Abstract
The on-board pose estimation of uncooperative target is an essential ability for close-proximity formation flying missions, on-orbit servicing, active debris removal and space exploration. However, the main issues of this research are: first, traditional pose determination algorithms result in a semantic gap and poor generalization abilities. Second, specific pose information cannot be accurately known in a complicated space target imaging environment. Deep learning methods can effectively solve these problems; thus, we propose a pose estimation algorithm that is based on deep learning. We use keypoints detection method to estimate the pose of space targets. For complicated space target imaging environment, we combined the high-resolution network with dilated convolution and online hard keypoint mining strategy. The improved network pays more attention to the obscured keypoints, has a larger receptive field, and improves the detection accuracy. Extensive experiments have been conducted and the results demonstrate that the proposed algorithms can effectively reduce the error rate of pose estimation and, compared with the related pose estimation methods, our proposed model has a higher detection accuracy and a lower pose determination error rate in the speed dataset.
1. Introduction
The on-board autonomous pose determination of noncooperative target spacecraft utilizing monocular vision is an essential capability for formation-flying, on-orbit servicing, and debris removal missions, such as PROBA-3 by ESA [1], ANGELS by US Air Force [2], PRISMA by OHB Sweden [3], OAAN [4] and Restore-L by NASA [5], and CPOD by Tyvak [6]. Because little knowledge regarding the kinematic characteristics of the target is available in noncooperative maneuvers before missions, the rendezvous and docking trajectory must be generated on-board while using the current state estimates during the proximity operations. Pose estimation that is based on monocular cameras has the advantages of rapid pose determination under mass requirements and low power, while stereo cameras and LIDAR sensors are less convenient and less flexible in terms of mass, power consumption, and operation range [7]. Thus, monocular cameras based pose determination systems are becoming an attractive option.
Previous monocular pose estimation algorithms for spaceborne applications mainly depend on conventional image processing methods [8,9,10,11], which identifies visible target features. Afterwards, matches the hand-engineered features against a reference texture model of the space target to estimate the pose, such as scale-invariant feature transformation [12] (SIFT), and sped up robust features [13] (SURF). However, there are two defects of these methods; firstly, they are not robust in conditions lacking adverse illumination; secondly, the computational complexity is high because of the numerous possible pose hypotheses [14]. In recent years, pose determination methods that are based on deep learning have solved these problems.
Because of the cheap computation and availability of large image datasets, deep learning based pose determination methods for terrestrial application have achieved great results [15,16]. Meanwhile, the pose determination methods for spaceborne applications are shifting towards deep learning techniques, such as Convolutional Neural Network (CNN). The CNNs have the advantages of higher robustness for adverse illumination condition and lower computational complexity over classical feature-based algorithms. Most of the CNN based pose determination methods [14,17,18,19,20,21] are designed to solve a classification or regression problem and then return the relative pose of the space target, which is describeed in detail in the related work section. However, compared with CNNs based on keypoints, these regression or classification models are less generalized and are more easily interfered by low signal-to-noise-ratio, and the multiscale characteristics of space target images are often ignored. The keypoint based deep learning methods achieve superior performance in both pose determination and object detection [22]. Both the translational and rotational errors are one degree of magnitude smaller than the ones mentioned before. Despite this, these keypoint based methods still can be improved. The current work ignores the global characteristics between the chosen keypoints of each image and it lacks attention to the obscured keypoints. Therefore, we are aiming to solve these problems.
We propose a monocular pose estimation algorithm for noncooperative space targets based on the HRNet landmark regression model [22]. The whole algorithm is divided into two parts: the pretreatment process and the main process. First, due to the continuous change in the shooting distance of the space target, the gained targets have multiscale characteristics [23], we propose a high-resolution, multiscale prediction of the space target detection network. A simplified three-dimensional (3D) wire-frame model of the spacecraft is also generated during the process. Subsequently, a high-resolution hard mining network that is based on dilated convolution is proposed. We fuse the multiscale features in HRNet by using dilated convolution, which expands the receptive field and promptes the network to infer keypoints from global information. An online hard keypoint mining method is proposed to makes deep networks focus on occluded keypoints. Finally, the two-dimensional (2D) and 3D keypoints features are used to calculate a relative pose by solving the Perspective-n-Point Problem [24]. The contributions of our work are summarized, as follows:
- Increased Network Inference Precision. We propose a feature fusion strategy based on dilated convolution. On the basis of the high-resolution network not reducing the resolution, we use dilated convolution to fuse features in different scales, which increases resolution and receptive field and makes the keypoint prediction more accurate.
- Detection of obscured keypoints is more accurate. Our model combines a high-resolution network and online hard landmark mining algorithm so that it can focus on a part of the landmarks obscured due to changes of space target pose.
- Effective Spacecraft Pose Estimation Model. We propose a monocular space target pose determination method that is based on keypoint detection. It achieves state-of-the-art performance on the speed dataset.
2. Related Work
2.1. Pose Determination for Cooperative Space Targets
The principle of cooperative pose determination is to extract a limited number of features from the acquired datasets in order to estimate the relative attitude and position of a Target Reference Frame (TRF) with respect to a Sensor Reference Frame (SRF) [25]. The Radio-Frequency (RF) antennas installed on board of the chaser and the target can be used in order to estimate pose for cooperative space targets, which was largely exploited at the beginning of the rendezvous era driven by the American and Russian space programs [26]. However, now, these RF technologies are out of date for six-DOF pose estimation, due to the strict requirements of measure performance, mass, and power budgets, especially for the space applications of small satellites. Using satellite navigation technology to estimate the position and attitude of cooperative targets is another solution. Specifically, it requires the presence of Global Navigation Satellite System (GNSS) receivers and antennas on board of the chaser and target, a reliable communication link between the two satellites is also needed in order to exchange measurement. Buist et al. proposed a GNSS-based relative position and attitude determination for distributed satellites [27]. Considering the multipath phenomena and partial occlusion of GNSS signals will lead to larger errors in measurement of the relative position during operating in close-proximity. GNSS is not suitable for close-proximity operations, but a valuable choice for the relative positioning of cooperative targets in mid or far range rendezvous scenarios. When compared with the RF-based and GNSS-based technologies, Electro-Optical (EO) sensors are the best option for cooperative pose estimation in close-proximity, because they are able to estimate the six-DOF pose of a target in close-proximity [28]. The EO sensors for spaceborne applications mainly refers to monocular cameras, stereo cameras, and LIDAR. Opromolla et al. descibe the applications of above sensors in cooperative pose determination [25].
2.2. Pose Determination for Noncooperative Space Targets
Different from cooperative pose determination, the general architecture of noncooperative pose determination process involves two steps, which are pose acquisition and pose tracking. The former refers to achieve the dateset first time by the adopted sensor and no a-priori information about the relative position and attitude of the target is available. The latter refers to update the pose parameters by using the knowledge of pose estimates at previous time instants [25]. For the known noncooperative target, a simplified geometric model is made according to its geometric shape information, and then a model-based algorithm is used in order to estimate the position and attitude of the noncooperative target. EO sensors represent the only valid technological option for noncooperative pose determination in close-proximity [25]. Because the monocular camera has the advantages of reduced mass, power consumption and system complexity, it has become an attractive alternative to LIDAR [29,30,31] or stereo cameras [32] in pose determination systems during close-proximity operation. Pasqualetto Cassinis et al. analyze the robustness and applicability of monocular pose estimation for noncooperative targets [7]. Sharma and D’Amico compare and evaluate the initial attitude estimation techniques of monocular navigation [33].
2.3. CNN Based Monocular Pose Determination Methods for Noncooperative Space Targets
CNN based pose determination methods perform better than classic feature-based algorithms, so the CNN based implementation in monocular pose determination has recently become more attractive. Su et al. propose the render CNN classification mode for predicting the viewpoint and trained a convolutional neural network to classify the three angles (pitch, yaw, roll) for pose estimation, finally turning the viewpoint prediction problem into three classification problems [17]. Xiang et al. propose the PoseCNN model for object pose estimation [18], whose model is divided into two branches in order to estimate the pose. Sharma et al. propose a CNN architecture based on AlexNet network [34] for noncooperative spacecraft to solve a classification problem and return the relative pose of the space target associated to each image [14]. Shi et al. use Inception-ResNet-V2 [35] and ResNet-101 [36], combined with an object detection engine [19], which improves their reliability. Sharma and D’Amico propose the SPN network [20,37] based on five convolutional layers, a Region Proposal Network (RPN) [38], and three fully-connected layers in order to generate the relative attitude of the target spacecraft. Proenca and Gao propose Urso network [21] and investigate the impact of training configuration and several aspects of the architecture. Furthermore, some keypoint based CNNs have achieved the state-of-the-art performance. Chen et al. combine deep learning and geometric optimization and propose a landmark regression model [22] based on HRNet [39]. Harvard et al. use CNN based keypoints and visibility maps [40] to determine the pose of the target spacecraft.
The CNN based regression or classification model’s generalization ability is poor and the current research work ignores the multiscale characteristics of space target images, and that is affected by pose transformation. In CNN based keypoint detection methods, some keypoints are difficult to detect because they are blocked, which ultimately affects the accuracy of pose estimation. Reducing the error rate of pose estimation is an important work in this paper.
3. Methodology
Figure 1 describes the algorithm structure of space target pose estimation, which is composed of two modules: the pretreatment process and the main process. The pretreatment process has two parts: first, select some images and their corresponding keypoint coordinates of the space target from the training set, and then reconstruct the three-dimensional structure of the space target through a multiview triangulation algorithm [41]. SUbsequently, in order to reduce the influence of background interference, we use an object detection network to predict the bounding box of the space target. Through this process, we can obtain the location information of the space target in images and the coordinates of keypoints. In main process, the cropped target image is sent into the keypoint detection network, and 11 keypoint coordinates containing satellite position and attitude features are output. Finally, the two-dimensional coordinates and three-dimensional space target models are fed into the PnP solver in order to obtain the estimated values of the space target position and attitude.
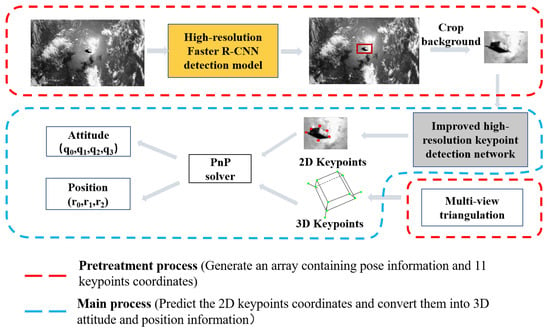
Figure 1.
Illustration of the proposed algorithm for space target pose estimation.
In particular, for the space target detection model, target images are small due to the long shooting distance, so the high-resolution feature is particularly important for the space target detection algorithm. ResNet [36] has the characteristics of residual connection and identity mapping. However, the downsampling of each stage of the network makes the feature map resolution increasingly lower. In order to solve this problem, we use a high-resolution network instead of the general deep residual network and use a multiscale prediction algorithm for space target detection.
For the keypoint detection model, some state-of-the-art algorithms do not consider the problem that some keypoints are blocked due to continuous adjustment of the space target’s pose [42,43]. Therefore, an online hard mining algorithm is introduced in order to make the network focus on obscured keypoints. The feature map’s high-resolution characteristic is important for keypoint detection, so the backbone network still uses a high-resolution network to maintain high resolution. In addition to using a high-resolution backbone deep network, the model introduces dilated convolution at each feature fusion stage to increase the receptive field of the feature to infer the keypoint information from the global information. We describe the operation process of space target pose estimation, as shown in Algorithm 1.
| Algorithm 1 Monocular space target pose estimation algorithm based on keypoint detection |
| Require: space target image ; reconstructed 3d initialization model of space target ; high-resolution multiscale spatial target detection model ; high-resolution keypoint detection model ; |
| Ensure:; |
| 1: Input into and output the frame coordinates of the space target; |
| 2: Input the predicted coordinates and into to get 11 sets of keypoint coordinates where ; |
| 3: The and predicted keypoint coordinates are sent to the PnP solver to obtain the estimated position and attitude ; |
3.1. Problem Formulation
Formally, the problem statement for this work is the estimation of the position and attitude of the camera frame C, with respect to the body frame of the space target B. is the relative position between the origin of the target’s body reference frame and the origin of the camera’s reference frame, as shown in Figure 2. Similarly, labels the quaternion containing the rotation relationship between the target’s body reference frame and the camera’s reference frame.
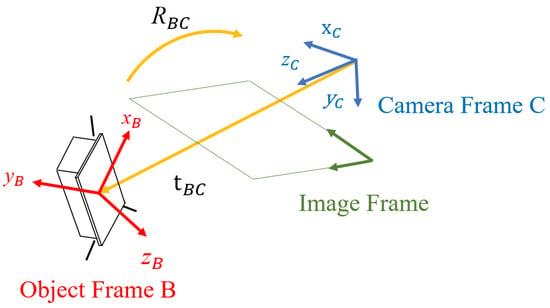
Figure 2.
Definition of the reference frames, relative position, and relative attitude.
The translation vector and rotation matrix are usually used to represent the relative position and attitude of the space target. However, the orthogonality of the rotation matrix makes it inconvenient to calculate the actual pose. In the aerospace field, Euler angles [44] (yaw, roll, and pitch) are sometimes used to represent the space target attitude, but Euler angles have the problem of universal lock. Therefore, Euler angles are not suitable for the attitude determination of space targets under omnidirectional changing angles. Quaternions can effectively avoid the problem of universal lock and are used to represent the pose of a space target. The quaternion definition formula is as follows:
The unit constraint relation in the formula is , where represent three imaginary units. The basic mathematical equation of quaternions is shown, as follows:
In the above formula, represents the rotation axis, and represents the rotation angle around the rotation axis. The corresponding relation between matrix R and quaternion is shown, as follows:
where , , .
The accuracy of pose estimation is evaluated by calculating the magnitude of the target rotation angle and translation error in the predicted space. Where represents the real label of the quaternions of the target image, q represents the prediction label of the quaternions, represents the translation vector label of the target image, t represents the predicted value of the translation vector, represents absolute value, represents dot product, represents the 2-norm, and i represents the i-th space target image. The rotation angle error of the estimated rotation angle of the i-th space target image is shown, as follows:
The translation vector error formula of the i-th space target estimation is illustrated as:
For the pose estimation of a space target image, the total error is the sum of the rotation angle error and the translation vector error:
Finally, the average pose error of all space targets in the test set is defined as , the number of images in the test set is N, and the error is demostrated, as follows:
3.2. Space Target Detection Algorithm
The space target detection network is mainly used to detect target areas, which is convenient for extracting targets from deep space backgrounds and feeding them into subsequent keypoint detection networks, so that keypoint detection networks focus on keypoint detection and eliminate interference from irrelevant backgrounds. In addition, in actual project research, it is found that the obtained image is generally large, such as , , and the size of the image sent into the deep network is generally , . Therefore, it is necessary to carry out space target detection before keypoint detection; otherwise, the space target image sent into the keypoint detection network will lose detailed information and easily blur the image.
Figure 3 is an example of a space target image in a simple background and a complex background. The space target only accounts for a small part of the whole image in the image taken, as shown in Figure 3a. If the whole image is sent into the keypoint detection network, the network cannot focus on the useful target information. The earth and clouds make the background of the space target more complex, causing accuracy interference from the background, as shown in Figure 3b. Therefore, it is necessary to implement space target detection before keypoint detection.
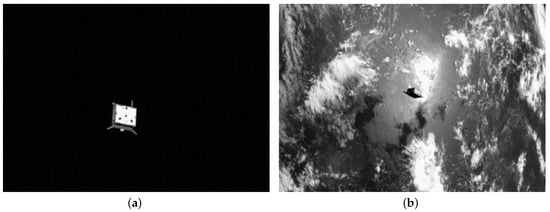
Figure 3.
Examples of space target images under simple and complex backgrounds.
Figure 4a shows the space target detection algorithm framework, which aims to solve the multiscale problem of space targets that are caused by changes in shooting distance. Multiscale prediction networks for feature extraction improves the detection performance of small targets. Because of the higher accuracy of the two-stage target detection algorithm, the space target detection algorithm uses the Faster R-CNN model [38,45], and network optimization is performed on the basis of the algorithm.
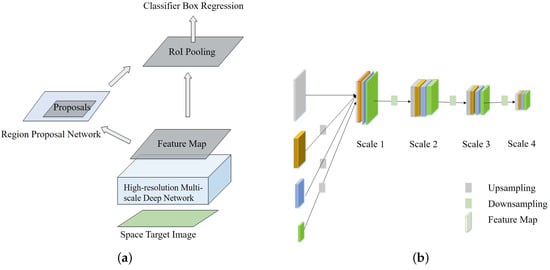
Figure 4.
(a) High-resolution space target detection framework (based on Faster R-CNN framework [38]) and (b) High-resolution multiscale detection network.
The proposed space target detection network adopts a High-Resolution Network (HRNet) [39] instead of the classic target detection backbone network ResNet. Compared with ResNet, HRNet adopts a feature fusion strategy, so that features extracted during the entire process of network learning always maintain high resolution. HRNet gradually adds high-resolution to low-resolution subnetworks, forming multiple network stages and connecting multiple subnetworks in parallel. During the entire feature extraction process in a high-resolution network, multiscale fusion is completed by repeatedly exchanging feature information through parallel multiresolution subnetworks, so that high-resolution features can be obtained from low-resolution characterization in other parallel representations. When compared with feature pyramid networks [46] (FPN), HRNet always maintains high-resolution features, unlike FPN networks, which recover from low resolution to high resolution to obtain high-resolution features.
The HRNet low-resolution feature is obtained by one or several convolution kernels with a continuous step size of 2, and then the different resolution features are fused by adding element by element. The HRNet high-resolution feature is obtained by the nearest neighbor interpolation upsampling method, while using a or upsampling rate method to increase the resolution of the feature map to the same size as the high-resolution feature map, and finally using convolution to change the number of channels, so that it can be added and fused with the original high-resolution feature map.
The space target detection network adopts Faster R-CNN, and the original backbone network ResNet is replaced with HRNet, which makes the detection effect of small targets better. The network has a parallel subnetwork structure and a multiscale fusion strategy. Figure 4b shows the multiscale characteristics of the space target image. There is a scale difference in the space target images due to the change in its shooting distance. If the network finally outputs only high-resolution feature maps, it will cause the large target detection accuracy rate to be low. Therefore, the detection network finally adopts a strategy similar to the feature pyramid. While the network continues to maintain high resolution, the high-resolution feature map is downsampled by average pooling in the final feature output stage, thus enabling multiscale detection. It is the network structure of the last stage of the high-resolution network, as shown in Figure 4b. Because of the multiscale characteristics of the obtained space target images, if only the scale 1 feature map is included, then the recognition rate of the spatial target image with a short shooting distance is low, similar to FPN. After adding feature scales 2, 3, and 4, the network model is no longer limited by the shooting distance, and then space targets at all scales are well detected.
The proposed high-resolution detection algorithm that is based on Faster R-CNN aims to improve the detection accuracy of small space targets. The high-resolution feature extraction network is used to reduce the downsampling loss of feature maps. In addition, the network finally adopts multiscale prediction to achieve significant performance for the detection of large and small targets.
3.3. High-Resolution Space Target Keypoint Detection Network
Selecting the keypoints of the target surface is more meaningful than selecting the vertices of the 3D box when processing keypoint prediction on the space target dataset, speed. The keypoints of the target surface are closer to the target features than the vertices of the 3D box [47]. Eleven space target 2D keypoints were selected, including four vertices at the bottom of the target, four vertices at the solar panel, and vertices at the ends of the three antennas of the target, as shown in Figure 5.
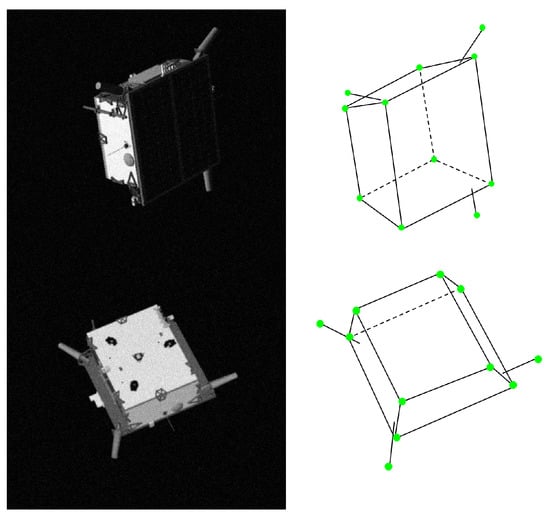
Figure 5.
Keypoint selection of space target for speed dataset.
Figure 6 illustrates the whole process of our improved keypoint detection network. The input image generates features through the network, and these multi-scale features are fused by dilated convolution. Then the network calculates the loss combined with the online hard keypoint mining method, and finally outputs the keypoints through the Gaussian kernel. In the space target detection section, the high-resolution network was introduced. The parallel structure of the subnetwork is adopted, so that the network always maintains high-resolution features without the need to sample and recover high-resolution features from the low-resolution features, and the exchange unit is used to perform different subnetworks. The communication between the networks can obtain the feature information of other subnetworks, and finally, HRNet can learn rich high-resolution features. However, unlike the high-resolution detection network for space targets, each keypoint belongs to detailed information, and the network model ultimately does not require multiplescale feature maps. In order to reduce the number of network parameters, only high-resolution feature maps are kept. The researches [39,48] have shown the importance of maintaining high-resolution representation during the whole process in object detection and pose estimation tasks. Specifically, the HRNet maintains the high-resolution representation while exchanging information across the parallel multi resolution subnetworks throughout the whole process; thus, it can generate heatmaps for keypoints with superior spatial precision [22]. It should be emphasized that keypoint detection has higher requirements for feature resolution, while FPN networks [46], Hourglass [42], U-Net [49], and other networks all obtain high-resolution features by upsampling low-resolution features. These methods of obtaining high-resolution features inevitably lose detailed information, which reduces the accuracy of keypoint detection.
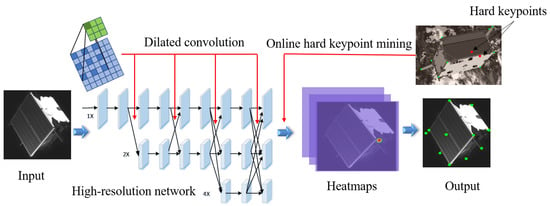
Figure 6.
Improved keypoint detection network.
In addition to the high resolution of the feature maps, increasing the perceptive field of space targets can also increase the accuracy of keypoint detection. For a space target, some keypoints are blocked due to its pose change. If the perceptive field of feature maps can be improved, the keypoint model can infer the position of the blocked keypoint according to the semantic information of feature maps. For this, we improve the high-resolution network. During feature fusion [50], an ordinary convolution is replaced with a dilated convolution, so that the perceptive field can be expanded and the corresponding position information of the keypoints that are occluded can be inferred from the global information.
Moreover, in the process of keypoint network training, the model tends to focus on the “simple keypoints”. However, the actual space target keypoint recognition faces invisible keypoints that are caused by pose changes and complex backgrounds, which makes it difficult to detect corresponding keypoints. To solve this problem, an “online hard keypoint mining” algorithm is introduced in the high-resolution network, so that the proposed model focuses on “hard keypoints”.
The keypoint detection network mainly predicts each keypoint’s coordinate values, and the coordinates of each keypoint are represented by a corresponding probability map. The value of the pixel where the keypoint is located is 1, and the value of other pixels is 0. The predicted pixels are difficult to match with the ground truth coordinates, so the Gaussian kernel with generates 11 heat maps on these keypoints in order to better match the predicted keypoints with the ground truth keypoints. Figure 7 shows an example of Gaussian kernel generating heatmaps on keypoints [51].

Figure 7.
The example of Gaussian kernel generating heatmaps on keypoints.
3.3.1. High-Resolution Network Based on Dilated Convolution
When compared with ordinary convolution, dilated convolution increases the expansion rate parameter, which is mainly used to expand the perceptive field of the convolution kernel. Additionally, the number of convolution kernel parameters remains unchanged; the difference is that the dilated convolution [52] has a larger perceptive field. Dilated convolution supports exponential expansion of the receptive field without loss of resolution or coverage and aggregates multi-scale features and global information without losing resolution. The research shows that the model that is based on dilated convolution can improve the accuracy of segmentation and detection [53], which is also suitable for keypoint detection. We found that the keypoints are not disorderly, they are distributed in various locations according to the structure of the space targets. Therefore, we want to use dilated convolution to improve the receptive field of the convolution kernel and make it pay more attention to the global information, so that the network can learn the internal relationship between each keypoint locations.
For the high-resolution keypoint detection network, convolutions of different resolutions are connected in parallel, and a variety of different resolution features are continuously exchanged. Each output resolution feature merges the features of two to four resolution inputs. The specific implementation method uses a convolution kernel with a step size of 2 in order to turn the high-resolution feature map into a low-resolution feature map, thereby achieving their fusion with low-resolution feature maps. Aiming at downsampling high-resolution features into low-resolution features, we introduce a dilated convolution with an expansion rate of 2. The specific improvement uses dilated convolution instead of ordinary convolution to increase the receptive field of extracted features. The whole network undergoes seven multiscale feature fusion. After each feature fusion, the connection between keypoints will be enhanced, and the overall structure of the space target will be clearer. Figure 8 shows the features of the network fusion. Each column of images represents the features before and after feature fusion. The outline and keypoints information of the space target in the feature map fused by dilated convolution will be clearer. Each row of images represents convolution features from shallow to deep. The deeper the feature map, the more abstract it will be.

Figure 8.
Contrast diagram before and after feature fusion using dilated convolution. The top seven feature maps represent the features before fusion and the bottom seven represent the features after fusion. From left to right represents the convolution features from shallow layers to deep layers. The morphological features are more blurred in deeper layers.
3.3.2. Robust Algorithm Design Based on Online Hard Keypoint Mining
Keypoint detection of space targets often faces the challenges that keypoints are occluded due to pose changes, and the keypoints are not easily detected in complex backgrounds. These keypoints can be regarded as “hard keypoints”, which are demostrated in Figure 9. During the training of high-resolution networks, more attention should be payed to these hard keypoints. In order to solve this problem, we introduced an “online hard keypoint mining” algorithm in the high-resolution network by focusing on these “hard keypoints” to optimize the prediction of keypoints.

Figure 9.
(a) The keypoints image of a space target. The blue dots represent the keypoints that are easy to predict, and the red one represents the hard keypoint. (b) The deconvolution of its final feature map. The blue dots represent all the keypoints, and the hard one is marked by red circle.
The keypoint model has a relatively large prediction error for “hard keypoints” of the space target, and these keypoints need to be specifically corrected. In the high-resolution network training phase, an online hard keypoint mining (OHKM) strategy can be introduced. The method is similar to OHEM [54] and the research shows that the training efficiency and performance can be improved by automatically selecting hard examples for training. The obscured keypoints can be regarded as the hard examples, and the OHKM algorithm improves the detection performance of hard keypoints in a similar way. During the training, the model divides some samples with higher confidence into positive samples and lower samples into negative samples, which can be shown by loss during training. However, there are some occluded space target keypoints in the image, which are divided into negative samples because of the high loss. The OHKM algorithm will focus on training with these negative samples, mining these difficult samples, so as to improve the accuracy. In the speed space target data, 11 keypoints are selected; usually, the network calculates the overall loss of 11 keypoints. All of the keypoints are given the same attention. However, some keypoints are easy to predict, while others are difficult. We want to make the network pay more attention to the hard keypoints. In the improved algorithm, only a partial loss of the eight keypoints with the largest error contributes to the overall loss. The specific method is to first generate the 11 most likely keypoints according to the original MSE loss method. Subsequently, the OHKM algorithm is applied to the 11 keypoints. The conventional method is to take the whole 11 keypoints into the loss function. However, we only select eight of the 11 keypoints with the largest loss value, the remaining three most likely keypoints are removed from the loss function. Therefore, only the eight keypoints with the largest loss value are taken into the loss function, so that the network model pays more attention to hard keypoints, which makes it more refined. The loss function of the detection network of keypoints of the space target is as follows:
where is the real coordinate value of the space target’s keypoint, the coordinate value of the keypoint predicted by the proposed model, k is the serial number of hard keypoints, and is the total number of selected “hard keypoints” in which we select as 8. The pseudocode of the high-resolution keypoint detection algorithm that are based on dilated convolution and hard keypoint mining is provided in Algorithm 2.
| Algorithm 2 High-resolution keypoint detection algorithm based on dilated convolution and hard keypoint mining |
| Require: space target image ; 11 groups of keypoint labels , where ; |
| Ensure: Trained keypoint detection network weight model; |
| 1: Preprocessing of input image data – Input image size is , random rotation is degrees; |
| 2: Input the image data into the high-resolution network, the feature fusion method is as follows: |
| 3: If feature map size → large: |
| 4: convolution (padding=0, stride=1)nearest neighbor upsampling; |
| 5: Else if feature map size → small: |
| 6: 3∗3 2-dilated convolution (padding=2, stride=2), BN, ReLU; |
| 7: Else: |
| 8: Identity mapping; |
| 9: Use the Gaussian kernel heat map to predict keypoint coordinates , where ; |
| 10: Use the OHKM algorithm to add the topk largest and in 11 groups; |
| 11: Backpropagate the residual computed in the previous step, adjust network weight; |
| 12: Repeat steps(1-11) until the loss converges, the keypoint detection model is trained. |
4. Results
In this section, we show the comprehensive process of our experiments, including the datasets, experimental setting, comparing baselines, and results analysis. Our algorithm is implemented in Torch-1.0.0 with a Python wrapper and it runs on an Intel Core i7-6700 CPU, NVIDIA GeForce GTX 1080Ti GPU.
4.1. Datasets and Comparison with Mainstream Methods
Speed is currently the first open source space target pose estimation dataset [55]. To date, only the training set is open source, and the test set is not yet open source. The dataset is composed of tango model spacecraft with high fidelity. Most of the datasets are synthetic images, and a small part of the images are real images. Two types of images are taken by the same camera model. The real image is taken by the 1.9/17 mm Grasshopper3 lens. The composite image that is captured by the camera is also obtained by the camera with the same parameter attributes. The training set has 12,000 sheets, each image label has relative position and attitude information, and the test set has 3000 sheets. The size of each image is , part of the dataset has a simple background (with deep space as the background), and part of the dataset has earth as the background, which is more complicated.
In a large number of comparative experiments, the proposed algorithm is superior to the current mainstream algorithm in various aspects. In terms of space target detection, the accuracy of the Faster R-CNN model that is based on the proposed high-resolution network is 5.32% higher than that of the Faster R-CNN model based on FPN and 0.68% higher than that of the Cascade R-CNN model [56] based on the high-resolution network. Regarding keypoint detection, the accuracy of our model is 4.39% higher than that of the HRNet keypoints network and 5.15% higher than that of the ResNet50 keypoints network. Finally, the error rate of the proposed model is 2.41% lower than that of the Urso network model. Specific experiments are shown in the following content.
4.2. Results and Analysis of Space Target Detection
We adopt the speed dataset and divide 2000 test images. The test set has half of the space targets in simple and complex backgrounds. Before sending space target data into the proposed model, the data are first preprocessed, including resizing all images according to the requirements of the mmdetection toolbox [57] and the normalization of the grayscale image (minus the mean and divided by the variance).
The test results output by the model are shown in Figure 10. Where (a) and (b) are the detection results of small and large space targets in simple backgrounds; (c) and (d) are small and large space targets in complex backgrounds, respectively; and, (e) and (f) are the detection results of dim targets under simple and complex backgrounds. The experimental results show that both large- and small-scale targets in simple and complex backgrounds can be detected, as well as dim targets, which indicates that the high-resolution target detection model is robust to scale and lighting conditions.

Figure 10.
Example of a space target detection result.
Table 1 shows the performance indicators of various space target detection model networks on the test set. The main detection indicators are the detection average precision AP (since only speed satellites are detected, so mAP and AP are equal) and mean intersection over union (mIoU). For a fair comparison, it is necessary to note that all four models use pretrained models.

Table 1.
Comparison of accuracy of various space target detection models.
According to the analysis presented in Table 1, the high-resolution Faster R-CNN detection model is higher than the other three detection models in AP and mIoU, mainly because the high-resolution network can continue to maintain the high resolution of the feature map and use multiscale feature map prediction, so that the space targets of different distances captured by the camera can be detected, indicating that the algorithm is robust to multiscale information. In addition, the Faster R-CNN model has a better detection effect on the space target image than the Cascade R-CNN model, mainly because the Cascade R-CNN model uses a cascade structure, the model is more complex, the space target image is relatively simple, and there is no need to learn function mapping relationships that are too complicated. Therefore, the target detection model uses Faster R-CNN.
Additionally, when comparing the complexity of the high-resolution network model (hrnetv2p-w18) and the feature pyramid model (fpn-resnet50) based on the Faster R-CNN detection framework, there are two measures: number of calculations (GFLOPs) and number of parameters (#param. (M)). It can be seen in Table 2 that the high-resolution network model maintains good detection accuracy and it has fewer parameters and calculations than ResNet50, and the model proposed has a lower complexity. There are two main reasons why the model is relatively simple: first, the network does not have a calculation process for low-resolution to high-resolution recovery, and this recovery process often requires a large amount of calculation; second, the network maintains high resolution at all times and makes it possible to obtain a high detection accuracy rate when the network structure is relatively simple. These two reasons allow for the proposed detection model to achieve 99.89% recognition accuracy and 90.03% mIoU, which is higher than that of the other detection models, and it has fewer model parameters and calculations than those of the ResNet-based feature pyramid network. 34.17% and 7.67%.

Table 2.
Comparison of the complexity of the high-resolution network based on Faster R-CNN and the feature pyramid model.
4.3. Results and Analysis of Keypoint Detection of Space Targets
After extracting the space target from the background through the object detection model, it is necessary to detect the target keypoints. Before inputting the keypoint detection model, the input data also need to be preprocessed and data-enhanced, including uniform input image size and random rotation.
The test picture output by the model is shown in Figure 11 below, (a) is the detection result of the keypoint with small background interference; (b) is the detection result of the keypoint with large background interference. From the above figure (a), it can be seen that the light is dark, its size is small, the keypoints of the space target can be detected, and its detection effect is good. The keypoints at the eight vertices of the calibration and the ends of the 3 antennas can be detected; from the above figure (b), it can be seen that under complex backgrounds and small targets, it can also accurately detect keypoints. The experimental results show that the proposed high-resolution online hard keypoint mining detection network has a good detection effect on keypoints of space targets and it is robust to light, scale, and background. Similar to the detection of space targets, we analyzed the accuracy and loss of the space target keypoint model on the validation set, as shown in Figure 12 and Figure 13. The model uses the Adam optimizer, where the momentum parameter is set to 0.9 and the model learning rate is 0.001. In order to illustrate the effectiveness of the high-resolution keypoint detection model (red curve, as represented by HRNet Keypoint Network), it is compared with the keypoint detection model based on residual network (blue curve, represented by ResNet50 keypoint network) comparison. In addition, we improved and optimized the high-resolution keypoint detection network (green curve, represented by HRNet+OHKM keypoint network) that introduces online hard keypoint mining and high-resolution dilated convolution keypoint detection. The model (black curve, represented by HRNet+OHKM+dilated Keypoint Network) was analyzed for performance. Regardless of whether it is in the accuracy curve or the loss curve, the result of the high-resolution net converges faster and more stably than the residual network. The improved algorithm that we proposed can improve the accuracy of keypoint detection. In addition, as seen from the blue curve, compared with the HRNet keypoint detection model, the ResNet-based keypoint detection model is not stable during the training process. The main reason is that the ResNet spatial sampling rate is too large, whose feature resolution cannot reach the pixel level requirement, and the network convergence speed is slow.
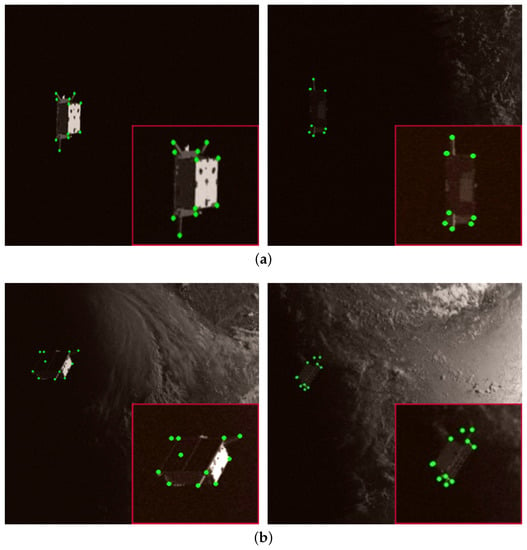
Figure 11.
Keypoint detection results under simple and complex space targets.
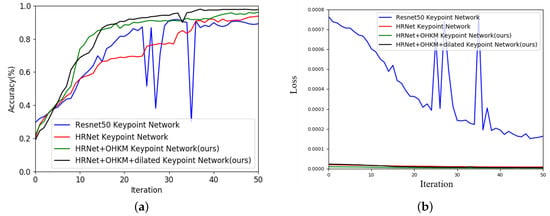
Figure 12.
(a) Comparison of the accuracy of each keypoint detection model on the verification set and (b) Comparison of the loss of each keypoint detection model on the verification set.
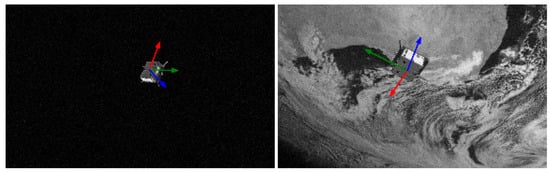
Figure 13.
Examples of pose visualization on two-dimensional images.
Table 3 shows the accuracy rate of each keypint detection model on the speed test set and the detection accuracy rate when 0.5 is taken. It can be seen that the high-resolution model has higher keypoint detection performance than the residual network model, because the network always maintains high-resolution features, which can provide rich details and effectively reduce the downsampling loss. After the network joined the online hard keypoint mining (OHKM), the accuracy rate improves again, from 93.19% to 95.53%, and the accuracy rate increases by 2.43%. The reason for the increase in accuracy is that the proposed model considers the problem of keypoints being blocked due to pose changes, and the network focuses on the “hard keypoints” that are blocked to increase the accuracy of keypoint detection. In addition to considering joining OHKM, the perceptive field is also very important for keypoint detection. When the corresponding perceptive field increases, global information increases, and keypoints can be inferred from global information. Therefore, after changing the convolution during feature fusion to a dilated convolution with an expansion rate of 2, the accuracy of keypoint detection is improved by 2.05%.

Table 3.
The comparison results of various space target keypoint detection models.
4.4. Results and Visualization of Space Target Pose Estimation
After detecting the keypoints, the coordinate information of the keypoints needs to be sent to the PnP solver in order to complete the pose estimation in three dimensions, and the estimateWorldCameraPose function packaged in MATLAB2018a is used to complete the three-dimensional pose estimation of the PnP solver. The position translation vector and attitude are obtained, and finally, the pose estimation evaluation is completed. In addition to the comparison with the model before optimization, it is also compared with the target pose estimation method (UrsoNet) that directly uses classification and regression [21] in Table 4, it can be concluded that the keypoint method is better than the direct regression or classification method, and the error rate can be reduced by approximately 2.41%. We also compare our method with some recent deep learning based networks presented in Table 5, and achieve better performance. Under the condition of using the same dataset, the high-resolution online hard keypoint mining detection network based on dilated convolution improves the final pose estimation effect and effectively reduced the error rate of the pose estimation algorithm. The poses of some test images are visualized. The quartet is first converted into a directional cosine matrix, and then the pose information is mapped to the two-dimensional image in combination with the camera parameters, as shown in Figure 13. That is, where the three arrows intersect, the red, green, and blue arrows represent the pitch angle, yaw angle, and roll angle, respectively.

Table 4.
Error rate of target pose estimation in each model space.

Table 5.
Comparison of Convolutional Neural Network (CNN) architecture for relative pose estimation.
The proposed pose estimation model that is based on keypoint detection achieves a high accuracy rate, mainly for the following four reasons. First, when compared to the pose estimation algorithm of direct regression and classification, the pose estimation that is based on the keypoint detection algorithm has better generalization performance, and fine-grained classification of angle information often has large model parameters and depends on a large quantity of label data. Second, in space target detection and keypoint detection stages, high-resolution deep networks are used in order to replace the depth residual network and feature pyramid network, so that the detection effect of small targets and keypoints in deep space becomes better. Fourth, by adding dilated convolution in the high-resolution feature fusion stage to improve the perceptive field of features, the occluded keypoint information can be inferred from the global information and, thus, improve the accuracy of keypoint detection.
5. Conclusions
This paper mainly studies the pose estimation of space targets based on keypoint detection. First, for the multiscale characteristics of space targets, a high-resolution, multiscale prediction target detection model is proposed, so that the model can detect multiscale target images. Next, when considering that some keypoints caused by continuous pose changes are blocked, a high-resolution hard keypoint mining detection network based on dilated convolution is proposed. By focusing on “occluded hard keypoints” and adding dilated convolution in the feature fusion stage to expand the perceptive field, global information can be used in order to infer the position of the keypoints. Finally, the experimental results show that improving the detection rate of small space targets and focusing the network on occluded keypoint information. The method that we proposed achieves better performance in estimating the translation and the rotation angle error than the classification or regression methods based on CNN. Additionally, under the same training conditions, our predicted position and pose errors are also lower than the baseline based on keypoints detection. Specifically, the pose estimation error rate is reduced by approximately 1.70%. When compared with the recently proposed UrsoNet pose estimation algorithm, it has more advantages in performance, and the error rate can be reduced by approximately 2.41%.
As part of future work, we are interested in investigating how to obtain a lower error rate and developing theoretical guarantees for pose estimation. Additionally, we will apply our method in order to solve real-world pose estimation problems.
Author Contributions
Conceptualization, J.X. and B.S.; Methodology, J.X. and X.N.; Experiments, J.X. and X.N.; Writing—original draft preparation, J.X. and X.N.; Writing—review and editing, J.X., B.S. and X.Y.; Supervision, B.S. and X.Y. All authors have read and agreed to the published this version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant (Nos. 61772387 and 62071354), the National Natural Science Foundation of Shaanxi Province (Grant Nos. 2019ZDLGY03-03) and also supported by the ISN State Key Laboratory.
Acknowledgments
The authors would like to thank anonymous reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Castellani, L.T.; Llorente, J.S.; Ibarz, J.M.F.; Ruiz, M. PROBA-3 mission. Int. J. Space Sci. Eng. 2013, 1, 349–366. [Google Scholar] [CrossRef]
- A. F. R. Laboratory. Fact sheet: Automated Navigation and Guidance Experiment for Local Space (ANGELS). Available online: http://www.kirtland.af.mil/shared/media/document/AFD-131204-039.pdf (accessed on 30 September 2014).
- D’Amico, S.; Ardaens, J.S.; Larsson, R. Spaceborne Autonomous Formation-Flying Experiment on the PRISMA Mission. J. Guid. Control Dyn. 2012, 35, 834–850. [Google Scholar] [CrossRef]
- Pei, J.; Walsh, M.; Roithmayr, C.; Karlgaard, C.; Murchison, L. Preliminary GN&C Design for the On-Orbit Autonomous Assembly of Nanosatellite Demonstration Mission. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Stevenson, WA, USA, 20–24 August 2017. [Google Scholar]
- Reed, B.B.; Smith, R.C.; Naasz, B.J.; Pellegrino, J.F.; Bacon, C.E. The Restore-L Servicing Mission. In Proceedings of the AIAA Space Forum, Long Beach, CA, USA, 13–16 September 2016; pp. 1–8. [Google Scholar]
- Bowen, J.; Villa, M.; Williams, M. CubeSat based Rendezvous, Proximity Operations, and Docking in the CPOD Mission. In Proceedings of the 29th Annual AIAA/USU Small Satellite, Logan, UT, USA, 8–13 August 2015. [Google Scholar]
- Pasqualetto Cassinis, L.; Fonod, R.; Gill, E. Review of the robustness and applicability of monocular pose estimation systems for relative navigation with an uncooperative spacecraft. Prog. Aerosp. Sci. 2019, 110, 100548. [Google Scholar] [CrossRef]
- Cropp, A.; Palmer, P. Pose Estimation and Relative Orbit Determination of a Nearby Target Microsatellite using Passive Imagery. In Proceedings of the 5th Cranfield Conference on Dynamics and Control of Systems and Structures in Space 2002, Cambridge, UK, 14–18 July 2002; pp. 389–395. [Google Scholar]
- Kanani, K.; Petit, A.; Marchand, E.; Chabot, T.; Gerber, B. Vision Based Navigation for Debris Removal Missions. In Proceedings of the 63rd International Astronautical Congress, Naples, Italy, 1–5 October 2012; pp. 1–8. [Google Scholar]
- D’Amico, S.; Benn, M.; Jorgensen, J. Pose Estimation of an Uncooperative Spacecraft. In Proceedings of the 5th International Conference on Spacecraft Formation Flying Missions and Technologies, Munich, Germany, 29–31 May 2013; pp. 1–17. [Google Scholar]
- Sharma, S.; Ventura, J. Robust Model-Based Monocular Pose Estimation for Noncooperative Spacecraft Rendezvous. J. Spacecr Rocket. 2018, 55, 1–16. [Google Scholar] [CrossRef]
- Lindeberg, T. Scale invariant feature transform. KTH Comput. Biol. CB 2012, 7, 10491. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded Up Robust Features. In Computer Vision—ECCV 2006; Leonardis, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Sharma, S.; Beierle, C. D’Amico, S. Pose Estimation for Non-Cooperative Spacecraft Rendezvous Using Convolutional Neural Networks. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2018; pp. 1–12. [Google Scholar]
- Toshev, A.; Szegedy, C. DeepPose: Human pose estimation via deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Columbus, OH, USA, 24–27 June 2014; pp. 1653–1660. [Google Scholar]
- Kendall, A.; Grimes, M.; Cipolla, R. PoseNet: A convolutional network for real-time 6-dof camera relocalization. In Proceedings of the IEEE International Conference on Computer Vision, Boston, MA, USA, 7–12 June 2015; pp. 2938–2946. [Google Scholar]
- Su, H.; Qi, C.R.; Li, Y.; Guibas, L.J. Render for CNN: Viewpoint Estimation in Images Using CNNs Trained With Rendered 3D Model Views. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Boston, MA, USA, 7–12 June 2015; pp. 2686–2694. [Google Scholar]
- Xiang, Y.; Schmidt, T.; Narayanan, V. PoseCNN: A Convolutional Neural Network for 6D Object Pose Estimation in Cluttered Scenes. arXiv 2017, arXiv:1711.00199. [Google Scholar]
- Shi, J.; Ulrich, S.; Ruel, S. CubeSat Simulation and Detection using Monocular Camera Images and Convolutional Neural Networks. In Proceedings of the 2018 AIAA GUidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Sharma, S.; D’Amico, S. Pose estimation for noncooperative rendezvous using neural networks. In Proceedings of the AIAA/AAS Space Flight Mechanics Meeting, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Proença, P.F.; Gao, Y. Deep Learning for Spacecraft Pose Estimation from Photorealistic Rendering. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 6007–6013. [Google Scholar]
- Chen, B.; Cao, J.; Parra, A.; Chin, T. Satellite Pose Estimation with Deep Landmark Regression and Nonlinear Pose Refinement. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–3 November 2019. [Google Scholar]
- Huang, G.; Chen, D.; Li, T.; Wu, F.; van der Maaten, L.; Weinberger, K.Q. Multi-Scale Dense Networks for Resource Efficient Image Classification. arXiv 2017, arXiv:1703.09844. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An Accurate O(n) Solution to the PnP Problem. Int. J. Comput. Vis. 2009, 81, 155–166. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A review of cooperative and uncooperative spacecraft pose determination techniques for close-proximity operations. Prog. Aerosp. Sci. 2017, 93, 53–72. [Google Scholar] [CrossRef]
- Woffinden, D.C.; Geller, D.K. ENavigating the road to autonomous orbital rendezvous. J. Spacecr. Rockets 2007, 44, 898–909. [Google Scholar] [CrossRef]
- Buist, P.; Teunissen, P.; Joosten, P. GNSS-guided relative positioning and attitude determination for missions with multiple spacecraft. In Proceedings of the International Symposium GPS/GNSS, Fort Worth, TX, USA, 26–29 September 2006; pp. 151–162. [Google Scholar]
- Woffinden, D.C.; Geller, D. Relative angles-only navigation and pose estimation for autonomous orbital rendezvous. J. Guid. Control Dyn. 2007, 30, 1455–1469. [Google Scholar] [CrossRef]
- Blais, F. Review of 20 years of range sensor development. J. Electron. Imaging 2004, 13, 231–243. [Google Scholar] [CrossRef]
- Crosby, F.; Kang, S. Object identification in 3D flash lidar images. J. Pattern Recognit. Res. 2011, 2, 193–200. [Google Scholar] [CrossRef]
- Kirmani, A.; Colaco, A.; Wong, F.; Goyal, V. Exploiting sparsity in time-of-flight range acquisition using a single time-resolved sensor. Opt. Express 2011, 19, 21485–21507. [Google Scholar] [CrossRef] [PubMed]
- Fasano, G.; Grassi, M.; Accardo, D. A stereo-vision based system for autonomous navigation of an in-orbit servicing platform. In Proceedings of the AIAA Infotech@Aero-space 2009, Seattle, WA, USA, 6–9 April 2009; p. 1934. [Google Scholar]
- Sharma, S.; D’Amico, S. Comparative assessment of techniques for initial pose estimation using monocular vision. Acta Astronaut 2016, 123, 435–445. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet classification with deep convolutional neural networks. In Proceedings of the 26th Annual Conference on Neural Information Processing Systems, Red Hook, NY, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–10 February 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sharma, S.; D’Amico, S. Neural Network-Based Pose Estimation for Noncooperative Spacecraft Rendezvous. IEEE Trans Aerosp Electron Syst 2020, 1. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Eds.; Curran Associates, Inc.: New York, NY, USA, 2015; pp. 91–99. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 5693–5703. [Google Scholar]
- Harvard, A.; Capuano, V.; Shao, E.; Chung, S. Inception-v4, Spacecraft Pose Estimation from Monocular Images Using Neural Network Based Keypoints and Visibility Maps. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1874. [Google Scholar]
- Labatut, P.; Pons, J.; Keriven, R. Efficient Multi-View Reconstruction of Large-Scale Scenes using Interest Points, Delaunay Triangulation and Graph Cuts. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Newell, A.; Yang, K.; Deng, J. Stacked Hourglass Networks for Human Pose Estimation. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 483–499. [Google Scholar]
- Wei, S.; Ramakrishna, V.; Kanade, T. Convolutional Pose Machines. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4724–4732. [Google Scholar]
- Diebel, J. Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Lin, T.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Hu, Y.; Hugonot, J.; Fua, P.; Salzmann, M. Segmentation-Driven 6D Object Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; pp. 3385–3394. [Google Scholar]
- Sun, K.; Zhao, Y.; Jiang, B.; Cheng, T. High-Resolution Representations for Labeling Pixels and Regions. arXiv 2019, arXiv:1904.04514. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Yang, J.; Yang, J.; Zhang, D.; Lu, J. Feature fusion: Parallel strategy vs. serial strategy. Pattern Recognit. 2003, 36, 1369–1381. [Google Scholar] [CrossRef]
- Payer, C.; Stern, D.; Bischof, H.; Urschler, M. Regressing Heatmaps for Multiple Landmark Localization Using CNNs. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2016; Ourselin, S., Joskowicz, L., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 230–238. [Google Scholar]
- Wei, Y.; Xiao, H.; Shi, H.; Jie, Z.; Feng, J.; Huang, T.S. Revisiting Dilated Convolution: A Simple Approach for Weakly- and Semi-Supervised Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 7268–7277. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Shrivastava, A.; Gupta, A.; Girshick, R. Training Region-Based Object Detectors With Online Hard Example Mining. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 761–769. [Google Scholar]
- Kisantal, M.; Sharma, S.; Park, T.H.; Izzo, D.; Märtens, M.; D’Amico, S. Satellite Pose Estimation Challenge: Dataset, Competition Design, and Results. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4083–4098. [Google Scholar] [CrossRef]
- Cai, Z.; Vasconcelos, N. Cascade R-CNN: Delving Into High Quality Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 6154–6162. [Google Scholar]
- Chen, K.; Wang, J.; Pang, J. MMDetection: Open MMLab Detection Toolbox and Benchmark. arXiv 2019, arXiv:1906.07155. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).