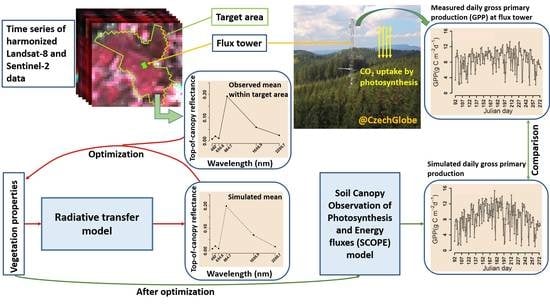
Analyzing Daily Estimation of Forest Gross Primary Production Based on Harmonized Landsat-8 and Sentinel-2 Product Using SCOPE Process-Based Model

Abstract

Vegetation top-of-canopy reflectance contains valuable information for estimating vegetation biochemical and structural properties, and canopy photosynthesis (gross primary production (GPP)). Satellite images allow studying temporal variations in vegetation properties and photosynthesis. The National Aeronautics and Space Administration (NASA) has produced a harmonized Landsat-8 and Sentinel-2 (HLS) data set to improve temporal coverage. In this study, we aimed to explore the potential and investigate the information content of the HLS data set using the Soil Canopy Observation of Photosynthesis and Energy fluxes (SCOPE) model to retrieve the temporal variations in vegetation properties, followed by the GPP simulations during the 2016 growing season of an evergreen Norway spruce dominated forest stand. We optimized the optical radiative transfer routine of the SCOPE model to retrieve vegetation properties such as leaf area index and leaf chlorophyll, water, and dry matter contents. The results indicated percentage differences less than 30% between the retrieved and measured vegetation properties. Additionally, we compared the retrievals from HLS data with those from hyperspectral airborne data for the same site, showing that HLS data preserve a considerable amount of information about the vegetation properties. Time series of vegetation properties, retrieved from HLS data, served as the SCOPE inputs for the time series of GPP simulations. The SCOPE model reproduced the temporal cycle of local flux tower measurements of GPP, as indicated by the high Nash–Sutcliffe efficiency value (>0.5). However, GPP simulations did not significantly change when we ran the SCOPE model with constant vegetation properties during the growing season. This might be attributed to the low variability in the vegetation properties of the evergreen forest stand within a vegetation season. We further observed that the temporal variation in maximum carboxylation capacity had a pronounced effect on GPP simulations. We focused on an evergreen forest stand. Further studies should investigate the potential of HLS data across different forest types, such as deciduous stand.

1. Introduction

Vegetation is an essential component of the terrestrial ecosystems that interacts with the atmosphere through the carbon and water cycles. The leaf stomata regulate the release of water by transpiration and the uptake of atmospheric carbon dioxide by photosynthesis. The sum of the gross photosynthesis by all leaves measured at the ecosystem scale is known as gross primary production (GPP) [1]. GPP, together with respiration, governs the exchange of CO${}_2$ between the biosphere and atmosphere, thereby providing the capacity of the terrestrial ecosystems to offset anthropogenic CO${}_2$ emissions [2]. Reliable estimation of spatio-temporal GPP variation in various terrestrial ecosystems is crucial because the changes of GPP over time reflect vital processes in plants and provide information about the plant–atmosphere feedback resolved over a large area [3,4].

Spatio-temporal variations in GPP can be quantified using either data-driven or data-assimilation approaches [5]. Data-driven approaches establish an empirical model between ground measurements of GPP (e.g., GPP partitioned from flux tower measurements of net ecosystem exchange [6]) and other explanatory variables that are commonly derived from remote sensing data (satellite images). The empirical model extrapolates the spatio-temporal variations in GPP. Among the widely-used explanatory variables, vegetation indices (VIs) (e.g., normalized difference vegetation index (NDVI), enhanced vegetation index (EVI), and photochemical reflectance index (PRI)) are the indices that have been mostly often used in various studies [7,8,9,10,11]. However, there are several limitations when using VIs as an explanatory variable connected with the upscaling of flux tower measurements [12]. For instance, the leaf greenness approximated from VIs (e.g., by means of NDVI and EVI) may not be necessarily proportional to the photosynthetic capacity and rate. Environmental stressors may affect the photosynthesis rate even during the early stages without the appearance of any significant visual symptoms at the leaf (e.g., leaf color change) or canopy levels (e.g., leaf area index change). This creates challenges to relating the maximum photosynthesis capacity to maximum vegetation greenness. The majority of VIs are derived at the leaf level (e.g., PRI as a proxy for the leaf conversion efficiency of absorbed light); therefore, further upscaling from the leaf to the canopy level is not always feasible due to the additional confounding effects of the canopy structure on VIs.

Data-assimilation approaches calibrate a process-based model (PBM) against the data on the output variables, e.g., flux tower measurements. The calibrated PBM is then used to estimate the spatio-temporal variations in GPP [13,14,15,16]. The limitations of VIs in the data-driven approach do not occur when adopting the data-assimilation approaches for GPP estimation. PBM can predict GPP by simulating various plant physiological responses to climatic and atmospheric conditions and stand structural properties [16,17,18,19], which are not explicitly included in the data-driven approach.

Overall, a PBM is required to effectively interpret remote sensing data and exploit their full potential for estimating GPP variations in various terrestrial ecosystems. Among the developed PBMs, the Soil Canopy Observation of Photochemistry and Energy fluxes (SCOPE, [19]) model has been widely used in various applications, all attempting to contribute to a better understanding and interpretation of remote sensing data over vegetation, for instance, by: (1) simulating multiple satellite radiances through coupling with an atmosphere radiative transfer model [20,21]; (2) retrieving biochemical and structural vegetation properties [22,23,24]; and (3) estimating vegetation functioning variations and their biases [20,25,26]. Further extensions of the SCOPE model have been recently proposed and examined in various ecosystems to improve their performance [27,28,29]. However, attempts to use the SCOPE model to estimate temporal variation in GPP of a forest stand by exploring the potential of combined remote sensing data are lacking.

The SCOPE model integrates radiative transfer, micrometeorology, and plant physiology to perform land surface process (e.g., GPP) simulations [20]. The SCOPE model uses a modular architecture, making it flexible and allowing the use of different modules as standalone instances. The radiative transfer module (RTMo) can be calibrated, i.e., a data-assimilation approach, against the surface reflectance obtained from remote sensing data to optimize its input parameters. These optimized parameters are the retrieved vegetation biochemical and structural properties. The retrieved information, together with the time series of meteorological variables, can be then directly used as inputs for the SCOPE model for GPP estimation. In general, the vegetation properties at one point in time can yield a rough estimate of GPP. However, temporal variations in the vegetation properties (i.e., vegetation phenology) are also needed to reflect the vegetation responses to climate variability and were found to improve the temporal GPP estimated by the SCOPE model [20,22].

Accurate description of the temporal variations in vegetation properties depends on the availability of rich time series of high quality remote sensing data. A single sensor may not provide the needed temporal coverage due to cloud cover and sensor temporal revisit limitations. More than 300 Earth observation satellites for optical imaging are orbiting the Earth, allowing us to combine observations from multiple sensors for improved temporal coverage. However, a simple combination of observations does not result in smooth spectral time series, e.g., due to the differences in radiometric characteristics and mismatch in spatial resolution between the sensors. It is not always suitable to assess the vegetation phenology and retrieve consistent time series of vegetation characteristics from the combined datasets. Recently, the National Aeronautics and Space Administration (NASA) produced the harmonized Landsat and Sentinel (HLS) data set by combining the surface reflectance data from the Operational Land Imager (OLI) and Multi-Spectral Instrument (MSI) sensors aboard Landsat-8 and Sentinel-2 satellites, respectively [30], to further improve the temporal resolution of the combined product. In HLS data, a smooth spectral time series is produced by accounting for the differences in spatial resolution, sensor-to-sensor differences in atmospheric correction approaches, and view geometry and radiometric characteristics of spectral bands. The potential of HLS time series data has not yet been fully explored with respect to GPP estimations. Recently, Lin et al. [31] applied a data-driven approach using HLS data to evaluate GPP variations in natural vegetation types. However, the full potential of HLS time series data has not yet been explored with respect to GPP estimation using data-assimilation approaches. The objective of this study was to fill this gap by assimilating multi-sensor spectral information obtained from the HLS data within the SCOPE model to retrieve the temporal variations in biochemical and structural vegetation properties to evaluate the improvement in GPP estimation. This research addresses the following two questions: (1) What information is preserved or lost in the retrieval of vegetation properties using multispectral HLS data? (2) What improvement in the GPP estimation can be expected by providing the SCOPE model with the temporal variations in the vegetation properties? We assumed that HLS multispectral data can provide sufficient information for retrieval of vegetation properties. However, whether such information can improve GPP estimation needs more investigation. We aimed to gain insights regarding these two aspects.

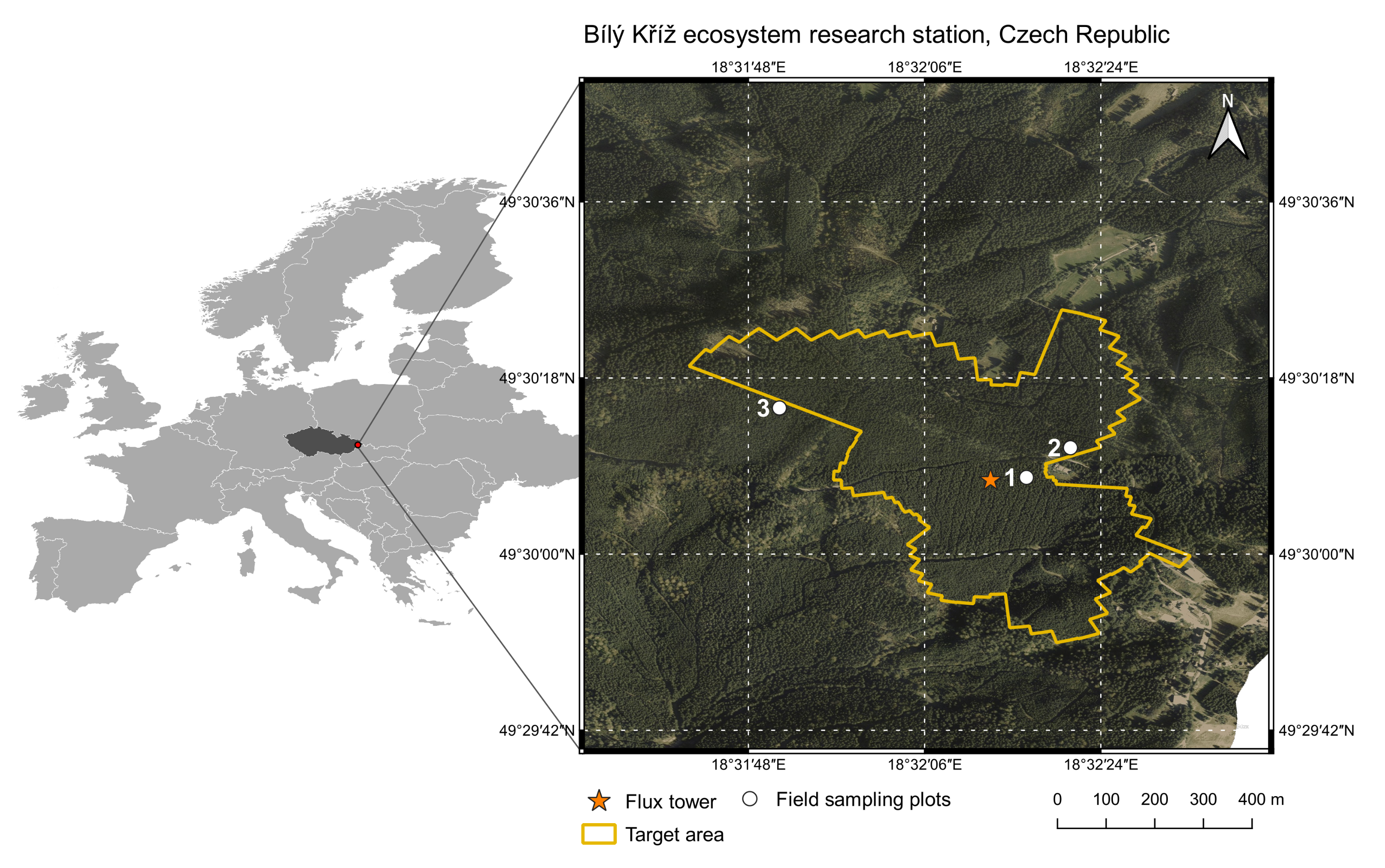
2. Study Area

We used measurements recorded at the Bílý Kříž ecosystem station in the Czech Republic, which is part of the Czech Carbon Observation System (CzeCOS; http://www.czecos.cz/) network. The Bílý Kříž site is situated in the northeast Czech Republic (${49}^{\circ }{30}^{\prime }07.{474}^{″}$ N, ${18}^{\circ }{32}^{\prime }12.{777}^{″}$ E) at an altitude of 875 m above sea level on a 13${}^{\circ }$ southwest-oriented planar slope that is approximately 100 m downslope of a mountain crest extending from west to east [32]. This site is a Class 2 candidate site of the Integrated Carbon Observation System (ICOS) (www.icos-cp.eu) and it regularly contributes to the FLUXNET dataset labeled as CZ-BK1 [33]. The site is predominated by a Norway spruce (Picea abies (L.) H. Karst) forest stand that represents the evergreen needle leaf forest vegetation class. The stand had a mean height of 17 m and the age of 35 years at the end of the 2016 vegetation growing season. This site is located in a moderately cold, humid, and precipitation-rich temperate climatic zone [34]. The soil at the Bílý Kříž site is an Entic Podsol type with a texture ranging from sandy loam to sandy clay with a 15–35% clay fraction [35]. The site is equipped with an eddy covariance flux tower system that has been measuring the energy and trace gas fluxes between the ecosystem and the atmosphere since 2004. We investigated the retrieval of vegetation properties and the estimation of GPP from remote sensing data for the 2016 vegetation growing season (April to September) when airborne hyperspectral data and ground measurements of vegetation biochemical and structural properties were available for this site.

3. Materials and Methods

3.1. Data

3.1.1. Remote Sensing Data

We obtained a time series of 39 images at 30 m resolution from the HLS data product that covered the study area from 1 April to 30 September 2016. The HLS data are atmospherically corrected with spatial coregistration, bidirectional reflectance distribution function normalization, and spectral bandpass adjustments of Landsat-8 MSI and Sentinel-2 OLI sensors. The MSI surface reflectance bands are also adjusted to Landsat-8 characteristics by applying the spectral response function of the OLI sensor. The HLS surface reflectance data product is distributed globally within the Sentinel-2 tiling system and is abbreviated as S30 (obtained from Sentinel-2 MSI sensor) and L30 (obtained from Landsat-8 OLI sensor). For more information about the processing of MSI and OLI observations within the HLS data product, the reader is referred to Skakun et al. [36] and Claverie et al. [30]. We included the time series of HLS data available between 11:38 to 11:54 a.m. Central European Time during the 2016 vegetation growing season. Further filtering of the HLS data was performed based on the quality indicators using NDVI and near infrared (NIR) reflectance (see Section 3.2 for more details).

We also obtained the hyperspectral airborne data over the study area. We compared the retrieval of vegetation properties from both airborne and HLS data to examine if multispectral HLS bands preserve the required information compared to hyperspectral bands. The airborne data were acquired around local solar noon between 11 a.m. and 2 p.m. on 31 August 2016 with two push broom spectroradiometers (Compact Airborne Spectrographic Imager (CASI) and shortwave Infrared (SWIR) Airborne Spectrographic Imager (SASI) from Itres Ltd., Calgary, AB, Canada) onboard the Flying Laboratory of Imaging Systems operated by the Global Change Research Institute [37,38]. The CASI operates in the visible and NIR regions between 372 and 1044 nm (72 spectral bands with a sampling distance of 9.4 nm) and a nominal spatial resolution of 1.0 m. SASI operates in the shortwave infrared region between 957 and 2442 nm (100 spectral bands with a sampling distance of 15 nm) and nominal spatial resolution of 2.5 m. The airborne data were corrected radiometrically (using the factory calibration coefficients in RCX software (Itres Ltd., Calgary, AB, Canada)), geometrically (using GeoCorr software (Itres Ltd., Calgary, AB, Canada)), and atmospherically (using ATCOR-4 software [39]), and combined into a single hypercube according to the processing chain established at Global Change Research Institute [37]. The quality of the atmospheric corrections was evaluated by comparing the airborne spectra extracted for homogeneous artificial surfaces with spectral signatures measured in the field during the overflight, which produced maximum differences of 3% in NIR and SWIR wavelengths for some targets (Figure S1). Both HLS and airborne data were used to retrieve vegetation properties at the Bílý Kříž site (Section 3.2). For this purpose, we extracted the surface reflectance of the vegetation canopy, i.e., top-of-canopy (TOC) reflectance, from the target area delineated by the ecosystem boundary (Section 3.1.2).

3.1.2. Ground Measurements

We obtained half-hourly eddy covariance (EC) measurements of net ecosystem exchange (NEE) to predict half-hourly GPP and standardized meteorological variables for the spruce forest stand during the 2016 growing season. The EC technique [40] was applied to measure turbulent fluxes of CO${}_2$ at the Bílý Kříž forest site. The EC system consisted of Gill ultrasonic anemometer (HS-50, Gill Instruments, Hampshire, UK) and a LI-COR infrared gas analyzer (LI-7200, LI-COR, Lincoln, NE, USA), and was installed on a meteorological tower at 20.5 m as of 1 October 2013 and moved to 25 m as of 7 June 2016 above ground level. The EC raw data measured at 20 Hz were processed using spike detection and removal [41], time lag compensation, sonic temperature correction [42], and high- [43,44] and low [45]-frequency spectral corrections. Coordinates were rotated using the planar-fit method [46]. Fluxes were computed at half-hourly time intervals using the block averaging method. Fetch filtering was applied to exclude half hours for which more than 30% of the signal originated from outside of the target area. This was achieved by comparing fetch distance at a given upwind direction with estimated distance providing 70% contribution to the EC fluxes using footprint modeling [47,48]. Fetch distance for all directions is represented as an ecosystem boundary, i.e., the target area (Figure 1), that delimits the area that is sufficiently homogeneous considering the canopy height and the species represented (Norway spruce at the Bílý Kříž site).

All EC processing and calculations were performed using EddyPro software (v6.2.0, LI-COR, Lincoln, NE, USA). A thorough data quality checking procedure was applied to EC measurements in this study using R package openeddy (R Core Team, 2020; https://github.com/lsigut/openeddy; see McGloin et al. [32] for details). Measured CO${}_2$ fluxes were filtered based on the friction velocity threshold computed using the moving point method [49]. After this filtering, half-hourly CO${}_2$ fluxes were assumed to represent the NEE (µmol CO₂ m⁻² s⁻¹). Gaps were filled using marginal distribution sampling [50] and NEE was partitioned into GPP (hereafter, GPP${}_{\mathrm{EC}}$) and ecosystem respiration according to Lasslop et al. [6] using the R package REddyProc [51]. Half-hourly GPP${}_{\mathrm{EC}}$ were then aggregated to daily sums of carbon, expressed as g C m⁻² s⁻¹.

Meteorological variables included half-hourly data of air temperature (T${}_{\mathrm{a}}$, in ${}^{\circ }\mathrm{C}$), TOC incoming shortwave radiation (R_in, in W m⁻²), TOC incoming longwave radiation (R_li in W m⁻²), vapor pressure deficit (e${}_{\mathrm{a}}$, in hPa), air pressure (p, in hPa), and wind speed (u, in m⁻²) for each day in the vegetation growing season of 2016. We additionally obtained half-hourly soil water content (SWC, in %) from the nine sensors installed at a 5 cm depth at different locations within the target area. For each half-hour, SWC values from all nine sensors were averaged to obtain the representative value of soil moisture of the target area. The half-hourly meteorological variables, mean SWC, along with HLS-, CASI-, and SASI-derived information served as the inputs to the SCOPE model to estimate (or simulate) half-hourly GPP, which was aggregated to daily sums of carbon (Section 3.3). We refer to simulated GPP as GPP${}_{\mathrm{SIM}}$ hereafter. We validated daily GPP${}_{\mathrm{SIM}}$ against daily GPP${}_{\mathrm{EC}}$. We also compared daily GPP${}_{\mathrm{SIM}}$ with daily means of half-hourly measurements of meteorological variables to show the relationship between them.

Table 1. Summary statistics of daily (means of half-hourly measurements) meteorological variables during the 2016 vegetation growing season. Min: minimum of daily means, Max: maximum of daily means, Mean: mean of daily means, SD: standard deviation of daily means.

Meteorological Variable	Symbol	Unit	Min	Max	Mean	SD
Air temperature	T${}_{\mathrm{a}}$	${}^{\circ }\mathrm{C}$	−0.66	24.69	13.77	5.09
Incoming shortwave radiation	R${}_{\mathrm{in}}$	$\mathrm{W}/{\mathrm{m}}^2$	32.57	523.19	297.87	123.21
Incoming longwave radiation	R${}_{\mathrm{li}}$	$\mathrm{W}/{\mathrm{m}}^2$	258.48	391.54	328.12	27.37
Vapor pressure	e${}_{\mathrm{a}}$	hPa	3.44	19.49	11.50	3.41
Air pressure	p	hPa	895.04	925.07	914.39	5.68
Wind speed	u	$\mathrm{m}/\mathrm{s}$	0.77	6.90	1.85	0.97

lists the summary statistics of daily meteorological variables during the 2016 vegetation growing season.

Additionally, we obtained ground measurements of vegetation properties characterizing spruce forest conditions at the site, which were collected during a joint ground/airborne campaign on 31 August 2016. The location of the field sampling plots was pre-determined by previously existing forest inventory plots established by the Institute of Forest Ecosystem Research (IFER), Czech Republic, in the vicinity of the ecosystem station. The coordinates of the central point of each plot were measured using a differential global positioning system. The measured biochemical vegetation properties included leaf chlorophyll content ($C_{\mathrm{ab}}$), leaf carotenoids content ($C_{\mathrm{ca}}$), leaf water content ($C_{\mathrm{w}}$), and leaf dry matter content ($C_{\mathrm{dm}}$). The biochemical properties were measured in a laboratory (leaf pigments were extracted according to Porra et al. [52]) for needles sampled from the top and bottom part of the crown of three representative trees selected at each sample plot. The measured structural property was the leaf area index $LAI$, which was determined at the plot level using a Plant Canopy Analyser LAI-2200 instrument (LI-COR, Lincoln, NE, USA). More details about the ground measurements and data pre-processing are reported in Homolová et al. [38]. These ground measurements were compatible with airborne hyperspectral data acquired on 31 August 2016. For this study, we used the minimum, mean, and maximum measurements of three plots that were located inside and right at the edge of the target area (Figure 1). These three plots represented a Norway-spruce-dominated forest stand.

Table 2. Input parameters for the radiative transfer module (RTMo) of the Soil Canopy Observation of Photosynthesis and Energy fluxes (SCOPE) model together with the lower bound (LB), upper bound (UP), prior mean ($\mu$), prior standard deviation (SD), and mean of the measurements acquired in August 2016 from three field sampling plots (Figure 1). The range of the measured soil water content (SWC) in the brightness-shape-moisture (BSM) submodel is provided from Table 3.

	Parameter	Symbol	Unit	LB	UB	$\mathit{\mu }$	SD	Measured Mean ${}^{†}$/Range ${}^{*}$
Biochemical properties	Leaf chlorophyll content	$C_{\mathrm{ab}}$	μg cm−2	0	100	50	28.8	38.42 ${}^{†}$
	Leaf water content	$C_{\mathrm{w}}$	g cm−2	0	0.05	0.025	0.01	0.02 ${}^{†}$
	Leaf dry matter content	$C_{\mathrm{dm}}$	g cm−2	0	0.04	0.02	0.01	0.015 ${}^{†}$
	Senescent material	$C_{\mathrm{s}}$	—	0	1.5	0.75	0.43	—
	Carotenoids	$C_{\mathrm{ca}}$	μg cm−2	0	20	10	5.77	7.91 ${}^{†}$
Structural properties	Leaf area index	$LAI$	m2 m−2	6	10	8	1.15	8.66 ${}^{†}$
	Leaf inclination distribution function	$LID{F}_{\mathrm{a}}$	—	–1	+1	0	0.58	—
	Bimodality of leaf inclination	$LID{F}_{\mathrm{b}}$	—	–1	+1	0	0.58	—
	Leaf structural parameter	N	—	1	3.5	2.25	0.72	—
BSM submodel parameters	Soil Brightness parameter	B	—	0	0.9	0.45	0.26	—
	Soil spectral shape latitude	$Lat$	deg	10	50	30	11.5	—
	Soil spectral shape longitude	$Lon$	deg	40	70	55	8.7	—
	Soil water content	SWC	%					15.61–31.54 ${}^{*}$

${}^{†}$ means mean and ${}^{*}$ means range.

provides the means of the measured vegetation properties. We validated the retrieved vegetation properties against the measured means.

3.2. Retrieval of Vegetation Properties Time Series Using HLS and Airborne Data and the SCOPE Model

The SCOPE model is an integration of four modules [19] that interact with each other to simulate the optical properties and physiological state of plants. The modules include: (a) the radiative transfer module in the optical domain (RTMo) for simulating TOC reflectance by tracking the propagation of incident solar and sky radiation; (b) the radiative transfer module for thermal radiation (RTMt), to simulate TOC outgoing thermal radiation; (c) energy balance and biochemical routines to simulate heat fluxes and photosynthesis; and (d) a radiative transfer module that simulates the TOC spectrum for chlorophyll fluorescence (RTMf). In this study, we inverted the RTMo module as a separate model to retrieve vegetation properties and finally simulated the photosynthesis (i.e., GPP${}_{\mathrm{SIM}}$) using forward SCOPE modeling.

The leaf level model PROSPECT5 [53] and the canopy-level reflectance model 4SAIL (scattering by arbitrary inclined leaves) [54] are combined in the RTMo model of SCOPE. The PROSPECT5 model simulates the leaf-level reflectance and transmittance from the input biochemical leaf properties. Leaf-level optical properties are further upscaled on canopy scale by accounting for the canopy architecture using the 4SAIL model. We also incorporated the effect of soil background (soil brightness and SWC) on the simulated reflectance using the brightness-shape-moisture (BSM) submodel as previously suggested [20,21]. Table 2 provides the input parameters of the RTMo model and the BSM submodel.

We evaluated the quality of HLS data before the retrieval of vegetation properties. For the 2016 vegetation growing season, we downloaded HLS data for 39 days. The HLS data are distributed with a per-pixel quality layer to mask the pixels of poor quality (e.g., due to the presence of clouds or other processing artifacts). However, the accuracy of the internal cloud mask is insufficient [30], and its use may lead to the omission of cloud detection. This was also the case for our study area for some days. Therefore, we did not use the internal cloud mask of the HLS data, but propose our method for filtering the time series based on the empirical threshold of NDVI and NIR reflectance. We only considered pixels to be of high quality when the NDVI varied between 0.5 and 0.99 (vegetation pixels) and the NIR reflectance between 0.1 and 0.4 (typical spruce canopy reflectance values as, for instance, reported by Rautiainen et al. [55]). Thresholds were set based on our previous experience with the reflectance characteristics of Norway spruce in the study area during the growing season. For each day, we calculated the mean of TOC reflectance in each HLS band within the target area if more than 50% of the pixels were of high quality (fulfilling both the NDVI and NIR thresholds). Of the original 39 days, 14 days were retained after the filtering. For the retrieval, we selected six HLS bands relevant for studying the vegetation properties that were common in both Sentinel-2 and Landsat-8 data. These selected bands were blue (482 nm), green (561.4 nm), red (654.6 nm), NIR narrow (864.7 nm), and two shortwave infrared bands (SWIR 1 (1608.9 nm) and SWIR 2 (2200.7 nm)).

Table 3. Overview of the harmonized Landsat-8 and Sentinel-2 (HLS) data used in this study, with the percentage of high-quality pixels and mean NDVI within the target area defined by flux footprint (delineated in Figure 1). CET: Central European time, NDVI: Normalized difference vegetation index, L30: Landsat-8 data, S30: Sentinel-2 data, SWC: soil water content.

Date of HLS Data	Sensing Satellite	Julian Day	Time of Observation in CET	% of High Quality Pixels	Mean NDVI	Mean SWC (%) at the Time of Observation
3 April 2016	S30	94	11:54:06	87.73	0.73	28.45
16 April 2016	L30	107	11:38:12	96.47	0.82	31.54
23 May 2016	S30	144	11:54:04	100	0.81	23.3
27 May 2016	L30	148	11:32:29	100	0.84	24.94
2 July 2016	S30	184	11:52:19	100	0.87	18.41
5 July 2016	L30	187	11:38:30	78.81	0.87	22.67
22 July 2016	S30	204	11:53:51	100	0.87	25.21
31 August 2016	L30	244	11:33:01	100	0.88	23.37
7 September 2016	L30	251	11:38:50	66.91	0.81	27.23
10 September 2016	S30	254	11:50:27	70.45	0.87	23.52
16 September 2016	L30	260	11:33:04	100	0.88	17.28
20 September 2016	S30	264	11:52:23	99.07	0.9	19.31
23 September 2016	L30	267	11:38:51	100	0.85	18.95
30 September 2016	S30	274	11:50:25	51.86	0.86	15.61

shows the 14 days with the percentage of high quality pixels within the target area.

For each of the 14 days with HLS data, we used an optimization method to invert the RTMo model against mean TOC reflectance to retrieve the dynamics of the vegetation properties, as described in van der Tol et al. [24]. To tune the parameters, we used nonlinear least squares optimization, implemented in the MATLAB (the MathWorks Inc., Natick, MA, USA) built-in function “lsqnonlin”, to minimize a cost function that calculated the sum of squared differences between the simulated and measured mean TOC reflectance in the selected six HLS optical bands. In this study, we chose to retrieve five biochemical parameters ($C_{\mathrm{ab}}$, $C_{\mathrm{w}}$, $C_{\mathrm{dm}}$, $C_{\mathrm{s}}$, and $C_{\mathrm{ca}}$; Table 2) and three structural parameters ($LAI$, leaf inclination distribution function ($LIDF$) and leaf structural parameter (N); Table 2). To run the optimization method, prior information, i.e., range, mean, and standard deviation of each vegetation property to be retrieved (Table 2) was needed. We used non-informative prior information following Verhoef et al. [21] and Bayat et al. [22] to ensure the significant impact of the measured HLS reflectance on the retrieved parameters. We used the middle of the total range (i.e., (lower bound + upper bound)/2) as a prior mean of each vegetation property. Assuming uniform prior distribution over the range between the lower and upper bound produced values of standard deviation equal to $1/\sqrt{12}\approx 0.3$ times the range of each vegetation property. We fixed the SWC based on the measurements of mean SWC within the target area measured at the observation time of HLS data (Section 3.1.2 and Table 3). We used the BSM submodel to describe soil background reflectance. The BSM submodel is based on the library of global soil vectors [56], which is extended via a brightness-shape component and SWC effect. This has two main advantages: (1) the model can simulate soil reflectance, providing an effective alternative to soil spectrum measurements; and (2) the model can scale the dry soil spectrum for any given SWC. Further, the BSM submodel can be inverted to retrieve BSM input parameters (soil brightness (B), $Lat$, and $Lon$) from the given dry soil spectrum. We took advantage of this possibility and retrieved these three input parameters by inverting the BSM submodel against a dry soil reflectance extracted from the airborne data.

We also calculated a mean TOC reflectance within the target area from the airborne hyperspectral data acquired on 31 August 2016. It was used to retrieve the vegetation properties using the RTMo inversion, where we used the same non-informative prior information of the vegetation properties and the BSM input parameters as we used for HLS data. We further used the ground measurements (Table 2) to compare the retrieved vegetation properties obtained from HLS and airborne data.

3.3. Simulating Gross Primary Production Using SCOPE Model

After retrieving the time series of the forest’s biochemical and structural properties, we set up the SCOPE model to simulate the half-hourly GPP${}_{\mathrm{SIM}}$ during the 2016 vegetation growing season. These half-hourly values were summed to daily GPP${}_{\mathrm{SIM}}$ values calculated in g C m⁻² s⁻¹. The SCOPE model inputs for GPP${}_{\mathrm{SIM}}$ included: (1) half-hourly meteorological variables, i.e., R${}_{\mathrm{in}}$, R${}_{\mathrm{li}}$, T${}_{\mathrm{a}}$, p, e${}_{\mathrm{a}}$, and u (introduced in Section 3.1.2); (2) vegetation properties, i.e., $C_{\mathrm{ab}}$, $C_{\mathrm{w}}$, $C_{\mathrm{dm}}$, $C_{\mathrm{s}}$, $C_{\mathrm{ca}}$, $LAI$, $LIDF$, and N (Table 2); (3) maximum rate of carboxylation ($V_{\mathrm{cmax}}$, in μmol m⁻² s⁻¹ ); and (4) the Bell–Berry stomatal parameter m. We ran the SCOPE model with three scenarios to investigate the impact of information retrieved from the HLS data on the accuracy of GPP${}_{\mathrm{SIM}}$:

“Fixed” scenario: We assumed no variations in the retrieved vegetation properties during the growing season. We fixed them either at the available measured means (Table 2) or at the prior means. $LID{F}_{\mathrm{a}}$ and $LID{F}_{\mathrm{b}}$ were fixed at –0.35 and –0.15, respectively, showing the spherical characteristics of Norway spruce [54]. We further fixed $V_{\mathrm{cmax}}$ = 80 μmol m⁻² s⁻¹ and m = 9, which are the typical values for evergreen needle leaf species as suggested in the SCOPE model. This scenario allowed us to monitor the temporal variation in GPP${}_{\mathrm{SIM}}$ determined by changes in radiation and atmospheric demand.

“HLS info” scenario: We used the time series of vegetation properties retrieved from the HLS data as the inputs to the SCOPE model. In this scenario, we also fixed $V_{\mathrm{cmax}}$ and m at the typical values for evergreen needle leaf species, since these two cannot be directly retrieved from the optical reflectance [20].

“HLS info & var Vcmax” scenario: We used the same time series of retrieved vegetation properties as in the HLS info scenario. Here, instead of using a fixed typical value of $V_{\mathrm{cmax}}$, we estimated its time series from the retrieved time series of $C_{\mathrm{ab}}$ from the HLS data. For this, we used the empirical relationship between $V_{\mathrm{cmax}}$ [μmol m⁻² s⁻¹] and $C_{\mathrm{ab}}$ [μg cm⁻²] proposed by Houborg et al. [57] for C${}_3$ plants:

$$V_{\mathrm{cmax}}=a\times C_{\mathrm{ab}}+b,$$

(1)

where a = 2.529 and b = –27.34. This scenario allowed us to monitor the temporal variation in GPP${}_{\mathrm{SIM}}$ when we relied on optical domain information both directly from the retrieved vegetation properties and indirectly from the empirical relationships.

3.4. Statistical Evaluation of Model Performance

We determined the performance of the SCOPE simulations using statistical criteria that evaluated the efficiency with which the SCOPE reproduced the flux tower GPP${}_{\mathrm{EC}}$. These criteria provided a measure of the SCOPE model efficiency in simulating daily GPP${}_{\mathrm{SIM}}$ over the 2016 vegetation growing season. We used the following criteria:

$$\mathrm{Root}\mathrm{mean}\mathrm{square}\mathrm{error}\left(\mathrm{RMSE}\right)=\sqrt{\frac{1}{n}\sum _{i=1}^n{(z_i-y_i)}^2},$$

(2)

$$\mathrm{Nash}-\mathrm{Sutcliffe}\mathrm{efficiency}\left(\mathrm{NSE}\right)=1-\frac{{\sum }_{i=1}^n{(z_i-y_i)}^2}{{\sum }_{i=1}^n{(z_i-\overline{z})}^2},$$

(3)

$$\mathrm{Correlation}\mathrm{coefficient}\left(\mathrm{COR}\right)=\frac{{\sum }_{i=1}^n(z_i-\overline{z})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^n{(z_i-\overline{z})}^2{\sum }_{i=1}^n{(y_i-\overline{y})}^2}},$$

(4)

where n is the number of daily simulated GPP${}_{\mathrm{SIM}}$ ($y_i$) and daily measured GPP${}_{\mathrm{EC}}$ ($z_i$), and $\overline{z}$ and $\overline{y}$ represent the mean over the vegetation growing period. The RMSE criterion has the unit of GPP. A low RMSE indicates high accuracy. It is appropriate to compare the simulations under different scenarios (Section 3.3). The NSE [58] can range from $-\infty$ to 1. An NSE value close to 1 indicates a perfect match of simulations to the observations. Following Dumont et al. [59], we assumed that an NSE ≥0.5 indicates adequate accuracy in GPP${}_{\mathrm{SIM}}$. The COR represents the linear relationship between simulations and observations, and can vary from –1 to 1. We also used Equations (3) and (4) to evaluate the efficiency with which the RTMo produced TOC reflectance on each day. In this case, $z_i$ and $y_i$ represent the observed and the RTMo-simulated HLS/airborne TOC reflectance at the wavelength i, respectively.

We compared the vegetation properties retrieved from the HLS data with those retrieved from the airborne data, and the measurements using the percentage difference:

$$\mathrm{Percentage}\mathrm{difference}=\left|\frac{A_i-B_i}{\frac{A_i-B_i}{2}}\right|\times 100,$$

(5)

where $A_i$ and $B_i$ represent the ith vegetation property retrieved from HLS data and airborne data, respectively. For comparison with the measurements, $B_i$ represents the ith measured vegetation property.

4. Results

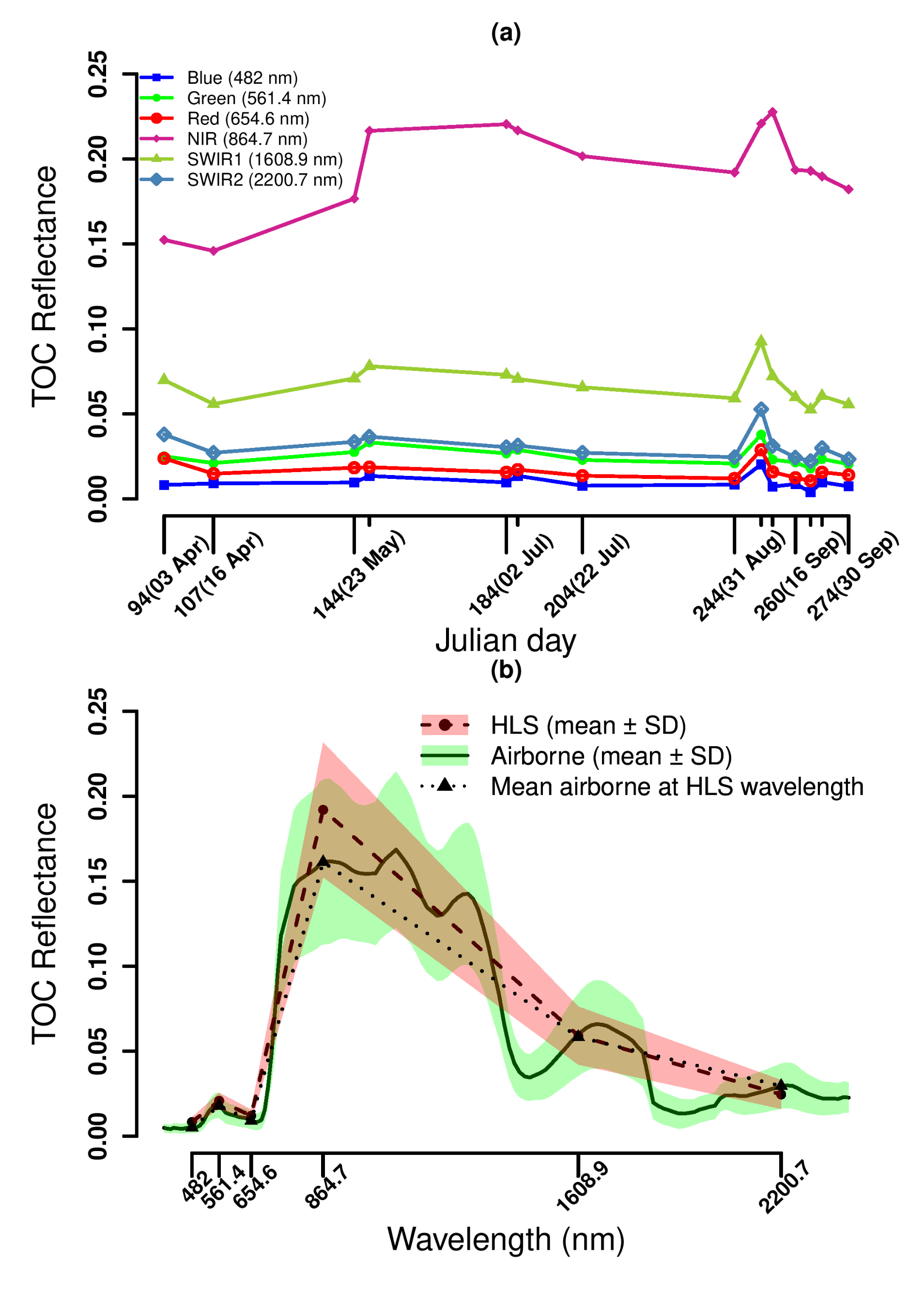
4.1. Variation in Observed Top-Of-Canopy Reflectance

Figure 2a shows the temporal variation in the mean TOC reflectance extracted from the HLS data within the target area. The highest variation was observed in the NIR band with increasing NIR reflectance from the start of the vegetation growing seasons, which then stabilized mid-season, and decreased at the end of vegetation growing season. Other bands exhibited the same pattern, but with smaller variations in the magnitude of reflectance compared to the NIR band.

The observed temporal variation in the TOC reflectance likely did not occur due to the variation in $LAI$ because the evergreen Norway spruce species can be expected to have stable $LAI$ (Section 4.3) throughout the year. Instead, change in leaf age distribution caused temporal variation in the reflectance. Both young and mature leaves contribute to the TOC reflectance when captured from the top of the crown by the sensors of HLS data. Young leaves, in particular, start becoming greener from the beginning of the vegetation growing season, and then they stay sufficiently green until September and then start browning. This phenological development of the young leaves was likely the cause of variation in the TOC reflectance observed in this study.

Figure 2b compares the mean and standard deviation, showing the variability of TOC reflectance within the target area, extracted from the HLS and airborne data acquired on 31 August 2016. To facilitate comparison, we also plotted the airborne reflectance resampled at the band centers of the HLS data. Both the HLS and airborne data exhibited similar magnitudes of mean TOC reflectance, with slightly higher NIR reflectance (0.19) in the HLS compared to airborne data (0.16). We found that both the HLS and airborne data exhibited similar variability within the target area even though the stand variability was poorly captured in the HLS data with coarse spatial resolution compared to the airborne data.

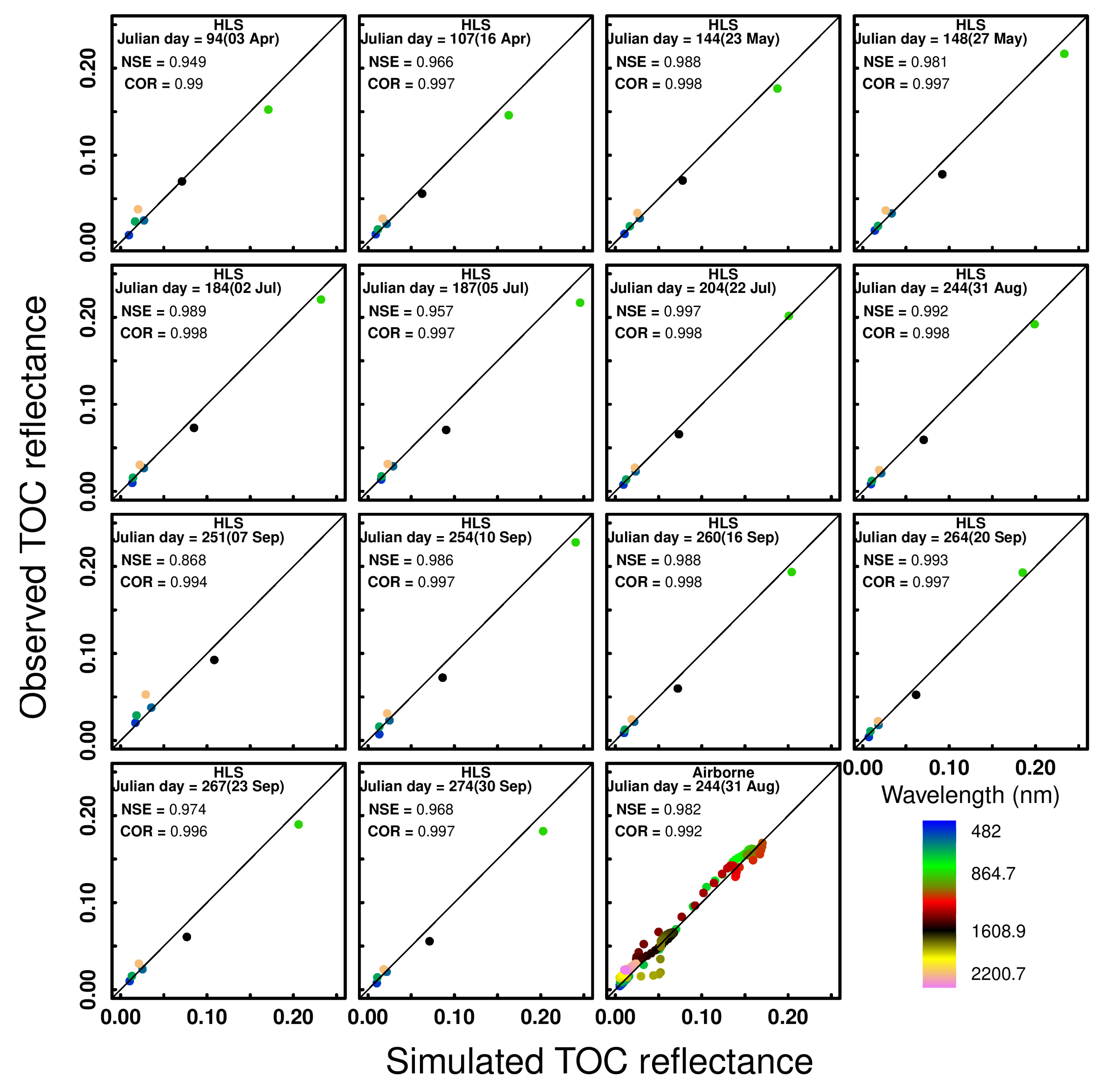
4.2. Simulation of TOC Reflectance

We assessed the performance of the RTMo model in retrieving vegetation properties by: (1) using the goodness-of-fit measured between the simulated and observed TOC reflectance; and (2) comparing the retrieved with the measured vegetation properties (Section 4.3). Figure 3 illustrates the goodness of fit using COR and NSE, and provides a spectral comparison between the observed mean TOC reflectance (by HLS and airborne) and the simulated TOC reflectance (by the RTMo model) for all 14 days during the vegetation growing season. We found that the NSE was close to one on each day, indicating a perfect match between the simulated and observed TOC reflectance. Strong positive correlations between simulations and observations were indicated by a COR value close to one. These showed that the RTMo model was able to successfully reproduce the observed HLS and airborne TOC reflectance. We presented the observed and simulated TOC reflectance curves for the selected Julian days in Figure S2.

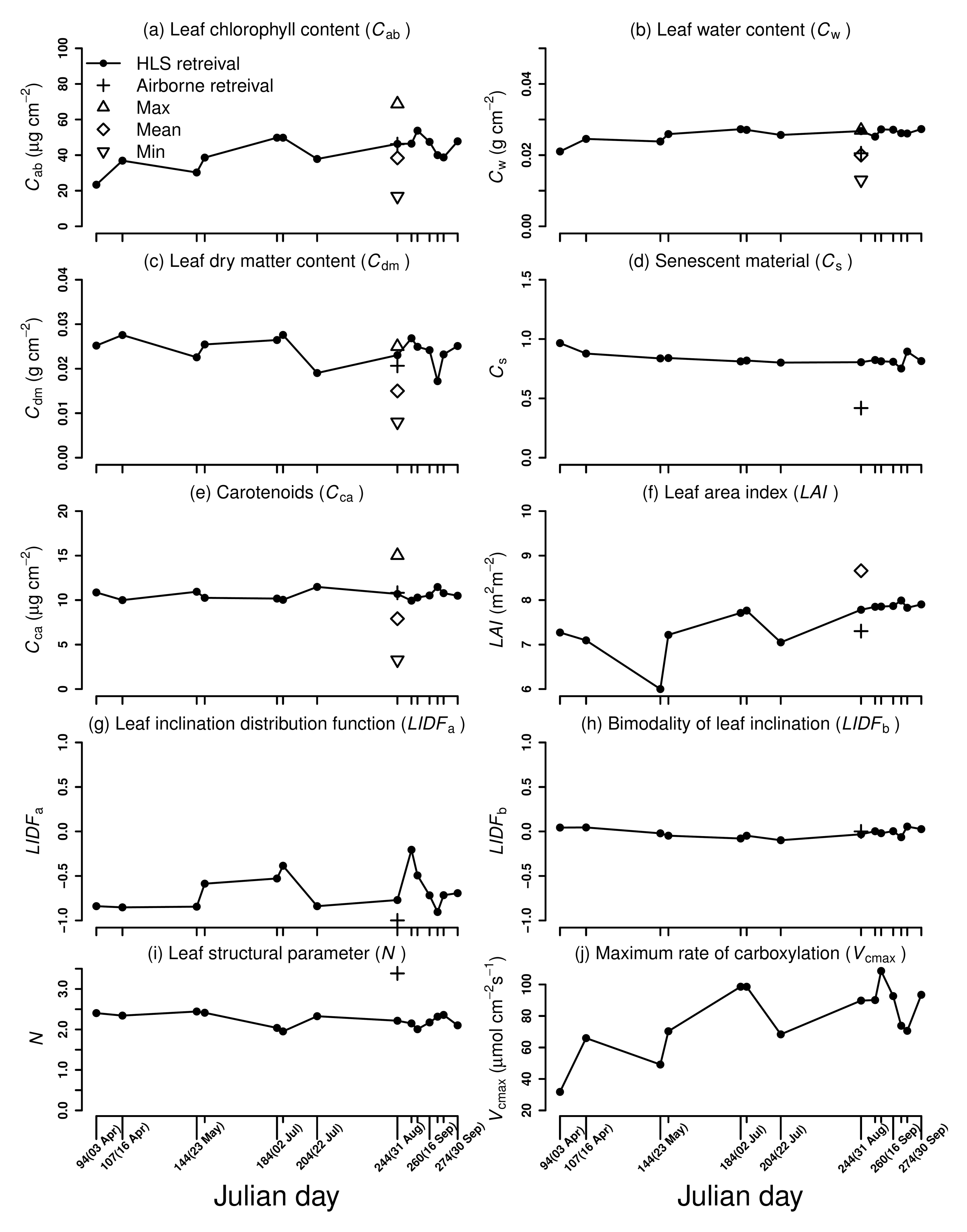
4.3. Retrieval of Vegetation Properties

Figure 4 illustrates the variations in the retrieved vegetation properties during the 2016 vegetation growing season. For comparison, Figure 4 also includes the retrieval from airborne data on 31 August 2016, and the minimum, maximum, and mean values obtained from the ground measurements. The y-axis represents the non-informative prior distribution range of each vegetation property (Table 2). An optimization process constrained the RTMo input by the TOC reflectance (either HLS or airborne). Each vegetation property was retrieved in a narrow range during the growing season, indicating the reduction in prior uncertainty after the optimization.

From HLS data, we were able to retrieve the vegetation properties at least once per month. Only in June was it not possible to find a reliable observation for use in the retrieval. These retrievals provide insight into the temporal patterns of vegetation properties. Except for $C_{\mathrm{ab}}$ and $C_{\mathrm{dm}}$, we did not observe any apparent temporal variation in any of the studied vegetation properties. We retrieved a low estimate of $C_{\mathrm{ab}}$ at the start of the growing season (23.4 μg cm⁻² on 3 April), which increased to 50 μg cm⁻² in mid-season (5 July), and then showed an overall decreasing trend toward the end. $C_{\mathrm{dm}}$ followed a similar pattern as $C_{\mathrm{ab}}$ during the growing season, i.e., both decreased or increased together between any two successive days. The retrieval of $LAI$ showed consistency during the growing season, and we retrieved the $LAI$ between 7 and 8 m² m⁻², except for 23 May, where it dropped to 6 m² m⁻². This drop is, however, not an unrealistic estimate of $LAI$ for Norway spruce.

We obtained the percentage difference between the vegetation properties retrieved from the HLS and airborne data using Equation (5) to show the similarity between them. We observed low percentage differences in most of the vegetation properties. The percent differences for $C_{\mathrm{ab}}$, $C_{\mathrm{dm}}$, $C_{\mathrm{ca}}$, and $LAI$ were less than 10%, with the lowest being 0.3% for $C_{\mathrm{ab}}$. $C_{\mathrm{w}}$ and $LID{F}_{\mathrm{a}}$ showed a difference of 25%. The maximum differences in $C_{\mathrm{s}}$ and N were observed at 63% and 42%, respectively.

Based on the percentage difference, we compared the vegetation properties retrieved from the HLS data on 31 August with the mean of the available ground measurements (Table 2 and Figure 4). We found that the percentage differences for $C_{\mathrm{ab}}$, $C_{\mathrm{w}}$, $C_{\mathrm{dm}}$, $C_{\mathrm{ca}}$, and $LAI$ were less than 30%. We found the lowest difference for $LAI$, with 7%, whereas $C_{\mathrm{ab}}$ showed a difference of 17%. These percentage differences appear to be acceptable given the aggregated effect of the target area compared with the three separate plots of measurements (Figure 1). Moreover, all the retrieved vegetation properties were within the minimum and maximum, i.e., the range of the measurements (Figure 4), indicating the retrievals were reasonable, at least on 31 August 2016.

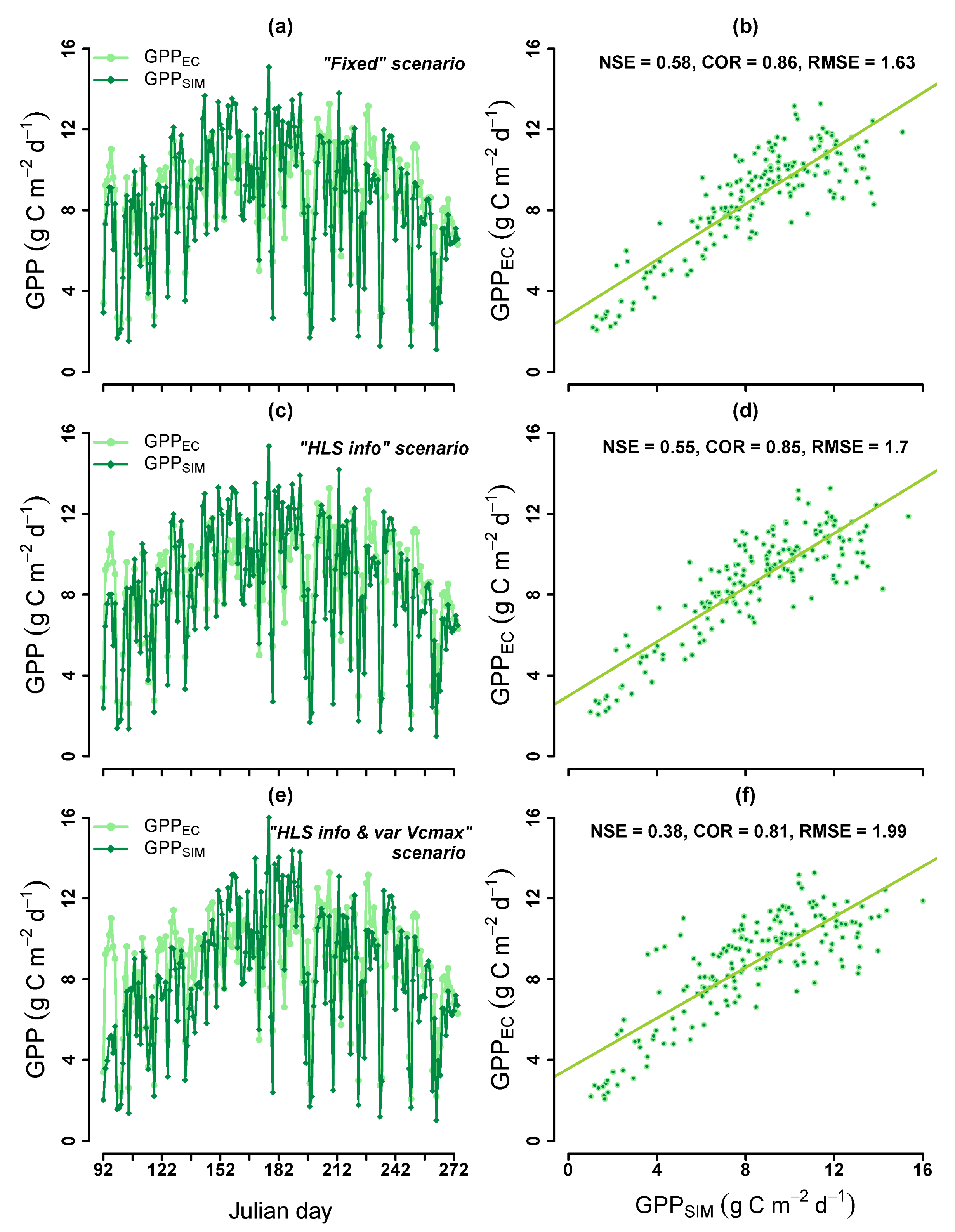
4.4. Simulations of GPP_SIM with SCOPE Model

Finally, we evaluated the performance of the SCOPE model by comparing the simulated daily GPP${}_{\mathrm{SIM}}$ with the daily GPP${}_{\mathrm{EC}}$ measured during the 2016 vegetation growing season. Figure 5 illustrates the temporal variation in daily GPP${}_{\mathrm{SIM}}$ for three designed scenarios (Section 3.3), together with the daily GPP${}_{\mathrm{EC}}$.

We also present the scatterplots between daily GPP${}_{\mathrm{SIM}}$ and GPP${}_{\mathrm{EC}}$ to show their correlation between them. Under both the Fixed and HLS info scenarios, daily GPP${}_{\mathrm{SIM}}$ closely followed the daily GPP${}_{\mathrm{EC}}$ (Figure 5a,c), visually indicating the accuracy of GPP${}_{\mathrm{SIM}}$. The quantitative description of the GPP${}_{\mathrm{SIM}}$ accuracy was confirmed with the estimated NSE value (Equation (3)), which was found to be greater than 0.5 for both scenarios. The high NSE value indicated the sufficient quality of the predictive power of the SCOPE model for simulating gross primary production. We, however, observed some under- and over-estimation in GPP${}_{\mathrm{SIM}}$ compared to the GPP${}_{\mathrm{EC}}$. The scatterplots (Figure 5b,d) further explain the positive linear relationship between GPP${}_{\mathrm{SIM}}$ and GPP${}_{\mathrm{EC}}$, with the value of COR being high (close to 0.9 for both scenarios). This high value indicated that the variation of GPP${}_{\mathrm{SIM}}$ between consecutive days were synchronized with that of GPP${}_{\mathrm{EC}}$. We also concluded that both Fixed and HLS info scenarios led to similar magnitude and variation in daily GPP${}_{\mathrm{SIM}}$ during the vegetation growing season, and both scenarios quantitatively produced similar NSE values, together with similar RMSE values (Equation (2)).

Under the HLS info & var Vcmax scenario, we estimated $V_{\mathrm{cmax}}$ from the time series of $C_{\mathrm{ab}}$ (Equation (1)) as ranging from 31.8 to 108.5 μmol m⁻² s⁻¹ during the vegetation growing season (Figure 4j). The variation in $V_{\mathrm{cmax}}$ resulted in the synchronization between daily GPP${}_{\mathrm{SIM}}$ and GPP${}_{\mathrm{EC}}$, but substantial differences in their magnitudes (Figure 5e) compared to the other two scenarios. These indicated the decrease in the quality of the predictive power of the SCOPE model for GPP${}_{\mathrm{SIM}}$. The drop in NSE below 0.5 and the increase in RMSE provided quantitative evidence of this decrease. The linearity in the relationship between GPP${}_{\mathrm{SIM}}$ and GPP${}_{\mathrm{EC}}$ also reduced, which resulted in a drop in COR (Figure 5f).

Most of the variability in daily GPP${}_{\mathrm{SIM}}$ can be explained by its response to meteorological variables. We showed that R${}_{\mathrm{in}}$ was the main driver of GPP${}_{\mathrm{SIM}}$, with strong dependence especially up to daily mean R${}_{\mathrm{in}}$ = 200 W m⁻² (Figure 6a). The GPP${}_{\mathrm{SIM}}$ response to R${}_{\mathrm{in}}$ was further modified by T${}_{\mathrm{a}}$ (Figure 6b). The GPP${}_{\mathrm{SIM}}$ response to T${}_{\mathrm{a}}$ can be roughly separated to two regimes by a threshold of ≈13 ${}^{\circ }\mathrm{C}$. The colder regime (<13 ${}^{\circ }\mathrm{C}$) was associated with generally lower GPP${}_{\mathrm{SIM}}$ than during the warmer regime (>13 ${}^{\circ }\mathrm{C}$). Most of the colder regime days occurred during the beginning of the growing season, whereas the warmer regime occurred during the core of the growing season. The GPP${}_{\mathrm{SIM}}$ values for the end of the growing season fell during both regimes but typically represented the lower end of the GPP${}_{\mathrm{SIM}}$ range within a given regime (Figure 6b). Although T${}_{\mathrm{a}}$ was the lowest mostly in the beginning of the growing season and could be expected to form the lower bound of the light response curve, GPP${}_{\mathrm{SIM}}$ values for the end of the growing season showed even lower values when accounting for R${}_{\mathrm{in}}$.

5. Discussion

This study provided insight into the potential of using newly produced HLS data for the retrieval of temporal variations in vegetation properties using the RTMo model, and we investigated if these temporal variations could improve GPP${}_{\mathrm{SIM}}$. In addition, we investigated the information contained about vegetation properties in the multispectral HLS data compared to hyperspectral airborne data.

The amount of HLS data contributing to the time-series was reduced by cloud coverage condition over the site. The cloud mask is not properly defined in the HLS data, and this was also observed in this study. The non-cloud pixels were defined based on the NDVI range (0.4 to 0.5) and NIR range (0.1 to 0.4). The NDVI range adopted in this study was based on the broad range of NDVI for vegetation, and the NIR range was based on our previous experience on the characteristics of Norway spruce during the growing period in the study area. The variations in these ranges can be observed for other species and the study period [60]. For example, the NIR reflectance can drop to below 0.1 outside the vegetation growing period and can rise to above 0.4 for grey alder tree species. Therefore, NDVI- and NIR-based filtering of cloud-free HLS data may be suitable at the local level and for shorter periods, like in this study. However, this filtering solution might be unsuitable if the study involves several tree species in a broad area and a longer study period. Therefore, the existing cloud mask of the HLS data, i.e., irrespective of tree species/land cover types, should be made more robust.

The RTMo model successfully reproduced the observed HLS and airborne TOC reflectance (Figure 3). The RTMo model is essentially a well-established combination of leaf-canopy radiative transfer models (PROSPECT5 leaf model and 4SAIL canopy reflectance model), which has been successfully used in numerous studies for the retrieval of vegetation properties. Therefore, the good fit between the observed and simulated TOC reflectance found in this study has already been reported in the literature [19,20,21,22,23,24,61,62,63,64,65,66,67].

We retrieved the time series of vegetation properties from the HLS data. We had a limited number of ground measurements for validation of the retrievals. However, the following points should be noted:

• A temporal increase in $C_{\mathrm{dm}}$ is positively correlated with $C_{\mathrm{ab}}$. A previous study, however, did not focus on the temporal aspects of evergreen as well as deciduous tree species, but also found a positive correlation between $C_{\mathrm{dm}}$ and $C_{\mathrm{ab}}$ [68].
• We observed a good fit between the retrieved vegetation properties and the ground measurements (Section 4.3) on 31 August. At least for one day in the time series, we could therefore validate the retrievals from the HLS TOC reflectance. The retrieved $C_{\mathrm{ab}}$, however, did not exhibit substantial temporal variation. Nevertheless, these variations followed the characteristics of the evergreen tree species, which shows young leaf development phenology during the growing season. These findings agree with those of a previous study on the global spatio-temporal distribution of leaf chlorophyll [69], which highlighted the consistency in the temporal leaf chlorophyll profile of evergreen tree species across the year with an increasing concentration within new needles in spring.

Considering the points described above, we inferred a successful retrieval of vegetation properties from the HLS data. In a future study, these two points could be considered together for validation of retrievals, at least for evergreen tree species, if limited measurements are available.

We compared the retrievals from HLS and airborne data. The low percentage differences in most of the vegetation properties indicated that switching from hyperspectral to multispectral observations did not prominently influence the retrieval of vegetation properties in our case. In other words, the multispectral HLS data preserve a considerable amount of information about vegetation properties. This finding is in agreement with Croft et al. [70] who reported similarity between the $C_{\mathrm{ab}}$ values over the range of tree species belonging to different biome types, retrieved from hyperspectral measurements and Landsat observations. Further, our finding is in line with Darvishzadeh et al. [71], who exploited the potential of Sentinel-2 data for the mapping of $C_{\mathrm{ab}}$ of Norway spruce. Our study highlighted the potential of the newly produced HLS data set to monitor the vegetation properties by taking advantage of its denser time series.

We further examined if the time series of vegetation properties, retrieved from the HLS data, could improve the simulation of GPP${}_{\mathrm{SIM}}$ by the SCOPE model. We observed that both constant (Fixed scenario) and time-varying vegetation properties (HLS info scenario) led to almost identical GPP${}_{\mathrm{SIM}}$ during the vegetation growing season (Section 4.4). These results confirmed that the GPP${}_{\mathrm{SIM}}$ in Norway spruce is mainly driven by meteorological conditions (Figure 6). Therefore, the time-varying vegetation properties’ information could be significant for GPP${}_{\mathrm{SIM}}$ only when the tree is either under stress condition (e.g., due to drought) or exhibits strong temporal phenology (such as deciduous tree species). In a previous study, Bayat et al. [20] reported an improvement in temporal GPP${}_{\mathrm{SIM}}$ of the plant under stress using the time-varying vegetation properties input to the SCOPE model. In our study, the SCOPE model was mainly driven by the meteorological conditions because the Norway spruce did not show pronounced temporal variations in vegetation properties (Section 4.3) and were under no significant stress condition during the selected episode [32]. Therefore, constant vegetation properties were sufficient for simulating temporal GPP${}_{\mathrm{SIM}}$ with reasonable accuracy. We further observed the influence of time-varying $V_{\mathrm{cmax}}$ (HLS info & var Vcmax scenario) on GPP${}_{\mathrm{SIM}}$. We expected that some fluctuations in GPP${}_{\mathrm{SIM}}$ (Figure 5a,c) would be further improved with time-varying $V_{\mathrm{cmax}}$ instead of using a constant value throughout the vegetation growing season. The time-varying $V_{\mathrm{cmax}}$, however, reduced the accuracy of GPP${}_{\mathrm{SIM}}$ (Figure 5f), which could be attributed to the empirical relationship of $V_{\mathrm{cmax}}$ and $C_{\mathrm{ab}}$ defined for C${}_3$ plants (Equation (1)). A more robust empirical relationship between the $C_{\mathrm{ab}}$ and $V_{\mathrm{cmax}}$ must thus be defined for this site. A biome specific definition [72] could improve the estimation of $V_{\mathrm{cmax}}$, but this should be tested at the local site in a future study.

6. Conclusions

The present analysis showed the potential of the newly produced multispectral harmonized Landsat-8 and Sentinel-2 (HLS) data to retrieve time series of vegetation properties (i.e., biochemical and structural), which were further used as inputs to the Soil Canopy Observation, Photochemistry and Energy fluxes (SCOPE) model to simulate the time series of gross primary production GPP${}_{\mathrm{SIM}}$. The study led to the following conclusions:

• HLS data can provide the dense time series of surface reflectance at the desired locations because it combines data from two existing satellites: Landsat-8 and Sentinel-2. The results demonstrated that the HLS data are capable of preserving the needed information about vegetation properties. We investigated the retrieval only for one evergreen tree species. Nevertheless, our analysis has an important implication for the future use of HLS data for the dense time series retrieval of vegetation properties, which is needed for other tree species, such as deciduous species, showing strong temporal phenology.
• We did not observe any improvement in GPP${}_{\mathrm{SIM}}$ using the time-varying vegetation properties retrieved from the HLS data. We observed the influence of the time-varying maximum rate of carboxylation ($V_{\mathrm{cmax}}$) on GPP${}_{\mathrm{SIM}}$. However, the empirical relationship used to estimate $V_{\mathrm{cmax}}$ from leaf chlorophyll content ($C_{\mathrm{ab}}$) decreased the accuracy of GPP${}_{\mathrm{SIM}}$. Future studies need to redefine this empirical relationship.