Glacier Ice Thickness Estimation and Future Lake Formation in Swiss Southwestern Alps—The Upper Rhône Catchment: A VOLTA Application
Abstract
1. Introduction
2. Study Area
3. Data
4. Methods
4.1. Glacier Ice Thickness Estimation and Distribution
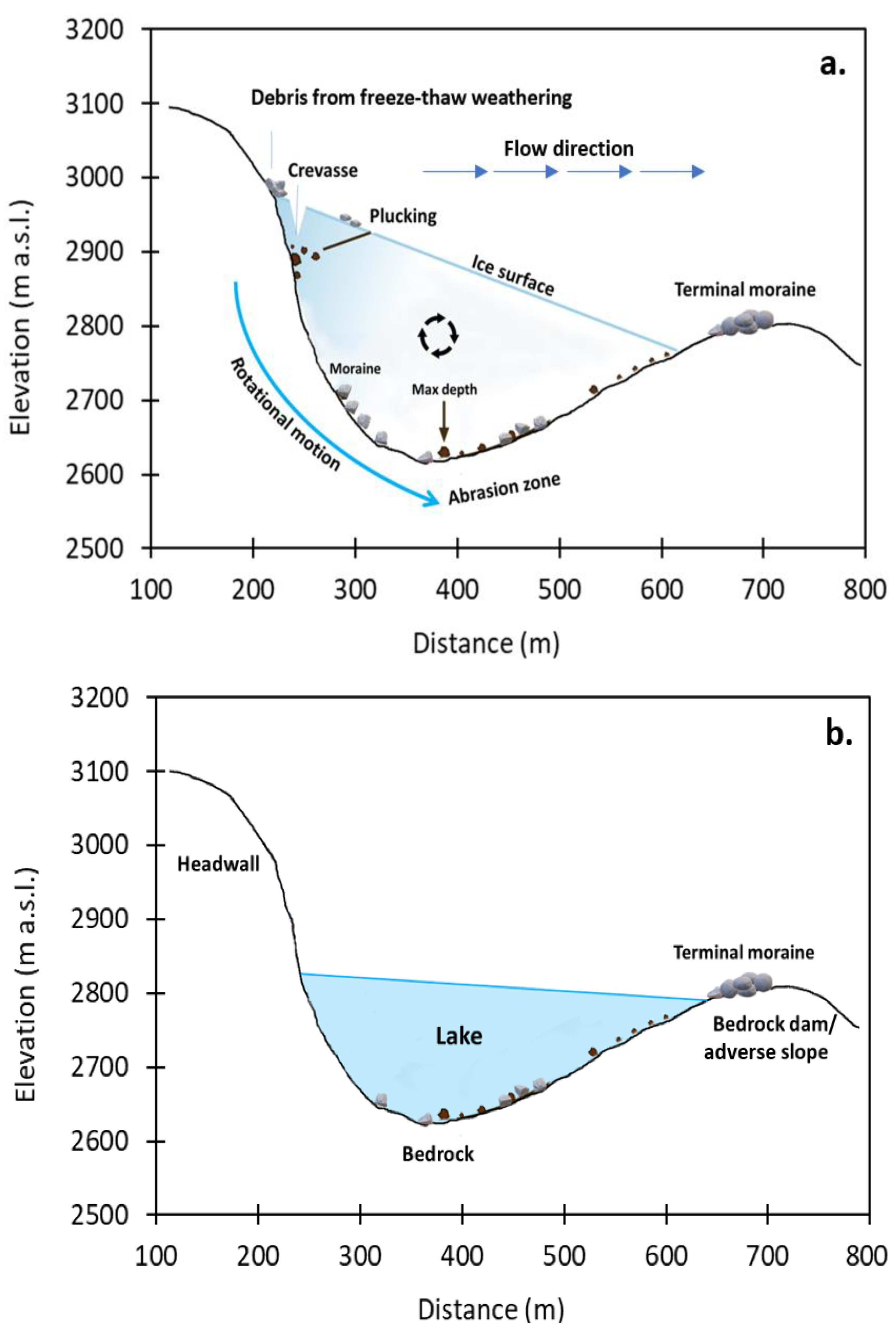
4.2. Detection of Glacier Bed Overdeepenings
4.3. Classification of Potential Future Lakes
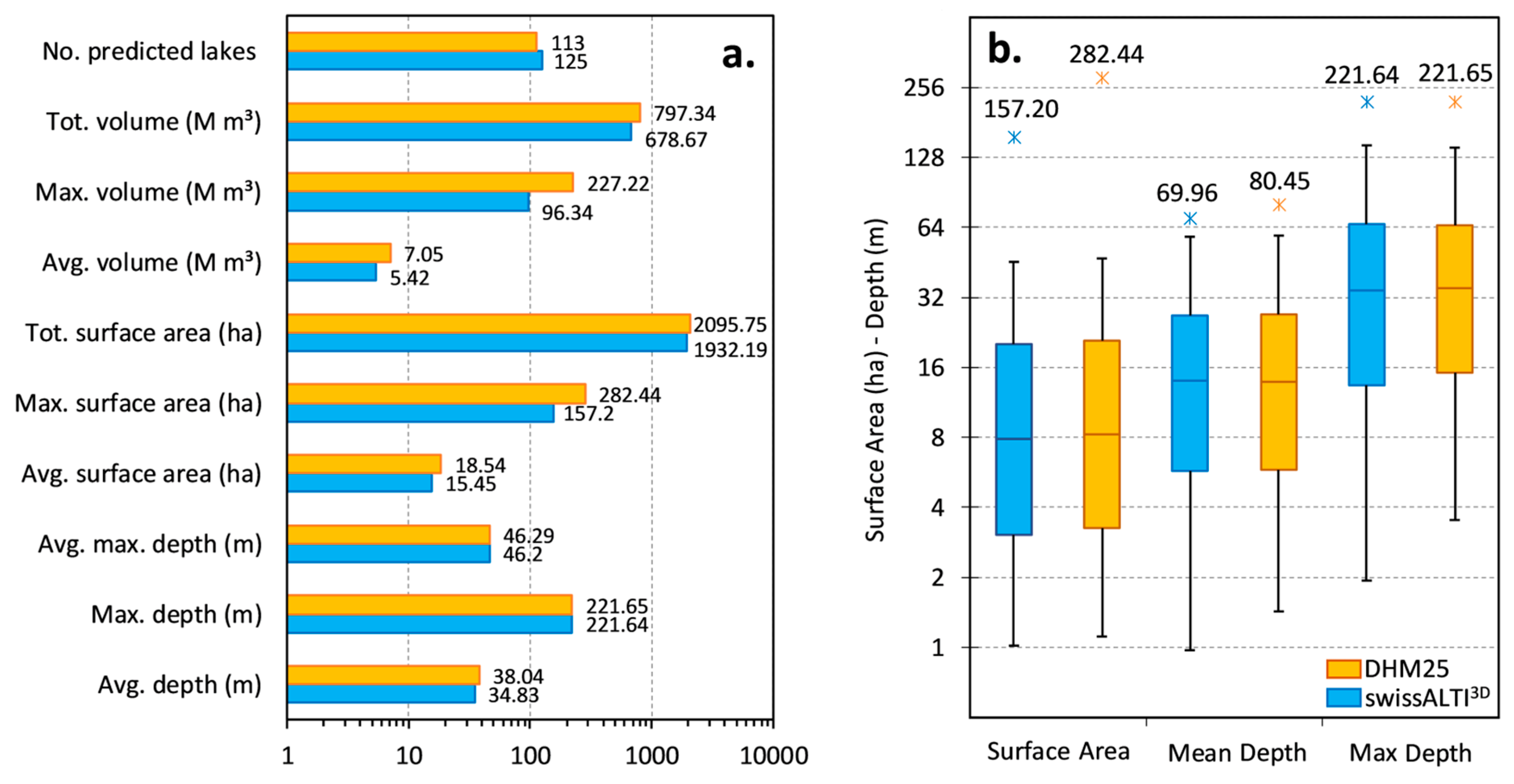
4.4. Evaluation of VOLTA and Intercomparison of Ice Thickness Models
5. Results
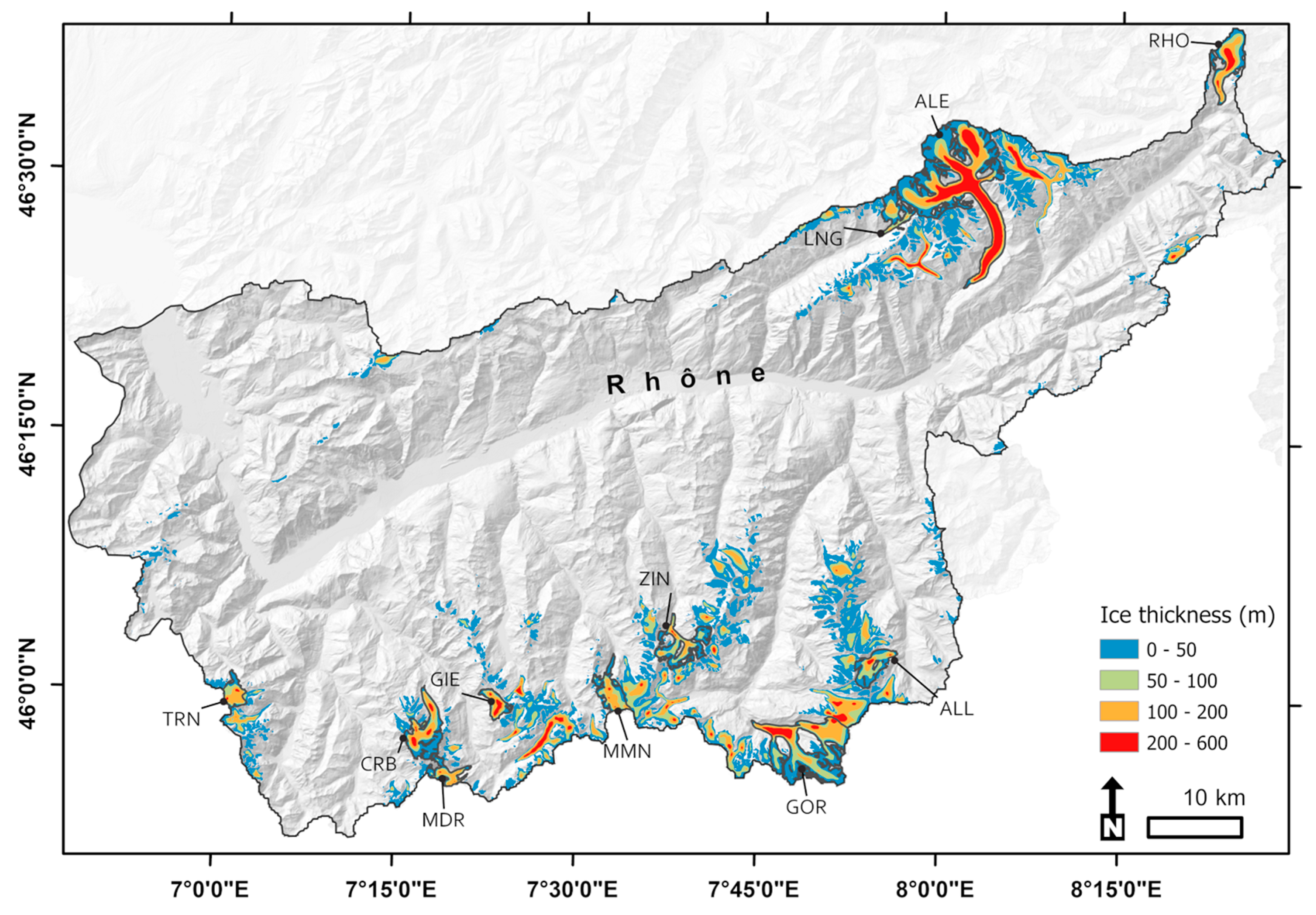
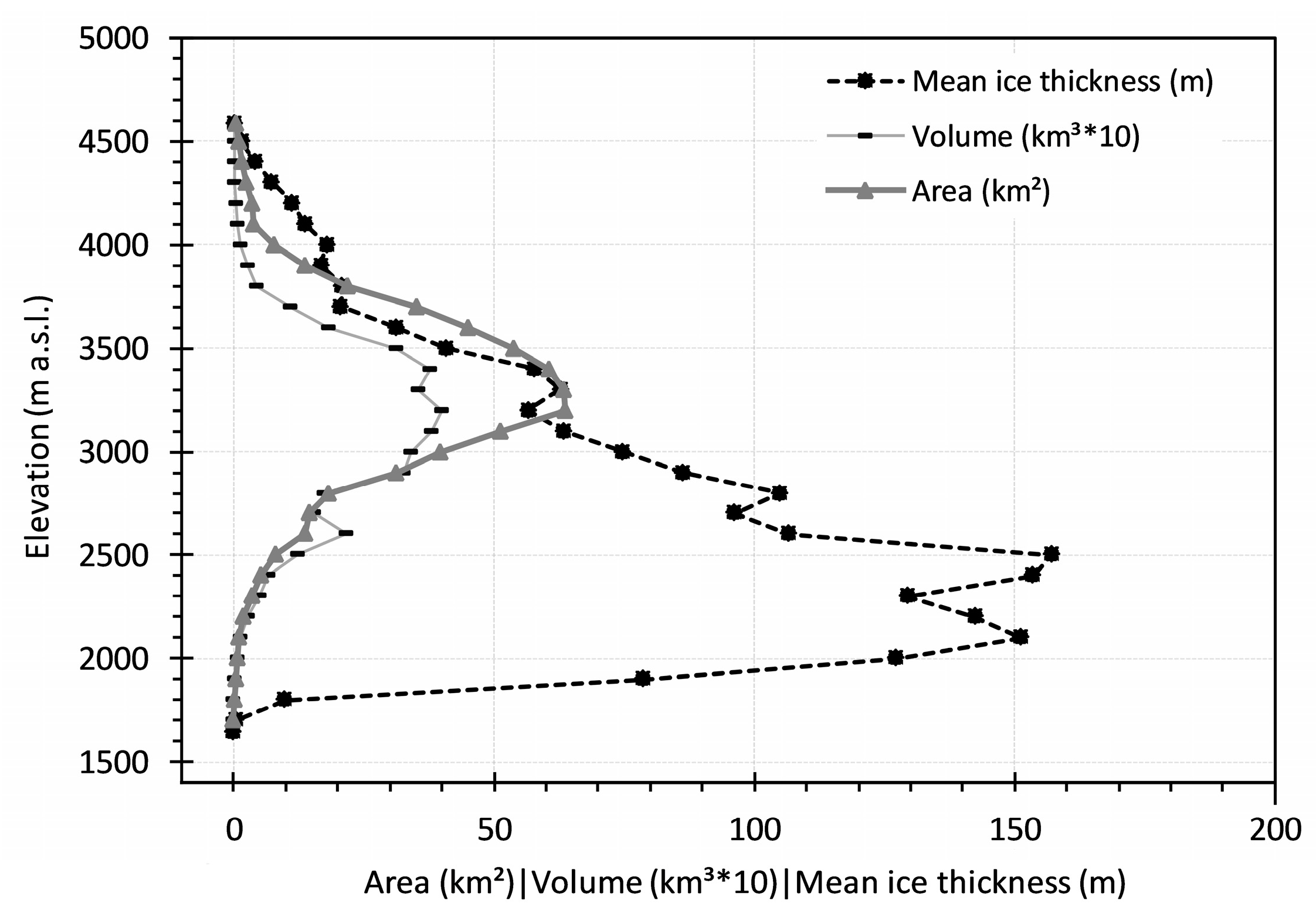
5.1. Ice Thickness and Glacier Volume
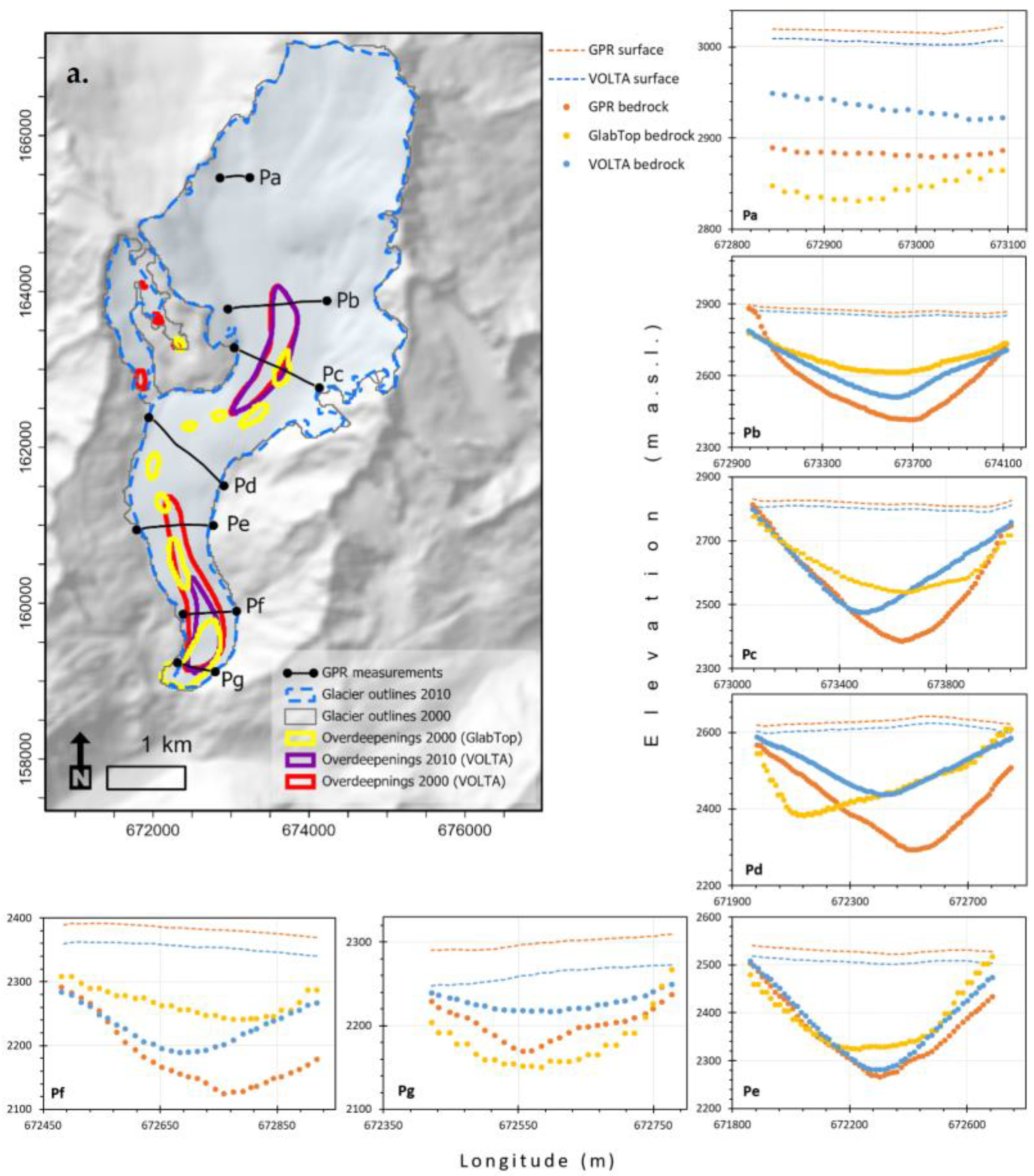
5.2. Subglacial Topography
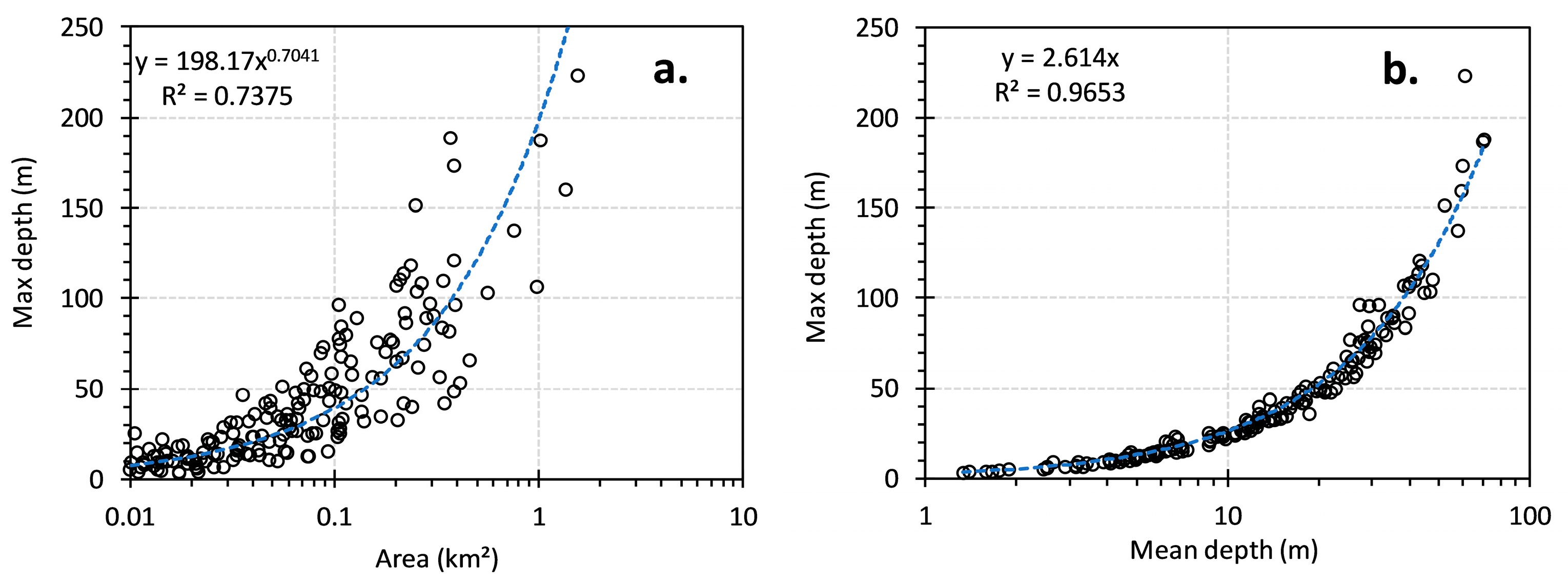
5.3. Model Performance and Morphological Analysis of Overdeepenings
5.4. Analysis of Potential Lakes
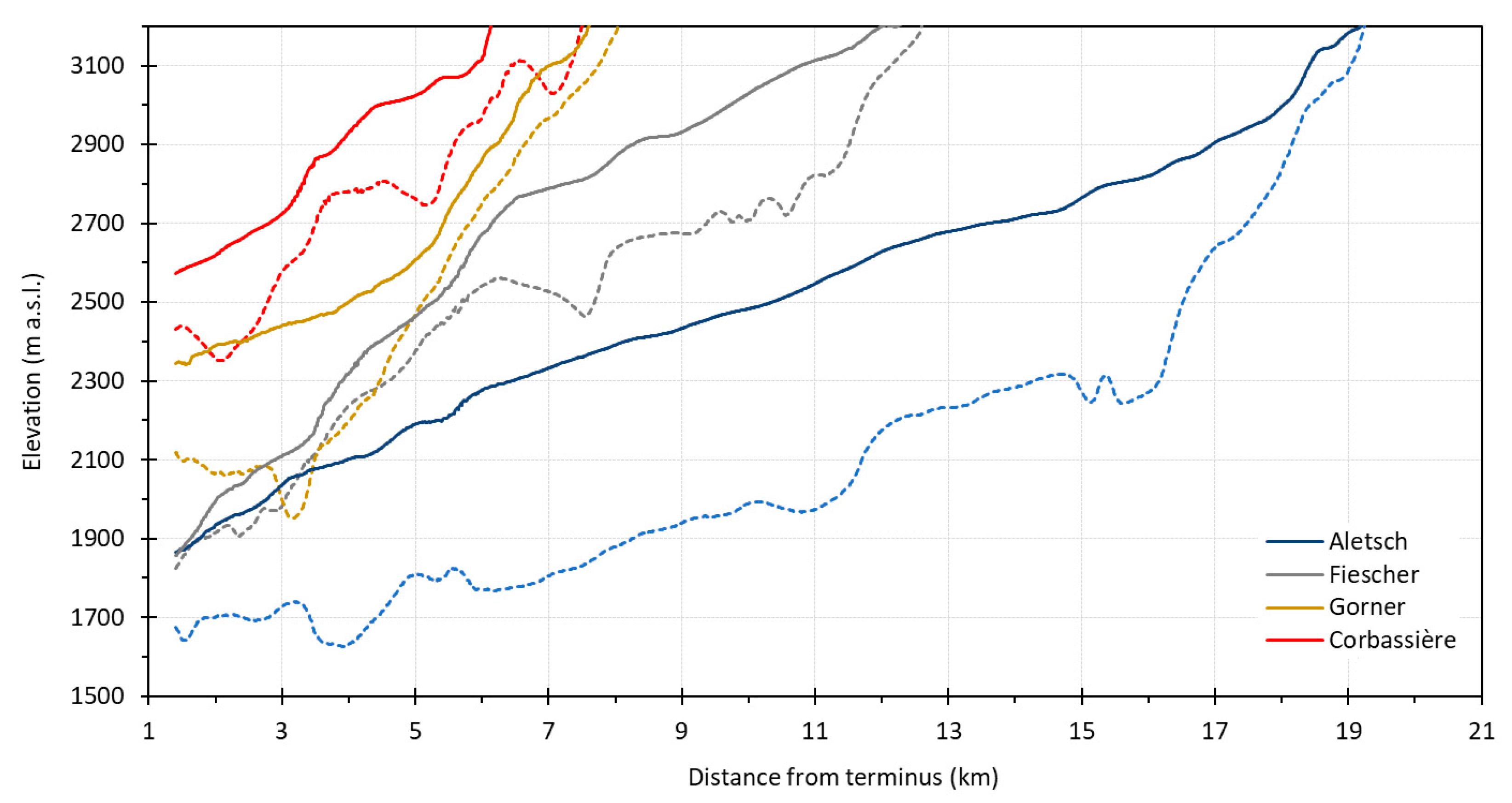
5.5. Evaluation of VOLTA and Intercomparison of Ice Thickness Models
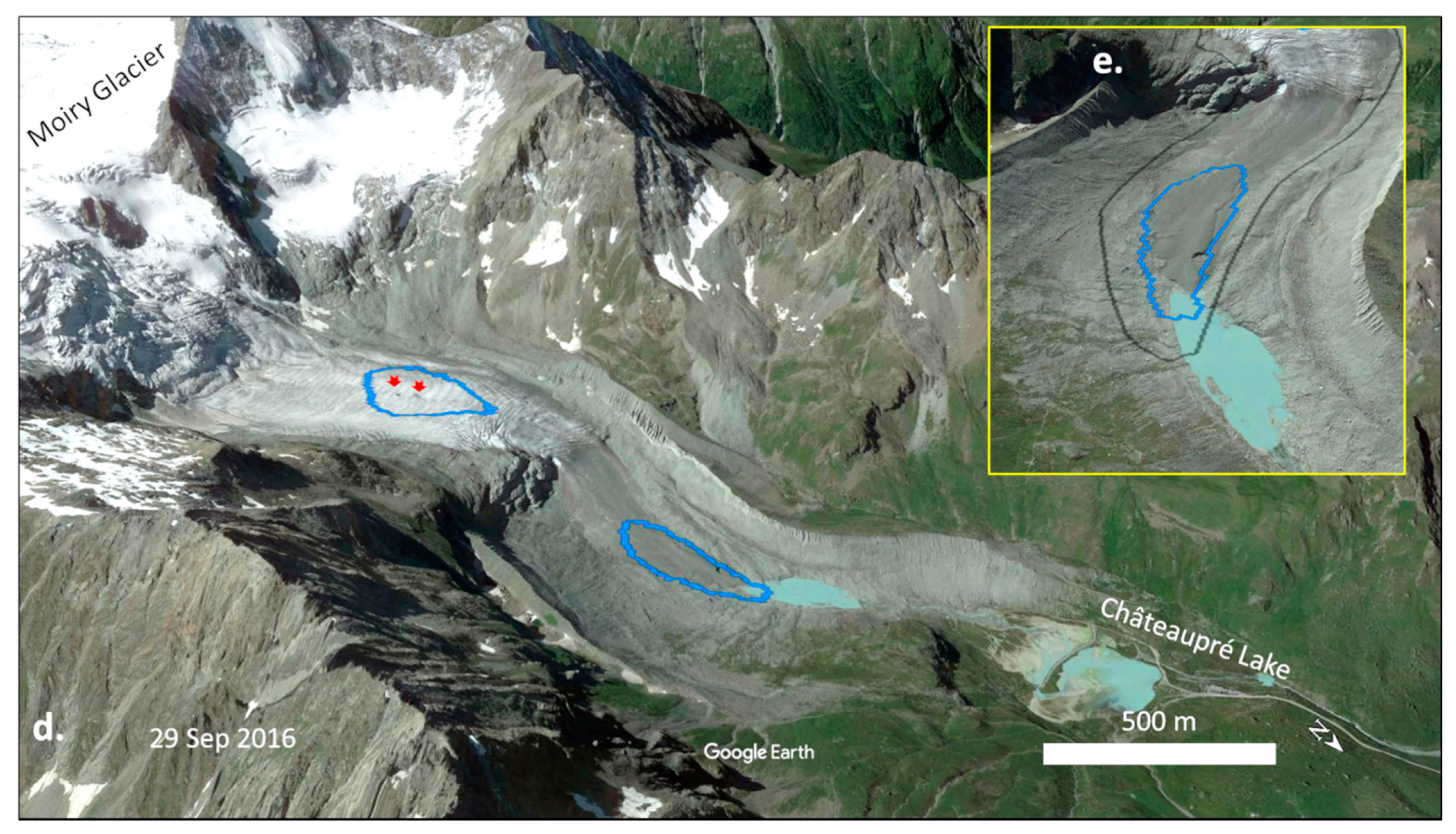
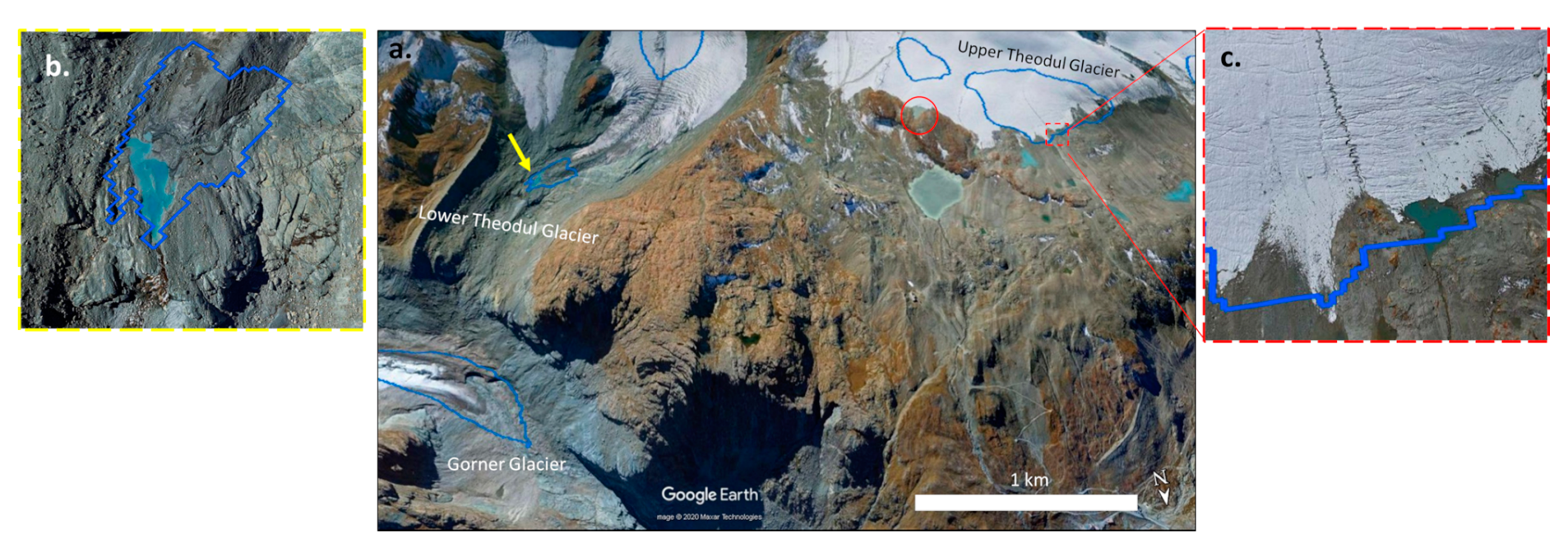
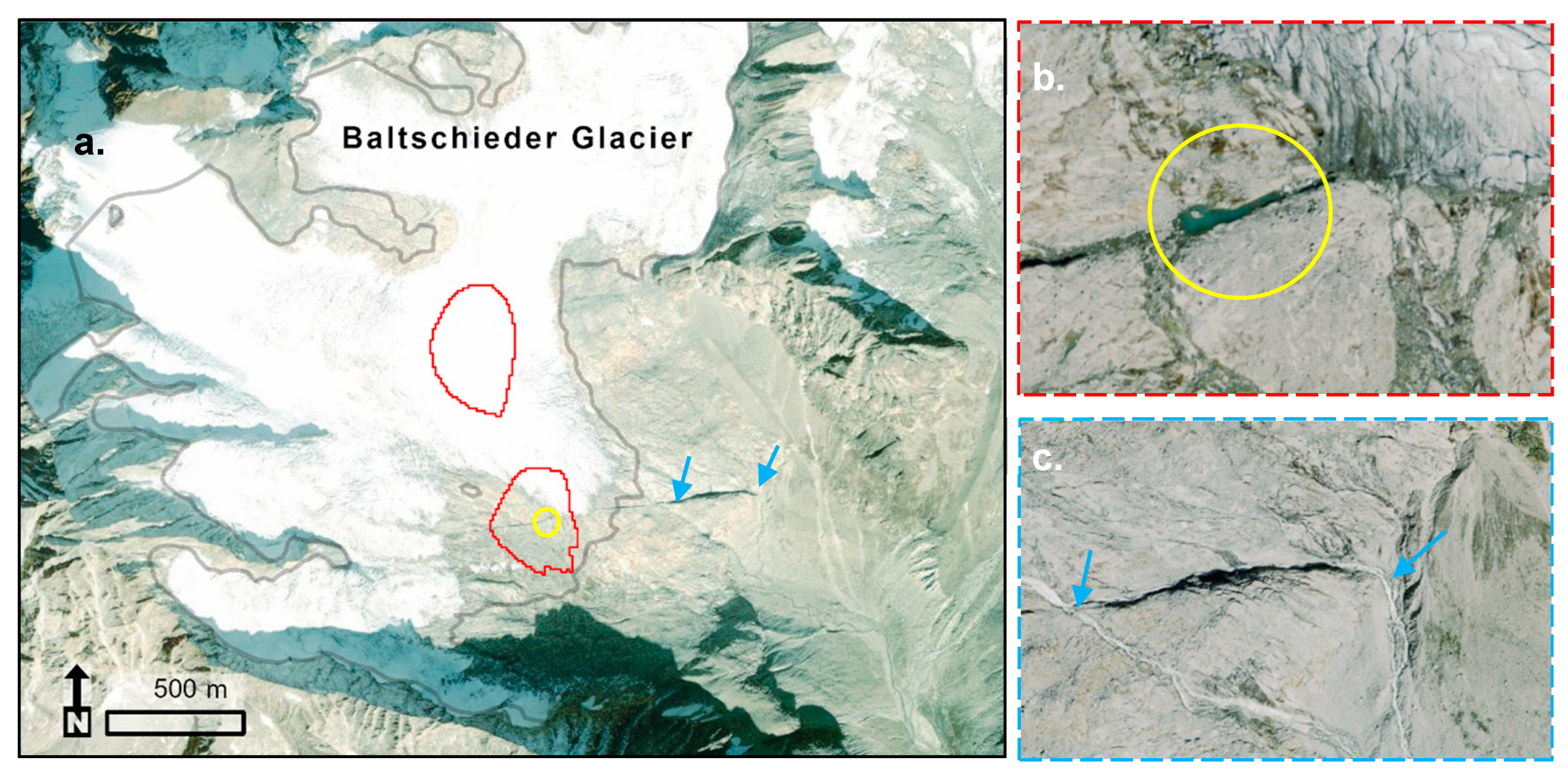
5.6. Visual Evaluation of Predicted Overdeepenings
6. Discussion
6.1. Model Performance in Ice Thickness Estimation
6.2. Overdeepenings and Future Lakes
6.3. Limitation of Methodology and Future Applications
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giaccone, E.; Colombo, N.; Acquaotta, F.; Paro, L.; Fratianni, S. Climate Variations in a High-Altitude Alpine Basin and Their Effects on a Glacial Environment (Italian Western Alps). Atmósfera 2015, 28, 117–128. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Global Warming of 1.5°C. An IPCC Special Report on the Impacts of Global Warming of 1.5°C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., Eds.; IPCC: Geneva, Switzerland, 2018; Available online: https://www.ipcc.ch/sr15/ (accessed on 24 July 2020).
- Zemp, M.; Haeberli, W.; Hoelzle, M.; Paul, F. Alpine Glaciers to Disappear within Decades? Geophys. Res. Lett. 2006, 33, L13504. [Google Scholar] [CrossRef]
- Zemp, M.; Frey, H.; Gärtner-Roer, I.; Nussbaumer, S.U.; Hoelzle, M.; Paul, F.; Haeberli, W.; Denzinger, F.; Ahlstrøm, A.P.; Anderson, B.; et al. Historically Unprecedented Global Glacier Decline in the Early 21st Century. J. Glaciol. 2015, 61, 745–762. [Google Scholar] [CrossRef]
- Beniston, M. Variations of Snow Depth and Duration in the Swiss Alps over the Last 50 Years: Links to Changes in Large-Scale Climatic Forcings. Clim. Chang. 1997, 36, 281–300. [Google Scholar] [CrossRef]
- Zekollari, H.; Huss, M.; Farinotti, D. Modelling the Future Evolution of Glaciers in the European Alps under the EURO-CORDEX RCM Ensemble. Cryosphere 2019, 13, 1125–1146. [Google Scholar] [CrossRef]
- Haeberli, W.; Buetler, M.; Huggel, C.; Friedli, T.L.; Schaub, Y.; Schleiss, A.J. New Lakes in Deglaciating High-Mountain Regions–Opportunities and Risks. Clim. Chang. 2016, 139, 201–214. [Google Scholar] [CrossRef]
- Watanabe, T.; Ives, J.D.; Hammond, J.E. Rapid Growth of a Glacial Lake in Khumbu Himal, Himalaya: Prospects for a Catastrophic Flood. Mt. Res. Dev. 1994, 14, 329–340. [Google Scholar] [CrossRef]
- Wang, X.; Siegert, F.; Zhou, A.; Franke, J. Glacier and Glacial Lake Changes and Their Relationship in the Context of Climate Change, Central Tibetan Plateau 1972–2010. Glob. Planet. Chang. 2013, 111, 246–257. [Google Scholar] [CrossRef]
- Vilímek, V.; Emmer, A.; Huggel, C.; Schaub, Y.; Würmli, S. Database of Glacial Lake Outburst Floods (GLOFs)–IPL Project No. 179. Landslides 2014, 11, 161–165. [Google Scholar] [CrossRef]
- Emmer, A. Glacier Retreat and Glacial Lake Outburst Floods (GLOFs). In Oxford Research Encyclopedia of Natural Hazard Science; Oxford University Press: New York, NY, USA, 2017; Available online: https://-oxfordre.com/natural-hazardscience/view/10.1093/acrefore/9780199389407.001.0001/acrefore-9780199389-407-e-275 (accessed on 16 October 2020).
- Kääb, A.; Huggel, C.; Fischer, L.; Guex, S.; Paul, F.; Roer, I.; Salzmann, N.; Schlaefli, S.; Schmutz, K.; Schneider, D.; et al. Remote Sensing of Glacier- and Permafrost-Related Hazards in High Mountains: An Overview. Nat. Hazards Earth Syst. Sci. 2005, 5, 527–554. [Google Scholar] [CrossRef]
- Clague, J.J.; Huggel, C.; Korup, O.; McGuire, B. Climate Change and Hazardous Processes in High Mountains. Asoc. Geológica Argent. 2012, 69, 328–338. [Google Scholar]
- Klimeš, J.; Novotný, J.; Novotná, I.; De Urries, B.J.; Vilímek, V.; Emmer, A.; Strozzi, T.; Kusák, M.; Rapre, A.C.; Hartvich, F.; et al. Landslides in Moraines as Triggers of Glacial Lake Outburst Floods: Example from Palcacocha Lake (Cordillera Blanca, Peru). Landslides 2016, 13, 1461–1477. [Google Scholar] [CrossRef]
- Haeberli, W.; Schaub, Y.; Huggel, C. Increasing Risks Related to Landslides from Degrading Permafrost into New Lakes in De-Glaciating Mountain Ranges. Geomorphology 2017, 293, 405–417. [Google Scholar] [CrossRef]
- Carrivick, J.L.; Tweed, F.S. A Global Assessment of the Societal Impacts of Glacier Outburst Floods. Glob. Planet. Chang. 2016, 144, 1–16. [Google Scholar] [CrossRef]
- Huggel, C.; Kääb, A.; Schneider, J. Climate and Geomorphic Risks in High-Mountain Environments: Glacier Hazards, Permafrost Hazards, and Glacier Lake Outburst Floods in Mountain Areas: Processes, Assessment, Prevention, Mitigation; Vienna, Austria, 10–13 November 2009. Eos Trans. Am. Geophys. Union 2010, 91, 103. [Google Scholar] [CrossRef]
- Sutherland, J.L.; Carrivick, J.L.; Shulmeister, J.; Quincey, D.J.; James, W.H.M. Ice-Contact Proglacial Lakes Associated with the Last Glacial Maximum across the Southern Alps, New Zealand. Quat. Sci. Rev. 2019, 213, 67–92. [Google Scholar] [CrossRef]
- Maanya, U.S.; Kulkarni, A.V.; Tiwari, A.; Bhar, E.D.; Srinivasan, J. Identification of Potential Glacial Lake Sites and Mapping Maximum Extent of Existing Glacier Lakes in Drang Drung and Samudra Tapu Glaciers, Indian Himalaya. Curr. Sci. 2016, 111, 553. [Google Scholar] [CrossRef]
- Farinotti, D.; Round, V.; Huss, M.; Compagno, L.; Zekollari, H. Large Hydropower and Water-Storage Potential in Future Glacier-Free Basins. Nature 2019, 575, 341–344. [Google Scholar] [CrossRef]
- Sam, L.; Bhardwaj, A.; Sinha, V.S.P.; Joshi, P.K.; Kumar, R. Use of Geospatial Tools to Prioritize Zones of Hydro-Energy Potential in Glaciated Himalayan Terrain. J. Indian Soc. Remote Sens. 2016, 44, 409–420. [Google Scholar] [CrossRef]
- Schaefli, B.; Manso, P.; Fischer, M.; Huss, M.; Farinotti, D. The Role of Glacier Retreat for Swiss Hydropower Production. Renew. Energy 2019, 132, 615–627. [Google Scholar] [CrossRef]
- Warren, C.R.; Kirkbride, M.P. Calving Speed and Climatic Sensitivity of New Zealand Lake-Calving Glaciers. Ann. Glaciol. 2003, 36, 173–178. [Google Scholar] [CrossRef]
- Cook, S.J.; Swift, D.A. Subglacial Basins: Their Origin and Importance in Glacial Systems and Landscapes. Earth-Sci. Rev. 2012, 115, 332–372. [Google Scholar] [CrossRef]
- Matthews, J.A. The Ecology of Recently-Deglaciated Terrain: A Geoecological Approach to Glacier Forelands; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Zhao, K.; Duan, Z.Y.; Peng, Z.G.; Guo, S.C.; Li, J.B.; He, S.P.; Zhao, X.Q. The Youngest Split in Sympatric Schizothoracine Fish (Cyprinidae) Is Shaped by Ecological Adaptations in a Tibetan Plateau Glacier Lake. Mol. Ecol. 2009, 18, 3616–3628. [Google Scholar] [CrossRef] [PubMed]
- Ryder, R.A. Ecological Heterogeneity between North-Temperate Reservoirs and Glacial Lake Systems Due to Differing Succession Rates and Cultural Uses. SIL Proc. 1922–2010 1978, 20, 1568–1574. [Google Scholar] [CrossRef]
- Stibal, M.; Bradley, J.A.; Edwards, A.; Hotaling, S.; Zawierucha, K.; Rosvold, J.; Lutz, S.; Cameron, K.A.; Mikucki, J.A.; Kohler, T.J.; et al. Glacial Ecosystems Are Essential to Understanding Biodiversity Responses to Glacier Retreat. Nat. Ecol. Evol. 2020, 4, 686–687. [Google Scholar] [CrossRef]
- Tolotti, M.; Cerasino, L.; Donati, C.; Pindo, M.; Rogora, M.; Seppi, R.; Albanese, D. Alpine Headwaters Emerging from Glaciers and Rock Glaciers Host Different Bacterial Communities: Ecological Implications for the Future. Sci. Total Environ. 2020, 717, 137101. [Google Scholar] [CrossRef]
- Gentili, R.; Baroni, C.; Panigada, C.; Rossini, M.; Tagliabue, G.; Armiraglio, S.; Citterio, S.; Carton, A.; Salvatore, M.C. Glacier Shrinkage and Slope Processes Create Habitat at High Elevation and Microrefugia across Treeline for Alpine Plants during Warm Stages. Catena 2020, 193, 104626. [Google Scholar] [CrossRef]
- Tiberti, R.; Buscaglia, F.; Callieri, C.; Rogora, M.; Tartari, G.; Sommaruga, R. Food Web Complexity of High Mountain Lakes Is Largely Affected by Glacial Retreat. Ecosystems 2019, 23, 1093–1106. [Google Scholar] [CrossRef]
- Čiamporová-Zaťovičová, Z.; Čiampor, F. Alpine Lakes and Ponds—A Promising Source of High Genetic Diversity in Metapopulations of Aquatic Insects. Inland Waters 2017, 7, 109–117. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Sam, L.; Martín-Torres, F.J.; Kumar, R. UAVs as Remote Sensing Platform in Glaciology: Present Applications and Future Prospects. Remote Sens. Environ. 2016, 175, 196–204. [Google Scholar] [CrossRef]
- Gaffey, C.; Bhardwaj, A. Applications of Unmanned Aerial Vehicles in Cryosphere: Latest Advances and Prospects. Remote Sens. 2020, 12, 948. [Google Scholar] [CrossRef]
- Hengl, T.; Reuter, H.I.; Institute for Environment and Sustainability (European Commission. Joint Research Centre) (Eds.) Geomorphometry: Concepts, Software, Applications, 1st ed.; Developments in Soil Science; Elsevier: Amsterdam, The Netherlands; Oxford, UK; Boston, MA, USA, 2009. [Google Scholar]
- Csatho, B. Remote Sensing of Glaciers: Techniques for Topographic, Spatial and Thematic Mapping of Glaciers, 1st ed.; Pellikka, P., Rees, W., Eds.; CRC Press: London, UK, 2010. [Google Scholar]
- Frey, H.; Paul, F. On the Suitability of the SRTM DEM and ASTER GDEM for the Compilation of Topographic Parameters in Glacier Inventories. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 480–490. [Google Scholar] [CrossRef]
- Bolch, T.; Kamp, U. Glacier Mapping in High Mountains Using DEMs, Landsat and ASTER Data. In Proceedings of the 8 th International Symposium on High Mountain Remote Sensing Cartography, La Paz, Bolivia, 21–27 March 2005; The University of Graz: Graz, Austria, 2006. [Google Scholar]
- Alifu, H.; Tateishi, R.; Johnson, B. A New Band Ratio Technique for Mapping Debris-Covered Glaciers Using Landsat Imagery and a Digital Elevation Model. Int. J. Remote Sens. 2015, 36, 2063–2075. [Google Scholar] [CrossRef]
- Smith, T.; Bookhagen, B.; Cannon, F. Improving Semi-Automated Glacier Mapping with a Multi-Method Approach: Applications in Central Asia. Cryosphere 2015, 9, 1747–1759. [Google Scholar] [CrossRef]
- Paul, F.; Winsvold, S.; Kääb, A.; Nagler, T.; Schwaizer, G. Glacier Remote Sensing Using Sentinel-2. Part II: Mapping Glacier Extents and Surface Facies, and Comparison to Landsat 8. Remote Sens. 2016, 8, 575. [Google Scholar] [CrossRef]
- Möri, A.; Wiederkehr, M. SwissALTI3D: A New Tool for Geological Mapping. Swiss Bull. Appl. Geol. 2013, 18, 61–69. [Google Scholar]
- Haeberli, W.; Hoelzle, M. Application of Inventory Data for Estimating Characteristics of and Regional Climate-Change Effects on Mountain Glaciers: A Pilot Study with the European Alps. Ann. Glaciol. 1995, 21, 206–212. [Google Scholar] [CrossRef]
- Linsbauer, A.; Paul, F.; Hoelzle, M.; Frey, H.; Haeberli, W. The Swiss Alps Without Glaciers—A GIS-Based Modelling Approach for Reconstruction of Glacier Beds. In Geomorphometry 2009 International Conference; Department of Geography, University of Zurich: Zurich, Switzerland, 2009. [Google Scholar]
- Haeberli, W.; Linsbauer, A.; Cochachin, A.; Salazar, C.; Fischer, U.H. On the Morphological Characteristics of Overdeepenings in High-Mountain Glacier Beds: Morphology of Glacier-Bed Overdeepenings. Earth Surf. Process. Landf. 2016, 41, 1980–1990. [Google Scholar] [CrossRef]
- Lang, H.; Musy, A. Hydrology in Mountainous Regions: Proceedings. 1: Hydrological Measurements: The Water Cycle; International Association of Hydrological Sciences, International Association of Hydrogeologists, Eds.; IAHS: Wallingford, UK, 1990. [Google Scholar]
- Bahr, D.B.; Meier, M.F.; Peckham, S.D. The Physical Basis of Glacier Volume-Area Scaling. J. Geophys. Res. Solid Earth 1997, 102, 20355–20362. [Google Scholar] [CrossRef]
- Nye, J.F. The Flow of a Glacier in a Channel of Rectangular, Elliptic or Parabolic Cross-Section. J. Glaciol. 1965, 5, 661–690. [Google Scholar] [CrossRef]
- Li, H.; Ng, F.; Li, Z.; Qin, D.; Cheng, G. An Extended “Perfect-Plasticity” Method for Estimating Ice Thickness along the Flow Line of Mountain Glaciers. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Linsbauer, A.; Paul, F.; Haeberli, W. Modeling Glacier Thickness Distribution and Bed Topography over Entire Mountain Ranges with GlabTop: Application of a Fast and Robust Approach. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Rasmussen, L.A. Bed Topography and Mass-Balance Distribution of Columbia Glacier, Alaska, U.S.A., Determined from Sequential Aerial Photography. J. Glaciol. 1988, 34, 208–216. [Google Scholar] [CrossRef][Green Version]
- Farinotti, D.; Huss, M.; Bauder, A.; Funk, M. An Estimate of the Glacier Ice Volume in the Swiss Alps. Glob. Planet. Chang. 2009, 68, 225–231. [Google Scholar] [CrossRef]
- Clarke, G.K.C.; Anslow, F.S.; Jarosch, A.H.; Radić, V.; Menounos, B.; Bolch, T.; Berthier, E. Ice Volume and Subglacial Topography for Western Canadian Glaciers from Mass Balance Fields, Thinning Rates, and a Bed Stress Model. J. Clim. 2013, 26, 4282–4303. [Google Scholar] [CrossRef]
- Huss, M. Extrapolating Glacier Mass Balance to the Mountain-Range Scale: The European Alps 1900–2100. Cryosphere 2012, 6, 713–727. [Google Scholar] [CrossRef]
- Clarke, G.K.C.; Berthier, E.; Schoof, C.G.; Jarosch, A.H. Neural Networks Applied to Estimating Subglacial Topography and Glacier Volume. J. Clim. 2009, 22, 2146–2160. [Google Scholar] [CrossRef]
- Brinkerhoff, D.J.; Aschwanden, A.; Truffer, M. Bayesian Inference of Subglacial Topography Using Mass Conservation. Front. Earth Sci. 2016, 4, 8. [Google Scholar] [CrossRef]
- James, W.H.M.; Carrivick, J.L. Automated Modelling of Spatially-Distributed Glacier Ice Thickness and Volume. Comput. Geosci. 2016, 92, 90–103. [Google Scholar] [CrossRef]
- Carrivick, J.L.; Davies, B.J.; James, W.H.M.; Quincey, D.J.; Glasser, N.F. Distributed Ice Thickness and Glacier Volume in Southern South America. Glob. Planet. Chang. 2016, 146, 122–132. [Google Scholar] [CrossRef]
- Carrivick, J.L.; Davies, B.J.; James, W.H.M.; McMillan, M.; Glasser, N.F. A Comparison of Modelled Ice Thickness and Volume across the entire Antarctic Peninsula Region. Geogr. Ann. Ser. Phys. Geogr. 2019, 101, 45–67. [Google Scholar] [CrossRef]
- James, W.H.M.; Carrivick, J.L.; Quincey, D.J.; Glasser, N.F. A Geomorphology Based Reconstruction of Ice Volume Distribution at the Last Glacial Maximum across the Southern Alps of New Zealand. Quat. Sci. Rev. 2019, 219, 20–35. [Google Scholar] [CrossRef]
- Frey, H.; Haeberli, W.; Linsbauer, A.; Huggel, C.; Paul, F. A Multi-Level Strategy for Anticipating Future Glacier Lake Formation and Associated Hazard Potentials. Nat. Hazards Earth Syst. Sci. 2010, 10, 339–352. [Google Scholar] [CrossRef]
- Magnin, F.; Haeberli, W.; Linsbauer, A.; Deline, P.; Ravanel, L. Estimating Glacier-Bed Overdeepenings as Possible Sites of Future Lakes in the de-Glaciating Mont Blanc Massif (Western European Alps). Geomorphology 2020, 350, 106913. [Google Scholar] [CrossRef]
- Frey, H.; Machguth, H.; Huss, M.; Huggel, C.; Bajracharya, S.; Bolch, T.; Kulkarni, A.; Linsbauer, A.; Salzmann, N.; Stoffel, M. Estimating the Volume of Glaciers in the Himalayan-Karakoram Region Using Different Methods. Cryosphere 2014, 8, 2313–2333. [Google Scholar] [CrossRef]
- Federal Statistical Office. Switzerland’s Population in 2018. Available online: https://www.swissstats.bfs.-admin.ch/collection/ch.admin.bfs.swissstat.en.n01 (accessed on 9 July 2020).
- Reynolds, K. The Swiss Alps, 1st ed.; World Mountain Ranges; Cicerone Press Limited: Kendal, UK, 2012. [Google Scholar]
- Tockner, K.; Uehlinger, U.; Robinson, C.T. Rivers of Europe, 1st ed.; Academic Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Federal Office of Topography, Swisstopo Online Shop. Available online: https://shop.swisstopo.admin-.ch/en/products/height_models/alti3D (accessed on 7 October 2019).
- Ayala, A.; Farinotti, D.; Stoffel, M.; Huss, M. Glaciers: Hydro-CH2018 Synthesis Report Chapters: “Future Changes in Hydrology”; ETH Zurich: Zurich, Switzerland; WSL: Birmensdorf, Switzerland; University of Fribourg: Fribourg, Switzerland; University of Geneva: Geneva, Switzerland, 2020. [Google Scholar]
- Etchevers, P. Impact of a Climate Change on the Rhône River Catchment Hydrology. J. Geophys. Res. 2002, 107, 4293. [Google Scholar] [CrossRef]
- Brandolini, F.; Reynard, E.; Pelfini, M. Multi-Temporal Mapping of the Upper Rhône Valley (Valais, Switzerland): Fluvial Landscape Changes at the End of the Little Ice Age (18th–19th Centuries). J. Maps 2020, 16, 212–221. [Google Scholar] [CrossRef]
- Fischer, M.; Huss, M.; Hoelzle, M. Surface Elevation and Mass Changes of All Swiss Glaciers 1980–2010. Cryosphere 2015, 9, 525–540. [Google Scholar] [CrossRef]
- Federal Office of Topography, Swisstopo OnlineShop. Available online: https://shop.swisstopo.admin.ch-/en/products/height_models/dhm25 (accessed on 28 March 2020).
- Paul, F.; Kääb, A.; Maisch, M.; Kellenberger, T.; Haeberli, W. The New Remote-Sensing-Derived Swiss Glacier Inventory: I. Methods. Ann. Glaciol. 2002, 34, 355–361. [Google Scholar] [CrossRef]
- Fischer, M.; Huss, M.; Barboux, C.; Hoelzle, M. The New Swiss Glacier Inventory SGI2010: Relevance of Using High-Resolution Source Data in Areas Dominated by Very Small Glaciers. Arct. Antarct. Alp. Res. 2014, 46, 933–945. [Google Scholar] [CrossRef]
- Swiss Glacier Ice Thickness: Glacier Monitoring Switzerland (GLAMOS). 2018. Available online: https://doi.glamos.ch/data/icethickness/icethickness_2015_r2018.html (accessed on 16 October 2020).
- Maisch, M.; Haeberli, W. Interpretation Geometrischer Parameter von Spätglazialgletschern Im Gebiet Mittelbünden, Schweizer Alpen. In Beiträge zur Quartärforschung in der Schweiz; Gamper, M., Ed.; Physische Geographie 1; Geographisches Institut der Universität: Zürich, Schweiz, 1982; pp. 111–126. [Google Scholar]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers; Elsevier Science: Burlington, ON, Canada, 2010. [Google Scholar]
- Driedger, C.L.; Kennard, P.M. Glacier Volume Estimation on Cascade Volcanoes: An Analysis and Comparison with Other Methods. Ann. Glaciol. 1986, 8, 59–64. [Google Scholar] [CrossRef]
- Hutchinson, M.F. A New Procedure for Gridding Elevation and Stream Line Data with Automatic Removal of Spurious Pits. J. Hydrol. 1989, 106, 211–232. [Google Scholar] [CrossRef]
- Balstrøm, T.; Crawford, D. Arc-Malstrøm: A 1D Hydrologic Screening Method for Stormwater Assessments Based on Geometric Networks. Comput. Geosci. 2018, 116, 64–73. [Google Scholar] [CrossRef]
- Colonia, D.; Torres, J.; Haeberli, W.; Schauwecker, S.; Braendle, E.; Giraldez, C.; Cochachin, A. Compiling an Inventory of Glacier-Bed Overdeepenings and Potential New Lakes in De-Glaciating Areas of the Peruvian Andes: Approach, First Results, and Perspectives for Adaptation to Climate Change. Water 2017, 9, 336. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Bauder, A.; Funk, M.; Truffer, M. A Method to Estimate the Ice Volume and Ice-Thickness Distribution of Alpine Glaciers. J. Glaciol. 2009, 55, 422–430. [Google Scholar] [CrossRef]
- Huss, M.; Farinotti, D. Distributed Ice Thickness and Volume of All Glaciers around the Globe. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Viani, C.; Machguth, H.; Huggel, C.; Godio, A.; Franco, D.; Perotti, L.; Giardino, M. Potential Future Lakes from Continued Glacier Shrinkage in the Aosta Valley Region (Western Alps, Italy). Geomorphology 2020, 355, 107068. [Google Scholar] [CrossRef]
- Linsbauer, A.; Frey, H.; Haeberli, W.; Machguth, H.; Azam, M.F.; Allen, S. Modelling Glacier-Bed Overdeepenings and Possible Future Lakes for the Glaciers in the Himalaya—Karakoram Region. Ann. Glaciol. 2016, 57, 119–130. [Google Scholar] [CrossRef]
- Rashid, I.; Majeed, U. Recent Recession and Potential Future Lake Formation on Drang Drung Glacier, Zanskar Himalaya, as Assessed with Earth Observation Data and Glacier Modelling. Environ. Earth Sci. 2018, 77, 429. [Google Scholar] [CrossRef]
- Zhang, G.; Bolch, T.; Allen, S.; Linsbauer, A.; Chen, W.; Wang, W. Glacial Lake Evolution and Glacier–Lake Interactions in the Poiqu River Basin, Central Himalaya, 1964–2017. J. Glaciol. 2019, 65, 347–365. [Google Scholar] [CrossRef]
- Drenkhan, F.; Guardamino, L.; Huggel, C.; Frey, H. Current and Future Glacier and Lake Assessment in the Deglaciating Vilcanota-Urubamba Basin, Peruvian Andes. Glob. Planet. Chang. 2018, 169, 105–118. [Google Scholar] [CrossRef]
- Small, E.E. Hypsometric Forcing of Stagnant Ice Margins: Pleistocene Valley Glaciers, San Juan Mountains, Colorado. Geomorphology 1995, 14, 109–121. [Google Scholar] [CrossRef]
- Vacco, D.A.; Alley, R.B.; Pollard, D.; Reusch, D.B. Numerical Modeling of Valley Glacier Stagnation as a Paleoclimatic Indicator. Quat. Res. 2010, 73, 403–409. [Google Scholar] [CrossRef]
- Bohorquez, P.; Darby, S.E. The Use of One- and Two-Dimensional Hydraulic Modelling to Reconstruct a Glacial Outburst Flood in a Steep Alpine Valley. J. Hydrol. 2008, 361, 240–261. [Google Scholar] [CrossRef]
- Grande Dixence—Technical Documentation; Grande Dixence SA: Sion, Switzerland, 2015; Available online: http://www.grande-dixence.ch/docs/default-source/documentation/brochure-technique/Grande-Dixence-technical-documentation-2.pdf?sfvrsn=7 (accessed on 16 October 2020).
- Farinotti, D.; Brinkerhoff, D.J.; Clarke, G.K.C.; Fürst, J.J.; Frey, H.; Gantayat, P.; Gillet-Chaulet, F.; Girard, C.; Huss, M.; Leclercq, P.W.; et al. How Accurate Are Estimates of Glacier Ice Thickness? Results from ITMIX, the Ice Thickness Models Intercomparison EXperiment. Cryosphere 2017, 11, 949–970. [Google Scholar] [CrossRef]
- Fischer, U.H.; Haeberli, W. Glacial Erosion Modelling: Results of a Workshop Held in Unterägeri, Switzerland; Arbeitsbericht NAB 10-34; Nagra (National Cooperative for the Disposal of Radioactive Waste): Unterägeri, Switzerland, 2010. [Google Scholar]
- Piccini, L.; Romeo, A.; Badino, G. Moulins and Marginal Contact Caves in the Gornergletscher, Switzerland. Nimbus 2000, 23–24, 94–99. [Google Scholar]
- Iken, A.; Fabri, K.; Funk, M. Water Storage and Subglacial Drainage Conditions Inferred from Borehole Measurements on Gornergletscher, Valais, Switzerland. J. Glaciol. 1996, 42, 233–248. [Google Scholar] [CrossRef][Green Version]
- Hock, R.; Iken, L.; Wangler, A. Tracer Experiments and Borehole Observations in the Over-Deepening of Aletschgletscher, Switzerland. Ann. Glaciol. 1999, 28, 253–260. [Google Scholar] [CrossRef]
- Hantz, D.; Lliboutry, L. Waterways, Ice Permeability at Depth, and Water Pressures at Glacier D’Argentière, French Alps. J. Glaciol. 1983, 29, 227–239. [Google Scholar] [CrossRef][Green Version]
- Alley, R.B.; Lawson, D.E.; Evenson, E.B.; Larson, G.J. Sediment, Glaciohydraulic Supercooling, and Fast Glacier Flow. Ann. Glaciol. 2003, 36, 135–141. [Google Scholar] [CrossRef]
- Cook, S.J.; Quincey, D.J. Estimating the Volume of Alpine Glacial Lakes. Earth Surf. Dyn. 2015, 3, 559–575. [Google Scholar] [CrossRef]
- Magrani, F.; Valla, P.G.; Gribenski, N.; Serra, E. Glacial Overdeepenings in the Swiss Alps and Foreland: Spatial Distribution and Morphometrics. Quat. Sci. Rev. 2020, 243, 106483. [Google Scholar] [CrossRef]
- Box, J.E.; Fettweis, X.; Stroeve, J.C.; Tedesco, M.; Hall, D.K.; Steffen, K. Greenland Ice Sheet Albedo Feedback: Thermodynamics and Atmospheric Drivers. Cryosphere Discuss. 2012, 6, 593–634. [Google Scholar] [CrossRef]
- Tedesco, M.; Fettweis, X.; Van den Broeke, M.R.; Van de Wal, R.S.W.; Smeets, C.J.P.P.; Van de Berg, W.J.; Serreze, M.C.; Box, J.E. The Role of Albedo and Accumulation in the 2010 Melting Record in Greenland. Environ. Res. Lett. 2011, 6, 014005. [Google Scholar] [CrossRef]
- Naegeli, K.; Huss, M.; Hoelzle, M. Change Detection of Bare-Ice Albedo in the Swiss Alps. Cryosphere 2019, 13, 397–412. [Google Scholar] [CrossRef]
- Naegeli, K.; Huss, M. Sensitivity of Mountain Glacier Mass Balance to Changes in Bare-Ice Albedo. Ann. Glaciol. 2017, 58 Pt 2, 119–129. [Google Scholar] [CrossRef]
- Heckmann, T.; Morche, D. Geomorphology of Proglacial Systems: Landform and Sediment Dynamics in Recently Deglaciated Alpine Landscapes; Geography of the Physical Environment; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Rutishauser, A.; Maurer, H.; Bauder, A. Helicopter-Borne Ground-Penetrating Radar Investigations on Temperate Alpine Glaciers: A Comparison of Different Systems and Their Abilities for Bedrock Mapping. Geophysics 2016, 81, WA119–WA129. [Google Scholar] [CrossRef]
- Gärtner-Roer, I.; Naegeli, K.; Huss, M.; Knecht, T.; Machguth, H.; Zemp, M. A Database of Worldwide Glacier Thickness Observations. Glob. Planet. Chang. 2014, 122, 330–344. [Google Scholar] [CrossRef]
- GlaThiDa Consortium. Glacier Thickness Database (GlaThiDa) 3.0.1; World Glacier Monitoring Service: Zurich, Switzerland, 2019; Available online: https://www.gtn-g.ch/data_catalogue_glathida/ (accessed on 16 October 2020).
- Michel, L.; Picasso, M.; Farinotti, D.; Bauder, A.; Funk, M.; Blatter, H. Estimating the Ice Thickness of Mountain Glaciers with an Inverse Approach Using Surface Topography and Mass-Balance. Inverse Probl. 2013, 29, 035002. [Google Scholar] [CrossRef]
- Mcnabb, R.W.; Hock, R.; O’Neel, S.; Rasmussen, L.A.; Ahn, Y.; Braun, M.; Conway, H.; Herreid, S.; Joughin, I.; Pfeffer, W.T.; et al. Using Surface Velocities to Calculate Ice Thickness and Bed Topography: A Case Study at Columbia Glacier, Alaska, USA. J. Glaciol. 2012, 58, 1151–1164. [Google Scholar] [CrossRef]







| Attributes | DEMs | |
|---|---|---|
| DHM25 Level 2 | swissALTI3D | |
| Resolution | 25 m | 10 m |
| Date of acquisition | 1996–2000/2001 | 2015–2016–2017 |
| Vertical accuracy | 1 m–3 m | 0.1 m–3 m |
| Data source | Swisstopo [72] | Swisstopo [67] |
| Glacier outlines (SGIs) | ||
| SGI2000 | SGI2010 | |
| Data source | Landsat TM4-5 | Orthophotos |
| Date of acquisition | 1998–1999 | 2008–2011 |
| Area | >5 km2 | All |
| Corresponding DEM | DHM25 L2 | swissALTI3D |
| Reference | Paul et al. [73] | Fischer et al. [74] |
| Criterion | Low | Very Low | Medium | High | Very High |
|---|---|---|---|---|---|
| Slope | ≥20° (>20%) | 15°–20° (>50%) | 10°–15° (>50%) | 5°–10° (>50%) | <5° (>50%) |
| Break in slope | ≤5° (>20%) | 5°–10° (> 50%) | 10°–15° (>50%) | 15°–20° (>50%) | >20° (>50%) |
| Bedrock/Glacier width change | Absent | Present | |||
| No crevasse→ heavy crevasse | Absent | Present | |||
| Ice Thickness (m) | Area (km2) | % | Volume (km3) | % |
|---|---|---|---|---|
| 0–50 | 354.20 | 62.20 | 7.70 ± 5.31 | 20.70 |
| 50–100 | 94.50 | 16.60 | 6.80 ± 1.40 | 18.20 |
| 100–200 | 81.30 | 14.30 | 11.32 ± 2.21 | 30.40 |
| >200 | 37.80 | 6.50 | 11.35 ± 3.33 | 30.50 |
| Total | 577 | 100 | 37.17 ± 12.26 | 100 |
| Area (km2) | ∑Area (km2) | α (°)mean | hmax(m) | hmean(m) |
| <0.01 | 0.98 | 39 | 15 | 13 |
| 0.01–1 | 85 | 37 | 43 | 34 |
| 1–3 | 85 | 26 | 311 | 35 |
| 3–10 | 156 | 21 | 333 | 56 |
| >10 | 241 | 20 | 578 | 94 |
| Likelihood | No. Potential Lakes | Area (km2) | Volume (km3) | Depthmean (m) |
|---|---|---|---|---|
| Very low | 11 | 5.37 | 0.028 | 17.10 |
| Low | 16 | 69.94 | 0.029 | 12.96 |
| Medium | 47 | 325.84 | 0.187 | 17.00 |
| High | 49 | 470.87 | 0.353 | 18.97 |
| Very high | 51 | 401.87 | 0.207 | 17.54 |
| Glacier * | Area (km2) | τb (kPa) | α (°) | Aspect | hmax (m) | hmean (m) | ||
|---|---|---|---|---|---|---|---|---|
| VOLTA | ITEM | GlabTop (IDW/TTR) | ||||||
| Aletsch (ALE) | 82.15 | 185.04 | 14.60 | SE | 584.13 | 133 | 187 | 140/160 |
| Gorner (GOR) | 55.80 | 172.19 | 20.46 | NW | 468.30 | 72 | 106 | 87/96 |
| Corbassière (COR) | 16.70 | 155.54 | 19.40 | NW | 290.70 | 80 | 92 | 97/110 |
| Rhône (RHO) | 15.76 | 153.81 | 15.19 | SW | 370.55 | 104 | 132 | 99/112 |
| Zinal (ZIN) | 14.02 | 153.49 | 24.00 | NE | 219.90 | 50 | 66 | 56/64 |
| Allalin (ALL) | 9.27 | 147.42 | 18.89 | NE | 260.58 | 50 | 91 | 62/74 |
| Mont Miné (MMN) | 8.98 | 147.31 | 15.90 | W | 241.27 | 74 | 76 | 79/88 |
| Lang (LNG) | 9.36 | 145.51 | 21.64 | S | 214.47 | 52 | 60 | 67/71 |
| Mont Durand (MDR) | 5.94 | 140.65 | 20.34 | E | 224.67 | 72 | 59 | 67/73 |
| Trient (TRN) | 5.99 | 140.11 | 17.74 | NW | 232.20 | 80 | 67 | 76/86 |
| Giétro (GIE) | 5.42 | 138.41 | 14.50 | NW | 270.29 | 104 | 88 | 99/104 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharehchahi, S.; James, W.H.M.; Bhardwaj, A.; Jensen, J.L.R.; Sam, L.; Ballinger, T.J.; Butler, D.R. Glacier Ice Thickness Estimation and Future Lake Formation in Swiss Southwestern Alps—The Upper Rhône Catchment: A VOLTA Application. Remote Sens. 2020, 12, 3443. https://doi.org/10.3390/rs12203443
Gharehchahi S, James WHM, Bhardwaj A, Jensen JLR, Sam L, Ballinger TJ, Butler DR. Glacier Ice Thickness Estimation and Future Lake Formation in Swiss Southwestern Alps—The Upper Rhône Catchment: A VOLTA Application. Remote Sensing. 2020; 12(20):3443. https://doi.org/10.3390/rs12203443
Chicago/Turabian StyleGharehchahi, Saeideh, William H. M. James, Anshuman Bhardwaj, Jennifer L. R. Jensen, Lydia Sam, Thomas J. Ballinger, and David R. Butler. 2020. "Glacier Ice Thickness Estimation and Future Lake Formation in Swiss Southwestern Alps—The Upper Rhône Catchment: A VOLTA Application" Remote Sensing 12, no. 20: 3443. https://doi.org/10.3390/rs12203443
APA StyleGharehchahi, S., James, W. H. M., Bhardwaj, A., Jensen, J. L. R., Sam, L., Ballinger, T. J., & Butler, D. R. (2020). Glacier Ice Thickness Estimation and Future Lake Formation in Swiss Southwestern Alps—The Upper Rhône Catchment: A VOLTA Application. Remote Sensing, 12(20), 3443. https://doi.org/10.3390/rs12203443











