Accuracy Assessment and Correction of SRTM DEM Using ICESat/GLAS Data under Data Coregistration
Abstract
1. Introduction
2. Materials
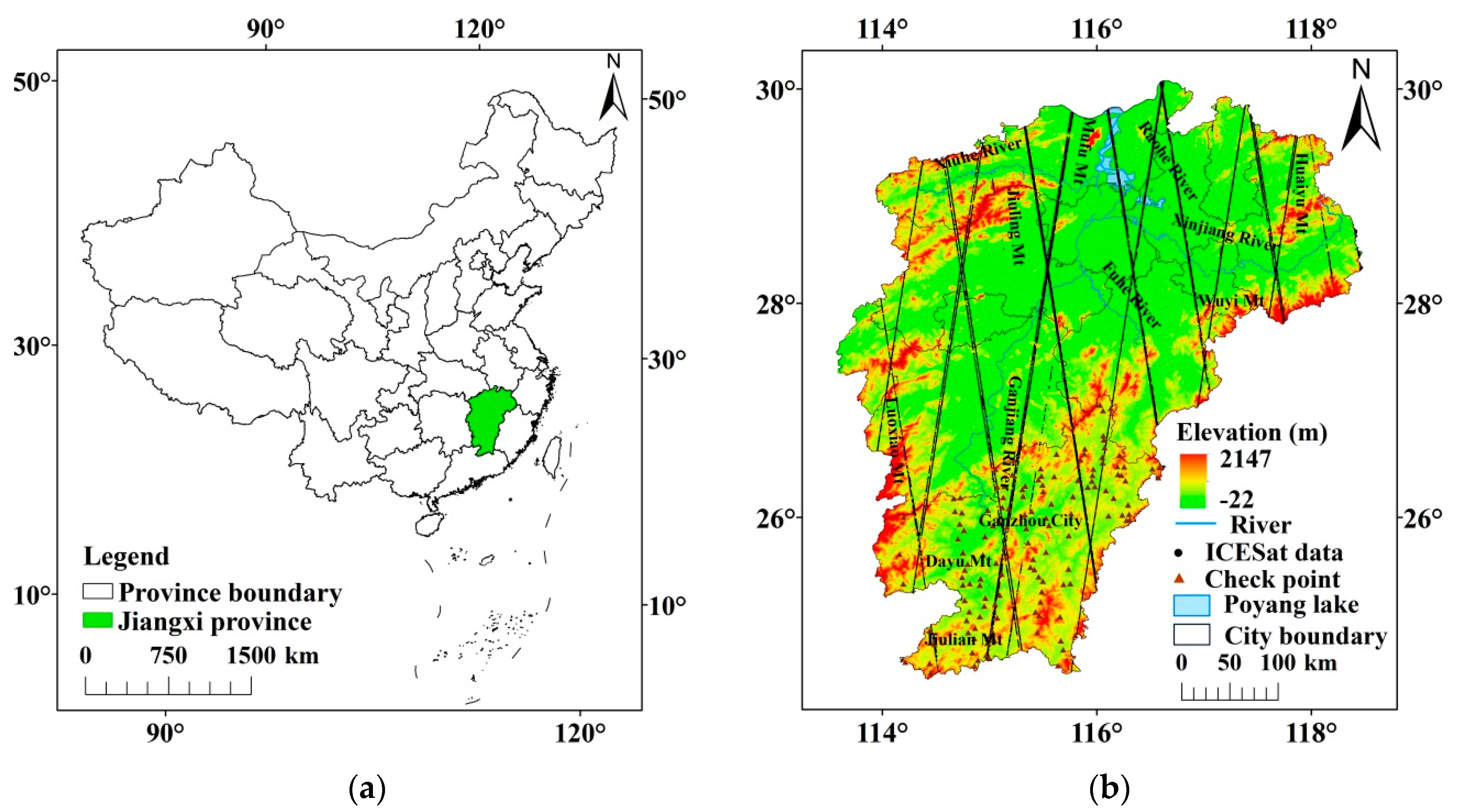
2.1. Study Area
2.2. Shuttle Radar Topography Mission (SRTM) Digital Elevation Model (DEM)
2.3. Geoscience Laser Altimeter System Onboard the Ice, Cloud, and Land Elevation Satellite (ICESat/GLAS) Data
2.4. Check Points
2.5. Terrain Factors and Land Use
3. Methods
3.1. Processing of ICESat/GLAS Data
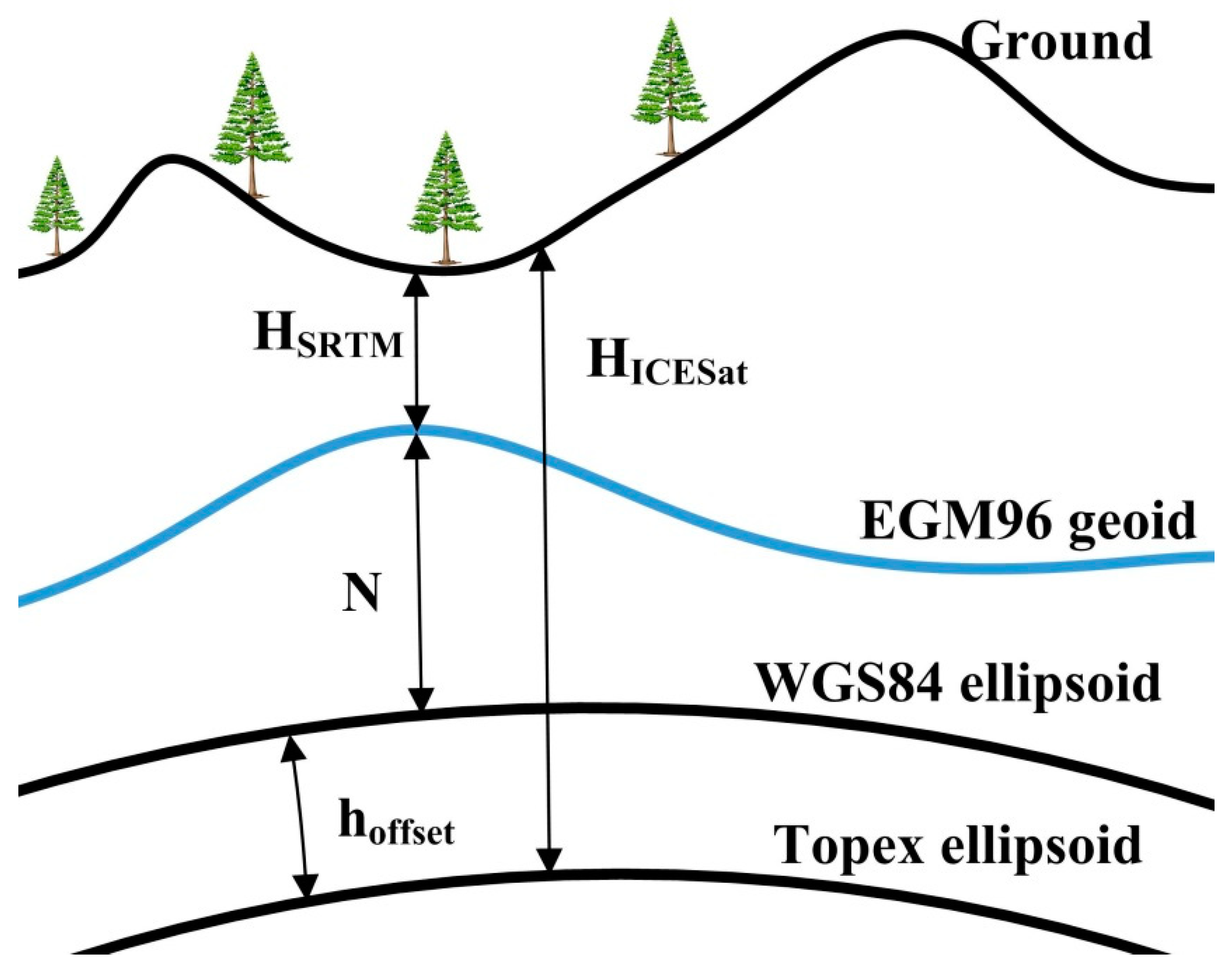
3.2. Coregistration of 3-Arc-Second Shuttle Radar Topography Mission (SRTM3) DEM and ICESat/GLAS Data
3.3. SRTM3 DEM Correction
3.3.1. Multiple Linear Regression (MLR)
3.3.2. Back Propagation Neural Network (BPNN)
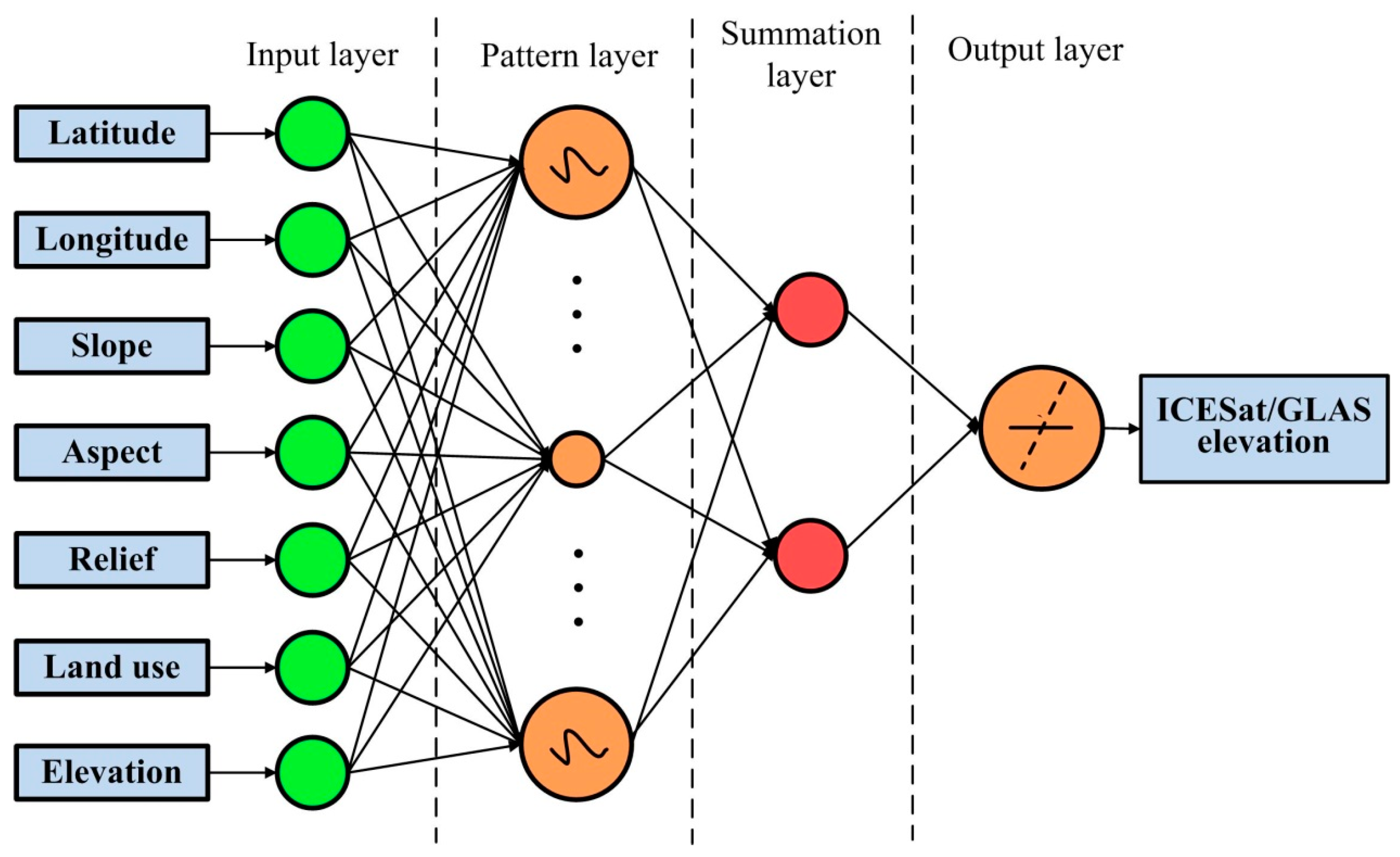
3.3.3. Generalized Regression Neural Network (GRNN)
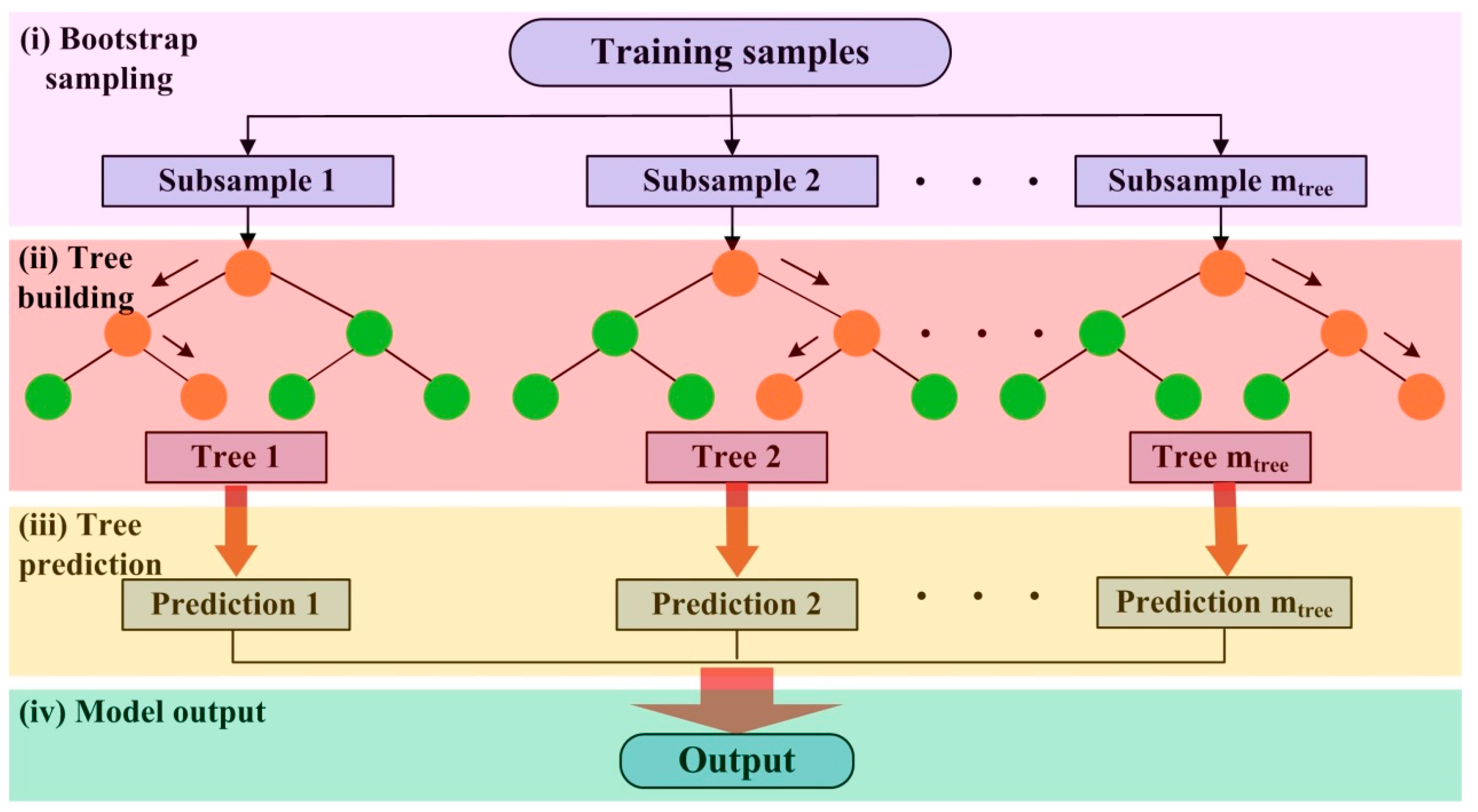
3.3.4. Random Forest (RF)
3.4. Accuracy Measures
4. Results and Discussion
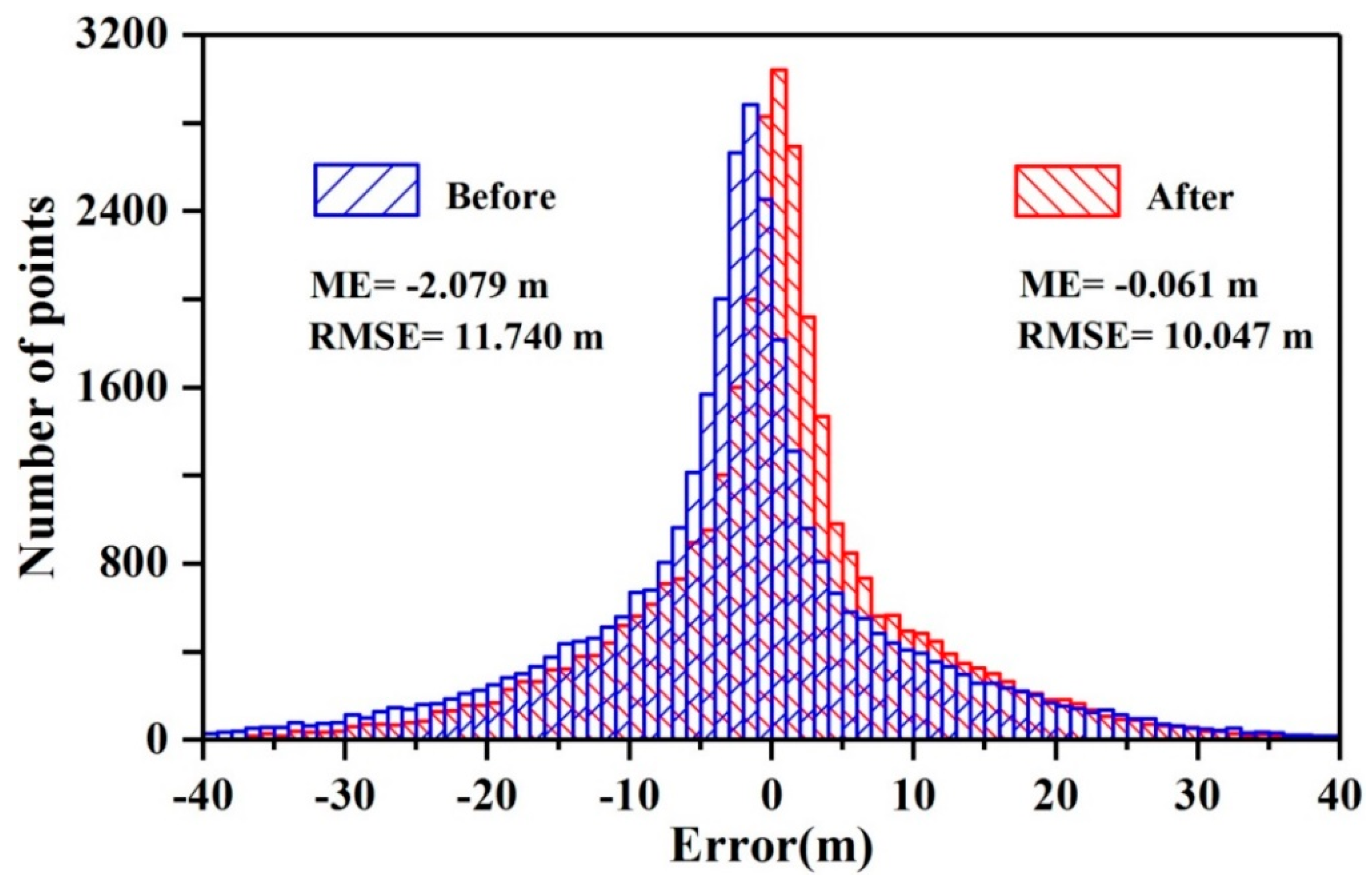
4.1. Overall Accuracy
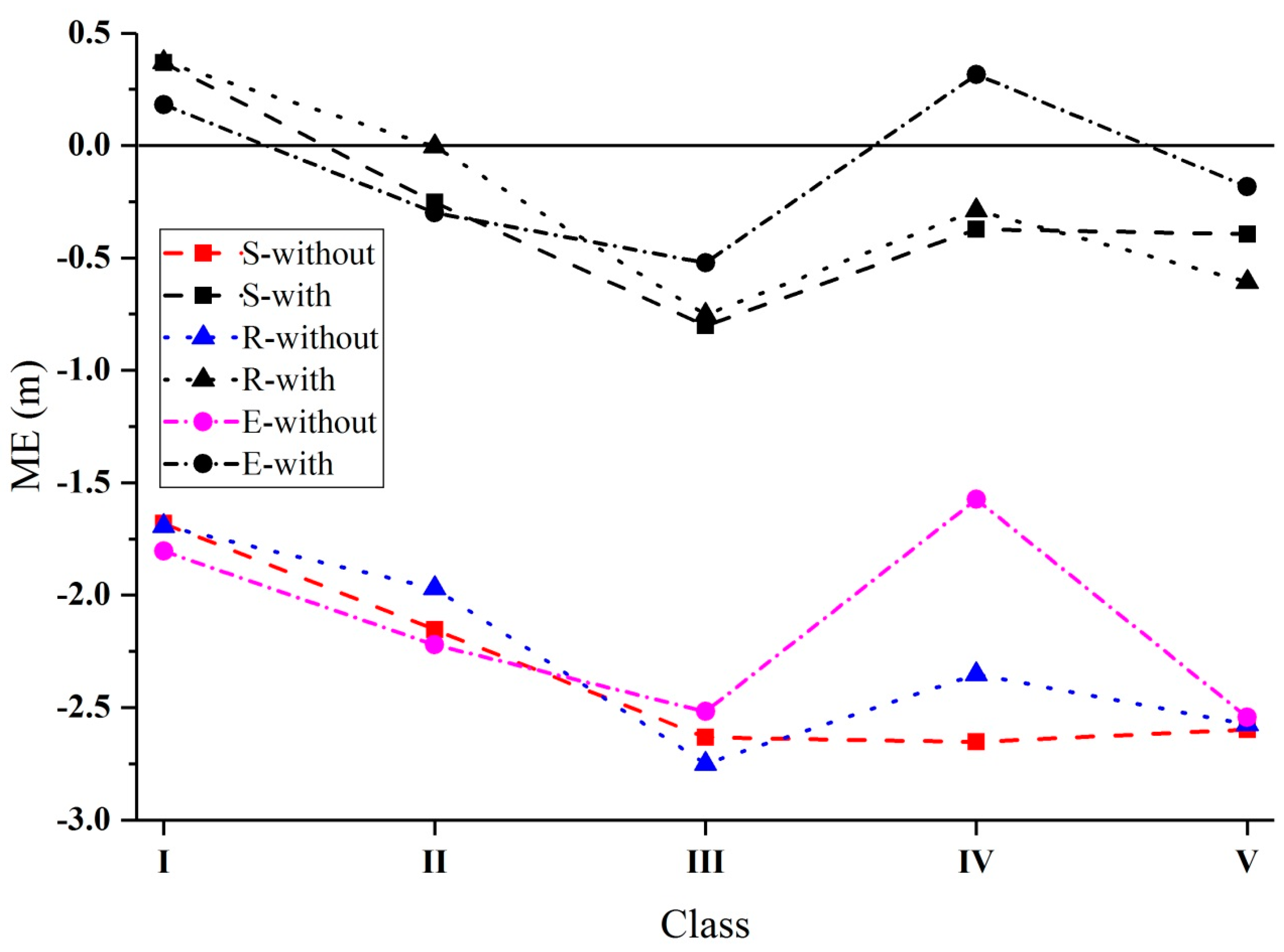
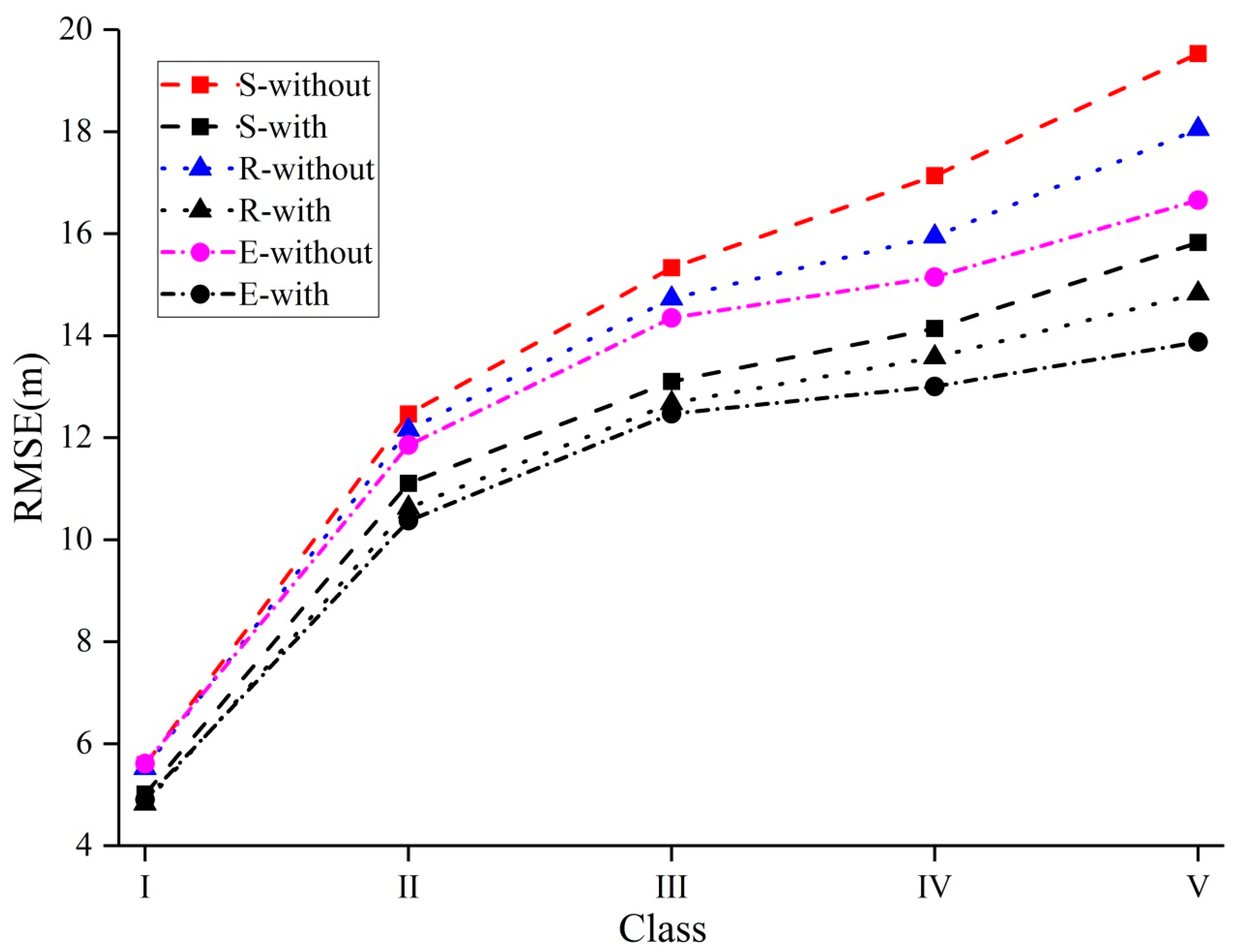
4.2. Effect of Terrain Factors and Land Use on SRTM3 DEM Errors Relative to ICESat/GLAS Data
4.2.1. Terrain Factors
4.2.2. Land Use
4.3. Model Performance Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shi, W.; Deng, S.; Xu, W. Extraction of multi-scale landslide morphological features based on local Gi* using airborne LiDAR-derived DEM. Geomorphology 2018, 303, 229–242. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Wang, T.; Isenburg, M.; Khoshelham, K. Effect of slope on treetop detection using a LiDAR Canopy Height Model. ISPRS J. Photogramm. Remote Sens. 2015, 104, 44–52. [Google Scholar] [CrossRef]
- Yamazaki, D.; Baugh, C.A.; Bates, P.D.; Kanae, S.; Alsdorf, D.E.; Oki, T. Adjustment of a spaceborne DEM for use in floodplain hydrodynamic modeling. J. Hydrol. 2012, 436–437, 81–91. [Google Scholar] [CrossRef]
- Razak, K.A.; Santangelo, M.; Van Westen, C.J.; Straatsma, M.W.; de Jong, S.M. Generating an optimal DTM from airborne laser scanning data for landslide mapping in a tropical forest environment. Geomorphology 2013, 190, 112–125. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y. A fast global interpolation method for digital terrain model generation from large LiDAR-derived data. Remote Sens. 2019, 11, 1324. [Google Scholar] [CrossRef]
- Wilson, J.P. Digital terrain modeling. Geomorphology 2012, 137, 107–121. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Shortridge, A.; Messina, J. Spatial structure and landscape associations of SRTM error. Remote Sens. Environ. 2011, 115, 1576–1587. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q. A practical method for SRTM DEM correction over vegetated mountain areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 216–228. [Google Scholar] [CrossRef]
- Hancock, G.R.; Martinez, C.; Evans, K.G.; Moliere, D.R. A comparison of SRTM and high-resolution digital elevation models and their use in catchment geomorphology and hydrology: Australian examples. Earth Surf. Process. Landf. 2006, 31, 1394–1412. [Google Scholar] [CrossRef]
- Sharma, A.; Tiwari, K.N. A comparative appraisal of hydrological behavior of SRTM DEM at catchment level. J. Hydrol. 2014, 519, 1394–1404. [Google Scholar] [CrossRef]
- Brock, J.; Schratz, P.; Petschko, H.; Muenchow, J.; Micu, M.; Brenning, A. The performance of landslide susceptibility models critically depends on the quality of digital elevations models. Geomat. Nat. Hazards Risk 2020, 11, 1075–1092. [Google Scholar] [CrossRef]
- Suwandana, E.; Kawamura, K.; Sakuno, Y.; Kustiyanto, E.; Raharjo, B. Evaluation of ASTER GDEM2 in Comparison with GDEM1, SRTM DEM and Topographic-Map-Derived DEM Using Inundation Area Analysis and RTK-dGPS Data. Remote Sens. 2012, 4, 2419–2431. [Google Scholar] [CrossRef]
- Mukherjee, S.; Joshi, P.K.; Mukherjee, S.; Ghosh, A.; Garg, R.D.; Mukhopadhyay, A. Evaluation of vertical accuracy of open source Digital Elevation Model (DEM). Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 205–217. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, Q.; Wang, C. SRTM error distribution and its associations with landscapes across China. Photogramm. Eng. Remote Sens. 2016, 82, 135–148. [Google Scholar] [CrossRef]
- Athmania, D.; Achour, H. External Validation of the ASTER GDEM2, GMTED2010 and CGIAR-CSI- SRTM v4.1 Free Access Digital Elevation Models (DEMs) in Tunisia and Algeria. Remote Sens. 2014, 6, 4600–4620. [Google Scholar] [CrossRef]
- Li, P.; Shi, C.; Li, Z.; Muller, J.-P.; Drummond, J.; Li, X.; Li, T.; Li, Y.; Liu, J. Evaluation of ASTER GDEM using GPS benchmarks and SRTM in China. Int. J. Remote Sens. 2013, 34, 1744–1771. [Google Scholar] [CrossRef]
- Yap, L.; Kandé, L.H.; Nouayou, R.; Kamguia, J.; Ngouh, N.A.; Makuate, M.B. Vertical accuracy evaluation of freely available latest high-resolution (30 m) global digital elevation models over Cameroon (Central Africa) with GPS/leveling ground control points. Int. J. Digit. Earth 2019, 12, 500–524. [Google Scholar] [CrossRef]
- Varga, M.; Bašić, T. Accuracy validation and comparison of global digital elevation models over Croatia. Int. J. Remote Sens. 2015, 36, 170–189. [Google Scholar] [CrossRef]
- Li, Y.Y.; Xu, C.J.; Chen, C.F.; Yin, H.; Yi, L.; He, X. Adaptive Denoising Approach for High-Rate GNSS Seismic Waveform Preservation: Application to the 2010 EI Mayor-Cucapah Earthquake and 2012 Brawley Seismic Swarm. IEEE Access 2019, 7, 173166–173184. [Google Scholar] [CrossRef]
- Satgé, F.; Bonnet, M.P.; Timouk, F.; Calmant, S.; Pillco, R.; Molina, J.; Lavado-Casimiro, W.; Arsen, A.; Crétaux, J.F.; Garnier, J. Accuracy assessment of SRTM v4 and ASTER GDEM v2 over the Altiplano watershed using ICESat/GLAS data. Int. J. Remote Sens. 2015, 36, 465–488. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, L.; Cheng, W.; Liu, H.; He, W. Rectification methods comparison for the ASTER GDEM V2 data using the ICESat/GLA14 data in the Lvliang mountains, China. Environ. Earth Sci. 2015, 74, 6571–6590. [Google Scholar] [CrossRef]
- Simard, M.; Neumann, M.; Buckley, S. Validation of the new SRTM digital elevation model (NASADEM) with ICESAT/GLAS over the United States. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3227–3229. [Google Scholar]
- Liu, Z.; Zhu, J.; Fu, H.; Zhou, C.; Zuo, T. Evaluation of the Vertical Accuracy of Open Global DEMs over Steep Terrain Regions Using ICESat Data: A Case Study over Hunan Province, China. Sensors 2020, 20, 4865. [Google Scholar] [CrossRef]
- Beaulieu, A.; Clavet, D. Accuracy assessment of Canadian Digital Elevation Data using ICESat. Photogramm. Eng. Remote Sens. 2009, 75, 81–86. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Harding, D.J. SRTM C-Band and ICESat Laser Altimetry Elevation Comparisons as a Function of Tree Cover and Relief. Photogramm. Eng. Remote Sens. 2006, 72, 287–298. [Google Scholar] [CrossRef]
- Huang, X.; Xie, H.; Liang, T.; Yi, D. Estimating vertical error of SRTM and map-based DEMs using ICESat altimetry data in the eastern Tibetan Plateau. Int. J. Remote Sens. 2011, 32, 5177–5196. [Google Scholar] [CrossRef]
- Du, X.; Guo, H.; Fan, X.; Zhu, J.; Yan, Z.; Zhan, Q. Vertical accuracy assessment of freely available digital elevation models over low-lying coastal plains. Int. J. Digit. Earth 2016, 9, 252–271. [Google Scholar] [CrossRef]
- Huber, M.; Wessel, B.; Kosmann, D.; Felbier, A.; Schwieger, V.; Habermeyer, M.; Wendleder, A.; Roth, A. Ensuring globally the TanDEM-X height accuracy: Analysis of the reference data sets ICESat, SRTM and KGPS-Tracks. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. II-769–II-772. [Google Scholar]
- Yue, L.; Shen, H.; Zhang, L.; Zheng, X.; Zhang, F.; Yuan, Q. High-quality seamless DEM generation blending SRTM-1, ASTER GDEM v2 and ICESat/GLAS observations. ISPRS J. Photogramm. Remote Sens. 2017, 123, 20–34. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Li, L.; Gallant, J.C.; Yang, Q. The impact of misregistration on SRTM and DEM image differences. Remote Sens. Environ. 2008, 112, 2430–2442. [Google Scholar] [CrossRef]
- Baugh, C.A.; Bates, P.D.; Schumann, G.; Trigg, M.A. SRTM vegetation removal and hydrodynamic modeling accuracy. Water Resour. Res. 2013, 49, 5276–5289. [Google Scholar] [CrossRef]
- Zhao, X.; Su, Y.; Hu, T.; Chen, L.; Gao, S.; Wang, R.; Jin, S.; Guo, Q. A global corrected SRTM DEM product for vegetated areas. Remote Sens. Lett. 2018, 9, 393–402. [Google Scholar] [CrossRef]
- O’Loughlin, F.E.; Paiva, R.C.D.; Durand, M.; Alsdorf, D.E.; Bates, P.D. A multi-sensor approach towards a global vegetation corrected SRTM DEM product. Remote Sens. Environ. 2016, 182, 49–59. [Google Scholar] [CrossRef]
- Wendi, D.; Liong, S.Y.; Sun, Y. An innovative approach to improve SRTM DEM using multispectral imagery and artificial neural network. J. Adv. Model. Earth Syst. 2016, 8, 691–702. [Google Scholar] [CrossRef]
- Wendleder, A.; Felbier, A.; Wessel, B.; Huber, M.; Roth, A. A Method to Estimate Long-Wave Height Errors of SRTM C-Band DEM. IEEE Geosci. Remote Sens. Lett. 2016, 13, 696–700. [Google Scholar] [CrossRef]
- Zhan, J.; Shi, N.; He, S.; Lin, Y. Factors and mechanism driving the land-use conversion in Jiangxi Province. J. Geogr. Sci. 2010, 20, 525–539. [Google Scholar] [CrossRef]
- Robinson, N.; Regetz, J.; Guralnick, R.P. EarthEnv-DEM90: A nearly-global, void-free, multi-scale smoothed, 90m digital elevation model from fused ASTER and SRTM data. ISPRS J. Photogramm. Remote Sens. 2014, 87, 57–67. [Google Scholar] [CrossRef]
- Lang, L.; Cheng, W.; Zhu, Q.; Long, E. A Comparative Analysis of the Multi-criteria DEM Extracted Relief—Taking Fujian Low Mountainous Region as an Example. Geo-Inf. Sci. 2007, 9, 1–6. [Google Scholar]
- Liu, J.; Liu, M.; Tian, H.; Zhuang, D.; Zhang, Z.; Zhang, W.; Tang, X.; Deng, X. Spatial and temporal patterns of China’s cropland during 1990–2000: An analysis based on Landsat TM data. Remote Sens. Environ. 2005, 98, 442–456. [Google Scholar] [CrossRef]
- Bhang, K.J.; Schwartz, F.W.; Braun, A. Verification of the Vertical Error in C-Band SRTM DEM Using ICESat and Landsat-7, Otter Tail County, MN. IEEE Trans. Geosci. Remote Sens. 2007, 45, 36–44. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, H.; Li, R.; Cheng, W.; Zhou, C. A quantitative model to simulate the vertical errors of SRTM3 DEM V4 data at the pixel level in the Shanbei Plateau of China. Int. J. Remote Sens. 2020, 41, 5257–5276. [Google Scholar] [CrossRef]
- Arefi, H.; Reinartz, P. Accuracy Enhancement of ASTER Global Digital Elevation Models Using ICESat Data. Remote Sens. 2011, 3, 1323–1343. [Google Scholar] [CrossRef]
- Harding, D.J.; Carabajal, C.C. ICESat waveform measurements of within-footprint topographic relief and vegetation vertical structure. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Harding, D.J. ICESat validation of SRTM C-band digital elevation models. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Aguilar, F.; Aguera, F.; Aguilar, M. A theoretical approach to modeling the accuracy assessment of digital elevation models. Photogramm. Eng. Remote Sens. 2007, 73, 1367. [Google Scholar] [CrossRef][Green Version]
- Guo, H.; Jiao, W.; Yang, Y. The Systematic Difference and Its Distribution between the 1985 National Height Datum and the Global Quasigeoid. Acta Geod. et Cartogr. Sin. 2004, 33, 100–104. [Google Scholar]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- Yang, X.; Li, L.; Chen, L.; Chen, L.; Shen, Z. Improving ASTER GDEM accuracy using land use-based linear regression methods: A case study of Lianyungang, East China. ISPRS Int. J. Geo-Inf. 2018, 7, 145. [Google Scholar] [CrossRef]
- Gorokhovich, Y.; Voustianiouk, A. Accuracy assessment of the processed SRTM-based elevation data by CGIAR using field data from USA and Thailand and its relation to the terrain characteristics. Remote Sens. Environ. 2006, 104, 409–415. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- An, S.; Liu, W.; Venkatesh, S. Fast cross-validation algorithms for least squares support vector machine and kernel ridge regression. Pattern Recognit. 2007, 40, 2154–2162. [Google Scholar] [CrossRef]
- Celikoglu, H.B. Application of radial basis function and generalized regression neural networks in non-linear utility function specification for travel mode choice modelling. Math. Comput. Model. 2006, 44, 640–658. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Du, P.; Bai, X.; Tan, K.; Xue, Z.; Samat, A.; Xia, J.; Li, E.; Su, H.; Liu, W. Advances of Four Machine Learning Methods for Spatial Data Handling: A Review. J. Geovisualization Spat. Anal. 2020, 4, 13. [Google Scholar] [CrossRef]
- He, X.; Chaney, N.W.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M.C. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Peters, J.; De Baets, B.; Verhoest, N.; Samson, R.; Degroeve, S.; De Becker, P.; Huybrechts, W. Random forests as a tool for ecohydrological distribution modelling. Ecol. Model. 2007, 207, 304–318. [Google Scholar] [CrossRef]
- Chen, C.; Wang, M.; Chang, B.; Li, Y. Multi-Level Interpolation-Based Filter for Airborne LiDAR Point Clouds in Forested Areas. IEEE Access 2020, 8, 41000–41012. [Google Scholar] [CrossRef]
- Chen, C.F.; Liu, F.Y.; Li, Y.Y.; Yan, C.Q.; Liu, G.L. A robust interpolation method for constructing digital elevation models from remote sensing data. Geomorphology 2016, 268, 275–287. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C. Comparison of free high resolution digital elevation data sets (ASTER GDEM2, SRTM v2.1/v4.1) and validation against accurate heights from the Australian National Gravity Database. Aust. J. Earth Sci. 2014, 61, 213–226. [Google Scholar] [CrossRef]
- Li, H.; Deng, Q.; Wang, L. Automatic Co-Registration of Digital Elevation Models Based on Centroids of Subwatersheds. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6639–6650. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J. Evaluation of the Newly Released Worldwide AW3D30 DEM over Typical Landforms of China Using Two Global DEMs and ICESat/GLAS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 1–11. [Google Scholar] [CrossRef]
- Toutin, T. Impact of terrain slope and aspect on radargrammetric DEM accuracy. ISPRS J. Photogramm. Remote Sens. 2002, 57, 228–240. [Google Scholar] [CrossRef]
- Szabó, G.; Singh, S.K.; Szabó, S. Slope angle and aspect as influencing factors on the accuracy of the SRTM and the ASTER GDEM databases. Phys. Chem. Earth 2015, 83–84, 137–145. [Google Scholar]
- Zhao, S.M.; Cheng, W.M.; Zhou, C.H. Accuracy assessment of the ASTER GDEM and SRTM3 DEM: An example in the Loess Plateau and North China Plain of China. Int. J. Remote Sens. 2011, 32, 8081–8093. [Google Scholar] [CrossRef]
- Hirt, C.; Filmer, M.S.; Featherstone, W.E. Comparison and validation of the recent freely available ASTER-GDEM ver1, SRTM ver4.1 and GEODATA DEM-9S ver3 digital elevation models over Australia. Aust. J. Earth Sci. 2010, 57, 337–347. [Google Scholar] [CrossRef]
- Chirico, P.G.; Malpeli, K.C.; Trimble, S.M. Accuracy evaluation of an ASTER-derived global digital elevation model (GDEM) version 1 and version 2 for two sites in western Africa. Gisci. Remote Sens. 2012, 49, 775–801. [Google Scholar] [CrossRef]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Hu, Z.; Peng, J.; Hou, Y.; Shan, J. Evaluation of Recently Released Open Global Digital Elevation Models of Hubei, China. Remote Sens. 2017, 9, 262. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Zhao, W.; Wu, H.; Yin, G.; Duan, S.-B. Normalization of the temporal effect on the MODIS land surface temperature product using random forest regression. ISPRS J. Photogramm. Remote Sens. 2019, 152, 109–118. [Google Scholar] [CrossRef]



| Influence Factors | Classes | ME (m) | RMSE (m) | ||
|---|---|---|---|---|---|
| Without | With | Without | With | ||
| Slope (°) | 0–5 | −1.681 | 0.369 | 5.589 | 5.013 |
| 5–10 | −2.153 | −0.253 | 12.463 | 11.104 | |
| 10–15 | −2.632 | −0.802 | 15.332 | 13.104 | |
| 15–20 | −2.653 | −0.372 | 17.135 | 14.143 | |
| >20 | −2.597 | −0.394 | 19.528 | 15.825 | |
| Relief (m) | 0–100 | −1.692 | 0.371 | 5.525 | 4.826 |
| 100–200 | −1.970 | −0.005 | 12.158 | 10.627 | |
| 200–300 | −2.750 | −0.753 | 14.728 | 12.677 | |
| 300–400 | −2.352 | −0.289 | 15.944 | 13.578 | |
| >400 | −2.574 | −0.607 | 18.053 | 14.826 | |
| Elevation (m) | 0–100 | −1.804 | 0.182 | 5.611 | 4.907 |
| 100–200 | −2.221 | −0.299 | 11.859 | 10.375 | |
| 200–300 | −2.517 | −0.522 | 14.351 | 12.472 | |
| 300–400 | −1.574 | 0.316 | 15.150 | 13.002 | |
| >400 | −2.543 | −0.184 | 16.660 | 13.880 | |
| Land use | Cultivated land | −2.550 | −0.282 | 6.980 | 5.752 |
| Forest cover | −2.027 | −0.117 | 13.843 | 11.879 | |
| Grassland | −1.751 | 0.096 | 10.793 | 9.231 | |
| Water area | −0.695 | 1.508 | 3.925 | 3.925 | |
| Built-up area | −2.036 | 0.070 | 4.982 | 3.532 | |
| Unused land | −1.329 | 0.686 | 1.782 | 1.316 | |
| Models | ME (m) | RMSE (m) | Computing Cost (s) | ||
|---|---|---|---|---|---|
| Without | With | Without | With | ||
| SRTM3 | −2.079 | −0.061 | 11.740 | 10.047 | - |
| 3CM | - | −0.061 | - | 10.047 | 0.598 |
| MLR | −0.045 | −0.042 | 10.345 | 9.501 | 0.120 |
| BPNN | −0.029 | −0.003 | 9.793 | 9.467 | 10.633 |
| GRNN | −0.245 | −0.047 | 11.452 | 10.379 | 9.594 |
| RF | −0.168 | −0.041 | 10.429 | 9.211 | 3964.742 |
| Data Coregistration | ME | RMSE |
|---|---|---|
| Without | −0.690 | 11.951 |
| With | −0.176 | 10.977 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Yang, S.; Li, Y. Accuracy Assessment and Correction of SRTM DEM Using ICESat/GLAS Data under Data Coregistration. Remote Sens. 2020, 12, 3435. https://doi.org/10.3390/rs12203435
Chen C, Yang S, Li Y. Accuracy Assessment and Correction of SRTM DEM Using ICESat/GLAS Data under Data Coregistration. Remote Sensing. 2020; 12(20):3435. https://doi.org/10.3390/rs12203435
Chicago/Turabian StyleChen, Chuanfa, Shuai Yang, and Yanyan Li. 2020. "Accuracy Assessment and Correction of SRTM DEM Using ICESat/GLAS Data under Data Coregistration" Remote Sensing 12, no. 20: 3435. https://doi.org/10.3390/rs12203435
APA StyleChen, C., Yang, S., & Li, Y. (2020). Accuracy Assessment and Correction of SRTM DEM Using ICESat/GLAS Data under Data Coregistration. Remote Sensing, 12(20), 3435. https://doi.org/10.3390/rs12203435






