Comparison of Remote Sensing Time-Series Smoothing Methods for Grassland Spring Phenology Extraction on the Qinghai–Tibetan Plateau
Abstract
1. Introduction
2. Study Area and Data
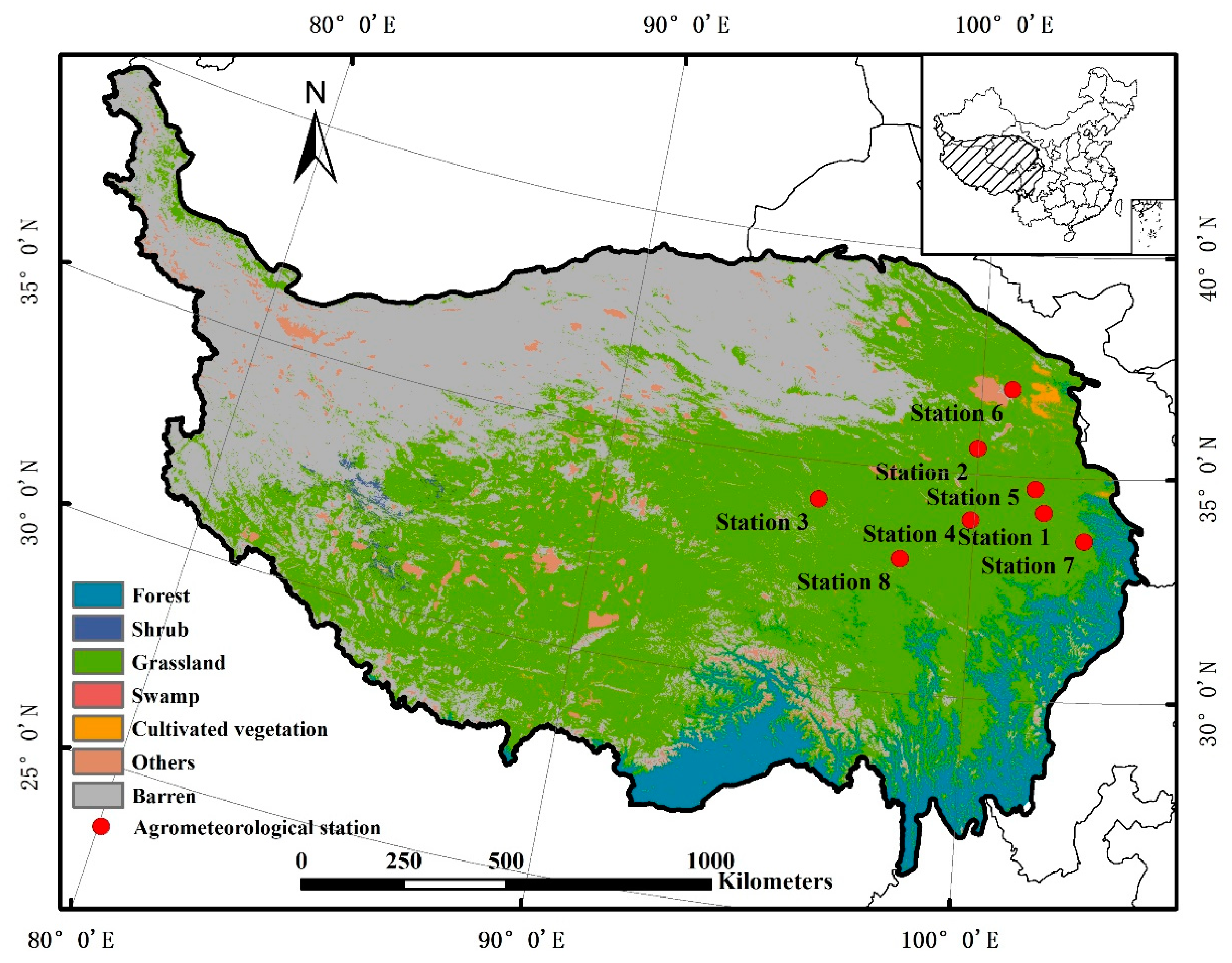
2.1. Study Area
2.2. Ground Observation Data
2.3. Remote Sensing Data and Processing
3. Methodology
3.1. The Time-Series Smoothing Methods
3.2. The Phenology Extraction Methods
3.2.1. Dynamic Threshold Method
3.2.2. Double-Logistic Method
3.3. The Evaluation of the Phenology Extraction Accuracy
3.4. Sensitivity Analysis of the Smoothing Parameters
3.5. Statistical Significance Test of the Results
4. Results
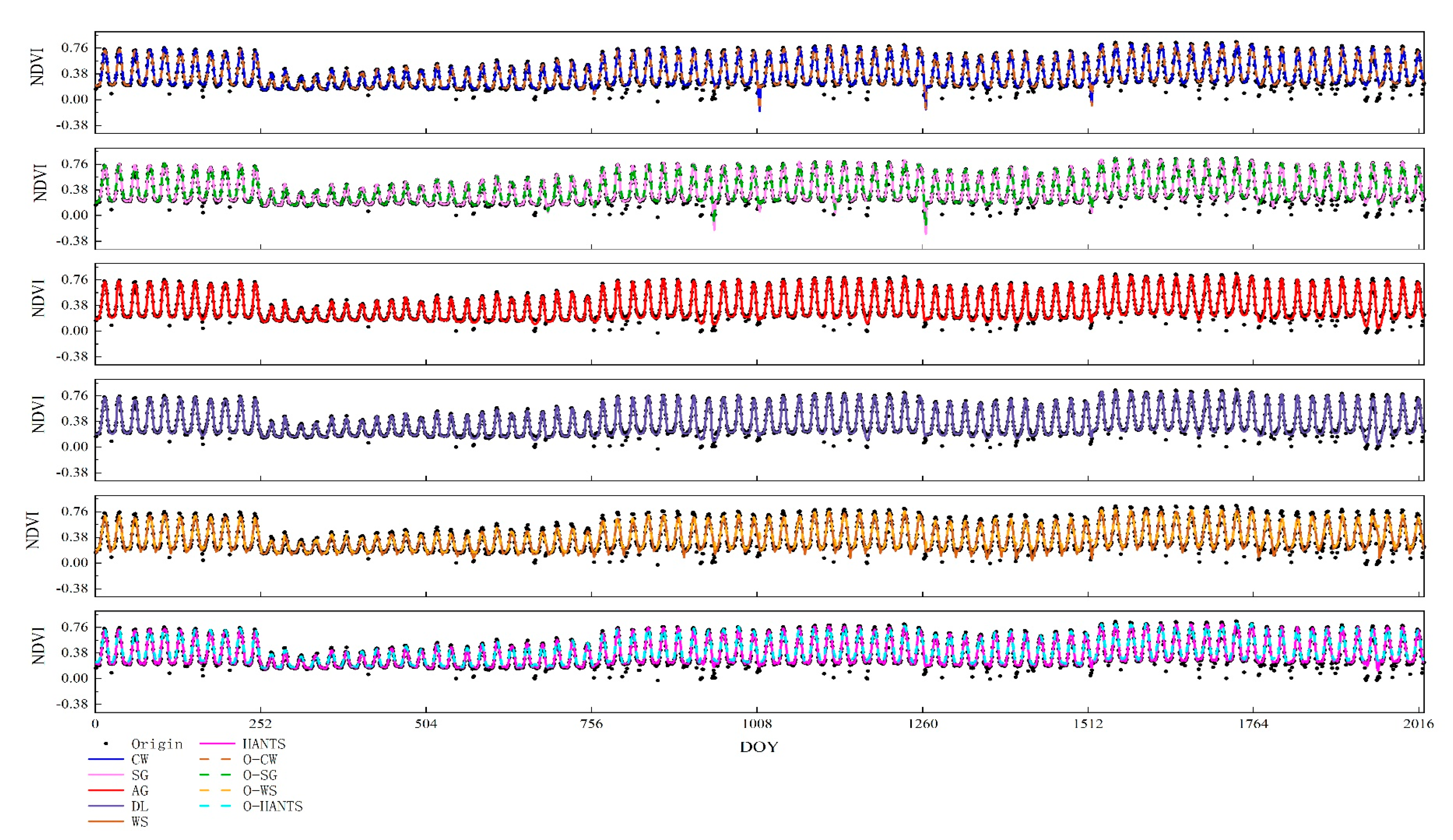
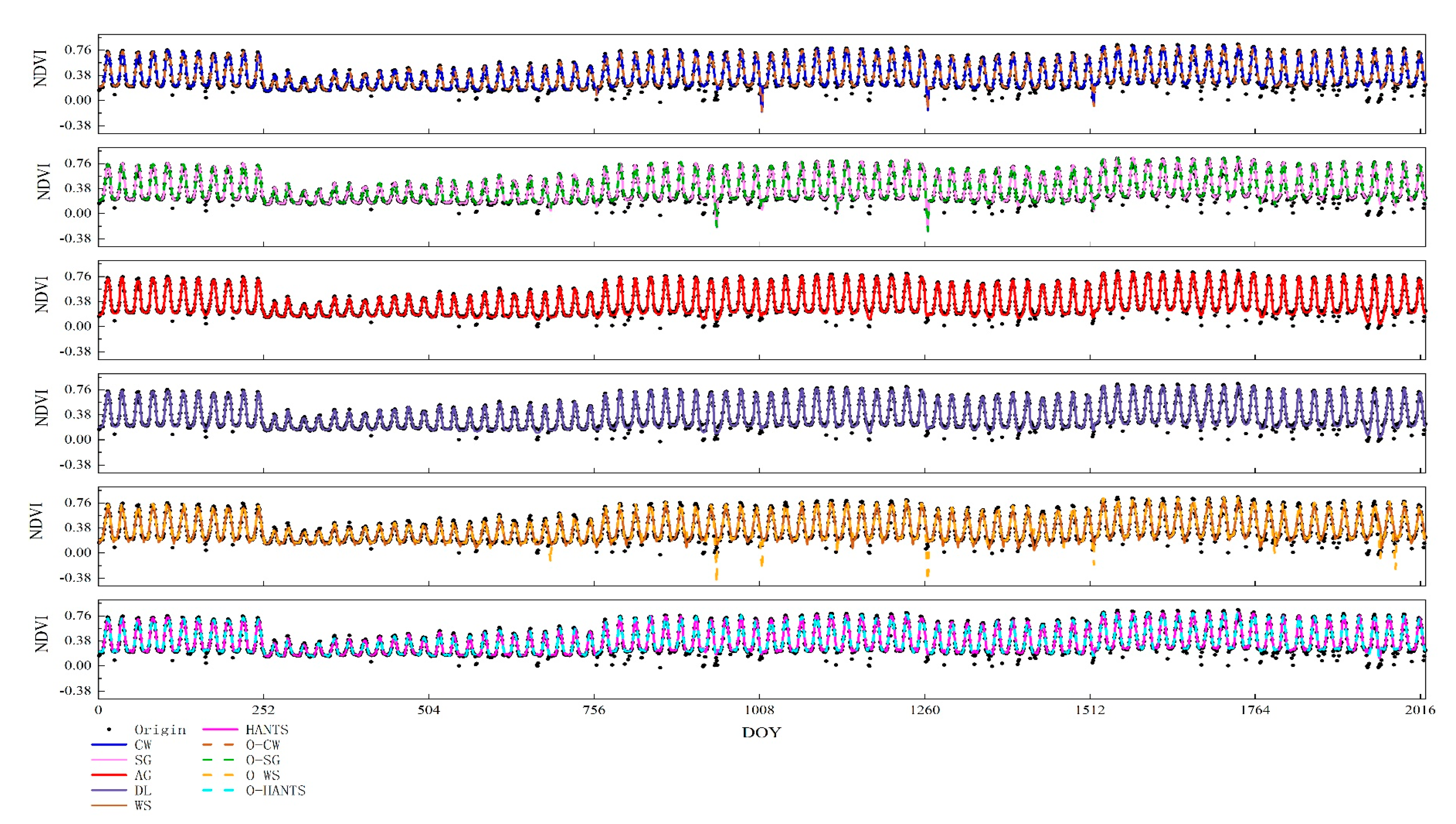
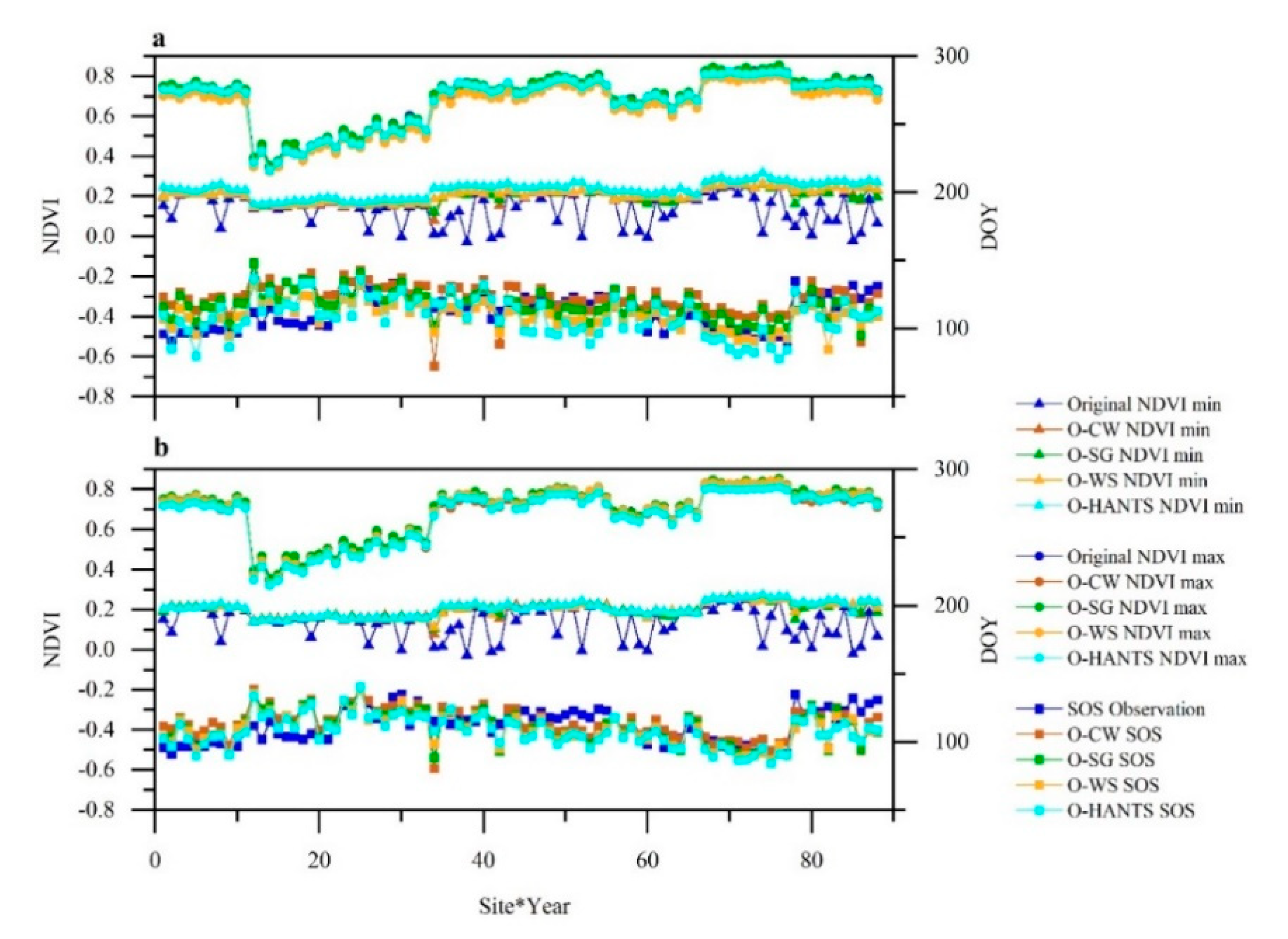
4.1. Performance of the Time-Series Smoothing Results
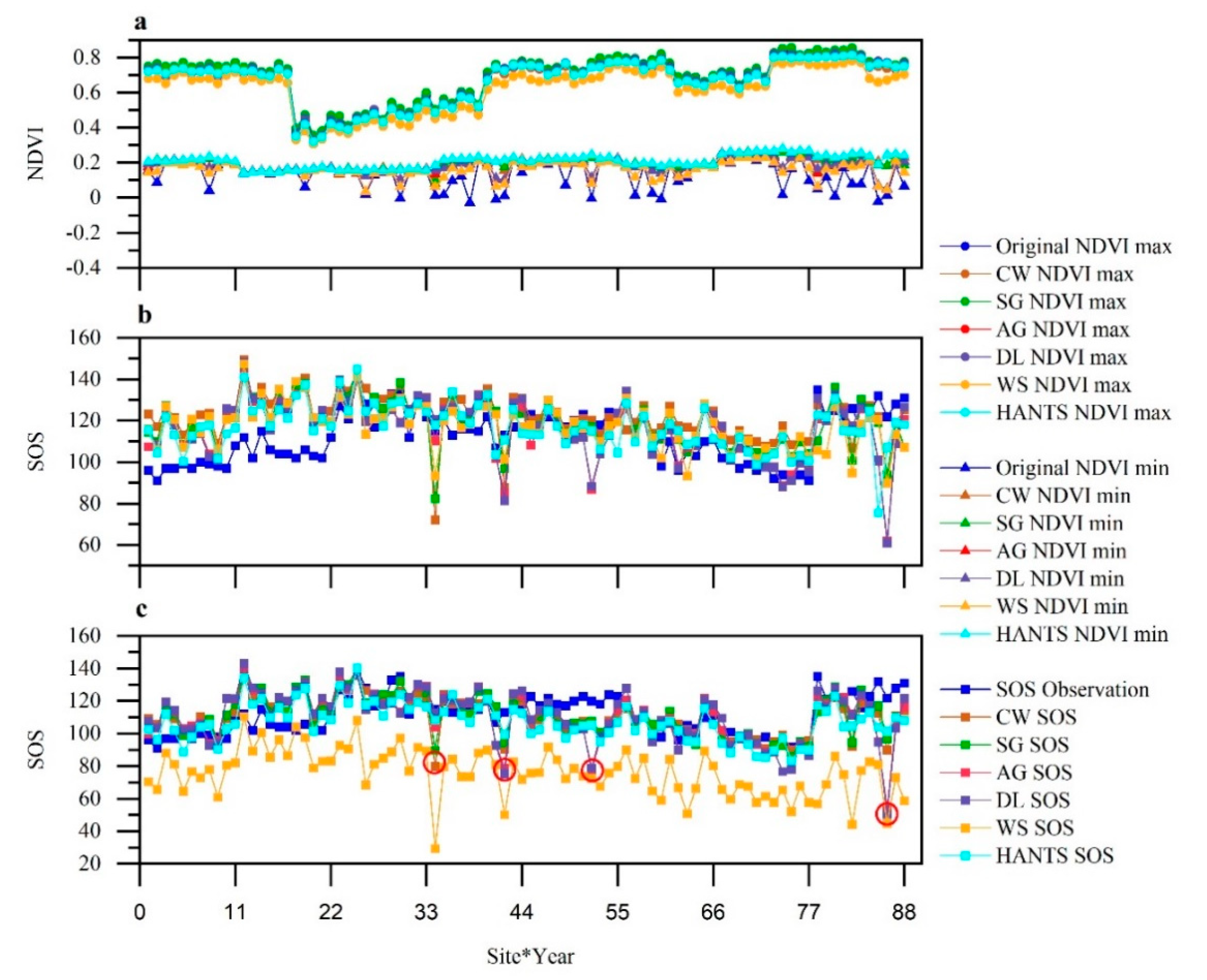
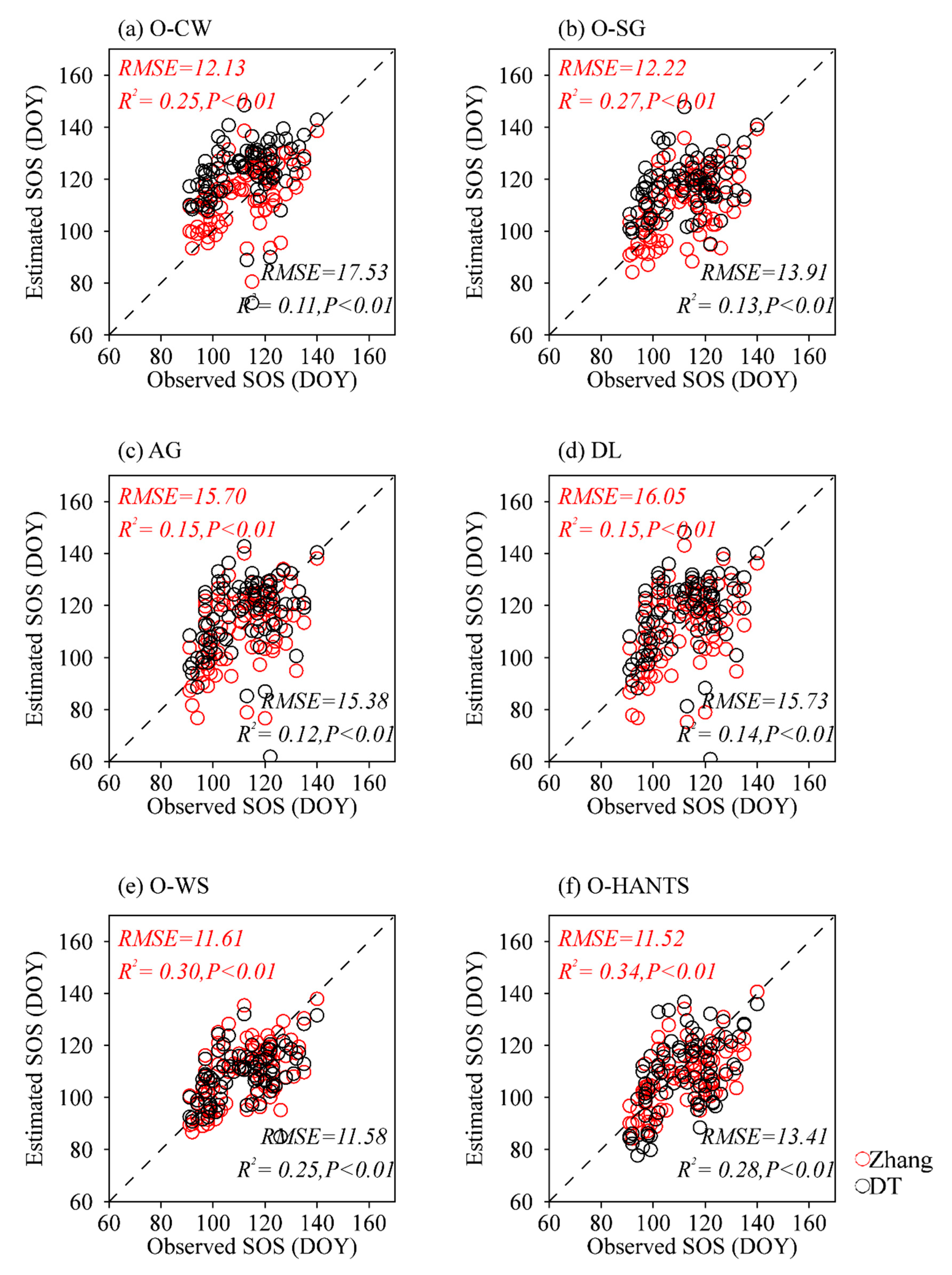
4.2. Inter-Comparison of SOS Extraction Using Different Smoothing Methods
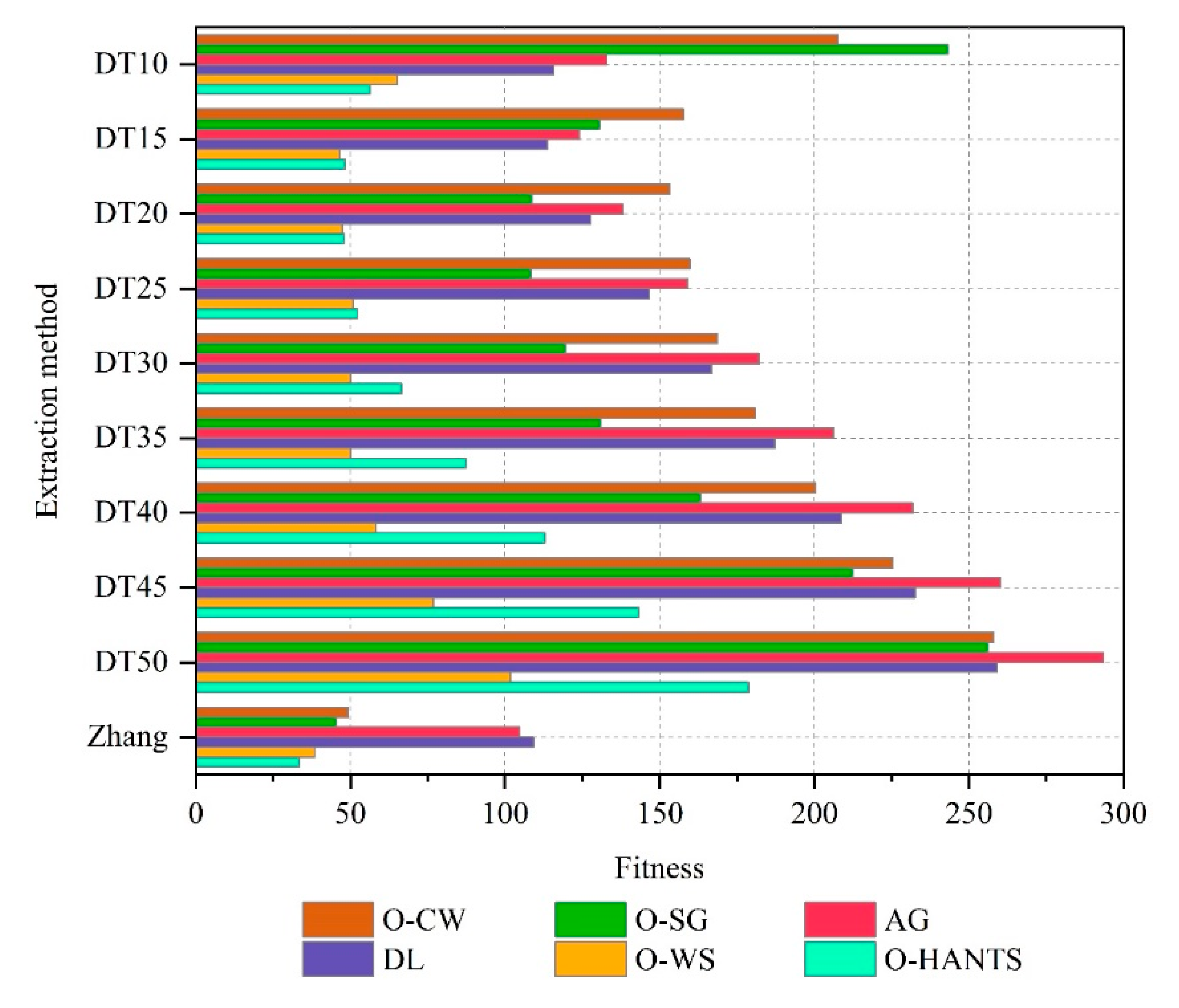
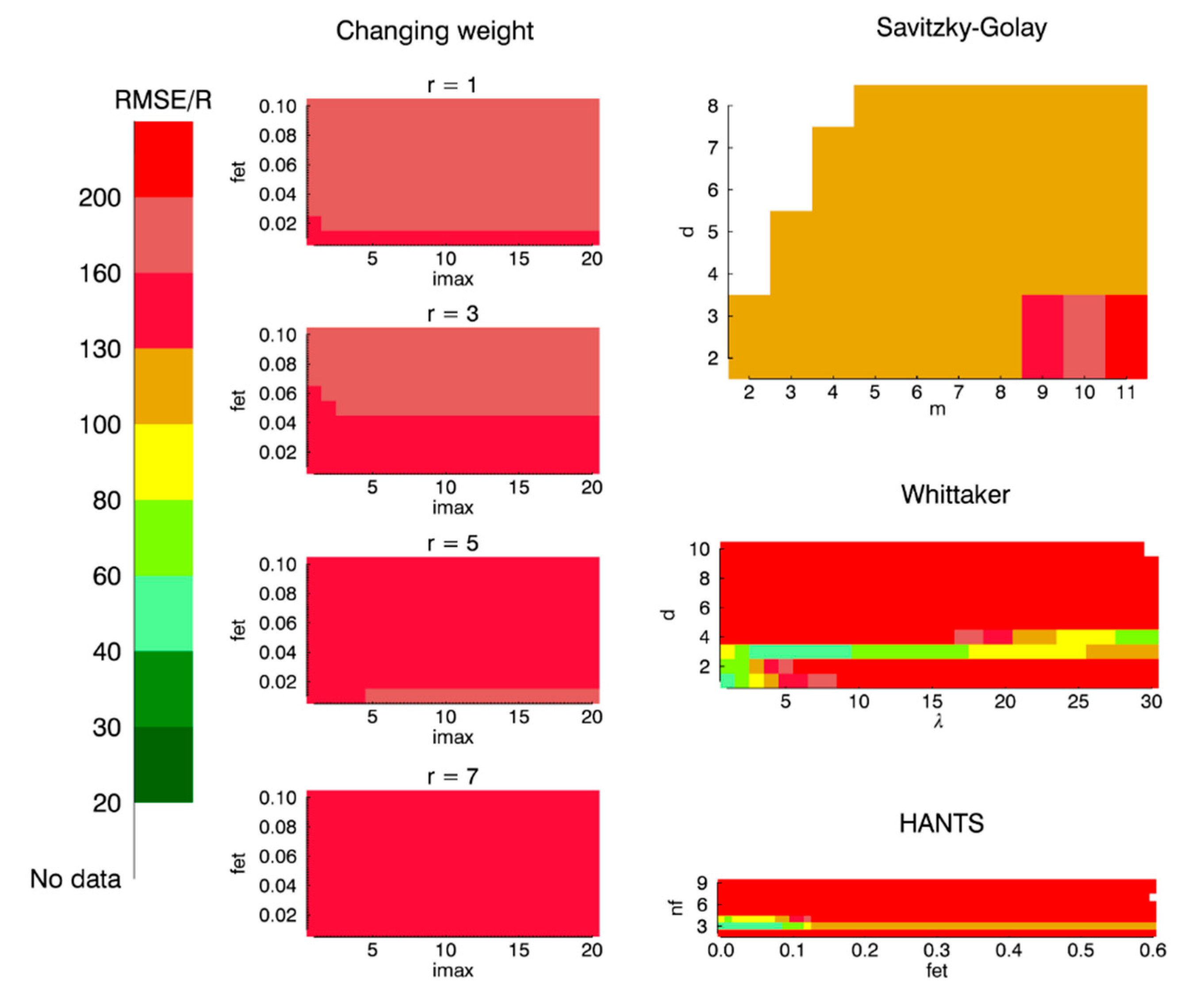
4.3. Parameter Sensitivity of Different Smoothing Methods
5. Discussion
5.1. The Impact of the Choice of Smoothing Methods on the Accuracy of SOS Extraction
5.2. The Impact of Smoothing Method Parameters on the Accuracy of SOS Extraction
5.3. The Impacting Factors on SOS Extraction Accuracies for Phenology Extraction Methods
5.4. Applicability of Different Smoothing Methods
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| O-CW | O-SG | AG | DL | O-WS | O-HANTS | Mean | SD | |
|---|---|---|---|---|---|---|---|---|
| DT10 | 207.67 | 243.26 | 132.89 | 115.75 | 65.27 | 56.39 | 136.87 | 68.80 |
| DT15 | 157.77 | 130.56 | 124.15 | 113.63 | 46.51 | 48.38 | 103.50 | 41.82 |
| DT20 | 153.16 | 108.57 | 138.11 | 127.68 | 47.52 | 48.10 | 103.86 | 41.79 |
| DT25 | 159.73 | 108.38 | 159.07 | 146.66 | 50.83 | 52.19 | 112.81 | 46.59 |
| DT30 | 168.76 | 119.56 | 182.08 | 166.58 | 50.03 | 66.59 | 125.60 | 51.58 |
| DT35 | 181.11 | 130.91 | 206.26 | 187.26 | 50.09 | 87.39 | 140.50 | 56.64 |
| DT40 | 200.31 | 163.31 | 231.97 | 208.82 | 58.25 | 112.83 | 162.58 | 60.19 |
| DT45 | 225.27 | 212.53 | 260.24 | 232.62 | 76.95 | 143.30 | 191.82 | 62.51 |
| DT50 | 258.02 | 256.32 | 293.48 | 258.99 | 101.78 | 178.68 | 224.54 | 64.86 |
| Zhang | 49.26 | 45.46 | 104.75 | 109.15 | 38.45 | 33.52 | 63.43 | 31.20 |
| Mean | 176.11 | 151.89 | 183.30 | 166.71 | 58.57 | 82.74 | / | / |
| SD | 52.92 | 63.32 | 59.83 | 50.70 | 17.68 | 45.27 | / | / |
References
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, B.; Midgley, P.M. Ipcc, 2013: Summary for policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group i to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Tylianakis, J.M.; Didham, R.K.; Bascompte, J.; Wardle, D.A. Global change and species interactions in terrestrial ecosystems. Ecol. Lett. 2008, 11, 1351–1363. [Google Scholar] [CrossRef]
- Badeck, F.W.; Bondeau, A.; Böttcher, K.; Doktor, D.; Lucht, W.; Schaber, J.; Sitch, S. Responses of spring phenology to climate change. New Phytol. 2004, 162, 295–309. [Google Scholar] [CrossRef]
- Menzel, A.; Fabian, P. Growing season extended in Europe. Nature 1999, 397, 659. [Google Scholar] [CrossRef]
- Yang, B.; He, M.; Shishov, V.; Tychkov, I.; Vaganov, E.; Rossi, S.; Ljungqvist, F.C.; Bräuning, A.; Grießinger, J. New perspective on spring vegetation phenology and global climate change based on tibetan plateau tree-ring data. Proc. Natl. Acad. Sci. USA 2017, 114, 6966–6971. [Google Scholar] [CrossRef] [PubMed]
- Piao, S.; Friedlingstein, P.; Ciais, P.; Viovy, N.; Demarty, J. Growing season extension and its impact on terrestrial carbon cycle in the northern hemisphere over the past 2 decades. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; Zhou, L.; Ciais, P.; Zhu, B. Variations in satellite-derived phenology in China’s temperate vegetation. Glob. Chang. Biol. 2006, 12, 672–685. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Dash, J.; Atkinson, P.M. Intercomparison of satellite sensor land surface phenology and ground phenology in Europe. Geophys. Res. Lett. 2015, 42, 2253–2260. [Google Scholar] [CrossRef]
- Richardson, A.D.; Hufkens, K.; Milliman, T.; Aubrecht, D.M.; Chen, M.; Gray, J.M.; Johnston, M.R.; Keenan, T.F.; Klosterman, S.T.; Kosmala, M.; et al. Tracking vegetation phenology across diverse North American biomes using phenocam imagery. Sci. Data 2018, 5, 180028. [Google Scholar] [CrossRef]
- Vrieling, A.; Meroni, M.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Zurita-Milla, R.; Oosterbeek, K.; O’Connor, B.; Paganini, M. Vegetation phenology from sentinel-2 and field cameras for a Dutch barrier island. Remote Sens. Environ. 2018, 215, 517–529. [Google Scholar] [CrossRef]
- Yang, W.; Kobayashi, H.; Wang, C.; Shen, M.; Chen, J.; Matsushit, B.; Tang, Y.; Kim, Y.; Bret-Harte, M.S.; Zona, D.; et al. A semi-analytical snow-free vegetation index for improving estimation of plant phenology in tundra and grassland ecosystems. Remote Sens. Environ. 2019, 228, 31–44. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Jeong, S.-J.; Ho, C.-H.; Gim, H.-J.; Brown, M.E. Phenology shifts at start vs. end of growing season in temperate vegetation over the Northern Hemisphere for the period 1982–2008. Glob. Chang. Biol. 2011, 17, 2385–2399. [Google Scholar] [CrossRef]
- Piao, S.; Wang, X.; Ciais, P.; Zhu, B.; Wang, T.; Liu, J. Changes in satellite-derived vegetation growth trend in temperate and boreal Eurasia from 1982 to 2006. Glob. Chang. Biol. 2011, 17, 3228–3239. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, Y.H.; Zhu, Z.; Liu, Y.; Liu, Z.; Huang, M.; Janssens, I.A.; Piao, S. Delayed autumn phenology in the Northern Hemisphere is related to change in both climate and spring phenology. Glob. Chang. Biol. 2016, 22, 3702–3711. [Google Scholar] [CrossRef]
- Stendardi, L.; Karlsen, S.R.; Niedrist, G.; Gerdol, R.; Zebisch, M.; Rossi, M.; Notarnicola, C. Exploiting time series of sentinel-1 and sentinel-2 imagery to detect meadow phenology in mountain regions. Remote Sens. 2019, 11, 542. [Google Scholar] [CrossRef]
- Pan, Z.; Huang, J.; Zhou, Q.; Wang, L.; Cheng, Y.; Zhang, H.; Blackburn, G.A.; Yan, J.; Liu, J. Mapping crop phenology using ndvi time-series derived from hj-1 a/b data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 188–197. [Google Scholar] [CrossRef]
- Yu, H.; Luedeling, E.; Xu, J. Winter and spring warming result in delayed spring phenology on the Tibetan plateau. Proc. Natl. Acad. Sci. USA 2010, 107, 22151–22156. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Dong, J.; Zhang, Y.; Xiao, X. Reply to shen et al.: No evidence to show nongrowing season NDVI affects spring phenology trend in the tibetan plateau over the last decade. Proc. Natl. Acad. Sci. USA 2013, 110, E2330–E2331. [Google Scholar] [CrossRef] [PubMed]
- White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van Leeuwen, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Chang. Biol. 2009, 15, 2335–2359. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Y.; Dong, J.; Xiao, X. Green-up dates in the Tibetan plateau have continuously advanced from 1982 to 2011. Proc. Natl. Acad. Sci. USA 2013, 110, 4309–4314. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Dai, J.; Ge, Q. Comparison of satellite and ground-based phenology in China’s temperate monsoon area. Adv. Meteorol. 2014. [Google Scholar] [CrossRef]
- White, K.; Pontius, J.; Schaberg, P. Remote sensing of spring phenology in northeastern forests: A comparison of methods, field metrics and sources of uncertainty. Remote Sens. Environ. 2014, 148, 97–107. [Google Scholar] [CrossRef]
- Ma, Y.; Niu, X.; Liu, J. A comparison of different methods for studying vegetation phenology in Central Asia. In Geo-Informatics in Resource Management and Sustainable Ecosystem; Springer: Heidelberg/Berlin, Germany, 2016; pp. 301–307. [Google Scholar] [CrossRef]
- Bao, G.; Bao, Y.; Alateng, T.; Bao, Y.; Qin, Z.; Wang, M.; Zhou, Y. Spatio-temporal dynamics of vegetation phenology in the Mongolian plateau during 1982~2011. Remote Sens. Technol. Appl. 2017, 32, 866–874. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
- Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations—Application to modis lai products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
- Geng, L.Y.; Ma, M.G.; Wang, X.F.; Yu, W.P.; Jia, S.Z.; Wang, H.B. Comparison of eight techniques for reconstructing multi-satellite sensor time-series NDVI data sets in the Heihe river basin, China. Remote Sens. 2014, 6, 2024–2049. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ. 2012, 123, 400–417. [Google Scholar] [CrossRef]
- Lara, B.; Gandini, M. Assessing the performance of smoothing functions to estimate land surface phenology on temperate grassland. Int. J. Remote Sens. 2016, 37, 1801–1813. [Google Scholar] [CrossRef]
- Zhu, W.; Pan, Y.; He, H.; Wang, L.; Mou, M.; Liu, J. A changing-weight filter method for reconstructing a high-quality NDVI time series to preserve the integrity of vegetation phenology. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1085–1094. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
- Vivó-Truyols, G.; Schoenmakers, P.J. Automatic selection of optimal Savitzky−Golay smoothing. Anal. Chem. 2006, 78, 4598–4608. [Google Scholar] [CrossRef]
- Zhao, A.; Tang, X.; Zhang, Z.; Liu, J. The parameters optimization selection of Savitzky-Golay filter and its application in smoothing pretreatment for FTIR spectra. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 516–521. [Google Scholar] [CrossRef]
- Spiess, A.-N.; Deutschmann, C.; Burdukiewicz, M.; Himmelreich, R.; Klat, K.; Schierack, P.; Rödiger, S. Impact of smoothing on parameter estimation in quantitative DNA amplification experiments. Clin. Chem. 2020, 61, 379–388. [Google Scholar] [CrossRef]
- Ding, M.; Zhang, Y.; Sun, X.; Liu, L.; Wang, Z.; Bai, W. Spatiotemporal variation in alpine grassland phenology in the Qinghai-Tibetan plateau from 1999 to 2009. Chin. Sci. Bull. 2013, 58, 396–405. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Y.; Xu, S.; Zhou, H.; Gu, S.; Yu, G.; Zhao, X. Diurnal, seasonal and annual variation in net ecosystem CO2 exchange of an alpine shrubland on Qinghai-Tibetan plateau. Glob. Chang. Biol. 2006, 12, 1940–1953. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Linderholm, H.W.; Chen, D.; Yu, Q.; Wu, D.; Haginoya, S. Observation and calculation of the solar radiation on the Tibetan plateau. Energy Convers. Manag. 2012, 57, 23–32. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; He, J. Variations in vegetation net primary production in the Qinghai-Xizang plateau, China, from 1982 to 1999. Clim. Chang. 2006, 74, 253–267. [Google Scholar] [CrossRef]
- Wang, B.; Bao, Q.; Hoskins, B.; Wu, G.; Liu, Y. Tibetan plateau warming and precipitation changes in east Asia. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Piao, S.; Cui, M.; Chen, A.; Wang, X.; Ciais, P.; Liu, J.; Tang, Y. Altitude and temperature dependence of change in the spring vegetation green-up date from 1982 to 2006 in the Qinghai-Xizang plateau. Agric. For. Meteorol. 2011, 151, 1599–1608. [Google Scholar] [CrossRef]
- Hwang, T.; Band, L.E.; Miniat, C.F.; Song, C.; Bolstad, P.V.; Vose, J.M.; Love, J.P. Divergent phenological response to hydroclimate variability in forested mountain watersheds. Glob. Chang. Biol. 2014, 20, 2580–2595. [Google Scholar] [CrossRef]
- Bart, R.R.; Tague, C.L.; Dennison, P.E. Modeling annual grassland phenology along the central coast of California. Ecosphere 2017, 8, e01875. [Google Scholar] [CrossRef]
- Marchin, R.M.; McHugh, I.; Simpson, R.R.; Ingram, L.J.; Balas, D.S.; Evans, B.J.; Adams, M.A. Productivity of an Australian mountain grassland is limited by temperature and dryness despite long growing seasons. Agric. For. Meteorol. 2018, 256–257, 116–124. [Google Scholar] [CrossRef]
- Bradley, B.A.; Jacob, R.W.; Hermance, J.F.; Mustard, J.F. A curve fitting procedure to derive inter-annual phenologies from time series of noisy satellite NDVI data. Remote Sens. Environ. 2007, 106, 137–145. [Google Scholar] [CrossRef]
- Tang, G.; Xiang, B.; Liang, S.; Ma, G.; Wang, J. Comparison of denoising multi-algorithms for the modis NDVI time-series signal. In Proceedings of the 2012 5th International Congress on Image and Signal Processing, Suzhou, China, 16–18 October 2012; pp. 1773–1777. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Chen, Y.; Tao, F.; Zhang, J.; Zhang, W. Comparing different smoothing methods to detect double-cropping rice phenology based on lai products—A case study in the Hunan province of China. Int. J. Remote Sens. 2018, 39, 6405–6428. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Eilers, P.H.C. A perfect smoother. Anal. Chem. 2003, 75, 3631–3636. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global modis NDVI time series: Performance of harmonic analysis of time series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Tang, G.; Arnone Iii, J.A.; Verburg, P.S.J.; Jasoni, R.L.; Sun, L. Trends and climatic sensitivities of vegetation phenology in semiarid and arid ecosystems in the us great basin during 1982–2011. Biogeosciences 2015, 12, 6985–6997. [Google Scholar] [CrossRef]
- Zhou, X.; Geng, X.; Yin, G.; Hänninen, H.; Hao, F.; Zhang, X.; Fu, Y.H. Legacy effect of spring phenology on vegetation growth in temperate China. Agric. For. Meteorol. 2020, 281, 107845. [Google Scholar] [CrossRef]
- Gan, L.; Cao, X.; Chen, J. Comparison of winter wheat spring phenology extraction by various remote sensing vegetation indices and methods. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 6302–6305. [Google Scholar] [CrossRef]
- Wu, C.; Peng, D.; Soudani, K.; Siebicke, L.; Gough, C.M.; Arain, M.A.; Bohrer, G.; Lafleur, P.M.; Peichl, M.; Gonsamo, A.; et al. Land surface phenology derived from normalized difference vegetation index (NDVI) at global fluxnet sites. Agric. For. Meteorol. 2017, 233, 171–182. [Google Scholar] [CrossRef]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar] [CrossRef]
- Cohen, J. Chapter 3—The significance of a product moment rs. In Statistical Power Analysis for the Behavioral Sciences, Cohen, J., Ed.; Academic Press: Cambridge, MA, USA, 1977; pp 75–107.rs. In Statistical Power Analysis for the Behavioral Sciences, Cohen, J., Ed.; Academic Press: Cambridge, MA, USA, 1977; pp. 75–107. [Google Scholar]
- Cong, N.; Wang, T.; Nan, H.; Ma, Y.; Wang, X.; Myneni, R.B.; Piao, S. Changes in satellite-derived spring vegetation green-up date and its linkage to climate in china from 1982 to 2010: A multimethod analysis. Glob. Chang. Biol. 2013, 19, 881–891. [Google Scholar] [CrossRef]
- Shen, M.; Piao, S.; Cong, N.; Zhang, G.; Jassens, I.A. Precipitation impacts on vegetation spring phenology on the Tibetan plateau. Glob. Chang. Biol. 2015, 21, 3647–3656. [Google Scholar] [CrossRef]
- Cai, Z.; Jonsson, P.; Jin, H.; Eklundh, L. Performance of smoothing methods for reconstructing NDVI time-series and estimating vegetation phenology from MODIS data. Remote Sens. 2017, 9, 1271. [Google Scholar] [CrossRef]
- Cao, R.; Chen, Y.; Shen, M.; Chen, J.; Zhou, J.; Wang, C.; Yang, W. A simple method to improve the quality of ndvi time-series data by integrating spatiotemporal information with the Savitzky-Golay filter. Remote Sens. Environ. 2018, 217, 244–257. [Google Scholar] [CrossRef]
- Tang, K.; Zhu, W.; Zhan, P.; Ding, S. An identification method for spring maize in northeast China based on spectral and phenological features. Remote Sens. 2018, 10, 193. [Google Scholar] [CrossRef]
- Jun, W.; Zhongbo, S.; Yaoming, M. Reconstruction of a cloud-free vegetation index time series for the Tibetan plateau. Mt. Res. Dev. 2004, 24, 348–353, 346. [Google Scholar] [CrossRef]
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ. 2009, 113, 248–258. [Google Scholar] [CrossRef]
- Bórnez, K.; Descals, A.; Verger, A.; Peñuelas, J. Land surface phenology from vegetation and proba-v data. Assessment over deciduous forests. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101974. [Google Scholar] [CrossRef]



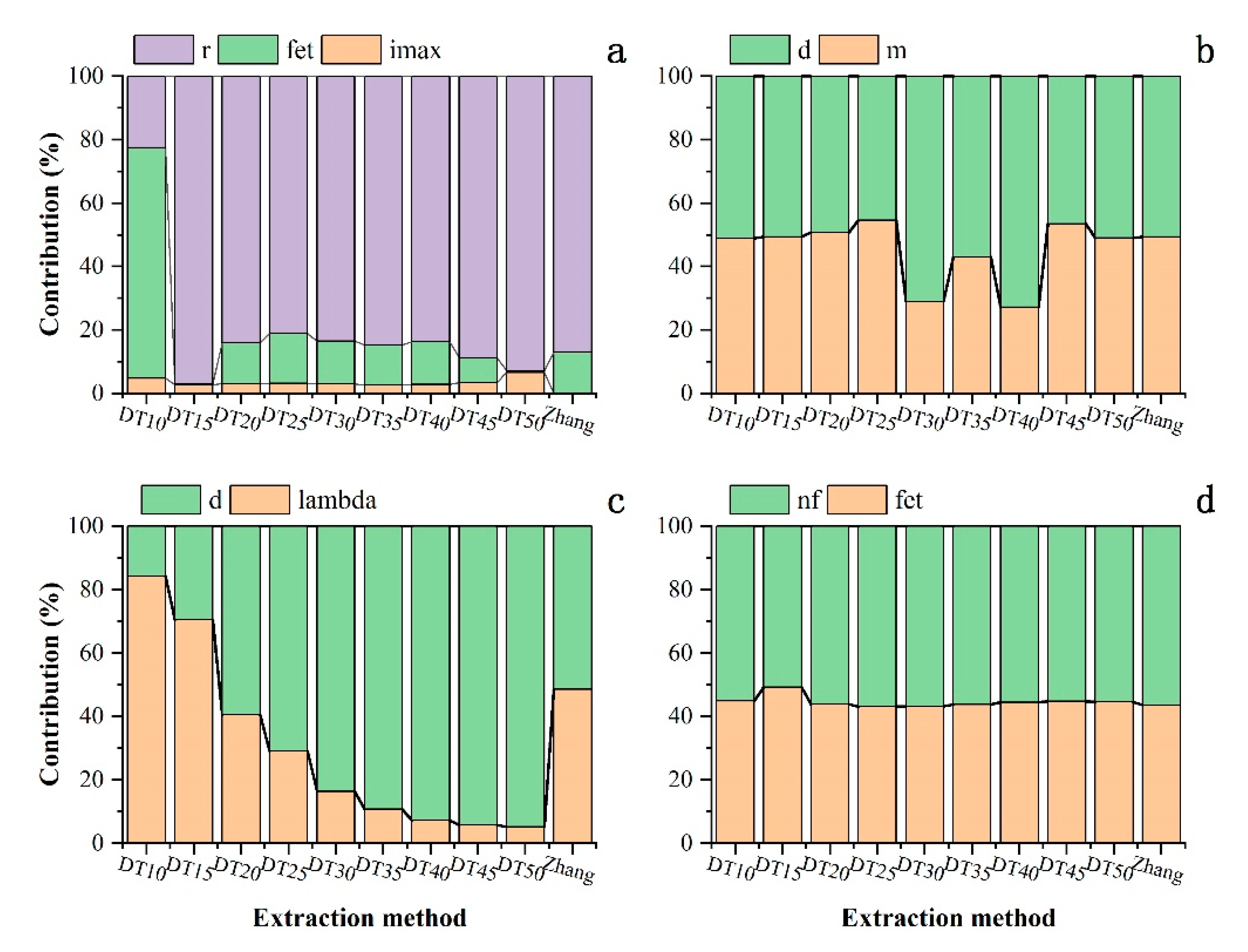

| Method | Category | Parameter Meaning | Default Value | Range | Step | Platform | Reference | Default Value Reference |
|---|---|---|---|---|---|---|---|---|
| CW | empirical | r:radius of sliding window | 7 | [1, 7] | 2 | IDL | [34] | [34] |
| fet: the threshold to determine the local maximum/minimum points | 0.05 | [0.01, 0.1] | 0.01 | |||||
| imax: the maximum iteration cycle | 10 | [1, 20] | 1 | |||||
| SG | curve fitting | m: the radius of smoothing window | 4 | [2, 11] | 1 | IDL | [35] | [35] |
| 6 | [2, 8] | 1 | ||||||
| d: the degree of the smoothing polynomial | ||||||||
| AG | curve fitting | / | / | / | / | TIMESAT | [52] | / |
| DL | curve fitting | / | / | / | / | TIMESAT | [52] | / |
| WS | curve fitting | λ: the weight parameter set by the user | 15 | [1, 30] | 1 | IDL | [53] | [32] |
| d: the order of the difference of sparse matrix | 2 | [1, 10] | 1 | |||||
| HANTS | data transformation | fet: the maximum fit error tolerance of the downward deviation between the Fourier fit and NDVI original values | 0.05 | [0, 0.6] | 0.01 | IDL | [36] | [54] |
| nf: the number of frequencies for the curve fitting | 4 | [2, 9] | 1 |
| Smoothing Method | Before Optimization | After Optimization | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 (%) | p1 | p2 | p3 | RMSE | R2 (%) | p1 | p2 | p3 | |
| CW | 17.54 | 11.21 | 7 | 0.05 | 10 | 17.53 | 11.45 | 3 | 0.02 | 1 |
| SG | 15.53 | 12.95 | 4 | 6 | 13.91 | 12.83 | 7 | 2 | ||
| WS | 15.40 | 5.77 | 15 | 2 | 11.58 | 24.90 | 1 | 1 | ||
| HANTS | 13.74 | 16.29 | 0.05 | 4 | 13.41 | 27.87 | 0.01 | 3 | ||
| Smoothing Method | Before Optimization | After Optimization | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 (%) | p1 | p2 | p3 | RMSE | R2 (%) | p1 | p2 | p3 | |
| CW | 12.20 | 22.77 | 7 | 0.05 | 10 | 12.13 | 24.63 | 1 | 0.09 | 1 |
| SG | 12.34 | 26.77 | 4 | 6 | 12.22 | 26.89 | 9 | 8 | ||
| WS | 39.42 | 6.51 | 15 | 2 | 11.61 | 30.20 | 1 | 3 | ||
| HANTS | 11.76 | 33.55 | 0.05 | 4 | 11.52 | 34.36 | 0.06 | 4 | ||
| Smoothing Method | Before Optimization | After Optimization | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 (%) | p1 | p2 | p3 | RMSE | R2 (%) | p1 | p2 | p3 | |
| cw | 12.06 | 24.54 | 7 | 0.05 | 10 | 12.02 | 25.22 | 3 | 0.04 | 1 |
| sg | 12.67 | 29.23 | 4 | 6 | 12.25 | 29.58 | 7 | 6 | ||
| ws | 10.64 | 31.04 | 15 | 2 | 10.56 | 37.03 | 6 | 3 | ||
| hants | 12.96 | 27.05 | 0.05 | 4 | 11.31 | 37.80 | 0.36 | 3 | ||
| O-CW | O-SG | AG | DL | O-WS | O-HANTS | Mean | SD | |
|---|---|---|---|---|---|---|---|---|
| DT-fix 10 | 1149.55 | 262.28 | 279.80 | 340.70 | 143.06 | 117.58 | 382.16 | 351.81 |
| DT-fix 15 | 993.49 | 260.06 | 249.89 | 293.73 | 145.82 | 117.18 | 343.36 | 297.48 |
| DT-fix20 | 756.71 | 274.98 | 191.61 | 219.83 | 138.31 | 115.03 | 282.74 | 218.31 |
| DT-fix25 | 494.03 | 285.51 | 102.39 | 115.69 | 101.27 | 92.19 | 198.51 | 148.19 |
| DT-fix30 | 116.22 | 75.77 | 59.01 | 62.85 | 50.15 | 48.86 | 68.81 | 23.00 |
| DT-fix35 | 47.67 | 41.39 | 52.14 | 54.55 | 35.17 | 29.91 | 43.47 | 8.88 |
| DT-fix40 | 59.32 | 51.01 | 62.25 | 62.72 | 42.29 | 33.63 | 51.87 | 10.85 |
| DT-fix45 | 81.26 | 61.91 | 78.30 | 77.08 | 56.04 | 40.41 | 65.83 | 14.59 |
| DT-fix50 | 107.54 | 74.26 | 100.50 | 97.63 | 73.07 | 55.74 | 84.79 | 18.36 |
| Zhang | 49.26 | 45.46 | 104.75 | 109.15 | 38.45 | 33.52 | 63.43 | 31.20 |
| Mean | 385.51 | 143.26 | 128.06 | 143.39 | 82.36 | 68.41 | / | / |
| SD | 409.75 | 104.78 | 78.23 | 98.33 | 43.33 | 35.74 | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Zhan, P.; Pan, Y.; Zhu, X.; Li, M.; Zhang, D. Comparison of Remote Sensing Time-Series Smoothing Methods for Grassland Spring Phenology Extraction on the Qinghai–Tibetan Plateau. Remote Sens. 2020, 12, 3383. https://doi.org/10.3390/rs12203383
Li N, Zhan P, Pan Y, Zhu X, Li M, Zhang D. Comparison of Remote Sensing Time-Series Smoothing Methods for Grassland Spring Phenology Extraction on the Qinghai–Tibetan Plateau. Remote Sensing. 2020; 12(20):3383. https://doi.org/10.3390/rs12203383
Chicago/Turabian StyleLi, Nan, Pei Zhan, Yaozhong Pan, Xiufang Zhu, Muyi Li, and Dujuan Zhang. 2020. "Comparison of Remote Sensing Time-Series Smoothing Methods for Grassland Spring Phenology Extraction on the Qinghai–Tibetan Plateau" Remote Sensing 12, no. 20: 3383. https://doi.org/10.3390/rs12203383
APA StyleLi, N., Zhan, P., Pan, Y., Zhu, X., Li, M., & Zhang, D. (2020). Comparison of Remote Sensing Time-Series Smoothing Methods for Grassland Spring Phenology Extraction on the Qinghai–Tibetan Plateau. Remote Sensing, 12(20), 3383. https://doi.org/10.3390/rs12203383







