Towards the Sea Ice and Wind Measurement by a C-Band Scatterometer at Dual VV/HH Polarization: A Prospective Appraisal

Abstract

Following the mission science plan of EPS/Metop-SG C-band scatterometer for 2023–2044, we consider the potential application of the sea ice/water discrimination method based on the minimum statistical distance of the measured normalized radar cross sections (NRCS) to the geophysical model functions (GMF) of the sea ice and water, respectively. The application of the method is considered for the classical spacecraft scatterometer geometry with three fixed fan-beam antennas and the hypothetical prospective scatterometer geometry with the five fixed fan-beam antennas. Joint vertical (VV) and horizontal (HH) transmit and receive polarization are considered for the spaceborne scatterometer geometries. We show explicitly that the hypothetical five fixed fan-beam antenna geometry combined with the dual VV and HH polarization for all antennas provides better estimates of the sea wind speed and direction as well as sea ice/water discrimination during single spacecraft pass. The sea ice/water discrimination algorithms developed for each scatterometer geometry and dual VV/HH polarization are presented. The obtained results can be used to optimize the design of new spaceborne scatterometers and will be beneficial to the forthcoming satellite missions.

1. Introduction

In recent years, there has been growing evidence of rapid climate change in the polar regions. On one hand, this leads to increasing interest in the economic development of these regions that, in turn, requires safe navigation, especially along the Northern Sea Route and Northwest Passage [1]. On the other hand, safe economic operations in these otherwise inhospitable regions require extensive monitoring of associated risks, including the development of extreme winds and waves, alterations to the ice shields, formation of ice cracks, and separation of floating ice. The Northern Sea Route [2] (also known as a part of the Northeast Passage [3]) and Northwest Passage [4] are shown in Figure 1. These regions are characterized by extremely cold temperatures and weather conditions. They are mostly covered with ice and barely populated, and so they are practically unequipped with local remote sensing facilities. Therefore, spaceborne remote sensing instruments are crucial for these regions [5,6,7,8].

One such instrument is a spacecraft scatterometer used for the sea wind retrieval as well as sea ice mapping [5,9,10,11,12,13]. Due to significant backscatter contrast between the sea ice and water, scatterometers mostly provide the sea ice mapping well [14]. Scatterometers are used to map the sea properties such as extent [15], motion [16], classification [17], and onset of melt [12]. In the last decades, scatterometers launched by NASA, ESA, and other space agencies have demonstrated their successful performance for the remote sensing in polar areas, and so their further development and application have long-term plans.

A summary of historical, current, and perspective spaceborne scatterometers for the measurement of the near-surface wind vector along with their measurement timelines is presented in [9,18]. Another review of sea ice type measuring instruments and timelines of their operations can be found in [9,19]. Following the EPS/Metop-SG scatterometer mission science plan for 2023–2044 [20], EUMETSAT continues its polar-orbiting satellite program by two satellite series of EPS-SG (EUMETSAT Polar System—Second Generation) Metop-SG A and B, involving three spacecraft each [21]. 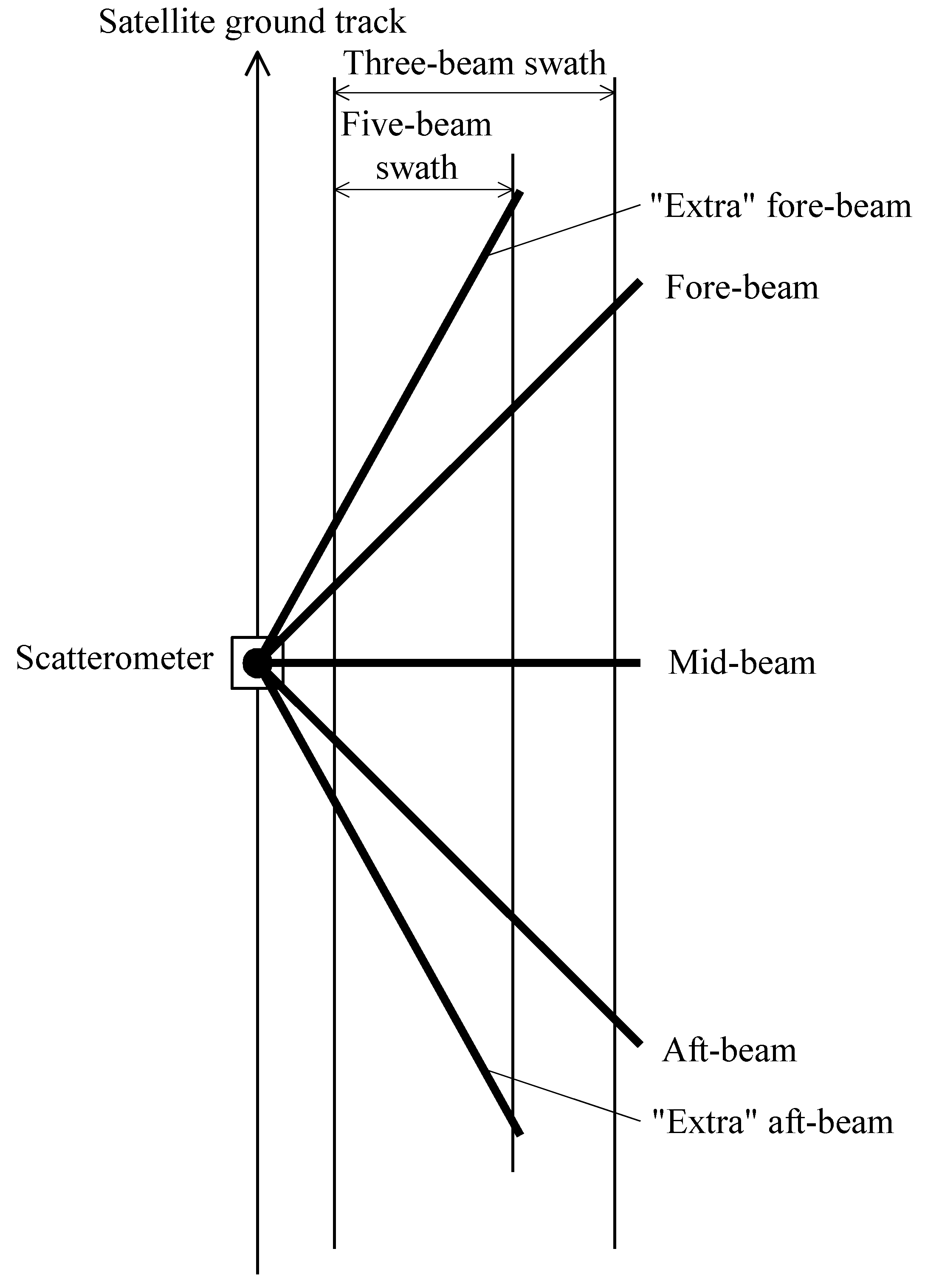Metop-SG B1, B2, and B3 will be equipped with a C-band scatterometer (SCA) [22,23]. SCA is a real aperture radar with a carrier frequency of 5.355 GHz. SCA measuring geometry slightly differs from the previous ASCAT geometry while having the same azimuthal orientation of beams relative to the satellite ground track (Figure 2).

The NRCS measurement is performed within the right and the left swathes of the 660 km wide span at the azimuthal angles of 45°, 90°, and 135° for the right-hand beams, and 225°, 270°, and 315° for the left-hand beams relative to the ground track. The mid-beam incidence angle varies between 20° and 53.7°, while it varies from 28.4° and 65° for the fore- and aft-beams. It is planned that the fore- and aft-antennas will transmit and receive vertical (VV) polarization only, while the mid-antennas will transmit and receive VV, horizontal (HH), and cross polarizations [22,24]. The major quantities of interest to be retrieved during the SCA mission are as follows [20]:

−

Sea wind vector and wind variability;

−

Sea-ice type and extent;

−

Freeze/thaw state;

−

Land soil moisture, vegetation, and accumulated rain.

Thus, the classical three fixed fan-beam scatterometer geometry (for a single swath) and C-band continues to be used in the coming decades. In addition to the single VV polarization used in ASCAT for all the antennas, extra HH and cross polarizations will be also used for the SCA mid-antennas.

Recently, we have proposed a method for the discrimination of sea ice and water by the current spacecraft scatterometers [25]. The method is based on the criterion of the statistical distance of measured NRCSs to the sea ice GMF and the water GMF. The method has been implemented for the classical three-beam and for the hypothetical five-beam C-band scatterometers operated only with the VV polarization for all antennas [25]. In this connection, here we focus on the extension of that method to the cases of the joint VV and HH polarizations for the SCA and some other possible fixed fan-beam scatterometers. Unlike consideration of the sea ice/water discrimination only at the VV polarization in [25], we are considering the sea ice/water discrimination at the VV polarization in conjunction with the additional HH polarization for various combinations of scatterometer beams in this paper.

2. Materials and Methods

Observing the underlying surface, scatterometer samples NRCSs from the cells observed (selected) by its antennas from various fixed azimuthal directions relative to the satellite ground track. Water and sea ice backscattering exhibit distinct features. The sea ice/water discrimination and evaluation of the sea ice extent and thickness (age) are based on the differences in their backscatter properties [26,27].

In the last decades, several approaches have been proposed for the discrimination between sea ice and water. Earlier, the factor of anisotropy k_a [28] or backscatter derivative k_d [29] have been used for that. Later discrimination methods using the lowest statistical distance between the measured NRCS values and GMFs of the sea ice or water [30], or Bayesian approaches [10,31,32] have also been proposed.

Very recently, we have proposed the following sea ice/water discrimination method in [25]. The method uses the statistical distance of measured NRCS values to GMFs of the sea ice or water when the sea ice S_ice and water S_water summation results, which are compared as follows to decide whether the sea ice or water is observed:

$$\{\begin{array}{l}{S}_{ice}<S_{water}\Rightarrow \mathrm{ice}\\ S_{ice}>S_{water}\Rightarrow \mathrm{water}\\ S_{ice}\approx S_{water}\Rightarrow \mathrm{uncertainty}\end{array}$$

(1)

where

$$S_{ice}={\displaystyle \sum _{i=1}^N{\left({\sigma }_i^{°*}-{\sigma }_{ice.i}^{°}\right)}^2}$$

(2)

$$S_{water}={\displaystyle \sum _{i=1}^N{\left({\sigma }_i^{°*}-{\sigma }_{water.i}^{°}\right)}^2}$$

(3)

and where $i=\overrightarrow{1,N}$, N is the number of scatterometer looks (beams) providing observation of the same cell from different azimuthal directions, ${\sigma }_i^{°*}$ is the measured i-NRCS value, and ${\sigma }_{ice.i}^{°}$ and ${\sigma }_{water.i}^{°}$ are the closest values of the sea ice and water GMFs, respectively, corresponding to the measured i-NRCS value.

To use this method, the appropriate sea ice and water GMFs related to the given frequency band and polarization of transmit and receive electromagnetic wave should be known.

Recently, we have considered the application of the method to the three fixed fan-beam ASCAT geometry [25]. ASCAT has been developed to operate at C-band with VV polarization only. Thus, the following GMF of the sea ice proposed for the C-band at VV polarization in [32,33] can be used:

$${\sigma }_{ice}^{°}(\theta )=\frac{1}{u(\theta )}\left({\sigma }_{ice}^{°}({\theta }_{ref})+{\displaystyle \underset{{\theta }_{ref}}{\overset{\theta }{\int }}u({\theta }^{\prime })A({\theta }^{\prime })d({\theta }^{\prime })}\right)$$

(4)

$$u({\theta }^{\prime })=\exp \left(-{\displaystyle \underset{{\theta }_{ref}}{\overset{{\theta }^{\prime }}{\int }}B({\theta }^{″})d({\theta }^{″})}\right)$$

(5)

where coefficients A(θ) and B(θ) are developed in [32] for each hemisphere,

$$A_{NH}(\theta )=0.257-0.00605\theta$$

(6)

$$B_{NH}(\theta )=0.004-0.169\cdot \exp (-0.075\theta )$$

(7)

$$A_{SH}(\theta )=-0.397+0.01314\theta -0.000131{\theta }^2$$

(8)

$$B_{SH}(\theta )=0.007-0.797\cdot \exp (-0.206\theta )$$

(9)

where NH is the Northern Hemisphere, and SH is the Southern Hemisphere. A 52.8° reference incidence angle θ_ref has been given in that study. Additionally, we have used the recent water VV polarization C-band GMF of CMOD7 [34]. Currently, CMOD7 is available in tabular form only.

At VV polarization, ASCAT (as well as SCA) provides three measured NRCSs ${\sigma }_{VV.1}^{°*}$, ${\sigma }_{VV.2}^{°*}$, and ${\sigma }_{VV.3}^{°*}$ for the same selected cell by the right-hand antennas located at the 45°, 90°, and 135° azimuthal angles to the spacecraft ground track (Figure 3). From the current NRCS triplet, the approximation of the sea ice GMF that provide with the best fit to the NRCS measured values can be calculated with the help of Equation (4) to find the sea ice summation result. Additionally, to find the water GMF approximation having the particular speed of wind U and up-wind direction α, and the best fit to the NRCS measured values, the following system of equations should be resolved:

$$\{\begin{array}{l}{\sigma }_{VV.1}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.1}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.1}^{°*}})\\ {\sigma }_{VV.2}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.2}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.2}^{°*}})\\ {\sigma }_{VV.3}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.3}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.3}^{°*}})\end{array}$$

(10)

where ${\theta }_{{\sigma }_{VV.1}^{°*}}$, ${\theta }_{{\sigma }_{VV.2}^{°*}}$, and ${\theta }_{{\sigma }_{VV.3}^{°*}}$ are the incidence angles complaint to NRCSs obtained from the same selected cell by the appropriate right-hand antennas at VV polarization, while ${\psi }_{{\sigma }_{VV.1}^{°*}}$, ${\psi }_{{\sigma }_{VV.2}^{°*}}$, and ${\psi }_{{\sigma }_{VV.3}^{°*}}$ are the azimuthal angles for observation of the selected cell by the appropriate antennas at VV polarization.

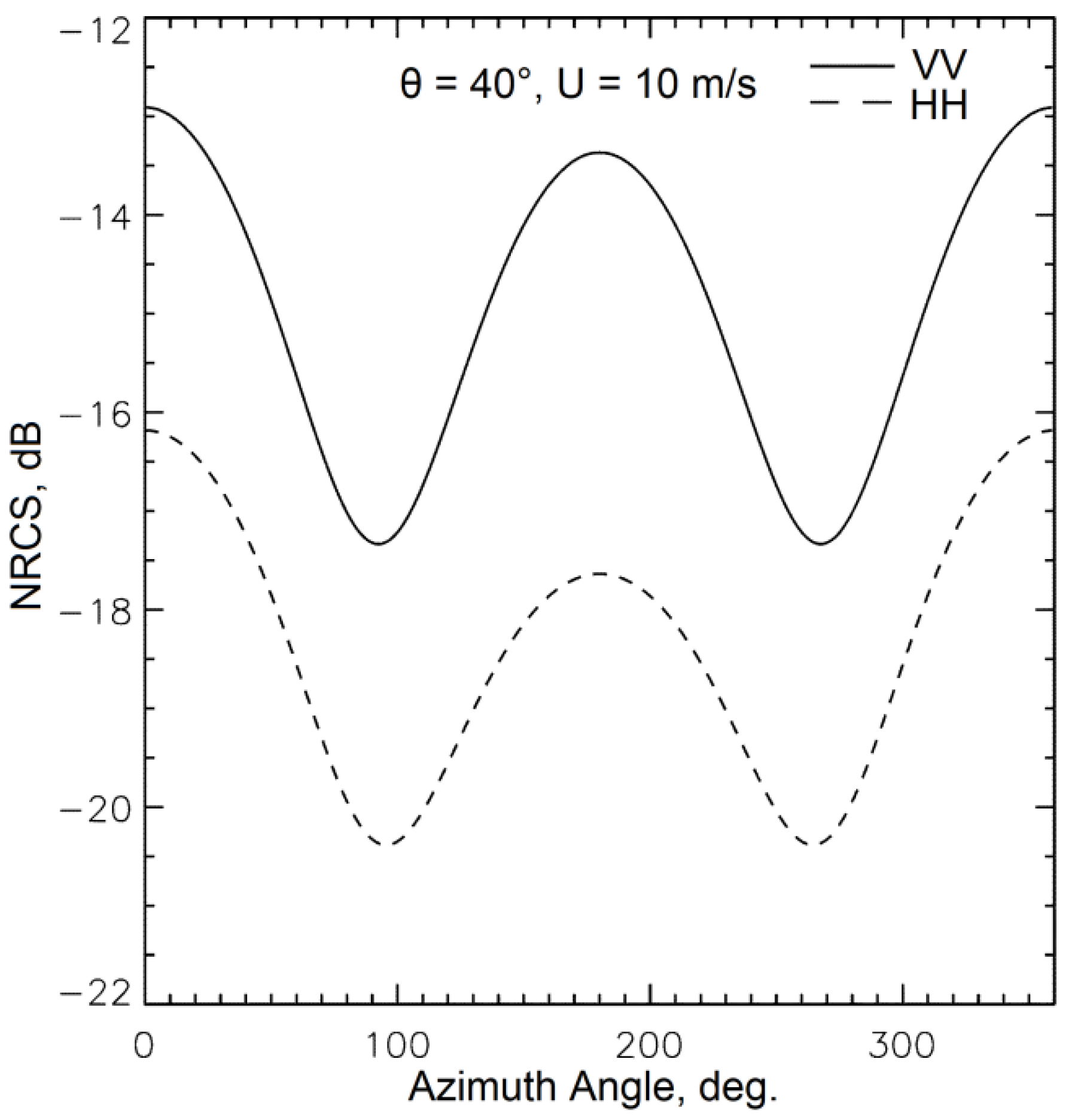
Potential ambiguity of the wind vector retrieval (providing different directions of wind from two to four) is a well-known disadvantage of such classical three fixed fan-beam satellite scatterometer geometry [35], especially when only a single polarization is being used. The ambiguity in the wind direction becomes apparent at the C-band when only the VV polarization is used due to peculiarities of the water backscattering at this band and the classical scatterometer geometry. Thus, the application of additional HH polarization in conjunction with VV polarization can provide a more accurate measurement of the wind vector as, in contrast to only one polarization measurement, two different GMF (different in azimuthal form) are used. An example of the different shapes of the azimuthal NRCS curves for VV and HH polarization at C-band is presented in Figure 4. It demonstrates clearly that at HH polarization the NRCS values are lower than at VV polarization. Another—and the most important—feature is that the difference in value between the main maximum and the second maximum is much higher at HH polarization than at VV polarization. Thus, this key polarization feature has been used here to improve the wind vector estimation and sea ice/water discrimination.

Unlike ASCAT, SCA allows to provide one more NRCS by the mid-antenna at HH polarization ${\sigma }_{HH.2}^{°*}$, and so the system of equations will have an additional equation related to the water HH polarization GMF:

$$\{\begin{array}{l}{\sigma }_{VV.1}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.1}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.1}^{°*}})\\ {\sigma }_{VV.2}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.2}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.2}^{°*}})\\ {\sigma }_{HH.2}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.2}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.2}^{°*}})\\ {\sigma }_{VV.3}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.3}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.3}^{°*}})\end{array}$$

(11)

where ${\theta }_{{\sigma }_{HH.2}^{°*}}$ is the incidence angle corresponding to measured NRCS from the same selected cell by the mid-antenna at HH polarization, ${\psi }_{{\sigma }_{HH.2}^{°*}}$ is the azimuthal angle of the selected cell at HH polarization by the mid-antenna relative to the satellite ground track, ${\theta }_{{\sigma }_{HH.2}^{°*}}={\theta }_{{\sigma }_{VV.2}^{°*}}$ and ${\psi }_{{\sigma }_{HH.2}^{°*}}={\psi }_{{\sigma }_{VV.2}^{°*}}$ in the case considered.

Unfortunately, in order to use the HH polarization in addition to VV polarization, the water HH polarization GMF should be available for the given frequency band as well. As appropriate operational water GMF for the HH polarization is currently not available at the C-band, a formula for the polarization ratio [36] can be used in that case until the appropriate water HH polarization C-band GMF is developed. As real azimuthal NRCS dependences are different at VV and HH polarizations, the polarization ratio should depend not only on the incidence angle but also on the azimuth angle. Otherwise, the use of the generated water HH polarization GMF could not be profitable, as it will have the same azimuthal NRCS shape like the initial VV polarization GMF only displaced in value. Unfortunately, the main disadvantage of using the polarization ratio to generate a HH polarization GMF from a VV polarization GMF is that such an NRCS transformation cannot provide a precise GMF (in comparison to the GMF obtained from a real NRCS data set) and will induce additional errors in the estimation of the wind speed and direction [36]. Thus, the polarization ratio can be used only in those cases where the operational water GMF for the HH polarization is unavailable.

For more accurate sea wind measurement and better sea ice/water discrimination, it is obvious that SCA measurement ability can be improved with the help of the HH polarization channel capable of providing two extra NRCSs ${\sigma }_{HH.1}^{°*}$ and ${\sigma }_{HH.3}^{°*}$, for the fore- and aft-antennas, respectively. In that case, the system of six equations has to be solved; three for the VV and three for the HH polarization, respectively:

$$\{\begin{array}{l}{\sigma }_{VV.1}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.1}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.1}^{°*}})\\ {\sigma }_{HH.1}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.1}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.1}^{°*}})\\ {\sigma }_{VV.2}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.2}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.2}^{°*}})\\ {\sigma }_{HH.2}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.2}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.2}^{°*}})\\ {\sigma }_{VV.3}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.3}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.3}^{°*}})\\ {\sigma }_{HH.3}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.3}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.3}^{°*}})\end{array}$$

(12)

where ${\theta }_{{\sigma }_{HH.1}^{°*}}$ and ${\theta }_{{\sigma }_{HH.3}^{°*}}$ are the incidence angles corresponding the measured NRCS values from the same selected cell observed at HH polarization with the fore- and aft-antennas, ${\psi }_{{\sigma }_{HH.1}^{°*}}$ and ${\psi }_{{\sigma }_{HH.3}^{°*}}$ are the selected cell azimuthal angles at HH polarization corresponding the fore- and aft-antennas directions relative to the spacecraft ground track, ${\theta }_{{\sigma }_{HH.1}^{°*}}={\theta }_{{\sigma }_{VV.1}^{°*}}$, ${\theta }_{{\sigma }_{HH.2}^{°*}}={\theta }_{{\sigma }_{VV.2}^{°*}}$, ${\theta }_{{\sigma }_{HH.3}^{°*}}={\theta }_{{\sigma }_{VV.3}^{°*}}$, ${\psi }_{{\sigma }_{HH.1}^{°*}}={\psi }_{{\sigma }_{VV.1}^{°*}}$, ${\psi }_{{\sigma }_{HH.2}^{°*}}={\psi }_{{\sigma }_{VV.2}^{°*}}$, and ${\psi }_{{\sigma }_{HH.3}^{°*}}={\psi }_{{\sigma }_{VV.3}^{°*}}$ in the case considered.

Thus, usage of both VV and HH channels for all three antennas, in contrast to two polarization channels used only for the mid-antenna of SCA, will allow providing better wind measurement and discrimination of the sea ice and water within the classical three fixed fan-beam geometry. As only the sea ice VV polarization GMF is used in the sea ice/water discrimination procedure (Equations (1)–(3)), the sea ice and water summation results are calculated only with NRCSs measured at VV polarization and so the number of looks in Equations (2) and (3) is still equal to three for the classical three-beam geometry.

Recently in [37], we have demonstrated that in order to provide an accurate and unambiguous retrieval of the wind vector, at least four azimuthally star-configured beams (looks) are required at the same incidence angle. The airborne star geometry [38] and some other earlier considered airborne one- [39] or multi-beam [40,41,42,43] geometries or sector scanning airborne instruments operated in the scatterometer mode [44,45,46,47,48,49] cannot be implemented for the satellite scatterometer to observe the same cell and to achieve better sea ice and water discrimination. Therefore, using the azimuthal isotropy of the sea ice backscattering in contrast to the anisotropy of the water surface backscattering, we considered another five hypothetical, fixed fan-beam scatterometer geometry constructed by adding an “extra” fore-antenna and an “extra” aft-antenna having 32.5° and 147.5° azimuthal directions relative to the spacecraft ground track, respectively, [25] as presented in Figure 3.

If only VV polarization is used, the hypothetical five fixed fan-beam scatterometer will provide five measured NRCSs ${\sigma }_{VV.1}^{°*}$, ${\sigma }_{VV.2}^{°*}$, ${\sigma }_{VV.3}^{°*}$, ${\sigma }_{VV.4}^{°*}$, and ${\sigma }_{VV.5}^{°*}$ (three by the “classical” beams, and two more by the “extra” beams), and thus the system of equations will contain five equations (each for its own azimuthal direction relative to the satellite ground track) [25]:

$$\{\begin{array}{l}{\sigma }_{VV.1}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.1}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.1}^{°*}})\\ {\sigma }_{VV.2}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.2}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.2}^{°*}})\\ {\sigma }_{VV.3}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.3}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.3}^{°*}})\\ {\sigma }_{VV.4}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.4}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.4}^{°*}})\\ {\sigma }_{VV.5}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.5}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.5}^{°*}})\end{array}$$

(13)

where ${\theta }_{{\sigma }_{VV.1}^{°*}}$, ${\theta }_{{\sigma }_{VV.2}^{°*}}$, ${\theta }_{{\sigma }_{VV.3}^{°*}}$, ${\theta }_{{\sigma }_{VV.4}^{°*}}$, and ${\theta }_{{\sigma }_{VV.5}^{°*}}$ are the incidence angles complaint to NRCS values obtained from the same selected cell observed by the “classical” three-beam antennas, and two “extra” antennas at VV polarization, respectively, ${\psi }_{{\sigma }_{VV.1}^{°*}}$, ${\psi }_{{\sigma }_{VV.2}^{°*}}$, ${\psi }_{{\sigma }_{VV.3}^{°*}}$, ${\psi }_{{\sigma }_{VV.4}^{°*}}$, and ${\psi }_{{\sigma }_{VV.5}^{°*}}$ are the azimuthal directions of the selected cell at VV polarization corresponding to the appropriate beams relative to the spacecraft ground track. Thus, this hypothetical five-antenna case compared to the classical three-antenna case at single VV polarization will significantly improve the estimation of the wind vector and discrimination of the sea ice and water as the number of directions observed is five, and the NRCS measurements are obtained from significantly different azimuthal directions than in the classical three-antenna case.

Considering further improvements of the hypothetical five-beam scatterometer, the use of both VV and HH channels for all antennas fully uncovers the advantages of the five fixed fan-beam geometry providing the wind direction retrieval without ambiguity, and, as a result, better discrimination of the sea ice and water. Consequently, the scatterometer will provide five NRCSs at VV polarization ${\sigma }_{VV.1}^{°*}$, ${\sigma }_{VV.2}^{°*}$, ${\sigma }_{VV.3}^{°*}$, ${\sigma }_{VV.4}^{°*}$, ${\sigma }_{VV.5}^{°*}$, and the same number of NRCSs at HH polarization ${\sigma }_{HH.1}^{°*}$, ${\sigma }_{HH.2}^{°*}$, ${\sigma }_{HH.3}^{°*}$, ${\sigma }_{HH.4}^{°*}$, ${\sigma }_{HH.5}^{°*}$. Thus, a system of 10 equations, including five for the VV and five for the HH polarization, respectively, has to be resolved in that case:

$$\{\begin{array}{l}{\sigma }_{VV.1}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.1}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.1}^{°*}})\\ {\sigma }_{HH.1}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.1}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.1}^{°*}})\\ {\sigma }_{VV.2}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.2}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.2}^{°*}})\\ {\sigma }_{HH.2}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.2}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.2}^{°*}})\\ {\sigma }_{VV.3}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.3}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.3}^{°*}})\\ {\sigma }_{HH.3}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.3}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.3}^{°*}})\\ {\sigma }_{VV.4}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.4}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.4}^{°*}})\\ {\sigma }_{HH.4}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.4}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.4}^{°*}})\\ {\sigma }_{VV.5}^{°*}=GMF(U,{\theta }_{{\sigma }_{VV.5}^{°*}},\alpha +{\psi }_{{\sigma }_{VV.5}^{°*}})\\ {\sigma }_{HH.5}^{°*}=GMF(U,{\theta }_{{\sigma }_{HH.5}^{°*}},\alpha +{\psi }_{{\sigma }_{HH.5}^{°*}})\end{array}$$

(14)

where ${\theta }_{{\sigma }_{HH.1}^{°*}}$, ${\theta }_{{\sigma }_{HH.2}^{°*}}$, ${\theta }_{{\sigma }_{HH.3}^{°*}}$, ${\theta }_{{\sigma }_{HH.4}^{°*}}$, and ${\theta }_{{\sigma }_{HH.5}^{°*}}$ are the incidence angles complaint to NRCS values obtained by the same antennas at HH polarization, respectively, ${\psi }_{{\sigma }_{HH.1}^{°*}}$, ${\psi }_{{\sigma }_{HH.2}^{°*}}$, ${\psi }_{{\sigma }_{HH.3}^{°*}}$, ${\psi }_{{\sigma }_{HH.4}^{°*}}$, and ${\psi }_{{\sigma }_{HH.5}^{°*}}$ are the azimuthal directions of the selected cell at HH polarization corresponded the appropriate beams relative to the spacecraft ground track, ${\theta }_{{\sigma }_{HH.1}^{°*}}={\theta }_{{\sigma }_{VV.1}^{°*}}$, ${\theta }_{{\sigma }_{HH.2}^{°*}}={\theta }_{{\sigma }_{VV.2}^{°*}}$, ${\theta }_{{\sigma }_{HH.3}^{°*}}={\theta }_{{\sigma }_{VV.3}^{°*}}$, ${\theta }_{{\sigma }_{HH.4}^{°*}}={\theta }_{{\sigma }_{VV.4}^{°*}}$, ${\theta }_{{\sigma }_{HH.4}^{°*}}={\theta }_{{\sigma }_{VV.4}^{°*}}$, ${\psi }_{{\sigma }_{HH.1}^{°*}}={\psi }_{{\sigma }_{VV.1}^{°*}}$, ${\psi }_{{\sigma }_{HH.2}^{°*}}={\psi }_{{\sigma }_{VV.2}^{°*}}$, ${\psi }_{{\sigma }_{HH.3}^{°*}}={\psi }_{{\sigma }_{VV.3}^{°*}}$, ${\psi }_{{\sigma }_{HH.4}^{°*}}={\psi }_{{\sigma }_{VV.4}^{°*}}$, and ${\psi }_{{\sigma }_{HH.5}^{°*}}={\psi }_{{\sigma }_{VV.5}^{°*}}$.

Thus, the combined use of VV and HH channels in this hypothetical five-antenna case comparing with previous geometries and polarization cases considered will significantly improve the estimation of the wind vector and discrimination of the sea ice and water.

Because the sea ice HH polarization GMF is currently unavailable, only the sea ice VV polarization GMF has to be used. So the sea ice/water discrimination procedure (Equations (1)–(3)) uses the sea ice and water summation results can be obtained only from the VV polarization NRCSs. For this reason, the number of scatterometer looks (in Equations (2) and (3)) is equal for the hypothetical five-beam geometry.

As CMOD7 is available in a tabular form only and taking into account the specifics of classical and hypothetical scatterometer antenna configurations, to speed up the calculation of the current wind speed (and up-wind direction) for a given cell under solving systems of Equations (10)–(14), a procedure similar to the procedure presented in [48] can be proposed. The procedure consists in finding the lower U_L and upper U_U values of the wind speed for ranges of possible wind speeds for each measured NRCS:

$$U_L=\max \{U_{1L.VV},U_{2L.VV},\dots ,U_{N_{VV}L.VV},U_{1L.HH},U_{2L.HH},\dots ,U_{N_{HH}L.HH}\}$$

(15)

$$U_U=\min \{U_{1U.VV},U_{2U.VV},\dots ,U_{N_{VV}U.VV},U_{1U.HH},U_{2U.HH},\dots ,U_{N_{HH}U.HH}\}$$

(16)

where $U_{1L.VV}$, $U_{2L.VV}$, …, $U_{N_{VV}L.VV}$ are the possible lower wind speeds obtained by appropriate antenna at VV polarization, N_VV is the number of antenna used at VV polarization, $U_{1L.HH}$, $U_{2L.HH}$, …, $U_{N_{HH}L.HH}$ are the possible lower wind speeds obtained by appropriate antenna at HH polarization, N_HH is the number of antenna used at HH polarization, $U_{1U.VV}$, $U_{2U.VV}$, …, $U_{N_{VV}U.VV}$ are the possible upper wind speeds obtained by appropriate antenna at VV polarization, $U_{1U.HH}$, $U_{2U.HH}$, …, $U_{N_{HH}U.HH}$ are the possible upper wind speeds obtained by appropriate antenna at HH polarization. To calculate the possible lower and upper wind speeds obtained by the appropriate antenna, the appropriate measured NRCSs, water GMFs, and polarizations are used.

3. Results and Discussion

The need of consideration of the hypothetical multiple fixed fan-beam spaceborne scatterometer geometries along with classical three fixed fan-beam geometry as well as the dual VV and HH polarizations case is based on the fact that classical three-antenna spaceborne scatterometer has a significant disadvantage that consists in ambiguous retrieval of the sea wind direction when instead of unique wind direction it provides from two to four directions. This disadvantage is also essential at the C-band application with VV polarization as at these band and polarization the water azimuthal NRCS dependence is smooth and the difference between the general maximum (up-wind) and the secondary maximum (down-wind) are relatively low even at medium incidence angles. From that point of view, this difference is relatively larger at HH polarization [50], which is more advantageous for decreasing the number of the ambiguous wind directions from three/four directions to two directions, especially when both VV and HH polarization are used at the wind measurement at the classical three fixed fan-beam geometry.

Currently, to eliminate such wind direction ambiguity, the wind information obtains from the neighbor cells, successive spacecraft passes over the same selected cell, or other external sources are used. Similarly, to eliminate uncertainties of the sea ice/water discrimination, several spacecraft passes are used to observe the same area. Such procedures make longer data acquisition and, consequently, real-time dissemination of results for several orbits.

As the water azimuthal NRCS dependence at the constant medium incidence angle is smooth and has four extremums (Figure 4), it is evident that to remove the wind direction ambiguity at a single spacecraft pass, a number of azimuthal looks for the same cell need to be increased. Recently, we have demonstrated that in case of an airborne scatterometer provided NRCS measurements at the same incidence angle, at least four star-configured antennas are required to achieve an unambiguous recovery of the sea wind direction [37]. In the case of the spacecraft scatterometer with the fixed antennas, it is impossible to realize the star geometry measurement observing the same cell as its antennas have different incidence angles and the maximum azimuthal difference of the antennas’ locations is limited by the right or left swath. Hence, the realistic number of antennas for such a spacecraft scatterometer needed to reveal the sea ice isotropy in contrast to the water anisotropy backscattering at the discrimination of the sea ice and water, and to increase a number of possible unambiguous estimations of the wind direction for a single spacecraft pass is equal to five [25].

To compare the classical three fan-beam geometry with the hypothetical five fan-beam geometry (Figure 2), we have estimated errors in the wind speed and direction measurement in the worst case scenario of the wind measurement for a single spacecraft pass and without taking into account the wind information from the neighbor cells or other external sources. For that purpose, we have performed a simulation using CMOD7 VV polarization GMF [34]. A Rayleigh Power (Exponential) distribution has been used to generate 9613 “measured” NRCS samples for each combination of the incidence and azimuthal angles with their further integration to obtain an appropriate “measured” NRCS value. A Monte Carlo simulation with 50 independent trials for each combination of the wind speed and direction have been used to evaluate the errors of the wind vector retrieval in the wind speed range from 2 to 30 m/s. They have been evaluated using Equations (10) and (12) for the classical three fan-beam geometry and hypothetical five fan-beam geometry, respectively.

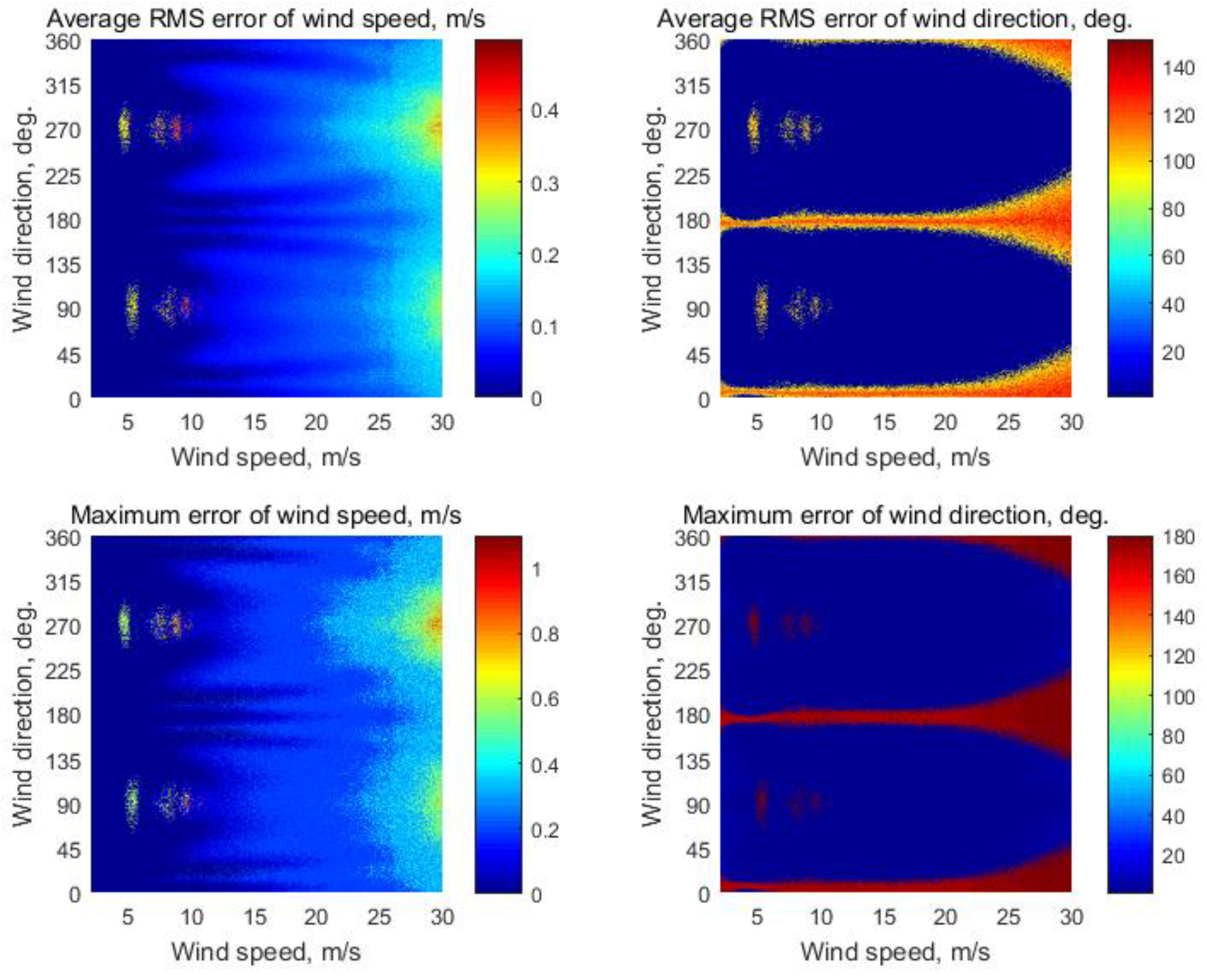
The simulation results for the classical three fan-beam geometry are presented in Figure 5. The maximum errors of the wind speed and direction retrieval, in this case, are 1.1 m/s and 180° that confirm that the wind direction ambiguity is typical for the classical three fan-beam geometry at the wind measurement for a single spacecraft pass and without taking into account the wind information from the neighbor cells or other sources.

Figure 6 demonstrates the simulation results for the hypothetical five fan-beam geometry. In that case, the maximum errors of the wind speed and direction retrieval are 0.8 m/s and about 180°. For the hypothetical five fan-beam geometry, the maximum error of the wind speed is significantly lower than for the classical three fan-beam geometry. Additionally, it provides a reduced number of possible ambiguous measurements of the wind direction. The simulation results demonstrate the superiority of the hypothetical five fan-beam geometry over the classical three fan-beam geometry providing more accurate wind speed and, especially, wind direction measurement even at the single (VV) polarization especially in the wind speed range of 2 to 27 m/s. This will lead to better sea ice/water discrimination by Equation (1).

Simulation examples of the sea ice/water discrimination at the single VV polarization by Equation (1) with the similar ASCAT classical three fan-beam geometry and hypothetical five fan-beam geometry using the system of Equations (10) and (13), respectively, demonstrate the applicability of the sea ice/water discrimination method as presented in [25]. They also demonstrate the superiority of the hypothetical five fan-beam geometry over the classical three fan-beam geometry at the sea ice/water discrimination.

Analyzing SCA capability (as the classical three fixed fan-beam antenna scatterometer using the additional HH channel to VV channel for the mid-antenna), it looks slightly better in comparison to the capability of ASCAT (previous classical three fixed fan-beam antenna scatterometer using only VV polarization for all the antennas). It is due to the sea wind direction recover with the system of Equation (11) of course is better than with the system of Equation (10) while both measuring geometries still have three antennas. To use the full potential of SCA measuring geometry, the ability of the three-antenna scatterometer measurement can be improved when the HH channel will be implemented for all three antennas in addition to the VV channel to provide wind direction retrieval with the system of Equation (12). At the same time, the hypothetical fixed five-beam configuration allows obtaining the required number of different azimuthal directions to observe the same cell to perform measurement the wind direction without ambiguity even at VV polarization only with the system of Equation (13), while the use of the additional HH channel for all antennas will provide better retrieval of the wind direction with the system of Equation (14), and discrimination of the sea ice and water. Whereupon, the five-antenna configuration will lead to narrowing the swath when the scatterometer operates in the five beam mode in comparison with the SCA classical three-antenna configuration, as the highest incidence angle of the “extra” fore- and aft-beams of the hypothetical five-beam scatterometer cannot exceed the highest incidence angle of the SCA fore- and aft-beams.

Lack of reliable water C-band GMF for the HH polarization can be supplied by the known polarization ratios [36] developed to convert the existent water VV polarization C-band GMF CMOD7 to its HH polarization version to use the systems of Equations (11)–(12) and (14) for estimation of the wind vector. The polarization ratio should also depend on the azimuth angle; otherwise, the generated water HH polarization GMF will have the same azimuthal form of the initial VV polarization GMF just shifted in the NRCS value having the identical azimuthal NRCS dependence, and so could not be profitable in such application. However, such NRCS transformation from VV to HH polarization certainly induces an error in the wind estimation [51]. Unfortunately, further quantitative assessment of the errors of the wind speed and direction retrieval using dual VV and HH polarization based on systems of Equations (11)–(12) and (14) was impossible due to unavailability of the azimuthally dependable C-band polarization ratio covering the range of SCA incidence angles; the only azimuthally dependable polarization ratio from [52] is valid only for the range of incidence angles from 10° to 43° and do not suit for simulations in those cases.

Recently, the first water HH polarization C-band GMF designed from the real HH polarization NRCS data but not by known polarization ratios has been presented in [53]. Unfortunately, this newest GMF has been developed for the sea wind retrieval by SAR in the analytical form similar to the water VV polarization C-band GMF CMOD5 [53,54] (different from the newest CMOD7). Its valid incidence angles do not cover in full the range of CSA incidence angles (especially for fore- and aft-antennas), and so it also cannot be used for simulations in the considered cases.

Currently, the sea ice C-band GMF for HH polarization is unavailable, and thus HH polarization measured NRCSs are used here only for the wind direction retrieval to improve the discrimination of the sea ice and water. Therefore, the algorithm for discrimination of the sea ice and water by Equation (1) relies upon the number of looks (antennas) within a VV channel only. However, to uncover the full potential of the dual VV and HH polarization measurement for the sea ice/water discrimination and sea ice classification, a reliable sea ice C-band GMF for HH polarization is required.

4. Conclusions

Analysis of the EPS/Metop-SG scatterometer mission science plan for 2023–2044 indicates that multiple fixed fan-beam spaceborne scatterometer geometries and polarization possibilities could be effectively used for the sea ice/water discrimination in the case of planned Metop-SG B1, B2, and B3 C-band scatterometers as well as in hypothetical cases with the increased number of antennas and polarizations.

The classical three fan-beam spacecraft scatterometer geometry at the single VV polarization at C-band is characterized by the ambiguous retrieval of the sea wind direction [35]. The hypothetical five fan-beam geometry can reduce this disadvantage and provide more accurate wind vector measurement for a single spacecraft pass. It, consequently, will improve the sea ice/water discrimination based on Equation (1). At the same time, the five-beam geometry narrows the swath compared to the SCA classical three-beam geometry as the highest incidence angle of the “extra” fore- and aft-beams of the hypothetical five-beam scatterometer cannot exceed the highest incidence angle of the SCA fore- and aft-beams.

Locations of the spacecraft scatterometer fixed fan-beam antenna are limited by the right or left swath to observe the same cell from various azimuthal directions, and so further improvement of the wind vector retrieval and sea ice/water discrimination can be achieved using the additional HH polarization channel for the beams because the VV and HH polarization azimuthal NRCS curves have different azimuthal dependences. The difference in the NRCS value between the main maximum and the second maximum is much higher at HH polarization than at VV polarization. Increasing the number of additional HH polarization channels in addition to VV polarization channels will therefore make the measurements more accurate.

To uncover the full potential of the dual VV and HH polarization measurement for the sea ice/water discrimination, sea ice classification, as well as wind vector retrieval, reliable sea ice and water C-band GMFs for HH polarization covering the incidence angle range of a scatterometer are required. Currently, the sea ice C-band GMF for HH polarization is unavailable, and thus the measured HH polarization NRCSs can be used here only for the wind direction retrieval to improve the discrimination of the sea ice and water. The water C-band GMF for the HH polarization suitable for the SCA or hypothetical five-beam spacecraft scatterometer configuration is also currently unavailable. The only water GMF was designed from the real HH polarization NRCS data [53] designed in the analytical form similar to the water VV polarization C-band GMF CMOD5. Unfortunately, the water GMF from [53] is different from the newest VV polarization CMOD7 and does not cover the full range of CSA incidence angles. Alternatively, the azimuth dependable polarization ratio, when available, could be used to generate the water HH polarization GMF from the suitable VV polarization GMF until the reliable water HH polarization C-band GMF corresponding the CMOD7 form and valid for the SCA range of the incidence angles will be developed.

Finally, the obtained results can be used for the development of new multiple fixed fan-beam and single fan-beam rotating spaceborne scatterometers, improving their capability in the measurement of the sea wind, sea ice/water discrimination, and classification of the sea ice in high latitude and polar regions providing near-real-time measurement and data acquisition within a single satellite pass to be a benefit for forthcoming spaceborne scatterometer missions.