Capability of Jason-2 Subwaveform Retrackers for Significant Wave Height in the Calm Semi-Enclosed Celebes Sea
Abstract
1. Introduction
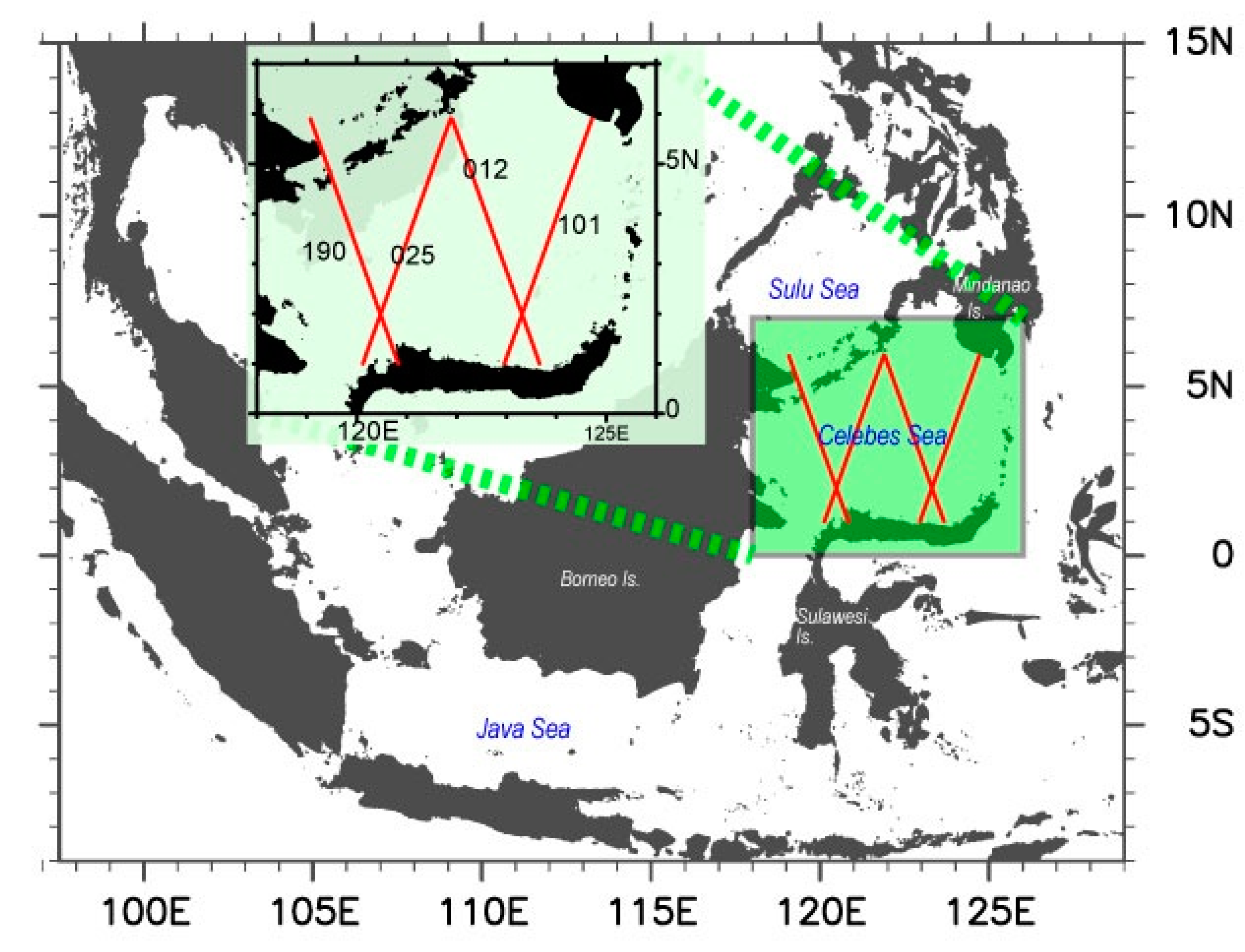
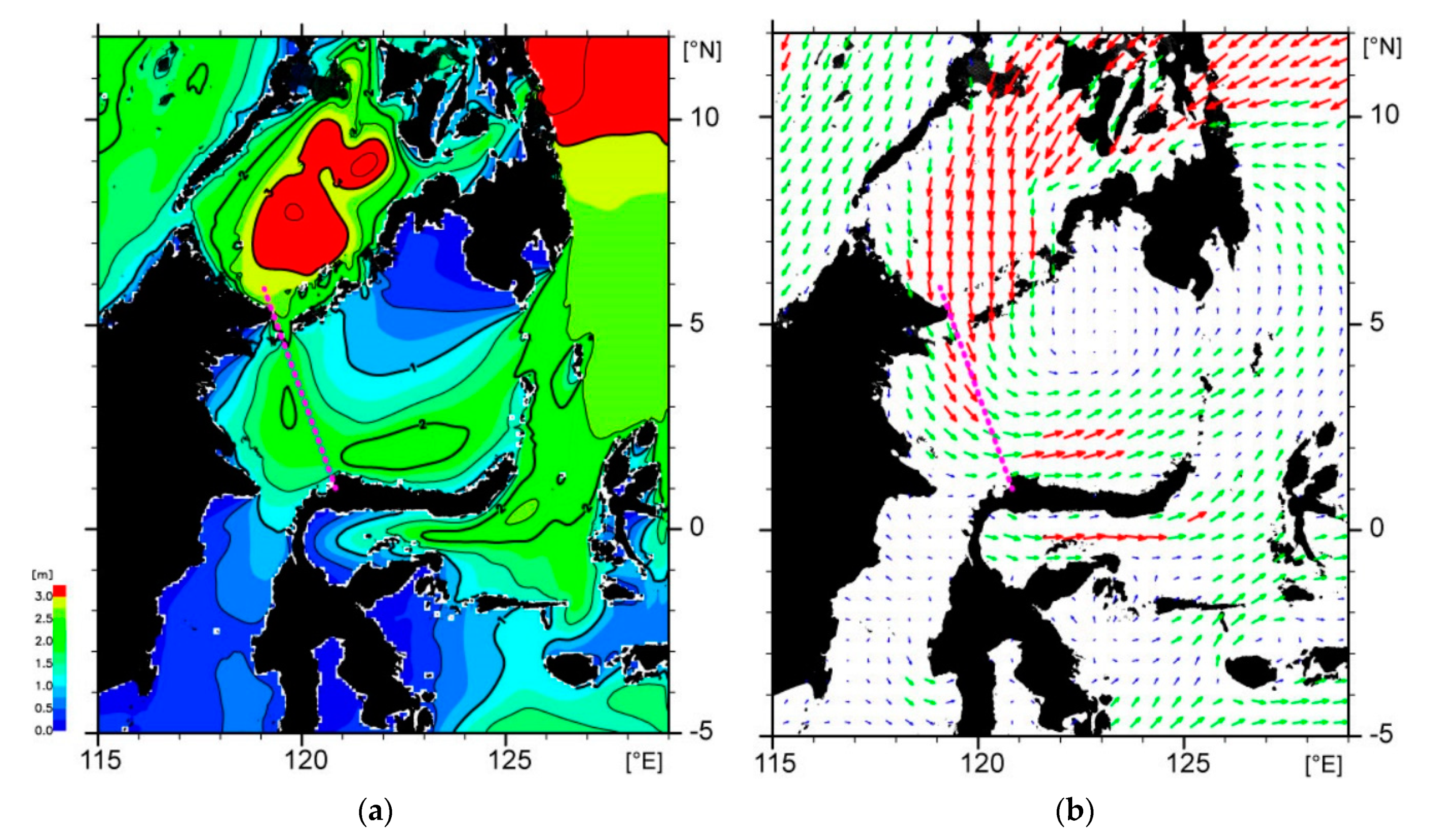
2. Materials and Methods
3. Results
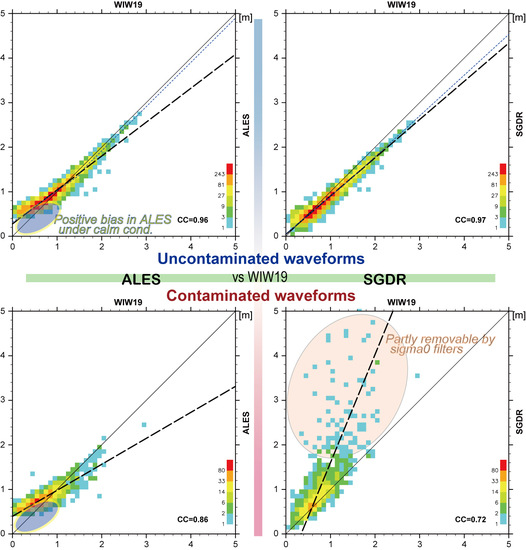
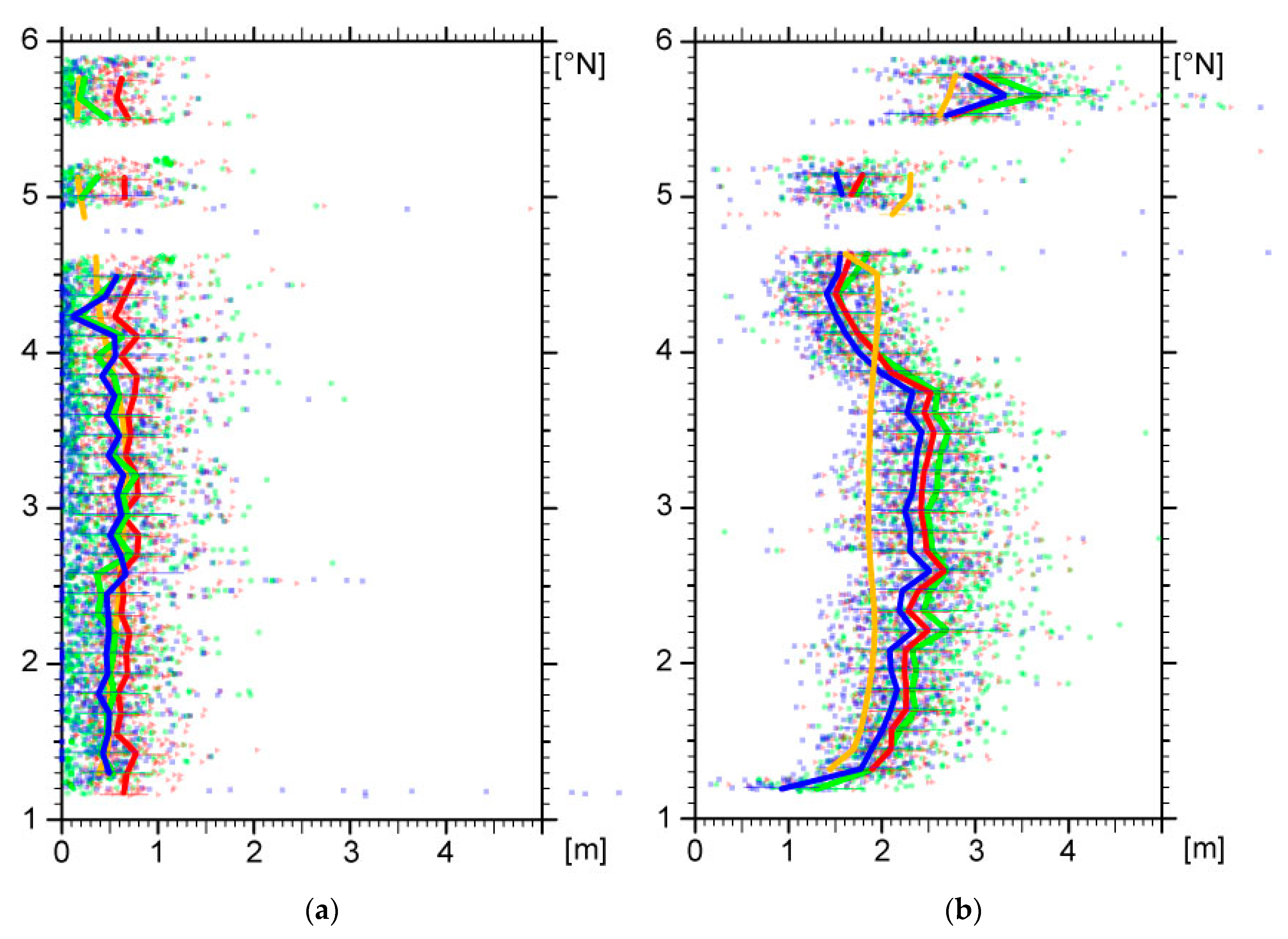
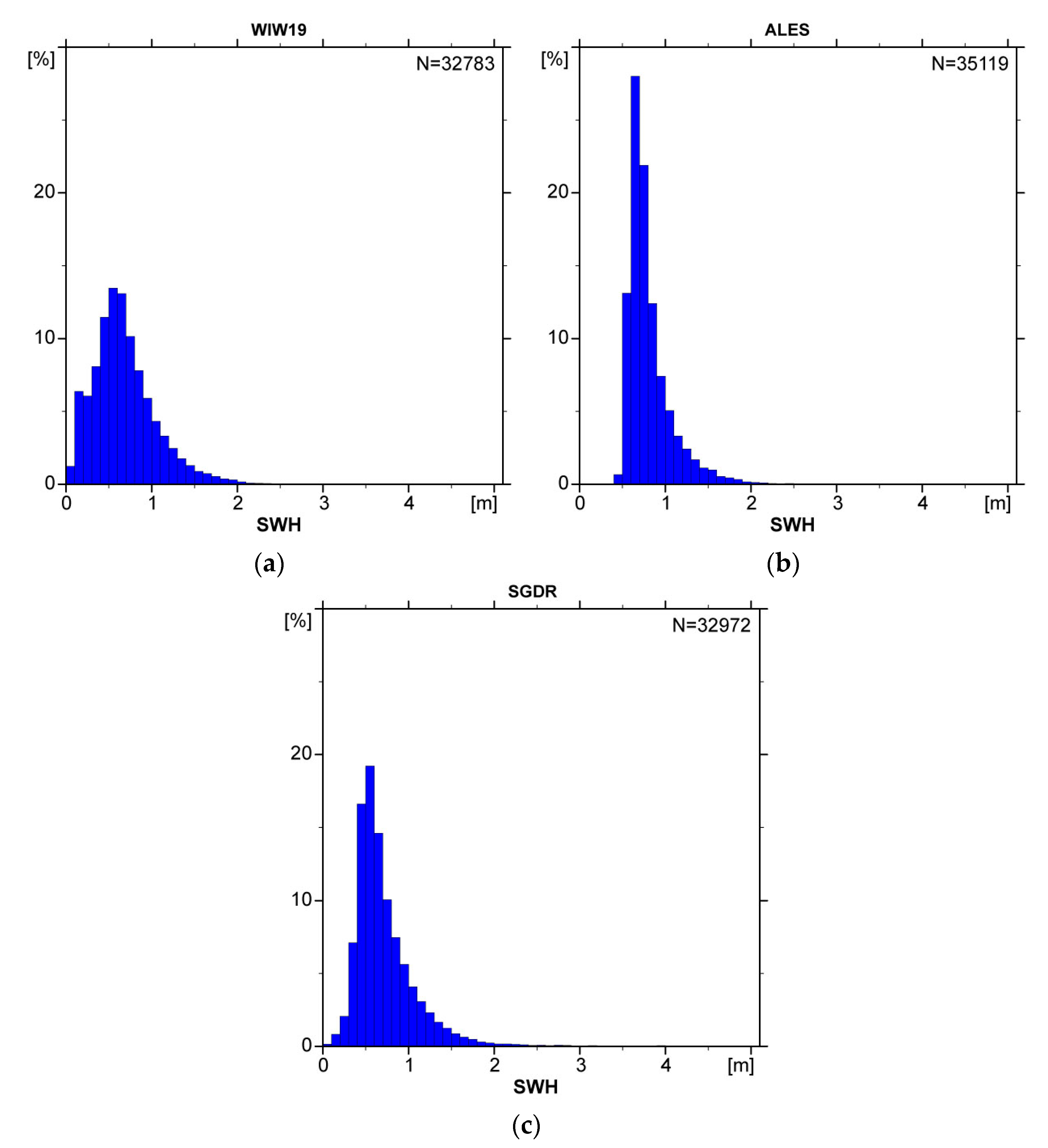
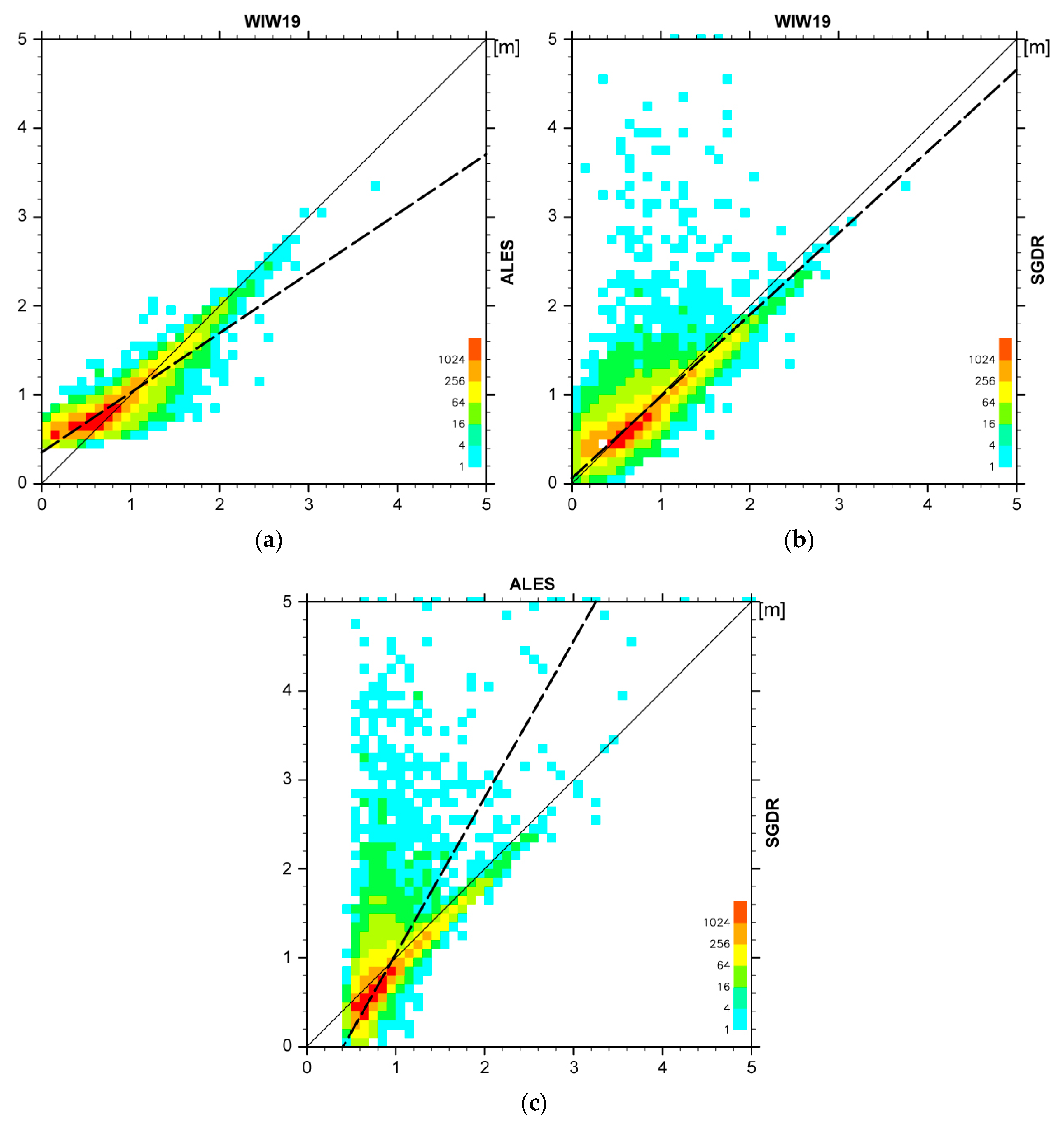
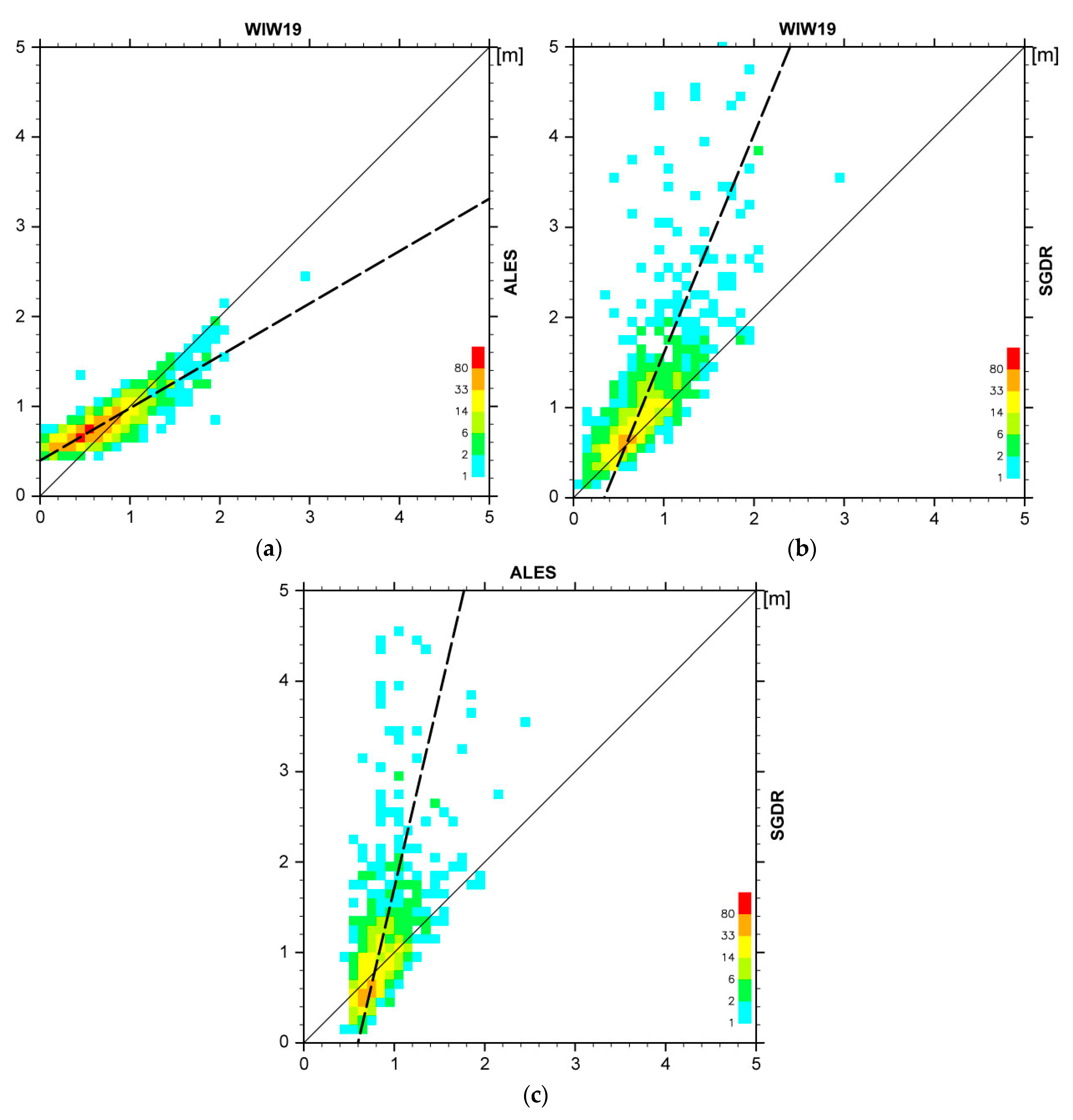
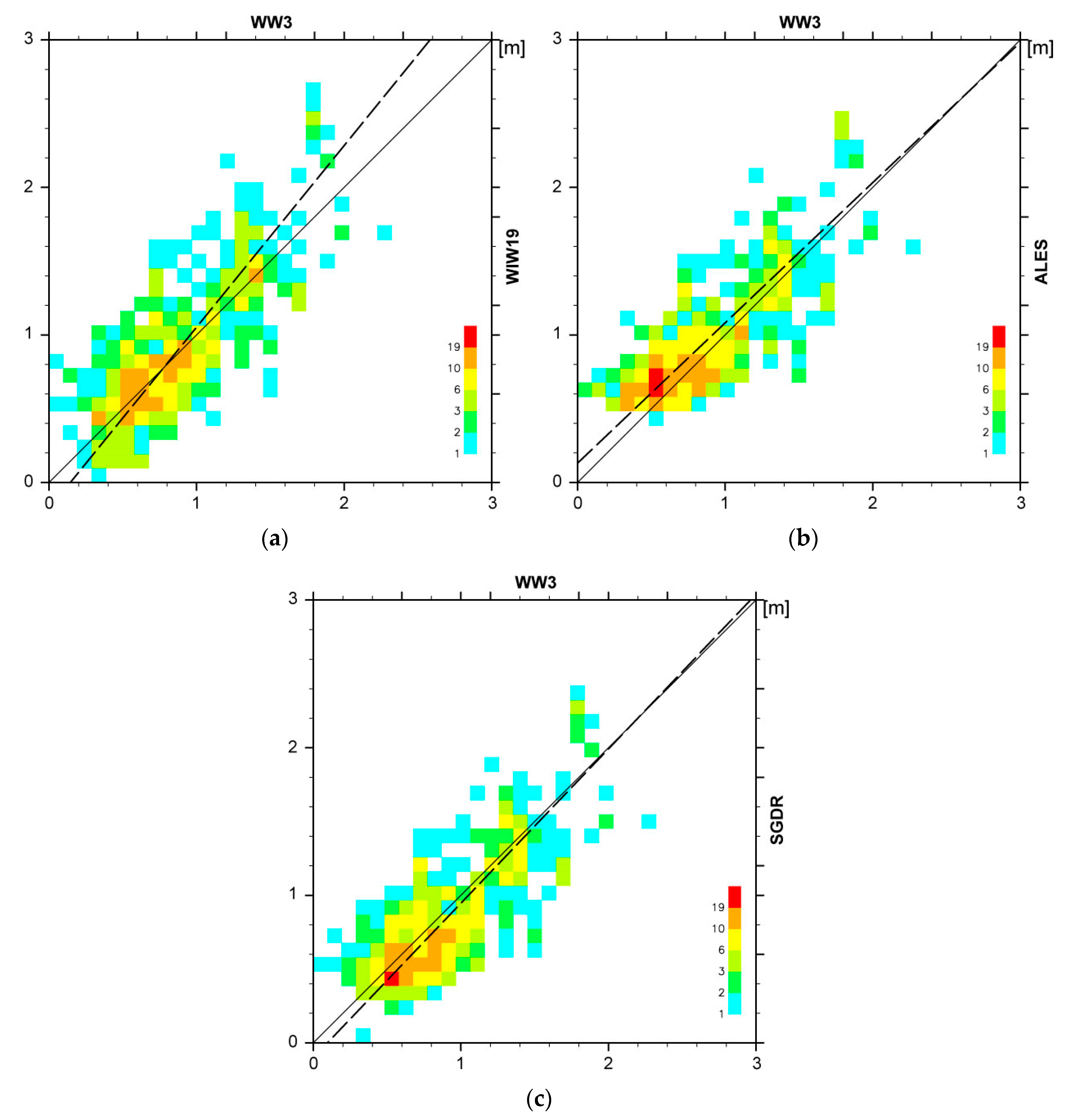
3.1. Inter-Comparisons among Three Algorithms
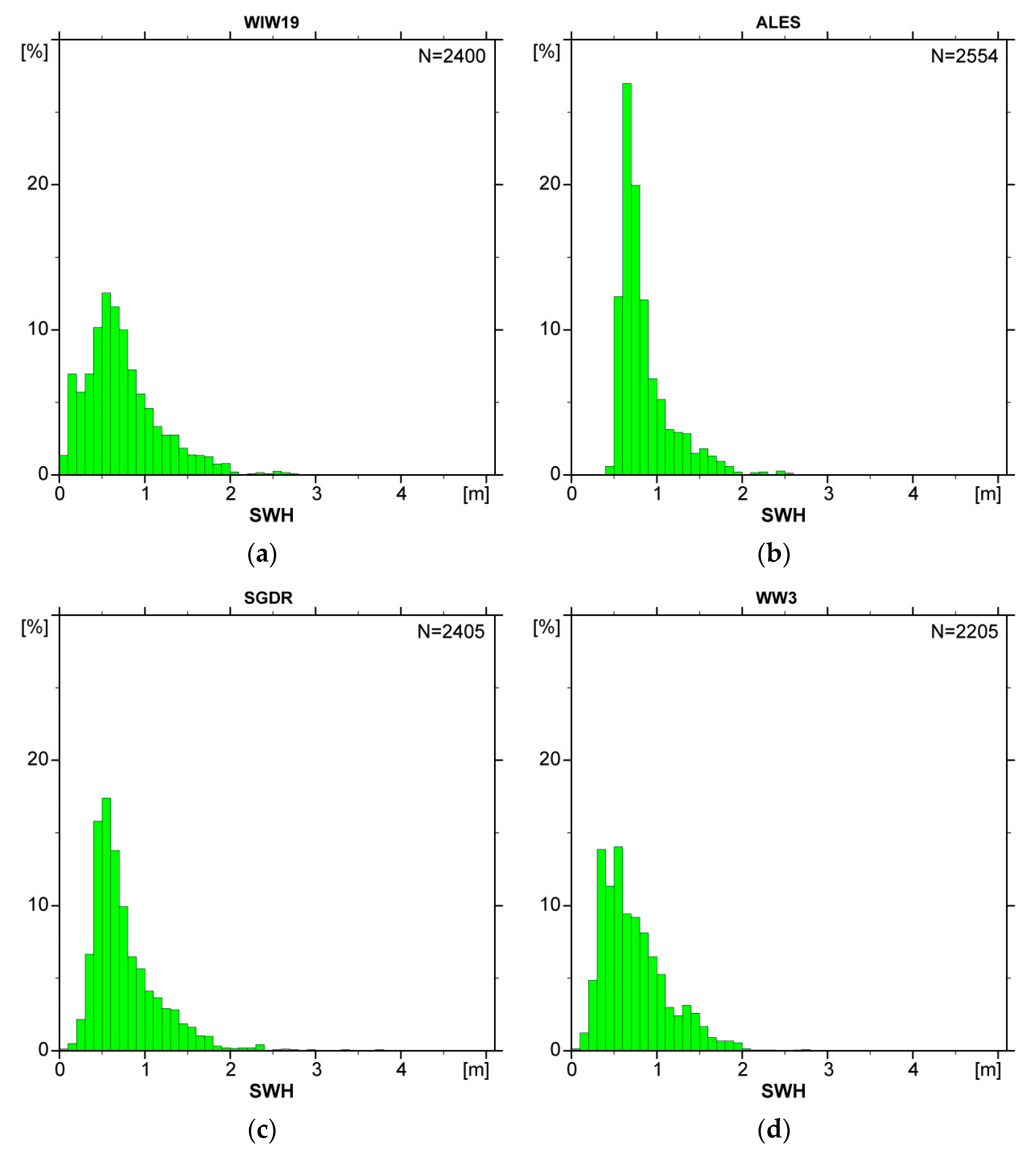
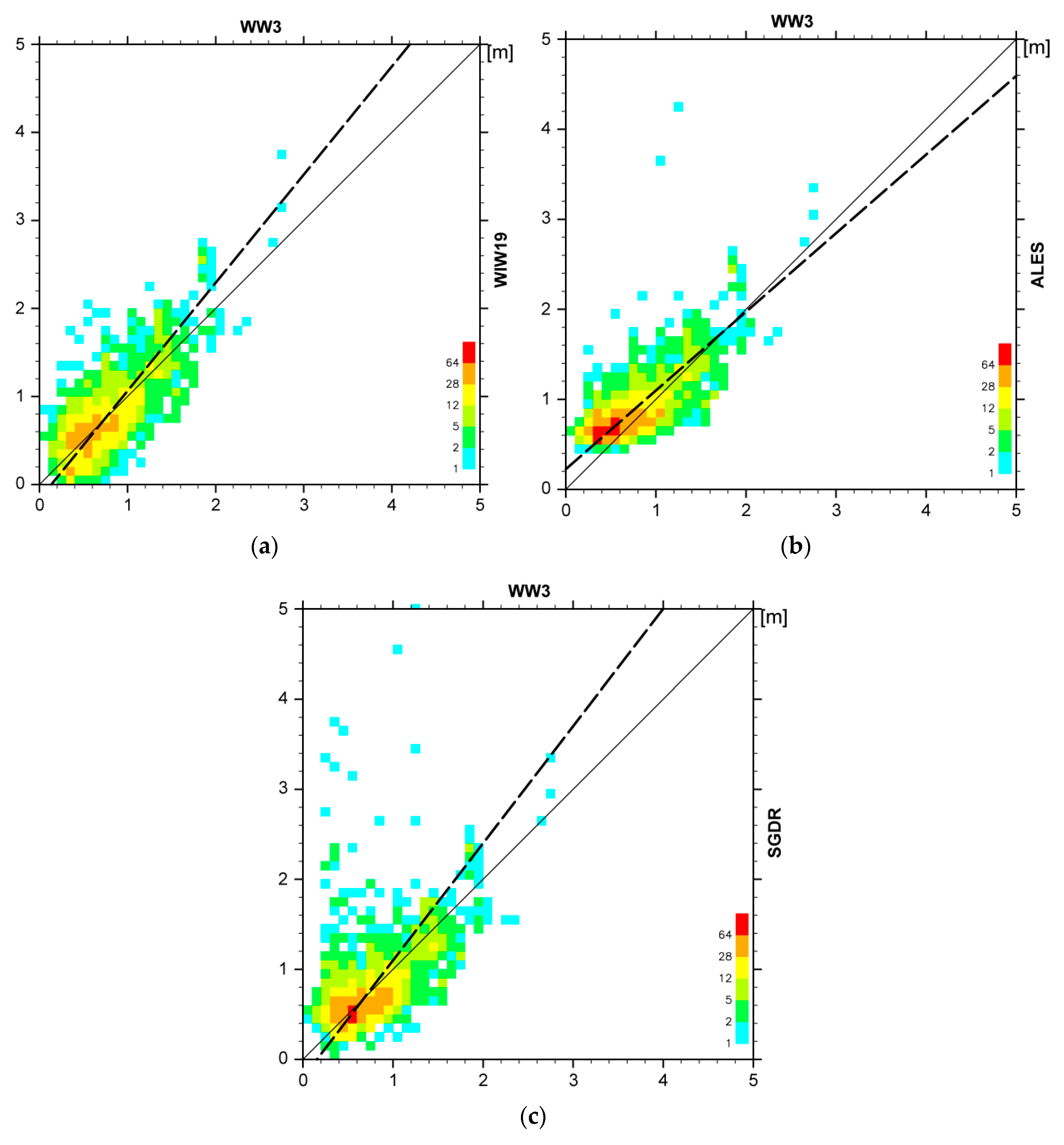
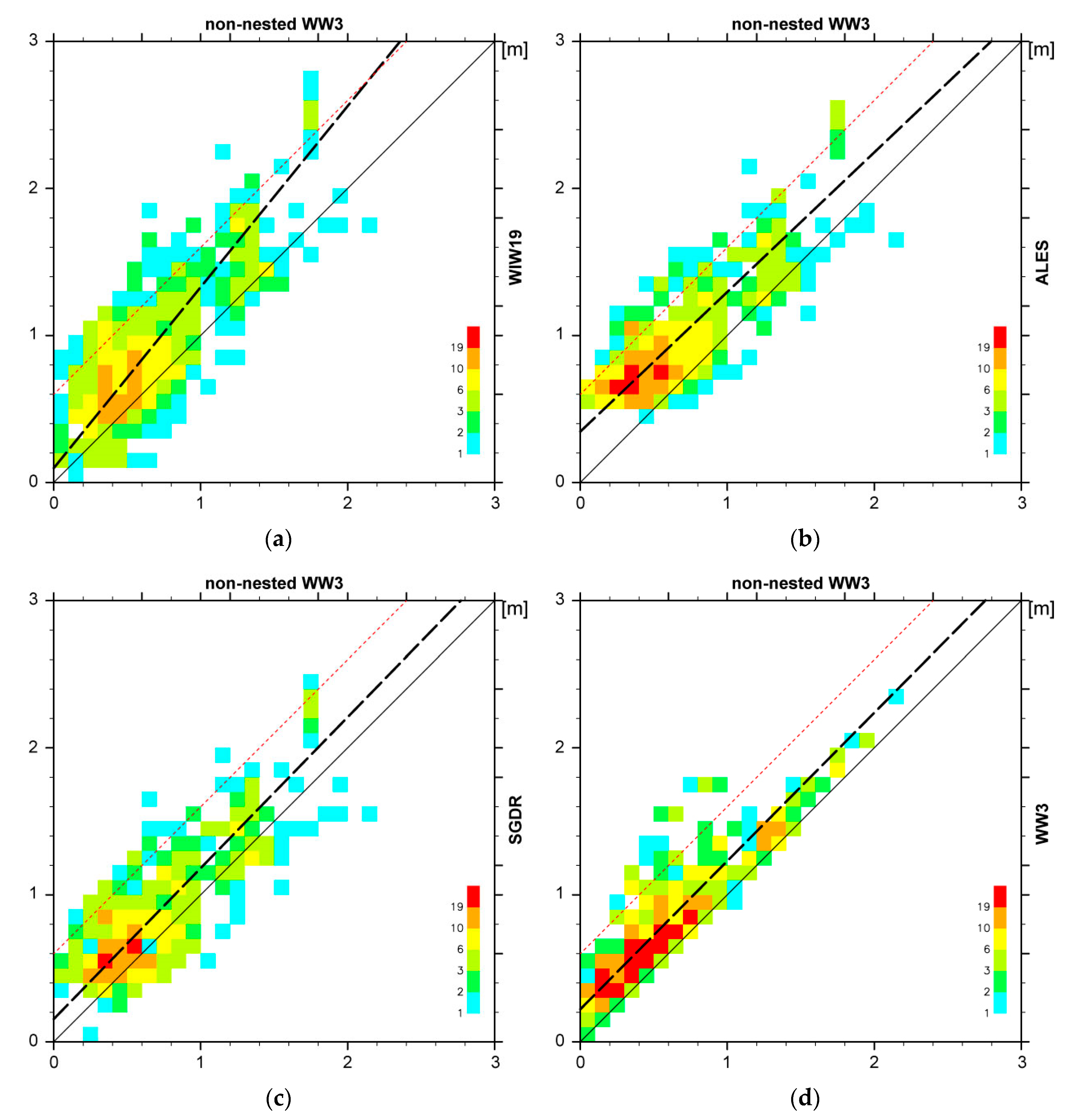
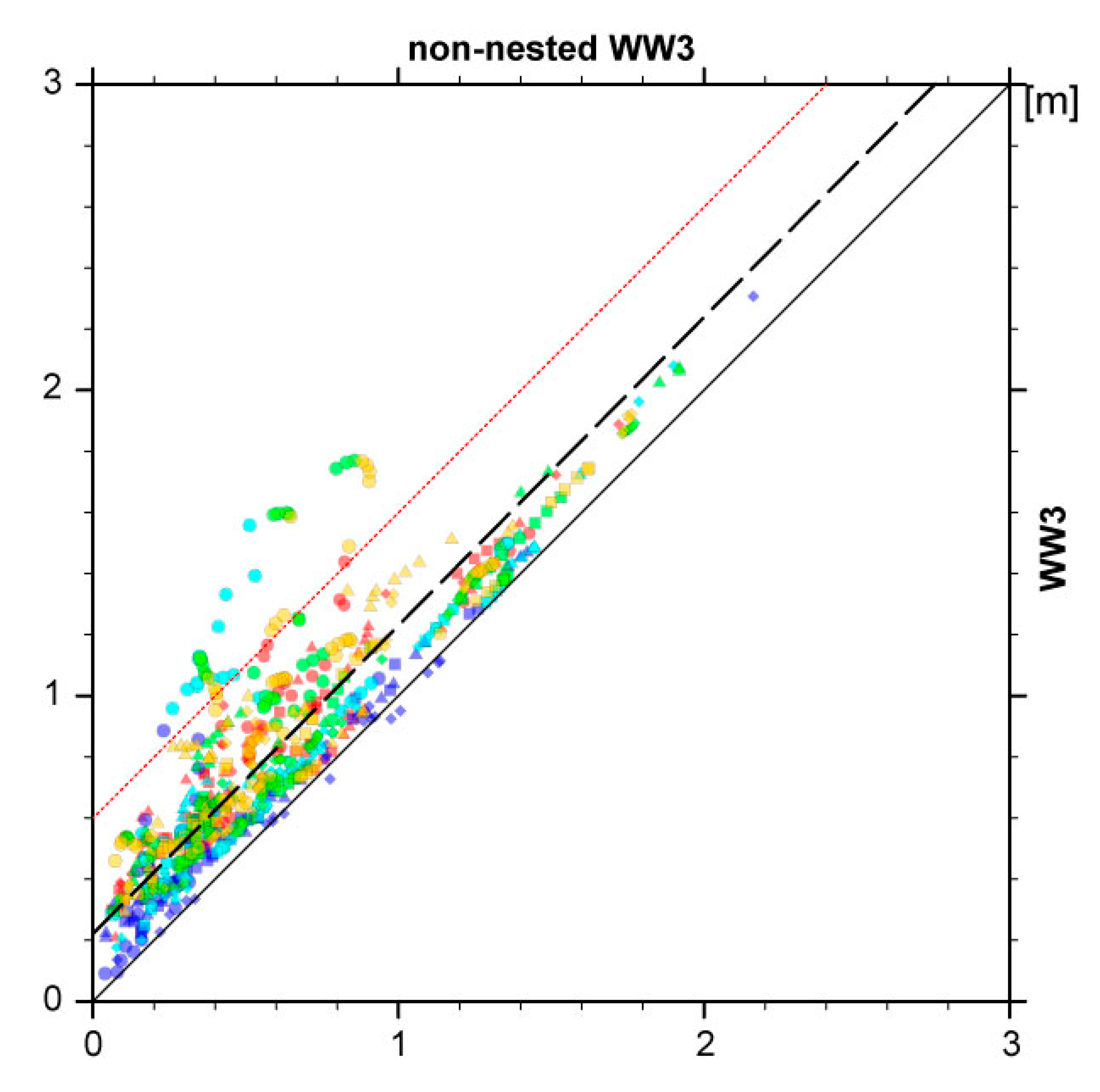
3.2. Comparison with WW3 Model
4. Discussion
4.1. Discrepancies of the Jason-2 Retrackers
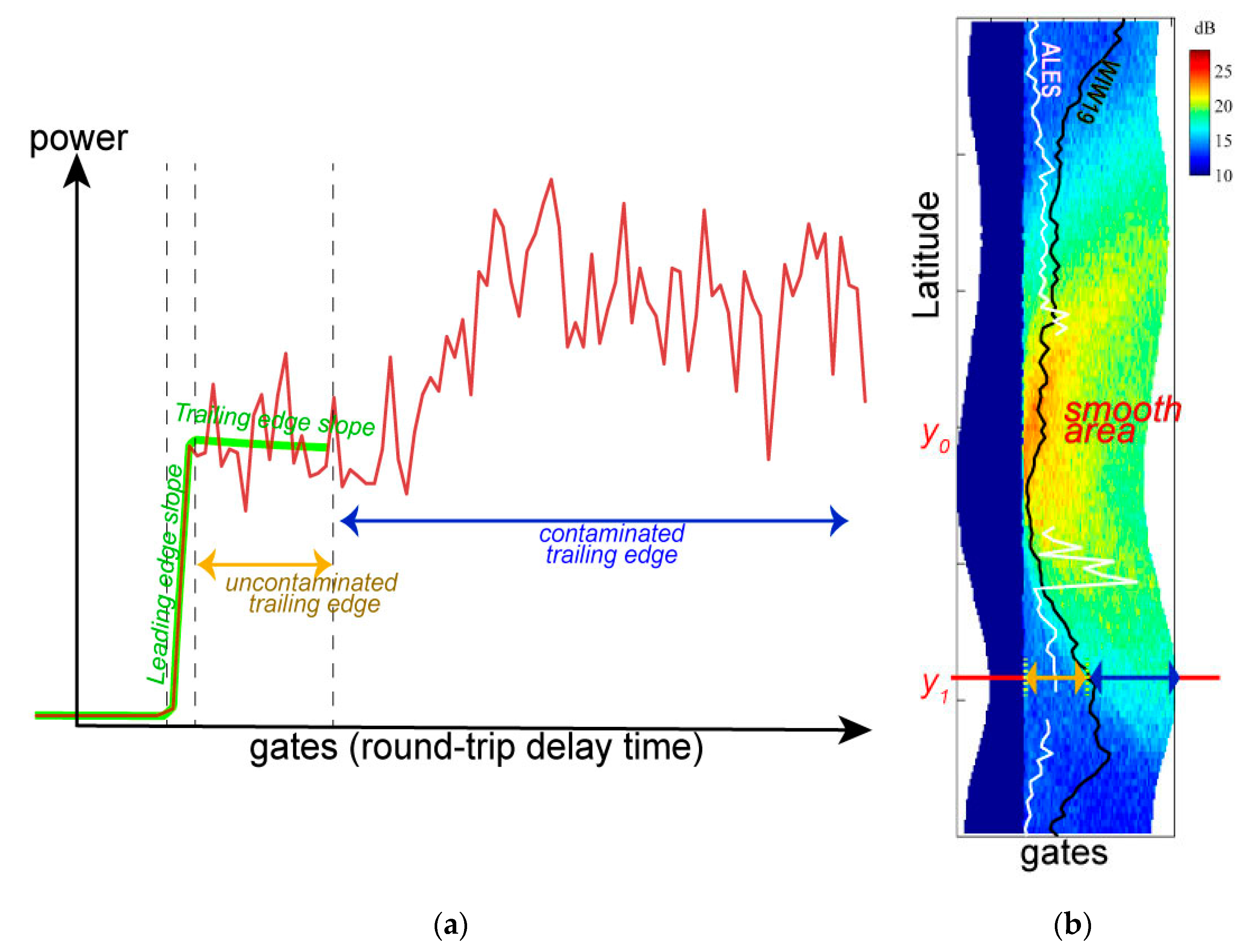
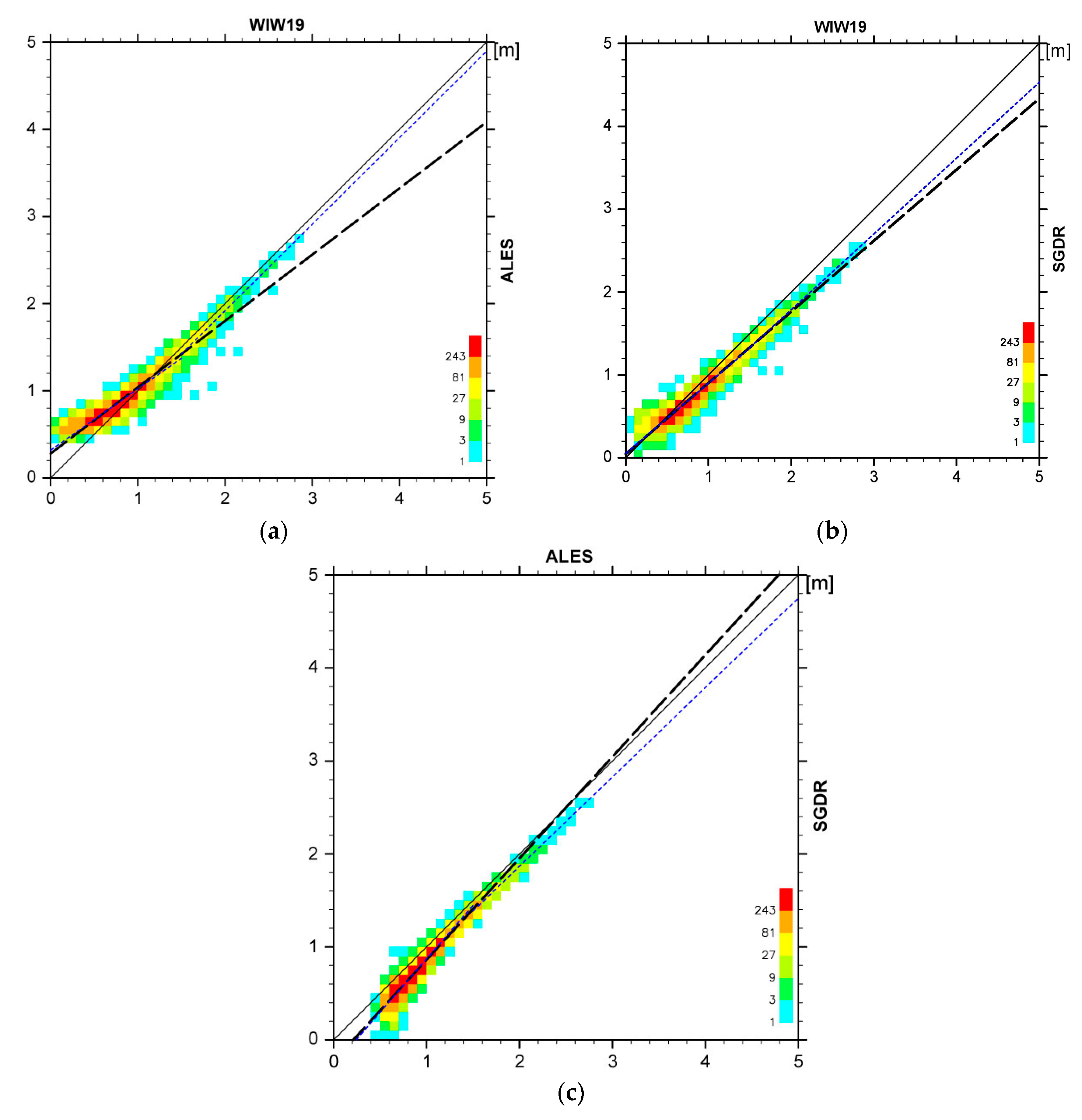
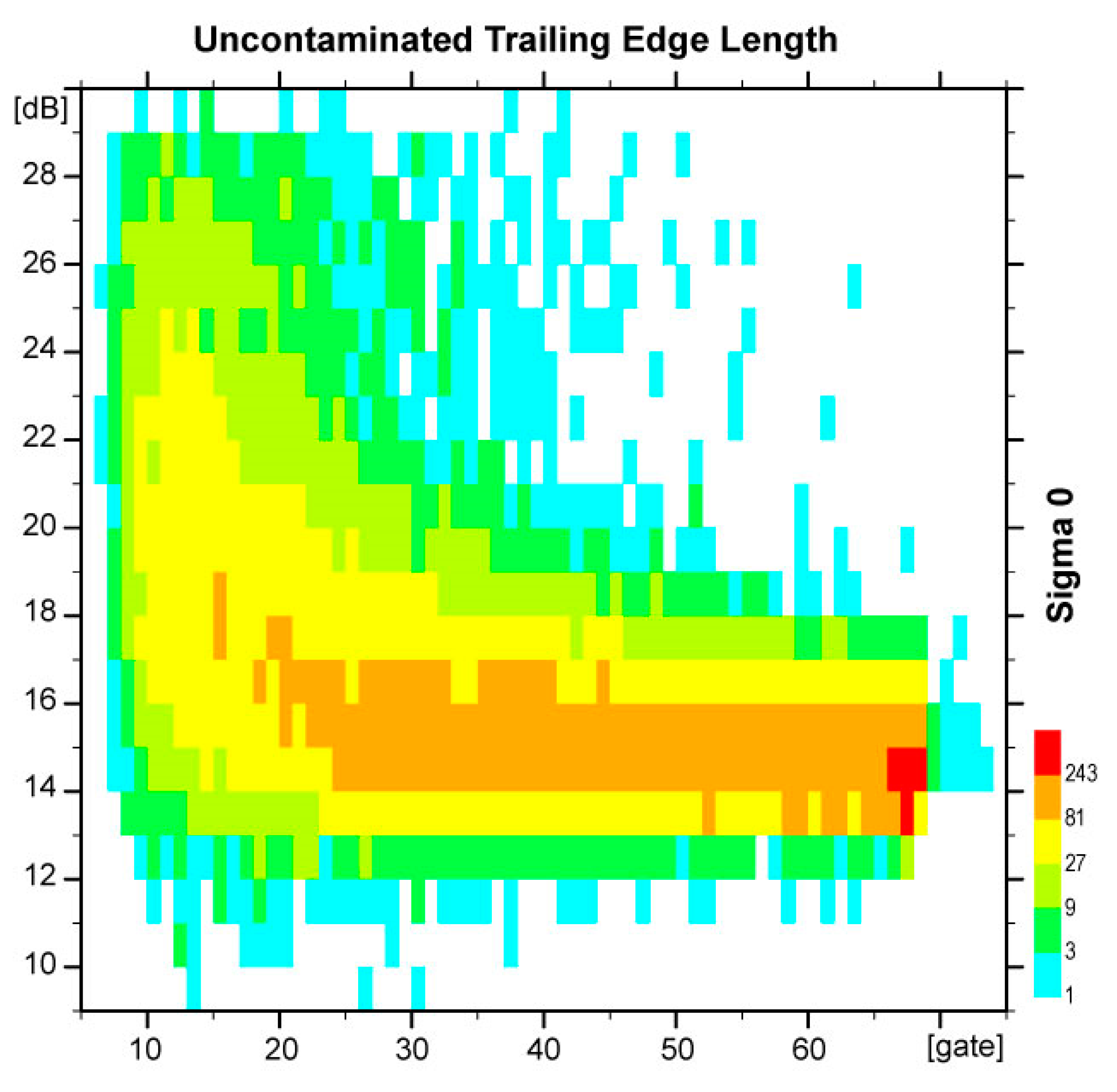
4.1.1. Dependency on the Length of the Uncontaminated Trailing Edge
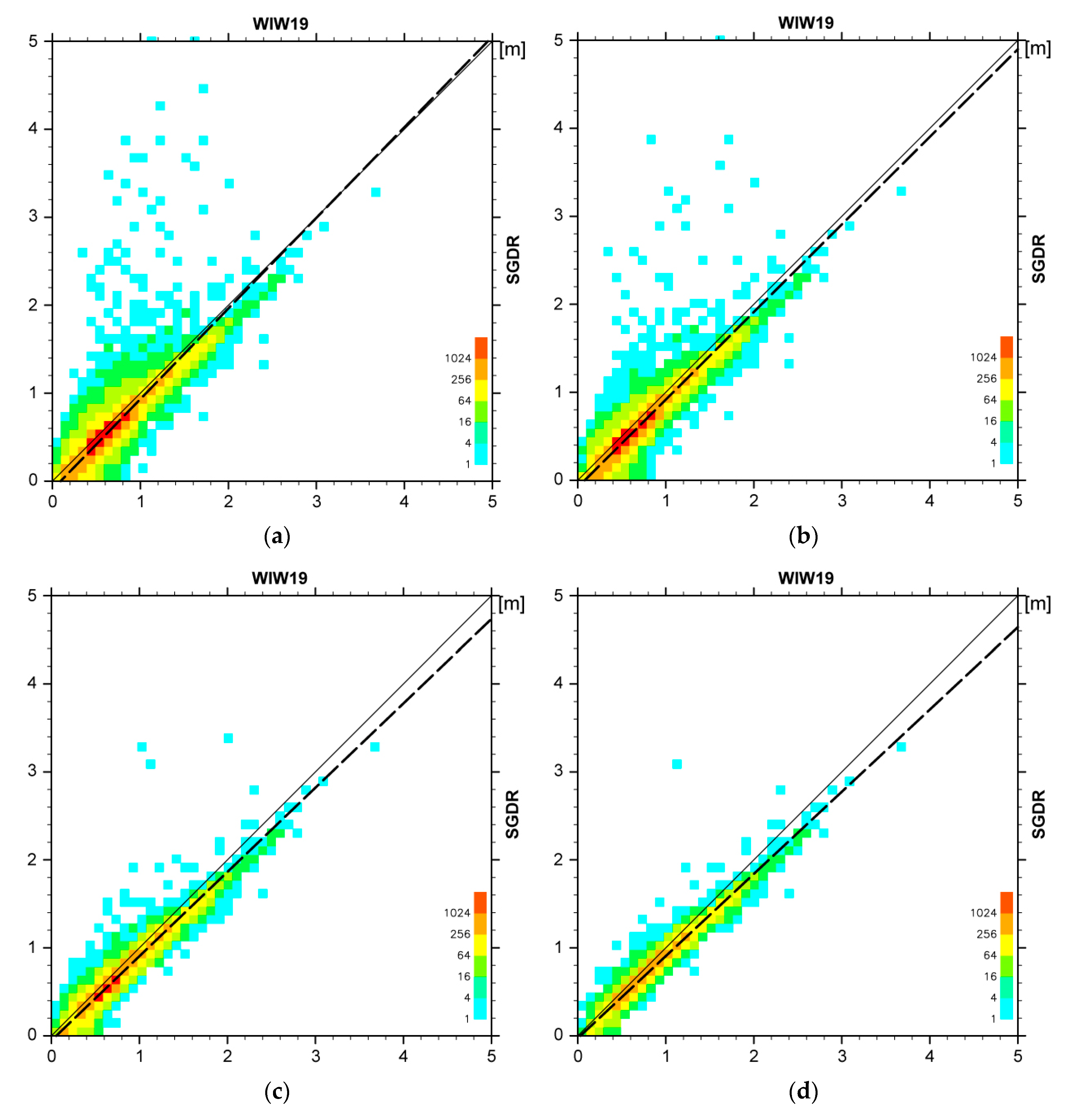
4.1.2. Filtering Sigma0 Blooms in SGDR Data
4.2. WW3 Model Representability
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zieger, S.; Vinoth, J.; Young, I.R. Join Calibration of Multiplatform Altimeter Measurements of Wind Speed and Wave Height over the Past 20 Years. J. Atmos. Ocean. Tech. 2009, 26, 2549–2564. [Google Scholar] [CrossRef]
- Ribal, A.; Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 2019, 6, 1–15. [Google Scholar] [CrossRef]
- Gommenginger, C.; Thibaut, P.; Fenoglio-Marc, L.; Quartly, G.; Deng, X.; Gomez-Enri, J.; Challenor, P.; Gao, Y. Retracking Altimeter Waveforms Near the Coasts. In Coastal Altimetry; Vignudelli, S., Kostianoy, A., Cipollini, P., Beneveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 61–102. [Google Scholar]
- Wang, X.F.; Ichikawa, K. Coastal Waveform Retracking for Jason-2 Altimeter Data based on along-track Echograms around the Tsushima Islands in Japan. Remote Sens. 2017, 9, 762. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudeli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef]
- Wang, X.F.; Ichikawa, K.; Wei, D.G. Coastal waveform retracking in the slick-rich Sulawesi Sea of Indonesia, based on variable footprint size with homogeneous sea surface roughness. Remote Sens. 2019, 11, 1274. [Google Scholar] [CrossRef]
- Idris, N.H.; Deng, X.; Md Din, A.H.; Idris, N.H. CAWRES: A Waveform Retracking Fuzzy Expert System for Optimizing Coastal Sea Levels from Jason-1 and Jason-2 Satellite Altimetry Data. Rem. Sens. 2017, 9, 603. [Google Scholar] [CrossRef]
- Thibaut, P.; Poisson, J.C.; Bronner, E.; Picot, N. Relative Performance of the MLE3 and MLE4 Retracing Algorithms on Jason-2 Altimeter Waveforms. Mar. Geod. 2010, 33, 217–335. [Google Scholar] [CrossRef]
- Dumont, J.P.; Rosmorduc, V.; Carrere, L.; Picot, N.; Bronner, E.; Couhert, A.; Desai, S.; Bonekamp, H.; Scharroo, R.; Leuliette, E. OSTM/Jason-2 Products Handbook, Iss. 1rev11, SALP-MU-M-OP-15815-CN; CNESS: Paris, France, 2017; pp. 1–66. [Google Scholar]
- Passaro, M.; Fenoglio-Marc, L.; Cipollini, P. Validation of significant wave height from improved satellite altimetry in the German bight. IEEE Trans. Geosc. Rem. Sens. 2015, 53, 2146–2156. [Google Scholar] [CrossRef]
- Tolman, H.L. User Manual and System Documentation of WAVEWATCH III TM Version 3.14; National Centers for Environmental Prediction, National Weather Service, NOAA: Camp Springs, MD, USA, 2009. [Google Scholar]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Bidlot, J.R.; Janssen, P.A.E.M.; Adballa, S. A Revised Formulation of Ocean Wave Dissipation and Its Model Impact. ECMWF Technical Memoranda 509; ECMWF: Reading, UK, 2007; pp. 1–27. [Google Scholar] [CrossRef]
- Hasselmann, S.; Hasselmann, K.; Allender, J.H.; Barnet, T.P. Computations and Parameterizations of the Nonlinear Energy Transfer in a Gravity-Wave Spectrum. Part II: Parameterizations of Nonlinear Energy Transfer for Application in Wave Models. J. Phys. Oceanogr. 1985, 15, 1378–1391. [Google Scholar] [CrossRef]
- Chawla, A.; Spindler, D.M.; Tolman, H.L. Validation of a thirty year wave hindcast using the Climate Forecast System Reanalysis winds. Ocean Model. 2013, 70, 189–206. [Google Scholar] [CrossRef]
- Perez, J.; Menendez, M.; Losada, I.J. GOW2: A global wave hindcast for coastal applications. Coast. Engin. 2017, 124, 1–11. [Google Scholar] [CrossRef]
- Ribal, A.; Babanin, A.V.; Zieger, S.; Liu, Q.X. A high-resolution wave energy resource assessment of Indonesia. Renew. Energy 2020. [Google Scholar] [CrossRef]
- Cavaleri, L.; Abdalla, S.; Benetazzo, A.; Bertotti, L.; Bidlot, J.-R.; Breivik, Ø.; Carniel, S.; Jensen, R.E.; Portilla-Yandun, J.; Rogers, W.E.; et al. Wave modelling in coastal and inner seas. Prog. Oceanogr. 2018, 167, 164–233. [Google Scholar] [CrossRef]
- Wang, X.F.; Ichikawa, K. Effect of High-Frequency Sea Waves on Wave Period Retrieval from Radar Altimeter and Buoy Data. Remote Sens. 2016, 8, 764. [Google Scholar] [CrossRef]
- Schlembach, F.; Passaro, M.; Quartly, G.D.; Kurekin, A.; Nencioli, F.; Dodet, G.; Piolle, J.F.; Ardhuin, F.; Bidlot, J.; Schwatke, C.; et al. Round Robin Assessment of Radar Altimeter Low Resolution Mode and Delay-Doppler Retracking Algorithms for Significant Wave Height. Rem. Sens. 2020, 12, 1254. [Google Scholar] [CrossRef]

| Parameter | Validity Conditions |
|---|---|
| MQE (ALES) MQE (SGDR) | 0 ≤ x(count) ≤ 0.15 0 ≤ x(count) ≤ 0.30 |
| SSH (ALES and SGDR) | −130 ≤ x (m) ≤ 100 |
| SWH (ALES and SGDR) | 0 < x (m) < 11 |
| Sigma0 (ALES and SGDR) | 7 ≤ x (dB) ≤ 30 |
| Uncontaminated trailing edge length (WIW19) | 5 ≤ x (gates) |
| Statistics | WIW19 vs. ALES | WIW19 vs. SGDR | ALES vs. SGDR |
|---|---|---|---|
| Number of data | 32,380 | 30,927 | 32,744 |
| RMS Diff. | 0.21 m | 0.21 m | 0.29 m |
| Slope of reg. line | 0.67 | 0.91 | 1.76 |
| Intercept of reg. line | 0.35 m | 0.06 m | −0.72 |
| Pearson Corr. Coef. | 0.91 | 0.82 | 0.74 |
| Statistics | WIW19 | ALES | SGDR |
|---|---|---|---|
| Number of data | 2010 | 2125 | 2018 |
| RMS Diff. | 0.30 m | 0.30 m | 0.40 m |
| Slope of reg. line | 1.23 | 0.87 | 1.30 |
| Intercept of reg. line | −0.17 m | 0.22 m | −0.20 m |
| Pearson Corr. Coef. | 0.76 | 0.74 | 0.55 |
| Statistics | WIW19 vs. ALES | WIW19 vs. SGDR | ALES vs. SGDR |
|---|---|---|---|
| Number of data | 1475 | 1024 | 937 |
| RMS Diff. | 0.23 m | 0.54 m | 0.53 m |
| Slope of reg. line | 0.58 | 2.43 | 4.27 |
| Intercept of reg. line | 0.40 m | −0.83 m | −2.56 |
| Pearson Corr. Coef. | 0.86 | 0.72 | 0.58 |
| Statistics | WIW19 vs. ALES | WIW19 vs. SGDR | ALES vs. SGDR |
|---|---|---|---|
| Number of data | 7838 | 7247 | 7199 |
| RMS Diff. | 0.16 m | 0.12 m | 0.16 m |
| Slope of reg. line | |||
| Whole | 0.76 | 0.86 | 1.09 |
| x ≥ 1.5m | 1.00 | 0.91 | 0.96 |
| x < 1.5m | 0.70 | 0.85 | 1.15 |
| Intercept of reg. line | |||
| Whole | 0.28 m | 0.05 m | −0.23 m |
| x ≥ 1.5m | −0.07 m | −0.04 m | −0.05 m |
| x < 1.5m | 0.32 m | 0.05 m | −0.28 m |
| Pearson Corr. Coef. | 0.96 | 0.97 | 0.98 |
| Statistics | 30 dB | 22 dB | 19 dB | 16 dB | 15 dB |
|---|---|---|---|---|---|
| Number of data | 30,927 | 29,995 | 27,596 | 19,492 | 12,771 |
| RMS Diff. | 0.21 m | 0.17 m | 0.15 m | 0.12 m | 0.12 m |
| Slope of reg. line | 0.91 | 1.03 | 1.00 | 0.96 | 0.93 |
| Intercept of reg. line | 0.06 m | −0.10 m | −0.08 m | −0.05 m | −0.03 m |
| Pearson Corr. Coef. | 0.82 | 0.91 | 0.94 | 0.97 | 0.98 |
| Statistics | WIW19 | ALES | SGDR |
|---|---|---|---|
| Number of data | 583 | 580 | 537 |
| RMS Diff. | 0.30 m | 0.27 m | 0.28 m |
| Slope of reg. line | 1.23 | 0.95 | 1.05 |
| Intercept of reg. line | −0.18 m | 0.13 m | −0.10 m |
| Pearson Corr. Coef. | 0.78 | 0.79 | 0.77 |
| Statistics | WIW19 | ALES | SGDR | WW3 |
|---|---|---|---|---|
| Number of data | 583 | 579 | 538 | 769 |
| RMS Diff. | 0.38 m | 0.39 m | 0.31 m | 0.29 m |
| Slope of reg. line | 1.23 | 0.95 | 1.03 | 1.00 |
| Intercept of reg. line | 0.10 m | 0.35 m | 0.15 m | 0.22 m |
| Pearson Corr. Coef. | 0.81 | 0.83 | 0.80 | 0.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ichikawa, K.; Wang, X.-F.; Tamura, H. Capability of Jason-2 Subwaveform Retrackers for Significant Wave Height in the Calm Semi-Enclosed Celebes Sea. Remote Sens. 2020, 12, 3367. https://doi.org/10.3390/rs12203367
Ichikawa K, Wang X-F, Tamura H. Capability of Jason-2 Subwaveform Retrackers for Significant Wave Height in the Calm Semi-Enclosed Celebes Sea. Remote Sensing. 2020; 12(20):3367. https://doi.org/10.3390/rs12203367
Chicago/Turabian StyleIchikawa, Kaoru, Xi-Feng Wang, and Hitoshi Tamura. 2020. "Capability of Jason-2 Subwaveform Retrackers for Significant Wave Height in the Calm Semi-Enclosed Celebes Sea" Remote Sensing 12, no. 20: 3367. https://doi.org/10.3390/rs12203367
APA StyleIchikawa, K., Wang, X.-F., & Tamura, H. (2020). Capability of Jason-2 Subwaveform Retrackers for Significant Wave Height in the Calm Semi-Enclosed Celebes Sea. Remote Sensing, 12(20), 3367. https://doi.org/10.3390/rs12203367