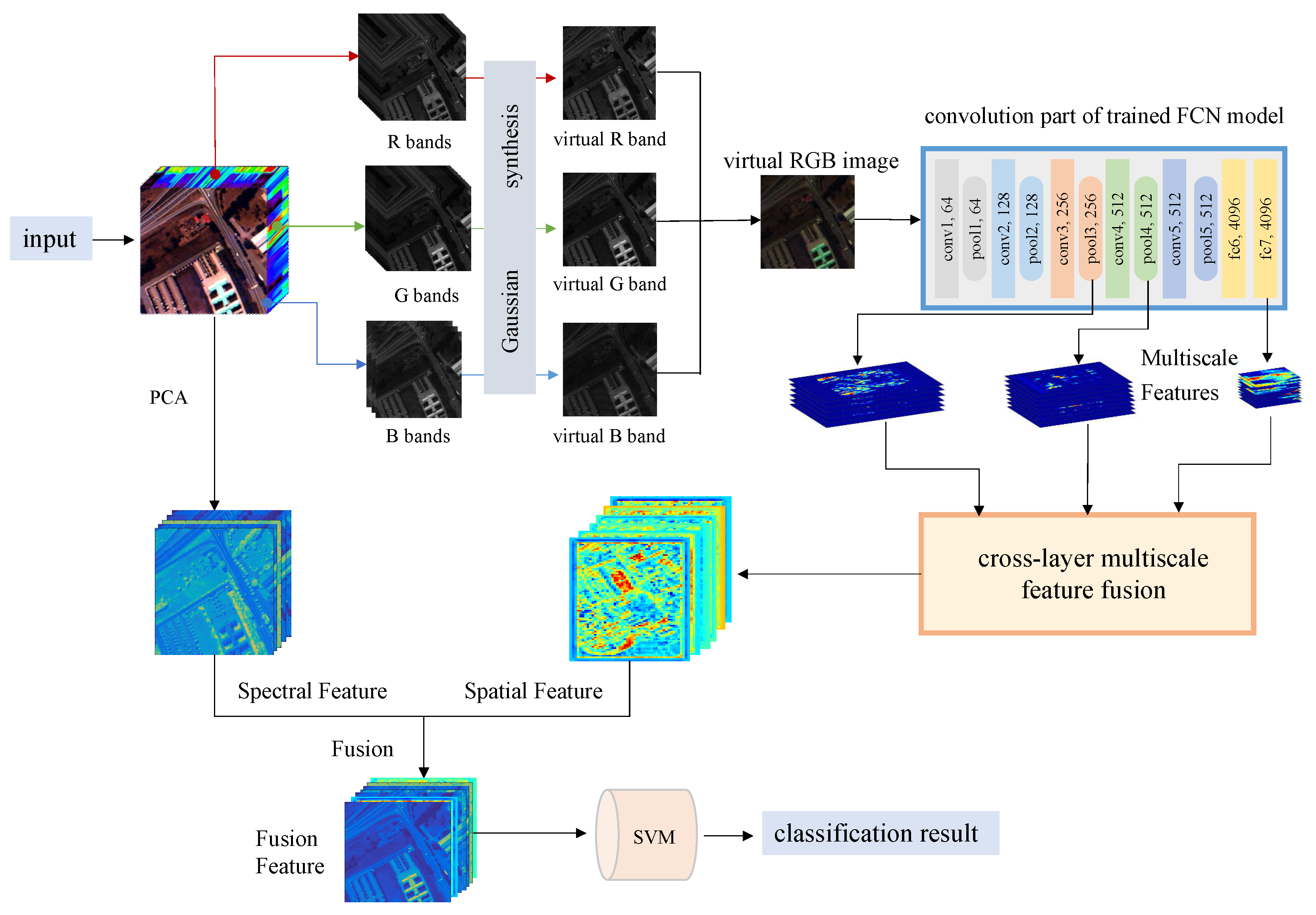
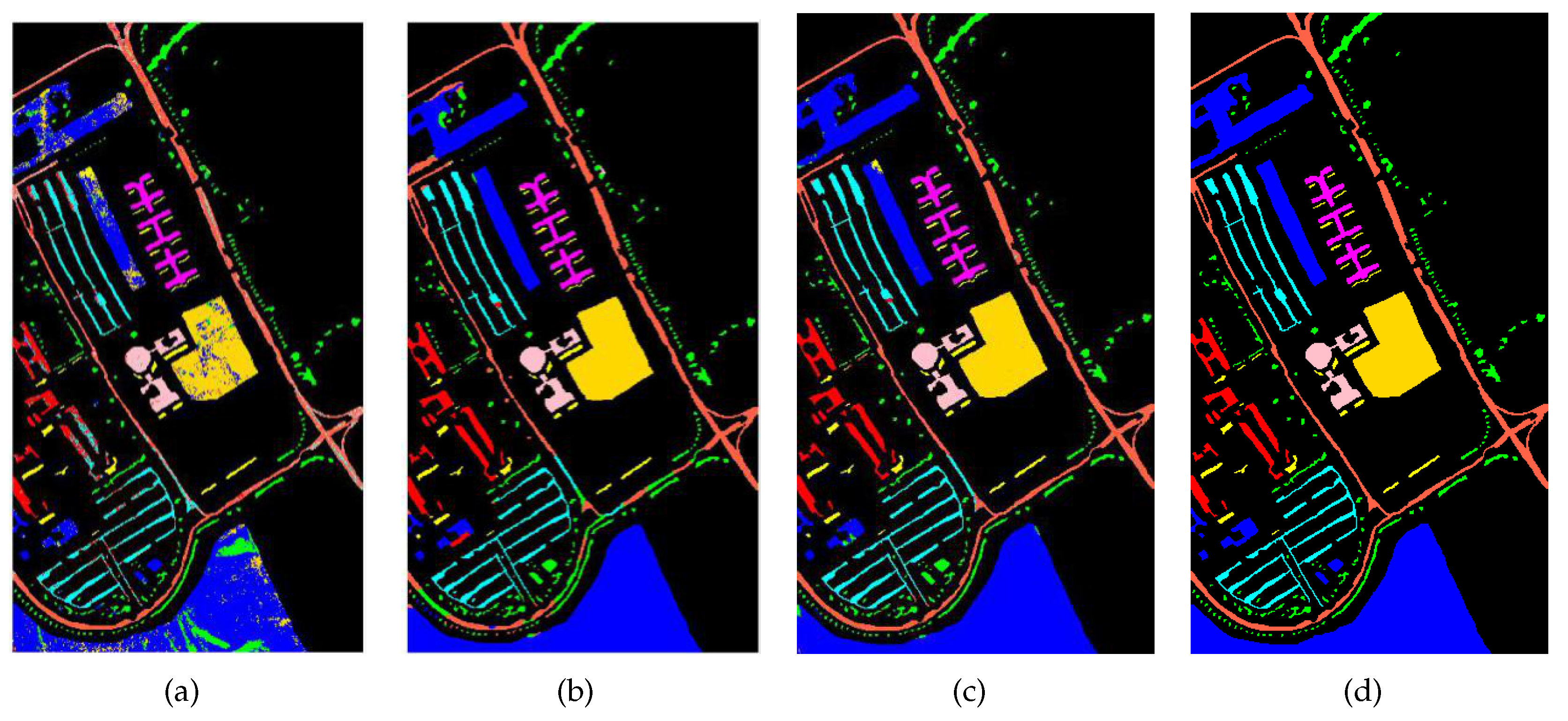
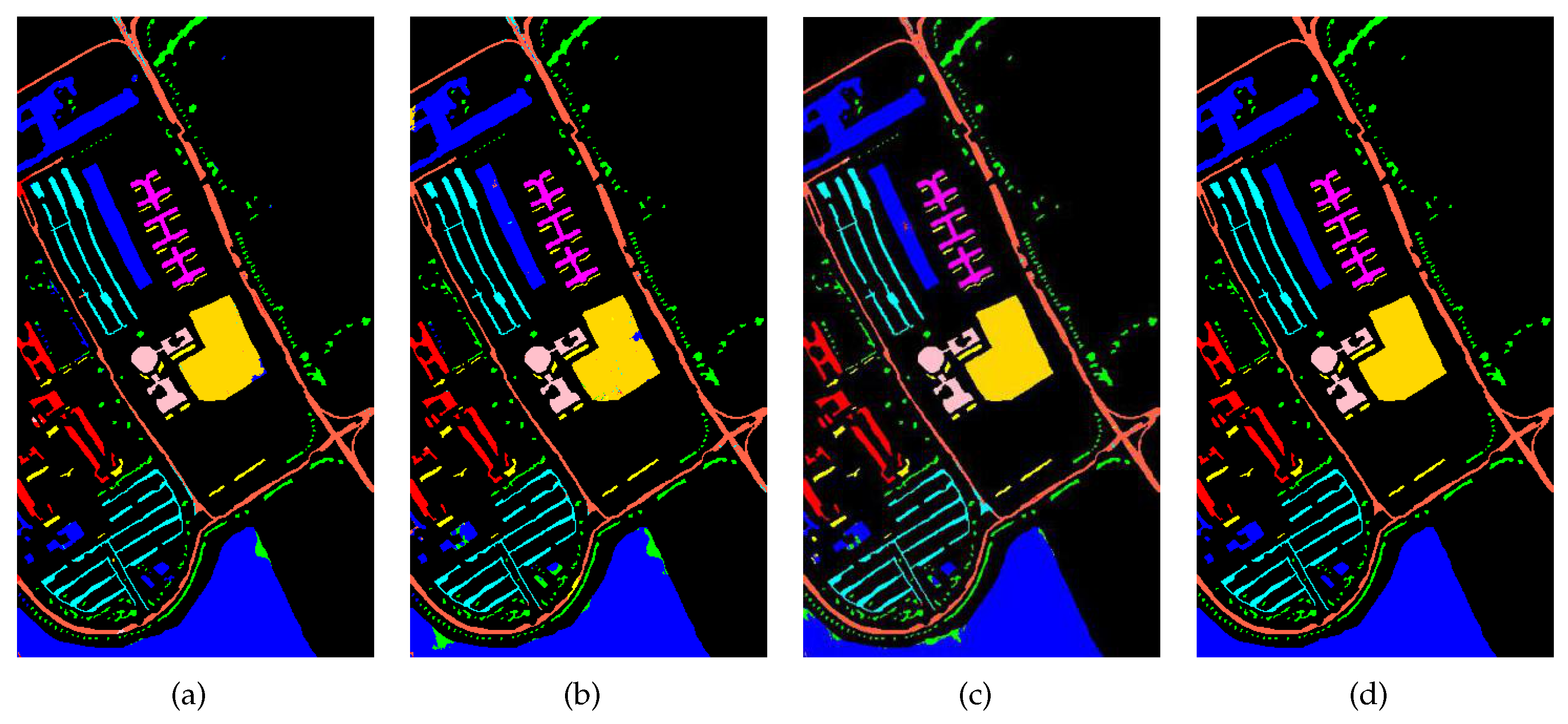
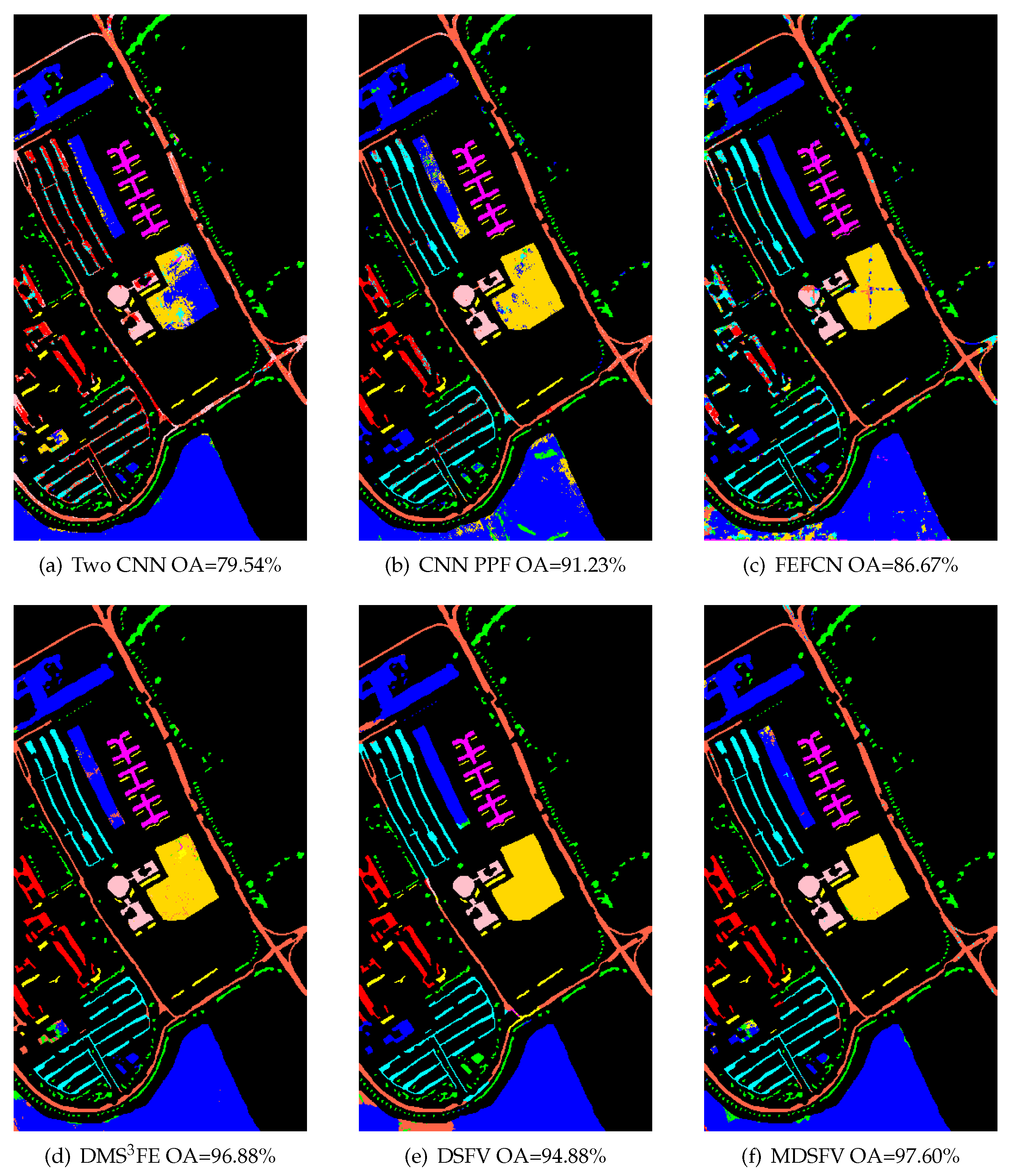
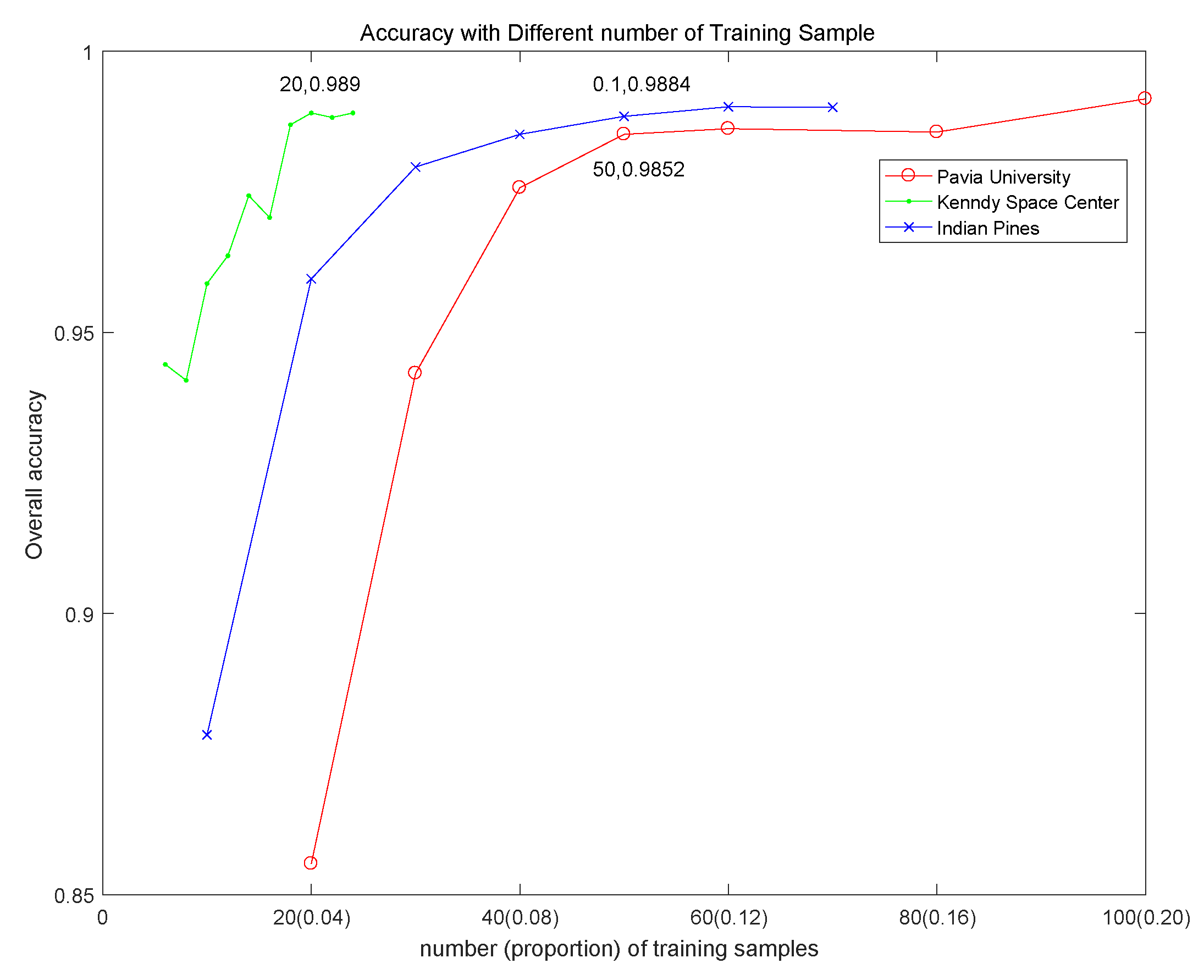
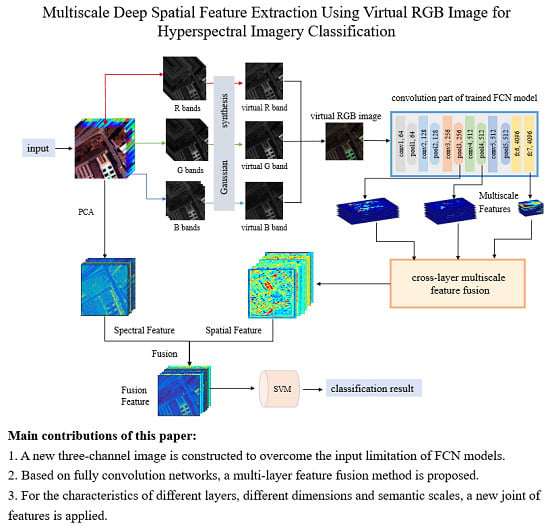
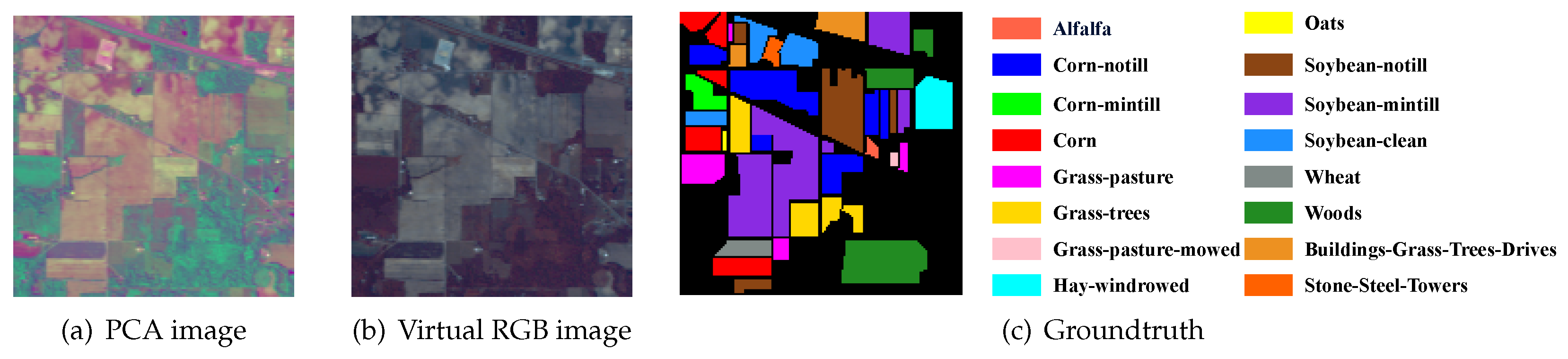The labeled hyperspectral image data is very limited. In addition, the imaging conditions of different hyperspectral images, the number of spectral bands and the ground objects are significantly different, which make different hyperspectral data that cannot be trained together like natural images and other remote sensing images. The fully convolutional network can be used to classify hyperspectral images because its task is to perform pixel-level class determination of the entire image, which is consistent with the goal of achieving classification of hyperspectral images. There are many parameters of the FCN, thus the single hyperspectral image cannot complete the update of all network parameters. By constructing a three-channel virtual RGB image, this paper simulates the trained network model on natural images for the pixel-level segmentation process, and better adapts to the characteristics of existing models. In this way, multi-layer and multiscale spatial features are extracted, and multiscale features joint is realized through various feature processing techniques, which enhances the feature expression ability. Finally, the spatial and spectral features are fused together to realize the classification of hyperspectral images. The procedure of the method is shown in
Figure 1, mainly concluding three-channel image construction, multi-layer multiscale feature extraction and jointing, the process of the feature fusion and classification.
2.2. Spatial Feature Extraction and Skip-Layer Jointing
The method acquires pixel-wise spatial features by deep and shallow feature fusion. Here we propose a method for extracting spatial features from models trained on natural images for hyperspectral classification. We select FCN for feature extraction. The advantage of FCN is that it has the same target with the hyperspectral image classification, aiming at pixel-wise classification. We reasonably guess that compared to a CNN, features from the FCN are more useful. We applied a well-trained network on natural images to extract multi-layer, multiscale features. Shallow features contain more edge and detailed information of the image, which is especially important for distinguishing the pixel categories of different objects intersections in hyperspectral images, while deep features contain more abstract semantic information, which is important for the determination of pixel categories. Therefore, we extracted both shallow edge texture information and deep semantic structure information, and combined them to obtain more expressive features. We selected VGG16 to extract spatial features from the virtual RGB images. The parameters were transferred from the FCN trained on ImageNet. In
Figure 1, the blue box shows the structure of the convolution part.
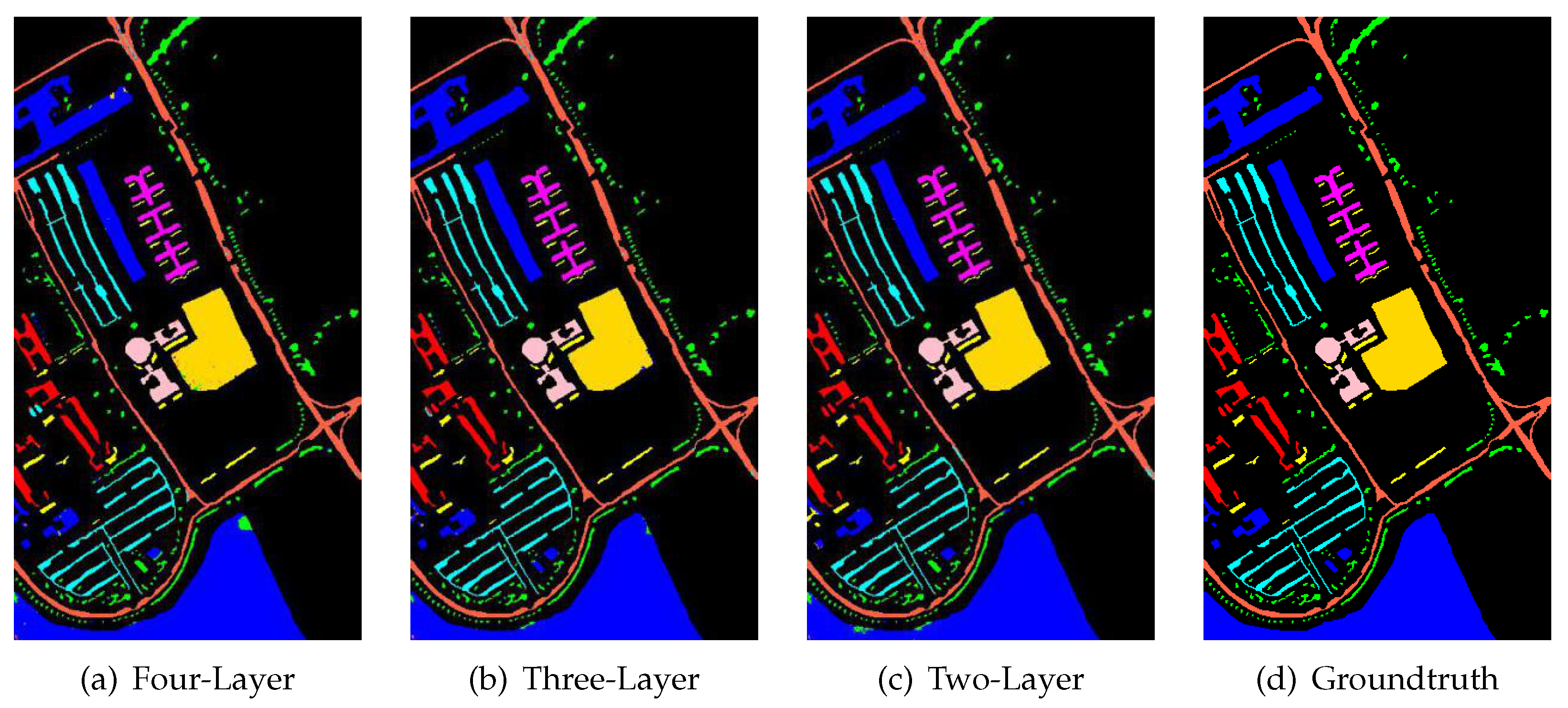
During the pooling operation of the fully convolutional network (FCN), the down-sampling multiples of spatial features increased gradually and the semantic properties of features were more and more abstract. The fc7 layer provided semantic information and the shallower layers provided more detailed information. So we chose both deep and shallow features, we extracted the detailed features of the pool3, pool4 and fc7 layers and combined them.The down-sampling multiples from the original image were 8, 16 and 32 times, respectively. We used a layer-by-layer upsampling skip-layer joint to combine the extracted features of the three layers and obtained the final spatial features.
The joint is shown in
Figure 2. The method mainly through the upsampling, cropping and two layer feature maps joint to realize layer-by-layer joint expecting improve the ability of expressing spatial characteristics. It can better preserve the depth of semantic information in the fc7 layer, and simultaneously combine the edge texture information of the shallow features to improve the ability of feature expression. Since the FCN adds a surrounding zero padding operation to ensure the full utilization of the edge information during the convolution process, mismatch of the feature map and the edge of the original image is caused. Therefore, we focused on the number of pixels that differ between the different layer feature maps when combining skip-layer features. It seriously affects the correspondence between different pixel information of each feature map, which is very important for the pixel-level hyperspectral classification task. The edge pixels of the feature map corresponding outside the reference map are usually defined as offset, and as is known to all, when passing the pooling layer, the offset halves, and when through the convolution layer, the offset caused is
The process is mainly divided into the three operations: upsampling, cropping and the deep features skip-layer joint. The upsampling is mainly based on bilinear interpolation, and in order not to lose the edge information, there is a surrounding padding = 1 to the map. The shallow feature maps occurred after the layer-to-layer convolution from the zero padded original image. The original image only corresponds to a part of its center, and the number of pixels in other areas are the offset. So in the cropping, we crop the maps by half of the multiple surrounding them. Since FCN’s upsampling and alignment operations are well known to many scholars, we will not cover them further here. We mainly introduce the skip-layer feature map jointing operation.
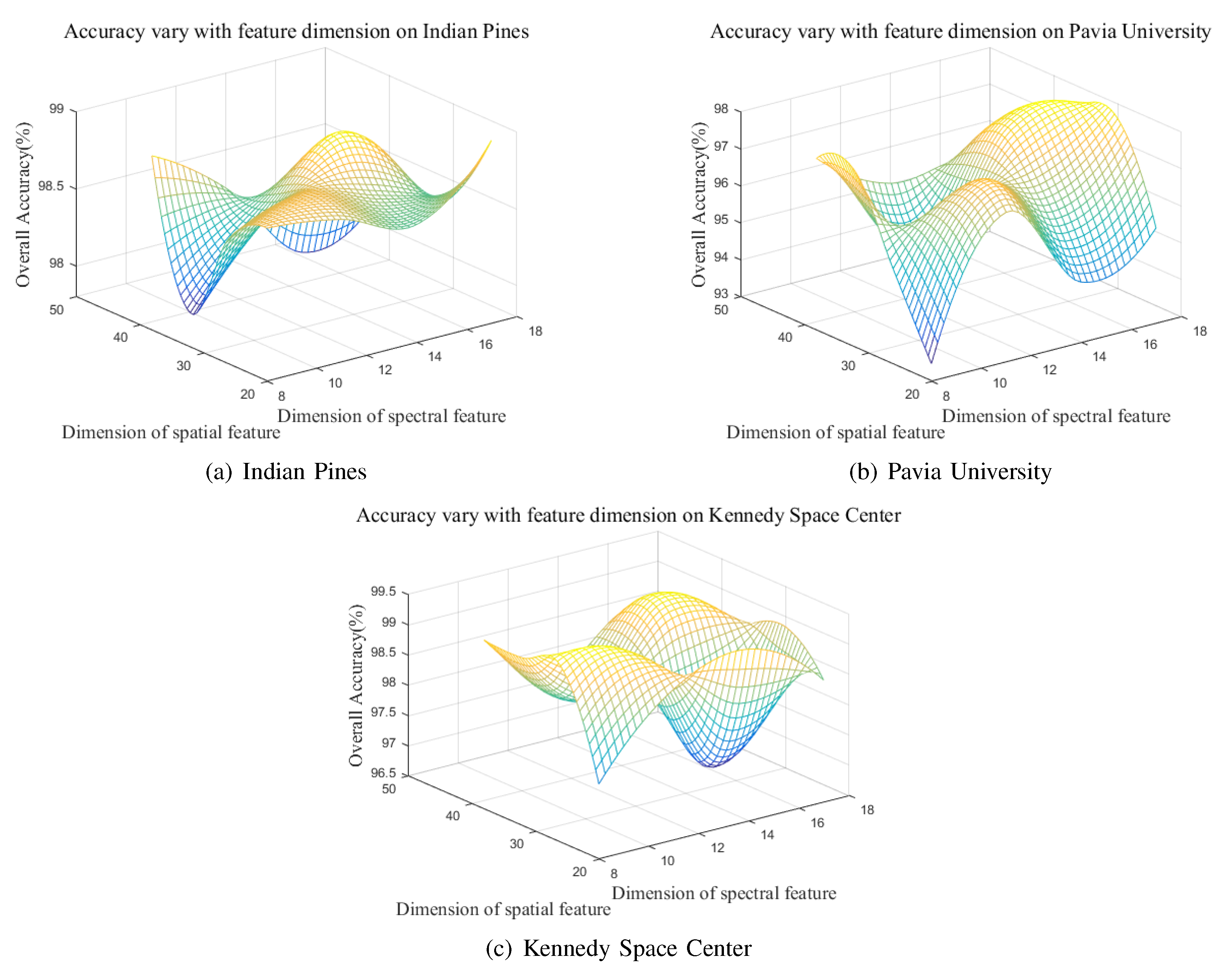
By cropping, we can guarantee that the two feature maps are equal in size and position, but the dimensions of the two layers are different and cannot be directly added. If the two layers of features are directly concatenated, the feature dimension is multiplied, which greatly affects the computational efficiency and classification performance. Here we used principal component analysis (PCA), reducing the dimension of the feature map with a high dimension to make the dimension of the two maps the same and adding them layer by layer. In order to ensure the spatial information contribution of the two-layer feature is equivalent, each dimension of the two layer feature map was normalized before the addition. In the process of dimensionality reduction, by the characteristics of the PCA itself, our available principal components are less than , is the size of feature to PCA. So if the dimension of the shallower is m and that of the deeper is n (), the size of the deeper map is , the dimension of the two maps is .
Combined with the convolution process of FCN, we conducted the following analyses for the feature joint.
Offset during the convolution process.
A series of operations of the FCN in the convolution process were analyzed to obtain the scale relationship and positional association before each feature map. According to (
5), the parameters of the convolution between the layers of the FCN are shown in
Table 1.
In
Table 1, we can find the offset of fc7 and the original image is 0, so we used the fc7 layer as the benchmark when combining skip-layer features, and the baseline was selected as the deeper feature map when cropping.
Offset calculation between feature maps.
We discuss the calculation of the offset between the two layers of feature maps before and after the pooling and other convolution operations. We assume that the offset of the deep feature relative to the original image is
, the offset generated by the convolution layer is
and during the upsampling padding = 1, the offset is 1, then the offset of a feature layer former relative to the latter layer
, is calculated as follows:
where
k represents the downsampling times of the two layers. There is a pooling layer between them, so
. The detailed offset between the layers through different feature levels are shown in
Table 2.
Unified dimension of deep and shallow feature maps.
We discuss the number of principal components retained by the deeper feature map after PCA and the dimension of the shallower feature map. We take the feature of the upsampled PCA to reduce the dimension, and finally take the dimension as the minumum of the shallower feature and the dimension of the deeper feature after PCA. If the shallower’s dimension is the larger, PCA will be also used on it to change the dimension to that of the deeper feature after PCA.
The detailed process of skip-layer feature joint is as follows:
Joint fc7 and pool4
First we upsampled the fc7 layer. The size of the fc7 and pool4 layer maps was different. Because of the padding operation, the relative offset between the two layers was generated. From
Table 1, we knew that offset between fc7 and the original image is 0. In
Table 2, the relative offset between the two layers was 5, the pool4 layer was cropped according to the offset. PCA was performed on the upsampled fc7 layer and we selected the same dimension of the upsampled fc7 and pool4. Then, we added their features layer-by-layer to obtain the feature map after fusion. We named it fuse-pool4 layer, which was offset from the original image by 5.
Joint fuse-pool4 and pool3
We combined the fuse-pool4 layer and the pool3 layer in the same way. We upsampled the fuse-pool4 and selected the feature map after upsampling according to the uniform rules of the deep and shallow feature dimensions. The relative offset between the two layers was 9 calculated, as shown in
Table 2. The pool3 layer was cropped according to the offset to obtain two layers of the same size. Then they were added layer-by-layer to get the feature map fuse-pool3 after the fusion.
Upsample to image size
The fuse-pool3 layer was 8 times downsampled relative to the original image. We applied the upsampling process to directly upsample the layer by 8 times, and then calculated the offset between it and the original image. The offset between the upsampled feature map and the original image was 31 and we cropped the feature map after upsampling according to offset = 31, and the spatial features corresponding to the pixel level of the original image were obtained.
So far, we have obtained the spatial features corresponding to the original image, which combines the features of 8 times, 16 times and 32 times downsampling of deep neural network. They not only include the edge and detail information required for hyperspectral pixel-level classification, but also contains semantic information needed to distinguish pixel categories. The feature map corresponds to the original image as much as possible, which can effectively reduce the possibility of generating classification errors in the two types of handover positions. In the process of deep and shallow feature fusion, we adopt the uniform of the dimension of two layer feature maps, and then add them layer by layer. Compared with directly concatenating the features, the feature dimensions are effectively reduced, and the ability of feature expression of the layers are maintained.
2.3. Spatial–Spectral Feature Fusion and Classification
We combined the hyperspectral bands of RGB-corresponding wavelengths to construct a virtual RGB image, and then use FCN to extract multi-layer, multiscale features of the image. Through the skip-layer joint of these features, the spatial features that characterize the spatial peculiarity of the pixel and the surrounding distribution are obtained. However, in the process of extracting the feature, we ignored the other hyperspectral bands and the close relationship between the bands. Therefore, we extracted the spectral features associated with each pixel’s spectral curve and fused it with the spatial features for classification.
Because the hyperspectral band is narrow and the sensitization range is wide, the number of hyperspectral bands is huge. To ensure that the feature dimension is not too high during the classification process and the expression ability of the feature is not affected as much as possible, we carried out the spectral curve for PCA. After the PCA, we selected the former masters of the composition as a spectral feature of the pixel.
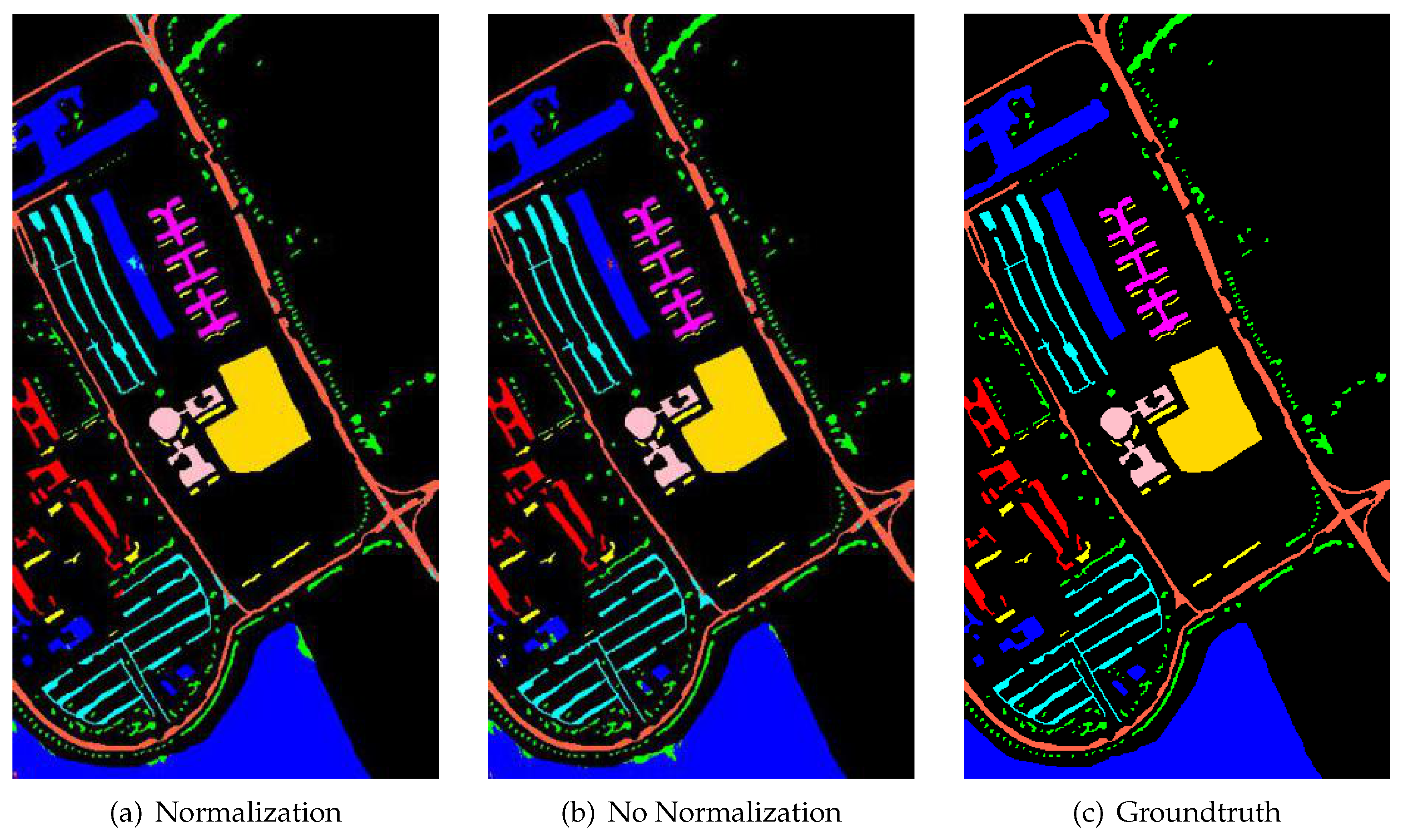
We combined the spatial and spectral features of the corresponding pixels. For the characteristics of different sources, the common joint was to directly concatenate the different features. Here, we considered that the range of values and the distribution of data were different between the spatial features obtained by the network extraction and the spectral characteristics represented by the spectral reflection values. We normalized the features and combined them according to the equations shown in Equations (
8) and (
9) to fuse spatial features and spectral features. Suppose
is a spectral feature, which is obtained from the original spectrum PCA taking the first
principal component, and
is the deep spatial feature with a dimension of
, so we know
where
is the size of the features to fuse. First, we do the following for
to normalize them in Equation (
8)
In Equation (
8), We perform the normalization operation of the layers of the spectral and spatial features, that is, subtract the average then divide by the variance operation on the corresponding features of each pixel, so as to achieve the uniformity of each feature dimension. Then we combine features by concatenating them, the size of the fused feature is shown in Equation (
9).
where
is discussed in
Section 4; the occurred
is the feature after fusion, we fed it into the classifier to implement classification.