Abstract
Solar radiation ground data is available in poor spatial resolution, which provides an opportunity and demonstrates the necessity to consider solar irradiance modeling based on satellite data. For the first time, solar energy monitoring in near real-time has been performed for India. This study focused on the assessment of solar irradiance from the Indian Solar Irradiance Operational System (INSIOS) using operational cloud and aerosol data from INSAT-3D and Copernicus Atmosphere Monitoring Service (CAMS)-Monitoring Atmospheric Composition Climate (MACC), respectively. Simulations of the global horizontal irradiance (GHI) and direct normal irradiance (DNI) were evaluated for 1 year for India at four Baseline Surface Radiation Network (BSRN) stations located in urban regions. The INSIOS system outputs as per radiative transfer model results presented high accuracy under clear-sky and cloudy conditions for GHI and DNI. DNI was very sensitive to the presence of cloud and aerosols, where even with small optical depths the DNI became zero, and thus it affected the accuracy of simulations under realistic atmospheric conditions. The median BSRN and INSIOS difference was found to vary from −93 to −49 W/m2 for GHI and −103 to −76 W/m2 for DNI under high solar energy potential conditions. Clouds were able to cause an underestimation of 40%, whereas for various aerosol inputs to the model, the overall accuracy was high for both irradiances, with the coefficient of determination being 0.99, whereas the penetration of photovoltaic installation, which exploits GHI, into urban environments (e.g., rooftop) could be effectively supported by the presented methodology, as estimations were reliable during high solar energy potential conditions. The results showed substantially high errors for monsoon season due to increase in cloud coverage that was not well-predicted at satellite and model resolutions.
1. Introduction
The United Nations’ Sustainable Development Goals (SDG) include steps to ensure universal access to modern, reliable, and affordable energy services; increase the share of renewable energy in the global energy production; double the global rate of enhancement in energy efficiency; and improve international cooperation and ease of access to clean energy research and development in technology. For instance, the stand-alone photovoltaic (PV) system installed at a location is dependent upon the amount of solar insolation available to the system [1]. This work is motivated by the need to understand the solar energy potential and support the evolving solar-based technologies. Solar monitoring provides support to the planning of installations of solar farms and rooftop panels [2,3,4]. The estimation of solar radiation using remote sensing technologies can also help the stakeholders to locate areas suitable for solar power production, which is a fast developing industry with huge potential. In [5], the authors have shown that the performance of a photovoltaic system is affected by the solar spectrum, and they quantitatively evaluated the influence of solar spectrum on photovoltaic performance under clear and cloudy weather conditions. Different quantities of solar radiation (SR) are used by electricity generation systems. The global horizontal irradiance (GHI) is applicable in PV systems and the direct normal irradiance (DNI) is applicable in concentrated solar power plants (CSP). A general conclusion is that in every single solar application, a detailed study of the cloud and aerosol climatology of the area is necessary for efficient energy planning. Before selecting the location and seeking investment, this specific planning is needed in order to decide when the performance will be at its maximum [6].
India receives more than 5000 trillion kWh/year of solar radiation [7], which is far more than its total annual energy consumption. The available radiation can be utilized for CSP as well as for PV applications. The Government of India is working on the implementation of schemes for the setting up of over 5 GW grid connected solar PV power projects under phase II of the Jawaharlal Nehru National Solar Mission (JNNSM) [8]. The solar energy market in India has seen a significant growth after 2014, when the government of India announced to set a target of installing 175 GW of renewable energy by 2022 [9]. In this target, the contribution of solar is 100 GW, which contains 40 GW contribution from rooftop solar plants. The current solar generation capacity in India as of October 2019 is 29.42 GWp from solar power that is ground mounted, 2.28 GWp from solar rooftop grid-interactive system, and 936.47 MWEQ from off-grid solar photovoltaic (SPV) systems [10]. In order to achieve this ambitious target of installing 100 GW of solar power capacity by 2022, an addition of 15 GW per year is needed [11]. Cumulative solar rooftop installation is 4.37 GW as of March 2019, which has to increase 10-fold to achieve the target of 40 GW by 2022 [12]. In this regard, the government has issued a scheme for setting up of 12 GW of grid connected solar PV power projects with the aim to achieve this target and also to enhance domestic solar PV manufacturing capacity.
Simultaneously, urbanization and economic development in India are causing a rapid increase in the demand for energy in urban regions, which is enhancing greenhouse gas emissions. The increase in demands is making it difficult for local governments and electricity utilities to cope with the situation, resulting in electricity shortages in most of the cities/towns. The “Development of Solar Cities” program is designed in order to support the urban local bodies to guide the cities towards becoming renewable energy cities. Various programs have been initiated for the urban sector by the Indian Government for promoting the design of solar buildings; solar water heating systems in industry, hospitals, hotels and homes; establishment of ‘Akshya Urja Shops’; promoting urban industrial waste and/or biomass to energy projects; and deployment of SPV systems/devices in urban areas for demonstration and creation of awareness [13]. The Ministry of Housing and Urban Affairs (MoHUA) under the Government of India launched the “Smart Cities Mission” in 2015 with an aim to make urban areas energy-efficient so as to reduce the load on existing resources. It had norms of making 80% of the smart cities’ buildings energy-efficient, with 10% of the energy requirement being fulfilled from solar energy [14].
The incident SR depends upon the geography of the region, azimuth and inclination angles, sun–earth position hour, and atmospheric attenuations [15]. Most parts of India receive daily SR of 4–7 kWh/m2 with sunny days, varying between 250 to 300 annually, with Western Rajasthan receiving the highest radiation energy annually and the north-eastern region receiving the lowest annual radiation [16]. SR is also affected by atmospheric parameters such as clouds, aerosols, suspended particles, water vapor, temperature, humidity, CO2, and SO2 soot.
The atmosphere satellite models can be classified as physical and statistical models, as mentioned in [17]. Statistical models tend to rely on straightforward regressions between ground measurements and data obtained from satellites [18], and the historical data is used to predict the future irradiance values [19]. In statistical models, the local atmospheric conditions are correlated with the clear sky (CS) irradiance in order to obtain solar irradiance at a particular time for a selected region. The time series analysis of global irradiance is the basis of statistical methods. Physical satellite models utilize the interactions of SR with participating atmospheric gasses, clouds, and aerosols. These models use the Radiative Transfer Model (RTM), which eliminates the requirement of ground data [17] and solves the equations of flow dynamics [20] and the radiative transfer equation (RTE), as described in [21,22,23,24,25].
In [26], the authors developed a fully physical model to estimate the global irradiances under clear-sky conditions that used aerosol properties, total ozone column, and total columnar water vapor produced by Monitoring Atmospheric Composition Climate (MACC). Hence, such a type of model is well suited for geostationary satellite retrievals with many grid points. A look-up table (LUT)-based eigenvector hybrid approach is described in [27]. It was used by authors in [28], combining the Moderate Resolution Imaging Spectro-Radiometer (MODIS) and Multifunctional Transport Satellite (MTSAT) data to produce surface solar irradiance for northern China. The model we developed in this study reproduces the irradiance produced by the Solar Energy Nowcasting System (SENSE), which is based on analytical LibRadtran RTM with much faster computational speed [29]. As a result, we introduce the Indian Solar Irradiance Operational System (INSIOS), which is optimized to run for the climatological and geographical conditions of India, as well as for the current Indian remote sensing capabilities (e.g., the Indian National Satellite System (INSAT-3D)).
INSIOS is capable of operating for SR estimation in near real-time and is based on LUTs calculated with libRadtran that span a broad range of cloud and atmospheric conditions, including cloud and aerosol optical parameters that are derived from a new tailor-made satellite product for the development of radiation budget applications; that recover the UV, visible, and near-infrared spectra at high resolution (1 nm); and that can produce almost instantaneous output. In [30,31,32], the authors pioneered the development of neural network (NN) models of SR. In place of NN, we used multi-polynomial regression analysis based on libRadtran outputs [33,34] with radiative transfer simulations using LUTs from a total of 0.3 million runs for CS and cloudy (CL) conditions (separately). The INSIOS system was developed here to carry out multivariate studies of interactions between radiation, clouds, and aerosols in the atmosphere, along with producing real-time maps of solar irradiance from real-time satellite inputs and aerosol forecasts.
Cloud optical thickness data for India were obtained from INSAT-3D; relevant aerosol data from Copernicus Atmosphere Monitoring Service (CAMS)-MACC near real-time; and ground-based data from the Baseline Surface Radiation Network (BSRN) stations of Gandhinagar, Delhi, Howrah, and Tiruvallur for the same time period. Ground-based data of GHI in India were used to compare with the simulated outputs. CAMS data were retrieved for the specific pixels as ground irradiance data. For the same pixels, the ground aerosol optical depth (AOD) was obtained from AERonotic Robotic NETwork (Aeronet) and the cloud optical thickness (COT) from the historical data of INSAT-3D. A matrix was produced at the end, with the data of latitude, longitude, year, month, day, hour, minute, solar zenith angle (SZA), CAMS AOD, INSAT-3D COT, ground-based AOD, BSRN GHI and DNI, and simulated GHI and DNI using near real-time modeling techniques. Near real-time solar irradiance was calculated from INSIOS. The validation was done against the ground-based data from BSRN stations. The methodology is presented in Section 2, the results are presented in Section 3, and the discussion is presented in Section 4, followed by the conclusions in Section 5.
2. Data and Methodology
2.1. Data
2.1.1. Ground Measurements
Ground data for verification were obtained from four BSRN stations of Gandhinagar, Delhi, Howrah, and Tiruvallur [35]. These stations are located in urban regions with populations varying from 0.21–11.03 million [36], as shown in Table 1. BSRN stations provide data of short-wave downward global radiation, direct radiation, diffuse radiation, and long-wave downward radiation in W/m2. Global radiation was measured using a pyranometer (Hukseflux, SR20-T2), direct radiation with a pyrheliometer (Hukseflux, DR02-T2), and diffuse radiation with a pyranometer (Hukseflux, SR20-T2). BSRN provided high-precision ground measured data of solar irradiance. The dataset used for the comparison was from January to December 2018. The location and description of the four BSRN stations of India are presented in Table 1, which were used for the validation of solar irradiance estimated from the near real-time modeling technique. Figure 1 gives the picturization of all the locations selected for this study [37]. The temporal resolution of the ground data obtained from BSRN stations was 1 min, whereas the INSAT-3D satellite data had a temporal resolution of 30 min. Hence, half-hourly analysis was done in this work. BSRN stations are widely placed in all corners of the Indian subcontinent. Delhi is located in the north, Gandhinagar in the west, Howrah in the east, and Tiruvallur in south. These locations have different geological features, atmospheric conditions, and aerosol levels. Hence, the models’ performance was studied under varied atmospheric conditions.

Table 1.
Latitude (degrees), longitude (degrees), elevation (meters above sea level), of Baseline Surface Radiation Network (BSRN) stations located in India, along with population levels.
Figure 1.
Study region and sun photometer locations.
Another form of ground data used in this analysis was AOD obtained from Aeronet for validation [38]. Sun photometer measurements of the SR provided information for the calculation of the columnar AOD. AOD was further used to compute columnar water vapor, as well as in the estimation of the aerosol size using the Ångstrom parameter relationship. Version 3 algorithm processing of the Aeronet data contained three quality levels (levels 1.0, 1.5, 2.0) for every product. Levels 1.0 and 1.5 are provided by Aeronet in near-real-time and 12 month or longer delay, ensuring that the highest quality data can be obtained from version 3, level 2.0 products. Fine and coarse mode AOD and fine mode fraction were provided by version 3 AOD processing. There were three quality levels provided by Aeronet. The pre-field deployment sun calibration was used by level 1.0. Level 1.0 data and a cloud-screening and automatic quality control procedures were used by level 1.5 data. After applying the final post-field deployment sun calibration to level 1.5 data, the data were upgraded to level 2.0. The total optical depth and other components such as ozone, NO2, and Rayleigh optical depths were included in the total optical depth. The unscreened and non-calibrated data were level 1.0 data, whereas the cloud-screened and cloud-cleared data were level 1.5 data, but were not quality assured and did not have final calibration applied. The quality-assured, pre-field and post-field calibration-applied, cloud-cleared, and manually inspected data were the level 2.0 data. Aeronet locations were selected on the basis of proximity to BSRN locations and available data were extracted on the basis of the time period of INSAT-3D data. The AOD data from Aeronet was available at 500 nm, which was converted to 550 nm using Ångstrom law [39,40].
2.1.2. Earth Observations
INSAT-3D is an exclusive Indian meteorological satellite to monitor the surface of the Earth and the atmosphere. INSAT-3D satellite imager covers the Asian region from −10.5°N to 45.5°N and 44.5°E to 104.5°E [41]. The India Meteorological Department (IMD) generates multiple data products in hierarchical data format with half-hourly temporal resolution and a spatial resolution of 4 km. Cloud microphysical parameters (CMP) are obtained from INSAT-3D imager observations for the Indian region, as described in [42]. INSAT-3D provides half-hourly cloud microphysical parameters such as cloud optical thickness and cloud effective radius, which is retrieved using the Daytime Cloud Optical and Microphysical Properties (DCOMP) algorithm that uses radiances from visible (0.65 μm) and shortwave-infrared (1.67 μm) channels [42]. In this paper, the operational retrieval algorithm for deriving half-hourly COT from INSAT-3D is described. The microphysical mechanisms of cloud play a significant role in climate change. For example, in [43], authors showed that the microphysical properties increased the greenhouse effect that was found to be more prominent in the case of deep convective clouds. It is also important in monitoring short-to-mesoscale processes.
Southern Asia provides an opportunity to explore the variation in SR due to varying, unstable, and extreme climatic conditions such as heavy fog and smog during winters, dust storms during summers, and heavy rainfall and cloud covers during monsoon season. In order to estimate the cloud microphysical parameters, observations with high temporal resolution are required. No satellite other than INSAT-3D provides continuous microphysical parameters over the Indian region. MODIS derives the cloud optical thickness at 1 km spatial resolution using reflectance measurements at 0.75, 2.16, and 3.75 µm that are used for several remote sensing applications [42]. It is incapable of providing a synoptic view of the earth at an instance because it is a polar orbiting sensor. Spinning Enhanced Visible and InfraRed Imager (SEVIRI), having a geostationary sensor, complements this phenomenon by observing a region on the earth’s surface continuously and provides COT by using 0.6 µm channel averaged over 15 × 15 km2. INSAT-3D offers continuous near global observations with high resolution in order to study various processes associated with cloud microphysics, and is advantageous as it offers a high spatial resolution of 1 km in the visible and short-wave infrared (SWIR) bands. The retrieval is on the basis of the principle that in a non-absorbing visible channel, the reflectance depends mainly on the cloud optical thickness. Hence, information on optical thickness can be obtained from a combination of visible and shortwave-infrared absorbing. The mean correlation between the MODIS COT and the INSAT-3D COT was found to be 0.73 for the cloudy month of July and 0.60 for the winter month of January, as shown in [42]. INSAT-3D CMP data were obtained from mosdac [44] in hierarchical data format for each location (Delhi (DEL), Gandhinagar (GAN), Howrah (HOW), and Tiruvallur (TIR)). COT data were extracted from the CMP files for each location and time step.
CAMS is a European commission service implemented by the European Centre for Medium-Range Weather Forecasts (ECMWF) under the Copernicus program [45]. MACC is a global reanalysis of aerosol optical depth at 550 nm, which provides a 10-year global reanalysis of aerosol optical depth at 550 nm. MACC near real-time provides daily global forecasts up to 5 days of aerosol optical depth at 550 nm [46]. The parameters include dust, organic carbon, black carbon, sulfates, AOD, and sea salt. It provides the data with hourly temporal resolution. The CAMS MACC near real-time system provides AOD-forecasted data at an interval of 6 h with 3 h time step. In this analysis, interpolation was used to obtain such values at selected locations at 30 min temporal resolution, as done in [47]. The uncertainty in CAMS AOD forecast varies from −0.1 to 0.2 for mean bias, as compared to Aeronet ground data, as shown in [48]. CAMS MACC near real-time data are available for the entire earth according to year and month. Data used in this analysis are a 1-day forecast of total AOD at 550 nm initialized at 0 UTC (Coordinated Universal Time) with 3 h time step from 0 to 12 UTC. CAMS AOD was extracted for all BSRN locations (respective latitude and longitude) for the respective time periods.
2.2. Methodology: Energy Management Systems
2.2.1. Solar Energy Nowcasting SystEm (SENSE)
SENSE was developed by the National Observatory of Athens in Greece in collaboration with the World Radiation Center in Switzerland and was a starting point in the investments related to energy with a vision of innovative high-end applications and technologies [49]. This method was developed and used in many European Union (EU)-funded projects [50] (e.g., Geo-cradle [51] and e-shape [52]). SENSE is based on near real-time atmospheric inputs and RTM simulations, and its technical background can be found in [53]. This work uses the modeling techniques for the near real-time assessment of the SR on the basis of LUTs calculated using libRadtran. The description of the RTM is available in [33,54]. The LUTs consist of millions of RTM simulations. The necessity and usefulness of the LUT-based approach, as presented in [26], is studied by the authors of [55], considering the interoperable exchange of similar GHI databases. The relevant studies related to LUT algorithms and RTM simulations have been located mainly in Europe, where the climate is much more stable with no extreme atmospheric phenomena. In the case of India, there are extreme climate events such as dust storms, anthropogenic aerosols, and heavy rainfall. The aim of this paper was to study the effect of such extreme atmospheric events on SR monitoring in near real-time.
The input parameters used for libRadtran simulations under clear-sky conditions were solar zenith angle (SZA), Ångström exponent (AE), AOD, total ozone column (TOC), single-scattering albedo (SSA), and columnar water vapor (CWV). In the case of the cloudy sky condition, the input parameters used were SZA, TOC, and COT. As the effects of aerosols are weak as compared to thick clouds under CL conditions, AOD was not used when COT was greater than 1. For the comparison of the model with BSRN station data, an altitude correction was applied on the basis of RTM (Libradtran) calculations on the solar energy output of different model simulations in order to take into account the altitude of the stations.
The RTM (Libradtran) outputs were high-resolution spectral irradiances (1 nm). The radiative transfer solver used was SDISORT [34] with pseudospherical approximation to produce valid outputs for SZA varying from 0–90°. The simulation calculations were made using a band parameterization method, which was based on the correlated-K approximation, as described in [56]. The determination of clouds and aerosol was done on the basis of the default aerosol model described in [57]. The detailed information about the RTM simulations, the input parameters, and the construction of the LUTs is presented in [58]. The LUT used for SZA was the same at 2:2:88 for both CS and CL conditions. The other LUTs included 0:0.05:1.5 for AOD for clear-sky and 0:1:30 for COT for cloudy conditions. AOD was obtained at a wavelength of 550 nm and COT at a channel width of 550–750 nm. We used TOC as 350 DU and WV as 0.5 cm. The methodology used for the SR estimation is shown in Figure 2. The coefficient of correlation between the RTM simulations of GHI and the BSRN ground measured data for entire datasets and period were found to be 0.88 and 0.69 for CS and CL conditions, respectively. The same results for DNI were 0.64 and 0.34 for CS and CL conditions, respectively.
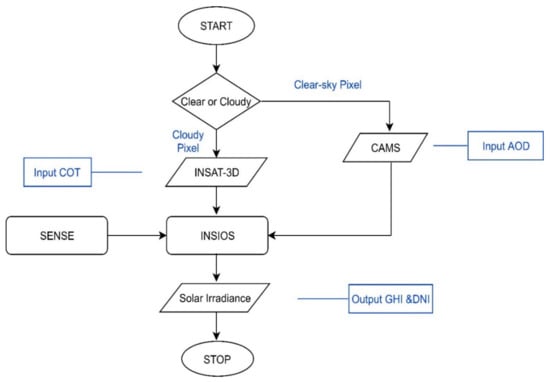
Figure 2.
Flowchart of the Indian Solar Irradiance Operational System (INSIOS) technique. COT: cloud optical thickness, INSAT-3D: Indian National Satellite System, CAMS: Copernicus Atmosphere Monitoring Service, AOD: aerosol optical depth, SENSE: Solar Energy Nowcasting System (SENSE), GHI: global horizontal irradiance, DNI: direct normal irradiance.
2.2.2. Indian Solar Irradiance Operational System (INSIOS)
The INSIOS technique was developed in order for the SENSE to be applied and optimized for the Indian climatological conditions and input data sources. It is an analytical method that uses RTM and SENSE outputs for training. The technique can be executed very fast and can be used for near real-time estimation of SR in India. In [29], the authors compared several models to estimate SR in near real-time, found that MRF approach was the most accurate, and estimated the GHI identical to the RTM simulations. The analytical functions for SR were constructed in this work and the polynomial coefficients are shown in Table 2. INSIOS is able to be placed in the future as a useful tool for solar energy production management in the region of India. An example of the GHI and DNI maps as produced from the near real-time SR techniques for 15 April 2018 at 07:00 UTC for India is shown in Figure 3. The INSIOS GHI and DNI were derived from SENSE using the multi-polynomial regression technique. INSIOS has the potential to be included in INSAT-3D operating and retrieving algorithms for on-the-fly surface irradiance calculations.

Table 2.
Values of coefficient used for the polynomial function in Equation (1) of INSIOS model for GHI and DNI estimation under clear-sky and cloudy conditions.
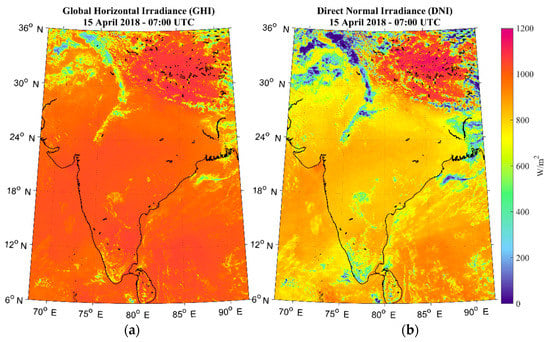
Figure 3.
Output map based on INSIOS for 15 April 2018 at 07:00 UTC (Coordinated Universal Time) for India for (a) GHI and (b) DNI.
The analytical functions for surface solar irradiance were constructed in order to perform SR near real-time estimations. SR is a function of COT, WV, SZA, SSA, AOD, AE, and TOC. In [29], the authors performed a sensitivity analysis of GHI to WV column and TOC. After comparing the integrated spectral GHI over the whole spectrum for different values of TOC, the authors found that there was a mean difference of only 0.5 between 300 DU (Dobson unit) and 400 DU. They found a mean difference of 3.2 for WV column, varying between 0.5 to 2. Hence, we chose to neglect AE, WV, TOC, and SSA variables for the construction of the analytical function. We constructed polynomial functions for CS and CL conditions according to the work presented in [59]. For clear-sky conditions, SR was taken as a function of SZA and AOD, whereas in cloudy conditions, SR was expressed as a function of SZA and COT. We used RTM and SENSE outputs for training the INSIOS function. Different orders of polynomials with two variables were tested in order to obtain the best fit (multi-regression analysis). It was found that the estimates closest to the RTM results were obtained with fourth and fifth degree polynomials in the case of GHI for clear and cloudy conditions, respectively, and fifth and sixth degree polynomials in the case of DNI for clear and cloudy conditions, respectively [60], as shown in Equation (1):
where is SZA and is COT for the cloudy case and AOD for the clear-sky case. Table 2 presents the analytical values of the coefficients of the best-fitted polynomial function for GHI and DNI under CS and CL conditions. Using this approach, the RTM simulations of SR can be derived in lesser computational times and hence can be used for near real-time applications. We can obtain the INSAT-3D near-real-time COT data [61] and CAMS 1 day AOD forecasts, which can be used for near real-time operation. The INSIOS system presented in this paper has a very fast processing speed which is capable of simulating solar irradiances in near real-time horizon. For the India maps, we were simulating at almost 300,000 pixels per minute. The inputs required were SZA and AOD/COT, depending upon the clear and cloudy conditions, respectively. As a result, INSIOS is operationally ready and it is hoped that it will be used as a solar energy potential tool for the Indian energy managing authorities and the energy producers in various scales (i.e., from the big solar farms to the roof-top installations).
2.2.3. Error Analysis
BSRN ground-based GHI and DNI data were used for the verification of the estimated GHI and DNI values, as obtained from INSIOS. The statistical equations used for the error analysis were as follows:
We used mean bias error (MBE) and root mean square error (RMSE) for validation purposes. MBE provided information about overestimation for positive MBE values and underestimation for negative values. RMSE showed the spread of the error distribution. On the basis of these error metrics, the relative MBE (rMBE) and relative RMSE (rRMSE) were calculated as follows:
Other parameters used for the analysis include the coefficient of correlation, the coefficient of determination, and the percentage difference. The percentage difference was calculated as follows:
3. Results
3.1. Reliability of INSIOS
This section focuses on the performance analysis of INSIOS as compared to the RTM simulations for all stations. Figure 4 represents the percentage difference between the INSIOS technique and the RTM simulations. The data used were the RTM GHI and DNI output with half-hourly temporal resolution. The box plot represents the interquartile range between the 25th and 75th percentiles with the in-box line to show the median and the upper and lower whiskers to represent the maximum and minimum error values that were within 2× the interquartile range of the box edges. The interquartile range was calculated as the difference between the first quartile and the third quartile. In [29], the authors showed the minimum and maximum error as being within 1.5 times the interquartile range of the box edges for a similar study. The largest difference was observed for DEL in the case of GHI for clear-sky conditions, for TIR in the case of GHI for cloudy conditions, for DEL and HOW in the case of DNI for clear-sky conditons, and for HOW and TIR in the case of DNI for cloudy conditions. INSIOS showed differences around zero (within ±0.04%) for all stations in all cases, except for GAN and HOW in the case of DNI for cloudy cloudy conditions. Hence, INSIOS shows the efficient representation of RTM simulations, which can be used for solar energy near real-time forecasting for faster operations.
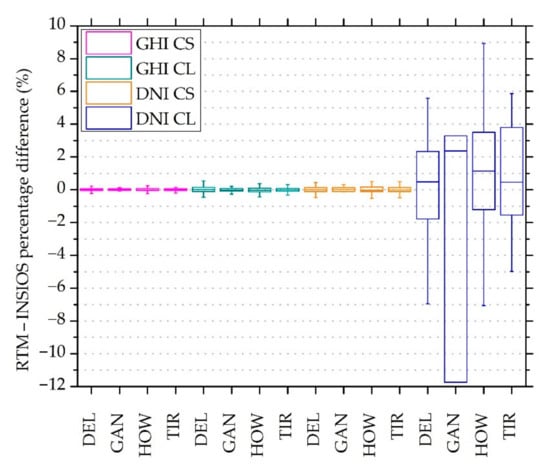
Figure 4.
Percentage difference of GHI and DNI estimated from INSIOS technique as compared to RTM simulations for clear and cloudy conditions for all stations. RTM: radiative transfer model, CS: clear-sky, CL: cloudy.
3.2. Comparison Against BSRN
The accuracy of the INSIOS model was verified against four BSRN stations in India. BSRN measurements are among the highest quality data available for SR [62]. We calculated the regression of mean GHI estimated from ground data and INSIOS method, as shown in Figure 5. It was found that the model overestimated the GHI and DNI for clear-sky conditions and underestimated the GHI for cloudy conditions for all stations. The overestimation of GHI and DNI under clear-sky conditions was justified, as the aerosol estimations may have been underpredicted. GHI and DNI were underestimated under cloudy conditions, which was due to the COT resolution available from INSAT-3D. In [63], the authors noticed that the percentage of missing data for global and direct irradiances was 4% and 13%, respectively, for BSRN data. The percentage of missing data in our case was 7.6% for GHI and 12.1% for DNI for DEL station, in which the missing data for May was at a maximum at 74.6% for GHI and 75.5% for DNI. For GAN, the missing data ranged from 2.76% to 17.3% for GHI and DNI, respectively, and for HOW it was from 9.8% to 12.3% for GHI and DNI, respectively. TIR showed a variation of missing data from 2.2% to 24.9% for GHI and DNI, respectively. The gaps in the initial field data may have occurred due to many reasons such as data loss, instrument failure, or calibration periods. The results show deviations in Figure 5, not due to adequate accuracy of aerosol and cloud input data sources in Southern Asia. In [64], the authors showed that for the Indian subcontinent, aerosol properties showed variations in regional, intraseasonal, and interannual contexts, and there were uncertainties in indirect radiative effects of aerosols. In [42], the authors presented the methodology of COT calculation from INSAT-3D satellite data and found that there was a moderate correlation between INSAT-3D and MODIS data. The coefficient of correlation was found to vary from 0.6 in January, to 0.4 in February, to 0.73 in July.
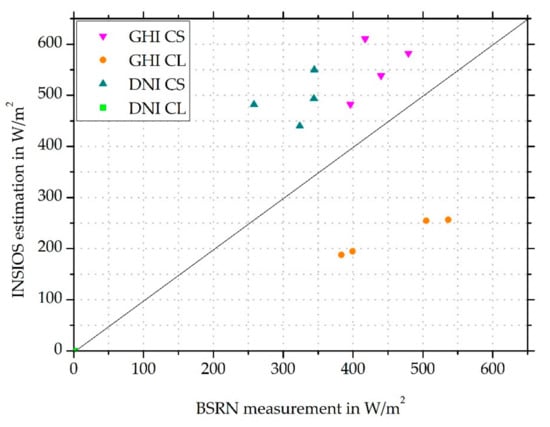
Figure 5.
Mean GHI and DNI estimated from INSIOS technique as compared to BSRN data for clear and cloudy conditions for all stations.
Figure 6 and Figure 7 present the seasonal relative RMSE and seasonal relative mean square errors for GHI and DNI estimated from INSIOS method, as compared to the ground data. For GAN, the results are shown for monsoon only, as the BSRN data were only available for the month of September for this area. Similarly, due to the unavailability of BSRN data, results of summer months for HOW and autumn months for TIR are not shown. In [53], the authors performed a global Köppen-Geiger-Photovoltaic climate classification that placed DEL in the temperate zone, GAN in the steppe, and HOW and TIR in tropical zone, according to temperature and precipitation. All these stations were classified as being in the high irradiation zone.
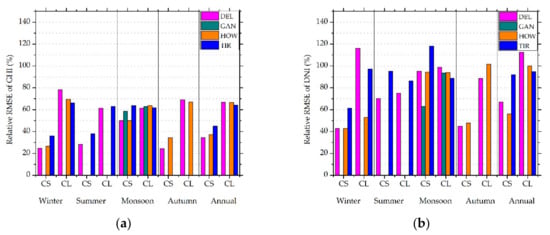
Figure 6.
Seasonal relative root mean square error (rRMSE) values of (a) GHI and (b) DNI estimations from RTM simulations and INSIOS technique, as compared to BSRN measurements.
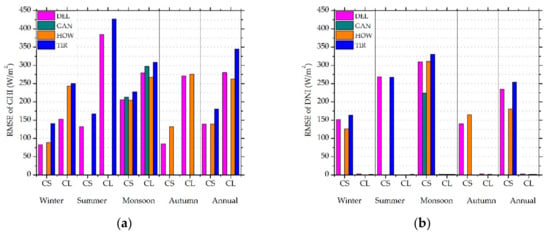
Figure 7.
Seasonal RMSE values of GHI (a) and DNI (b) estimations from RTM simulations and INSIOS technique, as compared to BSRN measurements.
The rRMSE for DEL ranged from 24.5–49.9% for CS and 61.2–78.4% under CL conditions, as can be seen from Figure 6a. In the case of DNI, the rRMSE for DEL ranged from 42.7–95.2% for CS and from 75.1–116.3% under CL conditions, as observed from Figure 6b. Larger errors in DNI as compared to GHI were justified, as there was a stronger impact of clouds and aerosols on DNI compared with GHI. The RMSE for DEL ranged from 75–380 W/m2 for GHI and 0.1–360 W/m2 for DNI under clear-sky and cloudy conditions, respectively. In [65], the authors showed that Delhi had the highest rate of fires within a radius of 200 km, and that fire intensity peaked in the post-monsoon period of October and pre-monsoon period from April to May. The concentration of particulate matter (PM10) in Delhi was the highest among the major Asian cities [66], reaching four times the Indian standard. Hence, in the case of DEL, the errors in the irradiance values for cloudy conditions were prominent because aerosols were not taken into consideration, though there were significantly high aerosol levels in DEL, especially during pre-monsoon and post-monsoon periods. GAN showed variation from 58.4–62.8% for GHI estimation under clear-sky and cloudy conditions during monsoon months, whereas the error varied from 63–93.6% for DNI. For GAN, the results are shown for the monsoon period only, as the BSRN data were available only for the month of September for this area. GAN showed an RMSE of 240 and 310 W/m2 for GHI estimation under CS and CL conditions, respectively, during monsoon months, whereas the error varied from 1.1–260 W/m2 for DNI. The error for HOW varied from 26.5–49.9% to 63.6–69.5% for GHI under clear-sky and cloudy conditions, respectively. In the case of DNI, the rRMSE values for HOW were from 42.9–94.4% for CS and 53–101.6% for CL conditions. The error for HOW varied from 100–270 W/m2 for GHI estimation and 0.5–350 W/m2 for DNI under CS and CL conditions. TIR showed a variation from 25–60% for GHI and 100–150% for DNI under clear-sky and cloudy conditions. TIR showed a variation from 110–410 W/m2 for GHI and 1.1–370 W/m2 for DNI under CS and CL conditions. TIR is on the eastern coast of India and receives heavy rainfall from the south-west monsoon in the months of June to September [67] and north-east monsoon from the calendar months of October to December [68]. Due to this, the errors were large during the monsoon season in the case of TIR. The detailed statistical analysis is presented in Table 3. The large rRMSE and RMSE values during monsoon season indicate the prominent effect of clouds on GHI and DNI. In [69], the authors developed two models in order to assess the solar irradiance at surface using satellite images, namely, the MT (HELIOSAT and Meteosat) model and the HT (HELIOSAT and INSAT-3D) model using multispectral satellite data along with the HELIOSAT model. The RMSE values were found to vary from 63.7 to 144 W/m2 and 84.9 to 167 W/m2 for MT and HT models, respectively, for dust events. The errors were found to be more frequent in the case of the HT model when compared with the MT model. The ratio of RMSE from the HT model and the MT model was found to vary from 0.75 to 1.99.

Table 3.
INSIOS model statistical scores of GHI and DNI estimation for clear-sky and cloudy conditions. MBE: mean bias error.
The deviations of the INSIOS estimations from BSRN ground data were not the same at the selected stations, as can be seen from Table 3, and also depended on the season, as shown in Figure 6 and Figure 7. The missing values were due to the unavailability of ground data from BSRN stations for the months of October and November for TIR, February to August for HOW, and all except September for GAN. Similar observations were observed by the authors in [47]. This observation can be explained by the problem with MACC in emulating the spatial and temporal complexity of the aerosol mixture. The AOD data from MACC near real-time analysis had a spatial resolution of 1.125° and a temporal resolution of 3 h. This caused difficulty in capturing the exact effect of the atmospheric parameters on the incident SR over a specific location and at a particular time.
The accuracy of GHI and DNI estimations from the INSIOS technique is shown in Figure 8, as compared to the BSRN measurements under CS and CL conditions for all stations. Figure 8 shows that the INSIOS is a reliable technique for GHI estimation under CS and CL conditions, as well as for DNI under clear-sky conditions, as presented in Figure 5. Figure 8 shows the overestimations of irradiance for clear-sky conditions and the underestimation in the case of cloudy conditions. The mean BSRN and INSIOS differences were found to vary from −93 W/m2 for GAN to −49 W/m2 for TIR in the case of GHI, and −103 W/m2 for GAN to −76 W/m2 for HOW in the case of DNI under clear-sky conditions. Under cloudy conditions, the GHI value varied from 194 W/m2 for DEL to 266 W/m2 for TIR. The clear-sky GHI estimations showed over-prediction of GHI and DNI in the presence of aerosols when the cloud effects were neglected. This is consistent with the results shown in Figure 5. The difference was more profound in the case of DNI as compared to GHI. In [26], the authors showed an overestimation of the fine, strongly diffusing pollution particles and an underestimation of the coarse, mineral dust particles that affect the GHI. Due to the underestimations of aerosols, there was an overestimation of irradiance. The underprediction of GHI and DNI under cloudy conditions, as shown in Figure 8, was consistent with the one shown in Figure 5. The difference in the case of DNI was substantially less, as the values of DNI were less for DNI estimation under cloudy conditions. Hence, the validations provided here qualify the intrinsic performances of the INSIOS model rather than its performances in real-life, as shown in [27,70,71,72]. Figure 8b shows the mean GHI and DNI differences derived from RTM simulations, as compared to the BSRN measured irradiance for CS and CL conditions. Hence, the errors highlight the fact that even the reference RTM simulations presented similar (almost identically highlighting the performance of INSIOS against the training RTM simulations) statistics in Southern Asia because of the specific atmospheric conditions (monsoon, dust storms, fog, and smog) and data sources (CAMS MACC and INSAT-3D). For Southern Asia or India, monsoon and the subsequent phenomena affect the reliability and accuracy of the observed atmospheric parameters such as cloud microphysics and aerosol loads. In order to address this issue, the sum of annual energy potential and the sum of errors for Delhi is shown in Figure 9. It shows realistic solar energy potential condition with sums of energy and errors from INSIOS. The percentage error in monthly GHI estimations, as compared to the BSRN measurements, was within 20%, and reached up to 70% in the case of DNI. The annual estimated values from INSIOS were 2071 and 1867 kWh/m2 for GHI and DNI, respectively. Annual average satellite estimations of GHI and DNI were found to vary from 1896–2043 and 1564–1992 kWh/m2, respectively, for various locations of India, as studied by the authors in [73].
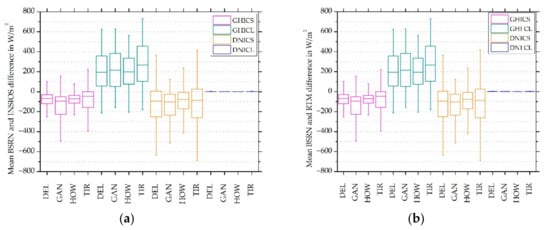
Figure 8.
Half-hourly mean GHI and DNI differences derived from (a) INSIOS and (b) RTM, as compared to BSRN data for clear and cloudy conditions.
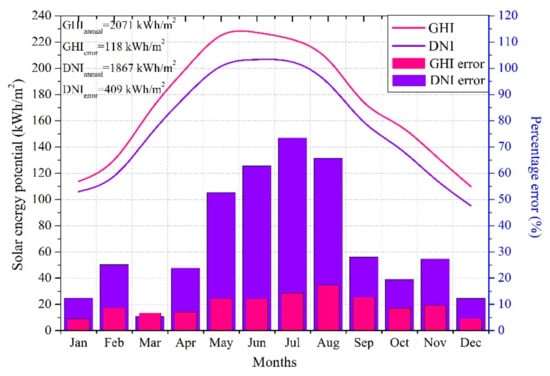
Figure 9.
Solar energy potential in kWh/m2 and percentage error (%) of GHI and DNI, as compared to the BSRN measurements in Delhi.
4. Discussion
The results found in this paper for all stations are similar to the findings of several studies, including [26,29,47]. MBE and RMSE are conventional statistical metrics widely used in the SR forecasting field for characterizing and validating forecasting models. These scores depend on several factors such as comparing spatial and temporal resolution of the data, the percentage of clear-sky days in the set of data, and the months used in the comparison, and the limitations of these metrics have been shown in [74]. Although these metrics provide comprehensive global information on forecast errors, it can be misleading and insufficient to characterize the behavior of the forecast. For DNI especially, there are no better statistics for real-time calculated irradiance [73], as the uncertainty of the atmospheric inputs is particularly high in Southern Asia (CAMS AOD and INSAT-3D COT). For GHI, the results were not so good compared to the bibliography because we dealt with the extreme conditions of monsoon [73,75,76], continuous fog [77,78], and haze [79,80,81]. The relevant studies that present better results were located mainly in Europe, where the climate is much more stable with no extreme atmospheric phenomena [27,29,82,83,84].
The results shown in Figure 6a are comparable to [29], in which the relative RMSE values were found to vary from 5–48%, considering the fact that the climate of Europe is mostly stable throughout the year, whereas the Indian climate shows drastic variations. In Figure 6b, better results were not obtained for estimated near real-time DNI, as DNI is very sensitive under cloudy conditions. In [85], the authors showed that radiation algorithms might produce unidentifiable and large errors. The same applies to climate modeling such as the estimation of SR from satellite data. In [86], the authors showed that clouds and aerosols increase radiative flux uncertainties. This occurs due to inaccurate spatiotemporal distribution of the physical properties of clouds and aerosols. Another factor responsible is the approximation and parameterization of the radiative properties of these elements. These factors affect the simulation of SR and burden the simulations with a high degree of uncertainty. Benchmarking by the University of Geneva [62] has shown the relative RMSE variation for GHI from 15–70% and DNI from 30–160% on the basis of the geographical conditions. Because India shows a great variation in the climatic and geographical conditions from east to west and north to south, the variation in the rRMSE is justified. In [83], the authors showed a difference in daily-mean surface solar irradiance for December, January, and March. The difference was found to be highest in June and at its minimum in December for the Netherlands, where June is characterized as spring and December as autumn. In our case also, the difference in the values of estimated and observed irradiances were at a minimum during the autumn season. Irradiance under cloud-free conditions is sensitive to aerosol production from atmospheric particulate matter, dust storms, and biomass burning [87]. Moreover, exclusion of SZA greater than 75 degrees would improve the statistics of rRMSE by almost 40%. In [88], the authors studied the performance of solar radiation components, obtained from meteorological radiation model (MRM) and satellite-based datasets, against pyranometer-based ground measurements. The rRMSE for GHI estimation was found to vary from 5.5–7.19% for MRM with different aerosol sources and 11.6% for CAMS under CS condition. Under CL conditions, the rRMSE for GHI varied from 62.2–63.1% for MRM and 95.5% for CAMS. In the case of DNI, the rRMSE varied from 10.5–17.0% for MRM and 17.3% for CAMS under the CS condition. Under the CL condition for DNI, the rRMSE was found to be around 184.9% for MRM and it was as high as 1146% for CAMS.
In [39], the authors found a correlation coefficient of 0.73, an average error around 46.15%, and an MBE of 0.045. It was also found that only 52.12% of CAMS MACC AOD values were within ±0.05 to ±0.15 of the Aeronet AOD. In [64], the authors pointed out that there is a need of a more detailed and appropriate measurements of atmospheric parameters in order to reduce the uncertainties in indirect radiative effects of aerosols. These include the establishment of a network of observatories in India to carry out in situ measurements of cloud parameters and shape, size, chemical composition, and mixing state of aerosols. Another important step is to carry out a detailed observation on the types of aerosol, as well as their horizontal and vertical distribution. In [73], the authors made a comparison between the AOD data obtained from MODIS and AERONET, finding that there was a high level of uncertainty in the data obtained from the two sources. This enhances the need for a more accurate and better spatial resolution AOD retrieval system for places such as India with complex climatology in order to improve the satellite-based estimations of solar radiation. In [89], the authors showed that there was a rapid dimming in the surface measurements of solar radiation post-2009. The cause of the decreasing solar radiation might have been due the changes in the clear-sky aerosol loading measurements, instrumentation biases, and aerosol climatology. The 1 day SR bias was found to vary from −100 to 200 W/m2.
4.1. Sensitivity Analysis
4.1.1. Effect of Cloud
Clouds are the biggest attenuators of SR. The quantity of solar energy that reaches the surface of the earth varies depending on the thickness of the cloud, the area it covers, and the water droplet content. The reflected irradiance from the cloud surface is also dependent on the type of cloud and its texture. The uncertainty in the simulation of SR due to the presence of clouds is high, and small fluctuations in cloudiness and cloud optical properties can affect GHI and DNI estimations. Figure 10 presents the annual frequency distribution of the percentage difference between the estimations from INSIOS and the ground measurements from BSRN stations for GHI and DNI values for cloudy sky conditions for all stations. The majority of the percentage differences were lower than −75%, with the maximum frequency encountered around −50% differences in the case of GHI. In the case of DNI, the majority of the percentage differences were lower than ±50%, with the maximum frequency encountered around 0. This indicates that INSIOS-derived forecasts of GHI and DNI have overall good accuracy, with the mean absolute percentage difference being −39.89 ± 37.96% for GHI and 6.78 ± 31.38% for DNI. This shows an underestimation of −39.89% for GHI and 6.78% for DNI from INSIOS as compared with BSRN that is imminent due to the overestimation of INSAT-3D COT. Figure 11 shows the effect of cloud optical thickness on GHI and DNI as compared to BSRN measurements. The mean percentage difference between the GHI/DNI produced by INSIOS and the values measured by all the BSRN stations is plotted as a function of COT. It can be seen from Figure 11a that for COT less than 40, the mean GHI percentage difference between INSIOS estimations and BSRN measurements varied from −60% to −20%, which is also visible in Figure 10a, and there were fluctuations for larger COT. For a similar study presented in [29], the authors found that there were underestimations from the MRF technique up to −60% when the COT was around 35. In the case of DNI, as shown in Figure 11b, the fluctuations in percentage difference between INSIOS and BSRN data were found to vary from −20% to 40%, which is consistent with the result shown in Figure 10b where the maximum percentage fluctuations were around zero. The maximum difference was seen to occur at COT around 35. The scattering of the incoming radiation in several directions other than the incidence one leads to an increase in the diffuse fraction of the radiation [47]. This underestimation might have been caused by an overestimation of INSAT-3D COT due to misclassifications of cloud-free conditions as cloudy. This might happen when the albedo at certain sun positions are abnormally high. Because INSIOS is a physical-based model, the errors occurring in the GHI and DNI estimations were expected to be predominantly the impact of errors in the inputs. Hence, higher quality inputs to INSIOS would improve the estimations.
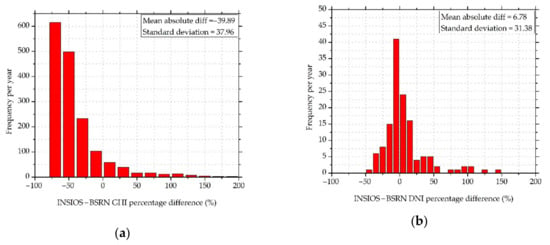
Figure 10.
Frequency histogram of the percentage difference between INSIOS estimations and BSRN measurements for (a) GHI and (b) DNI for all stations.
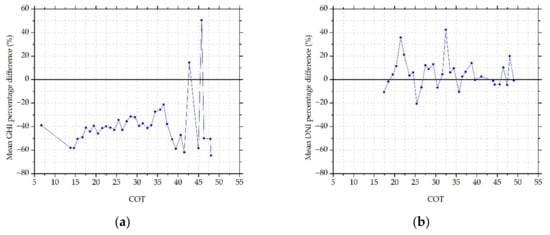
Figure 11.
Mean percentage difference of half-hourly (a) GHI and (b) DNI estimated from INSIOS as compared to BSRN measurements as a function of COT.
4.1.2. Effect of Aerosol
Apart from clouds, irradiance is also affected by scattering from dust, air molecules, and other suspended particulate matter in the atmosphere. Aerosols made up of dust, smoke particles, haze, and small water droplets cause scattering of SR, which varies depending upon the actual atmospheric conditions. In certain cases, aerosol can cause 80% reduction in SR, as shown in [46,90,91,92,93]. Under clear-sky conditions, when the atmosphere is free of clouds, aerosols play an important role in the transfer of SR. Uncertainty in the determination of aerosols can impact the SR estimations. For the purpose of validation of aerosol effect on SR estimation, Aeronet AOD was taken into account. In [48,84,92], the authors observed an underestimation of CAMS under high aerosol loads. In [26], the authors performed various tests for comparing outputs from McClear and libRadtran and found that they produced satisfactory similar results. Because we used libRadtran for RTM calculations, we can thus make a comparison between the two studies. The squared coefficient of correlation between the BSRN measurements and the McClear estimation was found to range from 0.37–0.83 [26]. In our case, the coefficient of correlation between the INSIOS estimations and BSRN measurements for GHI was found to be 0.88 for CS and 0.67 for CL conditions. In the case of DNI, the coefficient of correlation was found to be 0.64 for CS and 0.18 for CL conditions. This was within the range obtained from the McClear model. The global irradiance under clear-sky conditions is proportional to the inverse of the air mass at large solar zenith angles. However, more SR is received from the side by the atmosphere column above. Because of the side-lit bright atmosphere column above the selected point, scattering radiation back to the satellite, a cosine-corrected pixel appears to be brighter than expected [94]. This might be another reason for the overestimation of GHI and DNI under clear sky conditions. In this validation, the criteria used for discriminating the clear sky conditions from cloudy ones are very strict in the sense that it eliminates all the cloud-contaminated situations and rejects some events of heavy aerosol loadings. The severity of the cloud screening is the price to be paid to ensure that only the impact of the aerosols is taken into account in the examination of the so-called cloud-free cases. The first effect of the high aerosol loading situations leads to a pronounced reduction in the DNI.
Figure 12 shows a scatterplot of Aeronet and CAMS differences in AOD as a function of differences in GHI and DNI estimations between the INSIOS technique and BSRN measurements. The GHI differences were spread around zero depending upon the AOD difference. The spread was more in the case of DNI. This shows that the INSIOS estimations and BSRN measurement difference was the same for the variation in AOD differences. The effect of AOD difference was more for DNI as compared to GHI. Figure 13 shows the scatterplots of AOD forecasted by CAMS and AOD derived from INSAT-3D, as compared to Aeronet AOD. It was found that the variation of the two AOD sources compared to Aeronet AOD was large. In [94], the authors showed a comparison of AOD data as measured by Aeronet and the AOD modeled from MACC from January 2003 to January 2004, finding that at many points the fluctuations were as large as 66%. Mostly, there were underestimations from MACC modeling as compared to the Aeronet data. This justifies the fluctuations in the CAMS AOD from Aeronet AOD, visible from Figure 12. Figure 13 shows the plot between the absolute difference in GHI (W/m2) and DNI (W/m2) as estimated from INSIOS and the BSRN ground data as a function of the difference between Aeronet AOD and CAMS AOD for all stations. Figure 14 presents the scatter plot of CAMS AOD forecasts and Aeronet AOD. Figure 14b describes the SR derived from INSIOS using CAMS AOD and INSAT-3D AOD as input for clear-sky conditions. It shows that the difference in AOD between CAMS and INSAT-3D data minutely affected the SR estimation. The coefficient of correlation (R) for the CAMS-MACC AOD was 0.38 and for INSAT-3D AOD was 0.25, whereas the corresponding correlation for the irradiance obtained from INSIOS was significantly improved, reaching 0.9991 and 0.9997 for GHI and 0.9959 and 0.9980 for DNI for CAMS-MACC AOD and INSAT-3D AOD, respectively. This shows that the measured AOD differences between CAMS and INSAT-3D affect the SR minutely [53]. Such data behavior shows that the effect of AOD absolute differences in India in SR estimation is less than 1%, as discussed in various similar comparison approaches in [84,92,95]. In [53], the authors showed that the AOD differences between the CAMS forecasts and the MODIS’s observations had a minor impact on GHI estimation.
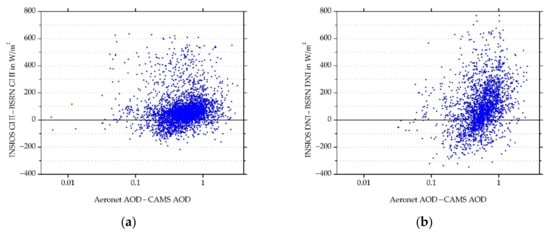
Figure 12.
Absolute difference in (a) GHI and (b) DNI (W/m2) derived by INSIOS from BSRN data as a function of differences in AOD from Aeronet and CAMS for all stations.
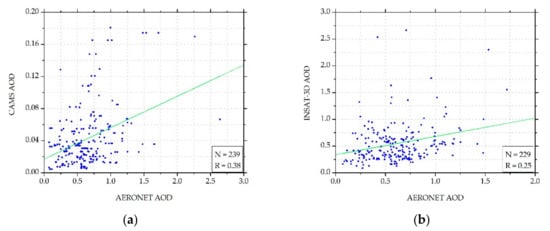
Figure 13.
Scatterplots of (a) AOD forecasted by CAMS and (b) AOD derived from INSAT-3D, as compared to Aeronet AOD.
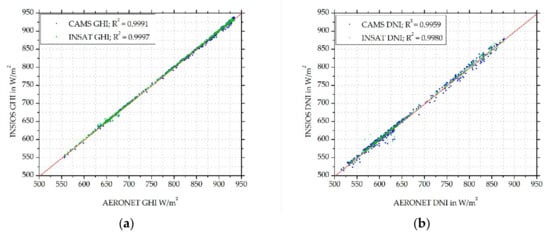
Figure 14.
Absolute difference in (a) GHI and (b) DNI (W/m2) derived by INSIOS from BSRN data as a function of differences in AOD from Aeronet and CAMS for all stations.
5. Conclusions
The study presented in this paper proposed a state-of-the-art modeling technique (INSIOS) for the estimation of SR in near real-time under clear and cloudy conditions. The validation was done against the BSRN ground measurements in urban areas. Firstly, the developed INSIOS modeling technique was described, followed by verification of models against ground measurements from four BSRN locations in India. The study revealed that the accuracy of the simulations was dependent on the resolution and quality of the input parameters (AOD and COT) to the model. INSIOS was found to overestimate the SR under clear-sky and underestimate the same under cloudy conditions. The correlation coefficient between the INSIOS estimations and BSRN measurements was found to vary from 0.64 to 0.88 for DNI and GHI under clear-sky conditions and 0.18 to 0.67 for DNI and GHI under cloudy conditions. The results shown in this paper present the potential use of the INSIOS technique for the applications related to solar energy and supporting the electricity grid services and smart grids on the urban scale. Several models for assessing the SR under clear sky conditions can be found in the literature, which is usually validated against the ground-measured data, as done in this study. Hence, the validations presented in this work qualify the performances of the model, rather than the real-life performances, as presented in [27,70,71,72].
Surface solar irradiance was provided by the solar radiation data (SoDa) (www.soda-is.org) [96] from the database HelioClim-3v3 [97,98]. SoDa services are used for monitoring the performances of solar powerplants, estimation of profitability of projects related to solar energy, management of electricity market using solar forecast data, and decision-making tools in health and agriculture sectors with spectral radiation datasets. However, the all-sky SR data available from these services is limited to the regions of Europe, the Middle East, Africa, and the eastern part of South America. CAMS McClear clear-sky irradiation service [26] provides solar irradiation for CS conditions with temporal resolution varying from 1 min to 1 month, and the data are provided with a delay of up to 2 days. The CAMS clear sky radiation service is based on the work presented in [26]. The products provided are global, direct, and diffuse horizontal, also having the beam normal irradiance for the entire globe. We compared the SoDa McClear [99] and INSIOS results with the BSRN measurements for the month of January for the station DEL and found that the MBE, RMSE, rMBE, and rRMSE values for GHI were 34.13 W/m2, 62.45 W/m2, 10.41%, and 19.06% from McClear, and −54.52 W/m2, 86.35 W/m2, −18.57%, and 29.41% from INSIOS, respectively. The MBE, RMSE, rMBE, and rRMSE values for DNI were −148.35 W/m2, 225.11 W/m2, −80.57%, and 122.26% from McClear, and −21.37 W/m2, 188.78 W/m2, −6.43%, and 56.78% from INSIOS, respectively. From the results shown here, it is clear that the performance of the INSIOS technique shows similar errors in the case of GHI and performs much better than those of McClear in the case of DNI. Knowing that McClear is a widely used model and used by SoDa services for SR estimations in Europe, Africa, and South America, one may have an interest in INSIOS for solar energy applications in other parts of the world.
Implementations of SENSE to Europe, North Africa, and the Middle East support regional energy planning and management through various solar energy applications [53,100]. INSIOS is going to be utilized for renewable energy management in India at various scales (from big solar farms to rooftop installations), exploiting the local earth observation capabilities (e.g., INSAT-3D). Future work may include the prediction of COT instead of using INSAT-3D COT followed by cloud motion vector analysis for the following 1–6 h. Uncertainties in aerosol properties from MACC are still too large, and more efforts are necessary for better modeling of the aerosols. Apart from this, the inclusion of multispectral data in the satellite input [69] may also improve the accuracy of the presented model.
Author Contributions
A.M. and P.K. designed and implemented the idea; A.M. and P.K. analyzed the data, prepared the graphs, and wrote the manuscript with contributions from all coauthors; P.K. and S.K. are the developers of SENSE; P.K., A.B. and S.K. reviewed the manuscript; A.B. and P.K. supervised A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
A.M., P.K., A.B., and S.K. acknowledge the Copernicus, Aeronet, BSRN, INSAT-3D, and SENSE services for providing the data related to clouds, aerosols, and irradiance that has been used in this study. P.K. and S.K. acknowledge the EuroGEO e-shape project under grant agreement 820852.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kumar, R.; Umanand, L. Estimation of Global Radiation Using Clearness Index Model for Sizing Photovoltaic System. Renew. Energy 2005, 30, 2221–2233. [Google Scholar] [CrossRef]
- McMahan, A.C.; Grover, C.N.; Vignola, F.E. Evaluation of Resource Risk in Solar-Project Financing; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Solar Forecasting–Iacharya Silicon Limited. Available online: https://www.iacharya.in/site/solar-forecasting/ (accessed on 9 December 2019).
- Self Forecasting for Australian Solar Farms. Available online: https://solcast.com/utility-scale/self-forecasting-for-australian-solar-farms/ (accessed on 9 December 2019).
- Ishii, T.; Otani, K.; Takashima, T.; Xue, Y. Solar Spectral Influence on the Performance of Photovoltaic (PV) Modules under Fine Weather and Cloudy Weather Conditions Tetsuyuki. Prog. Photovolt. Res. Appl. 2011. [Google Scholar] [CrossRef]
- Raptis, P.I.; Kazadzis, S.; Psiloglou, B.; Kouremeti, N.; Kosmopoulos, P.; Kazantzidis, A. Measurements and Model Simulations of Solar Radiation at Tilted Planes, towards the Maximization of Energy Capture. Energy 2017, 130, 570–580. [Google Scholar] [CrossRef]
- Renewable Energy in India: Progress, Vision and Strategy, Ministry of New and Renewable Energy Government of India 1. Available online: http://iitr.ac.in/wfw/web_ua_water_for_welfare/water/WRDM/mnre_paper_Rene_Energy_2010.pdf (accessed on 17 November 2019).
- Ministry of New and Renewable Energy. Available online: https://mnre.gov.in/node?page=2 (accessed on 16 November 2019).
- Jain, A.; Ram, R.; Gambhir, A.; Bharadwaj, A.; Gupta, D. Report of the Expert Group on 175 GW RE by 2022; Niti Aayog: New Delhi, India, 2015. [Google Scholar]
- Physical Progress (Achievements)|Ministry of New and Renewable Energy|Government of India. Available online: https://mnre.gov.in/physical-progress-achievements (accessed on 9 December 2019).
- Gulati, A.; Manchanda, S.; Kacker, R. Harvesting Solar Power in India. Indian Counc. Res. Int. Econ. Relat. 2012, 152. [Google Scholar] [CrossRef]
- State Rooftop Solar Attractiveness Index. Ministry of New and Renewable Energy: Government of India, 2018. Available online: http://solarrooftop.gov.in/notification/Notification-30082019-161516.pdf (accessed on 16 November 2019).
- Solar/Green Cities|Ministry of New and Renewable Energy|Government of India. Available online: https://mnre.gov.in/solar-cities (accessed on 7 December 2019).
- Rahiman, R.; Yenneti, K.; Panda, A. Making Indian Cities Energy Smart. The Energy and Resources Institute: New Delhi, India, 2019. Available online: http://teriin.org/sites/default/files/2019-04/Making-Indian-Cities-Energy-Smart_UNSW-TERI.pdf (accessed on 18 November 2019).
- Wald, L. Basics in Solar Radiation at Earth Surface. MINES ParisTech: PSL Research University, France. 2018. Available online: http://hal-mines-paristech.archives-ouvertes.fr/hal-01676634/file/2018_basics_solaire_wald_v1.pdf (accessed on 18 November 2019).
- Kumar, A.; Kumar, K.; Kaushik, N.; Sharma, S.; Mishra, S. Renewable Energy in India: Current Status and Future Potentials. Renew. Sustain. Energy Rev. 2010, 14, 2434–2442. [Google Scholar] [CrossRef]
- Inman, R.H.; Pedro, H.T.C.; Coimbra, C.F.M. Solar Forecasting Methods for Renewable Energy Integration Rich. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Masoom, A.; Kashap, Y.; Bansal, A. Solar Radiation Assessemnt and Forecasting Using Satellite Data; Tyagi, H., Agarwal, A.K., Chakraborty, P.R., Powar, S., Eds.; Springer: Singapore, 2019; pp. 45–71. [Google Scholar]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of Solar Irradiance Forecasting Methods and a Proposition for Small-Scale Insular Grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.C.; Coimbra, C.F.M. History and Trends in solar irradiance and PV power forecasting: A prelimenary assessment and review using text mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Liang, S.; Liang, S.; Zhang, X.; Wang, K.; Zhang, X.; Wild, M. Review on Estimation of Land Surface Radiation and Energy Budgets From Ground Measurement, Remote Sensing and Model Simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Tapiador, F.J. Assessment of Renewable Energy Potential through Satellite Data and Numerical Models. Energy Environ. Sci. 2009, 2, 1142–1161. [Google Scholar] [CrossRef]
- Gautier, C.; Diak, G.; Masse, S. A Simple Physical Model to Estimate Incident Solar Radiation at the Surface from GOES Satellite Data. J. Appl. Meteorol. 1980, 19, 1005–1012. [Google Scholar] [CrossRef]
- Noia, M.; Ratto, C.F.; Festa, R. Solar Irradiance Estimation from Geostationary Satellite Data: I. Statistical Models. Sol. Energy 1993, 51, 449–456. [Google Scholar] [CrossRef]
- Raphael, C.; Hay, J.E. An Assessment of Models Which Use Satellite Data to Estimate Solar Irradiance at the Earth’s Surface. J. Clim. Appl. Meteorol. 1984, 23, 832–844. [Google Scholar] [CrossRef]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A New Model Estimating Downwelling Solar Radiation at Ground Level in Clear-Sky Conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Mueller, R.W.; Matsoukas, C.; Gratzki, A.; Behr, H.D.; Hollmann, R. The CM-SAF Operational Scheme for the Satellite Based Retrieval of Solar Surface Irradiance—A LUT Based Eigenvector Hybrid Approach. Remote Sens. Environ. 2009, 113, 1012–1024. [Google Scholar] [CrossRef]
- Huang, G.; Ma, M.; Liang, S.; Liu, S.; Li, X. A LUT-Based Approach to Estimate Surface Solar Irradiance by Combining MODIS and MTSAT Data. J. Geophys. Res. Atmos. 2011, 116, 1–14. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; Taylor, M.; Raptis, P.I.; Keramitsoglou, I.; Kiranoudis, C.; Bais, A.F. Assessment of Surface Solar Irradiance Derived from Real-Time Modelling Te Chniques and Verification with Ground-Based Measurements. Atmos. Meas. Tech. 2018, 11, 907–924. [Google Scholar] [CrossRef]
- Zarzalejo, L.F.; Ramirez, L.; Polo, J. Artificial Intelligence Techniques Applied to Hourly Global Irradiance Estimation from Satellite-Derived Cloud Index. Energy 2005, 30, 1685–1697. [Google Scholar] [CrossRef]
- López, G.; Rubio, M.A.; Martínez, M.; Batlles, F.J. Estimation of Hourly Global Solar Radiation Using Artificial Neural Network. Agric. For. Meteorol. 2001, 107, 279–291. [Google Scholar] [CrossRef]
- Dorvloa Atsu, S.S.; Jervaseb, J.A.; Al-Lawatib, A. Solar Radiation Estimation Using Artificial Neural Networks. Appl. Energy 2002, 71, 307–319. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical Note: The LibRadtran Software Package for Radiative Transfer Calculations–Description and Examples of Use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A.; Emde, C.; Buras, R.; Hamann, U.; Gasteiger, J.; Richter, B. LibRadtran User’s Guide. 2019. Available online: http://libradtran.org/doc/libRadtran.pdf (accessed on 16 November 2019).
- Ramanathan, K. Basic Measurements of Radiation in India (2018-07). Natl. Inst. Wind Energy PANGAEA 2019. [Google Scholar] [CrossRef]
- Census 2011 India. Available online: https://www.census2011.co.in/ (accessed on 6 December 2019).
- Welcome to Bhuvan|ISRO’s Geoportal|Gateway to Indian Earth Observation. Available online: https://bhuvan.nrsc.gov.in/bhuvan_links.php (accessed on 21 November 2019).
- Giles, D.M.; Sinyuk, A.; Sorokin, M.G.; Schafer, J.S.; Smirnov, A.; Slutsker, I.; Eck, T.F.; Holben, B.N.; Lewis, J.R.; Campbell, J.R.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 Database-Automated near-Real-Time Quality Control Algorithm with Improved Cloud Screening for Sun Photometer Aerosol Optical Depth (AOD) Measurements. Atmos. Meas. Tech. 2019, 12, 169–209. [Google Scholar] [CrossRef]
- Singh, R.; Singh, C.; Ojha, S.P.; Kumar, A.S.; Kumar, A.S.K. Development of an Improved Aerosol Product over the Indian Subcontinent: Blending Model, Satellite, and Ground-Based Estimates. J. Geophys. Res. 2017, 122, 367–390. [Google Scholar] [CrossRef]
- Mhawish, A.; Banerjee, T.; Broday, D.M.; Misra, A.; Tripathi, S.N. Evaluation of MODIS Collection 6 Aerosol Retrieval Algorithms over Indo-Gangetic Plain: Implications of Aerosols Types and Mass Loading. Remote Sens. Environ. 2017, 201, 297–313. [Google Scholar] [CrossRef]
- INSAT-3D DATA PRODUCTS CATALOG. National Satellite Meteorological Centre; India Meteorological Department: New Delhi, India, 2014.
- John, J.; Dey, I.; Pushpakar, A.; Sathiyamoorthy, V.; Shukla, B.P. INSAT-3D Cloud Microphysical Product: Retrieval and Validation. Int. J. Remote Sens. 2019, 40, 1481–1494. [Google Scholar] [CrossRef]
- Stephens, G.L.; Greenwald, T.J. The Earth’s Radiation Budget and Its Relation to Atmospheric Hydrology: 2. Observations of Cloud Effects. J. Geophys. Res. 1991, 96, 15325–15340. [Google Scholar] [CrossRef]
- Meteorological &Amp; Oceanographic Satellite Data Archival Centre|Space Applications Centre. ISRO. Available online: https://www.mosdac.gov.in/ (accessed on 8 June 2019).
- Data|Copernicus. Available online: https://atmosphere.copernicus.eu/data (accessed on 16 November 2019).
- Schroedter-homscheidt, M.; Hoyer-klick, C.; Killius, N.; Lefèvre, M. Copernicus Atmosphere Monitoring Service User’s Guide to the CAMS Radiation Service. 2017. Available online: http://atmosphere.copernicus.eu/sites/default/files/FileRepository/Resources/Documentation/Radiation/CAMS72_2015SC2_D72.1.3.1_2017_UserGuide_v1.pdf (accessed on 17 November 2019).
- Eissa, Y.; Korany, M.; Aoun, Y.; Boraiy, M.; Wahab, M.M.A.; Alfaro, S.C.; Blanc, P.; El-Metwally, M.; Ghedira, H.; Hungershoefer, K.; et al. Validation of the Surface Downwelling Solar Irradiance Estimates of the HelioClim-3 Database in Egypt. Remote Sens. 2015, 7, 9269–9291. [Google Scholar] [CrossRef]
- Atmosphere, C.; Service, M. Validation Report of the CAMS Near-Real Time Global Atmospheric Composition Service March–May 2019. Available online: http://atmosphere.copernicus.eu/sites/default/files/2019-03/16_CAMS84_2018SC1_D1.1.1_SON2018_v1.pdf (accessed on 17 November 2019).
- SolarHub. Available online: http://beyond-eocenter.eu/index.php/web-services/solarhub (accessed on 17 November 2019).
- Horizon 2020, S.-18b-2015. GEOCRADLE: Coordinating and IntegRating State-of-the-Art Earth Observation Activities in the Regions of North Africa, Middle East, and Balkans and Developing Links with GEO Related Initiatives towards GEOSS. 2016. Available online: http://solea.gr/wp-content/uploads/2018/03/SENSE_PILOT_RESULTS.pdf (accessed on 18 November 2019).
- Geo-Cradle Portal. Available online: http://geocradle.eu/en/ (accessed on 9 December 2019).
- e-Shape. Available online: https://e-shape.eu/ (accessed on 9 December 2019).
- Kosmopoulos, P.G.; Kazadzis, S.; El-Askary, H.; Taylor, M.; Gkikas, A.; Proestakis, E.; Kontoes, C.; El-Khayat, M.M. Earth-Observation-Based Estimation and Forecasting of Particulate Matter Impact on Solar Energy in Egypt. Remote Sens. 2018, 10, 1870. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The LibRadtran Software Package for Radiative Transfer Calculations (Version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Ménard, L.; Nüst, D.; Ngo, K.M.; Blanc, P.; Jirka, S.; Masó, J.; Ranchin, T.; Wald, L. Interoperable Exchange of Surface Solar Irradiance Observations: A Challenge. Energy Procedia 2015, 76, 113–120. [Google Scholar] [CrossRef]
- Kato, S.; Ackerman, T.P.; Mather, J.H.; Clothiaux, E.E. The K-Distribution Method and Correlated-k Approximation for a Shortwave Radiative Transfer Model. J. Quant. Spectrosc. Radiat. Transf. 1999, 62, 109–121. [Google Scholar] [CrossRef]
- Shettle, E.P. Models of Aerosols, Clouds, and Precipitation for Atmospheric Propagation Studies. In Proceedings of the Atmospheric Propagation in the UV, Visible, IR and MM-Wave Region and Related Systems Aspects, Copenhagen, Denmark, 9–13 October 1989. [Google Scholar]
- Taylor, M.; Kosmopoulos, P.G.; Kazadzis, S.; Keramitsoglou, I.; Kiranoudis, C.T. Neural Network Radiative Transfer Solvers for the Generation of High Resolution Solar Irradiance Spectra Parameterized by Cloud and Aerosol Parameters. J. Quant. Spectrosc. Radiat. Transf. 2016, 168, 176–192. [Google Scholar] [CrossRef]
- Gasca, M.; Sauer, T. Polynomial Interpolation in Several Variables. Adv. Comput. Math. 2000, 12, 377–410. [Google Scholar] [CrossRef]
- Sauer, T.; Xu, Y. On Multivariate Lagrange Interpolation. Math. Comput. 1995, 64, 1147. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Goswami, D.R.; Padmanabhan, N.; Dube, N.; Darji, N.; Mahammad, S.; Pandya, K.S. Near Real Time Data Processing of INSAT Data and Dissemination of Data Products. Space Applications Centre: Ahmedabad, India. Available online: http://academia.edu/26888533/Near_Real_Time_Data_Processing_of_INSAT_Data_and_Dissemination_of_Data_Products (accessed on 2 December 2019).
- Beyer, H.G.; Martinez, J.P.; Suri, M.; Torres, J.L.; Lorenz, E.; Müller, S.C.; Hoyer-Klick, C.; Ineichen, P. Report on Benchmarking of Radiation Products. Management and Exploitation of Solar Resource Knowledge. 2009. Available online: http://www.mesor.org/docs/MESoR_Benchmarking_of_radiation_products.pdf (accessed on 6 November 2019).
- Roesch, A.; Wild, M.; Ohmura, A.; Dutton, E.G.; Long, C.N.; Zhang, T. Assessment of BSRN Radiation Records for the Computation of Monthly Means (Atmospheric Measurement Techniques (2011) 4 (339–354)). Atmos. Meas. Tech. 2011, 4, 973. [Google Scholar] [CrossRef]
- Ramachandran, S.; Kedia, S. Aerosol-Precipitation Interactions over India: Review and Future Perspectives. Adv. Meteorol. 2013, 2013, 20. [Google Scholar] [CrossRef]
- Liu, T.; Marlier, M.E.; DeFries, R.S.; Westervelt, D.M.; Xia, K.R.; Fiore, A.M.; Mickley, L.J.; Cusworth, D.H.; Milly, G. Seasonal Impact of Regional Outdoor Biomass Burning on Air Pollution in Three Indian Cities: Delhi, Bengaluru, and Pune. Atmos. Environ. 2018, 172, 83–92. [Google Scholar] [CrossRef]
- Kandlikar, M. Air Pollution at a Hotspot Location in Delhi: Detecting Trends, Seasonal Cycles and Oscillations. Atmos. Environ. 2007, 41, 5934–5947. [Google Scholar] [CrossRef]
- Indian Monsoon. Available online: https://www.cpc.ncep.noaa.gov/products/assessments/assess_96/india.html (accessed on 28 November 2019).
- Misra, V.; Bhardwaj, A. Defining the Northeast Monsoon of India. Mon. Weather Rev. 2019, 147, 791–807. [Google Scholar] [CrossRef]
- Kashyap, Y.; Bansal, A.; Sao, A.K.; Hammer, A. Model for Estimation of Global Horizontal Irradiance in the Presence of Dust, Fog, and Clouds. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7030–7037. [Google Scholar] [CrossRef]
- Gueymard, C.A. Clear-Sky Irradiance Predictions for Solar Resource Mapping and Large-Scale Applications: Improved Validation Methodology and Detailed Performance Analysis of 18 Broadband Radiative Models. Sol. Energy 2012, 86, 2145–2169. [Google Scholar] [CrossRef]
- Ineichen, P. Comparison of Eight Clear Sky Broadband Models against 16 Independent Data Banks. Sol. Energy 2011, 80, 468–478. [Google Scholar] [CrossRef]
- Rigollier, C.; Bauer, O.; Wald, L. On the Clear Sky Model of the ESRA—European Solar Radiation Atlas-With Respect to the Heliosat Method. Sol. Energy 2000, 68, 33–48. [Google Scholar] [CrossRef]
- Polo, J.; Zarzalejo, L.F.; Cony, M.; Navarro, A.A.; Marchante, R.; Martín, L.; Romero, M. Solar Radiation Estimations over India Using Meteosat Satellite Images. Sol. Energy 2011, 85, 2395–2406. [Google Scholar] [CrossRef]
- Vallance, L.; Charbonnier, B.; Paul, N.; Dubost, S.; Blanc, P. Towards a Standardized Procedure to Assess Solar Forecast Accuracy: A New Ramp and Time Alignment Metric. Sol. Energy 2017, 150, 408–422. [Google Scholar] [CrossRef]
- Dunning, C.M.; Turner, A.G.; Brayshaw, D.J. The Impact of Monsoon Intraseasonal Variability on Renewable Power Generation in India. Environ. Res. Lett. 2015, 10, 064002. [Google Scholar] [CrossRef]
- Sendanayake, S.; Miguntanna, N.P.; Jayasinghe, M.T.R. Predicting Solar Radiation for Tropical Islands from Rainfall Data. J. Urban Environ. Eng. 2015, 9, 109–118. [Google Scholar] [CrossRef]
- Das, S.K.; Chatterjee, A.; Ghosh, S.K.; Raha, S. Fog-Induced Changes in Optical and Physical Properties of Transported Aerosols over Sundarban, India. Aerosol Air Qual. Res. 2015, 15, 1201–1212. [Google Scholar] [CrossRef]
- Dey, S. On the Theoretical Aspects of Improved Fog Detection and Prediction in India. Atmos. Res. 2018, 202, 77–80. [Google Scholar] [CrossRef]
- The Effect of Haze on Solar Power Generation. Available online: https://www.azocleantech.com/news.aspx?newsID=25743 (accessed on 25 December 2019).
- Peters, I.M.; Karthik, S.; Liu, H.; Buonassisi, T.; Nobre, A. Urban Haze and Photovoltaics. Energy Environ. Sci. 2018, 11, 3043–3054. [Google Scholar] [CrossRef]
- Bergin, M.H.; Ghoroi, C.; Dixit, D.; Schauer, J.J.; Shindell, D.T. Large Reductions in Solar Energy Production Due to Dust and Particulate Air Pollution. Environ. Sci. Technol. Lett. 2017, 4, 339–344. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; Lagouvardos, K.; Kotroni, V.; Bais, A. Solar Energy Prediction and Verification Using Operational Model Forecasts and Ground-Based Solar Measurements. Energy 2015, 93, 1918–1930. [Google Scholar] [CrossRef]
- Deneke, H.M.; Feijt, A.J.; Roebeling, R.A. Estimating Surface Solar Irradiance from METEOSAT SEVIRI-Derived Cloud Properties. Remote Sens. Environ. 2008, 112, 3131–3141. [Google Scholar] [CrossRef]
- Eskes, H.; Huijnen, V.; Arola, A.; Benedictow, A.; Blechschmidt, A.M.; Botek, E.; Boucher, O.; Bouarar, I.; Chabrillat, S.; Cuevas, E.; et al. Validation of Reactive Gases and Aerosols in the MACC Global Analysis and Forecast System. Geosci. Model Dev. 2015, 8, 3523–3543. [Google Scholar] [CrossRef]
- Ellingson, R.G.; Fouquart, Y. The Intercomparison of Radiation Codes in Climate Models: An Overview. J. Geophys. Res. 1991, 96, 8925. [Google Scholar] [CrossRef]
- Oreopoulos, L.; Mlawer, E.; Delamere, J.; Shippert, T.; Cole, J.; Fomin, B.; Iacono, M.; Jin, Z.; Li, J.; Manners, J.; et al. The Continual Intercomparison of Radiation Codes: Results from Phase I. J. Geophys. Res. Atmos. 2012, 117, 1–19. [Google Scholar] [CrossRef]
- Eck, T.F.; Holben, B.N.; Slutsker, I.; Setzer, A.; Intercomparison, T. Measurements of Irradiance Attenuation and Estimation of Aerosol Single Scattering Albedo for Biomass Burning Aerosols in Amazonia. J. Geophys. Res. Atmos. 1998, 103, 31865–31878. [Google Scholar] [CrossRef]
- Psiloglou, B.E.; Kambezidis, H.D.; Kaskaoutis, D.G.; Karagiannis, D.; Polo, J.M. Comparison between MRM Simulations, CAMS and PVGIS Databases with Measured Solar Radiation Components at the Methoni Station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]
- Riihelä, A.; Kallio, V.; Devraj, S.; Sharma, A.; Lindfors, A.V. Validation of the SARAH-E Satellite-Based Surface Solar Radiation Estimates over India. Remote Sens. 2018, 10, 392. [Google Scholar] [CrossRef]
- Maghami, M.R.; Hizam, H.; Gomes, C.; Radzi, M.A.; Rezadad, M.I.; Hajighorbani, S. Power Loss Due to Soiling on Solar Panel: A Review. Renew. Sustain. Energy Rev. 2016, 59, 1307–1316. [Google Scholar] [CrossRef]
- Rieger, D.; Steiner, A.; Bachmann, V.; Gasch, P.; Förstner, J.; Deetz, K.; Vogel, B.; Vogel, H. Impact of the 4 April 2014 Saharan Dust Outbreak on the Photovoltaic Power Generation in Germany. Atmos. Chem. Phys. 2017, 17, 13391–13415. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; Taylor, M.; Athanasopoulou, E.; Speyer, O.; Raptis, P.I.; Marinou, E.; Proestakis, E.; Solomos, S.; Gerasopoulos, E.; et al. Dust Impact on Surface Solar Irradiance Assessed with Model Simulations, Satellite Observations and Ground-Based Measurements. Atmos. Meas. Tech. 2017, 10, 2435–2453. [Google Scholar] [CrossRef]
- Neher, I.; Buchmann, T.; Crewell, S.; Evers-Dietze, B.; Pfeilsticker, K.; Pospichal, B.; Schirrmeister, C.; Meilinger, S. Impact of Atmospheric Aerosols on Photovoltaic Energy Production Scenario for the Sahel Zone. Energy Procedia 2017, 125, 170–179. [Google Scholar] [CrossRef]
- Perez, R.; Cebecauer, T.; Šúri, M. Semi-Empirical Satellite Models. Sol. Energy Forecast. Resour. Assess. 2013, 21–48. [Google Scholar] [CrossRef]
- Akritidis, D.; Antonakaki, T.; Blechschmidt, M.; Clark, H.; Gielen, C.; Hendrick, F.; Kapsomenakis, J.; Kartsios, S.; Katragkou, E.; Melas, D.; et al. Validation of the CAMS Regional Services: Concentrations above the Surface Status Update for the Period March–May 2017. Available online: http://atmosphere.copernicus.eu/sites/default/files/2018-08/CAMS84_2015SC2_D84.5.1.8_D84.6.1.3_2017MAM_v1.pdf (accessed on 20 November 2019).
- SoDa. Available online: http://www.soda-pro.com/home (accessed on 7 December 2019).
- Blanc, P.; Wald, L. The SG2 Algorithm for a Fast and Accurate Computation of the Position of the Sun for Multi-Decadal Time Period. Sol. Energy 2012, 86, 3072–3083. [Google Scholar] [CrossRef]
- Espinar, B.; Blanc, P.; Wald, L.; Gschwind, B.; Ménard, L.; Wey, E.; Thomas, C.; Saboret, L. HelioClim-3: A near-real time and long-term surface solar irradiance database. MINES ParisTech: PSL Research University, France. 2012. Available online: http://hal-mines-paristech.archives-ouvertes.fr/hal-00741564/document (accessed on 8 November 2019).
- CAMS McClear. Available online: http://www.soda-pro.com/web-services/radiation/cams-mcclear (accessed on 7 December 2019).
- Solea|Solar Energy Applications. Available online: http://solea.gr/ (accessed on 17 November 2019).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).