A Priority Data Association Policy for Multitarget Tracking on Intelligent Vehicle Risk Assessment

Abstract

In order to conduct risk assessment for collision-free decision making of intelligent vehicles in a complex road traffic environment, it is essential to conduct stable tracking and state estimation of multiple vehicle targets. Therefore, this paper proposes a multitarget tracking method in line with the priority data association rule. Firstly, a standard coordinate turn process model is deduced as the existence of translation and rotation of the vehicle on the two-dimensional ground plane. Secondly, an unscented Kalman filter algorithm is developed due to the nonlinear radar measurement model. Thirdly, a priority data association rule, which puts the targets in a priority queue according to the number of times they are associated, is designed to filter out noise, given that it is unlikely for a vehicle target as an inertial system to appear or disappear instantly in practice. In addition, the data association rule specifies that the closer the target is to the front of the queue, the more prioritized the association with the newly observed target would be. Finally, the track management algorithm is constructed. On this basis, a series of real vehicle tests were conducted on real roads with four typical scenarios. According to the test results, the proposed algorithm is effective in filtering out noise and is suboptimal as the nearest neighbor data association.

1. Introduction

Due to the rapid development of artificial intelligence [1], sensor technology [2], computing systems [3], and so on, intelligent driving technology has advanced significantly over the most recent decades [4]. Taking into account the massive potential of intelligent vehicles in alleviating traffic congestion, improving road safety and reducing the emissions of air pollutants [5,6], many universities and enterprises have been increasing their efforts on the development and application of this technology, such as Waymo [7], Apollo [8], and Momenta [9].

However, the frequent occurrence of accidents [10] and complaints made by passengers [11] suggest that there remain various problems needing to be solved for the absolute safety of autonomous driving [12]. One of them is how to keep track of multiple traffic targets effectively for the accuracy of risk assessment, based on which sensible decisions can be taken to avoid the prospect of collisions or false alarms [13,14]. Popular works in multitargets tracking follow a scheme composed of four parts: a motion model, a state estimation algorithm, a data association method, and track management [15]. Purposed to describe the behaviors of the target vehicle, the motion model consists of a process model and measurement model, both of which could be either linear or nonlinear [16,17]. The most commonly used motion models for target dynamics include constant velocity (CV) [18], constant acceleration (CA) [19], and constant coordinate turn (CT) [20]. As for the state estimation algorithm, the premise of its design lies in whether the motion model is linear or nonlinear. If the motion model (both the process model and measurement model) is linear, the Kalman filter can be applied in practice [21]. If the process model or the measurement model are nonlinear, however, it is necessary to consider extended Kalman filtering [22] or unscented Kalman filtering [23]. With regard to the data association method, the nearest neighbor data association (NNDA) [24], the probabilistic data association (PDA) [25], and the joint probabilistic data association (JPDA) [26] algorithms have been developed. In respect to track management, there are three key processes involved, namely track update, track dieout, and track initiation [27]. By applying a millimeter wave radar for a collision warning system, Lee et al. [28] conducted a study on the target recognition and tracking algorithm of different radar signals, based on which a multi-target detection and tracking algorithm was proposed in combination with a Kalman filter. Schuster at al. [29] used a set of millimeter wave radars to detect adjacent lanes of vehicles, based on the different positions of radar signals, manage track (such as track creation, track update and track deletion), at the same time as tracking the vehicle’s motion state and geometrical size. The method for real target tracking and recognition is relatively accurate for size, but millimeter wave radars will capture multiple false targets and fail to achieve accurate estimations due to many noise signals being tracked [29].

In order to filter out noise signals at the time of multi-target tracking, this paper proposes a novel multi-target tracking method within the framework of the priority data association rule for intelligent vehicles fitted with a millimeter-wave radar system. This approach is innovative in making use of prior information that a vehicle target as an inertial system cannot appear or disappear instantaneously. On the one hand, the introduction of prior information can help filter out noise. On the other hand, the suboptimal data association is preserved. To put the proposed method into practice, some efforts were made as follows. Firstly, to describe the track problem, the stochastic system was exemplified as a standard coordinate turn (CT) process model and a radar nonlinear measurement model, and the CT model was deduced as the existence of translation and rotation of the vehicle on the two-dimensional ground plane. Secondly, since the radar measurement model is nonlinear, an unscented Kalman filter algorithm was applied. Thirdly, to make full use of prior information on the object that a vehicle target as an inertial system cannot appear or disappear instantaneously, the historical tracking data was ranked by the number of times the target got associated before being classified into four scenarios, namely Unclassified, Candidate, Activation, and Dieout. The transition between different scenarios was managed using a finite state machine. Additionally, all targets were sorted out as a priority queue according to the number of times they were associated, based on which the data association rule was developed that the closer the target is to the front of the queue, the more prioritized the association with the newly observed target would be. Finally, a track management algorithm was developed in combination with all the formulas and rules. The performance of the proposed method was verified via real-world tests under the four typical scenarios as mentioned above.

This article is organized as follows. Section 2 presents the problem formulation, which describes the derivation process of the coordinate turn process model, radar nonlinear measurement model, and unscented Kalman filter. Section 3 introduces the priority data association rule and track management algorithm. In Section 4, the performance evaluation results are shown and the impact of the proposed method on four typical scenarios is discussed, based on which a comparison is drawn with the nearest neighbor data association. Section 5 concludes the paper by summarizing the findings made in this study.

2. Problem Formulation

For the tracking of multiple vehicle objects, a stochastic system was developed. Given the translation and rotation of the vehicle on the two-dimensional ground plane, a standard coordinate turn process model was constructed. Apart from that, a standard nonlinear measurement model is regarded as taking the characteristics of radar into account. Finally, an unscented Kalman filter algorithm was developed to address the approximation issues encountered by the extended Kalman filter [30,31,32,33].

2.1. Stochastic System

According to the study of Beomjun and Li [13,14], a general format for a stochastic system of vehicle object during the sampling period (k, k + 1) is expressed as follows:

$$\{\begin{array}{c}X\left(k+1\right)=f\left(X\left(k\right),u\left(k\right)\right)+w\left(k\right)\\ Y\left(k\right)=h\left(X\left(k\right),u\left(k\right)\right)+v\left(k\right)\end{array},$$

(1)

where X(.) represents the state vector of the vehicle object, u(.) indicates the input vector, f(.) and h(.) refer to the linear or nonlinear functions, respectively, Y(.) denotes the measurement vector, w(.) means the process noise, and v(.) stands for measurement noise. Both w(.) and v(.) are mutually uncorrelated zero-mean white Gaussian noise with covariances Q and R, respectively.

2.2. Coordinate Turn Process Model

The vehicle target movement in the two-dimensional ground plane is comprised mainly of two degrees of freedom and one degree of free rotation. It is assumed that the accelerations in the steady state are quite slight; linear accelerations or decelerations can be rationally described by process noise w with a constant velocity [34] and the constant rotation. Based on the above assumptions, the constant coordinate turn (CT) motion could be written as follows:

$$X={\left[\begin{array}{ccccc}x& y& \dot{x}& \dot{y}& \omega \end{array}\right]}^T,$$

(2)

where (x, y) represents vehicle target position, $\left(\dot{x},\dot{y}\right)$ indicates the translational velocity of the two horizontal axes, and $\omega$ refers to the rotary motion in the vertical direction.

The recursive relation of vehicle position from time k to time k + 1 is expressed as:

$$\{\begin{array}{c}x\left(k+1\right)=x\left(k\right)+\dot{x}\left(k\right)T+\frac{1}{2}{\sigma }_{x}T\\ y\left(k+1\right)=y\left(k\right)+\dot{y}\left(k\right)T+\frac{1}{2}{\sigma }_{y}T\end{array},$$

(3)

where ${\sigma }_x$ represents velocity noise covariance in the x axis, ${\sigma }_y$ refers to velocity noise covariance in the y axis, and T denotes the sampling period.

Likewise, the velocity transfer relation is expressed as:

$$\{\begin{array}{c}\dot{x}\left(k+1\right)=\dot{x}\left(k\right)T+{\sigma }_{x}T\\ \dot{y}\left(k+1\right)=\dot{y}\left(k\right)T+{\sigma }_{y}T\end{array}.$$

(4)

From the geometric relations, it can be known that the rotary motion satisfies the following equations:

$$\{\begin{array}{l}v=\sqrt{\dot{x}{\left(k\right)}^2+\dot{y}{\left(k\right)}^2}\hfill \\ \dot{x}\left(k+1\right)=v\cos \theta \left(k\right)\hfill \\ \dot{y}\left(k+1\right)=v\sin \theta \left(k\right)\hfill \\ \omega \left(k\right)=\dot{\theta }\left(k\right)\hfill \end{array}.$$

(5)

According to Equations (5), the following differential formulas can be obtained:

$$\{\begin{array}{c}\ddot{x}\left(k+1\right)=-\dot{y}\left(k\right)\omega \left(k\right)\\ \ddot{y}\left(k+1\right)=\dot{x}\left(k\right)\omega \left(k\right)\end{array}.$$

(6)

Finally, with Formulas (3)–(6) combined, the constant coordinate turn (CT) process model is obtained as:

$$\left[\begin{array}{l}x\left(k+1\right)\hfill \\ y\left(k+1\right)\hfill \\ \dot{x}\left(k+1\right)\hfill \\ \dot{y}\left(k+1\right)\hfill \\ \omega \left(k+1\right)\hfill \end{array}\right]=\left[\begin{array}{ccccc}1& 0& \frac{\sin \left(\omega \left(k\right)T\right)}{\omega \left(k\right)}& \frac{\cos \left(\omega \left(k\right)T\right)-1}{\omega \left(k\right)}& 0\\ 0& 1& \frac{1-\cos \left(\omega \left(k\right)T\right)}{\omega \left(k\right)}& \frac{\sin \left(\omega \left(k\right)T\right)}{\omega \left(k\right)}& 0\\ 0& 0& \cos \left(\omega \left(k\right)T\right)& -\sin \left(\omega \left(k\right)T\right)& 0\\ 0& 0& \sin \left(\omega \left(k\right)T\right)& \cos \left(\omega \left(k\right)T\right)& 0\\ 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{l}x\left(k\right)\hfill \\ y\left(k\right)\hfill \\ \dot{x}\left(k\right)\hfill \\ \dot{y}\left(k\right)\hfill \\ \omega \left(k\right)\hfill \end{array}\right]+\left[\begin{array}{lll}\frac{T^2}{2}\hfill & 0\hfill & 0\hfill \\ 0\hfill & \frac{T^2}{2}\hfill & 0\hfill \\ T\hfill & 0\hfill & 0\hfill \\ 0\hfill & T\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right]\left[\begin{array}{l}{\sigma }_x\hfill \\ {\sigma }_y\hfill \\ {\sigma }_{\omega }\hfill \end{array}\right],$$

(7)

where ${\sigma }_{\omega }$ represents the covariance of rotation-induced noise, so that the state transition matrix of the system A(k) and process noise distribution matrix $\Gamma \left(k\right)$ are expressed as:

$$A\left(k\right)=\left[\begin{array}{ccccc}1& 0& \frac{\sin \left(\omega \left(k\right)T\right)}{\omega \left(k\right)}& \frac{\cos \left(\omega \left(k\right)T\right)-1}{\omega \left(k\right)}& 0\\ 0& 1& \frac{1-\cos \left(\omega \left(k\right)T\right)}{\omega \left(k\right)}& \frac{\sin \left(\omega \left(k\right)T\right)}{\omega \left(k\right)}& 0\\ 0& 0& \cos \left(\omega \left(k\right)T\right)& -\sin \left(\omega \left(k\right)T\right)& 0\\ 0& 0& \sin \left(\omega \left(k\right)T\right)& \cos \left(\omega \left(k\right)T\right)& 0\\ 0& 0& 0& 0& 1\end{array}\right], \Gamma \left(k\right)=\left[\begin{array}{lll}\frac{T^2}{2}\hfill & 0\hfill & 0\hfill \\ 0\hfill & \frac{T^2}{2}\hfill & 0\hfill \\ T\hfill & 0\hfill & 0\hfill \\ 0\hfill & T\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right].$$

2.3. Radar Nonlinear Measurement Model

The radar system is applied to track the target in the polar coordinate system, based on which the radial distance r(k) and azimuth angle φ(k) of the target are output. Combined with the position (x, y) in the rectangular coordinate system, the measurement model is constructed as follows:

$$Y\left(k\right)=\left[\begin{array}{c}r\left(k\right)\\ \phi \left(k\right)\end{array}\right]=h\left(X\left(k\right),u\left(k\right)\right)=\left[\begin{array}{c}\sqrt{x{\left(k\right)}^2+y{\left(k\right)}^2}\\ \arctan \frac{y\left(k\right)}{x\left(k\right)}\end{array}\right].$$

(8)

2.4. Unscented Kalman Filter

According to the measurement model (8), the filter is definitely capable of dealing with nonlinearity, as radar tracking is a nonlinear system. In this case, an unscented Kalman filter (UKF) is applicable. The core idea of a UKF is to rely on the unscented transform (UT) for sampling a set of deterministic sigma points that capture the mean and covariance of the original distribution of the target state.

For the specified mean target state X_m and covariance P, the sigma points are sampled in line with the following rules:

$$\{\begin{array}{cc}{X}^{\left(0\right)}=X_m,& i=0\\ X^{\left(i\right)}=X_m+{\left(\sqrt{\left(n+\lambda \right)P}\right)}^{\left(i\right)},& i=1~n\\ X^{\left(i\right)}=X_m-{\left(\sqrt{\left(n+\lambda \right)P}\right)}^{\left(i\right)},& i=n+1~2n\end{array},$$

(9)

where X⁽ⁱ⁾ represents the i-th sigma point state, n indicates the dimension of the state, λ denotes the scale with formula λ = α²(n + κ) − n, α (0 ≤ α ≤ 1) refers to a scaling parameter that determines the spread of the sigma points that are supposed to be ideally a small number, and κ stands for the other tuning parameter. The condition κ ≥ 0 must be satisfied to ensure that the covariance matrix is positive semidefinite [30].

The weight of these sigma points is determined using the following equations:

$$\{\begin{array}{cc}{w}_m^{\left(0\right)}=\frac{\lambda }{n+\lambda },& i=0\\ w_c^{\left(0\right)}=\frac{1}{n+\lambda }+\left(1-{\alpha }^2+\beta \right),& i=0\\ w_m^{\left(i\right)}=w_c^{\left(i\right)}=\frac{1}{2\left(n+\lambda \right)},& i=1~2n\end{array},$$

(10)

where $w_m^{\left(i\right)}$ represents the i-th sigma weight for the mean target state, $w_c^{\left(i\right)}$ indicates the i-th sigma weight for covariance, and β (β ≥ 0) denotes weight parameter.

The process of running the proposed unscented Kalman filter algorithm is detailed below.

(1)

Initialization: Parameters λ, $w_m^{\left(i\right)}$, $w_c^{\left(i\right)}$, Q, and R are chosen for a given initiation state X(0|0), covariance P(0|0), A(0), and Γ(0). If k ≥ 1, the following steps are taken:

(2)

Step 1: state prediction:

$$X\left(k+1|k\right)=A\left(k\right)X\left(k|k\right),$$

(11)

(3)

Step 2: covariance prediction:

$$P\left(k+1|k\right)=A\left(k\right)P\left(k|k\right)A{\left(k\right)}^T+\Gamma \left(k\right)Q\Gamma {\left(k\right)}^T,$$

(12)

(4)

Step 3: generate sigma points:

$$X^{\left(i\right)}\left(k+1|k\right)=\left[\begin{array}{c}{\left(X\left(k+1|k\right)\right)}^T\\ {\left(X\left(k+1|k\right)+\sqrt{\left(n+\lambda \right)P\left(k+1|k\right)}\right)}^T\\ {\left(X\left(k+1|k\right)-\sqrt{\left(n+\lambda \right)P\left(k+1|k\right)}\right)}^T\end{array}\right],$$

(13)

(5)

Step 4: measurement prediction based on sigma points:

$$Y^{\left(i\right)}\left(k+1|k\right)=h\left(X^{\left(i\right)}\left(k+1|k\right)\right),$$

(14)

(6)

Step 5: mean measurement prediction:

$$Y_m\left(k+1|k\right)={\displaystyle \sum _{i=0}^{2n}{w}_m{}^{\left(i\right)}\left(k+1|k\right)}{Y}^{\left(i\right)}\left(k+1|k\right),$$

(15)

(7)

Step 6: mean measurement covariance prediction:

$$P^{zz}\left(k+1|k\right)={\displaystyle \sum _{i=0}^{2n}{w}_c{}^{\left(i\right)}\left(k+1|k\right)}\left[Y^{\left(i\right)}\left(k+1|k\right)-Y_m\left(k+1|k\right)\right]{\left[Y^{\left(i\right)}\left(k+1|k\right)-Y_m\left(k+1|k\right)\right]}^T+R,$$

(16)

$$P^{xz}\left(k+1|k\right)={\displaystyle \sum _{i=0}^{2n}{w}_c{}^{\left(i\right)}\left(k+1|k\right)}\left[X^{\left(i\right)}\left(k+1|k\right)-X\left(k+1|k\right)\right]{\left[Y^{\left(i\right)}\left(k+1|k\right)-Y_m\left(k+1|k\right)\right]}^T,$$

(17)

(8)

Step 7: calculate Kalman gain:

$$K\left(k+1\right)=P^{xz}\left(k+1|k\right){\left[P^{zz}\left(k+1|k\right)\right]}^{-1},$$

(18)

(9)

Step 8: update state estimation:

$$X\left(k+1|k+1\right)=X\left(k+1|k\right)+K\left(k+1\right)\left[Y\left(k+1\right)-Y_m\left(k+1|k\right)\right],$$

(19)

(10)

Step 9: update covariance estimation:

$$P\left(k+1|k+1\right)=P\left(k+1|k\right)-K\left(k+1\right)P^{zz}\left(k+1|k\right){\left[K\left(k+1\right)\right]}^T,$$

(20)

3. Multitarget Tracking

In general, multitarget tracking involves two critical steps, namely data association and track management. The former is purposed to match the newly observed data with historical data, thus keeping target tracking updated, whereas the latter is aimed at updating the trajectory of the target according to the certainty rules, which could mainly consists of either the start, maintenance, or end of the tracking trajectory, corresponding to the entry, maintenance, and departure of the target.

3.1. Priority Data Association Policy

Conventional data association methods, such as nearest neighbor data association (NNDA), probabilistic data association (PDA), and joint PDA (JPDA) algorithms, commonly rely on the spatial distance relationship of the target, but without using prior information on the target, which leads to noise data being treated as the real target. Considering that a target vehicle as an inertial system is unlikely to appear or disappear instantly, the number of times the target is associated can be taken as prior information, and historical data can be ranked, with priority given to the data that were continuously observed for the highest number of times and the latest data, which allows the tracking process to be described by a finite state machine for each target tracked, as shown in Figure 1. All targets in different stages of tracking are categorized into four types, namely Unclassified, Candidate, Activation, and Dieout. The transfer process of target type is as following: the process from the Unclassified target to the Candidate target corresponds to the candidate initial stage, the process from the Candidate target to the activation target corresponds to the track initiation stage, and the process from other types of targets to the Dieout target corresponds to the dieout stage.

Furthermore, targets of different types are combined into a priority queue according to prior information on the number of times of association, as shown in Figure 2. At the beginning of each tracking cycle, the order of precedence associated with the new observed data is set as: Activation targets, Candidate targets, and Unclassified targets. Similarly, for the targets of the same type, the priority associated with the new data is also ranked by the number of successful associations. In each tracking cycle, each type of target accumulates the number of successful association counts, which means the count is increased by 1 if the association is successful, and otherwise the count is reduced by 1. Additionally, targets of different types rely on different sliding time windows; for example, the maximum sliding time window of an Unclassified target is NM, which means that the Unclassified target will disappear when the cumulative number of unassociated times reaches NM + 1 and the Unclassified target type is converted into a Candidate target once the target association is successful, with the count being 1. If the Candidate target is successfully correlated for M consecutive times, the target state is shifted to the Activation state and the count is 1. If the Candidate target is not associated for M times in a row, however, the candidate target will disappear.

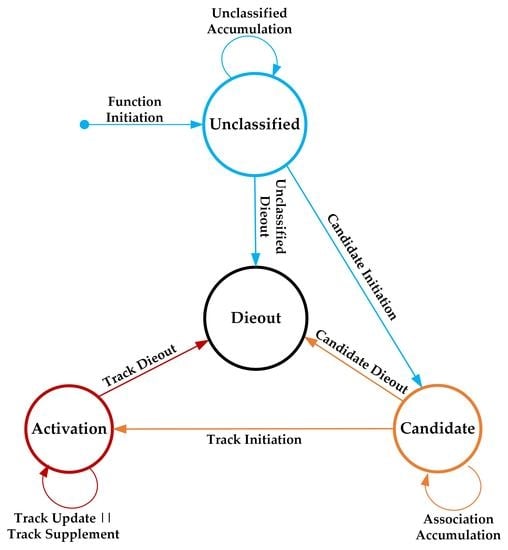
3.2. Track Management

Combining the finite-state machine illustrated in Figure 1 and priority data association rule shown in Figure 2, the complete technical route to track management is presented in Algorithm 1.

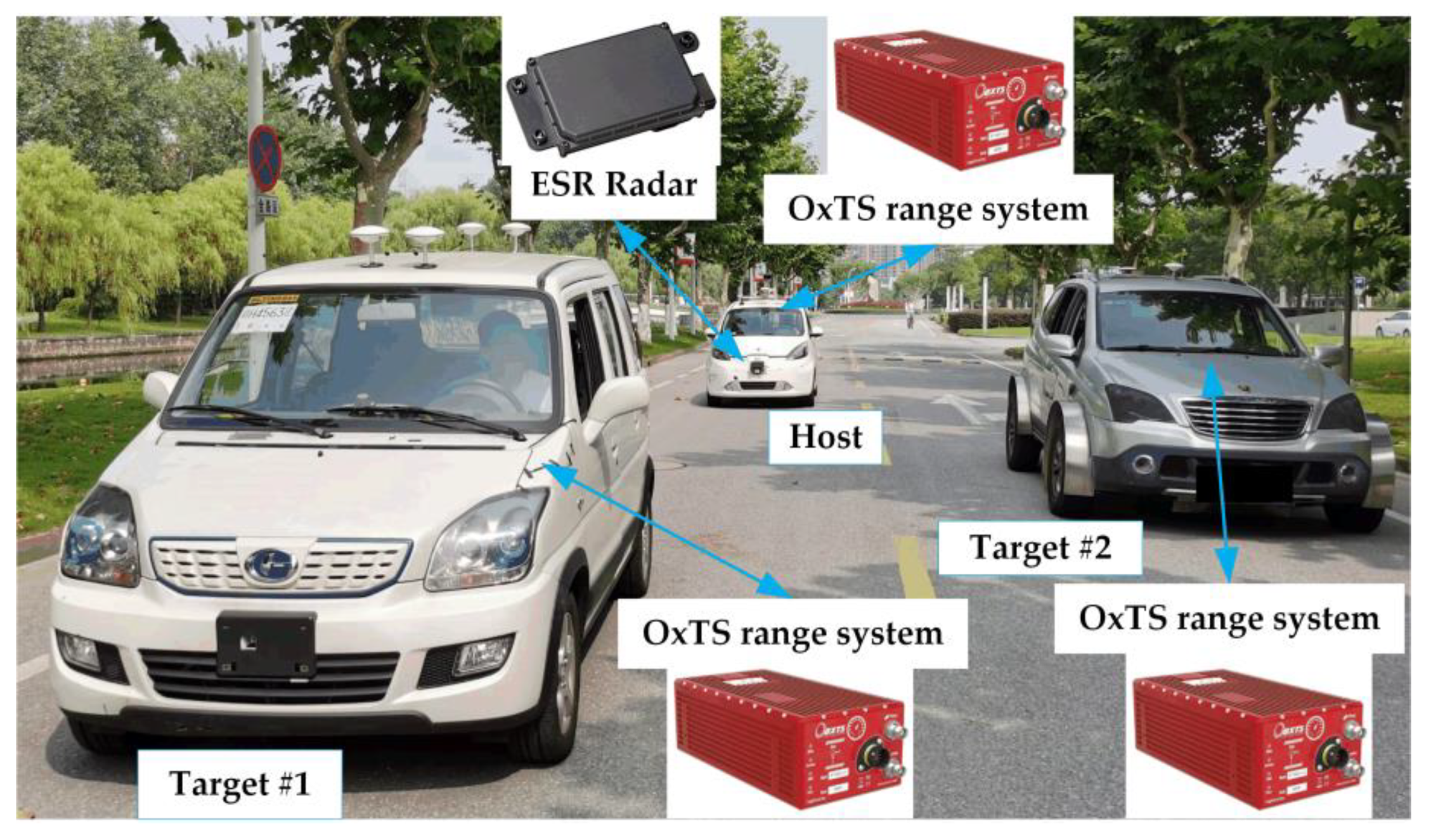
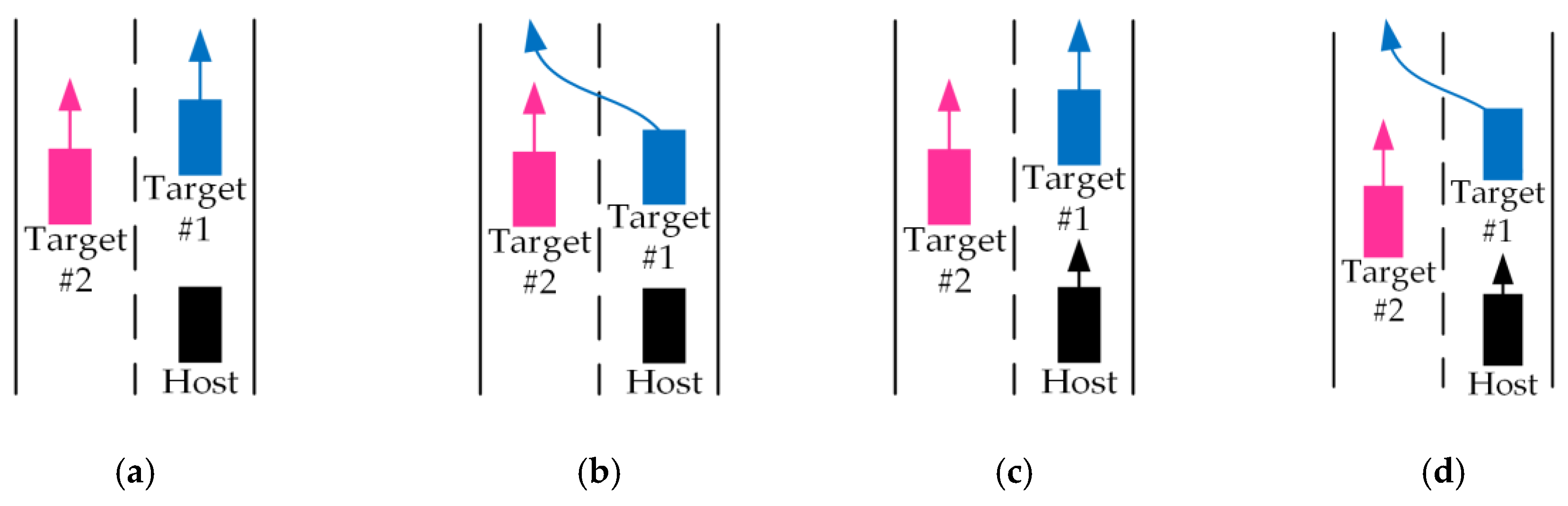
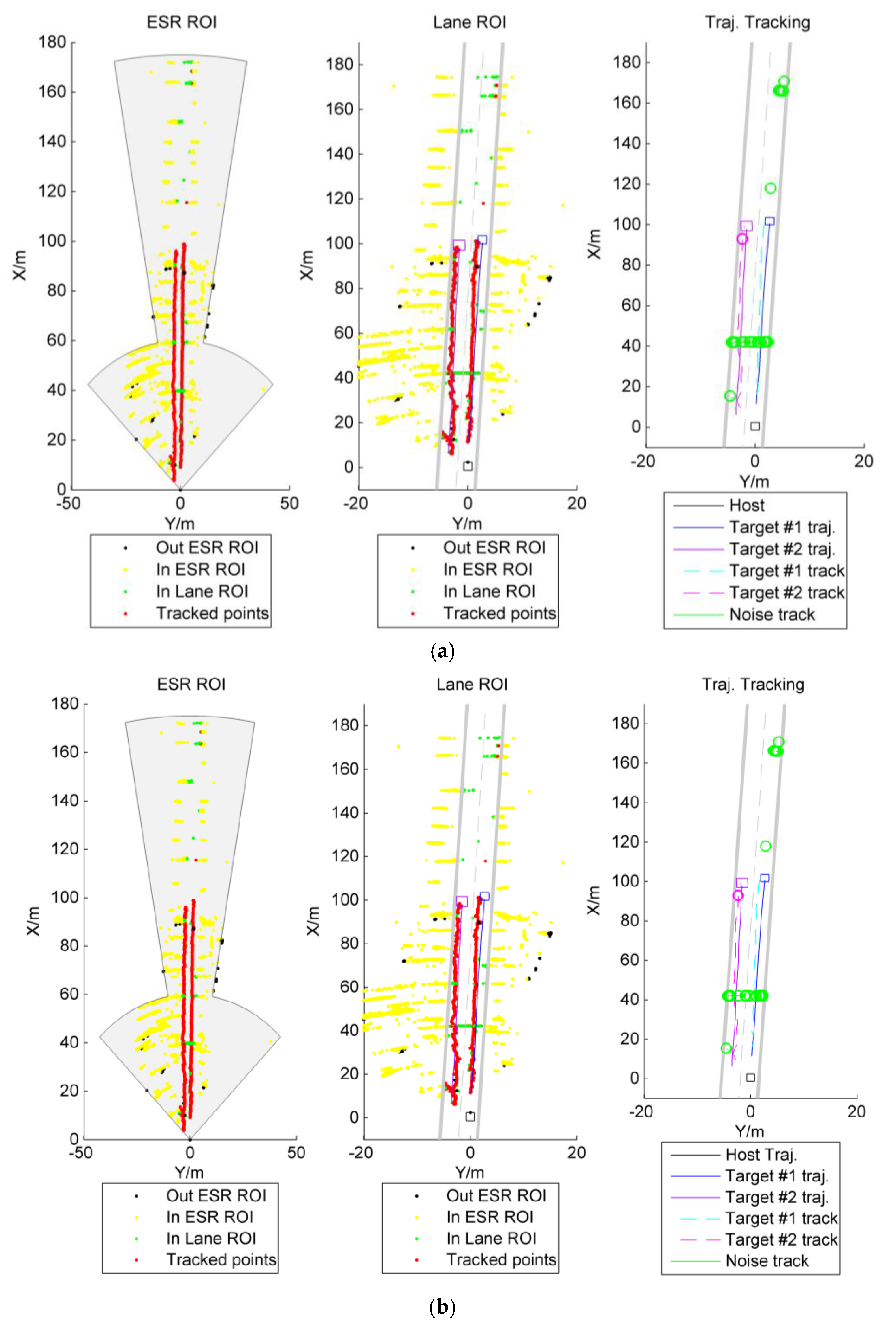
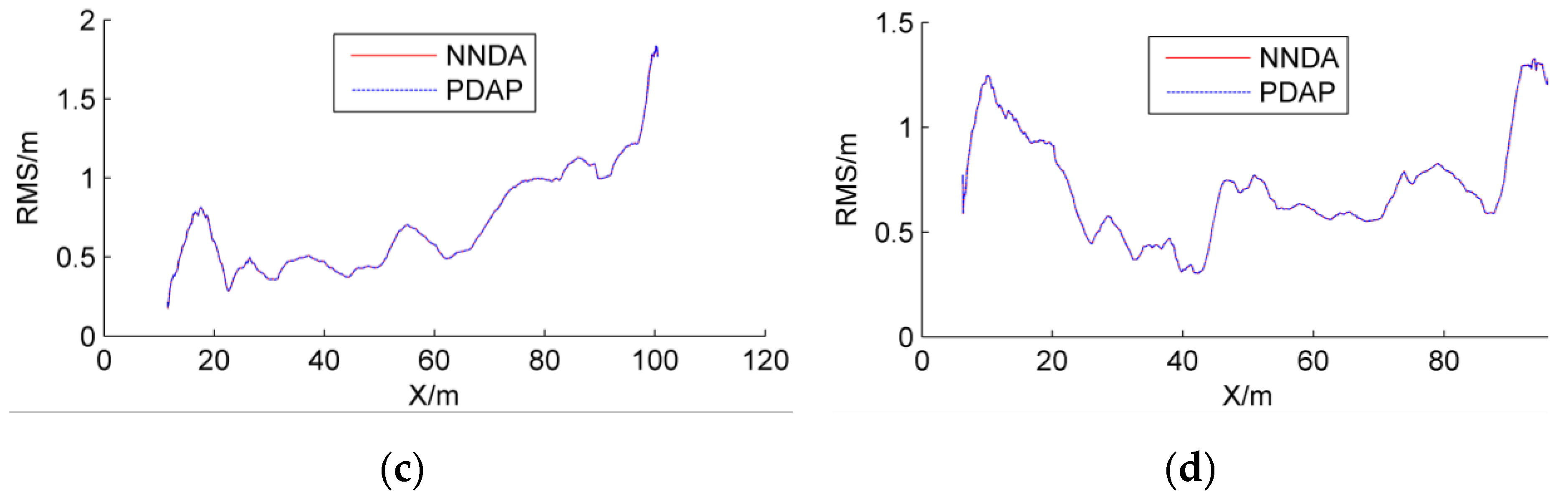
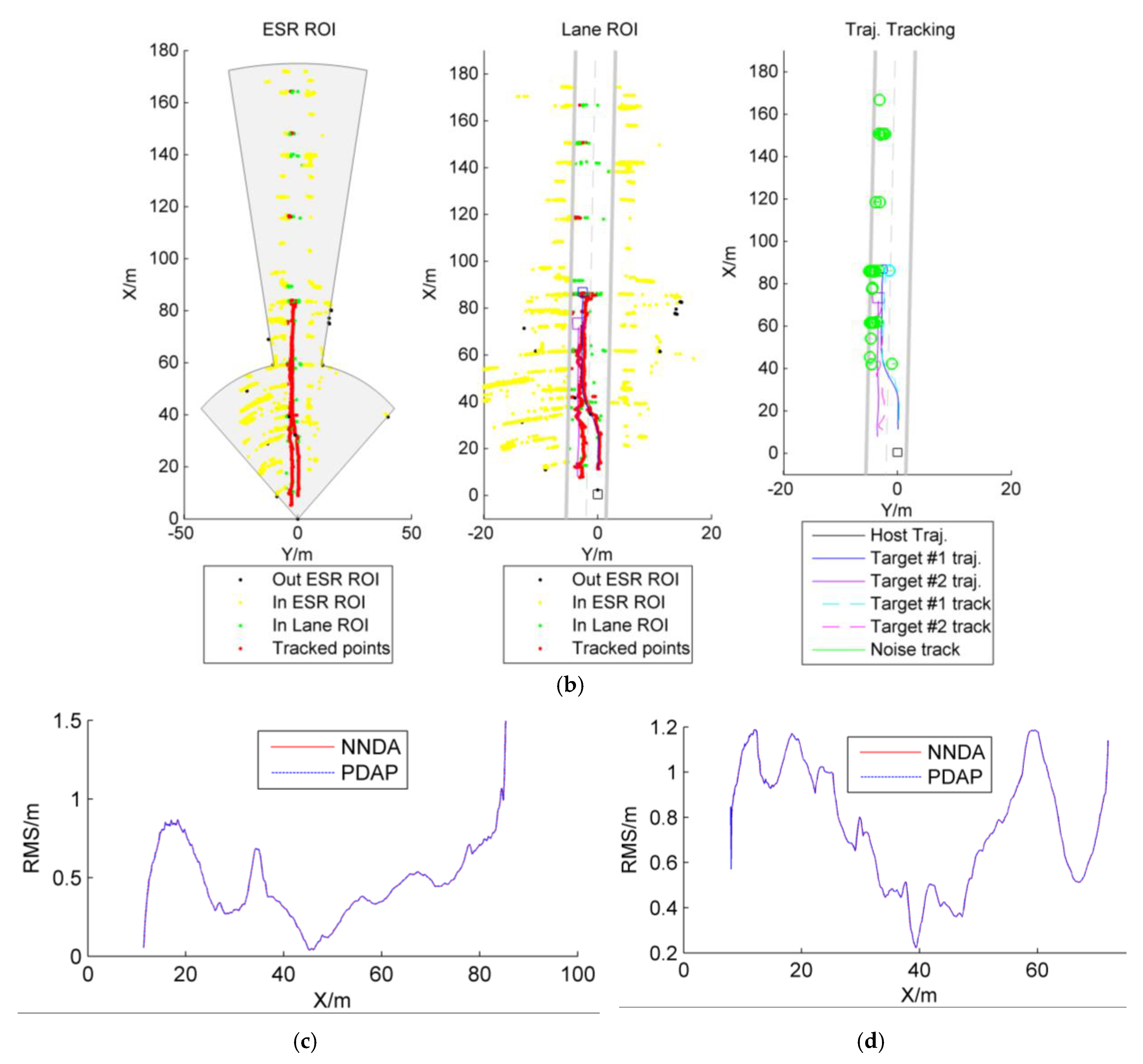
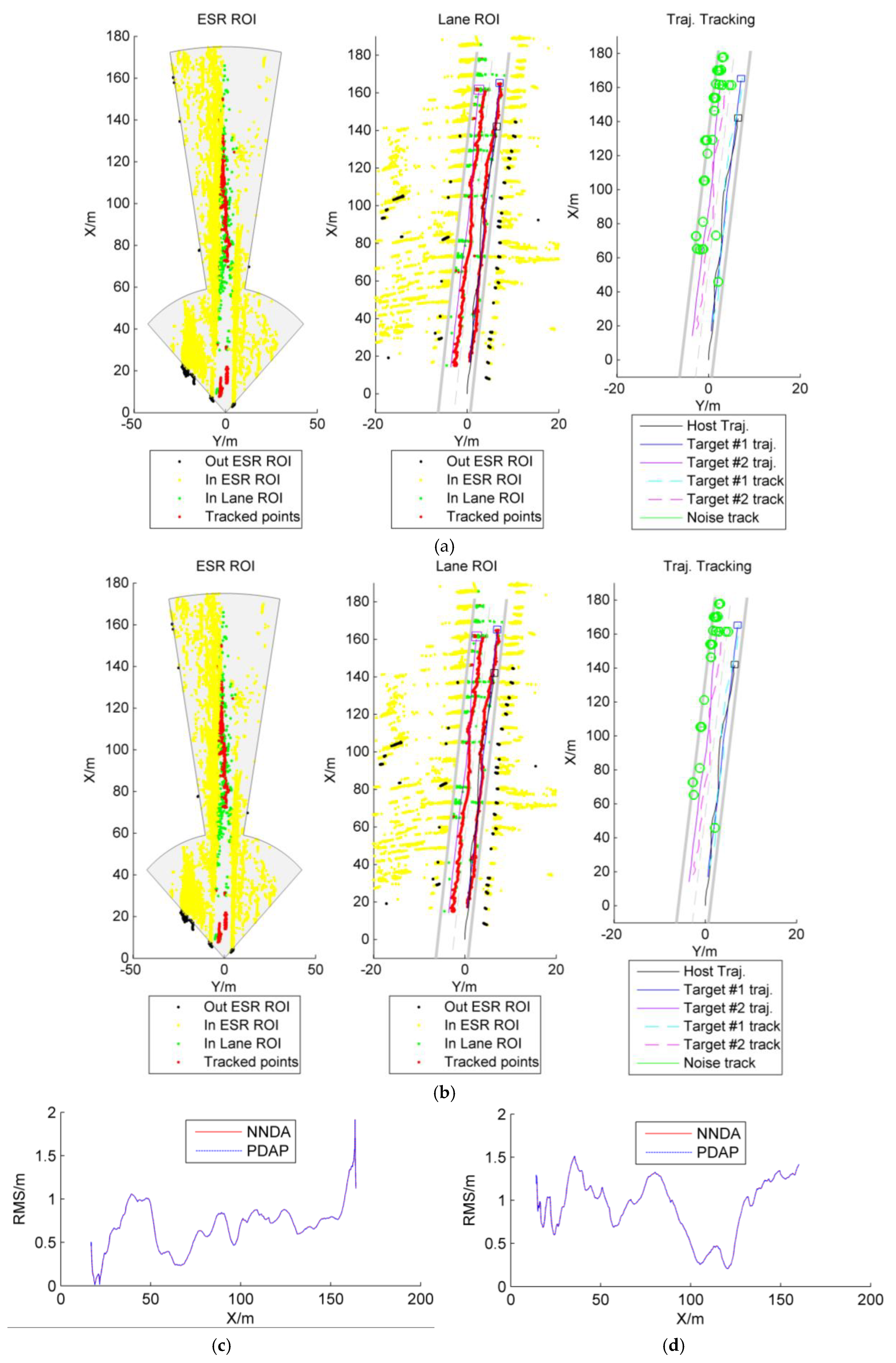
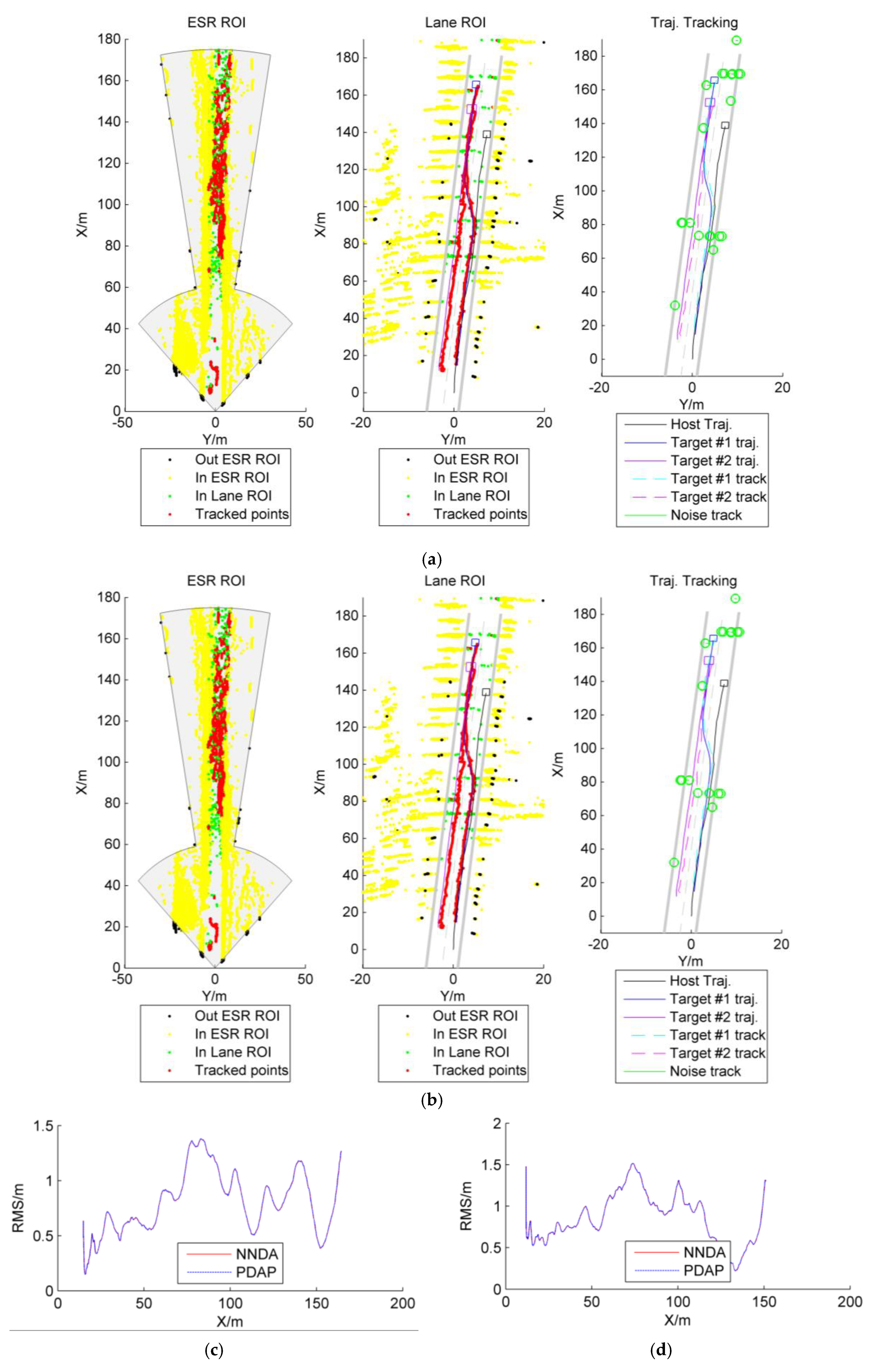
4. Discussion

The proposed multitarget algorithm was implemented with ESR radar as the basis, and a series of real-world vehicle tests were conducted to verify the algorithm. As shown in Figure 3, one host vehicle (the white car at the back) and two target vehicles (the two cars in the front) were involved in the tests. All of the vehicles were equipped with an OxTS high-precision positioning system applied to record the position of the vehicle in real time. As shown in Figure 4, there were four typical scenarios put to test, including:

(1)

Scenario 1: the host vehicle is stationary and the two target vehicles drive on a straight route;

(2)

Scenario 2: the car is stationary, target car #1 changes lanes, and target car #2 drives on a straight route;

(3)

Scenario 3: the host vehicle drives on a straight route and the two target cars drive on a straight route;

(4)

Scenario 4: the host vehicle drives on a straight route, target car #1 changes lanes, and target car #2 drives on a straight route.

Algorithm 1. Pseudocode of track management.

Input:  dnew: the new detected data by radar

Data:  Tuo: the Unclassified targets from the last cycle

Tco: the Candidate targets from the last cycle

Tao: the Activation targets from the last cycle

Output: Tun: the updated Unclassified targets

Tcn: the updated Candidate targets

Tan: the updated Activation targets

begin

if dnew is empty

if system is not initiation

if Tuo is nonempty

Ttp ← Unclassified_accumulation (Tuo)

Tun ← Unclassified_dieout (Ttp)

end

if Tco is nonempty

Ttp ← Candidate_accumulation (Tco)

Tcn ← Candidate_dieout (Ttp)

end

if Tao is nonempty

Ttp ← Track_dieout (Tao)

Tcn ← Track_supplement (Ttp)

end

else

Tun ← empty;   Tcn ← empty;   Tan ← empty

end

else

if system is not initiation

if Tao is nonempty

Ttp ← Track_update (Tao, dnew)

Tttp ← Track_dieout (Ttp)

Tant ← Track_supplement (Tttp)

end

if Tco is nonempty

Tantt, Ttp ← Track_initiation (Tco, dnew)

Tttp ← Candidate_accumulation (Ttp)

Tcnt ← Candidate_dieout (Tttp)

end

if Tuo is nonempty

Tcntt, Ttp ← Unclassified_accumulation (Tuo, dnew)

Tun ← Unclassified_dieout (Ttp)

end

else

Tun ← Unclassified_accumulation (dnew)

Tcn ← empty

Tan ← empty

end

Tcn = Tcnt + Tcntt;   Tan = Tant + Tantt

end

Tuo = Tun;   Tco = Tcn;  Tao = Tan

end

In order to verify the performance of the proposed algorithm, the nearest neighbor data association (NNDA) was adopted as a comparison algorithm; it is the most widely used and suboptimal Bayesian algorithm [24]. As both algorithms rely on a coordinate turn process model and an unscented Kalman filter, the proposed method is denoted as priority data association policy for coordinate turn process model with unscented Kalman filter (PDAP-CT-UKF) and the compared algorithm is denoted by nearest neighbor data association for coordinate turn process model with unscented Kalman filter (NNDA-CT-UKF). The root-mean-square error (RMS) and the mean value of RMS (MRMS) are taken as the index used to assess the performance in tracking real targets, while the total tracked targets are taken as the index used to evaluate the performance in filtering fake targets. As shown in Figure 5, Figure 6, Figure 7 and Figure 8, the region-of-interest (ROI), both ESR ROI and Lane ROI, is used to filter out targets, which beyond the ROI. Both PDAP-CT-UKF and NNDA-CT-UKF performed well in tracking multiple targets and had the same RMS, which means the proposed method (PDAP) and the NNDA are suboptimal in the four typical scenarios in real-time. The tracking data are listed in

Table 1. Tracking statistics.

		NNDA-CT-UKF		PDAP-CT-UKF
		MRMS	Total Tracked Targets	MRMS	Total Tracked Targets
Scenario 1	Target #1	0.7416 m	25	0.7416 m	23
	Target #2	0.7498 m		0.7498 m
Scenario 2	Target #1	0.4348 m	39	0.4348 m	36
	Target #2	0.7854 m		0.7854 m
Scenario 3	Target #1	0.7032 m	46	0.7032 m	40
	Target #2	0.9493 m		0.9493 m
Scenario 4	Target #1	0.7645 m	68	0.7645 m	64
	Target #2	0.8497 m		0.8497 m

. According to the MRMS results, both the PDAP and NNDA showed suboptimal results. Compared with NNDA, however, the total number of targets tracked by PDAP was smaller, which means the proposed algorithm has the capability to filter noise. However, both for NNDA and PDAP, the total number of tracked targets was significantly greater than the number of real targets, which means there should be only two real targets, target #1 and target #2. This suggests that there remains room for the algorithm to be improved significantly.

5. Conclusions

Aiming to improve the performance of multi-target tracking for risk assessment by intelligent vehicles, a priority data association rule was developed. In the rule, to filter out unwanted noise, the number of times that the target is associated is taken as prior information, and the tracking process is described by a finite state machine for each target tracked. Different types of targets are combined into a priority queue according to prior information on the number of times of association, based on which a rule was developed that the further in the queue the target is, the more prioritized the data association would be. Given that the movement of vehicles targeted in the two-dimensional ground plane is comprised mainly of two degrees of freedom and one degree of free rotation, a constant coordinate turn process model was constructed. Due to the nonlinear measurement model, an unscented Kalman filter was developed and applied.

Based on ESR radar, the proposed multi-target algorithm was implemented. Furthermore, real-world vehicle tests were conducted. Four typical scenarios were examined, with the nearest neighbor data association (NNDA) method applied as a comparison algorithm. As indicated by the test results, the proposed algorithm is effective in filtering out noise but is suboptimal in multitargets tracking, similarly to the NNDA.

In the future, our research will be focused on integrating multisensory information, such as lidar and machine vision, to further filter out noise. Due to multi-sensor fusion, the tracking algorithm will be verified and an improvement strategy will be designed. Further research into applications for risk assessment, such as decision making and emergency control, will be conducive to the development of intelligent vehicles.