Mapping the Urban Population in Residential Neighborhoods by Integrating Remote Sensing and Crowdsourcing Data
Abstract
1. Introduction
2. Study Area and Data
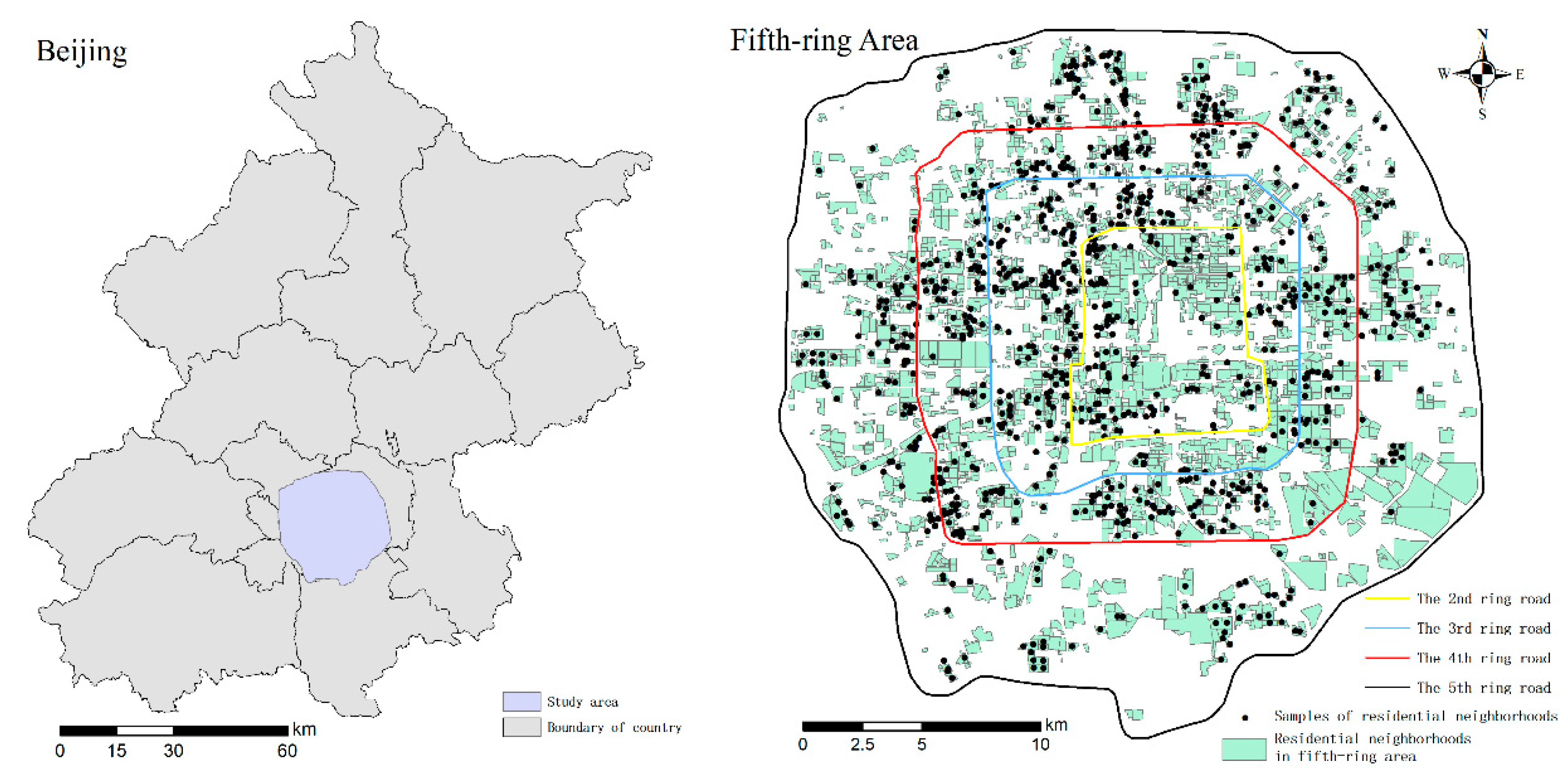
2.1. Study Area
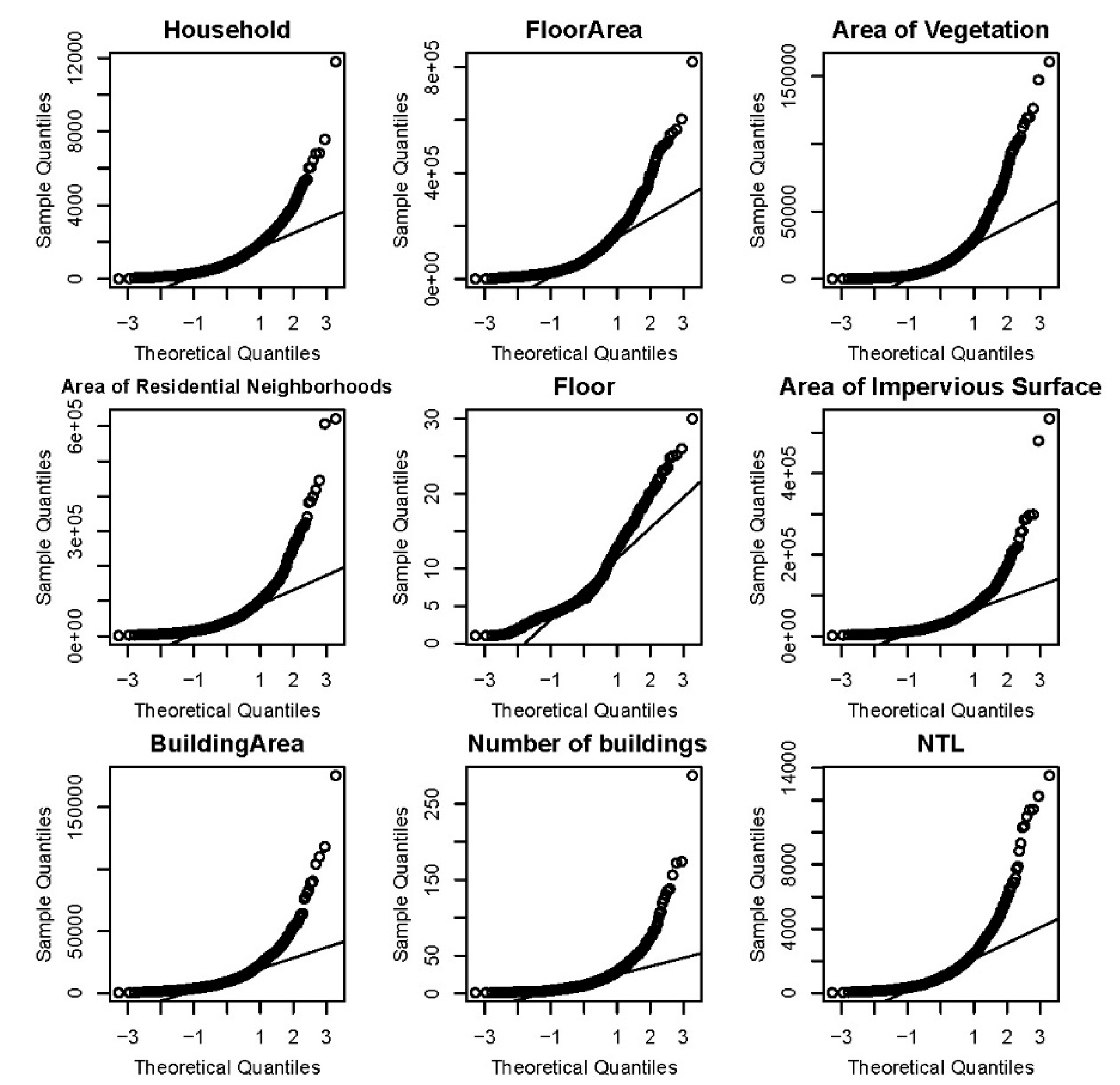
2.2. Data and Processing
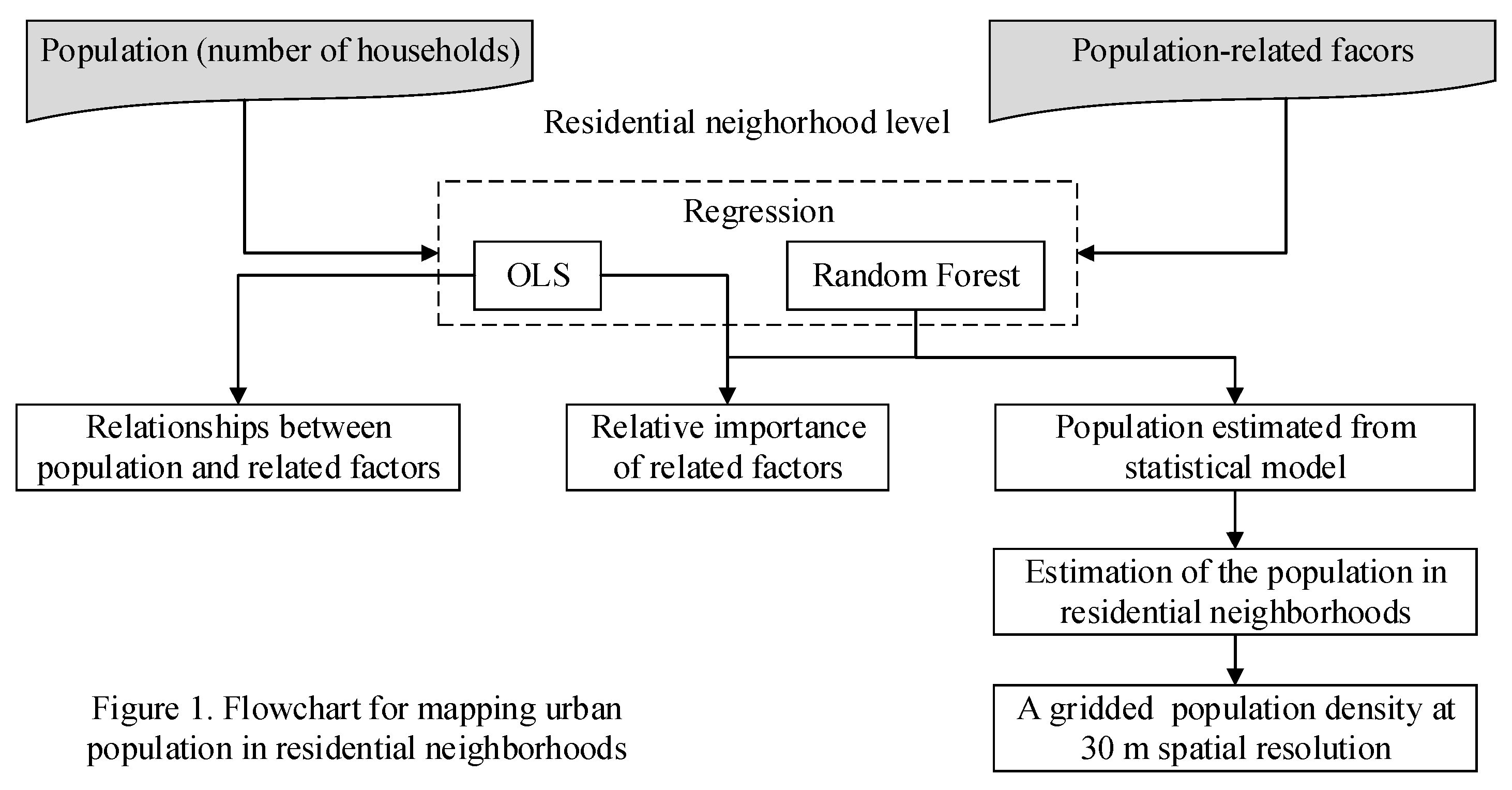
3. Methods
3.1. Relationships between Population and Related Factors and Their Relative Importance
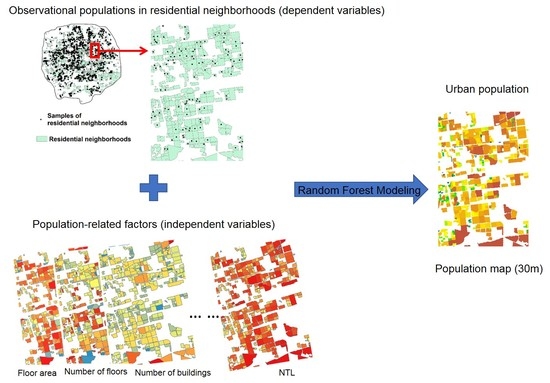
3.2. Mapping the Population
3.3. Accuracy Assessment
4. Results
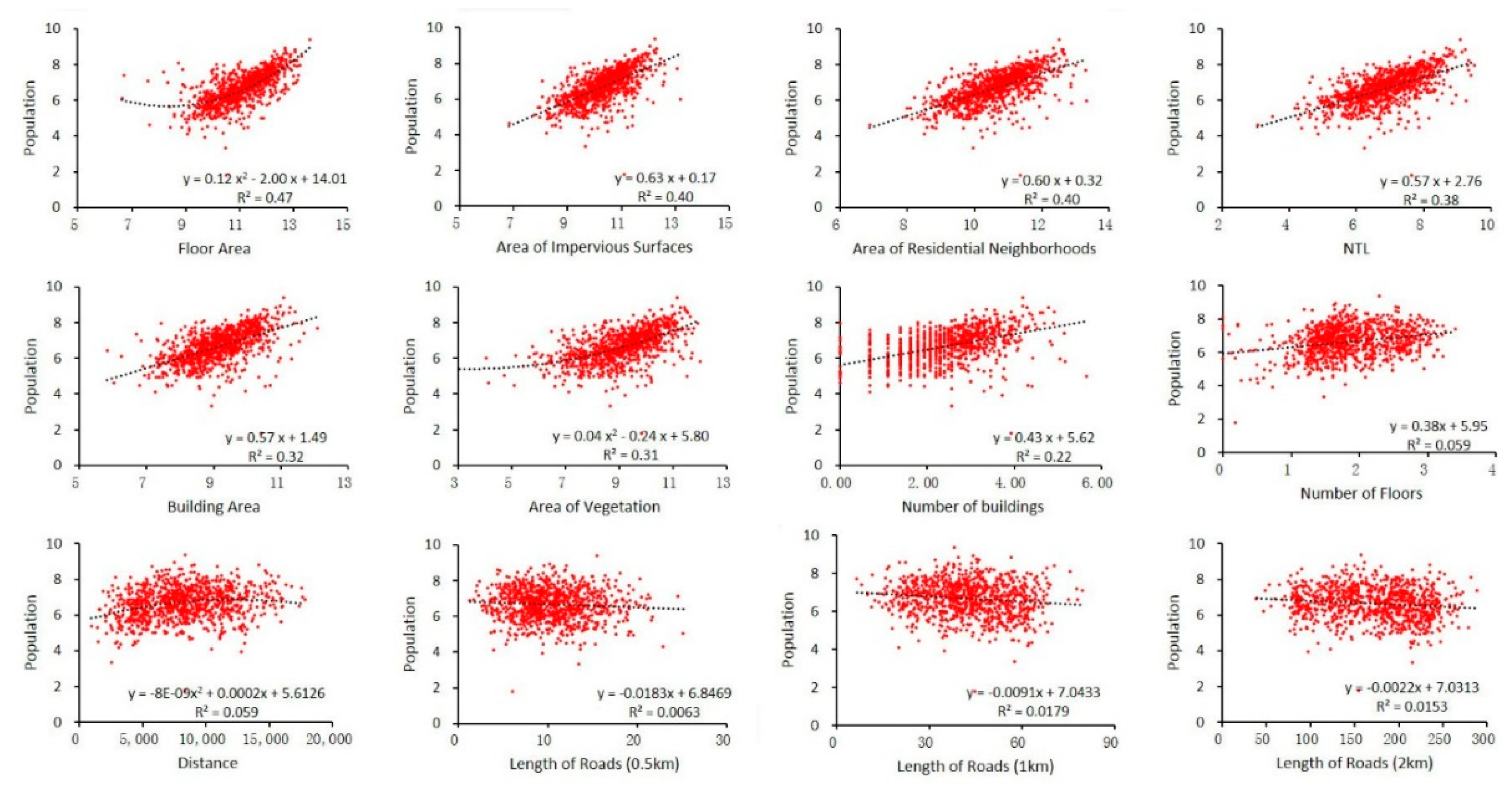
4.1. Relationships between Population and Population-Related Factors
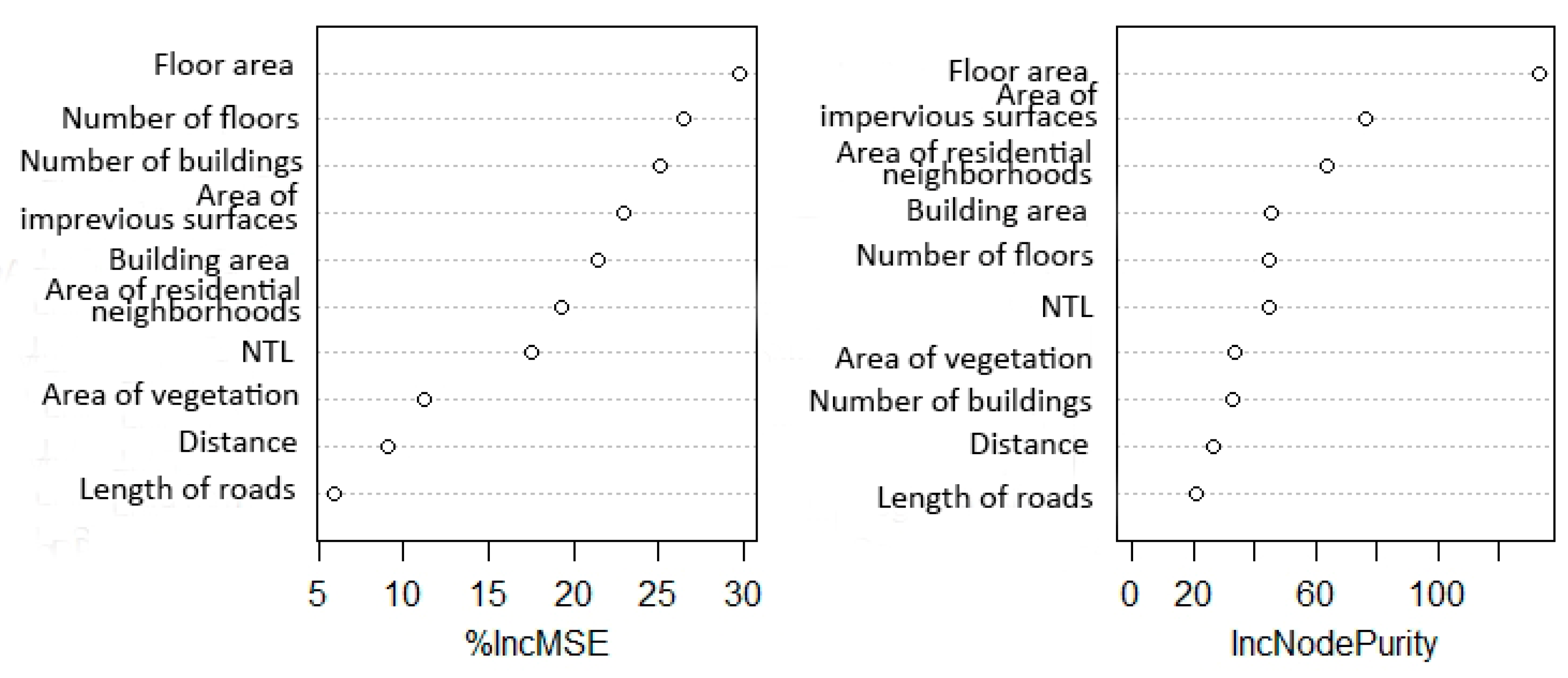
4.2. Relative Importance of Population-Related Factors
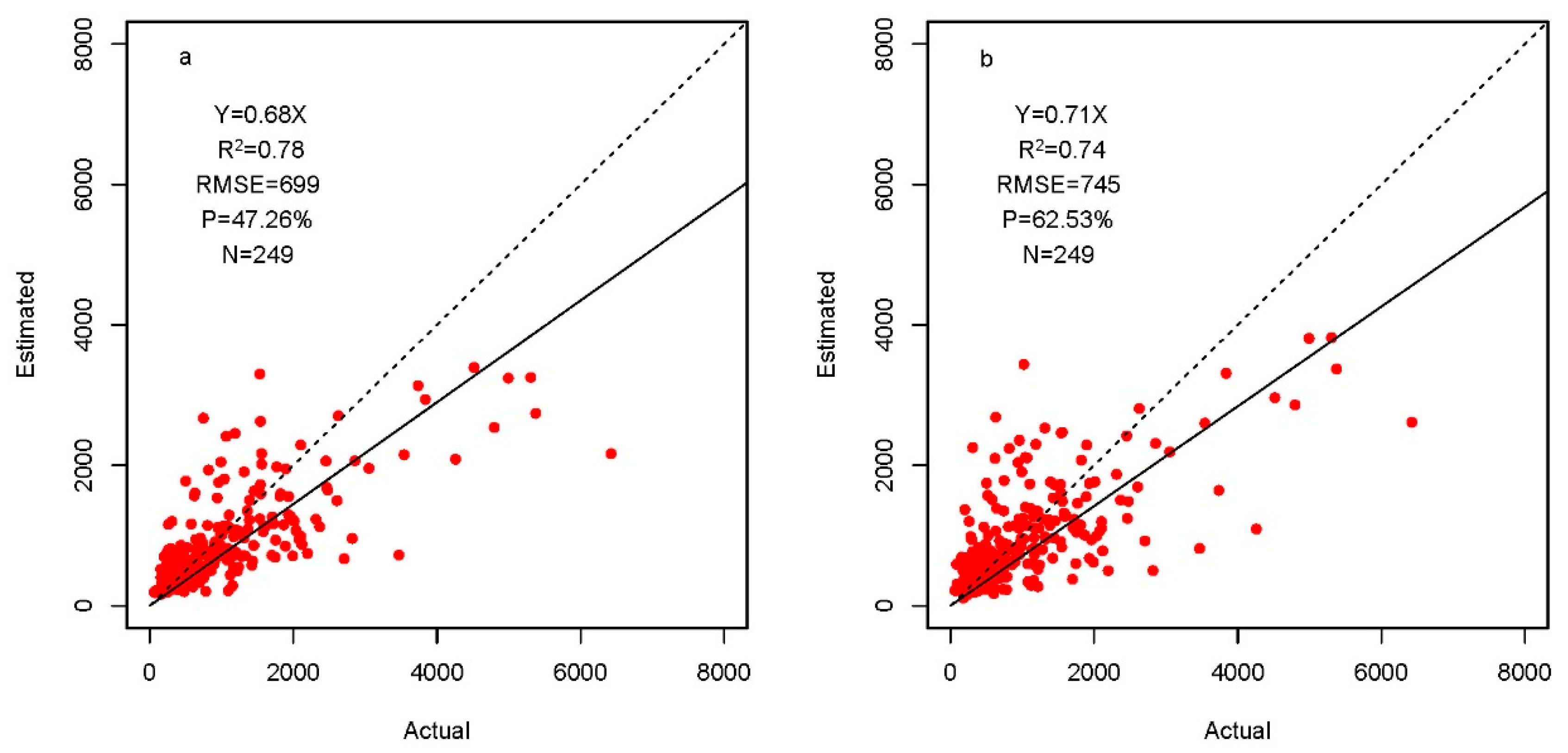
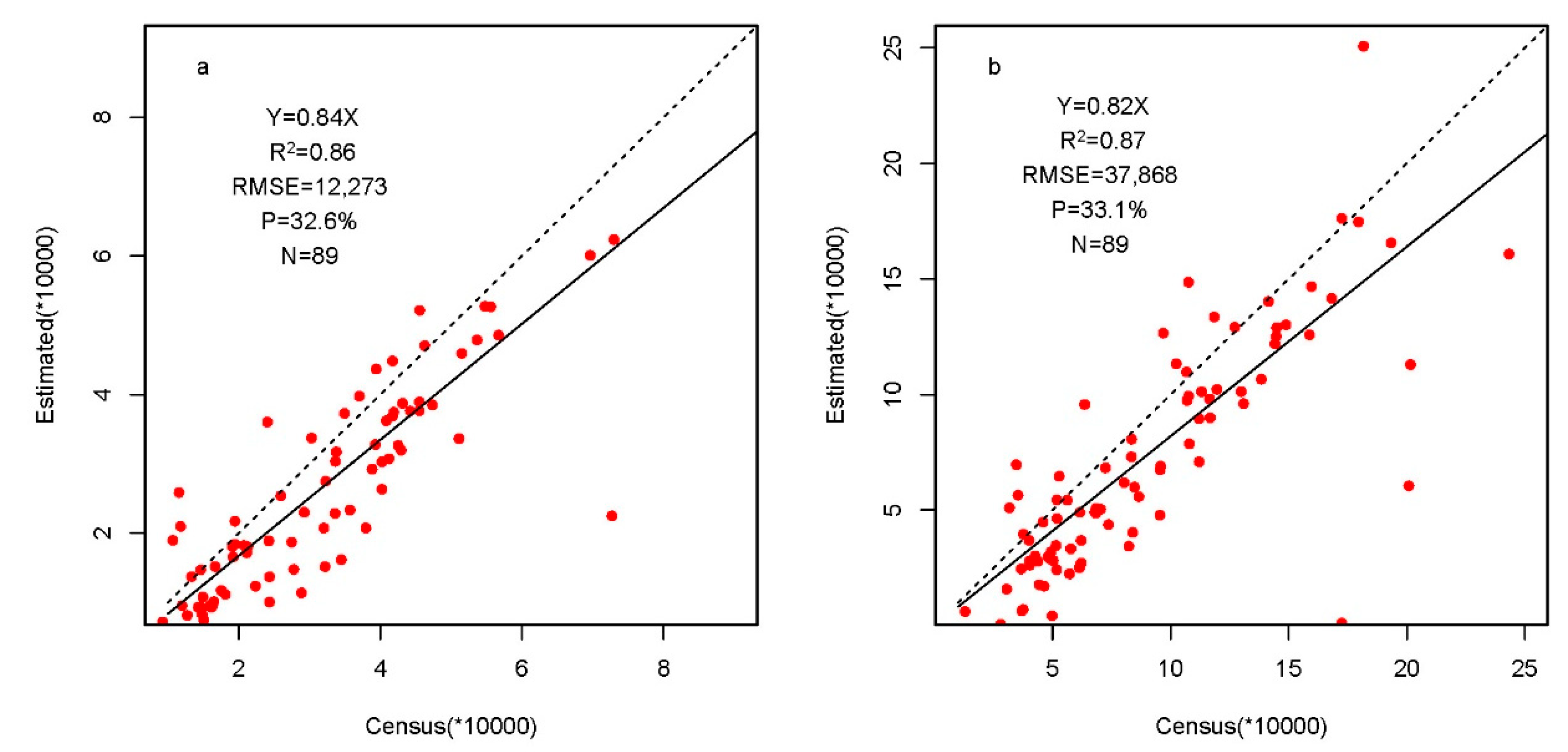
4.3. Population Accuracy and Methods Comparison
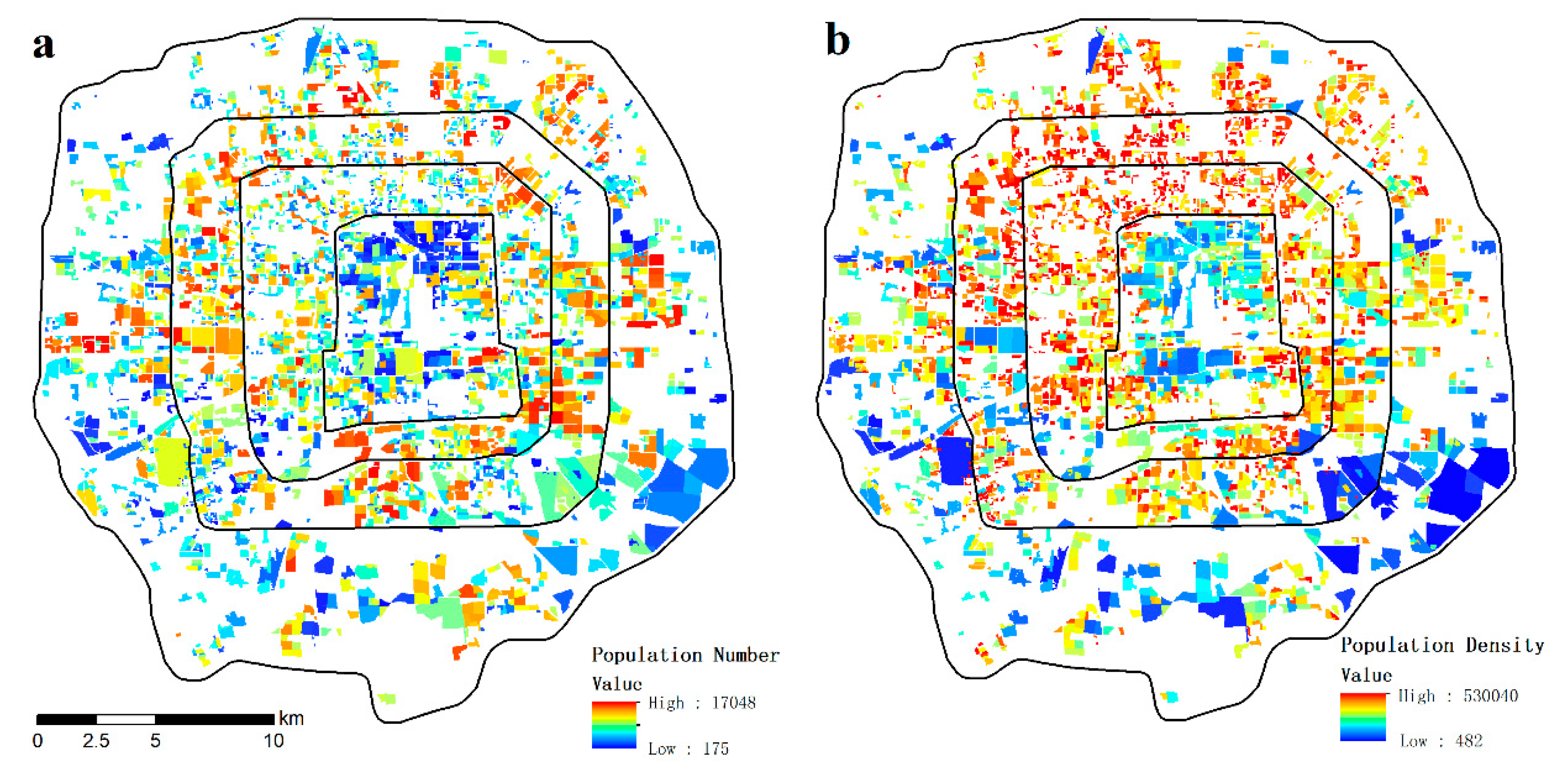
4.4. Distribution Features of the Urban Population in the Fifth-Ring of Beijing
5. Discussion
5.1. Relationships between Population and Population-Related Factors
5.2. Relative Importance of Population Related Factors
5.3. Difference between Dasymetric Mapping and Statistical Modeling Approach
5.4. Real Time Updating of Population Using Statistical Modeling Approach
5.5. Population Data from Different Sources
5.6. Prospects for Future Research
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alahmadi, M.; Atkinson, P.M.; Martin, D. A comparison of small-area population estimation techniques using built-area and height data, Riyadh, Saudi Arabia. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1959–1969. [Google Scholar] [CrossRef]
- Wardrop, N.A.; Jochem, W.C.; Bird, T.J.; Chamberlain, H.R.; Clarke, D.; Kerr, D.; Bengtsson, L.; Juran, S.; Seaman, V.; Tatem, A.J. Spatially disaggregated population estimates in the absence of national population and housing census data. Proc. Natl. Acad. Sci. USA 2018, 115, 3529–3537. [Google Scholar] [CrossRef] [PubMed]
- Gallego, F.J.; Batista, F.; Rocha, C.; Mubareka, S. Disaggregating population density of the European Union with CORINE land cover. Int. J. Geogr. Inf. Sci. 2011, 25, 2051–2069. [Google Scholar] [CrossRef]
- Azar, D.; Engstrom, R.; Graesser, J.; Comenetz, J. Generation of fine-scale population layers using multi-resolution satellite imagery and geospatial data. Remote Sens. Environ. 2013, 130, 219–232. [Google Scholar] [CrossRef]
- Leyk, S.; Gaughan, A.E.; Adamo, S.B.; de Sherbinin, A.; Balk, D.; Freire, S.; Rose, A.; Stevens, F.R.; Blankespoor, B.; Frye, C.; et al. The spatial allocation of population: A review of large-scale gridded population data products and their fitness for use. Earth Syst. Sci. Data 2019, 11, 1385–1409. [Google Scholar] [CrossRef]
- Silva, R.A.; West, J.J.; Lamarque, J.-F.; Shindell, D.T.; Collins, W.J.; Dalsoren, S.; Faluvegi, G.; Folberth, G.; Horowitz, L.W.; Nagashima, T.; et al. The effect of future ambient air pollution on human premature mortality to 2100 using output from the ACCMIP model ensemble. Atmos. Chem. Phys. 2016, 16, 9847–9862. [Google Scholar] [CrossRef]
- Jia, P.; Shi, X.; Xierali, I.M. Teaming up census and patient data to delineate fine-scale hospital service areas and identify geographic disparities in hospital accessibility. Environ. Monit. Assess. 2019, 191, 303. [Google Scholar] [CrossRef]
- Ahola, T.; Virrantaus, K.; Krisp, J.M.; Hunter, G.J. A spatio-temporal population model to support risk assessment and damage analysis for decision-making. Int. J. Geogr. Inf. Sci. 2007, 21, 935–953. [Google Scholar] [CrossRef]
- Tayman, J.; Pol, L. Retail site selection and geographic information systems. J. Appl. Bus. Res. 2011, 11, 46–54. [Google Scholar] [CrossRef][Green Version]
- Bennett, M.M.; Smith, L.C. Advances in using multitemporal night-time lights satellite imagery to detect, estimate, and monitor socioeconomic dynamics. Remote Sens. Environ. 2017, 192, 176–197. [Google Scholar] [CrossRef]
- Wang, L.Y.; Fan, H.; Wang, Y.K. Fine-resolution population mapping from international space station nighttime photography and multisource social sensing data based on similarity matching. Remote Sens. 2019, 11, 1900. [Google Scholar] [CrossRef]
- Balk, D.L.; Deichmann, U.; Yetman, G.; Pozzi, F.; Hay, S.I.; Nelson, A. Determining global population distribution: Methods, applications and data. Adv. Parasitol. 2006, 62, 119–156. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, B.; Bright, E.; Coleman, P.; Urban, M.L. LandScan USA: A high-resolution geospatial and temporal modeling approach for population distribution and dynamics. GeoJournal 2007, 69, 103–117. [Google Scholar] [CrossRef]
- Dong, P.; Ramesh, S.; Nepali, A. Evaluation of small-area population estimation using LiDAR, Landsat TM and parcel data. Int. J. Remote Sens. 2010, 31, 5571–5586. [Google Scholar] [CrossRef]
- Silvan-Cardenas, J.L.; Wang, L.; Rogerson, P.; Wu, C.; Feng, T.; Kamphaus, B.D. Assessing fine-spatial-resolution remote sensing for small-area population estimation. Int. J. Remote Sens. 2010, 31, 5605–5634. [Google Scholar] [CrossRef]
- Weber, E.M.; Seaman, V.Y.; Stewart, R.N.; Bird, T.J.; Tatem, A.J.; McKee, J.J.; Bhaduri, B.L.; Moehl, J.J.; Reith, A.E. Census-independent population mapping in northern Nigeria. Remote Sens. Environ. 2018, 204, 786–798. [Google Scholar] [CrossRef]
- Wu, S.S.; Qiu, X.; Wang, L. Population estimation methods in GIS and remote sensing: A review. Mapp. Sci. Remote Sens. 2005, 42, 80–96. [Google Scholar] [CrossRef]
- Song, J.; Tong, X.; Wang, L.; Zhao, C.; Prishchepov, A.V. Monitoring finer-scale population density in urban functional zones: A remote sensing data fusion approach. Landsc. Urban. Plan. 2019, 190, 103580. [Google Scholar] [CrossRef]
- Batista e Silva, F.; Gallego, J.; Lavalle, C. A high-resolution population grid map for Europe. J. Maps 2013, 9, 16–28. [Google Scholar] [CrossRef]
- Briggs, D.J.; Gulliver, J.; Fecht, D.; Vienneau, D.M. Dasymetric modelling of small-area population distribution using land cover and light emissions data. Remote Sens. Environ. 2007, 108, 451–466. [Google Scholar] [CrossRef]
- Mennis, J.; Hultgren, T. Intelligent dasymetric mapping and its application to areal interpolation. Am. Cartogr. 2006, 33, 179–194. [Google Scholar] [CrossRef]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating census data for population mapping using random forests with remotely-sensed and ancillary data. PLoS ONE 2015, 10, e0107042. [Google Scholar] [CrossRef] [PubMed]
- Deville, P.; Linard, C.; Martin, S.; Gilbert, M.; Stevens, F.R.; Gaughan, A.E.; Blondel, V.D.; Tatem, A.J. Dynamic population mapping using mobile phone data. Proc. Natl. Acad. Sci. USA 2014, 111, 15888–15893. [Google Scholar] [CrossRef] [PubMed]
- Mennis, J. Generating surface models of population using dasymetric mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar]
- Wright, J.K. A method of mapping densities of population with cape cod as an example. Geogr. Rev. 1936, 26, 103–110. [Google Scholar] [CrossRef]
- Mennis, J. Dasymetric mapping for estimating population in small areas. Geogr. Compass 2009, 3, 727–745. [Google Scholar] [CrossRef]
- Levin, N.; Duke, Y. High spatial resolution night-time light images for demographic and socio-economic studies. Remote Sens. Environ. 2012, 119, 1–10. [Google Scholar] [CrossRef]
- Li, X.M.; Zhou, W.Q. Dasymetric mapping of urban population in China based on radiance corrected DMSP-OLS nighttime light and land cover data. Sci. Total Environ. 2018, 643, 1248–1256. [Google Scholar] [CrossRef]
- Ye, T.; Zhao, N.; Yang, X.; Ouyang, Z.; Liu, X.; Chen, Q.; Hu, K.; Yue, W.; Qi, J.; Li, Z.; et al. Improved population mapping for China using remotely sensed and points-of-interest data within a random forests model. Sci. Total Environ. 2019, 658, 936–946. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Gao, S.; Gong, L.; Kang, C.; Zhi, Y.; Chi, G.; Shi, L. Social Sensing: A New Approach to understanding our socioeconomic environments. Ann. Assoc. Am. Geogr. 2015, 105, 512–530. [Google Scholar] [CrossRef]
- Qiu, G.; Bao, Y.; Yang, X.; Wang, C.; Ye, T.; Stein, A.; Jia, P. Local population mapping using a random forest model based on remote and social sensing data: A case study in Zhengzhou, China. Remote Sens. 2020, 12, 1618. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, X.P.; Li, X.; Zhang, J.B.; Liang, Z.T.; Mai, K.; Zhang, Y.T. Mapping fine-scale population distributions at the building level by integrating multisource geospatial big data. Int. J. Geogr. Inf. Sci. 2017, 31, 1220–1244. [Google Scholar] [CrossRef]
- Ural, S.; Hussain, E.; Shan, J. Building population mapping with aerial imagery and GIS data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 841–852. [Google Scholar] [CrossRef]
- Wang, S.X.; Tian, Y.; Zhou, Y.; Liu, W.L.; Lin, C.X. Fine-scale population estimation by 3D reconstruction of urban residential buildings. Sensors 2016, 16, 1755. [Google Scholar] [CrossRef] [PubMed]
- Kubicek, P.; Konecny, M.; Stachon, Z.; Shen, J.; Herman, L.; Reznik, T.; Stanek, K.; Stampach, R.; Leitgeb, S. Population distribution modelling at fine spatio-temporal scale based on mobile phone data. Int. J. Digit. Earth 2019, 12, 1319–1340. [Google Scholar] [CrossRef]
- Wu, J.G.; Shen, W.J.; Sun, W.Z.; Tueller, P.T. Empirical patterns of the effects of changing scale on landscape metrics. Landsc. Ecol. 2002, 17, 761–782. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z. Relationship between land surface temperature and spatial pattern of greenspace: What are the effects of spatial resolution? Landsc. Urban. Plan. 2013, 114, 1–8. [Google Scholar] [CrossRef]
- Botter, G.; Rinaldo, A. Scale effect on geomorphologic and kinematic dispersion. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Chen, K.-S.; Jia, Y.; Li, C.; Sun, X. Spatial-scale effect on the SEBAL model for evapotranspiration estimation using remote sensing data. Agric. For. Meteorol. 2013, 174, 28–42. [Google Scholar] [CrossRef]
- Cook, E.M.; Hall, S.J.; Larson, K.L. Residential landscapes as social-ecological systems: A synthesis of multi-scalar interactions between people and their home environment. Urban. Ecosyst. 2012, 15, 19–52. [Google Scholar] [CrossRef]
- Yan, J.; Zhou, W.; Zheng, Z.; Wang, J.; Tian, Y. Characterizing variations of greenspace landscapes in relation to neighborhood characteristics in urban residential area of Beijing, China. Landsc. Ecol. 2019, 35, 203–222. [Google Scholar] [CrossRef]
- Gaughan, A.E.; Stevens, F.R.; Huang, Z.J.; Nieves, J.J.; Sorichetta, A.; Lai, S.J.; Ye, X.Y.; Linard, C.; Hornby, G.M.; Hay, S.I.; et al. Spatiotemporal patterns of population in mainland China, 1990 to 2010. Sci. Data 2016, 3, 11. [Google Scholar] [CrossRef] [PubMed]
- Qiu, F.; Sridharan, H.; Chun, Y. Spatial autoregressive model for population estimation at the census block level using LIDAR-derived building volume information. Inf. Cartogr. Geogr. Inf. Sci. 2010, 37, 239–257. [Google Scholar] [CrossRef]
- Qian, Y.G.; Zhou, W.Q.; Li, W.F.; Han, L.J. Understanding the dynamic of greenspace in the urbanized area of Beijing based on high resolution satellite images. Urban. For. Urban. Green. 2015, 14, 39–47. [Google Scholar] [CrossRef]
- Sutton, P.; Roberts, D.; Elvidge, C.; Baugh, K. Census from Heaven: An estimate of the global human population using night-time satellite imagery. Int. J. Remote Sens. 2001, 22, 3061–3076. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bakillah, M.; Liang, S.; Mobasheri, A.; Arsanjani, J.J.; Zipf, A. Fine-resolution population mapping using OpenStreetMap points-of-interest. Int. J. Geogr. Inf. Sci. 2014, 28, 1940–1963. [Google Scholar] [CrossRef]
- Pavía, J.M.; Cantarino, I. Can dasymetric mapping significantly improve population data reallocation in a dense urban area? Geogr. Anal. 2017, 49, 155–174. [Google Scholar] [CrossRef]
- Kocifaj, M.; Komar, L.; Lamphar, H.; Wallner, S. Are population-based models advantageous in estimating the lumen outputs from light-pollution sources? Mon. Not. R. Astron. Soc. 2020, 496, L138–L141. [Google Scholar] [CrossRef]
- Kocifaj, M.; Solano-Lamphar, H.A.; Videen, G. Night-sky radiometry can revolutionize the characterization of light-pollution sources globally. Proc. Natl. Acad. Sci. 2019, 116, 7712. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, L.J.C. China’s urban population statistics: A critical evaluation. Eurasian Geogr. Econ. 2005, 46, 272–289. [Google Scholar] [CrossRef]
| Method | Spatial Resolution | References | |
|---|---|---|---|
| Global-scale | Areal interpolation (Dasymetric mapping) | 100–1000 m | Balk et al. 2006; Bhaduri et al. 2007; Leyk et al. 2019 |
| National/Regional-scale | Areal interpolation (Dasymetric mapping) | More than 100 m | Li and Zhou 2018; Azar et al. 2013; Deville et al. 2014 |
| Local-scale | Statistical modeling approach | Less than 100 m/block level | Dong et al. 2010; Silvan-Cardenas et al. 2010; Weber et al. 2018; Wang et al. 2019 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, C.; Zhou, W.; Qian, Y.; Yan, J. Mapping the Urban Population in Residential Neighborhoods by Integrating Remote Sensing and Crowdsourcing Data. Remote Sens. 2020, 12, 3235. https://doi.org/10.3390/rs12193235
Jing C, Zhou W, Qian Y, Yan J. Mapping the Urban Population in Residential Neighborhoods by Integrating Remote Sensing and Crowdsourcing Data. Remote Sensing. 2020; 12(19):3235. https://doi.org/10.3390/rs12193235
Chicago/Turabian StyleJing, Chuanbao, Weiqi Zhou, Yuguo Qian, and Jingli Yan. 2020. "Mapping the Urban Population in Residential Neighborhoods by Integrating Remote Sensing and Crowdsourcing Data" Remote Sensing 12, no. 19: 3235. https://doi.org/10.3390/rs12193235
APA StyleJing, C., Zhou, W., Qian, Y., & Yan, J. (2020). Mapping the Urban Population in Residential Neighborhoods by Integrating Remote Sensing and Crowdsourcing Data. Remote Sensing, 12(19), 3235. https://doi.org/10.3390/rs12193235