1. Introduction
The differential synthetic aperture radar (SAR) interferometric techniques are today well assessed and widely exploited in remote sensing of complex urban scenarios to measure the Earth’s surface displacement [
1,
2,
3]. Among them, the class of persistent scatterer (PS) SAR interferometry (PS-InSAR) [
1] has been recognized as one of the typical techniques for inspection of urban environments and natural terrains such as volcanoes and rural areas [
4,
5]. The approach mainly operates at the full spatial resolution and allows improved information extraction of coherent scatterers. The extracted information is commonly associated with the residual topography and the related deformation parameter, i.e., mean velocity of scatterers [
1]. It should be reminded that the term coherent scatterer mainly refers to the spatially concentrated backscattering responses, such as those obtained from the anthropic structures in the urban area that are persistent over the data acquisition time interval.
However, due to the side-looking intrinsic properties of SAR systems, the vertical structures of an urban environment can represent a challenging scenario for interferometric data-processing and consequently limit the PS-InSAR application for inspection of man-made constructions. In such a scenario, an alternative approach is SAR tomography (TomoSAR). The technique explores SAR data obtained over different orbits to reconstruct the backscattering distribution along the vertical direction and consequently resolves the backscattering confusion from the scatterers inside a resolution cell [
6]. It is important to note that besides the detection of superimposed PSs, SAR tomography permits the improved detection process of single scatterers with respect to interferometric techniques [
7]. Hence, TomoSAR completes and extends the application of PS-InSAR and it similarly allows estimation of the scatterer’s parameters related to possible deformation that may be given by the mean deformation velocity and the thermal dilation [
8,
9,
10].
TomoSAR principally relies on the persistence of the scatterers during the observation time interval. Although the tomographic distributed source model [
11] may mitigate the short term effect of decorrelating sources, the discrimination between reliable scatterers and false alarms is an imperative task, specifically when dealing with data obtained in a long time interval. Commonly, the key point in TomoSAR permanent scatterer detection framework, in the presence of noise, is related to increasing the number of detectable and reliable scatterers while keeping low the possibility of signal misinterpretation that leads to false alarm [
12]. This issue can be approached by the detection methods that allow controlling the false alarm rate (FAR) such as Generalized Likelihood Ratio Test (GLRT). In the framework of GLRT scheme, an efficient strategy for the detection of multiple PSs lying in the same range-azimuth pixel is the support GLRT technique [
13] that is based on the best support of the unknown signal which matches the data. Recently, the efficiency of this typical GLRT-based approach was significantly improved by the use of multi-looking in [
14]. The main objective of multi-look GLRT is improving the detection capability over the scene and in particular over the areas characterized by a low Signal to Noise Ratio (SNR). Thus, by applying the adaptive spatial filtering techniques, the probability of detection is improved at the cost of spatial resolution loss. More precisely, by a slight multi-looking and trading off the spatial resolution, a significant improvement can be obtained by multi-looking operation [
14].
Generally, the robust implementation of multi-look GLRT [
14] relies on the proper identification of similar samples, i.e., the realizations of the signal acquisitions or looks, through the estimation of the data covariance matrix (CM). From the fact that different realizations of each image are generally unavailable, the true covariance matrix is unknown. However, it is straightforward to approximate the true CM by the sample covariance matrix (SCM) that corresponds to the maximum likelihood estimation (MLE), when the data vector obeys the classical zero-mean complex circular Gaussian distribution model [
15]. Proper identification of similar pixels in the image that share a statistical similarity is a challenging issue. Traditionally, SCM can be estimated using a limited number of local pixels, which typically are selected in a neighborhood of the target cell, as it happens in the boxcar-based approach. The known boxcar technique is limited by losing the spatial resolution and overlapping the different backscattering contributions. To mitigate the effects of the resolution loss and scattering confusion, the adaptive multi-looking operations have been employed in the literature [
16].
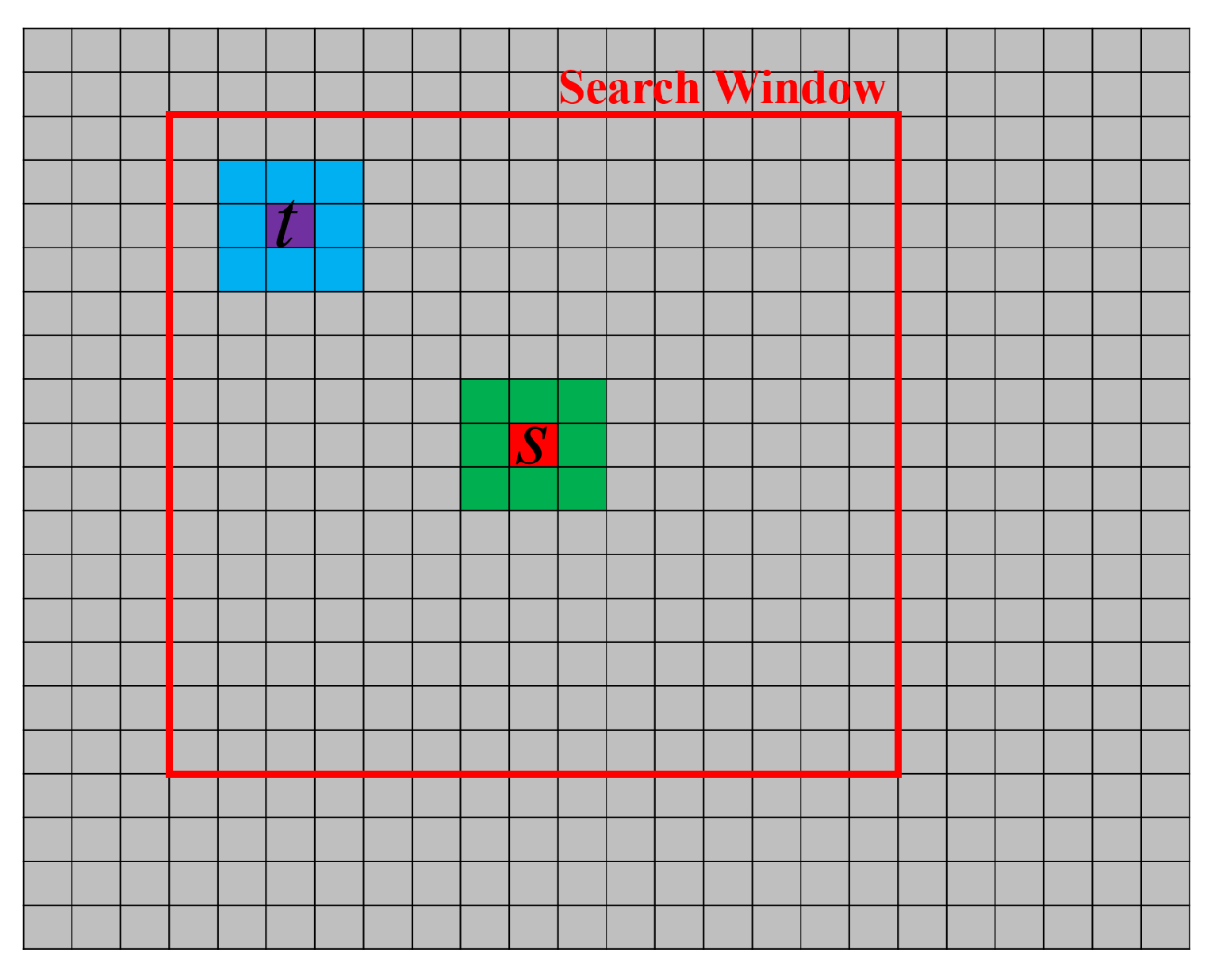
In the framework of adaptive multi-looking, a successful trend has been emerged with the non-local techniques, where rather than selecting neighborhood pixels, the main idea is to select the similar pixels within the image, usually, within a searching window. The similarity or the relative importance of pixels is defined by comparing their surrounding neighborhoods, known as patches [
16]. However, the efficiency of patch-based approaches depends on the definition of the similarity criterion that quantifies how much the patches are similar. To improve the discrimination power of the similarity criterion, the use of a pre-estimated covariance matrix of each patch is strongly recommenced in the literature [
17]. Among the different criteria, the generalized likelihood ratio (GLR) has shown several invariance properties [
18] and it has been frequently employed in the literature [
16,
17]. Nevertheless, the performance of GLR-based criterion drops when the pre-estimated CM departs from Wishart distribution, as it may happen when dealing with a large number of data obtained from long interferometric time-series acquisitions.
In this paper, the investigation on the role of covariance matrix estimation approaches for multiple PSs detection is deepened. In the context of the patch-based framework, the limitation of the similarity criterion based on the pre-estimated covariance matrix was highlighted. Accordingly, a more efficient and robust scheme based on the statistical distribution tests is adopted for identifying the similar pixels. Along this line, two different tests were assessed; one compares the distribution of two noisy patches [
19], while the other compares a pre-defined distribution model with the empirical distribution of the ratio between the patches [
20]. Typically, if the deterministic components of two noisy patches are equal, then their ratio will follow a known distribution. In this paper, these two statistical methods together with the classical boxcar-averaging approach were assessed and their potentials and limitations on multiple PSs detection using multi-look GLRT framework were discussed and evaluated.
This paper begins with an overview of the tomographic SAR signal model as well as the basic principles of multi-look GLRT detection framework in
Section 2. Moreover, the explanation of covariance matrix estimation using the two non-local statistical methods is provided in this section. Comparative analyses on the role of covariance matrix estimation using real data acquired by COSMO-SkyMED (CSK) and TerraSAR-X (TSX) are reported in
Section 3. Further discussions and conclusions on the results reported by the analyses are then given in
Section 4 and
Section 5.
3. Experimental Results
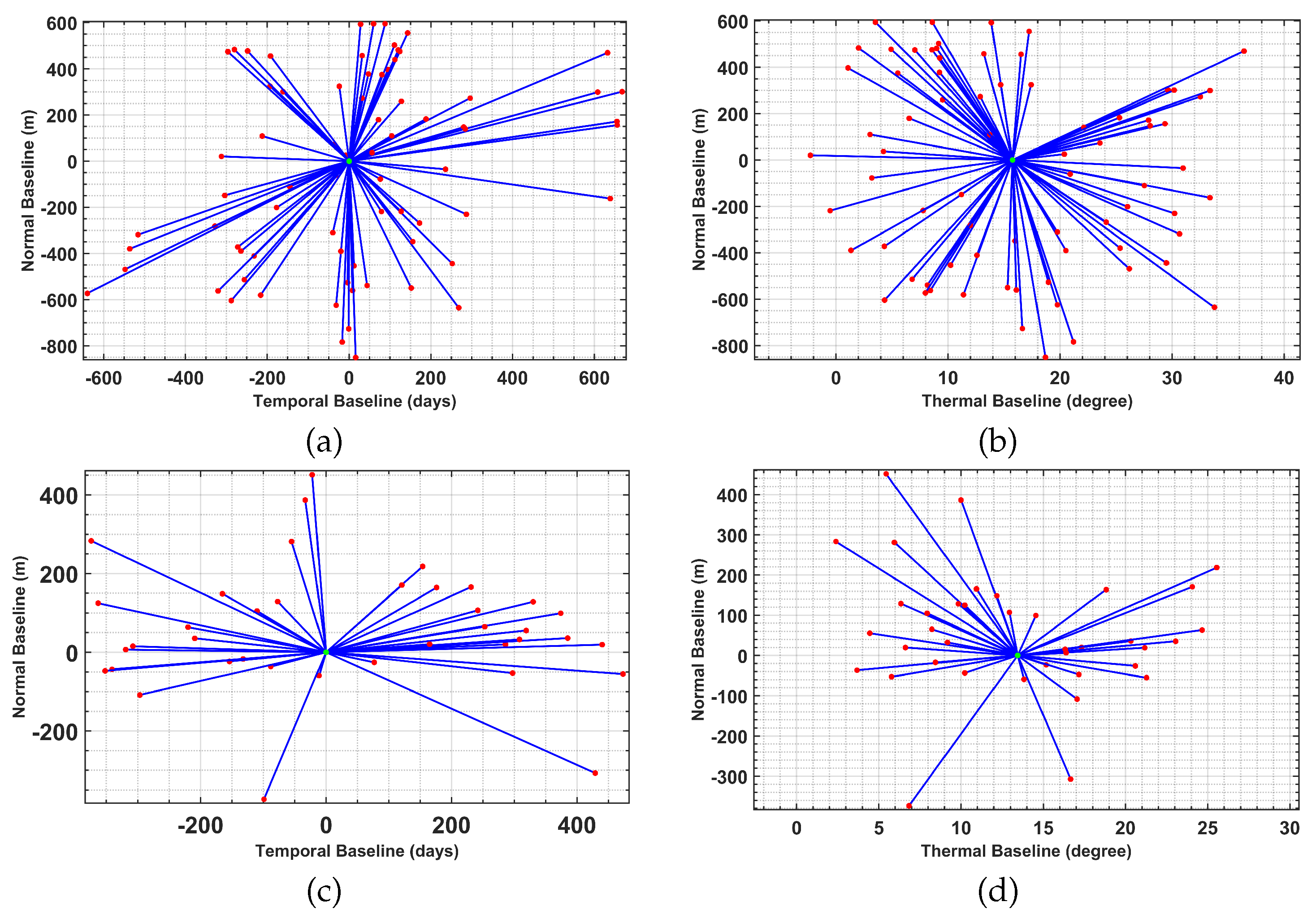
To assess the efficiency of robust SCM estimation, the experiments were carried out on two different datasets. The first dataset was acquired by COSMO-SkyMED sensor over Tehran metropolitan, and it consists of 75 single look complex images acquired between June 2011 and December 2014 with the system operating in the strip-map mode and HH polarization. The second dataset was captured by TerraSAR-X sensor over the city of Toulouse, France. The data are a 2.3 year (between September 2013 and November 2015) temporal stack of 39 Spotlight images in VV polarization. The datasets’ characteristics are summarized in
Table 2 and the baseline configurations are represented in
Figure 3. The figure presents the correlation of different baselines and the sensors’ configuration in spatial, temporal, and thermal domains.
The Rayleigh resolutions for CSK dataset are about 7.3 m, 0.43 cm/year, and 0.42 mm/degree, and for TSX stack data are about 14.2 m, 0.49 cm/year, and 0.53 mm/degree along the elevation, the linear deformation rate, and thermal dilation, respectively. It should be noted that according to the Nyquist sampling, the Rayleigh resolution is the highest achievable resolution [
10]. Moreover, both datasets were calibrated to the atmospheric effect and baseline errors by compensating for a constant phase offset, i.e., using a pixel in the image whose deformation is known (typically a high coherent pixel located in a non-deforming zone, which is characterized by a priori information about the test site) [
30].
To assess the role of the covariance matrix, the performance of support GLRT in single-look [
13] and multi-look detection frameworks was evaluated, in which the data covariance matrix for multi-look processing was estimated using the traditional boxcar, and the above-mentioned non-local approaches (ADS and RDS). The boxcar approach was implemented with a
window size, while the non-local techniques were implemented with an
search window and a
patch window. After the estimation of sample covariance matrix, the support GLRT detection frameworks have been employed for the detection of single and double scatterers. It should be noted that all estimations and detection processes were carried in 5D space. Finally, both detection tests were performed by the threshold values from FAR approach (
).
3.1. CSK Data Experiments: Tall Buildings
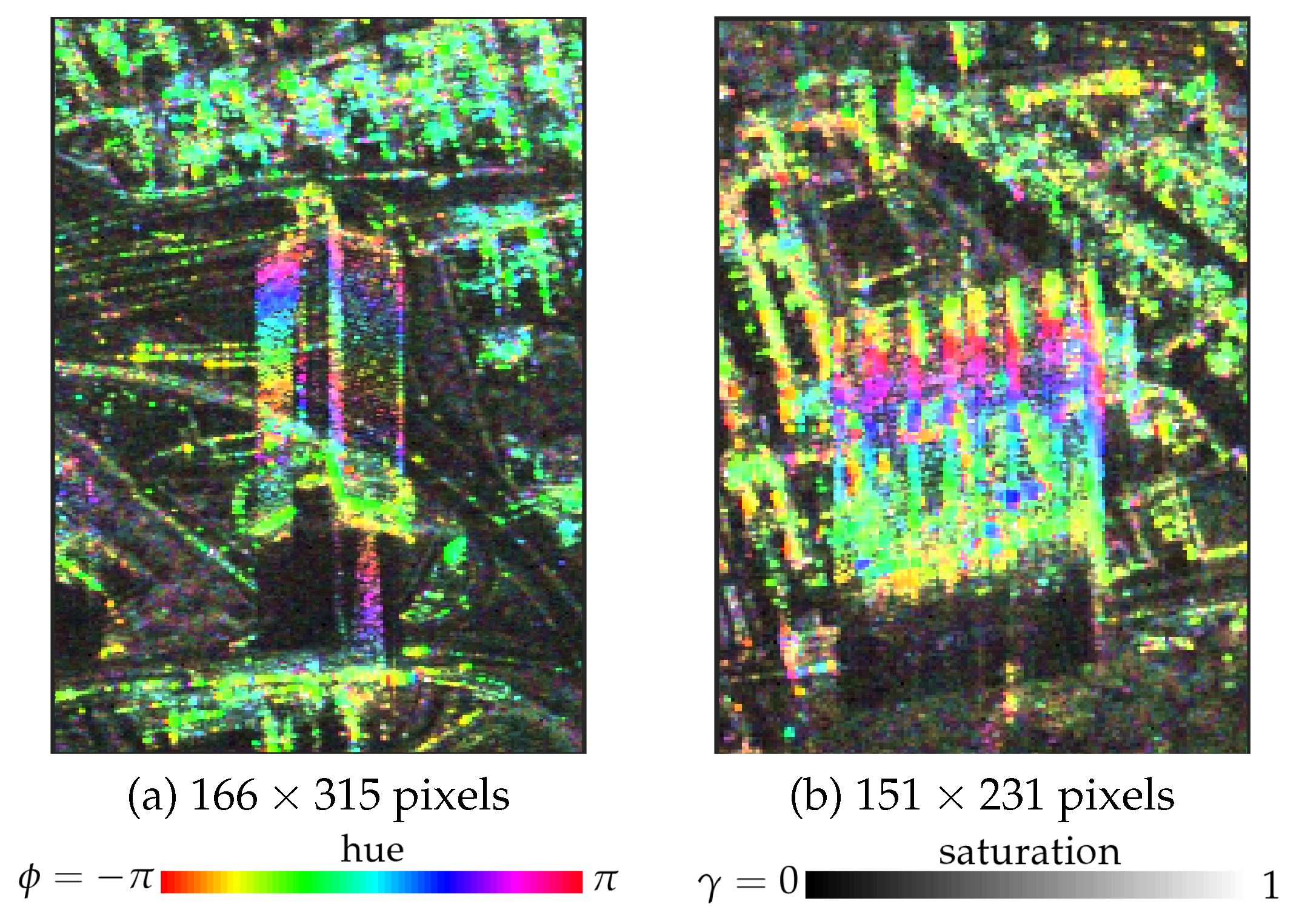
The first experiment is dedicated to assess the scatterer detection performance from tall buildings, which are corresponding to the layover regions in the SAR images. The studied buildings are the International tower and Millennium building in Tehran, where their corresponding interferometric fringes, between two specific CSK acquisition dates, are represented in
Figure 4. The International tower and Millennium building are 162 and 118 m tall, respectively. The interferometric fringes in
Figure 4 are represented in HSV color-coded, and they are generated when the interferometric phase, the absolute value of ensemble coherence, and the intensity image are coded by the hue, saturation, and value, respectively.
The trilateral shape of the International tower (
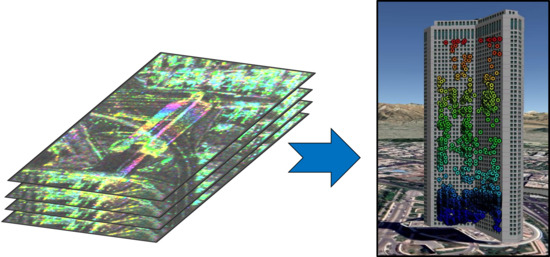
Figure 4a) makes ground-wall interaction perfectly sensible at CSK image spatial resolution scale. The tower’s layover mainly is expected to compose of the contribution of the scatterers situated on the ground and on the wall with single and double bounces scattering mechanisms. From the implementation of the single-look and multi-look support GLRT, the detected single/double scatterers are projected onto the optical 3D Google Earth image of the tower. The first row of
Figure 5 reports the elevation of the detected scatterers estimated using the employed approaches over the International tower. The color of the scatterers on the 3D images represents the elevation of detected scatterers. As can be seen, the color changes from blue to red by passing from the scatterers on the ground to the ones on top of the tower.
Additionally, the analysis of reconstruction of the single and double scatterers from the second building has been implemented. The corresponding results from different frameworks are presented in the second row of
Figure 5. Similarly, the color represents the elevation of the detected scatterers. For quantitative evaluation of the role of robust multi-looking in the detection process, the number of identified (single and double) scatterers using single-look and the different multi-look frameworks are represented in
Table 3. From experimental results, the performance of employed multi-look frameworks over the single-look detection process can be verified, while the potential of multi-look support GLRT was affected by the estimation approaches of the sample covariance matrix. It should be noted that within the time interval of CSK image acquisition, the Millennium building was under construction and it was completed in 2017. This might be the main reason that no reliable scatterer is detected from the top of the building, while other elements such as baseline distribution can also be an effective factor for this issue.
3.2. CSK Data Experiments: Urban Area
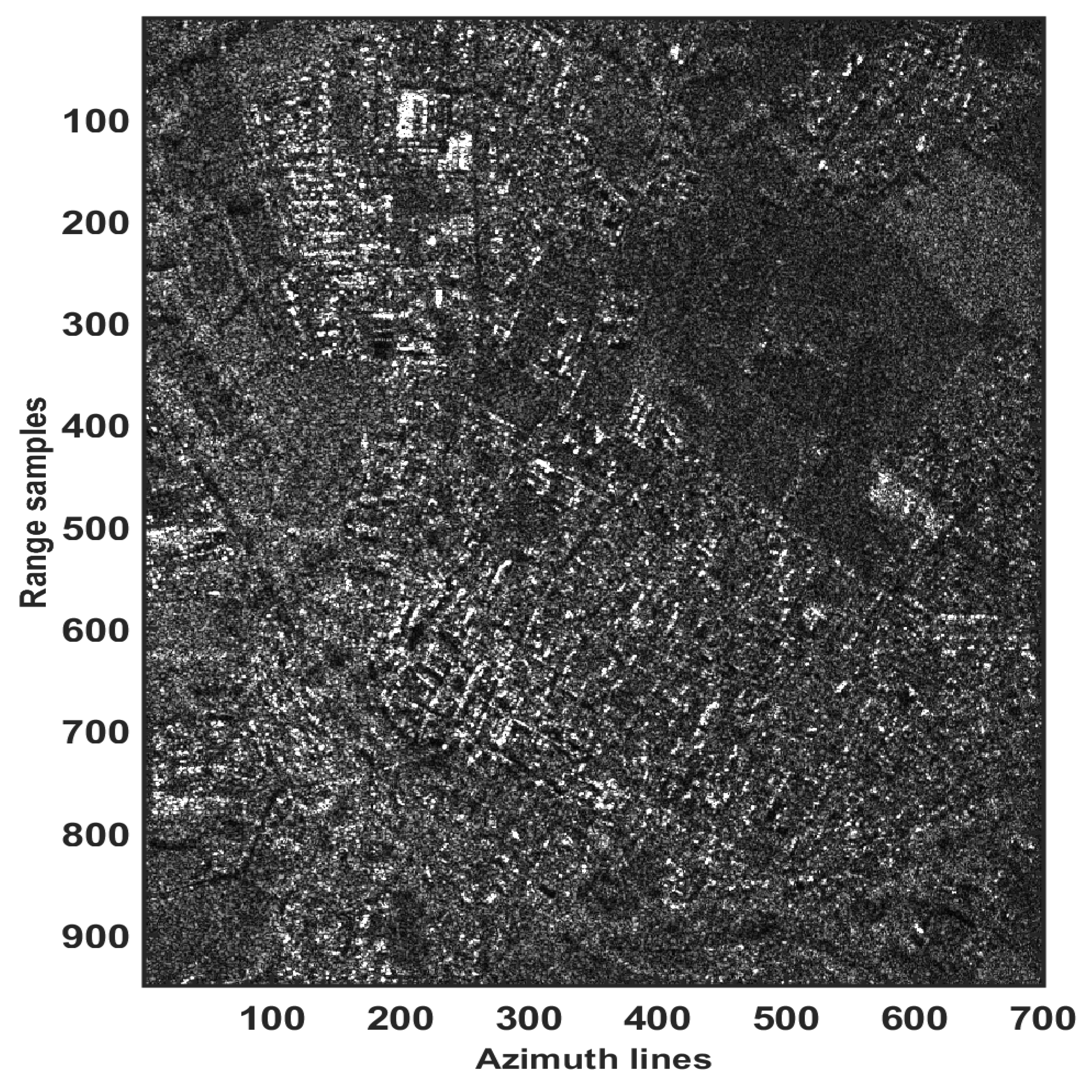
In order to assess the behavior of multi-looking operation when dealing with different targets, further experiments with CSK dataset in a larger region including different target scattering mechanisms have been performed. The amplitude image of the selected subset of the data with a size of
pixels is shown in
Figure 6. The data were processed and the detection tests in Equations (
8) and (
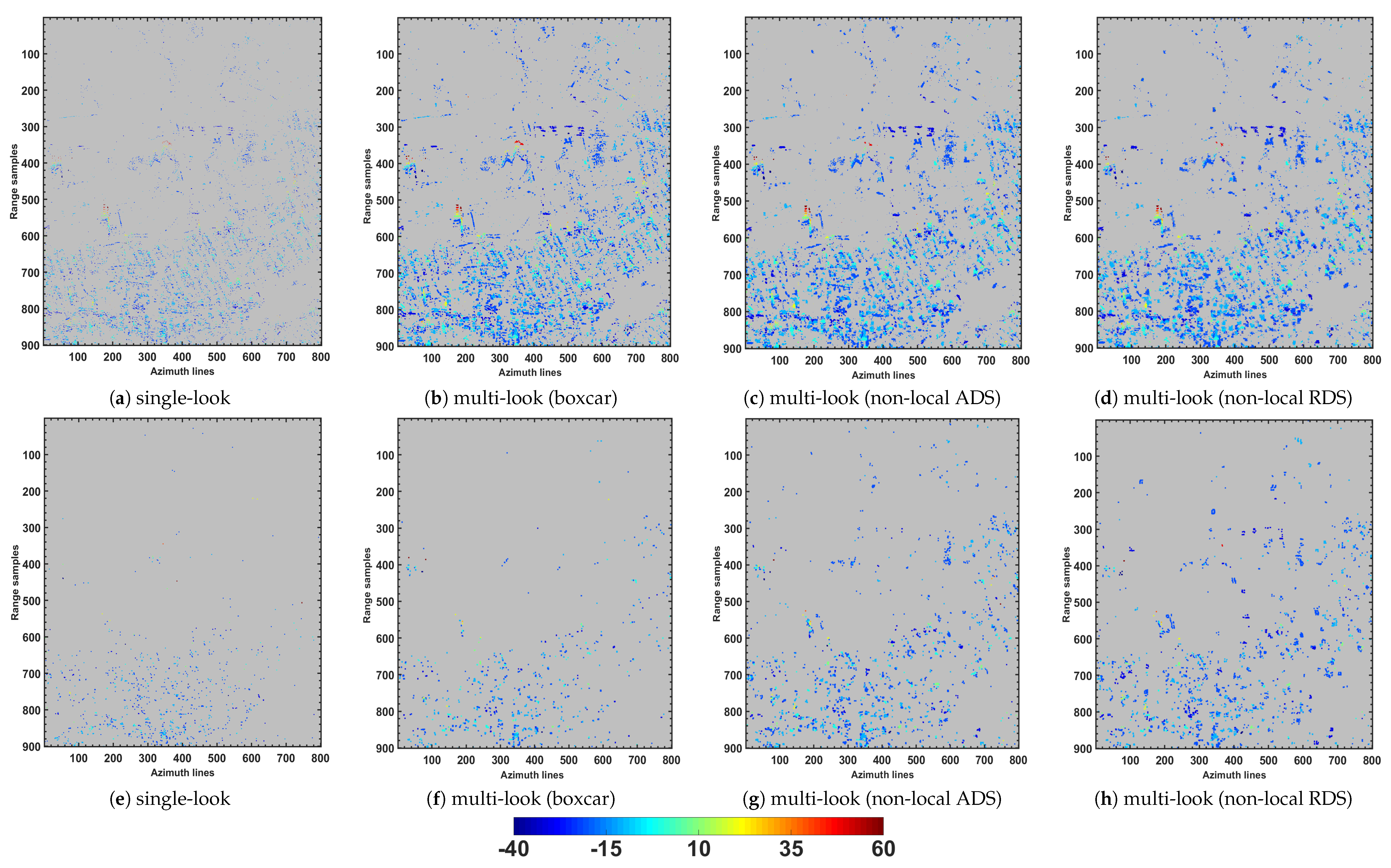
9) were carried out in the 5D space, in which, the scanned intervals of elevation (residual height), mean deformation velocity, and thermal dilation were set to [−60 60] m, [−3 3] cm/year, and [1.5 1.5] mm/°C, respectively. The test were preformed by exploiting the estimated covariance matrix from local and non-local approaches. Additionally, for the sake of comparison, the results from single-look support GLRT are reported. The residual heights of the detected single (
Figure 7a–d) and double (
Figure 7e–h) PSs are represented in the coordinate system of the SAR image. Moreover, to quantitatively compare the detection performance, the number of characterized single and double PSs are presented in
Table 4. From the results, the performance of multi-look approaches over the single-look detection is evident. Moreover, comparison of the employed multi-look frameworks shows that the densities of detected single scatterers using the three multi-look techniques are slightly different. Instead, the density of double scatterers using the non-local techniques is improved with respect to the one obtained by the boxcar approach. It should be noted that the linear velocity and thermal dilation maps of the detected PSs, which are not reported for the sake of brevity, showed generally zero linear and non-linear deformations of the test site.
3.3. CSK Data Experiments: Non-Urban Area
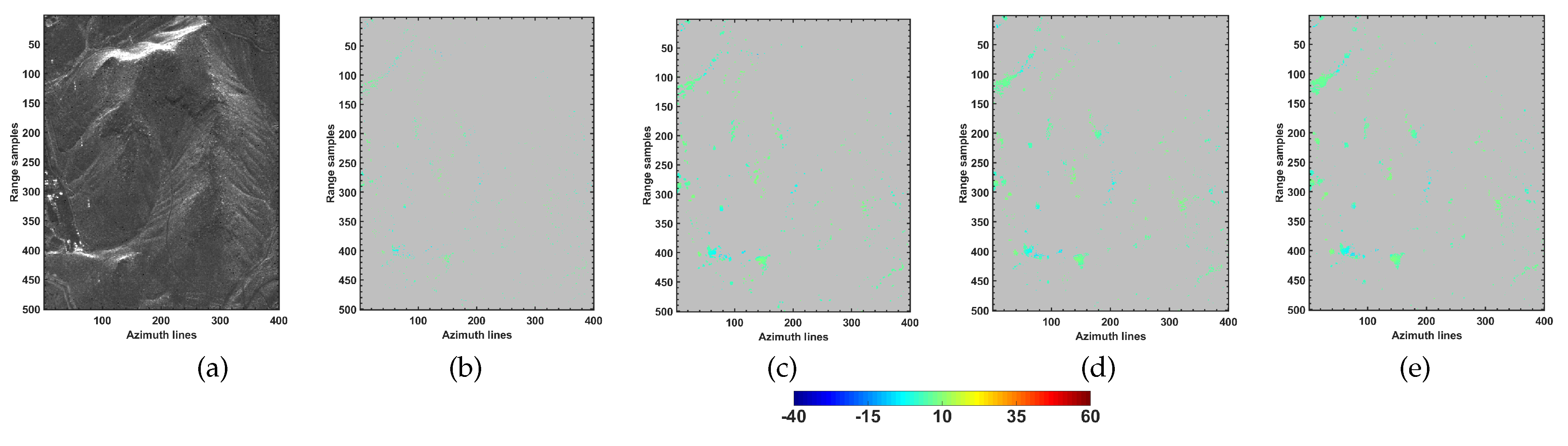
Additional experiments using CSK datasets were carried out over the non-urban and mainly non-layover area. The amplitude image of the selected subset of CSK dataset as well as the detected single scatterers using different employed frameworks are reported in
Figure 8. Since the area does not encompass the layover phenomenon, the presence of double scatterers is minimal or negligible (see the number of detected double scatterers in
Table 5). However, from the reported single scatterers, significant improvements were obtained by the use of multi-look operations in comparison with the single-look framework.
3.4. TSX Data Experiments
Further evaluation of the single-look and multi-look processes was executed using the TerraSAR-X dataset.
Figure 9 shows the average amplitude (averaged across dataset’s acquisitions) or super image of the investigated area related to the city of Toulouse, France. The sample covariance matrix of the dataset is estimated again by three different employed approaches. Both single and multi-look support GLRT detection methods were carried out in the 5D space, while the parameter of the detected PSs (i.e., residual height, mean deformation velocity, and thermal dilation) were computed using the Equation (
10). In particular, the residual height (elevation) interval was set to [−70, 70] m with an increment step of 2.5 m, the mean deformation velocity was scanned in the range of [−3 3] cm/year with a spacing of 0.25 cm/year, while the thermal coefficient interval [−1.5 1.5] mm/°C was scanned with an increment step of 0.1 mm/°C. The thermal maps of the dominant scatterers are reported in the first row of
Figure 10, where the color-map is set according to the range of the thermal dilation. Additionally, the thermal information of the detected double scatterers is represented in the second row of
Figure 10. In analogy to the previous experiments, considerable improvement in detection of double scatterers is reported by the non-local techniques in comparison with the boxcar approach. For a quantitative comparison of the results,
Table 6 presents the number of detected single and double scatterers. Both qualitative and quantitative comparisons verify the influence of multi-looking in PS density.
4. Discussion
It is understood that the capability of the detection tests (
8) and (
9) in providing higher densities of PSs may rely on the robust estimation of data covariance matrix. The role of covariance matrix can be affirmed from the reported results achieved by the processing of CSK and TSX datasets. In particular, different lines were followed to assess the impact of robust covariance matrix estimation.
First, the role of multi-looking operation was analyzed for the reconstruction of the reliable multiple scatterers from tall buildings, i.e., in layover regions. In this case, the role of covariance matrix estimation is analyzed with respect to the detection of superimposed scatterers and particularly the detection of double scatterers from the upper part of the buildings. The qualitative (
Figure 5) and quantitative (
Table 3) results over the two investigated towers (International and Millennium) indicate the significance of multi-look process over the single-look detection framework reported in the literature [
13]. Moreover, comparison of the obtained results by the employed multi-look frameworks indicates that the increased number of the detected scatterers was achieved by the non-local covariance matrix estimation approaches. The improvement by non-local techniques was obtained for both single and double scatterers. In particular, for the International tower, and in comparison with the boxcar-based detection framework, around 128 and 70 additional single scatterers were detected when SCM is computed using ADS and RDA, respectively. Furthermore, from the experimental results (specifically the results of the International tower), the appealing achievement by the NL techniques is related to the detection of additional double scatterers from the upper layers of the towers. The robust covariance matrix estimation by both NL approaches enabled to reveal the presence of the additional weaker scatterers and reach the top layers of the towers, where their presences were not detected using the traditional boxcar-based framework and single-look support GLRT. This achievement is confirmed by the results in
Figure 5 and
Table 3, where 226 and 239 additional double scatterers from the International tower were detected using ADS and RDS, respectively, in comparison with the boxcar technique. Although, the boxcar-based framework outperforms the single-look detection process, in comparison with the NL-based approaches, it fails to properly resolve the layover of scatterers from ground and upper layers of the towers, where the selection of similar samples is limited to the neighborhood pixels that may lead to some scattering confusion and consequently poor estimation of covariance matrix. Instead, the definition of search window allows NL approaches to be more convenient techniques by the selection of non-local similar samples leading to better noise reduction and consequently revealing the weaker scatterers.
On the basis of the performance evaluation of the experimental results from the investigated towers, some remarks are in order. The non-local framework fulfills tangible advantages over the local technique and single-look support GLRT. Indeed, in the boxcar approach, on the one hand, the limited number of neighborhood samples my not provide a robust estimation of covariance matrix; and on the other hand, increasing the window size and the number of local samples brings scattering confusion and resolution issues. Instead, the NL approaches are able to select more pixels with the same distribution within the defined search window and consequently resolve the local estimation problems. Moving to the non-local techniques, the comparable results were reported by both approaches. This affirms the applicability of the employed RDS in tomographic detection framework. It is worth pointing out that the model’s assumption in RDS may cause mismatches. However, generation of super image mitigates the mismatches’ issues related to the presence of additive noise and temporally decorrelated speckle from an image to image. Finally, it should be noted that the detected targets from both buildings were geocoded and overlapped to the 3D Google Earth images. The tomographic geocoded points fit well the shape of the buildings in the 3D view, thus providing evidence of the reliability of detected scatterers.
Moreover, to conclude on the importance of multi-looking operation, further experiments were presented using a larger subset of CSK data in the urban area including the pixels from different objects (
Figure 6). In such a scenario, and unlike the boxcar approach, the patch-based framework is expected to perform optimally and avoid the potentially dangerous identification between closeness and similarity [
18]. From both qualitative (
Figure 7) and quantitative (
Table 4) comparisons, it can be observed that the employed non-local techniques provided a higher density of detected PSs and they outperform over the boxcar and single-look detection methods. Particularly, single-look support GLRT detected 21,445 single scatterers and 1293 double scatterers, while using boxcar framework, 63,130 single and 3112 double scatterers were characterized. Instead, by the non-local ADS, 65,204 singles and 4266 doubles were detected. Moreover, the NL RDS provided 64,539 singles and 4291 doubles. In analogy to the experiments from the towers, the main improvements by the non-local approaches are related to the detection of double scatterers. This is confirmed in the reported residual height maps of double scatterers in
Figure 7, indicating the role of covariance matrix estimation in TomoSAR PS detection framework. The robust NL estimation of the sample covariance matrix allowed improving signal quality and consequently revealing the presence of weaker (double) scatterers, that were not detected by the classical boxcar and single-look estimation approaches.
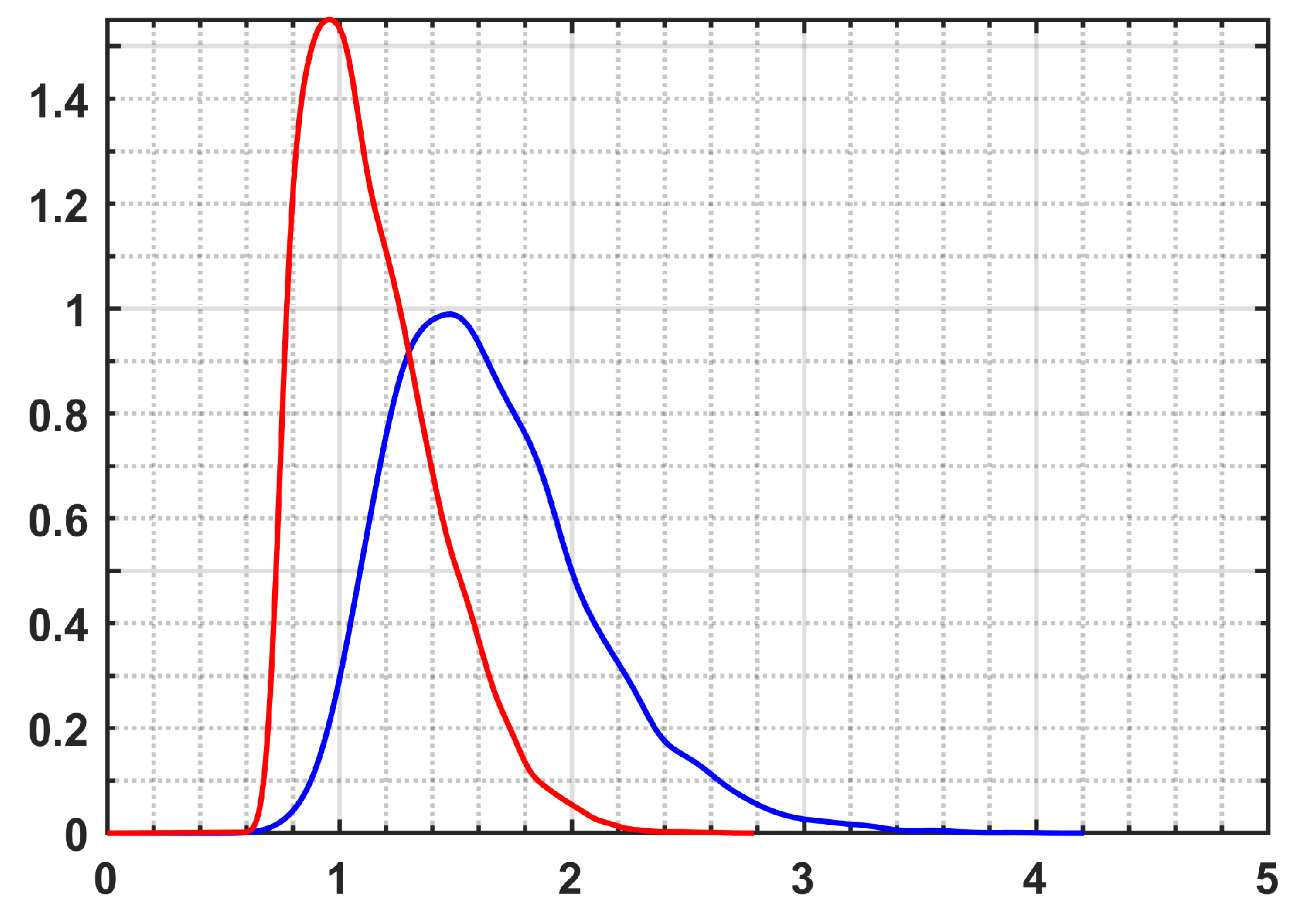
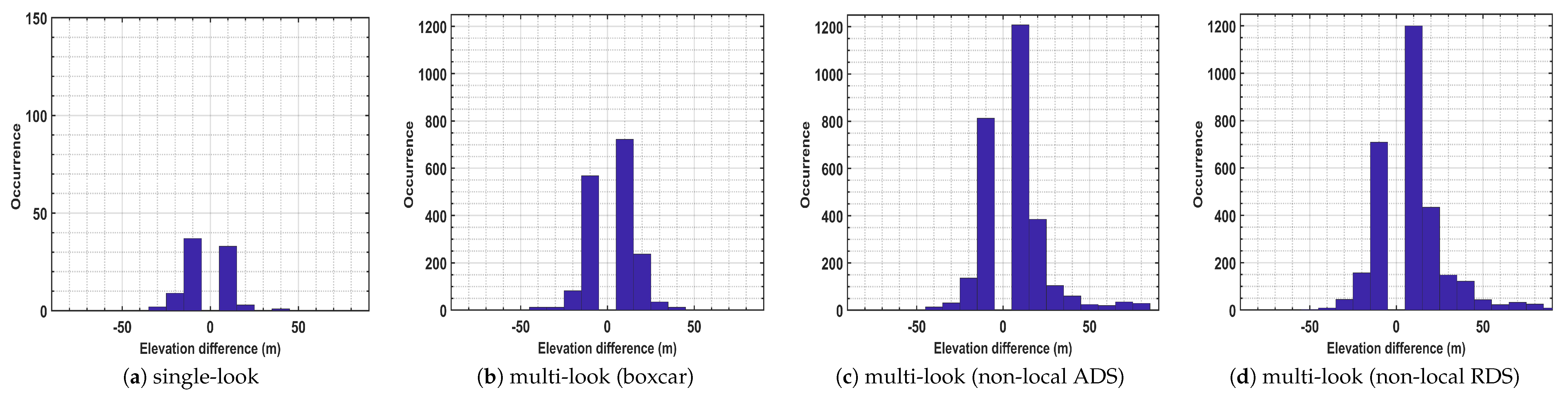
Additionally, the super-resolution capability (ability to detect the superimposed scatterers that are situated below the Rayleigh resolution) of the employed support GLRT detection frameworks with respect to the covariance matrix estimation approach is assessed. To this aim, for all pixels contains more than one PSs, the height differences between single and double scatterers were computed and the results are represented in
Figure 11. The reported histograms provide two important indications:
More double scatterers below the Rayleigh resolution were detected by the non-local approaches (around 2000 PSs by both NL approaches, while about 1200 PSs using the boxcar method, and less than 100 PSs using single-look framework, see the occurrences related to the height difference around ).
Double scatterers from upper layers of buildings were properly detected by non-local techniques, while those were missed by boxcar approach and specifically by the single-look framework (see the occurrences related to the higher values of height difference). This is consistent with the reported results from the towers.
These improvements achieved by the non-local techniques are typically related to the robust covariance matrix estimation through the proper sample selection framework. Unlike boxcar approach, the non-local techniques avoid overlapping different backscattering contributions and allow better signal improvement; consequently, revealing the presence of additional weaker scatterers. Moreover, it should be noted that the visual comparison of the estimated residual heights (
Figure 7) for the single and double scatterers achieved by different detection operations provides evidence of spatial consistency, which can validate the residual height maps.
Additional experiments from the employed approaches over a rural area were reported in
Figure 8 and
Table 5. The area mainly covers the distributed scatterers and non-layover region (except over the existing buildings and top of the mountain in the upper part of
Figure 8a). Hence, the test site is consistent with the model assumptions of the RDS approach in (
16), such that speckle follows the known fully developed model [
29]. From the reported results in
Figure 8, the NL RDS approach slightly outperforms the ADS technique, while generally comparable results were obtained by local and non-local multi-look approaches in the test site. This could be due to the fact that in the considered area the distributed scattering mechanisms are mainly encountered, where the non-local samples in the search window may not fulfill a tangible advantage over the local samples. Instead, a significant increase in the total number of single scatterers was obtained by the employed multi-look GLRT techniques with respect to the single-look framework. The estimation of covariance matrix permits noise reduction and consequently reveals the presence of the partially coherent scatterers in the rural test site, in which the single-look processing could not detect them.
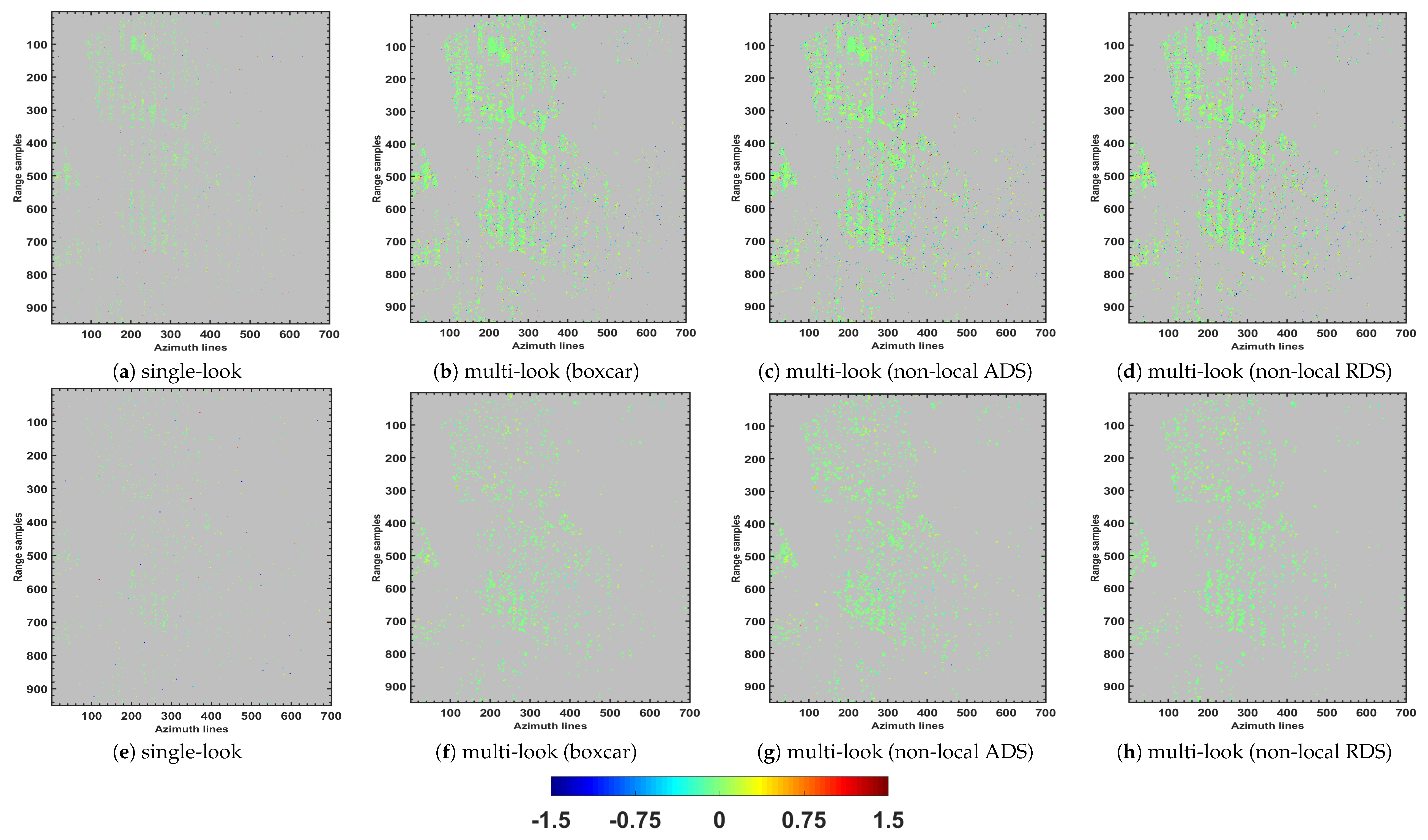
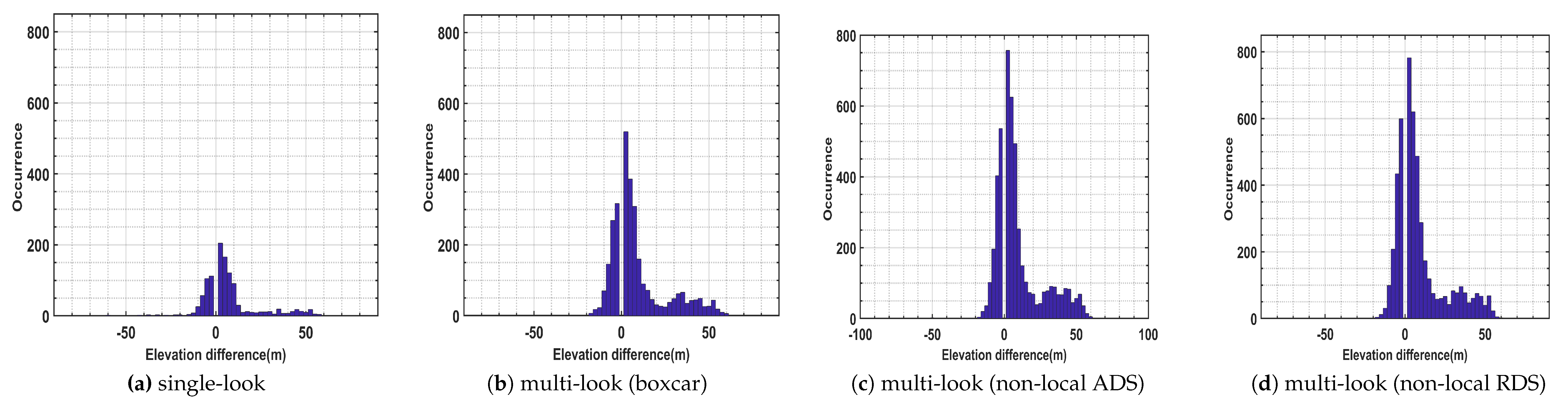
Furthermore, in analogy to the CSK data experiment from the urban area, the analyses of the covariance matrix to detect the single and double scatterers using TerraSAR-X images have been performed. From the provided thermal dilation maps in
Figure 10 and
Table 6, again the efficiency of the non-local techniques over the conventional boxcar approach as well as single-look support GLRT was proven in urban areas. In general, 1977 and 2180 additional double scatterers were revealed by the non-local ADS and RDS, respectively, where those scatterers were not characterized using the multi-look boxcar-based framework. Further analyses on the elevation separation have been made using the histogram of height difference between detected single and double scatterers (see
Figure 12). In consistence with the indications reported using the CSK dataset over the urban area, the detected additional double scatterers (
Figure 12) using non-local approaches are mainly related to top parts of buildings and also the situation where the scatterers’ distance in the elevation space is below the Rayleigh resolution.
As a final remark, the performance of the non-local ADS and RDS approaches over the different window and patch sizes were assessed. The results of detection processes using the image of the International building (
Figure 4a), including the tower and surrounding areas, are represented in
Table 7. Analysis of the detected single and double scatterers using both employed NL techniques showed that by increasing the size of the search window, the performance of detection frameworks was improved. The higher window size adds more similar samples to the search window, leading to a more robust estimation of the data covariance matrix at the cost of a higher computational process. Hence, the intermediate search window size is preferred to guarantee the presence of enough similar samples, while incurring the computational cost. From the results, the higher patch size generally increased the number of detected single scatterers. However, when a
patch is employed, the double scatterers are slightly decreased. Typically, by increasing the patch size, the information of different objects are added to the patches which can affect the efficiency of similarity measure and the estimated covariance matrix. Hence, this might be a reason that support GLRT could not increase the detection of weaker (double) scatterers with the largest patch. Moreover, it should be noted that smaller patches are suitable to capture the edges and prevent the blurring effects. Generally, the optimal sizes of the patch and the search window in NL-based tomography are a complex task and it mainly relies on the spatial resolution, the number of images, and the study area.
5. Conclusions
In this paper, the role of the multi-looking operation in the detection of single and double scatterers using TomoSAR PSs detection framework was analyzed and evaluated. It has been shown that under the same TomoSAR configuration parameters and the same system resolutions, the detection of multiple scatterers can be affected by the non-robust estimation of the sample covariance matrix. The tomographic experimental results achieved by the processing of high-resolution COSMO-SkyMED and TerraSAR-x images in different study areas affirmed the role of data covariance matrix in the detection frameworks. It has been shown that the multi-look frameworks with respect to the conventional single-look detection approach allows efficient noise reduction and revealing the presence of the additional scatterers, and consequently increasing the density of the detected PSs. Additionally, evaluation of detection performance over the different multi-looking approaches provided important indications on the efficiency of robust covariance matrix estimations.
In the urban area, the main achievement obtained by the employment of non-local techniques was related to the detection of double scatterers. The efficient estimation of covariance matrix using non-local techniques allows further noise reduction and reveals the presence of weaker (double) scatterers, which may not be detectable when the covariance matrix is estimated using the conventional boxcar approach. In particular, detection of double scatterers below the Rayleigh resolution and the scatterers from upper layers of buildings were the main improvements reported by the employment of non-local techniques over the local-based framework. Note that sample selection in the neighborhood of the target pixel by the boxcar approach may mix the different signals, while the non-local approaches avoid overlapping the different backscattering by taking into account only NL pixels belonging to a same distribution model. Hence, the proper sample selection by non-local techniques allowed detection of further weaker scatterers due to the better SNR improvement.
In rural areas, where the data are recorded from homogeneous regions without encompassing the edge structures and layover phenomenon, the non-local techniques may not fulfill a tangible advantage over the local techniques. In such a case, the classical boxcar technique can be applicable for a multi-look detection process. The patch-based adaptive sample selection methods generally suit the urban PS applications, where the detailed scatterers of the building can be optimally detected.
It should be noted that the amplitude statistical sample selection approaches might be seen as the typical methods for the identification of similar pixels using the big TomoSAR dataset. However, extending the statistical distribution tests to the complex data without relying on the pre-estimation of the sample covariance matrix and incorporating the tests with information related to the parameters of the scatterers might be a more effective similarity criterion. Hence, the benefit of such a criterion should be assessed.