From Drones to Phenotype: Using UAV-LiDAR to Detect Species and Provenance Variation in Tree Productivity and Structure
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. UAV-LiDAR Collection, Processing and Trait Calculation
2.3. Statistical Analysis
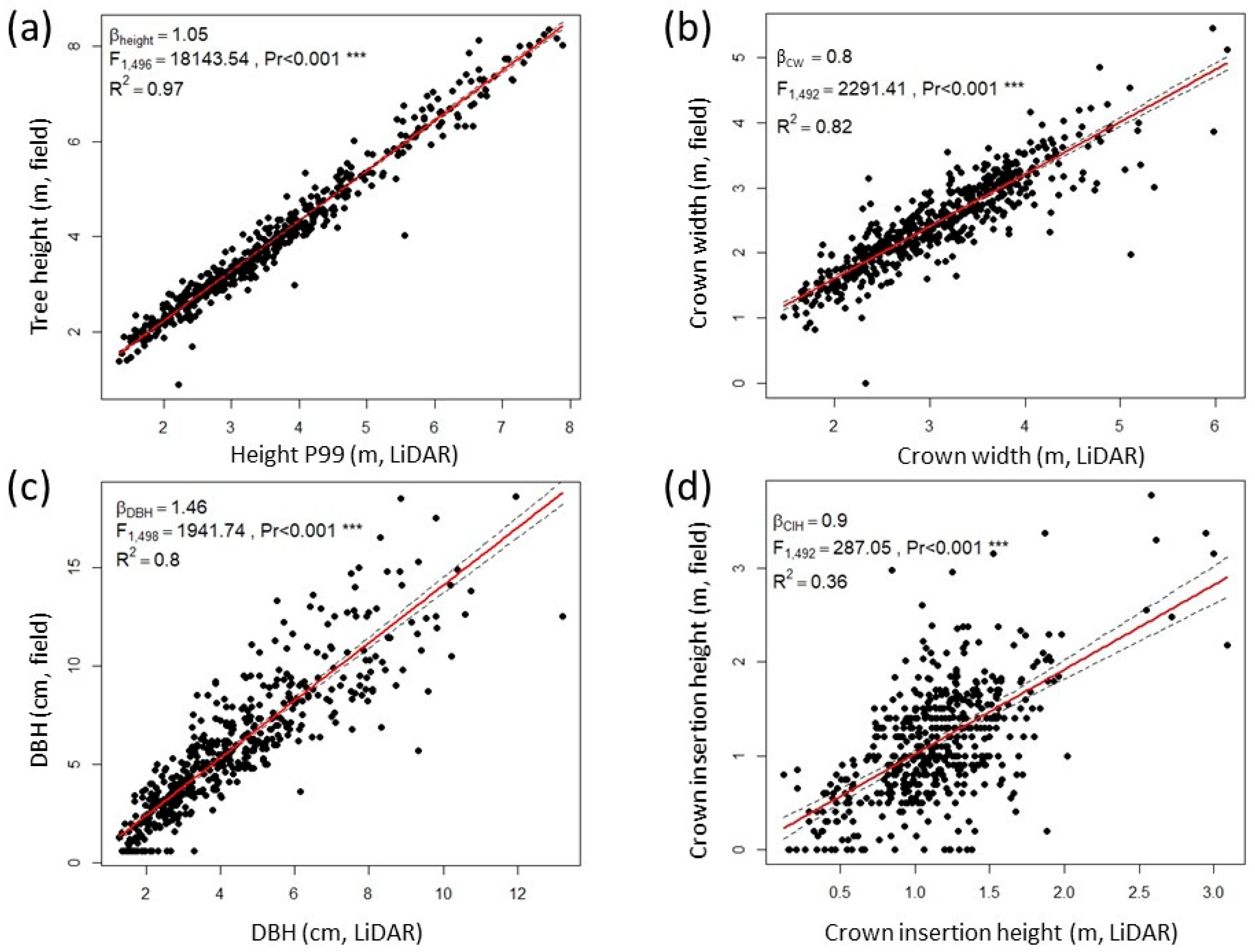
2.4. Field Validation
3. Trait Filtering
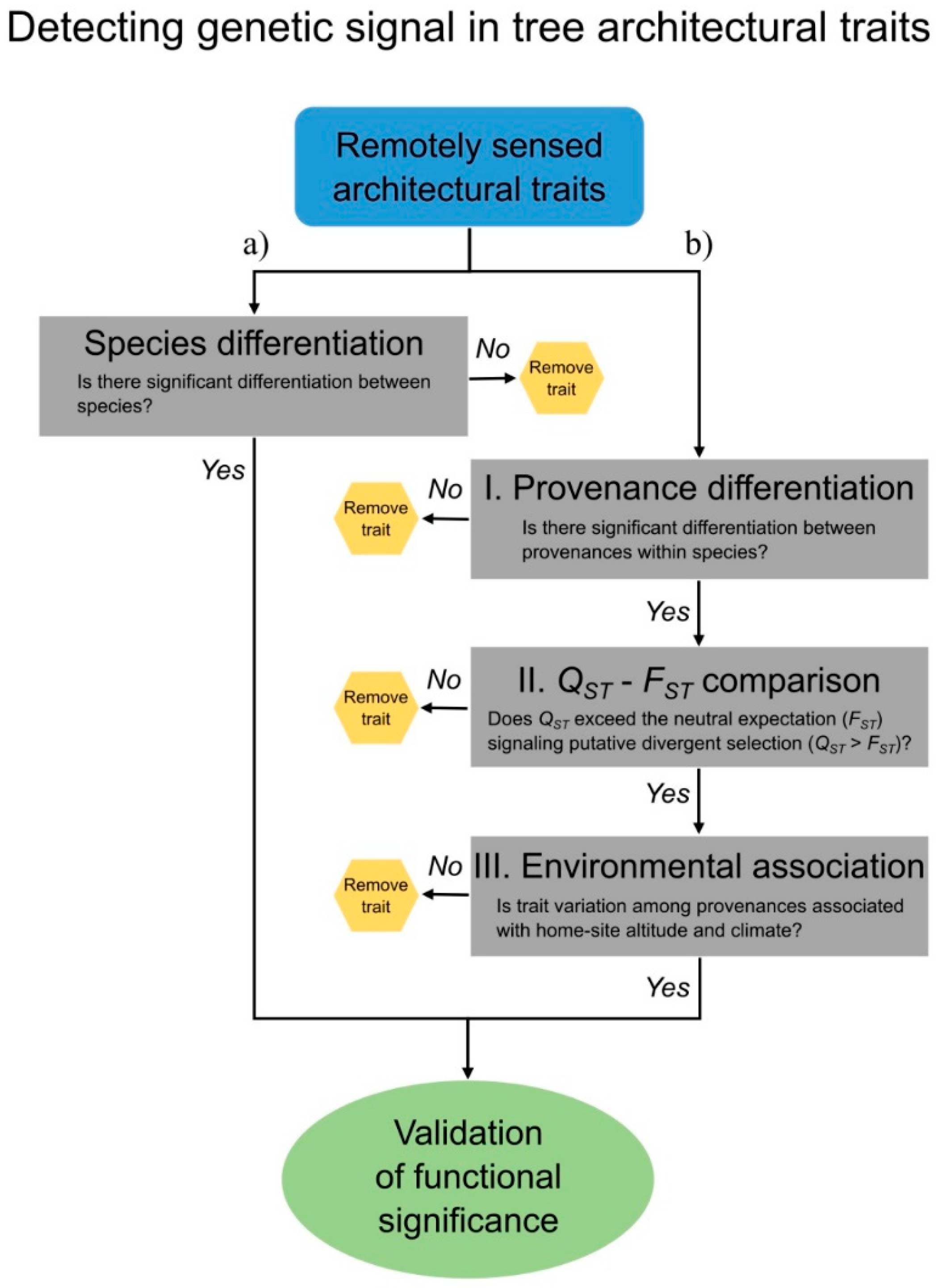
4. Results
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kellner, J.R.; Albert, L.P.; Burley, J.T.; Cushman, K.C. The case for remote sensing of individual plants. Am. J. Bot. 2019, 106, 1139–1142. [Google Scholar] [CrossRef] [PubMed]
- Krause, S.; Sanders, T.G.M.; Mund, J.P.; Greve, K. UAV-based photogrammetric tree height measurement for intensive forest monitoring. Remote Sens. 2019, 11, 758. [Google Scholar] [CrossRef]
- Alberto, F.J.; Aitken, S.N.; Alía, R.; González-Martínez, S.C.; Hänninen, H.; Kremer, A.; Lefèvre, F.; Lenormand, T.; Yeaman, S.; Whetten, R.; et al. Potential for evolutionary responses to climate change - evidence from tree populations. Glob. Chang. Biol. 2013, 19, 1645–1661. [Google Scholar] [CrossRef] [PubMed]
- Dungey, H.S.; Dash, J.P.; Pont, D.; Clinton, P.W.; Watt, M.S.; Telfer, E.J. Phenotyping whole forests will help to track genetic performance. Trends Plant Sci. 2018, 23, 854–864. [Google Scholar] [CrossRef] [PubMed]
- Fankhauser, K.E.; Strigul, N.S.; Gatziolis, D. Augmentation of traditional forest inventory and Airborne laser scanning with unmanned aerial systems and photogrammetry for forest monitoring. Remote Sens. 2018, 10, 1562. [Google Scholar] [CrossRef]
- Solvin, T.M.; Puliti, S.; Steffenrem, A. Use of UAV photogrammetric data in forest genetic trials: Measuring tree height, growth, and phenology in Norway spruce (Picea abies L. Karst.). Scand. J. For. Res. 2020, 1–12. [Google Scholar] [CrossRef]
- Wallace, L.; Musk, R.; Lucieer, A. An assessment of the repeatability of automatic forest inventory metrics derived from UAV-borne laser scanning data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7160–7169. [Google Scholar] [CrossRef]
- Grubinger, S.; Coops, N.C.; Stoehr, M.; El-Kassaby, Y.A.; Lucieer, A.; Turner, D. Modeling realized gains in Douglas-fir (Pseudotsuga menziesii) using laser scanning data from unmanned aircraft systems (UAS). For. Ecol. Manage. 2020, 473, 118284. [Google Scholar] [CrossRef]
- du Toit, F.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; El-Kassaby, Y.A.; Stoehr, M.; Turner, D.; Lucieer, A. Characterizing variations in growth characteristics between Douglas-fir with different genetic gain levels using airborne laser scanning. Trees-Struct. Funct. 2020, 34, 649–664. [Google Scholar] [CrossRef]
- Camarretta, N.; Harrison, P.A.; Bailey, T.; Potts, B.; Lucieer, A.; Davidson, N.; Hunt, M. Monitoring forest structure to guide adaptive management of forest restoration: A review of remote sensing approaches. New For. 2019, 1–24. [Google Scholar] [CrossRef]
- Breed, M.F.; Harrison, P.A.; Bischoff, A.; Durruty, P.; Gellie, N.J.C.C.; Gonzales, E.K.; Havens, K.; Karmann, M.; Kilkenny, F.F.; Krauss, S.L.; et al. Priority actions to improve provenance decision-making. Bioscience 2018, 68, 510–516. [Google Scholar] [CrossRef]
- Prober, S.M.; Byrne, M.; McLean, E.H.; Steane, D.A.; Potts, B.M.; Vaillancourt, R.E.; Stock, W.D. Climate-adjusted provenancing: A strategy for climate-resilient ecological restoration. Front. Ecol. Evol. 2015, 3, 40–53. [Google Scholar] [CrossRef]
- White, T.L.; Adams, W.; Neale, D. Forest Genetics; CABI: Wallingford, UK, 2007. [Google Scholar]
- Aitken, S.N.; Bemmels, J.B. Time to get moving: Assisted gene flow of forest trees. Evol. Appl. 2016, 9, 271–290. [Google Scholar] [CrossRef] [PubMed]
- Camarretta, N.; Harrison, P.A.; Bailey, T.; Davidson, N.; Lucieer, A.; Hunt, M.; Potts, B.M. Stability of species and provenance performance when translocated into different community assemblages. Restor. Ecol. 2020, 28, 447–458. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Turner, D.; Watson, C. Error assessment and mitigation for hyper-temporal UAV-borne LiDAR surveys of forest inventory. In Proceedings of the SilviLaser 2011, Hobart, Australia, 16–20 October 2011; pp. 1–14. [Google Scholar]
- Stone, C.; Caccamo, G.; Osborn, J.; Lucieer, A.; Iqbal, I.; McCoull, C.; Harwin, S.; Turner, D.; Pishchugin, A.; Gautam, D.; et al. Optimising Remotely Acquired, Dense Point Cloud Data for Plantation Inventory; Forest and Wood Products Australia: Melbourne, VIC, Australia, 2018; Volume 61.
- R Core Team R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org (accessed on 9 January 2017).
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef] [PubMed]
- Zuur, A.F.; Ieno, E.N. A protocol for conducting and presenting results of regression-type analyses. Methods Ecol. Evol. 2016, 7, 636–645. [Google Scholar] [CrossRef]
- Gauli, A.; Vaillancourt, R.E.; Bailey, T.G.; Steane, D.A.; Potts, B.M. Evidence for local climate adaptation in early-life traits of Tasmanian populations of Eucalyptus pauciflora. Tree Genet. Genomes 2015, 11, 14. [Google Scholar] [CrossRef]
- Gilmour, A.R.; Gogel, B.J.; Cullis, B.R.; Thompson, R. ASReml User Guide Release 3.0; VSN International Ltd.: Hemel Hempstead, UK, 2009. [Google Scholar]
- Gauli, A.; Steane, D.A.; Vaillancourt, R.E.; Potts, B.M. Molecular genetic diversity and population structure in Eucalyptus pauciflora subsp. pauciflora (Myrtaceae) on the island of Tasmania. Aust. J. Bot. 2014, 62, 175–188. [Google Scholar] [CrossRef]
- Turner, C.; Wiltshire, R.J.E.; Potts, B.M.; Vaillancourt, R.E. Allozyme variation and conservation of the Tasmanian endemics, Eucalyptus risdonii, E. Tenuiramis and E. coccifera. Conserv. Genet. 2000, 1, 209–216. [Google Scholar] [CrossRef]
- Dutkowski, G.W.; Potts, B.M. Genetic variation in the susceptibility of Eucalyptus globulus to drought damage. Tree Genet. Genomes 2012, 8, 757–773. [Google Scholar] [CrossRef]
- Leinonen, T.; McCairns, R.J.S.; O’Hara, R.B.; Merilä, J. QST–FST comparisons: Evolutionary and ecological insights from genomic heterogeneity. Nat. Rev. Genet. 2013, 14, 179–190. [Google Scholar] [CrossRef]
- Xu, T.; Hutchinson, M.F. New developments and applications in the ANUCLIM spatial climatic and bioclimatic modelling package. Environ. Model. Softw. 2013, 40, 267–279. [Google Scholar] [CrossRef]
- Prober, S.M.; Potts, B.M.; Bailey, T.; Byrne, M.; Dillon, S.; Harrison, P.A.; Hoffmann, A.A.; Jordan, R.; Mclean, E.H.; Steane, D.A.; et al. Climate adaptation and ecological restoration in eucalypts. Proc. R. Soc. Victoria 2016, 128, 40–53. [Google Scholar] [CrossRef]
- Harrison, P.A. Integrating Climate Change into Conservation and Restoration Strategies: The Case of the Tasmanian Eucalypts. Ph.D. Thesis, University of Tasmania, Hobart, Australia, 2017. [Google Scholar]
- Santini, F.; Kefauver, S.C.; Resco de Dios, V.; Araus, J.L.; Voltas, J. Using unmanned aerial vehicle-based multispectral, RGB and thermal imagery for phenotyping of forest genetic trials: A case study in Pinus halepensis. Ann. Appl. Biol. 2019, 174, 262–276. [Google Scholar] [CrossRef]
- Dalponte, M.; Frizzera, L.; Gianelle, D. How to map forest structure from aircraft, one tree at a time. Ecol. Evol. 2018, 8, 5611–5618. [Google Scholar] [CrossRef] [PubMed]
- Burt, A.; Disney, M.; Calders, K. Extracting individual trees from lidar point clouds using treeseg. Methods Ecol. Evol. 2019, 10, 438–445. [Google Scholar] [CrossRef]
- Duncanson, L.; Dubayah, R. Monitoring individual tree-based change with airborne lidar. Ecol. Evol. 2018, 8, 5079–5089. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Hamann, A. Genetic adaptation of aspen ( Populus tremuloides ) populations to spring risk environments: A novel remote sensing approach. Can. J. For. Res. 2010, 40, 2082–2090. [Google Scholar] [CrossRef]
- Bombrun, M.; Dash, J.P.; Pont, D.; Watt, M.S.; Pearse, G.D.; Dungey, H.S. Forest-Scale Phenotyping: Productivity Characterisation Through Machine Learning. Front. Plant Sci. 2020, 11, 1–14. [Google Scholar] [CrossRef]
- Kattenborn, T.; Sperlich, M.; Bataua, K.; Koch, B. Automatic Single Tree Detection in Plantations using UAV-based Photogrammetric Point clouds. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-3, 139–144. [Google Scholar] [CrossRef]
- Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; et al. A benchmark of lidar-based single tree detection methods using heterogeneous forest data from the Alpine Space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef]
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.; et al. Individual tree detection and classification with UAV-based photogrammetric point clouds and hyperspectral imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef]
- Mohan, M.; Silva, C.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.; Dia, M. Individual Tree Detection from Unmanned Aerial Vehicle (UAV) Derived Canopy Height Model in an Open Canopy Mixed Conifer Forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef]
- Weinstein, B.G.; Marconi, S.; Bohlman, S.; Zare, A.; White, E. Individual tree-crown detection in rgb imagery using semi-supervised deep learning neural networks. Remote Sens. 2019, 11, 1309. [Google Scholar] [CrossRef]
- Balsi, M.; Esposito, S.; Fallavollita, P.; Nardinocchi, C. Single-tree detection in high-density LiDAR data from UAV-based survey. Eur. J. Remote Sens. 2018, 51, 679–692. [Google Scholar] [CrossRef]
- Williams, K.J.; Potts, B.M. The natural distribution of Eucalyptus species in Tasmania. Tasforests 1996, 8, 39–149. [Google Scholar]
- Schellenberger Costa, D.; Gerschlauer, F.; Kiese, R.; Fischer, M.; Kleyer, M.; Hemp, A. Plant niche breadths along environmental gradients and their relationship to plant functional traits. Divers. Distrib. 2018, 24, 1869–1882. [Google Scholar] [CrossRef]
- Barry, K.M.; Stone, C.; Mohammed, C.L. Crown-scale evaluation of spectral indices for defoliated and discoloured eucalypts. Int. J. Remote Sens. 2008, 29, 47–69. [Google Scholar] [CrossRef]
- Moore, T.L.; Ruthrof, K.X.; Craig, M.D.; Valentine, L.E.; Hardy, G.E.S.J.; Fleming, P.A. Living (and reproducing) on the edge: Reproductive phenology is impacted by rainfall and canopy decline in a Mediterranean eucalypt. Aust. J. Bot. 2016, 64, 129–141. [Google Scholar] [CrossRef]
- Low, C.B.; Shelbourne, C.J.A. Performance of Eucalyptus globulus, E. maidenii, E. nitens, and other eucalypts in Northland and Hawke’s Bay at ages 7 and 11 years. New Zeal. J. For. Sci. 1999, 29, 274–288. [Google Scholar]
- Müller, J.; Bae, S.; Röder, J.; Chao, A.; Didham, R.K. Airborne LiDAR reveals context dependence in the effects of canopy architecture on arthropod diversity. For. Ecol. Manage. 2014, 312, 129–137. [Google Scholar] [CrossRef]
- Setiawan, N.N.; Vanhellemont, M.; Baeten, L.; Gobin, R.; De Smedt, P.; Proesmans, W.; Ampoorter, E.; Verheyen, K. Does neighbourhood tree diversity affect the crown arthropod community in saplings? Biodivers. Conserv. 2016, 25, 169–185. [Google Scholar] [CrossRef]
- Müller, J.; Stadler, J.; Brandl, R. Composition versus physiognomy of vegetation as predictors of bird assemblages: The role of lidar. Remote Sens. Environ. 2010, 114, 490–495. [Google Scholar] [CrossRef]
- Munro, N.T.; Fischer, J.; Barrett, G.; Wood, J.; Leavesley, A.; Lindenmayer, D.B. Bird’s response to revegetation of different structure and floristics-Are ‘restoration plantings’ restoring bird communities? Restor. Ecol. 2011, 19, 223–235. [Google Scholar] [CrossRef]
- North, M.P.; Kane, J.T.; Kane, V.R.; Asner, G.P.; Berigan, W.; Churchill, D.J.; Conway, S.; Gutiérrez, R.J.; Jeronimo, S.; Keane, J.; et al. Cover of tall trees best predicts California spotted owl habitat. For. Ecol. Manag. 2017, 405, 166–178. [Google Scholar] [CrossRef]
- Froidevaux, J.S.P.; Zellweger, F.; Bollmann, K.; Jones, G.; Obrist, M.K. From field surveys to LiDAR: Shining a light on how bats respond to forest structure. Remote Sens. Environ. 2016, 175, 242–250. [Google Scholar] [CrossRef]
- Hanzelka, J.; Reif, J. Effects of vegetation structure on the diversity of breeding bird communities in forest stands of non-native black pine (Pinus nigra A.) and black locust (Robinia pseudoacacia L.) in the Czech Republic. For. Ecol. Manag. 2016, 379, 102–113. [Google Scholar] [CrossRef]


| Traits | Description of LiDAR-derived traits |
|---|---|
| 1–Number of points | Number of points within individual point cloud. |
| 2–Height skewness | Skewness of the distribution of heights of each point cloud. |
| 3–Height CV | Coefficient of variation of heights from each point cloud. |
| 4–Quantile coefficient of dispersion | A measure of dispersion of the height measurements comparable between trees and across studies. Calculated as Q3 − Q1/Q3 + Q1. |
| 5–Height mode (m) | Mode of height within the point cloud. |
| 6–Height median (m) | Median of height within the point cloud. |
| 7–Height P50 (m) | 50th percentile of height within point cloud. |
| 8–Height P75 (m) | 75th percentile of height within point cloud. |
| 9–Height P99 (m) | 99th percentile of height within point cloud. |
| 10–DBH (cm) | Diameter at 1.3 m, derived from a general allometric equation using total tree height and maximum Euclidean crown width [19]. |
| 11–Above-ground biomass (AGB - kg) | AGB estimated through the allometric equation developed by Jucker et al. [19], using height P99 and max crown diameter. Measured as dry weight. |
| 12–Crown insertion height (m) | Mean height from the ground to the base of the crown. |
| 13–Max crown diameter (m) | The widest cross-section of the crown in any given direction. |
| 14–Crown surface area (m2) | The surface area of a 3D convex hull calculated using the point cloud defined above the canopy insertion point. |
| 15–Crown projected area (m2) | The area of the projected polygon (shapefile) describing the crown ground cover. |
| 16–Crown volume (convex hull) | Crown volume of a 3D convex hull calculated from the point cloud defined above crown insertion. It is calculated using the ‘convhulln’ function of the R geometry package. |
| 17–Height to area ratio (m/m2) | The ratio of crown height to crown area. It represents the crown height per unit of area. |
| 18–Height to volume ratio (m/m3) | The ratio of crown height to crown volume. It represents the crown height per unit of volume |
| 19–Height of widest cross-section (m) | Height of the crown at its widest cross-section. |
| 20–Mean height to height of widest cross-section ratio | Ratio between mean tree height and the height of its widest cross-section. |
| 21–Points to area ratio (points/m2) | The ratio of the number of points to crown area, representing a measure of crown density. |
| 22–Points to volume ratio (points/m3) | The ratio of the number of points to crown volume, representing a measure of crown density. |
| 23–Crown skewness | Skewness of the height distribution within each tree (median − Q1)/(Q3 − median). |
| 24–Area (3D:2D) | The ratio between crown volume calculated from the point cloud (i.e., convex hull) and the crown area obtained from the shapefile. |
| 25–Rumple index | Calculated as the ratio between crown surface area and ground-projected surface area, this index reflects crown structural complexity. Calculated using the “rumple_index” function from the lidR package. |
| Trait | Least-Square Mean | Degrees of Freedom | F | P | ||
|---|---|---|---|---|---|---|
| E. pauciflora | E. tenuiramis | Num | Den | |||
| 1 | 5035 | 8434 | 1 | 4.9 | 17.3 | 0.009 |
| 2 | −0.76 | −0.61 | 1 | 5.8 | 8.0 | 0.032 |
| 3 | 0.33 | 0.35 | 1 | 5.0 | 10.0 | 0.025 |
| 4 | 0.21 | 0.24 | 1 | 5.1 | 12.7 | 0.016 |
| 5 | 2.18 | 3.29 | 1 | 5.0 | 22.3 | 0.005 |
| 6 | 2.29 | 3.36 | 1 | 5.0 | 49.5 | 0.001 |
| 7 | 0.51 | 0.95 | 1 | 5.0 | 25.3 | 0.004 |
| 8 | 2.10 | 3.33 | 1 | 5.0 | 46.3 | 0.001 |
| 9 | 3.14 | 4.78 | 1 | 4.9 | 63.5 | 0.001 |
| 10 | 3.58 | 5.82 | 1 | 4.8 | 90.3 | 0.000 |
| 11 | 1.91 | 6.40 | 1 | 4.9 | 71.0 | 0.000 |
| 12 | 1.05 | 1.31 | 1 | 5.0 | 19.8 | 0.007 |
| 13 | 2.90 | 3.50 | 1 | 4.8 | 54.6 | 0.001 |
| 14 | 16.50 | 30.70 | 1 | 4.9 | 63.9 | 0.001 |
| 15 | 5.15 | 7.39 | 1 | 4.9 | 43.8 | 0.001 |
| 16 | 5.75 | 14.17 | 1 | 4.9 | 57.5 | 0.001 |
| 17 | 0.22 | 0.18 | 1 | 4.7 | 25.0 | 0.005 |
| 18 | 0.71 | 0.43 | 1 | 4.7 | 39.3 | 0.002 |
| 19 | 1.63 | 2.15 | 1 | 4.7 | 35.2 | 0.002 |
| 20 | 2.16 | 2.46 | 1 | 5.3 | 8.6 | 0.031 |
| 21 | 264 | 235 | 1 | 4.6 | 7.3 | 0.047 |
| 22 | 815 | 540 | 1 | 4.6 | 69.2 | 0.001 |
| 23 | 1.33 | 1.30 | 1 | 4.9 | 0.2 | 0.704 |
| 24 | 3.30 | 4.25 | 1 | 4.9 | 36.6 | 0.002 |
| 25 | 3.89 | 5.01 | 1 | 4.8 | 76.1 | 0.000 |
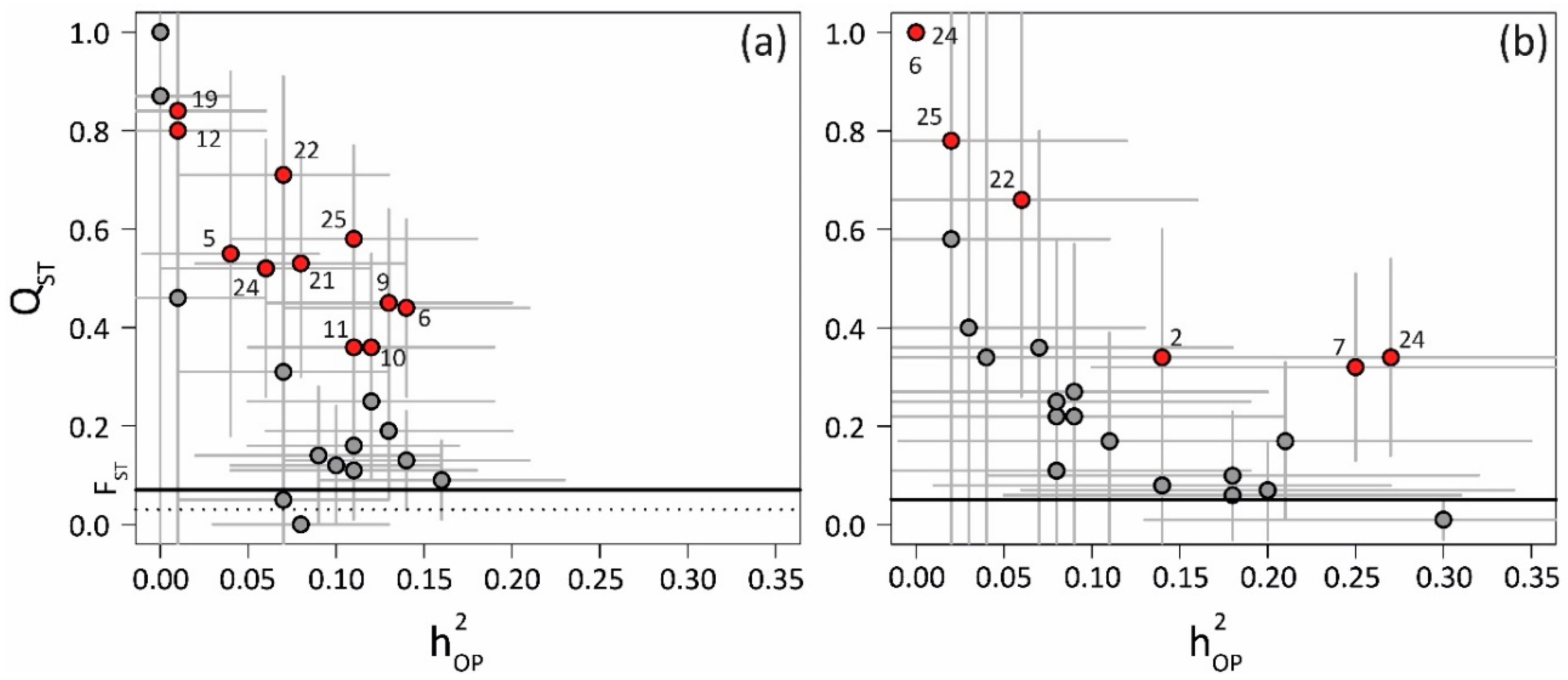
| Trait | Eucalyptus Pauciflora | Eucalyptus Tenuiramis | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Provenance | Genetic Parameters | QST > FST | Environmental Association | Provenance | Genetic Parameters | QST > FST | Environmental Association | |||
| QST | Qst | |||||||||
| 1 | 0.4 ns | 0.00 ± 0.00 | 0.08 ± 0.05 | 6.9 ** | 0.08 ± 0.12 | 0.14 ± 0.13 | ||||
| 2 | 31.0 *** | 0.31 ± 0.23 | 0.07 ± 0.06 | 7.7 ** | 29.7 *** | 0.34 ± 0.26 | 0.14 ± 0.12 | 7.2 ** | (+) TMNCW 50% * | |
| 3 | 6.0 ** | 0.87 ± 3.16 | 0.00 ± 0.04 | 12.0 *** | 0.36 ± 0.44 | 0.07 ± 0.11 | 5 * | |||
| 4 | 12.8 *** | 0.11 ± 0.10 | 0.11 ± 0.07 | 0.5 ns | 15.7 *** | 0.17 ± 0.16 | 0.21 ± 0.14 | 3.1 * | ||
| 5 | 48.2 *** | 0.55 ± 0.37 | 0.04 ± 0.05 | 15.5 *** | (+) TMNCW 50% * | 1.9 ns | 0.34 ± 0.72 | 0.04 ± 0.11 | ||
| 6 | 136.4 *** | 0.44 ± 0.18 | 0.14 ± 0.07 | 17.0 *** | (+) TMNCW 62% * | 22.6 *** | 1.00 ± 0.00 | 0.00 ± 0.00 | 14.3 *** | (−) TMNCW 64% * |
| 7 | 23.3 *** | 0.13 ± 0.10 | 0.14 ± 0.07 | 1.9 ns | 82.2 *** | 0.32 ± 0.19 | 0.25 ± 0.15 | 7.6 ** | (+) AIANN 44% ns | |
| 8 | 17.0 *** | 0.09 ± 0.08 | 0.16 ± 0.07 | 0.3 ns | 1.7 ns | 0.11 ± 0.20 | 0.08 ± 0.11 | |||
| 9 | 134.3 *** | 0.45 ± 0.19 | 0.13 ± 0.07 | 17.7 *** | (−) AIANN 63% * | 6.9 ** | 0.58 ± 1.17 | 0.02 ± 0.09 | ||
| 10 | 81.3 *** | 0.36 ± 0.19 | 0.12 ± 0.07 | 12.9 *** | (−) AIANN 63% * | 10.1 ** | 0.27 ± 0.30 | 0.09 ± 0.11 | 4.4 * | |
| 11 | 70.4 *** | 0.36 ± 0.19 | 0.11 ± 0.06 | 12.3 *** | (−) AIANN 54% * | 7.1 ** | 0.17 ± 0.22 | 0.11 ± 0.12 | ||
| 12 | 66.3 *** | 0.80 ± 0.53 | 0.01 ± 0.05 | 20.6 *** | (+) TMNCW 69% ** | 5.3 * | 1.00 ± 0.00 | 0.00 ± 0.00 | ||
| 13 | 20.5 *** | 0.16 ± 0.13 | 0.11 ± 0.06 | 2.3 ns | 5.8 ** | 0.07 ± 0.10 | 0.20 ± 0.14 | |||
| 14 | 45.3 *** | 0.25 ± 0.16 | 0.12 ± 0.07 | 7.4 ** | 6.4 ** | 0.25 ± 0.33 | 0.08 ± 0.11 | |||
| 15 | 12.3 *** | 0.12 ± 0.12 | 0.10 ± 0.06 | 0.9 ns | 4.5 * | 0.06 ± 0.09 | 0.18 ± 0.13 | |||
| 16 | 33.5 *** | 0.19 ± 0.14 | 0.13 ± 0.07 | 4.5 * | 0.5 ns | 1.00 ± 0.00 | 0.00 ± 0.00 | |||
| 17 | 2.6 ns | 0.05 ± 0.10 | 0.07 ± 0.06 | 4.8 * | 0.22 ± 0.29 | 0.09 ± 0.12 | ||||
| 18 | 11.1 *** | 0.14 ± 0.14 | 0.09 ± 0.07 | 1.2 ns | 5.4 * | 0.40 ± 0.78 | 0.03 ± 0.10 | |||
| 19 | 73.8 *** | 0.84 ± 0.52 | 0.01 ± 0.05 | 22.7 *** | (+) TMNCW 71% ** | 7.3 ** | 0.10 ± 0.13 | 0.18 ± 0.14 | ||
| 20 | 4.5 * | 1.00 ± 0.00 | 0.00 ± 0.00 | 3.5 * | 0.01 ± 0.04 | 0.30 ± 0.17 | ||||
| 21 | 109.7 *** | 0.53 ± 0.23 | 0.08 ± 0.06 | 19.9 *** | (−) TMNCW 77% ** | 83.0 *** | 0.34 ± 0.20 | 0.27 ± 0.16 | 7.2 ** | (−) TMXWW 67% * |
| 22 | 203.0 *** | 0.71 ± 0.20 | 0.07 ± 0.06 | 29.4 *** | (−) TMNCW 76% ** | 65.9 *** | 0.66 ± 0.40 | 0.06 ± 0.10 | 14.6 *** | (+) TMNCW 56% ns |
| 23 | 4.4 * | 0.46 ± 1.13 | 0.01 ± 0.05 | 6.2 ** | 0.22 ± 0.31 | 0.08 ± 0.11 | ||||
| 24 | 84.5 *** | 0.52 ± 0.26 | 0.06 ± 0.06 | 17.4 *** | (−) AIANN 62% * | 10.3 ** | 1.00 ± 0.00 | 0.00 ± 0.00 | 9.6 ** | (−) TMNCW 81% ** |
| 25 | 182.9 *** | 0.58 ± 0.19 | 0.11 ± 0.07 | 23.7 *** | (−) AIANN 64% ** | 32.7 *** | 0.78 ± 0.91 | 0.02 ± 0.10 | 10.6 ** | (−) TMNCW 30% ns |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camarretta, N.; A. Harrison, P.; Lucieer, A.; M. Potts, B.; Davidson, N.; Hunt, M. From Drones to Phenotype: Using UAV-LiDAR to Detect Species and Provenance Variation in Tree Productivity and Structure. Remote Sens. 2020, 12, 3184. https://doi.org/10.3390/rs12193184
Camarretta N, A. Harrison P, Lucieer A, M. Potts B, Davidson N, Hunt M. From Drones to Phenotype: Using UAV-LiDAR to Detect Species and Provenance Variation in Tree Productivity and Structure. Remote Sensing. 2020; 12(19):3184. https://doi.org/10.3390/rs12193184
Chicago/Turabian StyleCamarretta, Nicolò, Peter A. Harrison, Arko Lucieer, Brad M. Potts, Neil Davidson, and Mark Hunt. 2020. "From Drones to Phenotype: Using UAV-LiDAR to Detect Species and Provenance Variation in Tree Productivity and Structure" Remote Sensing 12, no. 19: 3184. https://doi.org/10.3390/rs12193184
APA StyleCamarretta, N., A. Harrison, P., Lucieer, A., M. Potts, B., Davidson, N., & Hunt, M. (2020). From Drones to Phenotype: Using UAV-LiDAR to Detect Species and Provenance Variation in Tree Productivity and Structure. Remote Sensing, 12(19), 3184. https://doi.org/10.3390/rs12193184







