A Vector Operation to Extract Second-Order Terrain Derivatives from Digital Elevation Models
Abstract
1. Introduction
2. Methods
2.1. Calculation Principle of Second-Order Terrain Derivatives
2.2. Vectorization Expression of First-Order Terrain Derivatives
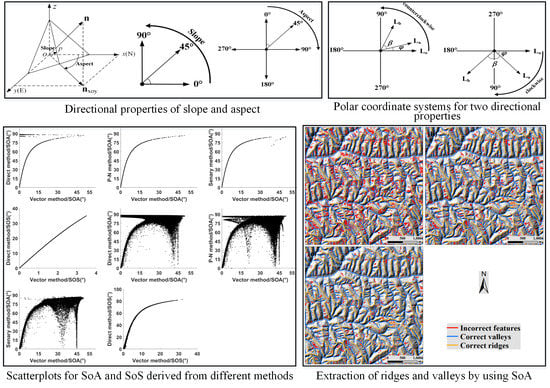
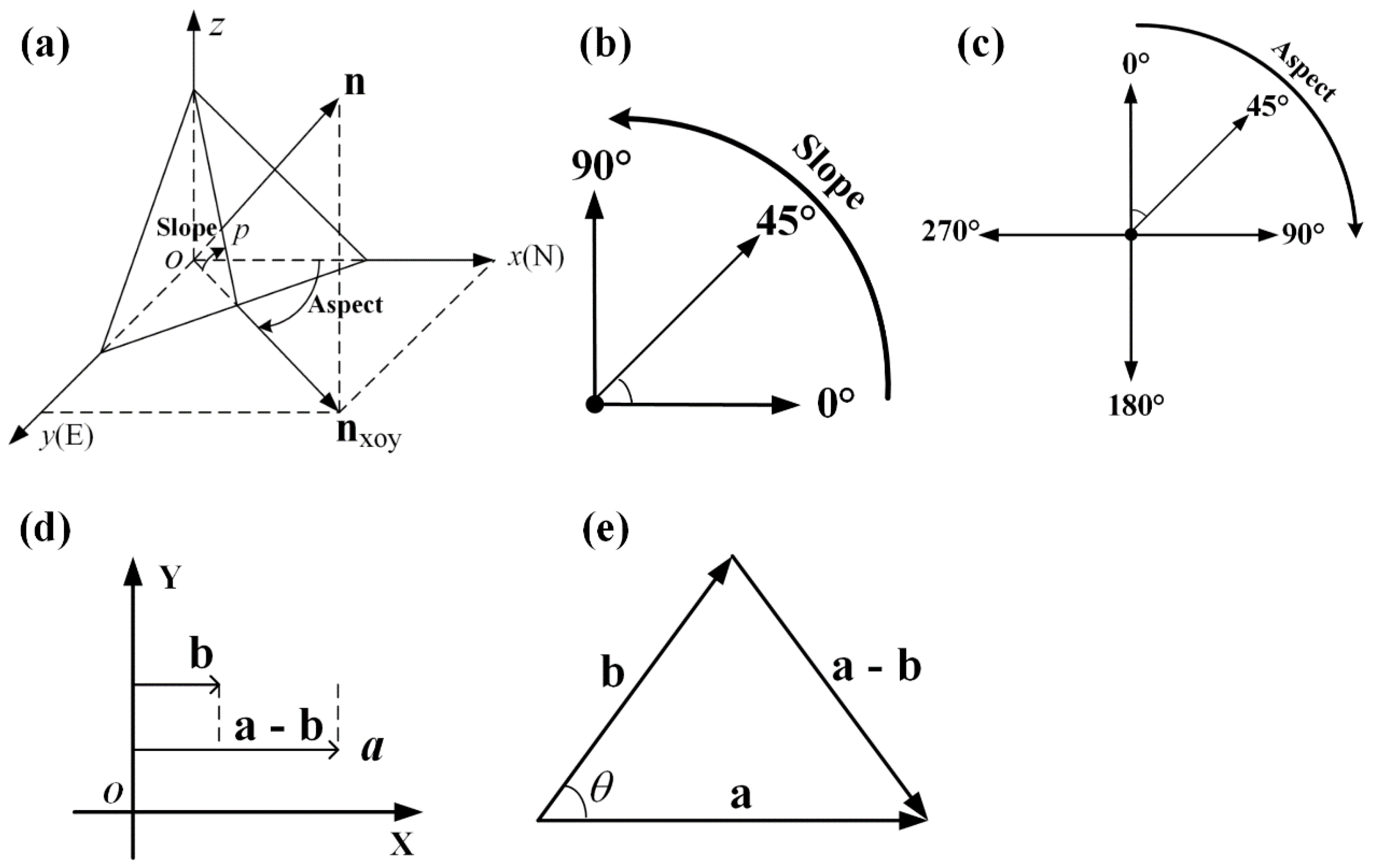
- Rotation-type judgment. Two rotation types, namely, counterclockwise (slope) and clockwise (aspect), can be observed in the directional property of first-order terrain derivatives (Figure 1). In the counterclockwise or clockwise systems, initial direction, end direction, and rotation angle consist of the aforementioned systems. These systems follow the characteristics of a polar coordinate system (Figure 2). Given the differences between counterclockwise and clockwise systems, a standard polar coordinate system corresponds to a counterclockwise directional property of first-order terrain derivatives, i.e., slope as an example in Figure 2a. By contrast, a reverse polar coordinate system corresponds to a clockwise directional property of first-order terrain derivatives, i.e., aspect as an example in Figure 2b. The initial direction of the polar coordinate system is Lo, which is also the initial direction of the reverse polar coordinate system.
- Standardization of initial direction. The initial direction of a polar coordinate system faces east, and the initial direction of several first-order terrain derivatives faces other directions, e.g., the initial direction of aspect faces north (Figure 1c). Thus, the initial direction must be standardized before calculating the vector operation of second-order terrain derivatives. For a first-order terrain derivative, its initial direction can be the same as that of the polar coordinate system, i.e., the initial direction of slope also faces east (Figure 2a). However, the angle can be 270° of the initial direction, which faces north in the polar coordinate system, i.e., aspect in Figure 2b. Thus, the initial direction of first-order terrain derivatives is defined as La, and the initial direction of the polar coordinate system is defined as Lo. The angle difference between the two initial directions should be a variable, which is defined as φ. Thus, for any direction of the first-order terrain derivative matrix, i.e., β, which is the angle between the initial direction (La) and the actual direction (Lb), the new direction (θ) of the first-order terrain derivatives in the polar coordinate system can be calculated using the following equation:where φ is the constant angle from Lo to La, β is the actual angle of the terrain derivative, and θ is the angle of the new direction in the polar coordinate system.
- Vector representation. These angles can be expressed as vectors in their respective polar coordinate systems based on the transformed directional property in the polar coordinate system.where r is the length, which should be the cell size of raster data; and θ is the transformed directions in the polar coordinate system. However, if the polar coordinate system is a reverse system, then this system should be further transformed into a standard system using following equation:
2.3. Vectorization Expression of First-Order Terrain Derivatives
3. Case Study Areas and Data
4. Results
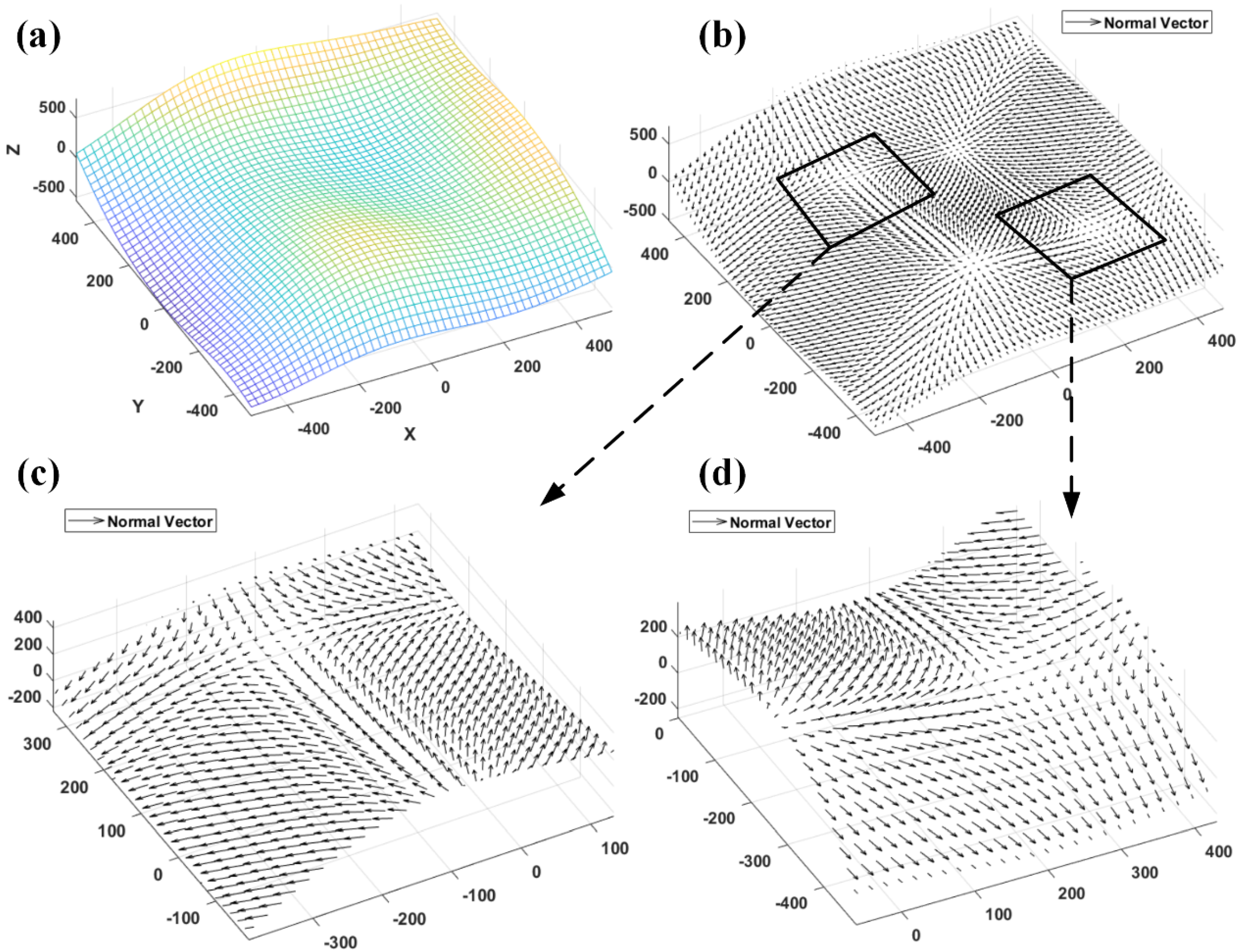
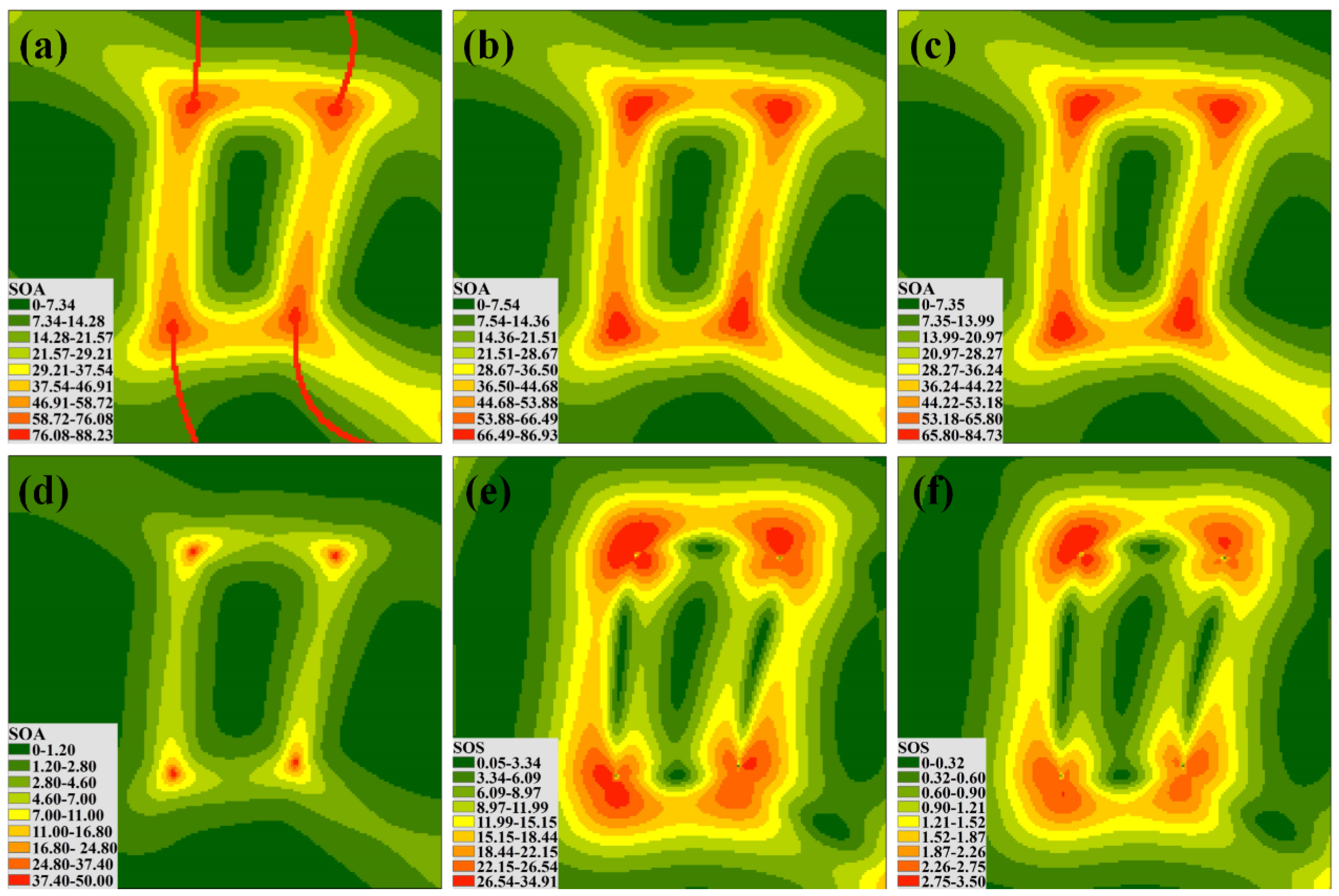
4.1. SoA and SoS of the Gaussian Surface
4.2. SoA and SoS of Different Landform Areas
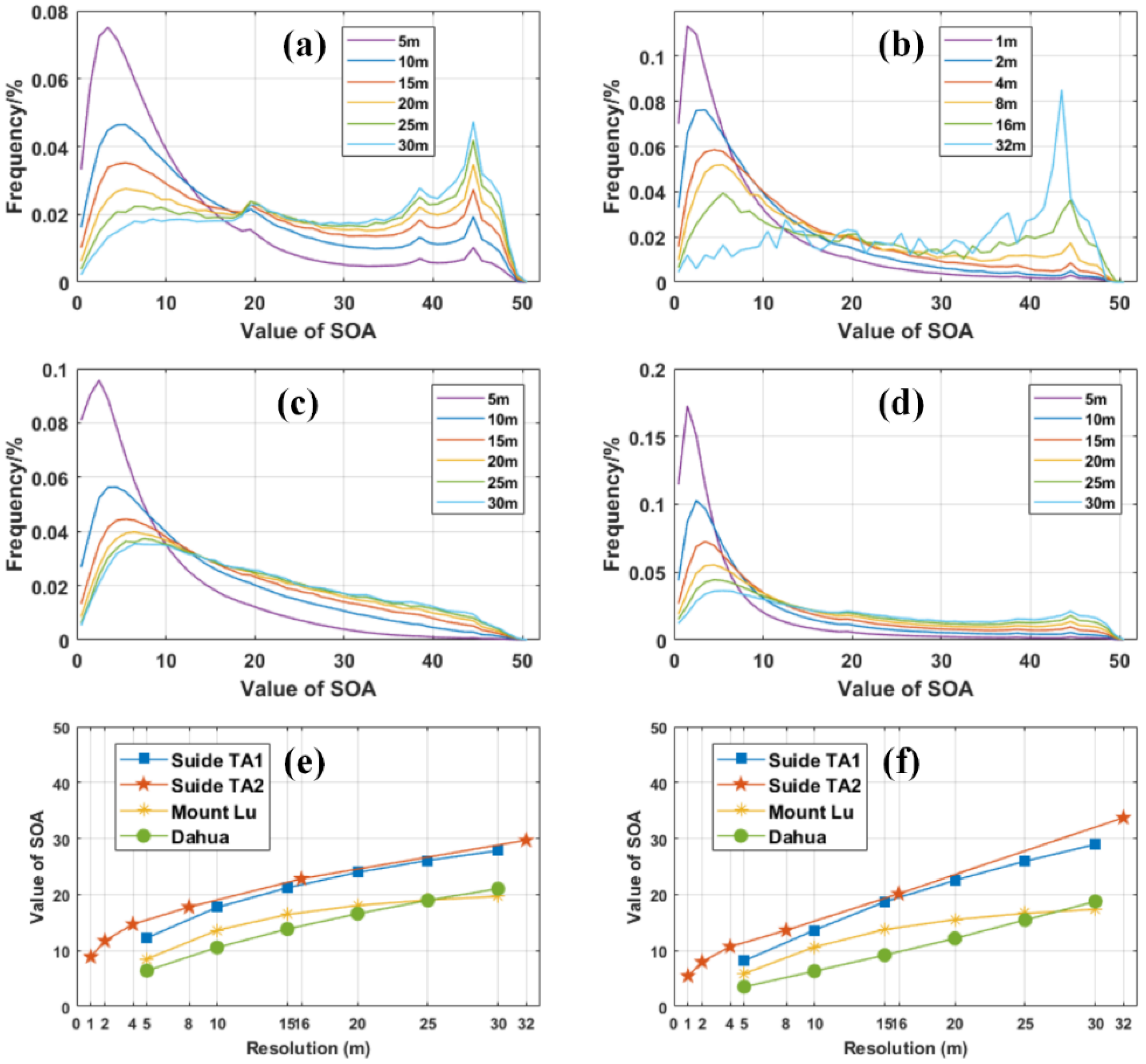
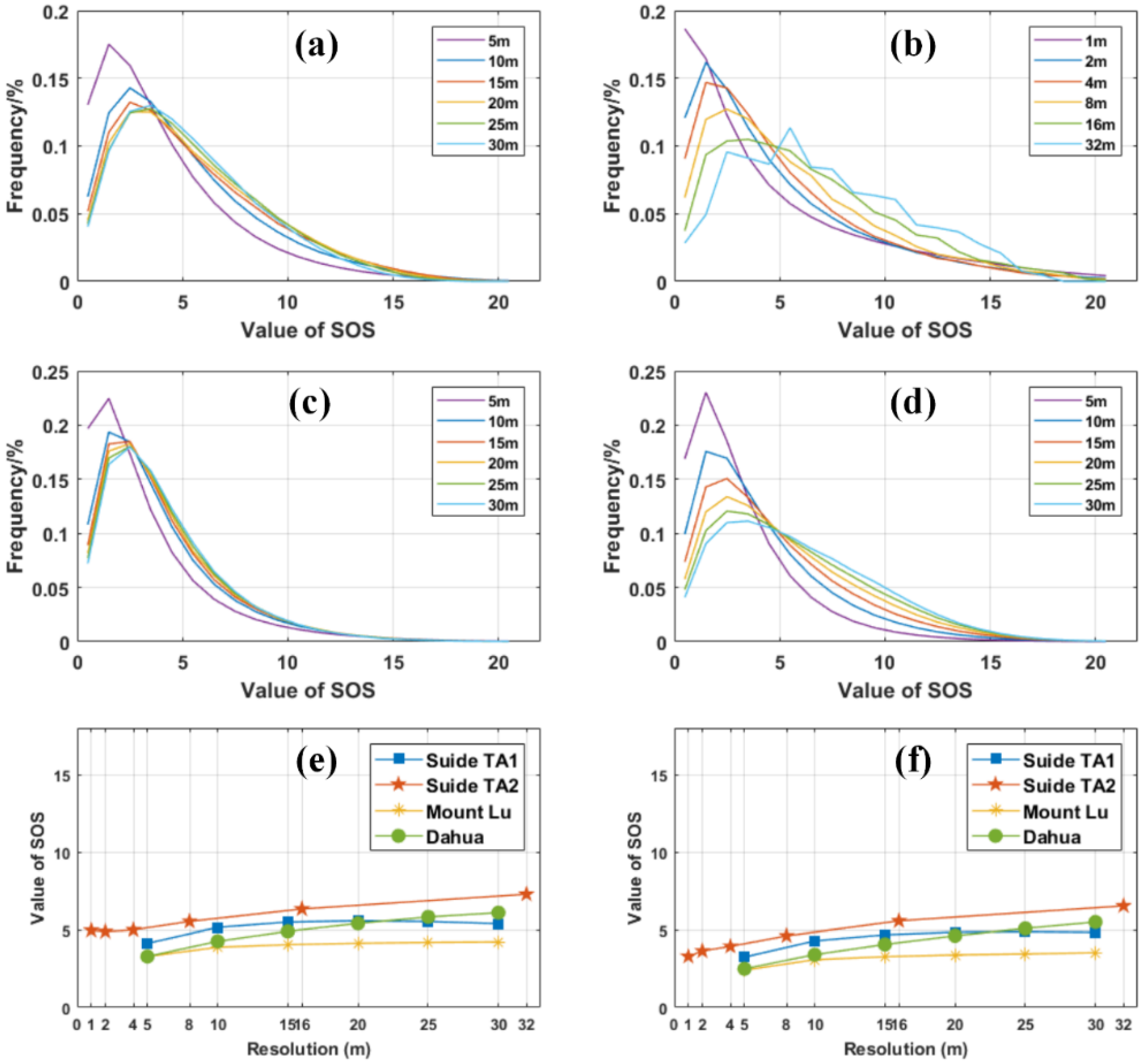
4.3. Assessment of DEM Resolution Effects
5. Discussion
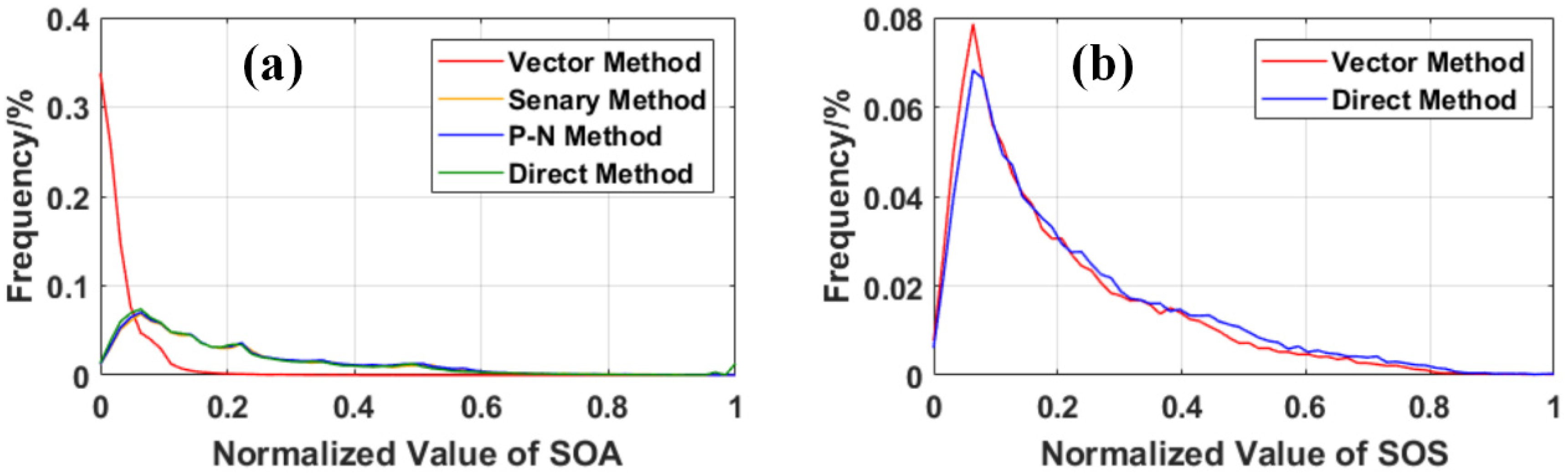
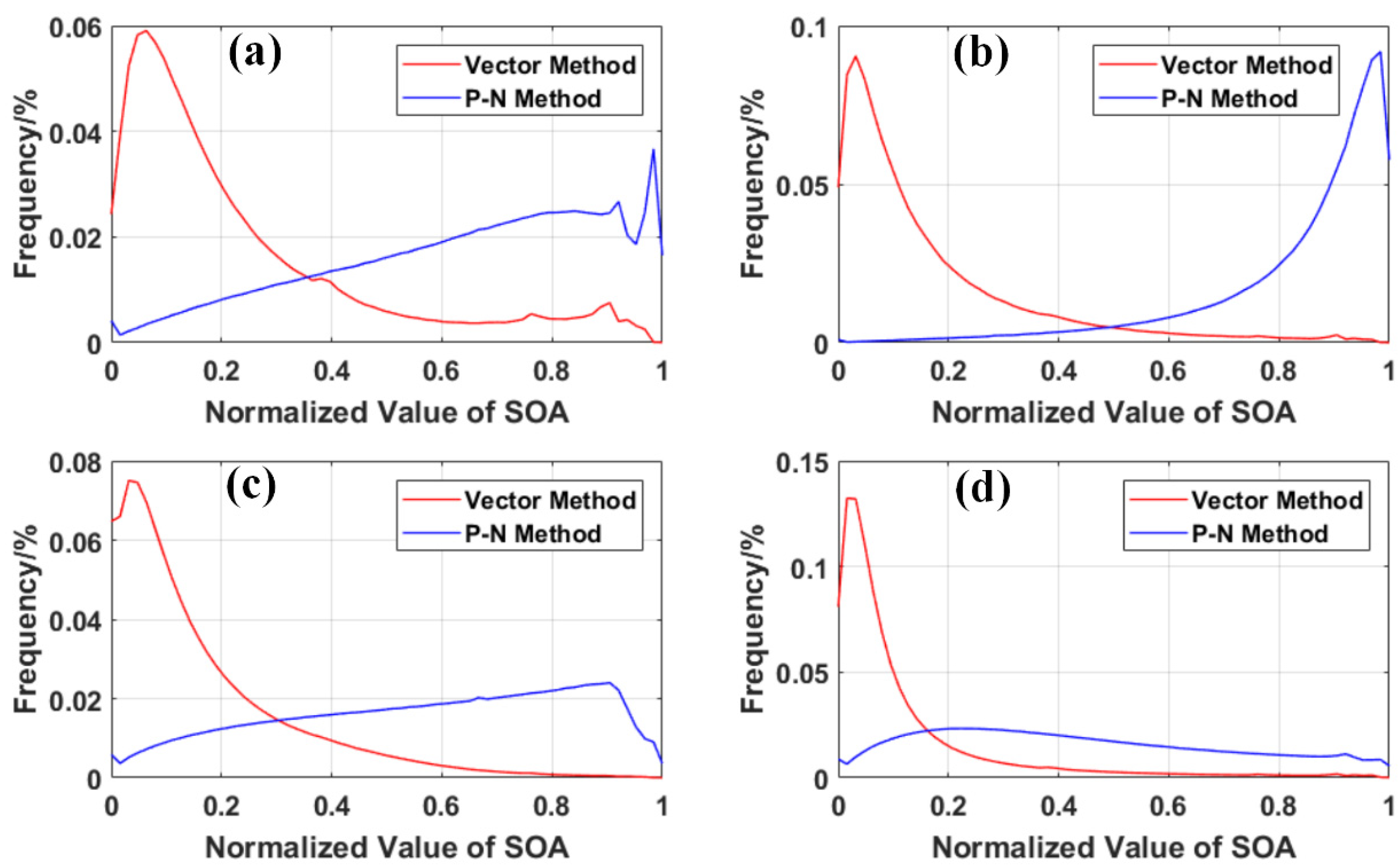
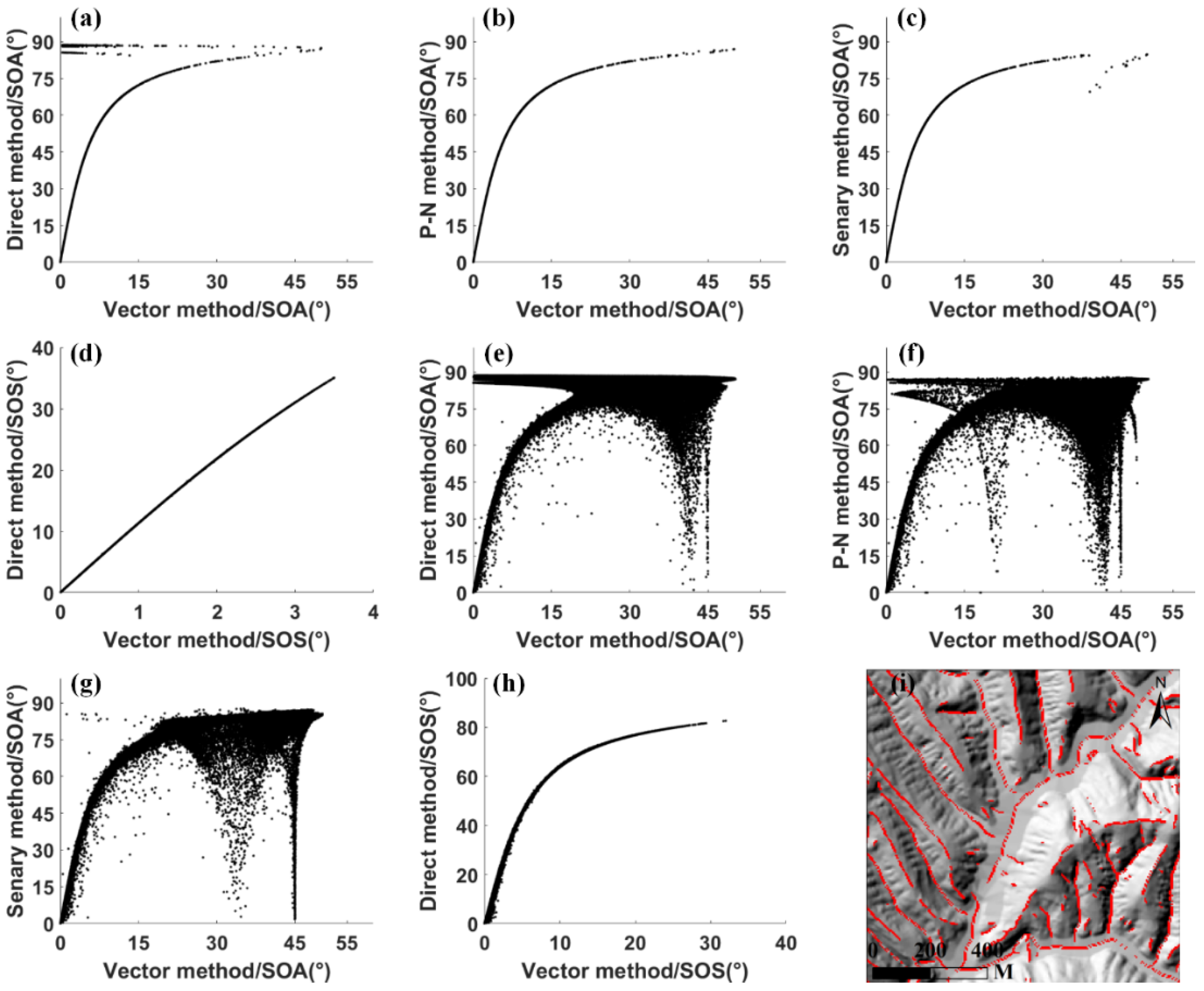
5.1. Correlation among Different Methods
5.2. Comparison of the Vector and Scalar Methods in Terrain Feature Extraction
5.3. Implications of the Vector Method for Other Terrain Derivative Calculation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Florinsky, I.V. Digital Terrain Analysis in Soil Science and Geology; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Wilson, J.P. Environmental Applications of Digital Terrain Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Xiong, L.-Y.; Tang, G.-A.; Zhu, A.-X.; Qian, Y.-Q. A peak-cluster assessment method for the identification of upland planation surfaces. Int. J. Geogr. Inf. Sci. 2017, 31, 387–404. [Google Scholar] [CrossRef]
- Florinsky, I.V. An illustrated introduction to general geomorphometry. Prog. Phys. Geogr. 2017, 41, 723–752. [Google Scholar] [CrossRef]
- Evans, I.S. Geomorphometry and landform mapping: What is a landform? Geomorphology 2012, 137, 94–106. [Google Scholar] [CrossRef]
- Gumindoga, W.; Rwasoka, D.; Murwira, A. Simulation of streamflow using TOPMODEL in the Upper Save River catchment of Zimbabwe. Phys. Chem. Earth Parts A/B/C 2011, 36, 806–813. [Google Scholar] [CrossRef]
- Callow, J.N.; Van Niel, K.P.; Boggs, G.S. How does modifying a DEM to reflect known hydrology affect subsequent terrain analysis? J. Hydrol. 2007, 332, 30–39. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Tang, G.A.; Strobl, J.; Zhu, A.X. Paleotopographic controls on loess deposition in the Loess Plateau of China. Earth Surf. Proc. Land. 2016, 41, 1155–1168. [Google Scholar] [CrossRef]
- Minár, J.; Jenčo, M.; Evans, I.S.; Minár, J., Jr.; Kadlec, M.; Krcho, J.; Pacina, J.; Burian, L.; Benová, A. Third-order geomorphometric variables (derivatives): Definition, computation and utilization of changes of curvatures. Int. J. Geogr. Inf. Sci. 2013, 27, 1381–1402. [Google Scholar] [CrossRef]
- Song, X.; Tang, G.; Li, F.; Jiang, L.; Zhou, Y.; Qian, K. Extraction of loess shoulder-line based on the parallel GVF snake model in the loess hilly area of China. Comput. Geosci. 2013, 52, 11–20. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, H.; Chen, M.; Tu, J.; Yan, L. Automatic detection of lunar craters based on DEM data with the terrain analysis method. Planet. Space Sci. 2018, 160, 1–11. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.; Tovar-Pescador, J.; Pozo-Vázquez, D.; Alsamamra, H. A comparative analysis of DEM-based models to estimate the solar radiation in mountainous terrain. Int. J. Geogr. Inf. Sci. 2009, 23, 1049–1076. [Google Scholar] [CrossRef]
- Shary, P.A.; Sharaya, L.S.; Mitusov, A.V. Fundamental quantitative methods of land surface analysis. Geoderma 2002, 107, 1–32. [Google Scholar] [CrossRef]
- Schmidt, J.; Evans, I.S.; Brinkmann, J. Comparison of polynomial models for land surface curvature calculation. Int. J. Geogr. Inf. Sci. 2003, 17, 797–814. [Google Scholar] [CrossRef]
- Florinsky, I.V. Accuracy of local topographic variables derived from digital elevation models. Int. J. Geogr. Inf. Sci. 1998, 12, 47–62. [Google Scholar] [CrossRef]
- Wilson, J.P. Geomorphometry: Today and Tomorrow. PeerJ Prepr. 2018, 6, e27197v27191. [Google Scholar] [CrossRef][Green Version]
- Hodgson, M.E.; Gaile, G.L. Characteric mean and dispersion in surface orientations for a zone. Int. J. Geogr. Inf. Syst. 1996, 10, 817–830. [Google Scholar] [CrossRef]
- Li, X.; Hodgson, M.E. Vector field data model and operations. GISci. Remote Sens. 2004, 41, 1–24. [Google Scholar] [CrossRef]
- Tang, G. A Research on the Accuracy of Digital Elevation Models; Science Press: Beijing, China, 2000. [Google Scholar]
- Cheng, G.; Liu, L.; Jing, N.; Chen, L.; Xiong, W. General-purpose optimization methods for parallelization of digital terrain analysis based on cellular automata. Comput. Geosci. 2012, 45, 57–67. [Google Scholar] [CrossRef]
- Cao, M.; Tang, G.; Zhang, F.; Yang, J. A cellular automata model for simulating the evolution of positive–negative terrains in a small loess watershed. Int. J. Geogr. Inf. Sci. 2013, 27, 1349–1363. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, Y.; Wang, X.; Liu, X.; Zhang, X.; Zhang, S. Comparing interpolation methods to predict soil total phosphorus in the Mollisol area of Northeast China. Catena 2019, 174, 59–72. [Google Scholar] [CrossRef]
- Hu, Q.; Zhou, Y.; Wang, S.; Wang, F. Machine learning and fractal theory models for landslide susceptibility mapping: Case study from the Jinsha River Basin. Geomorphology 2020, 351, 106975. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, G.; Jiang, L. Characteristics and correcting methods of errors in extraction of SOA based on DEMs. Geogr. Geo Inf. Sci. 2013, 29, 49–53. (In Chinese) [Google Scholar]
- She, J.; Li, X. Map algebra based analysis for directed flow networks. Trans. GIS 2016, 20, 356–367. [Google Scholar] [CrossRef]
- Ritter, P. A vector-based slope and aspect generation algorithm. Photogr. Eng. Remote Sens. 1987, 53, 1109–1111. [Google Scholar]
- Horn, B.K. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef]
- Skidmore, A.K. A comparison of techniques for calculating gradient and aspect from a gridded digital elevation model. Int. J. Geogr. Inf. Syst. 1989, 3, 323–334. [Google Scholar] [CrossRef]
- Bolstad, P.V.; Stowe, T. An evaluation of DEM accuracy: Elevation, slope, and aspect. Photogr. Eng. Remote Sens. 1994, 60, 1327–1332. [Google Scholar]
- Zhou, Q.; Liu, X. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Xiong, L.-Y.; Tang, G.-A.; Zhu, A.-X.; Li, J.-L.; Duan, J.-Z.; Qian, Y.-Q. Landform-derived placement of electrical resistivity prospecting for paleotopography reconstruction in the loess landforms of China. J. Appl. Geophys. 2016, 131, 1–13. [Google Scholar] [CrossRef]
- Yang, X.; Tang, G.; Meng, X.; Xiong, L. Classification of Karst Fenglin and Fengcong Landform Units Based on Spatial Relations of Terrain Feature Points from DEMs. Remote Sens. 2019, 11, 1950. [Google Scholar] [CrossRef]
- Hu, G.; Xiong, L.; Tang, G. Vector geometry based method for the extraction of slope of aspect by using DEMs. Acta Geod. Cartogr. Sin. 2019, 48, 1404–1414. [Google Scholar] [CrossRef]
- Goodchild, M.F. Scale in GIS: An overview. Geomorphology 2011, 130, 5–9. [Google Scholar] [CrossRef]
- Dai, W.; Yang, X.; Na, J.; Li, J.; Brus, D.; Xiong, L.; Tang, G.; Huang, X. Effects of DEM resolution on the accuracy of gully maps in loess hilly areas. Catena 2019, 177, 114–125. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Omidavr, E.; Pham, B.T.; Talebpour Asl, D.; Khaledian, H.; Pradhan, B.; Panahi, M.; et al. A Novel Ensemble Artificial Intelligence Approach for Gully Erosion Mapping in a Semi-Arid Watershed (Iran). Sensors 2019, 19, 2444. [Google Scholar] [CrossRef]
- Li, S.; Xiong, L.; Tang, G.; Strobl, J. Deep learning-based approach for landform classification from integrated data sources of digital elevation model and imagery. Geomorphology 2020, 354, 107045. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Jiang, R.Q.; Lu, Q.H.; Yang, B.S.; Li, F.Y.; Tang, G.A. Improved Priority-Flood method for depression filling by redundant calculation optimization in local micro-relief areas. Trans. GIS 2019, 23, 259–274. [Google Scholar] [CrossRef]
- Byun, J.; Seong, Y.B. An algorithm to extract more accurate stream longitudinal profiles from unfilled DEMs. Geomorphology 2015, 242, 38–48. [Google Scholar] [CrossRef]
- Dorsaz, J.M.; Gironás, J.; Escauriaza, C.; Rinaldo, A. The geomorphometry of endorheic drainage basins: Implications for interpreting and modelling their evolution. Earth Surf. Proc. Landf. 2013, 38, 1881–1896. [Google Scholar] [CrossRef]
- Dai, W.; Na, J.; Huang, N.; Hu, G.; Yang, X.; Tang, G.; Xiong, L.; Li, F. Integrated edge detection and terrain analysis for agricultural terrace delineation from remote sensing images. Int. J. Geogr. Inf. Sci. 2020, 34, 484–503. [Google Scholar] [CrossRef]
- Dai, W.; Hu, G.; Huang, N.; Zhang, P.; Yang, X.; Tang, G. A Contour-Directional Detection for Deriving Terrace Ridge From Open Source Images and Digital Elevation Models. IEEE Access 2019, 7, 129215–129224. [Google Scholar] [CrossRef]
- Dai, W.; Hu, G.; Yang, X.; Yang, X.W.; Cheng, Y.; Xiong, L.; Strobl, J.; Tang, G. Identifying ephemeral gullies from high-resolution images and DEMs using flow-directional detection. J. Mt. Sci. 2020. accepted. [Google Scholar] [CrossRef]
- Hickey, R. Slope angle and slope length solutions for GIS. Cartography 2000, 29, 1–8. [Google Scholar] [CrossRef]

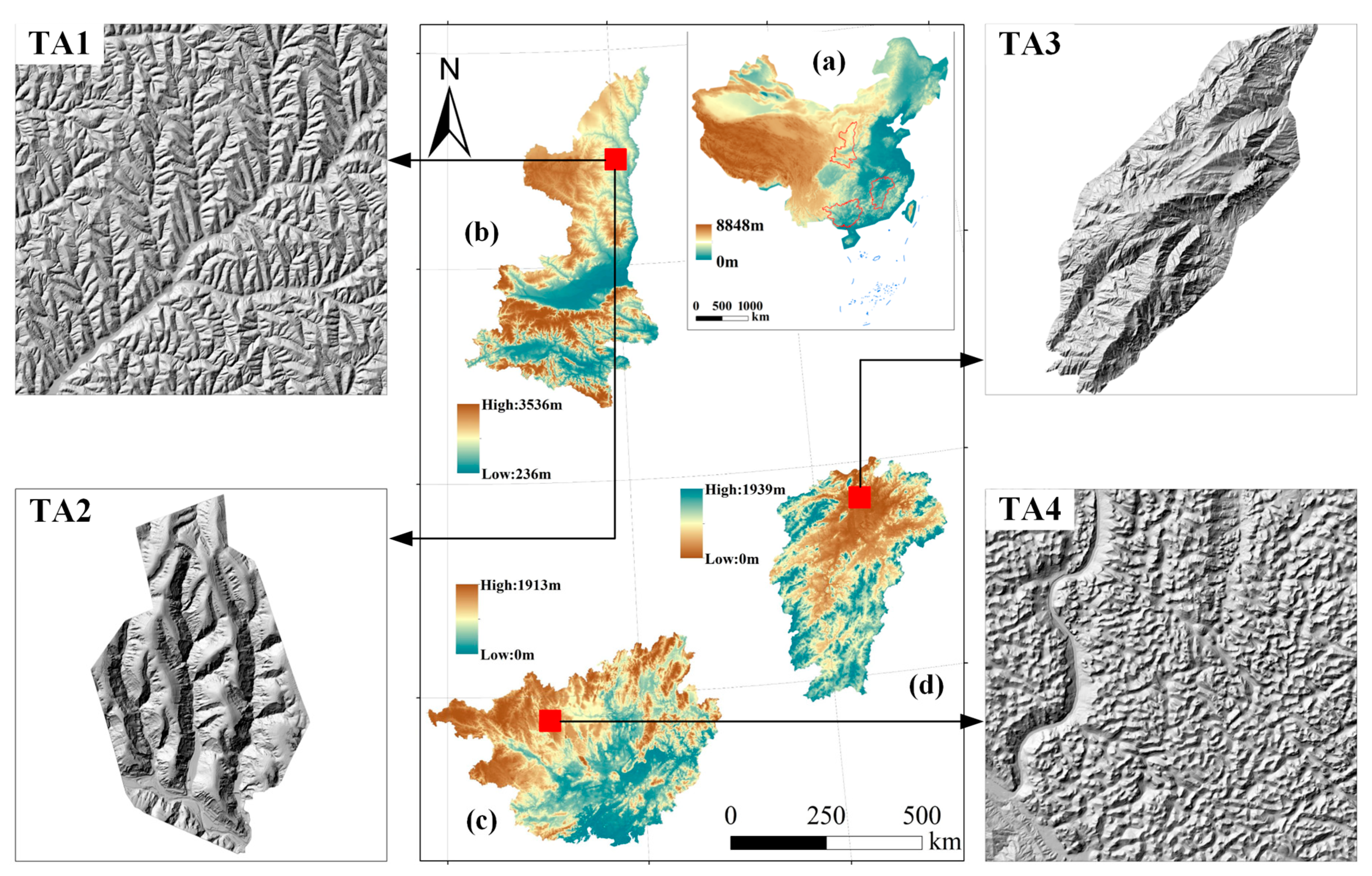





| Sample Areas | Elevation (m) | Average Height (m) | SD Height (m) | Average Slope (°) | Min–Max Slope (°) | SD Slope (°) | Area (km2) | Landform Type |
|---|---|---|---|---|---|---|---|---|
| TA1 | 814–1188 | 996.96 | 7.78 | 29.28 | 0–82.88 | 3.41 | 97.15 | Loess landform |
| TA2 | 784–987 | 883.06 | 7.03 | 32.97 | 0–83.04 | 4.21 | 1.92 | Loess landform |
| TA3 | 89–1470 | 710.33 | 17.92 | 31.58 | 0–86.94 | 3.52 | 180.43 | Structural landform |
| TA4 | 166–1163 | 821.45 | 12.87 | 29.70 | 0–89.41 | 3.69 | 361.19 | Karst landform |
| SoA Threshold | Lc | Le | Lr | Precision | Recall | F-Measure |
|---|---|---|---|---|---|---|
| 15 | 182,000.77 | 326,021.61 | 182,971.37 | 55.82% | 99.47% | 71.51% |
| 20 | 178,168.25 | 247,039.42 | 182,971.37 | 72.12% | 97.37% | 82.87% |
| 25 | 173,473.66 | 205,916.77 | 182,971.37 | 84.24% | 94.81% | 89.22% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Dai, W.; Li, S.; Xiong, L.; Tang, G. A Vector Operation to Extract Second-Order Terrain Derivatives from Digital Elevation Models. Remote Sens. 2020, 12, 3134. https://doi.org/10.3390/rs12193134
Hu G, Dai W, Li S, Xiong L, Tang G. A Vector Operation to Extract Second-Order Terrain Derivatives from Digital Elevation Models. Remote Sensing. 2020; 12(19):3134. https://doi.org/10.3390/rs12193134
Chicago/Turabian StyleHu, Guanghui, Wen Dai, Sijin Li, Liyang Xiong, and Guoan Tang. 2020. "A Vector Operation to Extract Second-Order Terrain Derivatives from Digital Elevation Models" Remote Sensing 12, no. 19: 3134. https://doi.org/10.3390/rs12193134
APA StyleHu, G., Dai, W., Li, S., Xiong, L., & Tang, G. (2020). A Vector Operation to Extract Second-Order Terrain Derivatives from Digital Elevation Models. Remote Sensing, 12(19), 3134. https://doi.org/10.3390/rs12193134