Detection of Chlorophyll a and CDOM Absorption Coefficient with a Dual-Wavelength Oceanic Lidar: Wavelength Optimization Method
Abstract
1. Introduction
2. Method
2.1. Inversion Formula
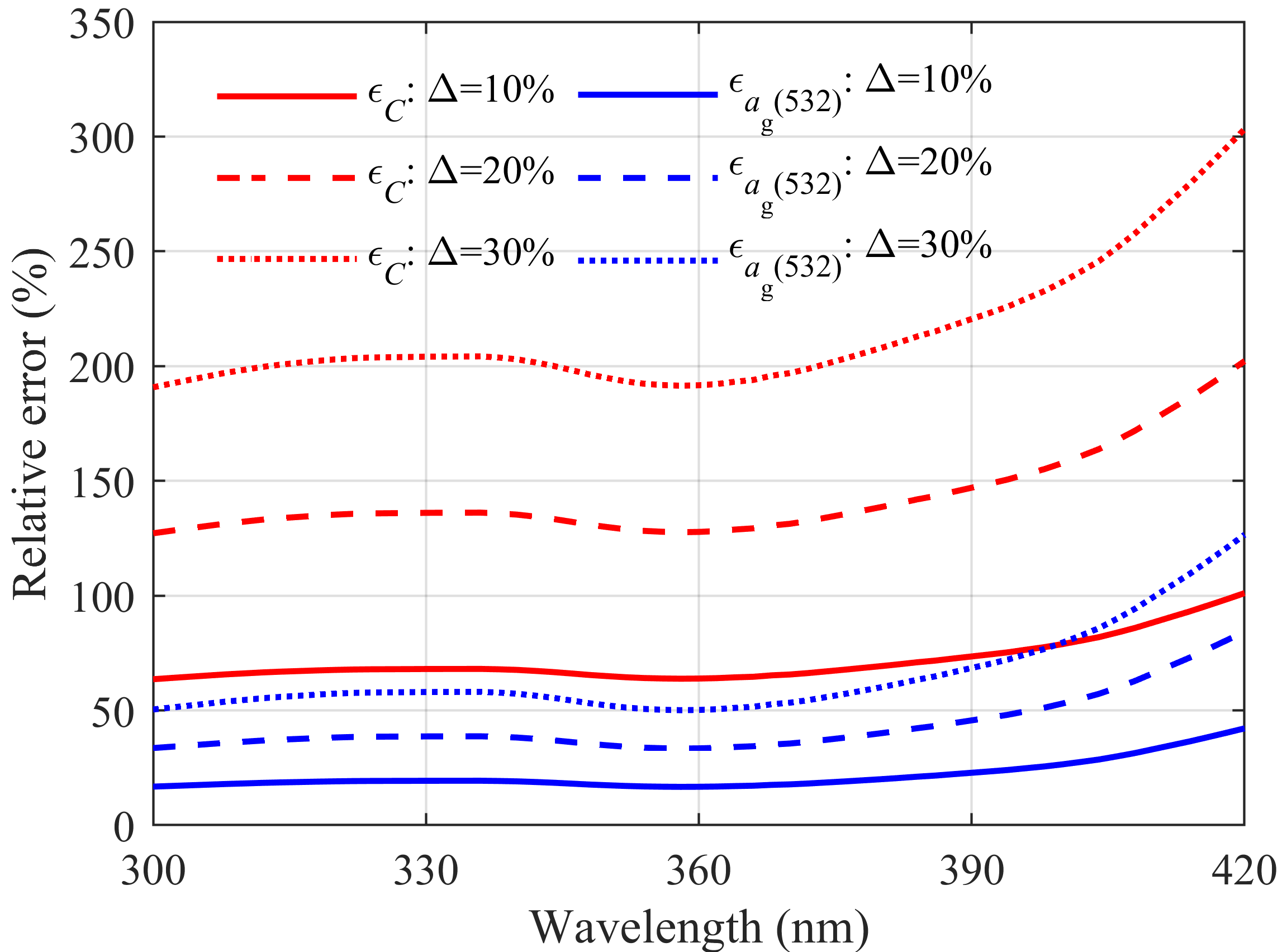
2.2. Error Analysis
3. Results
3.1. Dual-Wavelength Analysis
3.2. One Fixed Wavelength at 532 nm
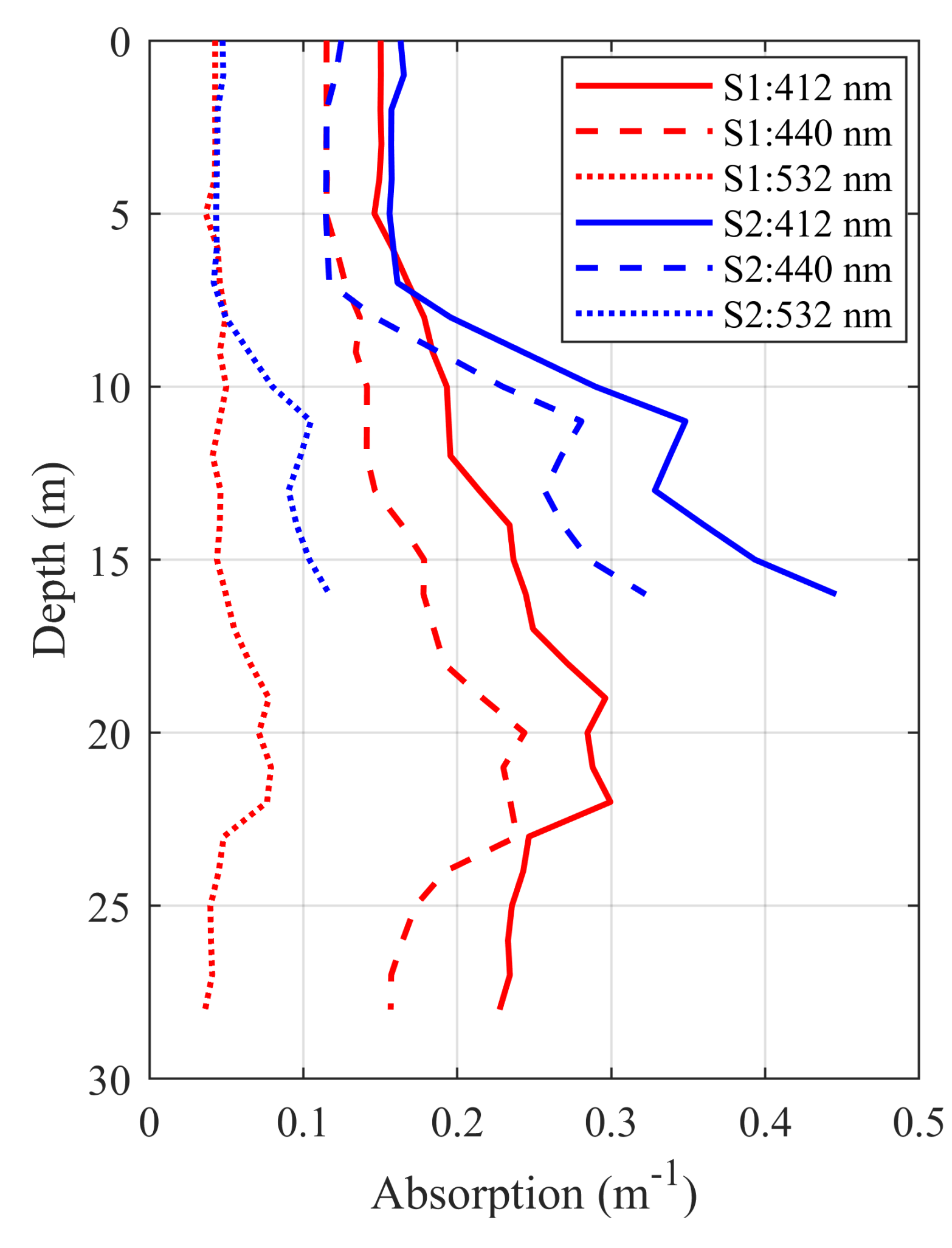
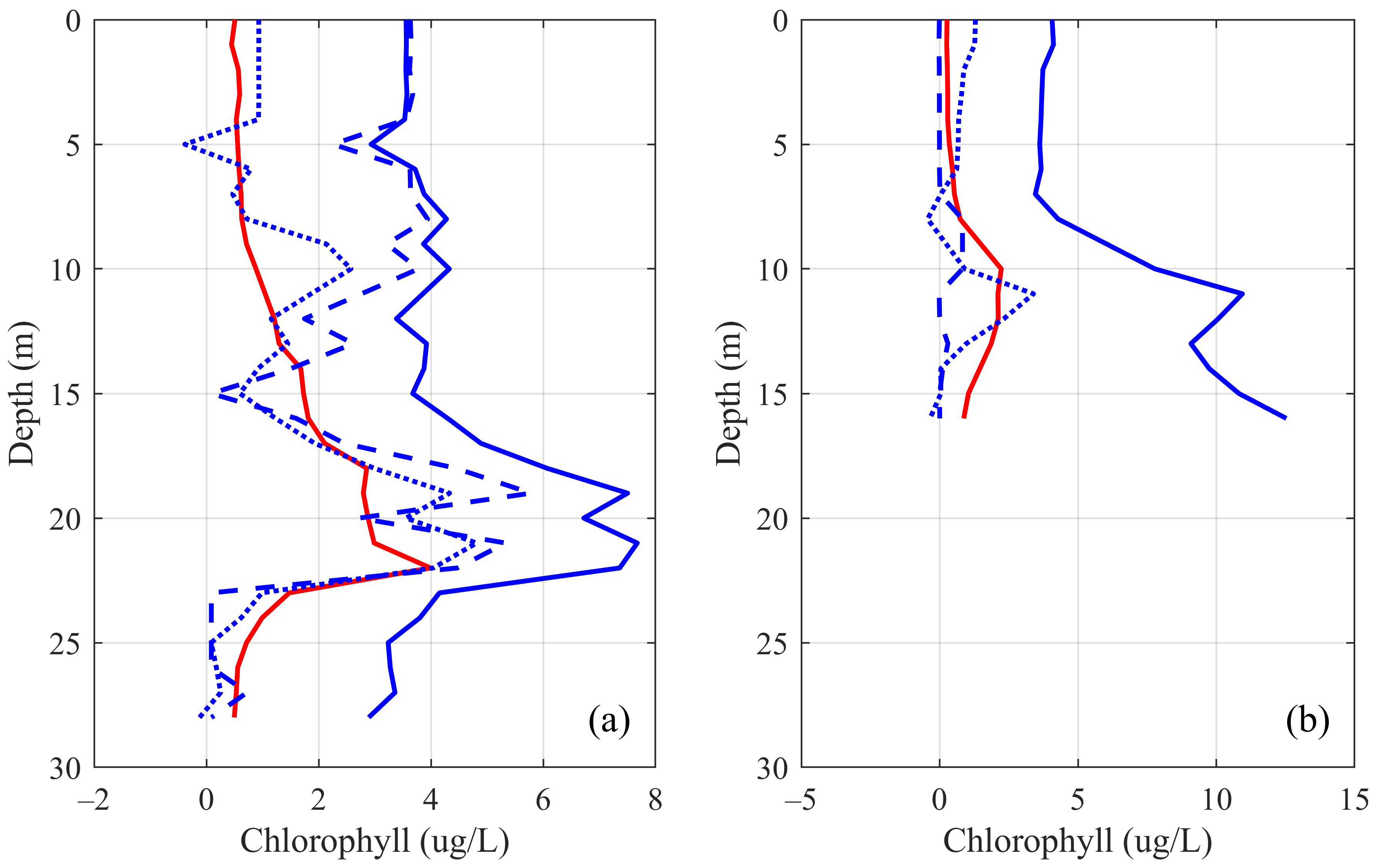
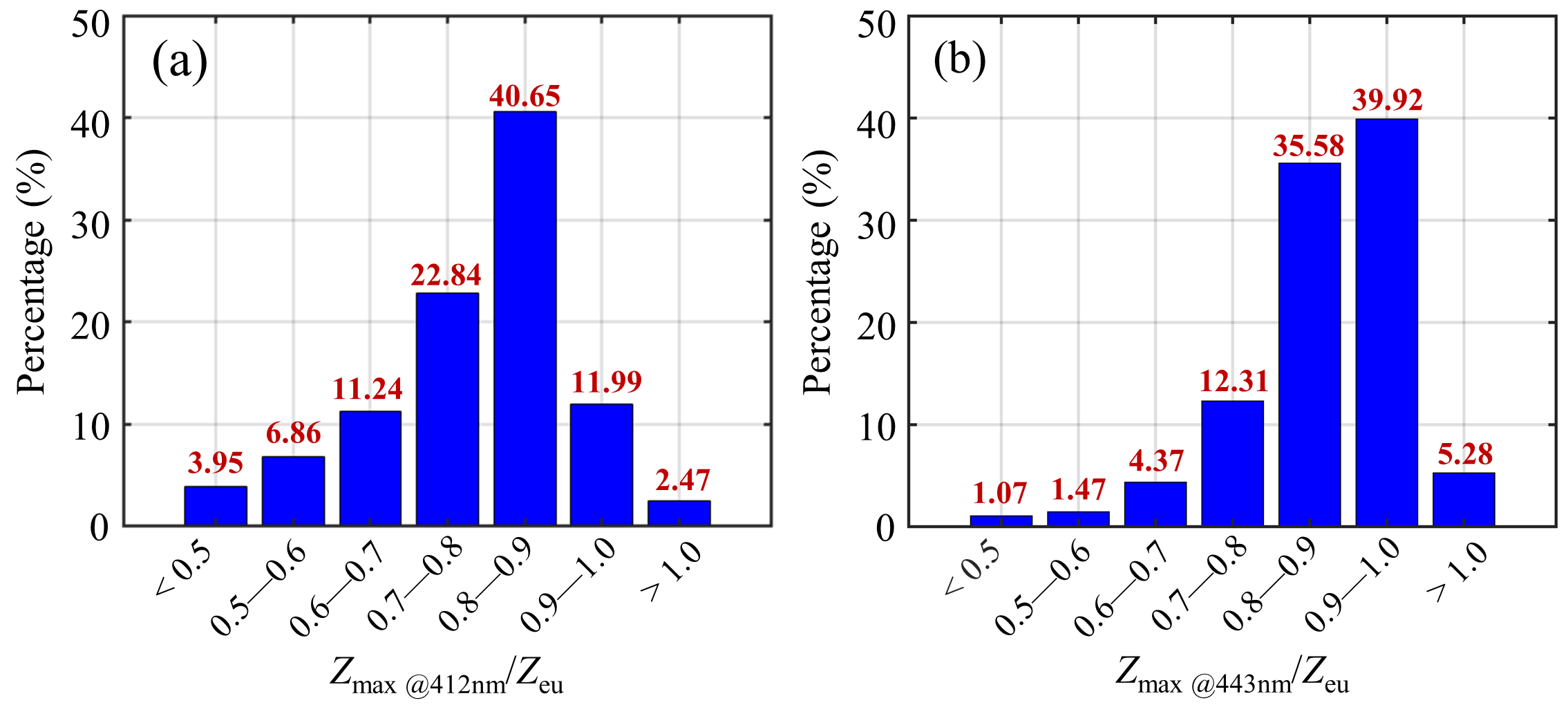
3.3. Real Water Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dickey, T.; Lewis, M.; Chang, G. Optical oceanography: Recent advances and future directions using global remote sensing and in situ observations. Rev. Geophys. 2006, 44. [Google Scholar] [CrossRef]
- Behrenfeld, J.M. Biospheric Primary Production During an ENSO Transition. Science 2001, 291, 2594–2597. [Google Scholar] [CrossRef]
- Sagan, S.; Weeks, A.R.; Robinson, I.S.; Moore, G.F.; Aiken, J. The relationship between beam attenuation and chlorophyll concentration and reflectance in Antarctic waters. Deep Sea Res. Part II Top. Stud. Oceanogr. 1995, 42, 983–996. [Google Scholar] [CrossRef]
- Mcclain, C.R. A Decade of Satellite Ocean Color Observations*. Ann. Rev. Mar. Sci. 2009, 1, 19. [Google Scholar] [CrossRef]
- Schulien, J.A.; Behrenfeld, M.J.; Hair, J.W.; Hostetler, C.A.; Twardowski, M.S. Vertically- resolved phytoplankton carbon and net primary production from a high spectral resolution lidar. Opt. Express 2017, 25, 13577–13587. [Google Scholar] [CrossRef]
- Zhou, Y.D.; Liu, D.; Xu, P.T.; Liu, C.; Bai, J.; Yang, L.M.; Cheng, Z.T.; Tang, P.J.; Zhang, Y.P.; Su, L. Retrieving the seawater volume scattering function at the 180° scattering angle with a high-spectral-resolution lidar. Opt. Express 2017, 25, 11813. [Google Scholar] [CrossRef]
- Hostetler, C.A.; Behrenfeld, M.J.; Hu, Y.; Hair, J.W.; Schulien, J.A. Spaceborne Lidar in the Study of Marine Systems. Annu. Rev. Mar. Sci. 2018, 10, 121–147. [Google Scholar] [CrossRef]
- Hair, J.; Hostetler, C.; Hu, Y.; Behrenfeld, M.; Butler, C.; Harper, D.; Hare, R.; Berkoff, T.; Cook, A.; Collins, J. Combined Atmospheric and Ocean Profiling from an Airborne High Spectral Resolution Lidar. EDP Sci. 2016, 119, 22001. [Google Scholar] [CrossRef]
- Liu, D.; Xu, P.T.; Zhou, Y.D.; Chen, W.B.; Han, B.; Zhu, X.L.; He, Y.; Mao, Z.H.; Le, C.F.; Chen, P.; et al. Lidar Remote Sensing of Seawater Optical Properties: Experiment and Monte Carlo Simulation. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9489–9498. [Google Scholar] [CrossRef]
- Collister, B.L.; Zimmerman, R.C.; Sukenik, C.I.; Hill, V.J.; Balch, W. MRemote sensing of optical characteristics and particle distributions of the upper ocean using shipboard lidar. Remote Sens. Environ. 2018, 215, 85–96. [Google Scholar] [CrossRef]
- Churnside, J.H.; Donaghay, P.L. Thin scattering layers observed by airborne lidar. Ices J. Mar. Sci. 2009, 66, 778–789. [Google Scholar] [CrossRef]
- Liu, H.; Chen, P.; Mao, Z.H.; Pan, D.L.; He, Y. Subsurface plankton layers observed from airborne lidar in Sanya Bay, South China Sea. Opt. Express 2018, 29134–29147. [Google Scholar] [CrossRef]
- Gray, D.J.; Anderson, J.; Nelson, J.; Edwards, J. Using a multiwavelength LiDAR for improved remote sensing of natural waters. Appl. Opt. 2015, 54, 232–242. [Google Scholar] [CrossRef]
- Twardowski, M.S.; Dalgleish, F.R.; Tonizzo, A.; Dalgleish, A.K.V.; Strait, C. Development and assessment of lidar modeling to retrieve IOPs. In Proceedings of the Ocean Sensing and Monitoring X, Orlando, FL, USA, 17–18 April 2018. [Google Scholar]
- Hoge, F.E. Validation of satellite-retrieved oceanic inherent optical properties: Proposed two-color elastic backscatter lidar and retrieval theory. Appl. Opt. 2003, 42, 7197–7201. [Google Scholar] [CrossRef]
- Fernald, F.G. Analysis of atmospheric lidar observations—Some comments. Appl. Opt. 1984, 23, 652–653. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, D.; Xu, P.; Mao, Z.; Chen, P.; Liu, Z.; Liu, Q.; Tang, P.; Zhang, Y.; Wang, X.; et al. Detecting atmospheric-water optical properties profiles with a polarized lidar. J. Remote Sens. 2019, 23, 108–115. [Google Scholar] [CrossRef]
- Churnside, J.H.; Marchbanks, R.D. Inversion of oceanographic profiling lidars by a perturbation to a linear regression. Appl. Opt. 2017, 56, 5228–5233. [Google Scholar] [CrossRef]
- Churnside, J.; Marchbanks, R.; Lembke, C.; Beckler, J. Optical Backscattering Measured by Airborne Lidar and Underwater Glider. Remote Sens. 2017, 9, 379. [Google Scholar] [CrossRef]
- Churnside, J.H.; Hair, J.W.; Hostetler, C.A.; Scarino, A.J. Ocean Backscatter Profiling Using High-Spectral-Resolution Lidar and a Perturbation Retrieval. Remote Sens. 2018, 10, 2003. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, Y.D.; Chen, W.B.; Liu, Q.; Huang, T.Y.; Liu, W.; Chen, Q.K.; Liu, Z.P.; Xu, P.T.; Cui, X.Y.; et al. Phase function effects on the retrieval of oceanic high-spectral-resolution lidar. Opt. Express 2019, 27, A654. [Google Scholar] [CrossRef]
- Gordon, H.R. Interpretation of airborne oceanic lidar: Effects of multiple scattering. Appl. Opt. 1982, 21, 2996–3001. [Google Scholar] [CrossRef]
- Kullenberg, G. Scattering of light by Sargasso Sea water. Deep Sea Res. 1968, 15, 423–424. [Google Scholar] [CrossRef]
- Lee, Z.P.; Du, K.P.; Arnone, R. A model for the diffuse attenuation coefficient of downwelling irradiance. J. Geophys. Res. 2005, 110, C02016. [Google Scholar]
- Liu, Q.; Liu, D.; Bai, J.; Zhang, Y.P.; Zhou, Y.D.; Xu, P.T.; Liu, Z.P.; Chen, S.J.; Che, H.C.; Wu, L.; et al. Relationship between the effective attenuation coefficient of spaceborne lidar signal and the IOPs of seawater. Opt. Express 2018, 26, 30278–30291. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption Spectrum (380–700 nm) of Pure Water. II. Integrating Cavity Measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variations of light absorption by suspended particles with chlorophyll a concentration in oceanic (case 1) waters: Analysis and implications for bio-optical models. J. Geophys. Res. Oceans 1998, 103, 31033–31044. [Google Scholar] [CrossRef]
- Ocean Optics Web Book. Available online: https://www.oceanopticsbook.info/view/optical-constituents-of-the-ocean/level-2/new-iop-model-case-1-water (accessed on 28 August 2020).
- Nelson, N.B.; Siegel, D.A. The Global Distribution and Dynamics of Chromophoric Dissolved Organic Matter. Ann. Rev. Mar. Sci. 2013, 5, 447–476. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Qin, B.Q.; Yang, L.Y. Spectral absorption coefficients of particulate matter and chromophoric dissolved organic matter in Meiliang Bay of Lake Taihu. Acta Ecol. Sin. 2006, 26, 3969–3979. [Google Scholar]
- Babin, M.; Stramski, D.; Ferrari, G.; Claustre, H.; Bricaud, A.; Obolensky, G.; Hoepffner, N. Variations in the light absorption coefficients of phytoplankton, nonalgal particles, and dissolved organic matter in coastal waters around Europe. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Morrison, J.R.; Nelson, N.B. Seasonal cycle of phytoplankton UV absorption at the Bermuda Atlantic Time-series Study (BATS) site. Limnol. Oceanogr. 2004, 49, 215–224. [Google Scholar] [CrossRef]
- Whitehead, K.; Vernet, M. Influence of mycosporine-like amino acids (MAAs) on UV absorption by particulate and dissolved organic matter in La Jolla Bay. Limnol. Oceanogr. 2000, 45, 1788–1796. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical-properties of the clearest natural-Waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Vasilkov, A.; Herman, J.; Ahmad, Z.; Kahru, M. Assessment of the ultraviolet radiation field in ocean waters from space-based measurements and full radiative-transfer calculations. Appl. Opt. 2005, 44, 2863–2869. [Google Scholar] [CrossRef]
- GlobColour. Available online: http://www.globcolour.info/ (accessed on 20 August 2020).
- Blough, N.V.; Del Vecchio, R. Chapter 10—Chromophoric DOM in the Coastal Environment. In Biogeochemistry of Marine Dissolved Organic Matter; Hansell, D.A., Carlson, C.A., Eds.; Academic Press: San Diego, CA, USA, 2002; pp. 509–546. [Google Scholar] [CrossRef]
- Roesler, C.S.; Perry, M.J.; Carder, K.L. Modeling insitu phytoplankton absorption from total absorption-spectra in productive inland marine waters. Limnol. Oceanogr. 1989, 34, 1510–1523. [Google Scholar] [CrossRef]
- Fitzwater, S.E.; Johnson, K.S.; Gordon, R.M.; Coale, K.H.; Smith, W.O. Trace metal concentrations in the Ross Sea and their relationship with nutrients and phytoplankton growth. Deep Sea Res. Part II Top. Stud. Oceanogr. 2000, 47, 3159–3179. [Google Scholar] [CrossRef]
- Zaneveld, J.R.; Kitchen, J.; Moore, C. Scattering Error Correction of Reflection-Tube Absorption Meters; SPIE: Washington, DC, USA, 1994; Volume 2258. [Google Scholar]
- Zhou, F.X.; Gao, X.L.; Song, J.M.; Chen, C.T.A.; Yuan, H.M.; Xing, Q.G. Absorption properties of chromophoric dissolved organic matter (CDOM) in the East China Sea and the waters off eastern Taiwan. Cont. Shelf Res. 2018, 159, 12–23. [Google Scholar] [CrossRef]
- Haltrin, V.I. Absorption and Scattering of Light in Natural Waters; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Liu, Q.; Liu, C.; Zhu, X.L.; Zhou, Y.D.; Le, C.F.; Bai, J.; He, Y.; Bi, D.C.; Liu, D. Analysis of the optimal operating wavelength of spaceborne oceanic lidar. Chin. Opt. 2020, 13, 148–155. [Google Scholar]
- Li, C.L.; Zhang, Q.Q.; Wang, L.; Wang, X.L.; Wu, Y.L. The Application of the Absorbance Ratio Medthod to the Identification of Diatoms and Dinoflagellates. J. Ocean Univ. China 2007, 37, 161–164. [Google Scholar]
- Fu, Y.; Wei, Y.C.; Zhou, Y. The Measurement and Changes of Chromophoric Dissolved Organic Matter in Water. J. Nanjing Norm. Univ. (Nat. Sci. Ed.) 2012, 35, 95–103. [Google Scholar]

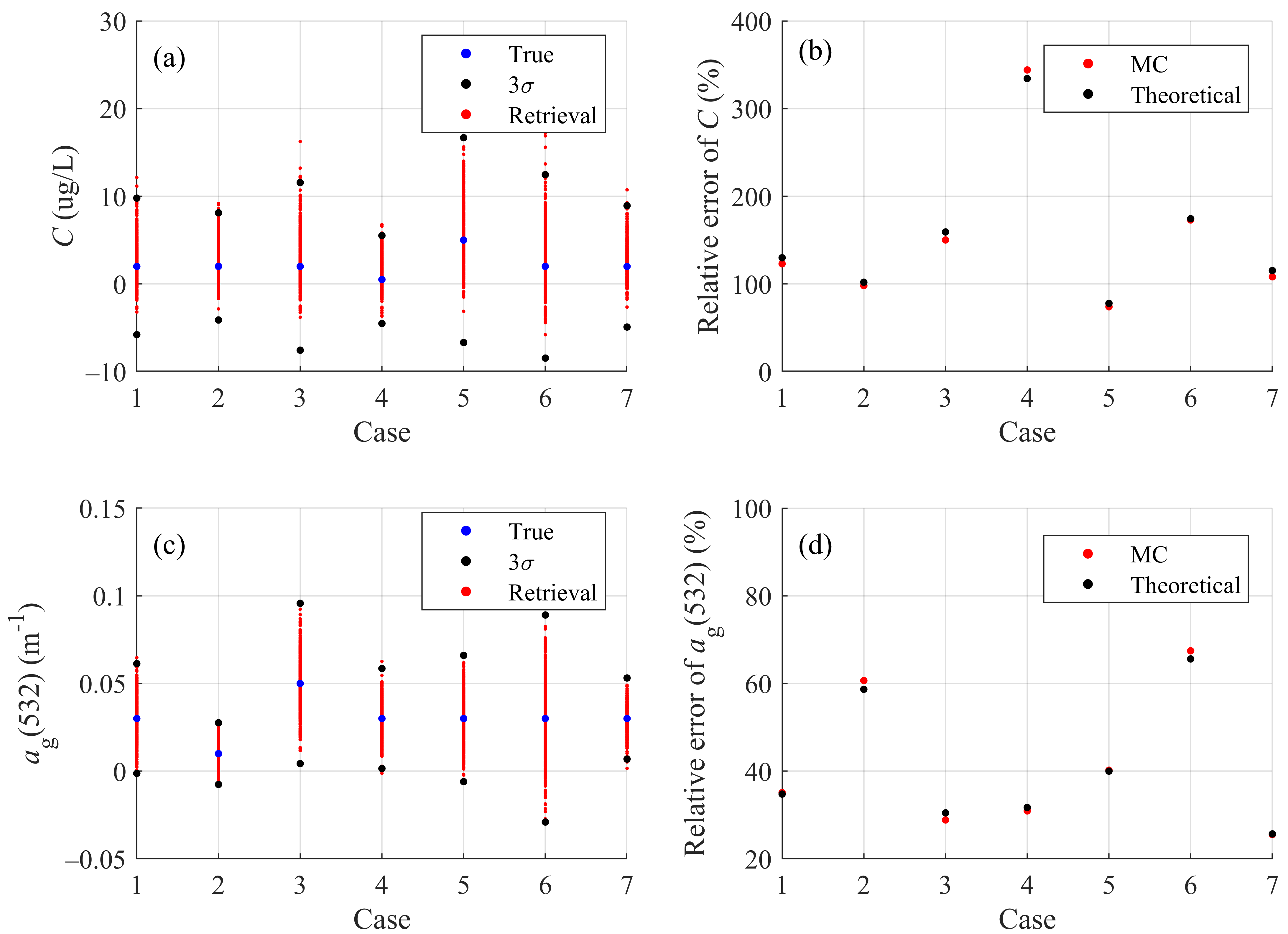
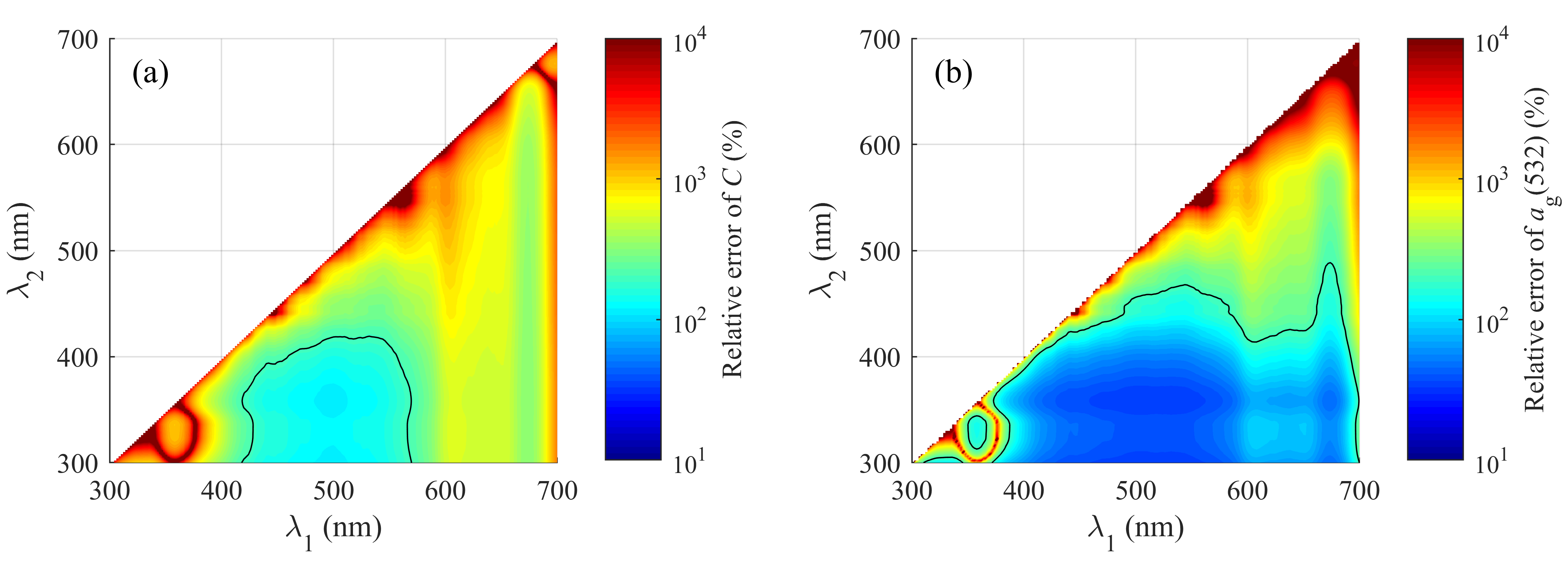
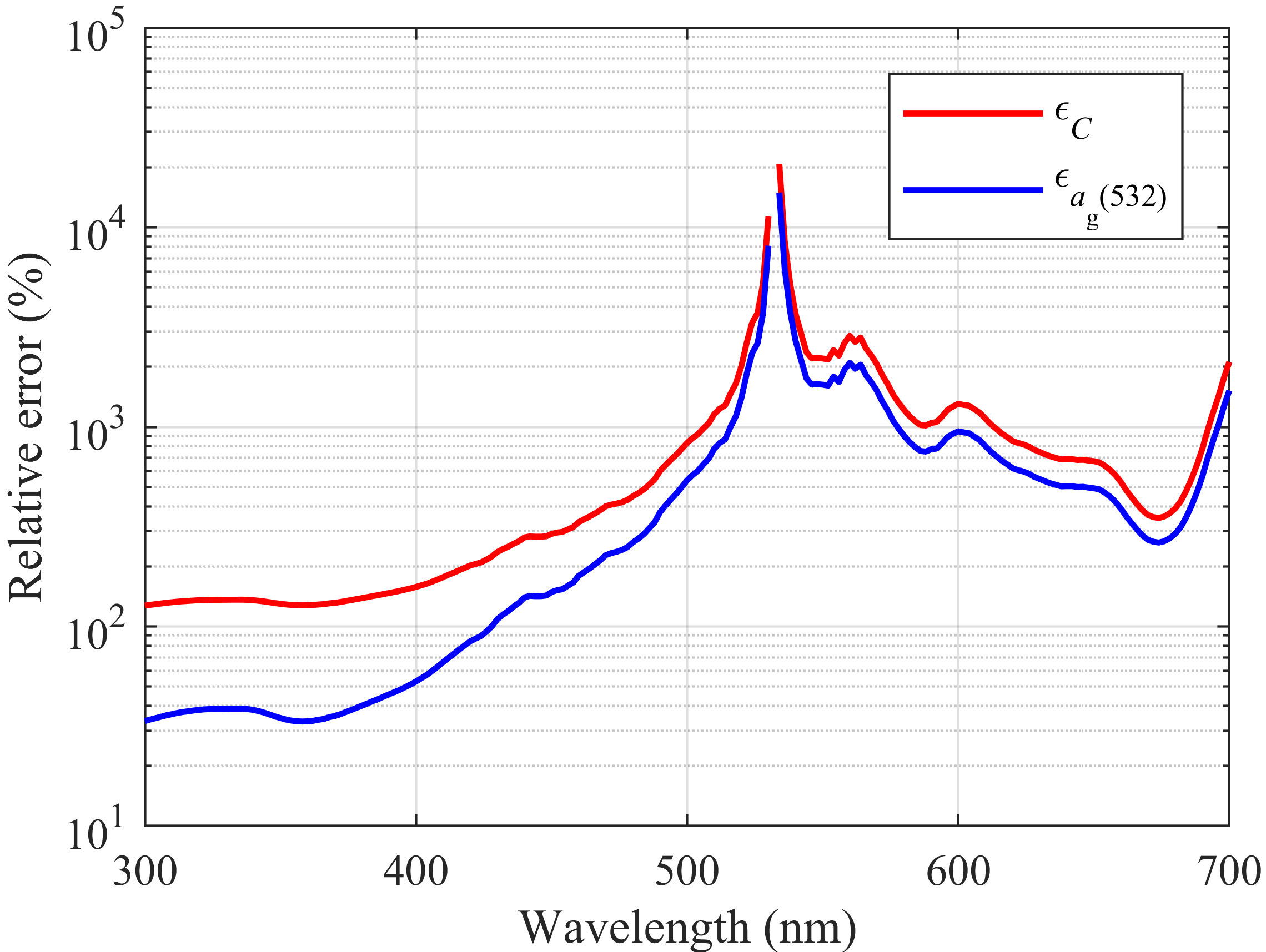
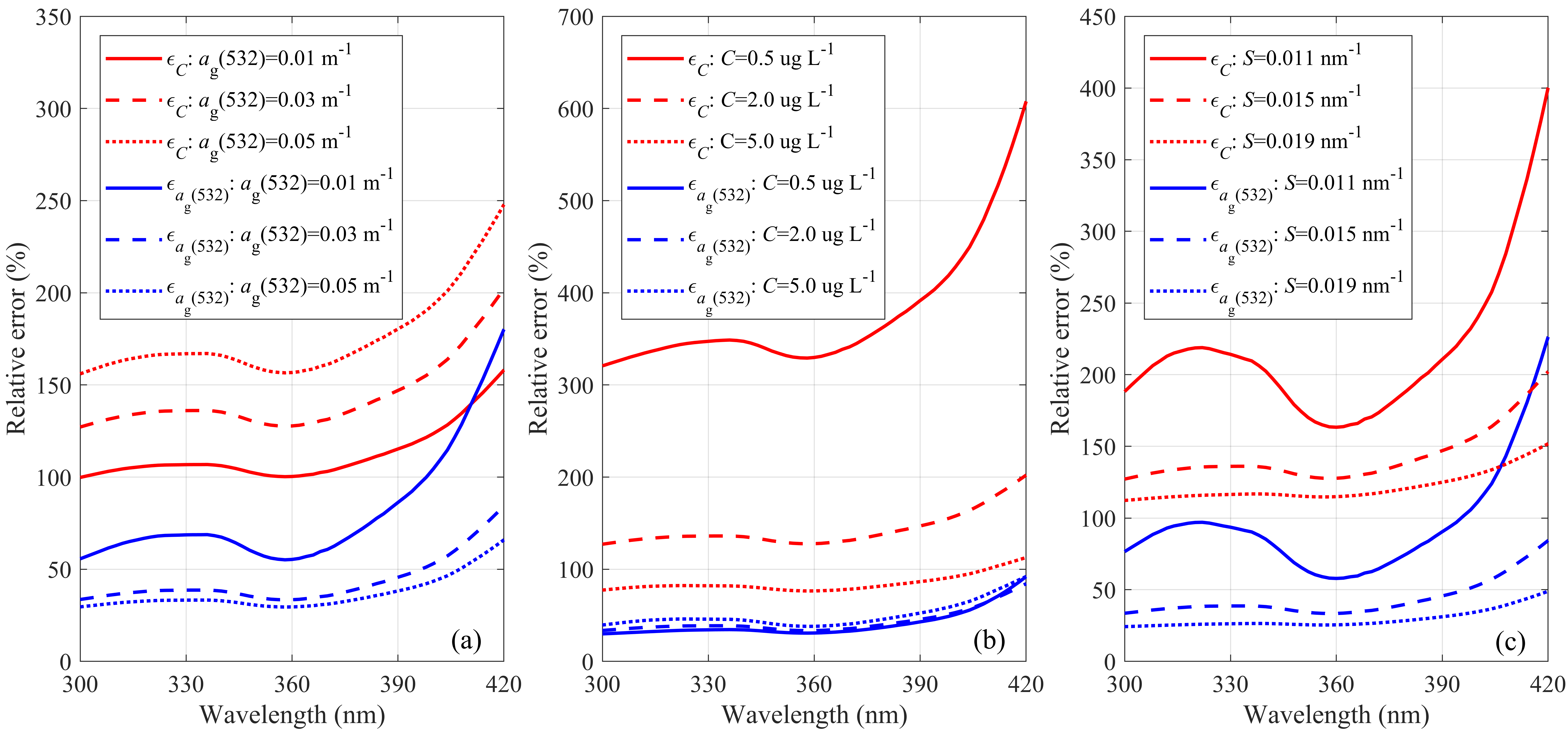
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| ag(532) (m−1) | 0.03 | 0.01 | 0.05 | 0.03 | 0.03 | 0.03 | 0.03 |
| C (μg L−1) | 2.00 | 2.00 | 2.00 | 0.50 | 5.00 | 2.00 | 2.00 |
| S (nm−1) | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 | 0.011 | 0.019 |
| Retrieval | λ1 | λ2 | Relative Errors |
|---|---|---|---|
| C | 412 nm | 300 nm | 230.84% |
| 440 nm | 140.80% | ||
| 500 nm | 111.76% | ||
| 532 nm | 127.16% | ||
| 672 nm | 325.96% | ||
| C | 412 nm | 358 nm | 233.66% |
| 440 nm | 141.42% | ||
| 500 nm | 112.06% | ||
| 532 nm | 127.62% | ||
| 672 nm | 326.10% | ||
| ag(532) | 412 nm | 300 nm | 47.64% |
| 440 nm | 37.58% | ||
| 502 nm | 33.64% | ||
| 532 nm | 33.60% | ||
| 672 nm | 45.98% | ||
| ag(532) | 412 nm | 358 nm | 48.08% |
| 440 nm | 37.46% | ||
| 502 nm | 33.38% | ||
| 532 nm | 33.52% | ||
| 672 nm | 47.28% |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Relative error (Δ = 10 %) | 168.27% | 66.13% | 282.32% | 569.08% | 79.63% | 168.27% | 168.27% |
| Relative error (Δ = 20 %) | 203.37% | 102.12% | 318.17% | 660.92% | 100.48% | 203.37% | 203.37% |
| Relative error (Δ = 30 %) | 243.39% | 142.93% | 360.77% | 793.77% | 126.38% | 243.39% | 243.39% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Ling, Q.; Zhang, Q.; Zhou, Y.; Le, C.; Chen, Y.; Liu, Q.; Chen, W.; Tang, J.; Liu, D. Detection of Chlorophyll a and CDOM Absorption Coefficient with a Dual-Wavelength Oceanic Lidar: Wavelength Optimization Method. Remote Sens. 2020, 12, 3021. https://doi.org/10.3390/rs12183021
Liu R, Ling Q, Zhang Q, Zhou Y, Le C, Chen Y, Liu Q, Chen W, Tang J, Liu D. Detection of Chlorophyll a and CDOM Absorption Coefficient with a Dual-Wavelength Oceanic Lidar: Wavelength Optimization Method. Remote Sensing. 2020; 12(18):3021. https://doi.org/10.3390/rs12183021
Chicago/Turabian StyleLiu, Ruoran, Qiaolv Ling, Qiangbo Zhang, Yudi Zhou, Chengfeng Le, Yatong Chen, Qun Liu, Weibiao Chen, Junwu Tang, and Dong Liu. 2020. "Detection of Chlorophyll a and CDOM Absorption Coefficient with a Dual-Wavelength Oceanic Lidar: Wavelength Optimization Method" Remote Sensing 12, no. 18: 3021. https://doi.org/10.3390/rs12183021
APA StyleLiu, R., Ling, Q., Zhang, Q., Zhou, Y., Le, C., Chen, Y., Liu, Q., Chen, W., Tang, J., & Liu, D. (2020). Detection of Chlorophyll a and CDOM Absorption Coefficient with a Dual-Wavelength Oceanic Lidar: Wavelength Optimization Method. Remote Sensing, 12(18), 3021. https://doi.org/10.3390/rs12183021






