1. Introduction
High latitude lakes are considered sentinels for a climate in change, due to their coupling with ice phenology, response to changes in humidity and precipitation patterns, and the high sensitivity of photosynthetic organisms to changing temperatures [
1,
2]. In particular, the growth rates, abundance, and species composition of phytoplankton are an indicator of changing environmental conditions [
2,
3,
4]. Nevertheless, monitoring water bodies has been difficult because in situ methods are very localized and cannot always be performed routinely. In situ datasets might also contain data gaps, and data gathering is not coherent across different regions and field sampling is deemed expensive.
A powerful way to have synoptic views of changes in water bodies is to monitor them from space. Phytoplankton biomass, which can be proxied from the chlorophyll
a (Chl) concentration, can be used to estimate primary production in aquatic environments. Satellites have now been collecting decades of remotely sensed optical imagery over large areas. Due to the characteristic reflectance of Chl pigments, we can estimate concentrations from such images. Earth Observation satellites have been designed and launched with the specific purpose of studying phytoplankton from space with sensors specifically suited to the assessment of aquatic ecosystems. For example, NASA’s Sea-viewing Wide Field-of-View Sensor (SeaWiFS), launched in August 1997 onboard the SeaStar satellite, collected data until 2010 at a resolution of 1.1 km. The Terra and Aqua Satellites both collect data through the 36-band MODIS sensor at wavelengths between 0.41 and 14.24 µm applicable to extensive ocean color algorithms [
5]. Additionally, the MERIS sensor was an imaging spectrometer at fifteen spectral bands and a spatial resolution of 300 m over land. Its visible to near-infrared sensitivity ranged from 390 nm to 1400 nm at programmable bandwidths between 2.5 and 30 nm. Following the loss of the Envisat-1 payload in 2012, the MERIS data spans until April 2012, having started in May 2002. Recently, the European Space Agency (ESA) has launched the Sentinel 3 constellation as part of the Copernicus Programme. Onboard the two sentinels, the Ocean and Land Colour Instruments (OCLI) are collecting data at wavelengths from 0.4 µm to 1.02 µm at 21 spectral bands, allowing for algal pigment discrimination and the further development of phytoplankton functional types characterization from space [
6]. The resolution of the new OCLI sensor is 300 m, which is not suitable for studying lakes smaller than 30 ha.
The use of the above-mentioned satellites hampers the study of small lakes due to their coarse resolution in relation to the size of the lakes. In fact, 95% of the roughly 56,000 Finnish lakes have an area <1 km
2 [
7]. Additionally, consistent data from the Ocean Colour missions’ dates to 1997, which provides a relatively short time series. Given these limitations, the high-resolution Landsat satellites (LT) can be advantageous to use on small water bodies. LT satellites have collected one of the most comprehensive datasets, with almost 40 years of observations. LT 5 was launched in March 1984 providing data for the following 28 years. LT 5 carried the 7-band Thematic Mapper (TM) multispectral sensor. LT 7, launched in April 1999, is still in operation and carries the 8-band Enhanced Thematic Mapper Plus (ETM+). Exploring this archive for assessing Chl concentrations offers an excellent opportunity to evaluate how changes in phenology (i.e., timing of the blooms and their duration) have occurred in previous decades, due to both climate change and eutrophication. Furthermore, the high spatial resolution of LT data (30 m) allows the assessment of smaller lakes or lakes with complex shapes, minimizing the influence of surrounding land vegetation.
Given Finland’s geographical location, the country can experience a faster warming with respect to the global average. Warming in Finland is estimated to be roughly 50% higher than the global average, which corresponds to a 0.15–0.20 °C increase per decade [
2]. Most Finnish lakes are from glacial origin and during most winters the lakes in Finland have ice cover, resulting in an annual cycle of water quality parameters that also affect primary production dynamics [
8].
Phytoplankton phenologies vary within the lake’s trophic state and climate induced changes in the environmental conditions affect both the species composition and dynamics of the phytoplankton community [
9]. In many lakes, the effects of eutrophication are common with algal blooms being exacerbated by climate change [
3], it is therefore critical to have extensive temporal and spatial information on Boreal lakes [
10].
The LT data has been used for the assessment of regional lake water clarity with reliable empirical relationships between satellite data and ground observations in the north American glaciated lakes [
11] and in Europe [
12]. Similarly, the interest on studying Finnish lakes through LT data dates back to the 1980s, leading to research that proved that spectral differences due to aquatic vegetation were possible to detect [
13]. An important early study on Finnish lakes also approached the configurations of ETM+ sensor for lake water quality estimations [
7]. Feasibility studies conducted in Finland in the early 2000s identified that it is possible to estimate the average Chl level of an individual lake through matchups of airborne sensing data from another lake [
14]. Notwithstanding the limitation on spectral and radiometric resolutions, other previous efforts outlined the importance of ETM+ data on monitoring small lakes for colored dissolved organic materials (CDOM), turbidity and Secchi disk transparency [
15]. We find that these approaches should be revisited with LT data for two reasons, first, taking the advantages of long data series is paramount for studying change [
16], secondly, exploring alternative high-resolution imagery is a necessary step to enhance the monitoring of small water bodies. Previous studies used semi-empirical approaches to conclude that Chl assessment is limited by the band configuration of LT, and this type of activity goes beyond the design of the TM sensor [
17]. Our study revisits this assumption by gathering more in situ data and a vast collection of imagery.
Studies of single lakes using LT data are well described in the literature [
12,
18,
19,
20]. For example, imagery from LT and samples from a transect were combined achieving a R
2 = 0.9 over Lake Erken, Sweden [
12]. Another study [
21] used the band ratio of B2/B1 (green/blue) for Chl assessment on Lake Champlain, USA, reporting an R of 0.82. Having such space-derived estimates has been proved useful to study the changing patterns [
22]. Nevertheless, the challenges increase with smaller lakes. For example, a set of 131 small lakes (averaging 100 ha) in Maine revealed an R
2 of 0.25 [
23]. LT5-TM and LT7-ETM+ are not ideal for waterbodies, but they are the only available dataset at enough resolution with a significant temporal span.
The models derived in these previous studies were limited by validation campaigns carried at specific validation campaigns, in specific time frames. Our approach is to engage on an innovative in situ and remote sensing match up. We used many years of consistent in situ data, collected at different locations and created a validation method, using more than three decades of satellite data. To take full advantage of the long LT time series, models should robustly incorporate data from both LT5-TM and LT7-ETM+. Vicent et al. argued that a model developed for LT5 cannot be applied to LT7 images [
24]. Nonetheless, their methods involved the use of dark-object-subtracted radiance instead of surface reflectance. Hence, further studies are still needed to fully explore the combined use of LT5-TM and LT7-ETM+, using surface reflectance derived from state-of-the-art atmospheric correction algorithms [
25].
The focus of our study is to demonstrate whether Chl assessments using surface reflectance retrieved from LT sensors can be generalized for these different circumstances. In other words, we aim to understand how different Chl might affect LT reflectance, as a preliminary approach to develop advanced bio-optical models for inland and coastal waters. Such models, in turn, are an essential tool not only for global water quality monitoring, but to also study temporal dynamics of phytoplankton across large areas, allowing the identification of shifts in the temporal characteristics of phytoplankton blooms related to climate variability and land-use changes [
26].
The water-leaving signal is especially complex for the case of inland waters due to the high concentrations of CDOM, tripton, floating and submerged aquatic vegetation, suspended matter (e.g clay) and finally phytoplankton. The tripton component, composed of detritus and minerals from dead phytoplankton and decaying organic matter, varies significantly in optical signatures and concentration ranges. High concentrations of humic and fulvic acids from surrounding vegetation are leached into lakes and reduce the light availability in the blue spectral region in boreal and brackish waters [
26], both being the case of most of Finland’s lakes. The lakes considered in this paper are, thus, some of the most difficult cases for bio-optical models of phytoplankton proxying from space.
Our objective is to better understand spatiotemporal factors affecting the relationship between LT reflectance data and surface Chl concentration over high latitude lakes. We drive our research by asking: 1) how does the performance of models based on LT data vary with different lakes’ trophic state? 2) How does the performance of models based on LT data vary at different temporal scales? 3) Can the LT data archive be used to assess the spatial and temporal variability of lakes’ average Chl levels across large areas?
3. Results
3.1. Daily Aggregated Data
Model and Variable Selection
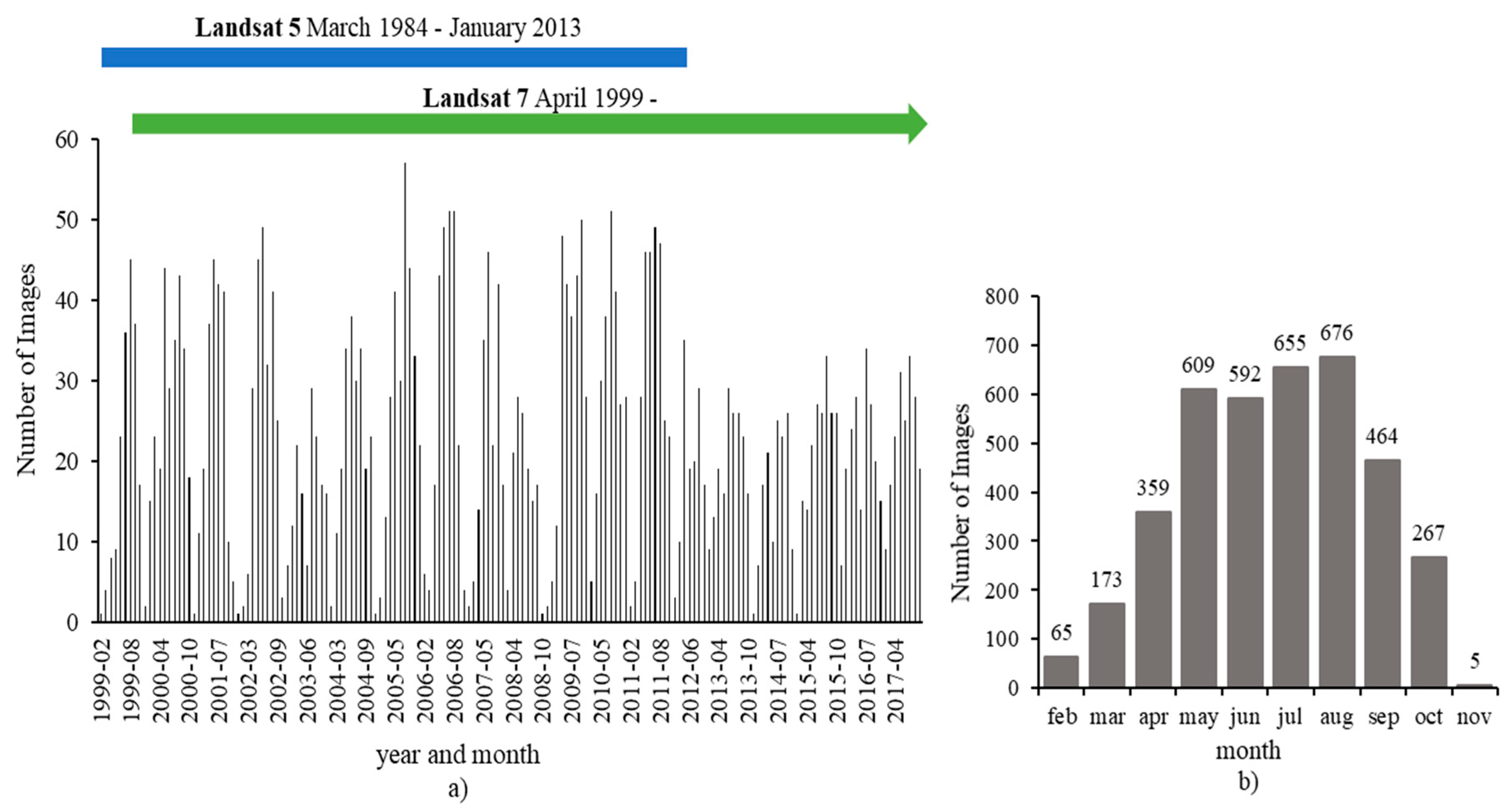
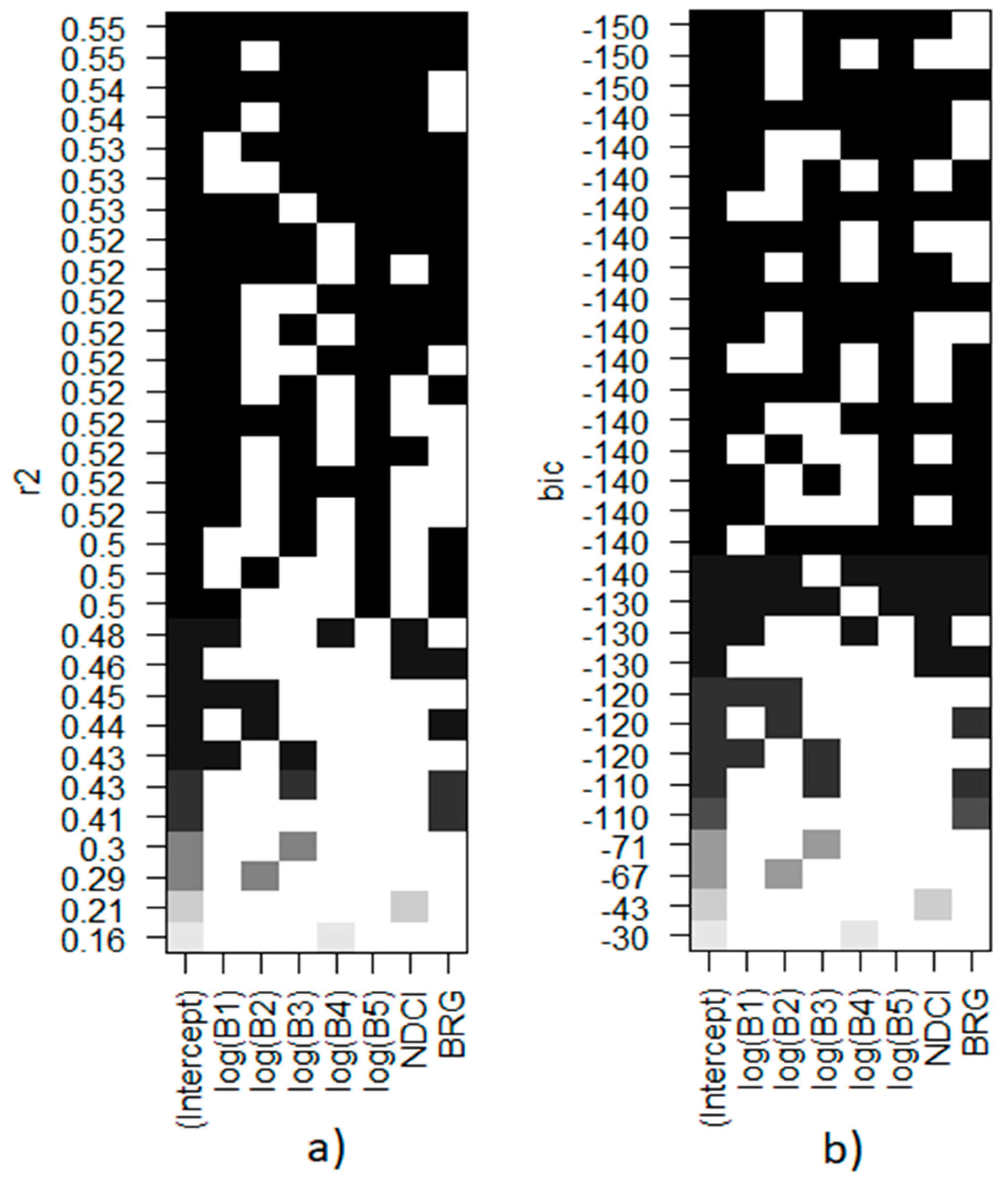
Of all models derived through intra-annual data, the best performance was achieved with a buffer of 700 m and a time-window of ±1 day from the satellite acquisition. For this configuration, the results of the LEAPS exhaustive variable search are presented in
Figure 4. The R
2 varied from 0.16, using only one explanatory variable (band 4 - NIR), to 0.55, using all possible bands and indices. The highest R
2 value could also be achieved when excluding band 2 (green) and including all other variables. The BIC values varied from -30, using only band 4, to −150, using bands 1, 3, 4 and 5.
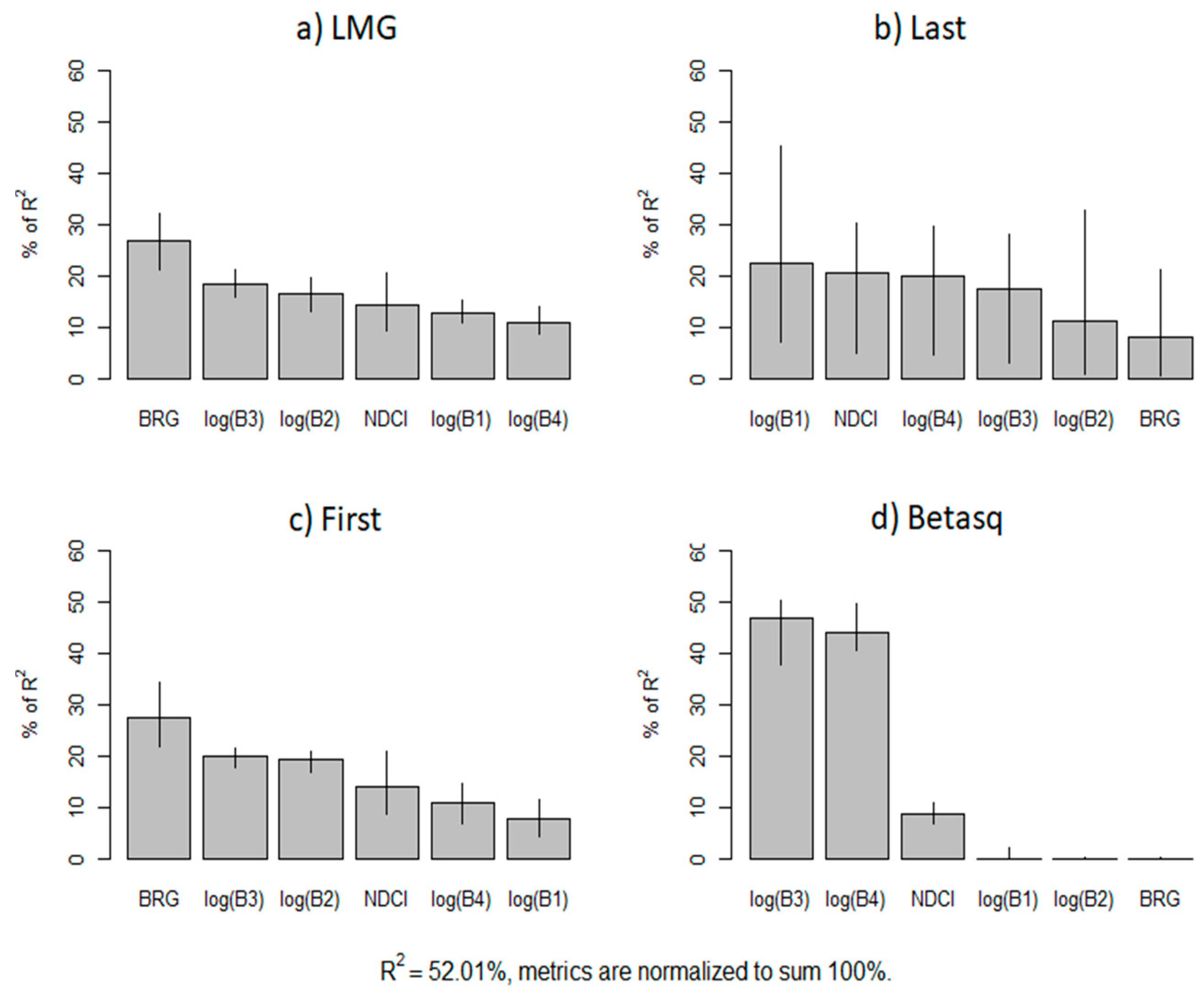
Figure 5 depicts the relative importance of each band for the overall R
2 of the achieved model. All bands 1–4 are significant (
p-value < 0.05) for the construction of the model, although the different models used to evaluate their relative importance did not always agree on the most important variables. Across all methods, band 3 and BRG index has the strongest explanatory power. Band 2 was selected as the second-best explanatory variable by two methods (LMG and First).
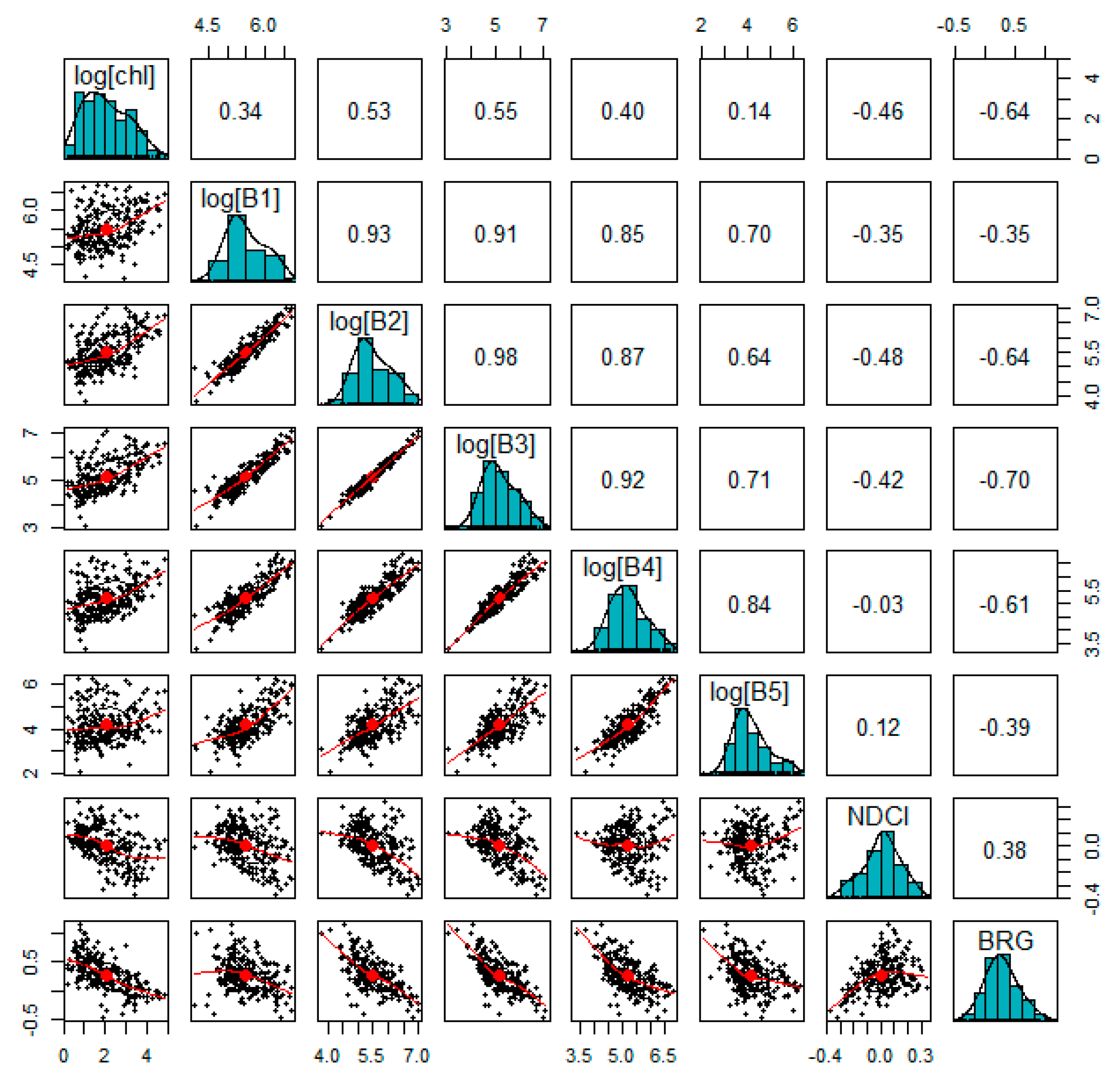
Figure 6 provides the correlations matrix of all bands and the NDCI and BRG indices. As evidenced, relationships between individual explanatory variables and Chl are not linear. Pearson’s coefficient of correlation (R) is shown for each band, and indices, with relation to the Chl concentration.
As a result of the small contribution of the shortwave infrared (SWIR) band 5, we considered a final model for the daily aggregated data comprising all these bands and indices.
All individual bands 1–5 correlate positively with in situ Chl, but bands 2 (R = 0.53) and band 3
(R = 55) are more strongly correlated. Both indices NDCI and BRG are negatively correlated with in situ Chl.
Model Performance
As expected, shortwave infrared (SWIR) band 5 of LT 5 and 7 provided only a marginal contribution to the overall performance of the model by 0.04 in the R
2 coefficient. Extracting that band to assess the performance of only visible and NIR bands also produced important results, summarized in
Table 1. All models derived from single bands 1–4 were significant, but not all models that included reflectance indices, NDCI and BRG, are significant. Henceforth, for the best models, we checked if all coefficients are significant, i.e., we checked if all variables significantly contribute for the resulting model. For the best performing model, a R
2 = 52.01 was achieved, including bands 1–4 and both indices. Reducing the time-window between satellite collection and in situ sampling has a relevant impact on the overall performance of the model, as it increases the R
2, whilst maintaining a
p-value < 0.05.
The choice of the size of the buffer around the sampling location has a small impact when compared to the choice of the time-windows (
Table 1). It is advisable to maintain a buffer size of either 60 m or above 500 m. Between 90 and 300 m, we observed that the number of additional pixels has created more noise than valuable signal from Chl content, thus creating a lower performing model.
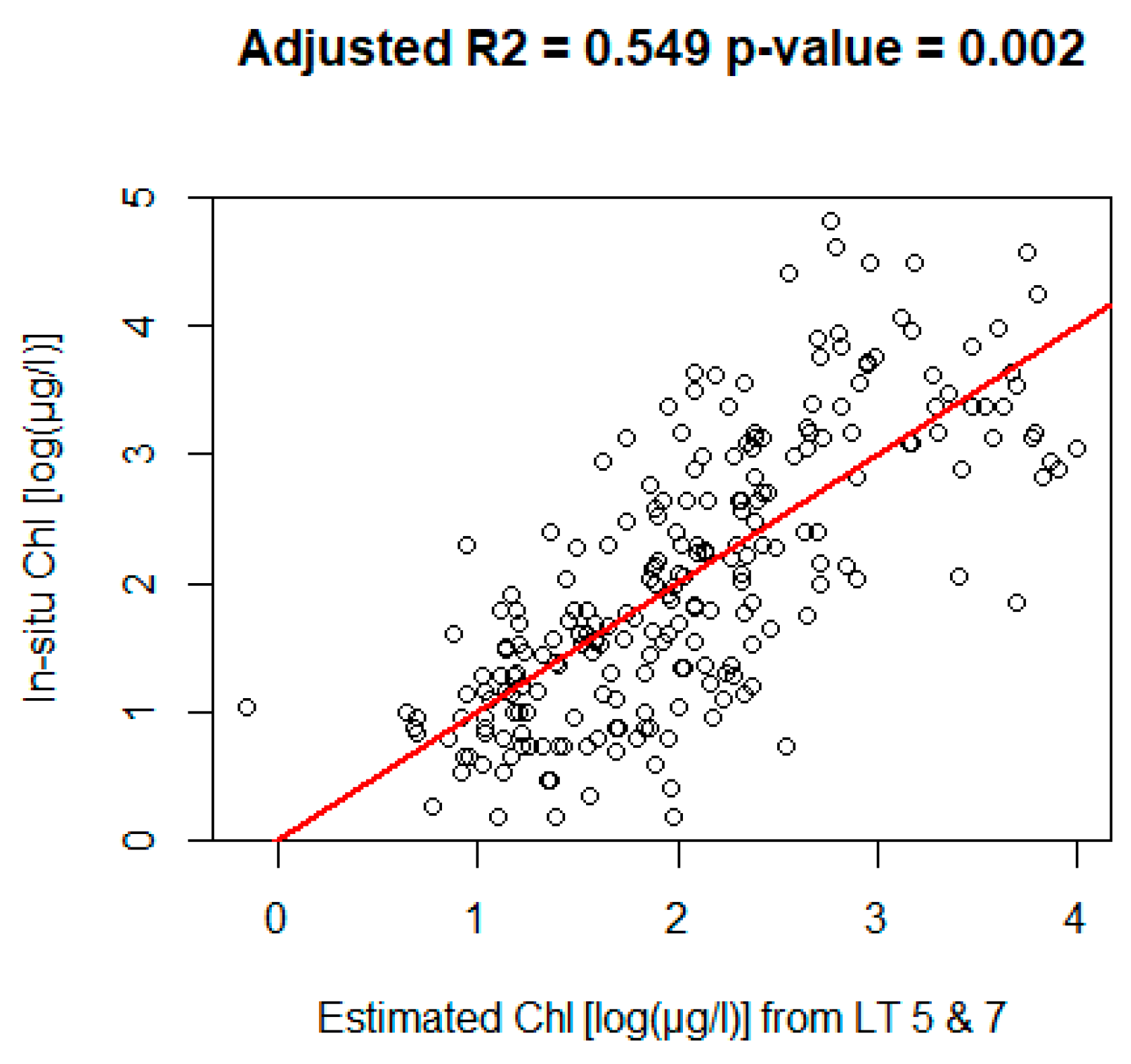
Figure 7 shows the best performing model found with a buffer of 700 m and ±1-day time window; this model includes all visible bands plus near infrared (NIR, band 4) and shortwave infrared (SWIR, band 5). The inclusion of SWIR slightly increases the overall correlation but also the
p-value of the model.
Using satellite images from ±1 day of in situ sampling comes with the disadvantage of a small number of data pairs (
Figure 7).
Indeed, the tests in
Table 1 and the model in
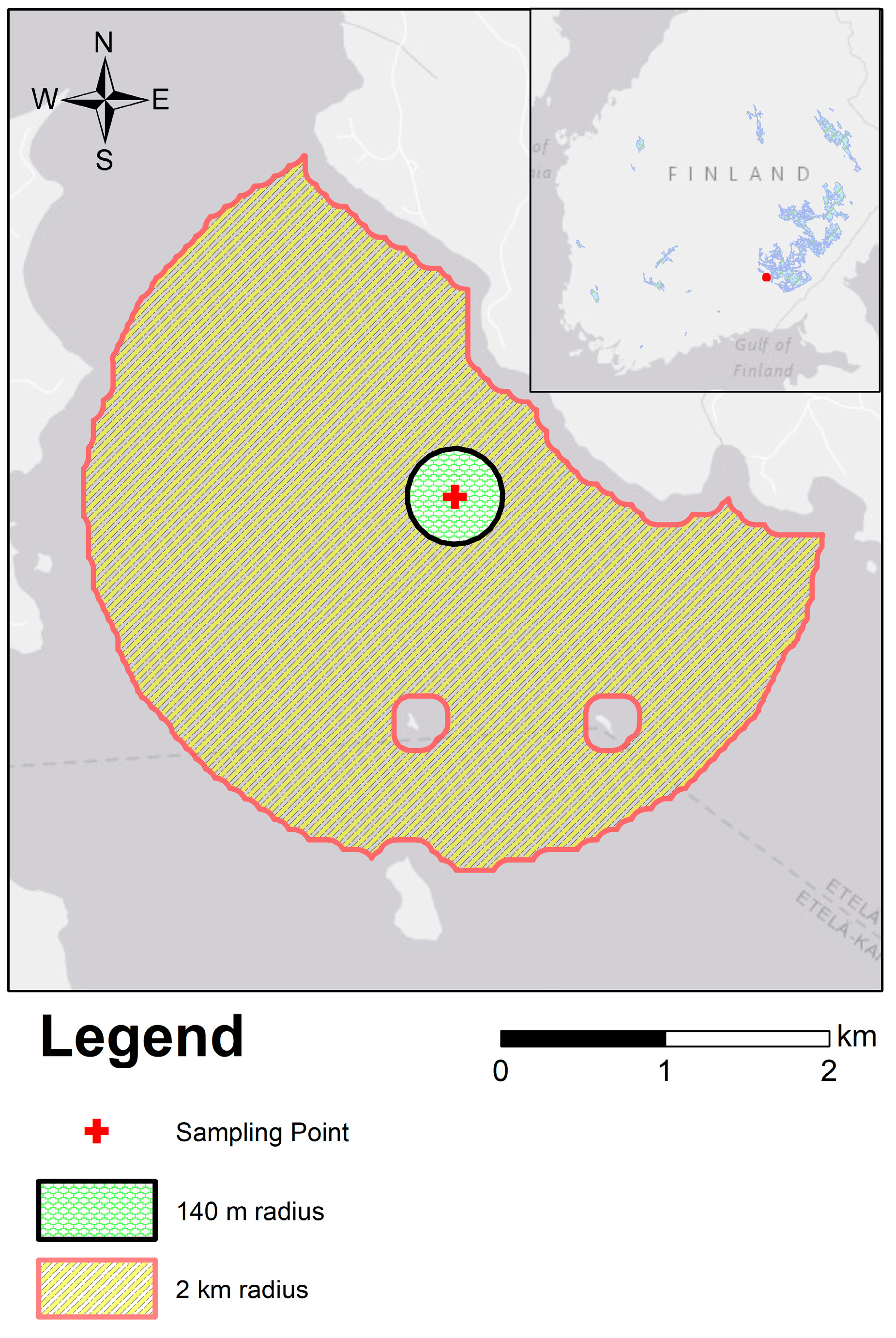
Figure 7 incorporate data from 6–11 out of the 19 lakes—for the remaining lakes, there are no satellite passes free of cloud cover, enough quality control standards, sun elevation or snow-free for the match-up. To assess Chl detection levels from different lakes, we have widened the time-window to ±4 days and lowered the radius to 500 m and included band 5 (SWIR). We have compared results obtained for individual lakes by addressing the lakes’ characteristics like depth, size and proximity of the sampling to the lakes’ margins.
Results from the individual multivariate models for each lake (
Figure 8) reveal that model performance is highly dependent on the Chl level. In
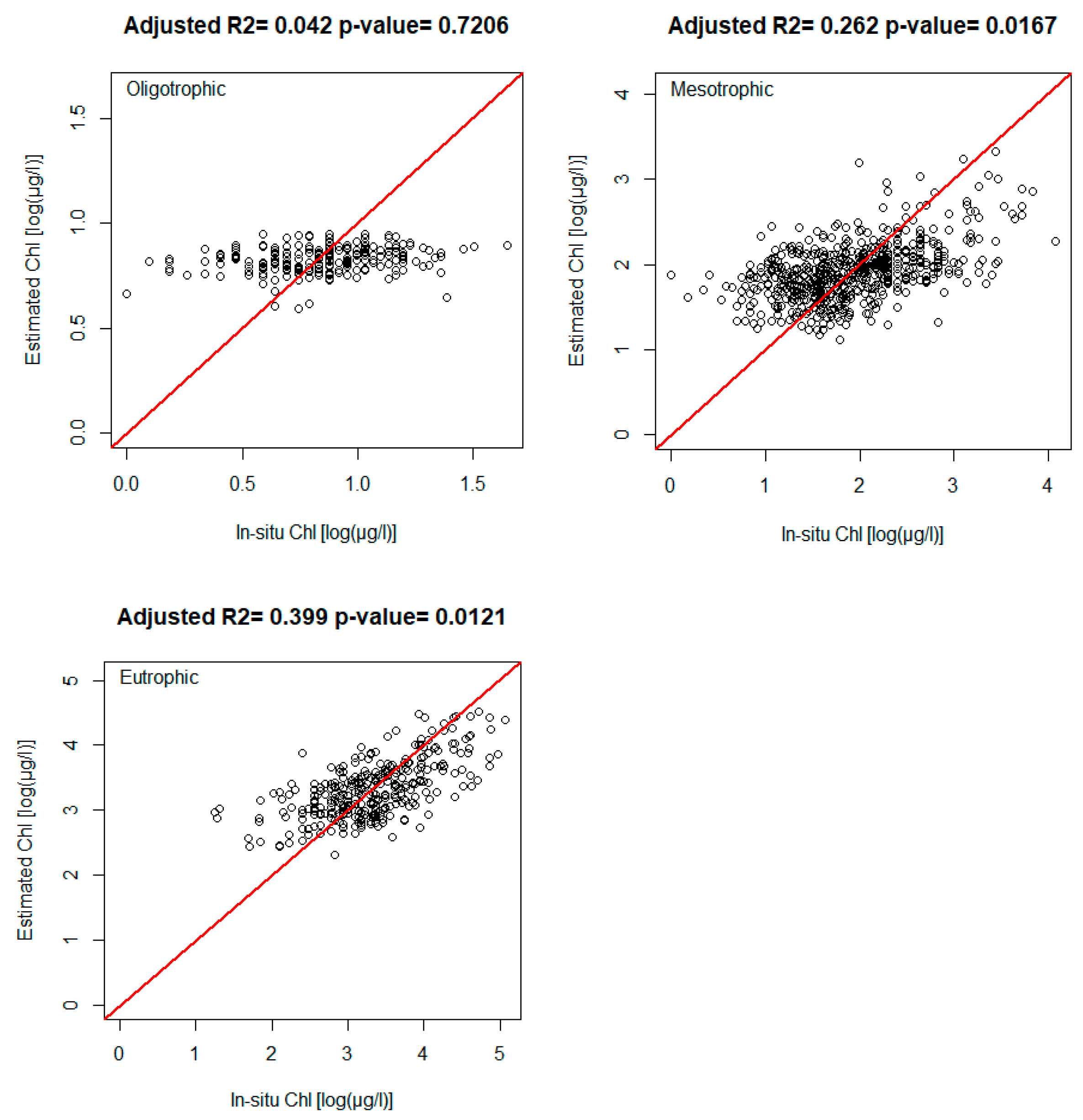
Figure 9, we show that the coefficient of determination, R
2, varies depending on the mean Chl concentration of each lake which we categorise as oligotrophic, mesotrophic and eutrophic. For each trophic state of a lake, the accuracy of the estimates from satellite imagery can vary greatly, but there are significantly better performances for eutrophic lakes.
Model Performance and Trophic State
The trophic state of lakes greatly influences the performance of the model built on the individual samples match-up. According to our results in
Figure 9, eutrophic lakes have better-resolved Chl estimations. Our results show that for eutrophic lakes the model performs twice as better as for mesotrophic lakes. All data points in
Figure 10 were filtered to the spring and summer season, i.e., DOY = [100:280].
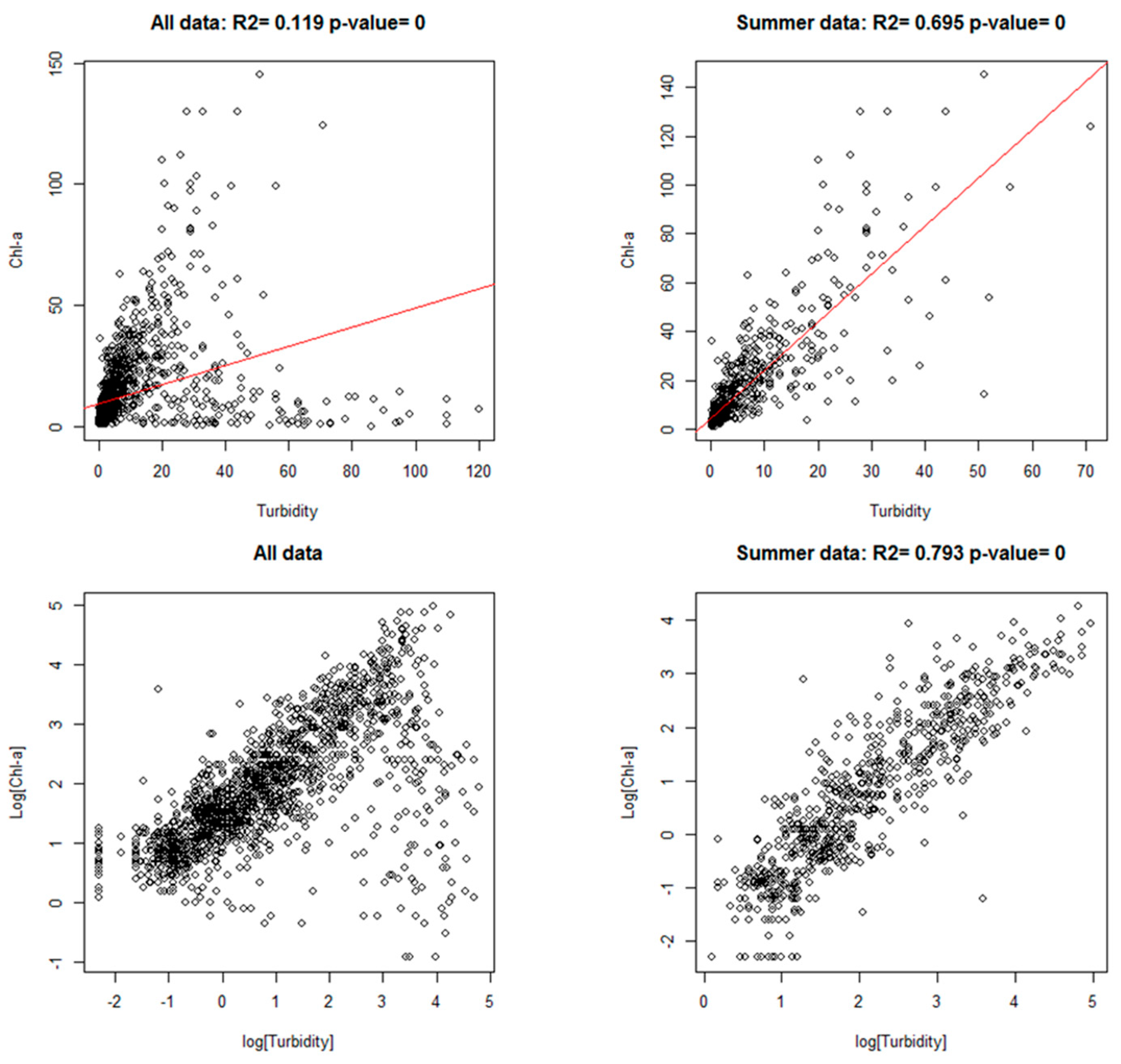
Model Performance Against In Situ Measurements of Chl and Turbidity
Our results show that turbidity and Chl are strongly correlated during summer months, i.e., DOY = [200:280]. Turbidity is therefore highly coupled with Chl during ~2.5 months of the year and before that the relationship is not present. The fact that during spring and until July the Chl is decoupled from turbidity provides a ground for phenology studies on phytoplankton blooms in lakes. Even in summer period, a model of LT reflectance and turbidity does not perform nearly as well as for Chl.
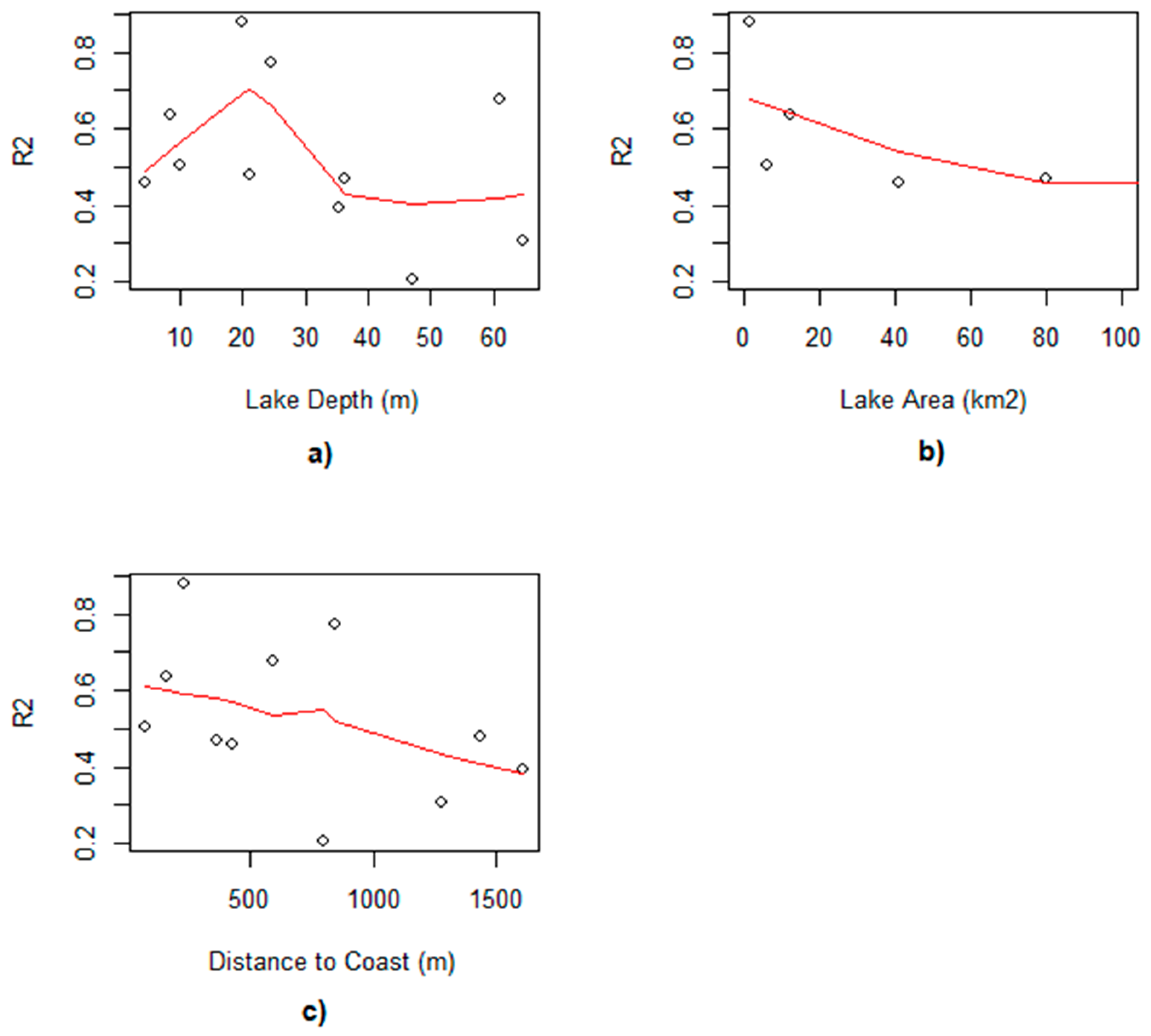
Performance of the Model Vis-a-Vis Sampling Location and Geophysical Characteristics
Sample collection set-up greatly influenced how well Chl concentrations at particular locations can be estimated using remote sensing (
Figure 11). Therefore, model performance is likely to vary within lakes that are close to each other. There is no linear trend relating depth and R
2, but the smaller the lake the better this model performs. Indeed, small lakes of less than 40 km
2, are better suited to be studied under this model. The relationship between the small lakes signal and the surrounding vegetation will be discussed further. Sampling locations that are very close to the shore (less than 200 m) have poor relation with the model estimates. On the other hand, the performance of the model is better for sampling locations between 200 and 700 m to the lakes’ margins (
Figure 11c). As will be discussed further, proximity to a lake’s margins can imply higher Chl if surrounding vegetation does not interfere with the optical characteristics of a lake’s water.
3.2. Seasonally Aggregated Data
We showed that the signal-to-noise ratio on the remotely sensed Chl is higher on the spring and summer period for eutrophic lakes. Hence, we aggregated images collected only during the summer period, i.e., between DOY 100 and 280. These images, when matched-up with the in situ samples, produce a well-performing model.
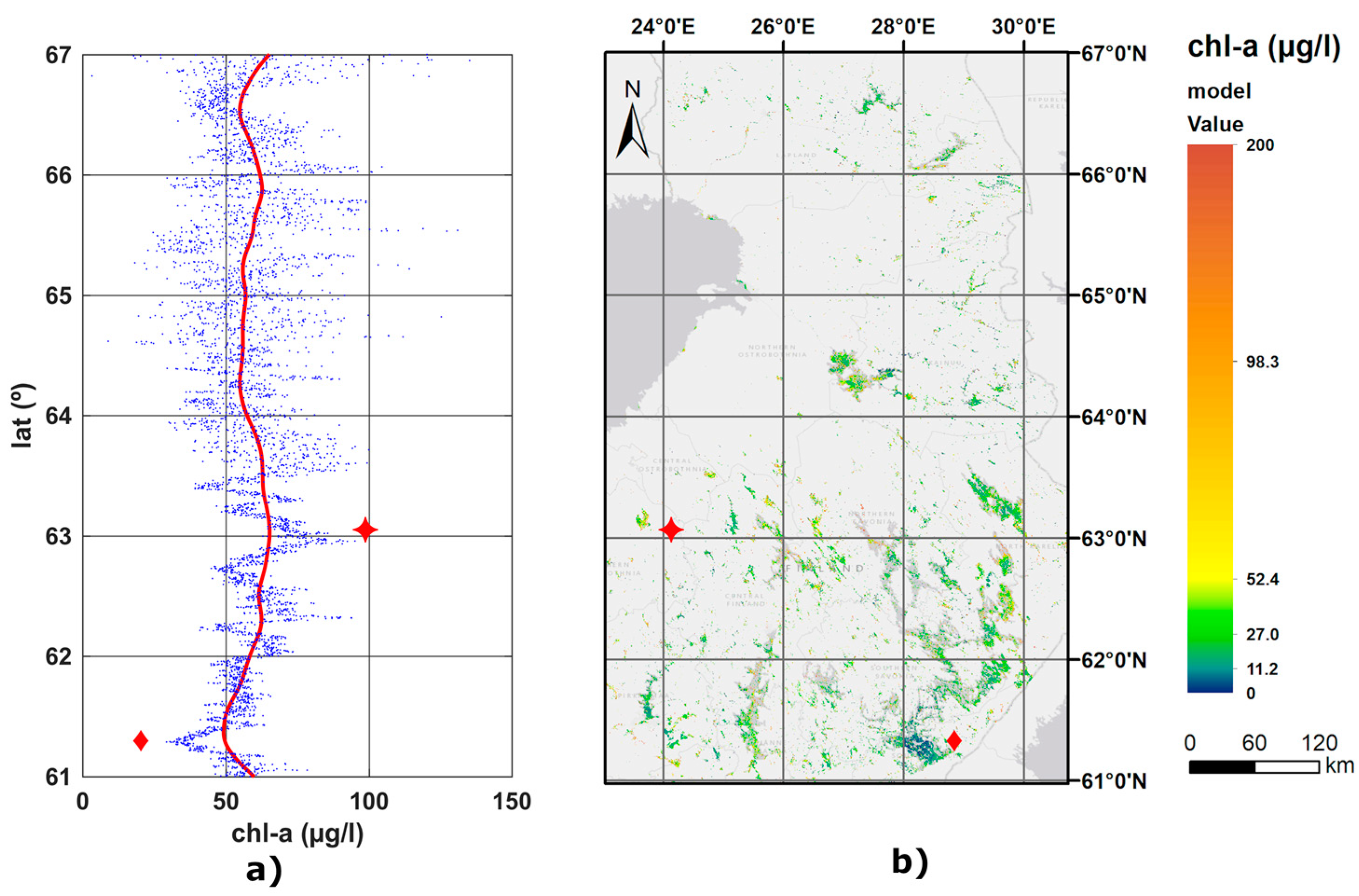
The seasonally aggregated model (
Figure 12) is the result of using a 500 m buffer with a ±2 day with averaged summer results for each lake. This result shows that the model performs well for large-scale estimation of Chl between DOY 100 and 280. The results of the Chl estimation for the whole of Finland, using the corresponding model, is shown in
Figure 13. As we expect that a gradient of rising latitudes has a large influence on the primary production of the lakes, we averaged the mean Chl in our model for the same latitude. For latitudes between 61.5°N to 63.5°N, there seems to be a clear positive trend on the increase of seasonal Chl. Lake Saimaa (red diamond in
Figure 13) is one of the less eutrophic ones, which contributes to the lowest average Chl concentration at the 61.2°N parallel. On the other hand, Lappajärvi (red star in
Figure 13 and detailed in
Figure 14) is Finland’s largest crater lake, it has been given by our model as a very eutrophic lake, which corresponds to the same concerns in the literature.
The clear trend contrasts with the northernmost areas where lakes are less abundant, smaller or sparser. Above 63.5°N, extreme variance of Chl can be seen. Under 63.5°N latitude, the model correctly identifies lakes that are typically eutrophic, due to the presence of agriculture or arable land.
4. Discussion
In this paper, we aim to better understand how statistical models based on LT perform considering different lakes across an extended time period, from 1984 to mid-2017 and an extended area. There are several differences between the TM and ETM+ sensors, onboard LT 5 and 7, respectively. TM is a multispectral scanning radiometer and ETM+ a whiskbroom scanning radiometer with an additional panchromatic band of 15 m resolution and two 8-bit “gain” ranges. ETM+ also features a 60 m resolution thermal band, replacing the one of 120 m resolution of TM. Nevertheless, these differences do not affect the bands considered in this paper, and we assume we can merge data from both sensors. Regarding the bands used in this study, it should be noted that, as land sensors, most of LT sensing capability (256 gray-levels) is used for the highly reflective surface of the land. Dark lakes are therefore harder to discern, and results are highly dependent on turbidity and trophic levels—benchmarking the differences between these sensing regimes (as the ones in
Figure 14) leads to the discussion of whether using atmospheric correction would lead to different results. Previous results showed that using atmospherically corrected data improved models only slightly [
15].
The choice of the spatial buffer around the sampling location has a small effect on the relationship between Chl and satellite data, but a buffer of 500–700 m was found to be the best choice for the models tested in this study. Additionally, a time window of ± 1 day performs better than a ± 2 day, meaning that satellite observations closer to the date when the field samples were collected are preferred. This is in line with previous studies that have assessed Chl over lakes, even in different geographic conditions (e.g., Minnesota, USA) [
29]. We also assessed the impact of extending this time-window up to ± 10 days. By doing so, the goodness of predictive Chl estimations has decreased significantly. The same is described by other authors, pointing out the decrease in certainty of the model with a longer time-window [
23]. Despite this, our models for non-averaged data performed better than other match-up activities for lakes at lower latitudes. As an example, the best model for a selection of water bodies in Maine, USA provided a correlation coefficient of at most 0.25 [
23].
As expected, the use of the SWIR 1 band did not improve the performance of the model derived from intra-annual data. In fact, SWIR bands have been used on the enhancement of the atmospheric correction algorithms for ocean color [
37] and their calibration for inland and coastal waters [
38]. However, under certain circumstances, the direct use of SWIR bands for Chl detection is fruitful, applicable to floating-bloom events and typical of cyanobacterial communities, where most of the biomass is at surface level [
39]. In the oceans, MODIS data from SWIR bands has also been used on the concept of a floating algae index [
40]. Our study does not focus on depth-resolved data and thus the use of SWIR was omitted.
On the other hand, our results demonstrate that we can determine, with good confidence, the lake specific mean Chl concentration in Finnish lakes (
Figure 12). This general model for all lakes must be used carefully. From
Figure 8, we see that the model performance varies amongst the sampled lakes on the daily aggregation approach. However, it is the level of Chl concentration that has the most significant impact on model accuracy. For timely estimations of Chl, the LT bands are not ideal as turbidity has a significant influence on the estimated Chl. Specifically, during the spring months, it was not possible to detect how turbidity is affecting our results. Studies have concluded that turbidity detection was feasible through TM data, but not Chl [
17]. It should be noted that if a lake is oligotrophic or CDOM-dominated (like most Finnish lakes) the radiometric resolution of LT data is insufficient to detect different Chl levels—lakes must be eutrophic for signal on both LT5-TM and LT7-ETM+ to be discerned (
Figure 9). Authors have argued that high CDOM levels shadow the optical signature of phytoplankton in the blue region of the spectrum rendering the blue/green ratio based Chl algorithms useless [
7]. Despite this, we have seen that seasonally aggregating data from satellite and in situ campaigns provides a reliable model. In this model, some concerns must be addressed. For example, the land adjacency effect is particularly relevant in small lakes. As seen in
Figure 11c, preliminary results on the performance of the model with respect to how close the sampling locations are to the margins provide insights that need to be further studied.
The adjacency effect is known to reduce apparent surface contrast [
41] and is particularly severe in the case of dark water bodies surrounded by dense vegetation. As LT imagery is developed mostly for land applications, there is a mask for the lakes’ adjacency effect to land but not the converse. In areas near the lakes’ margins, the adjacency effect can overestimate Chl concentration as it acts by changing reflectance at shorter wavelengths [
26]. Boreal waters are known for their high concentrations of humic and fluvic acids (CDOM) leached from the surrounding vegetation and soils. These, in turn, reduce the light availability in the blue spectral region [
26]. In Finnish lakes, high CDOM absorbs nearly all water leaving radiance. Thus, the radiance measured above lakes consist of radiation backscattered from the atmosphere, radiation reflected from the water surface and the radiation backscattered from the adjacent land. Water signal is often negligible in the blue band and can be discarded for such lakes. It is paramount to have in situ studies that sample a lake at different distances from the coast—such results would greatly improve our capability to quantify the adjacency effect in these types of lakes where sun elevation is low and most of their waters are brown. From our results, one factor that seems to ameliorate detection performance—including the minimization of the adjacency effect—is the trophic level of the lake. Another evident source of error is the potential effect of shallow lake grounds. Our methodology is robust on defining the lakes’ margins by creating a permanent water mask. The use of a buffer away from the lakes margins and small islets can render unlikely the presence of shallow banks under water—nor can we guarantee the avoidance of underwater vegetation. Some of these banks can also appear and disappear over the extensive timespan of this study. The revision of earlier studies on aquatic vegetation could influence resolving phytoplankton from our detection methodology [
13].
As seen in lakes Lappajärvi (
= 86.95 µg/L) and Saimaa (
= 10.1 µg/L), the model correctly identified them as eutrophic and oligotrophic lakes, respectively. Lappajärvi, being a brown water lake, contains humic material and has a high phosphorus content. The phosphorus load into Lappajärvi comes from agriculture and cattle farming, and measures have been considered to decrease the impact of eutrophication and mitigate algae bloom occurrence [
42]. Our results also corroborate the trends in eutrophication, such as Lake Keurusselkä (
= 31.83 µg/L), reported as having an increasing trophic status, which corresponded to 10 µg/l in 2010 [
43]. In Lake Saimaa, depicted in
Figure 14b), the average Chl during the summer period is 10.1 µg/l, which also corresponds to the literature, as this is a typical oligotrophic lake [
44]. The results of this study are particularly timely now that new data is emerging and Finnish lakes like Kallavesi, Näsijärvi and Vesijärvi have already been reported to experience later freeze dates and earlier ice break-up dates [
45]. Understanding the impact of such geophysical changes on lake Chl content is of utmost importance, and can be applied to better understand phenology changes of phytoplankton in freshwater systems [
16]. As
Figure 15 shows, having a product for Chl can improve environmental management by addressing the surrounding land use changes and their impacts.
Early semi-operative approaches pointed out the possibility of studying small lakes (and their small details,
Figure 16) if not for the medium and low resolution of conventional ocean color sensors [
14]. Our study also revisits the application of in situ data reference data in the conception of empirical Chl models [
12,
14,
46,
47] by applying new cloud computing technology like Google Earth Engine [
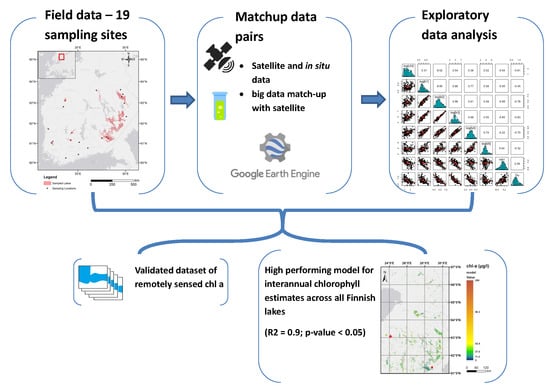
27] to the analysis of thousands of images and in situ measurements corresponding to long time series of data. The use of our methodology can allow for the application of a model to smaller lake, more remote, or simply less studied than a bigger “control” lake used for in the validation campaign.
Additionally, we underline the acute need to monitor Boreal lakes. In other regions, like Alberta, Canada, variations of trophic levels have been linked to climate, biotic variations and geology [
10]. A similar approach based on a model for all Finnish lakes is of the utmost importance.
5. Conclusions
Despite its relatively high spatial resolution, LT imagery is often overlooked for the remote sensing of Chl, due to the low spectral resolution of the sensors. Nevertheless, our results demonstrate that estimations over aggregated time windows can be done with high accuracy. Our results show that LT imagery can fill the resolution gap when it comes to monitoring the small, numerous and adjacent lakes found in the Finnish geophysical context.
Calculating representative monthly means for the satellite images can produce useful results of the model allowing for higher correlations and typical characterizations of the different water bodies within specified timeframes. Assessing Chl is possible due to its strong relationship with turbidity, although multi-linear models of LT data to estimate turbidity do not produce results as good as the Chl models. The relationship between Chl and turbidity is most robust during summer, and, since the model performs better during this period, the derived model can be used for further studies of phenology shifts during the blooming seasons.
The adjacency effect, when quantified, could explain the high variations of our model when applied to the calculation of Chl concentration in small lakes. During this study, we came across the difficulty of identifying the impacts of the adjacency effect both through our analysis and the timely literature. Therefore, we believe that the work here can open the discussion for retrieving more sophisticated models for Chl estimation, giving a better suited measurement of adjacency effects from land on small water bodies remotely sensed through LT imagery. Similar studies have already been carried for the adjacency effect on MODIS, SeaWiFS, MERIS, OLCI, OLI and MSI for the case of mid-latitude coastal environments [
48]. Although our methodology features a buffer from the lakes’ margins, this might not be enough to completely eradicate the impact of the adjacency effect.
Satellites can provide valuable information in cases where required sampling density is high, or field surveys are expensive or even impossible to carry out. Especially, satellite images may provide informative prior information for field sampling estimates, in a Bayesian setting. As lakes are sensitive to many climate factors, they are certainly useful in climate change monitoring.