Modelling Water Colour Characteristics in an Optically Complex Nearshore Environment in the Baltic Sea; Quantitative Interpretation of the Forel-Ule Scale and Algorithms for the Remote Estimation of Seawater Composition
Abstract
1. Introduction
- (1).
- Formulas based on those inherent optical properties (IOPs) of seawater that are relatively easily measured in situ using commercially available oceanographic instruments. These formulas use coefficients of light scattering by suspended particles bp(λ), coefficients of light absorption by such particles ap(λ), or the backscattering ratio bbp/bp in different spectral bands; with the developed formulas, we can estimate the concentrations of SPM, POM, POC, Chla, and the ratio POM/SPM (see [14,21]);
- (2).
- Formulas based on seawater IOPs that can be simply estimated by remote sensing. These formulas employ parameters like the coefficient of light backscattering by particles bbp(λ) or the light absorption coefficient by the sum of suspended and dissolved substances in seawater an (λ); with the developed formulas, we can estimate levels of SPM, POM and POC (see [22]);
- (3).
- Formulas based directly on the remote-sensing reflectance Rrs(λ)—both the magnitude of Rrs in certain red or near infrared bands (e.g., 625, 645, 665 and 710 nm) or the colour ratios for specific pairs of spectral bands (e.g., 490 and 589 nm, 555 and 589 nm, or 490 and 625 nm); with the developed formulas, we can estimate SPM, POM, POC and Chla levels (see [22,23]).
2. Materials and Methods
2.1. Empirical Data from the Nearshore Environment
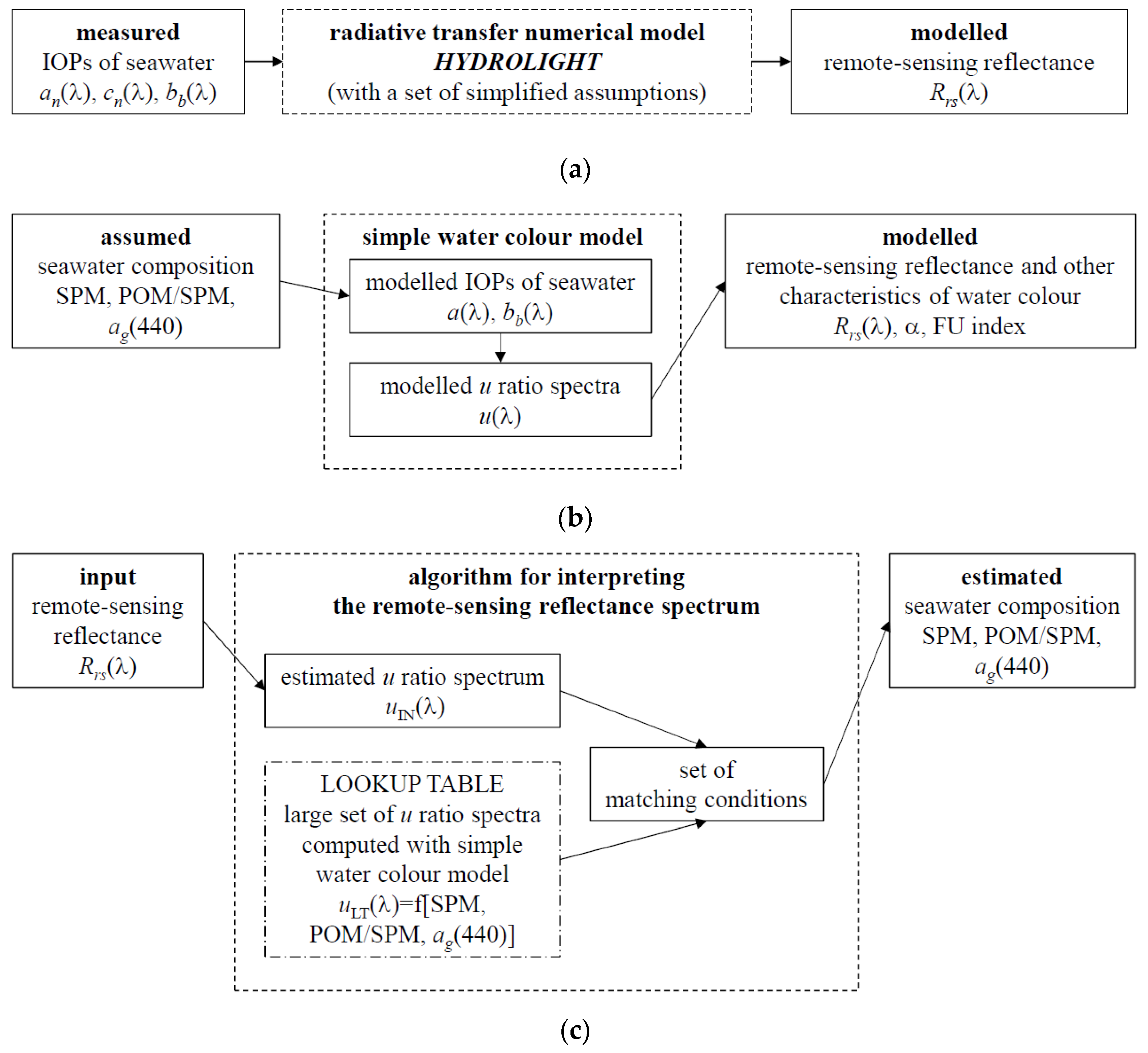
2.2. Main Modelling and Computational Approaches
- Representing the use of the standard version of the Hydrolight model to calculate Rrs spectra; such calculations are made on the basis of given (in this case measured) spectra of the absorption, attenuation and backscattering coefficients (an(λ) = ap(λ) + ag(λ), cn(λ) and bb(λ));
- Representing the application of a simple water colour model (a new version of the simple model proposed earlier, see [37]); with this model, for assumed values of the SPM concentration, POM/SPM and ag(440), one can approximately determine the spectrum of Rrs, and also estimate the hue angle α and the FU index according to the Forel-Ule scale. In its intermediate steps, this model estimates the spectra of coefficients a and bb, and calculates the spectrum of the u ratio (u(λ)), which is defined on the basis of these water IOPs;
- Representing the practical algorithm for interpreting a known (input) spectrum of Rrs based on the modelling results. The new algorithms will do this as follows: On the basis of the input Rrs spectrum, the spectrum of u(λ) will first be estimated (and used as the auxiliary quantity) and then compared with the numerous spectra contained in a lookup table that pools the results obtained with the simple water colour model. Possible variants of the operation of such an algorithm will be derived by adopting alternative sets of matching conditions. Finally, the algorithm will estimate a set of values characterising the composition of seawater: SPM concentration, POM/SPM and ag(440).
2.2.1. Hydrolight Model and Simplifying Assumptions Adopted
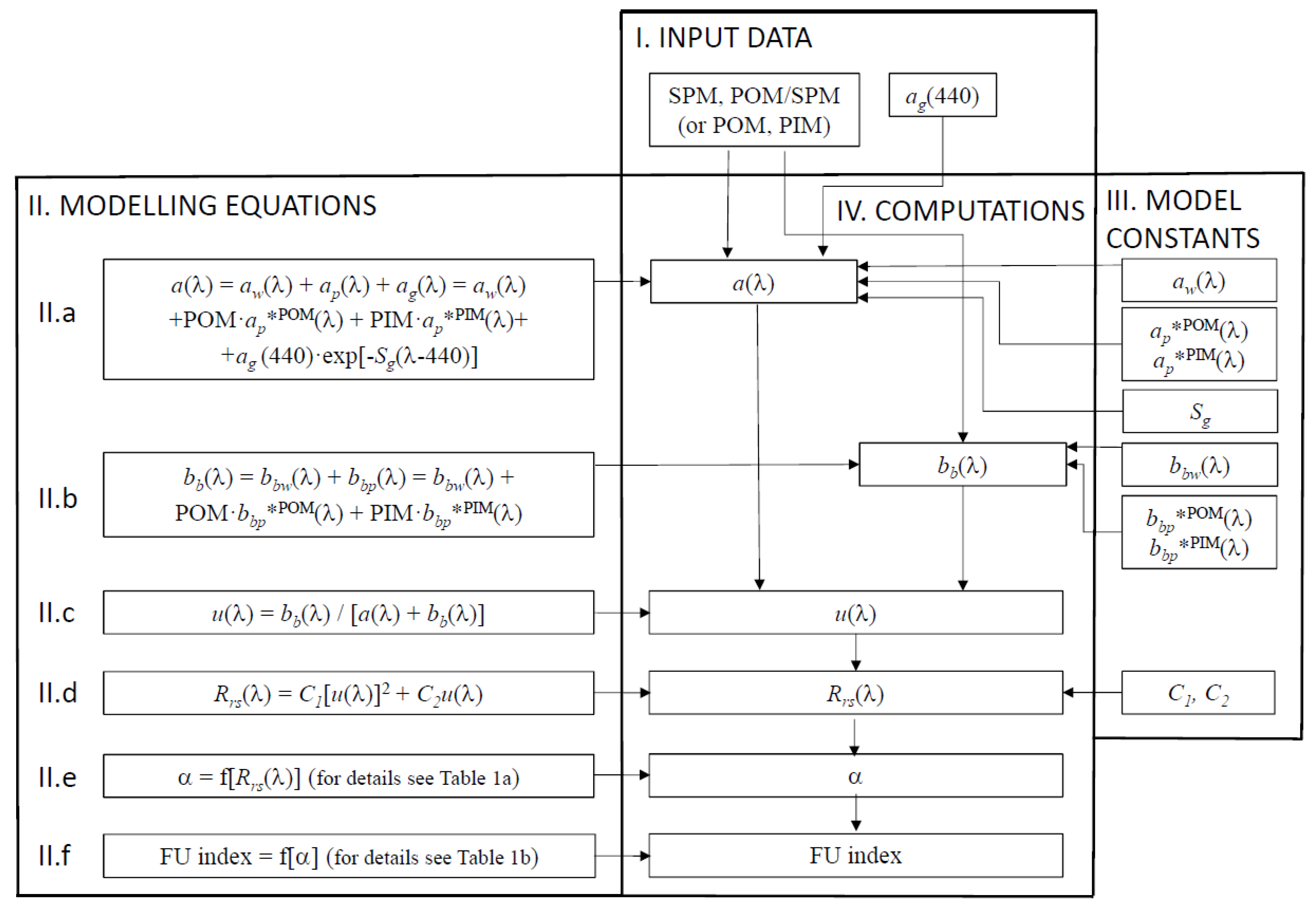
2.2.2. Simple Water Colour Model
- -
- -
- It was assumed that for both the organic and inorganic fractions of suspended particles (POM and PIM), typical/average values of the mass-specific optical coefficients could be taken into account, i.e., the coefficients respectively denoted by ap*POM, ap*PIM, bbp*POM or bbp*PIM (definitions are given later). The spectral values of these assumed constants will be determined on the basis of available empirical data and will be given in the next section;
- -
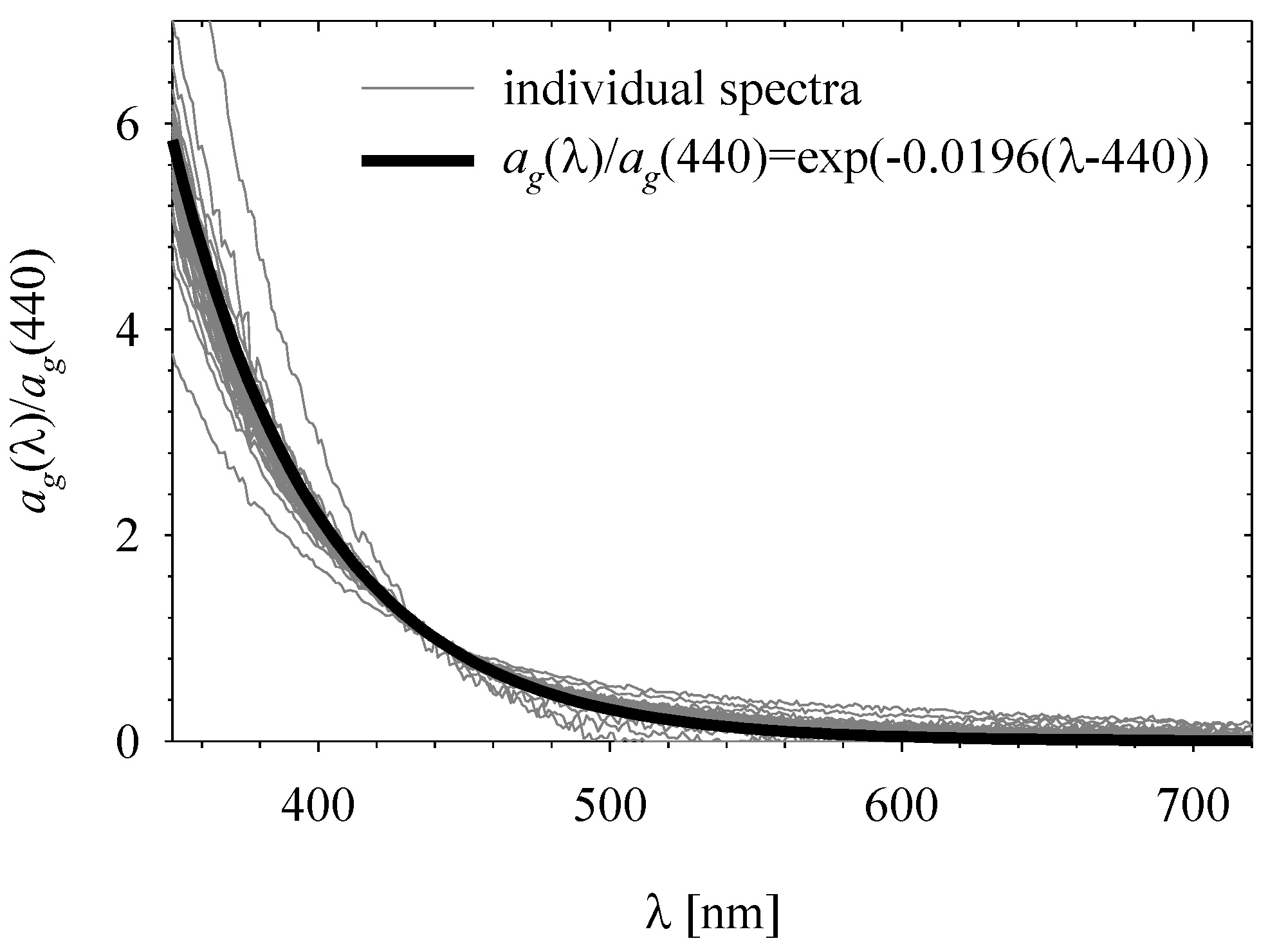
- It was assumed that the spectrum of the absorption coefficient by CDOM ag(λ) could be approximated by an exponential function (the last term of the sum presented in block II.a in Figure 2), which takes into account the constant value of the typical slope of this spectrum, denoted by Sg. A typical value of this constant determined on the basis of the available empirical material will be specified in the next section;
- -
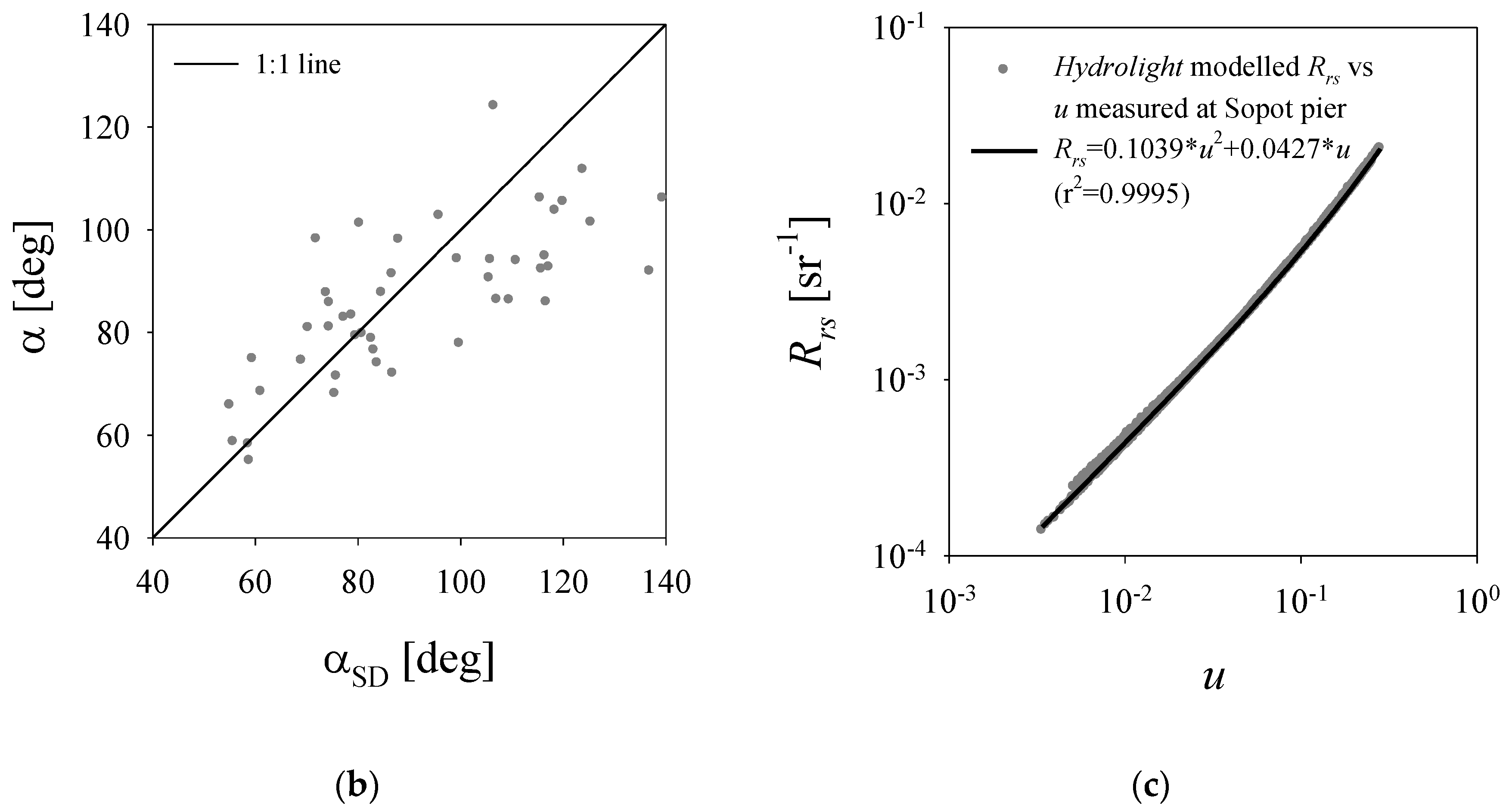
- It was assumed that the approximate dependence of the remote-sensing reflectance spectra Rrs(λ) on the spectra of u(λ) could be described by a quadratic function requiring only two constants, C1 and C2. The values of these constants, determined from the calculations done with the Hydrolight model, will be given in the next section.
3. Results and Discussion
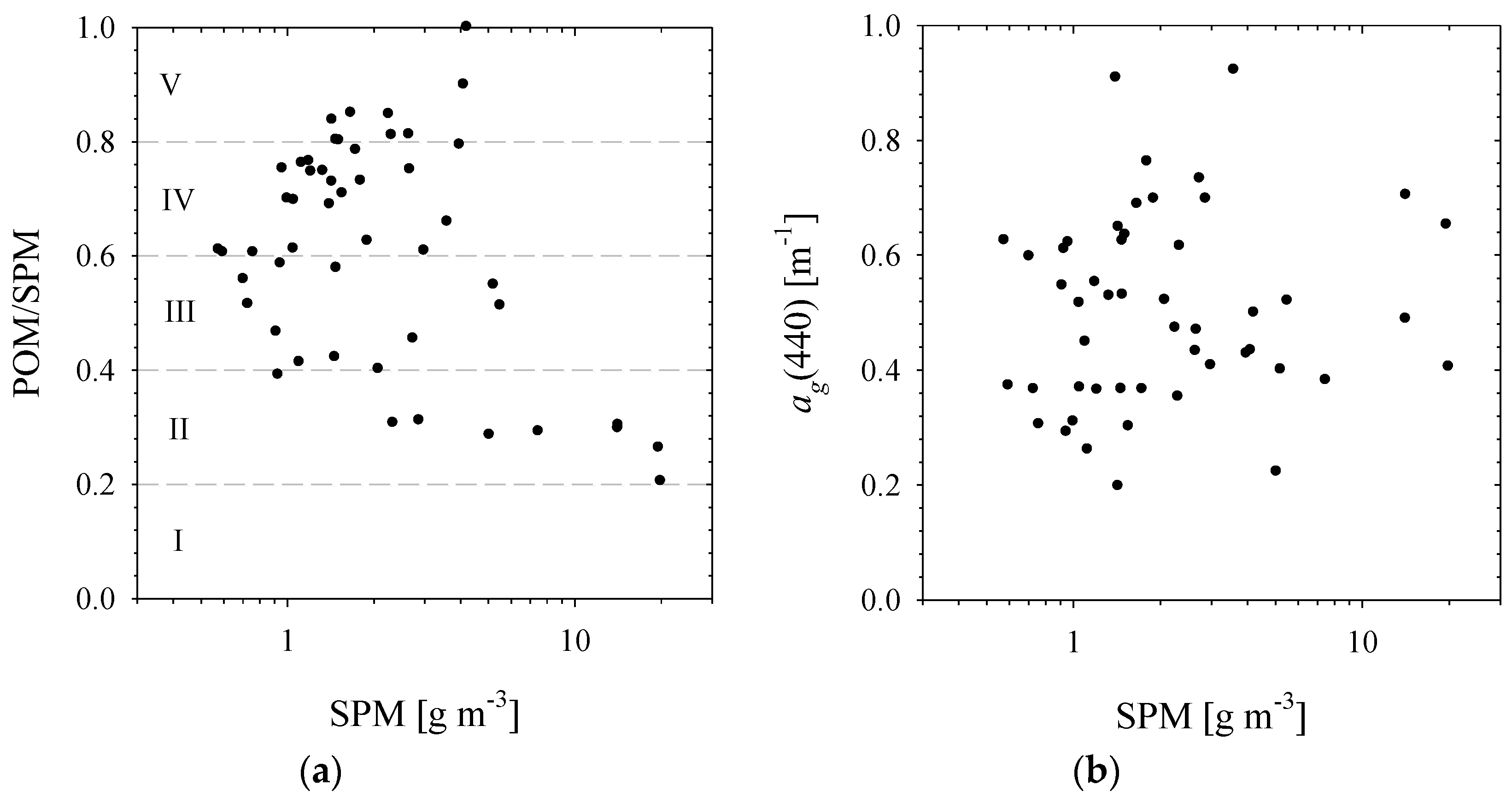
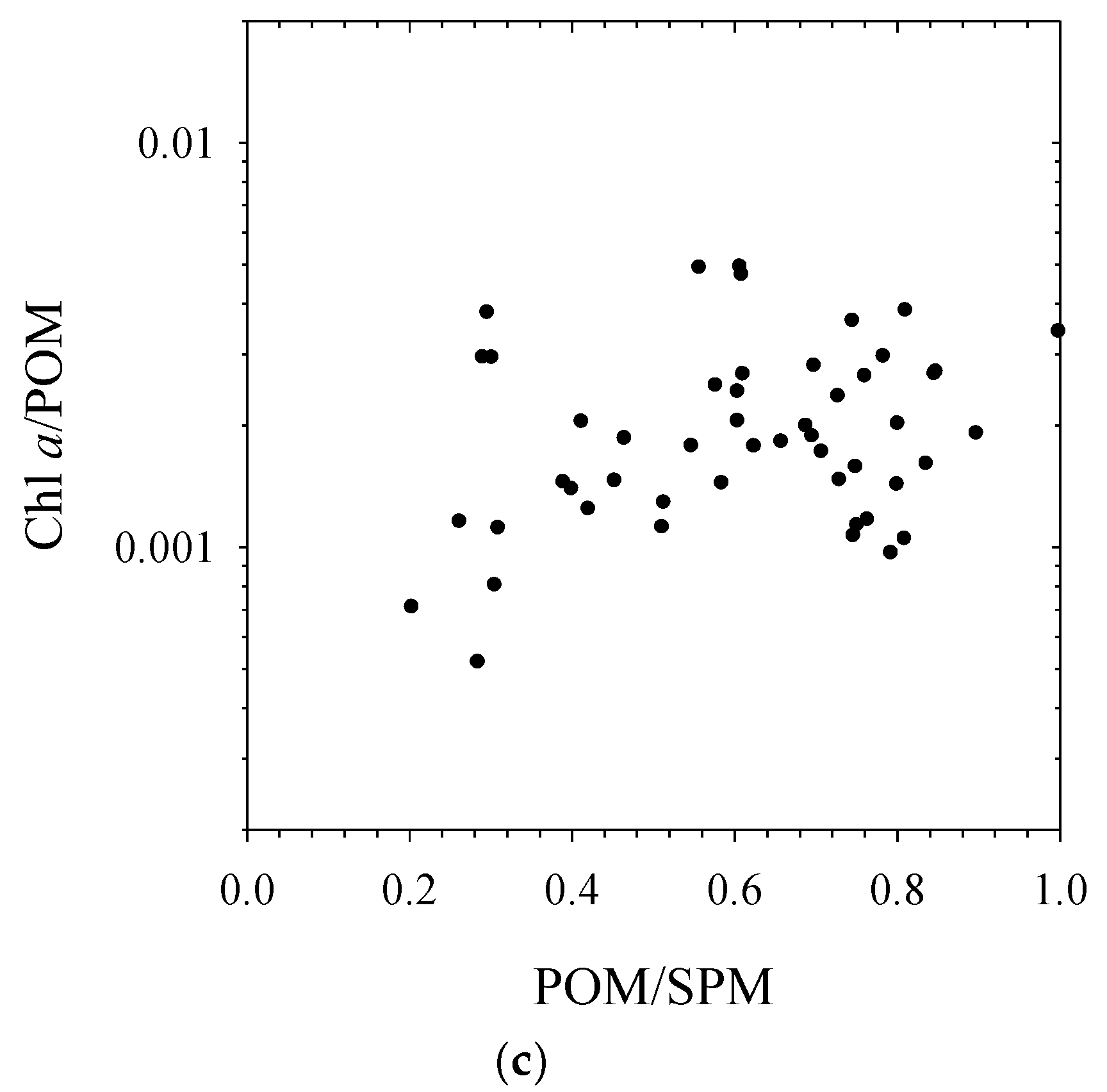
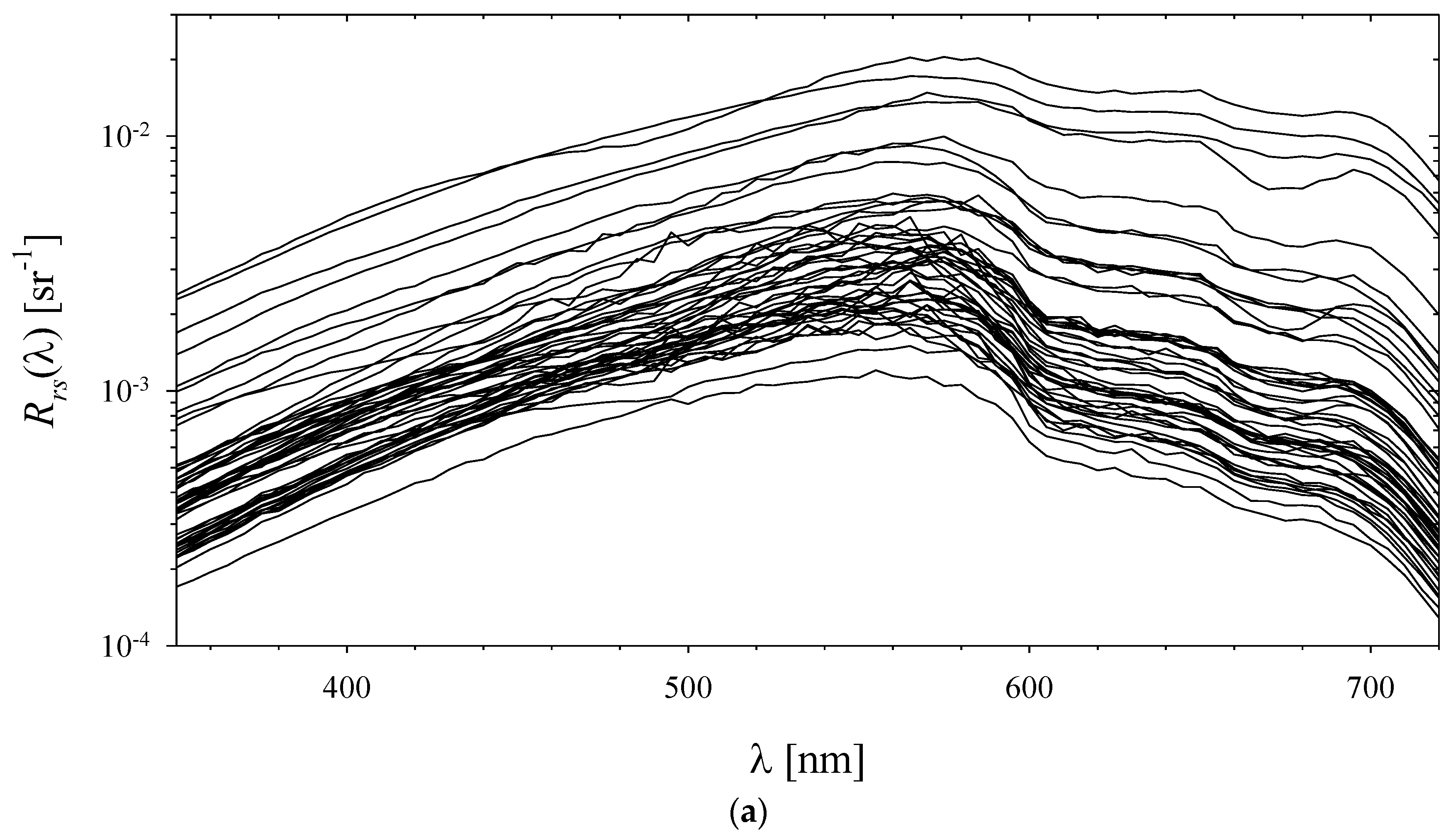
3.1. Variability of Biogeochemical and Optical Quantities in the Empirical Dataset
3.2. Average Specific Inherent Optical Properties—Constants for the Simple Water Colour Model
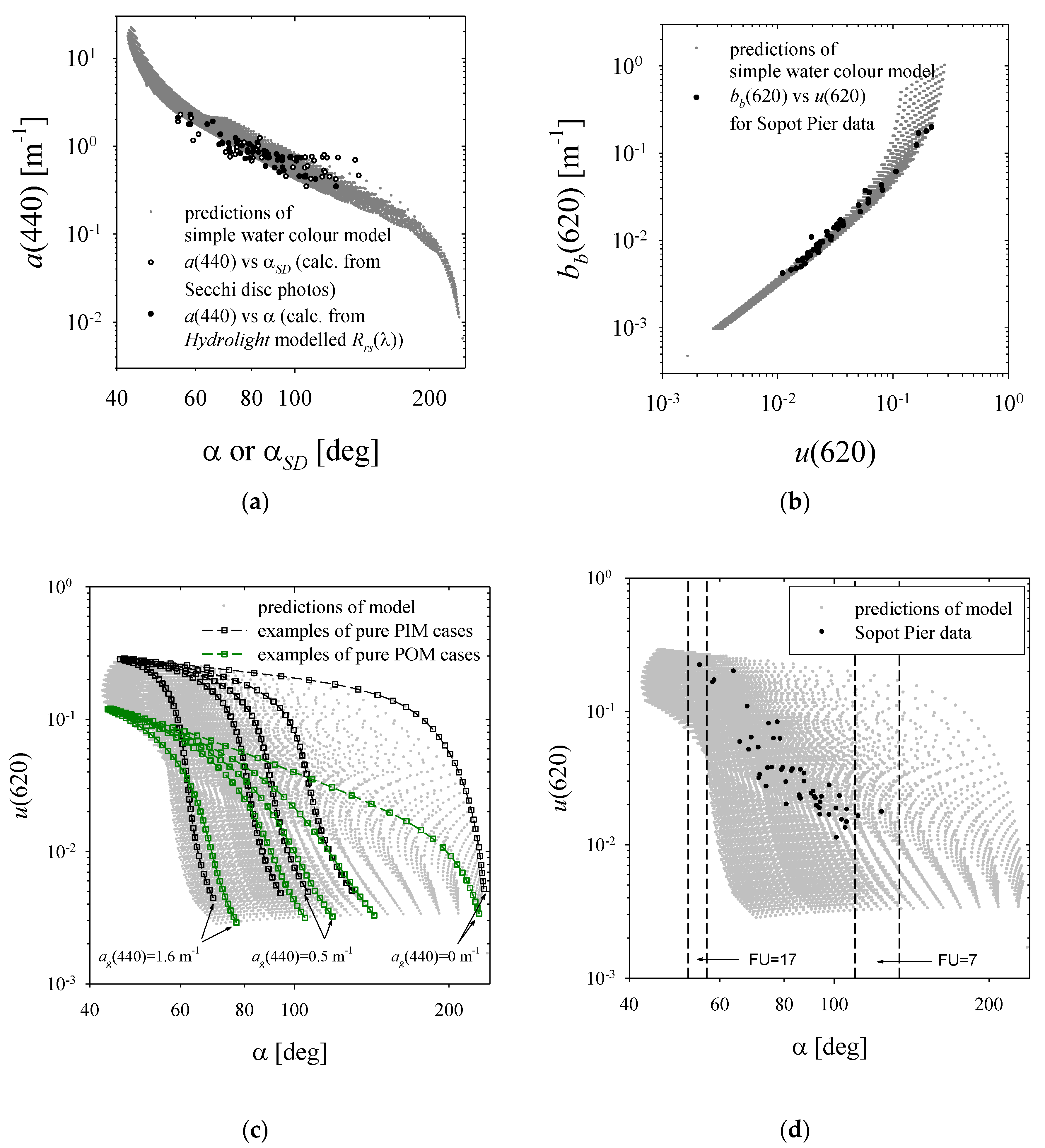
3.3. The Results of the Hydrolight Model
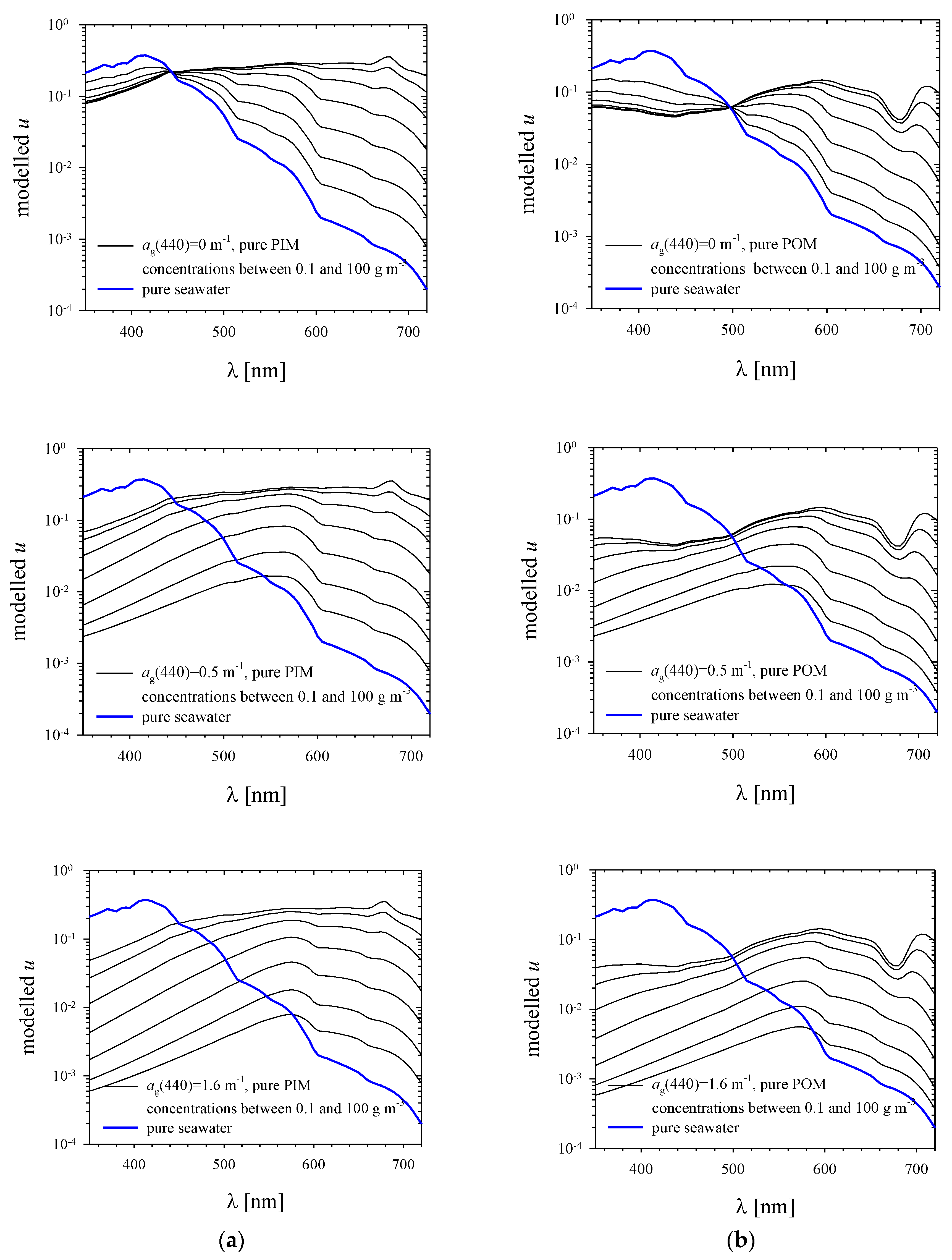
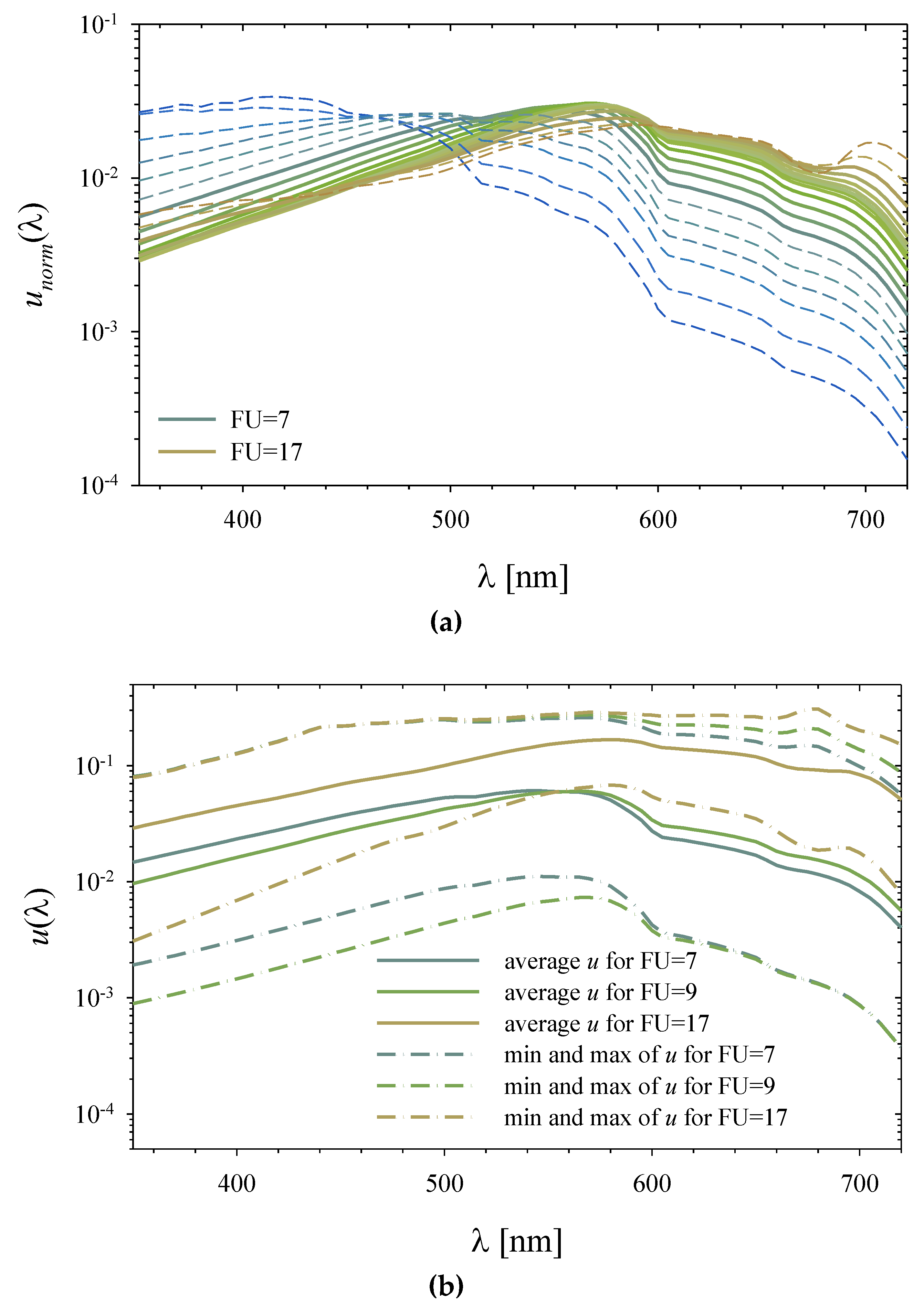
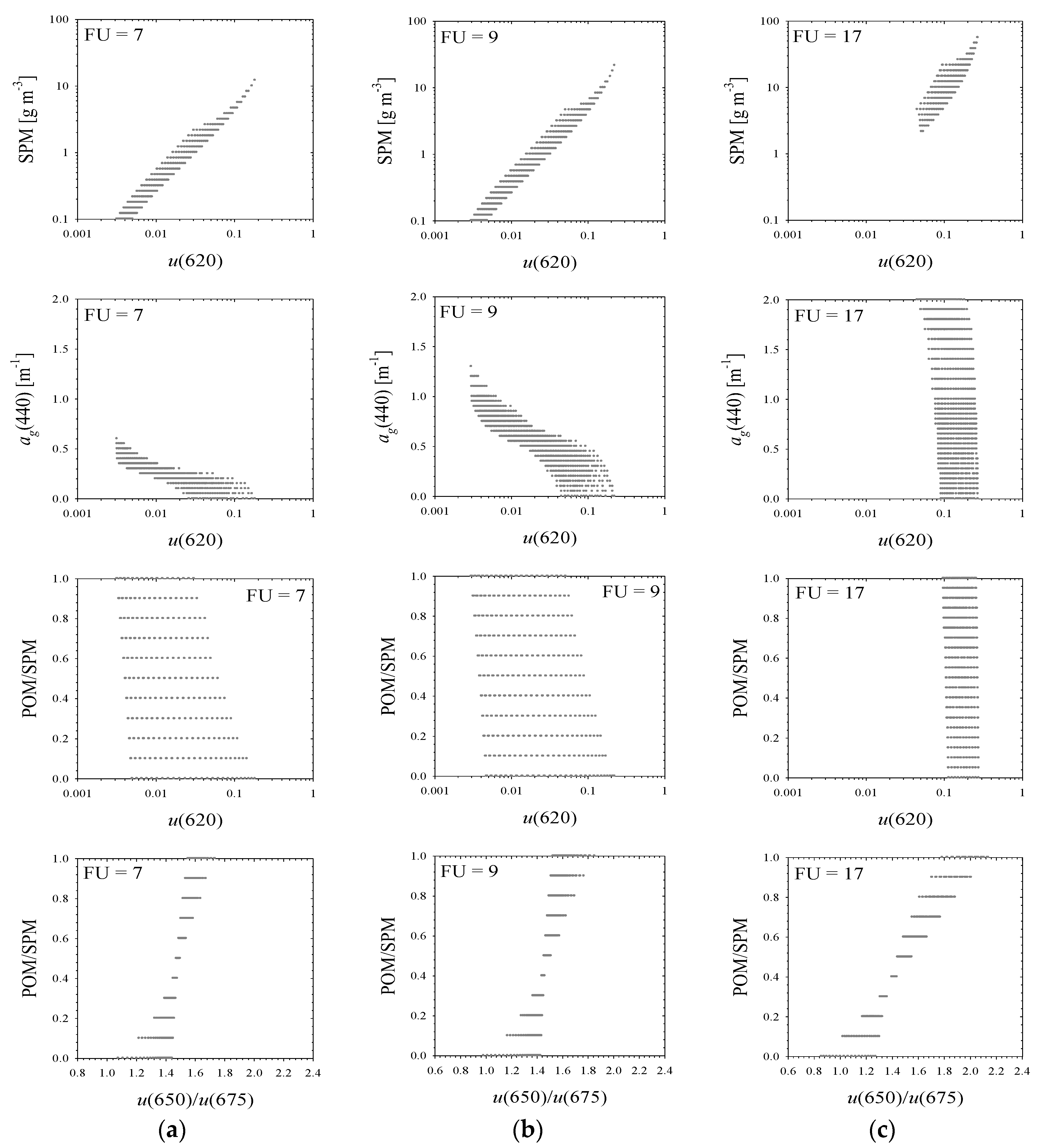
3.4. The Results of the Simple Water Colour Model
- -
- 37 different SPM concentrations, from 0.1 to 100 g m−3, obtained by using a fixed multiplier of , which yields 12 different values for each order of magnitude of variation in SPM concentration;
- -
- 11 POM/SPM ratios, from 0 to 1, with a constant step increasing consecutive values by 0.1;
- -
- 11 ag(440) coefficients, from 0 to 2 m−1, with a step of 0.05 m−1 for values <1 m−1, and a step of 0.1 m−1 for values >1 m−1.
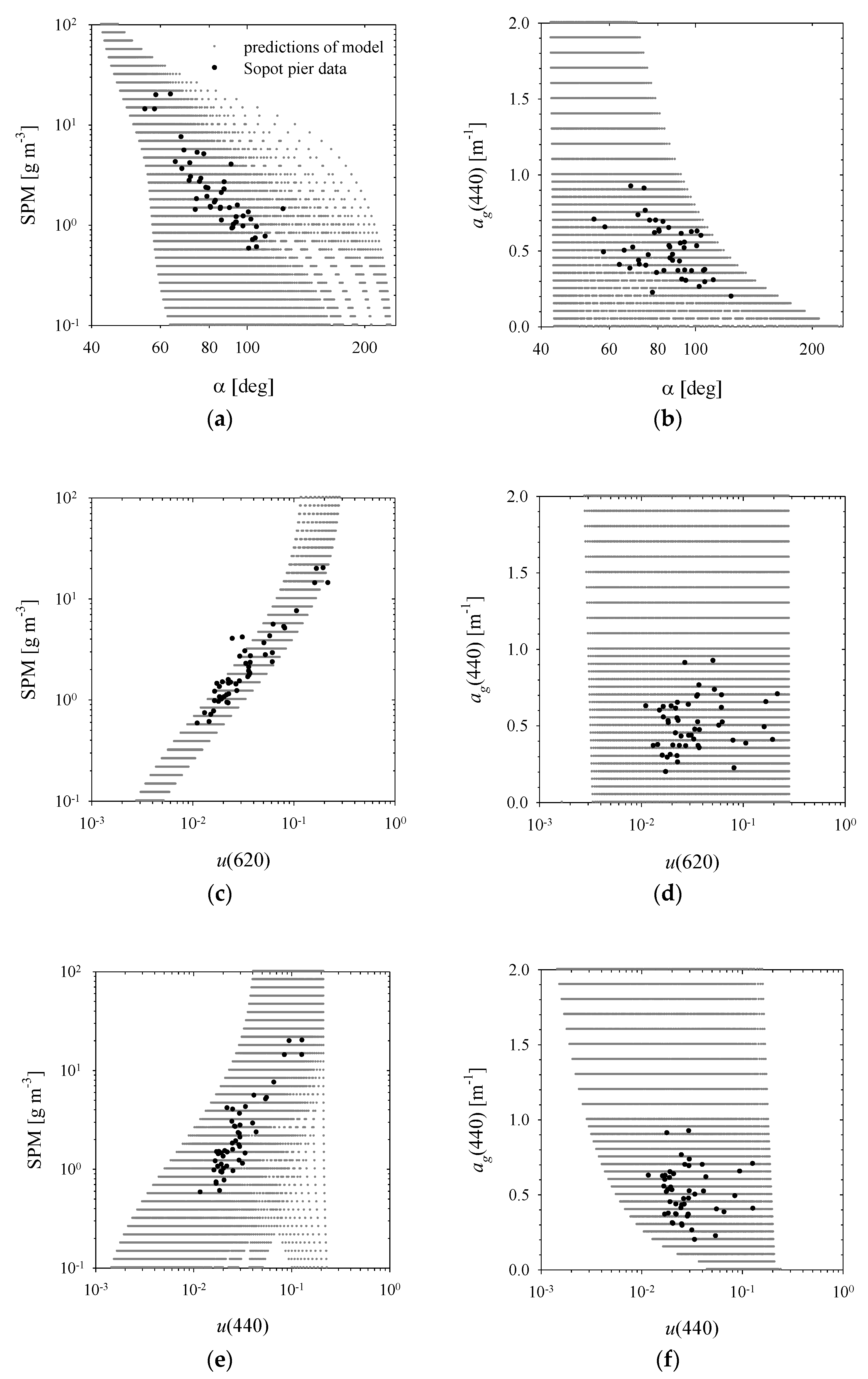
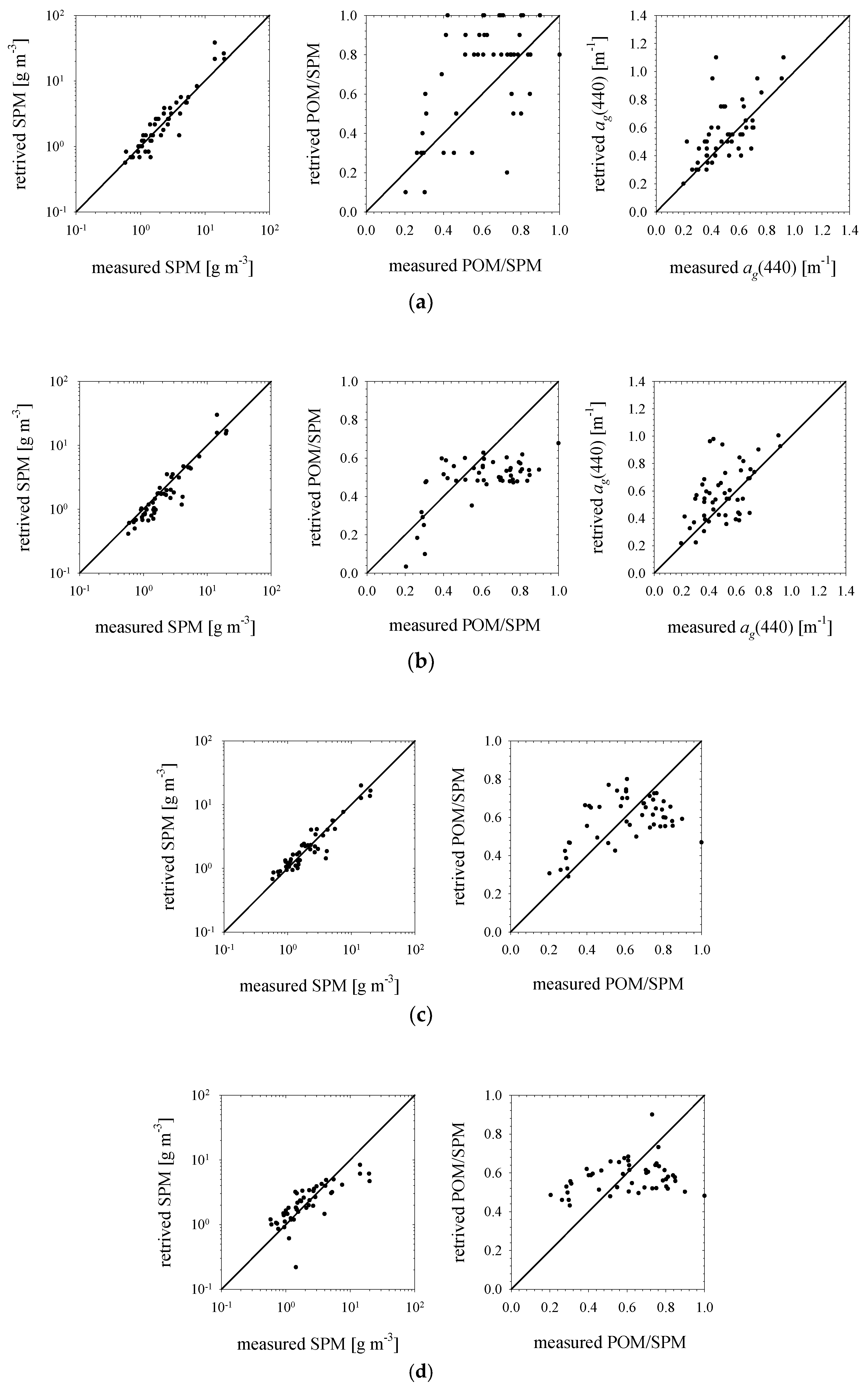
3.5. Examples of Algorithms for Estimating the Composition of Seawater Using the Modelling Results
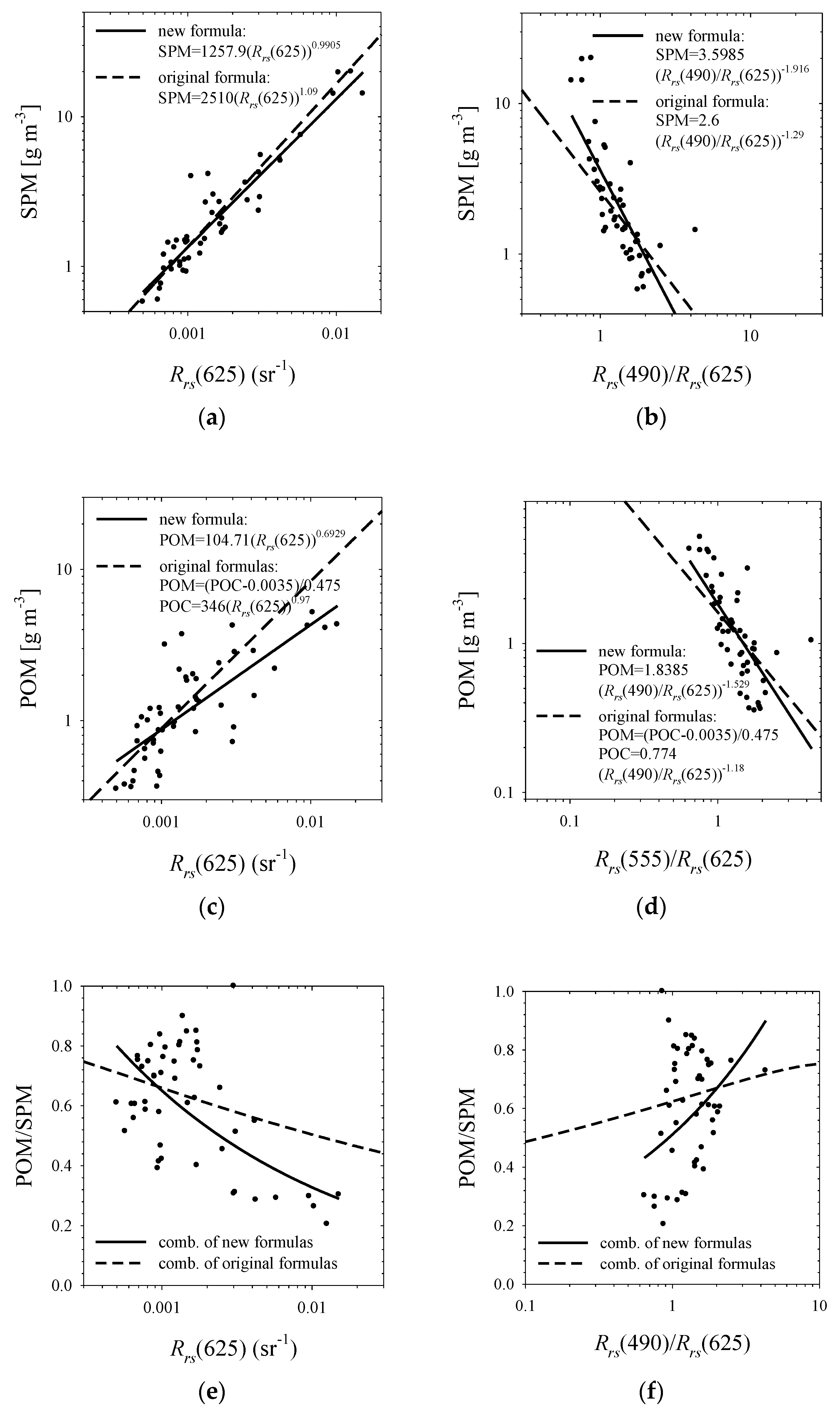
3.6. Existing Simple Statistical Formulas for Estimating Seawater Composition and Their Modified Versions Adapted to the Current Dataset
3.7. Comparison of the Accuracies of Estimation Using the New Algorithms and the Simple Statistical Formulas
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IOCCG. Synergy between Ocean Colour and Biogeochemical/Ecosystem Models. In IOCCG Report Series, No. 19; Dutkiewicz, S., Ed.; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2020; p. 184. [Google Scholar] [CrossRef]
- Wernand, M.R.; van der Woerd, H.J. Spectral analysis of the Forel-Ule ocean colour comparator scale. J. Europ. Opt. Soc. Rap. Public. 2010, 5, 10014. [Google Scholar] [CrossRef]
- Wernand, M.R.; Hommersom, A.; van der Woerd, H.J. MERIS-based ocean colour classification with the discrete Forel–Ule scale. Ocean Sci. 2013, 9, 477–487. [Google Scholar] [CrossRef]
- Novoa, S.; Wernand, M.R.; van der Woerd, H.J. The Forel-Ule scale revisited spectrally: Preparation, protocol, transmission measurements and chromaticity. J. Europ. Opt. Soc. Rap. Public. 2013, 8, 13057. [Google Scholar] [CrossRef]
- Novoa, S.; Wernand, M.R.; van der Woerd, H.J. The modern Forel-Ule scale: A ‘do-it-yourself’ colour comparator for water monitoring. J. Eur. Opt. Soc. Rap. Public 2014, 9, 14025. [Google Scholar] [CrossRef]
- Garaba, S.P.; Voss, D.; Zielinski, O. Physical, Bio-Optical State and Correlations in North–Western European Shelf Seas. Remote Sens. 2014, 6, 5042–5066. [Google Scholar] [CrossRef]
- Garaba, S.P.; Friedrichs, A.; Voss, D.; Zielinski, O. Classifying Natural Waters with the Forel-Ule Colour Index System: Results, Applications, Correlations and Crowdsourcing. Int. J. Environ. Res. Public Health 2015, 12, 16096–16109. [Google Scholar] [CrossRef] [PubMed]
- Van der Woerd, H.J.; Wernand, M.R. True Colour Classification of Natural Waters with Medium-Spectral Resolution Satellites: SeaWiFS, MODIS, MERIS and OLCI. Sensors 2015, 15, 25663–25680. [Google Scholar] [CrossRef]
- Van der Woerd, H.J.; Wernand, M.R. Hue-angle product for Low to medium spatial resolution optical satellite sensors. Remote Sens. 2018, 10, 180. [Google Scholar] [CrossRef]
- Busch, J.A.; Price, I.; Jeansou, E.; Zielinski, O.; van der Woerd, H.J. Citizens and satellites: Assessment of phytoplankton dynamics in a NW Mediterranean aquaculture zone. Int. J. Appl. Earth Obs. 2015, 47, 40–49. [Google Scholar] [CrossRef]
- Brewin, R.J.; Brewin, T.G.; Phillips, J.; Rose, S.; Abdulaziz, A.; Wimmer, W.; Sathyendranath, S.; Platt, T. A Printable Device for Measuring Clarity and Colour in Lake and Nearshore Waters. Sensors 2019, 19, 936. [Google Scholar] [CrossRef]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Kowalczuk, P. Seasonal variability of yellow substance absorption in the surface layer of the Baltic Sea. J. Geophys. Res. 1999, 104, 30047–30058. [Google Scholar] [CrossRef]
- Woźniak, S.B.; Meler, J.; Lednicka, B.; Zdun, A.; Stoń-Egiert, J. Inherent optical properties of suspended particulate matter in the southern Baltic Sea. Oceanologia 2011, 53, 691–729. [Google Scholar] [CrossRef]
- Darecki, M.; Stramski, D. An evaluation of MODIS and SeaWiFS bio-optical algorithms in the Baltic Sea. Remote Sens. Environ. 2004, 89, 326–350. [Google Scholar] [CrossRef]
- Simis, S.G.H.; Ylöstalo, P.; Kallio, K.Y.; Spilling, K.; Kutser, T. Contrasting seasonality in optical-biogeochemical properties of the Baltic Sea. PLoS ONE 2017, 12, e0173357. [Google Scholar] [CrossRef] [PubMed]
- Ligi, M.; Kutser, T.; Kallio, K.; Attila, J.; Koponen, S.; Paavel, B.; Soomets, T.; Reinart, A. Testing the performance of empirical remote sensing algorithms in the Baltic Sea waters with modelled and in situ reflectance data. Oceanologia 2017, 59, 57–68. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping water quality parameters with Sentinel-3 Ocean and Land Colour Instrument imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef]
- Kyryliuk, D.; Kratzer, S. Evaluation of Sentinel-3A OLCI products derived using the Case-2 Regional CoastColour Processor over the Baltic Sea. Sensors 2019, 19, 3609. [Google Scholar] [CrossRef]
- Kratzer, S.; Kyryliuk, D.; Brockmann, C. Inorganic suspended matter as an indicator of terrestrial influence in Baltic Sea coastal areas—Algorithm development and validation, and ecological relevance. Remote Sens. Environ. 2020, 237, 111609. [Google Scholar] [CrossRef]
- Woźniak, S.B.; Sagan, S.; Zabłocka, M.; Stoń-Egiert, J.; Borzycka, K. Light scattering and backscattering by particles suspended in the Baltic Sea in relation to the mass concentration of particles and the proportions of their organic and inorganic fractions. J. Mar. Syst. 2018, 182, 79–96. [Google Scholar] [CrossRef]
- Woźniak, S.B. Simple statistical formulas for estimating biogeochemical properties of suspended particulate matter in the southern Baltic Sea potentially useful for optical remote sensing applications. Oceanologia 2014, 56, 7–39. [Google Scholar] [CrossRef]
- Woźniak, S.B.; Darecki, M.; Zabłocka, M.; Burska, D.; Dera, J. New simple statistical formulas for estimating surface concentrations of suspended particulate matter (SPM) and particulate organic carbon (POC) from remote-sensing reflectance in the southern Baltic Sea. Oceanologia 2016, 58, 161–175. [Google Scholar] [CrossRef]
- Pearlman, S.R.; Costa, H.S.; Jung, R.A.; McKeown, J.J.; Pearson, H.E. Solids (section 2540). In Standard Methods for the Examination of Water and Wastewater; Eaton, A.D., Clesceri, L.S., Greenberg, A.E., Eds.; American Public Health Association: Washington, DC, USA, 1995; pp. 53–64. [Google Scholar]
- Stoń, J.; Kosakowska, A. Phytoplankton pigments designation–an application of RP-HPLC in qualitative and quantitative analysis. J. Appl. Phycol. 2002, 14, 205–210. [Google Scholar] [CrossRef]
- Stoń-Egiert, J.; Kosakowska, A. RP-HPLC determination of phytoplankton pigments comparison of calibration results for two columns. Mar. Biol. 2005, 147, 251–260. [Google Scholar] [CrossRef]
- Stoń-Egiert, J.; Łotocka, M.; Ostrowska, M.; Kosakowska, A. The influence of biotic factors on phytoplankton pigment composition and resources in Baltic ecosystems: New analytical results. Oceanologia 2010, 52, 101–125. [Google Scholar] [CrossRef]
- Stramski, D.; Reynolds, R.I.; Kaczmarek, S.; Uitz, J.; Zheng, G. Correction of pathlength amplification in the filter-pad technique for measurements of particulate absorption coefficient in the visible spectral region. Appl. Opt. 2015, 54, 6763–6782. [Google Scholar] [CrossRef]
- Maffione, R.A.; Dana, D.R. Instruments and methods for measuring the backward-scattering coefficient of ocean waters. Appl. Opt. 1997, 36, 6057–6067. [Google Scholar] [CrossRef]
- Dana, D.R.; Maffione, R.A. Determining the Backward Scattering Coefficient with Fixed-Angle Backscattering Sensors–Revisited. In Proceedings of the Ocean Optics XVI Conference, Santa Fe, NM, USA, 18–22 November 2002. [Google Scholar]
- HOBI Labs (Hydro-optics, Biology & Instrumentation Laboratories, Inc.). HydroScat-4 Spectral Backscattering Sensor, User’s Manual; Revision E.; HOBI Labs: Tucson, AZ, USA, 2008; p. 65. Available online: https://www.hobiservices.com/docs/HS4ManualRevE-2008-6-14.pdf (accessed on 21 July 2020).
- Morel, A. Optical properties of pure water and pure sea water. In Optical Aspects of Oceanography; Jerlov, N.G., Nielsen, E.S., Eds.; Academic Press: New York, NY, USA, 1974; pp. 1–24. [Google Scholar]
- Hanbury, A. Constructing cylindrical coordinate colour spaces. Pattern Recognit. Lett. 2008, 29, 494–500. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water; Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994; p. 592. [Google Scholar]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Woźniak, S.B.; Darecki, M.; Sagan, S. Empirical Formulas for Estimating Backscattering and Absorption Coefficients in Complex Waters from Remote-Sensing Reflectance Spectra and Examples of Their Application. Sensors 2019, 19, 4043. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K. Hydrolight 5, Ecolight 5, Technical Documentation; Sequoia Scientific, Inc.: Bellevue, WA, USA, 2008; p. 95. [Google Scholar]
- Mobley, C.D.; Sundman, L.K. Hydrolight 5, Ecolight 5, Users’ Guide; Sequoia Scientific, Inc.: Bellevue, WA, USA, 2008; p. 99. [Google Scholar]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Sogandares, F.M.; Fry, E.S. Absorption spectrum (340–640 nm) of pure water. I. Photothermal measurements. Appl. Opt. 1997, 36, 8699–8709. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef] [PubMed]
- CIE. Commission Internationale de l’Eclairage Proceedings, 1931; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]

| (a) | |||||
where:
| |||||
| ; | |||||
| |||||
| |||||
| (b) | |||||
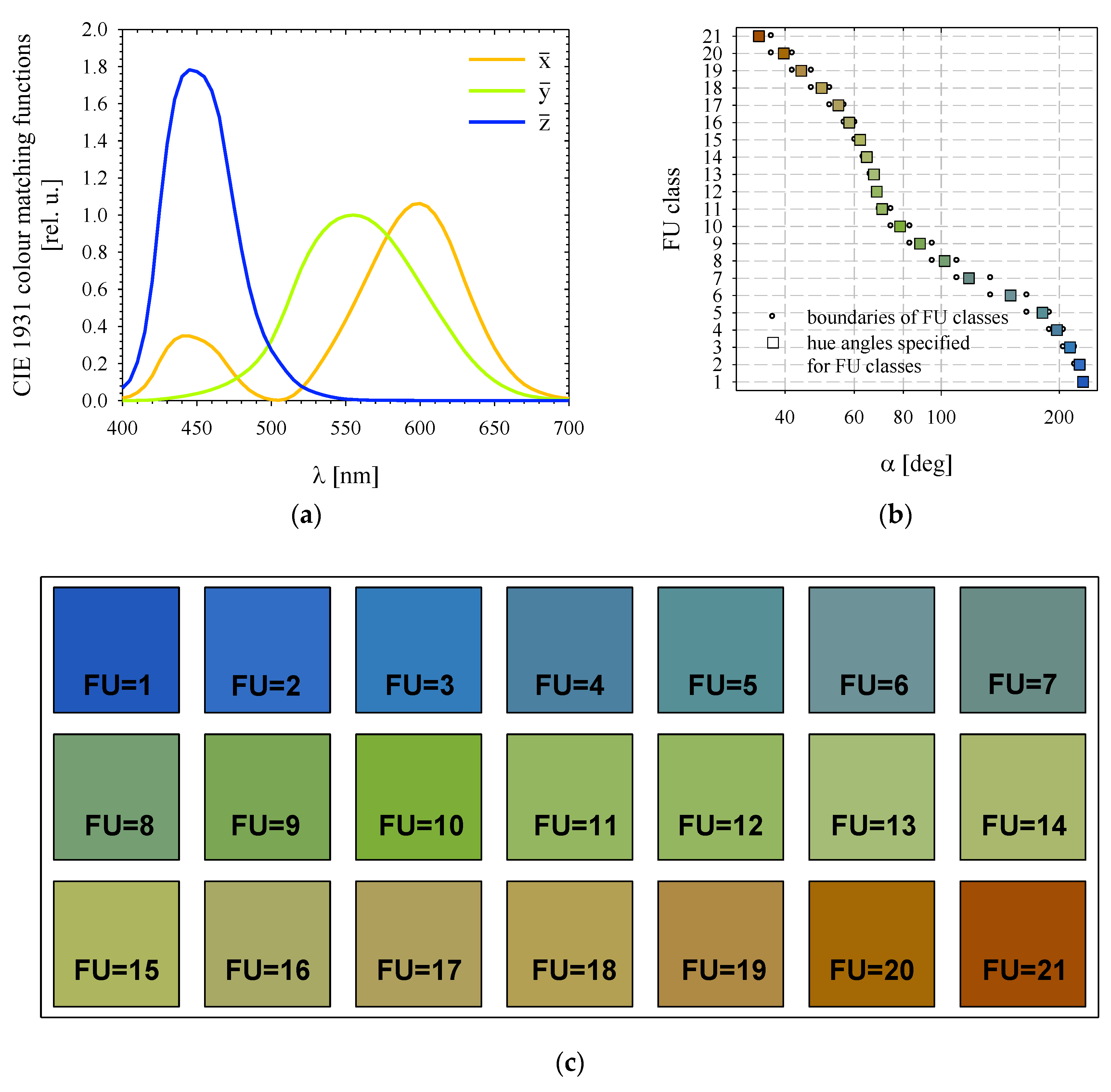
| FU Class | αFU[°] | αtransition[°] | FU Class | αFU[°] | αtransition[°] |
| 1 | 229.94 | 227.68 | 12 | 68.49 | 67.93 |
| 2 | 225.41 | 219.27 | 13 | 67.36 | 65.98 |
| 3 | 213.13 | 205.19 | 14 | 64.6 | 63.35 |
| 4 | 197.25 | 189.2 | 15 | 62.11 | 60.37 |
| 5 | 181.15 | 165.71 | 16 | 58.26 | 56.64 |
| 6 | 150.26 | 133.96 | 17 | 54.65 | 52.09 |
| 7 | 117.66 | 109.85 | 18 | 49.53 | 46.75 |
| 8 | 102.05 | 95.14 | 19 | 43.96 | 41.82 |
| 9 | 88.24 | 83.38 | 20 | 39.67 | 36.98 |
| 10 | 78.53 | 74.62 | 21 | 34.28 | (n. a.) |
| 11 | 70.71 | 69.6 | |||
| Quantities | Average (Standard Deviation) | Minimum | 5th Percentile | Median | 95th Percentile | Maximum |
|---|---|---|---|---|---|---|
| characteristics of particulate matter | ||||||
| SPM [g m−3] | 3.31 (4.36) | 0.58 | 0.66 | 1.61 | 16.7 | 20 |
| POM [g m−3] | 1.56 (1.22) | 0.35 | 0.36 | 1.15 | 4.26 | 5.18 |
| PIM [g m−3] | 1.75 (3.41) | 0 | 0.23 | 0.45 | 12 | 15.9 |
| Chla [mg m−3] | 3.26 (3.43) | 0.48 | 0.55 | 1.94 | 13.4 | 15.9 |
| main characteristic of CDOM | ||||||
| ag(440) [m−1] | 0.503 (0.164) | 0.197 | 0.243 | 0.494 | 0.828 | 0.922 |
| biogeochemical ratios | ||||||
| POM/SPM | 0.61 (0.20) | 0.2 | 0.28 | 0.62 | 0.87 | 1 |
| Chla/POM (×10−3) | 2.08 (1.06) | 0.52 | 0.76 | 1.83 | 4.77 | 4.9 |
| ag(440)/SPM [m2 g−1] | 0.314 (0.221) | 0.02 | 0.034 | 0.265 | 0.74 | 1.08 |
| optical properties of particulate matter | ||||||
| ap(440) [m−1] | 0.375 (0.36) | 0.066 | 0.082 | 0.282 | 1.34 | 1.56 |
| ap(675) [m−1] | 0.128 (0.119) | 0.015 | 0.026 | 0.092 | 0.473 | 0.494 |
| bbp(420) [m−1] | 0.0404 (0.0635) | 0.0061 | 0.0071 | 0.0203 | 0.249 | 0.328 |
| bbp(620) [m−1] | 0.0259 (0.0426) | 0.0036 | 0.0041 | 0.0105 | 0.169 | 0.193 |
| FU Class | Minimum of a(440) [m−1] | Maximum of a(440) [m−1] | Maximum of SPM (Maximum of PIM) [g m−3] | Maximum of POM [g m−3] |
|---|---|---|---|---|
| 1 | 0.011 | 0.0267 | 0.261 | 0.1 |
| 2 | 0.0211 | 0.049 | 0.562 | 0.215 |
| 3 | 0.0381 | 0.0822 | 1.21 | 0.383 |
| 4 | 0.0646 | 0.13 | 2.61 | 0.562 |
| 5 | 0.0948 | 0.223 | 4.64 | 0.9 |
| 6 | 0.133 | 0.391 | 8.25 | 1.47 |
| 7 | 0.224 | 0.626 | 12.1 | 2.15 |
| 8 | 0.338 | 0.926 | 14.7 | 3.16 |
| 9 | 0.488 | 1.33 | 21.5 | 4.64 |
| 10 | 0.689 | 1.73 | 26.1 | 5.62 |
| 11 | 0.952 | 2.03 | 26.1 | 6.81 |
| 12 | 1.15 | 2.04 | 26.1 | 8.25 |
| 13 | 1.24 | 2.07 | 31.6 | 8.25 |
| 14 | 1.34 | 2.14 | 31.6 | 10 |
| 15 | 1.52 | 2.51 | 38.3 | 12.1 |
| 16 | 1.75 | 3.16 | 46.4 | 14.7 |
| 17 | 2.09 | 4.62 | 56.2 | 21.5 |
| 18 | 2.84 | >9.45 | >100 | 46.4 |
| 19 | 5.07 | >21.8 | >100 | >100 |
| Quantity | n | Arithmetic Statistics of Absolute Error * | Arithmetic Statistics of Relative Error ** | Logarithmic Statistics *** | |||
|---|---|---|---|---|---|---|---|
| MB | RMSE | MNB [%] | RMSNE [%] | log.sys.err. [%] | X | ||
| Algorithm I | |||||||
| SPM | 49 | 0.36 g m−3 | 1.53 g m−3 | 4.3 | 28.2 | 0.2 | 1.35 |
| POM | 49 | 0.27 g m−3 | 0.91 g m−3 | 30.6 | 64.6 | 13.5 | 1.79 |
| PIM | 49 | 0.10 g m−3 | 1.13 g m−3 | −1.0 | 160.1 | −38.7 | 2.50 |
| POM/SPM | 50 | 0.11 | 0.23 | 21.5 | 42.8 | 13.3 | 1.50 |
| ag(440) | 49 | 0.06 m−1 | 0.17 m−1 | 16.4 | 38.8 | 11.4 | 1.33 |
| Algorithm II | |||||||
| SPM | 49 | −0.48 g m−3 | 0.99 g m−3 | −16.7 | 22.3 | −19.9 | 1.34 |
| POM | 49 | −0.53 g m−3 | 0.83 g m−3 | −26.0 | 41.3 | −35.3 | 1.70 |
| PIM | 49 | 0.06 g m−3 | 0.53 g m−3 | 24.2 | 57.5 | 13.7 | 1.51 |
| POM/SPM | 50 | −0.12 | 0.16 | −14.5 | 28.1 | −19.2 | 1.43 |
| ag(440) | 49 | 0.08 m−1 | 0.18 m−1 | 20.8 | 41.7 | 14.3 | 1.40 |
| functions of Rrs(625) | |||||||
| SPM | 49 | −0.26 g m−3 | 1.22 g m−3 | 3.3 | 27.1 | −0.7 | 1.34 |
| POM | 49 | −0.15 g m−3 | 0.77 g m−3 | 10.7 | 51.5 | −0.6 | 1.62 |
| PIM | 49 | −0.11 g m−3 | 1.11 g m−3 | 24.8 | 69.7 | 10.7 | 1.61 |
| POM/SPM | 50 | −0.02 | 0.18 | 4.5 | 30.8 | 0.1 | 1.35 |
| functions of Rrs(490)/Rrs(625) | |||||||
| SPM | 49 | −0.68 g m−3 | 3.25 g m−3 | 13.8 | 47.3 | 1.1 | 1.74 |
| POM | 49 | −0.20 g m−3 | 0.78 g m−3 | 13.2 | 52.8 | 0.4 | 1.69 |
| PIM | 49 | −0.48 g m−3 | 2.80 g m−3 | 60.6 | 119.0 | 17.9 | 2.44 |
| POM/SPM | 50 | −0.04 | 0.19 | 6.0 | 40.9 | −0.7 | 1.43 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woźniak, S.B.; Meler, J. Modelling Water Colour Characteristics in an Optically Complex Nearshore Environment in the Baltic Sea; Quantitative Interpretation of the Forel-Ule Scale and Algorithms for the Remote Estimation of Seawater Composition. Remote Sens. 2020, 12, 2852. https://doi.org/10.3390/rs12172852
Woźniak SB, Meler J. Modelling Water Colour Characteristics in an Optically Complex Nearshore Environment in the Baltic Sea; Quantitative Interpretation of the Forel-Ule Scale and Algorithms for the Remote Estimation of Seawater Composition. Remote Sensing. 2020; 12(17):2852. https://doi.org/10.3390/rs12172852
Chicago/Turabian StyleWoźniak, Sławomir B., and Justyna Meler. 2020. "Modelling Water Colour Characteristics in an Optically Complex Nearshore Environment in the Baltic Sea; Quantitative Interpretation of the Forel-Ule Scale and Algorithms for the Remote Estimation of Seawater Composition" Remote Sensing 12, no. 17: 2852. https://doi.org/10.3390/rs12172852
APA StyleWoźniak, S. B., & Meler, J. (2020). Modelling Water Colour Characteristics in an Optically Complex Nearshore Environment in the Baltic Sea; Quantitative Interpretation of the Forel-Ule Scale and Algorithms for the Remote Estimation of Seawater Composition. Remote Sensing, 12(17), 2852. https://doi.org/10.3390/rs12172852





