Estimation of Snow Depth in the Hindu Kush Himalayas of Afghanistan during Peak Winter and Early Melt Season
Abstract
1. Introduction
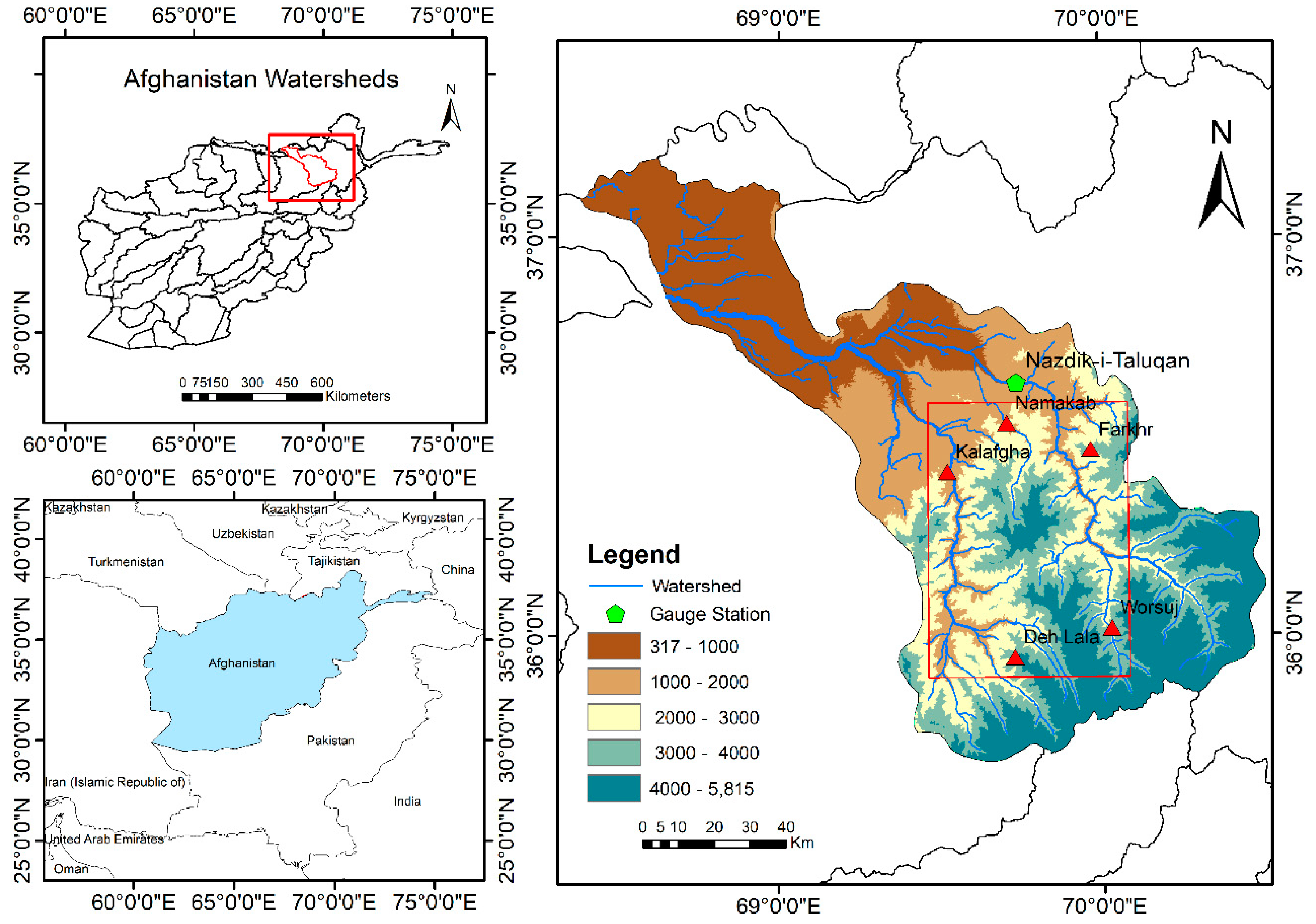
2. Study Area and Materials Used
2.1. Study Area and Test Data
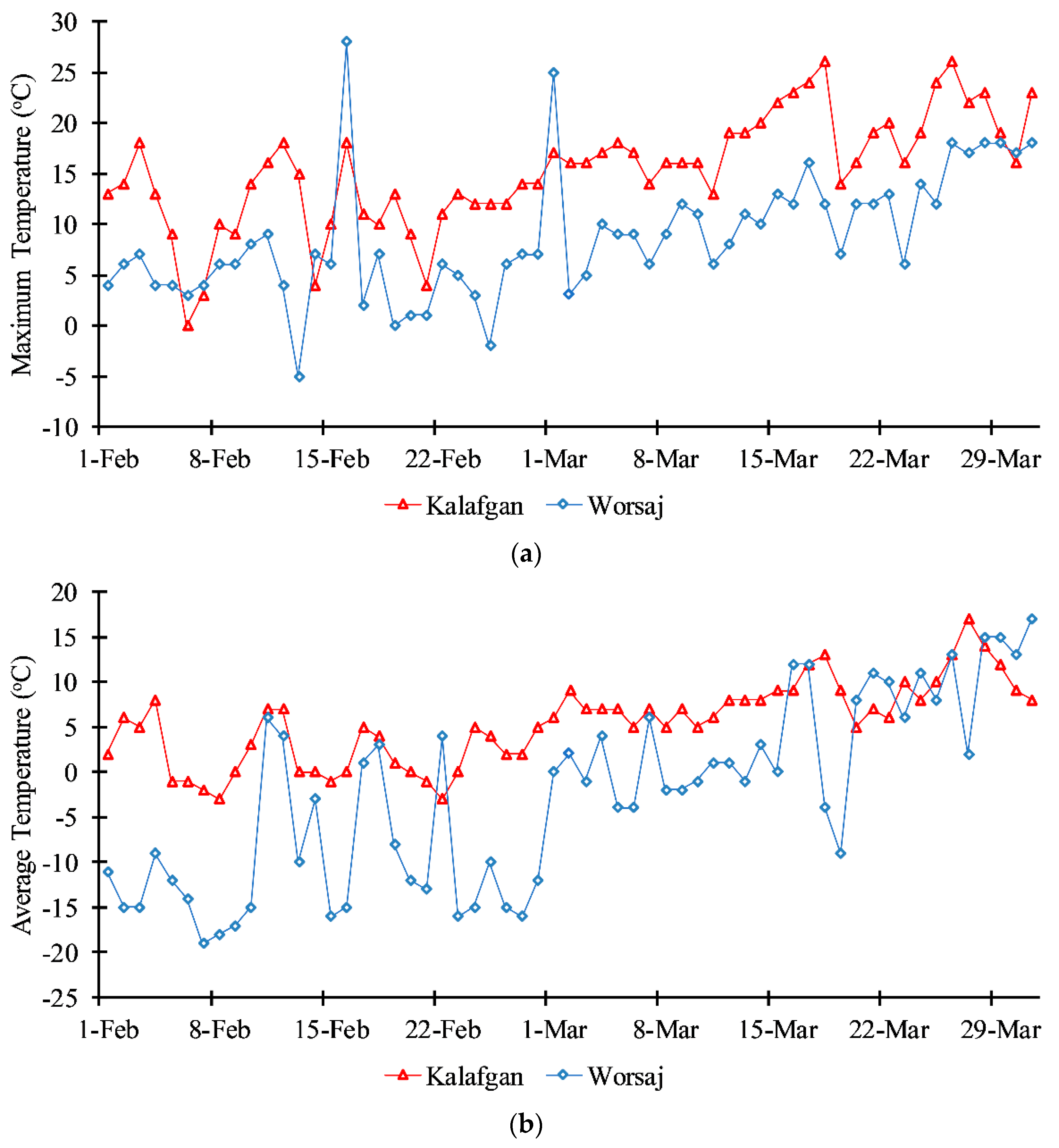
2.2. Field Data Collection
3. Methodology
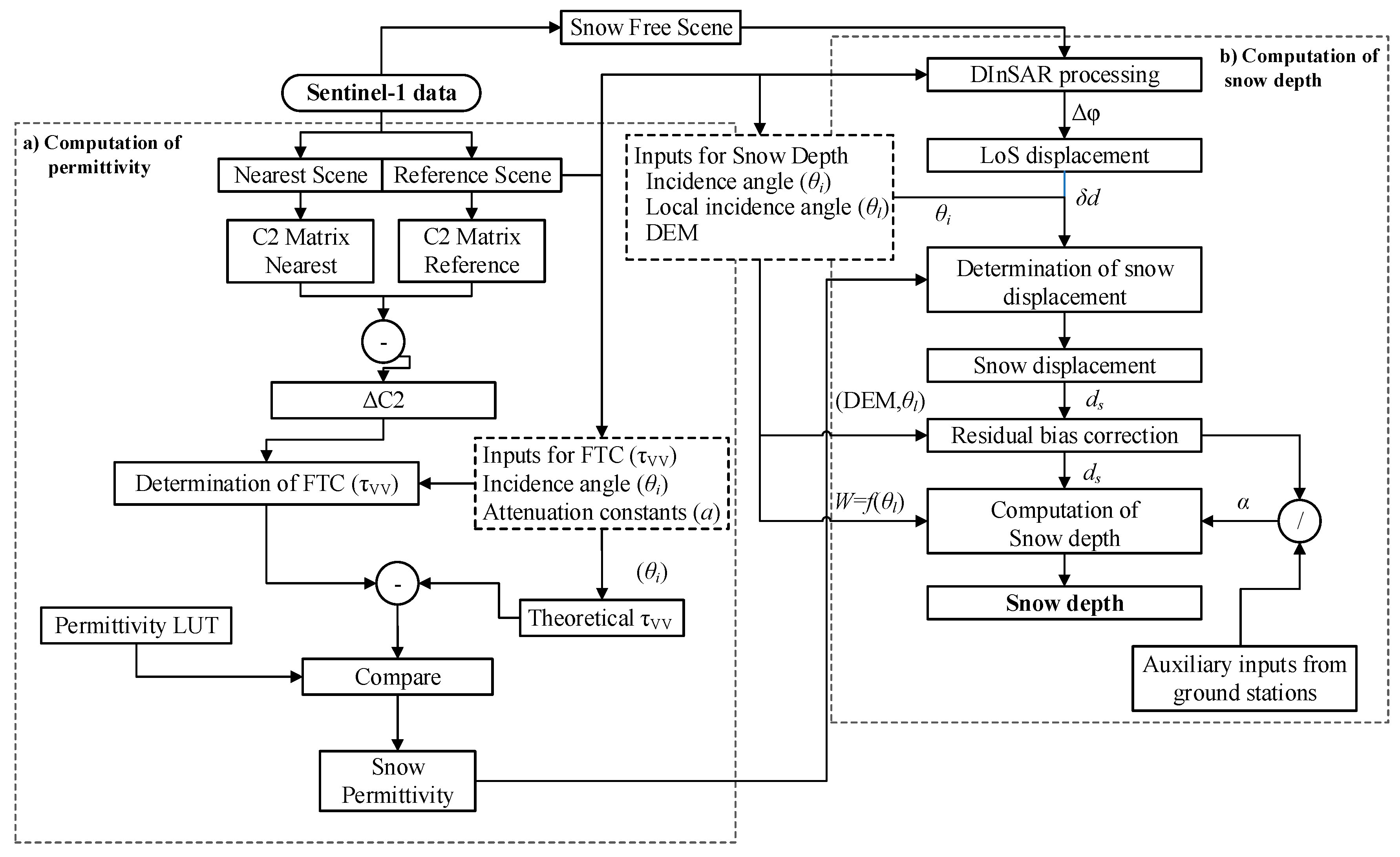
3.1. Proposed Framework
3.2. DInSAR Processing
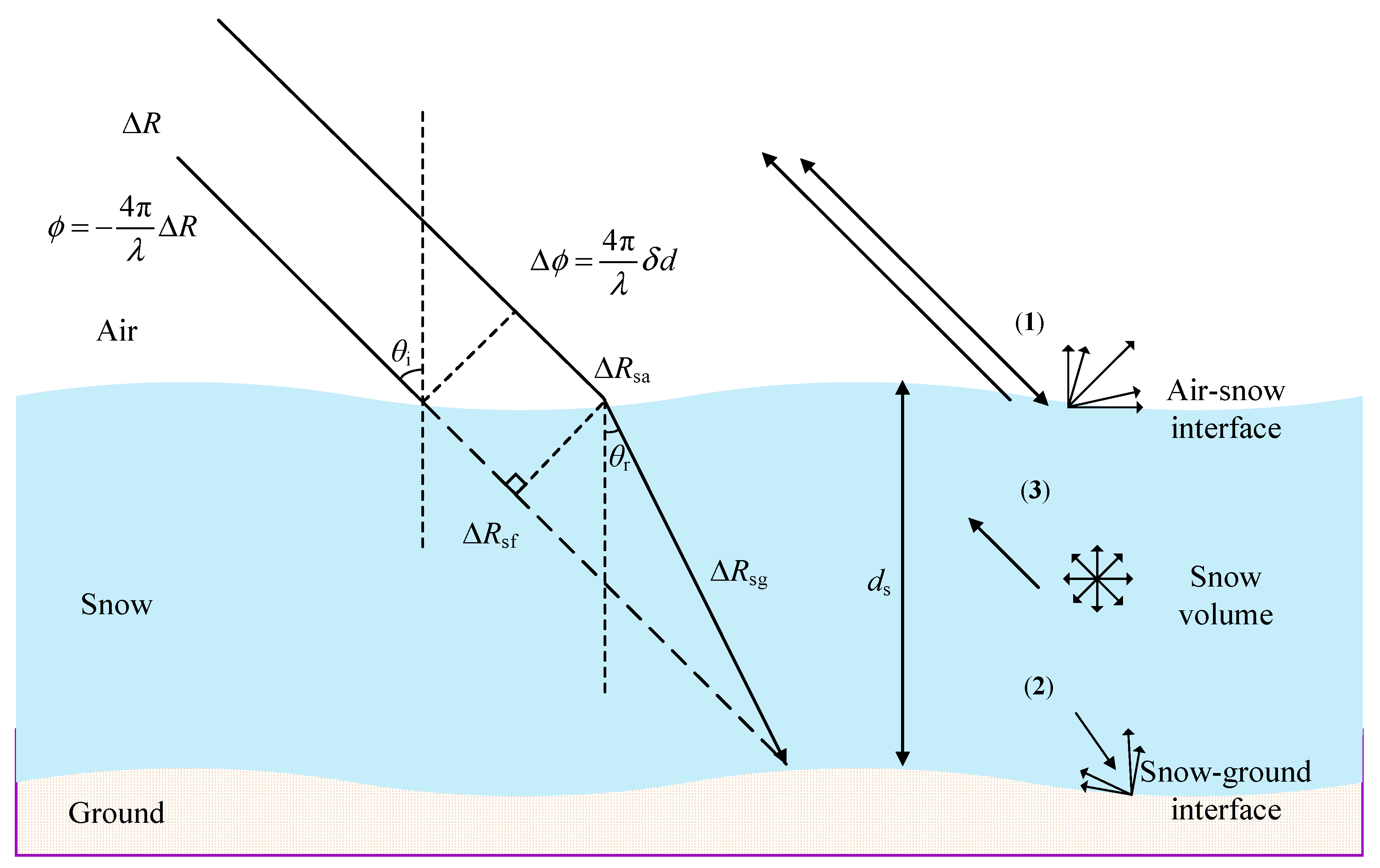
Background on the Estimation of Snow Depth
3.3. Approximation of Snow Depth
4. Results
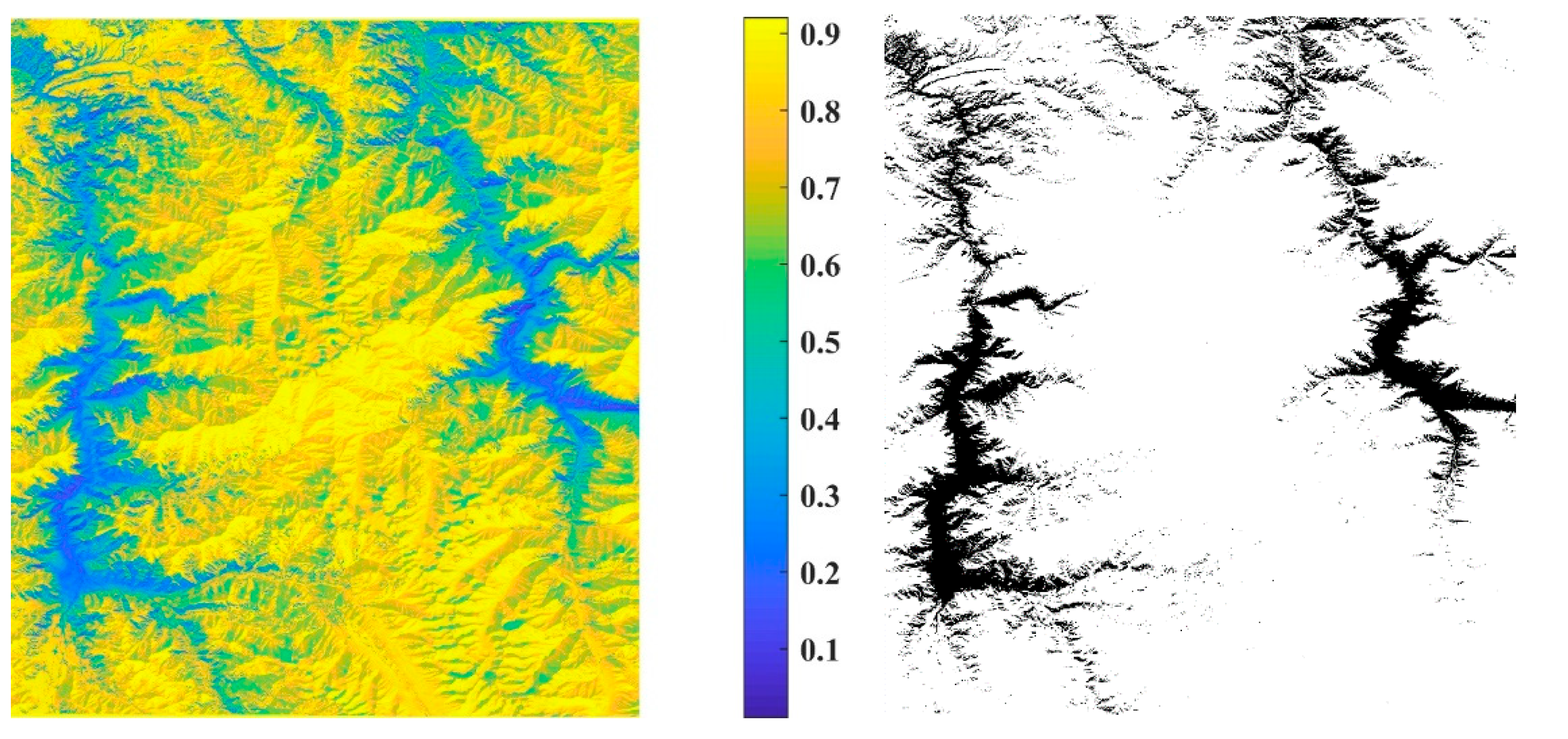
4.1. Masking for SCA and Layover-Shadow Pixels
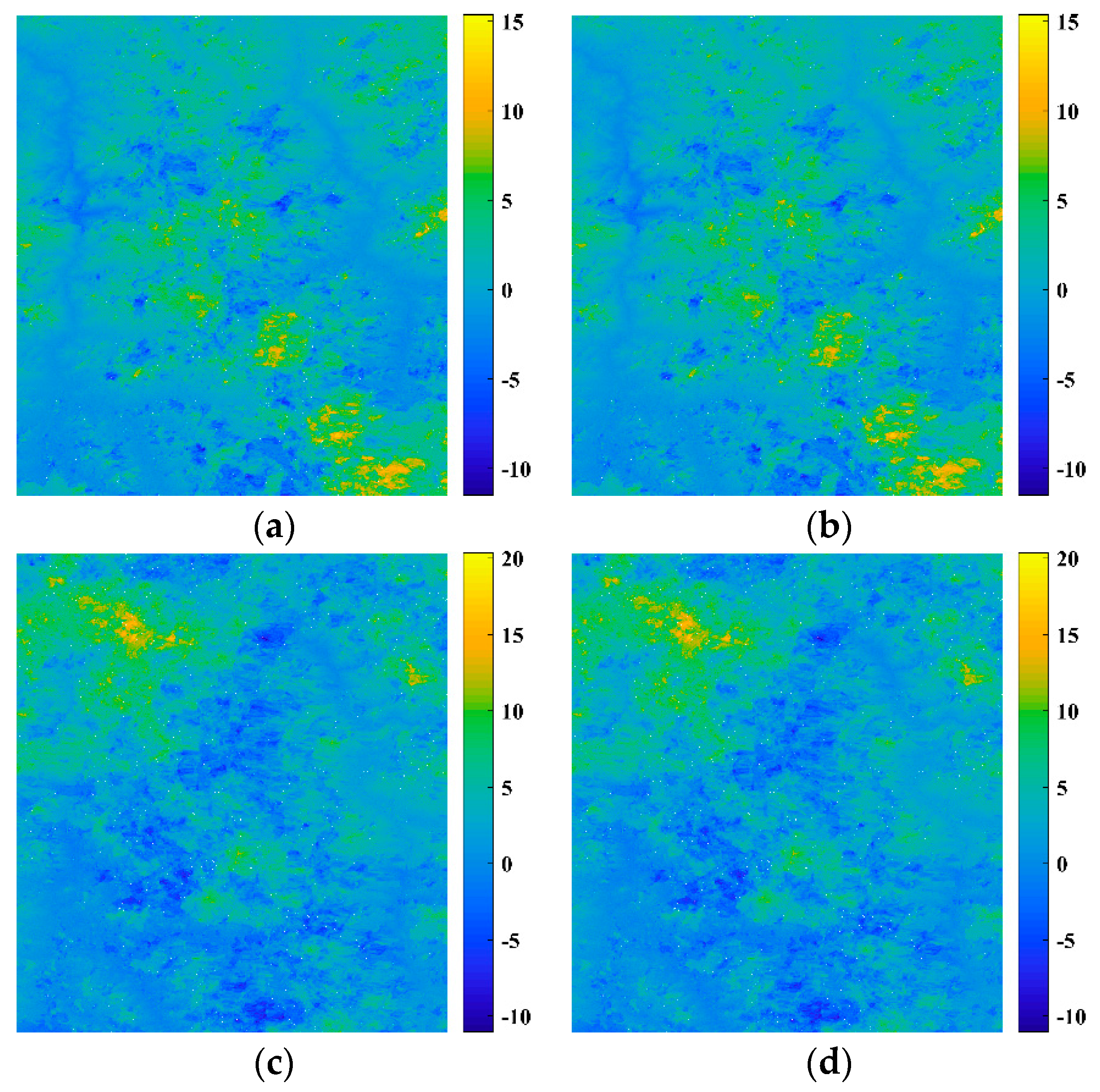
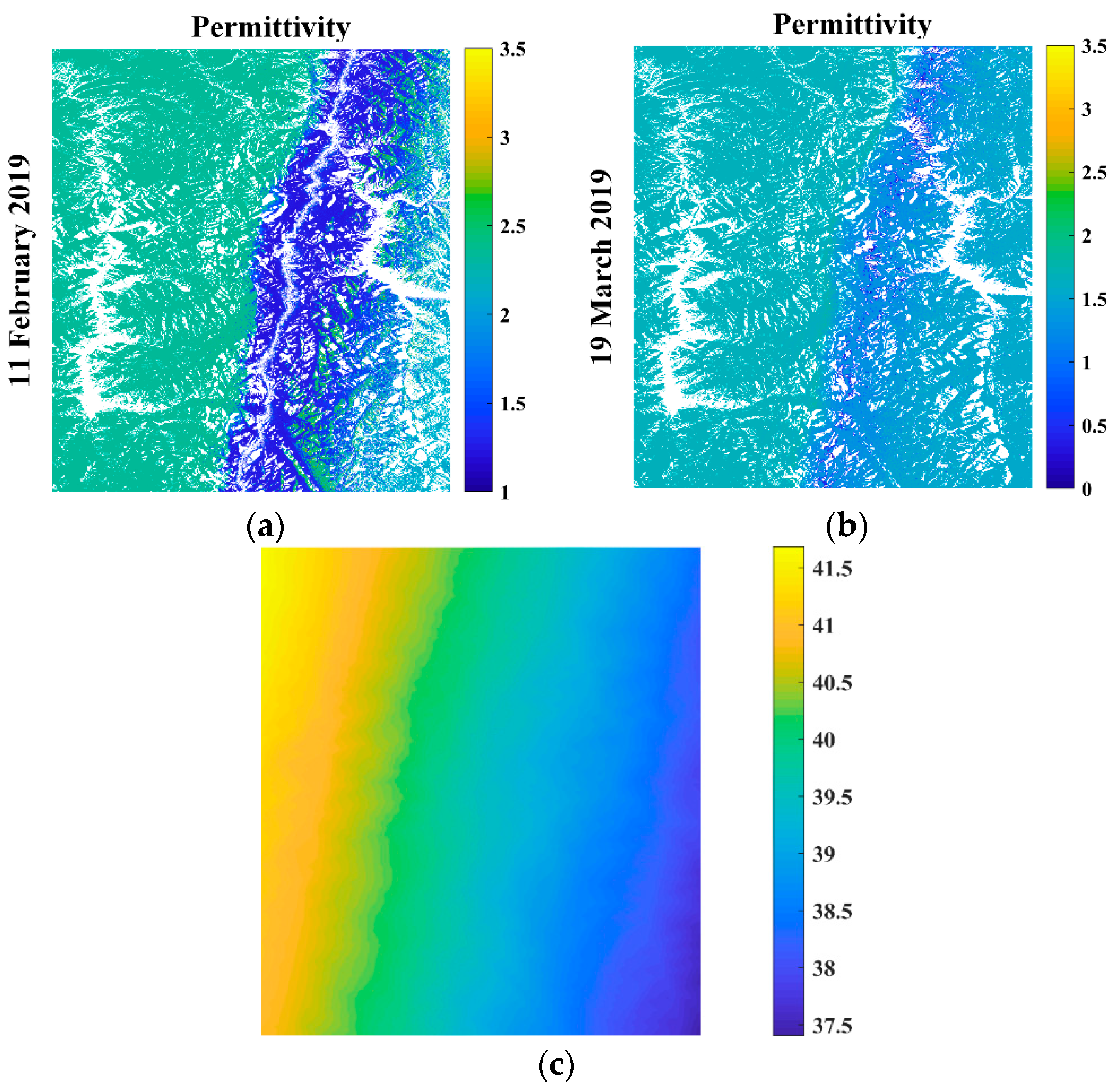
4.2. Spatial Distribution of the Snow Permittivity and Snow Depth
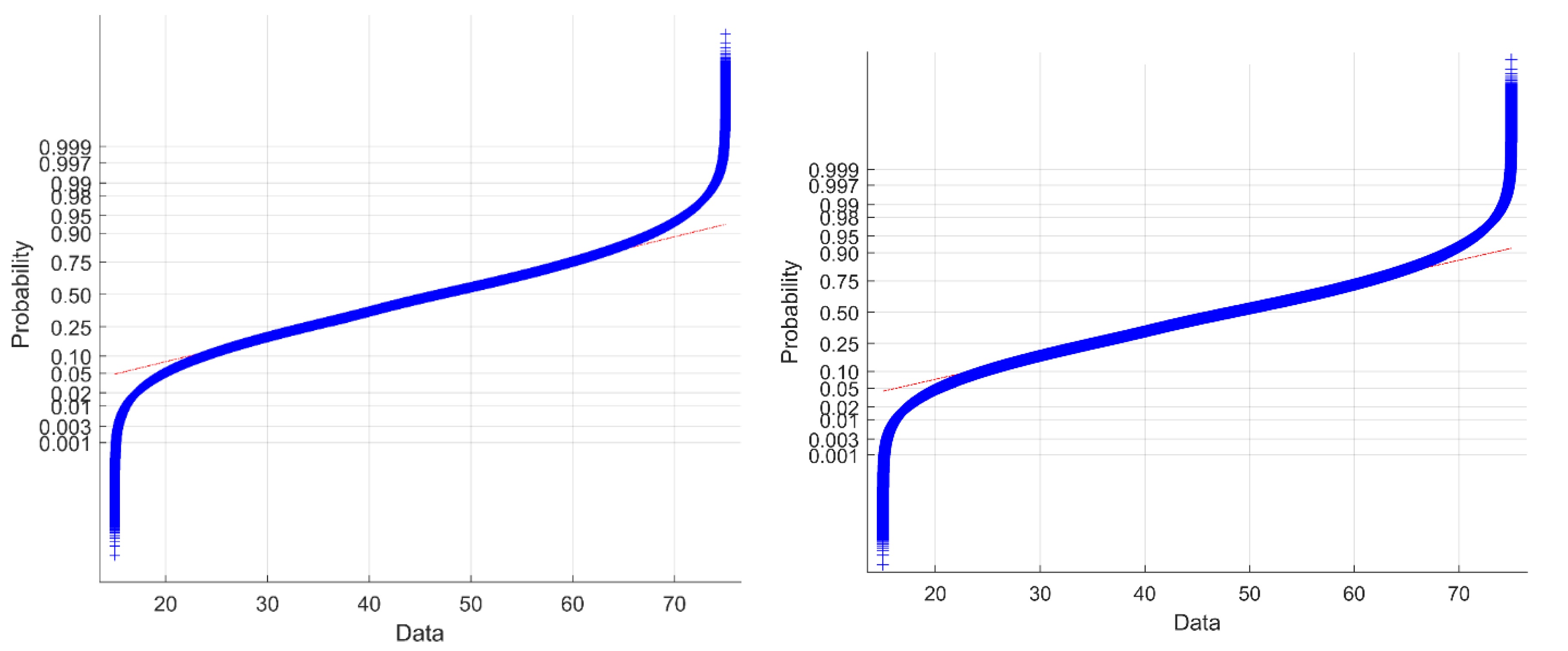
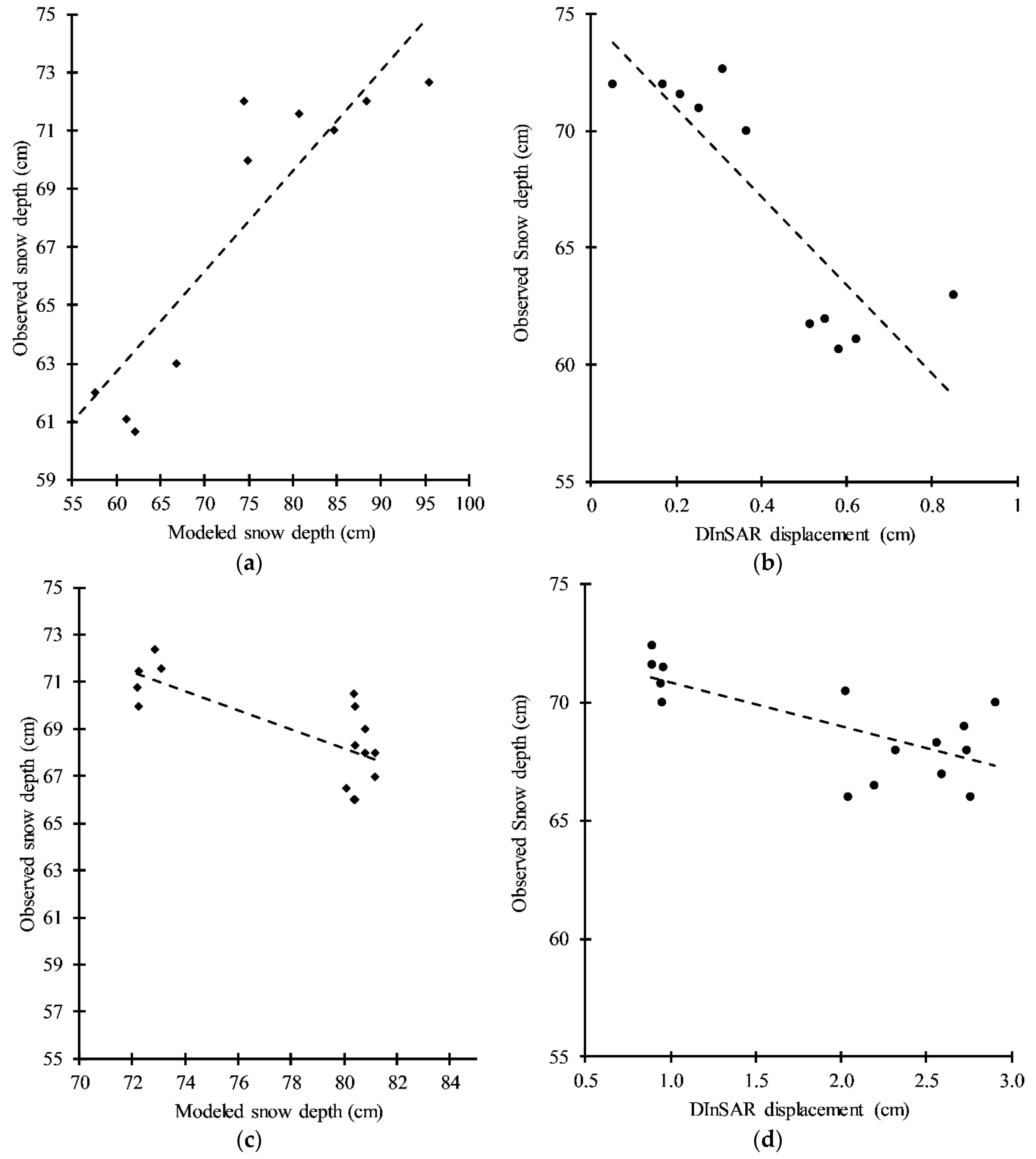
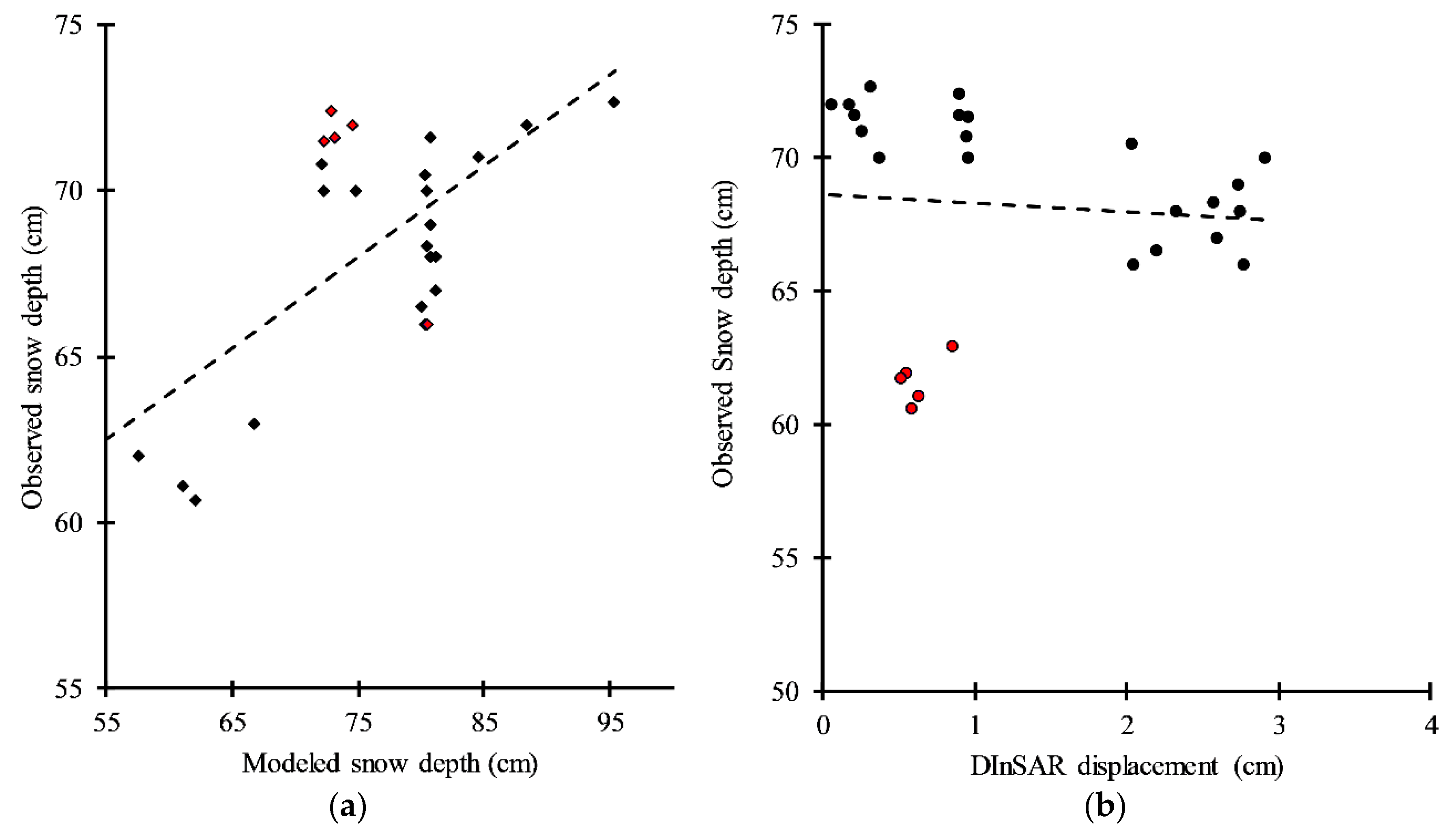
4.3. Accuracy Assessment of the Modeled Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Georgievsky, M.V. Application of the Snowmelt Runoff model in the Kuban river basin using MODIS satellite images. Environ. Res. Lett. 2009, 4, 045017. [Google Scholar] [CrossRef][Green Version]
- Kulkarni, A.V.; Rathore, B.; Singh, S.; Ajai, U. Distribution of seasonal snow cover in central and western Himalaya. Ann. Glaciol. 2010, 51, 123–128. [Google Scholar] [CrossRef]
- Gurung, D.R.; Kulkarni, A.V.; Giriraj, A.; Aung, K.S.; Shrestha, B.; Srinivasan, J. Changes in seasonal snow cover in Hindu Kush-Himalayan region. Cryosphere Discuss. 2011, 5, 755–777. [Google Scholar] [CrossRef]
- World Bank. Europe and Central Asia: Assessment of the Role of Glaciers in Stream Flow from the 564 Pamir and Tien Shan Mountains; The World Bank: Washington, DC, USA, 2015. [Google Scholar]
- Klemm. Impact of Irrigation in Northern Afghanistan on Water Use in the Amu Darya Basin Walter. 2009. Available online: https://www.unece.org/fileadmin/DAM/SPECA/documents/ecf/2010/FAO_report_e.pdf (accessed on 6 March 2020).
- Agal’Tseva, N.A.; Bolgov, M.V.; Spektorman, T.Y.; Trubetskova, M.D.; Chub, V.E. Estimating hydrological characteristics in the Amu Darya River basin under climate change conditions. Russ. Meteorol. Hydrol. 2011, 36, 681–689. [Google Scholar] [CrossRef]
- Kinar, N.J.; Pomeroy, J.W. Reviews of Geophysics Measurement of the physical properties of the snowpack. Rev. Geophys. 2015, 53, 481–544. [Google Scholar] [CrossRef]
- Ulaby, F.; Long, D.; Blackwell, W.J.; Elachi, C.; Fung, A.K. Microwave Radar and Radiometric Remote Sensing; The University of Michigan: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Dong, C. Remote sensing, hydrological modeling and in situ observations in snow cover research: A review. J. Hydrol. 2018, 561, 573–583. [Google Scholar] [CrossRef]
- Varade, D.; Dikshit, O. Potential of multispectral reflectance for assessment of snow geophysical parameters in Solang valley in the lower Indian Himalayas. GIScience Remote Sens. 2019, 57, 107–126. [Google Scholar] [CrossRef]
- Varade, D.; Dikshit, O. Estimation of surface snow wetness using sentinel-2 multispectral data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 223–228. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T. Snow depth derived from passive microwave remote-sensing data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef]
- Dozier, J.; Shi, J. Estimation of snow water equivalence using SIR-C/X-SAR. I. Inferring snow density and subsurface properties. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2465–2474. [Google Scholar] [CrossRef]
- Vuyovich, C.; Jacobs, J.M. Snowpack and runoff generation using AMSR-E passive microwave observations in the Upper Helmand Watershed, Afghanistan. Remote Sens. Environ. 2011, 115, 3313–3321. [Google Scholar] [CrossRef]
- Deems, J.; Painter, T.H.; Finnegan, D.C. Lidar measurement of snow depth: A review. J. Glaciol. 2013, 59, 467–479. [Google Scholar] [CrossRef]
- Leinss, S.; Parrella, G.; Hajnsek, I. Snow height determination by polarimetric phase differences in X-Band SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3794–3810. [Google Scholar] [CrossRef]
- Patil, A.; Mohanty, S.; Singh, G. Snow depth and snow water equivalent retrieval using X-band PolInSAR data. Remote Sens. Lett. 2020, 11, 817–826. [Google Scholar] [CrossRef]
- Abe, T.; Yamaguchi, Y.; Sengoku, M. Experimental study of microwave transmission in snowpack. IEEE Trans. Geosci. Remote Sens. 1990, 28, 915–921. [Google Scholar] [CrossRef]
- Ferretti, A.; Monti-guarnieri, A.; Prati, C.; Rocca, F. Part C InSAR P Rocessing: A Mathematical Approach. 2007, p. 115. Available online: https://www.esa.int/esapub/tm/tm19/TM-19_ptC.pdf (accessed on 12 May 2020).
- Deeb, E.; Forster, R.R.; Kane, D.L. Monitoring snowpack evolution using interferometric synthetic aperture radar on the North Slope of Alaska, USA. Int. J. Remote Sens. 2011, 32, 3985–4003. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; He, G.; Man, W. Estimating snow depth and snow water equivalence using repeat-pass interferometric SAR in the northern piedmont region of the Tianshan Mountains. J. Sens. 2017, 2017, 8739598. [Google Scholar] [CrossRef]
- Guneriussen, T.; Hogda, K.; Johnsen, H.; Lauknes, I. InSAR for estimation of changes in snow water equivalent of dry snow. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2101–2108. [Google Scholar] [CrossRef]
- Varade, D.; Maurya, A.; Dikshit, O.; Singh, G.; Manickam, S. Snow depth in Dhundi: An estimate based on weighted bias corrected differential phase observations of dual polarimetric bi-temporal Sentinel-1 data. Int. J. Remote Sens. 2019, 41, 3031–3053. [Google Scholar] [CrossRef]
- Gámez, P.S.; Navarro, F. Glacier surface velocity retrieval using D-InSAR and offset tracking techniques applied to ascending and descending passes of sentinel-1 data for Southern Ellesmere Ice Caps, Canadian Arctic. Remote Sens. 2017, 9, 442. [Google Scholar] [CrossRef]
- Strozzi, T.; Antonova, S.; Günther, F.; Mätzler, E.; Vieira, G.; Wegmuller, U.; Westermann, S.; Bartsch, A. Sentinel-1 SAR interferometry for surface deformation monitoring in low-land permafrost areas. Remote Sens. 2018, 10, 1360. [Google Scholar] [CrossRef]
- Liu, Y.; Li, L.; Yang, J.; Chen, X.; Hao, J. Estimating snow depth using multi-source data fusion based on the D-InSAR Method and 3DVAR fusion algorithm. Remote Sens. 2017, 9, 1195. [Google Scholar] [CrossRef]
- Ahmad, M.; Wasiq, M. Water Resource Development in Northern Afghanistan and Its Implications for Amu Darya Basin; World Bank: Washington, DC, USA, 2004. [Google Scholar]
- Kamal, G.M. River Basins and Watersheds of Afghanistan. 2004, pp. 1–7. Available online: http://www.nzdl.org/gsdl/collect/areu/Upload/1710/Kamal_River basins and watersheds2004.pdf (accessed on 20 February 2020).
- Rucci, A.; Ferretti, A.; Monti-Guarnieri, A.; Rocca, F. Sentinel 1 SAR interferometry applications: The outlook for sub millimeter measurements. Remote Sens. Environ. 2012, 120, 156–163. [Google Scholar] [CrossRef]
- Sarmap. SARscape Help Manual. 2014. Available online: http://sarmap.ch/tutorials/Basic.pdf (accessed on 20 May 2020).
- Description, D.S. SARscape Interferometry Module for Displacement Map Generation SARscape Processing Steps Baseline Estimation Digital Elevation Model/Ellipsoid Interferogram Flattening; European Space Agency (ESA): Paris, France, 2004; Volume 2003, pp. 1–4. [Google Scholar]
- Lensu, T. Synthetic aperture radar—Systems and signal processing. Signal. Process. 1992, 29, 107. [Google Scholar] [CrossRef]
- Klemm, R. Novel Radar Techniques and Applications Volume 1: Real Aperture Array Radar, Imaging Radar, and Passive and Multistatic Radar; Institution of Engineering and Technology: London, UK, 2017. [Google Scholar]
- Simonetto, E. DINSAR experiments using a free processing chain. SPIE Remote Sens. 2008, 7109, 71091G. [Google Scholar] [CrossRef]
- Moreira, P.A.; Prats-iraola, M.; Younis, G.; Krieger, I.; Hajnsek, K.; Papathanassiou, K.P. AR-Tutorial-March-2013. IEEE Geosci. Remote Sens. Mag. 2013, 6–43. [Google Scholar] [CrossRef]
- Rosen, P.; Hensley, S.; Joughin, I.; Li, F.; Madsen, S.; Rodriguez, E.; Goldstein, R. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Mätzler, C. Microwave permittivity of dry sand. IEEE Trans. Geosci. Remote Sens. 1998, 36, 317–319. [Google Scholar] [CrossRef]
- Rott, H.; Nagler, T.; Scheiber, R. Snow mass retrieval by means of SAR interferometry. Eur. Sp. Agency 2004, 550, 187–192. [Google Scholar]
- Singh, G.; Verma, A.; Kumar, S.; Snehmani; Ganju, A.; Yamaguchi, Y.; Kulkarni, A.V. Snowpack density retrieval using fully polarimetric TerraSAR-X data in the Himalayas. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6320–6329. [Google Scholar] [CrossRef]
- Varade, D.; Manickam, S.; Dikshit, O.; Singh, G. Snehmani Modelling of early winter snow density using fully polarimetric C-band SAR data in the Indian Himalayas. Remote Sens. Environ. 2020, 240, 111699. [Google Scholar] [CrossRef]
- Varade, D.; Dikshit, O.; Manickam, S.; Singh, G. Snehmani Capability assessment of Sentinel-1 bi-temporal dual polarimetric SAR data for inferences on snow density. In Proceedings of the 2019 IEEE MTT-S International Microwave and RF Conference (IMARC), Mumbai, India, 13–15 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Manickam, S.; Bhattacharya, A.; Singh, G.; Yamaguchi, Y. Estimation of snow surface dielectric constant from polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 211–218. [Google Scholar] [CrossRef]
- Zhang, B.; Li, J.; Ren, H. Using phase unwrapping methods to apply D-InSAR in mining areas. Can. J. Remote Sens. 2019, 45, 225–233. [Google Scholar] [CrossRef]
- Choi, H.; Bindschadler, R. Cloud detection in Landsat imagery of ice sheets using shadow matching technique and automatic normalized difference snow index threshold value decision. Remote Sens. Environ. 2004, 91, 237–242. [Google Scholar] [CrossRef]
- Varade, D.; Dikshit, O.; Manickam, S. Dry/wet snow mapping based on the synergistic use of dual polarimetric SAR and multispectral data. J. Mt. Sci. 2019, 16, 1435–1451. [Google Scholar] [CrossRef]
- Nagler, T.; Rott, H.; Ripper, E.; Bippus, G.; Hetzenecker, M. Advancements for snowmelt monitoring by means of sentinel-1 SAR. Remote Sens. 2016, 8, 348. [Google Scholar] [CrossRef]
- He, Y.; Wetterhall, F.; Cloke, H.L.; Pappenberger, F.; Wilson, M.D.; Freer, J.E.; McGregor, G. Tracking the uncertainty in flood alerts driven by grand ensemble weather predictions. Meteorol. Appl. 2009, 16, 91–101. [Google Scholar] [CrossRef]
- Colbeck, S.C. Grain clusters in wet snow. J. Colloid Interface Sci. 1979, 72, 371–384. [Google Scholar] [CrossRef]
- Colbeck, S.C. An overview of seasonal snow metamorphism. Rev. Geophys. 1982, 20, 45–61. [Google Scholar] [CrossRef]
- Surendar, M.; Bhattacharya, A.; Singh, G.; Venkataraman, G. Estimation of snow density using full-polarimetric Synthetic Aperture Radar (SAR) data. Phys. Chem. Earth 2015, 83–84, 156–165. [Google Scholar] [CrossRef]


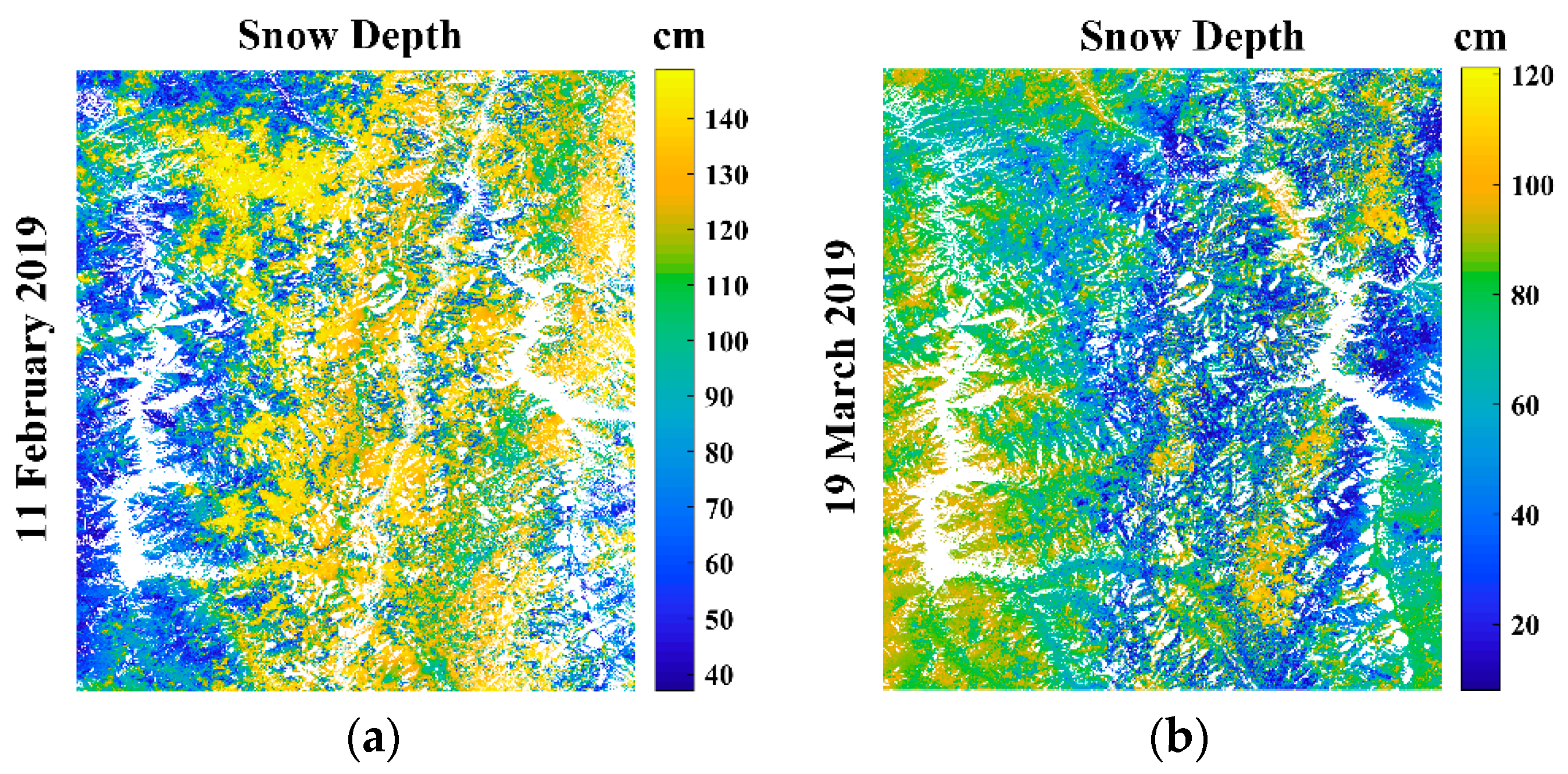
| Month | February | Incidence Angle | March | Incidence Angle |
|---|---|---|---|---|
| Reference Snow Covered Scene | 20190211 | 43.76 | 20190319 | 43.77 |
| Nearest Snow-Covered Scene | 20190210 | 45.36 | 20190307 | 43.77 |
| Snow Free Scene | 20180920 | 41.99 | 20180920 | 41.99 |
| DInSAR Temporal Baseline | 144 days | 182 days |
| Months | Total Number of Pixels Per Image = 27,240,402 Total Investigation Area = 6129.09 km2 | |||||
|---|---|---|---|---|---|---|
| Data | Source | Date | Total No of Pixels | Percentage of Valid Pixels | Percentage of Invalid Pixels | |
| February | SCA | Landsat-8 | 20190208 | 24,615,330 | 89.6 | 10.4 |
| Layover shadow | Sentinel-1 SLC | 20190211 | 24,163,647 | 88.0 | 12.0 | |
| Local incidence angle mask | Sentinel-1 SLC | 20190211 | 24,712,922 | 90.0 | 10.0 | |
| overall mask | Landsat-8 and Sentinel-1 | 20190208- | 18,945,394 | 69.0 | 31.0 | |
| March | SCA | Landsat-8 | 20190208- | 24,615,330 | 90.4 | 9.64 |
| Layover shadow | Sentinel-1 SLC | 20190319 | 24,163,448 | 88.7 | 11.30 | |
| Local incidence angle mask | Sentinel-1 SLC | 20190319 | 25,444,768 | 93.4 | 6.59 | |
| Overall mask | Landsat-8 and Sentinel-1 | 20190208- | 20,911,942 | 76.8 | 23.23 | |
| Months | Stations | Latitude, Longitude (°) | Elevation (m) | Permittivity | Depth (cm) |
|---|---|---|---|---|---|
| February | Kalafgan | 36.41168, 69.52226 | 2243 | 1.65 | 79.15 |
| Worsaj | 36.01873, 70.028075 | 2666 | 1.52 | 84.61 | |
| Namakab | 36.53367, 69.708233 | 1434 | 1.63 | 50.06 | |
| Farkhar | 36.46611, 69.968109 | 3358 | 1.22 | 70.17 | |
| Deh Lala | 35.94721, 69.72947 | 3650 | 1.63 | 109.05 | |
| March | Kalafgan | 36.41168, 69.52226 | 2243 | 1.66 | 65.18 |
| Worsaj | 36.01873, 70.028075 | 2666 | 1.55 | 72.24 | |
| Namakab | 36.53367, 69.708233 | 1434 | 1.66 | 94.80 | |
| Farkhar | 36.46611, 69.968109 | 3358 | 1.55 | 53.03 | |
| Deh Lala | 35.94721, 69.729476 | 3650 | 1.49 | 94.56 |
| Dataset | Parameter | DInSAR Displacement | Model f(x) = p1x + p2 (95% Confidence Bounds): | Modeled Snow Depth | Model f(x) = p1x + p2 (95% Confidence Bounds): |
|---|---|---|---|---|---|
| February | R2 | 0.735 | p1 = −18.87 (−27.42, −10.32) p2 = 74.73 (70.76, 78.7) | 0.8188 | p1 = 0.3456 (0.223, 0.4681) p2 = 41.96 (32.91, 51.01) |
| Adj R2 | 0.705 | 0.7987 | |||
| RMSE | 2.829 | 2.338 | |||
| MSE | 8.003 | 5.466 | |||
| MAE | 9.383 | 7.754 | |||
| March | R2 | 0.493 | p1 = −1.844 (−2.965, −0.7234) p2 = 72.65 (70.29, 75.02) | 0.567 | p1 = −0.4039 (−0.6155, −0.1924) p2 = 100.5 (84.01, 117) |
| Adj R2 | 0.454 | 0.534 | |||
| RMSE | 1.565 | 1.446 | |||
| MSE | 2.449 | 2.091 | |||
| MAE | 5.191 | 4.796 | |||
| Both | R2 | 0.007 | p1 = −0.7426 (−2.32, 0.8349) p2 = 69.76 (67.18, 72.33) | 0.476 | p1 = −0.4645 (−0.6455, −0.2834) p2 = 104.9 (90.81, 118.9) |
| Adj R2 | 0.034 | 0.454 | |||
| RMSE | 3.854 | 2.799 | |||
| MSE | 14.853 | 7.834 | |||
| MAE | 12.782 | 9.283 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoodzada, A.B.; Varade, D.; Shimada, S. Estimation of Snow Depth in the Hindu Kush Himalayas of Afghanistan during Peak Winter and Early Melt Season. Remote Sens. 2020, 12, 2788. https://doi.org/10.3390/rs12172788
Mahmoodzada AB, Varade D, Shimada S. Estimation of Snow Depth in the Hindu Kush Himalayas of Afghanistan during Peak Winter and Early Melt Season. Remote Sensing. 2020; 12(17):2788. https://doi.org/10.3390/rs12172788
Chicago/Turabian StyleMahmoodzada, Abdul Basir, Divyesh Varade, and Sawahiko Shimada. 2020. "Estimation of Snow Depth in the Hindu Kush Himalayas of Afghanistan during Peak Winter and Early Melt Season" Remote Sensing 12, no. 17: 2788. https://doi.org/10.3390/rs12172788
APA StyleMahmoodzada, A. B., Varade, D., & Shimada, S. (2020). Estimation of Snow Depth in the Hindu Kush Himalayas of Afghanistan during Peak Winter and Early Melt Season. Remote Sensing, 12(17), 2788. https://doi.org/10.3390/rs12172788







