Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data
Abstract
1. Introduction
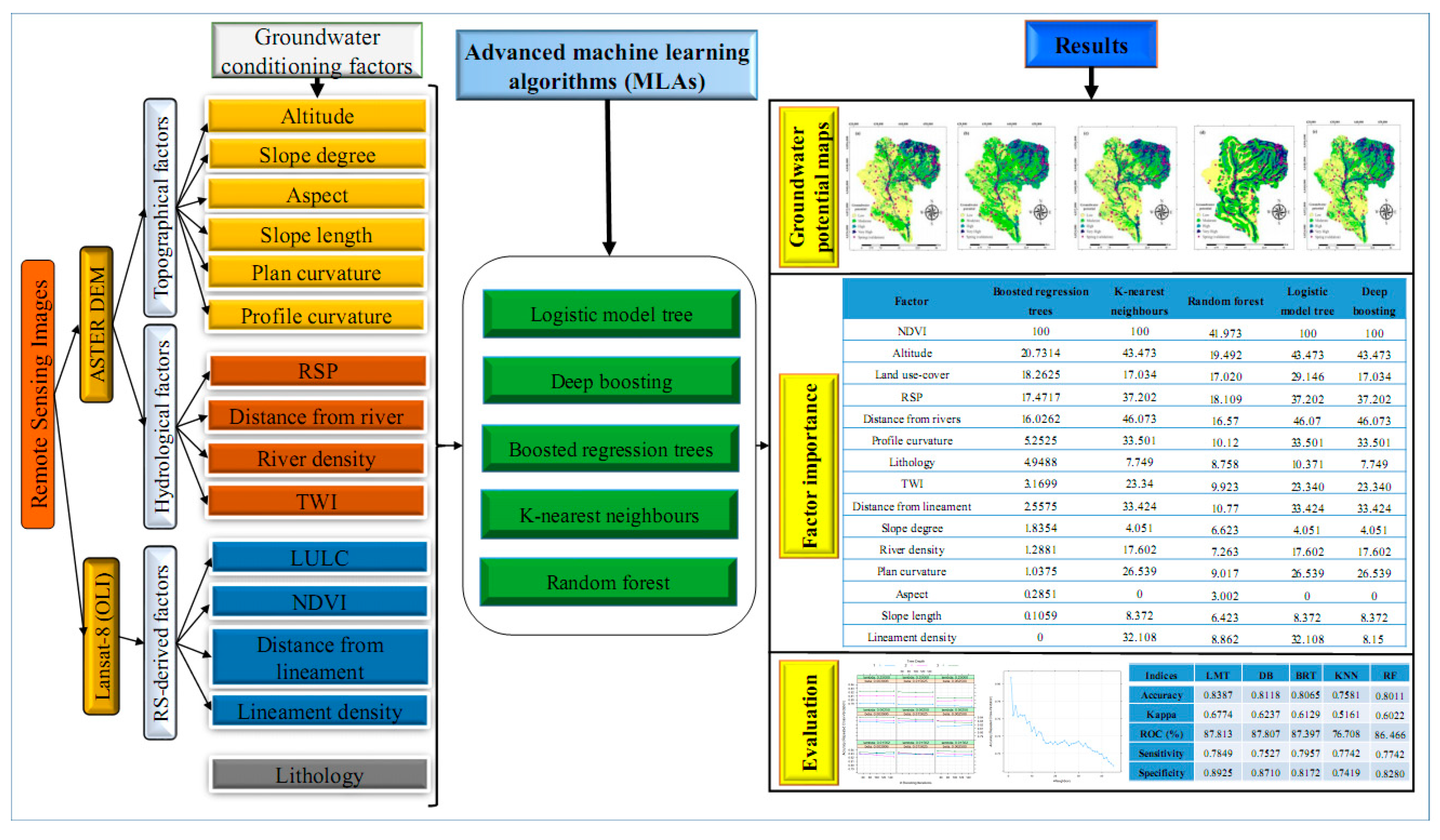
2. Materials and Methods
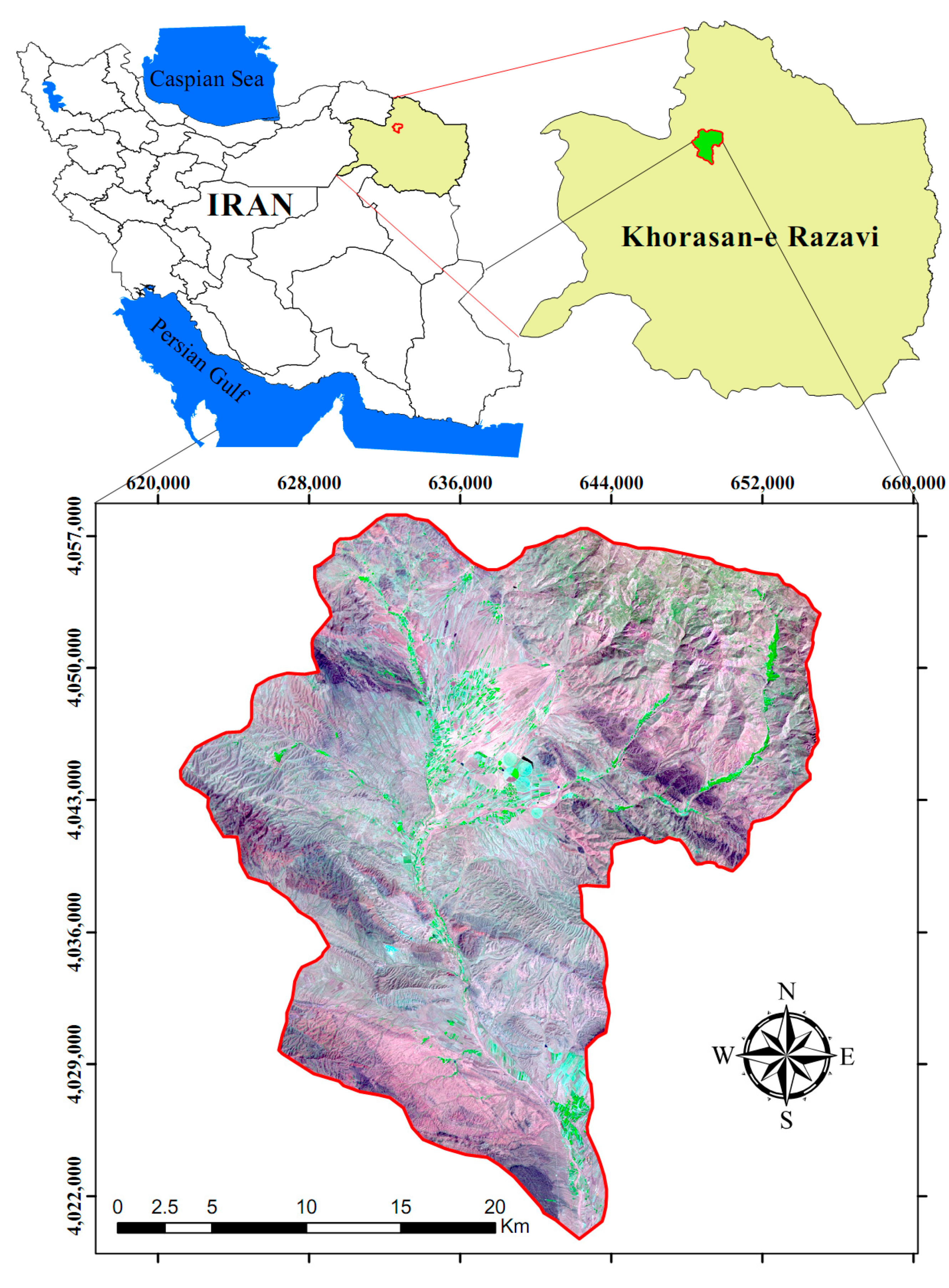
2.1. Study Area
2.2. GW Spring Driving Factors
2.2.1. Topographical Driving Factors
Altitude
Slope Degree
Aspect
Slope Length (LS)
Plan and Profile Curvatures
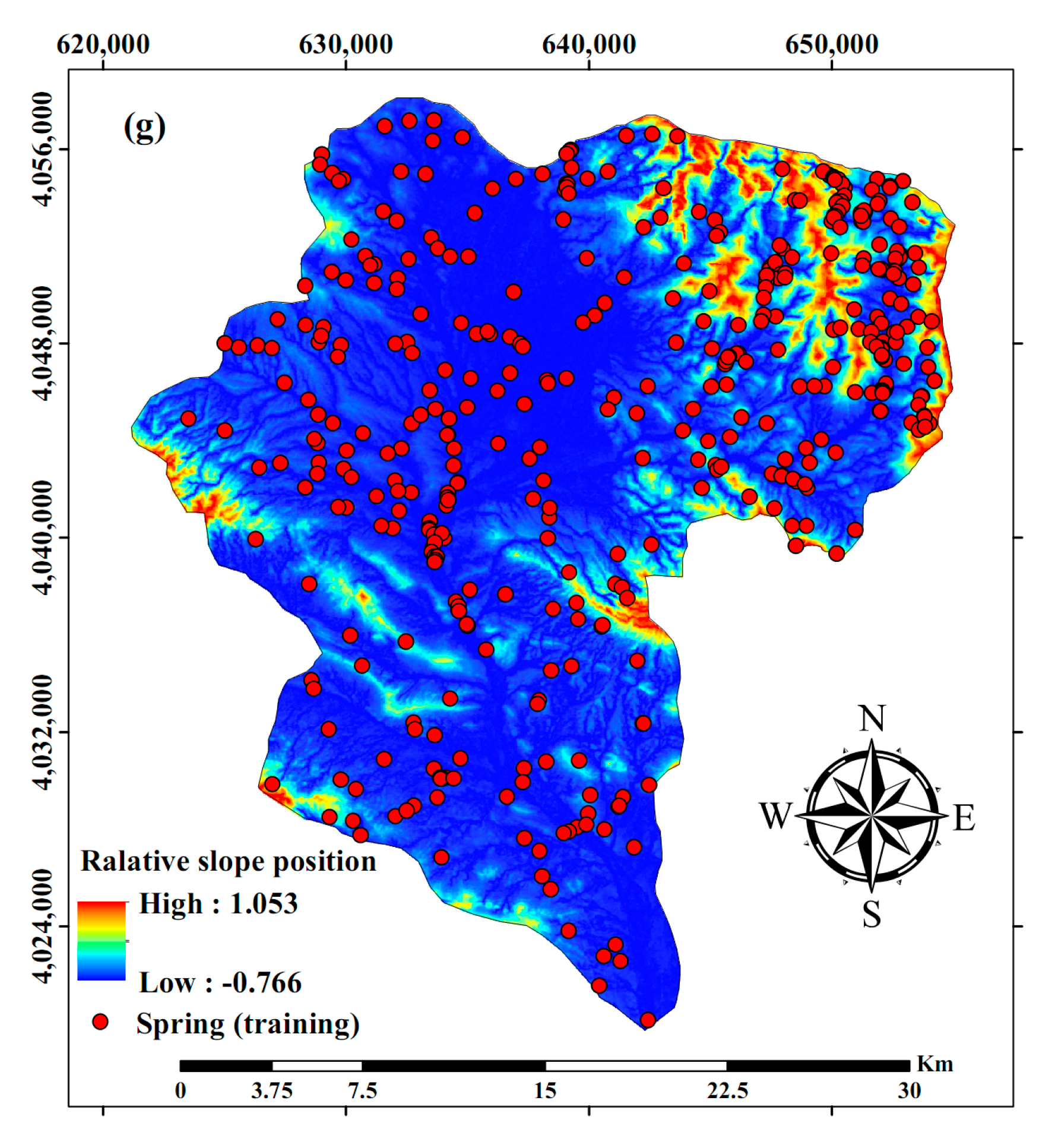
Relative Slope Position (RSP)
2.2.2. Hydrological Driving Factors
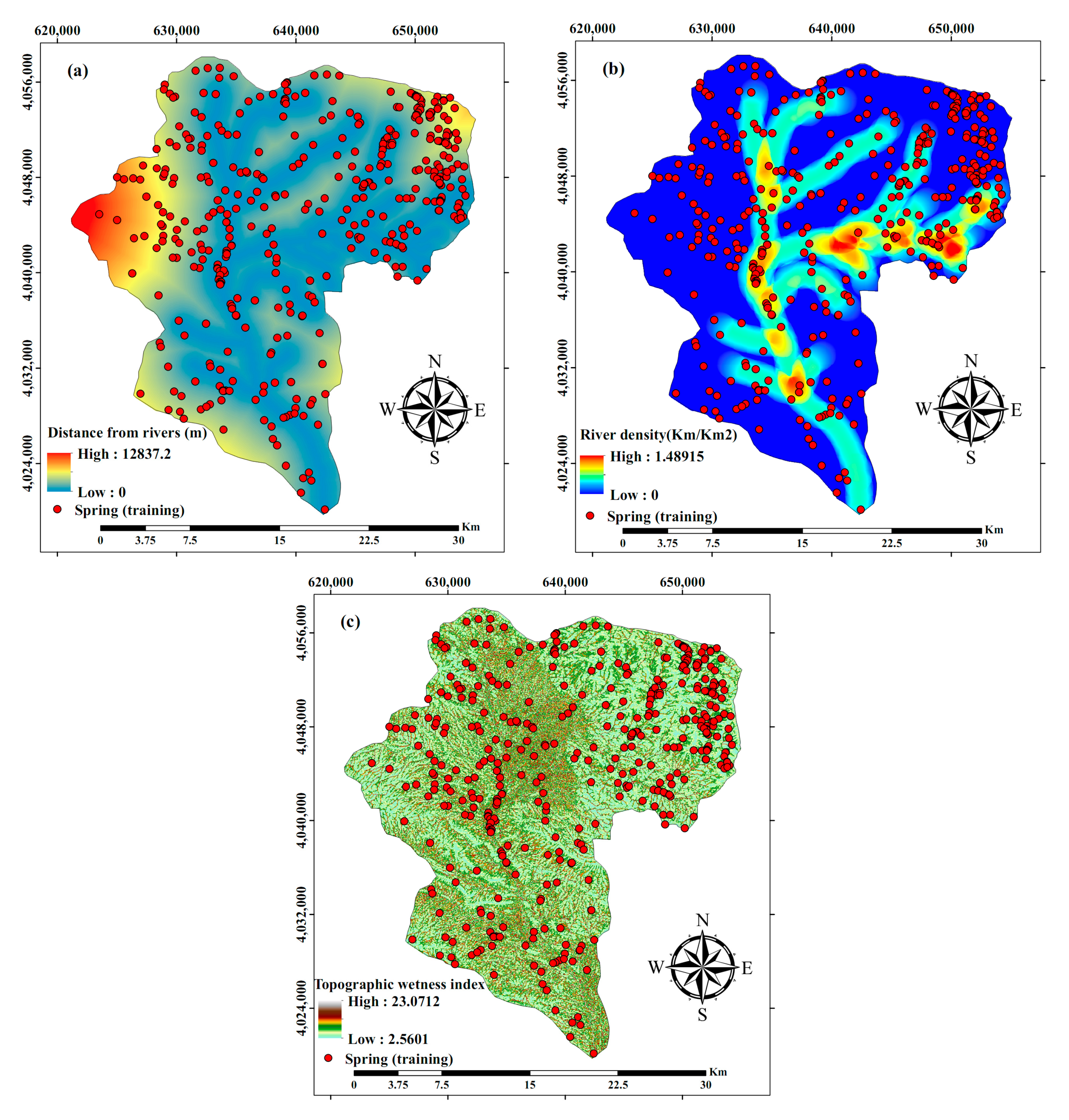
Distance from Rivers and River Density (Rd)
Topographic Wetness Index (TWI)
2.2.3. RS-Derived Factors
Satellite Data and Pre-Processing
Generation of Land Use/Land-Cover Classification and Accuracy Assessment
Retrieval of Normalized Difference Vegetation Index (NDVI)
Distance from Lineament and Lineament Density
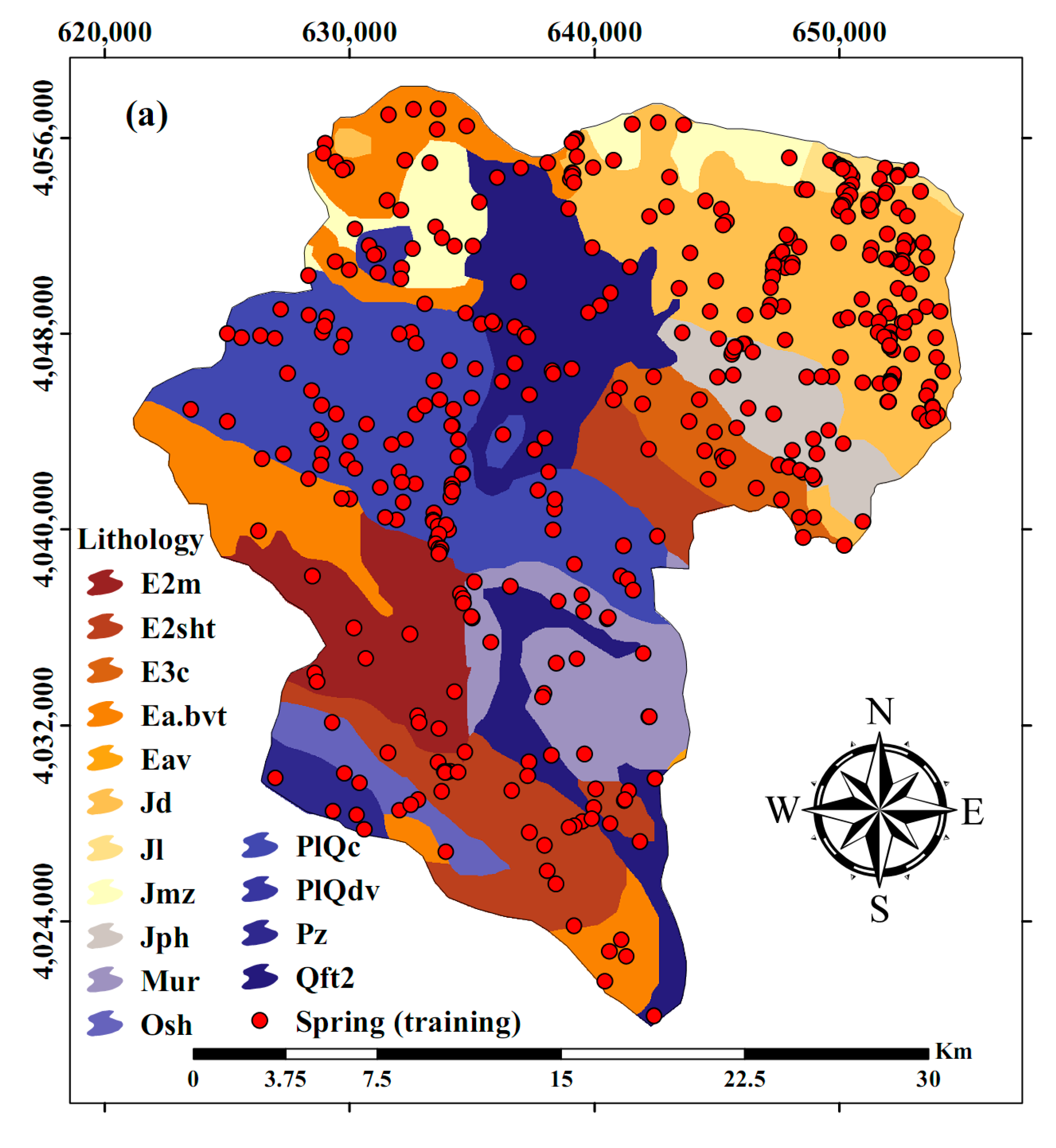
2.2.4. Lithology
2.3. Machine Learning Algorithms
2.3.1. Logistic Model Tree
2.3.2. Deep Boosting
2.3.3. Boosted Regression Trees
2.3.4. K-Nearest Neighbors
2.3.5. Random Forest
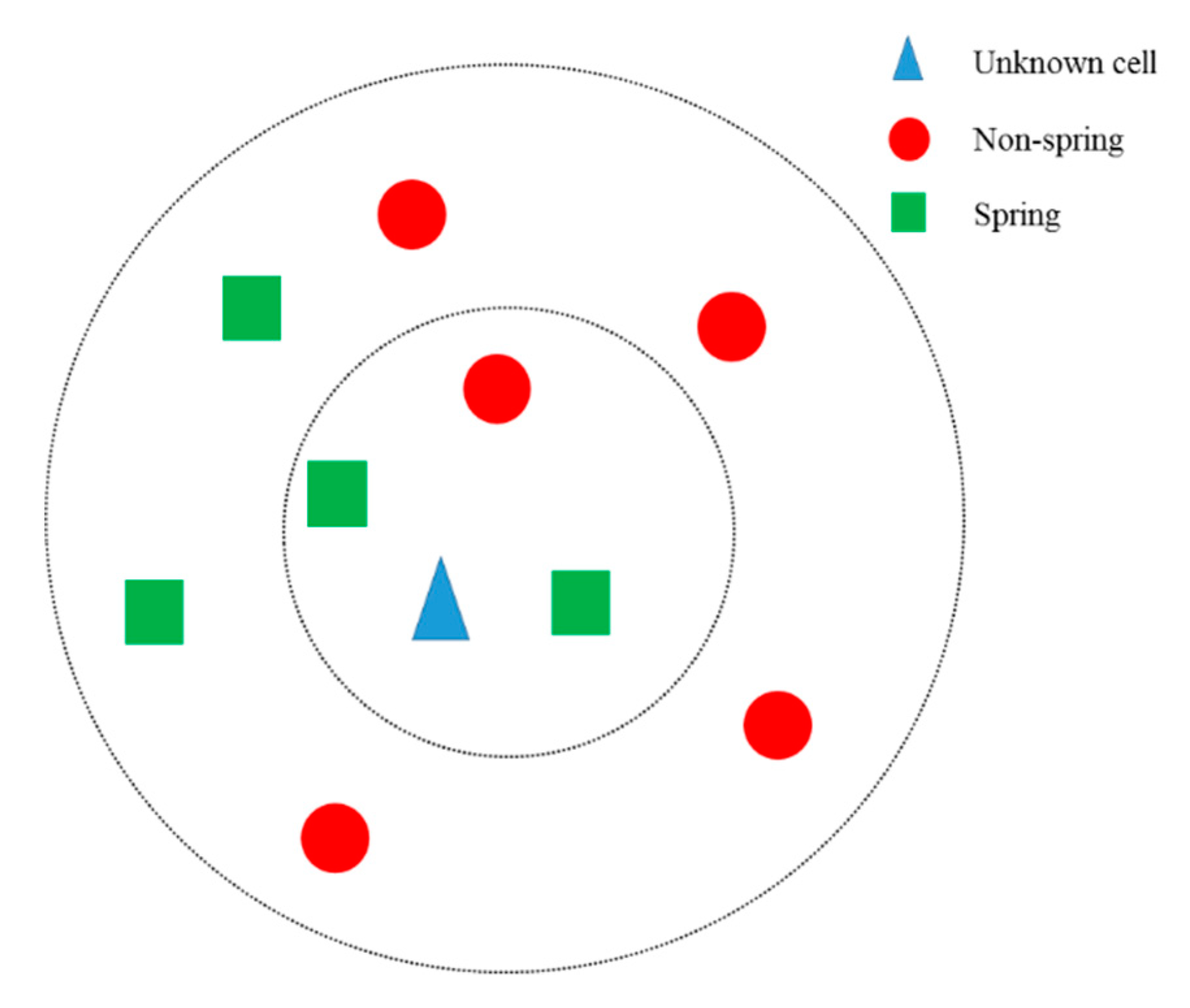
2.4. Validation of the Algorithms
3. Results
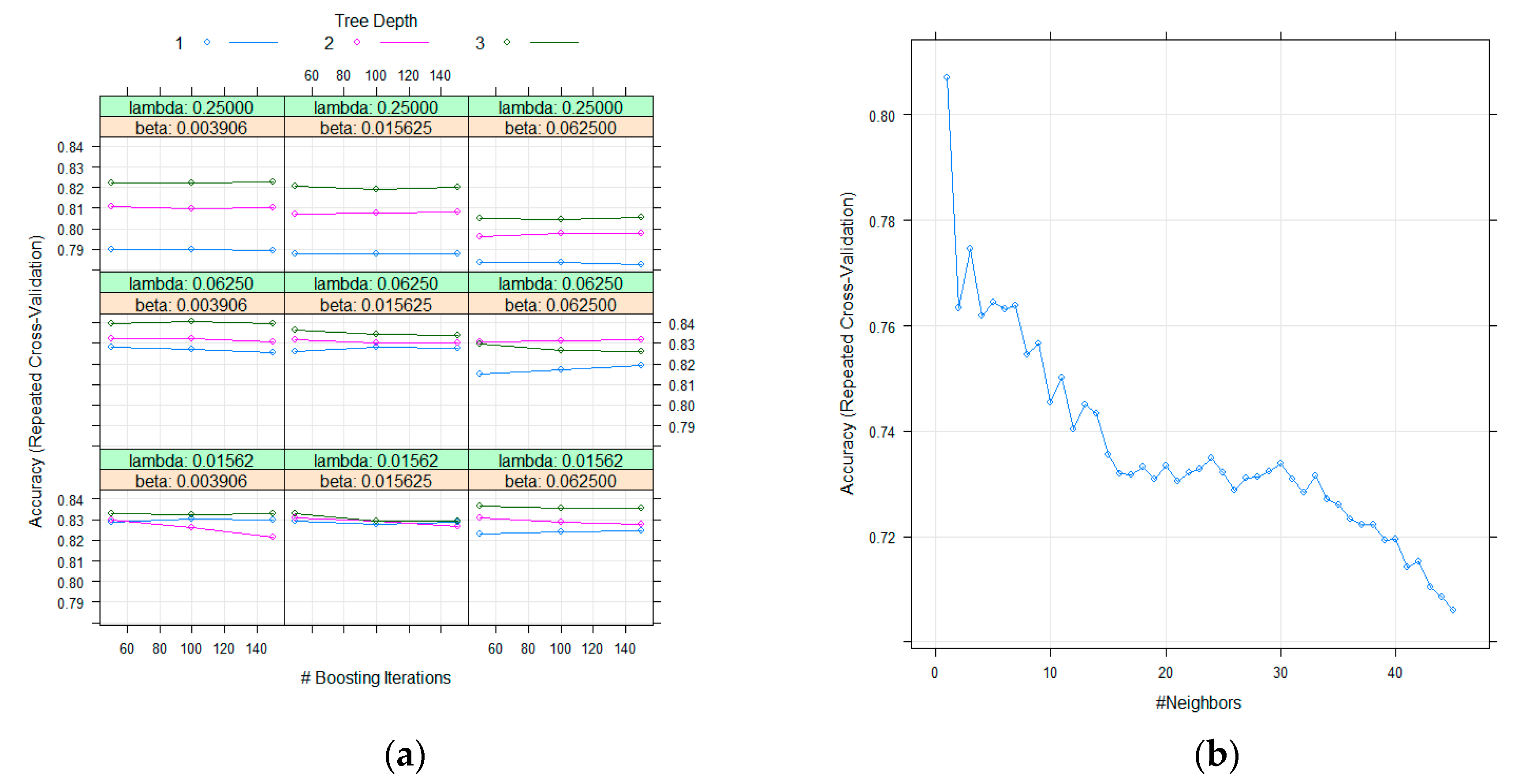
3.1. Machine Learning Algorithm Parameter Optimization Results
3.2. Validation of Maps and Performance Analysis of the Algorithms
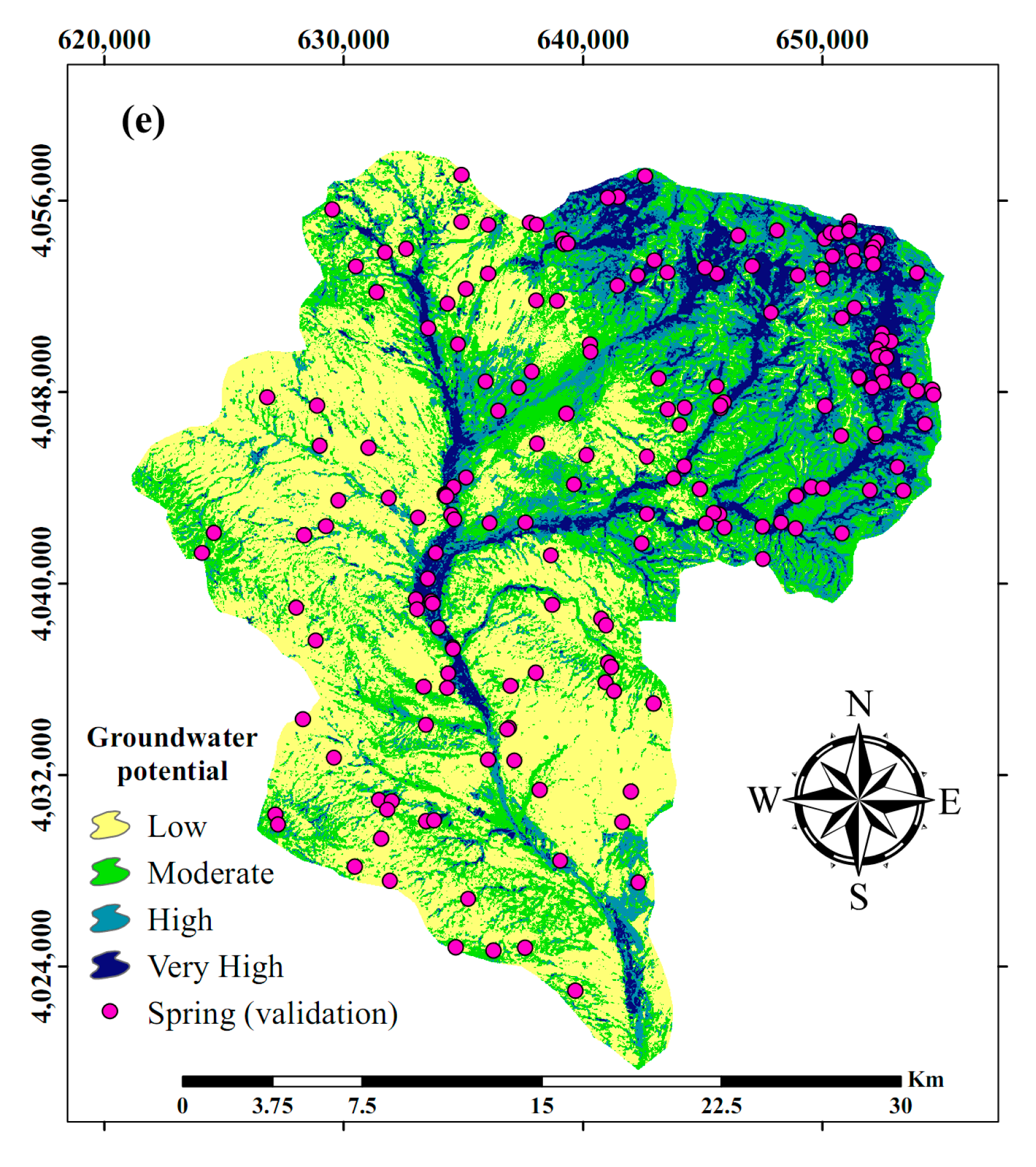
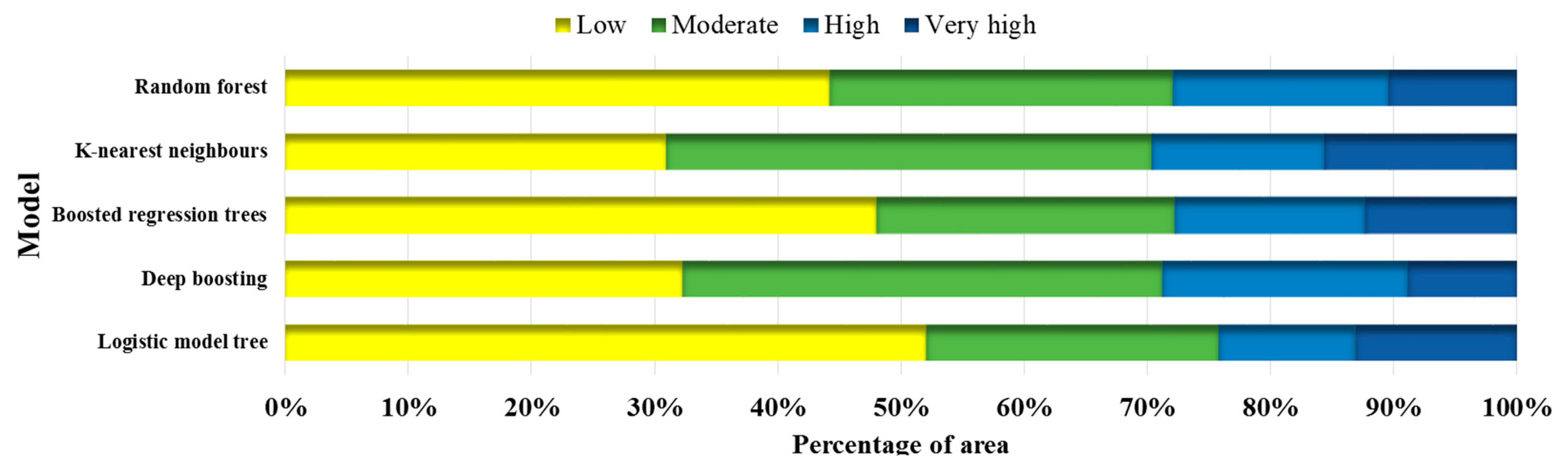
3.3. GW Potential Maps
3.4. Importance of Factors
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wada, Y.; Van Beek, L.P.H.; Van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Alcamo, J.; Henrich, T.; Rosch, T. World Water in 2025—Global Modelling and Scenario Analysis for the World Commission on Water for the 21st Century; Report A0002; Centre for Environmental System Research, University of Kassel: Kassel, Germany, 2000. [Google Scholar]
- Chezgi, J.; Pourghasemi, H.R.; Naghibi, S.A.; Moradi, H.R.; Kheirkhah Zarkesh, M. Assessment of a spatial multi-criteria evaluation to site selection underground dams in the Alborz Province, Iran. Geocarto Int. 2016, 31, 628–646. [Google Scholar] [CrossRef]
- Sahoo, S.; Munusamy, S.B.; Dhar, A.; Kar, A.; Ram, P. Appraising the accuracy of multi-class frequency ratio and weights of evidence method for delineation of regional groundwater potential zones in canal command system. Water Resour. Manag. 2017, 31, 4399–4413. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Abbaspour, K. A comparison between ten advanced and soft computing models for groundwater qanat potential assessment in Iran using R and GIS. Theor. Appl. Climatol. 2018, 131, 967–984. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Moradi Dashtpagerdi, M. Evaluation of four supervised learning methods for groundwater spring potential mapping in Khalkhal region (Iran) using GIS-based features. Hydrogeol. J. 2017, 25, 169–189. [Google Scholar] [CrossRef]
- Kim, J.C.; Jung, H.S.; Lee, S. Spatial mapping of the groundwater potential of the Geum River basin using ensemble models based on remote sensing images. Remote Sens. 2019, 11, 2285. [Google Scholar] [CrossRef]
- Moghaddam, D.D.; Rahmati, O.; Haghizadeh, A.; Kalantari, Z. A modeling comparison of groundwater potential mapping in a mountain bedrock aquifer: QUEST, GARP, and RF models. Water 2020, 12, 679. [Google Scholar] [CrossRef]
- Kalantar, B.; Al-Najjar, H.A.H.; Pradhan, B.; Saeidi, V.; Halin, A.A.; Ueda, N.; Naghibi, S.A. Optimized conditioning factors using machine learning techniques for groundwater potential mapping. Water 2019, 11, 1909. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Hashemi, H.; Berndtsson, R.; Lee, S. Application of extreme gradient boosting and parallel random forest algorithms for assessing groundwater spring potential using DEM-derived factors. J. Hydrol. 2020, 589, 125197. [Google Scholar] [CrossRef]
- Corsini, A.; Cervi, F.; Ronchetti, F. Weight of evidence and artificial neural networks for potential groundwater spring mapping: An application to the Mt. Modino area (Northern Apennines, Italy). Geomorphology 2009, 111, 79–87. [Google Scholar] [CrossRef]
- Lee, S.; Hyun, Y.; Lee, S.; Lee, M.-J. Groundwater potential mapping using remote sensing and GIS-based machine learning techniques. Remote Sens. 2020, 12, 1200. [Google Scholar] [CrossRef]
- Al-Djazouli, M.O.; Elmorabiti, K.; Rahimi, A.; Amellah, O.; Fadil, O.A.M. Delineating of groundwater potential zones based on remote sensing, GIS and analytical hierarchical process: A case of Waddai, eastern Chad. GeoJournal 2020, 1–14. [Google Scholar] [CrossRef]
- Martínez-Santos, P.; Renard, P. Mapping groundwater potential through an ensemble of big data methods. Groundwater 2020, 58, 583–597. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Panahi, M.; Khosravi, K.; Pourghasemi, H.R.; Rezaie, F.; Parvinnezhad, D. Spatial prediction of groundwater potentiality using ANFIS ensembled with teaching-learning-based and biogeography-based optimization. J. Hydrol. 2019, 572, 435–448. [Google Scholar] [CrossRef]
- Moghaddam, D.D.; Rahmati, O.; Panahi, M.; Tiefenbacher, J.; Darabi, H.; Haghizadeh, A.; Haghighi, A.T.; Nalivan, O.A.; Tien Bui, D. The effect of sample size on different machine learning models for groundwater potential mapping in mountain bedrock aquifers. CATENA 2020, 187, 104421. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Dolatkordestani, M.; Rezaei, A.; Amouzegari, P.; Heravi, M.T.; Kalantar, B.; Pradhan, B. Application of rotation forest with decision trees as base classifier and a novel ensemble model in spatial modeling of groundwater potential. Environ. Monit. Assess. 2019, 191, 1–20. [Google Scholar] [CrossRef]
- Ozdemir, A. Using a binary logistic regression method and GIS for evaluating and mapping the groundwater spring potential in the Sultan Mountains (Aksehir, Turkey). J. Hydrol. 2011, 405, 123–136. [Google Scholar] [CrossRef]
- Ozdemir, A. GIS-based groundwater spring potential mapping in the Sultan Mountains (Konya, Turkey) using frequency ratio, weights of evidence and logistic regression methods and their comparison. J. Hydrol. 2011, 411, 290–308. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Moghaddam, D.D.; Kalantar, B.; Pradhan, B.; Kisi, O. A comparative assessment of GIS-based data mining models and a novel ensemble model in groundwater well potential mapping. J. Hydrol. 2017, 548, 471–483. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Ha, D.H.; Avand, M.; Jaafari, A.; Nguyen, H.D.; Al-Ansari, N.; Van Phong, T.; Sharma, R.; Kumar, R.; Van Le, H.; et al. Soft computing ensemble models based on logistic regression for groundwater potential mapping. Appl. Sci. 2020, 10, 2469. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C.; et al. GIS-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.C.; Jung, H.S.; Lee, S. Groundwater productivity potential mapping using frequency ratio and evidential belief function and artificial neural network models: Focus on topographic factors. J. Hydroinformatics 2018, 20, 1436–1451. [Google Scholar] [CrossRef]
- Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Tien Bui, D.; Bui, Q.T.; Nguyen, Q.P.; Pradhan, B.; Nampak, H.; Trinh, P.T. A hybrid artificial intelligence approach using GIS-based neural-fuzzy inference system and particle swarm optimization for forest fire susceptibility modeling at a tropical area. Agric. For. Meteorol. 2017, 233, 32–44. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. CATENA 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Colkesen, I.; Kavzoglu, T. The use of logistic model tree (LMT) for pixel and object based classifications using high resolution WorldView 2 imagery. Geocarto Int. 2017, 32, 71–86. [Google Scholar] [CrossRef]
- Cortes, C.; Mohri, M.; Syed, U. Deep Boosting. In Proceedings of the 31st International Conference on International Conference on Machine Learning, Beijing, China, 21–26 June 2014; Volume 32, pp. 1179–1187. [Google Scholar]
- Pham, B.T.; Van Phong, T.; Nguyen, H.D.; Qi, C.; Al-Ansari, N.; Amini, A.; Ho, L.S.; Tuyen, T.T.; Yen, H.P.H.; Ly, H.-B.; et al. A comparative study of kernel logistic regression, radial basis function classifier, multinomial naïve bayes, and logistic model tree for flash flood susceptibility mapping. Water 2020, 12, 239. [Google Scholar] [CrossRef]
- Khosravi, K.; Melesse, A.M.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hong, H. Flood susceptibility mapping at Ningdu catchment, China using bivariate and data mining techniques. In Extreme Hydrology and Climate Variability; Elsevier: Amsterdam, The Netherlands, 2019; pp. 419–434. [Google Scholar]
- Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Singh, S.K.; Al-Ansari, N.; Clague, J.J.; Jaafari, A.; Chen, W.; Miraki, S.; Dou, J.; et al. Shallow landslide susceptibility mapping: A comparison between logistic model tree, logistic regression, naïve bayes tree, artificial neural network, and support vector machine algorithms. Int. J. Environ. Res. Public Health 2020, 17, 2749. [Google Scholar] [CrossRef]
- Jothibasu, A.; Anbazhagan, S. Modeling groundwater probability index in Ponnaiyar River basin of South India using analytic hierarchy process. Model. Earth Syst. Environ. 2016, 2, 109. [Google Scholar] [CrossRef]
- Aniya, M. Landslide susceptibility mapping in the Amahata River Basin, Japan. Ann. Assoc. Am. Geogr. 1985, 75, 102–114. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. Application of an evidential belief function model in landslide susceptibility mapping. Comput. Geosci. 2012, 44, 120–135. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Park, H.J.; Lee, J.H. A novel ensemble bivariate statistical evidential belief function with knowledge-based analytical hierarchy process and multivariate statistical logistic regression for landslide susceptibility mapping. CATENA 2014, 114, 21–36. [Google Scholar] [CrossRef]
- Sinha, D.D.; Mohapatra, S.N.; Pani, P. Mapping and assessment of groundwater potential in Bilrai watershed (Shivpuri District, M.P.) a geomatics approach. J. Indian Soc. Remote Sens. 2012, 40, 649–668. [Google Scholar] [CrossRef]
- Benjmel, K.; Amraoui, F.; Boutaleb, S.; Ouchchen, M.; Tahiri, A.; Touab, A. Mapping of groundwater potential zones in crystalline terrain using remote sensing, GIS techniques, and multicriteria data analysis (Case of the Ighrem Region, Western Anti-Atlas, Morocco). Water 2020, 12, 471. [Google Scholar] [CrossRef]
- Mogaji, K.A.; Lim, H.S.; Abdullah, K. Regional prediction of groundwater potential mapping in a multifaceted geology terrain using GIS-based Dempster–Shafer model. Arab. J. Geosci. 2015, 8, 3235–3258. [Google Scholar] [CrossRef]
- Razavi-Termeh, S.V.; Sadeghi-Niaraki, A.; Choi, S.M. Groundwater potential mapping using an integrated ensemble of three bivariate statistical models with random forest and logistic model tree models. Water 2019, 11, 1596. [Google Scholar] [CrossRef]
- Ahmed, R.; Sajjad, H. Analyzing factors of groundwater potential and its relation with population in the Lower Barpani Watershed, Assam, India. Nat. Resour. Res. 2018, 27, 503–515. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 1–27. [Google Scholar] [CrossRef]
- Moore, I.D.; Burch, G.J. Sediment transport capacity of sheet and rill flow: Application of unit stream power theory. Water Resour. Res. 1986, 22, 1350–1360. [Google Scholar] [CrossRef]
- Al-Abadi, A.M.; Al-Temmeme, A.A.; Al-Ghanimy, M.A. A GIS-based combining of frequency ratio and index of entropy approaches for mapping groundwater availability zones at Badra–Al Al-Gharbi–Teeb areas, Iraq. Sustain. Water Resour. Manag. 2016, 2, 265–283. [Google Scholar] [CrossRef]
- Choubin, B.; Rahmati, O.; Soleimani, F.; Alilou, H.; Moradi, E.; Alamdari, N. Regional groundwater potential analysis using classification and regression trees. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 485–498. [Google Scholar]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei-Sardooi, E.; Samani, A.N.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Horton, R.E. Drainage-basin characteristics. Trans. Am. Geophys. Union 1932, 13, 350. [Google Scholar] [CrossRef]
- Moglen, G.E.; Eltahir, E.A.B.; Bras, R.L. On the sensitivity of drainage density to climate change. Water Resour. Res. 1998, 34, 855–862. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Alilou, H.; Moghaddam Nia, A.; Keshtkar, H.; Han, D.; Bray, M. A cost-effective and efficient framework to determine water quality monitoring network locations. Sci. Total Environ. 2018, 624, 283–293. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Indhulekha, K.; Chandra Mondal, K.; Jhariya, D.C. Groundwater prospect mapping using remote sensing, GIS and resistivity survey techniques in Chhokra Nala Raipur district, Chhattisgarh, India. J. Water Supply Res. Technol. 2019, 68, 595–606. [Google Scholar] [CrossRef]
- Sultana, S.; Satyanarayana, A.N.V. Assessment of urbanisation and urban heat island intensities using landsat imageries during 2000–2018 over a sub-tropical Indian City. Sustain. Cities Soc. 2020, 52, 101846. [Google Scholar] [CrossRef]
- Dissanayake, D.; Morimoto, T.; Ranagalage, M.; Murayama, Y. Land-use/land-cover changes and their impact on surface urban heat islands: Case study of Kandy City, Sri Lanka. Climate 2019, 7, 99. [Google Scholar] [CrossRef]
- Nigatu, W.; Dick, Ø.B.; Tveite, H. GIS based mapping of land cover changes utilizing multi-temporal remotely sensed image data in Lake Hawassa Watershed, Ethiopia. Environ. Monit. Assess. 2014, 186, 1765–1780. [Google Scholar] [CrossRef]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ. 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Nag, S.K. Application of lineament density and hydrogeomorphology to delineate groundwater potential zones of Baghmundi block in Purulia District, West Bengal. J. Indian Soc. Remote Sens. 2005, 33, 521–529. [Google Scholar] [CrossRef]
- Acharya, T.; Nag, S.K.; Basumallik, S. Hydraulic significance of fracture correlated lineaments in precambrian rocks in Purulia district, West Bengal. J. Geol. Soc. India 2012, 80, 723–730. [Google Scholar] [CrossRef]
- Ghorbani Nejad, S.; Falah, F.; Daneshfar, M.; Haghizadeh, A.; Rahmati, O. Delineation of groundwater potential zones using remote sensing and GIS-based data-driven models. Geocarto Int. 2016, 32, 1–21. [Google Scholar] [CrossRef]
- Geology Survey of Iran (GSI). Geological Survey and Mineral Exploration of Iran. 1997. Available online: http://wwwgsiir/Main/Lang_en/indexhtml (accessed on 20 July 2020).
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Tien Bui, D. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, J.R. Simplifying decision trees. Int. J. Man. Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Wadsworth and Brooks/Cole: Monterey, CA, USA, 1984; p. 358. [Google Scholar]
- Kuhn, M.; Wing, J.; Weston, S.; Andre, W.; Chris, K.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Team, R.C.; et al. Classification and Regression Training. 2020. Available online: https://cran.r-project.org/web/packages/caret/caret.pdf (accessed on 15 March 2020).
- Hornik, K.; Buchta, C.; Hothorn, T.; Karatzoglou, A.; Meyer, D.; Zeileis, A. R/Weka Interface. 2020. Available online: https://cran.r-project.org/web/packages/RWeka/RWeka.pdf (accessed on 15 March 2020).
- Marcous, D.; Sandbank, Y. Deep Boosting Ensemble Modeling. Available online: https://cran.r-project.org/web/packages/deepboost/deepboost.pdf (accessed on 15 March 2020).
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. GIS-based groundwater spring potential mapping using data mining boosted regression tree and probabilistic frequency ratio models in Iran. AIMS Geosci. 2017, 3, 91–115. [Google Scholar]
- Liu, J.; Sui, C.; Deng, D.; Wang, J.; Feng, B.; Liu, W.; Wu, C. Representing conditional preference by boosted regression trees for recommendation. Inf. Sci. 2016, 327, 1–20. [Google Scholar] [CrossRef]
- Schonlau, M. Boosted Regression (Boosting): An Introductory Tutorial and a Stata Plugin. Stata J. Promot. Commun. Stat. Stata 2005, 5, 330–354. [Google Scholar] [CrossRef]
- Greenwell, B.; Boehmke, B.; Cunningham, J. Generalized Boosted Regression Models. 2020. Available online: https://cran.r-project.org/web/packages/gbm/gbm.pdf (accessed on 15 March 2020).
- Motevalli, A.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R.; Pradhan, B.; Gholami, V. Inverse method using boosted regression tree and k-nearest neighbor to quantify effects of point and non-point source nitrate pollution in groundwater. J. Clean. Prod. 2019, 228, 1248–1263. [Google Scholar] [CrossRef]
- Shahabi, H.; Shirzadi, A.; Ghaderi, K.; Omidvar, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S.; et al. Flood detection and susceptibility mapping using Sentinel-1 remote sensing data and a machine learning approach: Hybrid intelligence of bagging ensemble based on K-nearest neighbor classifier. Remote Sens. 2020, 12, 266. [Google Scholar] [CrossRef]
- Avand, M.; Janizadeh, S.; Naghibi, S.A.; Pourghasemi, H.R.; Khosrobeigi Bozchaloei, S.; Blaschke, T. A comparative assessment of random forest and k-nearest neighbor classifiers for gully erosion susceptibility mapping. Water 2019, 11, 2076. [Google Scholar] [CrossRef]
- He, Q.P.; Wang, J. Fault detection using the k-nearest neighbor rule for semiconductor manufacturing processes. IEEE Trans. Semicond. Manuf. 2007, 20, 345–354. [Google Scholar] [CrossRef]
- Betrie, G.D.; Tesfamariam, S.; Morin, K.A.; Sadiq, R. Predicting copper concentrations in acid mine drainage: A comparative analysis of five machine learning techniques. Environ. Monit. Assess. 2013, 185, 4171–4182. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–35. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Breiman and Cutler’s Random Forests for Classification and Regression. 2018. Available online: https://cran.r-project.org/web/packages/randomForest/randomForest.pdf (accessed on 15 March 2020).
- Sangchini, E.K.; Emami, S.N.; Tahmasebipour, N.; Pourghasemi, H.R.; Naghibi, S.A.; Arami, S.A.; Pradhan, B. Assessment and comparison of combined bivariate and AHP models with logistic regression for landslide susceptibility mapping in the Chaharmahal-e-Bakhtiari Province, Iran. Arab. J. Geosci. 2016, 9, 201. [Google Scholar] [CrossRef]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using C5.0, random forest, and multivariate adaptive regression spline models in GIS. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef]
- Naghibi, S.; Vafakhah, M.; Hashemi, H.; Pradhan, B.; Alavi, S. Groundwater augmentation through the site selection of floodwater spreading using a data mining approach (case study: Mashhad Plain, Iran). Water 2018, 10, 1405. [Google Scholar] [CrossRef]
- Andualem, T.G.; Demeke, G.G. Groundwater potential assessment using GIS and remote sensing: A case study of Guna tana landscape, upper blue Nile Basin, Ethiopia. J. Hydrol. Reg. Stud. 2019, 24, 100610. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of support vector machine, random forest, and genetic algorithm optimized random forest models in groundwater potential mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
- Shoombuatong, W.; Hongjaisee, S.; Barin, F.; Chaijaruwanich, J.; Samleerat, T. HIV-1 CRF01_AE coreceptor usage prediction using kernel methods based logistic model trees. Comput. Biol. Med. 2012, 42, 885–889. [Google Scholar] [CrossRef]
- Arabameri, A.; Chen, W.; Loche, M.; Zhao, X.; Li, Y.; Lombardo, L.; Cerda, A.; Pradhan, B.; Bui, D.T. Comparison of machine learning models for gully erosion susceptibility mapping. Geosci. Front. 2019. [Google Scholar] [CrossRef]
- Al-Fugara, A.; Pourghasemi, H.R.; Al-Shabeeb, A.R.; Habib, M.; Al-Adamat, R.; Al-Amoush, H.; Collins, A.L. A comparison of machine learning models for the mapping of groundwater spring potential. Environ. Earth Sci. 2020, 79, 206. [Google Scholar] [CrossRef]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd International Conference on Machine Learning—ICML ’06, Pittsburgh, Pennsylvania, 25–29 June 2006; pp. 161–168. [Google Scholar]
- Naghibi, S.A.; Vafakhah, M.; Hashemi, H.; Pradhan, B.; Alavi, S.J. Water resources management through flood spreading project suitability mapping using frequency ratio, k-nearest neighbours, and random forest algorithms. Nat. Resour. Res. 2020, 29, 1915–1933. [Google Scholar] [CrossRef]
| Indices | Classification Algorithm | ||
|---|---|---|---|
| Maximum Likelihood | Neural Network | Decision Tree | |
| Overall Accuracy (%) | 87 | 88 | 91 |
| Kappa Coefficient (%) | 76 | 78 | 82 |
| Geology Group | Description | Age |
|---|---|---|
| Jmz | Grey thick-bedded limestone and dolomite (Mozduran formation) | Middle-Late Jurassic |
| Jd | Well-bedded to thin-bedded, greenish-grey argillaceous limestone with intercalations of calcareous shale (Dalichai formation) | Jurassic |
| PlQc | Fluvial conglomerate, Piedmont conglomerate, and sandstone | Pliocene-Quaternary |
| Jl | Light grey, thin-bedded to massive limestone (Lar formation) | Jurassic-Cretaceous |
| Qft2 | Low level piedmont fan and valley terrace deposits | Quaternary |
| Ea.bvt | Andesitic to basaltic volcanic tuff | Eocene |
| PlQdv | Rhyolitic to Rhyodacitic volcanics | Pliocene-Quaternary |
| Jph | Phyllite, slate, and meta-sandstone (Hamadan Phyllites) | Jurassic |
| E3c | Conglomerate and sandstone | Eocene |
| E2sht | Tuffaceous shale and tuff | Eocene |
| E2m | Pale red marl, gypsiferous marl, and limestone | Eocene |
| Mur | Red marl, gypsiferous marl, sandstone, and conglomerate (Upper Red formation) | Miocene |
| Pz | Undifferentiated lower Paleozoic rocks | Early Palaeozoic |
| Osh | Greenish-grey siltstone and shale with intercalations of flaggy limestone (Shirgesht formation) | Ordovician |
| Eav | Andesitic volcanics | Middle Eocene |
| Indices | Logistic Model Tree | Deep Boosting | Boosted Regression Trees | K-Nearest Neighbors | Random Forest |
|---|---|---|---|---|---|
| Accuracy | 0.8387 | 0.8118 | 0.8065 | 0.7581 | 0.8010 |
| Kappa | 0.6774 | 0.6237 | 0.6129 | 0.5161 | 0.6022 |
| ROC (%) | 87.813 | 87.807 | 87.397 | 76.708 | 86.466 |
| Sensitivity | 0.7849 | 0.7527 | 0.7957 | 0.7742 | 0.7750 |
| Specificity | 0.8925 | 0.8710 | 0.8172 | 0.7419 | 0.8270 |
| Mean Rank | p-Value (α = 0.05) | χ2 (Chi-Square) | ||||
|---|---|---|---|---|---|---|
| Logistic Model Tree | Deep Boosting | Boosted Regression Trees | K-Nearest Neighbors | Random Forest | ||
| 4.80 | 3.40 | 3.20 | 1.20 | 2.40 | 0.007 | 14.08 |
| Model/Class | Low | Moderate | High | Very High | |
|---|---|---|---|---|---|
| Logistic model tree | Range | 0–0.11 | 0.11–0.37 | 0.37–0.70 | 0.70–1 |
| Area (km2) | 371.02 | 169 | 79.22 | 92.9 | |
| Deep boosting | Range | 0.02–0.27 | 0.27–0.43 | 0.43–0.60 | 0.60–0.98 |
| Area (km2) | 230.23 | 277.32 | 141.73 | 62.83 | |
| Boosted regression trees | Range | 0.09–0.21 | 0.21–0.39 | 0.39–0.62 | 0.62–0.89 |
| Area (km2) | 342.25 | 172.48 | 109.87 | 87.44 | |
| K-nearest neighbors | Range | 0–0.04 | 0.04–0.42 | 0.42–0.71 | 0.71–1 |
| Area (km2) | 220.9 | 280.68 | 99.8 | 110.77 | |
| Random forest | Range | 0–0.16 | 0.16–0.36 | 0.36–0.61 | 0.61–1 |
| Area (km2) | 315.06 | 198.71 | 124.42 | 73.93 |
| Factor | Boosted Regression Trees (Relative Influence) | K-Nearest Neighbors | Random Forest(Mean Decrease Gini) | Logistic Model Tree |
|---|---|---|---|---|
| NDVI | 100 | 100 | 41.973 | 100 |
| Distance from rivers | 16.03 | 46.073 | 16.57 | 46.07 |
| Altitude | 20.73 | 43.473 | 19.492 | 43.473 |
| RSP | 17.47 | 37.202 | 18.109 | 37.202 |
| Profile curvature | 5.25 | 33.501 | 10.12 | 33.501 |
| Distance from lineament | 2.558 | 33.424 | 10.77 | 33.424 |
| Lineament density | 0 | 32.108 | 8.862 | 32.108 |
| Land use-cover | 18.26 | 17.034 | 17.02 | 29.146 |
| Plan curvature | 1.038 | 26.539 | 9.017 | 26.539 |
| TWI | 3.17 | 23.34 | 9.923 | 23.34 |
| River density | 1.288 | 17.602 | 7.263 | 17.602 |
| Lithology | 4.949 | 7.749 | 8.758 | 10.371 |
| Slope length | 0.105 | 8.372 | 6.423 | 8.372 |
| Slope degree | 1.835 | 4.051 | 6.623 | 4.051 |
| Aspect | 0.285 | 0 | 3.002 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamali Maskooni, E.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R. Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data. Remote Sens. 2020, 12, 2742. https://doi.org/10.3390/rs12172742
Kamali Maskooni E, Naghibi SA, Hashemi H, Berndtsson R. Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data. Remote Sensing. 2020; 12(17):2742. https://doi.org/10.3390/rs12172742
Chicago/Turabian StyleKamali Maskooni, Ehsan, Seyed Amir Naghibi, Hossein Hashemi, and Ronny Berndtsson. 2020. "Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data" Remote Sensing 12, no. 17: 2742. https://doi.org/10.3390/rs12172742
APA StyleKamali Maskooni, E., Naghibi, S. A., Hashemi, H., & Berndtsson, R. (2020). Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data. Remote Sensing, 12(17), 2742. https://doi.org/10.3390/rs12172742







