GNSS-Based Machine Learning Storm Nowcasting
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Integrated Water Vapour Observations
2.1.2. Wet Refractivity Data
2.1.3. Storms
2.2. Application of Random Forest Classifier
2.2.1. Input Features
2.2.2. Random Forest Classifier
2.2.3. Data Preprocessing
2.2.4. Implementation of Storm Classifier
- Max depth—the maximum depth of the tree (from 1 to 11).Each tree in RF makes multiple splits. The depth of the tree relates to how much information is captured. Larger depth in a tree allows to explain more variation in the data. However, too many splits can cause overfitting.
- Max features—the number of features to consider when looking for the best split (from 1 to 216).Before determining the best split RF model randomly resamples features. Trees with a large selection of features from which the best split is chosen might have better performance. However, when many features are considered, trees can be less diverse which will decrease their RF algorithm accuracy.
- N estimators—the number of trees in the forest (from 10 to 2000).Increased number of estimators improves the accuracy of the model, but this is done at the expense of a longer learning process and might be computationally expensive.
- Min sample leaf—the minimum number of samples required to be at a leaf node (from 1 to 21).The optimal value of the minimum number of samples at the leaf depends on the size of the learning set. Too large values may not be able to capture sufficient variation in the data.
2.2.5. Evaluation Metrics
3. Results
3.1. Random Forest Classifier for Storm Nowcasting
3.1.1. Attribute Selection
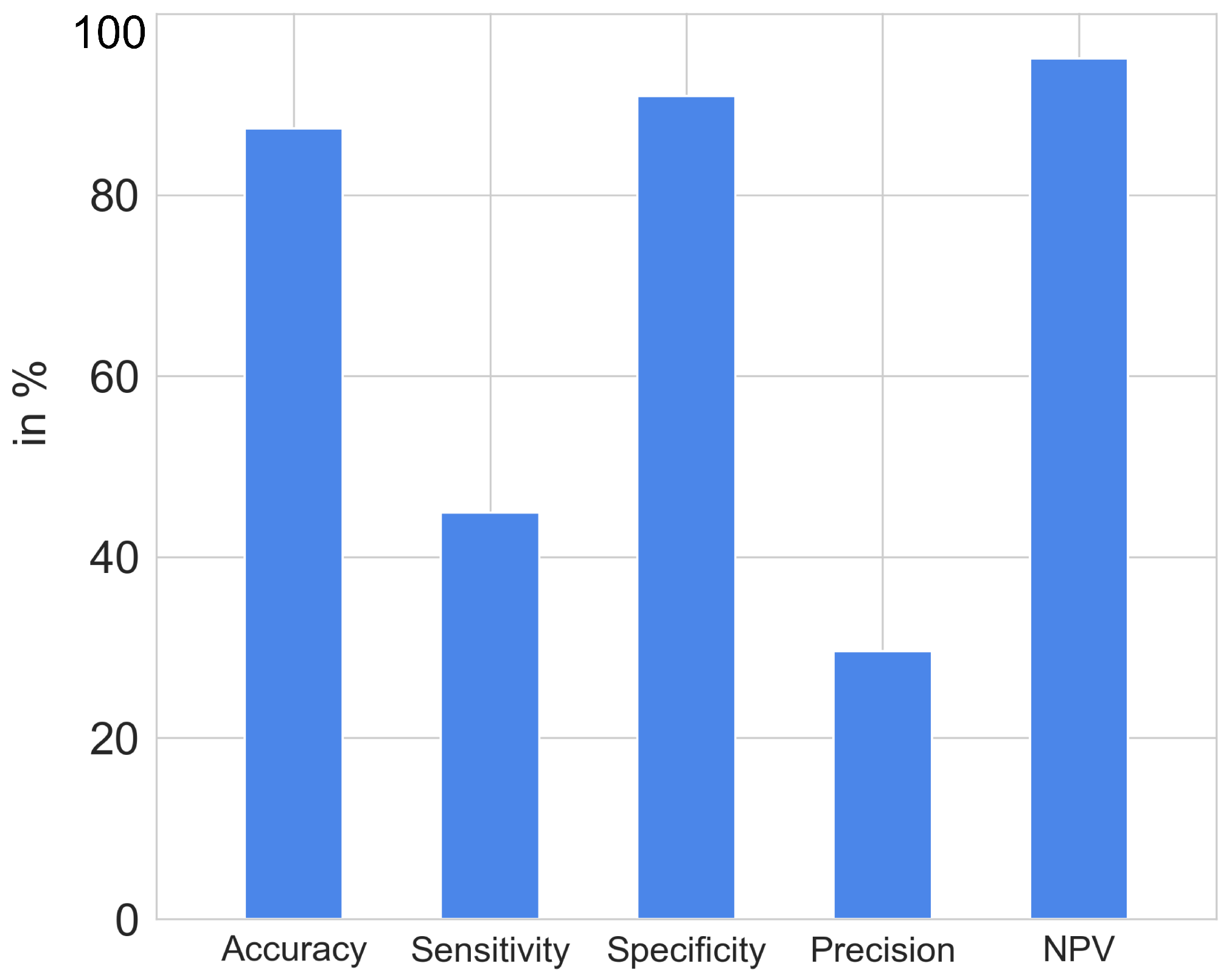
3.1.2. Classifier Performance
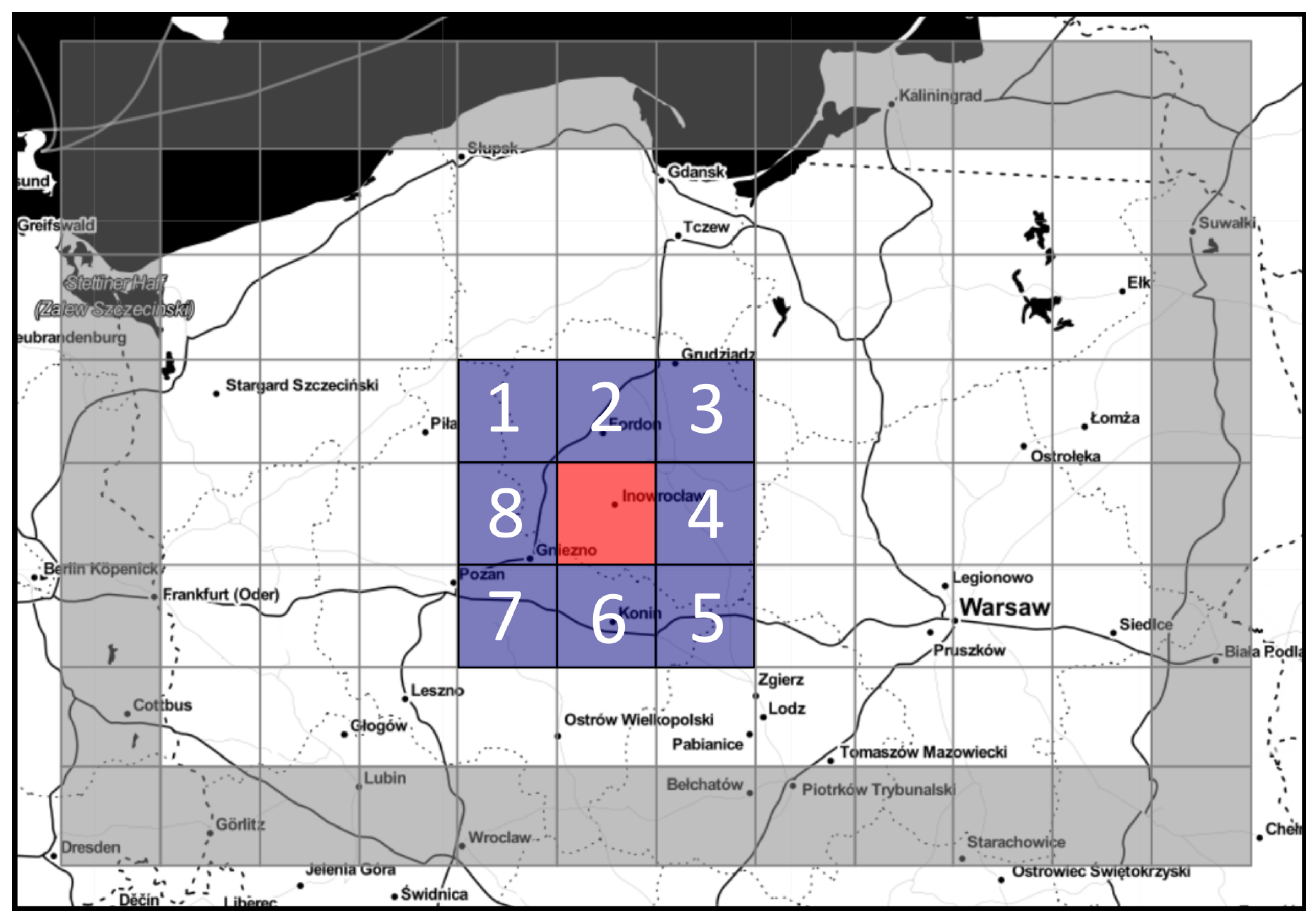
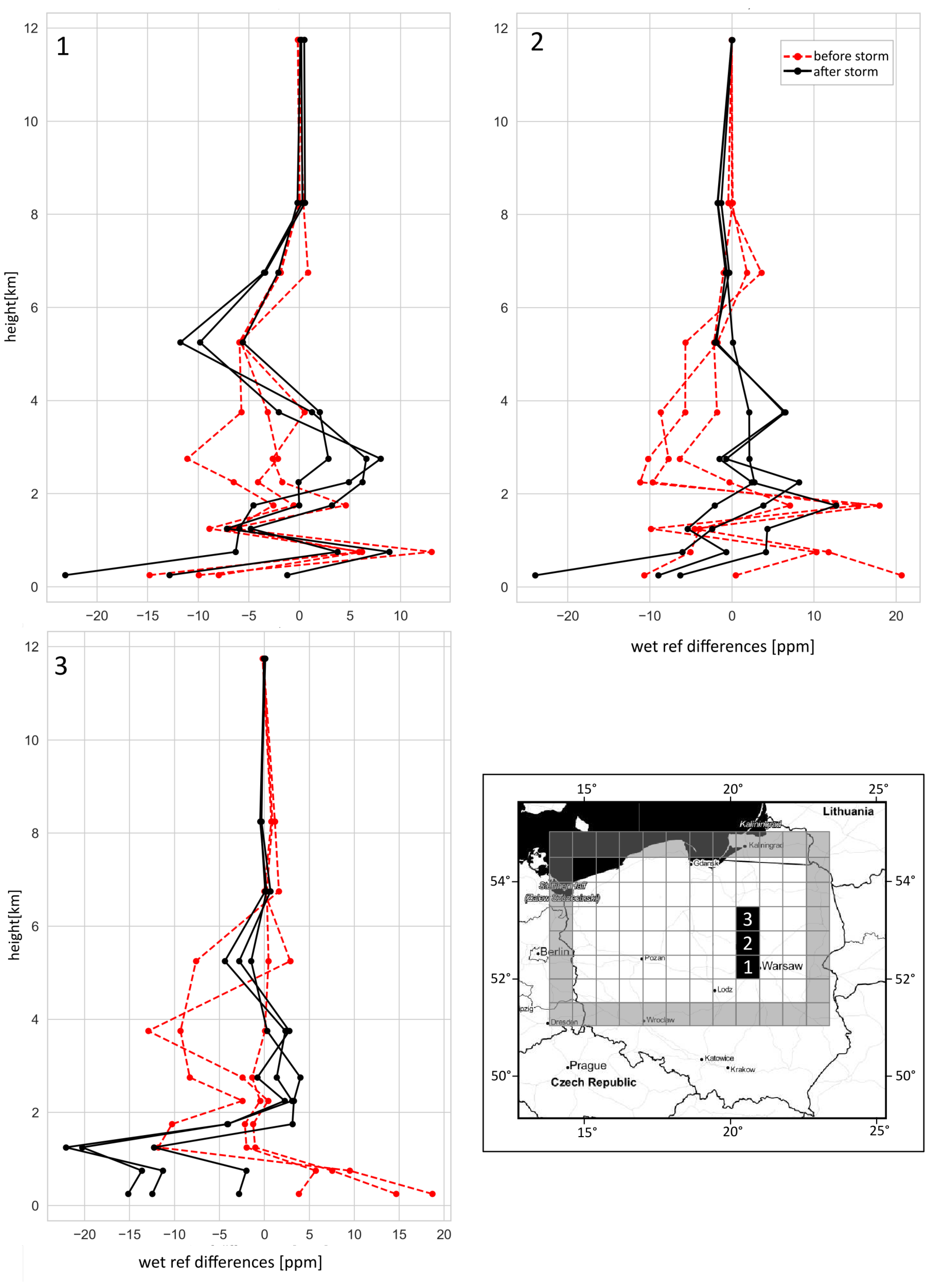
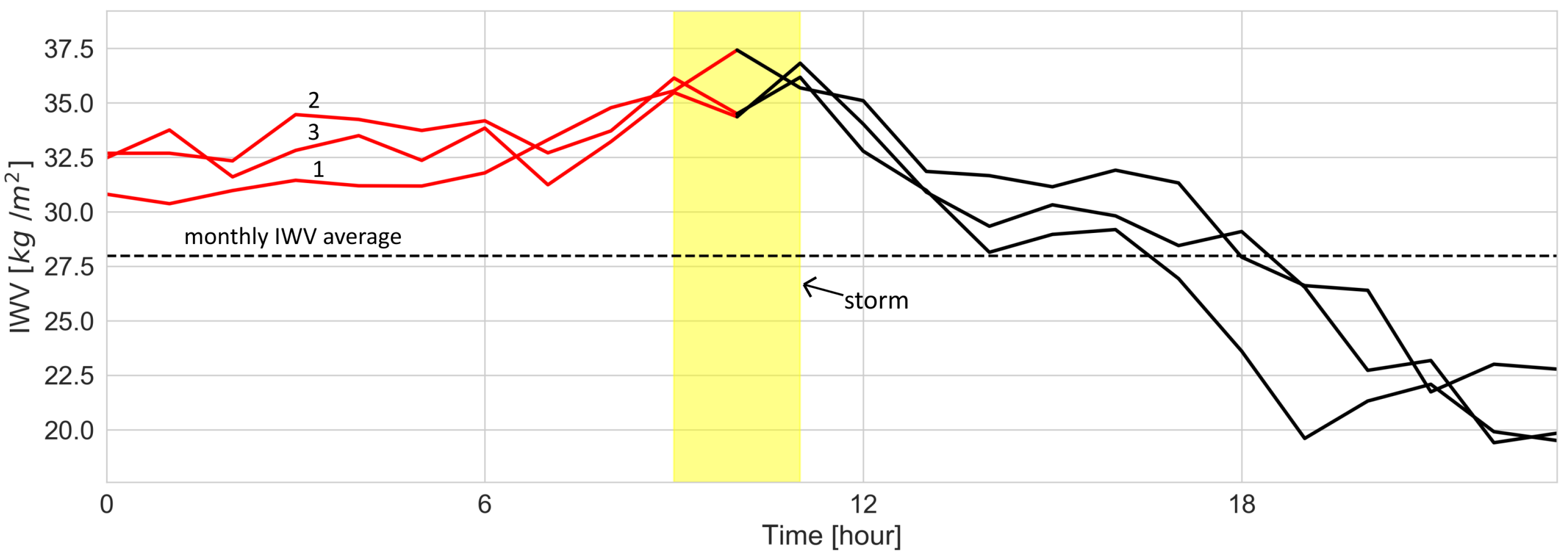
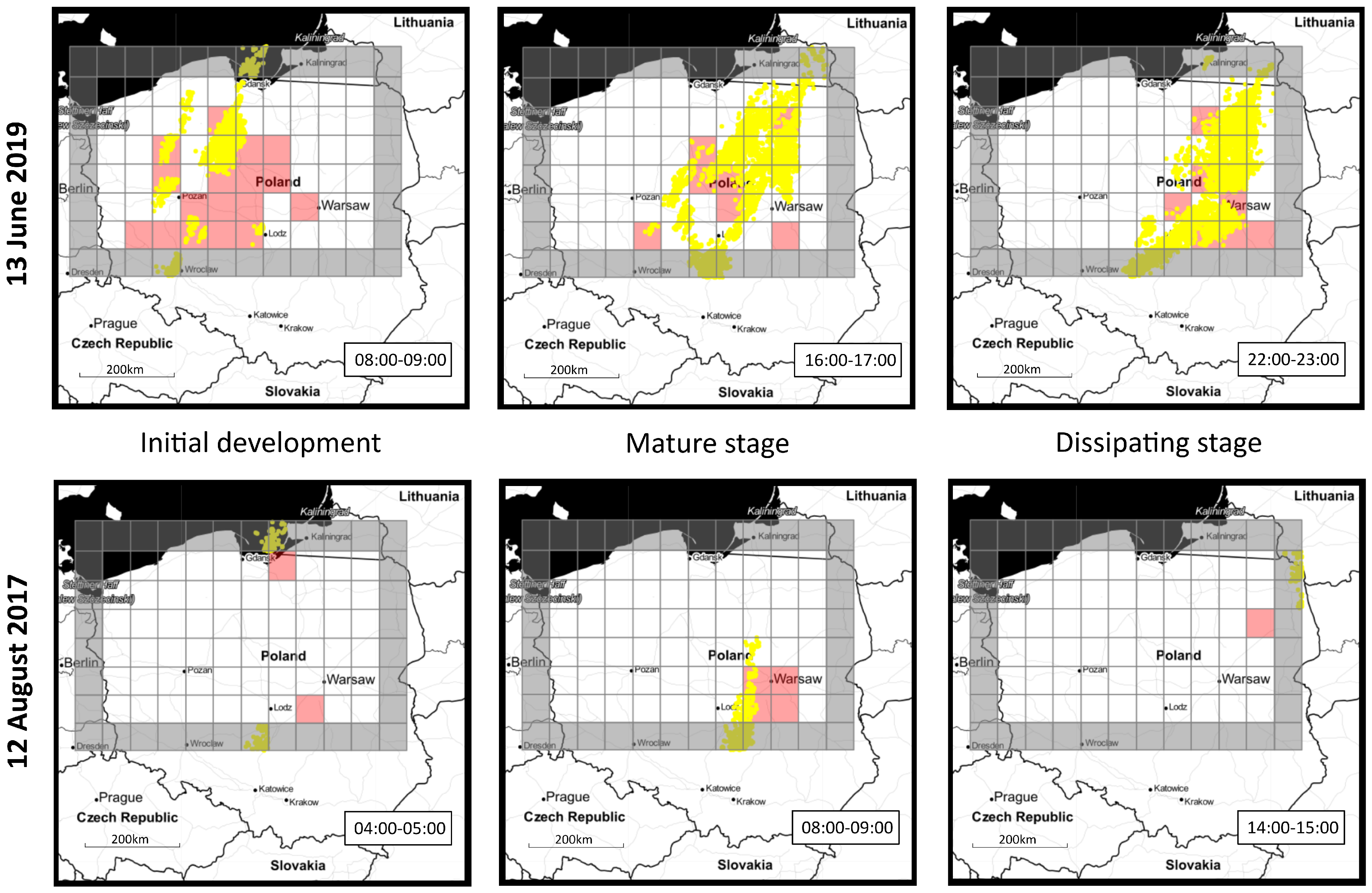
3.1.3. Case Studies
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite Systems |
| GPS | Global Positioning System |
| PWV | Precipitable Water Vapour |
| IWV | Integrated Water Vapour |
| ZTD | Zenith Troposphere Delay |
| WRF | Weather Research and Forecasting |
| E-GVAP | The EUMETNET EIG GNSS water vapour programme |
| NPV | Negative Predicted Value |
| MDI | Mean Decrease in Impurity |
| UPWr | Wroclaw University of Environmental and Life Sciences |
References
- Wang, Y.; Coning, E.; Harou, A.; Jacobs, W.; Joe, P.; Nikitina, L.; Roberts, R.; Wang, J.; Wilson, J.; Atencia, A.; et al. Guidelines for Nowcasting Techniques; Number 1198; World Meteorological Organization (WMO): Geneva, Switzerland, 2017. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.k.; Woo, W.c. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 2015, 802–810. [Google Scholar]
- Browning, K.A.; Collier, C.G. Nowcasting of precipitation systems. Rev. Geophys. 1989, 27, 345–370. [Google Scholar] [CrossRef]
- Guerova, G.; Jones, J.; Douša, J.; Dick, G.; de Haan, S.; Pottiaux, E.; Bock, O.; Pacione, R.; Elgered, G.; Vedel, H.; et al. Review of the state of the art and future prospects of the ground-based GNSS meteorology in Europe. Atmos. Meas. Tech. 2016, 9, 5385–5406. [Google Scholar] [CrossRef]
- Douša, J.; Dick, G.; Kačmařík, M.; Bro Řková, R.; Zus, F.; Brenot, H.; Stoycheva, A.; Möller, G.; Kaplon, J. Benchmark campaign and case study episode in central Europe for development and assessment of advanced GNSS tropospheric models and products. Atmos. Meas. Tech. 2016, 9, 2989–3008. [Google Scholar] [CrossRef]
- Václavovic, P.; Douša, J.; Teferle, F. GNSS Real-Time PPP Demonstration Campaign; Springer: Cham, Switzerland, 2020; pp. 45–48. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Miranda, P.M.A. On the inclusion of GPS precipitable water vapour in the nowcasting of rainfall. Nat. Hazards Earth Syst. Sci. 2015, 15, 2605–2616. [Google Scholar] [CrossRef]
- Yao, Y.; Shan, L.; Zhao, Q. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application. Sci. Rep. 2017, 7, 12465. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Nico, G. Neural Network Approach to Forecast Hourly Intense Rainfall Using GNSS Precipitable Water Vapor and Meteorological Sensors. Remote Sens. 2019, 11, 966. [Google Scholar] [CrossRef]
- Wilson, J.W.; Crook, N.A.; Mueller, C.K.; Sun, J.; Dixon, M. Nowcasting Thunderstorms: A Status Report. Bull. Am. Meteorol. Soc. 1998, 79, 2079–2099. [Google Scholar] [CrossRef]
- Cooper, M.A.; Holle, R.L. Reducing Lightning Injuries Worldwide; Springer: Cham, Switzerland, 2019; Number June; pp. 153–160. [Google Scholar] [CrossRef]
- Suparta, W.; Adnan, J.; Mohd Ali, M.A. Nowcasting the lightning activity in Peninsular Malaysia using the GPS PWV during the 2009 inter-monsoons. Ann. Geophys. 2014, 57, 1–13. [Google Scholar] [CrossRef]
- Guerova, G.; Dimitrova, T.; Georgiev, S. Thunderstorm Classification Functions Based on Instability Indices and GNSS IWV for the Sofia Plain. Remote Sens. 2019, 11, 2988. [Google Scholar] [CrossRef]
- Brenot, H.; Rohm, W.; Kačmařík, M.; Möller, G.; Sá, A.; Tondaś, D.; Rapant, L.; Biondi, R.; Manning, T.; Champollion, C. Cross-Comparison and methodological improvement in GPS tomography. Remote Sens. 2020, 12, 30. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. 2000. [Google Scholar] [CrossRef]
- Rohm, W.; Zhang, K.; Bosy, J. Limited constraint, robust Kalman filtering for GNSS troposphere tomography. Atmos. Meas. Tech. 2014. [Google Scholar] [CrossRef]
- Kak, A.C.; Slaney, M.; Wang, G. Principles of Computerized Tomographic Imaging. Med. Phys. 2002. [Google Scholar] [CrossRef]
- Manning, T.; Rohm, W.; Zhang, K.; Hurter, F.; Wang, C. Determining the 4D dynamics of wet refractivity using GPS tomography in the Australian region. In Proceedings of the IAG General Assembly, Melbourne, Australia, 28 June–2 July 2011. [Google Scholar] [CrossRef]
- Zhang, K.; Manning, T.; Wu, S.; Rohm, W.; Silcock, D.; Choy, S. Capturing the Signature of Severe Weather Events in Australia Using GPS Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015. [Google Scholar] [CrossRef]
- Jiang, P.; Ye, S.R.; Liu, Y.Y.; Zhang, J.J.; Xia, P.F. Near real-time water vapor tomography using ground-based GPS and meteorological data: Long-term experiment in Hong Kong. Ann. Geophys. 2014. [Google Scholar] [CrossRef]
- Trzcina, E.; Rohm, W. Estimation of 3D wet refractivity by tomography, combining GNSS and NWP data: First results from assimilation of wet refractivity into NWP. Q. J. R. Meteorol. Soc. 2019. [Google Scholar] [CrossRef]
- Hanna, N.; Trzcina, E.; Möller, G.; Rohm, W.; Weber, R. Assimilation of GNSS tomography products into the Weather Research and Forecasting model using radio occultation data assimilation operator. Atmos. Meas. Tech. 2019. [Google Scholar] [CrossRef]
- Han, L.; Sun, J.; Zhang, W.; Xiu, Y.; Feng, H.; Lin, Y. A machine learning nowcasting method based on real-time reanalysis data. J. Geophys. Res. Atmos. 2017, 122, 4038–4051. [Google Scholar] [CrossRef]
- Zhang, W.; Han, L.; Sun, J.; Guo, H.; Dai, J. Application of Multi-channel 3D-cube Successive Convolution Network for Convective Storm Nowcasting. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 1705–1710. [Google Scholar] [CrossRef]
- Veillette, M.S.; Iskenderian, H.; Lamey, P.M.; Bickmeier, L.J. Convective Initiation Forecasts Through the Use of Machine Learning Methods. In Proceedings of the 16th Conference on Aviation, Range, and Aerospace Meteorology, Austin, TX, USA, 9 January 2013; American Meteorological Society: Boston, MA, USA, 2013. [Google Scholar]
- Ruiz, A.; Villa, N. Storms prediction: Logistic regression vs random forest for unbalanced data. Case Stud. Bus. Ind. Gov. Stat. 2007, 1, 91–101. [Google Scholar]
- Williams, J.K.; Ahijevych, D.; Dettling, S.; Steiner, M. Combining observations and model data for short-term storm forecasting. In Remote Sensing Applications for Aviation Weather Hazard Detection and Decision Support; Feltz, W.F., Murray, J.J., Eds.; Proc. SPIE: San Diego, CA, USA, 2008; Volume 7088, p. 708805. [Google Scholar] [CrossRef]
- Ahijevych, D.; Pinto, J.O.; Williams, J.K.; Steiner, M. Probabilistic Forecasts of Mesoscale Convective System Initiation Using the Random Forest Data Mining Technique. Weather Forecast. 2016, 31, 581–599. [Google Scholar] [CrossRef]
- Dymarska, N.; Rohm, W.; Sierny, J.; Kapłon, J.; Kubik, T.; Kryza, M.; Jutarski, J.; Gierczak, J.; Kosierb, R. An assessment of the quality of near-real time GNSS observations as a potential data source for meteorology. Meteorol. Hydrol. Water Manag. 2017, 5, 3–13. [Google Scholar] [CrossRef]
- Kryza, M.; Werner, M.; Wałszek, K.; Dore, A.J. Application and evaluation of the WRF model for high-resolution forecasting of rainfall—A case study of SW Poland. Meteorol. Z. 2013, 22, 595–601. [Google Scholar] [CrossRef]
- Emardson, T.R. The systematic behavior of water vapor estimates using four years of GPS observations. IEEE Trans. Geosci. Remote Sens. 2000. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS software version 5.2. 2015. [Google Scholar]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T.A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Tondaś, D.; Kapłon, J.; Rohm, W. Ultra-fast near real-time estimation of troposphere parameters and coordinates from GPS data. Measurement 2020, 162, 107849. [Google Scholar] [CrossRef]
- Karabatić, A.; Weber, R.; Haiden, T. Near real-time estimation of tropospheric water vapour content from ground based GNSS data and its potential contribution to weather now-casting in Austria. Adv. Space Res. 2011, 47, 1691–1703. [Google Scholar] [CrossRef]
- Bosy, J.; Kaplon, J.; Rohm, W.; Sierny, J.; Hadas, T. Near real-time estimation of water vapour in the troposphere using ground GNSS and the meteorological data. Ann. Geophys. 2012, 30. [Google Scholar] [CrossRef]
- Wilgan, K.; Rohm, W.; Bosy, J. Multi-observation meteorological and GNSS data comparison with Numerical Weather Prediction model. Atmos. Res. 2015, 156, 29–42. [Google Scholar] [CrossRef]
- Boehm, J.; Kouba, J.; Schuh, H. Forecast Vienna mapping functions 1 for real-time analysis of space geodetic observations. J. Geod. 2009. [Google Scholar] [CrossRef]
- Shoji, Y. Retrieval of water vapor inhomogeneity using the japanese nationwide GPS array and its potential for prediction of convective precipitation. J. Meteorol. Soc. Jpn. 2013. [Google Scholar] [CrossRef][Green Version]
- Wanke, E.; Andersen, R.; Volgnandt, T. A World-Wide Low-Cost Community-Based Time-of-Arrival Lightning Detection and Lightning Location Network 2014. pp. 1–95. Available online: www.blitzortung.org/Documents/TOA_Blitzortung_RED.pdf (accessed on 18 April 2020).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Geron, A. Hands-on Machine Learning With Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2017. [Google Scholar]
- More, A. Survey of resampling techniques for improving classification performance in unbalanced datasets. arXiv 2016, arXiv:1608.06048. [Google Scholar]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data; University of California, Berkeley: Berkeley, CA, USA, 2004; Volume 110, pp. 1–12. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Hossin, M.; Sulaiman, M.N. A Review on Evaluation Metrics for Data Classification Evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1–11. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Houze, R.A. Mesoscale convective systems. Rev. Geophys. 2004, 42, RG4003. [Google Scholar] [CrossRef]
- Guerova, G.; Dimitrova, T.; Vassileva, K.; Slavchev, M.; Stoev, K.; Georgiev, S. BalkanMed real time severe weather service: progress and prospects in Bulgaria. Adv. Space Res. 2020. [Google Scholar] [CrossRef]

| Actual Positive Class | Actual Negative Class | |
|---|---|---|
| Predicted Positive Class | True positive (TP) | False positive (FP) |
| Predicted Negative Class | False negative (FN) | True negative (TN) |
| Month | IWV(NST) | IWV(ST) |
|---|---|---|
| June | 20.40 | 25.67 |
| July | 23.00 | 28.92 |
| August | 22.79 | 27.98 |
| Class | Reported ‘Storm’ | Reported ‘No Storm’ |
|---|---|---|
| Predicted ‘Storm’ | 146 | 179 |
| Predicted ‘No storm’ | 347 | 3485 |
| Date | Reported ‘Storm’ | Reported ‘No Storm’ | Class |
|---|---|---|---|
| 1 August 2017 | 39 | 6 | Predicted ‘Storm’ |
| 32 | 432 | Predicted ‘No storm’ | |
| 12 August 2017 | 35 | 62 | Predicted ‘Storm’ |
| 12 | 1645 | Predicted ‘No storm’ | |
| 13 June 2019 | 72 | 111 | Predicted ‘Storm’ |
| 303 | 1408 | Predicted ‘No storm’ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łoś, M.; Smolak, K.; Guerova, G.; Rohm, W. GNSS-Based Machine Learning Storm Nowcasting. Remote Sens. 2020, 12, 2536. https://doi.org/10.3390/rs12162536
Łoś M, Smolak K, Guerova G, Rohm W. GNSS-Based Machine Learning Storm Nowcasting. Remote Sensing. 2020; 12(16):2536. https://doi.org/10.3390/rs12162536
Chicago/Turabian StyleŁoś, Marcelina, Kamil Smolak, Guergana Guerova, and Witold Rohm. 2020. "GNSS-Based Machine Learning Storm Nowcasting" Remote Sensing 12, no. 16: 2536. https://doi.org/10.3390/rs12162536
APA StyleŁoś, M., Smolak, K., Guerova, G., & Rohm, W. (2020). GNSS-Based Machine Learning Storm Nowcasting. Remote Sensing, 12(16), 2536. https://doi.org/10.3390/rs12162536






