The Potential of the Least-Squares Spectral and Cross-Wavelet Analyses for Near-Real-Time Disturbance Detection within Unequally Spaced Satellite Image Time Series
Abstract
1. Introduction
- Can SHP representing both inter-annual (gradual) and intra-annual (seasonal) variations be determined within the time series?
- How reliable is SHP for detecting a disturbance in MP?
- How much the weights obtained from the observational uncertainties can increase the probability of a disturbance detection in MP?
- How additional data sets, such as temperature and precipitation, can be used for assessment?
2. Materials and Methods
2.1. Study Region
2.2. Data Sets and Pre-Processing
2.2.1. Satellite Imagery
2.2.2. Validation Data Sets
2.3. Monitoring Method
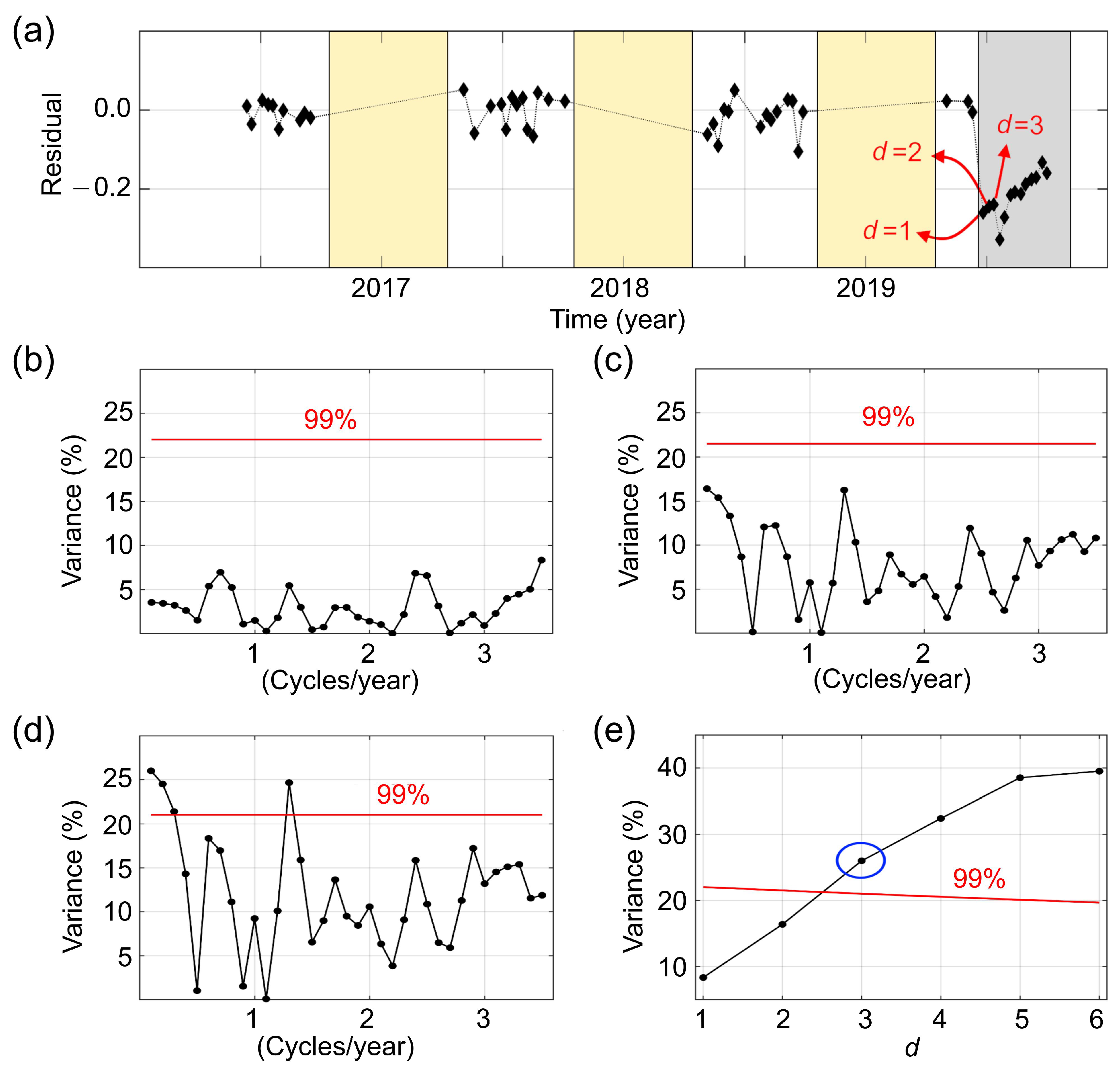
2.3.1. Stable History Period Selection
2.3.2. Near-Real-Time Disturbance Detection
2.4. Least-Squares Cross-Wavelet Analysis as an Assessment Method
3. Results
3.1. Simulation Experiment for Validation of the Monitoring Method
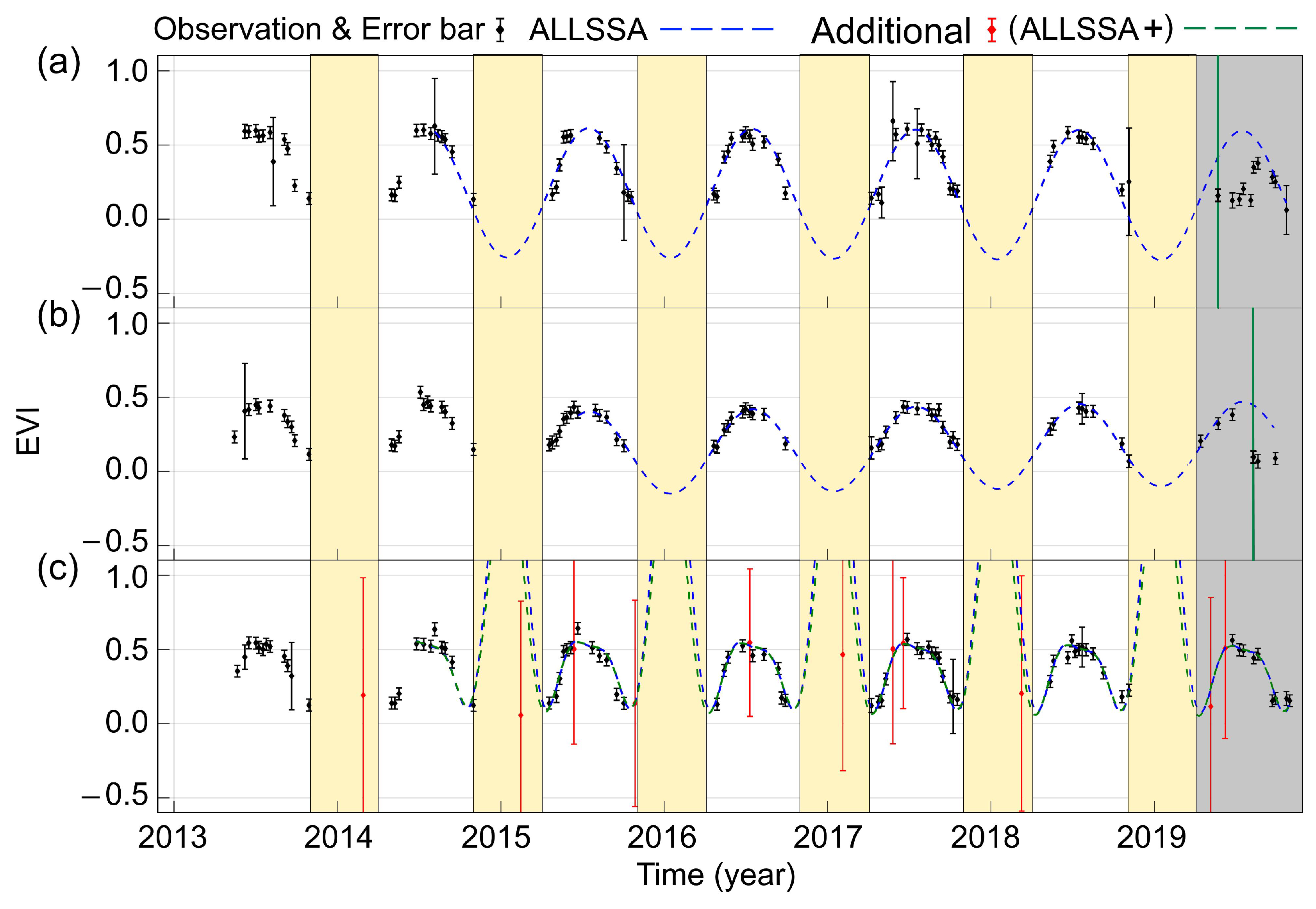
3.2. Disturbance Detection in the Study Region
3.3. Assessment of the Results Using the Coherency Analyses
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pickett, S.T.A.; White, P.S. The Ecology of Natural Disturbance and Patch Dynamics; Academic Press: New York, NY, USA, 1986; pp. 3–13. [Google Scholar]
- Lucht, W.; Schaphoff, S.; Erbrecht, T.; Heyder, U.; Cramer, W. Terrestrial vegetation redistribution and carbon balance under climate change. Carbon Balance Manag. 2006, 1, 7. [Google Scholar] [CrossRef] [PubMed]
- Xin, Q.; Olofsson, P.; Zhu, Z.; Tan, B.; Woodcock, C.E. Toward near real-time monitoring of forest disturbance by fusion of MODIS and Landsat data. Remote Sens. Environ. 2013, 135, 234–247. [Google Scholar] [CrossRef]
- Martell, D.L. Forest Fire Management. In Handbook Of Operations Research In Natural Resources; Weintraub, A., Romero, C., Bjorndal, T., Epstein, R., Miranda, J., Eds.; International Series in Operations Research & Mana; Springer: Boston, MA, USA, 2007; Volume 99. [Google Scholar]
- Roeder, A.; Hill, J. Recent Advances in Remote Sensing and Geoinformation Processing for Land Degradation Assessment; CRC Press: London, UK, 2009; p. 418. [Google Scholar]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near real-time disturbance detection using satellite image time series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Rouse, J.W.; Hass, R.H., Jr.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium 1 (A), Texas A&M Univ, College Station, TX, USA, 1 January 1974; pp. 309–317. [Google Scholar]
- Liu, H.Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- Watts, L.M.; Laffan, S.W. Effectiveness of the BFAST algorithm for detecting vegetation response patterns in a semi-arid region. Remote Sens. Environ. 2014, 154, 234–245. [Google Scholar] [CrossRef]
- Zhu, Z. Change detection using Landsat time series: A review of frequencies, preprocessing, algorithms, and applications. ISPRS J. Photogramm. Remote. Sens. 2017, 130, 370–384. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to topographic effects: A case study in high-density Cypress forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Loveland, T.R.; Dwyer, J.L. Landsat: Building a strong future. Remote Sens. Environ. 2012, 122, 22–29. [Google Scholar] [CrossRef]
- Kovalskyy, V.; Roy, D.P. The global availability of Landsat 5 TM and Landsat 7 ETM+ land surface observations and implications for global 30m Landsat data product generation. Remote Sens. Environ. 2013, 130, 280–293. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helderg, D.; Ironsh, J.R.; Johnsoni, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, A. Search algorithm for weak signals in unevenly spaced data. Comput. Phys. 1988, 2, 77–82. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Friedl, M.A.; Schaaf, C.B. Sensitivity of vegetation phenology detection to the temporal resolution of satellite data. Int. J. Remote Sens. 2009, 30, 2061–2074. [Google Scholar] [CrossRef]
- Samanta, A.; Costa, M.H.; Nunes, E.L.; Vieira, S.A.; Xu, L.; Myneni, R.B. Comment on “Drought-induced reduction in global terrestrial net primary production from 2000 through 2009”. Science 2011, 333, 1093. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4-7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Jeppesen, J.H.; Jacobsen, R.H.; Inceoglu, F.; Toftegaard, T.S. A cloud detection algorithm for satellite imagery based on deep learning. Remote Sens. Environ. 2019, 229, 247–259. [Google Scholar] [CrossRef]
- Shao, Z.; Pan, Y.; Diao, C.; Cai, J. Cloud detection in remote sensing images based on multiscale features-convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4062–4076. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Pagiatakis, S.D. Least-squares wavelet analysis of unequally spaced and non-stationary time series and its applications. Math Geosci. 2017, 49, 819–844. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Pagiatakis, S.D. LSWAVE: A MATLAB software for the least-squares wavelet and cross-wavelet analyses. GPS Solut. 2019, 23, 8. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2407. [Google Scholar] [CrossRef]
- White, M.A.; Nemani, R.R. Real-time monitoring and short-term forecasting of land surface phenology. Remote Sens. Environ. 2006, 104, 43–49. [Google Scholar] [CrossRef]
- Reiche, J.; Bruin, S.D.; Hoekman, D.; Verbesselt, J.; Herold, M. A Bayesian approach to combine Landsat and ALOS PALSAR time series for near real-time deforestation detection. Remote Sens. 2015, 7, 4973–4996. [Google Scholar] [CrossRef]
- Reiche, J.; Hamunyela, E.; Verbesselt, J.; Hoekman, D.; Herold, M. Improving near-real time deforestation monitoring in tropical dry forests by combining dense Sentinel-1 time series with Landsat and ALOS-2 PALSAR-2. Remote Sens. Environ. 2018, 204, 147–161. [Google Scholar] [CrossRef]
- Alberta Wildfire. Available online: https://wildfire.alberta.ca/ (accessed on 29 July 2020).
- Banfield, G.E.; Bhatti, J.S.; Jiang, H.; Apps, M.J. Variability in regional scale estimates of carbon stocks in boreal forest ecosystems: Results from West-Central Alberta. For. Ecol. Manag. 2002, 169, 15–27. [Google Scholar] [CrossRef]
- Strong, W.L.; La Roi, G.H. Root-system morphology of common boreal forest trees in Alberta, Canada. Can. J. For. Res. 1983, 13, 1164–1173. [Google Scholar] [CrossRef]
- USGS – Science for a changing world – Earth Explorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 29 July 2020).
- She, X.; Zhang, L.; Cen, Y.; Wu, T.; Huang, C.; Baig, M.H.A. Comparison of the continuity of vegetation indices derived from Landsat 8 OLI and Landsat 7 ETM+ data among different vegetation types. Remote Sens. 2015, 7, 13485–13506. [Google Scholar] [CrossRef]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 reflective wavelength and normalized difference vegetation index continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Murakami, K.; Nagai, S. Evaluation of sub-pixel cloud noises on MODIS daily spectral indices based on in situ measurements. Remote Sens. 2011, 3, 1644–1662. [Google Scholar] [CrossRef]
- Alberta Agriculture and Forestry. Available online: https://agriculture.alberta.ca/acis/ (accessed on 29 July 2020).
- Ruan, X.; Qiu, F.; Dyck, M. The effects of environmental and socioeconomic factors on land-use changes: A study of Alberta, Canada. Environ. Monit. Assess. 2016, 188, 446. [Google Scholar] [CrossRef] [PubMed]
- Eum, H.; Gupta, A. Hybrid climate datasets from a climate data evaluation system and their impacts on hydrologic simulations for the Athabasca River basin in Canada. Hydrol. Earth Sys. Sci. 2019, 23, 5151–5173. [Google Scholar] [CrossRef]
- Natural Resources Canada. Available online: https://nrcan.gc.ca/ (accessed on 29 July 2020).
- Jamali, S.; Jönsson, P.; Eklundh, L.; Ardö, J.; Seaquist, J. Detecting changes in vegetation trends using time series segmentation. Remote Sens. Environ. 2015, 156, 182–195. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Brandt, M.; Verger, A.; Diouf, A.A.; Baret, F.; Samimi, C. Local vegetation trends in the Sahel of Mali and Senegal using long time series FAPAR satellite products and field measurement (1982–2010). Remote Sens. 2014, 6, 2408–2434. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Timmermann, A. Market timing and return prediction under model instability. J. Empir. Financ. 2002, 9, 495–510. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Liao, W.; Lamoureux, M.P. Antileakage least-squares spectral analysis for seismic data regularization and random noise attenuation. Geophysics 2018, 8, V157–V170. [Google Scholar] [CrossRef]
- Vaníček, P. Approximate spectral analysis by least-squares fit. Astrophys. Space Sci. 1969, 4, 387–391. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Ghaderpour, E. Least-Squares Wavelet Analysis and Its Applications in Geodesy and Geophysics. Ph.D. Thesis, York University, Toronto, ON, Canada, 2018. [Google Scholar]
- Chen, S.; Luk, B.L. Adaptive simulated annealing for optimization in signal processing applications. Signal Process. 1999, 79, 117–128. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lass. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar]
- Bento, J. On the complexity of the weighted fused lasso. IEEE Signal Process. Lett. 2018, 25, 1595–1599. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Holden, C.; Yang, Z. Generating synthetic Landsat images based on all available Landsat data: Predicting Landsat surface reflectance at any given time. Remote Sens. Environ. 2015, 162, 67–83. [Google Scholar] [CrossRef]
- Verbesselt, J.; Jönsson, P.; Lhermitte, S.; van Aardt, J.; Coppin, P. Evaluating satellite and climate data derived indices as fire risk indicators in savanna ecosystems. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1622–1632. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Ben Abbes, A.; Rhif, M.; Pagiatakis, S.D.; Farah, I.R. Non-stationary and unequally spaced NDVI time series analyses by the LSWAVE software. Int. J. Remote Sens. 2019, 41, 2374–2390. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jeverjeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Proc. Geoph. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Ge, Z. Significance tests for the wavelet cross spectrum and wavelet linear coherence. Ann. Geophys. 2008, 26, 3819–3829. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Ince, E.S.; Pagiatakis, S.D. Least-squares cross-wavelet analysis and its applications in geophysical time series. J. Geod. 2018, 92, 1223–1236. [Google Scholar] [CrossRef]
- Wells, D.E.; Krakiwsky, E.J. The Method of Least-Squares; Department of Surveying Engineering, University of New Brunswick: Fredericton, NB, Canada, 1971. [Google Scholar]
- Özgür, C.; Colliau, T.; Rogers, G.; Hughes, Z.; Myer-Tyson, E. MATLAB vs. Python vs. R. J. Data Sci. 2017, 15, 355–372. [Google Scholar]
- Dover, J.W. Green Infrastructure: Incorporating Plants and Enhancing Biodiversity in Buildings and Urban Environments; Routledge: Abingdon, UK; Taylor and Francis: Abingdon, UK, 2015. [Google Scholar]
- Craymer, M.R. The Least-Squares Spectrum, Its Inverse Transform and Autocorrelation Function: Theory and Some Application in Geodesy. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1998. [Google Scholar]
- LSWAVE: A MATLAB Software for the Least-Squares Wavelet and Cross-Wavelet Analyses–by E. Ghaderpour and S. D. Pagiatakis. National Geodetic Survey (NGS)—National Oceanic and Atmospheric Administration (NOAA). Available online: https://www.ngs.noaa.gov/gps-toolbox/LSWAVE.htm (accessed on 29 July 2020).
- Signal Processing—by E. Ghaderpour. GitHub. Available online: https://github.com/Ghaderpour/LSWAVE-SignalProcessing/ (accessed on 29 July 2020).
- Bullock, D.G. Crop rotation. Crit. Rev. Plant Sci. 1992, 11, 309–326. [Google Scholar] [CrossRef]
- Deike, S.; Pallutt, B.; Melander, B.; Strassemeyer, J.; Christen, O. Long-term productivity and environmental effects of arable farming as affected by crop rotation, soil tillage intensity and strategy of pesticide use: A case-study of two long-term field experiments in Germany and Denmark. Eur. J. Agron. 2008, 29, 191–199. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arikan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514, 1–13. [Google Scholar] [CrossRef]
- Bekaert, D.; Hooper, A.; Wright, T. A spatially variable power law tropospheric correction technique for InSAR data. J. Geophys. Res. 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Murray, K.D.; Bekaert, D.P.S.; Lohman, R.B. Tropospheric corrections for InSAR: Statistical assessments and applications to the Central United States and Mexico. Remote Sens. Environ. 2019, 232, 111326. [Google Scholar] [CrossRef]
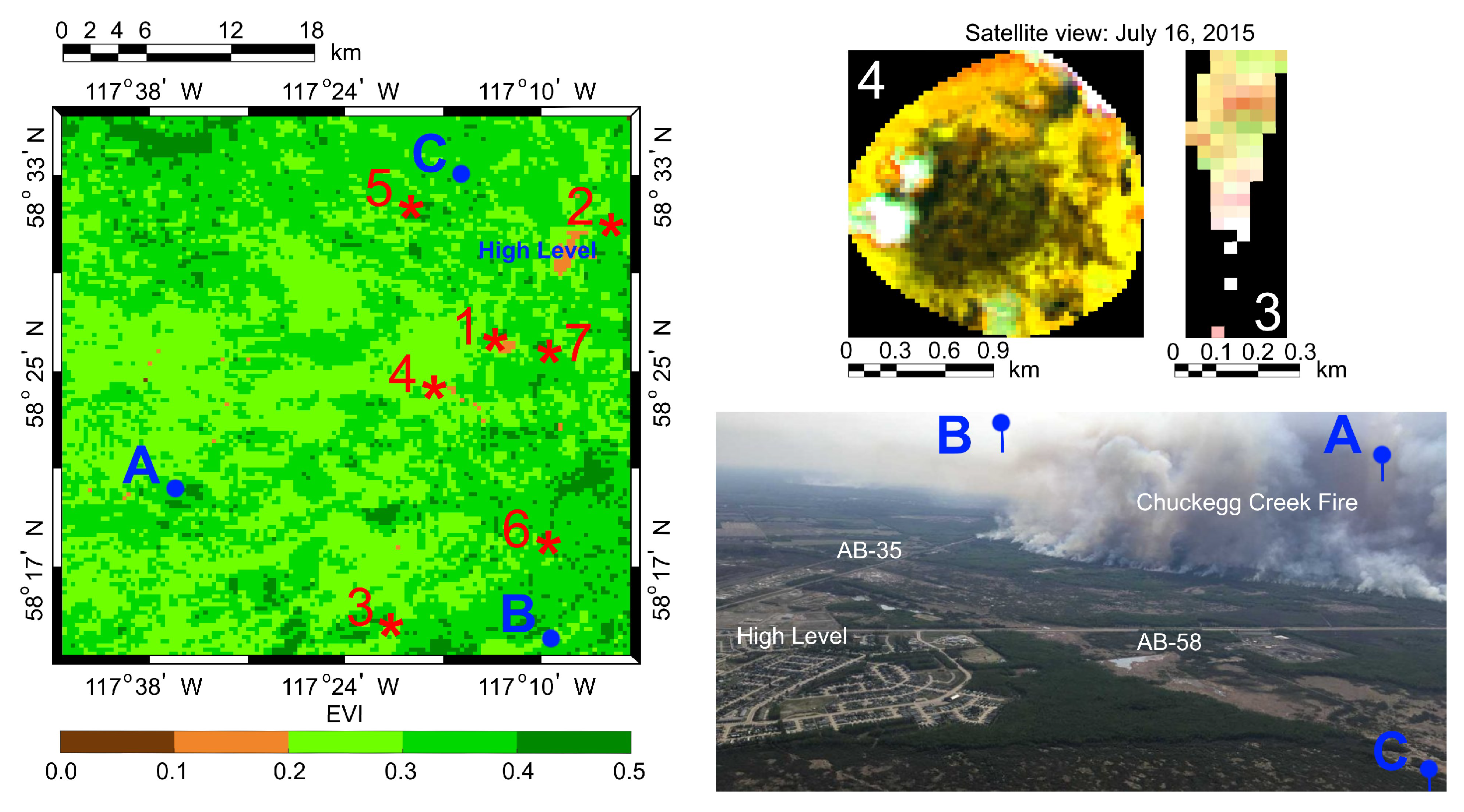




| Label | Date of Wildfire | Latitude | Longitude | Area Burned (ha) | Cause |
|---|---|---|---|---|---|
| 1 | 2014-05-10 | 0.7 | Railroad | ||
| 2 | 2015-04-28 | 0.5 | Resident | ||
| 3 | 2015-05-30 | 7.0 | Recreation | ||
| 4 | 2015-06-27 | 246.9 | Lightning | ||
| 5 | 2016-04-23 | 0.5 | Recreation | ||
| 6 | 2017-09-28 | 0.5 | Recreation | ||
| 7 | 2018-05-08 | 0.4 | Agriculture | ||
| 2019-05-12 | 350,135.0 | Lightning |
| Parameters | Values | |
|---|---|---|
| amplitude | ||
| noise level | ||
| magnitude | ||
| d |
| Pixel | Time Series | Frequency | Amplitude | Phase | Intercept | Slope |
|---|---|---|---|---|---|---|
| A | Temperature | |||||
| A | Precipitation | |||||
| B | Temperature | |||||
| B | Precipitation | |||||
| C | Temperature | |||||
| C | Precipitation | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaderpour, E.; Vujadinovic, T. The Potential of the Least-Squares Spectral and Cross-Wavelet Analyses for Near-Real-Time Disturbance Detection within Unequally Spaced Satellite Image Time Series. Remote Sens. 2020, 12, 2446. https://doi.org/10.3390/rs12152446
Ghaderpour E, Vujadinovic T. The Potential of the Least-Squares Spectral and Cross-Wavelet Analyses for Near-Real-Time Disturbance Detection within Unequally Spaced Satellite Image Time Series. Remote Sensing. 2020; 12(15):2446. https://doi.org/10.3390/rs12152446
Chicago/Turabian StyleGhaderpour, Ebrahim, and Tijana Vujadinovic. 2020. "The Potential of the Least-Squares Spectral and Cross-Wavelet Analyses for Near-Real-Time Disturbance Detection within Unequally Spaced Satellite Image Time Series" Remote Sensing 12, no. 15: 2446. https://doi.org/10.3390/rs12152446
APA StyleGhaderpour, E., & Vujadinovic, T. (2020). The Potential of the Least-Squares Spectral and Cross-Wavelet Analyses for Near-Real-Time Disturbance Detection within Unequally Spaced Satellite Image Time Series. Remote Sensing, 12(15), 2446. https://doi.org/10.3390/rs12152446







