Figure 1.
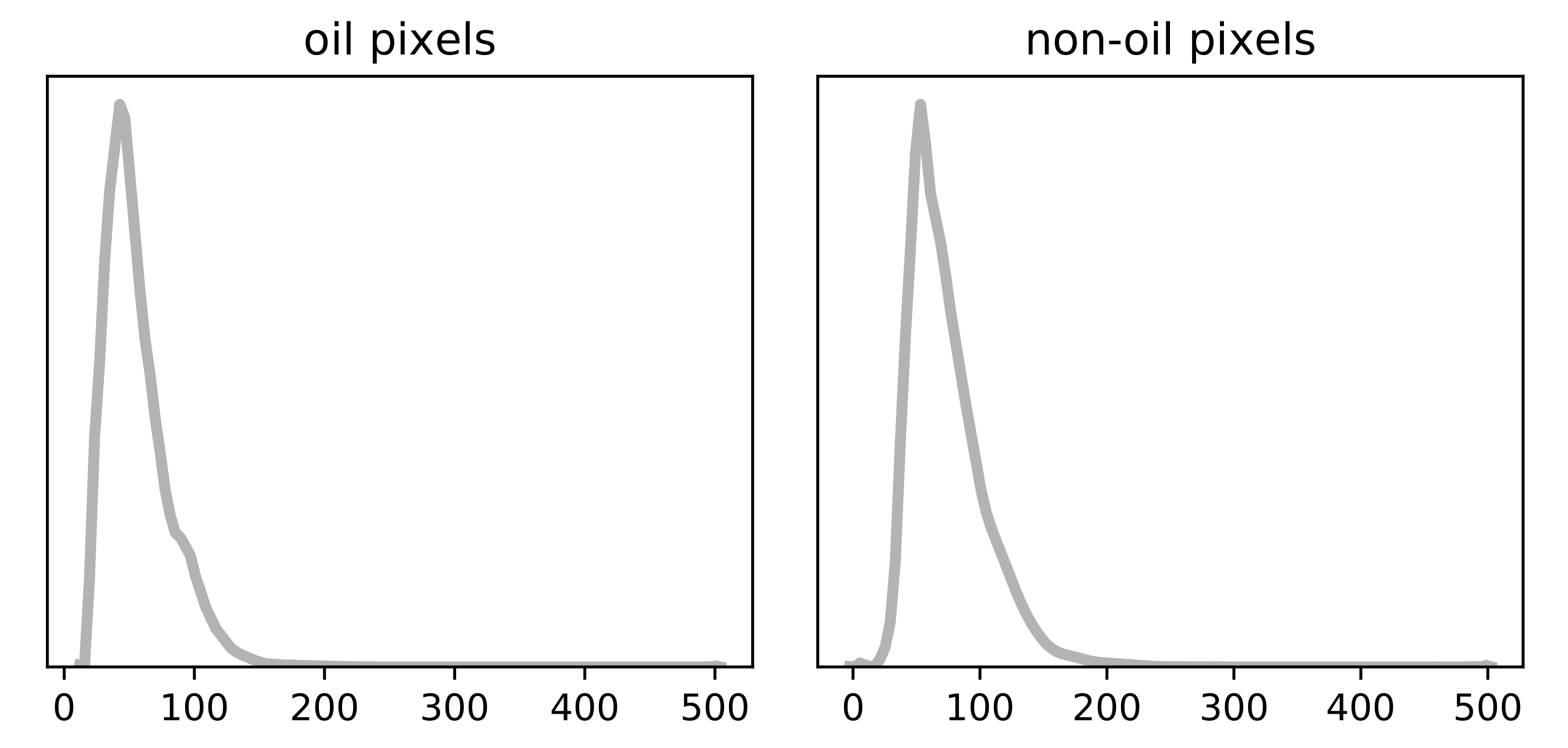
Distribution of the backscatter values in the VV images, across pixels belonging to class “oil” and “non-oil”. The plots show only the range , rather than .
Figure 1.
Distribution of the backscatter values in the VV images, across pixels belonging to class “oil” and “non-oil”. The plots show only the range , rather than .
Figure 2.
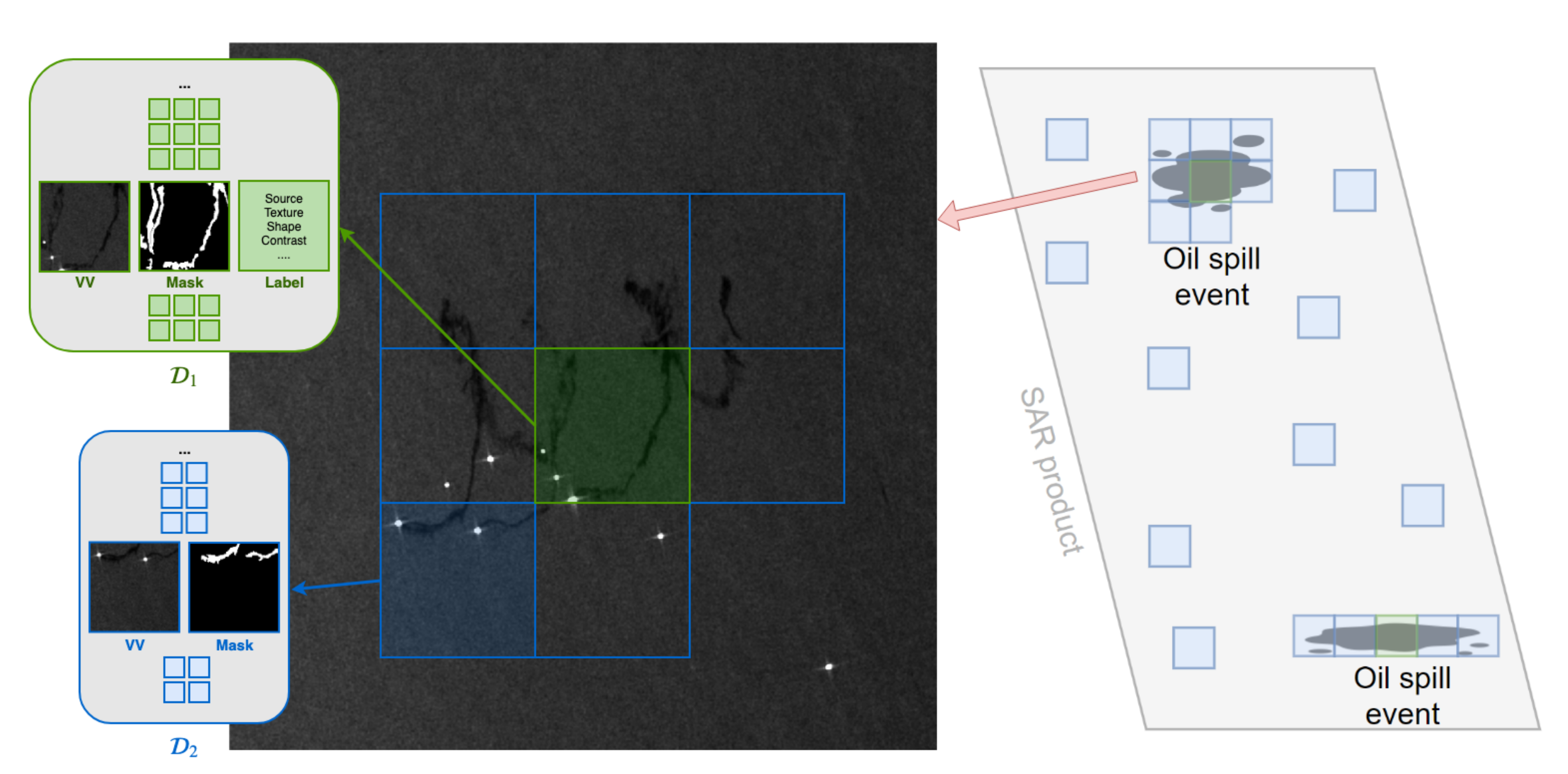
Illustration of patches extraction from the SAR products. The patches centered on the oil spill events (depicted in green) form the dataset and are associate with a label that indicates the values assumed by the 12 categories. The second dataset, , contains (i) all the patches of , (ii) all the patches with at least 1 oil spill pixel, (iii) an equal amount of patches without oil that is randomly sampled from other locations in the SAR product. Along with the VV channel, the segmentation masks are included in both datasets.
Figure 2.
Illustration of patches extraction from the SAR products. The patches centered on the oil spill events (depicted in green) form the dataset and are associate with a label that indicates the values assumed by the 12 categories. The second dataset, , contains (i) all the patches of , (ii) all the patches with at least 1 oil spill pixel, (iii) an equal amount of patches without oil that is randomly sampled from other locations in the SAR product. Along with the VV channel, the segmentation masks are included in both datasets.
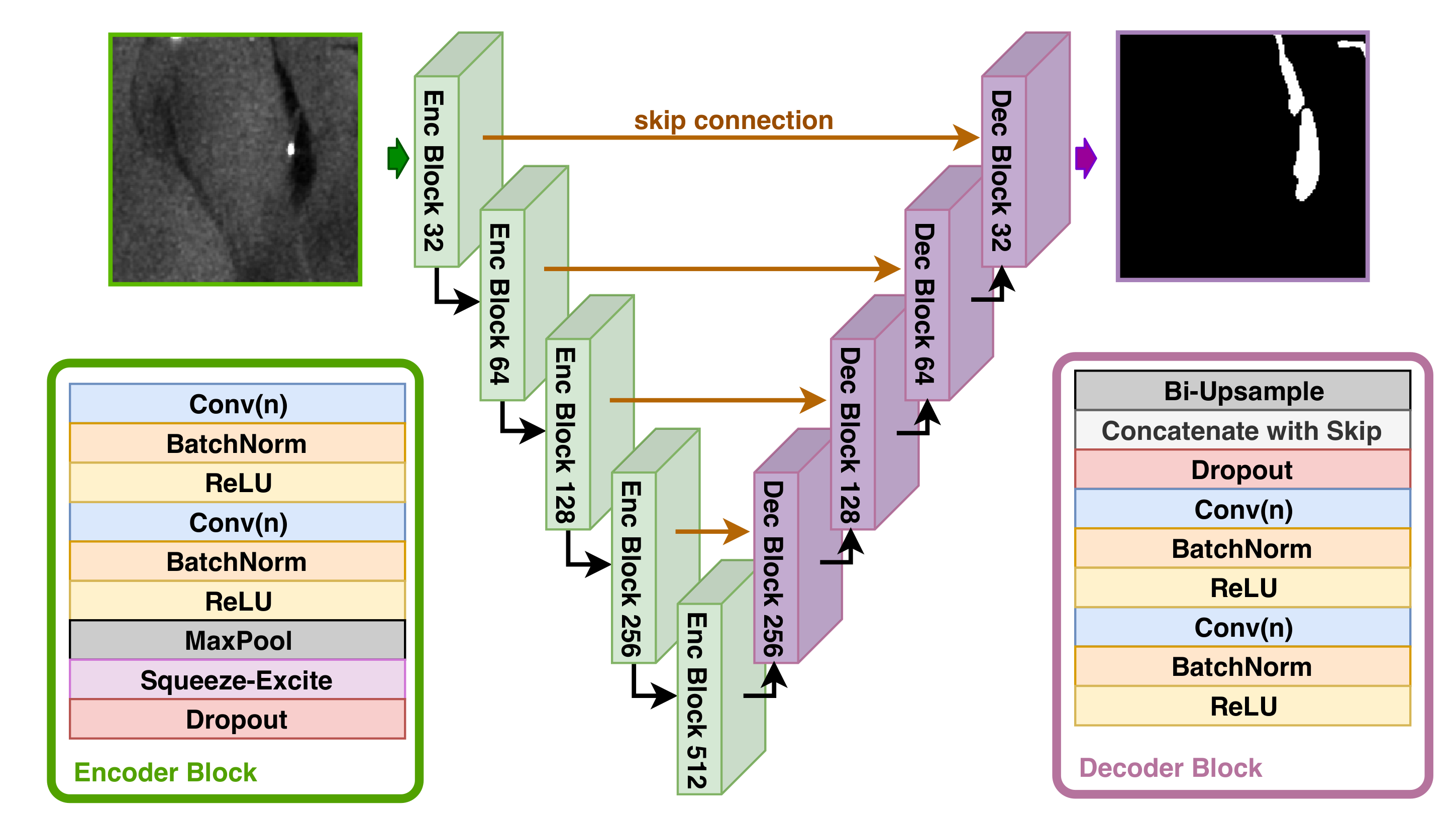
Figure 3.
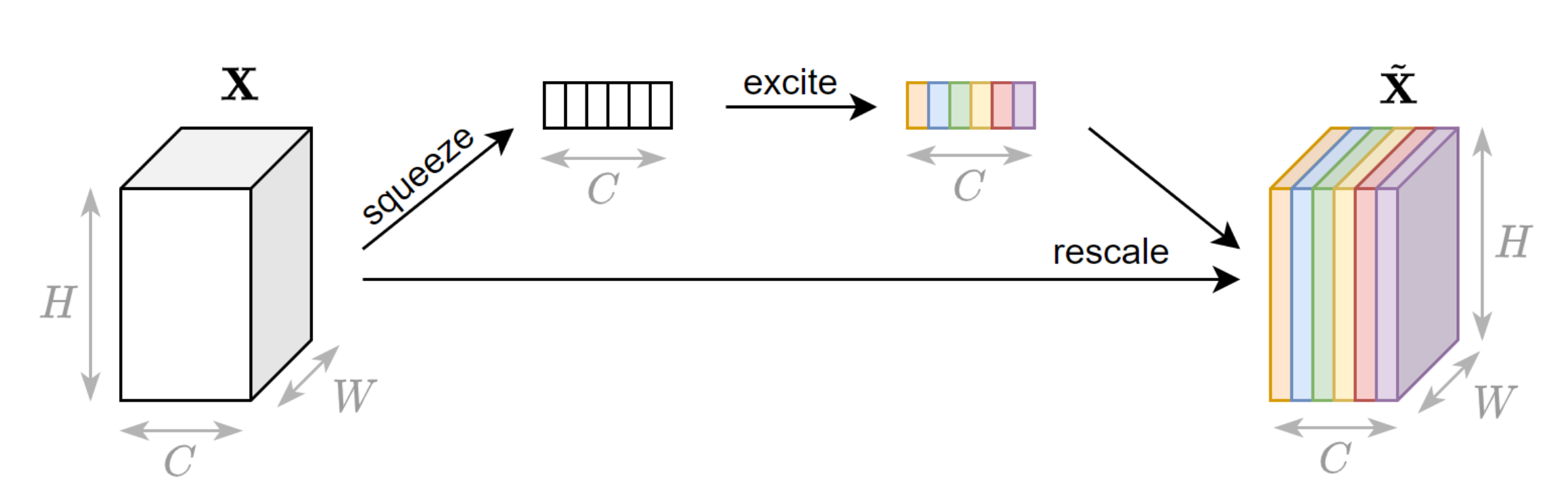
Schematic depiction of the OFCN architecture used for segmentation. Conv(n) stands for a convolutional layer with n neurons. For example, in the first Encoder Block, 64 in the second, and so on.
Figure 3.
Schematic depiction of the OFCN architecture used for segmentation. Conv(n) stands for a convolutional layer with n neurons. For example, in the first Encoder Block, 64 in the second, and so on.
Figure 4.
First the trained OFCN generates the segmentation masks from the SAR images. Then, both SAR images and predicted mask are fed in the classification network. A different architecture is trained to classify each one of the categories (e.g., the depicted one classifies the “texture” category).
Figure 4.
First the trained OFCN generates the segmentation masks from the SAR images. Then, both SAR images and predicted mask are fed in the classification network. A different architecture is trained to classify each one of the categories (e.g., the depicted one classifies the “texture” category).
Figure 5.
Evolution of training loss and F1 score on validation across the 400 training epochs on dataset . Bold lines indicate a running average with window of size 30.
Figure 5.
Evolution of training loss and F1 score on validation across the 400 training epochs on dataset . Bold lines indicate a running average with window of size 30.
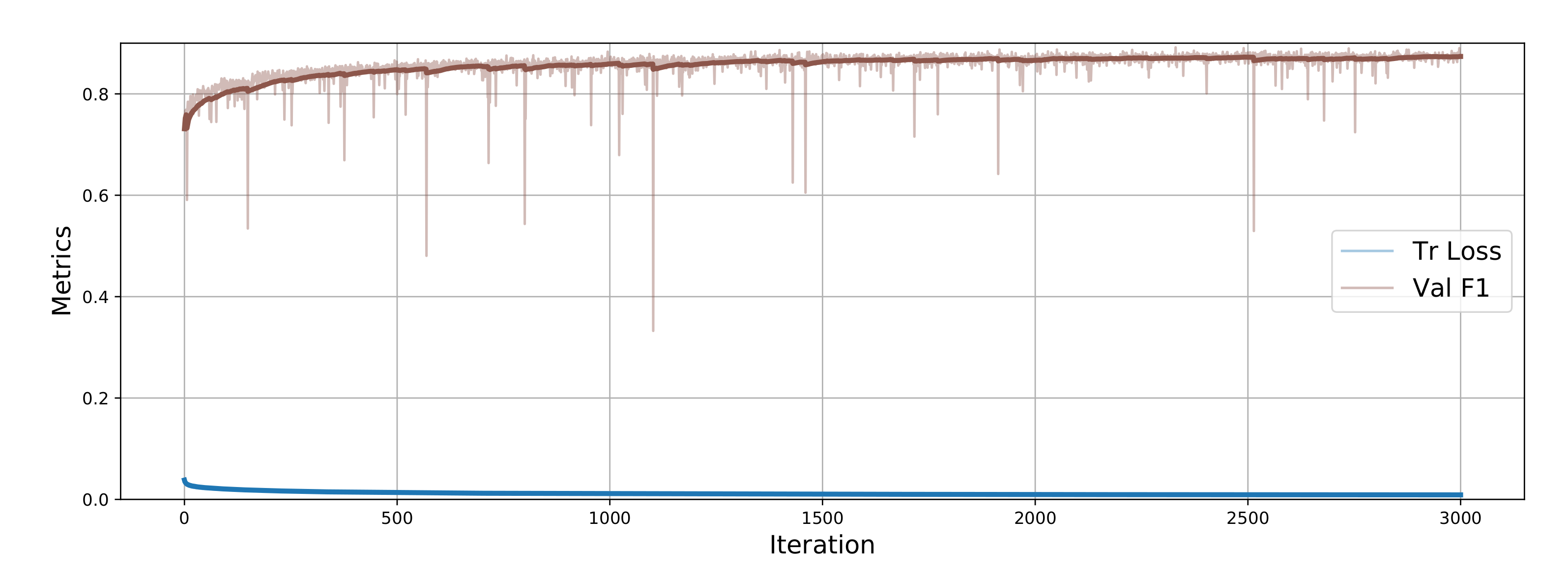
Figure 6.
Training history of the model configured with C1 with two-stage training (C1-2ST-Long) on dataset . The plot depicts the evolution of the training loss and F1 score on the validation set over the 3000 epochs in the second stage. Bold lines indicate a running average with window of size 30.
Figure 6.
Training history of the model configured with C1 with two-stage training (C1-2ST-Long) on dataset . The plot depicts the evolution of the training loss and F1 score on the validation set over the 3000 epochs in the second stage. Bold lines indicate a running average with window of size 30.
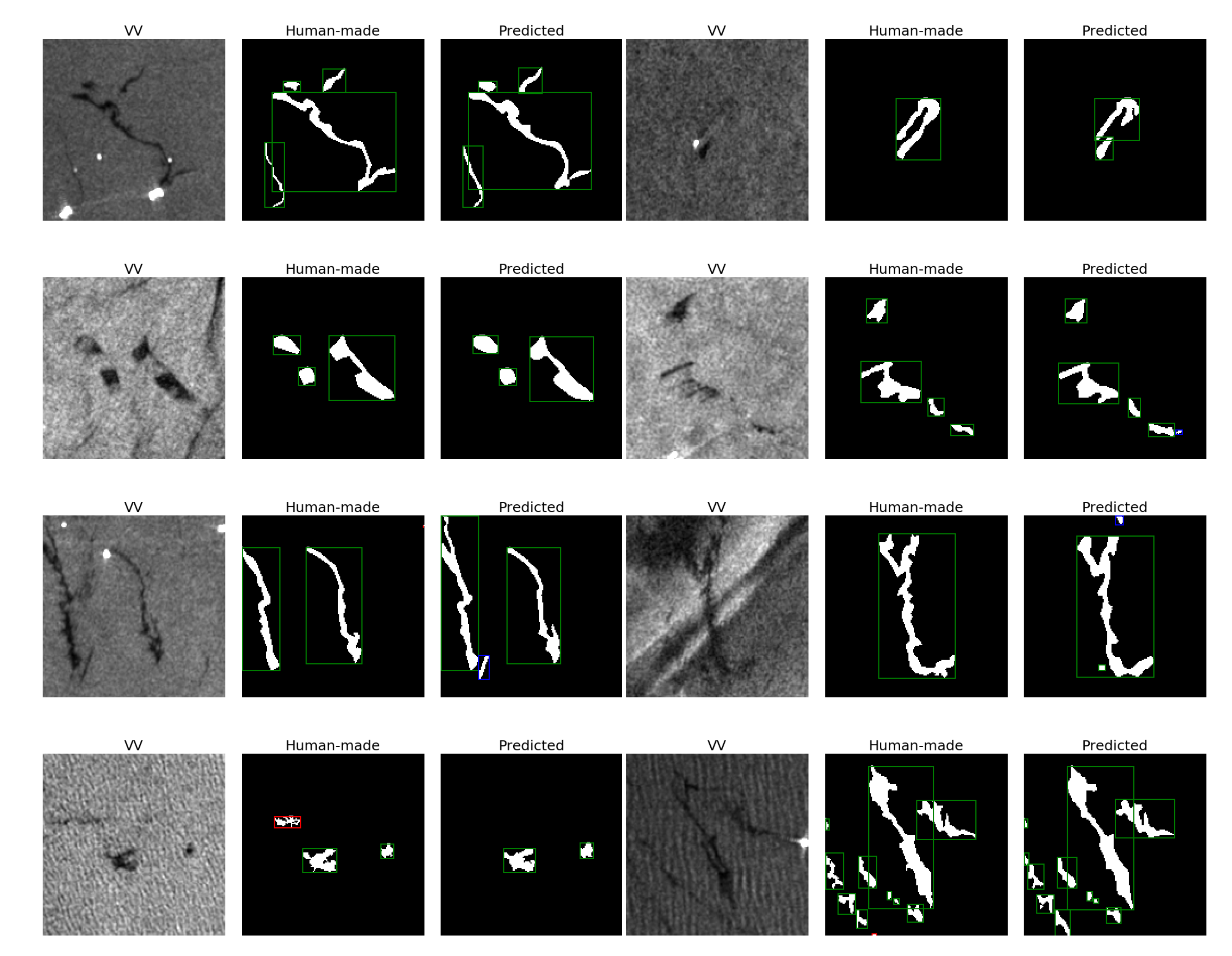
Figure 7.
Examples of segmentation masks predicted by the OFCN on the validation set of . From left to right: the VV input channel, the mask made by the human operator, the OFCN output thresholded at 0.5 (values , values ). Green bounding boxes are TP (the oil spill appears both in the human-made and the predicted mask), blue boxes are FP (the OFCN detects an oil spill that is not present in the human-made mask), and red boxes are FN (the oil spill is in the human-made mask but is not detected by the OFCN).
Figure 7.
Examples of segmentation masks predicted by the OFCN on the validation set of . From left to right: the VV input channel, the mask made by the human operator, the OFCN output thresholded at 0.5 (values , values ). Green bounding boxes are TP (the oil spill appears both in the human-made and the predicted mask), blue boxes are FP (the OFCN detects an oil spill that is not present in the human-made mask), and red boxes are FN (the oil spill is in the human-made mask but is not detected by the OFCN).
Figure 8.
Variation of the F1 score on the validation set according to the incidence angle of the satellite.
Figure 8.
Variation of the F1 score on the validation set according to the incidence angle of the satellite.
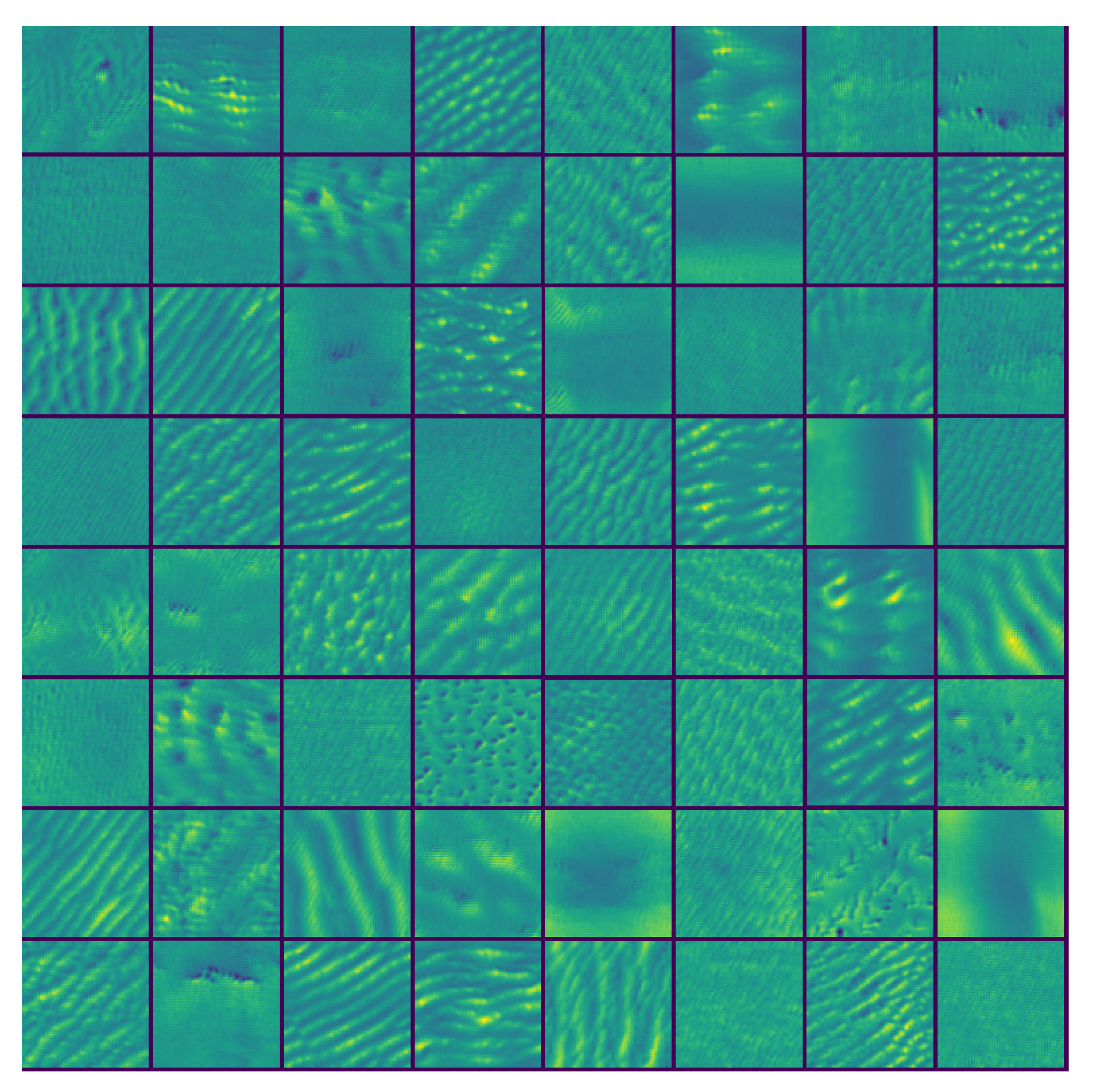
Figure 9.
Filters visualization. We synthetically generated the input images that maximally activate 64 of the 512 filters in the first convolutional layer of the “Enc Block 512” at the bottom of the OFCN.
Figure 9.
Filters visualization. We synthetically generated the input images that maximally activate 64 of the 512 filters in the first convolutional layer of the “Enc Block 512” at the bottom of the OFCN.
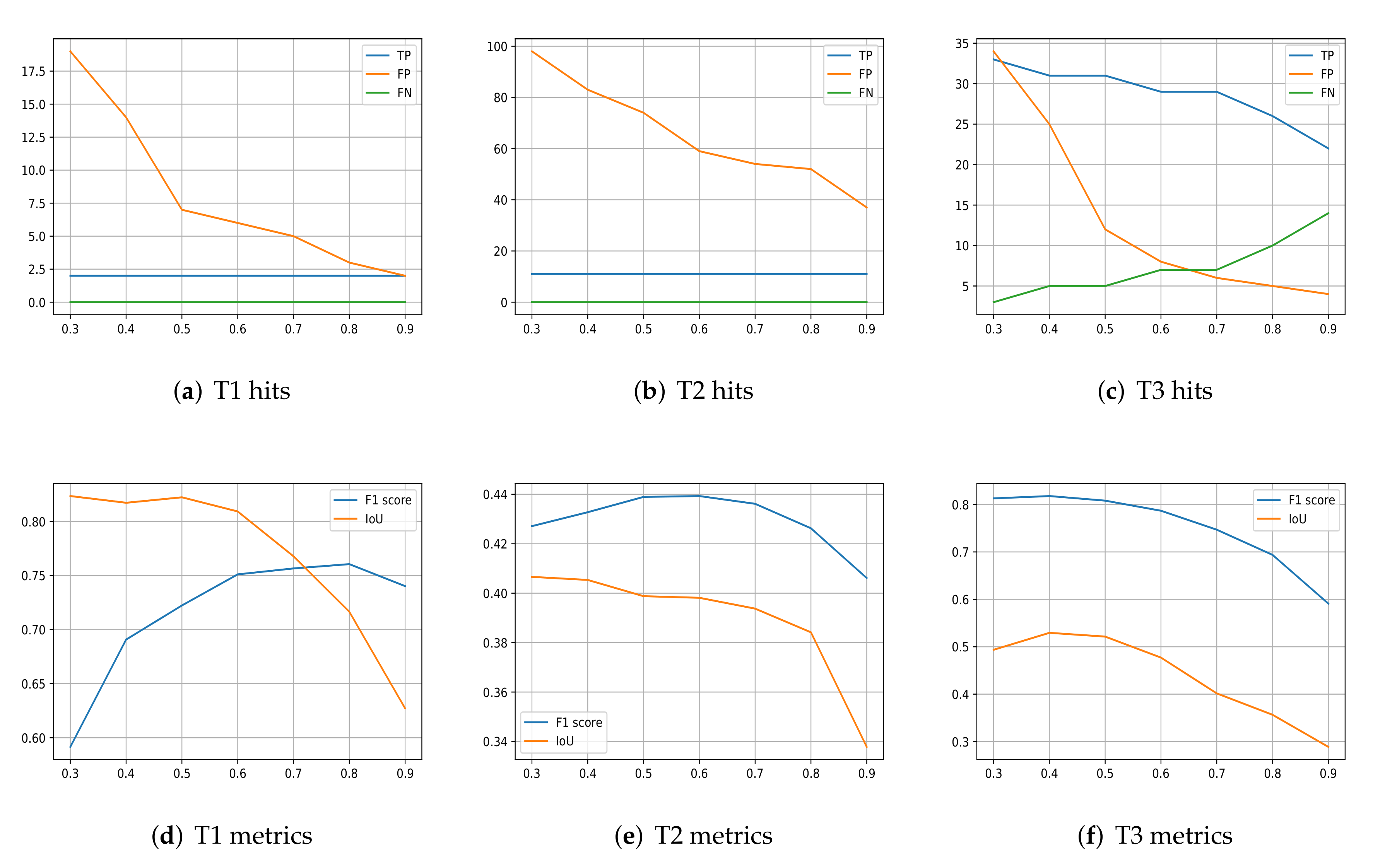
Figure 10.
The x-axis always denotes the value of the rounding threshold . (a–c) number of True Positive (TP), False Positive (FP), and False Negative (FN) detection obtained by using a different threshold on the soft output of the OFCN. (d–f) values of F1 score and IoU for different .
Figure 10.
The x-axis always denotes the value of the rounding threshold . (a–c) number of True Positive (TP), False Positive (FP), and False Negative (FN) detection obtained by using a different threshold on the soft output of the OFCN. (d–f) values of F1 score and IoU for different .
Figure 11.
Results on the 3 Sentinel-1 products used for testing. The first column contains the original SAR images (VV-intensity); the second column contains the segmentation masks of oil spills that are manually drawn by human operators (yellow masks); the third column contains the segmentation masks of oil spills that are predicted by the OFCN (blue masks). Only small sections of the whole SAR products are shown in the figures. The number on the top of the images represent the incident angle.
Figure 11.
Results on the 3 Sentinel-1 products used for testing. The first column contains the original SAR images (VV-intensity); the second column contains the segmentation masks of oil spills that are manually drawn by human operators (yellow masks); the third column contains the segmentation masks of oil spills that are predicted by the OFCN (blue masks). Only small sections of the whole SAR products are shown in the figures. The number on the top of the images represent the incident angle.
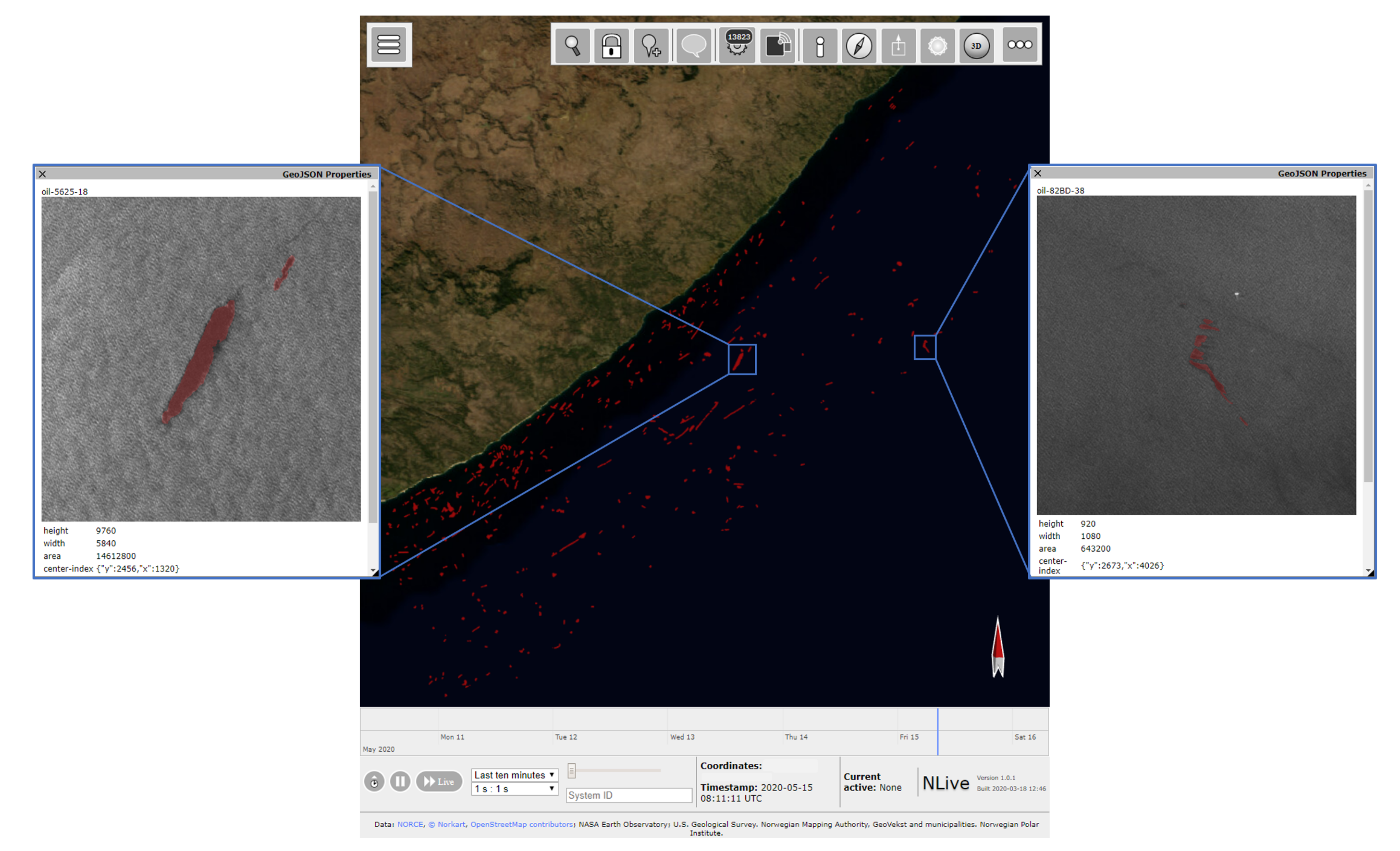
Figure 12.
Visualization in NLive of oil spills detected in a large area (approximately ) in the South hemisphere between 2014 and 2020.
Figure 12.
Visualization in NLive of oil spills detected in a large area (approximately ) in the South hemisphere between 2014 and 2020.
Table 1.
The 12 categories used to classify each oil spill. The possible values assumed by each category are reported in the second column. The distribution of the values for each category assumed by the elements in the dataset is reported in the third column, by using both numerical percentages and a histogram; e.g., 61.8% of the data samples do not have a linear shape and 38.2% have a linear shape.
Table 1.
The 12 categories used to classify each oil spill. The possible values assumed by each category are reported in the second column. The distribution of the values for each category assumed by the elements in the dataset is reported in the third column, by using both numerical percentages and a histogram; e.g., 61.8% of the data samples do not have a linear shape and 38.2% have a linear shape.
| Category | Values | Values Distribution |
|---|
| Patch shape | {False, True} | {48.2%, 51.8%} | ![Remotesensing 12 02260 i001 Remotesensing 12 02260 i001]() |
| Linear shape | {False, True} | {61.8%, 38.2%} | ![Remotesensing 12 02260 i002 Remotesensing 12 02260 i002]() |
| Angular shape | {False, True} | {90.4%, 9.6%} | ![Remotesensing 12 02260 i003 Remotesensing 12 02260 i003]() |
| Weathered texture | {False, True} | {71.3%, 28.7%} | ![Remotesensing 12 02260 i004 Remotesensing 12 02260 i004]() |
| Tailed shape | {False, True} | {83.2%, 16.8%} | ![Remotesensing 12 02260 i005 Remotesensing 12 02260 i005]() |
| Droplets texture | {False, True} | {98.3%, 1.7%} | ![Remotesensing 12 02260 i006 Remotesensing 12 02260 i006]() |
| Winding texture | {False, True} | {92.5%, 7.5%} | ![Remotesensing 12 02260 i007 Remotesensing 12 02260 i007]() |
| Feathered texture | {False, True} | {97.7%, 2.3%} | ![Remotesensing 12 02260 i008 Remotesensing 12 02260 i008]() |
| Shape outline | {Fragmented, Continuous} | {78.4%, 21.6%} | ![Remotesensing 12 02260 i009 Remotesensing 12 02260 i009]() |
| Texture | {Rough, Smooth, Strong, Variable} | {29.2%, 14.3%, 5.1%, 51.2%} | ![Remotesensing 12 02260 i010 Remotesensing 12 02260 i010]() |
| Contrast | {Strong, Weak, Variable} | {23%, 52.8%, 24.1%} | ![Remotesensing 12 02260 i011 Remotesensing 12 02260 i011]() |
| Edge | {Sharp, Diffuse, Variable} | {33.7%, 13.3%, 52.9%} | ![Remotesensing 12 02260 i012 Remotesensing 12 02260 i012]() |
Table 2.
Summary of the datasets details.
Table 2.
Summary of the datasets details.
| Original Data | | | |
|---|
| • 713 SAR prod. | • 1843 tr. patches | • 149,856 tr. patches | • 3 SAR products |
| • 4 years period | • 150 val. patches | • 37,465 val. patches | • Details in Table 3 |
| • 2,093 oil events | • 100 test patches | | |
| • 227,964 oil spills | | | |
Table 3.
Further details on , i.e., the three SAR products used as test set. The image size is reported as the number of pixels.
Table 3.
Further details on , i.e., the three SAR products used as test set. The image size is reported as the number of pixels.
| ID | Image Size | # Oil Spills | # Oil Pixels | # Non-Oil Pixels |
|---|
| T1 | 9836 × 14,894 | 2 | 552 (0.00067%) | 81,877,550 |
| T2 | 21,738 | 11 | 19,336 (0.017%) | 112,071,385 |
| T3 | 10,602 × 21,471 | 36 | 22,793 (0.018%) | 127,436,689 |
Table 4.
Hyperparameters selection results. We report the 3 best configurations (C1, C2, C3) found with cross-validation on . Acronyms: BN (Batch Normalization), SE (Squeeze-and-Excitation), L2 reg. (strength of the L2 regularization on the network parameters), LR (Learning Rate), CW (weight of the oil class).
Table 4.
Hyperparameters selection results. We report the 3 best configurations (C1, C2, C3) found with cross-validation on . Acronyms: BN (Batch Normalization), SE (Squeeze-and-Excitation), L2 reg. (strength of the L2 regularization on the network parameters), LR (Learning Rate), CW (weight of the oil class).
| ID | BN | SE | L2 reg. | Dropout | LR | CW | Var F1 () |
|---|
| C1 | True | True | 0.0 | 0.1 | | 2 | 0.731 |
| C2 | False | True | | 0.1 | | 3 | 0.723 |
| C3 | True | False | 0.0 | 0.0 | | 2 | 0.708 |
Table 5.
Comparison with baselines. Reported is the number of trainable parameters, training time for 400 epochs, training accuracy, training loss, and F1 score on the validation. Best results are in bold. Models are trained on an Nvidia RTX 2080.
Table 5.
Comparison with baselines. Reported is the number of trainable parameters, training time for 400 epochs, training accuracy, training loss, and F1 score on the validation. Best results are in bold. Models are trained on an Nvidia RTX 2080.
| Model | # Params. | Tr Time (Hours) | Tr Acc. | Tr Loss | Val F1 () |
|---|
| U-net | 7,760,069 | 10.1 | 0.984 | 0.058 | 0.741 |
| DeepLabV3+ | 41,049,697 | 15.2 | 0.987 | 0.039 | 0.765 |
| OFCN | 7,873,729 | 10.9 | 0.988 | 0.038 | 0.775 |
Table 6.
Validation performance obtained on using the three best configurations C1, C2, and C3, the two-step training (2ST) strategy with configuration C1, and a long training of 3000 epochs (Long). We also report the training time, the accuracy, and loss achieved on the training set.
Table 6.
Validation performance obtained on using the three best configurations C1, C2, and C3, the two-step training (2ST) strategy with configuration C1, and a long training of 3000 epochs (Long). We also report the training time, the accuracy, and loss achieved on the training set.
| ID | Epochs | Time (Days) | Tr Acc. | Tr Loss | Val F1 () |
|---|
| C1 | 400 | 6.8 | 0.995 | 0.016 | 0.857 |
| C2 | 400 | 6.9 | 0.990 | 0.047 | 0.750 |
| C3 | 400 | 6.2 | 0.993 | 0.018 | 0.802 |
| C1-2ST | 400 + 400 | 9.4 | 0.996 | 0.014 | 0.861 |
| C1-2ST-Long | 500 + 3000 | 54.3 | 0.997 | 0.009 | 0.892 |
Table 7.
Performance obtained on the 3 SAR products in used as test set.
Table 7.
Performance obtained on the 3 SAR products in used as test set.
| ID | F1 | IoU | TP | FP | FN |
|---|
| T1 | 0.73 | 0.81 | 2 | 7 | 0 |
| T2 | 0.44 | 0.36 | 11 | 59 | 0 |
| T3 | 0.83 | 0.52 | 31 | 14 | 5 |
Table 8.
Classification accuracy and F1 score for each one of the 12 categories on the validation set.
Table 8.
Classification accuracy and F1 score for each one of the 12 categories on the validation set.
| Category | Accuracy | F1 |
|---|
| Patch shape | 80.0% | 0.80 |
| Linear shape | 76.8% | 0.77 |
| Angular shape | 93.2% | 0.91 |
| Weathered texture | 70.4% | 0.64 |
| Tailed texture | 78.4% | 0.73 |
| Droplets texture | 98.8% | 0.98 |
| Winding texture | 94.4% | 0.92 |
| Feathered texture | 97.2% | 0.96 |
| Shape outline | 93.8% | 0.91 |
| Texture | 55.6% | 0.49 |
| Contrast | 61.6% | 0.59 |
| Edge | 61.6% | 0.58 |