Figure 1.
Polynomial and radial basis function (RBF) kernel representations. Polynomial kernels of degree (a) 2, (b) 3, and (c) 5; RBF kernels with the parameter of (d) 0.2, (e) 0.6, and (f) 1.0.
Figure 1.
Polynomial and radial basis function (RBF) kernel representations. Polynomial kernels of degree (a) 2, (b) 3, and (c) 5; RBF kernels with the parameter of (d) 0.2, (e) 0.6, and (f) 1.0.
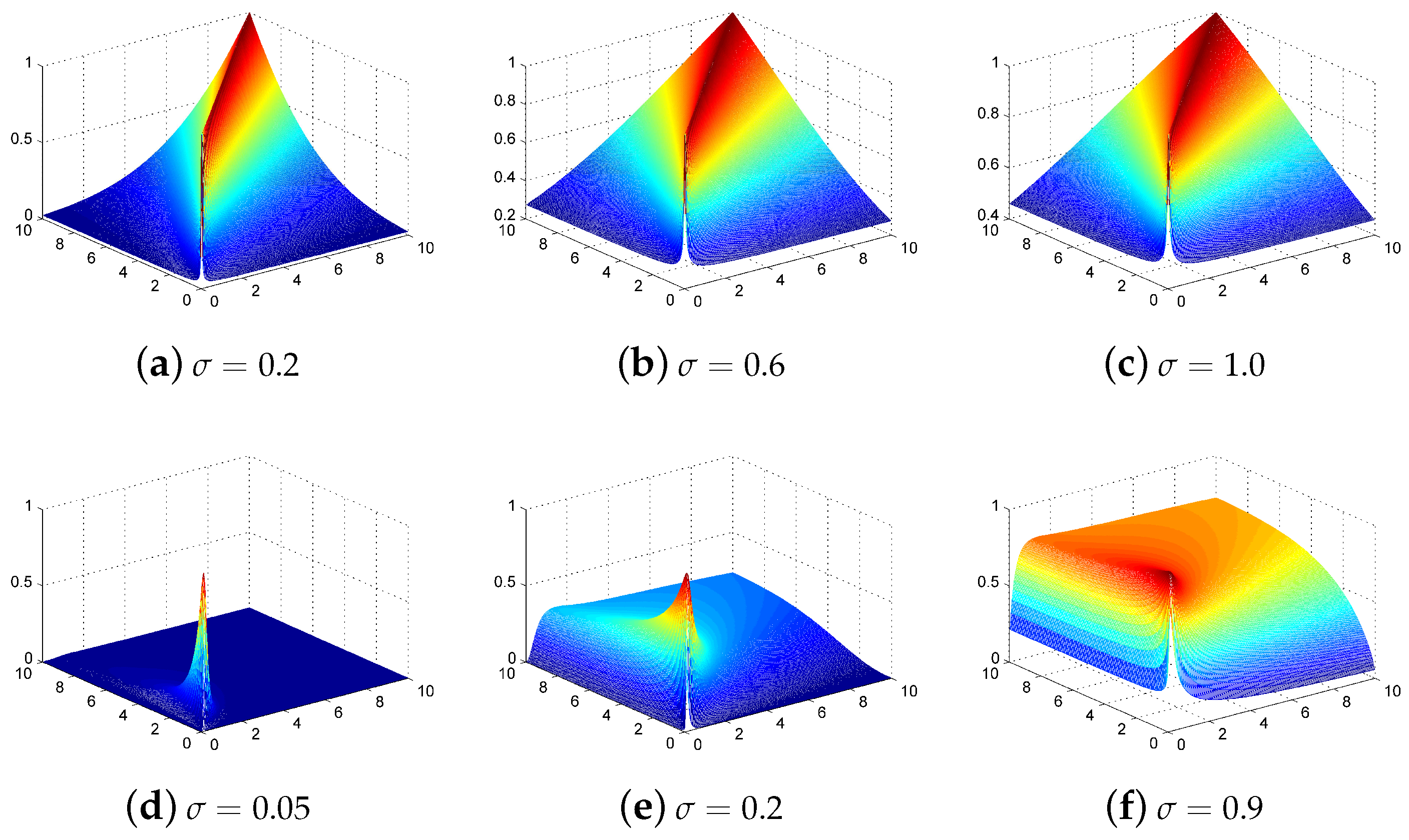
Figure 2.
Spectral angle mapper (SAM)-RBF kernel and spectral information divergence (SID)-RBF kernel representation. SAM-RBF kernel with parameter values of (a) 0.2, (b) 0.6, and (c) 1.0. SID-RBF kernel with parameter values of (d) 0.05, (e) 0.2, and (f) 0.9.
Figure 2.
Spectral angle mapper (SAM)-RBF kernel and spectral information divergence (SID)-RBF kernel representation. SAM-RBF kernel with parameter values of (a) 0.2, (b) 0.6, and (c) 1.0. SID-RBF kernel with parameter values of (d) 0.05, (e) 0.2, and (f) 0.9.
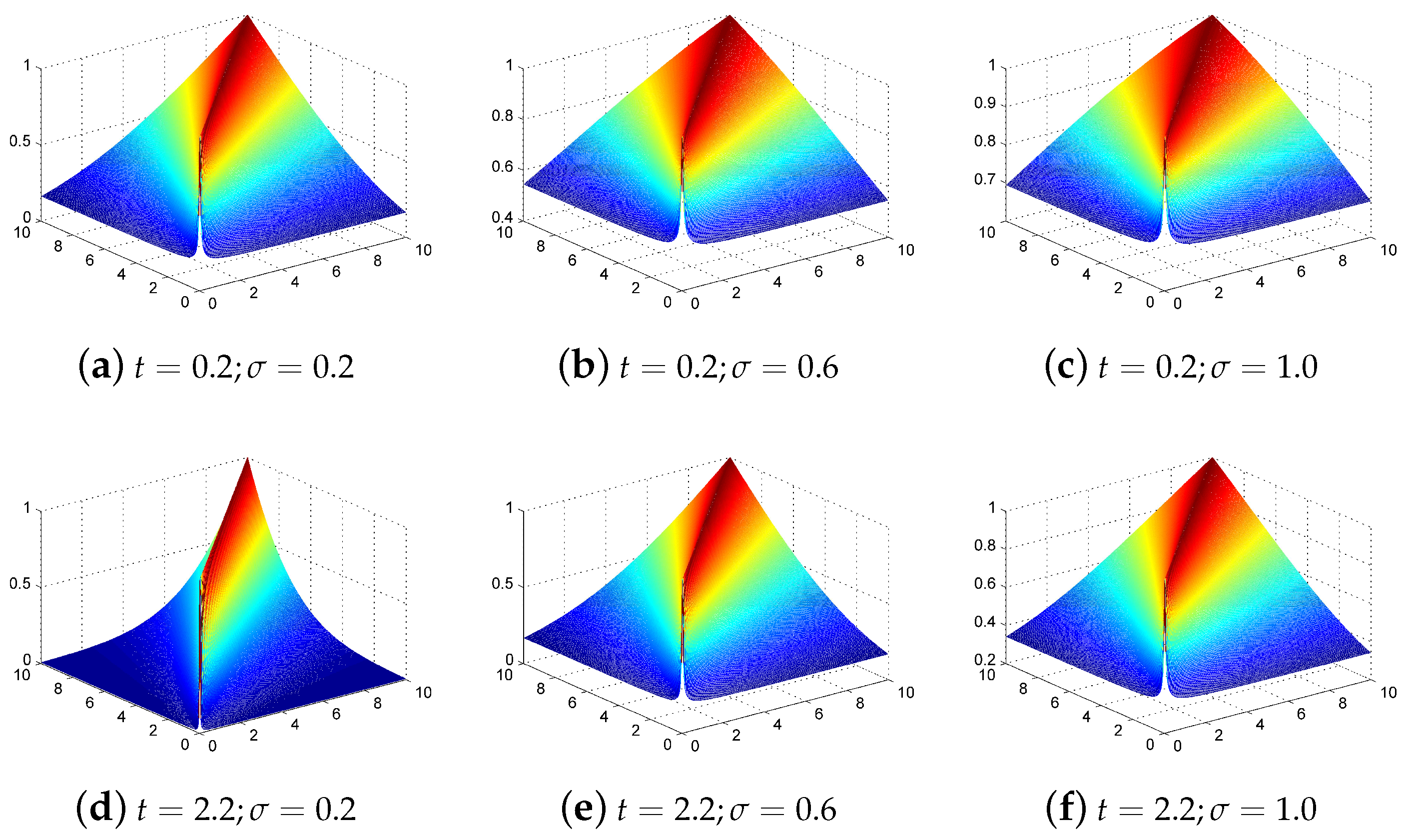
Figure 3.
Power-SAM-RBF kernel characteristics with different parameters of t and .
Figure 3.
Power-SAM-RBF kernel characteristics with different parameters of t and .
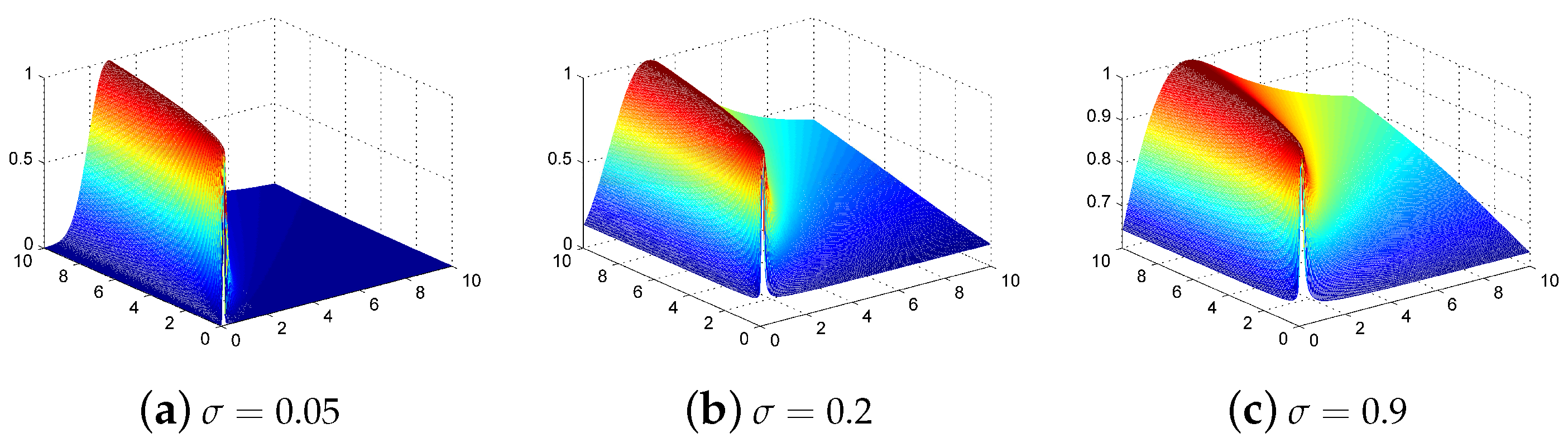
Figure 4.
Normalized-SID-RBF kernel representation with parameter values of (a) 0.05, (b) 0.2, and (c) 0.9.
Figure 4.
Normalized-SID-RBF kernel representation with parameter values of (a) 0.05, (b) 0.2, and (c) 0.9.
Figure 5.
(a) False color hyperspectral remote sensing image over the Indian Pines test site (using bands 50, 27, and 17). (b) Ground truth of the labeled area with nine classes of land cover: Corn-notill, Corn-mintill, Grass-pasture, Grass-trees, Hay-windrowed, Soybean-notill, Soybean-mintill, Soybean-clean, and Woods.
Figure 5.
(a) False color hyperspectral remote sensing image over the Indian Pines test site (using bands 50, 27, and 17). (b) Ground truth of the labeled area with nine classes of land cover: Corn-notill, Corn-mintill, Grass-pasture, Grass-trees, Hay-windrowed, Soybean-notill, Soybean-mintill, Soybean-clean, and Woods.
Figure 6.
(a) False color hyperspectral data over the University of Pavia (using bands 105, 63, and 29). (b) Ground truth of the labeled area with nine classes of land cover: Asphalt, meadows, gravel, trees, painted metal sheets, bare soil, bitumen, self-blocking bricks, and shadows.
Figure 6.
(a) False color hyperspectral data over the University of Pavia (using bands 105, 63, and 29). (b) Ground truth of the labeled area with nine classes of land cover: Asphalt, meadows, gravel, trees, painted metal sheets, bare soil, bitumen, self-blocking bricks, and shadows.
Figure 7.
(a) False color hyperspectral image (HSI) over Salinas Valley (using bands 68, 30, and 18); (b) Ground truth of the labeled area with 16 classes of land cover: Broccoli green weeds 1, Broccoli green weeds 2, Fallow, Fallow rough plow, Fallow smooth, Stubble, Celery, Grapes untrained, Soil vineyard develop, Corn senesced green weeds, Lettuce romaine 4 wk, Lettuce romaine 5 wk, Lettuce romaine 6 wk, Lettuce romaine 7 wk, Vineyard untrained, and Vineyard vertical trellis.
Figure 7.
(a) False color hyperspectral image (HSI) over Salinas Valley (using bands 68, 30, and 18); (b) Ground truth of the labeled area with 16 classes of land cover: Broccoli green weeds 1, Broccoli green weeds 2, Fallow, Fallow rough plow, Fallow smooth, Stubble, Celery, Grapes untrained, Soil vineyard develop, Corn senesced green weeds, Lettuce romaine 4 wk, Lettuce romaine 5 wk, Lettuce romaine 6 wk, Lettuce romaine 7 wk, Vineyard untrained, and Vineyard vertical trellis.
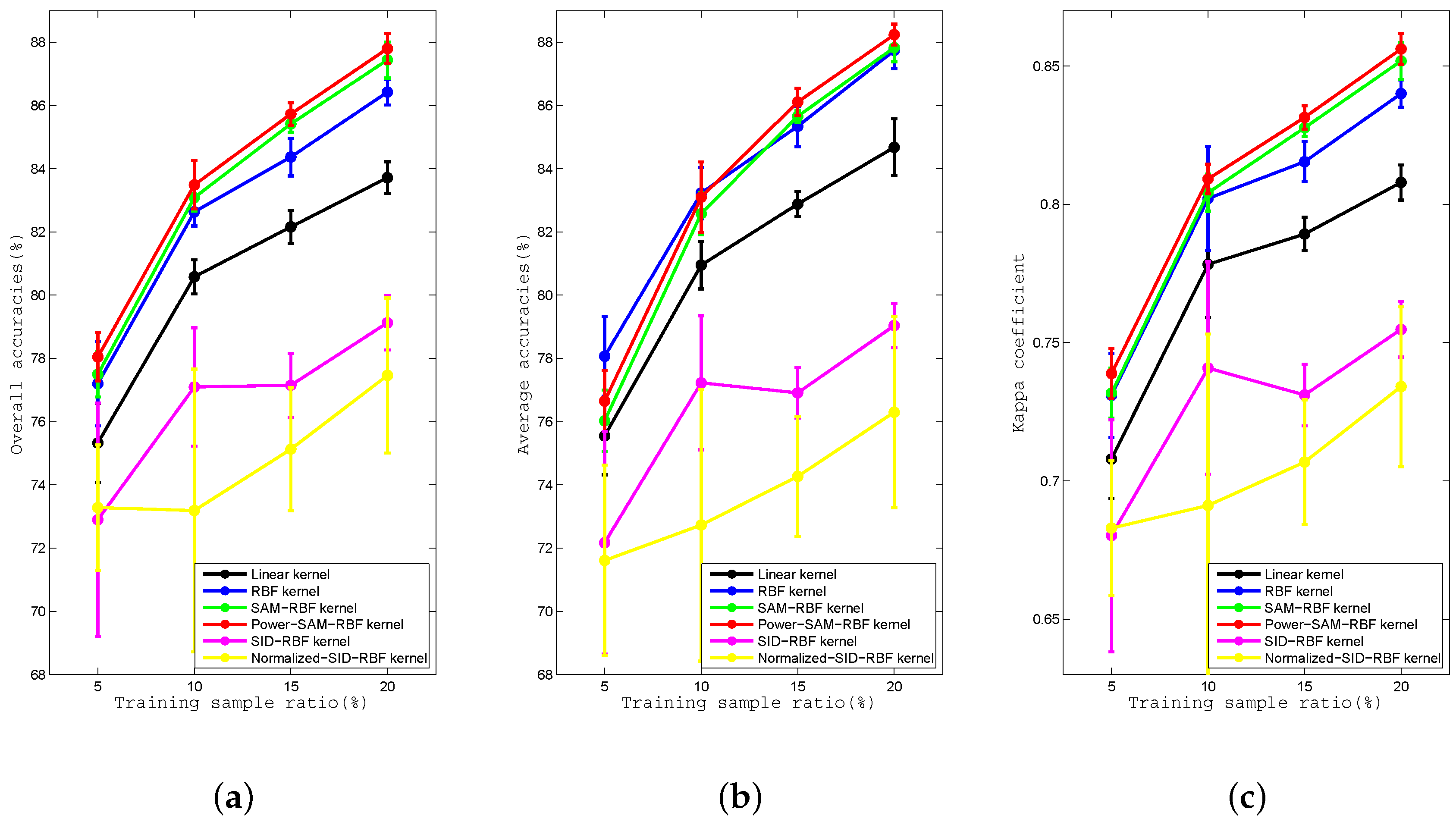
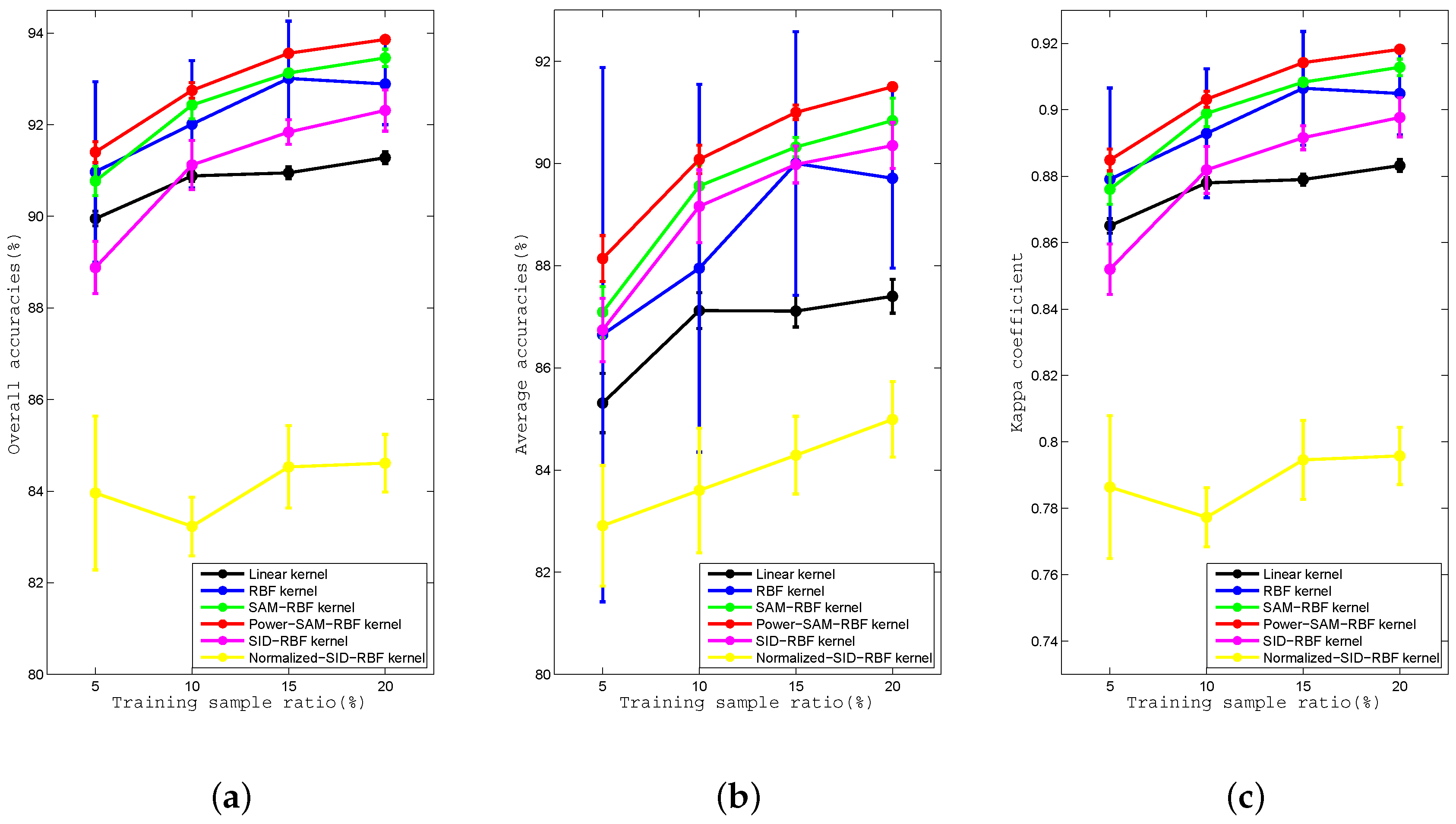
Figure 8.
Curves of the (a) OA, (b) AA, and (c) kappa coefficient for the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels with proportions of training data of , , , and for the Indian Pines dataset.
Figure 8.
Curves of the (a) OA, (b) AA, and (c) kappa coefficient for the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels with proportions of training data of , , , and for the Indian Pines dataset.
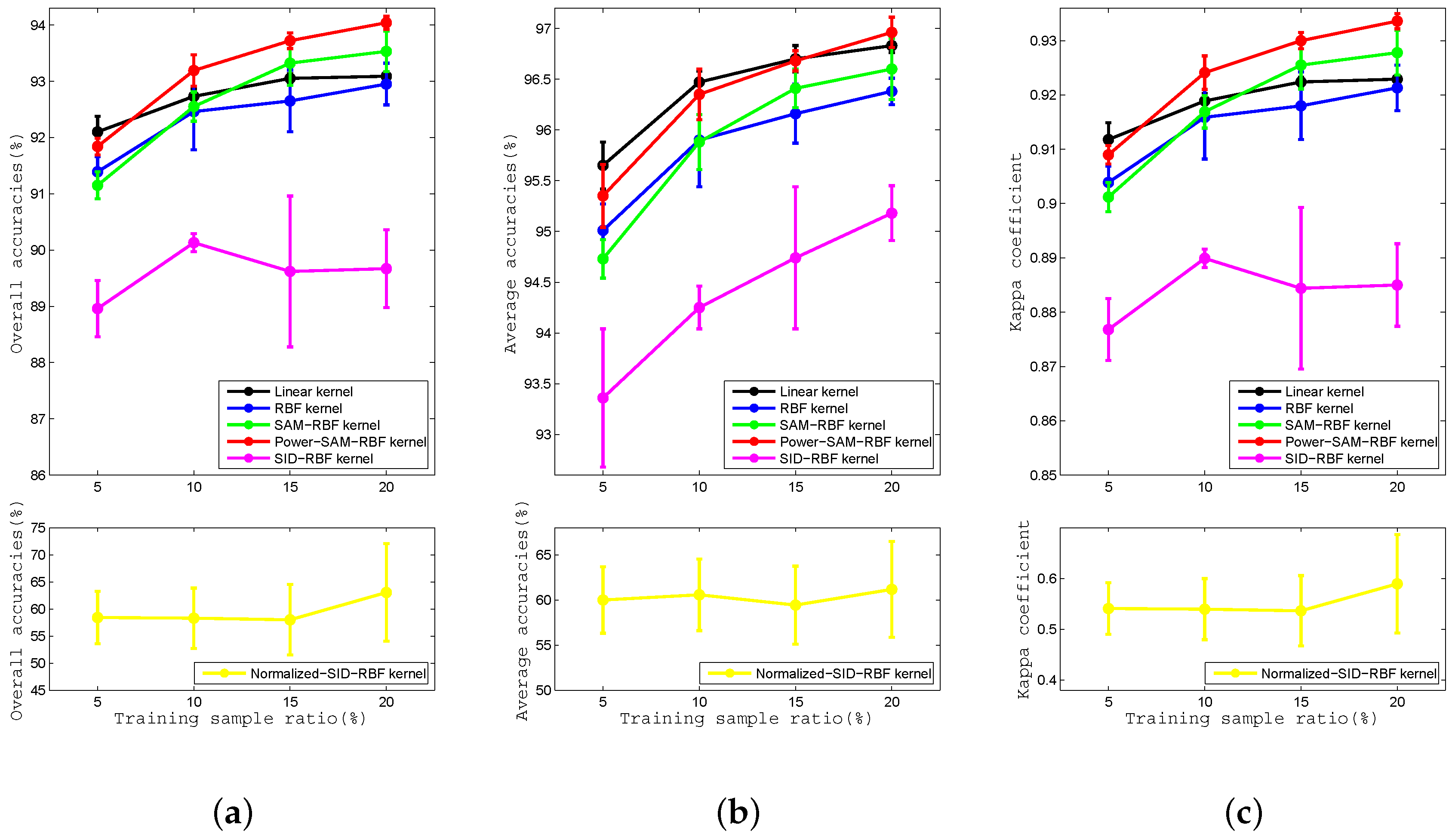
Figure 9.
Curves of the (a) OA, (b) AA, and (c) kappa coefficient for the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels for proportions of training data of , , , and for the University of Pavia dataset.
Figure 9.
Curves of the (a) OA, (b) AA, and (c) kappa coefficient for the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels for proportions of training data of , , , and for the University of Pavia dataset.
Figure 10.
Curves of (a) OA, (b) AA, and (c) kappa coefficient for the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels with proportions of training data of , , , and for the Salinas Valley dataset.
Figure 10.
Curves of (a) OA, (b) AA, and (c) kappa coefficient for the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels with proportions of training data of , , , and for the Salinas Valley dataset.
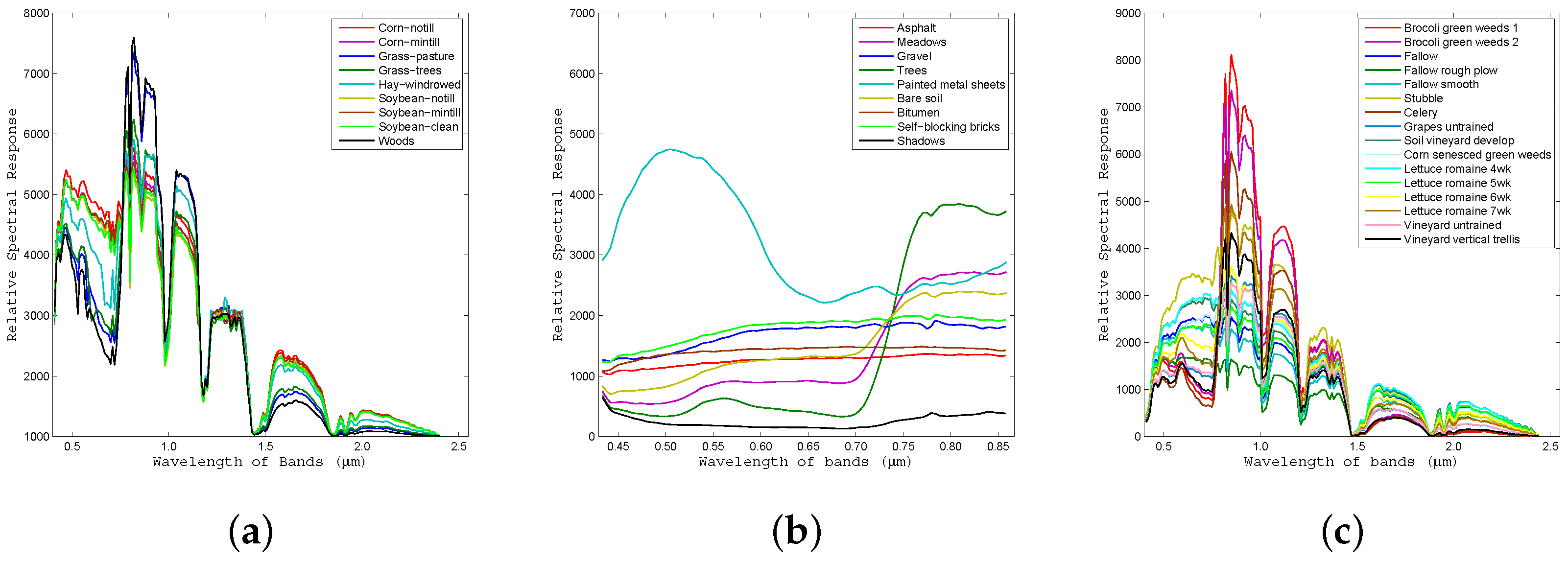
Figure 11.
Average spectral signature of each class for all labeled pixels in the ground-truth data for the (a) Indian Pines, (b) University of Pavia, and (c) Salinas Valley datasets.
Figure 11.
Average spectral signature of each class for all labeled pixels in the ground-truth data for the (a) Indian Pines, (b) University of Pavia, and (c) Salinas Valley datasets.
Figure 12.
Curves of when the training set being (a) and (b) .
Figure 12.
Curves of when the training set being (a) and (b) .
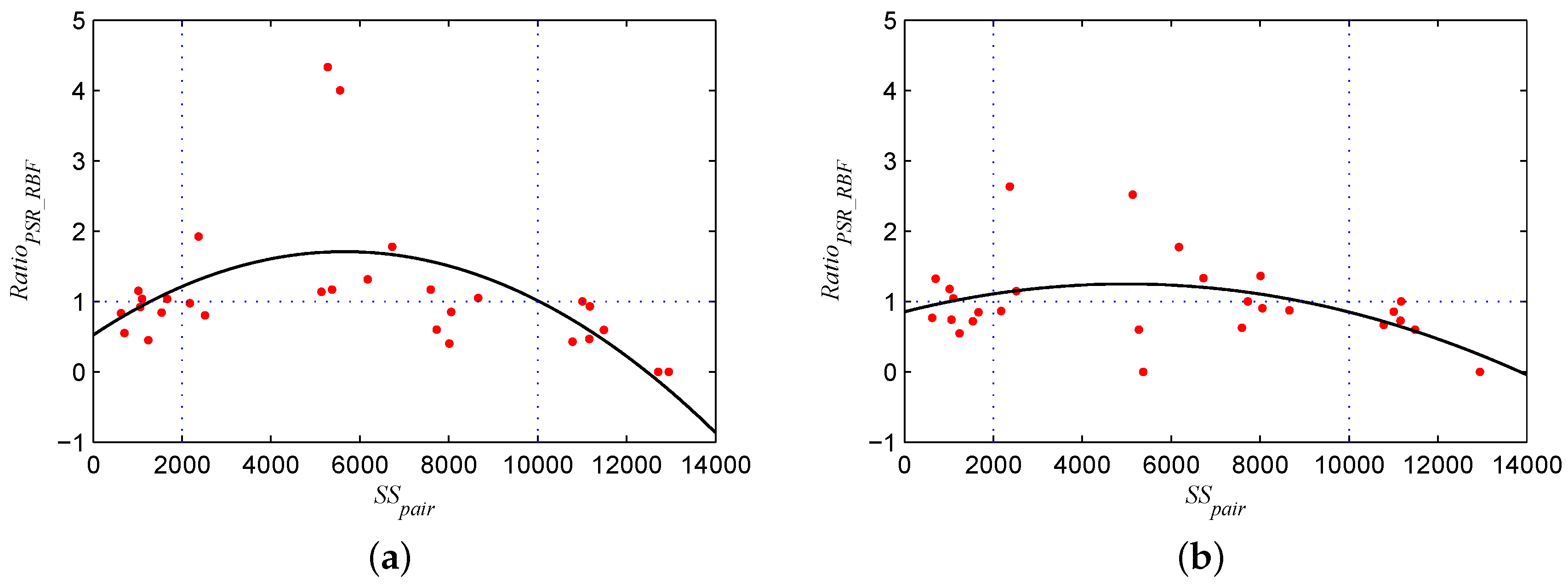
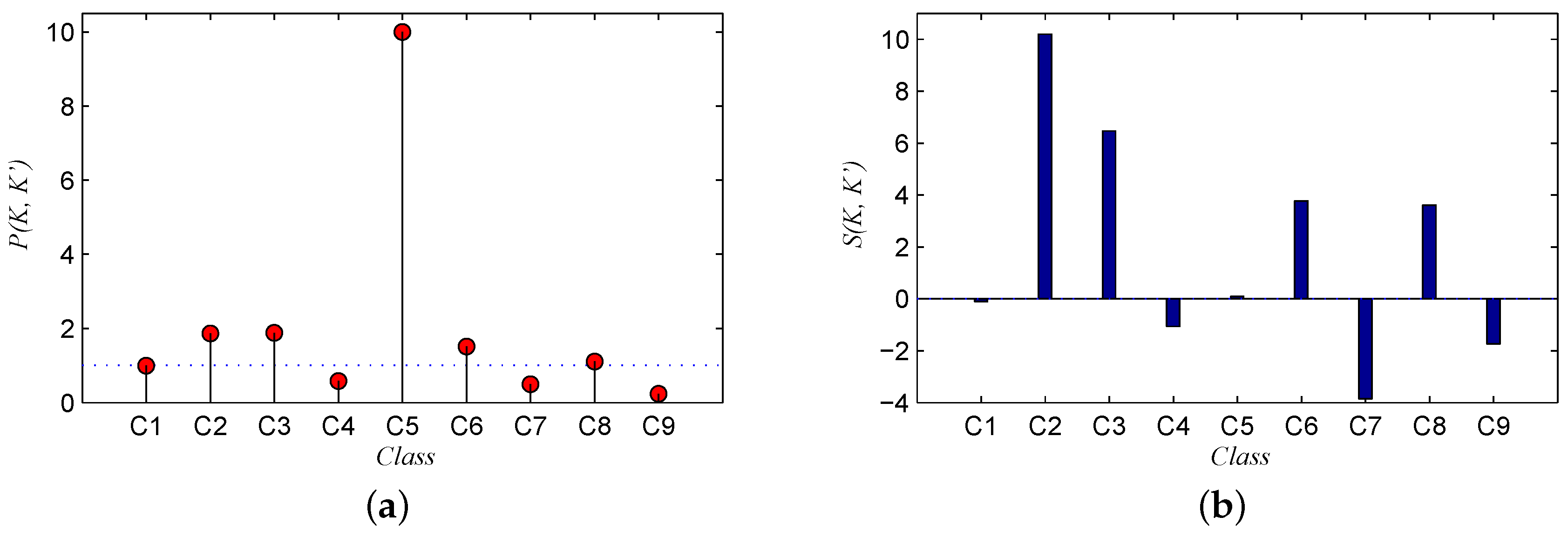
Figure 13.
Curves of (a) (the ratio of the accuracy improvement with the kernel k to that with another kernel ) and (b) (the D-value of the superiority of the kernel k over another kernel ) for the Power-SAM-RBF kernel versus the RBF kernel for the Indian Pines dataset.
Figure 13.
Curves of (a) (the ratio of the accuracy improvement with the kernel k to that with another kernel ) and (b) (the D-value of the superiority of the kernel k over another kernel ) for the Power-SAM-RBF kernel versus the RBF kernel for the Indian Pines dataset.
Table 1.
Ground truth classes for the Indian Pines dataset and their corresponding numbers of samples.
Table 1.
Ground truth classes for the Indian Pines dataset and their corresponding numbers of samples.
| Label | Indian Pines | University of Pavia | Salinas Valley |
|---|
| C1 | Corn-notill | Asphalt | Brocoli green weeds 1 |
| C2 | Corn-mintill | Meadows | Brocoli green weeds 2 |
| C3 | Grass-pasture | Gravel | Fallow |
| C4 | Grass-trees | Trees | Fallow rough plow |
| C5 | Hay-windrowed | Painted metal sheets | Fallow smooth |
| C6 | Soybean-notill | Bare Soil | Stubble |
| C7 | Soybean-mintill | Bitumen | Celery |
| C8 | Soybean-clean | Self-Blocking Bricks | Grapes untrained |
| C9 | Woods | Shadows | Soil vinyard develop |
| C10 | - | - | Corn senesced green weeds |
| C11 | - | - | Lettuce romaine 4wk |
| C12 | - | - | Lettuce romaine 5wk |
| C13 | - | - | Lettuce romaine 6wk |
| C14 | - | - | Lettuce romaine 7wk |
| C15 | - | - | Vinyard untrained |
| C16 | - | - | Vinyard vertical trellis |
Table 2.
Parameter settings for the PSO method.
Table 2.
Parameter settings for the PSO method.
| Label | Class | Samples |
|---|
| Acceleration constants | and | 1.5 and 1.7 |
| maximal number of generations | | 5 |
| Swarm scale | | 10 |
| Inertia weight | | 1 |
| Constriction factor | k | 1 |
Table 3.
Overall accuracies (OA), average accuracies (AA), kappa coefficients of Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels on the Indian Pines dataset.
Table 3.
Overall accuracies (OA), average accuracies (AA), kappa coefficients of Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels on the Indian Pines dataset.
| Training Sample | Accuracies | Linear Kernel | RBF Kernel | SAM-RBF Kernel | Power-SAM-RBF Kernel | SID-RBF Kernel | Normalized-SID-RBF Kernel |
|---|
| 5% | OA | 75.33 ± 1.25 | 77.20 ± 1.33 | 77.50 ± 0.72 | 78.05 ± 0.76 | 72.90 ± 3.69 | 73.28 ± 1.99 |
| AA | 75.55 ± 1.23 | 78.07 ± 1.26 | 76.03 ± 0.97 | 76.65 ± 0.96 | 72.17 ± 3.52 | 71.61 ± 3.01 |
| Kappa | 0.7079 ± 0.0142 | 0.7309 ± 0.0152 | 0.7317 ± 0.0090 | 0.7389 ± 0.0092 | 0.6803 ± 0.0420 | 0.6830 ± 0.0245 |
| 10% | OA | 80.58 ± 0.54 | 82.64 ± 0.45 | 83.09 ± 0.42 | 83.49 ± 0.76 | 77.10 ± 1.87 | 73.19 ± 4.47 |
| AA | 80.95 ± 0.75 | 83.23 ± 0.81 | 82.58 ± 0.67 | 83.10 ± 1.11 | 77.23 ± 2.12 | 72.73 ± 4.30 |
| Kappa | 0.7783 ± 0.0193 | 0.8020 ± 0.0188 | 0.8042 ± 0.0068 | 0.8091 ± 0.0053 | 0.7408 ± 0.0384 | 0.6912 ± 0.0619 |
| 15% | OA | 82.16 ± 0.52 | 84.37 ± 0.60 | 85.42 ± 0.27 | 85.73 ± 0.36 | 77.15 ± 1.01 | 75.13 ± 1.94 |
| AA | 82.88 ± 0.39 | 85.34 ± 0.64 | 85.66 ± 0.19 | 86.11 ± 0.43 | 76.91 ± 0.80 | 74.27 ± 1.90 |
| Kappa | 0.7892 ± 0.0060 | 0.8154 ± 0.0073 | 0.8276 ± 0.0031 | 0.8314 ± 0.0043 | 0.7311 ± 0.0112 | 0.7068 ± 0.0226 |
| 20% | OA | 83.72 ± 0.50 | 86.42 ± 0.40 | 87.44 ± 0.57 | 87.80 ± 0.48 | 79.13 ± 0.86 | 77.46 ± 2.45 |
| AA | 84.68 ± 0.90 | 87.74 ± 0.57 | 87.83 ± 0.44 | 88.24 ± 0.33 | 79.04 ± 0.70 | 76.30 ± 3.02 |
| Kappa | 0.8079 ± 0.0064 | 0.8400 ± 0.0050 | 0.8518 ± 0.0067 | 0.8561 ± 0.0056 | 0.7548 ± 0.0100 | 0.7341 ± 0.0289 |
Table 4.
OAs, AAs, kappa coefficients of the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels on the University of Pavia dataset.
Table 4.
OAs, AAs, kappa coefficients of the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels on the University of Pavia dataset.
| Training Sample | Accuracies | Linear Kernel | RBF Kernel | SAM-RBF Kernel | Power-SAM-RBF Kernel | SID-RBF Kernel | Normalized-SID-RBF Kernel |
|---|
| 5% | OA | 89.95 ± 0.16 | 90.97 ± 1.97 | 90.77 ± 0.32 | 91.40 ± 0.23 | 88.88 ± 0.57 | 83.96 ± 1.68 |
| AA | 85.31 ± 0.58 | 86.65 ± 5.23 | 87.09 ± 0.50 | 88.14 ± 0.45 | 86.74 ± 0.62 | 82.91 ± 1.18 |
| Kappa | 0.8651 ± 0.0022 | 0.8791 ± 0.0275 | 0.8761 ± 0.0045 | 0.8849 ± 0.0033 | 0.8520 ± 0.0076 | 0.7864 ± 0.0215 |
| 10% | OA | 90.88 ± 0.12 | 92.01 ± 1.39 | 92.43 ± 0.30 | 92.75 ± 0.17 | 91.12 ± 0.54 | 83.23 ± 0.64 |
| AA | 87.12 ± 0.35 | 87.95 ± 3.60 | 89.56 ± 0.41 | 90.08 ± 0.28 | 89.16 ± 0.71 | 83.60 ± 1.22 |
| Kappa | 0.8780 ± 0.0016 | 0.8929 ± 0.0194 | 0.8989 ± 0.0040 | 0.9032 ± 0.0024 | 0.8819 ± 0.0071 | 0.7773 ± 0.0089 |
| 15% | OA | 90.95 ± 0.13 | 93.01 ± 1.25 | 93.13 ± 0.07 | 93.56 ± 0.07 | 91.84 ± 0.27 | 84.53 ± 0.90 |
| AA | 87.11 ± 0.31 | 90.00 ± 2.58 | 90.32 ± 0.19 | 91.00 ± 0.14 | 89.98 ± 0.36 | 84.29 ± 0.76 |
| Kappa | 0.8790 ± 0.0017 | 0.9065 ± 0.0171 | 0.9083 ± 0.0010 | 0.9142 ± 0.0010 | 0.8916 ± 0.0036 | 0.7946 ± 0.0119 |
| 20% | OA | 91.28 ± 0.13 | 92.89 ± 0.89 | 93.46 ± 0.19 | 93.86 ± 0.08 | 92.31 ± 0.45 | 84.61 ± 0.63 |
| AA | 87.40 ± 0.33 | 89.71 ± 1.76 | 90.84 ± 0.44 | 91.50 ±0.06 | 90.35 ± 0.45 | 84.99 ± 0.74 |
| Kappa | 0.8832 ± 0.0018 | 0.9049 ± 0.0124 | 0.9128 ± 0.0025 | 0.9182 ± 0.0010 | 0.8977 ± 0.0059 | 0.7958 ± 0.0086 |
Table 5.
OAs, AAs, and kappa coefficients of the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels on the Salinas Valley dataset.
Table 5.
OAs, AAs, and kappa coefficients of the Linear, RBF, SAM-RBF, Power-SAM-RBF, SID-RBF, and Normalized-SID-RBF kernels on the Salinas Valley dataset.
| Training Sample | Accuracies | Linear Kernel | RBF Kernel | SAM-RBF Kernel | Power-SAM-RBF Kernel | SID-RBF Kernel | Normalized-SID-RBF Kernel |
|---|
| 5% | OA | 92.10 ± 0.28 | 91.39 ± 0.27 | 91.15 ± 0.24 | 91.84 ± 0.15 | 88.96 ± 0.50 | 58.42 ± 4.83 |
| AA | 95.65 ± 0.23 | 95.01 ± 0.26 | 94.73 ± 0.19 | 95.35 ± 0.31 | 93.36 ± 0.68 | 60.00 ± 3.68 |
| Kappa | 0.9118 ± 0.0031 | 0.9039 ± 0.0030 | 0.9012 ± 0.0027 | 0.9090 ± 0.0017 | 0.8768 ± 0.0057 | 0.5410 ± 0.0506 |
| 10% | OA | 92.73 ± 0.13 | 92.46 ± 0.68 | 92.55 ± 0.26 | 93.19 ± 0.28 | 90.13 ± 0.16 | 58.30 ± 5.58 |
| AA | 96.47 ± 0.11 | 95.98 ± 0.46 | 95.88 ± 0.27 | 96.35 ± 0.25 | 94.25 ± 0.21 | 60.57 ± 3.96 |
| Kappa | 0.9189 ± 0.0014 | 0.9159 ± 0.0077 | 0.9169 ± 0.0030 | 0.9241 ± 0.0031 | 0.8899 ± 0.0017 | 0.5398 ± 0.0600 |
| 15% | OA | 93.05 ± 0.08 | 92.65 ± 0.55 | 93.32 ± 0.39 | 93.72 ± 0.14 | 89.62 ± 1.34 | 58.02 ± 6.51 |
| AA | 96.70 ± 0.13 | 96.16 ± 0.29 | 96.41 ± 0.19 | 96.68 ± 0.10 | 94.74 ± 0.70 | 59.43 ± 4.32 |
| Kappa | 0.9224 ± 0.0009 | 0.9180 ± 0.0062 | 0.9255 ± 0.0044 | 0.9300 ± 0.0015 | 0.8844 ± 0.0149 | 0.5366 ± 0.0692 |
| 20% | OA | 93.09 ± 0.07 | 92.95 ± 0.37 | 93.53 ± 0.36 | 94.04 ± 0.12 | 89.67 ± 0.69 | 63.06 ± 8.99 |
| AA | 96.83 ± 0.07 | 96.38 ± 0.13 | 96.60 ± 0.30 | 96.96 ± 0.15 | 95.18 ± 0.27 | 61.17 ± 5.31 |
| Kappa | 0.9229 ± 0.0008 | 0.9213 ± 0.0042 | 0.9278 ± 0.0041 | 0.9336 ± 0.0014 | 0.8850 ± 0.0076 | 0.5896 ± 0.0969 |
Table 6.
Summation of five experimental results in the confusion matrix for the Indian Pines dataset with a proportion of training data of .
Table 6.
Summation of five experimental results in the confusion matrix for the Indian Pines dataset with a proportion of training data of .
| | | | Predicted Class |
|---|
| | | | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|
| Ground truth class | RBF kernel | C1 | 4608 | 287 | 15 | 15 | 4 | 583 | 1219 | 54 | 0 |
| C2 | 253 | 2376 | 3 | 5 | 0 | 58 | 984 | 261 | 0 |
| C3 | 15 | 11 | 1980 | 88 | 27 | 21 | 12 | 35 | 106 |
| C4 | 6 | 0 | 71 | 3323 | 0 | 11 | 32 | 1 | 21 |
| C5 | 2 | 0 | 9 | 0 | 2259 | 0 | 0 | 0 | 0 |
| C6 | 401 | 65 | 21 | 4 | 2 | 3103 | 989 | 30 | 0 |
| C7 | 960 | 749 | 46 | 55 | 6 | 629 | 8949 | 265 | 1 |
| C8 | 255 | 224 | 9 | 11 | 0 | 236 | 597 | 1483 | 0 |
| C9 | 0 | 0 | 179 | 55 | 0 | 0 | 1 | 1 | 5774 |
| Power-SAM-RBF kernel | C1 | 4529 | 126 | 6 | 18 | 5 | 453 | 1522 | 126 | 0 |
| C2 | 329 | 2095 | 1 | 3 | 0 | 32 | 1155 | 325 | 0 |
| C3 | 8 | 5 | 1794 | 128 | 57 | 9 | 19 | 40 | 235 |
| C4 | 4 | 0 | 53 | 3348 | 12 | 1 | 16 | 9 | 22 |
| C5 | 2 | 0 | 7 | 4 | 2256 | 0 | 1 | 0 | 0 |
| C6 | 336 | 23 | 16 | 5 | 8 | 3171 | 1008 | 48 | 0 |
| C7 | 738 | 288 | 35 | 58 | 25 | 482 | 9907 | 127 | 0 |
| C8 | 468 | 233 | 4 | 5 | 0 | 98 | 767 | 1240 | 0 |
| C9 | 0 | 0 | 43 | 78 | 0 | 0 | 0 | 0 | 5889 |
Table 7.
Summation of five experimental results in the confusion matrix for the Indian Pines dataset with a proportion of training data of .
Table 7.
Summation of five experimental results in the confusion matrix for the Indian Pines dataset with a proportion of training data of .
| | | | Predicted Class |
|---|
| | | | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|
| Ground truth class | RBF kernel | C1 | 4754 | 106 | 4 | 11 | 0 | 245 | 569 | 21 | 0 |
| C2 | 241 | 2392 | 0 | 2 | 0 | 12 | 583 | 90 | 0 |
| C3 | 7 | 3 | 1807 | 20 | 2 | 18 | 28 | 24 | 21 |
| C4 | 5 | 0 | 9 | 2874 | 0 | 2 | 22 | 0 | 8 |
| C5 | 2 | 0 | 4 | 0 | 1901 | 0 | 3 | 0 | 0 |
| C6 | 216 | 30 | 17 | 9 | 0 | 2903 | 714 | 1 | 0 |
| C7 | 632 | 272 | 32 | 31 | 2 | 427 | 8282 | 142 | 0 |
| C8 | 58 | 89 | 11 | 8 | 0 | 30 | 149 | 2025 | 0 |
| C9 | 0 | 0 | 46 | 32 | 0 | 0 | 6 | 0 | 4976 |
| Power-SAM-RBF kernel | C1 | 4682 | 72 | 3 | 13 | 0 | 278 | 591 | 71 | 0 |
| C2 | 178 | 2494 | 0 | 2 | 0 | 10 | 510 | 126 | 0 |
| C3 | 5 | 2 | 1775 | 44 | 5 | 10 | 28 | 23 | 38 |
| C4 | 1 | 0 | 29 | 2864 | 0 | 4 | 6 | 0 | 16 |
| C5 | 0 | 0 | 3 | 6 | 1900 | 1 | 0 | 0 | 0 |
| C6 | 250 | 13 | 11 | 11 | 0 | 3107 | 486 | 12 | 0 |
| C7 | 426 | 144 | 32 | 42 | 3 | 360 | 8710 | 103 | 0 |
| C8 | 137 | 85 | 7 | 5 | 0 | 29 | 201 | 1906 | 0 |
| C9 | 0 | 0 | 20 | 55 | 0 | 0 | 0 | 0 | 4985 |
Table 8.
Similarity () between the spectral signatures of each pair of classes. Note that the high-similarity group is shown in green, the medium-similarity group is shown in yellow, and the low-similarity group is shown in red.
Table 8.
Similarity () between the spectral signatures of each pair of classes. Note that the high-similarity group is shown in green, the medium-similarity group is shown in yellow, and the low-similarity group is shown in red.
| | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|
| C1 | - | 1.7 | 11.4 | 7.9 | 5.0 | 2.6 | 1.7 | 2.5 | 13.2 |
| C2 | - | - | 11.0 | 7.4 | 4.8 | 1.0 | 0.6 | 0.9 | 12.7 |
| C3 | - | - | - | 4.1 | 6.8 | 11.5 | 11.4 | 11.1 | 2.1 |
| C4 | - | - | - | - | 4.6 | 7.9 | 7.9 | 7.5 | 5.6 |
| C5 | - | - | - | - | - | 5.4 | 5.2 | 4.9 | 8.6 |
| C6 | - | - | - | - | - | - | 1.1 | 0.6 | 13.3 |
| C7 | - | - | - | - | - | - | - | 1.1 | 13.3 |
| C8 | - | - | - | - | - | - | - | - | 12.8 |
| C9 | - | - | - | - | - | - | - | - | - |
Table 9.
Ground truth classes for the Indian Pines dataset and their corresponding numbers of samples.
Table 9.
Ground truth classes for the Indian Pines dataset and their corresponding numbers of samples.
| Class | Samples | |
|---|
| C1 | Corn-notill | 1428 |
| C2 | Corn-mintill | 830 |
| C3 | Grass-pasture | 483 |
| C4 | Grass-trees | 730 |
| C5 | Hay-windrowed | 478 |
| C6 | Soybean-notill | 972 |
| C7 | Soybean-mintill | 2455 |
| C8 | Soybean-clean | 593 |
| C9 | Woods | 1265 |
Table 10.
Average product accuracy (PA) for each class with the RBF and Power-SAM-RBF kernels with and proportions of training data.
Table 10.
Average product accuracy (PA) for each class with the RBF and Power-SAM-RBF kernels with and proportions of training data.
| Class | RBF Kernel | Power-SAM-RBF Kernel |
|---|
| 5% | 20% | 5% | 20% |
|---|
| C1 | 67.91 | 83.26 | 66.75 | 82.00 |
| C2 | 60.30 | 72.05 | 53.17 | 75.12 |
| C3 | 86.27 | 93.63 | 78.17 | 92.00 |
| C4 | 95.90 | 98.42 | 96.62 | 98.08 |
| C5 | 99.52 | 99.53 | 99.38 | 99.48 |
| C6 | 67.24 | 74.63 | 68.71 | 79.87 |
| C7 | 76.75 | 84.34 | 84.97 | 88.70 |
| C8 | 52.68 | 85.44 | 44.05 | 80.42 |
| C9 | 96.07 | 98.34 | 97.99 | 98.52 |