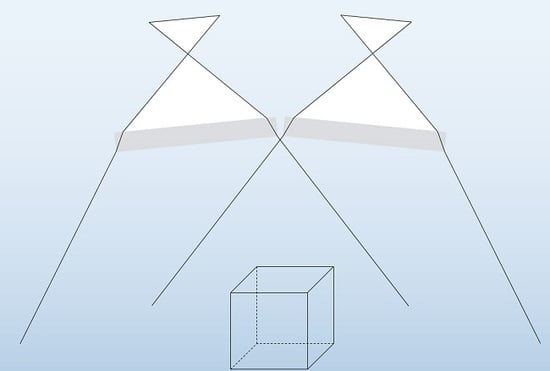
Impact of Stereo Camera Calibration to Object Accuracy in Multimedia Photogrammetry
Abstract
:1. Introduction
2. Calibration Techniques in Multimedia Photogrammetry
2.1. Planar Interfaces
2.2. Hemispherical Interfaces
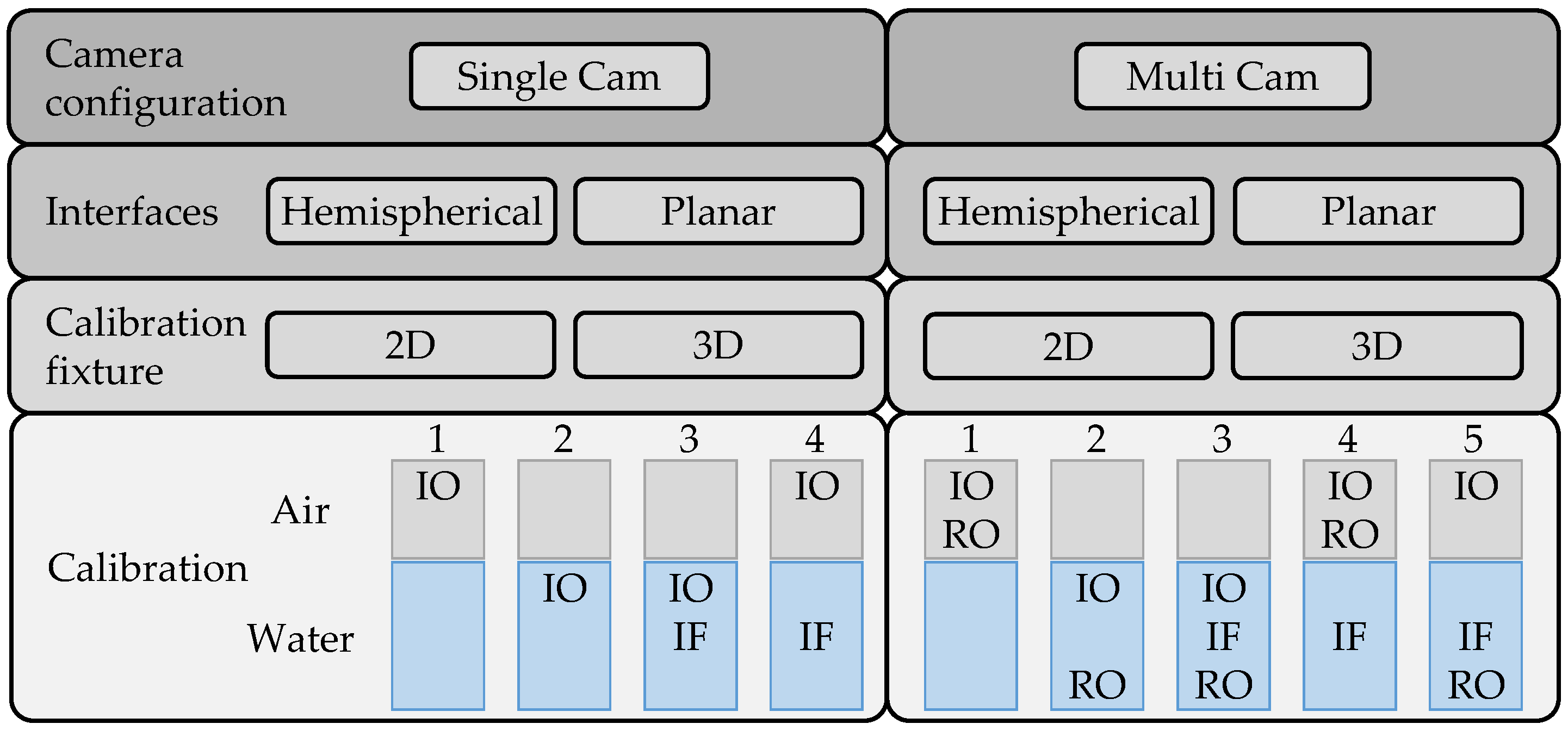
2.3. System Configurations and Calibration Strategies
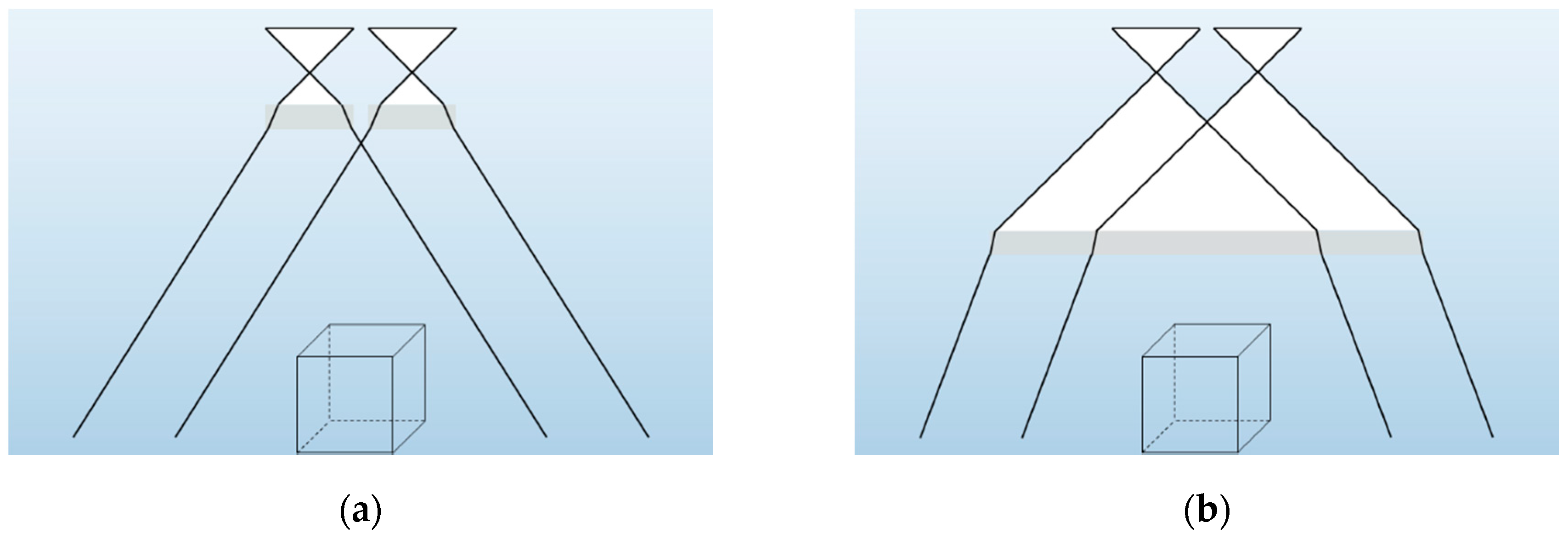
2.4. Calibration Fixtures
3. Synthetic Datasets
3.1. Notation and Assumptions
- Isotropic glass interface of 10 mm thickness
- Refractive index of air = 1.000
- Refractive index of water = 1.3318
- Refractive index of glass = 1.490
- Perpendicular arrangement of the interface with respect to the optical axis
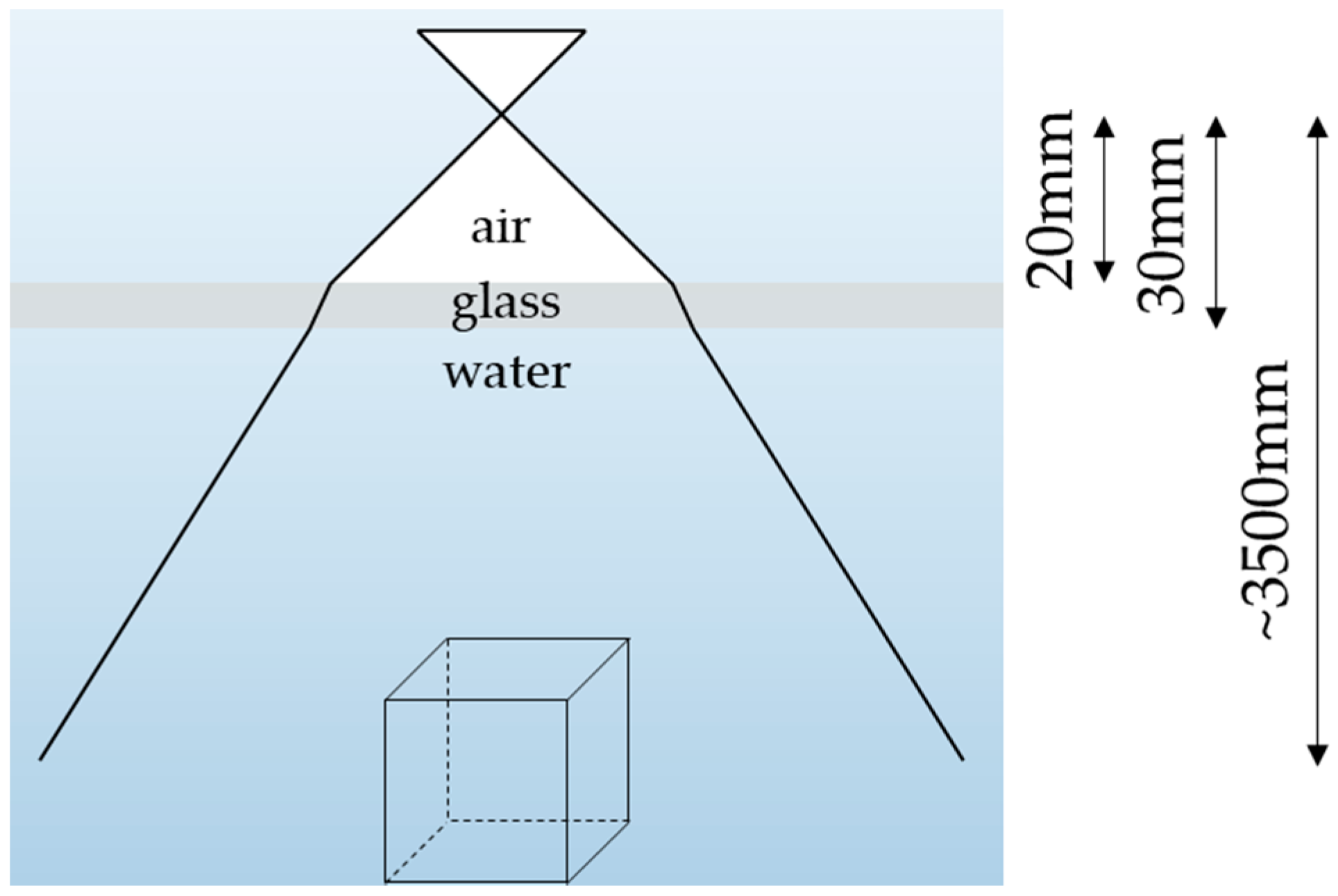
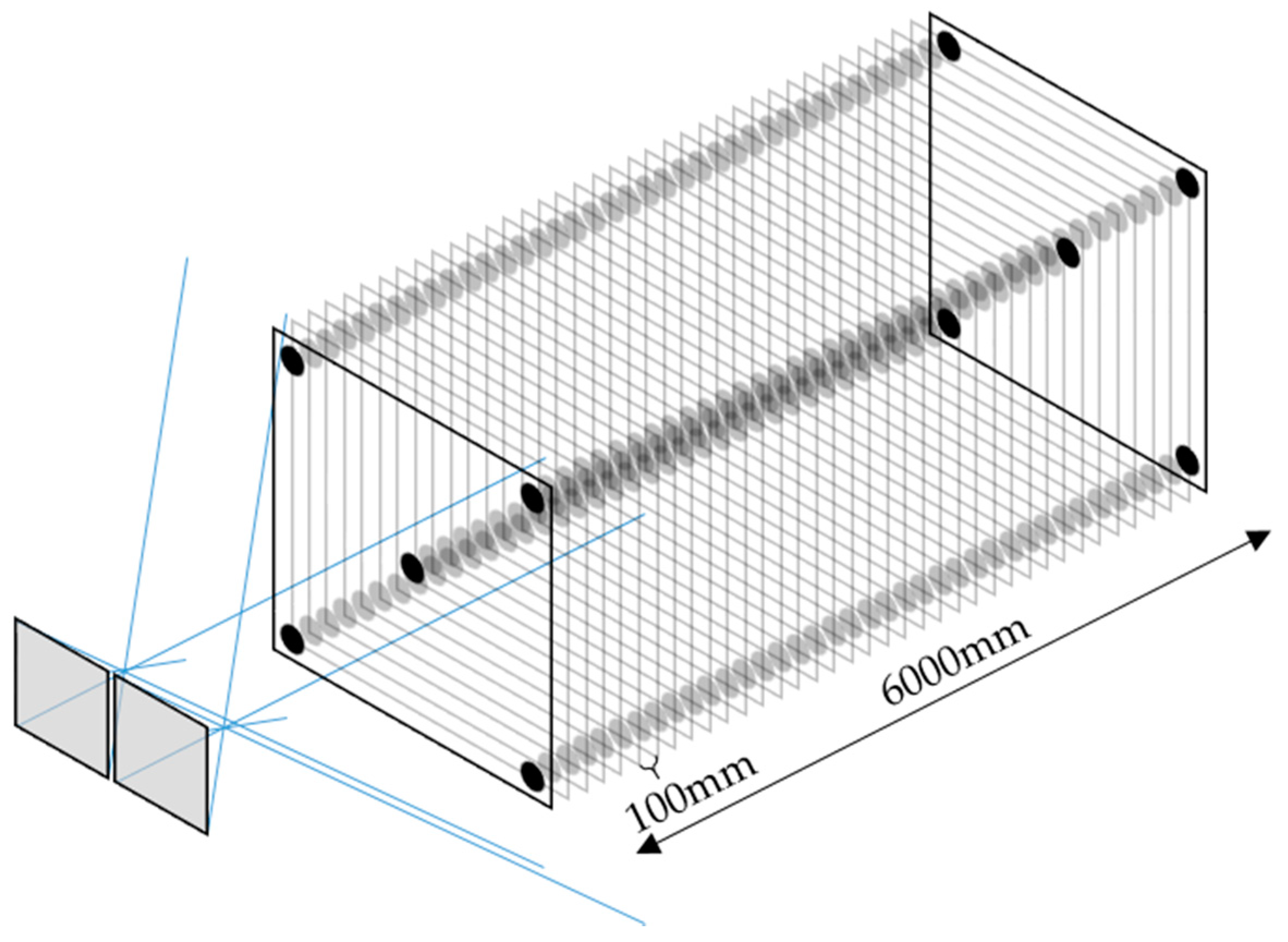
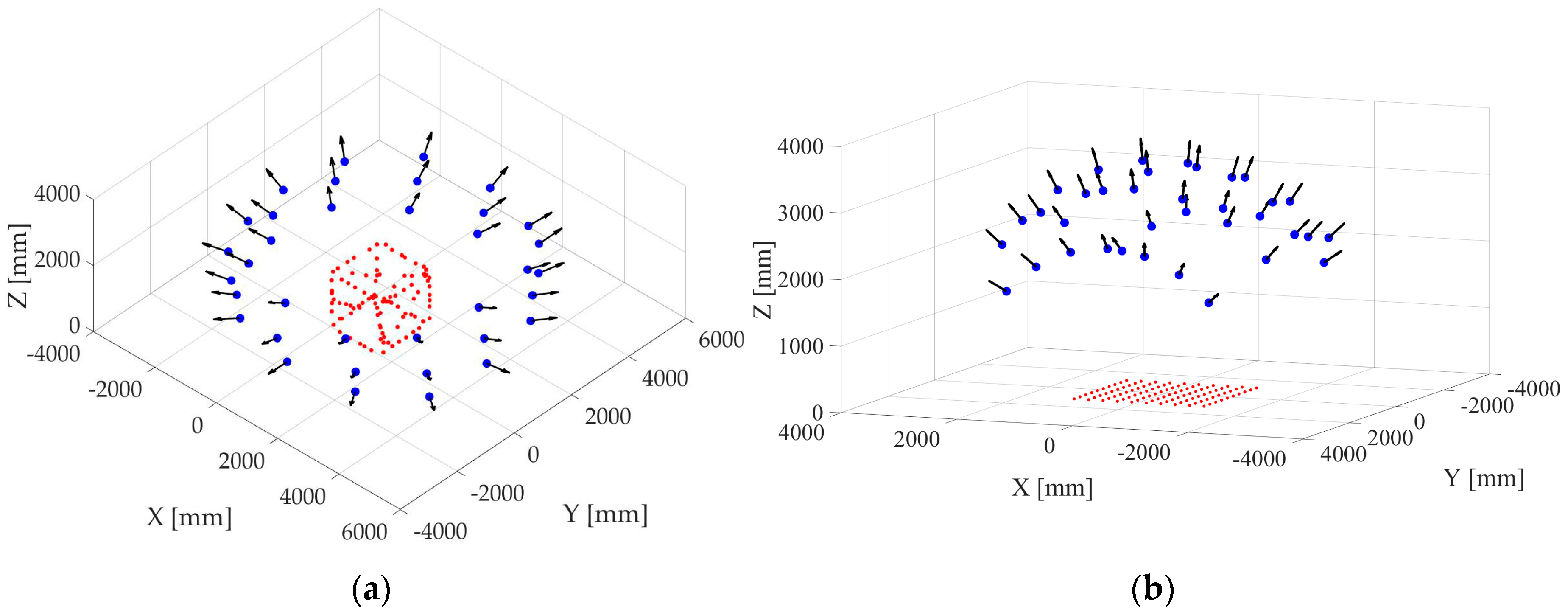
3.2. Dataset Cube
3.3. Dataset HS
3.4. Variation of Convergence
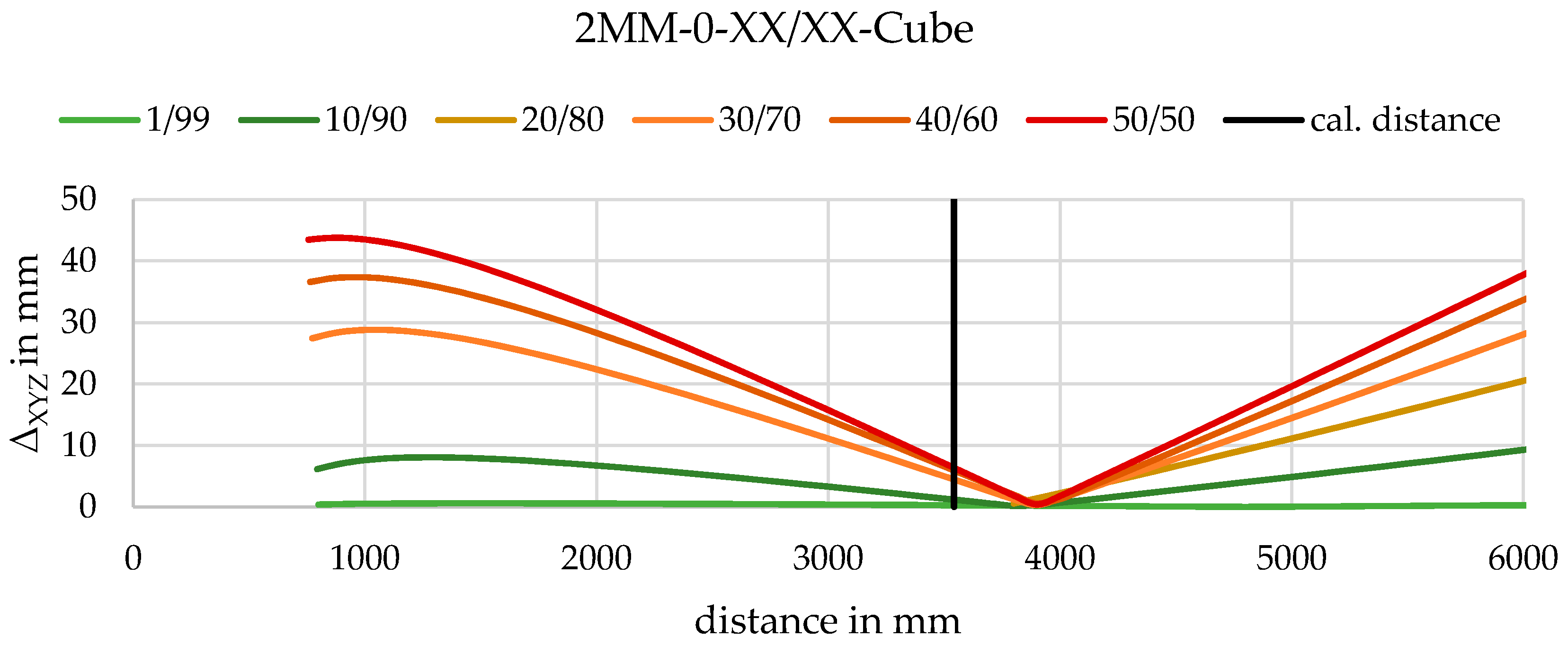
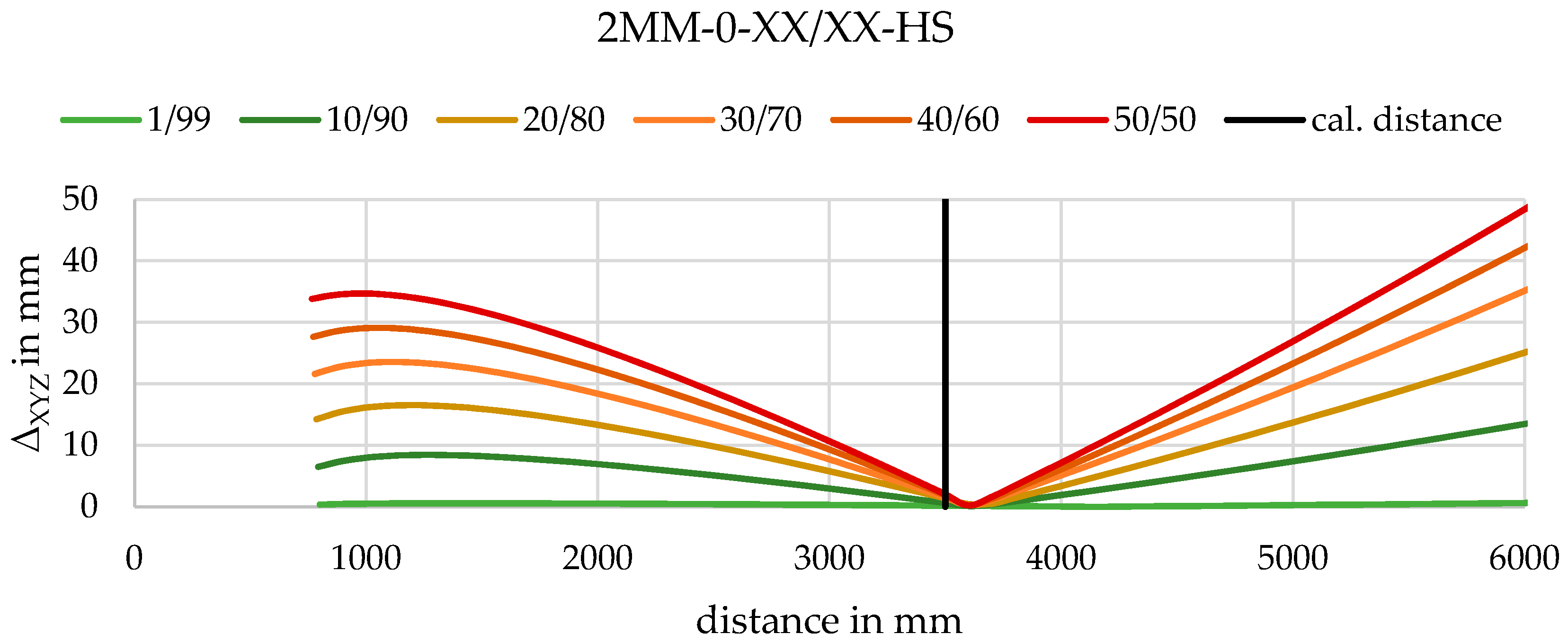
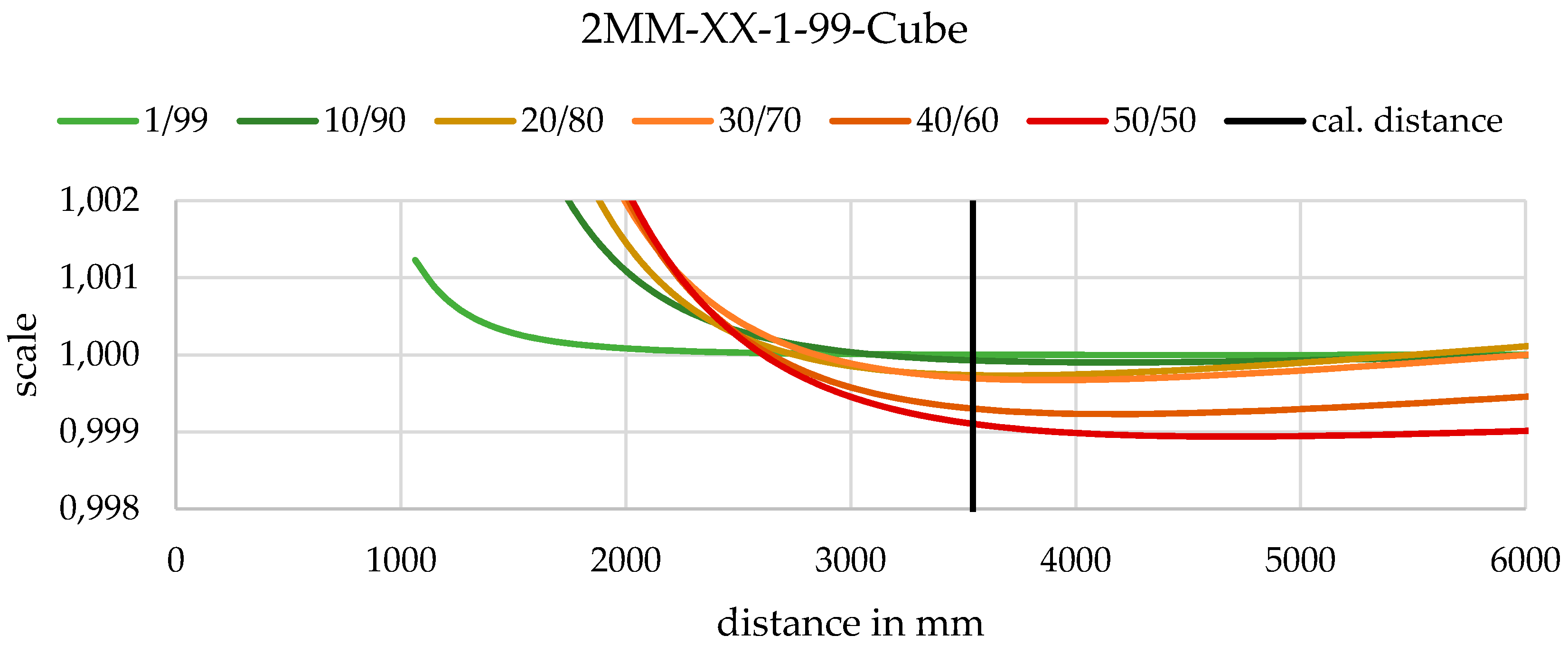
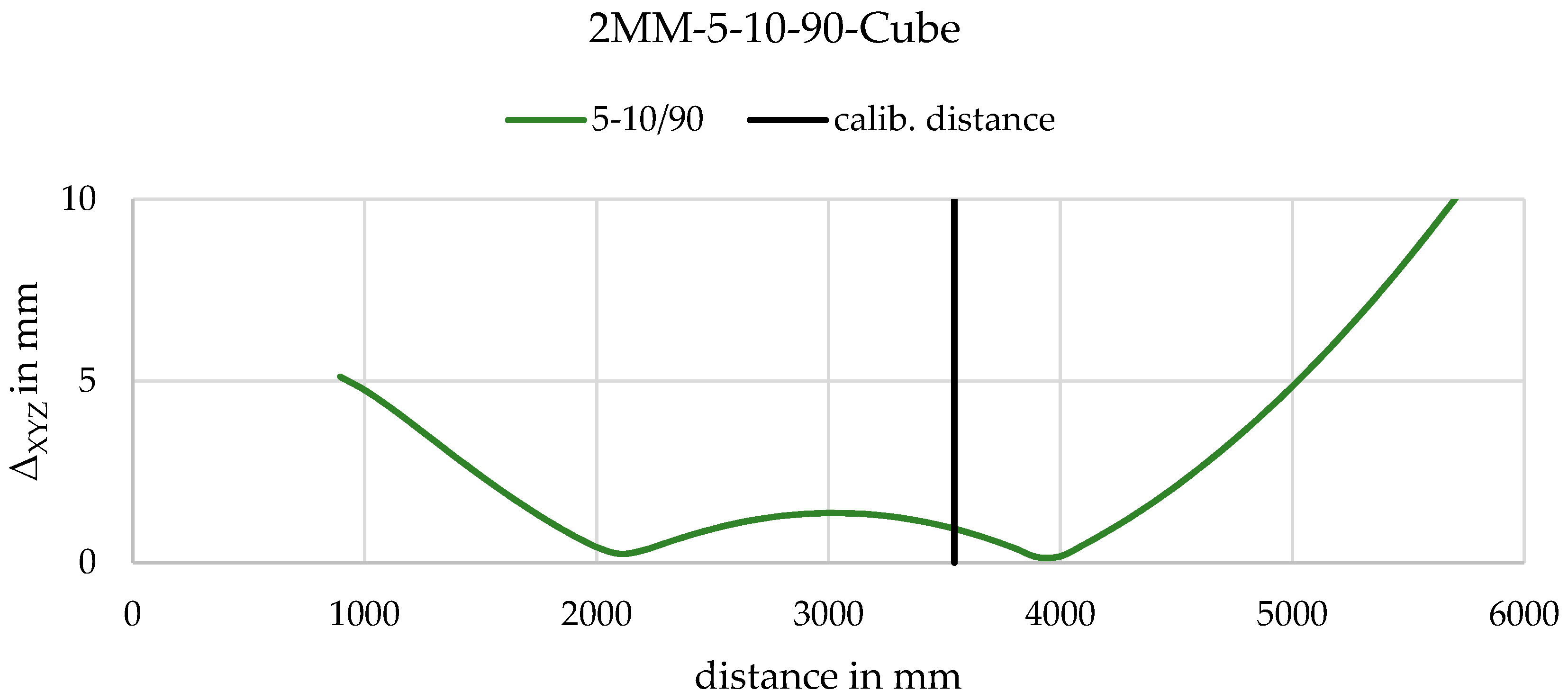
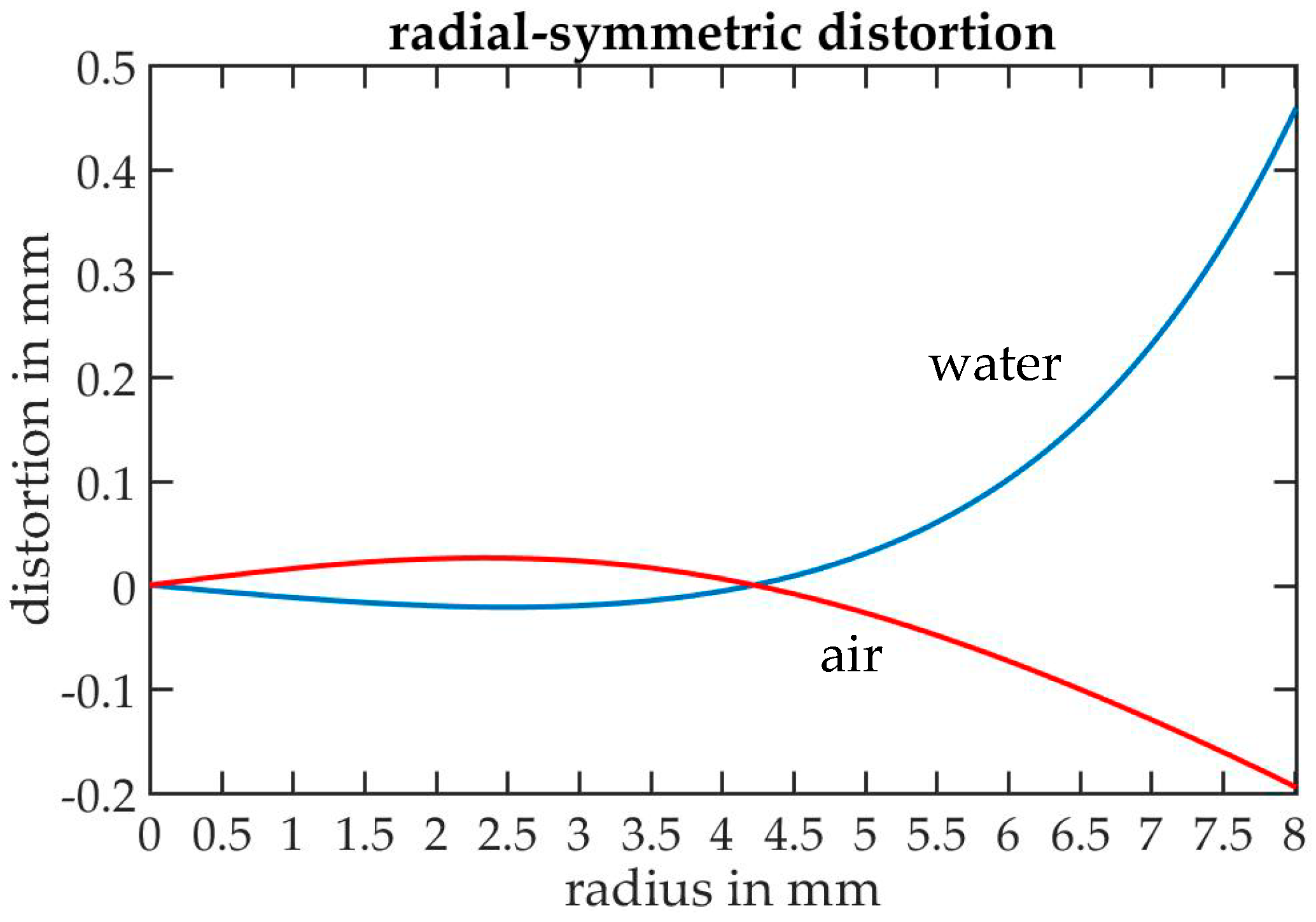
3.5. Variation of Air/Water Ratio
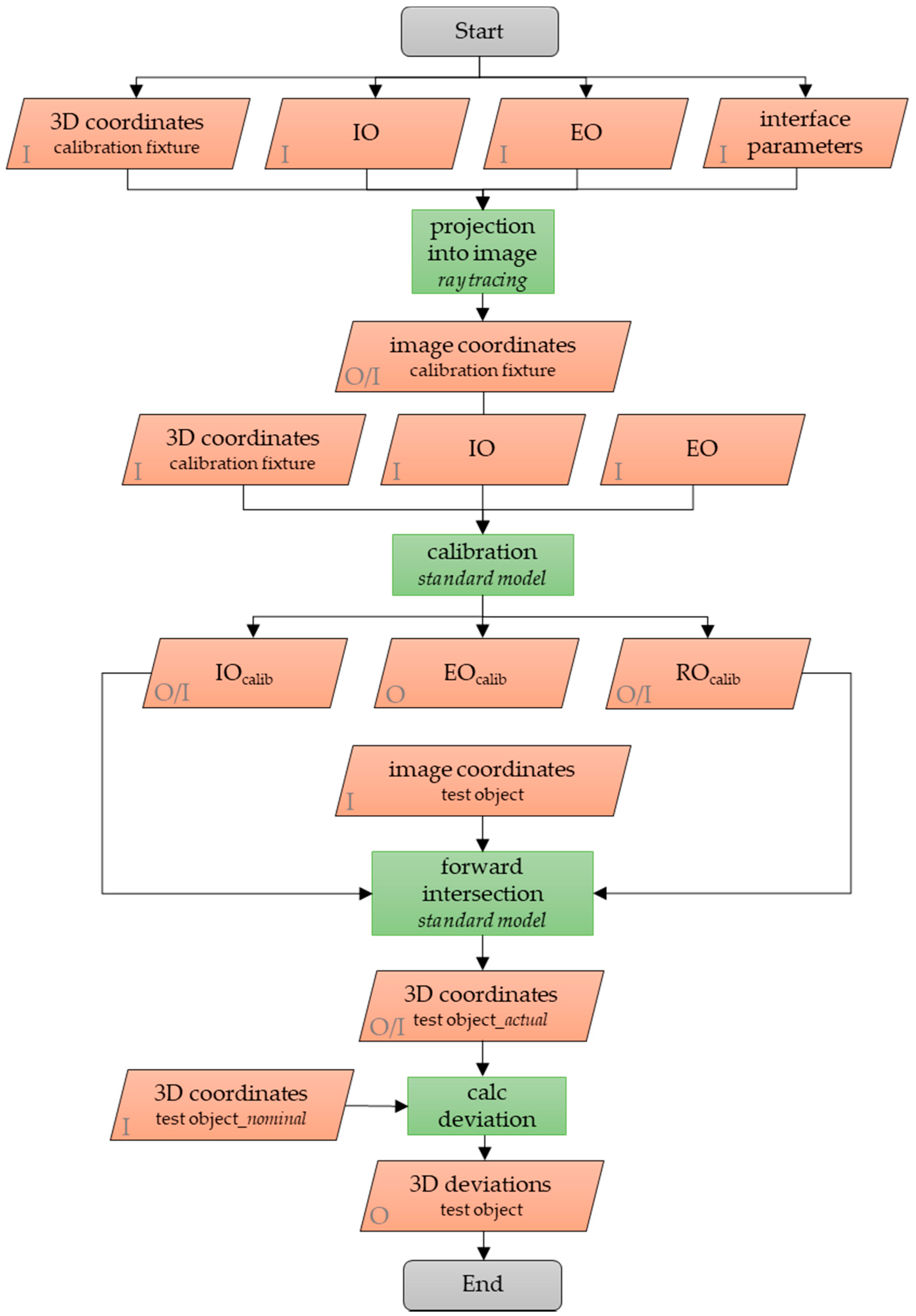
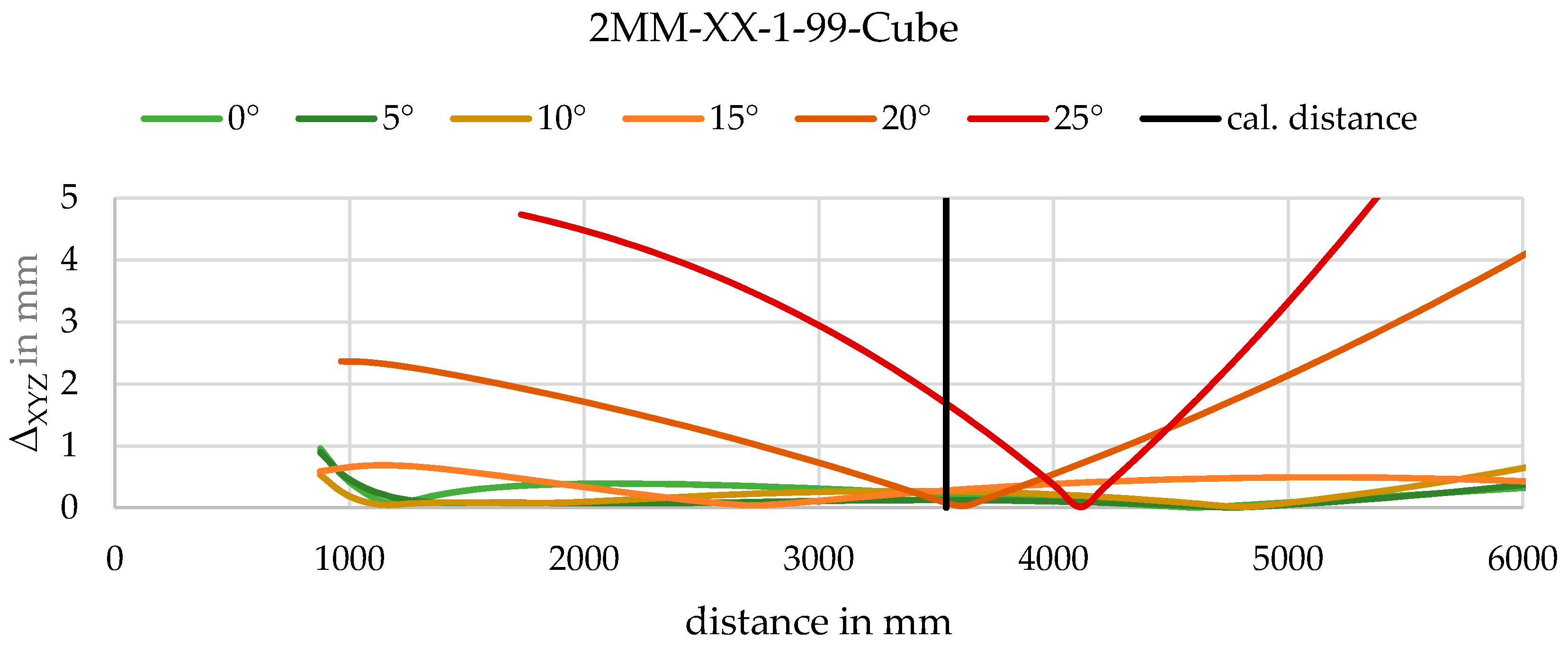
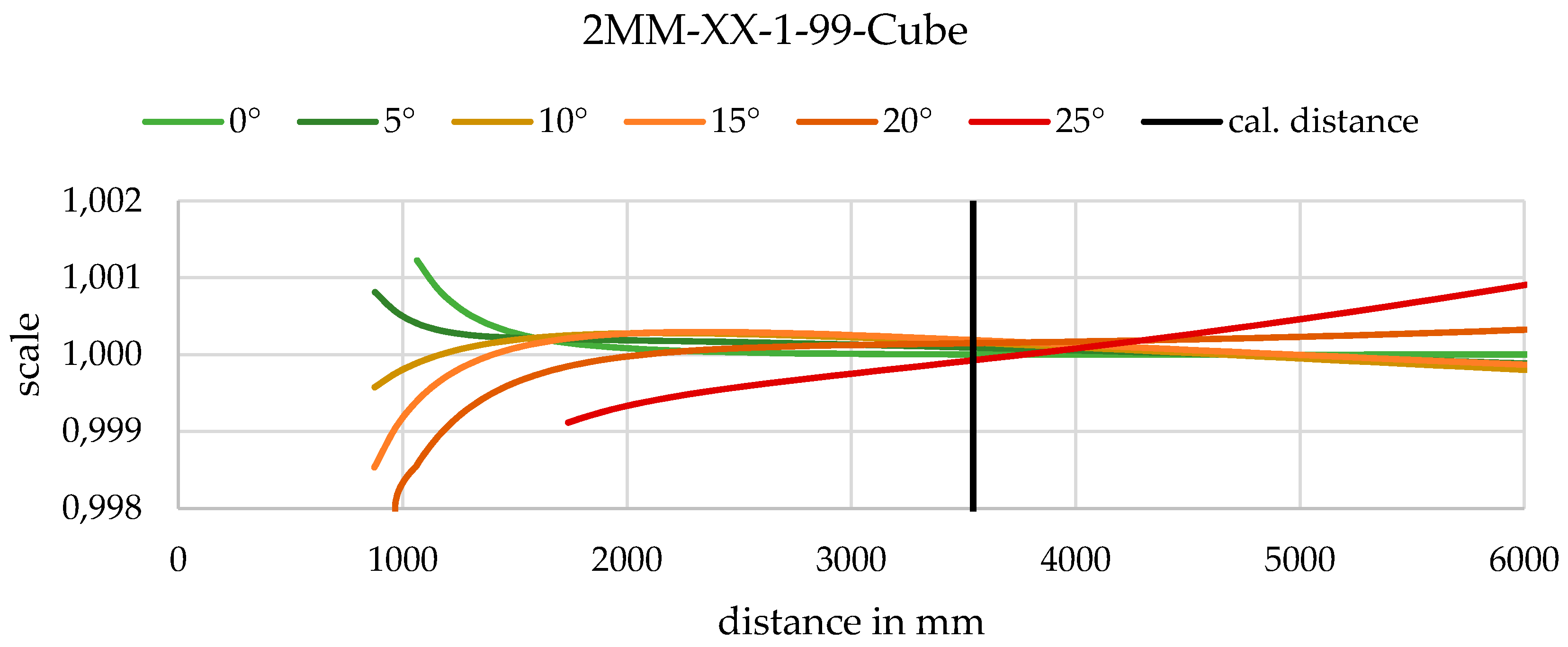
3.6. Quality Evaluation in Object Space via Forward Intersection
4. Analysis of Calibration and Orientation for Planar Interfaces in Implicit Form
4.1. Single-Camera Bundle Adjustment
4.2. Stereo Camera Bundle Adjustment
- 2SM-0°-1/99
- 2MM-0°-1/99
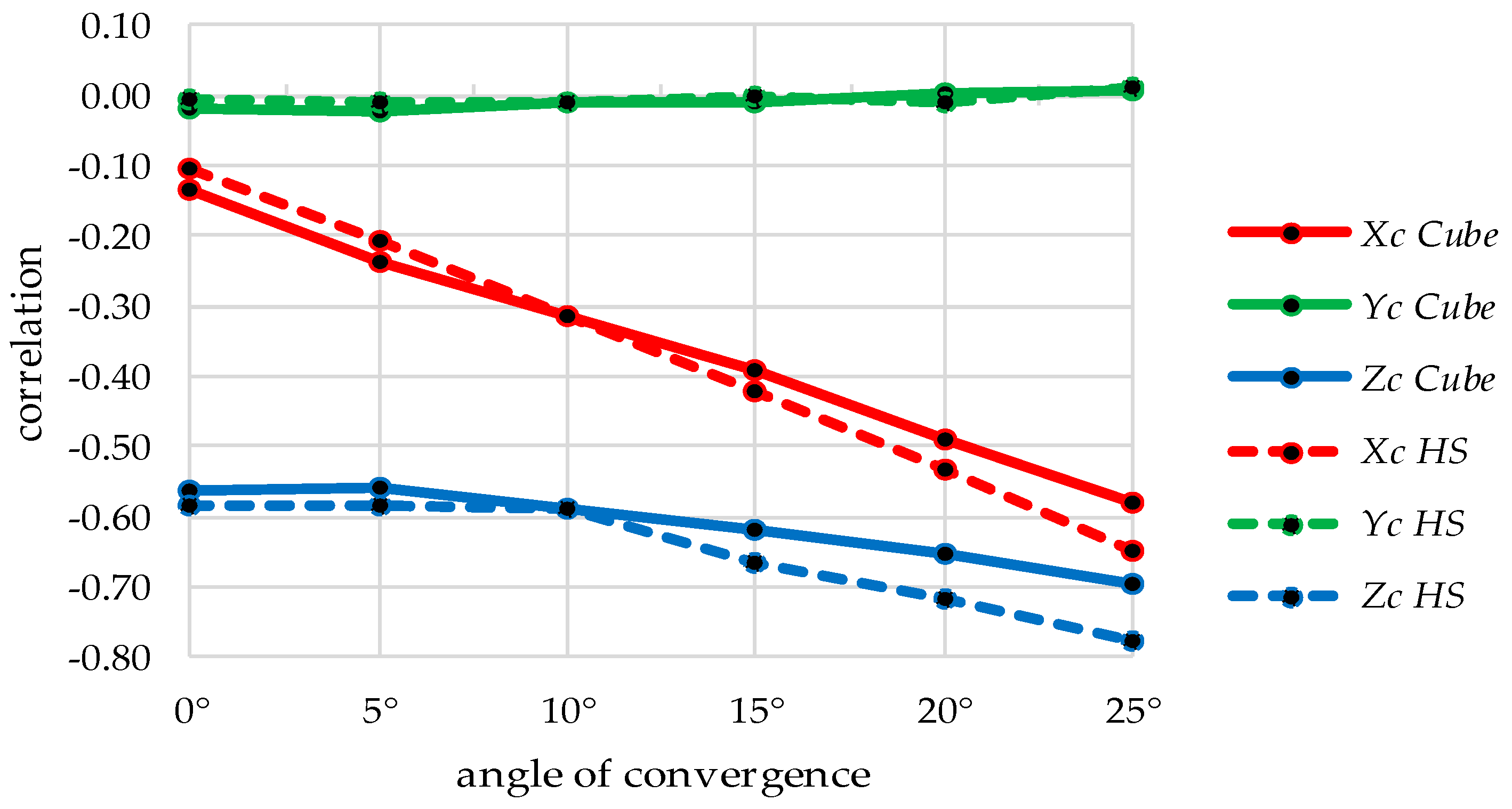
4.2.1. Variation of Convergence
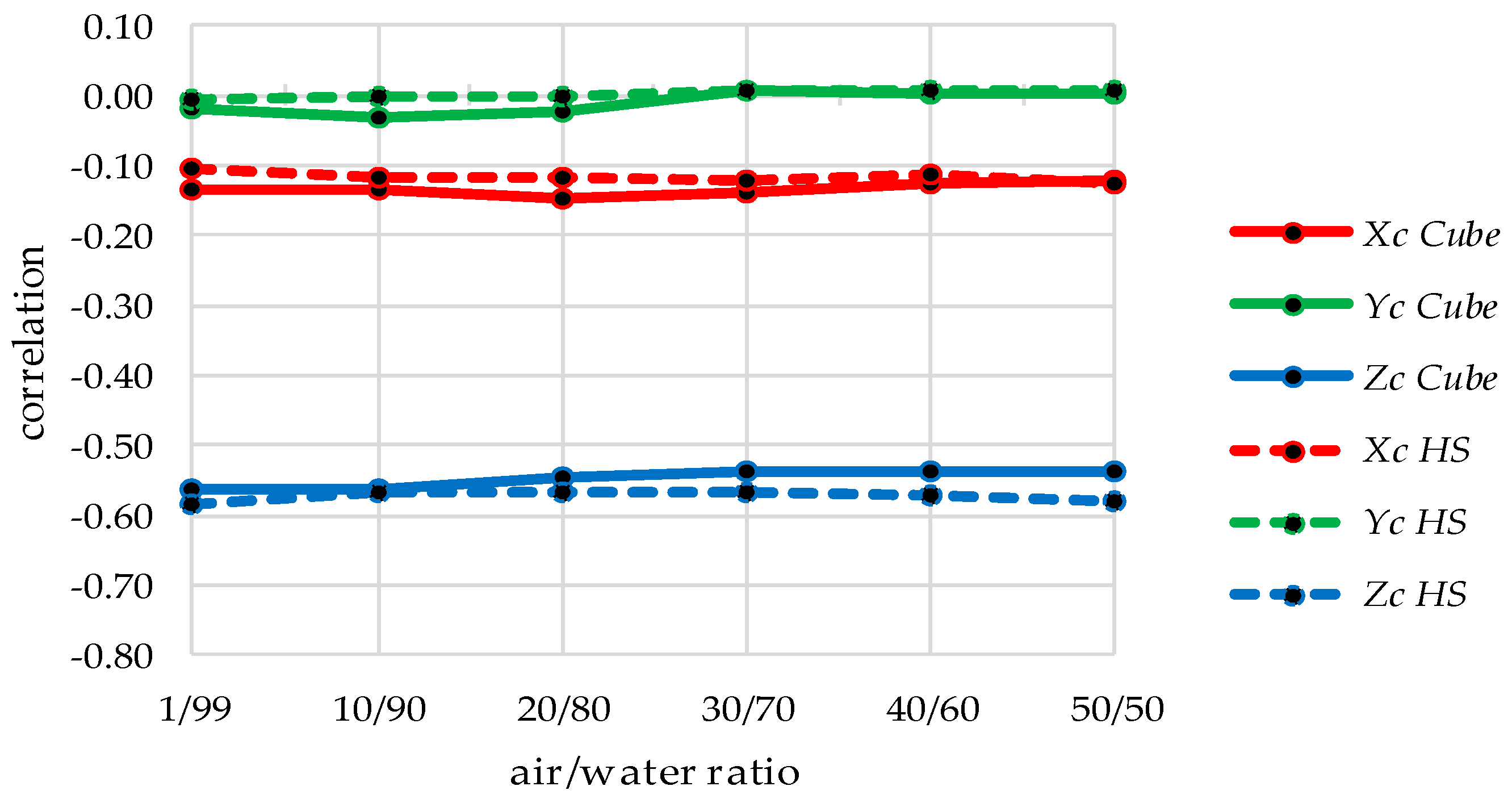
4.2.2. Variation of Air/Water Ratio
4.3. Assessment of Simulated Data
5. Analysis of Calibration and Orientation for Planar Interfaces in Explicit Form
5.1. Explicit Modelling
| nair | = refractive index of air |
| nglass | = refractive index of glass |
| nwater | = refractive index of water |
| N1x, N1y, N1z, d | = plane parameters of interface 1 |
| N2x, N2y, N2z, d2 | = plane parameters of interface 2 |
| X0, Y0, Z0 | = translation of the relative orientation |
| ω, φ, κ | = rotation of relative orientation |
5.2. Synthetic Data
| nwater | ± 0.01 |
| Image coordinates | ± 1 pixel |
| Translation of exterior orientations | ± 200 mm |
| Rotation of exterior orientations | ± 1° |
6. Experiments
6.1. Description of the Experiments
6.2. Calibration Parameters
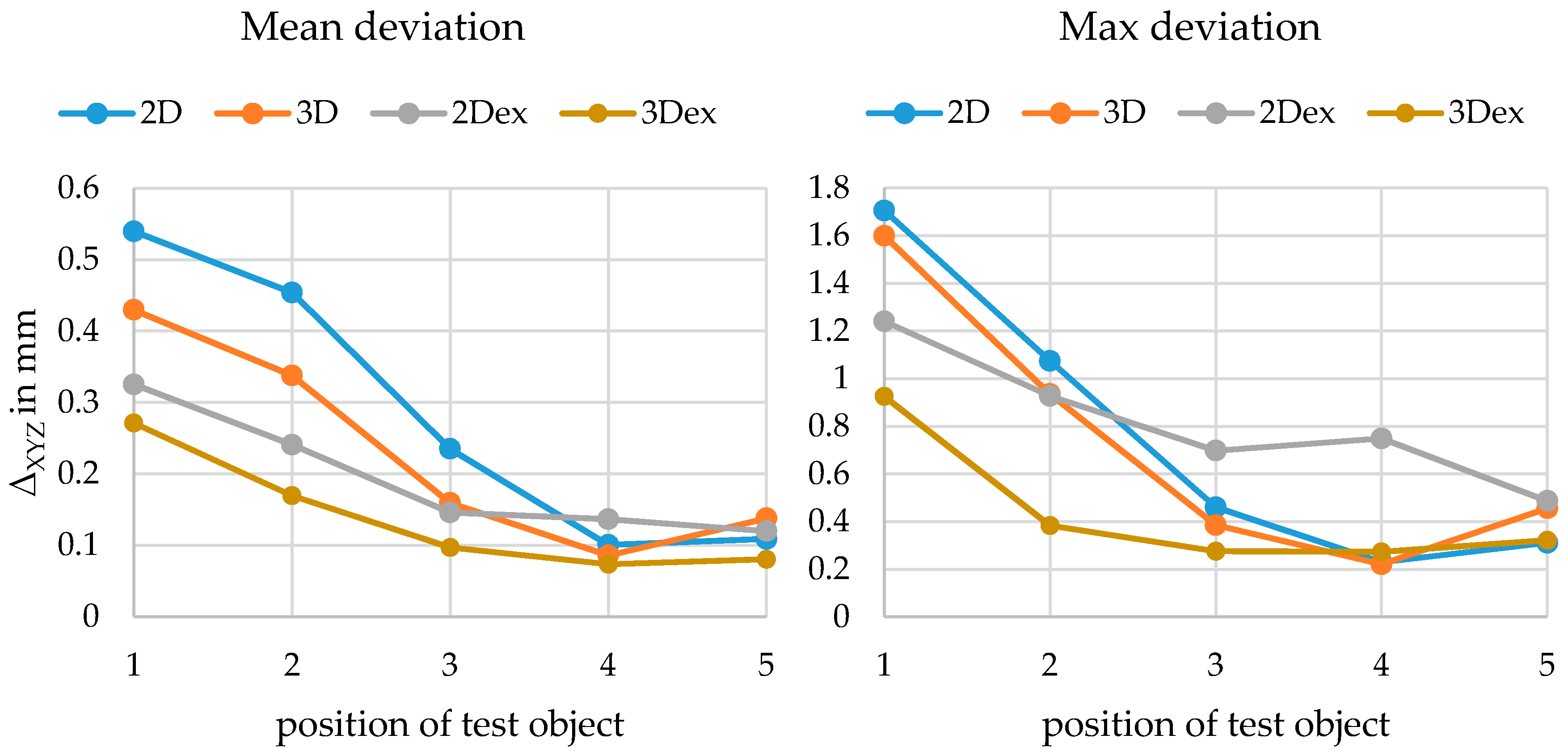
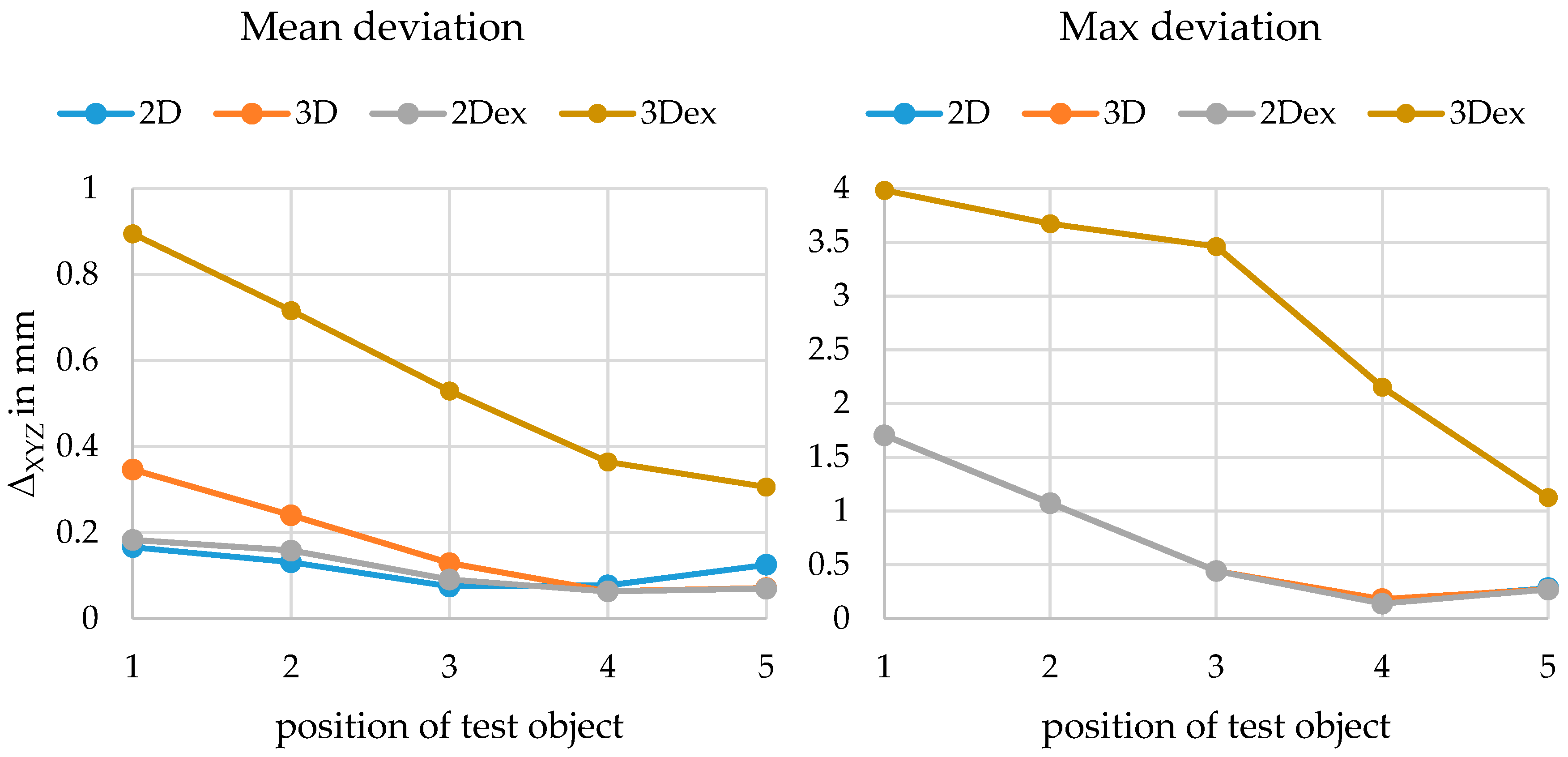
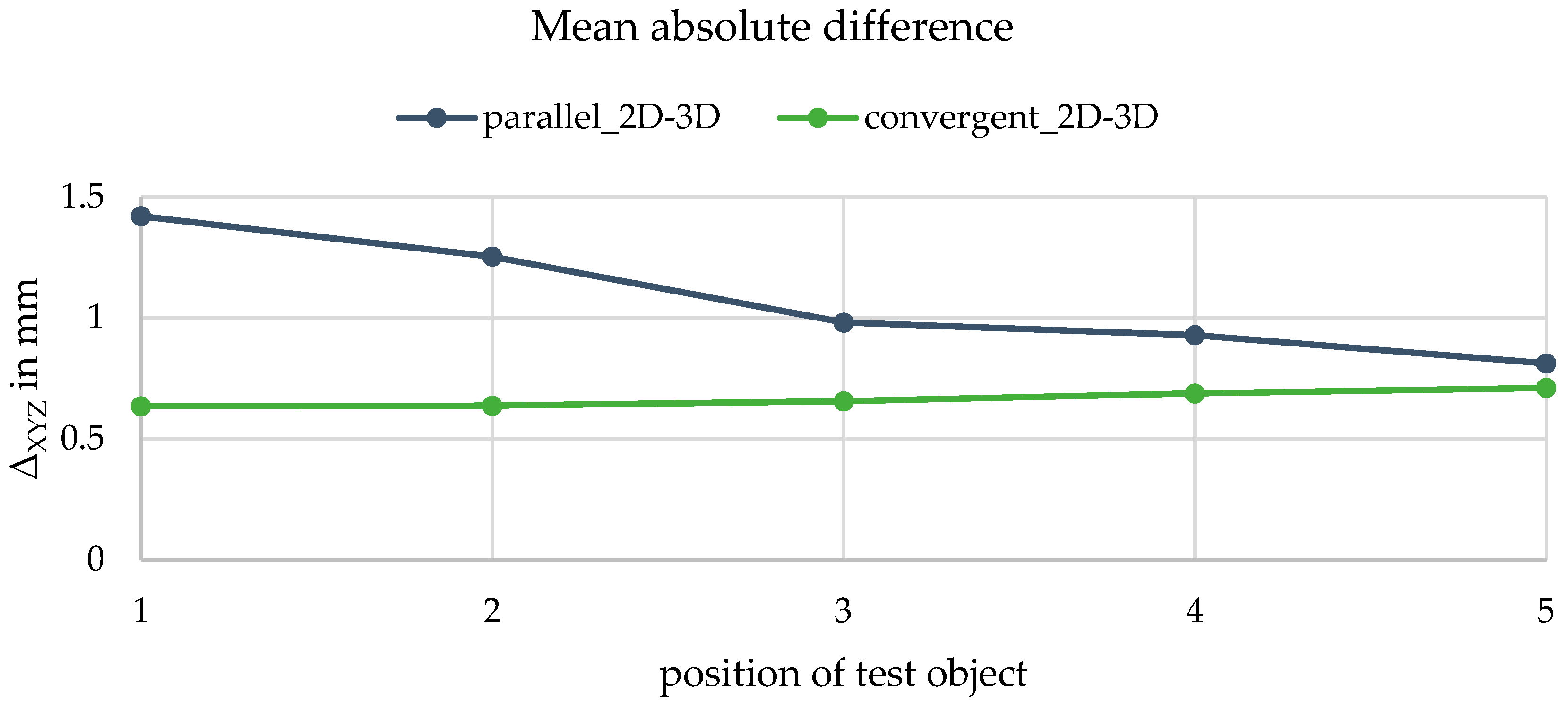
6.3. Deviations in Object Space
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- kbvresearch.com. Underwater Camera Market Size. Available online: https://www.kbvresearch.com/underwater-camera-market-size/ (accessed on 28 November 2019).
- Datainsightspartner.com. Underwater Drones Market Size Estimation, in-Depth Insights, Historical Data, Price Trend, Competitive Market Share & Forecast 2019–2027. Available online: https://datainsightspartner.com/report/underwater-drones-market/61 (accessed on 28 November 2019).
- Shortis, M.; Ravanbakskh, M.; Shaifat, F.; Harvey, E.S.; Mian, A.; Seager, J.W.; Culverhouse, P.F.; Cline, D.E.; Edgington, D.R. A review of techniques for the identification and measurement of fish in underwater stereo-video image sequences. In SPIE Optical Metrology; Remondino, F., Shortis, M.R., Beyerer, J., Puente León, F., Eds.; SPIE: Munich, Germany, 2013. [Google Scholar]
- Torisawa, S.; Kadota, M.; Komeyama, K.; Suzuki, K.; Takagi, T. A digital stereo-video camera system for three-dimensional monitoring of free-swimming Pacific bluefin tuna, Thunnus orientalis, cultured in a net cage. Aquat. Living Resour. 2011, 24, 107–112. [Google Scholar] [CrossRef] [Green Version]
- Menna, F.; Nocerino, E.; Nawaf, M.M.; Seinturier, J.; Torresani, A.; Drap, P.; Remondino, F.; Chemisky, B. Towards real-time underwater photogrammetry for subsea metrology applications. In OCEANS 2019; IEEE: Marseille, France, 2019; pp. 1–10. [Google Scholar]
- Bruno, F.; Lagudi, A.; Collina, M.; Medaglia, S.; Davidde Petriaggi, B.; Petriaggi, R.; Ricci, S.; Sacco Perasso, C. Documentation and monitoring of underwater archaeological sites using 3d imaging techniques: The case study of the “nymphaeum of punta epitaffio” (baiae, naples). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W10, 53–59. [Google Scholar] [CrossRef] [Green Version]
- Costa, E. The progress of survey techniques in underwater sites: The case study of cape stoba shipwreck. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W10, 69–75. [Google Scholar] [CrossRef] [Green Version]
- Kahmen, O.; Rofallski, R.; Conen, N.; Luhmann, T. On scale definition within calibration of multi-camera systems in multimedia photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W10, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Shortis, M. Calibration Techniques for Accurate Measurements by Underwater Camera Systems. Sensors (Basel) 2015, 15, 30810–30826. [Google Scholar] [CrossRef] [Green Version]
- Boutros, N.; Shortis, M.R.; Harvey, E.S. A comparison of calibration methods and system configurations of underwater stereo-video systems for applications in marine ecology. Limnol. Oceanogr. Methods 2015, 13, 224–236. [Google Scholar] [CrossRef]
- Massot-Campos, M.; Oliver-Codina, G. Optical Sensors and Methods for Underwater 3D Reconstruction. Sensors (Basel) 2015, 15, 31525–31557. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Höhle, J. Zur Theorie und Praxis der Unterwasser-Photogrammetrie; Deutsche Geodätische Kommission: München, Germany, 1971. [Google Scholar]
- Maas, H.-G. Digitale Photogrammetrie in der Dreidimensionalen Strömungsmesstechnik. Ph.D. Thesis, ETH Zürich—Dissertation Nr. 9665, Zürich, Switzerland, 1992. [Google Scholar]
- Mandlburger, G. A case study on through-water dense image matching. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-2, 659–666. [Google Scholar] [CrossRef] [Green Version]
- Brown, D.C. Close-Range Camera Calibration. Photogramm. Eng. 1971, 37, 855–866. [Google Scholar]
- Kotowski, R. Zur Berücksichtigung Lichtbrechender Flächen im Strahlenbündel; Zugl.: Bonn, Univ., Diss., 1986; Beck: München, Germany, 1987; ISBN 3769693795. [Google Scholar]
- Bräuer-Burchardt, C.; Heinze, M.; Schmidt, I.; Kühmstedt, P.; Notni, G. Compact handheld fringe projection based underwater 3d-scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W5, 33–39. [Google Scholar] [CrossRef] [Green Version]
- Maas, H.-G. A modular geometric model for underwater photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W5, 139–141. [Google Scholar] [CrossRef] [Green Version]
- Mulsow, C. A flexible multi-media bundle approach. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, XXXVIII/5, 472–477. [Google Scholar]
- Menna, F.; Nocerino, E.; Remondino, F. Flat versus hemispherical dome ports in underwater photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W3, 481–487. [Google Scholar] [CrossRef] [Green Version]
- Nocerino, E.; Menna, F.; Fassi, F.; Remondino, F. Underwater calibration of dome port pressure housings. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XL-3/W4, 127–134. [Google Scholar] [CrossRef] [Green Version]
- Menna, F.; Nocerino, E.; Fassi, F.; Remondino, F. Geometric and Optic Characterization of a Hemispherical Dome Port for Underwater Photogrammetry. Sensors (Basel) 2016, 16, 48. [Google Scholar] [CrossRef] [Green Version]
- Menna, F.; Nocerino, E.; Remondino, F. Optical aberrations in underwater photogrammetry with flat and hemispherical dome ports. In Videometrics, Range Imaging, and Applications XIV; SPIE: Munich, Germany, 2017; pp. 26–27. [Google Scholar]
- Shortis, M.; Harvey, E.; Seager, J. A Review of the Status and Trends in Underwater Videometric Measurement. In Proceedings of the SPIE Conference 6491, Videometrics IX, IS&T/SPIE Electronic Imaging, San Jose, CA, USA, 28 January–1 February 2007. Invited paper. [Google Scholar]
- Menna, F.; Nocerino, E.; Troisi, S.; Remondino, F. A photogrammetric approach to survey floating and semi-submerged objects. In SPIE Optical Metrology; Remondino, F., Shortis, M.R., Beyerer, J., Puente León, F., Eds.; SPIE: Munich, Germany, 2013; 87910H. [Google Scholar]
- Johnson-Roberson, M.; Pizarro, O.; Williams, S.B.; Mahon, I. Generation and visualization of large-scale three-dimensional reconstructions from underwater robotic surveys. J. Field Robotics 2010, 27, 21–51. [Google Scholar] [CrossRef]
- Rofallski, R.; Luhmann, T. Fusion von Sensoren mit optischer 3D-Messtechnik zur Positionierung von Unterwasserfahrzeugen. In Hydrographie 2018, Trend zu Unbemannten Messsystemen; Wißner-Verlag: Augsburg, Germany, 2018; pp. 223–234. ISBN 978-3-95786-165-8. [Google Scholar]
- Luhmann, T.; Fraser, C.; Maas, H.-G. Sensor modelling and camera calibration for close-range photogrammetry. ISPRS J. Photogramm. Remote Sens. 2016, 37–46. [Google Scholar] [CrossRef]
- Wester-Ebbinghaus, W. Verfahren zur Feldkalibrierung von photogrammetrischen Aufnahmekammern im Nahbereich. In Kammerkalibrierung in der Photogrammetrischen Praxis; Reihe, B., Kupfer, G., Wester-Ebbinghaus, W., Eds.; Heft Nr. 275; Deutsche Geodätische Kommission: München, Germany, 1985; pp. 106–114. [Google Scholar]
- Luhmann, T. Erweiterte Verfahren zur Geometrischen Kamerakalibrierung in der Nahbereichsphotogrammetrie; Beck: München, Germany, 2010; ISBN 978-3-7696-5057-0. [Google Scholar]
- Bruno, F.; Bianco, G.; Muzzupappa, M.; Barone, S.; Razionale, A.V. Experimentation of structured light and stereo vision for underwater 3D reconstruction. ISPRS J. Photogramm. Remote Sens. 2011, 66, 508–518. [Google Scholar] [CrossRef]
- Drap, P.; Seinturier, J.; Hijazi, B.; Merad, D.; Boi, J.-M.; Chemisky, B.; Seguin, E.; Long, L. The ROV 3D Project. J. Comput. Cult. Herit. 2015, 8, 1–24. [Google Scholar] [CrossRef]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging, 3rd ed.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2020; ISBN 9783110607246. [Google Scholar]
- Wester-Ebbinghaus, W. Einzelstandpunkt-Selbstkalibrierung. Ein Beitrag zur Feldkalibrierung von Aufnahmekammern; Zugl.: Bonn, Univ., Habil.-Schr., 1982; Beck: München, Germany, 1983; ISBN 3769693396. [Google Scholar]
- Ekkel, T.; Schmik, J.; Luhmann, T.; Hastedt, H. Precise laser-based optical 3d measurement of welding seams under water. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W5, 117–122. [Google Scholar] [CrossRef]
- VDI. VDI/VDE. 2634.1: Optical 3-D Measuring Systems—Imaging Systems with Point-by-Point Probing; VDI: Düsseldorf, Geramny, 2002. [Google Scholar]
- Costa, C.; Loy, A.; Cataudella, S.; Davis, D.; Scardi, M. Extracting fish size using dual underwater cameras. Aquac. Eng. 2006, 35, 218–227. [Google Scholar] [CrossRef]
- Buschinelli, P.D.V.; Matos, G.; Pinto, T.; Albertazzi, A. Underwater 3D shape measurement using inverse triangulation through two flat refractive surfaces. In OCEANS 2016 MTS/IEEE, Monterey, CA, USA, 19–23 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–7. ISBN 978-1-5090-1537-5. [Google Scholar]
- Lavest, J.M.; Rives, G.; Laprest, J.T. Dry camera calibration for underwater applications. Mach. Vis. Appl. 2003, 13, 245–253. [Google Scholar] [CrossRef]
- Rahman, T.; Anderson, J.; Winger, P.; Krouglicof, N. Calibration of an Underwater Stereoscopic Vision System. In 2013 OCEANS—San Diego; IEEE: San Diego, CA, USA, 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Agrafiotis, P.; Georgopoulos, A. Camera constant in the case of two media photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W5, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Sedlazeck, A.; Koch, R. Calibration of Housing Parameters for Underwater Stereo-Camera Rigs. In British Machine Vision Conference 2011; Hoey, J., McKenna, S., Trucco, E., Zhang, J., Eds.; BMVA Press: Dundee, UK, 2011; pp. 118.1–118.11. [Google Scholar]
- Sedlazeck, A.; Koch, R. Perspective and Non-perspective Camera Models in Underwater Imaging—Overview and Error Analysis. In Outdoor and Large-Scale Real-World Scene Analysis; Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Pandu Rangan, C., Steffen, B., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 212–242. ISBN 978-3-642-34090-1. [Google Scholar]
- Maas, H.-G. On the Accuracy Potential in Underwater/Multimedia Photogrammetry. Sensors (Basel) 2015, 15, 18140–18152. [Google Scholar] [CrossRef] [PubMed]

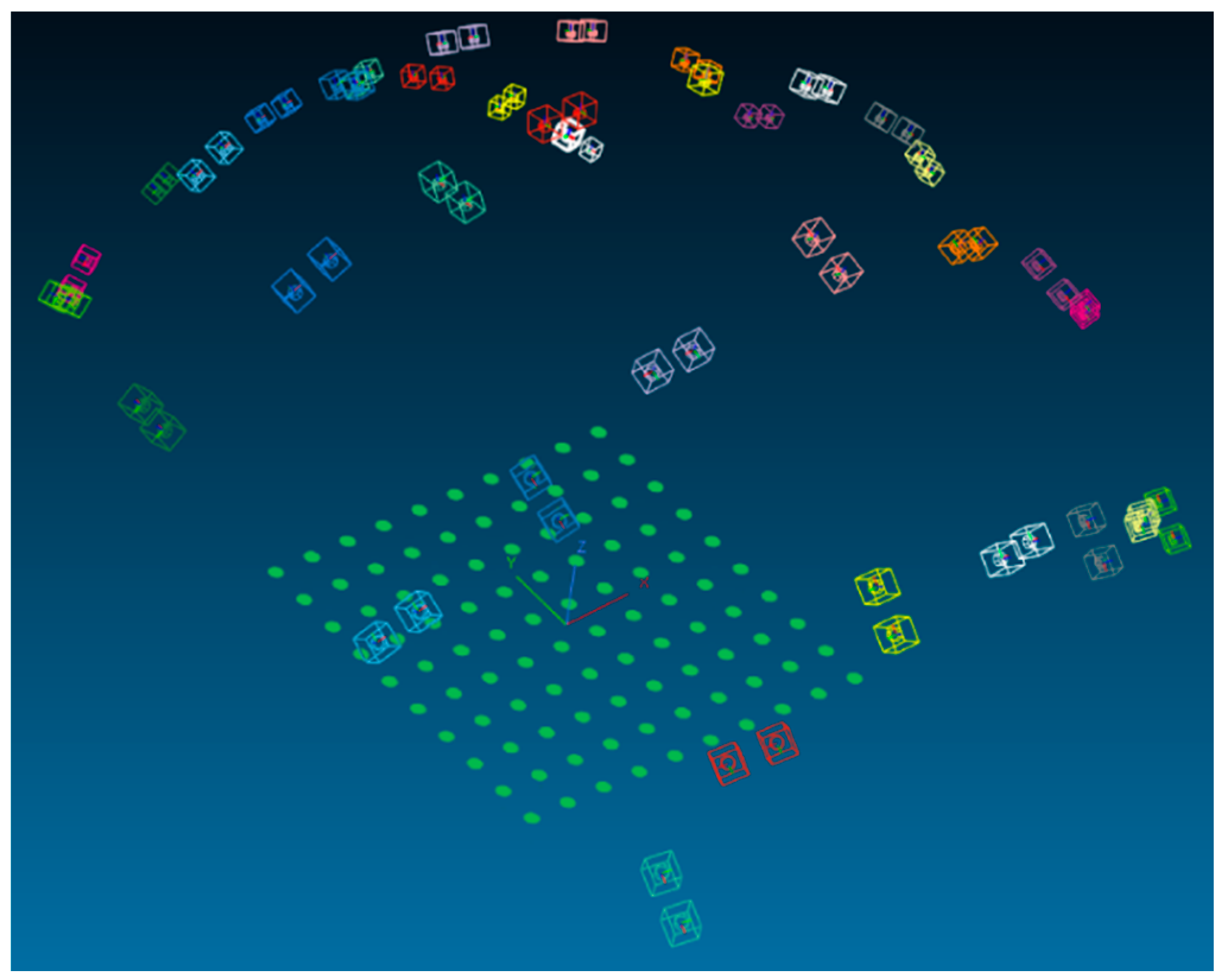


| Cube | HS |
|---|---|
| 2SM-0-Cube | 2SM-0-HS |
| 2MM-0-XX-Cube | 2MM-0-XX-HS |
| 2MM-5-XX-Cube | 2MM-5-XX-HS |
| 2MM-10-XX-Cube | 2MM-10-XX-HS |
| 2MM-15-XX-Cube | 2MM-15-XX-HS |
| 2MM-20-XX-Cube | 2MM-20-XX-HS |
| 2MM-25-XX-Cube | 2MM-25-XX-HS |
| Cube | HS |
|---|---|
| 2SM-XX-Cube | 2SM-XX-HS |
| 2MM-XX-1/99-Cube | 2MM-XX-1/99-HS |
| 2MM-XX-10/90-Cube | 2MM-XX-10/90-HS |
| 2MM-XX-20/80-Cube | 2MM-XX-20/80-HS |
| 2MM-XX-30/70-Cube | 2MM-XX-30/70-HS |
| 2MM-XX-40/60-Cube | 2MM-XX-40/60-HS |
| 2MM-XX-50/50-Cube | 2MM-XX-50/50-HS |
| No. | Experiment | Principal Distance c [mm] | A1 | A2 | A3 |
|---|---|---|---|---|---|
| 1 | nominal | −23.908 | 0.0 | 0.0 | 0.0 |
| 2 | 1SM-1/99-Cube | −23.908 | 0.0 | 0.0 | 0.0 |
| 3 | 1SM-1/99-HS | −23.908 | 0.0 | 0.0 | 0.0 |
| 4 | 1MM-1/99-Cube | −33.980 | 3.1e-4 | 1.4e-7 | 1.3e-10 |
| 5 | 1MM-1/99-HS | −33.979 | 3.1e-4 | 1.5e-7 | 1.1e-10 |
| No. | Dataset | Relative Orientation | c [mm] | |||||
|---|---|---|---|---|---|---|---|---|
| X0 [mm] | Y0 [mm] | Z0 [mm] | ω [°] | φ [°] | κ [°] | |||
| 0 | nominal | 200.000 | 0.000 | 0.000 | 0.000 | 0–25 | 0.000 | −23.908 |
| 1 | 2SM-0°-1/99-Cube | 200.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −23.908 |
| 2 | 2MM-0°-1/99-Cube | 199.994 | 0.000 | 0.019 | 0.000 | 0.000 | 0.000 | −33.979 |
| 3 | 2MM-5°-1/99-Cube | 200.572 | 0.000 | −0.062 | 0.000 | 5.001 | 0.000 | −33.978 |
| 4 | 2MM-10°-1/99-Cube | 201.143 | −0.002 | −0.116 | 0.000 | 10.000 | 0.000 | −33.978 |
| 5 | 2MM-15°-1/99-Cube | 201.715 | −0.007 | −0.192 | 0.000 | 15.003 | 0.000 | −33.979 |
| 6 | 2MM-20°-1/99-Cube | 202.266 | −0.010 | −0.339 | −0.001 | 20.003 | 0.000 | −33.979 |
| 7 | 2MM-25°-1/99-Cube | 202.884 | −0.011 | −0.378 | 0.001 | 25.004 | 0.000 | −33.981 |
| No. | Dataset | Relative Orientation | c [mm] | |||||
|---|---|---|---|---|---|---|---|---|
| X0 [mm] | Y0 [mm] | Z0 [mm] | ω [°] | φ [°] | κ [°] | |||
| 0 | nominal | 200.000 | 0.000 | 0.000 | 0.000 | 0–25 | 0.000 | −23.908 |
| 1 | 2SM-0°-1/99-HS | 200.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −23.908 |
| 2 | 2MM-0°-1/99-HS | 199.987 | 0.000 | 0.007 | 0.000 | 0.000 | 0.000 | −33.978 |
| 3 | 2MM-5°-1/99-HS | 200.573 | 0.000 | −0.047 | 0.000 | 5.000 | 0.000 | −33.977 |
| 4 | 2MM-10°-1/99-HS | 201.164 | −0.001 | −0.037 | 0.000 | 10.000 | 0.000 | −33.978 |
| 5 | 2MM-15°-1/99-HS | 201.736 | −0.004 | −0.082 | 0.000 | 15.000 | 0.000 | −33.979 |
| 6 | 2MM-20°-1/99-HS | 202.314 | −0.008 | −0.113 | 0.002 | 20.001 | 0.000 | −33.980 |
| 7 | 2MM-25°-1/99-HS | 202.845 | −0.005 | −0.290 | 0.001 | 25.000 | 0.000 | −33.981 |
| Parameter | Dataset | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cube | HS | Cube | HS | Cube | HS | Cube | HS | Cube | HS | |
| X | −0.58 | −0.65 | ||||||||
| Y | ||||||||||
| Z | −0.69 | −0.78 | ||||||||
| ω | 0.75 | 0.81 | 0.76 | 0.80 | ||||||
| φ | −0.82 | −0.82 | −0.79 | −0.74 | ||||||
| κ | −0.88 | −0.90 | −0.85 | −0.87 | ||||||
| c | Xh | Yh | B1 | B2 | ||||||
| No. | Dataset | Relative Orientation | c [mm] | |||||
|---|---|---|---|---|---|---|---|---|
| X0 [mm] | Y0 [mm] | Z0 [mm] | ω [°] | Φ [°] | κ [°] | |||
| 0 | nominal | 200.000 | 0.000 | 0.000 | 0.000 | 0–25 | 0.000 | −23.908 |
| 1 | 2SM-0°-1/99-Cube | 200.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −23.908 |
| 2 | 2MM-0°-1/99-Cube | 199.994 | 0.000 | 0.019 | 0.000 | 0.000 | 0.000 | −33.979 |
| 3 | 2MM-0°-10/90-Cube | 199.912 | −0.018 | 0.012 | −0.001 | −0.008 | 0.001 | −33.891 |
| 4 | 2MM-0°-20/80-Cube | 199.780 | 0.021 | 1.491 | 0.003 | 0.018 | 0.001 | −33.806 |
| 5 | 2MM-0°-30/70-Cube | 199.732 | 0.142 | 1.501 | 0.019 | 0.002 | −0.002 | −33.744 |
| 6 | 2MM-0°-40/60-Cube | 199.664 | 0.219 | 1.594 | 0.018 | 0.015 | −0.001 | −33.654 |
| 7 | 2MM-0°-50/50-Cube | 199.702 | 0.234 | 2.345 | 0.021 | 0.033 | 0.000 | −33.549 |
| No. | Dataset | Relative Orientation | c [mm] | |||||
|---|---|---|---|---|---|---|---|---|
| X0 [mm] | Y0 [mm] | Z0 [mm] | ω [°] | Φ [°] | κ [°] | |||
| 0 | nominal | 200.000 | 0.000 | 0.000 | 0.000 | 0–25 | 0.000 | −23.908 |
| 1 | 2SM-0°-1/99-HS | 200.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −23.908 |
| 2 | 2MM-0°-1/99-HS | 199.987 | 0.000 | 0.007 | 0.000 | 0.000 | 0.000 | −33.978 |
| 3 | 2MM-0°-10/90-HS | 199.782 | −0.019 | 0.616 | −0.001 | 0.000 | 0.000 | −33.878 |
| 4 | 2MM-0°-20/80-HS | 199.586 | −0.039 | 1.288 | −0.004 | 0.004 | 0.000 | −33.758 |
| 5 | 2MM-0°-30/70-HS | 199.441 | −0.056 | 2.092 | −0.006 | 0.007 | 0.000 | −33.630 |
| 6 | 2MM-0°-40/60-HS | 199.345 | −0.028 | 2.187 | −0.003 | 0.011 | 0.000 | −33.496 |
| 7 | 2MM-0°-50/50-HS | 199.287 | −0.028 | 2.254 | −0.001 | 0.013 | 0.000 | −33.362 |
| Parameter | Dataset | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cube | HS | Cube | HS | Cube | HS | Cube | HS | Cube | HS | |
| X | ||||||||||
| Y | ||||||||||
| Z | −0.54 | −0.58 | ||||||||
| ω | 0.55 | 0.63 | 0.54 | 0.63 | ||||||
| φ | −0.64 | −0.64 | −0.64 | −0.62 | ||||||
| κ | ||||||||||
| c | Xh | Yh | B1 | B2 | ||||||
| No. | Dataset | Relative Orientation | |||||
|---|---|---|---|---|---|---|---|
| X0 [mm] | Y0 mm] | Z0 [mm] | ω [°] | φ [°] | κ [°] | ||
| 0 | nominal | 200.000 | 0.000 | 0.000 | 0.000 | 0–25 | 0.000 |
| 1 | 2MM-25°-1/99-Cube | 200.000 | 0.000 | 0.000 | 0.000 | 25.000 | 0.000 |
| 2 | 2MM-0°-50/50-Cube | 200.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 3 | 2MM-25°-50/50-Cube | 200.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Data | c | xh | yh | A1 | A2 | A3 | B1 | B2 | C1 | C2 |
|---|---|---|---|---|---|---|---|---|---|---|
| [mm] | [mm] | [mm] | ||||||||
| σc | σxh | σyh | σA1 | σA2 | σA3 | σB1 | σB2 | σC1 | σC2 | |
| IO AIR | −10.52 | −6.84E-02 | −4.24E-02 | −1.13E-03 | 1.04E-05 | −4.45E-08 | −4.08E-05 | −3.79E-05 | −1.83E-04 | −6.51E-05 |
| 1.08E-03 | 7.43E-04 | 7.96E-04 | 4.88E-06 | 2.25E-07 | 3.18E-09 | 2.50E-06 | 2.02E-06 | 1.16E-05 | 1.15E-05 | |
| IO Water | −14.49 | −4.41E-02 | −3.01E-02 | 6.35E-04 | 2.64E-06 | 6.87E-08 | 4.62E-05 | −1.34E-05 | −1.30E-04 | −2.02E-04 |
| 3.07E-03 | 2.73E-03 | 2.85E-03 | 9.32E-06 | 4.41E-07 | 6.31E-09 | 8.22E-06 | 8.39E-06 | 2.53E-05 | 3.09E-05 |
| No. | Dataset | Relative Orientation | c [mm] | |||||
|---|---|---|---|---|---|---|---|---|
| X0 [mm] | Y0 [mm] | Z0 [mm] | ω [°] | Φ [°] | κ [°] | |||
| 0 | air, parallel | −37.914 | 0.886 | 0.214 | 0.120 | −0.022 | −0.180 | −10.520 |
| 1 | parallel-2D | −37.817 | 0.916 | 0.251 | 0.197 | 0.040 | −0.194 | −14.547 |
| 2 | parallel-3D | −37.814 | 0.939 | 0.510 | 0.139 | 0.022 | −0.180 | −14.492 |
| 3 | parallel-2Dex | −37.544 | 0.838 | 0.940 | 0.079 | −0.053 | −0.197 | −10.520 |
| 4 | parallel-3Dex | −37.744 | 0.935 | 0.450 | 0.080 | 0.069 | −0.193 | −10.520 |
| 5 | convergent-2D | −75.961 | −2.683 | −17.026 | 2.461 | −27.792 | −2.859 | −14.555 |
| 6 | convergent-3D | −75.611 | −2.735 | −16.769 | 2.452 | −27.556 | −2.862 | −14.501 |
| 7 | convergent-2Dex | −72.735 | −2.602 | −15.273 | 2.446 | −27.334 | −2.846 | −10.520 |
| 8 | convergent-3Dex | −74.194 | −4.169 | 5.248 | 3.285 | −28.640 | −2.828 | −10.520 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahmen, O.; Rofallski, R.; Luhmann, T. Impact of Stereo Camera Calibration to Object Accuracy in Multimedia Photogrammetry. Remote Sens. 2020, 12, 2057. https://doi.org/10.3390/rs12122057
Kahmen O, Rofallski R, Luhmann T. Impact of Stereo Camera Calibration to Object Accuracy in Multimedia Photogrammetry. Remote Sensing. 2020; 12(12):2057. https://doi.org/10.3390/rs12122057
Chicago/Turabian StyleKahmen, Oliver, Robin Rofallski, and Thomas Luhmann. 2020. "Impact of Stereo Camera Calibration to Object Accuracy in Multimedia Photogrammetry" Remote Sensing 12, no. 12: 2057. https://doi.org/10.3390/rs12122057