1. Introduction
Soybean is one of the main crops in the global agro-industrial complex [
1]. Worldwide, soybean production ranks fourth among all grain and leguminous crops (after rice, wheat, and corn) (
http://fao.org/faostat), while the gross yield of the crop has increased by more than 50% in the 10 years from 2008 to 2018—that is, from 220 million to 340 million tons (
http://www.indexbox.ru). In the Russian Far East, soybean is the main cultivated crop; in 2018, the share of the four southern Far Eastern regions that have a common border with China accounted for more than 50% of the total soybean sowing area in Russia (
https://www.gks.ru). That is why soybean is one of the main crops that allows to formulate a food security strategy at the government level in different countries, which is an urgent task in conditions of economic crisis [
2] and, in particular, the expected consequences of COVID-19 [
3]. Thus, in order to fulfill a number of tasks, for example, in planning sown areas and making decisions related to the product’s sale, it is necessary to pre-evaluate yield at the regional level.
The assessment of soybean yield at the field level was carried out in Reference [
4,
5]. These studies show that vegetation indexes (i.e., the Normalized Difference Vegetation Index (NDVI) and the Triangular Vegetation Index (TVI)) are related to cover crop biomass and, hence, yield [
5]. However, widely used yield analysis methods applied to individual fields, taking into account soil and agrochemical characteristics, along with remote sensing indicators, are not always applicable at the regional level [
6].
Remote sensing data are often extracted using arable land masks in crop yield modeling at the territory level. The applicability of this method for a specific region requires additional study, which is associated with a different degree of signal influence from different cultures on the final result. The influence of arable land structure on the values of vegetative indices was estimated in Reference [
7,
8]. For example, in the Canadian prairies, where most annual crops have similar phenological cycles, it is easy enough to define the plot of the seasonal vegetation indices’ variation, and, accordingly, to set aside arable land and use it in crop modeling [
9]. In other cases, due to the different phenological cycles of annual and perennial grasses and winter and spring crops, applying an arable land mask to assess the yield of a particular crop is not a priori possible. These results are very interesting from a practical point of view; they highlight the possibility of using remote sensing data obtained for arable land masks in the Russian Far East, similar in climatic conditions to some provinces of Canada. In the Russian Far East regions, due to cold winters, winter crops are practically not cultivated and it can be expected that the main crops have similar phenological cycles. In Reference [
10], the authors used a static mask throughout the European Union (EU) to study the correlation of remote sensing data with official crop statistics. An empirical model for predicting crop yields in areas with crop diversity is presented in Reference [
11]. Remote sensing data obtained from a common arable land mask were used to calculate wheat yield in Europe (in which the wheat share in the total sown area of different regions was used as a correction factor). Researchers from the USA [
12] compared the effectiveness of using a single crop mask with a common arable land mask as part of a study to predict corn and soybean yields. As a result, inclusion of information related to crop phenology significantly improved model performance. In Reference [
13], the researchers estimated the relationship between major USA crops’ yield and different time series of Moderate Resolution Imaging Spectroradiometer (MODIS) products for specific crops, including NDVI. In particular, it was shown that the yields from nine crops (i.e., barley, canola, corn, cotton, potatoes, sorghum, soybeans, sugar beets, and wheat) exhibited positive correlations with all vegetation indexes.
Recently, along with traditional trend methods and year-analog methods, regression models with climatic indicators and Earth remote sensing data as independent variables have been used to predict crop yield at the district or regional level [
14,
15]. The main indicators reflecting the state of arable land at certain times are the values of vegetation indices calculated from satellite images [
16,
17,
18]. At the same time, a set of meteorological factors that include both individual indicators (temperature, humidity, etc.) and integrated climate characteristics can determine a municipality’s production conditions and crop yields [
19]. For example, Balaghi et al. [
20] found a strong relation between rainfall in vegetation periods and wheat yield in most provinces of Morocco, and Maas et al. [
21] used photosynthetically active radiation (PAR) to predict crop yield.
Differences in the climatic conditions of neighboring municipalities are especially characteristic of the regions and subsequent districts in the Russian Far East due to their significant area. The agriculture in these regions is influenced by the complex relief and the specifics of a monsoon climate, which, first of all, is manifested for the Primorskiy and Khabarovsk territories [
22,
23].
Crop yield modeling studies at the regional level using remote sensing data in Russia have suggested the use of maximum NDVI values as one of the predictors of the regression model. In Reference [
24], it was indicated that the maximum NDVI calculated from the mask of the determined culture is the most stable indicator among all possible NDVI composites, and is also the most suitable for predicting spring crops. Bereza et al. [
25] used the term early forecasting for winter crops—in particular, wheat—and described yield forecasting at the regional level using NDVI from mid-May to mid-June when plants are heading and flowering begins. However, this NDVI value is actually the first maximum of early cultures; the second maximum characteristic of later cultures (for the Belgorod region) is observed at the end of July [
26]. Thus, the considered approach can also be called yield prediction using the maximum NDVI. In general, the use of such methods is characteristic of the western regions of Russia. At the same time, in the Russian Far East, which is the main producer of soybeans in Russia, there are no structured ground-based observation data that make it possible to accurately identify soybean masks for most municipalities in the retrospective period and to compare them with remote sensing data. According to previous studies for various municipalities in the south of the Far East, it was found that the maximum NDVI values for soybeans correspond to mid-July to early August (28th–32nd calendar weeks) [
27]. These calendar dates correspond to the R4–R6 stages (i.e., full pod, beginning seed, and full seed) for soybeans in the south of the Russian Far East [
28].
The main objective of this article was to assess the relationships between soybean yield and the NDVI maximum and meteorological variables at the regional scale in the Khabarovsk District. Obtaining actual NDVI maximum values using weekly composites reduces the effectiveness of early forecasting, which is associated with the expectation of the next composite following the maximum value, as well as time-consuming data processing. Thus, it is proposed to apply the method of approximating NDVI seasonal variation using Gaussian function parameters for previous years for the prediction of the maximum value. This approach makes it possible to determine the maximum NDVI at an earlier stage and to further use this indicator in the regression model to predict soybean yield in the study area. The results obtained in different studies do not deny the possibility of using NDVI values of different periods of the vegetation cycle as one of the predictors of the regression model [
29]. However, NDVI maxima are mainly used to ensure the highest accuracy of crop yield prediction.
Thus, at the first stage of the study, we investigated the dynamics of the seasonal NDVI variation for the main crops of the district based on experimental fields to establish the proportions of growing crops in the Khabarovsk District arable land area. As mentioned above, the use of arable land masks to predict individual crops is justified only if the main crops have similar phenological cycles. Although winter crops do not grow in the territory of the Khabarovsk region, it seems quite logical to assess the NDVI dynamics for the main crops grown in experimental fields, as well as to construct a model of arable land (taking into account the ratio of main crops). Using the same approach to calculate the NDVI index in the model and for the arable land of the entire municipal region provides the possibility of using remote sensing data on the arable land mask to predict soybean yield (as soybean is the main crop of this region).
3. Results
3.1. NDVI Seasonal Dynamics for Different Crops in the Experimental Fields in 2014–2018
Figure 3 shows the NDVI seasonal dynamics for the experimental soybean fields from 2014 to 2018. The average soybean weekly NDVI was calculated as the weighted sum of all soybean fields’ NDVI values (taking into account the area of the fields). Then, we determined the maximum NDVI value for each season using these average NDVI series. It was found that the average expressed maximum for soybeans fell on the 31st and 32nd calendar weeks (corresponding to the last decade of July to the first decade of August). The selected Gaussian function satisfactorily approximated the initial NDVI series. Parameter
c in the researched years ranged from 7.5 to 8.7, and parameter
b from 31.0 to 31.5 (
Table 2). It is remarkable that 2015 is characterized by the maximum peak width and the lowest maximum NDVI values. In contrast, in 2016 and 2018, the maximum NDVI values, respectively, were 0.859 and 0.854, while the
b values were minimal—7.5 and 7.6. The approximation accuracies in 2014 and 2015 were, respectively, 8.5% and 6.0%; in 2016, 13.9%; and in 2017 and 2018, 10.2% and 10.9%. Approximation RMSE varied from 0.029 in 2015 to 0.063 in 2016.
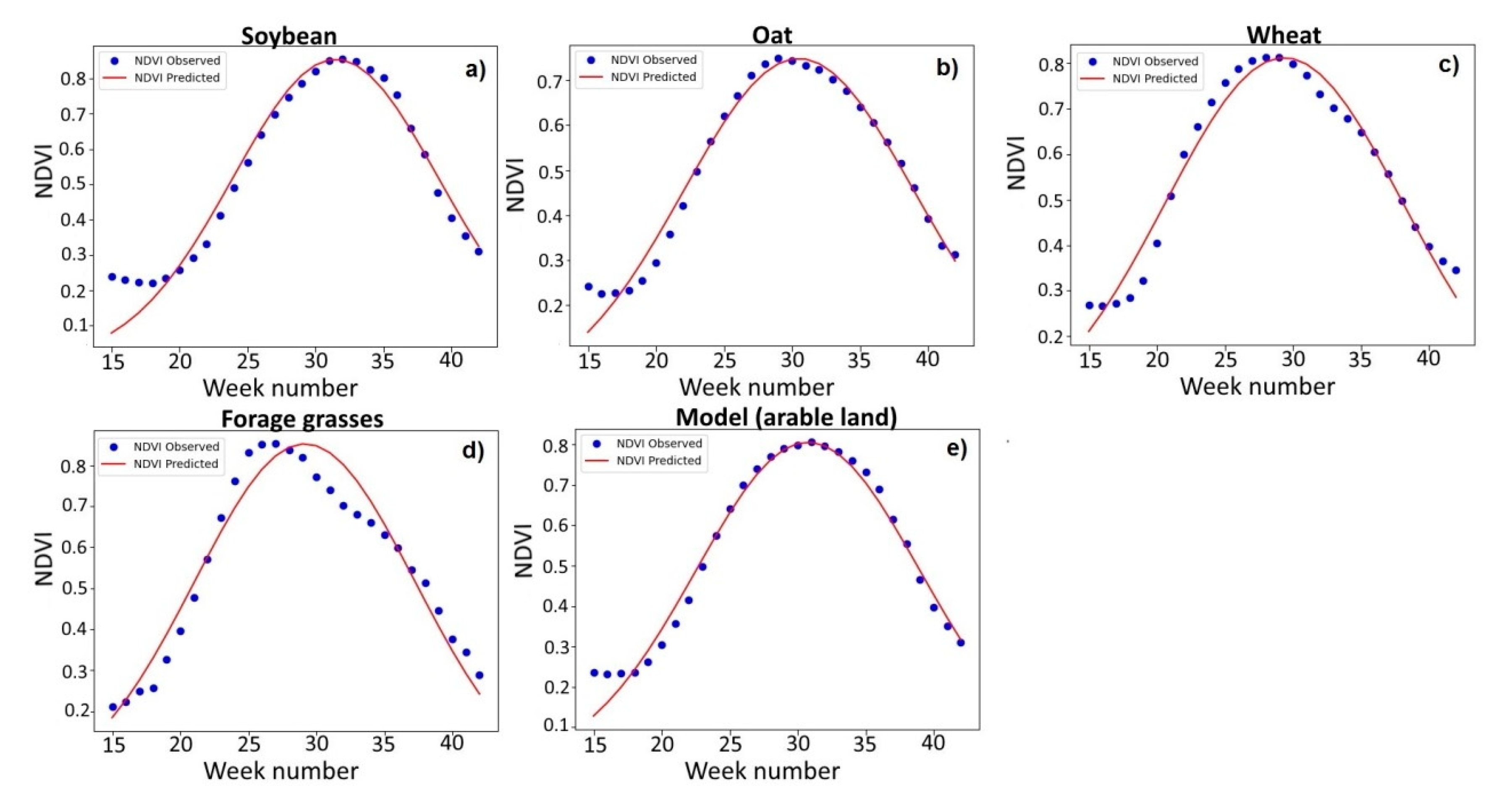
Figure 4 shows the seasonal NDVI approximating graphs for the main crops of the study area in 2018 (obtained from the experimental fields). It is easy to notice that the seasonal NDVI variation for oat and wheat corresponds to the Gaussian curve, while the corresponding curve for forage grasses has a displaced maximum. The figure also shows the seasonal NDVI variation for a model that takes into account the structure of the arable land in the Khabarovsk District. We multiplied the NDVI values by a fraction of a particular crop-sown area from the total area of the arable fields in the region and then summarized them for all of the researched cultures to calculate the weekly NDVI composites in the model of the arable land.
As follows from
Table 3, the
b values in 2018 for wheat and forage grasses were 29.4 and 29.2, respectively, while for oat and the arable land model, they were 30.5 and 30.4. The range of
c values for the different crops varied from 7.6 to 8.7, and for the arable land model, the corresponding parameter was 9.2. The Gaussian bell’s widening in the arable land model is explainable because different crops are characterized by different growing season lengths and different maximum NDVI values, which, accordingly, contribute to the peak’s expansion and the maximum decrease relative to the leading crop, while the total area under the curve can remain at the individual crop level. The model MAPE for spring wheat, oat, and arable land at the end of 2018 did not exceed 7%; the corresponding indicator for forage grasses was 9.1%, and for soybean was 10.9%. The RMSE for the arable land of the Khabarovsk District was 0.032.
In 2018, the maximum NDVI values for soybeans corresponded to the 32nd calendar week; for oat, to the 29th week; for wheat, to the 28th week; and for forage grasses, to the 26th week (i.e., the third decade of June) (
Figure 5). Thus, the maximum NDVI values for different crops vary noticeably in timing (from June 20 to August 10, i.e., for more than a month and a half). The maximum NDVI value was assumed to correspond to the period of the 30th and 31st calendar weeks in the arable land model. At the same time, the numerical value of the maximum NDVI for the arable land model was 0.805, which is lower than the corresponding indicator for the main crop-soybean. The NDVI
max (NDVI maximum) for soybean in 2018 was 0.852.
3.2. NDVI Seasonal Dynamics for the Arable Land in the Khabarovsk District in 2014–2018
Figure 6 shows the weekly NDVI composites’ dynamics for the arable land in the Khabarovsk District in 2014–2018. The maximum value of NDVI is reached earlier than the maximum of the approximating function. This shift can be explained by errors in arable land mask generation. We suppose that natural meadows, quite widely represented in the study area, were partially erroneously classified as arable lands. From 2014 to 2018, the maximum NDVI corresponded to the 26th–30th weeks (earlier in 2014, 2015, and 2018, and later in 2016 and 2017). The average maximum for 2014–2018 fell on the 28th calendar week.
Table 4 provides the parameters of the approximation curves. The
b values in 2014, 2016, and 2018 were at the level of 29.8–29.9, while in 2017, it was 29.4, and in 2015, it was 30.5. Parameter
c varied from 10.1 to 10.4. The calculated parameters for the averaged seasonal variation over the five years were, accordingly, 29.9 and 10.3. MAPE ranged from 3.9% in 2017 to 7.7% in 2014. The maximum NDVI value ranged from 0.708 in 2016 to 0.756 in 2017 (the variability was 2.6%, while the variability for the experimental soybean fields was 5.1%). The averaged (2014–2018) maximum NDVI value was 0.727, and MAPE was 6.5% (RMSE was 0.038).
Correlation analysis showed that the maximum NDVI values (2014–2018) of the arable land in the Khabarovsk District strongly correlate with the maximum NDVI values of the experimental soybean fields (R = 0.73).
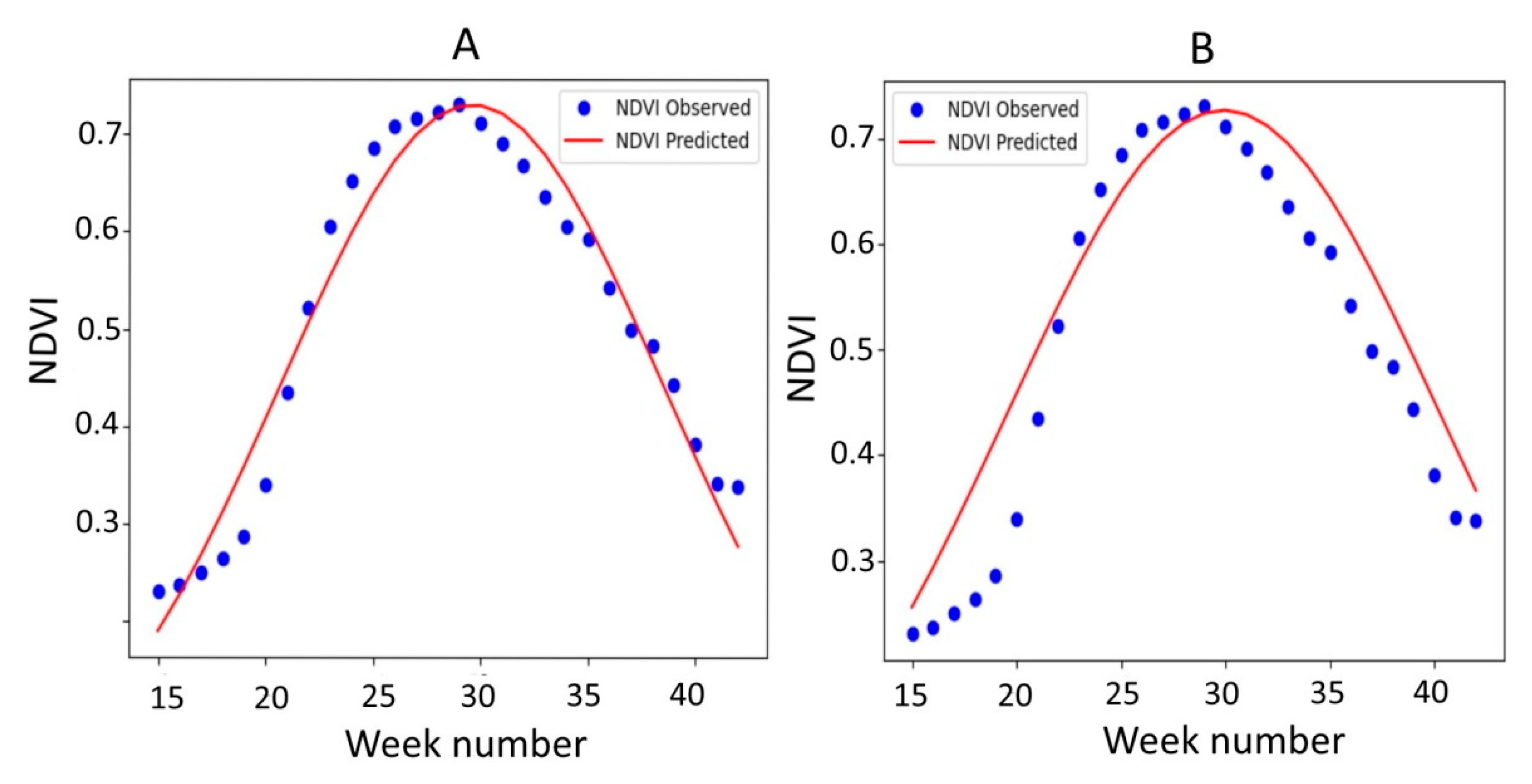
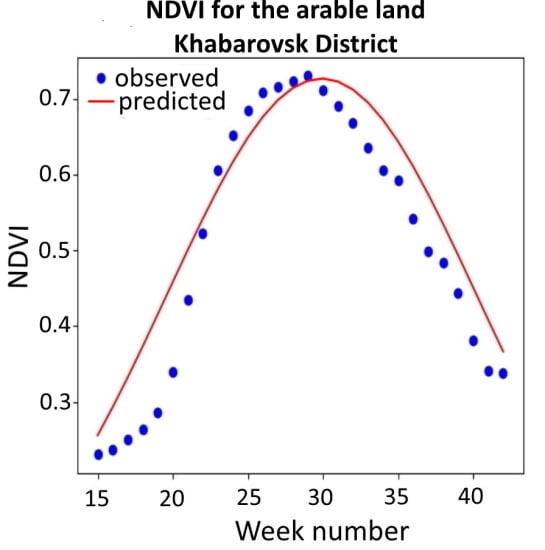
Figure 7 shows the NDVI composites from the 15th to the 42nd calendar weeks, while the approximation was carried out in two ways—i.e., using the observed NDVI composites in 2019 (
Figure 7A) and using the parameters of the approximating function obtained according to the averaged data for 2014–2018 (
Figure 7B). The maximum NDVI was reached in the 29th calendar week and equaled 0.73. The
b values were 29.6 (
Figure 7A) and 29.9 (
Figure 7B), while the
c values were 8.9 (
Figure 7A) and 10.3 (
Figure 7B). MAPE (
Figure 7A) was equal to 7.3%. Applying the approximating function (calculated according to the parameters of 2014–2018), MAPE increased to 12.6% (RMSE increased to 0.054), and the simulated maximum value of NDVI was 0.733. The deviation of the predicted maximum from the observed maximum was 0.4%.
Analysis a posteriori was not the only goal of our work. For early prediction of soybean yields, it is important to predict the maximum NDVI in previous weeks.
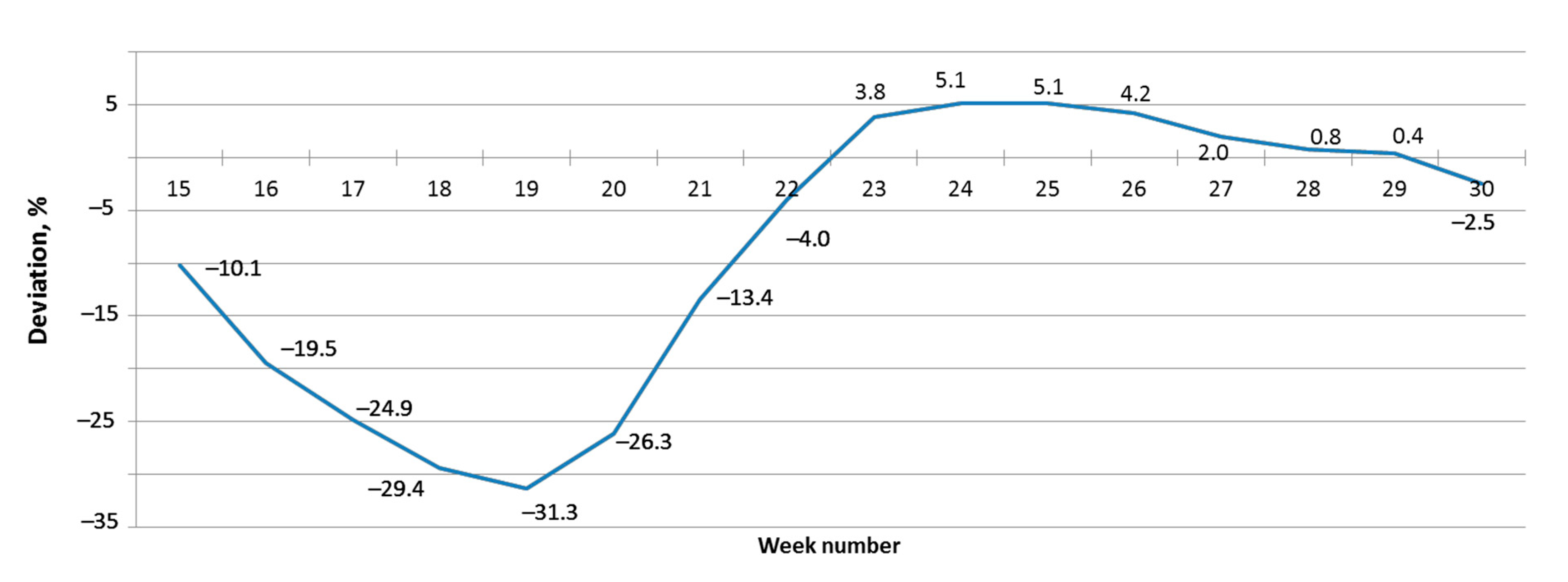
Figure 8 shows the deviation of the forecasted maximum NDVI value, calculated from the composite values of the current week, from the observed maximum. For this calculation, we used the function approximating composites averaged over 2014–2018.
In
Figure 8, we can see that the accuracy of determining the maximum NDVI value becomes sufficient from the 22nd calendar week (within 5%), which corresponds to the first decade of June. When approaching the calendar maximum, the error of the maximum determination decreases to 0.4%. Due to the fact that the passage point of the maximum value cannot always be determined immediately from the seasonal NDVI schedule and that image processing is expensive, we recommend using the average value for the three weeks preceding the maximum value as the maximum NDVI. The
in 2019 was 0.5%.
Thus, the analysis of the NDVI seasonal variation of the experimental fields and the arable land with approximation functions showed the possibility of using the maximum NDVI values of arable land in the early prediction of soybean yield.
3.3. Mathematical Model for Calculating Soybean Yield in the Khabarovsk District
During the construction of the forecast model, we calculated the values of the meteorological factors that potentially affect crop yields. It was shown that the maximum NDVI value of the arable land in the Khabarovsk District is reached by the 30th calendar week (
Figure 6 and
Figure 7).
Table 5 provides the soybean yield estimations, the maximum NDVI values (x
1), and the values of the climatic characteristics (x
2–x
6).
Soybean yield is a fairly variable indicator, the coefficient of variation for which is 17%. The minimum value of this indicator (i.e., 1.01 t/ha) corresponds to 2016, while the maximum was observed in 2018—1.67 t/ha. The independent variables x2 and x4 have a high coefficient of variation. The total soil temperature (x4) in the first 30 weeks of 2014 was 2.5 times higher than the same value in 2016 (769.5 °С and 311.9 °С, respectively). The maximum NDVI values have the least variation—2.4%—while the variability of x3, x5, and x6 is in the range of 7–8.5%. In general, 2010, 2011, 2013, and 2015–2017 are characterized by a late start to the growing season (x3 ranged from 71 to 75 days). For 2012, 2014, and 2018, x3 (growing duration) ranged from 82 to 84 days. Similarly, the variable x6 (photosynthetically active radiation) changed during the study period. High PAR values were observed in 2012, 2014, and 2017–2018 and ranged from 0.86 to 0.89 GJ∙m2. The highest values of the indicators characterizing humidity/aridity were observed in 2011 and 2015. The average relative soil moisture (x5) was 38.0% and 38.1%, and the Selyaninov hydrothermal coefficient (x2) was 3.03 and 3.07, respectively.
The analysis showed that a number of the variables share a certain relationship, suggesting their exclusion from the regression model.
Table 6 provides the Kendall rank correlation coefficients for the dependent and independent variables of the regression model. A rather high correlation coefficient value can be observed between the indices x
3 and x
6 (τ = 0.73), and x
2 and x
5 (τ = 0.56). Thus, it is advisable to leave only one of the two variables characterizing the degree of aridity (x
2) and to exclude x
6 from the regression model. It is also possible to preliminarily characterize the impact of the indicators on soybean yield using the correlation table. Thus, the maximum NDVI value, the duration of the growing season, the total temperature of the soil, and the PAR are all directly related to the average crop yield. Conversely, soil moisture and SHC are inversely related to soybean yield.
Variables x
5 and x
6 were excluded during the correlation analysis, and variables x
2 and x
4 were automatically excluded during stepwise model construction as insignificant indicators. As a result, the multiple regression equation, which characterizes the dependence of soybean yield in the Khabarovsk District on the variables included in the model, constructed according to the data of 2010–2018, has the following form:
The model’s coefficient of determination (R
2) is 0.72. The standardized values of the regression coefficients are approximately equal, which indicates the same effect of the predictors on soybean yield (
Table 7). All of the coefficients of the regression equation are significant (
p < 0.05).
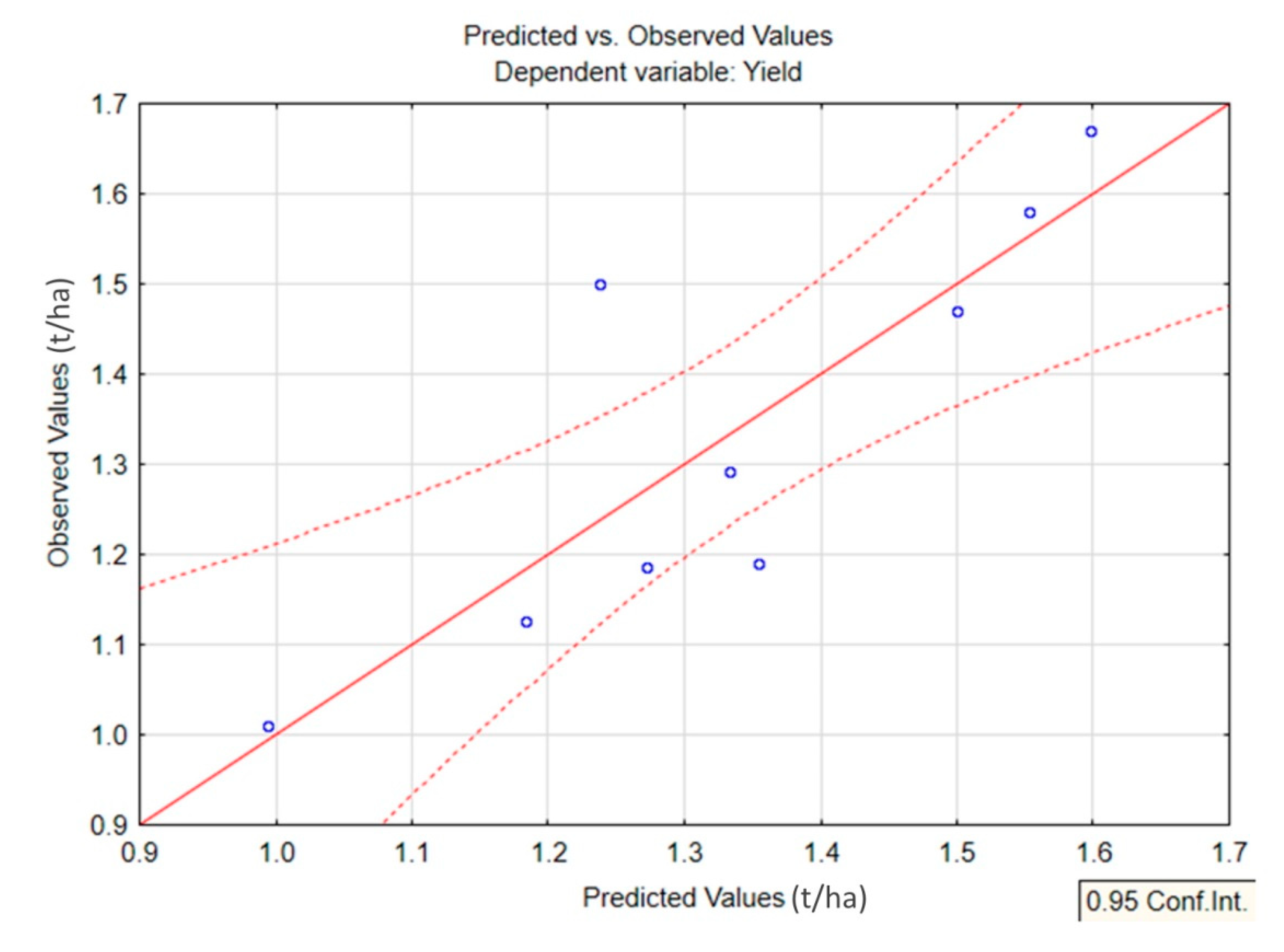
An analysis of the results showed that the predicted values for most of the observed years are within the confidence interval (γ = 0.95) for the actual soybean yield (
Figure 9). The largest deviation was observed in 2013, which is due, possibly, to an inaccurate estimate of soybean yield in the Khabarovsk District, caused by the largest flood in the history of observations of the Amur River. As a result of the flood, 16,000 hectares of farmland in the Khabarovsk Territory were affected, including the lands of the Big Ussuriysky Island (90% flooded). The final statistics of the Federal State Statistics Service of Russia in 2013 were affected by the high proportion of soybean fields in the non-flooded sown areas of the Khabarovsk Territory.
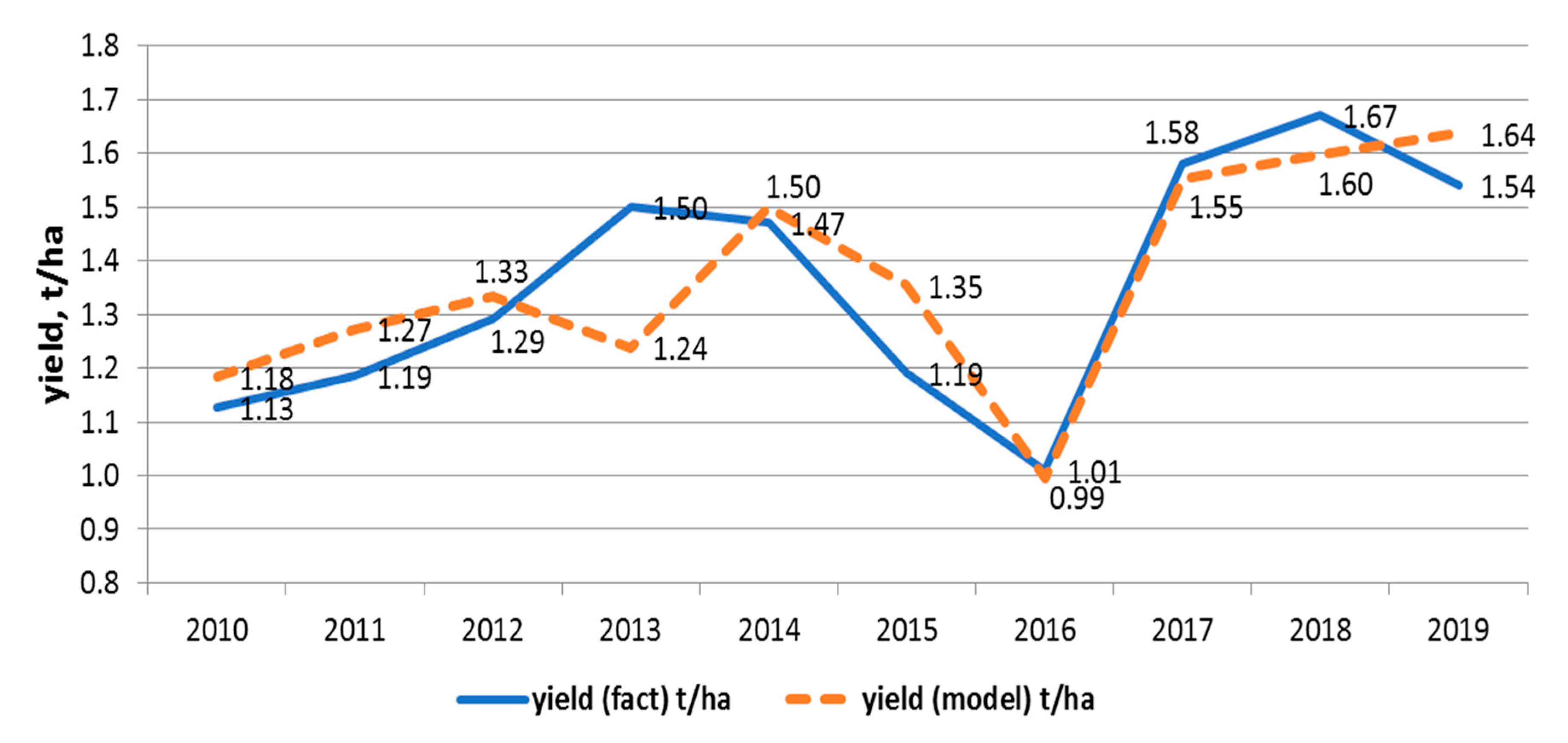
Figure 10 shows the actual and estimated values of the average soybean yield for 2010–2018. Moreover, we forecasted soybean yield in the Khabarovsk region in 2019 using the regression model. The predicted and real values of soybean yield in 2019 are also reflected in
Figure 10. The MAPE of the model was 6.2%, the RMSE was 0.13 t/ha, and the APE was 6.3% (using the actual values of the maximum NDVI). Thus, the developed model shows fairly high accuracy when calculating soybean yield in the Khabarovsk District for 2018.
The regression model had high accuracy, as evidenced in R
2cv, RMSE
cv, and MAPE
cv values obtained using a leave-one-year-out (2010–2019) cross-validation procedure (
Table 8). APE
cv was mainly within 8% (except 2013 and 2015).
We evaluated model accuracy using approximated NDVI maxima to solve the problem of early forecasting and calculated the NDVI maxima from the 22nd to the 30th calendar weeks in 2010–2019 using the Gaussian approximation function.
Table 9 provides an estimate of the model accuracy using the RMSE and APE, where the predicted NDVI values were used as an independent model variable in regression equations for each year from 2010 to 2019. Regression equations were obtained using a leave-one-year-out cross-validation procedure.
The model’s average APE increased from 5.9% (actual average NDVI maxima) to 7.6–9.9% (predicted NDVI maxima, calculated using NDVI 28th, 29th, 30th weeks). The average RMSE increased from 0.11 t/ha to 0.15–0.18 t/ha.
Table 10 presents the calculated NDVI maxima for
i weeks in 2019, as well as the corresponding yield values. The parameters of the Gaussian approximation function (average for 2014−2018) are given in
Table 4.
The calculated crop yields ranged from 1.36 to 1.99 t/ha for different weeks. Prediction error (APE) in the 23rd to 26th weeks ranged from 23% to 29%, did not exceed 10% in the 28th and 29th weeks, and was 4.3% in the 30th week.
3.4. Soybean Yield Prediction in Other Municipalities of Far East Based on Proposed Model
We predicted soybean yield in 11 soybean-producing municipalities of the Russian Far East, using our regression model with the maximum NDVI value and the growing season duration (as of 30 weeks) as independent variables.
Table 11 provides the average errors of forecasting, the R
2 values, and the
p-values.
The RMSE, the R2 values, and the p-values for some regions (i.e., the Khabarovsk, Vyasemskiy, Tambovskiy, Mikhailovskiy, and Khankaiskiy districts) are quite satisfactory. The early forecasting method development for soybean and other crops for different territories is a priority area for future research.
4. Discussion
Various researchers have investigated the seasonal course of NDVI, as well as other vegetative indices, for different crops obtained using remote sensing data. For example, the use of the asymmetric Gaussian and double logistical functions for modeling seasonal changes in vegetation indices was considered in Reference [
44]. The paper [
45] presented the application of the iterative logistic fitting method for Enhanced Vegetation Index (EVI) modeling in grasslands. Seo et al. [
46] used two logistic curves (one for the early and one for the later parts of the growth period) for corn and soybean NDVI approximation. Berger et al. [
47] presented NDVI prediction according to historical data using soybean in Uruguay as an example. In their study, a set of fields, each at least 250 ha in size, were studied; to approximate the seasonal course of NDVI, the authors used two models: one with a polynomial and the other a double logistic function interpolation.
The RMSE for the studied soybean fields was 0.15 for the polynomial approximation and 0.11 for the logistic approximation. All of the RMSEs in our model using Gaussian as an approximating function are below 0.1, which is a fairly good result. The time interval for approximation in our model from the 15th to the 42nd calendar weeks (196 days) approximately corresponds to the time interval considered in [
47]—from November 11 to May 5 of the next year (adjusted for the season in the Southern Hemisphere). Consideration of the arable land as a whole (instead of as individual fields) contributed to the superiority of our model. We suppose that the main goal of approximation is to determine the maximum NDVI value as accurately as possible in order to enable early forecasting. Therefore, as a further development of our work, the phenological stages of soybean, including the emergence, flowering, and maturation dates of the soybean, should be studied. Papers [
48,
49] calculated the relationship of the quantitative and qualitative indicators of soybean with vegetation indices using the remote sensing data of different phenological stages.
In our study, we used the maximum value of the NDVI index as one of the independent variables of the model. However, a reasonable question arises: Is it not more appropriate to use the NDVI values of other days (weeks) in early yield forecasting? This is most reasonable for winter crops because their first maximum is observed in early spring [
50]. On the other hand, some researchers have noted that the best results in predicting crop yields may not be achieved during the passage of the maximum NDVI value. Magney et al. [
51] showed that the best results for predicting wheat yields are observed over two periods—on days 37–46, and also on days 75–85 after the emergence of seedlings. Ren et al. [
52] compared regression models using NDVI values in different weeks of April and May. They showed that errors of the predicted yield using MODIS–NDVI varied between 4.62% and 5.40% depending on the NDVI values, as well as that the average RMSE was 0.21 t/ha. Lopresti et al. [
53] estimated wheat yields in Argentina using NDVI values between the 289th and 305th calendar days of the year, which in the Southern Hemisphere corresponds to March in the Northern Hemisphere, and the RMSE varied from 0.40 to 0.46 t ha
−1 for the different regions of Argentina. Using early NDVI values in soybean analysis is, in our opinion, quite a difficult task.
Thus, the use of NDVI before it reaches its maximum value significantly decreases the accuracy of the model. The solution to this problem could be a promising research area. In general, an analysis of recent works devoted to assessing crop yields at the region or municipality level using remote sensing data showed that the developed model has enough accuracy. Thus, in Reference [
54], the average error of the regression model for corn yield prediction in the period of 2010–2014 was 4.5%. Neravuori et al. proposed a method for predicting crop yields in mixed-crop fields (the predominant crop being mainly wheat) using vegetation indices in the model during the early period of the growth season (i.e., in June) [
55]. The MAPE of this model was 8.8%; however, when using data acquired later in July and August, the MAPE increased to 12.6%.
Wei et al. [
56] showed an approach combining the SIMDualKc water balance model and the Stewart water-yield model for soybean. The accuracy of this model is of particular interest because the work was performed in Northeast China—that is, in the adjacent region to the Russian Far East. The RMSE of the model was 0.38 t/ha—about 11.5% of the maximum observed yield. Sacamoto [
57] compared three methods for assessing crop yields, that is, linear regression, polynomial regression (PM), and the random forest (RF) method, where temperature, precipitation, and shortwave radiation were used in addition to NDVI. The obtained equations were used to estimate soybean yield in a few regions of Nebraska (USA). Averaged by regions, the RMSE was 0.28 t/ha for PM and 0.21 t/ha for RF.
Other meteorological factors can be used to improve the yield forecasting model. For example, in Reference [
58], atmospheric pressure was used in wheat yield prediction in China. The influence of air temperature in the surface layer on wheat productivity was considered in References [
20,
59]. However, the experiments for the Khabarovsk District showed that these climatic indicators do not significantly affect soybean yield. Both of these indicators are inversely correlated with the maximum NDVI value (which prevents their use in the model). Such a negative correlation can be explained by the fact that high atmospheric pressure, which causes a lack of precipitation, high temperature, and hot weather in late spring and early summer, leads to destructive effects on plant maturation. However, at the same time, they do not correlate with crop yield at the end of the year.
Various climatic indices are used for yield modeling; for example, Pacific Decadal Oscillation (PDO) and MEI (Multivariate El Niño/Southern Oscillation index) [
60] and monthly drought index (DI) [
61]. In agrometeorological studies in Russia and the Commonwealth of Independent States (CIS), the most commonly used indices are the Selyaninov hydrothermal coefficient (SHC), the climate biological effectiveness (CBE), and the Budyko dryness index (BDI) [
62,
63]. Correlation analysis showed that all of the listed climatic indices are significantly (
p < 0.05) correlated with each other; therefore, it was decided to choose just one of the indices—the SHC. During our research, the SHC index (for the first 30 weeks of the year) was excluded at the stage of regression equation building. Application of the other indices gives similar results: The corresponding variables are excluded during stepwise regression process.
In Reference [
45], it was stated that the addition of various soil characteristics (i.e., soil temperature and moisture in different layers) increases the determination coefficient of the wheat yield regression model by 0.12. In this work, the temperature and soil moisture in the upper layer (at a depth of 10 cm) were previously considered as independent variables. Both of these indicators were excluded from the model during the model building process. Using soil temperature and soil moisture in a 10–40 cm layer instead of similar indicators for the top layer allows to build an alternative model for early yield prediction:
where x
1 is the maximum NDVI value, and x
2 is the total soil temperature in the 10–40 cm layer during the vegetation season (before the 30th week). The model’s determination coefficient (R
2 = 0.68) is slightly less than the corresponding coefficient for our equation from
Section 3. Thus, this equation proves the relationship between soil temperature in deep layers and soybean yield. Further study of the influence of soil characteristics on crop yields looks promising.