Quad-Polarimetric Multi-Scale Analysis of Icebergs in ALOS-2 SAR Data: A Comparison between Icebergs in West and East Greenland
Abstract
1. Introduction
1.1. Icebergs in SAR
1.2. Aims and Objectives
2. Materials and Methods
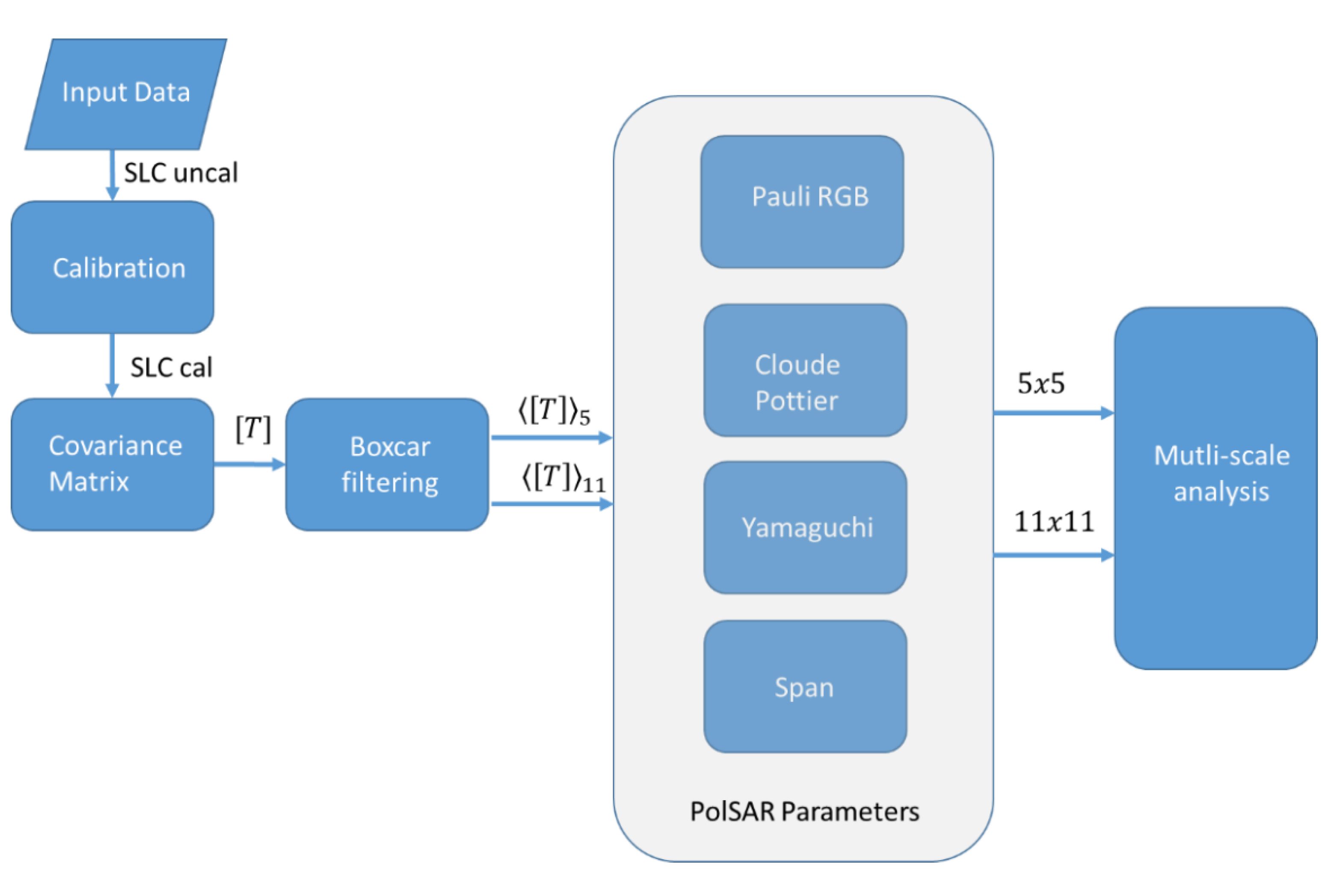
2.1. SAR Processing and Iceberg Detection
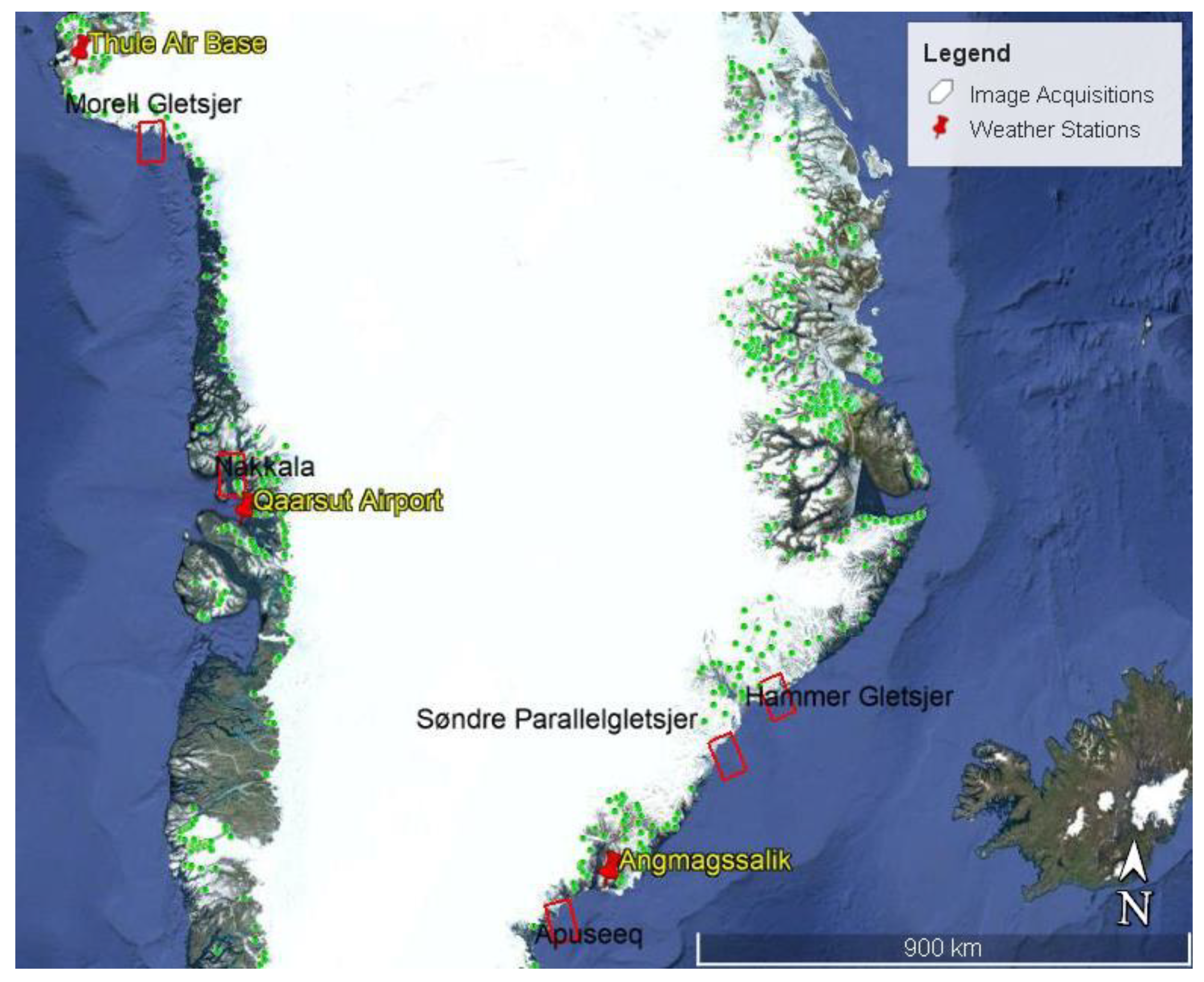
2.2. Geographical Location and Meteorological Data
2.3. Meteorological Conditions
2.4. Glaciers that Calved Icebergs
2.5. SAR Dataset
2.6. PolSAR
2.6.1. Cloude–Pottier Decomposition
2.6.2. Yamaguchi Decomposition
3. Results
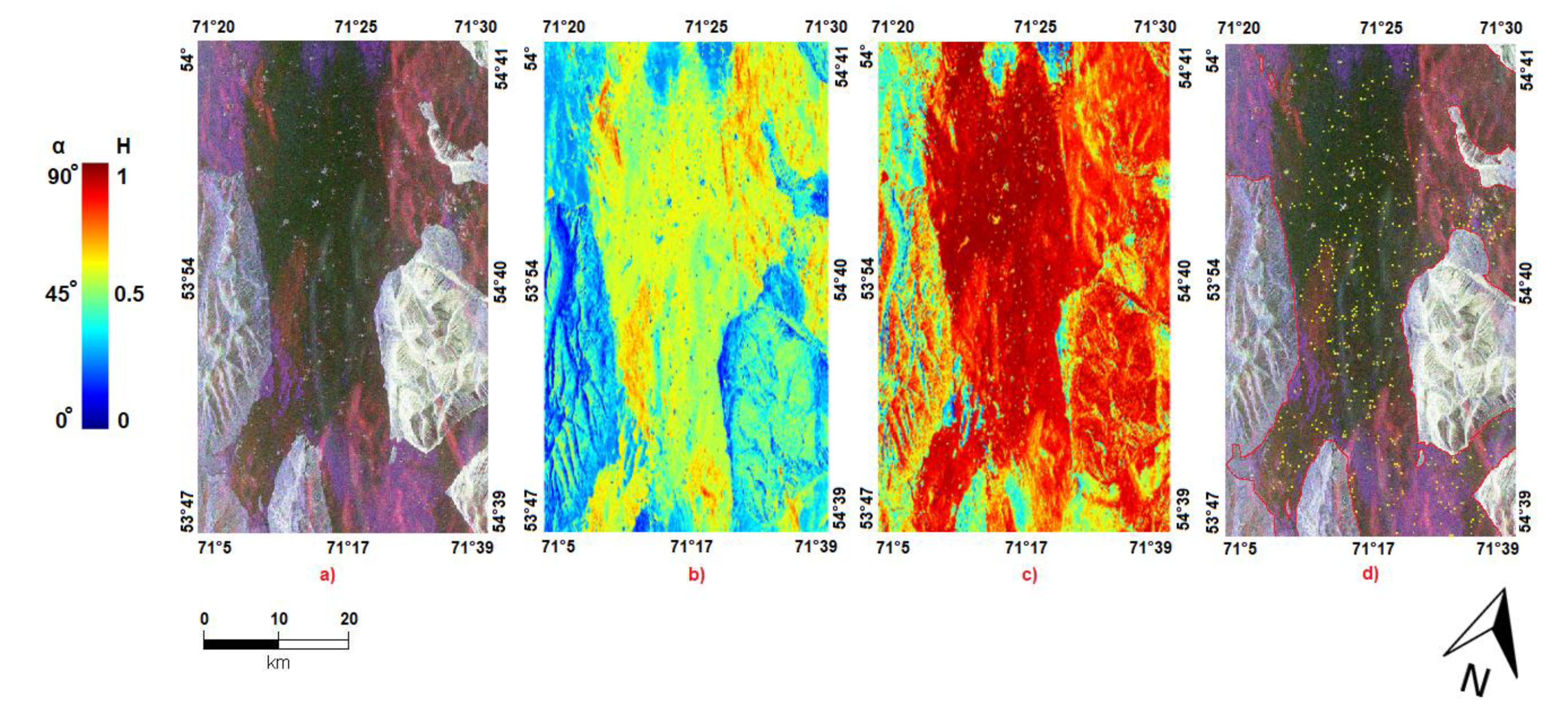
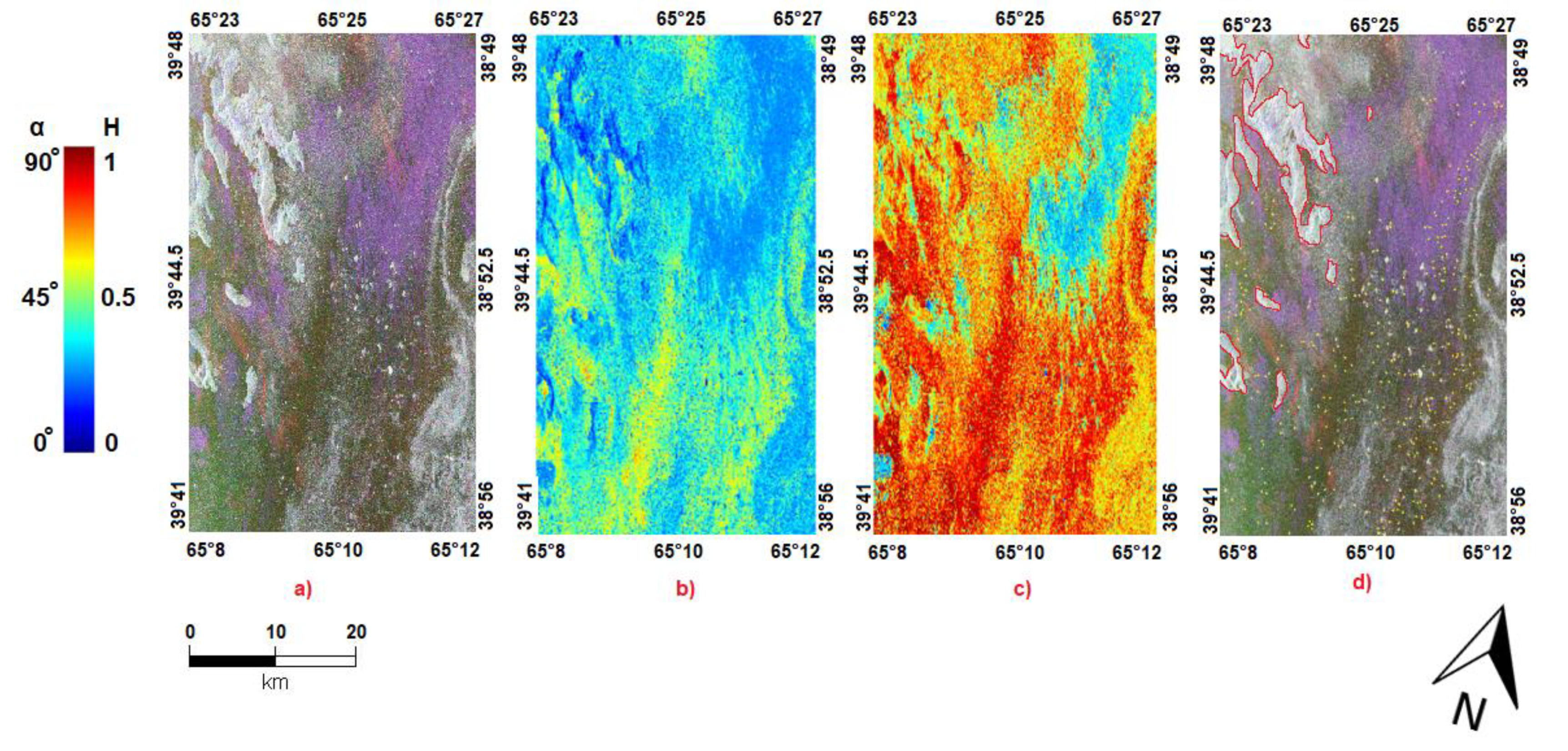
3.1. Preliminary Image Analysis
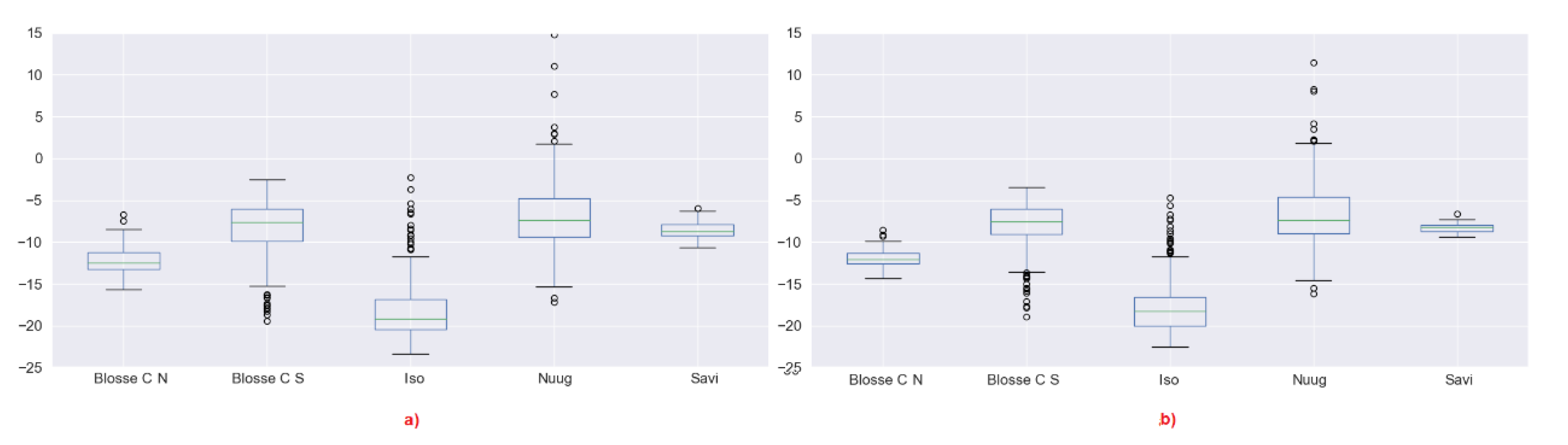
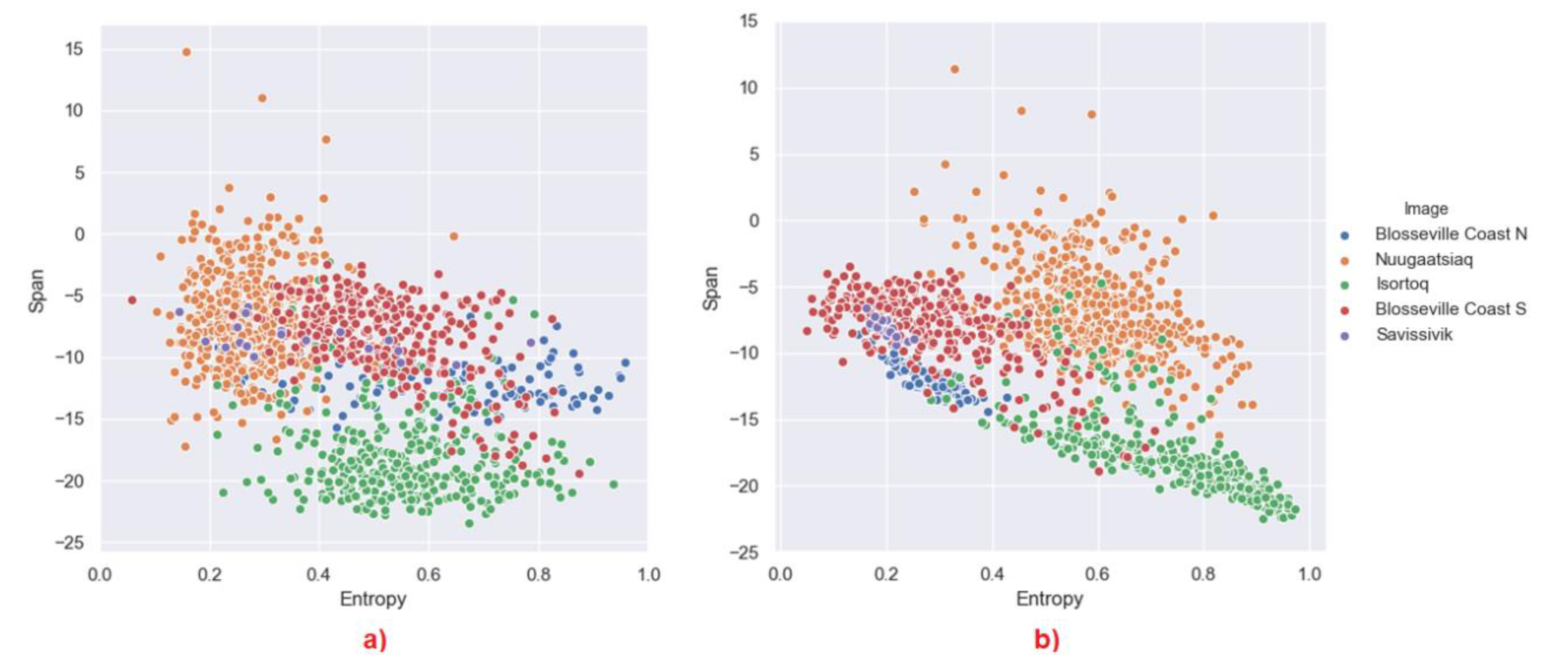
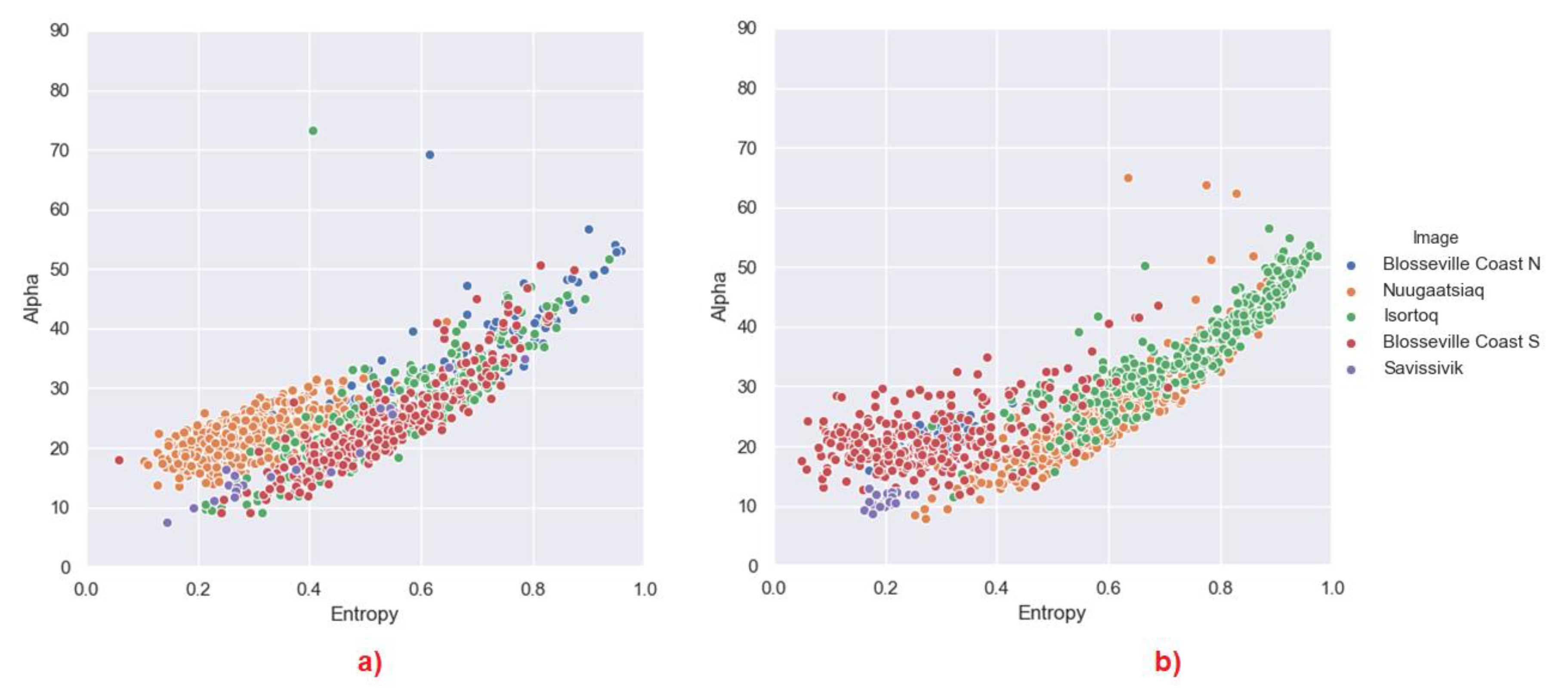
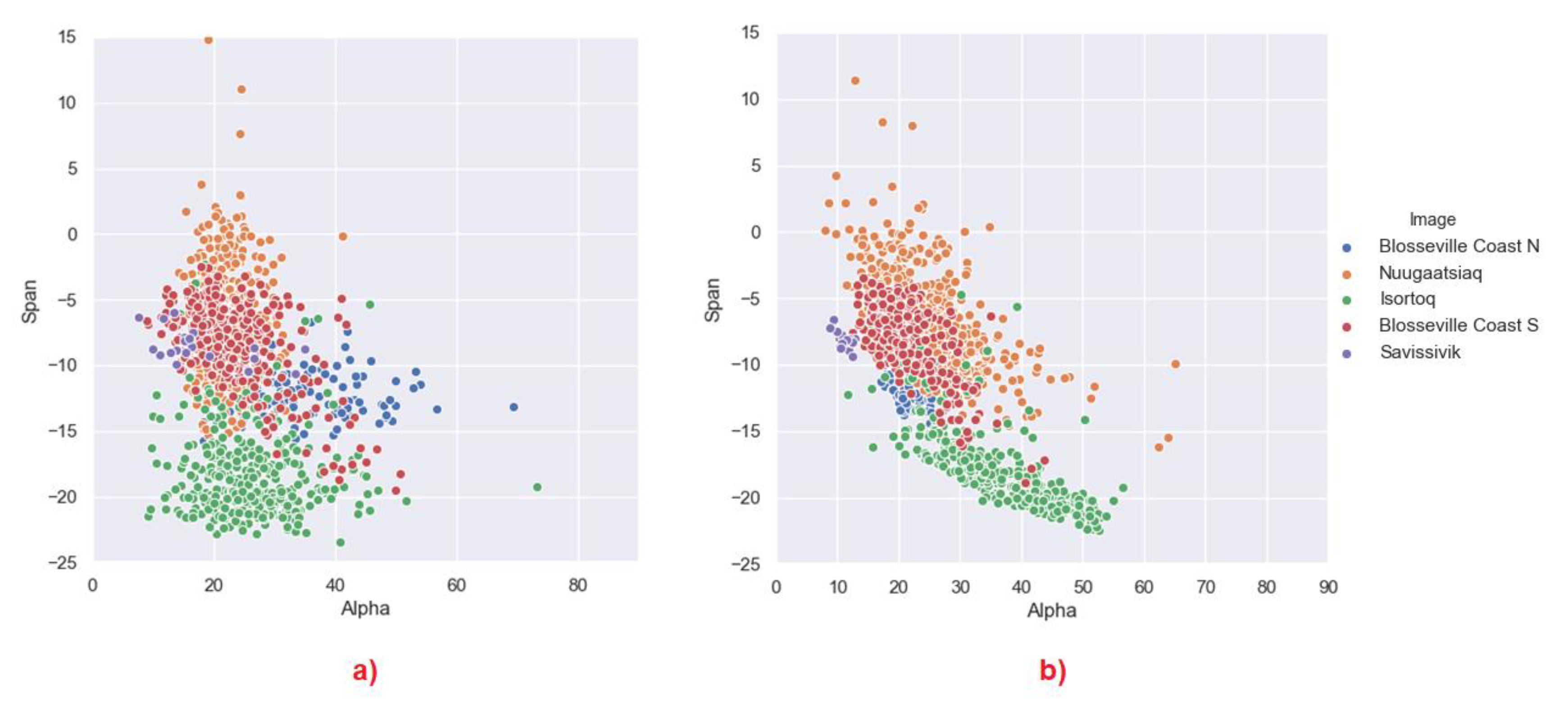
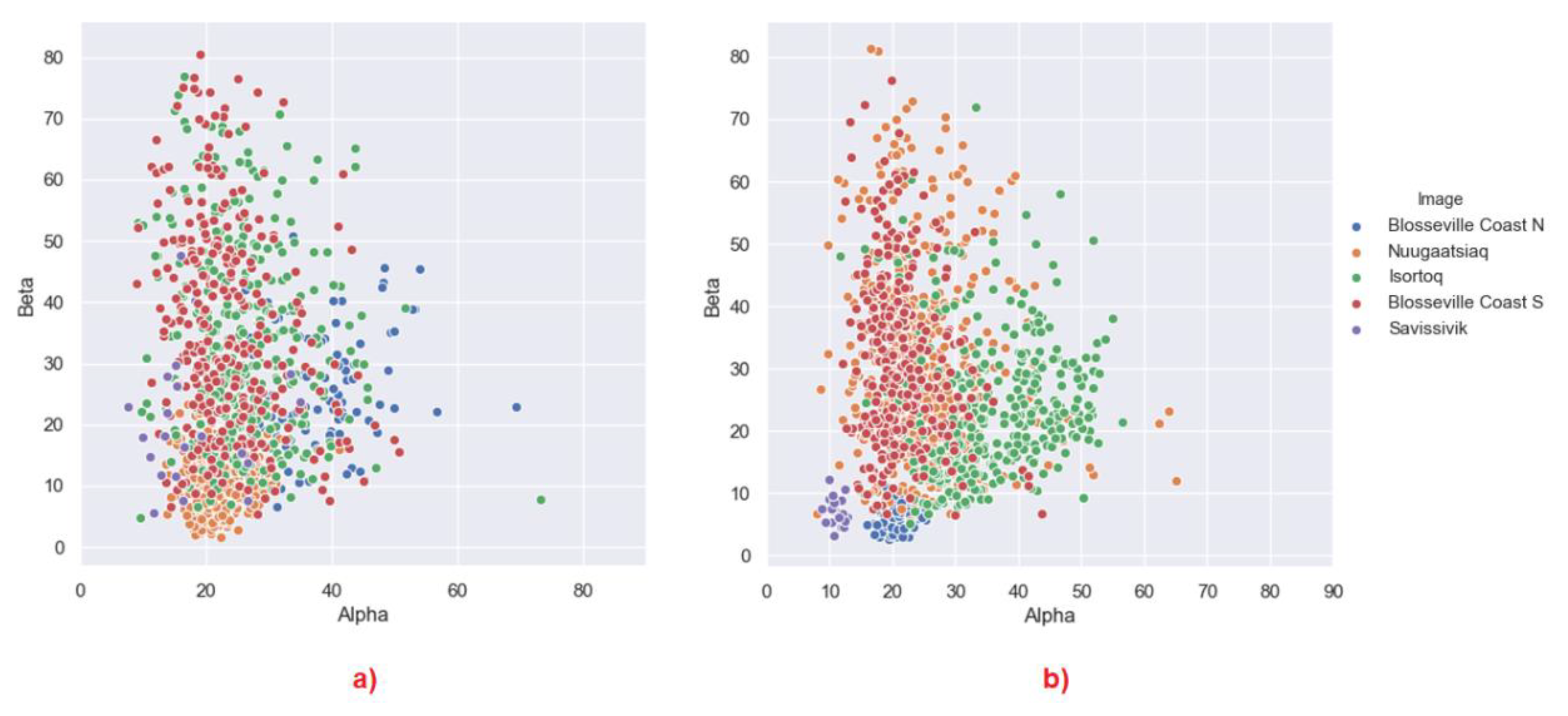
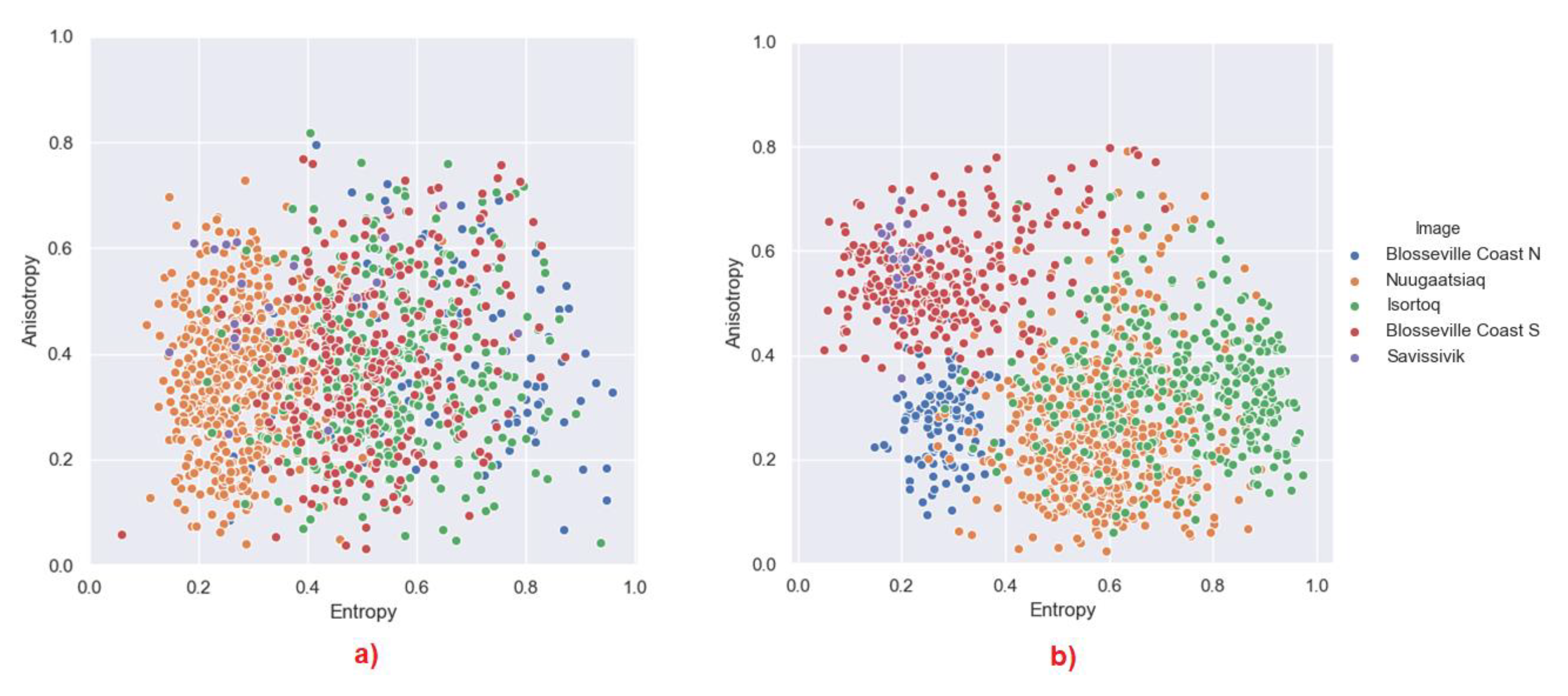
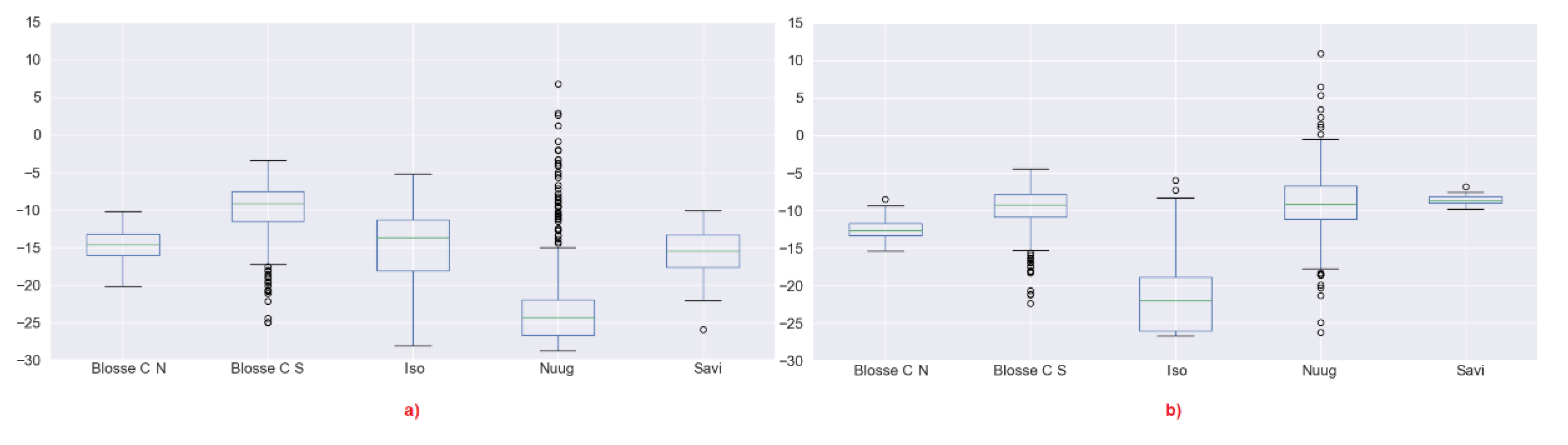
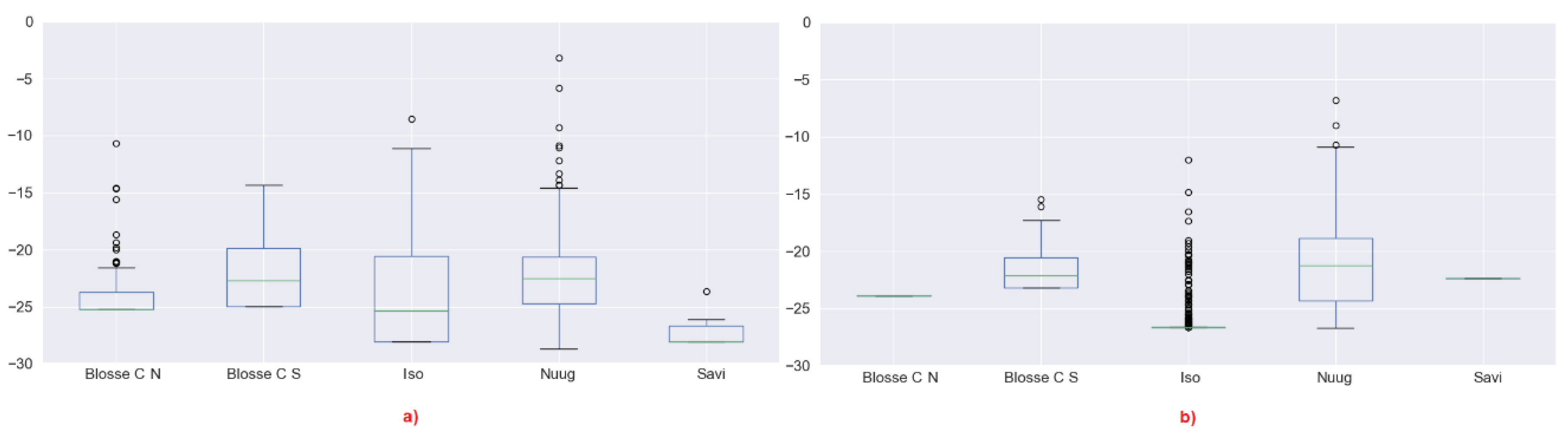
3.2. Polarimetric Behaviour
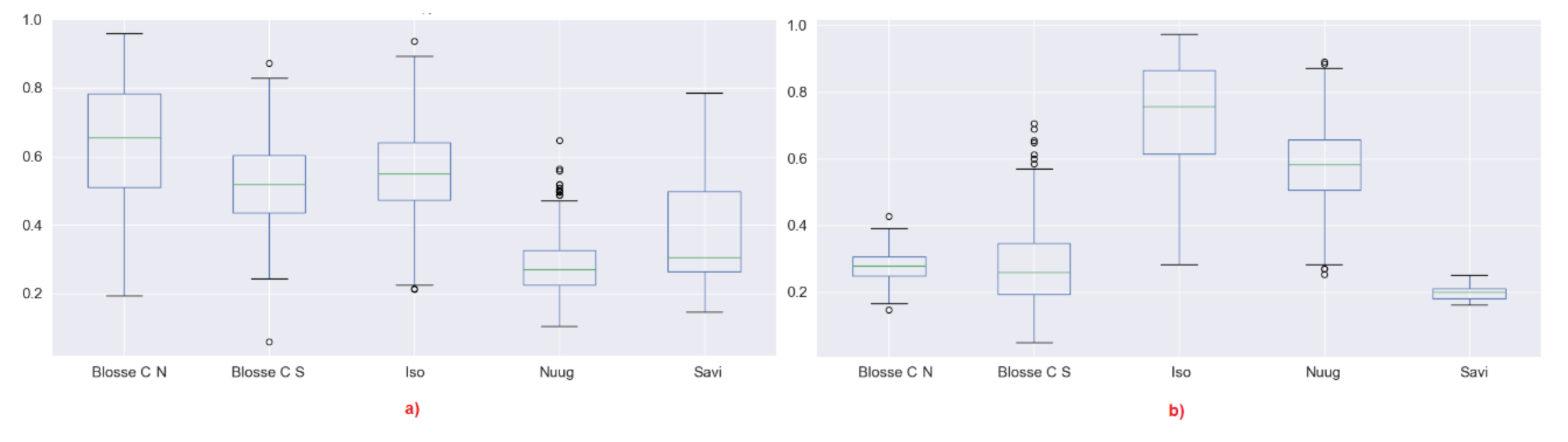
3.2.1. Cloude–Pottier
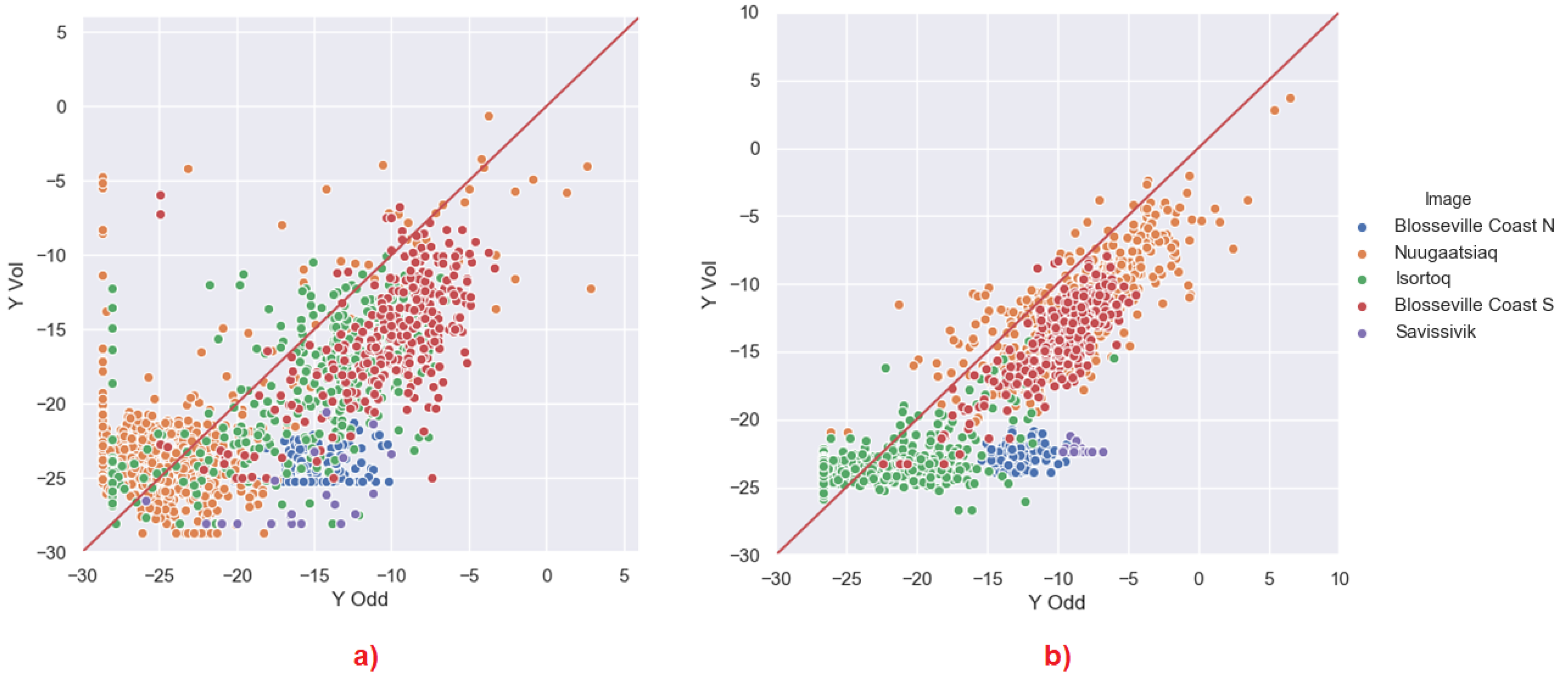
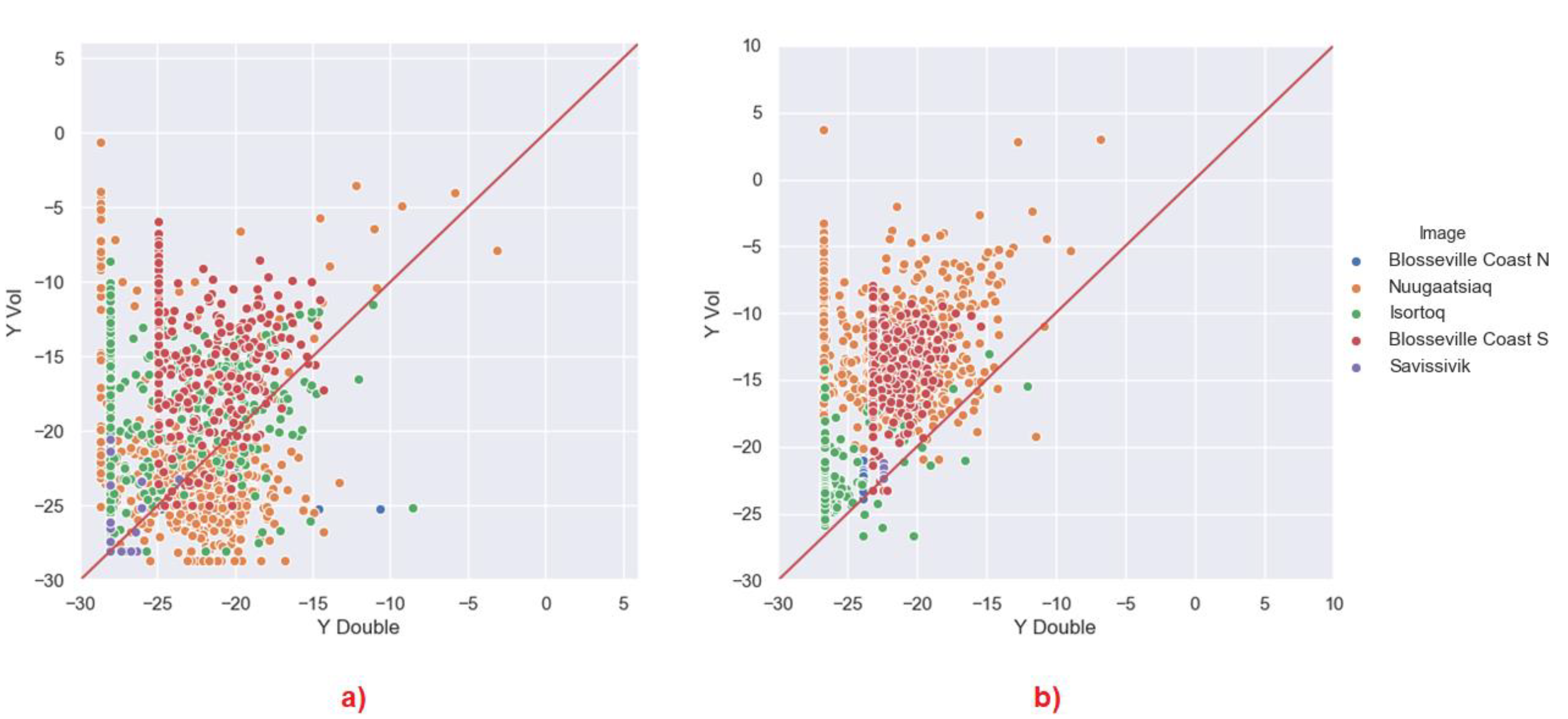
3.2.2. Yamaguchi
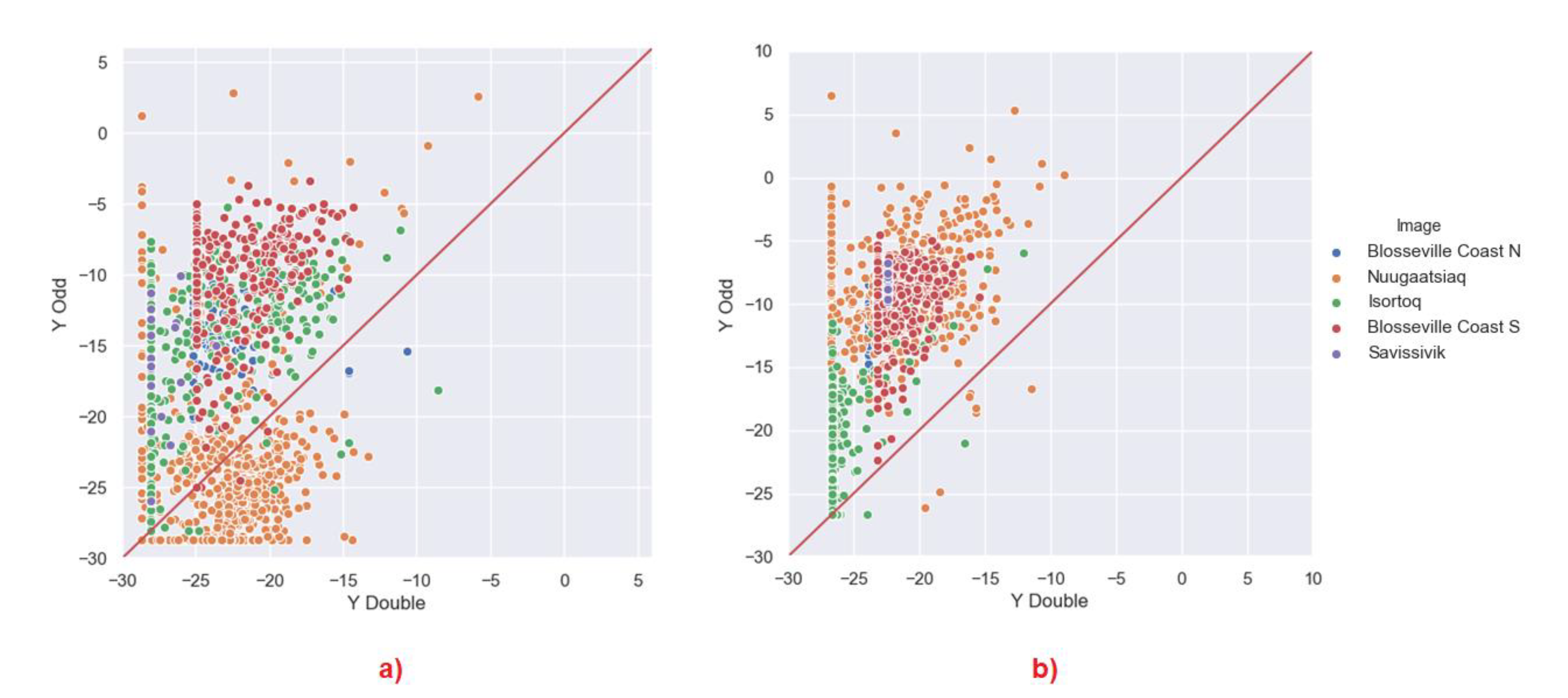
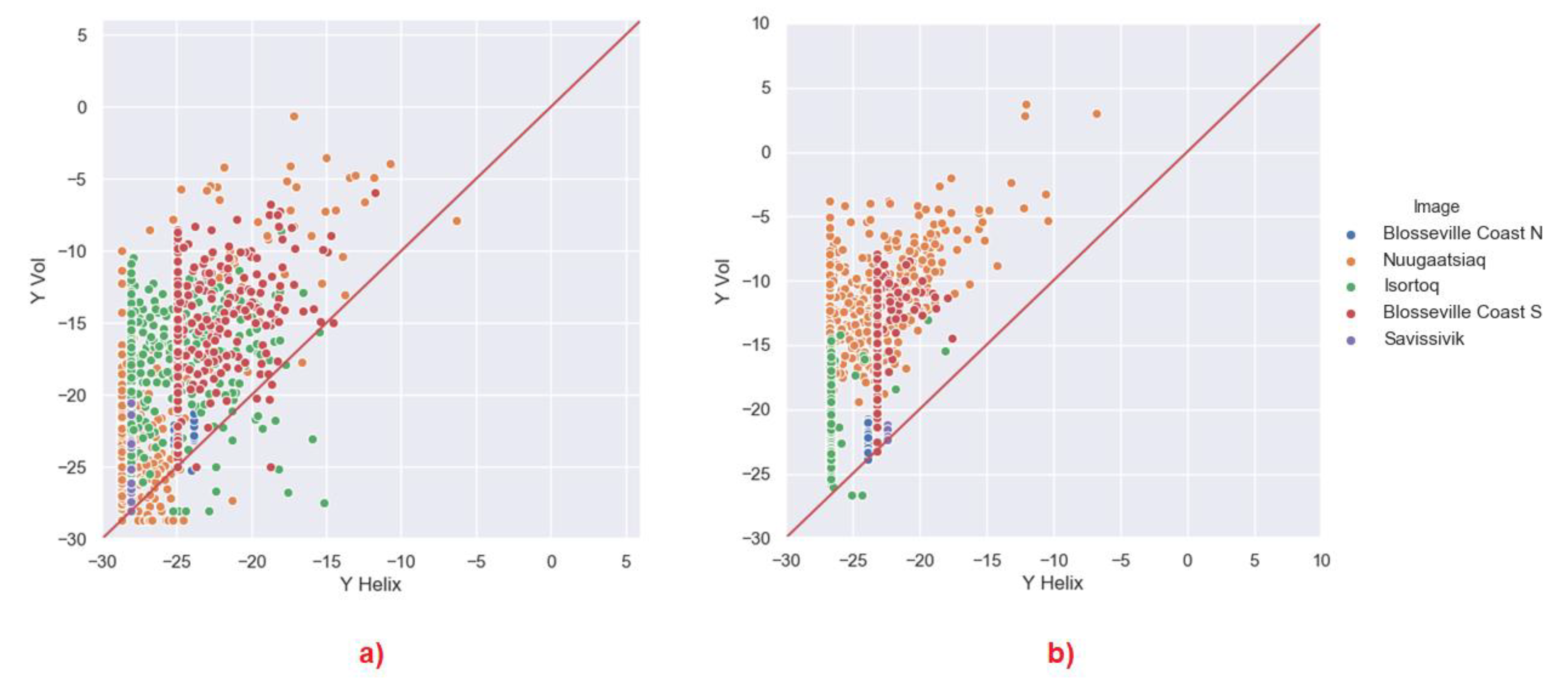
4. Discussion
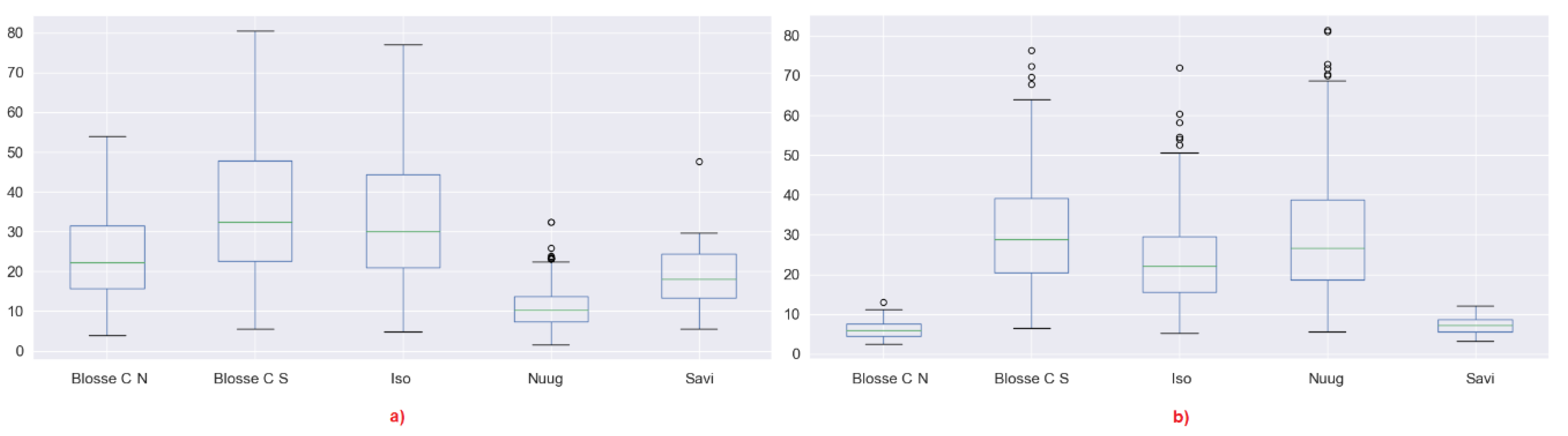
4.1. Depolarisation
- (a)
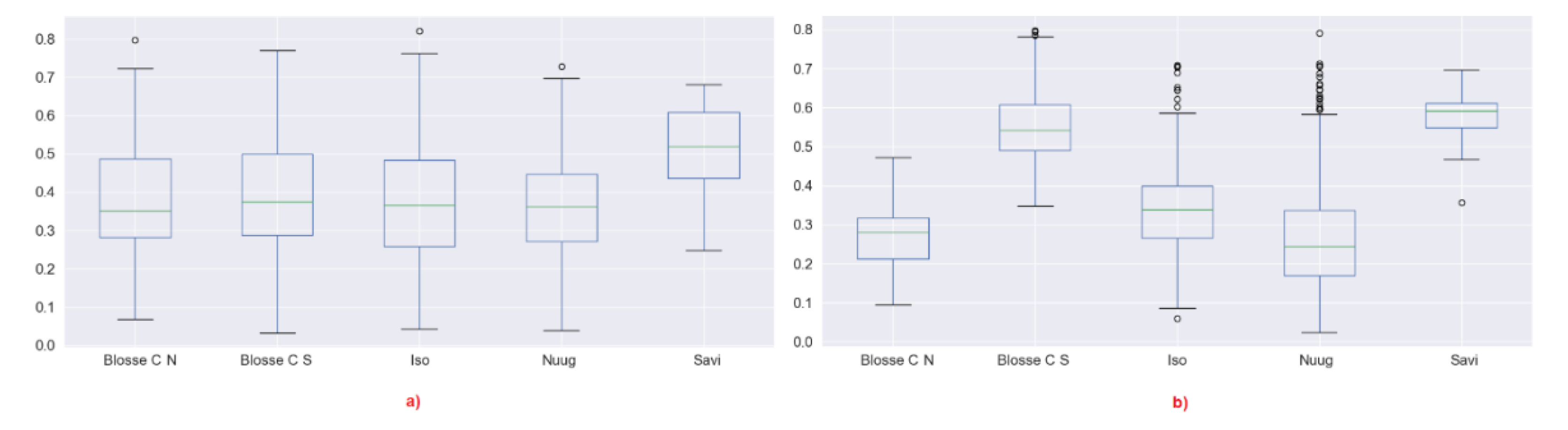
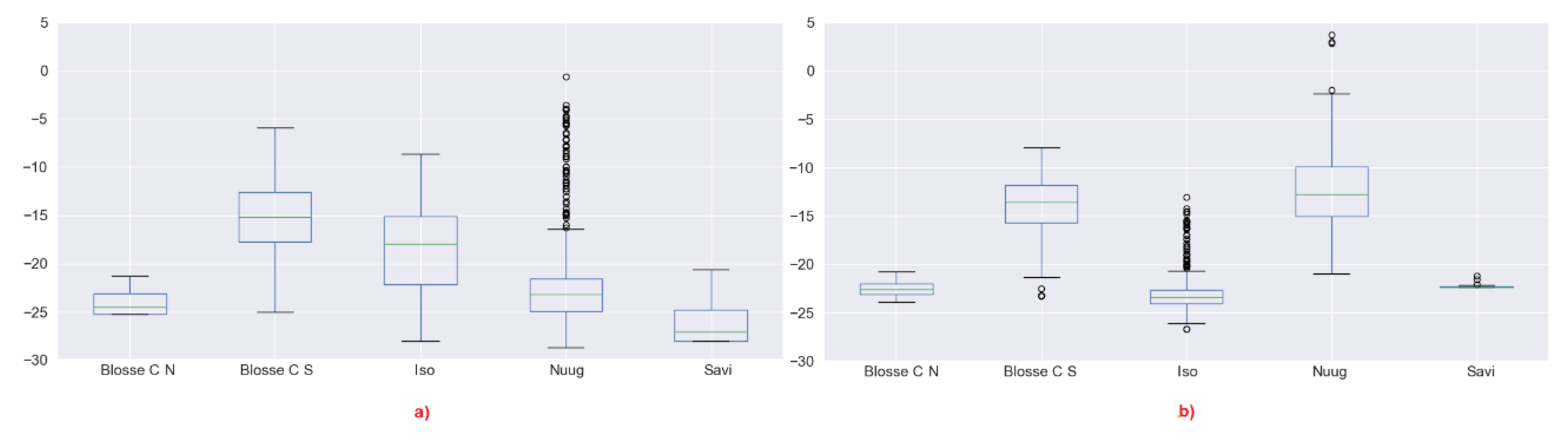
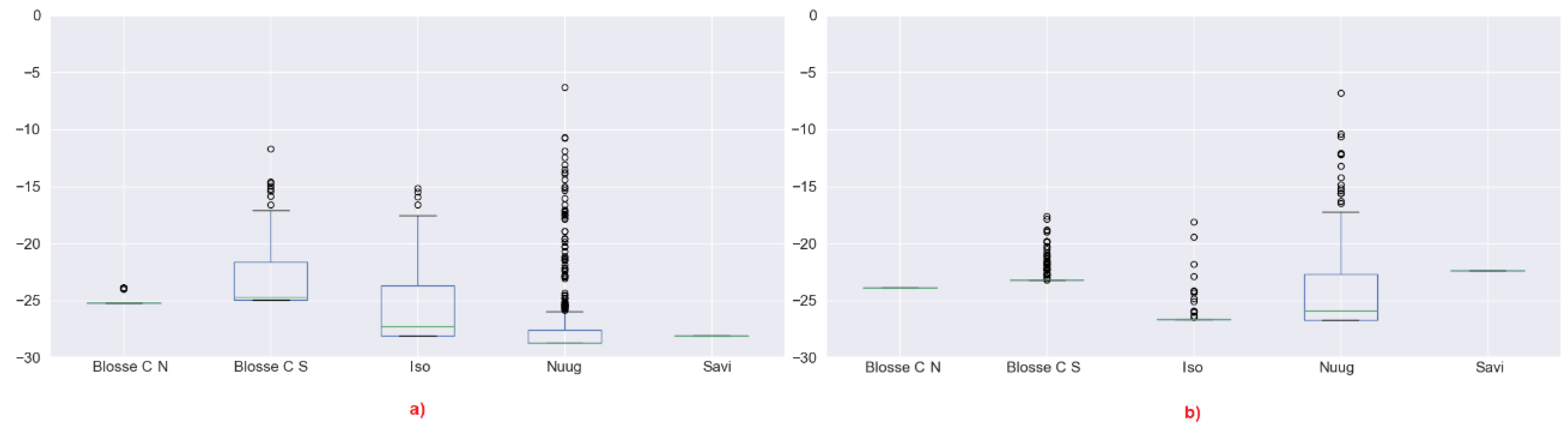
- We may expect that by reducing the window, the entropy may tend to increase because in a smaller window, we expect that it is less likely to have lots of dominant scatterers. This is the case for instance for Nuugaatsiaq and partially for Isortoq. This is an indicator that dominant scatterers in these icebergs are not packed uniformly and very close to each other. When we use a smaller window, we include less dominant scatterers and increase the entropy. Considering the window sizes, we may expect strong scatterers being located no closer than a few tens of metres. This may represent some topographic features of the iceberg. From a more theoretical point of view, it indicates that scattering from those icebergs is not well approximated by a partial target with fully developed speckle. A uniform distribution of scatterers is slightly more realistic for Isortoq, where the reduction is not very large, although the values are already quite high to start with due to the low backscattering and the effect of noise.
- (b)
- Blosseville Coast N and S and Savissivik are an interesting case, since several icebergs reduce their entropy when increasing the window. Inspecting the images, we revealed that these are smaller icebergs and when increasing the window, we included the edge pixels, which are generally brighter. We therefore included in the window other dominant scatterers that increase the entropy. Please note, we used the middle pixels of the icebergs because we are interested in the scattering behaviour of the ice body, in order to improve our understanding of icebergs. If we had to include the edges for all the icebergs, we may have masked the inner behaviour. Nevertheless, when the icebergs are small, excluding the edge is simply not an option. This is also true for detection studies in which iceberg edges could be critical to identify icebergs [30].
4.2. Target Characteristics
4.3. Model Based Analysis
4.4. Summary
5. Conclusions and Further Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wesche, C.; Dierking, W. Estimating iceberg paths using a wind-driven drift model. Cold Reg. Sci. Technol. 2016, 125, 31–39. [Google Scholar] [CrossRef]
- Denbina, M.; Collins, M.J. Iceberg detection using compact polarimetric synthetic aperture radar. Atmos.-Ocean 2012, 50, 437–446. [Google Scholar] [CrossRef][Green Version]
- Vincent, W.F. Arctic Climate Change: Local Impacts, Global Consequences, and Policy Implications. In The Palgrave Handbook of Arctic Policy and Politics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 507–526. [Google Scholar]
- Xie, S.; Dixon, T.H.; Holland, D.M.; Voytenko, D.; Vaňková, I. Rapid iceberg calving following removal of tightly packed pro-glacial mélange. Nat. Commun. 2019, 10, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Akbari, V.; Doulgeris, A.P.; Brekke, C. Subaperture analysis of polarimetric SAR data for iceberg detection. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5666–5669. [Google Scholar]
- Zakharov, I.; Power, D.; Bobby, P.; Randell, C. Multi-resolution SAR data analysis for automated retrieval of sea ice and iceberg parameters. In Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 9–13 September 2013. [Google Scholar]
- Hannevik, T.N. Literature review on ship and ice discrimination; 824642985X; Norwegian Defence Research Establishment: Kjeller, Norway, 2017; p. 34. [Google Scholar]
- Ferdous, M.S.; Himi, U.H.; McGuire, P.; Power, D.T.; Johnson, T.; Collins, M.J. C-Band Simulations of Melting Icebergs Using GRECOSAR and an EM Model: Varying Wind Conditions at Lower Beam Mode. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2019, 12, 5134–5146. [Google Scholar] [CrossRef]
- Hanna, E.; Mernild, S.H.; Cappelen, J.; Steffen, K. Recent warming in Greenland in a long-term instrumental (1881–2012) climatic context: I. Evaluation of surface air temperature records. Environ. Res. Lett. 2012, 7, 045404. [Google Scholar] [CrossRef]
- Fettweis, X.; Hanna, E.; Huybrechts, P.; Erpicum, M. Estimation of the Greenland ice sheet surface mass balance for the 20th and 21st centuries. Cryosphere 2008, 2, 117–129. [Google Scholar] [CrossRef]
- Dowdeswell, J.A.; Jeffries, M.O. Arctic ice shelves: An introduction. In Arctic Ice Shelves and Ice Islands; Springer: Berlin/Heidelberg, Germany, 2017; pp. 3–21. [Google Scholar]
- Romanov, Y.A.; Romanova, N.A.; Romanov, P. Geographical distribution and volume of Antarctic icebergs derived from ship observation data. Ann. Glaciol. 2017, 58, 28–40. [Google Scholar] [CrossRef]
- Wadhams, P.; Woodwort-Lynas, C. Icebergs; Butterworth-Heinemann Limited: Oxford, UK, 2004. [Google Scholar]
- Soldal, I.H.; Dierking, W.; Korosov, A.; Marino, A. Automatic Detection of Small Icebergs in Fast Ice Using Satellite Wide-Swath SAR Images. Remote Sens. 2019, 11, 806. [Google Scholar] [CrossRef]
- Young, N.; Turner, D.; Hyland, G.; Williams, R. Near-coastal iceberg distributions in East Antarctica, 50-145 E. Ann. Glaciol. 1998, 27, 68–74. [Google Scholar] [CrossRef]
- Wesche, C.; Dierking, W. Iceberg signatures and detection in SAR images in two test regions of the Weddell Sea, Antarctica. J. Glaciol. 2012, 58, 325–339. [Google Scholar] [CrossRef]
- Sudom, D.; Timco, G.; Tivy, A. Iceberg sightings, shapes and management techniques for offshore Newfoundland and Labrador: Historical data and future applications. In Proceedings of the 2014 Oceans-St. John’s, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–8. [Google Scholar]
- Nunziata, F.; Buono, A.; Migliaccio, M.; Moctezuma, M.; Parmiggiani, F.; Aulicino, G. Multi-Frequency and Multi-Polarization Synthetic Aperture Radar for the Larsen-C A-68 Iceberg Monitoring. In Proceedings of the 2018 IEEE 4th International Forum on Research and Technology for Society and Industry (RTSI), Palermo, Italy, 10–13 September 2018; pp. 1–4. [Google Scholar]
- Parmiggiani, F.; Moctezuma-Flores, M.; Guerrieri, L.; Battagliere, M. SAR analysis of the Larsen-C A-68 iceberg displacements. Int. J. Remote Sens. 2018, 39, 5850–5858. [Google Scholar] [CrossRef]
- Marino, A. Iceberg Detection with L-Band ALOS-2 Data Using the Dual-POL Ratio Anomaly Detector. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6067–6070. [Google Scholar]
- Bayer, T.; Winter, R.; Schreier, G. Terrain influences in SAR backscatter and attempts to their correction. IEEE Trans. Geosci. Remote. Sens. 1991, 29, 451–462. [Google Scholar] [CrossRef]
- Kirkham, J.D.; Rosser, N.J.; Wainwright, J.; Jones, E.C.V.; Dunning, S.A.; Lane, V.S.; Hawthorn, D.E.; Strzelecki, M.C.; Szczuciński, W. Drift-dependent changes in iceberg size-frequency distributions. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Dierking, W.; Wesche, C. C-band radar polarimetry—Useful for detection of icebergs in sea ice? IEEE Trans. Geosci. Remote. Sens. 2013, 52, 25–37. [Google Scholar] [CrossRef]
- Willis, C.; Macklin, J.; Partington, K.; Teleki, K.; Rees, W.; Williams, R. Iceberg detection using ERS-1 synthetic aperture radar. Int. J. Remote. Sens. 1996, 17, 1777–1795. [Google Scholar] [CrossRef]
- Marino, A.; Walker, N.; Woodhouse, I. Ship detection with RADARSAT-2 quad-pol SAR data using a notch filter based on perturbation analysis. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3704–3707. [Google Scholar]
- Marino, A.; Dierking, W.; Wesche, C. A depolarization ratio anomaly detector to identify icebergs in sea ice using dual-polarization SAR images. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 5602–5615. [Google Scholar] [CrossRef]
- Akbari, V.; Brekke, C.; Doulgeris, A.P.; Storvold, R.; Sivertsen, A.H. Quad-polarimetric SAR for detection and characterization of icebergs. Proceedings of ESA Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Herdes, E.; Copland, L.; Danielson, B.; Sharp, M. Relationships between iceberg plumes and sea-ice conditions on northeast Devon Ice Cap, Nunavut, Canada. Ann. Glaciol. 2012, 53, 1–9. [Google Scholar] [CrossRef]
- Viehoff, T.; Li, A. Iceberg observations and estimation of submarine ridges in the western Weddell Sea. Int. J. Remote Sens. 1995, 16, 3391–3408. [Google Scholar] [CrossRef]
- Williams, R.; Rees, W.; Young, N. A technique for the identification and analysis of icebergs in synthetic aperture radar images of Antarctica. Int. J. Remote Sens. 1999, 20, 3183–3199. [Google Scholar] [CrossRef]
- Wesche, C.; Dierking, W. Near-coastal circum-Antarctic iceberg size distributions determined from Synthetic Aperture Radar images. Remote Sens. Environ. 2015, 156, 561–569. [Google Scholar] [CrossRef]
- Xiang, D.; Ban, Y.; Su, Y. The cross-scattering component of polarimetric SAR in urban areas and its application to model-based scattering decomposition. Int. J. Remote Sens. 2016, 37, 3729–3752. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Bjørk, A.A.; Kruse, L.; Michaelsen, P. Brief communication: Getting Greenland’s glaciers right–a new data set of all official Greenlandic glacier names. Cryosphere 2015, 9, 2215–2218. [Google Scholar] [CrossRef]
- Ultee, L.; Bassis, J.N. SERMeQ model produces realistic retreat of 155 Greenland outlet glaciers. Earth Space Sci. Open Arch. 2020, 15. [Google Scholar] [CrossRef]
- Sinclair, G. The transmission and reception of elliptically polarized waves. Proc. IRE 1950, 38, 148–151. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Lee, J.-S.; Jurkevich, L.; Dewaele, P.; Wambacq, P.; Oosterlinck, A. Speckle filtering of synthetic aperture radar images: A review. Remote Sens. Rev. 1994, 8, 313–340. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; Schuler, D.L.; Pottier, E.; Ferro-Famil, L. Scattering-model-based speckle filtering of polarimetric SAR data. IEEE Trans. Geosci. Remote. Sens. 2005, 44, 176–187. [Google Scholar]
- Chandrasekhar, S. Radiative Transfer; Dover: New York, NY, USA, 1960. [Google Scholar]
- Cloude, S.R. Uniqueness of target decomposition theorems in radar polarimetry. In Direct and Inverse Methods in Radar Polarimetry; Springer: Berlin/Heidelberg, Germany, 1992; pp. 267–296. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote. Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote. Sens. 1998, 32, 963–973. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote. Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Muhuri, A.; De, S.; Manickam, S.; Frery, A.C. Modifying the Yamaguchi four-component decomposition scattering powers using a stochastic distance. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2015, 8, 3497–3506. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Minetani, Y.; Umemura, M.; Yamada, H. Experimental Validation of Conifer and Broad-Leaf Tree Classification Using High Resolution PolSAR Data above X-Band. Ieice Trans. Commun. 2019, 1345–1350. [Google Scholar] [CrossRef]





| Image ID | Location | Lat/Lon (DMS) | Resolution | Incidence Angle Range (°) | Date/Time |
|---|---|---|---|---|---|
| ALOS2066231360-150815 | Blosseville Coast N | 68°02’13.2”N 30°19’58.8”W | 4.3 × 5.1 | 37, 39, 41.5 | 15/08/2015 01:26 |
| ALOS2064761430-150805 | Nuugaatsiaq | 71°25’26.4”N 53°26’52.8”W | 4.3 × 5.1 | 37, 39, 41.5 | 05/08/2015 02:48 |
| ALOS2064461300-150803 | Isortoq | 65°07’08.4”N 39°13’37.2”W | 4.3 × 5.1 | 37, 39, 41.5 | 03/08/2015 02:07 |
| ALOS2057951350-150620 | Blosseville Coast S | 67°19’1.2’’N 32°37’33.6’’W | 4.3 × 5.1 | 29, 31, 33.6 | 20/06/2015 01:26 |
| ALOS2191031530-171206 | Savissivik | 75°52’19.2’’N 62°10’48’’W | 4.3 × 5.1 | 29, 31, 33.6 | 06/12/2017 02:52 |
| Parameter | Type | Notes |
|---|---|---|
| Alpha | Cloude–Pottier Decomposition | - |
| Entropy | Cloude–Pottier Decomposition | - |
| Beta | Cloude–Pottier Decomposition | - |
| Anisotropy | Cloude–Pottier Decomposition | - |
| Span | Observable | - |
| Y Double | Yamaguchi Decomposition | Orientation removed |
| Y Helix | Yamaguchi Decomposition | Orientation removed |
| Y Surface | Yamaguchi Decomposition | Orientation removed |
| Y Volume | Yamaguchi Decomposition | Orientation removed |
| Location | Min Temperature (°C) | Average Rainfall (mm) | Average Wind Speed (km/h) | Date Taken |
|---|---|---|---|---|
| Angmagssalik | −3 | 5.44 | 6.9 | 03/08/2015 |
| Angmagssalik | −4 | 25.18 | 7.6 | 20/06/2015 |
| Angmagssalik | −3 | 5.44 | 6.9 | 15/08/2015 |
| Qaarsut Airport | 1 | 78.94 | 6.2 | 05/08/2015 |
| Thule Air Base | −18 | 4.83 | 11.7 | 06/12/2017 |
| Name of Glacier | Tongue Width (km) | Estimated Calving Rate (km/yr) | Location | Iceberg Size |
|---|---|---|---|---|
| Hammer | 16 | <5 | Blosseville Coast N | Small |
| Nakkala | 15 | <5 | Nuugaatsiaq | Medium |
| Apuseeq | 4 | <5 | Isortoq | Small |
| Søndre Parallelgletsjer | 12 | <5 | Blosseville Coast S | Large |
| Morell | 10 | <5 | Savissivik | Small |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bailey, J.; Marino, A. Quad-Polarimetric Multi-Scale Analysis of Icebergs in ALOS-2 SAR Data: A Comparison between Icebergs in West and East Greenland. Remote Sens. 2020, 12, 1864. https://doi.org/10.3390/rs12111864
Bailey J, Marino A. Quad-Polarimetric Multi-Scale Analysis of Icebergs in ALOS-2 SAR Data: A Comparison between Icebergs in West and East Greenland. Remote Sensing. 2020; 12(11):1864. https://doi.org/10.3390/rs12111864
Chicago/Turabian StyleBailey, Johnson, and Armando Marino. 2020. "Quad-Polarimetric Multi-Scale Analysis of Icebergs in ALOS-2 SAR Data: A Comparison between Icebergs in West and East Greenland" Remote Sensing 12, no. 11: 1864. https://doi.org/10.3390/rs12111864
APA StyleBailey, J., & Marino, A. (2020). Quad-Polarimetric Multi-Scale Analysis of Icebergs in ALOS-2 SAR Data: A Comparison between Icebergs in West and East Greenland. Remote Sensing, 12(11), 1864. https://doi.org/10.3390/rs12111864






