Simulating Multi-Directional Narrowband Reflectance of the Earth’s Surface Using ADAM (A Surface Reflectance Database for ESA’s Earth Observation Missions)
Abstract
1. Introduction
- For the soil/vegetation pixels, the spectral interpolation/extrapolation of the MODIS broad-bands/normalized reflectances between 240 and 4000 nm is performed using empirical orthogonal functions (EOFs) derived from spectral reflectance databases of soil/vegetation/leaf optical properties (similar to [1]). The Ross–Li-HS kernel based BRDF model [35] is used to calculate the reflectance spectrum in any illumination/observation geometry. A separate processing scheme is applied for snow covered surfaces: It relies on the Asymptotic Radiative Transfer (ART) model [36], fitted to the normalized reflectances, to simulate the spectro-directional variations of snow reflectance. Moreover, it is possible to calculate the uncertainty attached to the land surface reflectance: the calculation relies on the variance covariance matrix of the reflectance values between the seven MODIS bands for each 0.1° × 0.1° pixel.
- Over water surfaces, the reflectance is simulated by a combination of three components: (i) the water column and (ii) foam, that mainly shape reflectance spectral variations, and (iii) the specular reflection that essentially drives reflectance directionality. The water column reflectance is parameterized as a function of the chlorophyll content and specular reflection (also referred to as sunglint), which mostly depends on the wind speed.
2. ADAM Spectral and Directional Calculation Models (API Toolkit)
2.1. Land Surfaces
2.1.1. Vegetation and Soil
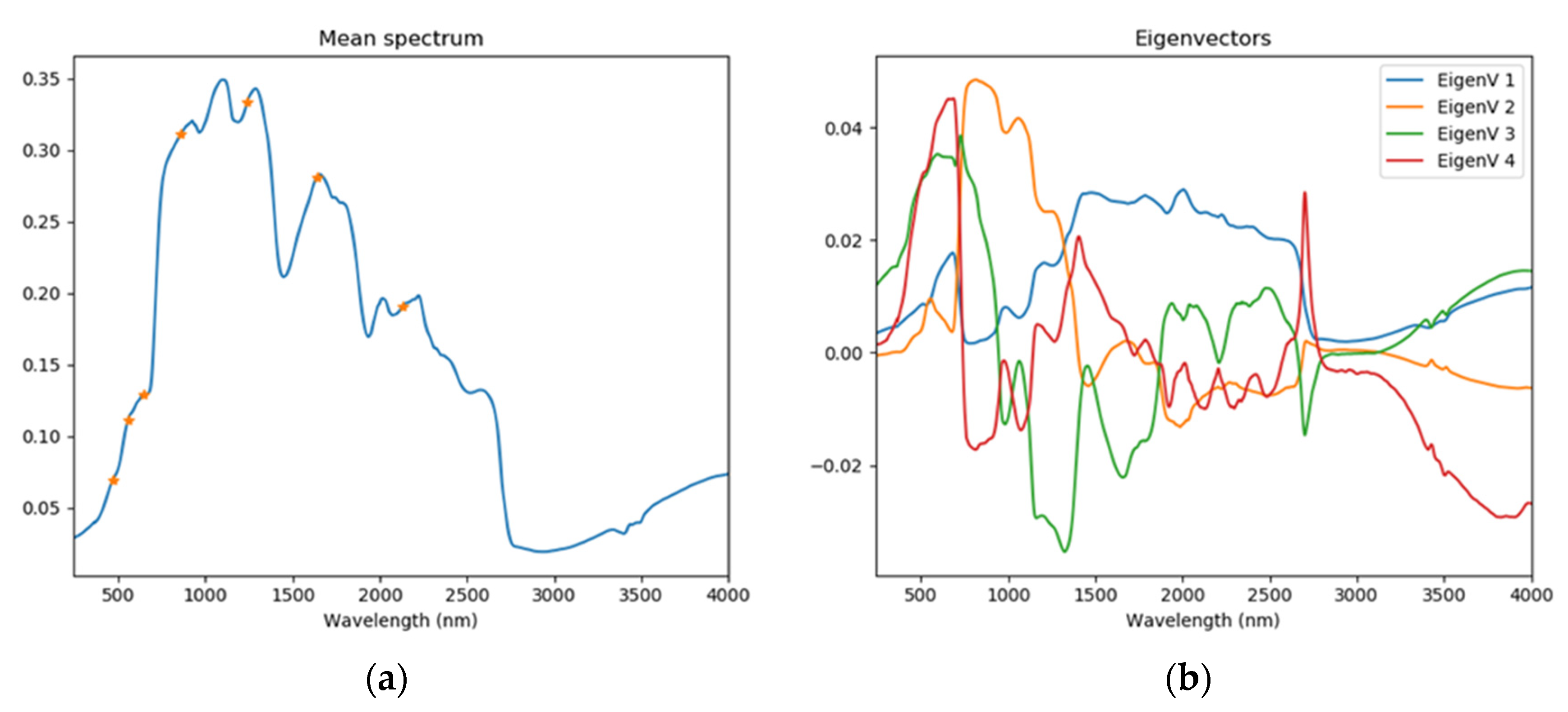
Spectral Modeling
Directional Modeling
2.1.2. Snow and Sea Ice
2.2. Water Surfaces (Ocean and Inland Lakes)
- the column reflectance, that has a strong spectral variation but limited directional variation. Here, we consider only waters of Case 1 (using the definition of [46]), corresponding mostly to open ocean (i.e., excluding coastal areas), for which the absorption and scattering properties can be correlated with chlorophyll concentration (chl);
- the specular reflectance, which has a strong directional effect with negligible spectral variation, that mostly depends on the wind speed (ws);
- the foam reflectance, that has limited spectral and directional effects.
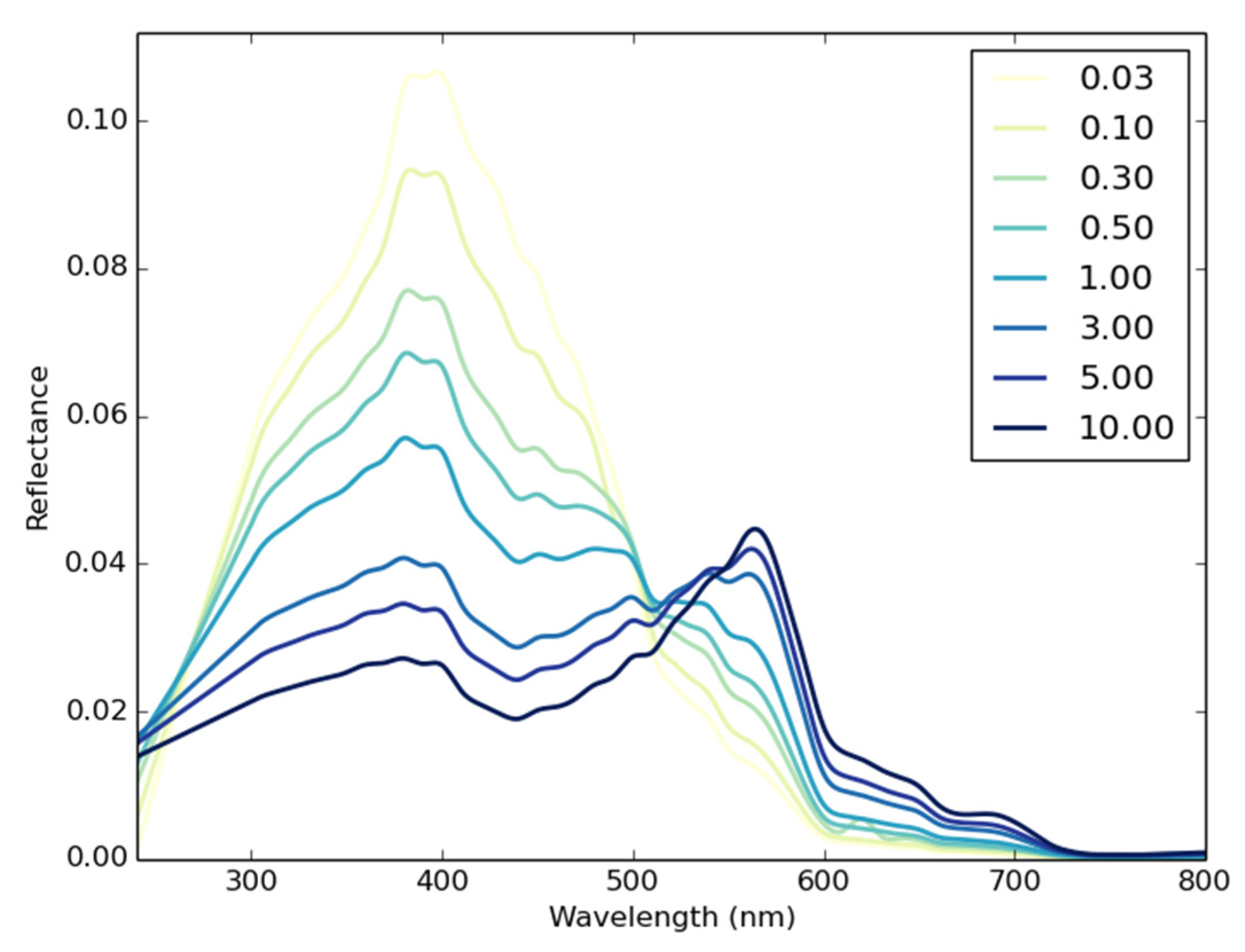
2.2.1. Water Column Reflectance
2.2.2. Glint Reflectance
2.2.3. Foam Reflectance
3. Input Data and Processing
3.1. Land
3.2. Ocean
3.2.1. Chlorophyll Content
3.2.2. Wind Speed
3.3. Gap-Filling
3.3.1. Polar Land Regions
3.3.2. Water Surface Products
3.3.3. Sea Ice
3.4. Ancillary Data
3.4.1. Land
3.4.2. Water Surfaces
4. ADAM Products
4.1. ADAM Database Format
4.2. Availability of the ADAM Product and Online Calculation Tools for Plotting
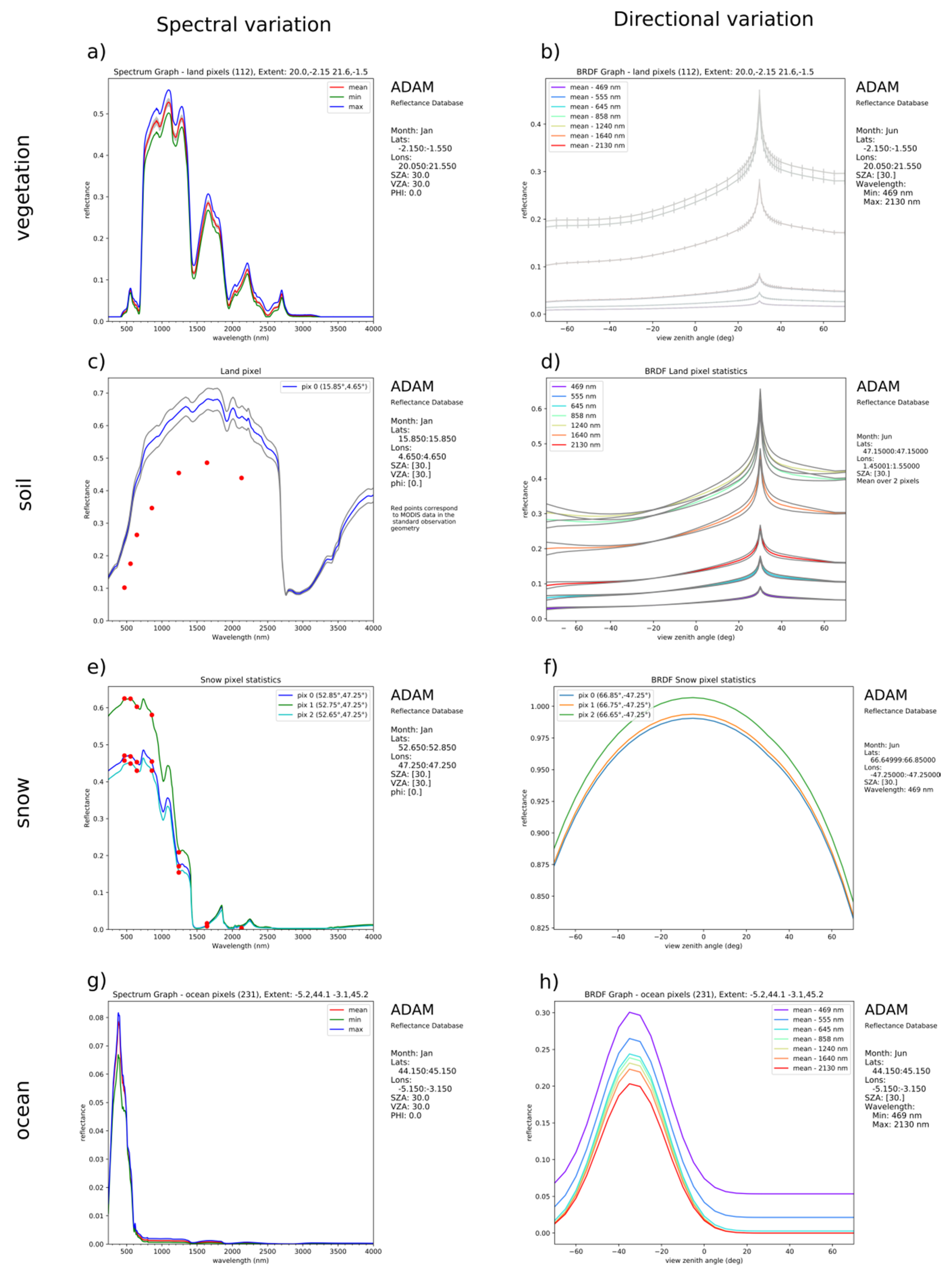
4.3. Representative Simulations with ADAM API and Database
5. Evaluation of the ADAM Product over Land
5.1. Comparison of ADAM with POLDER Multi-Spectral/Multi-Directional Observations
5.1.1. Evaluation Dataset
5.1.2. Methods
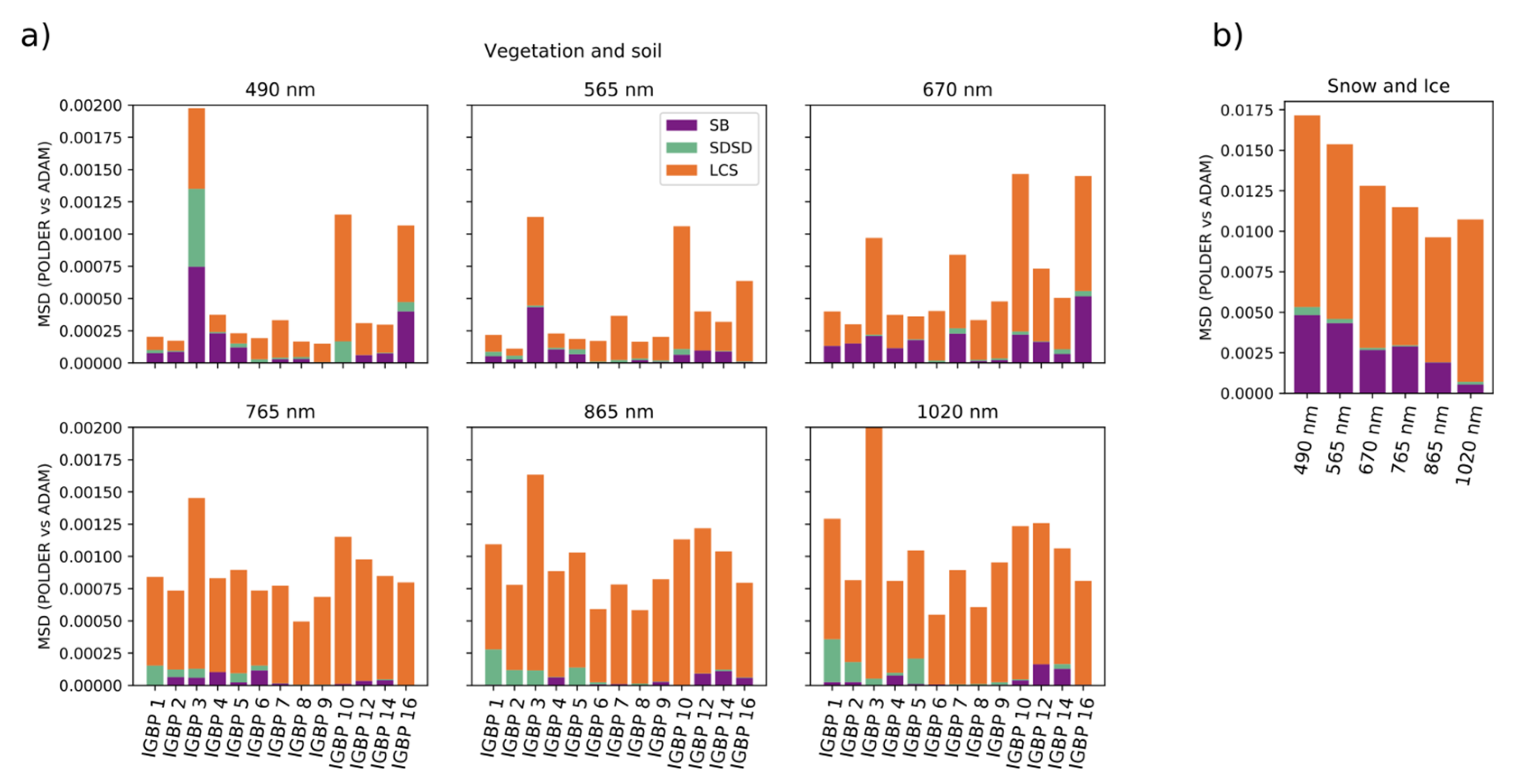
5.1.3. Results
5.2. Comparison with CALIPSO Lidar Observations at 532 nm
5.2.1. Rationales
5.2.2. Evaluation Dataset
5.2.3. Methods
5.2.4. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Vidot, J.; Borbás, É. Land surface VIS/NIR BRDF atlas for RTTOV-11: Model and validation against SEVIRI land SAF albedo product: Land Surface VIS/NIR BRDF Atlas for RTTOV-11. Q. J. R. Meteorol. Soc. 2014, 140, 2186–2196. [Google Scholar] [CrossRef]
- Hou, W.; Wang, J.; Xu, X.; Reid, J.S. An algorithm for hyperspectral remote sensing of aerosols: 2. Information content analysis for aerosol parameters and principal components of surface spectra. J. Quant. Spectrosc. Radiat. Transf. 2017, 192, 14–29. [Google Scholar] [CrossRef]
- Peltoniemi, J.I.; Kaasalainen, S.; Naranen, J.; Matikainen, L.; Piironen, J. Measurement of directional and spectral signatures of light reflectance by snow. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2294–2304. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Sobrino, J.A.; Fédèle, E. Analysis of directional effects on atmospheric correction. Remote Sens. Environ. 2013, 128, 276–288. [Google Scholar] [CrossRef]
- Vermote, E.F.; Kotchenova, S. Atmospheric correction for the monitoring of land surfaces. J. Geophys. Res. Atmos. 2008, 113, D23. [Google Scholar] [CrossRef]
- Wang, Y.; Lyapustin, A.I.; Privette, J.L.; Cook, R.B.; SanthanaVannan, S.K.; Vermote, E.F.; Schaaf, C.L. Assessment of biases in MODIS surface reflectance due to Lambertian approximation. Remote Sens. Environ. 2010, 114, 2791–2801. [Google Scholar] [CrossRef]
- Zhang, H.; Jiao, Z.; Chen, L.; Dong, Y.; Zhang, X.; Lian, Y.; Qian, D.; Cui, T. Quantifying the Reflectance Anisotropy Effect on Albedo Retrieval from Remotely Sensed Observations Using Archetypal BRDFs. Remote Sens. 2018, 10, 1628. [Google Scholar] [CrossRef]
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. MODIS Collection 6 MAIAC algorithm. Atmos. Meas. Tech. 2018, 11. [Google Scholar] [CrossRef]
- von Hoyningen-Huene, W.; Freitag, M.; Burrows, J.B. Retrieval of aerosol optical thickness over land surfaces from top-of-atmosphere radiance. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Mei, L.; Rozanov, V.; Vountas, M.; Burrows, J.P.; Levy, R.C.; Lotz, W. Retrieval of aerosol optical properties using MERIS observations: Algorithm and some first results. Remote Sens. Environ. 2017, 197, 125–140. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.M.; Liu, H.; Laszlo, I.; Kondragunta, S.; Remer, L.A.; Huang, J.; Huang, H.-C. Suomi-NPP VIIRS aerosol algorithms and data products. J. Geophys. Res. Atmos. 2013, 118, 12–673. [Google Scholar] [CrossRef]
- Boersma, K.F.; Eskes, H.J.; Dirksen, R.J.; Veefkind, J.P.; Stammes, P.; Huijnen, V.; Kleipool, Q.L.; Sneep, M.; Claas, J.; Leitão, J. An improved tropospheric NO2 column retrieval algorithm for the Ozone Monitoring Instrument. Atmos. Meas. Tech. 2011, 4, 1905–1928. [Google Scholar] [CrossRef]
- Bucsela, E.J.; Krotkov, N.A.; Celarier, E.A.; Lamsal, L.N.; Swartz, W.H.; Bhartia, P.K.; Boersma, K.F.; Veefkind, J.P.; Gleason, J.F.; Pickering, K.E. A new stratospheric and tropospheric NO2 retrieval algorithm for nadir-viewing satellite instruments: Applications to OMI. Atmos. Meas. Tech. 2013, 6, 2607–2626. [Google Scholar] [CrossRef]
- Acarreta, J.R.; De Haan, J.F.; Stammes, P. Cloud pressure retrieval using the O2-O2 absorption band at 477 nm. J. Geophys. Res. Atmos. 2004, 109, D5. [Google Scholar] [CrossRef]
- Koelemeijer, R.B.A.; Stammes, P.; Hovenier, J.W.; de Haan, J. A fast method for retrieval of cloud parameters using oxygen A band measurements from the Global Ozone Monitoring Experiment. J. Geophys. Res. Atmos. 2001, 106, 3475–3490. [Google Scholar] [CrossRef]
- Joiner, J.; Vasilkov, A.P. First results from the OMI rotational Raman scattering cloud pressure algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1272–1282. [Google Scholar] [CrossRef]
- Noguchi, K.; Richter, A.; Rozanov, V.; Rozanov, A.; Burrows, J.P.; Irie, H.; Kita, K. Effect of surface BRDF of various land cover types on geostationary observations of tropospheric NO2. Atmos. Meas. Tech. 2014, 7, 3497–3508. [Google Scholar] [CrossRef]
- Lorente, A.; Folkert Boersma, K.; Stammes, P.; Gijsbert Tilstra, L.; Richter, A.; Yu, H.; Kharbouche, S.; Muller, J.-P. The importance of surface reflectance anisotropy for cloud and NO2 retrievals from GOME-2 and OMI. Atmos. Meas. Tech. 2018, 11, 4509–4529. [Google Scholar] [CrossRef]
- Zhou, Y.; Brunner, D.; Spurr, R.J.D.; Boersma, K.F.; Sneep, M.; Popp, C.; Buchmann, B. Accounting for surface reflectance anisotropy in satellite retrievals of tropospheric NO2. Atmos. Meas. Tech. 2010, 3, 1185. [Google Scholar] [CrossRef]
- Popp, C.; Wang, P.; Brunner, D.; Stammes, P.; Zhou, Y.; Grzegorski, M. MERIS albedo climatology for FRESCO+ O2 A-band cloud retrieval. Atmos. Meas. Tech. 2011, 4, 463–483. [Google Scholar] [CrossRef]
- Vasilkov, A.; Qin, W.; Krotkov, N.; Lamsal, L.; Spurr, R.; Haffner, D.; Joiner, J.; Eun-Su, Y.; Marchenko, S. Accounting for the effects of surface BRDF on satellite cloud and trace-gas retrievals: A new approach based on geometry-dependent Lambertian equivalent reflectivity applied to OMI algorithms. Atmos. Meas. Tech. 2017, 10, 333. [Google Scholar] [CrossRef]
- Herman, J.R.; Celarier, E.A. Earth surface reflectivity climatology at 340–380 nm from TOMS data. J. Geophys. Res. Atmos. 1997, 102, 28003–28011. [Google Scholar] [CrossRef]
- Koelemeijer, R.B.A.; De Haan, J.F.; Stammes, P. A database of spectral surface reflectivity in the range 335–772 nm derived from 5.5 years of GOME observations. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Kleipool, Q.L.; Dobber, M.R.; de Haan, J.; Levelt, P.F. Earth surface reflectance climatology from 3 years of OMI data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Tilstra, L.G.; Wang, P.; Stammes, P. Surface reflectivity climatologies from UV to NIR determined from Earth observations by GOME-2 and SCIAMACHY. J. Geophys. Res. Atmos. 2017, 122, 4084–4111. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Martonchik, J.V.; Diner, D.J.; Pinty, B.; Verstraete, M.M.; Myneni, R.B.; Knyazikhin, Y.; Gordon, H.R. Determination of land and ocean reflective, radiative, and biophysical properties using multiangle imaging. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1266–1281. [Google Scholar] [CrossRef]
- Muller, J.-P.; López, G.; Watson, G.; Shane, N.; Kennedy, T.; Yuen, P.; Lewis, P.; Fischer, J.; Guanter, L.; Domench, C. The ESA GlobAlbedo Project for mapping the Earth’s land surface albedo for 15 Years from European Sensors. In Proceedings of the EGU, Vienna, Austria, 22–27 April 2012; Volume 13, p. 10969. [Google Scholar]
- Gonzalez, L.; Bréon, F.-M.; Caillault, K.; Briottet, X. A sub km resolution global database of surface reflectance and emissivity based on 10-years of MODIS data. ISPRS J. Photogramm. Remote Sens. 2016, 122, 222–235. [Google Scholar] [CrossRef]
- Bicheron, P.; Leroy, M. Bidirectional reflectance distribution function signatures of major biomes observed from space. J. Geophys. Res. Atmos. 2000, 105, 26669–26681. [Google Scholar] [CrossRef]
- Bréon, F.-M.; Maignan, F. A BRDF–BPDF database for the analysis of Earth target reflectances. Earth Syst. Sci. Data 2017, 9, 31–45. [Google Scholar] [CrossRef]
- Kharbouche, S.; Muller, J.-P.; Lewis, P.E. A 15 Year Climatology of Spectral BRDF Derived from MODIS for a Priori Optimal Estimation of Global Surface Albedo within the EU-FP7 QA4ECV Project; International Symposium on Remote Sensing of the Environment: Berlin, Germany, 2014. [Google Scholar]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Maignan, F.; Bréon, F.-M.; Lacaze, R. Bidirectional reflectance of Earth targets: Evaluation of analytical models using a large set of spaceborne measurements with emphasis on the Hot Spot. Remote Sens. Environ. 2004, 90, 210–220. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Zege, E.P. Scattering optics of snow. Appl. Opt. 2004, 43, 1589–1602. [Google Scholar] [CrossRef] [PubMed]
- Bacour, C.; Gonzalez, L.; Bréon, F.-M. A Surface Reflectance DAtabase for ESA’s Earth Observation Missions (ADAM). Improvement and/or Expension of Existing Surface Datasets—Algorithmic Theoretical Basis Document. Technical Note 4 for ESA Study Contract Nr C4000102979/CCN No6. NOVELTIS: Labège, France, 2019; 109p, Available online: https://adam.noveltis.fr/permalink/NOV-FE-0724-ATBD.pdf (accessed on 15 March 2020).
- Bell, I.E.; Baranoski, G.V. Reducing the dimensionality of plant spectral databases. IEEE Trans. Geosci. Remote Sens. 2004, 42, 570–576. [Google Scholar] [CrossRef]
- Liu, L.; Song, B.; Zhang, S.; Liu, X. A novel principal component analysis method for the reconstruction of leaf reflectance spectra and retrieval of leaf biochemical contents. Remote Sens. 2017, 9, 1113. [Google Scholar] [CrossRef]
- Hou, W.; Mao, Y.; Xu, C.; Li, Z.; Li, D.; Ma, Y.; Xu, H. Study on the spectral reconstruction of typical surface types based on spectral library and principal component analysis. In Proceedings of the Fifth Symposium on Novel Optoelectronic Detection Technology and Application, Xi’an, China, 24–26 October 2018; International Society for Optics and Photonics, 2019; Volume 11023, p. 110232T. [Google Scholar]
- Jiao, Z.; Dong, Y.; Schaaf, C.B.; Chen, J.M.; Román, M.; Wang, Z.; Zhang, H.; Ding, A.; Erb, A.; Hill, M.J. An algorithm for the retrieval of the clumping index (CI) from the MODIS BRDF product using an adjusted version of the kernel-driven BRDF model. Remote Sens. Environ. 2018, 209, 594–611. [Google Scholar] [CrossRef]
- Bréon, F.-M.; Maignan, F.; Leroy, M.; Grant, I. Analysis of hot spot directional signatures measured from space. J. Geophys. Res. Atmos. 2002, 107, AAC-1. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Breon, F.-M. Validation of an analytical snow BRDF model using PARASOL multi-angular and multispectral observations. IEEE Geosci. Remote Sens. Lett. 2012, 9, 928–932. [Google Scholar] [CrossRef]
- Jiao, Z.; Ding, A.; Kokhanovsky, A.; Schaaf, C.; Bréon, F.-M.; Dong, Y.; Wang, Z.; Liu, v; Zhang, X.; Yin, S. Development of a snow kernel to better model the anisotropic reflectance of pure snow in a kernel-driven BRDF model framework. Remote Sens. Environ. 2019, 221, 198–209. [Google Scholar] [CrossRef]
- Ding, A.; Jiao, Z.; Dong, Y.; Zhang, X.; Peltoniemi, J.I.; Mei, L.; Guo, J.; Yin, S.; Cui, L.; Chang, Y. Evaluation of the Snow Albedo Retrieved from the Snow Kernel Improved the Ross-Roujean BRDF Model. Remote Sens. 2019, 11, 1611. [Google Scholar] [CrossRef]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. Oceans 2001, 106, 7163–7180. [Google Scholar] [CrossRef]
- Jin, Z.; Charlock, T.P.; Rutledge, K.; Stamnes, K.; Wang, Y. Analytical solution of radiative transfer in the coupled atmosphere-ocean system with a rough surface. Appl. Opt. 2006, 45, 7443–7455. [Google Scholar] [CrossRef] [PubMed]
- Coupled Ocean and Atmosphere Radiative Transfer (COART). Available online: https://cloudsgate2.larc.nasa.gov/jin/coart.html (accessed on 15 March 2020).
- Bréon, F.M.; Henriot, N. Spaceborne observations of ocean glint reflectance and modeling of wave slope distributions. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Frouin, R.; Schwindling, M.; Deschamps, P.-Y. Spectral reflectance of sea foam in the visible and near-infrared: In situ measurements and remote sensing implications. J. Geophys. Res. Oceans 1996, 101, 14361–14371. [Google Scholar] [CrossRef]
- Koepke, P. Effective reflectance of oceanic whitecaps. Appl. Opt. 1984, 23, 1816–1824. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Spectral reflectance of whitecaps. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Vermote, E.F.; Vermeulen, A. Atmospheric correction algorithm: Spectral reflectances (MOD09). Version 4.0. Algorithm Theor. Basis Doc. NASA EOS-ID 1999, 4, 1–107. [Google Scholar]
- NASA Goddard Space Flight Center, Ocean Biology Processing Group. (2014): Sea-viewing Wide Field-of-view Sensor (SeaWiFS) Ocean Color Data. NASA OB.DAAC: Greenbelt, MD, USA, Maintained by NASA Ocean Biology Distibuted Active Archive Center (OB.DAAC), Goddard Space Flight Center, Greenbelt MD. Available online: https://oceandata.sci.gsfc.nasa.gov/SeaWiFS/Mapped/Monthly/9km/chlor_a (accessed on 15 March 2020). [CrossRef]
- Ricciardulli, L.; Wentz, F. Reprocessed QuikSCAT (V04) wind vectors with Ku-2011 geophysical model function. Remote Sens. Syst. Tech. Rep. 2011, 43011. [Google Scholar]
- Remote Sensing Systems QuikScat/SeaWinds Page. Available online: http://www.remss.com/missions/qscat (accessed on 15 March 2020).
- CryoClim Service Documentation Page. Available online: http://www.cryoclim.net/cryoclim/index.php/Service_documentation (accessed on 15 March 2020).
- CryoClim Data Portal. Available online: http://www.cryoclim.net/cryoclim/subsites/data_portal/ (accessed on 15 March 2020).
- Goyens, C.; Marty, S.; Leymarie, E.; Antoine, D.; Babin, M.; Bélanger, S. High angular resolution measurements of the anisotropy of reflectance of sea ice and snow. Earth Space Sci. 2018, 5, 30–47. [Google Scholar] [CrossRef]
- DLR Spectral Archive. Available online: http://cocoon.caf.dlr.de/intro_en.html (accessed on 15 March 2020).
- ASTER Spectral Library. Available online: http://speclib.jpl.nasa.gov/ (accessed on 15 March 2020).
- USGS Spectral Database. Available online: http://speclab.cr.usgs.gov/spectral.lib06/ (accessed on 15 March 2020).
- Gerber, F.; Marion, R.; Olioso, A.; Jacquemoud, S.; Da Luz, B.R.; Fabre, S. Modeling directional–hemispherical reflectance and transmittance of fresh and dry leaves from 0.4 μm to 5.7 μm with the PROSPECT-VISIR model. Remote Sens. Environ. 2011, 115, 404–414. [Google Scholar] [CrossRef]
- Warren, S.G. Optical constants of ice from the ultraviolet to the microwave. Appl. Opt. 1984, 23, 1206–1225. [Google Scholar] [CrossRef] [PubMed]
- Refractive Index Database. Available online: http://refractiveindex.info/?group=CRYSTALS&material=H2O-ice (accessed on 15 March 2020).
- Segelstein, D.J. The Complex Refractive index of Water. Ph.D. Thesis, University of Missouri–Kansas City, Kansas City, MO, USA, 1981. [Google Scholar]
- Available online: https://omlc.org/spectra/water/data/segelstein81.txt (accessed on 15 March 2020).
- Hale, G.M.; Querry, M.R. Optical constants of water in the 200-nm to 200-μm wavelength region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Refractive Index Database. Available online: http://refractiveindex.info/?group=LIQUIDS&material=Water (accessed on 15 March 2020).
- ESA Earth Observation Portal Database. Available online: https://earth.esa.int (accessed on 15 March 2020).
- ADAM Portal. Available online: https://adam.noveltis.fr (accessed on 15 March 2020).
- Tanré, D.; Bréon, F.M.; Deuzé, J.L.; Dubovik, O.; Ducos, F.; François, P.; Goloub, P.; Herman, M.; Lifermann, A.; Waquet, F. Remote sensing of aerosols by using polarized, directional and spectral measurements within the A-Train: The PARASOL mission. Atmos. Meas. Tech. 2011, 4, 1383–1395. [Google Scholar] [CrossRef]
- Kobayashi, K.; Salam, M.U. Comparing simulated and measured values using mean squared deviation and its components. Agron. J. 2000, 92, 345–352. [Google Scholar] [CrossRef]
- Gauch, H.G.; Hwang, J.T.; Fick, G.W. Model evaluation by comparison of model-based predictions and measured values. Agron. J. 2003, 95, 1442–1446. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO mission and CALIOP data processing algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bacour, C.; Bréon, F.-M.; Gonzalez, L.; Price, I.; Muller, J.-P.; Straume, A.G. Simulating Multi-Directional Narrowband Reflectance of the Earth’s Surface Using ADAM (A Surface Reflectance Database for ESA’s Earth Observation Missions). Remote Sens. 2020, 12, 1679. https://doi.org/10.3390/rs12101679
Bacour C, Bréon F-M, Gonzalez L, Price I, Muller J-P, Straume AG. Simulating Multi-Directional Narrowband Reflectance of the Earth’s Surface Using ADAM (A Surface Reflectance Database for ESA’s Earth Observation Missions). Remote Sensing. 2020; 12(10):1679. https://doi.org/10.3390/rs12101679
Chicago/Turabian StyleBacour, Cédric, François-Marie Bréon, Louis Gonzalez, Ivan Price, Jan-Peter Muller, and Anne Grete Straume. 2020. "Simulating Multi-Directional Narrowband Reflectance of the Earth’s Surface Using ADAM (A Surface Reflectance Database for ESA’s Earth Observation Missions)" Remote Sensing 12, no. 10: 1679. https://doi.org/10.3390/rs12101679
APA StyleBacour, C., Bréon, F.-M., Gonzalez, L., Price, I., Muller, J.-P., & Straume, A. G. (2020). Simulating Multi-Directional Narrowband Reflectance of the Earth’s Surface Using ADAM (A Surface Reflectance Database for ESA’s Earth Observation Missions). Remote Sensing, 12(10), 1679. https://doi.org/10.3390/rs12101679






