Abstract
Disturbance monitoring is an important application of the Landsat times series, both to monitor forest dynamics and to support wise forest management at a variety of spatial and temporal scales. In the last decade, there has been an acceleration in the development of approaches designed to put the Landsat archive to use towards these causes. Forest disturbance mapping has moved from using individual change-detection algorithms, which implement a single set of decision rules that may not apply well to a range of scenarios, to compiling ensembles of such algorithms. One approach that has greatly reduced disturbance detection error has been to combine individual algorithm outputs in Random Forest (RF) ensembles trained with disturbance reference data, a process called stacking (or secondary classification). Previous research has demonstrated more robust and sensitive detection of disturbance using stacking with both multialgorithm ensembles and multispectral ensembles (which make use of a single algorithm applied to multiple spectral bands). In this paper, we examined several additional dimensions of this problem, including: (1) type of algorithm (represented by processes using one image per year vs. all historical images); (2) spectral band choice (including both the basic Landsat reflectance bands and several popular indices based on those bands); (3) number of algorithm/spectral-band combinations needed; and (4) the value of including both algorithm and spectral band diversity in the ensembles. We found that ensemble performance substantially improved per number of model inputs if those inputs were drawn from a diversity of both algorithms and spectral bands. The best models included inputs from both algorithms, using different variants of shortwave-infrared (SWIR) and near-infrared (NIR) reflectance. Further disturbance detection improvement may depend upon the development of algorithms which either interrogate SWIR and NIR in new ways or better highlight disturbance signals in the visible wavelengths.
1. Introduction
Forests are critically important for global ecological functions, including processes such as moderating climate, conserving biodiversity, and maintaining the hydrologic cycle [1,2,3]. Consequently, the monitoring of forest disturbance is a key concern globally [4,5], and remote-sensing via earth orbiting satellites has played an increasingly important role [6,7,8].
Landsat data have become the premier remote sensing dataset for monitoring forest disturbance [9,10,11] since the opening in 2008 of the global, high-quality, and well-calibrated multidecade data archive, offering free access to its collections [12]. Methods for characterizing forest disturbance with Landsat time series have greatly advanced over the recent past. Perhaps the most important advancements have been the greater use of denser time series [13], which has led to automated solutions for removal of clouds, cloud shadows, and snow [14,15], and the development of a number of highly sophisticated algorithms to detect and characterize disturbance [16].
As discussed by Zhu [16], two of the most widely used algorithms for processing Landsat time series to monitor disturbance have been LandTrendr [17] and Continuous Change Detection and Classification (CCDC), [18]). Cohen et al. [19] compared these and several other contemporary algorithms against a reference disturbance dataset that encompassed a broad range of forest types, disturbance intensities, and disturbance agents. That study highlighted the challenges of broadening the application domain of somewhat locally and finely tuned automated algorithms, revealing a propensity for increased detection errors when tested outside the conditions for which the algorithms were originally developed and tested. This was especially true when the algorithms encountered lower-severity disturbances, a ubiquitous class of disturbances that tend to have rather subtle spectral change magnitudes [20].
Following the algorithm comparison study of Cohen et al. [19], Healey et al. [21] tested an ensemble approach called stacking (or stacked generalization, [22]) that combined outputs from a number of algorithms in a secondary classification model trained with reference data. Specifically, a Random Forests (RF, [23]) model was applied to several disturbance-related outputs (e.g., spectral change magnitude, duration) from nine different algorithms and a few ancillary datasets (i.e., topography, forest type, Landsat spectral data). The RF model was calibrated with the broadly encompassing disturbance reference dataset of Cohen et al. [19]. Stacking greatly reduced disturbance classification errors relative to those associated with the original algorithm classifications.
Most of the algorithms included in the Cohen et al. [19] and Healey et al. [21] studies, including LandTrendr, relied on a single Landsat spectral band or index (hereafter collectively referred to as bands). Given the success of secondary classification based on a reference disturbance dataset and ensemble modeling by Healey et al. [21], Cohen et al. [24] used the approach to integrate LandTrendr outputs from multiple spectral bands. That study revealed the power of an explicitly multispectral approach, when relying on a single algorithm such as LandTrendr, to classify forest disturbance with Landsat data. In addition, the Cohen et al. [24] study highlighted the importance of shortwave-infrared bands and spectral indices that include those bands for the accurate detection of forest disturbances.
With evidence of stacking’s effectiveness using inputs both from different algorithms [21] and from different bands using the same algorithm [24], there was an outstanding operational question of whether applications should focus on building ensembles from multiple algorithms, multiple bands, or both. Subsidiary to that question was a need for insight into the relative strengths of different classes of algorithms and bands in an ensemble context. We address these questions in this study by testing alternate ensembles composed of different numbers of inputs from varying bands and two different algorithms: LandTrendr and Continuous Monitoring of Land Disturbance, [25] (COLD). COLD is based on CCDC, but, whereas CCDC searched for breakpoints in a time series associated with relatively large spectral change magnitudes, it was not sensitive to the subtler change magnitudes often associated with forest disturbance. COLD was designed to address this deficiency.
This study had several objectives, including: (1) comparing the performance of LandTrendr and COLD for forest disturbance detection in a Landsat multispectral ensemble modeling context; (2) evaluating the power of integrated, multialgorithm (LandTrendr+COLD) ensemble models for forest disturbance detection; and (3) determining which Landsat spectral bands and regions are most important for forest disturbance detection in a multialgorithm, multispectral context.
2. Methods
2.1. Sample-Based Disturbance Reference Data
A sample of 3828 forested Landsat pixel (i.e., plot) locations, selected via a two-stage stratified cluster design, was used in this study (Figure 1). This sample (trimmed from the original 3861 locations), along with the broad mix of forest types it contained and the estimation strategy, was thoroughly described in Cohen et al. [20], where it was used to estimate forest disturbance trends between 1985 and 2012 across the conterminous United States. For that study, disturbance data for the sample were collected with TimeSync, a tool for Landsat time-series visualization and disturbance data collection [26]. For a given plot, the Landsat time series consisted of, to the extent possible, one growing season cloud-free Landsat image chip (256-by-256 image pixels, centered on the plot) per year.
Figure 1.
Location of plots used in this study (dots) superimposed on a forest mask (dark gray, [27]).
As described by Cohen et al. [20], using TimeSync, Landsat time-series data (1984–2013) for each plot was examined to determine if there was a disturbance (e.g., harvest, fire, etc.) at some time during the time series (between 1985 and 2012) and, if so, the year the disturbance occurred. As TimeSync provides segment-based observations, similar to LandTrendr [17], where disturbances lasted for multiple years (e.g., progressive tree mortality within a plot associated insect and disease spread), both the start date and end date were noted and the disturbance observations were annualized. Disturbance interpretations were supported by multiyear high-resolution image chips for the same locations available in Google Earth and other related data.
2.2. Landsat Data Preparation and Algorithm Application
For each of the 3828 sample plot locations, two new Landsat time-series datasets (1984-2013) were created for the current study: one for LandTrendr and one for COLD. The data used were from the Landsat Collection 1 dataset (https://www.usgs.gov/land-resources/nli/landsat/landsat-collection-1?qt-science_support_page_related_con=1#qt-science_support_page_related_con). Note that the 33 plots trimmed from the original Cohen et al. [20] sample were scattered across many individual Landsat scenes containing few or no other plots and were thus not cost-effective to recover for this study using the newer Collection 1 datasets. Both algorithms were run on the six primary spectral reflectance bands (i.e., blue, green, red, near-infrared, and two shortwave-infrared). Additionally, seven common spectral indices were used, including Tasseled Cap brightness (TCB), greenness (TCG), wetness (TCW), and angle (TCA), the normalized difference vegetation index (NDVI), the normalized difference moisture index (NDMI), and the normalized burn ratio (NBR), as described in Table 1 of Ref. [24]. Because most of the Landsat data were from TM and ETM+, we used the conventional assignment of band numbers to spectral regions: for visible (VIS) b1 = blue, b2 = green, b3 = red; b4 = near-infrared (NIR); and shortwave-infrared (SWIR) b5 = SWIR1, and b7 = SWIR2.
We sought a simple classification for the various indices that was consistent with the VIS, NIR, and SWIR terminology above. Among the included indices (see Table 1 in [24] for formulations), TCW, NDMI, and NBR exploit the contrast between SWIR and other spectral regions (NIR for NDMI and NBR; both NIR and VIS for TCW). Consequently, we refer to these as SWIR-based bands. As NDVI contrasts NIR against red, and TCG contrasts NIR against both VIS and SWIR, we refer to these as NIR-based bands. TCB expresses more balance among the three spectral regions and was originally designed to encompass pixels having little to no vegetation [28,29]. Because TCA contrasts TCG with TCB, it can be thought of as strongly related to NDVI; thus, in this context, we consider it an NIR-based band. In keeping with our earlier statement that we will refer to indices and bands alike simply as bands, for further simplification, we will refer to b5, b7, and SWIR-based indices as SWIR bands and b4 and NIR-based indices as NIR bands.
2.2.1. LandTrendr
LandTrendr is a time-series segmentation algorithm that processes a temporal stack of spectral data for a single cloud-free observation from the mid-growing season for each year, using a standard compositing approach to reduce cloud-contaminated observations [17]. Following the methods (Section 2.2) of Cohen et al. [24], for the current study, LandTrendr was run on each plot once for each of the aforementioned 13 bands. For each band examined, the plot-level segmentations used the LandTrendr segmentation parameter value set from Table 2 of Kennedy et al. [30]. Initial segments had either a positive or negative slope, or, in rare cases, a slope of zero (stable). The sign of the slope and its interpretation as disturbance or recovery/regrowth (i.e., non-disturbance) is band-dependent. To reduce disturbance omission and commission, LandTrendr normally uses a spectral change filter applied to the resulting segment slopes [17]. However, our approach utilized a secondary statistical classification model (Random Forests) which obviated the need for a spectral change filter. To minimize omission, we declared as a tentative disturbance any LandTrendr segment having a non-zero slope of spectral change in the band-relevant direction of disturbance. Due to this intentional tolerance for disturbance, and inherent LandTrendr segmentation errors, this knowingly increased false positive disturbances. As such, the primary function of the RF model was to minimize commission. The labels for all tentative disturbance and non-disturbance segments were annualized prior to use of the RF modeling. For example, a disturbance segment lasting four years from, say from 1999-2002, would contain a disturbance call for each year in that time span: 1999, 2000, 2001, and 2002.
Band-specific application of the RF model used a purposively selected band-specific training dataset derived from a combination of TimeSync interpretations of real disturbance and false positive disturbances from the LandTrendr segmentation (called the union dataset). For all model runs, regardless of band, the annualized disturbance observations from any plot where TimeSync declared a disturbance were used to represent the disturbance class. For a specific band in a given year, where LandTrendr declared a disturbance that was not matched by a TimeSync disturbance, those observations represented the non-disturbance (false positive) class. This purposive, union dataset sample had the effect of minimizing the imbalance in annualized disturbance and non-disturbance observations in the training dataset, and had the collateral benefit of feeding the model the most challenging observations [24].
The RF prediction of disturbance probability for any given band in any given year, as described in Cohen et al. [24], was a function of three predictor variables: the band value for that year, the spectral difference between that year and the previous year, and the number of years duration of the original segment containing that year. Each RF model used 500 trees, and out-of-bag (OOB) errors for the training dataset were reported as a function of RF probability threshold. As we sought a balance of omission and commission errors, we adjusted the threshold until that balance was realized among the two relevant cells of the disturbance/non-disturbance error matrix. Although models were trained with a subset of the full dataset that focused on TimeSync disturbance observations and false-positive LandTrendr detections, the probability threshold adjustment was applied to the entire reference dataset. As in Cohen et al. [24], we created multispectral LandTrendr ensembles using all combinations of all bands, taken 2–13 at a time (Table 1). The above approaches based on training via a union dataset, followed by full dataset OOB error balance adjustment, were applied to each combination.

Table 1.
Number of bands (N) included for models based on the individual algorithms and their combination, the number of unique band combinations for each N, and balanced error rates for the medians of all models and the means of the top five models for each N. Also shown are error differences for the means of the top five models based on the individual and combined algorithms, using both the six best and six worst bands for the combined models.
2.2.2. COLD
In parallel with LandTrendr, a COLD-specific time-series (1984-2013) Landsat dataset was constructed for each of the 3828 sample plot locations using the process described by Zhu et al. [25]. First, for each plot, all available Landsat data were downloaded and then, using the Landsat metadata and a new variant of the Tmask algorithm [15], screened for clouds, cloud shadow, and snow.
As described by Zhu et al. [25], using all clear observations, COLD fitted a harmonic time-series model separately for each band. Once established in the early period of the time series, the model was used to predict future observations. When four or more consecutive future observations (adjusted to the density of time series data) were not within the expected range of both spectral change magnitude and direction, a breakpoint was identified. After the initial breakpoint, a new harmonic model was established, future predictions were compared to future observations, and new breakpoints were declared as specified. This process was repeated for the full time series for each band. Four consecutive observations were less than the six used by Zhu et al. [25]. Likewise, here a change probability threshold of 0.90 was used, compared to the 0.99 value used by Zhu et al. [25]. As for LandTrendr, the expectation here was that these parameter adjustments were more tolerant of commission error and would thus help to minimize COLD disturbance omissions, while the RF model was expected to minimize commissions.
The spectral direction of most breakpoint changes was in the band-specific direction of disturbance and, as such, declared as a disturbance. Typically, the post-disturbance harmonic model trended in the opposite spectral direction associated with disturbance (i.e., towards recovery/regrowth) and lasted for several years. In this case, for our application of COLD, the duration of the disturbance was declared as one year. If the new post-disturbance model trended in the direction of disturbance, a disturbance with multiyear duration was detected and the duration of the disturbance was declared. The duration of the multiyear disturbance was equivalent to the number of years before a new breakpoint was established that trended in the direction of recovery/regrowth. As with LandTrendr, for multiyear disturbances the spectral change magnitude was annualized. This enabled the extraction of the same predictor variables as those used for LandTrendr to calculate the probability of disturbance occurrence in any given year via secondary RF classification: the band value for the prediction year, the spectral difference between the prediction year and the previous year, and the number of years’ duration of the original segment containing that year.
RF modeling for secondary classification was handled exactly as for LandTrendr, with band-specific model runs using purposively selected band-specific union training datasets. Likewise, for any given band, the probability of disturbance in any given year was a function the band value for that year, the spectral difference between that year and the previous year, and the number of years duration of the original segment containing that year. Each RF model used 500 trees and OOB errors for the training dataset were reported as a function of RF probability threshold, and the thresholds were adjusted using the full dataset to achieve error balance. Similarly, we created multispectral COLD ensembles using all combinations of all bands taken 2–13 at a time (Table 1). Relevant union datasets were created, and full dataset error balances were achieved by adjusting the RF threshold.
2.2.3. LandTrendr+COLD
The primary objective of this study was to test a multialgorithm, multispectral RF ensemble approach to forest disturbance detection. For this purpose, we had available results from 13 individual bands run through two algorithms, for a total of 26 possible predictor variable sets (i.e., N = 26). Testing models using all possible combinations of inputs from N = 1 to 26 would involve over 67 million RF models, each involving the production of 500 decision trees, which was not computationally feasible. Cohen et al. [24] demonstrated that most of the predictive power was achieved with an N≤10. Thus, for this study we sought to select the six most important (i.e., best) bands from each of the two algorithms (for a total N = 12). We did so with an algorithm-specific band-importance weighting scheme.
For a given algorithm, each N (from 1–13) of the RF runs for an individual algorithm produced results for a different number of combinations (from 1–1716, Table 1). For each N, this resulted in a concomitant number of balanced error predictions which could be ordered from low to high (note that N = 13 was not used here because it included all bands, and thus added no information). From these results, we selected the five models having the lowest errors (top five models) for each N (from 1–12 for a total of 60), and then scored the bands according to how often they were used in the collection of models. For each band in each of the 60 models, we applied a weight of 1-model error (balanced) and then summed the scores by band. We then chose the six bands with the highest (best) weighted scores for the given algorithm to use in the multialgorithm ensembles. As for the multispectral ensembles for the individual algorithms, the multialgorithm ensembles used all combinations of all bands taken 2–12 at a time (Table 1). Relevant union training datasets were created, and error balances were achieved by adjusting the RF threshold.
To gain additional insight into the importance of which bands were selected for the multialgorithm, multispectral ensembles we ran an additional test based on a second set of RF models. This new test used the six bands with the lowest (i.e., worst) weighted scores from the runs of the individual algorithms (N = 12). This informed our understanding of the importance of thoughtful band selection in a multialgorithm ensemble context where band selection is conservative (i.e., only a modest number of bands are used).
3. Results and Discussion
3.1. Individual Algorithm Detection Errors
Distributions of balanced model errors as a function of number of input bands (N) revealed quite similar patterns for both algorithms (Figure 2a,b, Table 1). Specifically, as N increased the range of errors tightened and the median error values decreased. Although median error values continued to decrease through the range of N, the greatest impact was realized from the first 2–3 bands.
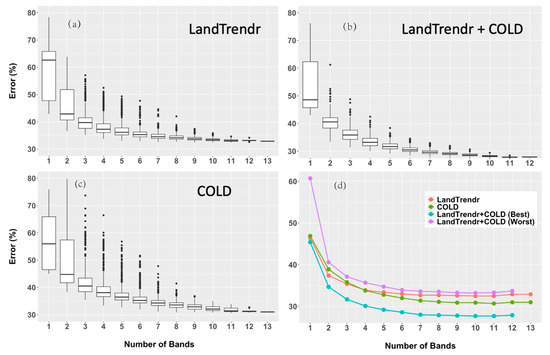
Figure 2.
Distributions of balanced omission and commission errors among all combinations for each number of bands used, for (a) LandTrendr, (b) COLD, and (c) their combination. Also shown are the mean errors for the top five models of each modeling set, including those from the best and worst six bands for the combined models (d). Note that, for all modeling sets, error balances were achieved using probability thresholds of considerably less than 0.5, increasing and converging at approximately 0.3 as number of bands approached 4 or greater.
As described earlier for the band weighting scheme, the top five models for each N were used to select the six best bands from each algorithm to include in the multialgorithm, multispectral ensembles. Examining the mean errors for the top five models we see that those decreased with increasing N, but generally reached an asymptote by N = 7 (LT) or 9 (COLD) (Figure 2d, Table 1). It is worth noting that the distribution of errors for LandTrendr were somewhat greater here compared to similar results in Cohen et al. [24]. This is likely due the fact that different Landsat plot locations were used between the two studies, suggesting that LandTrendr performed less well across the greater diversity of forests represented by the plots in this study (a similar observation to that of Cohen et al. [19]).
The median errors for each algorithm at different values of N were mixed (Figure 2a,b, Table 1). At N = 1 and N > 5, COLD had a lower median error, whereas LT had lower median errors for N of between 2 and 5. However, the median error differences between the algorithms were all generally low (<0.02) above N = 1. Similarly, the mean errors for the top five models (Figure 2d, Table 1) were higher for COLD at lower N (1–3), but lower than LandTrendr for higher N (>3). However, those differences were all generally low (<0.02).
3.2. Combined Algorithm Detection Errors
The multialgorithm ensembles based on the best six bands from each algorithm clearly performed better than either of the individual algorithm ensembles. This was expressed both in the tighter error distributions among models for a given N (Figure 2a–c) and among the errors for the top five models (Figure 2d, Table 1). Relative to LandTrendr, the error differences for the means of the top five models varied from −0.010 (N = 1) to −0.050 (N = 12) for the multialgorithm ensembles. Because COLD generally performed better than LandTrendr at higher N, for COLD the mean errors for the top five models compared to the multialgorithm ensemble models were slightly less than for LandTrendr at higher N (<−0.035 at N>5).
In comparison to using the best six bands, the multialgorithm ensembles based on the worst six bands from each algorithm had considerably higher mean errors for the top five performing models (Figure 2d, Table 1). For example, errors for models using the best bands were between 0.053 and 0.059 lower than errors for models using the worst bands for N = 2 and greater. Although this may not be surprising in general, errors differences between the multialgorithm ensemble models based on the best and worst bands (>0.05 above N = 2) were substantially greater than comparative differences between the single algorithm multispectral models (<0.02 at all N) (Table 1, Figure 2d). This suggests a need for the thoughtful selection of bands to use for disturbance detection in either the single algorithm or multialgorithm context.
3.3. Band Importance
For reference to bands in the context of the multialgorithm ensembles, we use lower case for LandTrendr (b1–b5, b7, tcb, tcg, tcw, tca, ndvi, ndmi, and nbr) and upper case for COLD. Based on the weighted scores (Table 2), the best six bands from the LandTrendr ensembles were, in rank order: nbr (35.17), b5, twc, tcg, b7, and tca (23.44). For COLD, the ranks from highest to lowest were: NBR (36.29), B4, TCB, B7, NDMI, and NDVI (25.39). The bottom-ranked six bands for LandTrendr were (from worst to best): b1 (8.07), b3, b2, tcb, b4, and ndvi (16.78). For COLD, the bottom ranked bands were: B1 (6.90), TCG, B3, B2, TCW, and TCA (17.93). Clearly, based on these weighted scores (ranks 11–13 for LandTrendr and 10, 11, and 13 for COLD), VIS bands appear to have had low information content for forest disturbance detection. In contrast, the NIR and SWIR bands provided most of the detection power.

Table 2.
Weighted scores and ranks for each band used in the LandTrendr, COLD, and combined models.
To highlight the relative importance of SWIR and NIR bands for forest disturbance detection, we summed the weighted scores for the relevant bands from each region and then divided the sums. For LandTrendr and COLD, respectively, the sums of scores for the SWIR bands were 140.85 and 127.62 (Table 2), revealing a somewhat greater dependence of the former on SWIR. In comparison to COLD (sum = 84.21), LandTrendr (sum = 81.73) relied slightly less on NIR. The ratio of score sums for SWIR to NIR for each provides an objective measure of the relative reliance of SWIR vs. NIR bands by the algorithms for disturbance detection in this study: 1.72 and 1.52 for LandTrendr vs. COLD, respectively.
One possible reason for the greater reliance of non-SWIR bands by COLD could be the use of harmonic functions that rely on all available images for the time series. This enabled COLD to more fully exploit the shoulders of the growing season where many disturbances occur and where non-SWIR (particularly NIR) bands may be more important. The propensity of studies using NDVI and related NIR bands for forest phenology characterizations, focusing on such metrics as the start and end of the growing season would seem to support this contention [31,32,33]. In contrast, LandTrendr uses only one clear image per year taken from the mid-growing season where, possibly, SWIR reflectance is more critical for detecting forest disturbance. This suggestion is well supported by the numerous studies that rely on SWIR bands relative to non-SWIR bands for forest disturbance detection [24,34,35]. However, there are many examples in the literature where non-SWIR bands are successfully employed to detect forest disturbance [36,37] and where SWIR bands have proved useful for phenology characterizations [38,39,40]. Given the results of this study and conflicting information regarding band preferences from the literature, exploring the relationships between forest phenology and disturbance in relation to spectral band strengths and their timing would be a fruitful area of future research.
Weighted scores and band ranks for the combined (best) ensemble models (LandTrendr+COLD) revealed unequivocally the importance of SWIR bands relative to NIR bands for forest disturbance detection in this study (Table 2). First, this is clearly evident from the fact that the top four and five of the top six bands weighted most highly were SWIR bands. Interestingly, the normalized burn ratio from both algorithms was included in the top two bands. Second, and more quantitatively, the ratio of summed weighted scores (SWIR/NIR bands; 162.88/64.78) was 2.51, considerably higher than for either algorithm individually. The interpretation of this ratio, of course, must be tempered by the fact that seven of the 12 bands used were SWIR-based, vs. the five of the 12 that were NIR-based.
Examining the specific bands selected by the top five ensemble models from each algorithm and the combined ensembles based on the best bands (for N = 1-7, given the asymptotic nature of the models at higher N) provides more detailed insight into which bands and band combinations were most important for the ensembles (Table 3). Tasseled Cap wetness was the single most important variable (i.e., lowest error) for models when N = 1, with tcw from LandTrendr having the lowest error (0.429) followed by TCW from COLD (0.450). Consequently, tcw was chosen as the most important single spectral band for the combined ensemble based on the best bands from each algorithm. The normalized burn ratio, normalized difference moisture index, and bands 5 and 7 were selected as the next most important bands for the top five models by both algorithms, clearly highlighting the importance of SWIR when only a single band is used.

Table 3.
Balanced errors and bands used for the top five models for N = 1–7 from LandTrendr, COLD, and the combined modeling sets.
Not unexpectedly, for higher N, non-SWIR bands were increasingly included in the top five models. For N = 2, this occurred for ranks 4 and 5 (tcg and tca) for LandTrendr and for rank 4 (TCB) for COLD (Table 3). For the combined ensembles, only SWIR bands were included for N = 2. For N = 3–7, LandTrendr, COLD, and the combined ensemble models (and consistent with the ratio of the sums of weighted scores), SWIR bands represented more than half the total number of bands in the models.
Patterns in the top-performing band combinations for the combined models (Table 3) showed that ensemble diversity was positively correlated with classification accuracy. When inputs from both algorithms were available, the top 2-band models all had one output from LandTrendr and one from COLD. Moreover, with increasing N, a mix of bands from both algorithms was consistently chosen. Additionally, several of the combined models (e.g., N = 2, rank 2, N = 3, rank 1, and others) selected the same spectral band from the two algorithms. The only plausible explanation for the algorithm predictor variables derived from the same input bands being co-selected by a given combined model is that differences between the algorithms themselves are an important factor. These differences included the use of all available data and harmonic functions to find breakpoints for COLD vs. the use of only one image per year and an iterative temporal segmentation approach by LandTrendr. The relative importance for the disturbance detection of multiple algorithms compared to multiple spectral bands cannot be determined from this study, but should be worth exploring in different contexts.
Finally, while Table 2 and Table 3 both indicate the dominance of SWIR, the importance of NIR should not be minimized. Although we categorize Tasseled Cap wetness and three of the five normalized spectral indices as SWIR bands, all three are dependent on the contrast of NIR (band 4) against SWIR. The physical explanation for why NIR and SWIR appeared complimentary with respect to identifying forest disturbance is beyond the scope of this paper. However, ensemble diversity is generally recognized as an important element in the combination of classifiers [41,42] and Figure 2d shows that combining inputs from both different algorithms and different bands consistently improved forest disturbance detection.
4. Conclusions
This study confirmed the high value of stacking (secondary classification)—in this case using Random Forests (RF) ensemble models—as an effective means of combining predictor variables derived from single-band runs of a given disturbance algorithm to predict forest disturbance occurrence from Landsat time series. In particular, we retested LandTrendr in this context using Landsat Collection 1 data and a significantly broader set of plot locations relative to our earlier test [24]. Moreover, for comparison, we tested a second algorithm (COLD) using the same stacking methods and found similar trends in improvement as additional bands were added. As LandTrendr was developed with the expectation that only a single band would be used for disturbance classification, the specific band chosen was an important decision [17]. With stacking, this decision was less important because results from several bands could be combined. Although COLD algorithmically combines information from multiple bands to detect disturbance, it does so without the advantage of reference data training. In the context of earlier studies (e.g., [19,21,24]), the results of the current study strongly suggest that a combination of using multiple bands and reference data training significantly improved the performance of a given, single algorithm for forest disturbance detection.
Differences in the performance of the two algorithms across N (from 1–13 bands) were generally small (Table 1, Figure 1). Far more important were the differences between the multialgorithm ensembles using the best bands from each algorithm and either of the individual algorithm ensembles. However, it is not enough to simply combine bands from different algorithms to improve results; the specific bands chosen are also important, as indicated by the comparison of results from the combined models using the best and the worst six bands from each algorithm.
Using a weighting scheme based on the top five models for each N (from 1–12), we determined that, for both LandTrendr and COLD, SWIR bands were more important than non-SWIR bands for forest disturbance detection. However, given that several of the spectral indices used contrast NIR and SWIR, NIR reflectance is also important. Although the spectral change-disturbance information relationship for any given date of image and pixel location would be exactly the same, differences between the LandTrendr and COLD algorithms enabled improvements in disturbance detection from otherwise collinear inputs. Further change detection improvement may depend upon the development of algorithms which either interrogate SWIR and NIR in new ways or better highlight disturbance signals in the visible wavelengths. Additionally, taking advantage of newer datasets such as those from Sentinel satellites, to incorporate new spectral regions, could improve the results of forest disturbance monitoring [43].
Author Contributions
Conceptualization, W.B.C., S.P.H. and Z.Y.; Methodology, W.B.C., S.P.H., Z.Y., Z.Z. and N.G.; Software, Z.Y., Z.Z. and N.G.; Validation, W.B.C., S.P.H., Z.Y. and Z.Z.; Formal Analysis, W.B.C., S.P.H., Z.Y., Z.Z. and N.G.; Investigation, W.B.C., S.P.H. and Z.Y.; Resources, Z.Y., Z.Z. and N.G.; Data Curation, Z.Y., Z.Z. and N.G.; Writing—Original Draft Preparation, W.B.C., S.P.H., Z.Y. and Z.Z.; Writing—Review and Editing, W.B.C., S.P.H., Z.Y., Z.Z. and N.G.; Visualization, W.B.C., S.P.H. and Z.Y.; Supervision, W.B.C., S.P.H. and Z.Y.; Project Administration, W.B.C., S.P.H. and Z.Y.; Funding Acquisition, W.B.C., S.P.H., Z.Y. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the US Forest Service (IRDB-LCMS) Landscape Change Monitoring System, the Northwest Forest Plan, the NASA Carbon Monitoring System (NASA reference numbers: NNH13AW62I and 80HQTR18T0016), the NASA SERVIR Program (NNH16AD021), and the USGS Landsat Science Program (140G0119C0008).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Houghton, R.A.; Byers, B.; Nassikas, A.A. A role for tropical forests in stabilizing atmospheric CO2. Nat. Clim. Chang. 2015, 5, 1022–1023. [Google Scholar] [CrossRef]
- Miura, S.; Amacher, M.; Hofer, T.; San-Miguel-Ayanz, J.; Ernawati; Thackway, R. Protective functions and ecosystem services of global forests in the past quarter-century. For. Ecol. Manag. 2015, 352, 35–46. [Google Scholar] [CrossRef]
- Watson, J.E.M.; Evans, T.; Venter, O.; Williams, B.; Tulloch, A.; Stewart, C.; Thompson, I.; Ray, J.C.; Murray, K.; Salazar, A.; et al. The exceptional value of intact forest ecosystems. Nat. Ecol. Evol. 2018, 2, 599–610. [Google Scholar] [CrossRef] [PubMed]
- Ninan, K.N.; Inoue, M. Valuing forest ecosystem services: What we know and what we don’t. Ecol. Economics 2013, 93, 137–149. [Google Scholar] [CrossRef]
- Sexton, J.; Noojipady, P.; Song, X.; Feng, M.; Song, D.; Kim, D.; Anand, A.; Huang, C.; Channan, S.; Pimm, S.L.; et al. Conservation policy and the measurement of forests. Nat. Clim. Chang. 2016, 6, 192–196. [Google Scholar] [CrossRef]
- Frolking, S.; Palace, M.W.; Clark, D.B.; Chambers, J.Q.; Shugart, H.H.; Hurtt, G.C. Forest disturbance and recovery: A general review in the context of spaceborne remote sensing of impacts on aboveground biomass and canopy structure. J. Geophys. Res. 2009, 114, G00E02. [Google Scholar] [CrossRef]
- Negron-Juarez, R.I.; Chambers, J.Q.; Hurtt, G.C.; Annane, B.; Cocke, S.; Powell, M.; Stott, M.; Goosem, S.; Metcalfe, D.J.; Saatchi, S.S. Remote sensing assessment of forest disturbance across complex mountainous terrain: The pattern and severity of impacts of tropical cyclone Yasi on Australian rainforests. Remote Sens. 2014, 6, 5633–5649. [Google Scholar] [CrossRef]
- Birdsey, R.A.; Dugan, A.J.; Healey, S.P.; Dante-Wood, K.; Zhang, F.; Mo, G.; Chen, J.M.; Hernandez, A.J.; Raymond, C.L.; McCarter, J. Assessment of the Influence of Disturbance, Management Activities, and Environmental Factors on Carbon Stocks of US National Forests; Gen. Tech. Rep. RMRS-GTR-402; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2019; 116 pages plus Appendices. Available online: https://www.fs.usda.gov/treesearch/pubs/59157 (accessed on 10 April 2020).
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.E.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat pro-gram, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.B.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free access to Land-sat data, Letter. Science 2008, 320, 1011. [Google Scholar] [CrossRef] [PubMed]
- Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest monitoring using Landsat time series data: A review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance data set for North America, 1990–2000. Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Automated cloud, cloud shadow, and snow detection in multitemporal Landsat data: An algorithm designed specifically for monitoring land cover change. Remote Sens. Environ. 2014, 152, 217–234. [Google Scholar] [CrossRef]
- Zhu, Z. Change detection using Landsat time series: A review of frequencies, preprocessing, algorithms, and applications. ISPRS J. Photogramm. Remote Sens. 2017, 130, 370–384. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Cohen, W.B.; Healey, S.P.; Yang, Z.; Stehman, S.V.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Huang, C.; Hughes, M.J.; Kennedy, R.E.; et al. How similar are forest disturbance maps derived from different Landsat time series algorithms? Forests 2017, 8, 98. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Stehman, S.V.; Schroeder, T.A.; Bell, D.M.; Masek, J.G.; Huang, C.; Meigs, G.W. Forest disturbance in the conterminous US from 1985-2012: The emerging dominance of forest decline. For. Ecol. Manag. 2016, 360, 242–252. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Hughes, M.J.; Kennedy, R.E.; et al. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Healey, S.P.; Kennedy, R.E.; Gorelick, N. A LandTrendr multi-spectral ensemble for forest disturbance detection. Remote Sens. Environ. 2018, 205, 131–140. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, J.; Yang, Z.; Aljaddani, A.H.; Cohen, W.B.; Qiu, S.; Zhou, C. Continuous monitoring of land disturbance based on Landsat time series. Remote Sens. Environ. 2020, 238, 111116. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Kennedy, R.E. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync—Tools for calibration and validation. Remote Sens. Environ. 2010, 114, 2911–2924. [Google Scholar] [CrossRef]
- Homer, C.G.; Dewitz, J.A.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.D.; Wickham, J.D.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States—Representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Kauth, R.J.; Thomas, G.S. The tasseled cap—a graphic description of the spectral–temporal development of agricultural crops as seen by Landsat. In Proceedings of the Symposium on Machine Processing of Remotely Sensed Data, Purdue University, West Lafayette, IN, USA, 29 June–1 July 1976; pp. 41–51. [Google Scholar]
- Crist, E.P.; Cicone, R.R.C. A physically-based transformation of thematic mapper data—The TM tasseled cap. IEEE Trans. Geosci. Remote Sens. 1984, 22, 256–263. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B.; Pfaff, E.; Braaten, J.; Nelson, P. Spatial and temporal patterns of forest disturbance and regrowth within the area of the Northwest Forest Plan. Remote Sens. Environ. 2012, 122, 117–133. [Google Scholar] [CrossRef]
- Nagai, S.; Inoue, T.; Ohtsuka, T.; Kobayashi, H.; Kurumado, K.; Muraoka, H.; Nasahara, K.N. Relationship between spatio-temporal characteristics of leaf-fall phenology and seasonal variations in near surface- and satellite-observed vegetation indices in a cool-temperate deciduous broad-leaved forest in Japan. Int. J. Remote Sens. 2014, 35, 3520–3536. [Google Scholar] [CrossRef]
- Nijland, W.; Bolton, D.K.; Coops, N.C.; Stenhouse, G. Imaging phenology; scaling from camera plots to landscapes. Remote Sens. Environ. 2016, 177, 13–20. [Google Scholar] [CrossRef]
- Verma, M.; Friedl, M.A.; Finzi, A.; Phillips, N. Multi-criteria evaluation of the suitability of growth functions for modeling remotely sensed phenology. Ecol. Model. 2016, 323, 123–132. [Google Scholar] [CrossRef]
- Gerard, F.; Plummer, S.; Wadsworth, R.; Sanfeliu, A.F.; Iliffe, L.; Balzter, H.; Wyatt, B. Forest fire scar detection in the boreal forest with multitemporal SPOT-VEGETATION data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2575–2585. [Google Scholar] [CrossRef]
- Ozdogan, M. A practical and automated approach to large area forest disturbance mapping with remote sensing. PLoS ONE 2014, 9, e78438. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.-F.; Lin, T.-C.; Vadeboncoeur, M.A.; Hwong, J.-L. Remote sensing assessment of forest damage in relation to the 1996 strong typhoon Herb at Lienhuachi Experimental Forest, Taiwan. For. Ecol. Manag. 2008, 255, 3297–3306. [Google Scholar] [CrossRef]
- Brooks, E.B.; Wynne, R.H.; Thomas, V.A.; Blinn, C.E.; Coulston, J.W. On-the-fly massively multitemporal change detection using statistical quality control charts and Landsat data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3316–3332. [Google Scholar] [CrossRef]
- Rautiainen, M.; Heiskanen, J.; Korhonen, L. Seasonal changes in canopy leaf area index and MODIS vegetation products for a boreal forest site in central Finland. Boreal Environ. Res. 2012, 17, 72–84. [Google Scholar]
- Liu, Y.; Liu, R.; Pisek, J.; Chen, J.M. Separating overstory and understory leaf area indices for global needleleaf and deciduous broadleaf forests by fusion of MODIS and MISR data. Biogeosciences 2017, 14, 1093–1110. [Google Scholar] [CrossRef]
- Pastor-Guzman, J.; Dash, J.; Atkinson, P.M. Remote sensing of mangrove forest phenology and its environmental drivers. Remote Sens. Environ. 2018, 205, 71–84. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Whitaker, C.J. Ten measures of diversity in classifier ensembles: Limits for two classifiers. IEE Colloquium 2001, 73–82. [Google Scholar] [CrossRef]
- Mellor, A.; Boukir, S.S. Exploring diversity in ensemble classification: Applications in large area land cover mapping. ISPRS J. Photogramm. Remote Sens. 2017, 129, 151–161. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Hernández-Clemente, A.H.R.; Beck, P.S.A. Understanding the temporal dimension of the red-edge spectral region for forest decline detection using high-resolution hyperspectral and Sentinel-2a imagery. ISPRS J. Photogramm. Remote Sens. 2018, 137, 134–148. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).