Spatiotemporal Characterization of Land Cover Impacts on Urban Warming: A Spatial Autocorrelation Approach
Abstract
1. Introduction
2. Materials and Methods
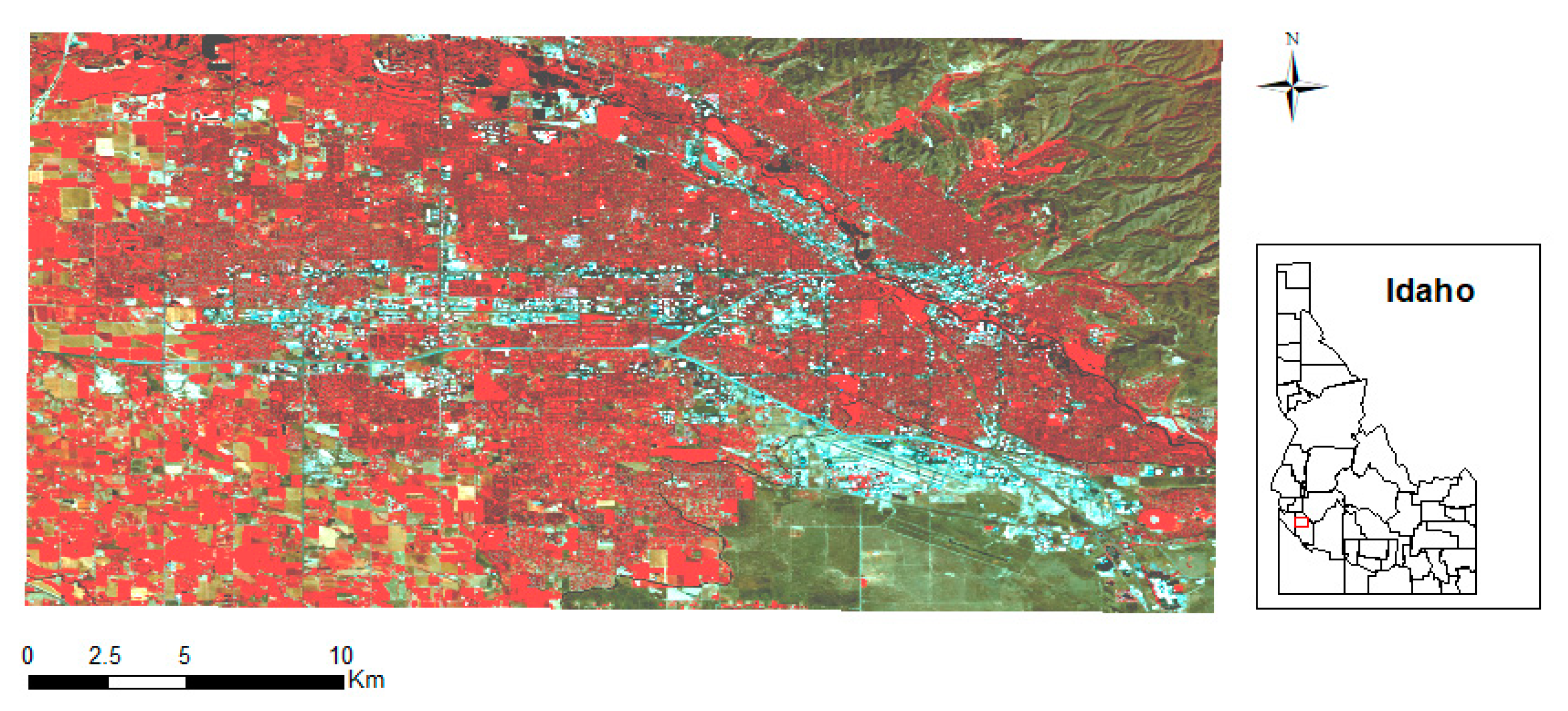
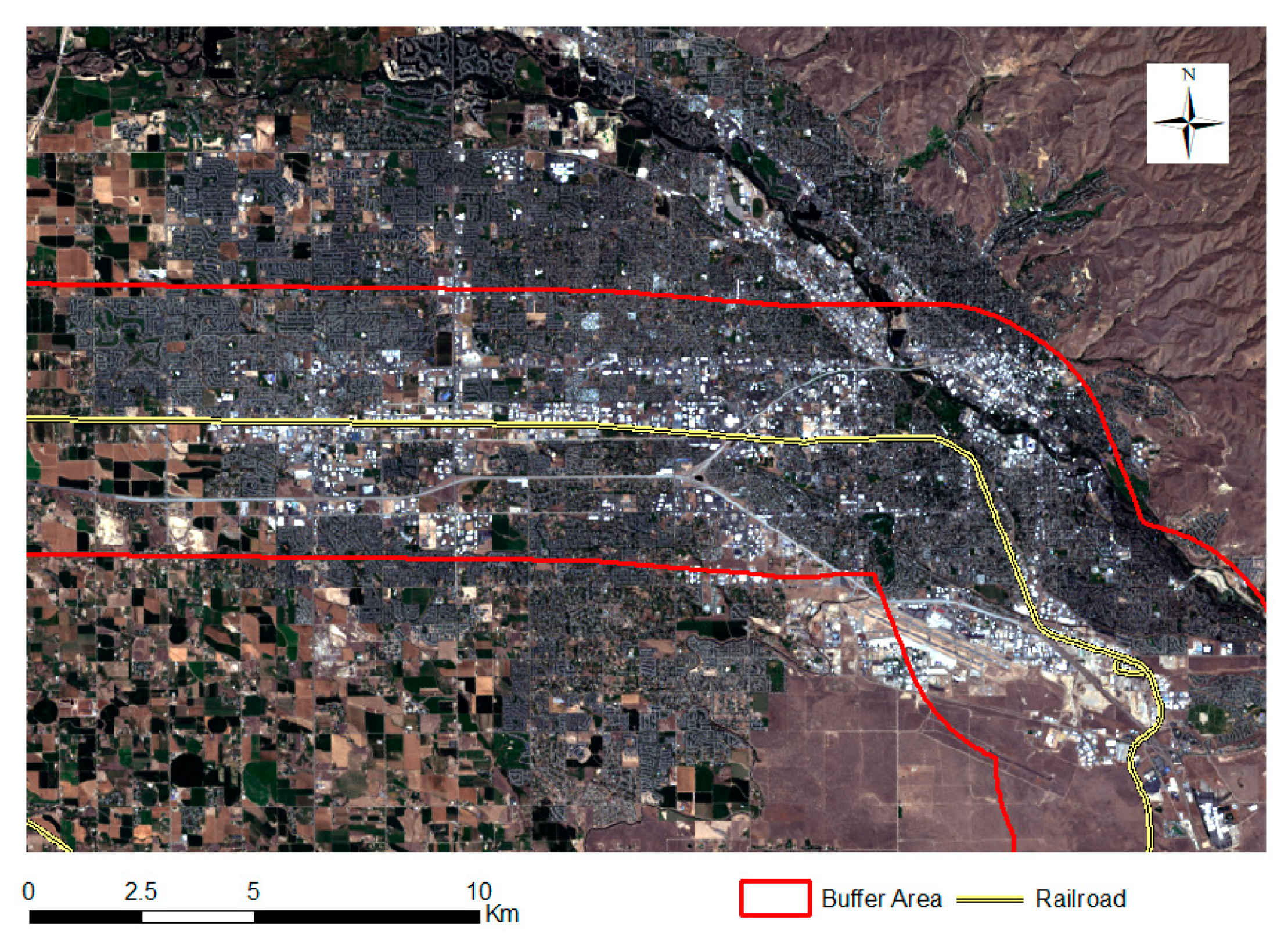
2.1. Study Area
2.2. Data Processing and Analysis
2.3. LST Retrival
2.4. Urban–Rural Gradient Analysis
2.5. Spatial Pattern Analysis
2.6. Statistical Analysis
3. Results
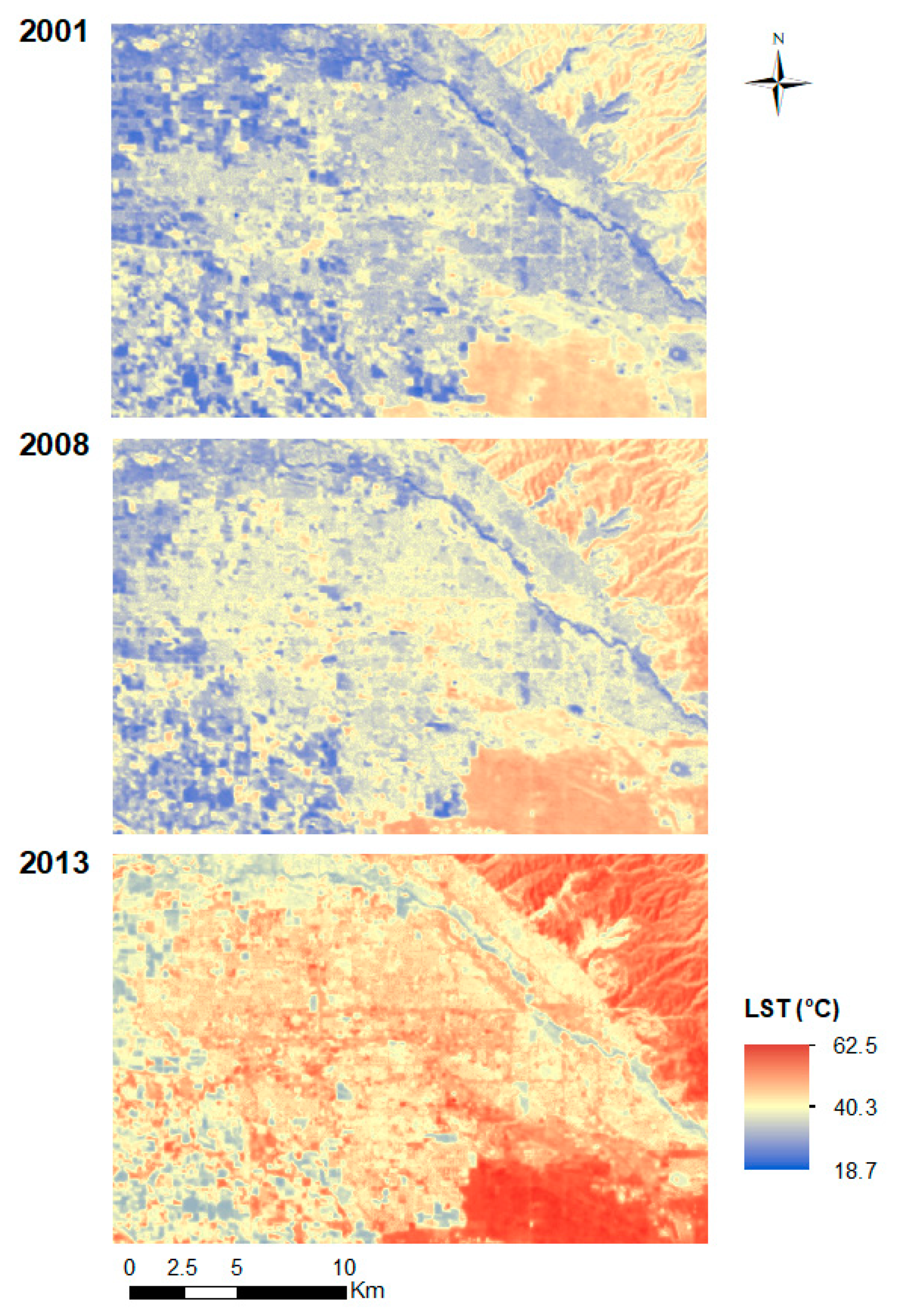
3.1. Spatiotemporal Patterns of the LST
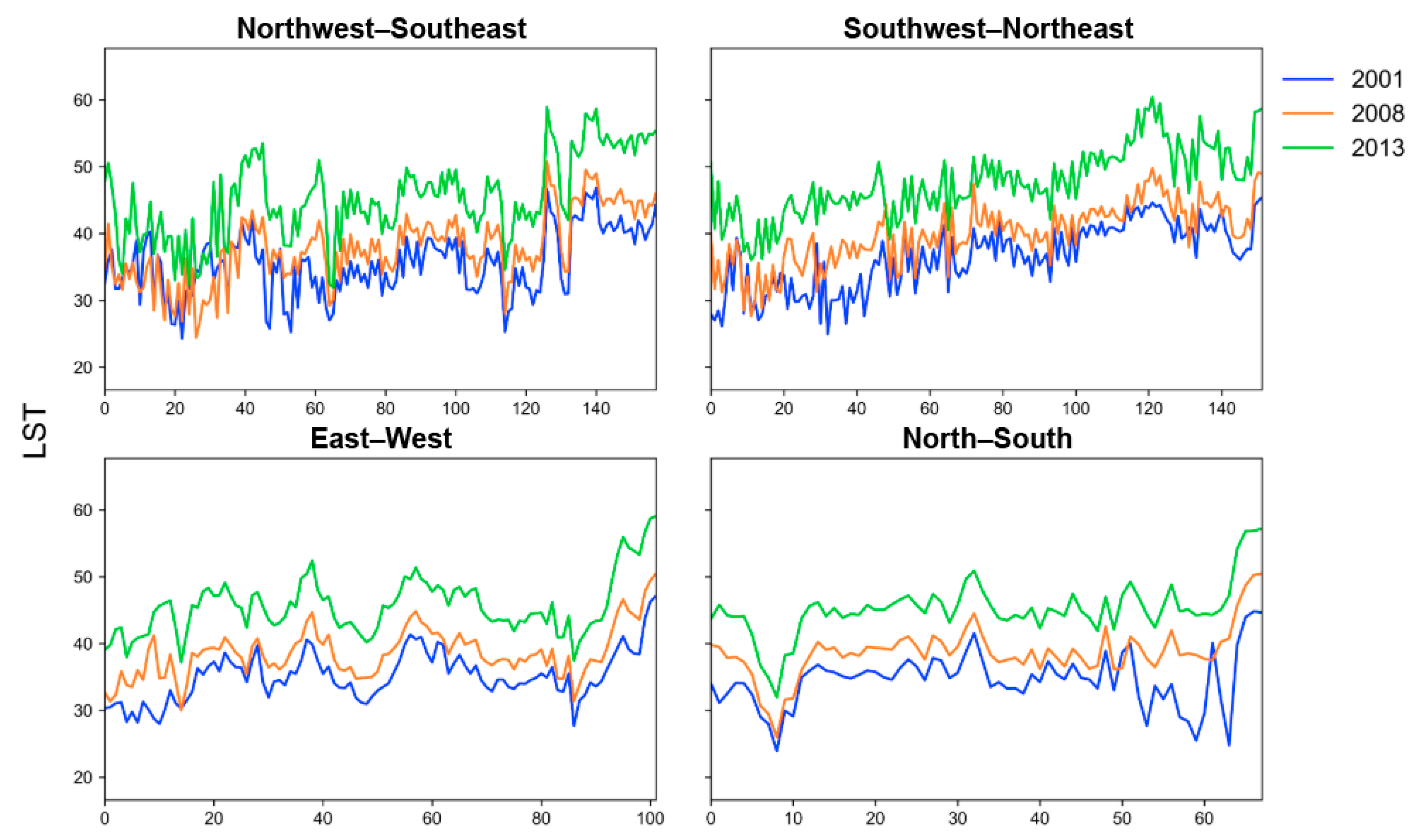
3.2. LST Profiles along Urban–Rural Transects
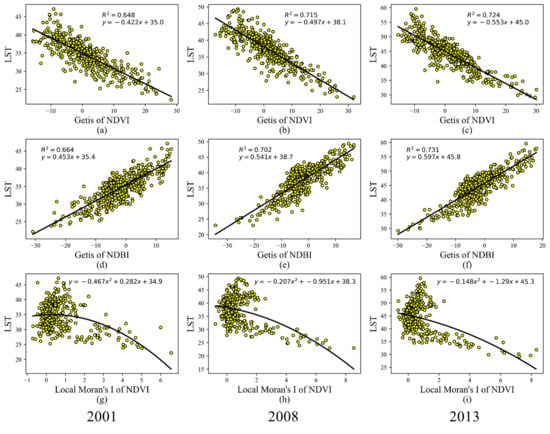
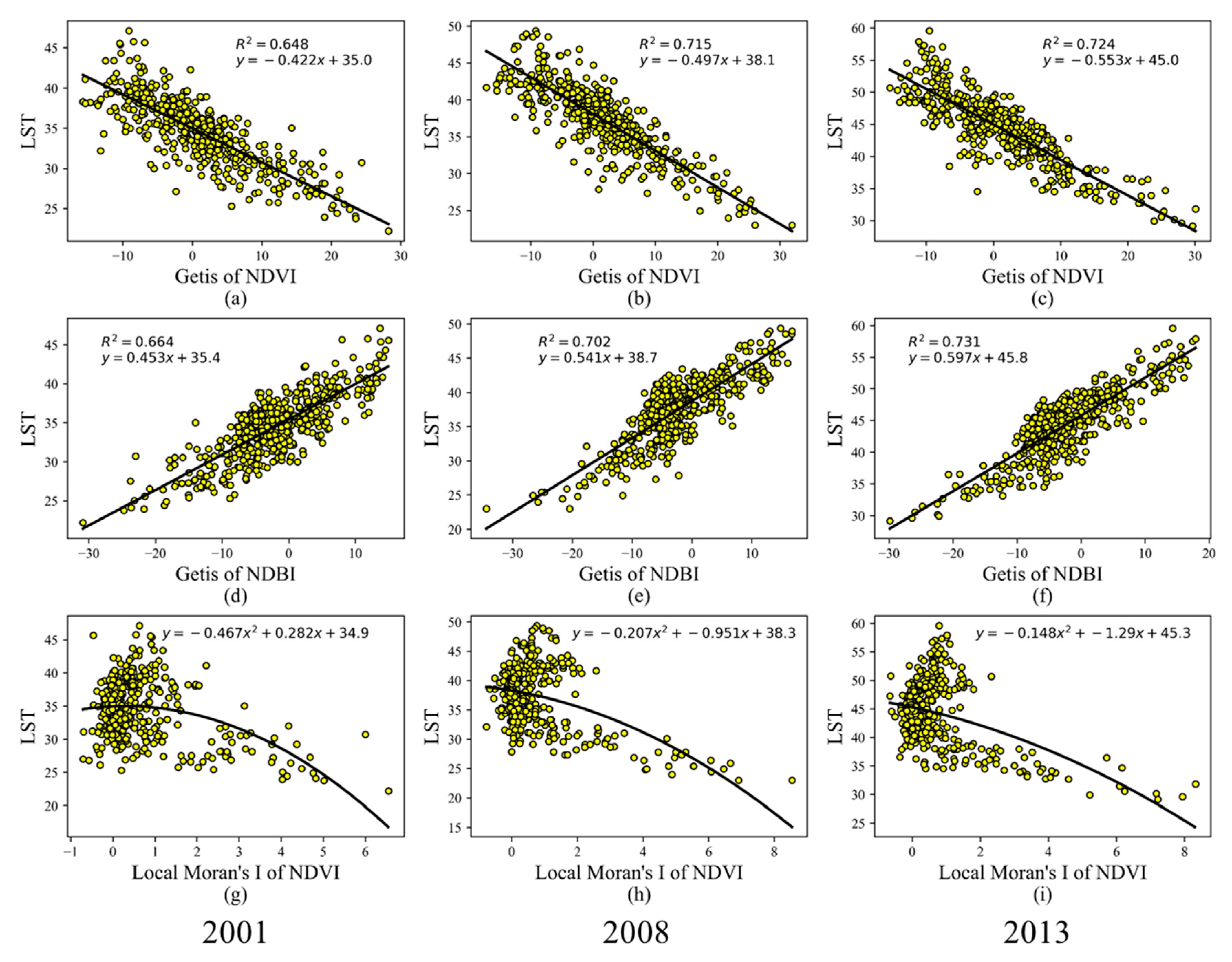
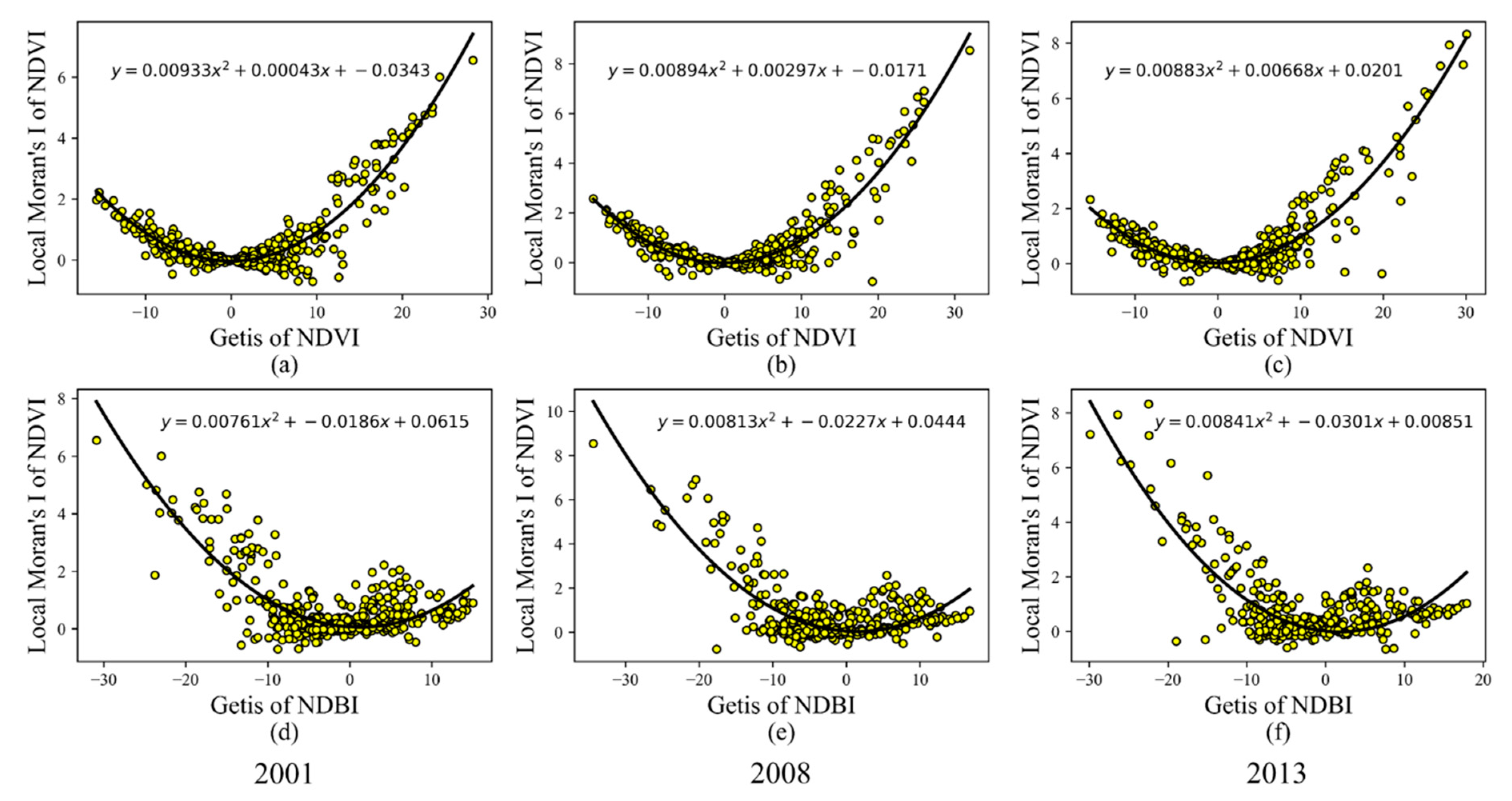
3.3. Bivariate Relationship between LST and Spatial Autocorrelation Variables
3.4. Impacts of Spatial Autocorrelation Indices on the LST
4. Discussion
4.1. Changing Climate in Boise
4.2. The Interacting Effect of Land Cover Abundance and Spatial Pattern on the LST
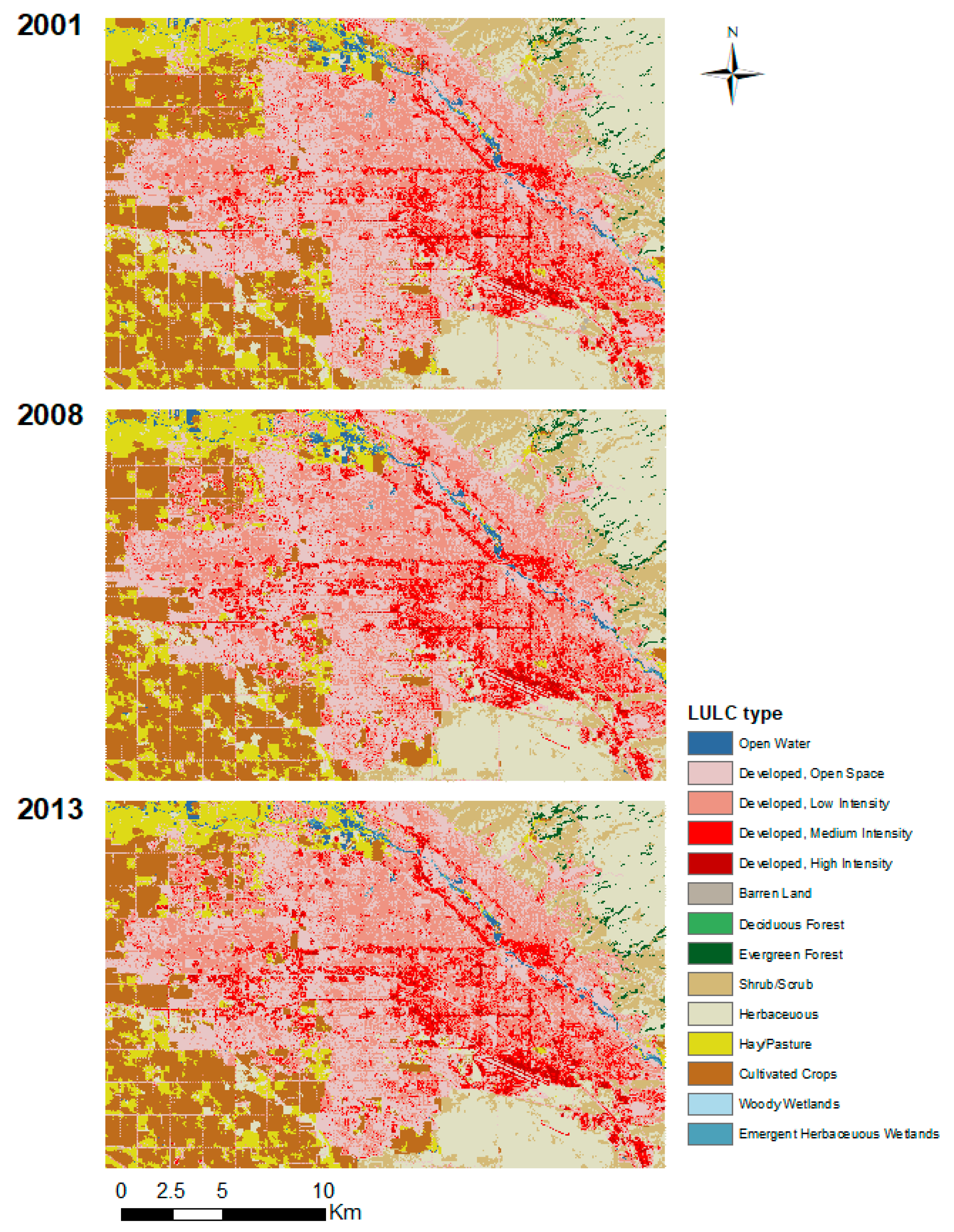
4.3. Urbanization Impacts on the Spatiotemporal Pattern of LST
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- United States Environmental Protection Agency, Heat Island Impacts. Available online: https://www.epa.gov/heat-islands/heat-island-impacts (accessed on 7 February 2020).
- Myint, S.W.; Zheng, B.; Talen, E.; Fan, C.; Kaplan, S.; Middel, A.; Smith, M.; Huang, H.-P.; Brazel, A. Does the spatial arrangement of urban landscape matter? Examples of urban warming and cooling in Phoenix and Las Vegas. Ecosyst. Health Sustain. 2015, 1, 1–15. [Google Scholar] [CrossRef]
- Tran, D.X.; Pla, F.; Latorre-Carmona, P.; Myint, S.W.; Caetano, M.; Kieu, H.V. Characterizing the relationship between land use land cover change and land surface temperature. ISPRS J. Photogramm. Remote Sens. 2017, 124, 119–132. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ. 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Essa, W.; van der Kwast, J.; Verbeiren, B.; Batelaan, O. Downscaling of thermal images over urban areas using the land surface temperature–impervious percentage relationship. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 95–108. [Google Scholar] [CrossRef]
- Mallick, J.; Rahman, A. Impact of population density on the surface temperature and micro-climate of Delhi. Curr. Sci. 2012, 102, 1708–1713. [Google Scholar]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: Evidence from the heavily urbanized Beijing metropolitan area, China. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Tiyip, T.; Pla, F.; Latorre-Carmona, P.; Halik, Ü.; Sawut, M.; Caetano, M. Effects of green space spatial pattern on land surface temperature: Implications for sustainable urban planning and climate change adaptation. ISPRS J. Photogramm. Remote Sens. 2014, 89, 59–66. [Google Scholar] [CrossRef]
- Rhee, J.; Park, S.; Lu, Z. Relationship between land cover patterns and surface temperature in urban areas. GIScience Remote Sens. 2014, 51, 521–536. [Google Scholar] [CrossRef]
- Connors, J.P.; Galletti, C.S.; Chow, W.T. Landscape configuration and urban heat island effects: Assessing the relationship between landscape characteristics and land surface temperature in Phoenix, Arizona. Landsc. Ecol. 2013, 28, 271–283. [Google Scholar] [CrossRef]
- Fan, C.; Myint, S.W.; Zheng, B. Measuring the spatial arrangement of urban vegetation and its impacts on seasonal surface temperatures. Prog. Phys. Geogr. 2015, 39, 199–219. [Google Scholar] [CrossRef]
- Li, W.; Cao, Q.; Lang, K.; Wu, J. Linking potential heat source and sink to urban heat island: Heterogeneous effects of landscape pattern on land surface temperature. Sci. Total Environ. 2017, 586, 457–465. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Myint, S.W.; Fan, C. Spatial configuration of anthropogenic land cover impacts on urban warming. Landsc. Urban Plan. 2014, 130, 104–111. [Google Scholar] [CrossRef]
- Gage, E.A.; Cooper, D.J. Relationships between landscape pattern metrics, vertical structure and surface urban heat island formation in a Colorado suburb. Urban Ecosyst. 2017, 20, 1229–1238. [Google Scholar] [CrossRef]
- Seto, K.C.; Fragkias, M. Quantifying Spatiotemporal Patterns of Urban Land-use Change in Four Cities of China with Time Series Landscape Metrics. Landsc. Ecol. 2005, 20, 871–888. [Google Scholar] [CrossRef]
- Fan, C.; Myint, S. A comparison of spatial autocorrelation indices and landscape metrics in measuring urban landscape fragmentation. Landsc. Urban Plan. 2014, 121, 117–128. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S. The gradient concept of landscape structure [Chapter 12]. In Issues and Perspectives in Landscape Ecology; Wiens, J.A., Moss, M.R., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 112–119. [Google Scholar]
- Fan, C.; Myint, S.W.; Rey, S.J.; Li, W. Time series evaluation of landscape dynamics using annual Landsat imagery and spatial statistical modeling: Evidence from the Phoenix metropolitan region. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 12–25. [Google Scholar] [CrossRef]
- Southworth, J.; Munroe, D.; Nagendra, H. Land cover change and landscape fragmentation—Comparing the utility of continuous and discrete analyses for a western Honduras region. Agric. Ecosyst. Environ. 2004, 101, 185–205. [Google Scholar] [CrossRef]
- Kowe, P.; Mutanga, O.; Odindi, J.; Dube, T. A quantitative framework for analysing long term spatial clustering and vegetation fragmentation in an urban landscape using multi-temporal landsat data. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102057. [Google Scholar] [CrossRef]
- United States Census Bureau. Available online: https://www.census.gov/en.html (accessed on 9 April 2020).
- US Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service. NOAA’s National Weather Service—National Climate. Available online: https://w2.weather.gov/climate/ (accessed on 9 April 2020).
- Dahal, K.R.; Benner, S.; Lindquist, E. Analyzing spatiotemporal patterns of urbanization in Treasure Valley, Idaho, USA. Appl. Spat. Anal. Policy 2018, 11, 205–226. [Google Scholar] [CrossRef]
- Baeza, S.; Paruelo, J.M. Land Use/Land Cover Change (2000–2014) in the Rio de la Plata Grasslands: An Analysis Based on MODIS NDVI Time Series. Remote Sens. 2020, 12, 381. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Shao, Y.; Ediriwickrema, J.; Lyon, J.G. Monitoring agricultural cropping patterns across the Laurentian Great Lakes Basin using MODIS-NDVI data. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 81–88. [Google Scholar] [CrossRef]
- Rani, M.; Kumar, P.; Pandey, P.C.; Srivastava, P.K.; Chaudhary, B.S.; Tomar, V.; Mandal, V.P. Multi-temporal NDVI and surface temperature analysis for Urban Heat Island inbuilt surrounding of sub-humid region: A case study of two geographical regions. Remote Sens. Appl. Soc. Environ. 2018, 10, 163–172. [Google Scholar] [CrossRef]
- Soudani, K.; Hmimina, G.; Delpierre, N.; Pontailler, J.-Y.; Aubinet, M.; Bonal, D.; Caquet, B.; de Grandcourt, A.; Burban, B.; Flechard, C.; et al. Ground-based Network of NDVI measurements for tracking temporal dynamics of canopy structure and vegetation phenology in different biomes. Remote Sens. Environ. 2012, 123, 234–245. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y. Urban heat island analysis using the Landsat TM data and ASTER data: A case study in Hong Kong. Remote Sens. 2011, 3, 1535–1552. [Google Scholar] [CrossRef]
- Chen, X.-L.; Zhao, H.-M.; Li, P.-X.; Yin, Z.-Y. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Baño, D.; Salazar, J.; Delgado, M. Remote Sensing in the Design of Urban Planning Strategies, Case Study Urban Heat Island of the Metropolitan District of Quito, Ecuador. Lat. Am. J. Comput. Fac. Syst. Eng. Esc. Politécnica Nac. Quito Ecuad. 2018, 5, 17–26. [Google Scholar]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. Atmos. 2003, 108, 4688–4695. [Google Scholar]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd Edition. Pearson. Available online: https://www.pearson.com/us/higher-education/program/Jensen-Remote-Sensing-of-the-Environment-An-Earth-Resource-Perspective-2nd-Edition/PGM200207.html (accessed on 9 April 2020).
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An atmospheric correction parameter calculator for a single thermal band earth-sensing instrument. In Proceedings of the IGARSS 2003—2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 5, pp. 033747721–2520033014. [Google Scholar]
- Zhang, S.; York, A.M.; Boone, C.G.; Shrestha, M. Methodological advances in the spatial analysis of land fragmentation. Prof. Geogr. 2013, 65, 512–526. [Google Scholar] [CrossRef]
- Myint, S.W.; Brazel, A.; Okin, G.; Buyantuyev, A. Combined effects of impervious surface and vegetation cover on air temperature variations in a rapidly expanding desert city. GIScience Remote Sens. 2010, 47, 301–320. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J. Urban heat islands and landscape heterogeneity: Linking spatiotemporal variations in surface temperatures to land-cover and socioeconomic patterns. Landsc. Ecol. 2010, 25, 17–33. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Florax, R.J.; Folmer, H.; Rey, S.J. Specification searches in spatial econometrics: The relevance of Hendry’s methodology. Reg. Sci. Urban Econ. 2003, 33, 557–579. [Google Scholar] [CrossRef]
- Climate Central, AMERICAN WARMING: The Fastest-Warming Cities and States in the U.S. Available online: https://www.climatecentral.org/news/report-american-warming-us-heats-up-earth-day (accessed on 9 April 2020).
- Climate Action. City of Boise. Available online: https://www.cityofboise.org/programs/climate-action/ (accessed on 9 April 2020).
- Masoudi, M.; Tan, P.Y. Multi-year comparison of the effects of spatial pattern of urban green spaces on urban land surface temperature. Landsc. Urban Plan. 2019, 184, 44–58. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y.; Myint, S.W. Effects of landscape composition and pattern on land surface temperature: An urban heat island study in the megacities of Southeast Asia. Sci. Total Environ. 2017, 577, 349–359. [Google Scholar] [CrossRef] [PubMed]

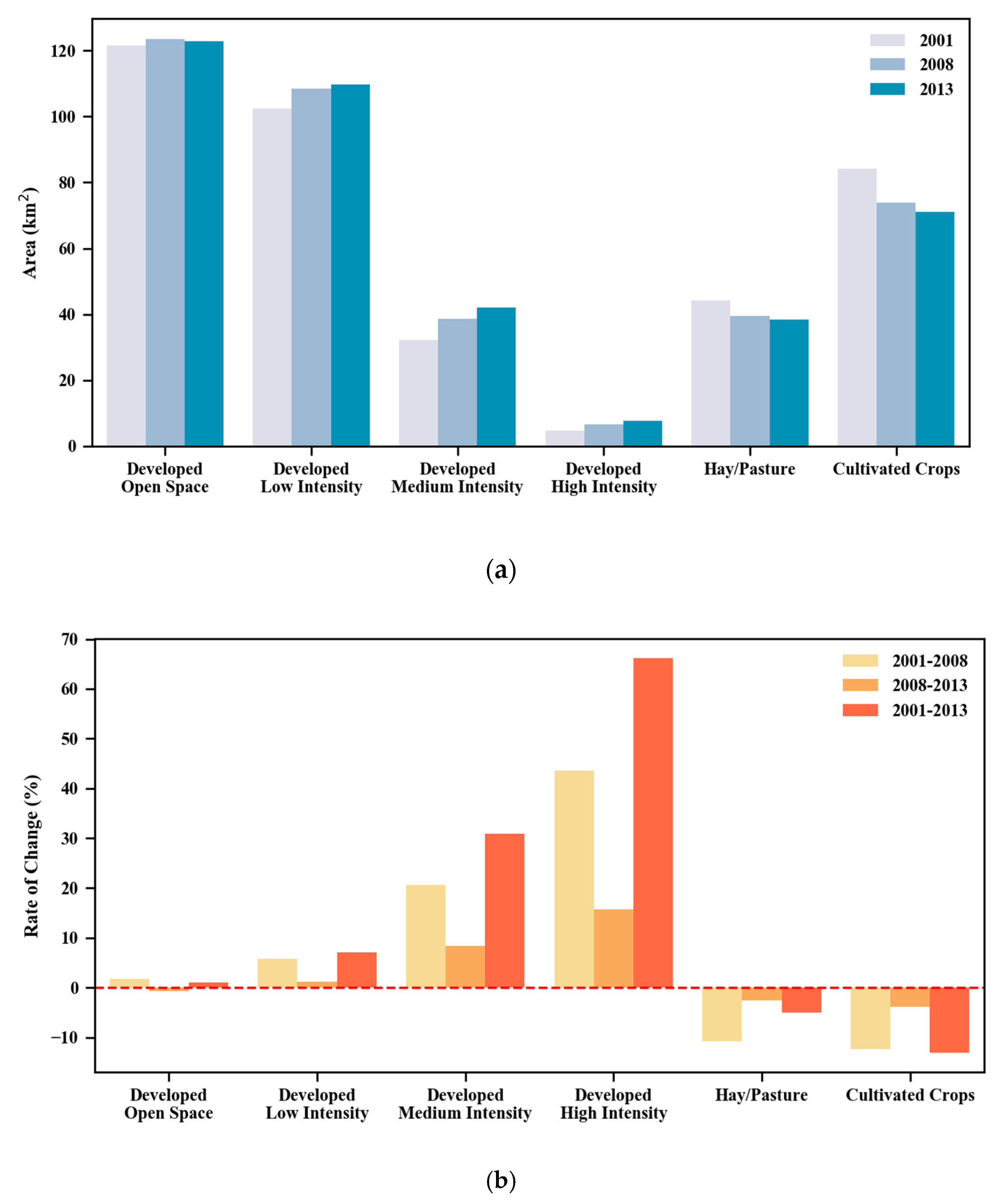
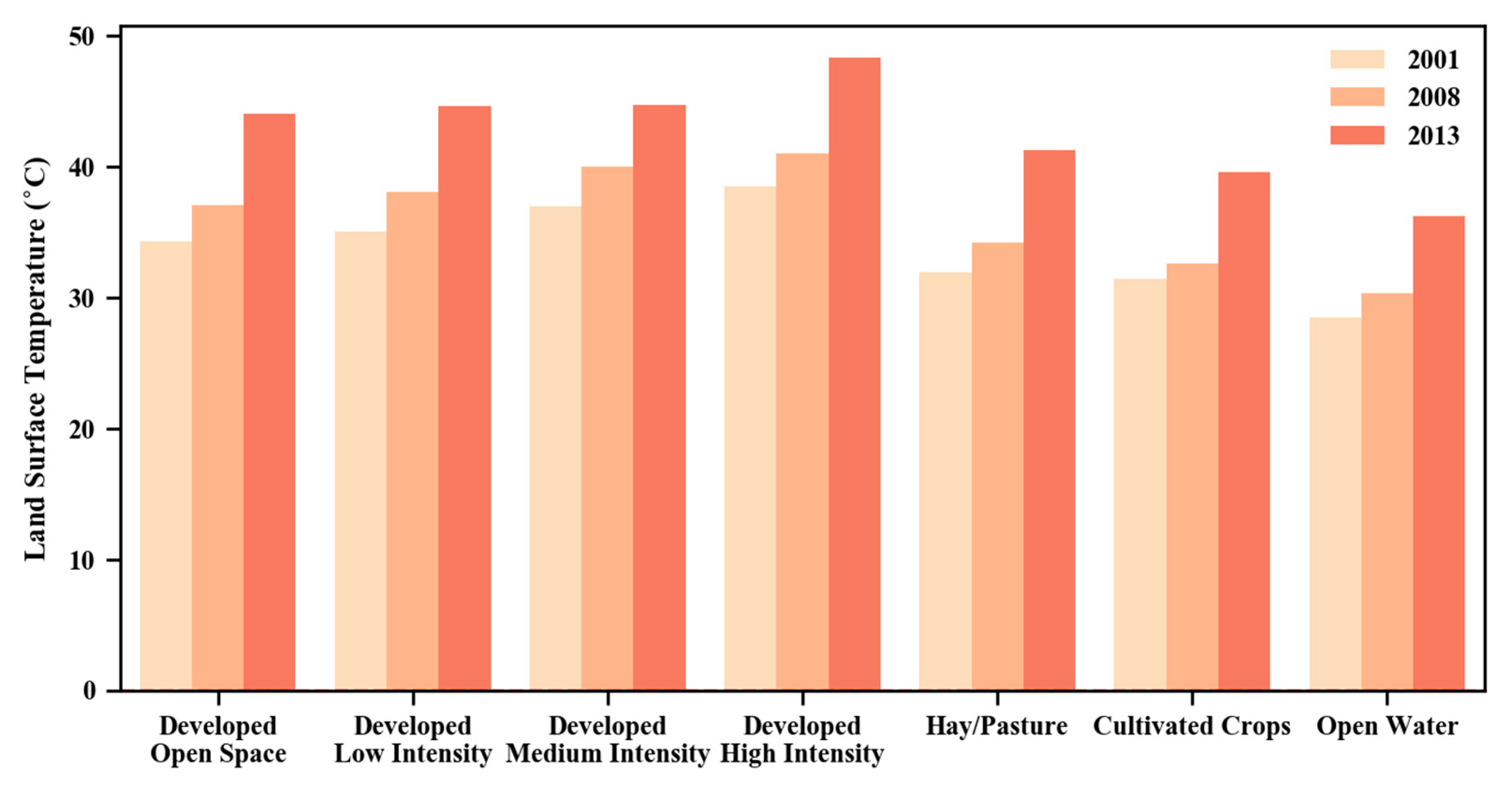
| Year | G of NDVI | G of NDBI | Local Moran’s I |
|---|---|---|---|
| 2001 | −0.807 * | 0.767 * | −0.075 |
| 2008 | −0.833 * | 0.779 * | −0.152 * |
| 2013 | −0.837 * | 0.786 * | −0.135 * |
| 2001 | ||||
|---|---|---|---|---|
| Coefficient | Std Error | Standardized Coefficient | VIF | |
| G of NDVI | −0.16 * | 0.031 | −0.317 | 4.496 |
| G of NDBI | 0.294 * | 0.033 | 0.524 | 4.431 |
| Local Moran’s I of NDVI | 0.121 | 0.113 | −0.04 | 1.313 |
| AIC: 2185.6 (AIC for OLS: 2219.9) Pseudo R2: 0.7 | ||||
| 2008 | ||||
| Coefficient | Std error | Standardized coefficient | VIF | |
| G of NDVI | −0.181 * | 0.024 | −0.317 | 4.165 |
| G of NDBI | 0.316 * | 0.028 | 0.524 | 3.83 |
| Local Moran’s I of NDVI | −0.394 * | 0.09 | −0.043 | 1.298 |
| AIC: 2177.6 (AIC for OLS: 2188.1) Pseudo R2: 0.77 | ||||
| 2013 | ||||
| Coefficient | Std error | Standardized coefficient | VIF | |
| G of NDVI | −0.24 * | 0.033 | −0.369 | 4.766 |
| G of NDBI | 0.319 * | 0.034 | 0.457 | 4.286 |
| Local Moran’s I of NDVI | −0.278 * | 0.105 | −0.062 | 1.358 |
| AIC: 2253.4 (AIC for OLS: 2286.6) Pseudo R2: 0.78 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, C.; Wang, Z. Spatiotemporal Characterization of Land Cover Impacts on Urban Warming: A Spatial Autocorrelation Approach. Remote Sens. 2020, 12, 1631. https://doi.org/10.3390/rs12101631
Fan C, Wang Z. Spatiotemporal Characterization of Land Cover Impacts on Urban Warming: A Spatial Autocorrelation Approach. Remote Sensing. 2020; 12(10):1631. https://doi.org/10.3390/rs12101631
Chicago/Turabian StyleFan, Chao, and Zhe Wang. 2020. "Spatiotemporal Characterization of Land Cover Impacts on Urban Warming: A Spatial Autocorrelation Approach" Remote Sensing 12, no. 10: 1631. https://doi.org/10.3390/rs12101631
APA StyleFan, C., & Wang, Z. (2020). Spatiotemporal Characterization of Land Cover Impacts on Urban Warming: A Spatial Autocorrelation Approach. Remote Sensing, 12(10), 1631. https://doi.org/10.3390/rs12101631