Potential for the Detection of Irrigation Events on Maize Plots Using Sentinel-1 Soil Moisture Products
Abstract
1. Introduction
2. Study Site and Data
2.1. Experimental Plots and In-Situ Data
2.2. Satellite Data
3. Method
3.1. Step 1—Adjusting from Instantaneous to Daily Values
3.2. Step 2—Estimation of the Soil Water Content of the Upper Layer
3.3. Step 3—Irrigation Detection
3.4. Step 4: Irrigation Injection
3.5. Accounting
4. Results
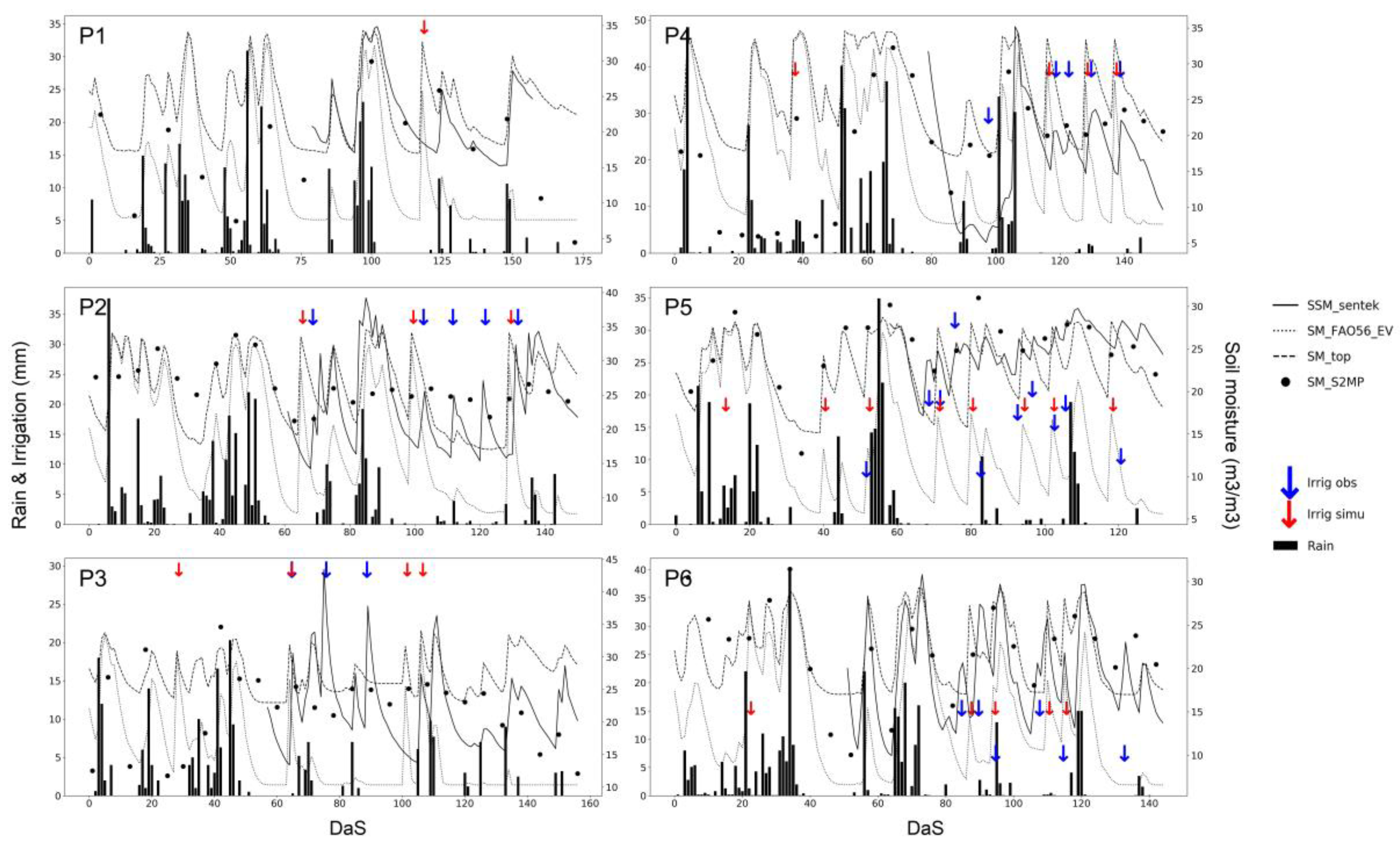
4.1. Analysis of Soil Moisture Changes for the Detection of Irrigation Events
4.2. Detection of Water Turns Using In-Situ SSM Measurements
4.3. Detection of Water Turns Using the S2MP Product
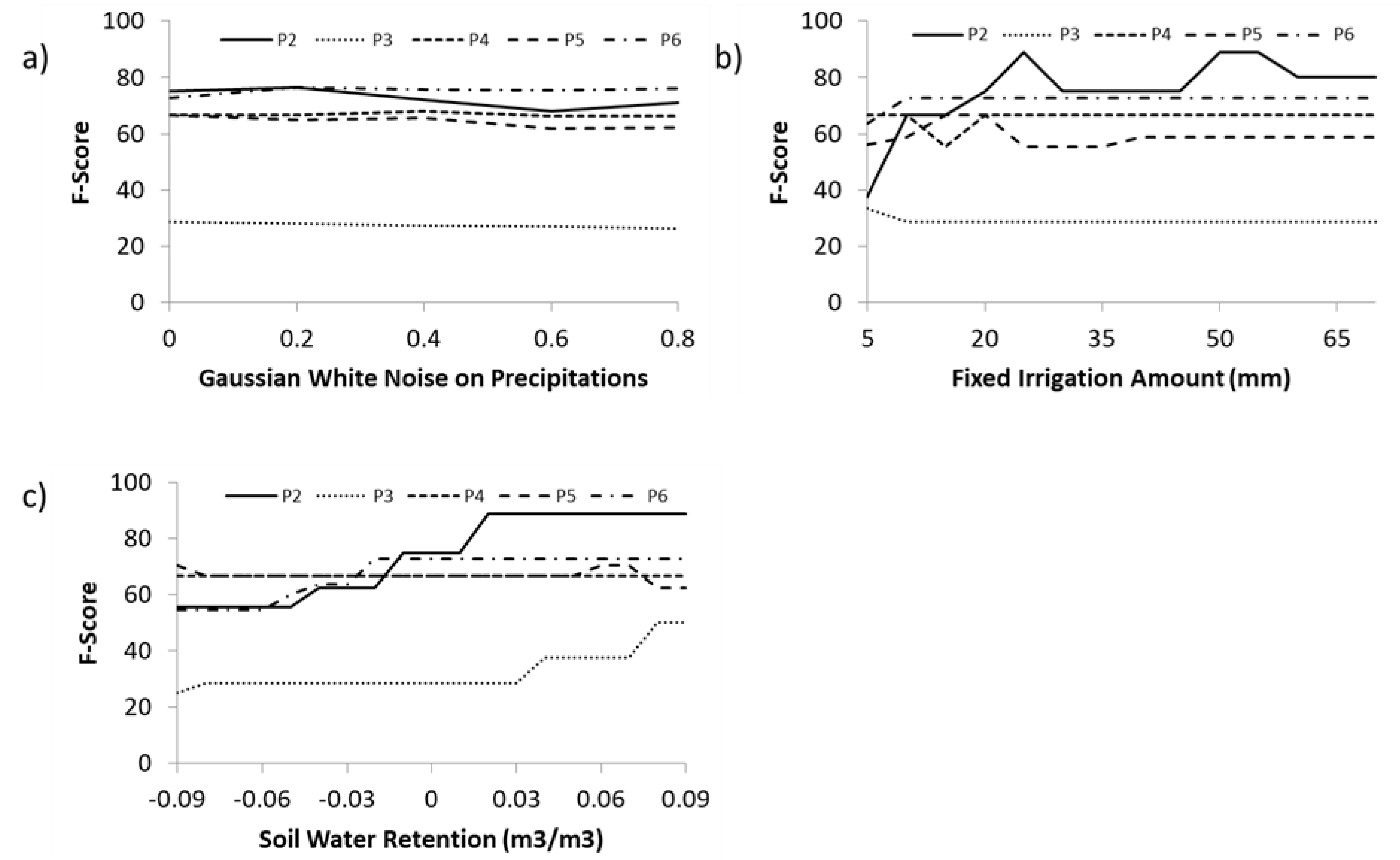
4.4. Sensitivity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AMSR | Advanced Microwave Scanning Radiometer | |
| Δθm | Difference of SSM computed by model between two observation time step | m3·m−3 |
| Δθobs | Difference of SSM observed between two observation time step | m3·m−3 |
| Drdown | Depletion of the bottom of the root bucket | mm |
| Drtop | Depletion of the top of the root bucket | mm |
| E | Evaporation | mm |
| ET | Evapotranspiration | mm |
| ET0 | Reference Evapotranspiration | mm |
| Etc | Crop Evapotranspiration | mm |
| ETcadj | Adjusted Crop Evapotranspiration | mm |
| F1 | Fscore | |
| FAO-56 | The approach described by Allen et al. (1998) | |
| Fc | Fraction cover | % |
| FP | False Positive | |
| i | observation time step | days |
| j | daily time step | days |
| κ | A threshold to account for the spacing of observations | m3·m−3 |
| k | A parameter to calibrate for the threshold κ | |
| Kc | Crop Coefficient | |
| Kcb | Basal Crop Coefficient | |
| Kstop | Stress coefficient of the top of the root bucket | |
| MAE | Mean Absolute eError | |
| MBE | Mean Bias eError | |
| NDVI | Normalized Difference Vegetation Index | |
| p | Precision | |
| padjust | Fraction of TAW that can be depleted from the root zone before water stress occurs | |
| θfc | Field Capacity | m3·m−3 |
| θwp | Wilting Point | m3·m−3 |
| r | Recall | |
| R2 | Determination Coefficient | |
| RMSE | Root Mean Square Error | |
| S2MP | Sentinel-1/Sentinel-2-derived Soil Moisture Product at plot scale | |
| SAR | Synthetic Aperture Radar | |
| SD | Standard Deviation | |
| SMAP | Soil Moisture Active Passive | |
| SMOS | Soil Moisture and Ocean Salinity mission | |
| SSM | Surface Soil Moisture | m3·m−3 |
| SSMsentek | SSM measured at 5 cm depth by the Sentek Enviroscan instrument | m3·m−3 |
| SWCtop | Soil Water Content of the top bucket | mm |
| T | Transpiration | mm |
| TAWdown | Total Available Water at the bottom of the root bucket | mm |
| TAWtop | Total Available Water at the top of the root bucket | mm |
| TP | True Positive | |
| Ttop | Transpiration of the top layer | mm |
| WCM | Water Cloud Model | |
| Ψ | A threshold to account for dry soils | m3·m−3 |
| Ze | Depth of the evaporation bucket | mm |
| Zr | Root Depth | m |
| Zrmax | Root Depth | m |
References
- Khabba, S.; Jarlan, L.; Er-Raki, S.; Le Page, M.; Ezzahar, J.; Boulet, G.; Simonneaux, V.; Kharrou, M.H.; Hanich, L.; Chehbouni, G. The SudMed Program and the Joint International Laboratory TREMA: A Decade of Water Transfer Study in the Soil-plant-atmosphere System over Irrigated Crops in Semi-arid Area. Procedia Environ. Sci. 2013, 19, 524–533. [Google Scholar] [CrossRef]
- FAO. The State of the World’s Land and Water Resources for Food and Agriculture; FAO: Rome, Italy; Earthscan: London, UK, 2011; ISBN 978-1-84971-326-9. [Google Scholar]
- Campbell, G.S.; Campbell, M.D. Irrigation Scheduling Using Soil Moisture Measurements: Theory and Practice. In Advances in Irrigation; Academic Press: London, UK, 1982; Volume 1, pp. 25–42. ISBN 978-0-12-024301-3. [Google Scholar]
- Pereira, L.S. Higher performance through combined improvements in irrigation methods and scheduling: A discussion. Agric. Water Manag. 1999, 40, 153–169. [Google Scholar] [CrossRef]
- Yaron, D.; Dinar, A.; Meyers, S. Irrigation Scheduling - Theoretical Approach and Application Problems. Water Resour. Manag. 1987, 1, 17–31. [Google Scholar] [CrossRef]
- Romano, N. Soil moisture at local scale: Measurements and simulations. J. Hydrol. 2014, 516, 6–20. [Google Scholar] [CrossRef]
- Susha Lekshmi, S.U.; Singh, D.N.; Shojaei Baghini, M. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Mekala, M.S.; Viswanathan, P. A Survey: Smart agriculture IoT with cloud computing. In Proceedings of the 2017 International conference on Microelectronic Devices, Circuits and Systems (ICMDCS), Vellore, India, 10–12 August 2017; pp. 1–7. [Google Scholar]
- Shafi, U.; Mumtaz, R.; García-Nieto, J.; Hassan, S.A.; Zaidi, S.A.R.; Iqbal, N. Precision Agriculture Techniques and Practices: From Considerations to Applications. Sensors 2019, 19, 3796. [Google Scholar] [CrossRef]
- Maqbool, S. Arising Issues In Wireless Sensor Networks: Current Proposals And Future Developments. J. Comput. Eng. 2013, 8, 56–73. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely sensed soil moisture: Downscale Satellite-Based Soil Moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Pan, M.; Wanders, N.; Kumar, D.N.; Wood, E.F. Four decades of microwave satellite soil moisture observations: Part 1. A review of retrieval algorithms. Adv. Water Resour. 2017, 109, 106–120. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; O’Neill, P.E.; Njoku, E.; Jackson, T.; Colliander, A.; Chen, F.; Burgin, M.; Dunbar, S.; Piepmeier, J.; et al. Assessment of the SMAP Passive Soil Moisture Product. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4994–5007. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; de Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT Soil Moisture Product: A Review of its Specifications, Validation Results, and Emerging Applications. Meteorologische Zeitschrift 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Kim, S.; Liu, Y.Y.; Johnson, F.M.; Parinussa, R.M.; Sharma, A. A global comparison of alternate AMSR2 soil moisture products: Why do they differ? Remote Sens. Environ. 2015, 161, 43–62. [Google Scholar] [CrossRef]
- Lawston, P.M.; Santanello, J.A.; Kumar, S.V. Irrigation Signals Detected From SMAP Soil Moisture Retrievals: Irrigation Signals Detected From SMAP. Geophys. Res. Lett. 2017, 44, 11860–11867. [Google Scholar] [CrossRef]
- Malbéteau, Y.; Merlin, O.; Balsamo, G.; Er-Raki, S.; Khabba, S.; Walker, J.P.; Jarlan, L. Toward a Surface Soil Moisture Product at High Spatiotemporal Resolution: Temporally Interpolated, Spatially Disaggregated SMOS Data. J. Hydrometeor. 2018, 19, 183–200. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data: Using the soil as a natural raingauge. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Brocca, L.; Tarpanelli, A.; Filippucci, P.; Dorigo, W.; Zaussinger, F.; Gruber, A.; Fernández-Prieto, D. How much water is used for irrigation? A new approach exploiting coarse resolution satellite soil moisture products. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 752–766. [Google Scholar] [CrossRef]
- Jalilvand, E.; Tajrishy, M.; Ghazi Zadeh Hashemi, S.A.; Brocca, L. Quantification of irrigation water using remote sensing of soil moisture in a semi-arid region. Remote Sens. Environ. 2019, 231, 111226. [Google Scholar] [CrossRef]
- Zaussinger, F.; Dorigo, W.; Gruber, A.; Tarpanelli, A.; Filippucci, P.; Brocca, L. Estimating irrigation water use over the contiguous United States by combining satellite and reanalysis soil moisture data. Hydrol. Earth Syst. Sci. 2019, 23, 897–923. [Google Scholar] [CrossRef]
- Zribi, M.; Gorrab, A.; Baghdadi, N.; Lili-Chabaane, Z.; Mougenot, B. Influence of Radar Frequency on the Relationship Between Bare Surface Soil Moisture Vertical Profile and Radar Backscatter. IEEE Geosci. Remote Sensing Lett. 2014, 11, 848–852. [Google Scholar] [CrossRef]
- Gorrab, A.; Zribi, M.; Baghdadi, N.; Mougenot, B.; Fanise, P.; Chabaane, Z. Retrieval of Both Soil Moisture and Texture Using TerraSAR-X Images. Remote Sens. 2015, 7, 10098–10116. [Google Scholar] [CrossRef]
- Paloscia, S.; Pampaloni, P.; Pettinato, S.; Santi, E. Generation of soil moisture maps from ENVISAT/ASAR images in mountainous areas: A case study. Int. J. Remote Sens. 2010, 31, 2265–2276. [Google Scholar] [CrossRef]
- Srivastava, H.S.; Patel, P.; Manchanda, M.L.; Adiga, S. Use of multiincidence angle RADARSAT-1 SAR data to incorporate the effect of surface roughness in soil moisture estimation. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1638–1640. [Google Scholar] [CrossRef]
- Zribi, M.; Chahbi, A.; Shabou, M.; Lili-Chabaane, Z.; Duchemin, B.; Baghdadi, N.; Amri, R.; Chehbouni, A. Soil surface moisture estimation over a semi-arid region using ENVISAT ASAR radar data for soil evaporation evaluation. Hydrol. Earth Syst. Sci. 2011, 15, 345–358. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Amini, J.; Notarnicola, C.; Greifeneder, F. Synergetic Use of Sentinel-1 and Sentinel-2 Data for Soil Moisture Mapping at Plot Scale. Remote Sens. 2018, 10, 1285. [Google Scholar] [CrossRef]
- Bao, Y.; Lin, L.; Wu, S.; Kwal Deng, K.A.; Petropoulos, G.P. Surface soil moisture retrievals over partially vegetated areas from the synergy of Sentinel-1 and Landsat 8 data using a modified water-cloud model. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 76–85. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Bazzi, H. Synergic Use of Sentinel-1 and Sentinel-2 Images for Operational Soil Moisture Mapping at High Spatial Resolution over Agricultural Areas. Remote Sens. 2017, 9, 1292. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.J.; Baghdadi, N. Synergetic use of sentinel-1 and sentinel-2 data for soil moisture mapping at 100 m resolution. Sensors 2017, 17, 1966. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, L.; Xie, Q.; Yao, S.; Chen, X.; Zhang, Y. Combined Use of GF-3 and Landsat-8 Satellite Data for Soil Moisture Retrieval over Agricultural Areas Using Artificial Neural Network. Adv. Meteorol. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Ouaddi, N.; Jarlan, L.; Ezzahar, J.; Zribi, M.; Khabba, S.; Bouras, E.; Bousbih, S.; Frison, P.-L. Monitoring of wheat crops using the backscattering coefficient and the interferometric coherence derived from Sentinel-1 in semi-arid areas. Remote Sens. Environ. 2020. [Google Scholar]
- Pulvirenti, L.; Squicciarino, G.; Cenci, L.; Boni, G.; Pierdicca, N.; Chini, M.; Versace, C.; Campanella, P. A surface soil moisture mapping service at national (Italian) scale based on Sentinel-1 data. Environ. Model. Softw. 2018, 102, 13–28. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G. Application of artificial neural networks for the soil moisture retrieval from active and passive microwave spaceborne sensors. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 61–73. [Google Scholar] [CrossRef]
- Greifeneder, F.; Khamala, E.; Sendabo, D.; Wagner, W.; Zebisch, M.; Farah, H.; Notarnicola, C. Detection of soil moisture anomalies based on Sentinel-1. Phys. Chem. Earth Parts A/B/C 2018. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Smith, M.; Raes, D.; Wright, J. FAO-56 Dual Crop Coefficient Method for Estimating Evaporation from Soil and Application Extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.; Raes, D.; Smith, M. FAO Irrigation and Drainage n°56: Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998; Volume 300, ISBN 92-5-104219-5. [Google Scholar]
- Allen, R.G. Skin layer evaporation to account for small precipitation events—An enhancement to the FAO-56 evaporation model. Agric. Water Manag. 2011, 99, 8–18. [Google Scholar] [CrossRef]
- Neale, C.M.U.; Bausch, W.C.; Heermann, D.F. Development of Reflectance-Based Crop Coefficients for Corn. Trans. ASAE 1990, 32, 1891. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Khabba, S.; Simonneaux, V.; Jarlan, L.; Ouldbba, A.; Rodriguez, J.C.; Allen, R. Assessment of reference evapotranspiration methods in semi-arid regions: Can weather forecast data be used as alternate of ground meteorological parameters? J. Arid Environ. 2010, 74, 1587–1596. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Kimball, B.A. Wheat basal crop coefficients determined by normalized difference vegetation index. Irrig. Sci. 2005, 24, 1–14. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Barnes, E.M.; Kimball, B.A. Estimating cotton evapotranspiration crop coefficients with a multispectral vegetation index. Irrig. Sci. 2003, 22, 95–104. [Google Scholar] [CrossRef]
- Jayanthi, H.; Neale, C.M.U.; Wright, J.L. Development and validation of canopy reflectance-based crop coefficient for potato. Agric. Water Manag. 2007, 88, 235–246. [Google Scholar] [CrossRef]
- López-Urrea, R.; Montoro, A.; González-Piqueras, J.; López-Fuster, P.; Fereres, E. Water use of spring wheat to raise water productivity. Agric. Water Manag. 2009, 96, 1305–1310. [Google Scholar] [CrossRef]
- Toureiro, C.; Serralheiro, R.; Shahidian, S.; Sousa, A. Irrigation management with remote sensing: Evaluating irrigation requirement for maize under Mediterranean climate condition. Agric. Water Manag. 2017, 184, 211–220. [Google Scholar] [CrossRef]
- Calera, A.; Campos, I.; Osann, A.; D’Urso, G.; Menenti, M. Remote Sensing for Crop Water Management: From ET Modelling to Services for the End Users. Sensors 2017, 17, 1104. [Google Scholar] [CrossRef]
- D’Urso, G. Current Status and Perspectives for the Estimation of Crop Water Requirements from Earth Observation. Ital. J. Agron. 2010, 5, 107–120. [Google Scholar] [CrossRef]
- Le Page, M.; Toumi, J.; Khabba, S.; Hagolle, O.; Tavernier, A.; Kharrou, M.; Er-Raki, S.; Huc, M.; Kasbani, M.; Moutamanni, A.; et al. A Life-Size and Near Real-Time Test of Irrigation Scheduling with a Sentinel-2 Like Time Series (SPOT4-Take5) in Morocco. Remote Sens. 2014, 6, 11182–11203. [Google Scholar] [CrossRef]
- Vuolo, F.; D’Urso, G.; De Michele, C.; Bianchi, B.; Michael, C. Satellite-based Irrigation Advisory Services: A common tool for different experiences from Europe to Australia. WaterEnviron. Agric. Chall. Sustain. Dev. 2013, 147, 82–95. [Google Scholar] [CrossRef]
- Rocha, J.; Perdigo, A.; Melo, R.; Henriques, C. Remote Sensing Based Crop Coefficients for Water Management in Agriculture. In Sustainable Development—Authoritative and Leading Edge Content for Environmental Management; InTechOpen: London, UK, 2012; pp. 167–192. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.; Sobrino, J.; Plaza, A.; Guanter, L.; Moreno, J.; Martinez, P. Comparison Between Fractional Vegetation Cover Retrievals from Vegetation Indices and Spectral Mixture Analysis: Case Study of PROBA/CHRIS Data Over an Agricultural Area. Sensors 2009, 9, 768–793. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef]
- Fung, A.K. Microwave Scattering and emission Models and Their Applications; The Artech House Remote Sensing Library; Artech House: Boston, MA, USA, 1994; ISBN 978-0-89006-523-5. [Google Scholar]
- Raes, D. BUDGET, a Soil Water and Salt Balance Model: Reference Manual; K.U. Leuven: Leuven, Belgium, 2002. [Google Scholar]
- Lascano, R. Review of models for predicting soil water balance. In Proceedings of the Niamey Workshop, Niamey, Niger, 18–23 February 1991; Volume 199, pp. 443–458. [Google Scholar]
- Ranatunga, K.; Nation, E.; Barratt, D. Review of soil water models and their applications in Australia. Environ. Model. Softw. 2008, 23, 1182–1206. [Google Scholar] [CrossRef]
- Noilhan, J.; Mahfouf, J.F. The ISBA land surface parameterization scheme. Glob. Planet. Chang. 1996, 13, 145–159. [Google Scholar] [CrossRef]
- Noilhan, J.; Planton, S. A Simple Parameterization of Land Surface Processes for Meteorological Models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Ritchie, J.T. Soil water balance and plant water stress. In Understanding Options for Agricultural Production; Tsuji, G.Y., Hoogenboom, G., Thornton, P.K., Eds.; Springer: Dordrecht, The Netherlands, 1998; Volume 7, pp. 41–54. ISBN 978-90-481-4940-7. [Google Scholar]
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. Aquacrop 6.0-6.1, reference manual. In Aquacrop Reference Manual Version 4.0; FAO, Land and Water Division: Rome, Italy, 2018; p. 125. [Google Scholar]
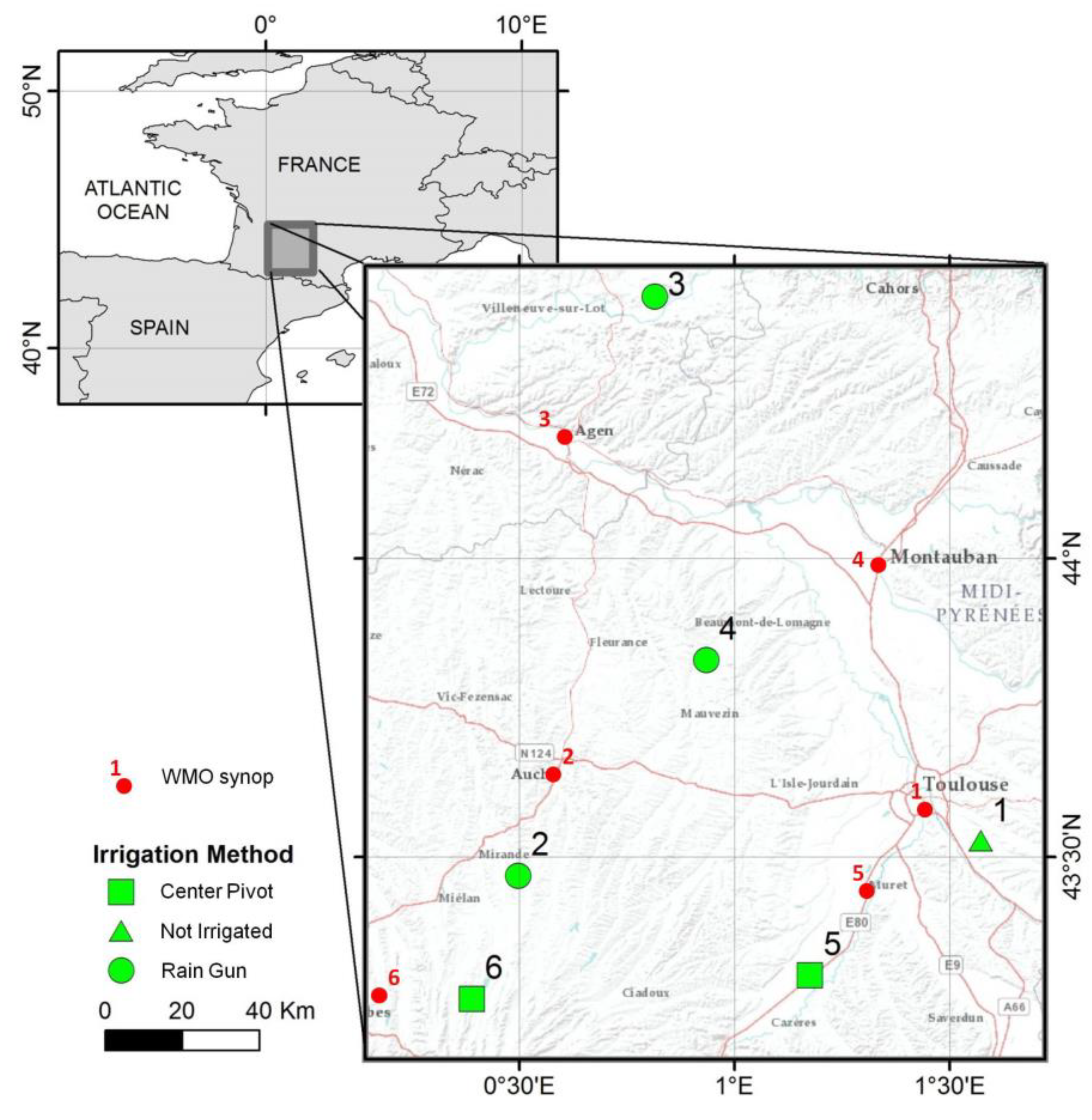
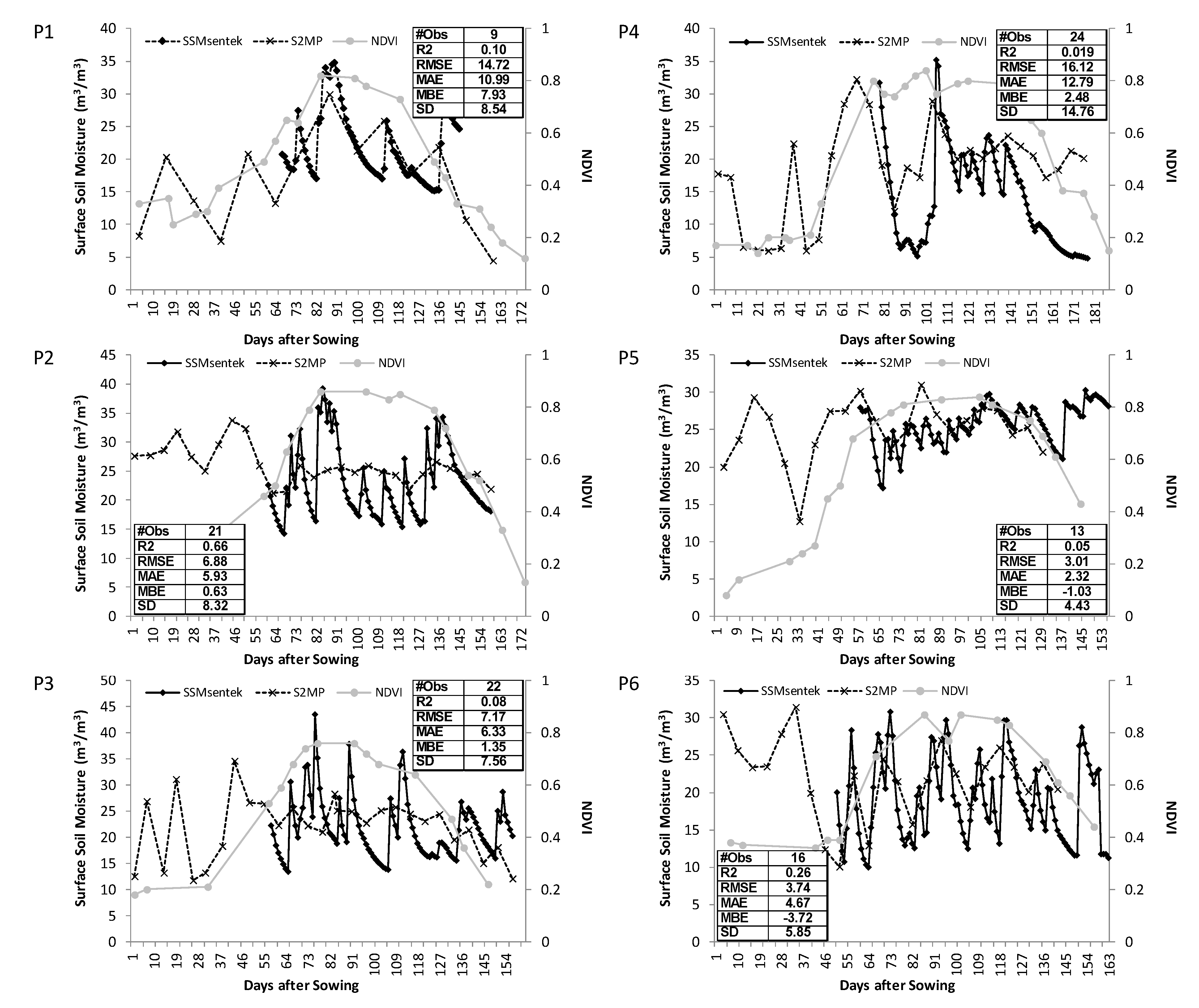

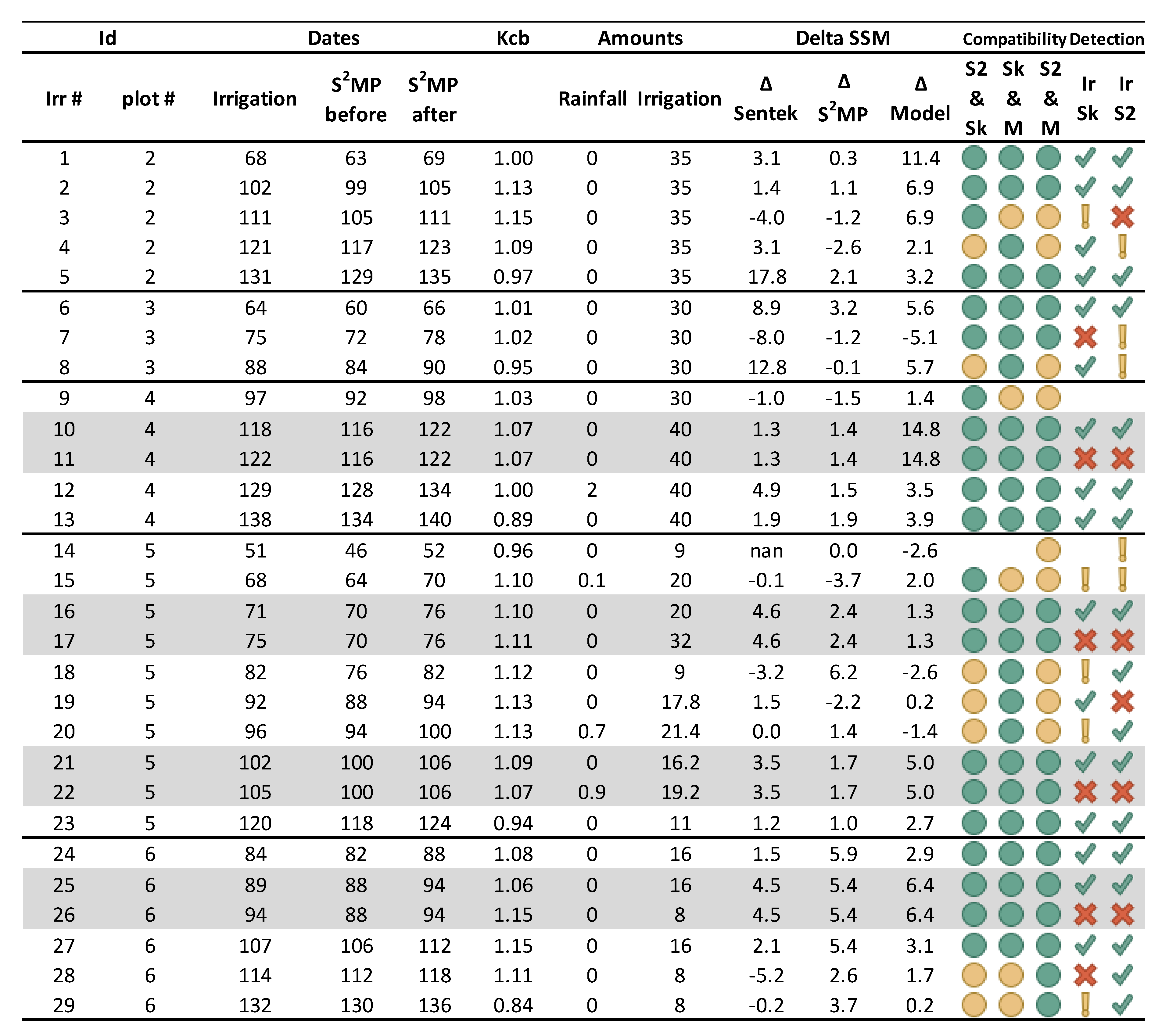
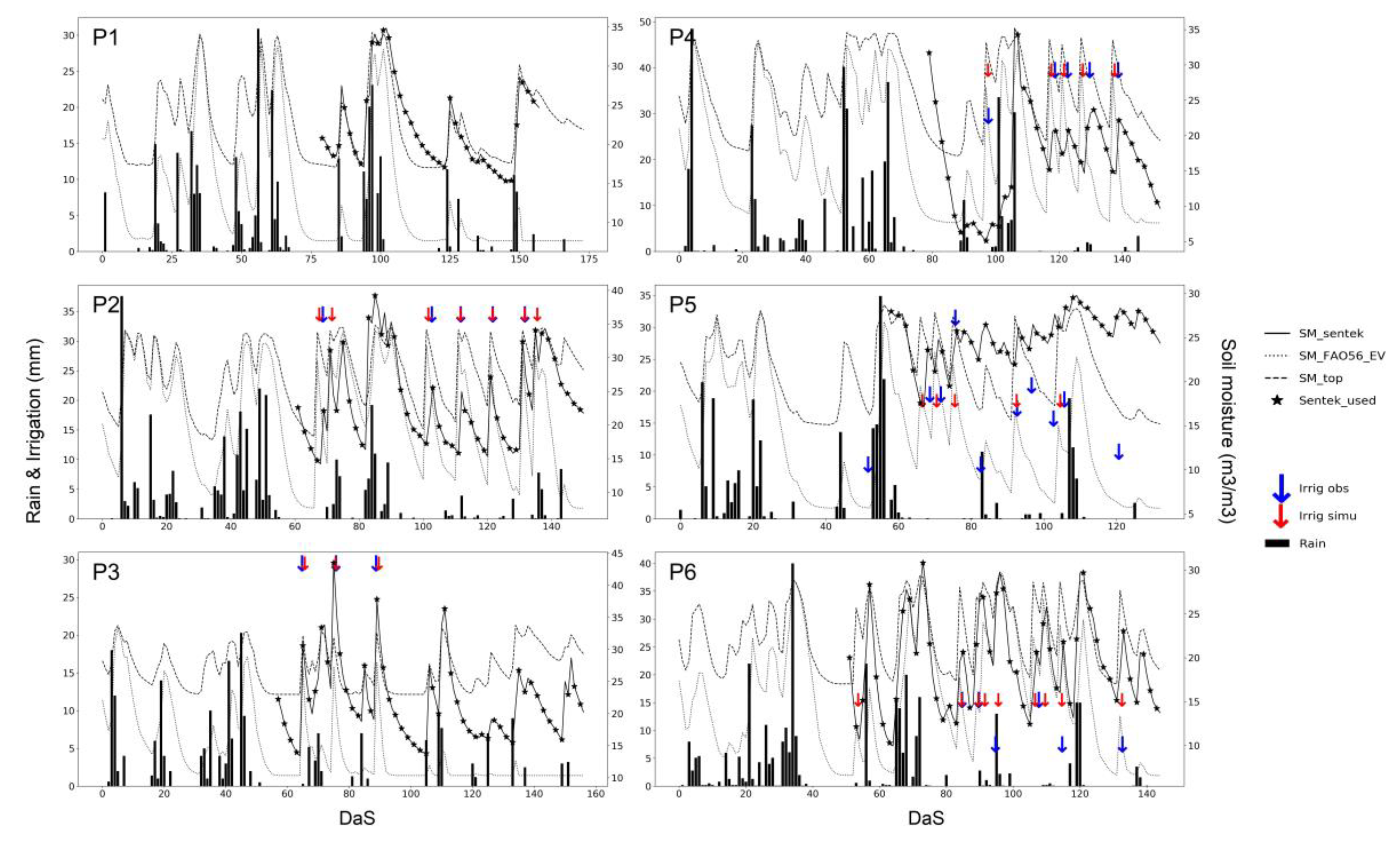
| ID | Area (ha) | Sowing Date | Sentek Installation Date | Soil | θwp (m3·m−3) | θfc (m3·m−3) | Zrmax (m) | Irrigation Type | Number of Irrigation Events | Cumulated Irrigation (mm) | Cumulated Rainfall (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 7.6 | April, 23 | May, 9 | Silt Loam | 0.17 | 0.33 | 0.45 | Not Irrigated | 0 | 0 | 333 |
| Depth: 60 cm | |||||||||||
| P2 | 4.7 | April, 23 | May, 31 | Silt Loam | 0.18 | 0.35 | 0.50 | Rain Gun | 5 | 175 | 347 |
| Depth: 90 cm | |||||||||||
| P3 | 12.4 | April, 25 | June, 1 | Silty clay | 0.23 | 0.36 | 0.30 | Rain Gun | 3 | 90 | 229 |
| Depth: 90 cm | |||||||||||
| P4 | 11.1 | April, 6 | May, 9 | Clay loam | 0.17 | 0.36 | 0.50 | Rain Gun | 5 | 190 | 452 |
| Depth: 90 cm | |||||||||||
| P5 | 25.2 | May, 22 | July, 18 | Gravelly Silt | 0.15 | 0.30 | 0.50 | Center Pivot | 10 | 175 | 279 |
| Depth: 60 cm | |||||||||||
| P6 | 26.8 | May, 10 | June, 29 | Silt Loam | 0.17 | 0..31 | 0.30 | Center Pivot | 6 | 72 | 334 |
| Depth: 90 cm |
| Plot ID | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| Fixed irrigation amount (mm) | 30 | 35 | 30 | 40 | 19 | 16 |
| Lapse | TP | FP | FN | Precision | Recall | F-score | Rank | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k-> | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |||
| P1 (0 dosis) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||||||||||
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||||||||||
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||||
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||||
| P2 (5 dosis) | 1 | 4 | 5 | 5 | 5 | 2 | 2 | 3 | 3 | 1 | 0 | 0 | 0 | 67 | 71 | 63 | 63 | 80 | 100 | 100 | 100 | 73 | 83 | 77 | 77 | 6 | 77 |
| 2 | 5 | 5 | 5 | 5 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 71 | 71 | 71 | 71 | 100 | 100 | 100 | 100 | 83 | 83 | 83 | 83 | 4 | 83 | |
| 3 | 5 | 5 | 5 | 5 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 71 | 71 | 71 | 71 | 100 | 100 | 100 | 100 | 83 | 83 | 83 | 83 | 4 | 83 | |
| 4 | 5 | 5 | 5 | 5 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 100 | 83 | 83 | 83 | 100 | 100 | 100 | 100 | 100 | 91 | 91 | 91 | 2 | 93 | |
| 5 | 5 | 5 | 5 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 1 | 100 | |
| 6 | 4 | 4 | 4 | 4 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 100 | 100 | 100 | 100 | 80 | 80 | 80 | 80 | 89 | 89 | 89 | 89 | 3 | 89 | |
| P3 (3 dosis) | 1 | 3 | 3 | 3 | 3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 100 | 100 | 75 | 75 | 100 | 100 | 100 | 100 | 100 | 100 | 86 | 86 | 2 | 93 |
| 2 | 3 | 3 | 3 | 3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 100 | 100 | 75 | 75 | 100 | 100 | 100 | 100 | 100 | 100 | 86 | 86 | 2 | 93 | |
| 3 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 67 | 67 | 67 | 67 | 67 | 67 | 67 | 67 | 67 | 67 | 67 | 67 | 5 | 67 | |
| 4 | 2 | 3 | 3 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 | 100 | 100 | 100 | 67 | 100 | 100 | 100 | 80 | 100 | 100 | 100 | 1 | 95 | |
| 5 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 100 | 100 | 100 | 100 | 67 | 67 | 67 | 67 | 80 | 80 | 80 | 80 | 4 | 80 | |
| 6 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 75 | 75 | 75 | 75 | 50 | 50 | 50 | 50 | 60 | 60 | 60 | 60 | 6 | 60 | |
| P4 (5 dosis) | 1 | 3 | 3 | 3 | 3 | 0 | 0 | 0 | 1 | 2 | 2 | 2 | 2 | 100 | 100 | 100 | 75 | 60 | 60 | 60 | 60 | 75 | 75 | 75 | 67 | 4 | 73 |
| 2 | 3 | 5 | 5 | 5 | 0 | 0 | 1 | 1 | 2 | 0 | 0 | 0 | 100 | 100 | 83 | 83 | 60 | 100 | 100 | 100 | 75 | 100 | 91 | 91 | 2 | 89 | |
| 3 | 2 | 5 | 5 | 5 | 1 | 1 | 1 | 1 | 3 | 0 | 0 | 0 | 67 | 83 | 83 | 83 | 40 | 100 | 100 | 100 | 50 | 91 | 91 | 91 | 3 | 81 | |
| 4 | 3 | 5 | 5 | 5 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 100 | 100 | 100 | 100 | 60 | 100 | 100 | 100 | 75 | 100 | 100 | 100 | 1 | 94 | |
| 5 | 3 | 3 | 3 | 3 | 2 | 1 | 1 | 1 | 3 | 2 | 2 | 2 | 63 | 75 | 75 | 75 | 50 | 60 | 60 | 60 | 56 | 67 | 67 | 67 | 5 | 64 | |
| 6 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 3 | 67 | 67 | 67 | 67 | 40 | 40 | 40 | 40 | 50 | 50 | 50 | 50 | 6 | 50 | |
| P5 (10 dosis) | 1 | 1 | 2 | 4 | 9 | 0 | 0 | 0 | 1 | 9 | 8 | 6 | 1 | 100 | 100 | 100 | 90 | 10 | 20 | 40 | 90 | 18 | 33 | 57 | 90 | 6 | 50 |
| 2 | 2 | 5 | 8 | 8 | 0 | 0 | 1 | 1 | 8 | 5 | 2 | 2 | 100 | 100 | 89 | 89 | 20 | 50 | 80 | 80 | 33 | 67 | 84 | 84 | 1 | 67 | |
| 3 | 2 | 7 | 7 | 7 | 0 | 1 | 1 | 1 | 8 | 3 | 3 | 3 | 100 | 88 | 88 | 88 | 20 | 70 | 70 | 70 | 33 | 78 | 78 | 78 | 1 | 67 | |
| 4 | 4 | 6 | 6 | 6 | 0 | 1 | 1 | 1 | 6 | 4 | 4 | 4 | 100 | 86 | 86 | 86 | 40 | 60 | 60 | 60 | 57 | 71 | 71 | 71 | 1 | 67 | |
| 5 | 4 | 4 | 4 | 4 | 0 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 100 | 100 | 100 | 100 | 40 | 40 | 40 | 40 | 57 | 57 | 57 | 57 | 4 | 57 | |
| 6 | 4 | 4 | 4 | 4 | 0 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 100 | 100 | 100 | 100 | 40 | 40 | 40 | 40 | 57 | 57 | 57 | 57 | 4 | 57 | |
| P6 (6 dosis) | 1 | 4 | 6 | 6 | 6 | 1 | 3 | 5 | 5 | 3 | 1 | 1 | 1 | 88 | 69 | 55 | 55 | 58 | 92 | 92 | 92 | 70 | 79 | 69 | 69 | 3 | 72 |
| 2 | 6 | 6 | 6 | 6 | 1 | 3 | 4 | 4 | 0 | 0 | 0 | 0 | 86 | 67 | 60 | 60 | 100 | 100 | 100 | 100 | 92 | 80 | 75 | 75 | 1 | 81 | |
| 3 | 3 | 5 | 5 | 5 | 0 | 1 | 1 | 1 | 3 | 1 | 1 | 1 | 100 | 83 | 83 | 83 | 50 | 83 | 83 | 83 | 67 | 83 | 83 | 83 | 2 | 79 | |
| 4 | 1 | 4 | 4 | 4 | 0 | 2 | 2 | 2 | 5 | 2 | 2 | 2 | 100 | 67 | 67 | 67 | 17 | 67 | 67 | 67 | 29 | 67 | 67 | 67 | 5 | 57 | |
| 5 | 3 | 3 | 3 | 3 | 0 | 0 | 0 | 0 | 3 | 3 | 3 | 3 | 100 | 100 | 100 | 100 | 50 | 50 | 50 | 50 | 67 | 67 | 67 | 67 | 4 | 67 | |
| 6 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 5 | 5 | 5 | 5 | 100 | 100 | 100 | 100 | 17 | 17 | 17 | 17 | 29 | 29 | 29 | 29 | 6 | 29 | |
| Total (29 dosis) | 1 | 15 | 19 | 21 | 26 | 3 | 5 | 9 | 11 | 15 | 11 | 9 | 4 | 85 | 80 | 71 | 71 | 50 | 64 | 71 | 88 | 63 | 71 | 71 | 78 | 5 | 71 |
| 2 | 19 | 24 | 27 | 27 | 3 | 5 | 10 | 10 | 10 | 5 | 2 | 2 | 86 | 83 | 73 | 73 | 66 | 83 | 93 | 93 | 75 | 83 | 82 | 82 | 1 | 80 | |
| 3 | 14 | 24 | 24 | 24 | 4 | 7 | 7 | 7 | 15 | 5 | 5 | 5 | 78 | 77 | 77 | 77 | 48 | 83 | 83 | 83 | 60 | 80 | 80 | 80 | 3 | 75 | |
| 4 | 15 | 23 | 23 | 23 | 0 | 4 | 4 | 4 | 14 | 6 | 6 | 6 | 100 | 85 | 85 | 85 | 52 | 79 | 79 | 79 | 68 | 82 | 82 | 82 | 2 | 79 | |
| 5 | 17 | 17 | 17 | 17 | 2 | 1 | 1 | 1 | 13 | 12 | 12 | 12 | 92 | 94 | 94 | 94 | 57 | 59 | 59 | 59 | 70 | 72 | 72 | 72 | 4 | 72 | |
| 6 | 13 | 13 | 13 | 13 | 2 | 2 | 2 | 2 | 17 | 17 | 17 | 17 | 89 | 89 | 89 | 89 | 43 | 43 | 43 | 43 | 58 | 58 | 58 | 58 | 6 | 58 | |
| TP | FP | FN | Precision | Recall | f-Score | |
|---|---|---|---|---|---|---|
| P1 | 0 | 1 | 0 | |||
| P2 | 3 | 0 | 2 | 100 | 60 | 75 |
| P3 | 1 | 2.5 | 2 | 29 | 33 | 31 |
| P4 | 3 | 0 | 2 | 100 | 60 | 75 |
| P5 | 6 | 0 | 4 | 100 | 60 | 75 |
| P6 | 4 | 0 | 2 | 100 | 67 | 80 |
| Total | 17 | 3.5 | 12 | 83 | 59 | 69 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Page, M.; Jarlan, L.; El Hajj, M.M.; Zribi, M.; Baghdadi, N.; Boone, A. Potential for the Detection of Irrigation Events on Maize Plots Using Sentinel-1 Soil Moisture Products. Remote Sens. 2020, 12, 1621. https://doi.org/10.3390/rs12101621
Le Page M, Jarlan L, El Hajj MM, Zribi M, Baghdadi N, Boone A. Potential for the Detection of Irrigation Events on Maize Plots Using Sentinel-1 Soil Moisture Products. Remote Sensing. 2020; 12(10):1621. https://doi.org/10.3390/rs12101621
Chicago/Turabian StyleLe Page, Michel, Lionel Jarlan, Marcel M. El Hajj, Mehrez Zribi, Nicolas Baghdadi, and Aaron Boone. 2020. "Potential for the Detection of Irrigation Events on Maize Plots Using Sentinel-1 Soil Moisture Products" Remote Sensing 12, no. 10: 1621. https://doi.org/10.3390/rs12101621
APA StyleLe Page, M., Jarlan, L., El Hajj, M. M., Zribi, M., Baghdadi, N., & Boone, A. (2020). Potential for the Detection of Irrigation Events on Maize Plots Using Sentinel-1 Soil Moisture Products. Remote Sensing, 12(10), 1621. https://doi.org/10.3390/rs12101621








