Quantitative Airborne Inventories in Dense Tropical Forest Using Imaging Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
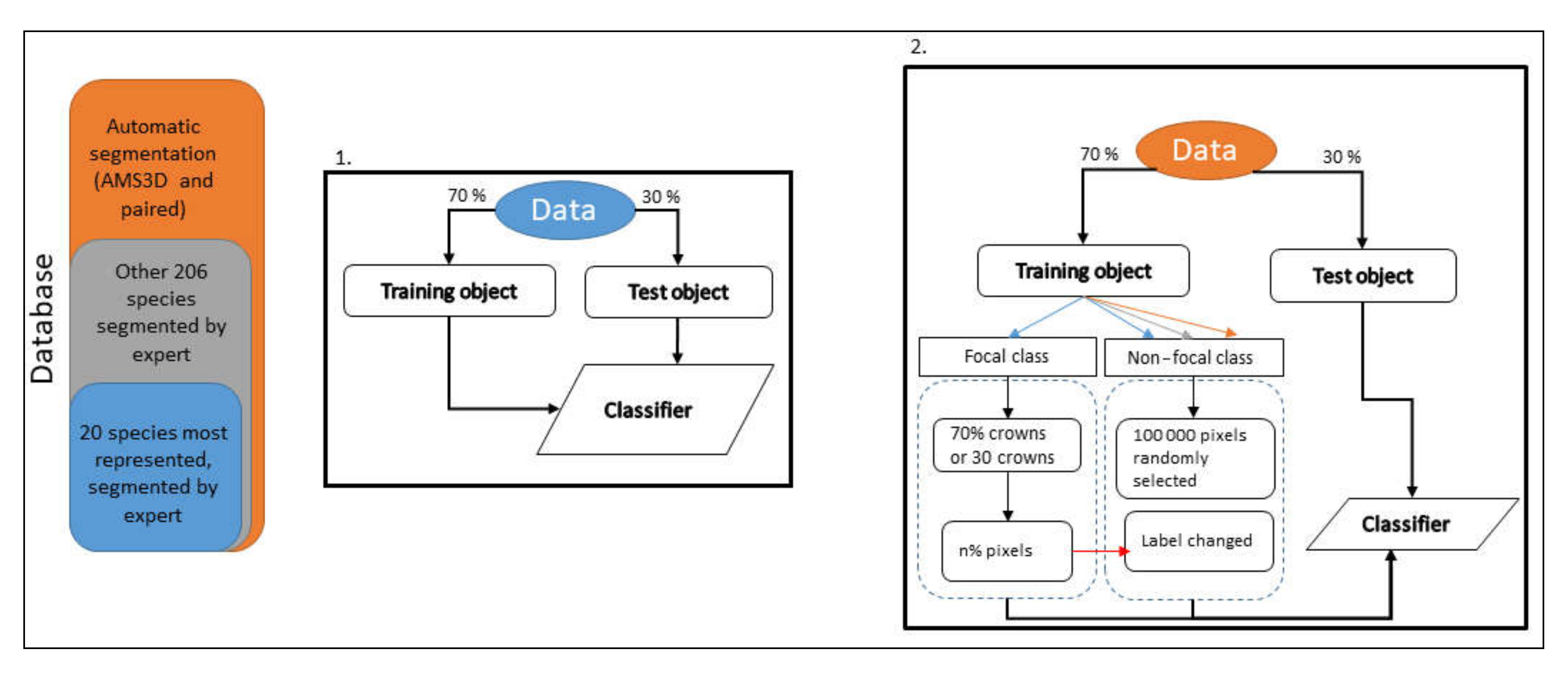
2.2. General Methodology Outline
2.3. Remote Sensing Data
2.3.1. Hyperspectral Imaging
2.3.2. LiDAR Data and RGB Imagery
2.3.3. Ground Reference Data
2.4. Automatic Segmentation Method
2.4.1. AMS-3D Method
2.4.2. Correspondence between ITC and Inventory Data
2.5. Classification Method
2.5.1. Classifier Evaluation Criteria
2.5.2. Optimization Step
2.6. Experimental Set-Up
2.6.1. Experiment 1—VNIR versus VNIR+ SWIR
2.6.2. Experiment 2—Increasing Background Spectral Diversity
2.6.3. Experiment 3—Effect of Noise in the Training Data
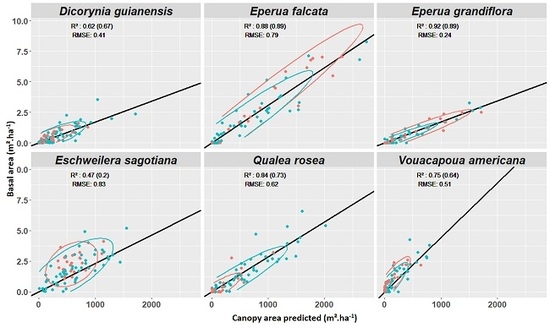
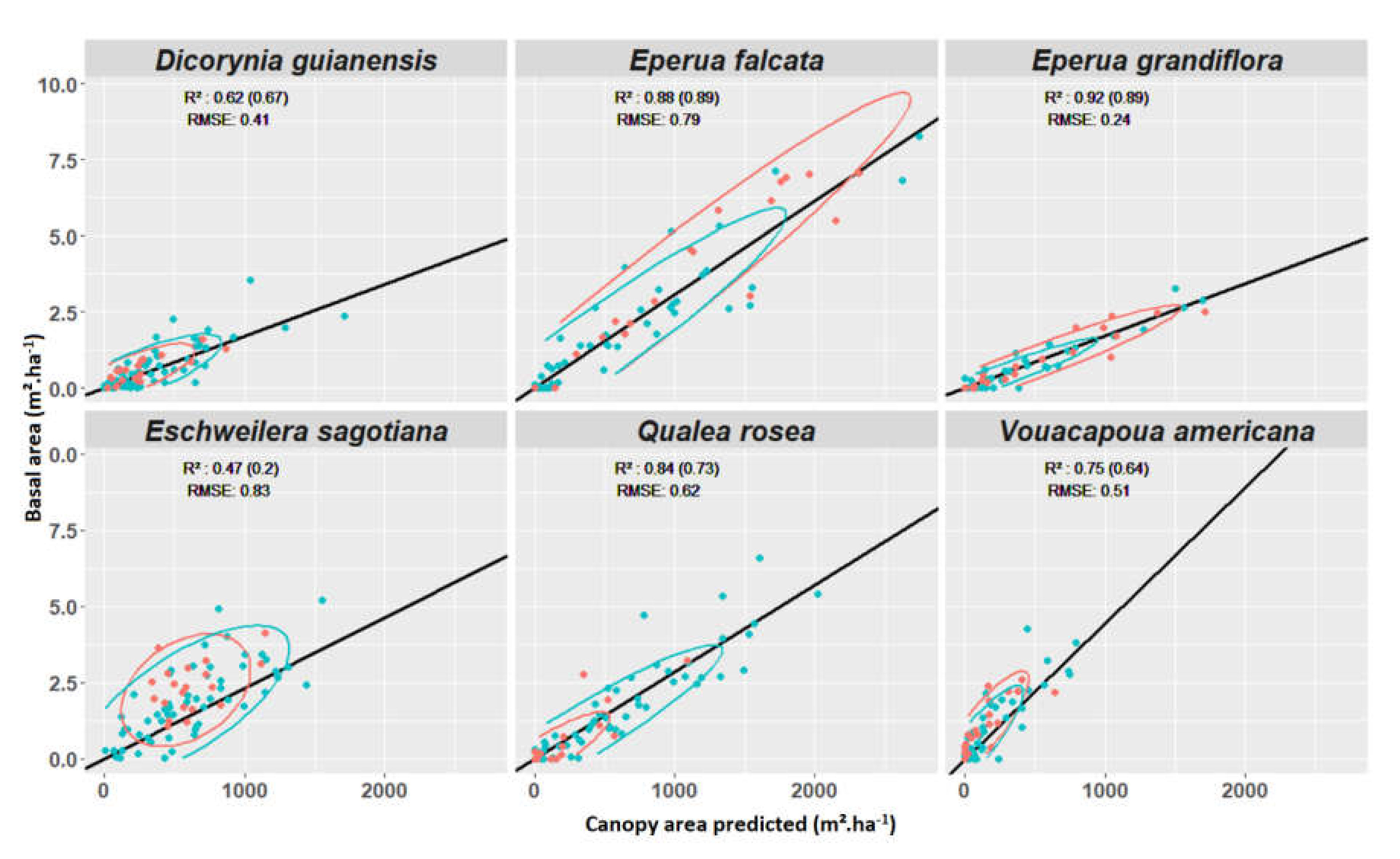
2.6.4. Experiment 4—Predicting Basal Area per Species per Plot
3. Results
3.1. Experiment 1
3.2. Experiment 2
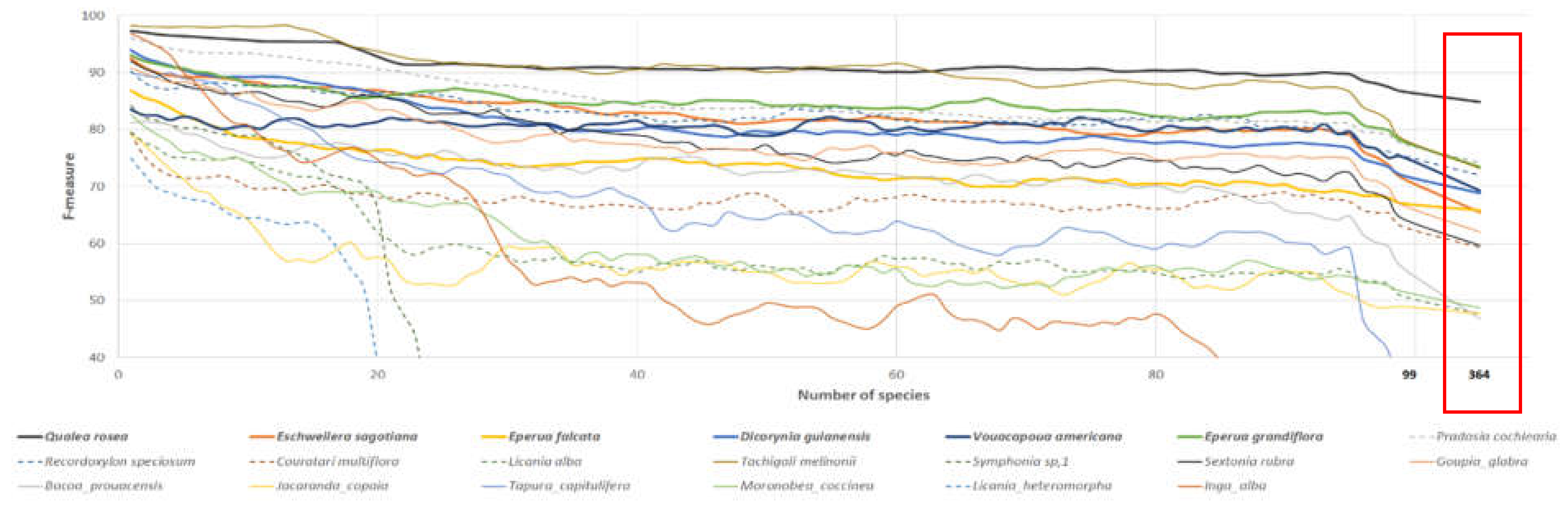
3.3. Experiment 3 –Exploring the Impact of Training Set Impurity
3.3.1. Low Level of Impurity (All Species)
3.3.2. High Level of Impurity (Most Abundant Species)
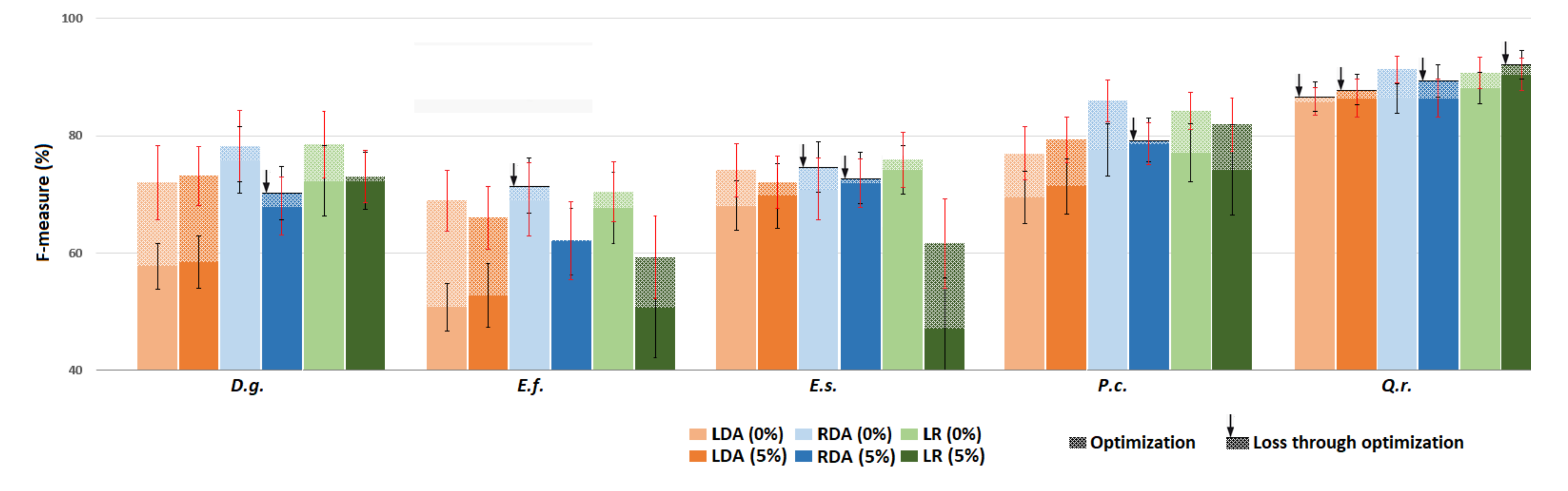
3.3.3. High Level of Impurity—Smaller Focal Training Class
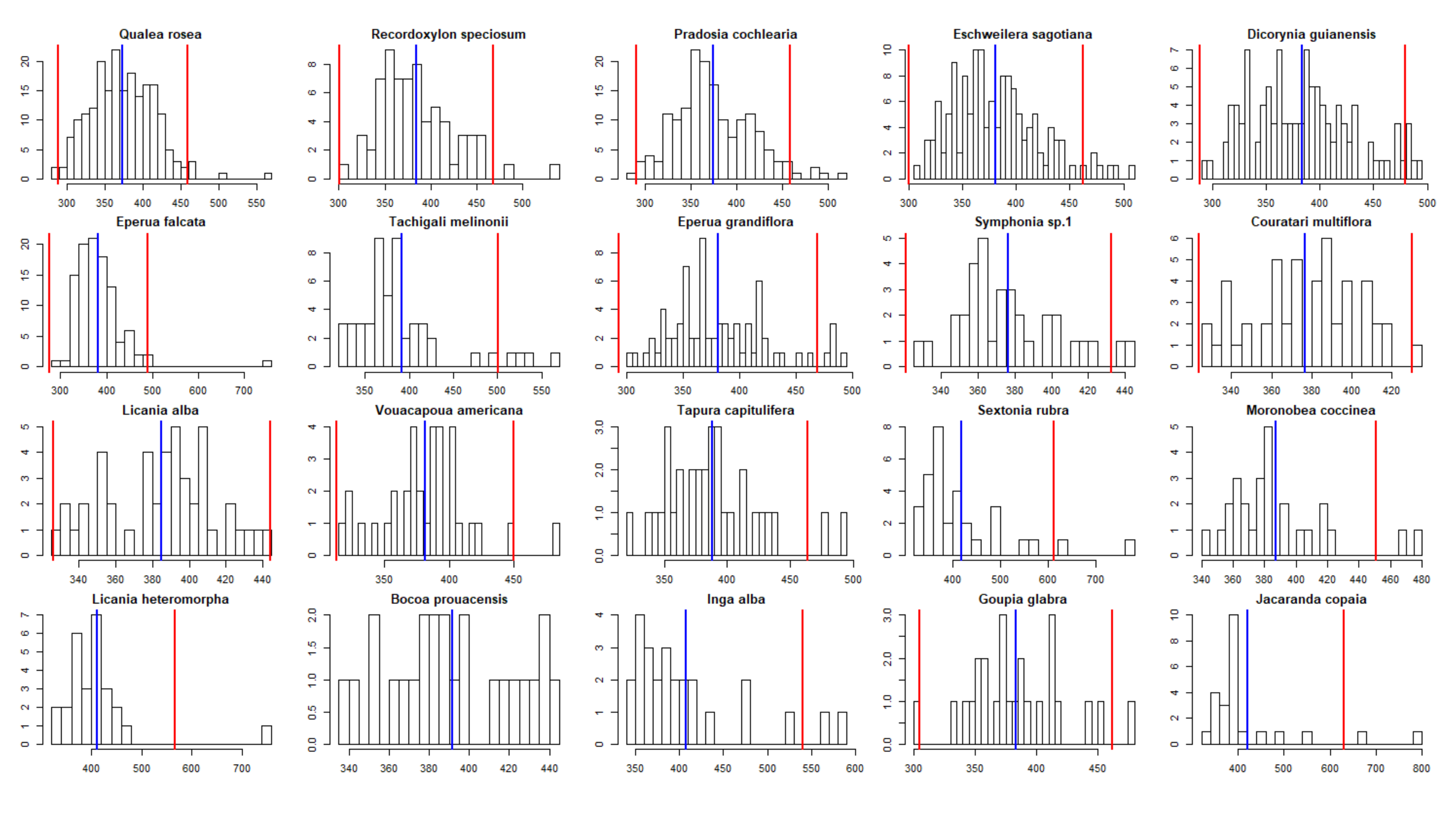
3.3.4. Focal Class Purification
3.4. Experiment 4
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Experiment 1
| Species | VNIR | VSWIR | ||||
|---|---|---|---|---|---|---|
| LDA | RDA | LR | LDA | RDA | LR | |
| B.p. | 13.2 (±6.5) | 18.2 (±10.4) | 24.1 (±12.8) | 42.7 (±7.7) | 65.2 (±6.5) | 54.7 (±7.8) |
| C.m. | 66.8 (±12.0) | 65.0 (±12.6) | 67.2 (±10.5) | 75.3 (±8.0) | 72.2 (±8.5) | 75.6 (±5.9) |
| D.g. | 54.2 (±4.3) | 51.9 (±5.8) | 60.1 (±4.8) | 76.1 (±3.3) | 75.0 (±3.6) | 78.9 (±3.0) |
| E.f. | 33.6 (±4.5) | 14.1 (±3.2) | 36.5 (±4.5) | 59.3 (±5.2) | 66.6 (±6.2) | 69.4 (±4.8) |
| E.g. | 49.2 (±6.5) | 56.3 (±4.9) | 69.6 (±4.2) | 74.6 (±3.5) | 79.9 (±3.4) | 81.5 (±2.7) |
| E.s. | 59.3 (±3.4) | 66.2 (±3.9) | 65.7 (±4.2) | 75.8 (±3.0) | 78.2 (±3.0) | 75.6 (±3.4) |
| G.g. | 37.8 (±9.7) | 62.2 (±9.1) | 67.4 (±9.3) | 80.6 (±6.2) | 81.3 (±8.2) | 77.2 (±10.2) |
| I.a. | 38.1 (±11.0) | 45.9 (±13.9) | 64.6 (±12.0) | 63.6 (±9.5) | 69.2 (±7.5) | 64.6 (±8.1) |
| J.c. | 58.8 (±19.4) | 59.5 (±22.7) | 54.5 (±20.4) | 56.8 (±16.9) | 53.4 (±20.5) | 55.3 (±12.5) |
| L.a. | 34.0 (±7.3) | 52.1 (±9.4) | 54.0 (±9.7) | 58.0 (±7.9) | 67.4 (±8.7) | 64.2 (±6.0) |
| L.h. | 9.4 (±3.9) | 5.6 (±4.8) | 5.6 (±4.8) | 20.3 (±8.3) | 46.5 (±12.3) | 36.0 (±9.4) |
| M.c. | 45.5 (±9.3) | 50.0 (±11.3) | 64.4 (±9.1) | 68.8 (±9.0) | 70.0 (±11.1) | 71.1 (±5.9) |
| P.c. | 78.2 (±3.2) | 78.8 (±1.5) | 81.3 (±1.6) | 89.1 (±1.6) | 88.2 (±1.4) | 88.9 (±1.6) |
| Q.r. | 88.4 (±2.0) | 88.1 (±1.6) | 90.8 (±0.8) | 94.0 (±0.8) | 93.0 (±1.0) | 94.4 (±0.8) |
| R.s. | 76.6 (±5.0) | 75.1 (±5.3) | 81.3 (±3.4) | 84.1 (±3.5) | 82.4 (±4.4) | 81.7 (±3.5) |
| S.r. | 36.4 (±7.8) | 52.3 (±10.3) | 55.3 (±10.0) | 53.8 (±10.4) | 69.2 (±6.6) | 71.7 (±4.6) |
| S.s. | 13.2 (±3.8) | 0.4 (±0.4) | 10.4 (±2.7) | 33.9 (±8.4) | 54.6 (±6.1) | 52.4 (±6.6) |
| T.m. | 63.3 (±7.8) | 67.8 (±7.6) | 68.5 (±5.8) | 87.7 (±3.4) | 87.1 (±3.5) | 85.5 (±3.4) |
| T.c. | 7.4 (±2.7) | 8.8 (±6.3) | 40.5 (±9.0) | 30.3 (±7.6) | 60.0 (±12.1) | 59.2 (±8.7) |
| V.a. | 31.2 (±8.6) | 48.6 (±10.0) | 46.3 (±12.5) | 69.6 (±5.8) | 72.4 (±7.8) | 63.0 (±7.1) |
| Mean F-measue | 44.7 | 48.3 | 55.4 | 64.7 | 71.6 | 70.1 |
Appendix B. Experiment 3 (Low Level of Impurity)—Complement
| Bias | 0% | 1% | 2% | 5% | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Plain | Optimized | Plain | Optimized | Plain | Optimized | Plain | Optimized | |||||||||||||||||
| Species | LDA | RDA | LR | LDA | RDA | LR | LDA | RDA | LR | LDA | RDA | LR | LDA | RDA | LR | LDA | RDA | LR | LDA | RDA | LR | LDA | RDA | LR |
| B.p. | 35.8 (±10.3) | 57.7 (±12.4) | 37.5 (±15.5) | 65.4 (±12.6) | 57.5 (±17.4) | 42.1 (±16.0) | 36.4 (±9.8) | 58.5 (±12.4) | 43.4 (±13.6) | 64.3 (±12.7) | 56.2 (±17.3) | 43.0 (±16.0) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| C.m. | 68.3 (±10.8) | 64.7 (±10.1) | 68.0 (±10.5) | 69.8 (±11.2) | 68.3 (±11.3) | 71.4 (±7.9) | 67.4 (±11.2) | 65.1 (±10.3) | 66.5 (±9.5) | 69.8 (±11.6) | 68.0 (±11.3) | 69.4 (±8.4) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| D.g. | 57.7 (±3.9) | 72.3 (±6.0) | 78.2 (±6.1) | 75.8 (±5.6) | 72.0 (±6.3) | 78.5 (±5.7) | 57.5 (±3.8) | 72.6 (±5.7) | 78.2 (±5.5) | 74.8 (±6.3) | 72.2 (±5.4) | 78.3 (±5.5) | 56.2 (±4.2) | 69.6 (±4.7) | 76.5 (±5.7) | 72.5 (±5.2) | 67.2 (±4.9) | 73.2 (±5.0) | 58.5 (±4.4) | 70.3 (±4.6) | 72.3 (±4.8) | 73.1 (±5.0) | 68.0 (±4.9) | 73.1 (±4.4) |
| E.f. | 50.8 (±4.1) | 67.7 (±6.1) | 69.2 (±6.2) | 71.5 (±4.6) | 68.9 (±5.2) | 70.5 (±5.0) | 51.5 (±4.2) | 67.9 (±5.2) | 68.0 (±5.4) | 72.1 (±4.8) | 69.2 (±4.5) | 70.5 (±4.9) | 51.4 (±4.1) | 62.5 (±6.1) | 61.9 (±6.5) | 67.3 (±6.0) | 63.4 (±5.9) | 65.0 (±5.5) | 52.8 (±5.4) | 62.0 (±5.7) | 50.7 (±8.5) | 66.0 (±5.4) | 62.2 (±6.6) | 59.3 (±7.0) |
| E.g. | 65.1 (±7.0) | 82.0 (±5.3) | 84.4 (±4.6) | 82.4 (±6.2) | 82.7 (±6.2) | 84.8 (±4.5) | 64.9 (±6.9) | 81.9 (±5.6) | 82.5 (±6.0) | 82.0 (±6.2) | 82.5 (±6.0) | 84.7 (±4.2) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| E.s. | 68.1 (±4.2) | 74.2 (±4.1) | 71.0 (±5.2) | 74.7 (±4.3) | 74.1 (±4.6) | 75.9 (±4.7) | 68.5 (±4.5) | 74.7 (±3.9) | 69.2 (±6.0) | 74.1 (±4.3) | 73.4 (±4.1) | 74.9 (±5.0) | 67.4 (±5.0) | 74.1 (±4.3) | 69.0 (±6.2) | 74.2 (±4.4) | 74.2 (±4.0) | 73.3 (±4.6) | 69.8 (±5.5) | 72.8 (±4.4) | 47.1 (±8.7) | 72.0 (±4.5) | 72.0 (±4.0) | 61.7 (±7.6) |
| G.g. | 62.5 (±12.6) | 73.4 (±11.5) | 76.4 (±12.5) | 74.5 (±10.1) | 73.5 (±10.9) | 77.3 (±12.3) | 62.8 (±14.2) | 72.6 (±10.5) | 74.8 (±11.6) | 74.5 (±10.6) | 74.4 (±11.2) | 75.0 (±12.9) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| I.a. | 38.3 (±11.5) | 42.3 (±12.7) | 38.5 (±11.6) | 43.0 (±12.9) | 41.0 (±13.3) | 41.4 (±13.1) | 38.9 (±11.2) | 42.7 (±12.5) | 36.6 (±10.7) | 43.0 (±14.4) | 41.4 (±13.5) | 40.9 (±14.2) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| J.c. | 50.7 (±19.7) | 51.4 (±16.8) | 52.4 (±17.1) | 50.9 (±16.9) | 49.3 (±17.5) | 53.1 (±17.2) | 52.2 (±17.2) | 49.0 (±16.9) | 51.6 (±16.6) | 51.5 (±17.6) | 50.4 (±16.5) | 52.6 (±18.7) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| L.a. | 41.6 (±8.7) | 56.3 (±10.8) | 53.9 (±10.5) | 56.6 (±11.1) | 54.4 (±10.6) | 62.3 (±10.3) | 41.9 (±9.9) | 56.8 (±10.2) | 48.5 (±12.1) | 57.0 (±10.5) | 54.7 (±10.1) | 59.7 (±8.8) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| L.h. | 25.6 (±8.9) | 43.6 (±11.0) | 22.8 (±8.1) | 44.0 (±12.3) | 34.2 (±13.1) | 25.5 (±7.6) | 26.5 (±8.9) | 43.5 (±13.6) | 23.5 (±8.3) | 46.6 (±9.4) | 33.7 (±11.5) | 26.0 (±10.6) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| M.c. | 58.5 (±13.8) | 55.5 (±16.9) | 60.0 (±14.5) | 56.3 (±15.9) | 54.9 (±16.0) | 62.7 (±12.0) | 58.6 (±12.8) | 56.1 (±16.5) | 56.5 (±16.9) | 55.4 (±16.5) | 56.2 (±15.6) | 61.7 (±14.8) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| P.c. | 69.5 (±4.5) | 77.1 (±4.9) | 85.9 (±3.6) | 77.6 (±4.5) | 77.0 (±4.6) | 84.3 (±3.2) | 69.6 (±4.9) | 78.0 (±4.9) | 85.8 (±3.2) | 78.2 (±4.7) | 77.4 (±4.8) | 84.0 (±3.8) | 70.4 (±4.9) | 80.4 (±3.4) | 84.6 (±4.6) | 79.9 (±3.6) | 79.8 (±3.5) | 84.2 (±3.4) | 71.4 (±4.8) | 79.3 (±3.8) | 74.2 (±7.7) | 79.3 (±3.8) | 78.7 (±3.5) | 81.9 (±4.5) |
| Q.r. | 86.6 (±2.5) | 88.1 (±2.7) | 91.3 (±2.3) | 86.4 (±2.6) | 85.8 (±2.4) | 90.7 (±2.6) | 86.9 (±2.5) | 88.1 (±2.5) | 91.2 (±2.2) | 86.6 (±2.6) | 86.2 (±2.8) | 90.8 (±2.4) | 88.0 (±2.5) | 89.0 (±2.5) | 92.2 (±2.0) | 85.6 (±3.1) | 85.7 (±2.7) | 90.6 (±1.8) | 87.9 (±2.6) | 89.4 (±2.7) | 92.1 (±2.4) | 86.6 (±3.2) | 86.4 (±3.0) | 90.4 (±2.6) |
| R.s. | 82.5 (±3.8) | 78.8 (±4.5) | 81.2 (±5.2) | 81.0 (±3.7) | 80.7 (±3.5) | 84.9 (±4.5) | 82.4 (±4.2) | 79.3 (±5.0) | 79.5 (±5.6) | 80.7 (±4.4) | 79.7 (±4.1) | 83.4 (±5.3) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| S.r. | 54.3 (±9.2) | 70.8 (±10.7) | 61.6 (±14.7) | 71.8 (±13.7) | 66.9 (±15.8) | 68.0 (±13.8) | 53.8 (±9.1) | 69.7 (±12.3) | 52.3 (±18.4) | 71.3 (±13.5) | 66.4 (±13.9) | 61.1 (±17.4) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| S.s. | 29.1 (±5.9) | 36.7 (±9.1) | 21.3 (±7.1) | 36.6 (±8.0) | 36.7 (±8.8) | 25.6 (±14.2) | 29.1 (±6.5) | 35.8 (±7.9) | 21.3 (±7.1) | 35.5 (±9.2) | 35.8 (±9.2) | 25.6 (±11.7) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| T.m. | 64.7 (±6.4) | 69.9 (±6.0) | 80.7 (±9.4) | 76.3 (±7.5) | 75.8 (±6.8) | 78.8 (±7.2) | 64.9 (±6.5) | 70.4 (±5.6) | 78.2 (±9.9) | 76.0 (±6.8) | 75.6 (±7.2) | 78.9 (±9.7) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| T.c. | 58.3 (±11.5) | 65.4 (±12.5) | 72.2 (±14.8) | 65.8 (±14.4) | 52.1 (±13.6) | 72.5 (±15.1) | 58.2 (±10.9) | 65.4 (±12.7) | 69.6 (±13.4) | 63.6 (±14.2) | 51.0 (±13.5) | 70.6 (±14.2) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| V.a. | 68.2 (±8.7) | 72.8 (±12.2) | 65.1 (±12.8) | 74.4 (±12.0) | 74.4 (±12.2) | 66.9 (±13.3) | 66.5 (±10.4) | 74.1 (±12.0) | 63.9 (±13.3) | 74.4 (±12.1) | 73.6 (±11.1) | 64.6 (±12.5) | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| Average | 56.8 | 65.0 | 63.6 | 66.7 | 64.0 | 65.9 | 56.9 | 65.1 | 62.0 | 66.6 | 63.9 | 64.8 | 66.7 | 75.1 | 76.9 | 75.9 | 74.1 | 77.3 | 68.0 | 74.7 | 67.3 | 75.4 | 73.4 | 73.3 |
Appendix C. Experiment 3 (High Level of Impurity—Smaller Focal Training Class)—Complement
| SPID | Bias | LDA | RDA | LR | |||
|---|---|---|---|---|---|---|---|
| Plain | Optimized | Plain | Optimized | Plain | Optimized | ||
| D.g. | 0 | 58.9 (±8.0) | 69.7 (±6.4) | 67.1 (±6.5) | 66.7 (±6.7) | 71.6 (±7.4) | 74.6 (±6.5) |
| E.f. | 0 | 53.4 (±7.2) | 68.3 (±6.9) | 66.0 (±4.9) | 64.7 (±7.1) | 61.2 (±9.1) | 63.6 (±7.6) |
| E.s. | 0 | 68.6 (±5.7) | 71.7 (±6.4) | 73.0 (±5.6) | 71.5 (±6.3) | 61.2 (±9.0) | 68.4 (±8.4) |
| P.c. | 0 | 73.6 (±4.4) | 79.9 (±5.6) | 79.5 (±5.7) | 79.2 (±5.1) | 83.6 (±4.2) | 84.9 (±5.1) |
| Q.r. | 0 | 88.8 (±2.7) | 89.5 (±2.6) | 89.4 (±2.6) | 89.4 (±2.7) | 90.2 (±2.9) | 90.9 (±3.0) |
| Average | 68.7 | 75.8 | 75.0 | 74.3 | 73.5 | 76.5 | |
| D.g. | 1% | 58.8 (±8.3) | 71.0 (±7.9) | 67.8 (±7.7) | 67.1 (±8.5) | 70.5 (±8.7) | 75.3 (±7.0) |
| E.f. | 1% | 54.1 (±6.6) | 66.8 (±7.8) | 65.2 (±5.7) | 65.1 (±5.8) | 59.0 (±10.0) | 63.6 (±6.7) |
| E.s. | 1% | 69.0 (±6.6) | 73.2 (±5.1) | 73.4 (±5.3) | 72.5 (±5.5) | 52.9 (±8.1) | 62.9 (±7.0) |
| P.c. | 1% | 71.9 (±5.7) | 76.5 (±5.8) | 75.8 (±6.7) | 76.7 (±5.9) | 77.1 (±5.0) | 79.5 (±4.7) |
| Q.r. | 1% | 89.2 (±2.9) | 89.2 (±2.3) | 89.2 (±2.9) | 88.9 (±2.7) | 87.2 (±3.6) | 88.5 (±3.6) |
| Average | 68.6 | 75.3 | 74.3 | 74.0 | 69.4 | 74.0 | |
| D.g. | 2% | 57.0 (±8.2) | 71.5 (±5.8) | 68.3 (±6.2) | 67.4 (±6.7) | 68.5 (±9.5) | 72.9 (±7.0) |
| E.f. | 2% | 53.7 (±6.1) | 66.4 (±7.7) | 64.4 (±6.7) | 64.6 (±7.3) | 54.7 (±10.5) | 62.2 (±9.6) |
| E.s. | 2% | 68.2 (±6.1) | 73.3 (±5.1) | 73.6 (±5.3) | 71.9 (±6.7) | 48.6 (±11.3) | 62.0 (±10.0) |
| P.c. | 2% | 74.1 (±5.2) | 79.6 (±4.0) | 78.5 (±4.2) | 78.6 (±5.0) | 78.6 (±3.5) | 82.3 (±3.4) |
| Q.r. | 2% | 88.7 (±2.9) | 89.3 (±2.9) | 89.3 (±2.7) | 89.3 (±2.9) | 84.2 (±3.0) | 87.5 (±2.7) |
| Average | 68.3 | 76.0 | 74.8 | 74.3 | 66.9 | 73.4 | |
| D.g. | 5% | 58.8 (±6.8) | 71.6 (±5.2) | 68.2 (±6.2) | 68.1 (±6.3) | 61.3 (±5.8) | 70.9 (±5.4) |
| E.f. | 5% | 52.2 (±5.9) | 67.5 (±6.2) | 66.1 (±6.4) | 66.2 (±5.9) | 45.8 (±13.2) | 59.0 (±8.6) |
| E.s. | 5% | 69.2 (±5.9) | 73.2 (±5.5) | 73.7 (±4.8) | 72.0 (±5.8) | 41.6 (±11.2) | 58.7 (±10.0) |
| P.c. | 5% | 74.0 (±5.7) | 80.5 (±5.3) | 80.2 (±6.1) | 79.9 (±5.8) | 71.4 (±5.7) | 78.4 (±4.9) |
| Q.r. | 5% | 88.6 (±2.9) | 89.4 (±2.9) | 89.9 (±2.6) | 89.2 (±3.1) | 74.5 (±5.5) | 83.4 (±6.0) |
| Average | 68.6 | 76.4 | 75.6 | 75.1 | 58.9 | 70.1 | |
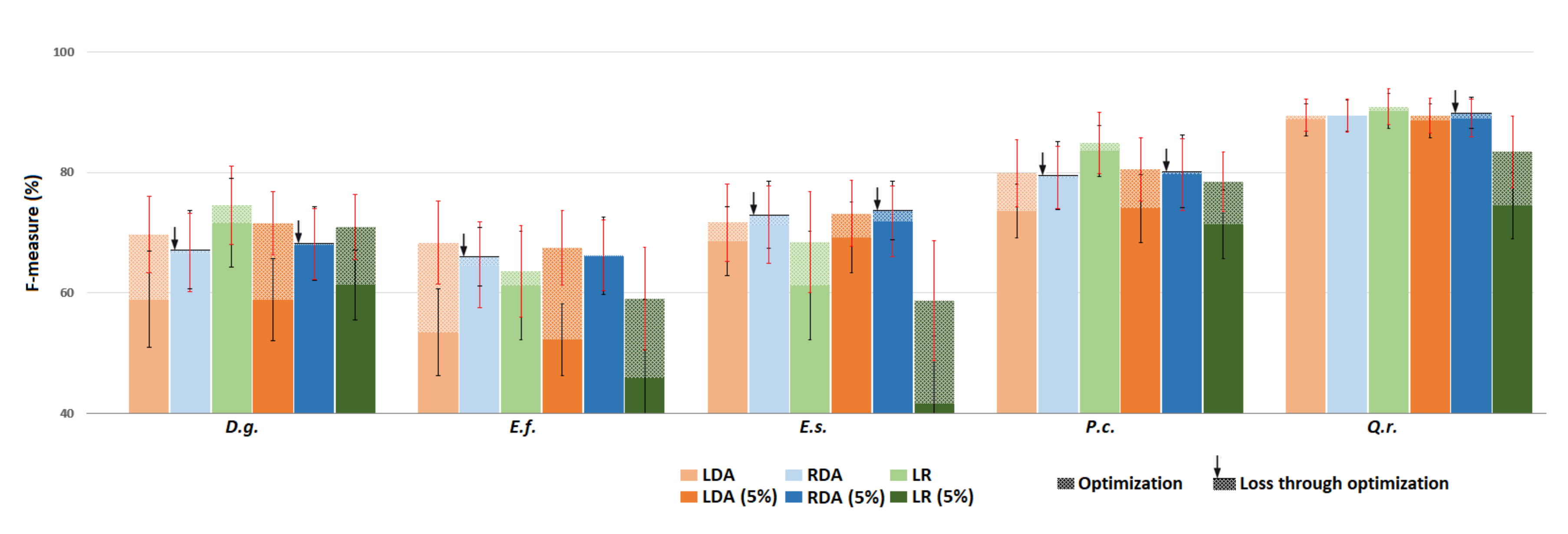
Appendix D. Experiment 3 (Focal Class Purification)—Complement
| Removing | Without | With | Total Crowns | Potential Outliers | Proportion (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| SPID | LDA | RDA | LR | LDA | RDA | LR | |||
| B.p. | 35.8 (±10.3) | 57.7 (±12.4) | 37.5 (±15.5) | 40.4 (±10.2) | 60.3 (±14.0) | 35.0 (±13.3) | 24 | 0 | 0.0 |
| C.m. | 68.3 (±10.8) | 64.7 (±10.1) | 68.0 (±10.5) | 68.4 (±11.6) ** | 65.5 (±9.8) ** | 71.8 (±9.1) *** | 49 | 1 | 2.0 |
| D.g. | 57.7 (±3.9) | 72.3 (±6.0) | 78.2 (±6.1) | 55.9 (±5.2) | 69.6 (±5.9) | 76.6 (±5.7) | 108 | 5 | 4.6 |
| E.f. | 50.8 (±4.1) | 67.7 (±6.1) | 69.2 (±6.2) | 50.3 (±6.1) | 66.4 (±6.1) | 69.3 (±5.9)* | 106 | 2 | 1.9 |
| E.g. | 65.1 (±7.0) | 82.0 (±5.3) | 84.4 (±4.6) | 64.2 (±5.9) | 81.9 (±5.2) | 84.6 (±5.4) | 74 | 5 | 6.8 |
| E.s. | 68.1 (±4.2) | 74.2 (±4.1) | 71.0 (±5.2) | 66.7 (±4.7) | 74.6 (±3.9) | 73.9 (±4.8)* | 139 | 7 | 5.0 |
| G.g. | 62.5 (±12.6) | 73.4 (±11.5) | 76.4 (±12.5) | 58.4 (±8.3) | 68.3 (±11.6) | 73.7 (±14.8) | 25 | 2 | 8.0 |
| I.a. | 38.3 (±11.5) | 42.3 (±12.7) | 38.5 (±11.6) | 38.4 (±9.9) | 43.0 (±8.1) | 33.4 (±13.2) | 26 | 2 | 7.7 |
| J.c. | 50.7 (±19.7) | 51.4 (±16.8) | 52.4 (±17.1) | 59.2 (±10.6) ** | 58.5 (±10.2) | 57.4 (±12.6) | 24 | 2 | 8.3 |
| L.a. | 41.6 (±8.7) | 56.3 (±10.8) | 53.9 (±10.5) | 43.3 (±7.0) | 53.3 (±8.3) | 50.1 (±13.7) | 46 | 0 | 0.0 |
| L.h. | 25.6 (±8.9) | 43.6 (±11.0) | 22.8 (±8.1) | 27.9 (±10.9) | 44.0 (±16.7) | 26.9 (±8.6) | 27 | 1 | 3.7 |
| M.c. | 58.5 (±13.8) | 55.5 (±16.9) | 60.0 (±14.5) | 60.1 (±11.1) | 59.9 (±14.9) | 66.7 (±12.1) | 27 | 2 | 7.4 |
| P.c. | 69.5 (±4.5) | 77.1 (±4.9) | 85.9 (±3.6) | 69.2 (±4.2) | 79.0 (±3.7) | 85.7 (±3.7) | 164 | 6 | 3.7 |
| Q.r. | 86.6 (±2.5) | 88.1 (±2.7) | 91.3 (±2.3) | 88.5 (±3.0) | 89.9 (±2.4) | 91.9 (±2.2) | 206 | 7 | 3.4 |
| R.s. | 82.5 (±3.8) | 78.8 (±4.5) | 81.2 (±5.2) | 83.1 (±7.6) | 80.5 (±7.7) | 83.8 (±6.3) ** | 69 | 2 | 2.9 |
| S.r. | 54.3 (±9.2) | 70.8 (±10.7) | 61.6 (±14.7) | 55.6 (±8.3) *** | 71.3 (±7.6) | 64.7 (±12.9) *** | 32 | 2 | 6.3 |
| S.s. | 29.1 (±5.9) | 36.7 (±9.1) | 21.3 (±7.1) | 29.8 (±7.6) | 36.1 (±11.5) | 22.4 (±6.9) | 34 | 2 | 5.9 |
| T.m. | 64.7 (±6.4) | 69.9 (±6.0) | 80.7 (±9.4) | 64.6 (±11.5) | 69.6 (±11.8) | 82.0 (±6.4) | 51 | 4 | 7.8 |
| T.c. | 58.3 (±11.5) | 65.4 (±12.5) | 72.2 (±14.8) | 55.8 (±9.0) | 68.0 (±12.8) * | 73.3 (±13.9) | 32 | 2 | 6.3 |
| V.a. | 68.2 (±8.7) | 72.8 (±12.2) | 65.1 (±12.8) | 70.0 (±8.6) | 78.4 (±7.0) | 67.8 (±10.7) | 34 | 1 | 2.9 |
| Average | 56.8 | 65.0 | 63.6 | 57.5 | 65.9 | 64.5 | 1297.0 | 55 | 4.2 |

Appendix E. Experiment 4—Complement
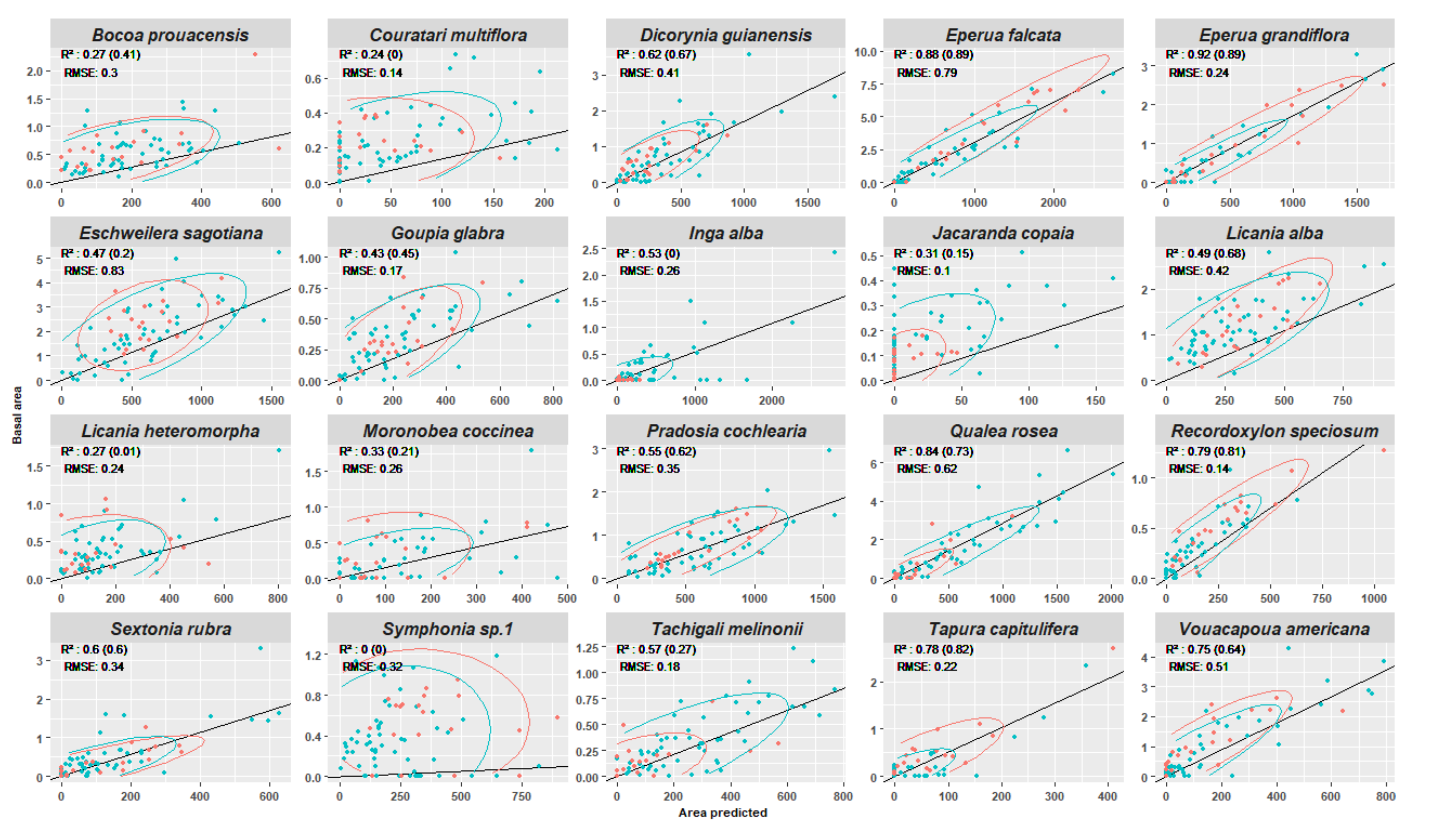
Appendix F. Test of Correlation
| Species | F-Measure (Object Level) | BA~CA r2 | Number of Pixels | Number of Crowns | Intra Group Variance | Mean Species Mahalanobis Distance | Pseudo Outlier (%) |
|---|---|---|---|---|---|---|---|
| B.p. | 65.4 | 0.27 | 2375 | 24 | 60716044 | 398 | 0 |
| C.m. | 69.8 | 0.24 | 4850 | 49 | 42710171 | 382 | 2 |
| D.g. | 75.8 | 0.62 | 18,589 | 108 | 88937469 | 383 | 4.6 |
| E.f. | 71.5 | 0.84 | 15,355 | 106 | 41768295 | 383 | 1.9 |
| E.g. | 82.4 | 0.92 | 10,859 | 74 | 37064303 | 378 | 6.8 |
| E.s. | 74.7 | 0.47 | 12,559 | 139 | 42879098 | 382 | 5 |
| G.g. | 74.5 | 0.43 | 4998 | 25 | 45436876 | 387 | 8 |
| I.a. | 43.0 | 0.53 | 3846 | 26 | 73845080 | 394 | 7.7 |
| J.c. | 50.9 | 0.31 | 1705 | 24 | 50504397 | 417 | 8.3 |
| L.a. | 56.6 | 0.49 | 3894 | 46 | 49323222 | 386 | 0 |
| L.h. | 44.0 | 0.27 | 1437 | 27 | 35529833 | 412 | 3.7 |
| M.c. | 56.3 | 0.33 | 3355 | 27 | 53471810 | 381 | 7.4 |
| P.c. | 77.6 | 0.55 | 38,349 | 164 | 46398429 | 374 | 3.7 |
| Q.r. | 86.4 | 0.84 | 27,828 | 206 | 51460549 | 374 | 3.4 |
| R.s. | 81.0 | 0.79 | 7944 | 69 | 120765823 | 382 | 2.9 |
| S.r. | 71.8 | 0.60 | 4070 | 32 | 31609536 | 417 | 6.3 |
| S.s. | 36.6 | 0.00 | 3355 | 34 | 38010280 | 378 | 5.9 |
| T.m. | 76.3 | 0.57 | 6745 | 51 | 80924196 | 392 | 7.8 |
| T.c. | 65.8 | 0.78 | 1224 | 32 | 36278962 | 388 | 6.3 |
| V.a. | 74.4 | 0.75 | 3218 | 34 | 137806130 | 387 | 2.9 |
| Pearson Cor. Coeff | -- | 0.71 ** | 0.54 * | 0.59 *** | 0.28 | 0.08 | 0.48 |
| Spearman Cor. Coeff. | -- | 0.69 ** | 0.77 ** | 0.71 *** | 0.22 | −0.44 | −0.09 |
References
- Corlett, R.T. Plant diversity in a changing world: Status, trends, and conservation needs. Plant Divers. 2016, 38, 10–16. [Google Scholar] [CrossRef]
- Peres, C.A.; Gardner, T.A.; Barlow, J.; Zuanon, J.; Michalski, F.; Lees, A.C.; Vieira, I.C.G.; Moreira, F.M.S.; Feeley, K.J. Biodiversity conservation in human-modified Amazonian forest landscapes. Biol. Conserv. 2010, 143, 2314–2327. [Google Scholar] [CrossRef]
- Leisher, C.; Touval, J.; Hess, S.M.; Boucher, T.M.; Reymondin, L. Land and Forest Degradation inside Protected Areas in Latin America. Diversity 2013, 5, 779–795. [Google Scholar] [CrossRef]
- Sala, O.E. Global Biodiversity Scenarios for the Year 2100. Science 2000, 287, 1770–1774. [Google Scholar] [CrossRef] [PubMed]
- Burivalova, Z.; Şekercioğlu, Ç.H.; Koh, L.P. Thresholds of Logging Intensity to Maintain Tropical Forest Biodiversity. Curr. Biol. 2014, 24, 1893–1898. [Google Scholar] [CrossRef] [PubMed]
- Putz, F.E.; Zuidema, P.A.; Pinard, M.A.; Boot, R.G.A.; Sayer, J.A.; Sheil, D.; Sist, P.; Vanclay, J.K. Improved Tropical Forest Management for Carbon Retention. PLoS Biol. 2008, 6, e166. [Google Scholar] [CrossRef]
- Sist, P.; Mazzei, L.; Blanc, L.; Rutishauser, E. Large trees as key elements of carbon storage and dynamics after selective logging in the Eastern Amazon. For. Ecol. Manag. 2014, 318, 103–109. [Google Scholar] [CrossRef]
- Putz, F.E. Woody vines and forest management in Malaysia. Commonw. For. Rev. 1985, 64, 359–365. [Google Scholar]
- The Biology of Vines; Putz, F.E., Mooney, H.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1991; ISBN 978-0-521-39250-1. [Google Scholar]
- Ouédraogo, D.-Y.; Beina, D.; Picard, N.; Mortier, F.; Baya, F.; Gourlet-Fleury, S. Thinning after selective logging facilitates floristic composition recovery in a tropical rain forest of Central Africa. For. Ecol. Manag. 2011, 262, 2176–2186. [Google Scholar] [CrossRef]
- Alroy, J. Effects of habitat disturbance on tropical forest biodiversity. Proc. Natl. Acad. Sci. USA 2017, 114, 6056. [Google Scholar] [CrossRef]
- Kennard, D.K.; Gould, K.; Putz, F.E.; Fredericksen, T.S.; Morales, F. Effect of disturbance intensity on regeneration mechanisms in a tropical dry forest. For. Ecol. Manag. 2002, 162, 197–208. [Google Scholar] [CrossRef]
- Chaudhary, A.; Burivalova, Z.; Koh, L.P.; Hellweg, S. Impact of Forest Management on Species Richness: Global Meta-Analysis and Economic Trade-Offs. Sci. Rep. 2016, 6, 23954. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Asner, G.P. Applications of Remote Sensing to Alien Invasive Plant Studies. Sensors 2009, 9, 4869–4889. [Google Scholar] [CrossRef] [PubMed]
- Ustin, S.L.; DiPietro, D.; Olmstead, K.; Underwood, E.; Scheer, G.J. Hyperspectral remote sensing for invasive species detection and mapping. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 3, pp. 1658–1660. [Google Scholar]
- Waite, C.E.; van der Heijden, G.M.F.; Field, R.; Boyd, D.S. A view from above: Unmanned aerial vehicles (UAVs) provide a new tool for assessing liana infestation in tropical forest canopies. J. Appl. Ecol. 2019. [Google Scholar] [CrossRef]
- Sist, P. Reduced-impact logging in the tropics: Objectives, principles and impacts. Int. For. Rev. 2000, 2, 3–10. [Google Scholar]
- Baldeck, C.; Asner, G. Improving Remote Species Identification through Efficient Training Data Collection. Remote Sens. 2014, 6, 2682–2698. [Google Scholar] [CrossRef]
- Baldeck, C.A.; Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E.; Kellner, J.R.; Wright, S.J. Operational Tree Species Mapping in a Diverse Tropical Forest with Airborne Imaging Spectroscopy. PLoS ONE 2015, 10, e0118403. [Google Scholar] [CrossRef]
- Feret, J.-B.; Asner, G.P. Tree Species Discrimination in Tropical Forests Using Airborne Imaging Spectroscopy. IEEE Trans. Geosci. Remote Sens. 2013, 51, 73–84. [Google Scholar] [CrossRef]
- Harrison, D.; Rivard, B.; Sánchez-Azofeifa, A. Classification of tree species based on longwave hyperspectral data from leaves, a case study for a tropical dry forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 93–105. [Google Scholar] [CrossRef]
- Laybros, A.; Schläpfer, D.; Féret, J.-B.; Descroix, L.; Bedeau, C.; Lefevre, M.-J.; Vincent, G. Across Date Species Detection Using Airborne Imaging Spectroscopy. Remote Sens. 2019, 11, 789. [Google Scholar] [CrossRef]
- Clark, M.; Roberts, D.; Clark, D. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Feret, J.B.; Shimabukuro, Y.E.; Filho, C.R. On the use of shortwave infrared for tree species discrimination in tropical semideciduous forest. In Proceedings of the ISPRS Geospatial Week 2015, La Grande Motte, France, 28 September–3 October 2015; Volume XL-3/W3, pp. 473–476. [Google Scholar]
- Clark, M.L.; Roberts, D.A. Species-Level Differences in Hyperspectral Metrics among Tropical Rainforest Trees as Determined by a Tree-Based Classifier. Remote Sens. 2012, 4, 1820–1855. [Google Scholar] [CrossRef]
- Dalponte, M.; Orka, H.O.; Gobakken, T.; Gianelle, D.; Naesset, E. Tree Species Classification in Boreal Forests with Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2632–2645. [Google Scholar] [CrossRef]
- Aubry-Kientz, M.; Dutrieux, R.; Ferraz, A.; Saatchi, S.; Hamraz, H.; Williams, J.; Coomes, D.; Piboule, A.; Vincent, G. A Comparative Assessment of the Performance of Individual Tree Crowns Delineation Algorithms from ALS Data in Tropical Forests. Remote Sens. 2019, 11, 1086. [Google Scholar] [CrossRef]
- Tochon, G.; Féret, J.B.; Valero, S.; Martin, R.E.; Knapp, D.E.; Salembier, P.; Chanussot, J.; Asner, G.P. On the use of binary partition trees for the tree crown segmentation of tropical rainforest hyperspectral images. Remote Sens. Environ. 2015, 159, 318–331. [Google Scholar] [CrossRef]
- Lee, W.S.; Liu, B. Learning with Positive and Unlabeled Examples Using Weighted Logistic Regression. ICML 2003, 3, 448–455. [Google Scholar]
- Ecology and Management of a Neotropical Rainforest: Lessons Drawn from Paracou, a Long-Term Experimental Research Site in French Guiana; Gourlet-Fleury, S.; Guehl, J.-M.; Laroussinie, O.; ECOFOR (Group). Elsevier: Paris, France, 2004; ISBN 978-2-84299-455-6. [Google Scholar]
- Richter, R.; Schlapfer, D. Atmospheric/Topographic Correction for Airborne Imagery (ATCOR-4 User Guide, Version 7.2.0); ReSe Applications LLC: Wil, Switzerland, 2018; p. 279. [Google Scholar]
- Schlapfer, D. PARametric Geocoding, Orthorectification for Airborne Scanner Data, User Manual Version 2.3; ReSe Applications Schlaepfer and Remote Sensing Laboratories (RSL) of the University of Zurich: Zurich, Switzerland, 2006. [Google Scholar]
- Galvão, L.S.; Ponzoni, F.J.; Epiphanio, J.C.N.; Rudorff, B.F.T.; Formaggio, A.R. Sun and view angle effects on NDVI determination of land cover types in the Brazilian Amazon region with hyperspectral data. Int. J. Remote Sens. 2004, 25, 1861–1879. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar detection of individual tree size in tropical forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Xiao, W.; Zaforemska, A.; Smigaj, M.; Wang, Y.; Gaulton, R. Mean Shift Segmentation Assessment for Individual Forest Tree Delineation from Airborne Lidar Data. Remote Sens. 2019, 11, 1263. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D.; De Boissieu, F.; Meador, A. lidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications; R Core Team: Vienna, Austria, 2018. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. Mach. Learn. PYTHON 2011, 12, 2825–2830. [Google Scholar]
- Kurtzer, G.M.; Sochat, V.; Bauer, M.W. Singularity: Scientific containers for mobility of compute. PLoS ONE 2017, 12, e0177459. [Google Scholar] [CrossRef]
- Yu, H.; Yang, J. A direct LDA algorithm for high-dimensional data—With application to face recognition. Pattern Recognit. 2001, 34, 2067–2070. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-1-118-58600-6. [Google Scholar]
- Friedman, J.H. Regularized Discriminant Analysis. J. Am. Stat. Assoc. 1989, 84, 165–175. [Google Scholar] [CrossRef]
- Guo, Y.; Hastie, T.; Tibshirani, R. Regularized Discriminant Analysis and Its Application in Microarrays; Dept. of Statistics, Stanford University: Stanford, CA, USA, 2005; p. 18. [Google Scholar]
- Pohar, M.; Blas, M.; Turk, S. Comparison of Logistic Regression and Linear Discriminant Analysis: A Simulation Study. Metodol. Zv. 2004, 1, 143. [Google Scholar]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; de Souza Filho, C.R. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Graves, S.J.; Asner, G.P.; Martin, R.E.; Anderson, C.B.; Colgan, M.S.; Kalantari, L.; Bohlman, S.A. Tree Species Abundance Predictions in a Tropical Agricultural Landscape with a Supervised Classification Model and Imbalanced Data. Remote Sens. 2016, 8, 161. [Google Scholar] [CrossRef]
- Naidoo, L.; Cho, M.A.; Mathieu, R.; Asner, G. Classification of savanna tree species, in the Greater Kruger National Park region, by integrating hyperspectral and LiDAR data in a Random Forest data mining environment. ISPRS J. Photogramm. Remote Sens. 2012, 69, 167–179. [Google Scholar] [CrossRef]
- Akbani, R.; Kwek, S.; Japkowicz, N. Applying Support Vector Machines to Imbalanced Datasets. In Proceedings of the Machine Learning: ECML 2004, Pisa, Italy, 20–24 September 2004; Boulicaut, J.-F., Esposito, F., Giannotti, F., Pedreschi, D., Eds.; Springer: Berlin, Heidelberg, 2004; pp. 39–50. [Google Scholar]
- Imam, T.; Ting, K.M.; Kamruzzaman, J. z-SVM: An SVM for Improved Classification of Imbalanced Data. In Proceedings of the AI 2006: Advances in Artificial Intelligence, Hobart, Australia, 4–8 December 2006; Sattar, A., Kang, B., Eds.; Springer: Berlin, Heidelberg, 2006; pp. 264–273. [Google Scholar]
- Lin, W.-J.; Chen, J.J. Class-imbalanced classifiers for high-dimensional data. Brief. Bioinform. 2013, 14, 13–26. [Google Scholar] [CrossRef]
- Wu, G.; Chang, E.Y. Adaptive Feature-Space Conformal Transformation for Imbalanced-Data Learning. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2013; p. 8. [Google Scholar]
- Baldeck, C.A.; Asner, G.P. Single-Species Detection with Airborne Imaging Spectroscopy Data: A Comparison of Support Vector Techniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2501–2512. [Google Scholar] [CrossRef]
- Xue, J.-H.; Titterington, D.M. Do unbalanced data have a negative effect on LDA? Pattern Recognit. 2008, 41, 1558–1571. [Google Scholar] [CrossRef]
- Ter Steege, H.; Pitman, N.C.A.; Sabatier, D.; Baraloto, C.; Salomao, R.P.; Guevara, J.E.; Phillips, O.L.; Castilho, C.V.; Magnusson, W.E.; Molino, J.-F.; et al. Hyperdominance in the Amazonian Tree Flora. Science 2013, 342, 1243092. [Google Scholar] [CrossRef]
- Sabatier, D.; Grimaldi, M.; Prévost, M.-F.; Guillaume, J.; Godron, M.; Dosso, M.; Curmi, P. The influence of soil cover organization on the floristic and structural heterogeneity of a Guianan rain forest. Plant Ecol. 1997, 131, 81–108. [Google Scholar] [CrossRef]
- Traissac, S. Dynamique Spatiale de Vouacapoua Americana, Arbre de Foret Tropicale Humide a Repartition Agregee; Université Claude Bernard Lyon 1: Villeurbanne, France, 2003. [Google Scholar]
- Traissac, S.; Pascal, J.-P. Birth and life of tree aggregates in tropical forest: Hypotheses on population dynamics of an aggregated shade-tolerant species. J. Veg. Sci. 2014, 25, 491–502. [Google Scholar] [CrossRef]
- Fonty, É.; Molino, J.-F.; Prévost, M.-F.; Sabatier, D. A new case of neotropical monodominant forest: Spirotropis longifolia (Leguminosae-Papilionoideae) in French Guiana. J. Trop. Ecol. 2011, 27, 641–644. [Google Scholar] [CrossRef]
- Pitman, N.C.A.; Terborgh, J.; Silman, M.R.; Nuñez, V.P. Tree Species Distributions in an Upper Amazonian Forest. Ecology 1999, 80, 2651–2661. [Google Scholar] [CrossRef]
- Marcon, E.; Scotti, I.; Hérault, B.; Rossi, V.; Lang, G. Generalization of the Partitioning of Shannon Diversity. PLoS ONE 2014, 9. [Google Scholar] [CrossRef]
- Laliberté, E.; Schweiger, A.K.; Legendre, P. Partitioning plant spectral diversity into alpha and beta components. Ecol. Lett. 2020, 23, 370–380. [Google Scholar] [CrossRef]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef]
- Antin, C.; Pélissier, R.; Vincent, G.; Couteron, P. Crown allometries are less responsive than stem allometry to tree size and habitat variations in an Indian monsoon forest. Trees 2013, 27, 1485–1495. [Google Scholar] [CrossRef]
- Harja, D.; Vincent, G.; Mulia, R.; Noordwijk, M. Tree shape plasticity in relation to crown exposure. Trees 2012, 26, 1275–1285. [Google Scholar] [CrossRef]
- Brell, M.; Rogass, C.; Segl, K.; Bookhagen, B.; Guanter, L. Improving Sensor Fusion: A Parametric Method for the Geometric Coalignment of Airborne Hyperspectral and Lidar Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3460–3474. [Google Scholar] [CrossRef]
- Tusa, E.; Laybros, A.; Monnet, J.-M.; Dalla Mura, M.; Barré, J.-B.; Vincent, G.; Dalponte, M.; Féret, J.-B.; Chanussot, J. Fusion of hyperspectral imaging and LiDAR for forest monitoring. In Data Handling in Science and Technology; Elsevier: Amsterdam, The Netherlands, 2020; Volume 32, pp. 281–303. ISBN 978-0-444-63977-6. [Google Scholar]
- Reich, P.B. Phenology of tropical forests: Patterns, causes, and consequences. Can. J. Bot. 1995, 73, 164–174. [Google Scholar] [CrossRef]
- Laurans, M.; Martin, O.; Nicolini, E.; Vincent, G. Functional traits and their plasticity predict tropical trees regeneration niche even among species with intermediate light requirements. J. Ecol. 2012, 100, 1440–1452. [Google Scholar] [CrossRef]
- Reich, P.B.; Uhl, C.; Walters, M.B.; Prugh, L.; Ellsworth, D.S. Leaf demography and phenology in Amazonian rain forest: A census of 40 000 leaves of 23 tree species. Ecol. Monogr. 2004, 74, 3–23. [Google Scholar] [CrossRef]
- Korpela, I.; Heikkinen, V.; Honkavaara, E.; Rohrbach, F.; Tokola, T. Variation and directional anisotropy of reflectance at the crown scale—Implications for tree species classification in digital aerial images. Remote Sens. Environ. 2011, 115, 2062–2074. [Google Scholar] [CrossRef]
- Loubry, D. Déterminisme du Comportement Phénologique des Arbres en Forêt Tropicale Humide de Guyane Française (5° lat. n.); Université de Paris 6: Paris, France, 1994. [Google Scholar]
- Saini, M.; Christian, B.; Joshi, N.; Vyas, D.; Marpu, P.; Krishnayya, N.S.R. Hyperspectral Data Dimensionality Reduction and the Impact of Multi-Seasonal Hyperion EO-1 Imagery on Classification Accuracies of Tropical Forest Species. Available online: https://www.ingentaconnect.com/content/asprs/pers/2014/00000080/00000008/art00005 (accessed on 2 May 2020).
- Yadava, U.L. A Rapid and Non-destructive Method to Determine Chlorophyll in Intact Leaves. HortScience 1986, 21, 1449–1450. [Google Scholar]
- Schlapfer, D.; Richter, R. Evaluation of brefcor BRDF effects correction for HYSPEX, CASI, and APEX imaging spectroscopy data. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; IEEE: Lausanne, Switzerland, 2014; pp. 1–4. [Google Scholar]

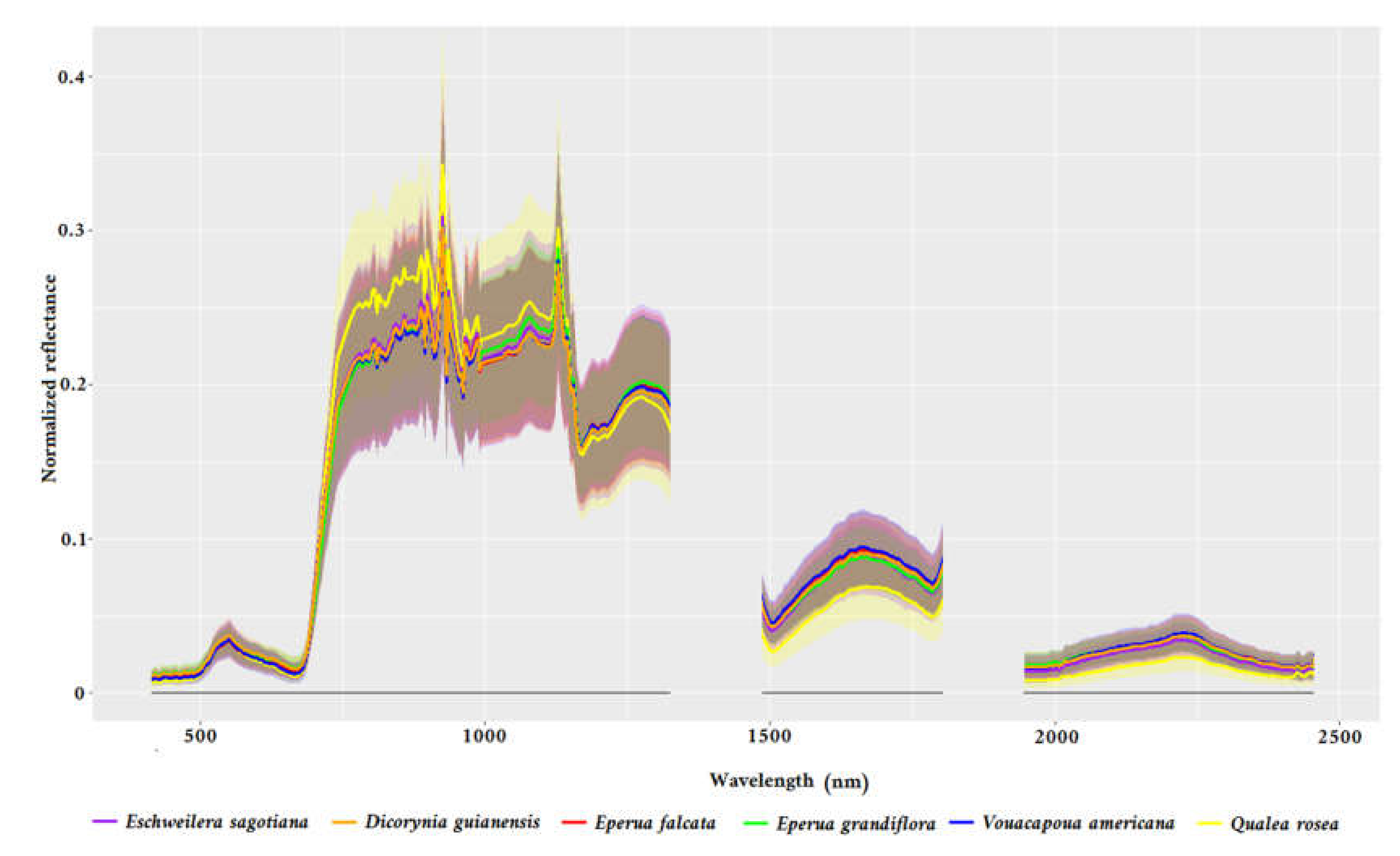
| Species (Acronyms) | Number of Crowns | Number of Pixels | Mean Crown Area (m2) (SD) | Sample Representation (%) |
|---|---|---|---|---|
| Qualea rosea (Q.r.) | 206 | 27,828 | 109.5 (59.4) | 9.2 |
| Pradosia cochlearia (P.c.) | 164 | 38,349 | 142.3 (122.5) | 7.3 |
| Eschweilera sagotiana (E.s.) | 139 | 12,559 | 49.1 (29.0) | 6.2 |
| Dicorynia guianensis (D.g.) | 108 | 18,589 | 102.7 (66.8) | 4.8 |
| Eperua falcata (E.f.) | 106 | 15,355 | 71.7 (41.3) | 4.7 |
| Eperua grandiflora (E.g.) | 74 | 10,859 | 87.3 (46.2) | 3.3 |
| Recordoxylon speciosum (R.s.) | 69 | 7944 | 69.6 (26.2) | 3.1 |
| Tachigali melinonii (T.m.) | 51 | 6745 | 106.2 (67.1) | 2.3 |
| Couratari multiflora (C.m.) | 49 | 4850 | 55.1 (33.8) | 2.2 |
| Licania alba (L.a.) | 46 | 3894 | 47.0 (18.4) | 2.0 |
| Symphonia sp.1 (S.s.) | 34 | 3355 | 50.2 (20.1) | 1.5 |
| Vouacapoua americana (V.a.) | 34 | 3218 | 65.4 (34.0) | 1.5 |
| Sextonia rubra (S.r.) | 32 | 4070 | 118.5 (99.3) | 1.4 |
| Tapura capitulifera (T.c.) | 32 | 1224 | 30.5 (12.2) | 1.4 |
| Licania heteromorpha (L.h.) | 27 | 1437 | 40.3 (21.7) | 1.2 |
| Moronobea coccinea (M.c.) | 27 | 3355 | 68.8 (36.7) | 1.2 |
| Inga alba (I.a.) | 26 | 3846 | 81.3 (58.7) | 1.2 |
| Goupia glabra (G.g.) | 25 | 4998 | 133.7 (77.3) | 1.1 |
| Bocoa prouacensis (B.p.) | 24 | 2375 | 54.9 (35.8) | 1.1 |
| Jacaranda copaia (J.c.) | 24 | 1705 | 40.4 (22.7) | 1.1 |
| Others | 949 | 84,713 | 80.8 (71.6) | 42.3 |
| Species | VNIR | VSWIR | ||||
|---|---|---|---|---|---|---|
| LDA | RDA | LR | LDA | RDA | LR | |
| B.p. | 25.4 (±11.6) | 22.3 (±8.5) | 26.4 (±7.2) | 66.9 (±11.3) | 83.3 (±10.4) | 61.0 (±18.0) |
| C.m. | 66.7 (±13.2) | 64.8 (±13.5) | 67.5 (±11.0) | 75.0 (±10.7) | 67.9 (±9.9) | 77.0 (±8.4) |
| D.g. | 61.2 (±4.5) | 61.3 (±4.7) | 69.2 (±7.0) | 88.6 (±2.5) | 86.3 (±3.6) | 90.3 (±2.4) |
| E.f. | 46.9 (±5.5) | 7.3 (±2.5) | 29.6 (±9.6) | 70.0 (±5.8) | 72.9 (±8.2) | 73.9 (±6.7) |
| E.g. | 63.1 (±6.4) | 61.8 (±7.4) | 79.4 (±5.0) | 82.1 (±5.3) | 87.6 (±4.4) | 89.7 (±3.6) |
| E.s. | 79.0 (±3.3) | 72.8 (±5.3) | 70.6 (±7.3) | 89.6 (±2.8) | 89.3 (±1.9) | 86.4 (±2.1) |
| G.g. | 44.3 (±8.9) | 63.3 (±12.1) | 67.6 (±12.9) | 84.1 (±7.3) | 83.9 (±12.0) | 80.4 (±12.7) |
| I.a. | 44.4 (±14.2) | 49.4 (±15.6) | 62.7 (±17.2) | 77.6 (±10.0) | 76.3 (±8.5) | 66.0 (±16.0) |
| J.c. | 58.4 (±16.7) | 59.2 (±12.6) | 57.1 (±16.6) | 59.2 (±19.1) | 58.2 (±18.1) | 70.2 (±16.8) |
| L.a. | 55.9 (±10.0) | 62.9 (±10.7) | 62.6 (±11.4) | 78.1 (±4.5) | 79.6 (±9.5) | 74.6 (±9.1) |
| L.h. | 22.2 (±8.0) | 16.7 (±0.0) | 20.0 (±0.0) | 65.2 (±11.3) | 60.7 (±13.7) | 49.0 (±14.6) |
| M.c. | 64.5 (±11.4) | 52.7 (±14.3) | 64.1 (±13.3) | 82.8 (±10.9) | 74.7 (±17.4) | 79.7 (±12.7) |
| P.c. | 80.5 (±4.2) | 83.6 (±3.8) | 88.4 (±3.3) | 93.5 (±1.9) | 93.6 (±1.9) | 94.1 (±1.6) |
| Q.r. | 94.8 (±1.6) | 94.6 (±1.5) | 95.6 (±1.2) | 96.9 (±1.1) | 96.2 (±1.4) | 97.2 (±1.1) |
| R.s. | 84.9 (±6.0) | 81.4 (±5.0) | 90.0 (±4.7) | 91.4 (±3.3) | 87.1 (±6.1) | 90.6 (±3.8) |
| S.r. | 55.0 (±9.2) | 50.6 (±14.5) | 53.7 (±13.2) | 77.6 (±11.5) | 82.9 (±8.4) | 85.2 (±7.3) |
| S.s. | 24.0 (±0.0) | 0.0 (±0.0) | 11.3 (±0.0) | 64.0 (±11.7) | 68.9 (±12.1) | 50.5 (±13.7) |
| T.m. | 73.3 (±7.7) | 79.2 (±6.0) | 84.1 (±5.6) | 93.5 (±4.1) | 93.3 (±4.3) | 93.4 (±4.1) |
| T.c. | 35.4 (±8.7) | 17.1 (±4.0) | 38.2 (±14.1) | 82.6 (±8.9) | 72.7 (±11.8) | 83.5 (±9.8) |
| V.a. | 48.7 (±13.8) | 52.8 (±13.7) | 43.0 (±14.7) | 85.1 (±8.3) | 83.8 (±10.0) | 77.1 (±10.1) |
| Mean F-measue | 56.4 | 52.7 | 59.1 | 80.2 | 80.0 | 78.5 |
| Bias | 0% | 1% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Plain | Optimized | Plain | Optimized | |||||||||
| Species | LDA | RDA | LR | LDA | RDA | LR | LDA | RDA | LR | LDA | RDA | LR |
| B.p. | 35.8 (±10.3) | 57.7 (±12.4) | 37.5 (±15.5) | 65.4 | 57.5 | 42.1 | 36.4 | 58.5 | 43.4 | 64.3 | 56.2 | 43.0 |
| C.m. | 68.3 (±10.8) | 64.7 (±10.1) | 68.0 (±10.5) | 69.8 | 68.3 | 71.4 | 67.4 | 65.1 | 66.5 | 69.8 | 68.0 | 69.4 |
| D.g. | 57.7 (±3.9) | 72.3 (±6.0) | 78.2 (±6.1) | 75.8 | 72.0 | 78.5 | 57.5 | 72.6 | 78.2 | 74.8 | 72.2 | 78.3 |
| E.f. | 50.8 (±4.1) | 67.7 (±6.1) | 69.2 (±6.2) | 71.5 | 68.9 | 70.5 | 51.5 | 67.9 | 68.0 | 72.1 | 69.2 | 70.5 |
| E.g. | 65.1 (±7.0) | 82.0 (±5.3) | 84.4 (±4.6) | 82.4 | 82.7 | 84.8 | 64.9 | 81.9 | 82.5 | 82.0 | 82.5 | 84.7 |
| E.s. | 68.1 (±4.2) | 74.2 (±4.1) | 71.0 (±5.2) | 74.7 | 74.1 | 75.9 | 68.5 | 74.7 | 69.2 | 74.1 | 73.4 | 74.9 |
| G.g. | 62.5 (±12.6) | 73.4 (±11.5) | 76.4 (±12.5) | 74.5 | 73.5 | 77.3 | 62.8 | 72.6 | 74.8 | 74.5 | 74.4 | 75.0 |
| I.a. | 38.3 (±11.5) | 42.3 (±12.7) | 38.5 (±11.6) | 43.0 | 41.0 | 41.4 | 38.9 | 42.7 | 36.6 | 43.0 | 41.4 | 40.9 |
| J.c. | 50.7 (±19.7) | 51.4 (±16.8) | 52.4 (±17.1) | 50.9 | 49.3 | 53.1 | 52.2 | 49.0 | 51.6 | 51.5 | 50.4 | 52.6 |
| L.a. | 41.6 (±8.7) | 56.3 (±10.8) | 53.9 (±10.5) | 56.6 | 54.4 | 62.3 | 41.9 | 56.8 | 48.5 | 57.0 | 54.7 | 59.7 |
| L.h. | 25.6 (±8.9) | 43.6 (±11.0) | 22.8 (±8.1) | 44.0 | 34.2 | 25.5 | 26.5 | 43.5 | 23.5 | 46.6 | 33.7 | 26.0 |
| M.c. | 58.5 (±13.8) | 55.5 (±16.9) | 60.0 (±14.5) | 56.3 | 54.9 | 62.7 | 58.6 | 56.1 | 56.5 | 55.4 | 56.2 | 61.7 |
| P.c. | 69.5 (±4.5) | 77.1 (±4.9) | 85.9 (±3.6) | 77.6 | 77.0 | 84.3 | 69.6 | 78.0 | 85.8 | 78.2 | 77.4 | 84.0 |
| Q.r. | 86.6 (±2.5) | 88.1 (±2.7) | 91.3 (±2.3) | 86.4 | 85.8 | 90.7 | 86.9 | 88.1 | 91.2 | 86.6 | 86.2 | 90.8 |
| R.s. | 82.5 (±3.8) | 78.8 (±4.5) | 81.2 (±5.2) | 81.0 | 80.7 | 84.9 | 82.4 | 79.3 | 79.5 | 80.7 | 79.7 | 83.4 |
| S.r. | 54.3 (±9.2) | 70.8 (±10.7) | 61.6 (±14.7) | 71.8 | 66.9 | 68.0 | 53.8 | 69.7 | 52.3 | 71.3 | 66.4 | 61.1 |
| S.s. | 29.1 (±5.9) | 36.7 (±9.1) | 21.3 (±7.1) | 36.6 | 36.7 | 25.6 | 29.1 | 35.8 | 21.3 | 35.5 | 35.8 | 25.6 |
| T.m. | 64.7 (±6.4) | 69.9 (±6.0) | 80.7 (±9.4) | 76.3 | 75.8 | 78.8 | 64.9 | 70.4 | 78.2 | 76.0 | 75.6 | 78.9 |
| T.c. | 58.3 (±11.5) | 65.4 (±12.5) | 72.2 (±14.8) | 65.8 | 52.1 | 72.5 | 58.2 | 65.4 | 69.6 | 63.6 | 51.0 | 70.6 |
| V.a. | 68.2 (±8.7) | 72.8 (±12.2) | 65.1 (±12.8) | 74.4 | 74.4 | 66.9 | 66.5 | 74.1 | 63.9 | 74.4 | 73.6 | 64.6 |
| Average | 56.8 | 65.0 | 63.6 | 66.7 | 64.0 | 65.9 | 56.9 | 65.1 | 62.0 | 66.6 | 63.9 | 64.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laybros, A.; Aubry-Kientz, M.; Féret, J.-B.; Bedeau, C.; Brunaux, O.; Derroire, G.; Vincent, G. Quantitative Airborne Inventories in Dense Tropical Forest Using Imaging Spectroscopy. Remote Sens. 2020, 12, 1577. https://doi.org/10.3390/rs12101577
Laybros A, Aubry-Kientz M, Féret J-B, Bedeau C, Brunaux O, Derroire G, Vincent G. Quantitative Airborne Inventories in Dense Tropical Forest Using Imaging Spectroscopy. Remote Sensing. 2020; 12(10):1577. https://doi.org/10.3390/rs12101577
Chicago/Turabian StyleLaybros, Anthony, Mélaine Aubry-Kientz, Jean-Baptiste Féret, Caroline Bedeau, Olivier Brunaux, Géraldine Derroire, and Grégoire Vincent. 2020. "Quantitative Airborne Inventories in Dense Tropical Forest Using Imaging Spectroscopy" Remote Sensing 12, no. 10: 1577. https://doi.org/10.3390/rs12101577
APA StyleLaybros, A., Aubry-Kientz, M., Féret, J.-B., Bedeau, C., Brunaux, O., Derroire, G., & Vincent, G. (2020). Quantitative Airborne Inventories in Dense Tropical Forest Using Imaging Spectroscopy. Remote Sensing, 12(10), 1577. https://doi.org/10.3390/rs12101577