Modelling Distributions of Rove Beetles in Mountainous Areas Using Remote Sensing Data
Abstract
1. Introduction
- How well can habitat suitability be modelled based on SRS data for rove beetles in mountainous ecosystems?
- How and why do SRS-based model predictions differ among years?
- What are the most important SRS predictors? How do they differ among species?
2. Materials and Methods
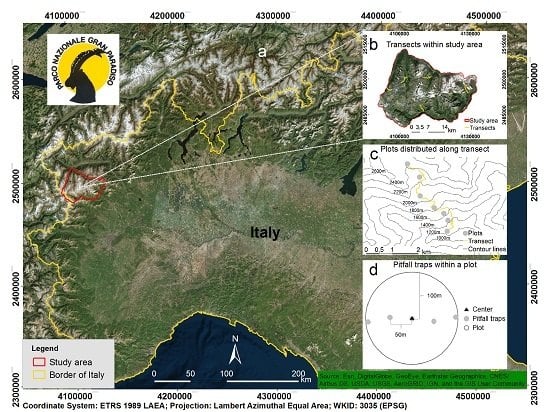
2.1. Study Area
2.2. Sampling Design for Biodiversity Data and Species Characteristics
Dinothenarus fossor | Platydracus stercorarius | Ocypus ophthalmicus | |
| Size | 15–20 mm | 12–15 mm | 15–23 mm |
| Macro-habitat | Sylvicolous (mainly) | Eurytopic | Often in open areas (eurytopic) |
| Micro-habitat | Phytodetriticolous (mainly) | Saprophilous (often close to dung) | Phytodetriticolous |
| Nutrition | Predator (mainly myrmecophagous) | Generalist predator (other insects) | Generalist predator (other insects, larvae, nematodes, snails) |
| Micro-climate | Xerophilus | NA | Xerophilus, heliophilous |
| Altitude | Montane (mainly) | Lowland to montane | Lowland to subalpine-alpine |
| Chorotype | Central European | Turano-European | Palearctic |
2.3. Species Presence/Pseudo-Absence Data for Model Training
2.4. Satellite Remote Sensing Data
2.5. Ensemble Modelling and Model Parametrization
2.6. Assessing Variable Importance of SRS Data
2.7. Model Evaluation
3. Results
3.1. Model Performance
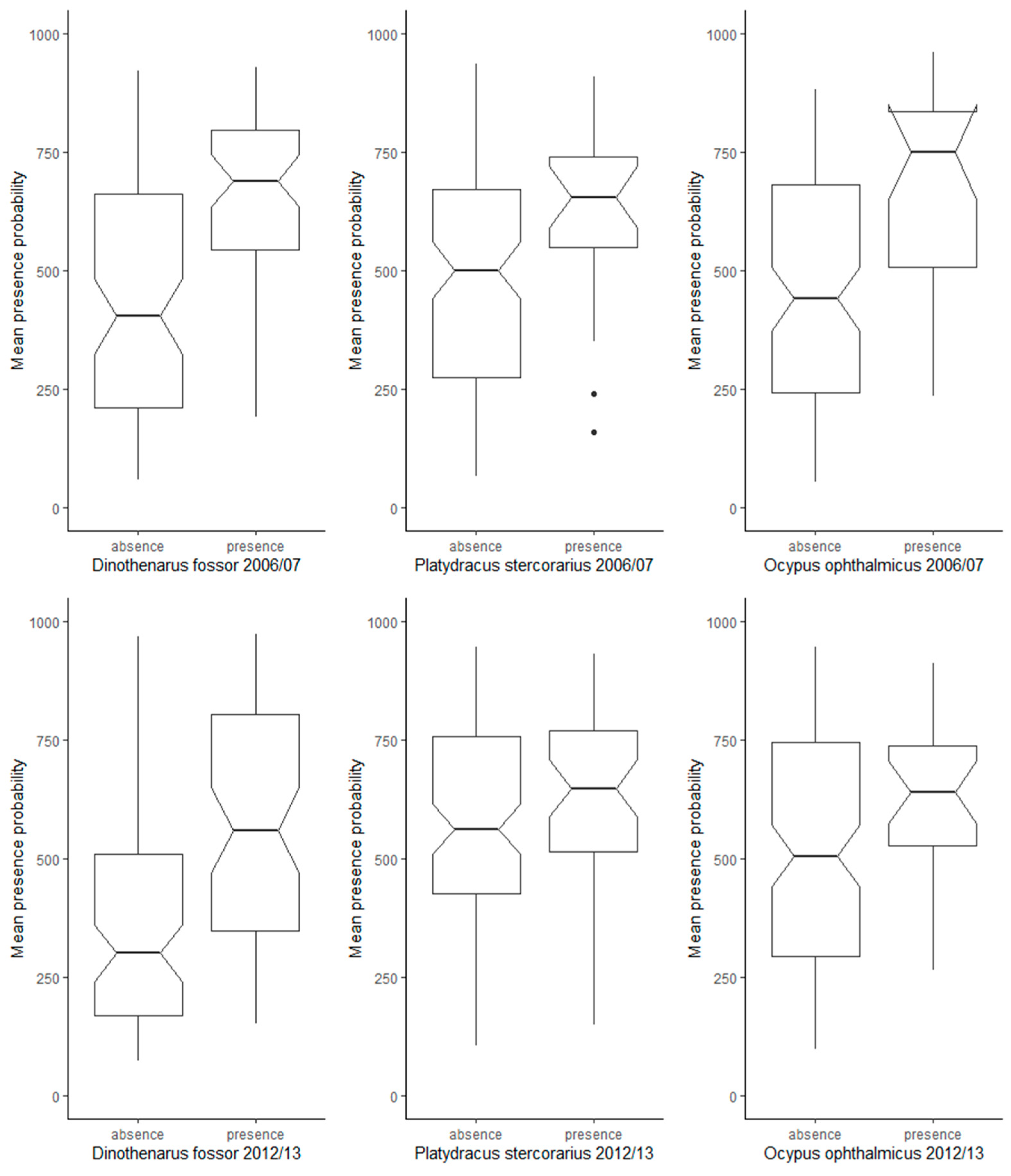
3.2. Effects of Inter-Annual Variability of Species Records on SRS-Based Training Data
3.3. Variable Importance
3.4. Species Distribution Maps
4. Discussion
4.1. Model Performances to Predict Invertebrate Species Distribution
4.2. Temporal Variability of Species Presence Records, SRS Data, and Modelled Distribution Ranges
4.3. Importance of SRS Predictors
4.4. Suggestions for Model Improvement
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Körner, C. Why Are There Global Gradients in Species Richness? Mountains Might Hold the Answer Rapoport Effect and Speciation/Extinction Rates. Trends Ecol. Evol. 2000, 15, 513–514. [Google Scholar] [CrossRef]
- Körner, C.; Paulsen, J.; Spehn, E.M. A Definition of Mountains and Their Bioclimatic Belts for Global Comparisons of Biodiversity Data. Alp. Bot. 2011, 121, 73–78. [Google Scholar] [CrossRef]
- Díaz, S.; Pascual, U.; Stenseke, M.; Martín-López, B.; Watson, R.T.; Molnár, Z.; Hill, R.; Chan, K.M.A.; Baste, I.A.; Brauman, K.A.; et al. Assessing Nature’s Contributions to People. Science 2018, 359, 270–272. [Google Scholar] [CrossRef] [PubMed]
- Viviroli, D.; Weingartner, R.; Messerli, B. Assessing the Hydrological Significance of the World’s Mountains. Mt. Res. Dev. 2003, 23, 32–40. [Google Scholar] [CrossRef]
- Kohler, T.; Wehrli, A.; Jurek, M. Mountains and Climate Change: A Global Concern. Sustainable Mountain Development Series; Centre for Development and Environment (CDE), Swiss Agency for Development and Cooperation (SDC) and Geographica Bernensia: Bern, Switzerland, 2014. [CrossRef]
- Pocock, M.J.O.; Newson, S.E.; Henderson, I.G.; Peyton, J.; Sutherland, W.J.; Noble, D.G.; Ball, S.G.; Beckmann, B.C.; Biggs, J.; Brereton, T.; et al. Developing and Enhancing Biodiversity Monitoring Programmes: A Collaborative Assessment of Priorities. J. Appl. Ecol. 2015, 52, 686–695. [Google Scholar] [CrossRef]
- Franklin, J. Mapping Species Distributions: Spatial Inference and Prediction; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Sardà-Palomera, F.; Brotons, L.; Villero, D.; Sierdsema, H.; Newson, S.E.; Jiguet, F. Mapping from Heterogeneous Biodiversity Monitoring Data Sources. Biodivers. Conserv. 2012, 21, 2927–2948. [Google Scholar] [CrossRef]
- Oke, O.A.; Thompson, K.A. Distribution Models for Mountain Plant Species: The Value of Elevation. Ecol. Model. 2015, 301, 72–77. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very High Resolution Interpolated Climate Surfaces for Global Land Areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Luoto, M.; Virkkala, R.; Heikkinen, R.K. The Role of Land Cover in Bioclimatic Models Depends on Spatial Resolution. Glob. Ecol. Biogeogr. 2007, 16, 34–42. [Google Scholar] [CrossRef]
- Bradley, B.A.; Fleishman, E. Can Remote Sensing of Land Cover Improve Species Distribution Modelling? J. Biogeogr. 2008, 35, 1158–1159. [Google Scholar] [CrossRef]
- Cord, A.F.; Klein, D.; Mora, F.; Dech, S. Comparing the Suitability of Classified Land Cover Data and Remote Sensing Variables for Modeling Distribution Patterns of Plants. Ecol. Model. 2014, 272, 129–140. [Google Scholar] [CrossRef]
- Li, X.; Ling, F.; Foody, G.M.; Ge, Y.; Zhang, Y.; Du, Y. Generating a Series of Fine Spatial and Temporal Resolution Land Cover Maps by Fusing Coarse Spatial Resolution Remotely Sensed Images and Fine Spatial Resolution Land Cover Maps. Remote Sens. Environ. 2017, 196, 293–311. [Google Scholar] [CrossRef]
- He, K.S.; Bradley, B.A.; Cord, A.F.; Rocchini, D.; Tuanmu, M.N.; Schmidtlein, S.; Turner, W.; Wegmann, M.; Pettorelli, N. Will Remote Sensing Shape the next Generation of Species Distribution Models? Remote Sens. Ecol. Conserv. 2015, 1, 4–18. [Google Scholar] [CrossRef]
- Weiss, D.J.; Walsh, S.J. Remote Sensing of Mountain Environments. Geogr. Compass 2009, 3, 1–21. [Google Scholar] [CrossRef]
- Liang, L.; Li, X.; Huang, Y.; Qin, Y.; Huang, H. Integrating Remote Sensing, GIS and Dynamic Models for Landscape-Level Simulation of Forest Insect Disturbance. Ecol. Model. 2017, 354, 1–10. [Google Scholar] [CrossRef]
- Dudov, S.V. Modeling of Species Distribution with the Use of Topography and Remote Sensing Data on the Example of Vascular Plants of the Tukuringra Ridge Low Mountain Belt (Zeya State Nature Reserve, Amur Oblast). Biol. Bull. Rev. 2017, 7, 246–257. [Google Scholar] [CrossRef]
- Lausch, A.; Bannehr, L.; Beckmann, M.; Boehm, C.; Feilhauer, H.; Hacker, J.M.; Heurich, M.; Jung, A.; Klenke, R.; Neumann, C.; et al. Linking Earth Observation and Taxonomic, Structural and Functional Biodiversity: Local to Ecosystem Perspectives. Ecol. Indic. 2016, 70, 317–339. [Google Scholar] [CrossRef]
- Turner, W.; Rondinini, C.; Pettorelli, N.; Mora, B.; Leidner, A.K.; Szantoi, Z.; Buchanan, G.; Dech, S.; Dwyer, J.; Herold, M.; et al. Free and Open-Access Satellite Data Are Key to Biodiversity Conservation. Biol. Conserv. 2015, 182, 173–176. [Google Scholar] [CrossRef]
- Vrieling, A.; Meroni, M.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Zurita-Milla, R.; Oosterbeek, K.; O’Connor, B.; Paganini, M. Vegetation Phenology from Sentinel-2 and Field Cameras for a Dutch Barrier Island. Remote Sens. Environ. 2018, 215, 517–529. [Google Scholar] [CrossRef]
- Kovacs, E.; Roelfsema, C.; Lyons, M.; Zhao, S.; Phinn, S. Seagrass Habitat Mapping: How Do Landsat 8 OLI, Sentinel-2, ZY-3A, and Worldview-3 Perform? Remote Sens. Lett. 2018, 9, 686–695. [Google Scholar] [CrossRef]
- Schmidt, J.; Fassnacht, F.E.; Förster, M.; Schmidtlein, S. Synergetic Use of Sentinel-1 and Sentinel-2 for Assessments of Heathland Conservation Status. Remote Sens. Ecol. Conserv. 2018, 4, 225–239. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the Archive: How Free Data Has Enabled the Science and Monitoring Promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current Status of Landsat Program, Science, and Applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Grimaldi, D.; Engel, M.S. Evolution of the Insect; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Bohac, J. Staphylinid Beetles as Bioindicators. Agric. Ecosyst. Environ. 1999, 74, 357–372. [Google Scholar] [CrossRef]
- Pohl, G.R.; Langor, D.W.; Spence, J.R. Rove Beetles and Ground Beetles (Coleoptera: Staphylinidae, Carabidae) as Indicators of Harvest and Regeneration Practices in Western Canadian Foothills Forests. Biol. Conserv. 2007, 137, 294–307. [Google Scholar] [CrossRef]
- Assing, V.; Schülke, M. (Eds.) Die Käfer Mitteleuropas, Bd. 4: Staphylinidae (Exklusive Aleocharinae, Pselaphinae Und Scydmaeninae), 2nd ed.; Springer Spektrum: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-8274-1677-3. [Google Scholar]
- Elith, J.; Leathwick, J.R. Species Distribution Models: Ecological Explanation and Prediction Across Space and Time. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 677–697. [Google Scholar] [CrossRef]
- Araújo, M.B.; New, M. Ensemble Forecasting of Species Distributions. Trends Ecol. Evol. 2007, 22, 42–47. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Monographs on Statistics and Applied Probability; Chapman and Hall/CRC: Boca Raton, FL, USA, 1989; ISBN 9780412317606. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized Additive Models. Stat. Sci. 1986, 249–307. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A Working Guide to Boosted Regression Trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M. Modeling of Species Distributions with Maxent: New Extensions and a Comprehensive Evaluation. Ecography 2008, 31, 161–175. [Google Scholar] [CrossRef]
- Marmion, M.; Parviainen, M.; Luoto, M.; Heikkinen, R.K.; Thuiller, W. Evaluation of Consensus Methods in Predictive Species Distribution Modelling. Divers. Distrib. 2009, 15, 59–69. [Google Scholar] [CrossRef]
- Gran Paradiso National Park—Italy. Available online: https://data.lter-europe.net/deims/site/lter_eu_it_109 (accessed on 20 October 2017).
- Viterbi, R.; Cerrato, C.; Bassano, B.; Bionda, R.; Hardenberg, A.; Provenzale, A.; Bogliani, G. Patterns of Biodiversity in the Northwestern Italian Alps: A Multi-Taxa Approach. Community Ecol. 2013, 14, 18–30. [Google Scholar] [CrossRef]
- Thomasset, F.; Ottino, M. Parco Nazionale Gran Paradiso. Piano del Parco. Relazione Illustrativa. Available online: http://www.pngp.it/documenti/Piano del parco/PNGP_Relazione.illustrativa.pdf (accessed on 2 March 2018).
- Cagnacci, F.; Lovari, S.; Meriggi, A. Carrion Dependence and Food Habits of the Red Fox in an Alpine Area. Ital. J. Zool. 2003, 70, 31–38. [Google Scholar] [CrossRef]
- Poussin, C.; Guigoz, Y.; Palazzi, E.; Terzago, S.; Chatenoux, B.; Giuliani, G. Snow Cover Evolution in the Gran Paradiso National Park, Italian Alps, Using the Earth Observation Data Cube. Data 2019, 4, 138. [Google Scholar] [CrossRef]
- Marcelino, J.A.P.; Giordano, R.; Borges, P.A.V.; Garcia, P.V.; Soto-Adames, F.N.; Soares, A.O. Distribution and Genetic Variability of Staphylinidae across a Gradient of Anthropogenically Influenced Insular Landscapes. Bull. Insectol. 2016, 69, 117–126. [Google Scholar]
- Work, T.T.; Klimaszewski, J.; Thiffault, E.; Bourdon, C.; Paré, D.; Bousquet, Y.; Venier, L.; Titus, B. Initial Responses of Rove and Ground Beetles (Coleoptera, Staphylinidae, Carabidae) to Removal of Logging Residues Following Clearcut Harvesting in the Boreal Forest of Quebec, Canada. Zookeys 2013, 258, 31–52. [Google Scholar] [CrossRef]
- Standen, V. The Adequacy of Collecting Techniques for Estimating Species Richness of Grassland Invertebrates. J. Appl. Ecol. 2000, 37, 884–893. [Google Scholar] [CrossRef]
- Ribera, I.; Dolédec, S.; Downie, I.S.; Foster, G.N. Effect of Land Disturbance and Stress on Species Traits of Ground Beetle Assemblages. Ecology 2001, 82, 1112–1129. [Google Scholar] [CrossRef]
- Tagliapietra, A.; Zanetti, A. Staphylinid Beetles in Natura 2000 Sites of Friuli Venezia Giulia. Gortania Botanica Zool. 2012, 33, 97–124. [Google Scholar]
- Zanetti, A.; Sette, A.; Poggi, R.; Tagliapietra, A. Biodiversity of Staphylinidae (Coleoptera) in the Province of Verona (Veneto, Northern Italy). Mem. Della Soc. Entomol. Ital. 2016, 93, 3–237. [Google Scholar] [CrossRef]
- Wisz, M.S.; Hijmans, R.J.; Li, J.; Peterson, A.T.; Graham, C.H.; Guisan, A. Effects of Sample Size on the Performance of Species Distribution Models. Divers. Distrib. 2008, 14, 763–773. [Google Scholar] [CrossRef]
- Van Proosdij, A.S.J.; Sosef, M.S.M.; Wieringa, J.J.; Raes, N. Minimum Required Number of Specimen Records to Develop Accurate Species Distribution Models. Ecography 2016, 39, 542–552. [Google Scholar] [CrossRef]
- Stockwell, D.R.B.; Peterson, A.T. Effects of Sample Size on Accuracy of Species Distribution Models. Ecol. Model. 2002, 148, 1–13. [Google Scholar] [CrossRef]
- Hao, T.; Elith, J.; Guillera-Arroita, G.; Lahoz-Monfort, J.J. A Review of Evidence about Use and Performance of Species Distribution Modelling Ensembles like BIOMOD. Divers. Distrib. 2019, 25, 839–852. [Google Scholar] [CrossRef]
- Elith, J.; Graham, C.H.; Anderson, R.P.; Dudík, M.; Ferrier, S.; Guisan, A.; Hijmans, R.J.; Huettmann, F.; Leathwick, J.R.; Lehmann, A.; et al. Novel Methods Improve Prediction of Species’ Distributions from Occurrence Data. Ecography 2006, 29, 129–151. [Google Scholar] [CrossRef]
- Fletcher, R.; Fortin, M.J. Spatial Ecology and Conservation Modeling: Applications with R; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jiménez-valverde, A.; Real, R. AUC: A Misleading Measure of the Performance of Predictive Distribution Models. Glob. Ecol. Biogeogr. 2008, 17, 145–151. [Google Scholar] [CrossRef]
- Earth Resources Observation and Science (EROS) Center Science Processing Architecture (ESPA) on Demand Interface. On Demand Interface. Available online: https://landsat.usgs.gov/sites/default/files/documents/espa_odi_userguide.pdf (accessed on 5 April 2018).
- Rödder, D.; Nekum, S.; Cord, A.F.; Engler, J.O. Coupling Satellite Data with Species Distribution and Connectivity Models as a Tool for Environmental Management and Planning in Matrix-Sensitive Species. Environ. Manag. 2016, 58, 130–143. [Google Scholar] [CrossRef]
- Regos, A.; Tapia, L.; Gil-Carrera, A.; Domínguez, J. Monitoring Protected Areas from Space: A Multi-Temporal Assessment Using Raptors as Biodiversity Surrogates. PLoS ONE 2017, 12, e0181769. [Google Scholar] [CrossRef]
- Crist, E.P.; Cicone, R.C. Application of the Tasseled Cap Concept to Simulated Thematic Mapper Data. Photogramm. Eng. Remote Sens. 1984, 50, 343–352. [Google Scholar]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a Tasselled Cap Transformation Based on Landsat 8 At-Satellite Reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. Interpretation of Spectral Vegetation Indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Parastatidis, D.; Mitraka, Z.; Chrysoulakis, N.; Abrams, M. Online Global Land Surface Temperature Estimation from Landsat. Remote Sens. 2017, 9, 1208. [Google Scholar] [CrossRef]
- ASTER Global Digital Elevation Map Announcement. Available online: https://asterweb.jpl.nasa.gov/gdem.asp (accessed on 10 May 2018).
- Hof, A.R.; Jansson, R.; Nilsson, C. The Usefulness of Elevation as a Predictor Variable in Species Distribution Modelling. Ecol. Model. 2012, 246, 86–90. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. A Terrain Ruggedness Index That Qauntifies Topographic Heterogeneity. Int. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Dormann, C.F.; Purschke, O.; Márquez, J.R.G.; Lautenbach, S.; Schröder, B. Components of Uncertainty in Species Distribution Analysis: A Case Study of the Great Grey Shrike. Ecology 2008, 89, 3371–3386. [Google Scholar] [CrossRef]
- Wehn, S.; Johansen, L. The Distribution of the Endemic Plant Primula Scandinavica, at Local and National Scales, in Changing Mountainous Environments. Biodiversity 2015, 16, 278–288. [Google Scholar] [CrossRef]
- Dirnböck, T.; Dullinger, S.; Grabherr, G. A Regional Impact Assessment of Climate and Land-Use Change on Alpine Vegetation. J. Biogeogr. 2003, 401–417. [Google Scholar] [CrossRef]
- Pepin, N.; Kidd, D. Spatial Temperature Variation in the Eastern Pyrenees. Weather 2006, 61, 300–310. [Google Scholar] [CrossRef]
- Kramer-Schadt, S.; Niedballa, J.; Pilgrim, J.D.; Schröder, B.; Lindenborn, J.; Reinfelder, V.; Stillfried, M.; Heckmann, I.; Scharf, A.K.; Augeri, D.M.; et al. The Importance of Correcting for Sampling Bias in MaxEnt Species Distribution Models. Divers. Distrib. 2013, 19, 1366–1379. [Google Scholar] [CrossRef]
- Cohen, W.B.; Goward, S.N. Landsat’s Role in Ecological Applications of Remote Sensing. Bioscience 2004, 54, 535–545. [Google Scholar] [CrossRef]
- Carroll, C.; Noss, R.F.; Paquet, P.C. Carnivores as Focal Species for Conservation Planning in the Rocky Mountain Region. Ecol. Appl. 2001, 11, 961–980. [Google Scholar] [CrossRef]
- Bartel, R.A.; Sexton, J.O. Monitoring Habitat Dynamics for Rare and Endangered Species Using Satellite Images and Niche-Based Models. Ecography 2009, 32, 888–896. [Google Scholar] [CrossRef]
- Cohen, W.B.; Spies, T.A.; Fiorella, M. Estimating the Age and Structure of Forests in a Multi-Ownership Landscape of Western Oregon, U.S.A. Int. J. Remote Sens. 1995, 16, 721–746. [Google Scholar] [CrossRef]
- Aguirre-Gutiérrez, J.; Carvalheiro, L.G.; Polce, C.; van Loon, E.E.; Raes, N.; Reemer, M.; Biesmeijer, J.C. Fit-for-Purpose: Species Distribution Model Performance Depends on Evaluation Criteria—Dutch Hoverflies as a Case Study. PLoS ONE 2013, 8, e63708. [Google Scholar] [CrossRef]
- Thuiller, W.; Georges, D.; Engler, R. Biomod2: Ensemble Platform for Species Distribution Modeling. R Package Version 3.1-48. 2014. Available online: http://cran.r-project.org/package=biomod2 (accessed on 20 May 2019).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014; Available online: http://www.r-project.org/ (accessed on 6 May 2019).
- Hijmans, R.J. Cross-Validation of Species Distribution Models: Removing Spatial Sorting Bias and Calibration with a Null Model. Ecology 2012, 93, 679–688. [Google Scholar] [CrossRef]
- Anderson, K.P.; Burnham, D.A. Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Wood, S.N. MGCV: Mixed GAM Computation Vehicle with Automatic Smoothness Estimation; R Package Version 1.8. Available online: https://cran.r-project.org/web/packages/mgcv/mgcv.pdf (accessed on 20 October 2019).
- Merow, C.; Smith, M.J.; Silander, J.A. A Practical Guide to MaxEnt for Modeling Species’ Distributions: What It Does, and Why Inputs and Settings Matter. Ecography 2013, 36, 1058–1069. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum Entropy Modeling of Species Geographic Distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Greenwell, B.; Boehmke, B.; Cunningham, J. GBM: Generalized Boosted Regression Models; R Package Version 2.1.5. Available online: https://cran.r-project.org/web/packages/gbm/gbm.pdf (accessed on 20 October 2019).
- Elith, J.; Ferrier, S.; Huettmann, F.; Leathwick, J. The Evaluation Strip: A New and Robust Method for Plotting Predicted Responses from Species Distribution Models. Ecol. Model. 2005, 186, 280–289. [Google Scholar] [CrossRef]
- Peterson, A.T.; Papeş, M.; Soberón, J. Rethinking Receiver Operating Characteristic Analysis Applications in Ecological Niche Modeling. Ecol. Model. 2008, 213, 63–72. [Google Scholar] [CrossRef]
- Swets, J.A. Measuring the Accuracy of Diagnostic Systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the Accuracy of Species Distribution Models: Prevalence, Kappa and the True Skill Statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
- González-Ferreras, A.M.; Barquín, J.; Peñas, F.J. Integration of Habitat Models to Predict Fish Distributions in Several Watersheds of Northern Spain. J. Appl. Ichthyol. 2016, 32, 204–216. [Google Scholar] [CrossRef]
- Elith, J.; Burgman, M.A.; Regan, H.M. Mapping Epistemic Uncertainties and Vague Concepts in Predictions of Species Distribution. Ecol. Model. 2002, 157, 313–329. [Google Scholar] [CrossRef]
- Bonn, A.; Schröder, B. Habitat Models and Their Transfer for Single and Multi Species Groups: A Case Study of Carabids in an Alluvial Forest. Ecography 2008, 24, 483–496. [Google Scholar] [CrossRef]
- De Groot, M.; Rebeušek, F.; Grobelnik, V.; Govedič, M.; Šalamun, A.; Verovnik, R. Distribution Modelling as an Approach to the Conservation of a Threatened Alpine Endemic Butterfly (Lepidoptera: Satyridae). Eur. J. Entomol. 2009, 106, 77–84. [Google Scholar] [CrossRef]
- Porfirio, L.L.; Harris, R.M.B.; Lefroy, E.C.; Hugh, S.; Gould, S.F.; Lee, G.; Bindoff, N.L.; Mackey, B. Improving the Use of Species Distribution Models in Conservation Planning and Management under Climate Change. PLoS ONE 2014, 9, e113749. [Google Scholar] [CrossRef] [PubMed]
- Luoto, M.; Kuussaari, M.; Toivonen, T. Modelling Butterfly Distribution Based on Remote Sensing Data. J. Biogeogr. 2002, 29, 1027–1037. [Google Scholar] [CrossRef]
- Eyre, M.D.; Rushton, S.P.; Luff, M.L.; Telfer, M.G. Predicting the Distributions of Ground Beetle Species (Coleoptera, Carabidae) in Britain Using Land Cover Variables. J. Environ. Manag. 2004, 72, 163–174. [Google Scholar] [CrossRef]
- Heikkinen, R.K.; Luoto, M.; Kuussaari, M.; Toivonen, T. Modelling the Spatial Distribution of a Threatened Butterfly: Impacts of Scale and Statistical Technique. Landsc. Urban Plan. 2007, 79, 347–357. [Google Scholar] [CrossRef]
- Widenfalk, L.A.; Ahrné, K.; Berggren, Å. Using Citizen-Reported Data to Predict Distributions of Two Non-Native Insect Species in Sweden. Ecosphere 2014, 5, 1–16. [Google Scholar] [CrossRef]
- Romo, H.; García-Barros, E.; Márquez, A.L.; Moreno, J.C.; Real, R. Effects of Climate Change on the Distribution of Ecologically Interacting Species: Butterflies and Their Main Food Plants in Spain. Ecography 2014, 37, 1063–1072. [Google Scholar] [CrossRef]
- Grenouillet, G.; Buisson, L.; Casajus, N.; Lek, S. Ensemble Modelling of Species Distribution: The Effects of Geographical and Environmental Ranges. Ecography 2011, 34, 9–17. [Google Scholar] [CrossRef]
- Wisz, M.S.; Guisan, A. Do Pseudo-Absence Selection Strategies Influence Species Distribution Models and Their Predictions? An Information-Theoretic Approach Based on Simulated Data. BMC Ecol. 2009, 9, 8. [Google Scholar] [CrossRef] [PubMed]
- Barbet-Massin, M.; Jiguet, F.; Albert, C.H.; Thuiller, W. Selecting Pseudo-Absences for Species Distribution Models: How, Where and How Many? Methods Ecol. Evol. 2012, 3, 327–338. [Google Scholar] [CrossRef]
- Krueger, T.; Page, T.; Hubacek, K.; Smith, L.; Hiscock, K. The Role of Expert Opinion in Environmental Modelling. Environ. Model. Softw. 2012, 36, 4–18. [Google Scholar] [CrossRef]
- Bélisle, A.C.; Asselin, H.; Leblanc, P.; Gauthier, S. Local Knowledge in Ecological Modeling. Ecol. Soc. 2018, 23, 14. [Google Scholar] [CrossRef]
- Anderson, C.B. Biodiversity Monitoring, Earth Observations and the Ecology of Scale. Ecol. Lett. 2018, 21, 1572–1585. [Google Scholar] [CrossRef]
- Guisan, A.; Graham, C.H.; Elith, J.; Huettmann, F.; Dudik, M.; Ferrier, S.; Hijmans, R.; Lehmann, A.; Li, J.; Lohmann, L.G.; et al. Sensitivity of Predictive Species Distribution Models to Change in Grain Size. Divers. Distrib. 2007, 13, 332–340. [Google Scholar] [CrossRef]
- Thiele, H.-U. Carabid Beetles in Their Environments; Springer: Berlin/Heidelberg, Germany, 1977; ISBN 978-3-642-81156-2. [Google Scholar]
- Saska, P.; van der Werf, W.; Hemerik, L.; Luff, M.L.; Hatten, T.D.; Honek, A. Temperature Effects on Pitfall Catches of Epigeal Arthropods: A Model and Method for Bias Correction. J. Appl. Ecol. 2013, 50, 181–189. [Google Scholar] [CrossRef]
- Southwood, T.R.E.; Henderson, P.A. Ecological Methods, 3rd ed.; Blackwell Science: Hoboken, NJ, USA, 2000; ISBN 978-0-632-05477-0. [Google Scholar]
- Buse, A.; Good, J.E.G. The Effects of Conifer Forest Design and Management on Abundance and Diversity of Rove Beetles (Coleoptera: Staphylinidae): Implications for Conservation. Biol. Conserv. 1993, 64, 67–76. [Google Scholar] [CrossRef]
- Hoffmann, H.; Michalik, P.; Görn, S.; Fischer, K. Effects of Fen Management and Habitat Parameters on Staphylinid Beetle (Coleoptera: Staphylinidae) Assemblages in North-Eastern Germany. Insect Conserv. 2016, 20, 129–139. [Google Scholar] [CrossRef]
- Fontana, F.; Rixen, C.; Jonas, T.; Aberegg, G.; Wunderle, S. Alpine Grassland Phenology as Seen in AVHRR, VEGETATION, and MODIS NDVI Time Series—A Comparison with in Situ Measurements. Sensors 2008, 8, 2833–2853. [Google Scholar] [CrossRef] [PubMed]
- Bino, G.; Levin, N.; Darawshi, S.; Van Der Hal, N.; Reich-Solomon, A.; Kark, S. Accurate Prediction of Bird Species Richness Patterns in an Urban Environment Using Landsat-Derived NDVI and Spectral Unmixing. Int. J. Remote Sens. 2008, 29, 3675–3700. [Google Scholar] [CrossRef]
- Sheeren, D.; Bonthoux, S.; Balent, G. Modeling Bird Communities Using Unclassified Remote Sensing Imagery: Effects of the Spatial Resolution and Data Period. Ecol. Indic. 2014, 43, 69–82. [Google Scholar] [CrossRef]
- Pickens, B.A.; King, S.L. Linking Multi-Temporal Satellite Imagery to Coastal Wetland Dynamics and Bird Distribution. Ecol. Model. 2014, 285, 1–12. [Google Scholar] [CrossRef]
- Cord, A.; Klein, D.; Dech, S. The Impact of Inter-Annual Variability in Remote Sensing Time Series on Modelling Tree Species Distributions. In Proceedings of the 6th International Workshop on the Analysis of Multi-Temporal Remote Sensing Images (Multi-Temp), Trento, Italy, 12–14 July 2011. [Google Scholar] [CrossRef]
- Young, N.E.; Anderson, R.S.; Chignell, S.M.; Vorster, A.G.; Lawrence, R.; Evangelista, P.H. A Survival Guide to Landsat Preprocessing. Ecology 2017, 98, 920–932. [Google Scholar] [CrossRef]
- Zanetti, A.; Tagliapietra, A. Studi Sulle Taxocenosi Di Staphylinidae in Boschi Di Latifoglie Italiani (Coleoptera, Staphylinidae). Stud. Trentini Sci. Nat. Acta Biol. 2004, 81, 207–231. [Google Scholar]
- Balog, A.; Markó, V.; Imre, A. Farming System and Habitat Structure Effects on Rove Beetles (Coleoptera: Staphylinidae) Assembly in Central European Apple and Pear Orchards. Biologia 2009, 64, 343–349. [Google Scholar] [CrossRef]
- Lupi, D.; Colombo, M.; Facchini, S. The Ground Beetles (Coleoptera: Carabidae) of Three Horticultural Farms in Lombardy, Northern Italy. Boll. Zool. Agr. Bachic. 2006, 39, 193–209. [Google Scholar]
- Dauber, J.; Purtauf, T.; Allspach, A.; Frisch, J.; Voigtländer, K.; Wolters, V. Local vs. Landscape Controls on Diversity: A Test Using Surface-Dwelling Soil Macroinvertebrates of Differing Mobility. Glob. Ecol. Biogeogr. 2005, 14, 213–221. [Google Scholar] [CrossRef]
- Magura, T.; Nagy, D.; Tóthmérész, B. Rove Beetles Respond Heterogeneously to Urbanization. J. Insect Conserv. 2013, 17, 715–724. [Google Scholar] [CrossRef]
- Raxworthy, C.J.; Martinez-Meyer, E.; Horning, N.; Nussbaum, R.A.; Schneider, G.E.; Ortega-Huerta, M.A.; Peterson, A.T. Predicting Distributions of Known and Unknown Reptile Species in Madagascar. Nature 2003, 426, 837–841. [Google Scholar] [CrossRef] [PubMed]
- Remelgado, R.; Leutner, B.; Safi, K.; Sonnenschein, R.; Kuebert, C.; Wegmann, M. Linking animal movement and remote sensing—Mapping resource suitability from a remote sensing perspective. Remote Sens. Ecol. Conserv. 2017, 4, 211–224. [Google Scholar] [CrossRef]
- Alexakis, D.D.; Mexis, F.D.K.; Vozinaki, A.E.K.; Daliakopoulos, I.N.; Tsanis, I.K. Soil Moisture Content Estimation Based on Sentinel-1 and Auxiliary Earth Observation Products. A Hydrological Approach. Sensors 2017, 17, 1455. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the Capabilities of Sentinel-2 for Quantitative Estimation of Biophysical Variables in Vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Belgiu, M.; Csillik, O. Sentinel-2 Cropland Mapping Using Pixel-Based and Object-Based Time-Weighted Dynamic Time Warping Analysis. Remote Sens. Environ. 2018, 204, 509–523. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Madrigal, V.P.; Mallinis, G.; Dor, E.B.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Cruzan, M.B.; Weinstein, B.G.; Grasty, M.R.; Kohrn, B.F.; Hendrickson, E.C.; Arredondo, T.M.; Thompson, P.G. Small Unmanned Aerial Vehicles (Micro-Uavs, Drones) in Plant Ecology. Appl. Plant Sci. 2016, 4, 160041. [Google Scholar] [CrossRef]
| Dinothenarus fossor | Platydracus stercorarius | Ocypus ophthalmicus | ||||||||||||||||
| Year(s) | 2006 | 2007 | 2012 | 2013 | 2006/2007 | 2012/2013 | 2006 | 2007 | 2012 | 2013 | 2006/2007 | 2012/2013 | 2006 | 2007 | 2012 | 2013 | 2006/2007 | 2012/2013 |
| Traps | 42 | 36 | 55 | 49 | 52 | 66 | 14 | 12 | 25 | 35 | 22 | 45 | 19 | 15 | 16 | 16 | 27 | 26 |
| Plots | 15 | 15 | 18 | 17 | 17 | 19 | 9 | 10 | 14 | 16 | 12 | 18 | 11 | 10 | 9 | 10 | 14 | 12 |
| Tran-sects | 4 | 5 | 4 | 4 | 5 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 5 | 5 | 5 |
| Variable | Ecological Relevance | References | Source |
|---|---|---|---|
| Altitude | Directly correlated with temperature, of particular importance in mountain ecosystems | [9,18,67] | ASTER GDEM |
| Eastness/Northness | Gradients represent differences in the aspect affecting irradiation and precipitation (e.g. an orientation towards east favours heating up in the morning while west-facing ensure higher temperatures in the afternoon) | [68,69] | ASTER GDEM |
| Slope | Terrain steepness reflects gradients in humidity, thickness of soil layer and transport dynamics of matter | [18] | ASTER GDEM |
| Terrain Ruggedness Index | Represents elevational differences among neighbouring grid cells (high values relate to large topographic heterogeneity and impenetrable terrain) | [65,70] | ASTER GDEM |
| Greenness (TCT) | Responds to photosynthetic capacity, vegetation cover and primary productivity (sensitive to topography) | [71,72] | Landsat imagery |
| Wetness (TCT) | Responds to soil/canopy moisture and standing water, being often highest in young forest stands (not sensitive to topography) | [73,74] | Landsat imagery |
| Dinothenarus fossor | ||||||||
| Years | 2006/2007 | 2012/2013 | ||||||
| mean AUC | ±SD | mean TSS | ±SD | mean AUC | ±SD | mean TSS | ±SD | |
| GLM | 0.549 | 0.11 | 0.164 | 0.17 | 0.67 | 0.104 | 0.354 | 0.19 |
| GAM | 0.717 | 0.118 | 0.455 | 0.185 | 0.782 | 0.064 | 0.557 | 0.128 |
| MAXENT | 0.725 | 0.083 | 0.454 | 0.126 | 0.801 | 0.102 | 0.574 | 0.191 |
| RF | 0.74 | 0.094 | 0.5 | 0.149 | 0.813 | 0.085 | 0.618 | 0.12 |
| GBM | 0.83 | 0.047 | 0.588 | 0.088 | 0.835 | 0.064 | 0.609 | 0.137 |
| Ensemble | 0.845 | 0.044 | 0.663 | 0.076 | 0.869 | 0.053 | 0.666 | 0.111 |
| Platydracus stercorarius | ||||||||
| Years | 2006/2007 | 2012/2013 | ||||||
| mean AUC | ±SD | mean TSS | ±SD | mean AUC | ±SD | mean TSS | ±SD | |
| GLM | 0.532 | 0.073 | 0.098 | 0.117 | 0.529 | 0.102 | 0.168 | 0.169 |
| GAM | 0.626 | 0.124 | 0.312 | 0.226 | 0.625 | 0.098 | 0.337 | 0.117 |
| MAXENT | 0.78 | 0.068 | 0.605 | 0.126 | 0.655 | 0.055 | 0.375 | 0.086 |
| RF | 0.638 | 0.115 | 0.368 | 0.161 | 0.754 | 0.077 | 0.505 | 0.121 |
| GBM | 0.664 | 0.133 | 0.391 | 0.221 | 0.77 | 0.059 | 0.542 | 0.085 |
| Ensemble | 0.798 | 0.058 | 0.618 | 0.1 | 0.788 | 0.051 | 0.551 | 0.095 |
| Ocypus ophthalmicus | ||||||||
| Years | 2006/2007 | 2012/2013 | ||||||
| mean AUC | ±SD | mean TSS | ±SD | mean AUC | ±SD | mean TSS | ±SD | |
| GLM | 0.685 | 0.137 | 0.391 | 0.267 | 0.573 | 0.149 | 0.186 | 0.268 |
| GAM | 0.8 | 0.142 | 0.615 | 0.26 | 0.587 | 0.125 | 0.22 | 0.214 |
| MAXENT | 0.809 | 0.148 | 0.707 | 0.217 | 0.709 | 0.112 | 0.474 | 0.141 |
| RF | 0.881 | 0.079 | 0.754 | 0.15 | 0.767 | 0.102 | 0.572 | 0.142 |
| GBM | 0.843 | 0.087 | 0.7 | 0.158 | 0.713 | 0.14 | 0.525 | 0.191 |
| Ensemble | 0.893 | 0.086 | 0.806 | 0.145 | 0.843 | 0.07 | 0.672 | 0.127 |
| Dinothenarus fossor | ||||||||||||
| Years | 2006/2007 | 2012/2013 | ||||||||||
| Algorithm | GLM | GAM | MAXENT | RF | GBM | Ensemble | GLM | GAM | MAXENT | RF | GBM | Ensemble |
| Altitude | 0.169 | 0.127 | 0.175 | 0.071 | 0.11 | 0.117 | 0.115 | 0.073 | 0.105 | 0.05 | 0.01 | 0.048 |
| Northness | 0.177 | 0.182 | 0.084 | 0.175 | 0.002 | 0.062 | 0.16 | 0.234 | 0.091 | 0.174 | 0.022 | 0.123 |
| Eastness | 0.137 | 0.211 | 0.02 | 0.171 | 0.003 | 0.079 | 0.152 | 0.227 | 0.035 | 0.133 | 0.022 | 0.11 |
| Slope | 0.083 | 0.05 | 0.046 | 0.095 | 0.001 | 0.021 | 0.12 | 0.053 | 0.074 | 0.075 | 0.022 | 0.04 |
| Ruggedness | 0.122 | 0.166 | 0.227 | 0.179 | 0.243 | 0.238 | 0.138 | 0.089 | 0.23 | 0.182 | 0.124 | 0.153 |
| Greenness | 0.204 | 0.182 | 0.388 | 0.24 | 0.642 | 0.458 | 0.228 | 0.237 | 0.379 | 0.292 | 0.792 | 0.488 |
| Wetness | 0.11 | 0.081 | 0.06 | 0.069 | 0.000 | 0.024 | 0.087 | 0.086 | 0.085 | 0.094 | 0.008 | 0.038 |
| Platydracus stercorarius | ||||||||||||
| Years | 2006/2007 | 2012/2013 | ||||||||||
| Algorithm | GLM | GAM | MAXENT | RF | GBM | Ensemble | GLM | GAM | MAXENT | RF | GBM | Ensemble |
| Altitude | 0.107 | 0.077 | 0.029 | 0.063 | 0.002 | 0.029 | 0.136 | 0.084 | 0.144 | 0.076 | 0.038 | 0.041 |
| Northness | 0.149 | 0.145 | 0.087 | 0.167 | 0.019 | 0.083 | 0.141 | 0.124 | 0.063 | 0.136 | 0.025 | 0.07 |
| Eastness | 0.133 | 0.096 | 0.029 | 0.155 | 0.003 | 0.033 | 0.149 | 0.128 | 0.051 | 0.139 | 0.02 | 0.064 |
| Slope | 0.123 | 0.131 | 0.005 | 0.052 | 0.001 | 0.019 | 0.142 | 0.118 | 0.156 | 0.071 | 0.086 | 0.076 |
| Ruggedness | 0.145 | 0.165 | 0.148 | 0.107 | 0.174 | 0.147 | 0.12 | 0.152 | 0.278 | 0.238 | 0.299 | 0.289 |
| Greenness | 0.189 | 0.268 | 0.516 | 0.294 | 0.649 | 0.532 | 0.178 | 0.254 | 0.227 | 0.247 | 0.494 | 0.403 |
| Wetness | 0.152 | 0.119 | 0.186 | 0.162 | 0.152 | 0.157 | 0.134 | 0.14 | 0.082 | 0.092 | 0.038 | 0.057 |
| Ocypus ophthalmicus | ||||||||||||
| Years | 2006/2007 | 2012/2013 | ||||||||||
| Algorithm | GLM | GAM | MAXENT | RF | GBM | Ensemble | GLM | GAM | MAXENT | RF | GBM | Ensemble |
| Altitude | 0.161 | 0.101 | 0.074 | 0.044 | 0.002 | 0.052 | 0.155 | 0.127 | 0.222 | 0.133 | 0.187 | 0.096 |
| Northness | 0.135 | 0.194 | 0.067 | 0.232 | 0.054 | 0.143 | 0.097 | 0.238 | 0.059 | 0.221 | 0.108 | 0.166 |
| Eastness | 0.133 | 0.16 | 0.043 | 0.122 | 0.005 | 0.076 | 0.163 | 0.208 | 0.025 | 0.139 | 0.002 | 0.081 |
| Slope | 0.05 | 0.076 | 0.031 | 0.06 | 0.057 | 0.037 | 0.045 | 0.054 | 0.02 | 0.042 | 0.027 | 0.029 |
| Ruggedness | 0.208 | 0.166 | 0.313 | 0.266 | 0.432 | 0.319 | 0.199 | 0.16 | 0.437 | 0.225 | 0.341 | 0.324 |
| Greenness | 0.231 | 0.2 | 0.409 | 0.18 | 0.425 | 0.32 | 0.196 | 0.144 | 0.176 | 0.176 | 0.313 | 0.256 |
| Wetness | 0.083 | 0.103 | 0.063 | 0.095 | 0.025 | 0.053 | 0.145 | 0.07 | 0.062 | 0.063 | 0.022 | 0.048 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dittrich, A.; Roilo, S.; Sonnenschein, R.; Cerrato, C.; Ewald, M.; Viterbi, R.; Cord, A.F. Modelling Distributions of Rove Beetles in Mountainous Areas Using Remote Sensing Data. Remote Sens. 2020, 12, 80. https://doi.org/10.3390/rs12010080
Dittrich A, Roilo S, Sonnenschein R, Cerrato C, Ewald M, Viterbi R, Cord AF. Modelling Distributions of Rove Beetles in Mountainous Areas Using Remote Sensing Data. Remote Sensing. 2020; 12(1):80. https://doi.org/10.3390/rs12010080
Chicago/Turabian StyleDittrich, Andreas, Stephanie Roilo, Ruth Sonnenschein, Cristiana Cerrato, Michael Ewald, Ramona Viterbi, and Anna F. Cord. 2020. "Modelling Distributions of Rove Beetles in Mountainous Areas Using Remote Sensing Data" Remote Sensing 12, no. 1: 80. https://doi.org/10.3390/rs12010080
APA StyleDittrich, A., Roilo, S., Sonnenschein, R., Cerrato, C., Ewald, M., Viterbi, R., & Cord, A. F. (2020). Modelling Distributions of Rove Beetles in Mountainous Areas Using Remote Sensing Data. Remote Sensing, 12(1), 80. https://doi.org/10.3390/rs12010080