Accurate Simulation of Ice and Snow Runoff for the Mountainous Terrain of the Kunlun Mountains, China
Abstract
1. Introduction
2. Materials and Methods
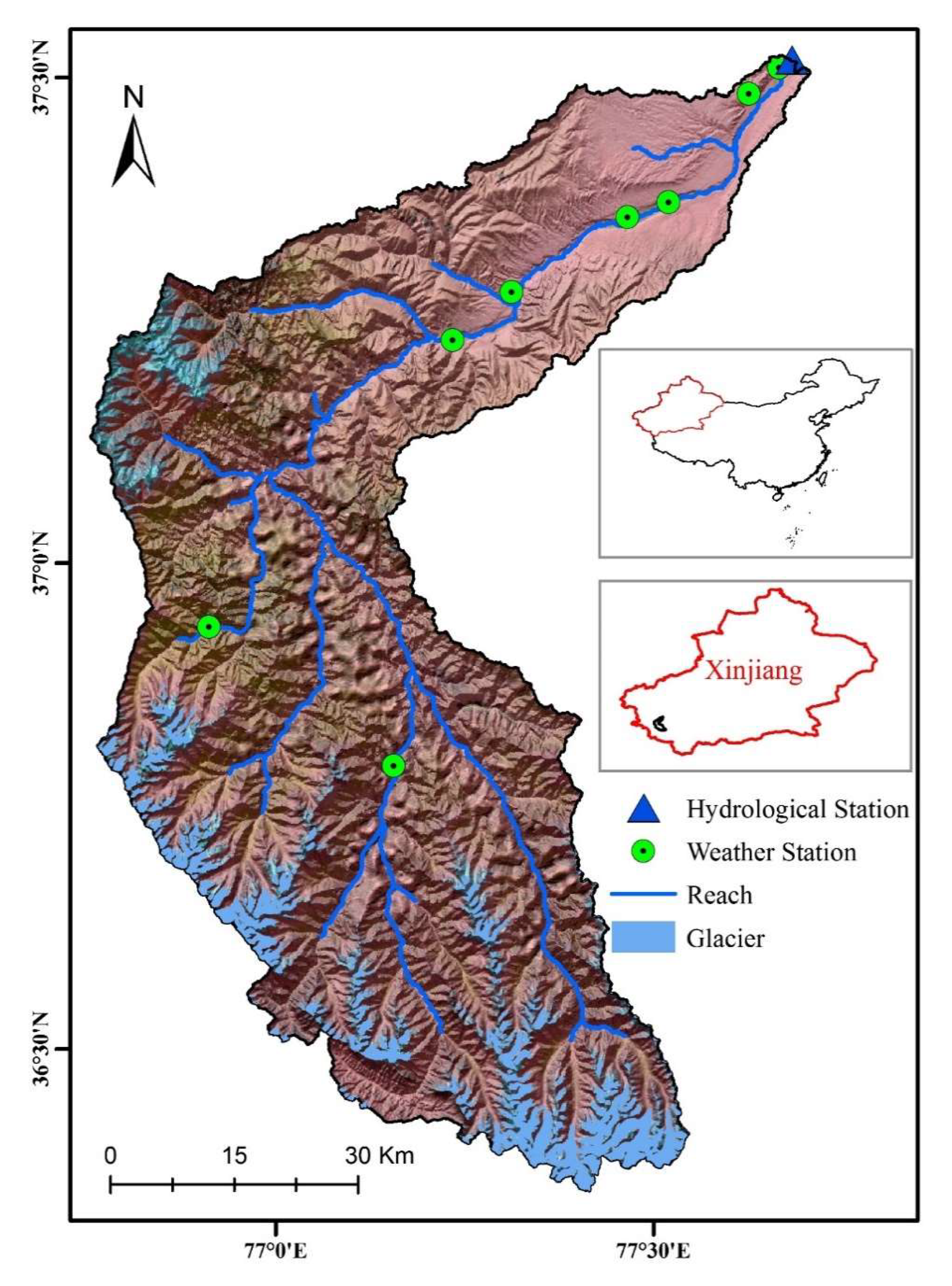
2.1. Study Area
2.2. Materials
2.3. Methods
2.3.1. Calculation of Accumulated Temperature
2.3.2. Calculation of Ice Melt
2.3.3. Calibration, Validation, and Sensitivity
3. Results
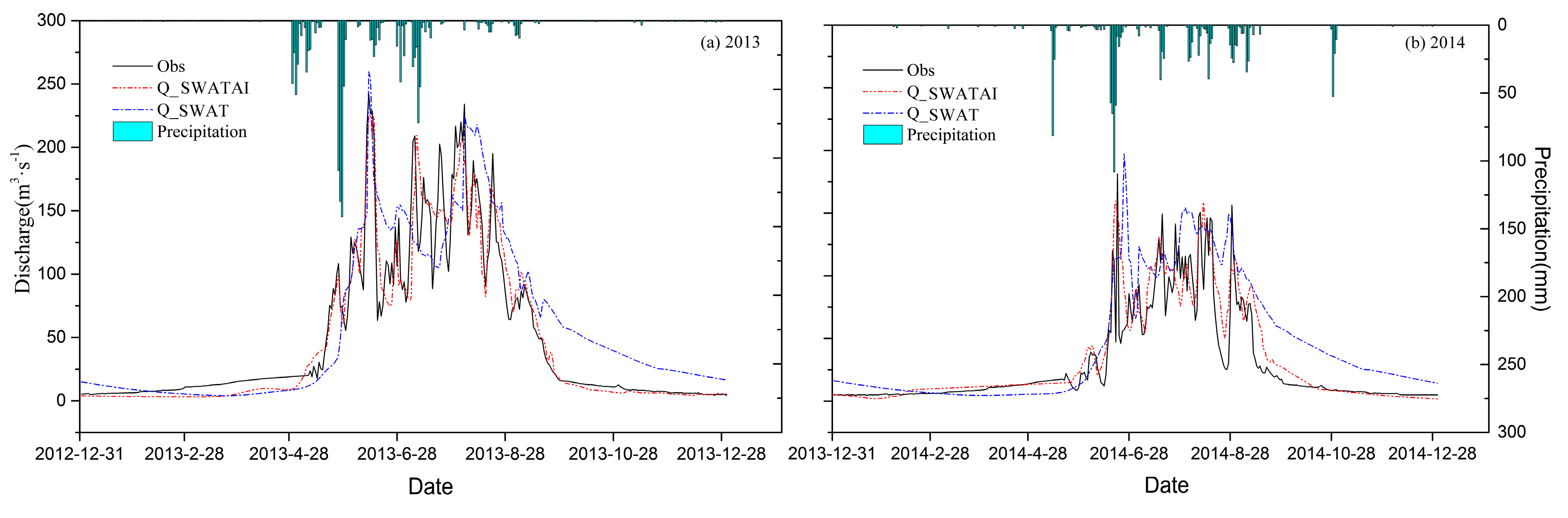
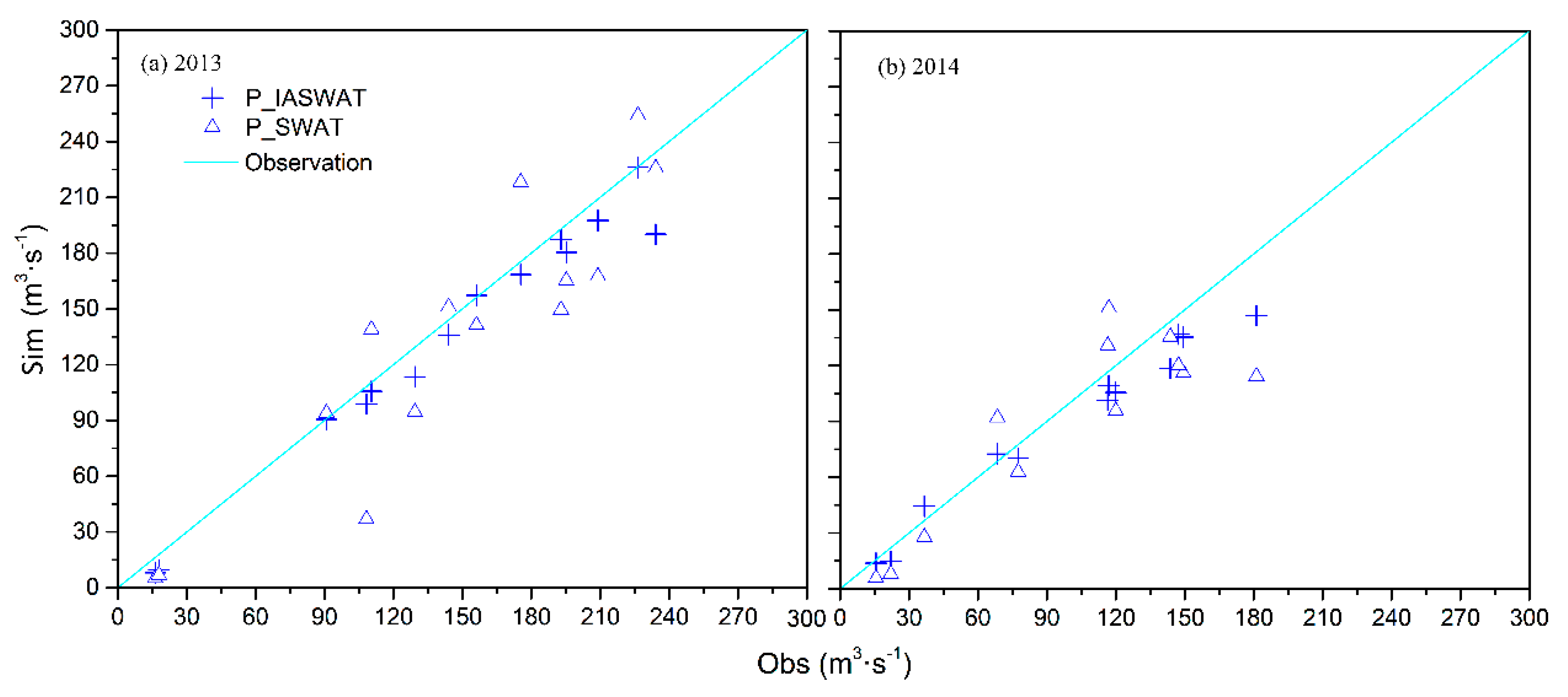
3.1. Daily Simulations
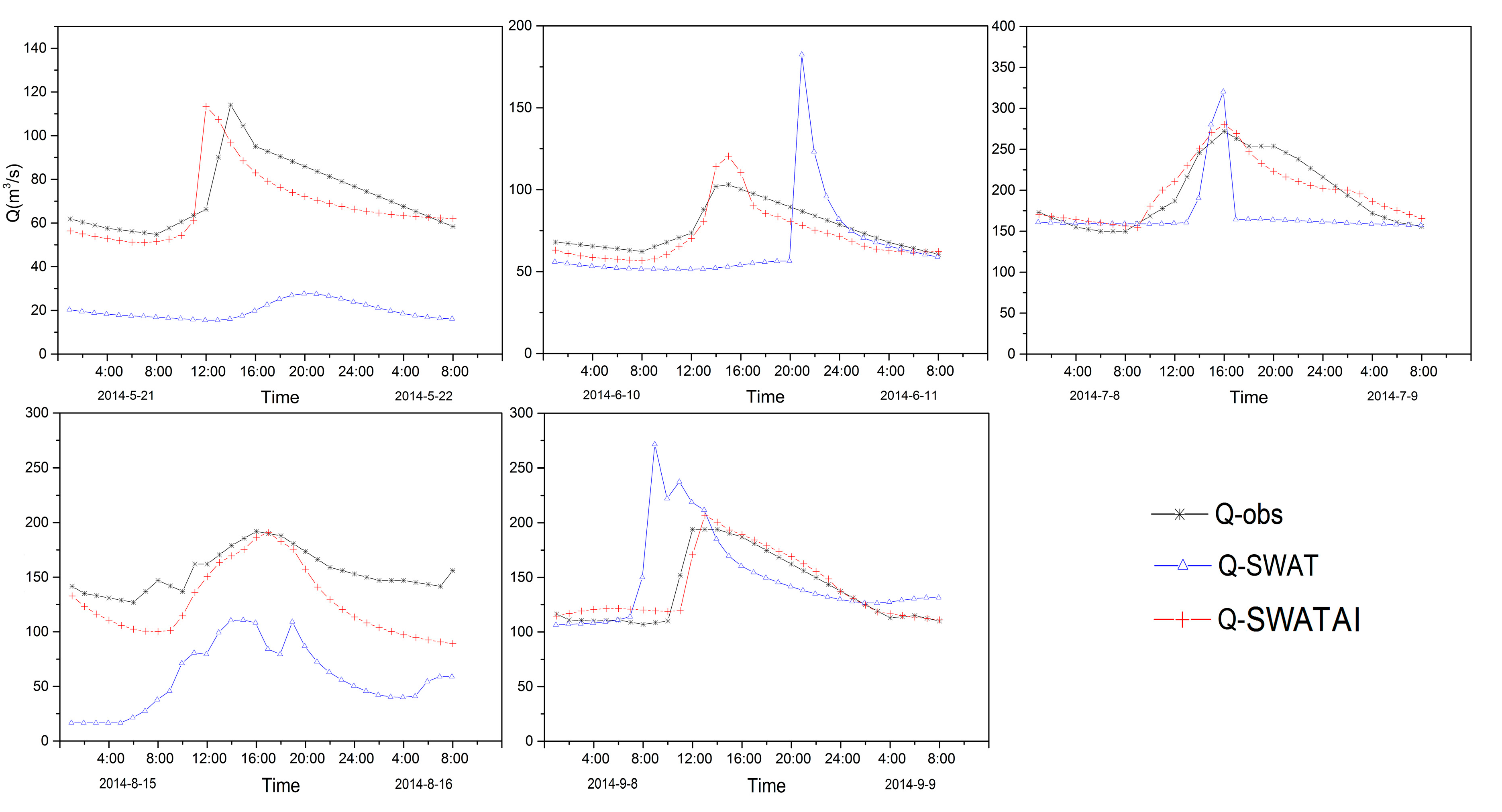
3.2. Sub-Daily Simulations
3.3. Effects of Parameters on the Simulated Results
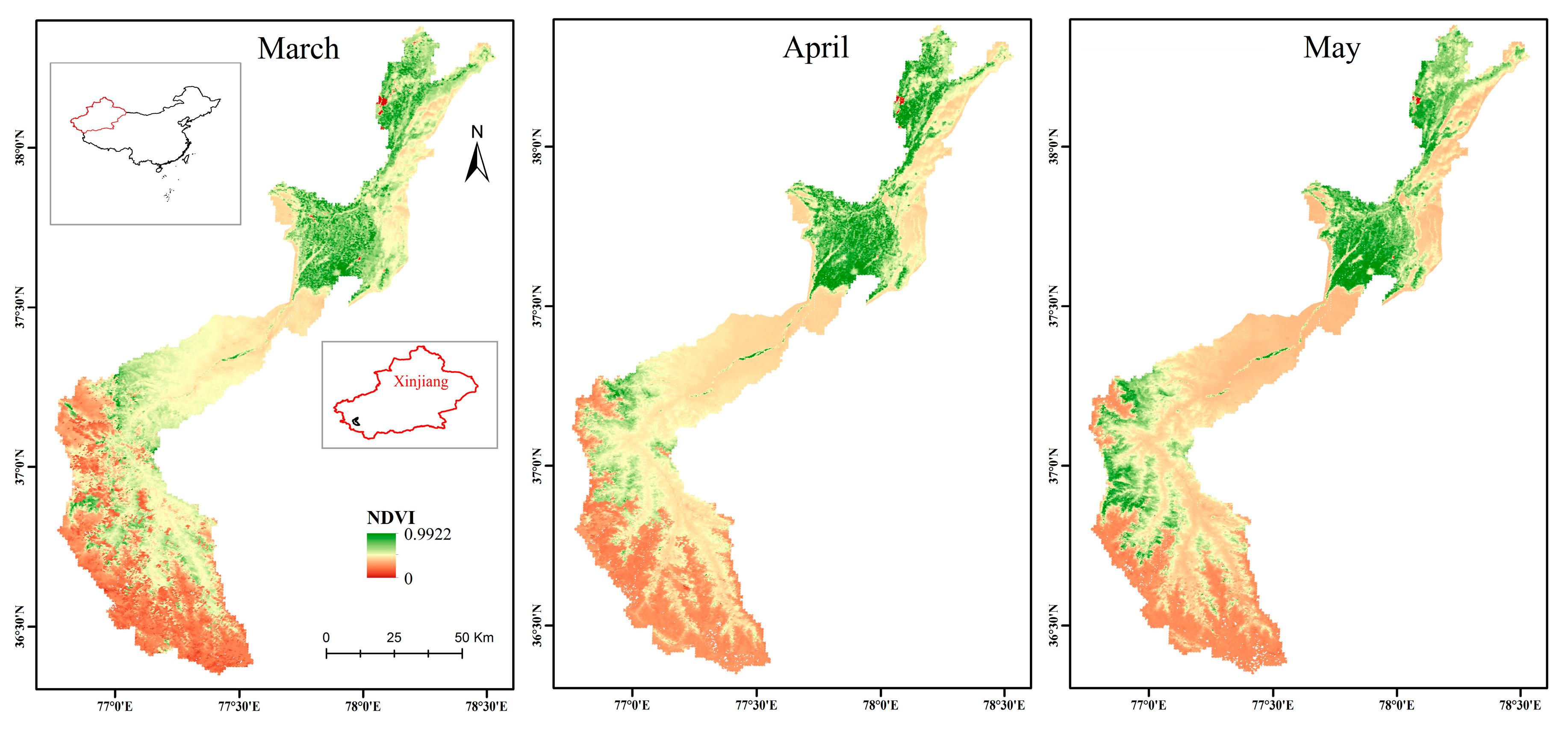
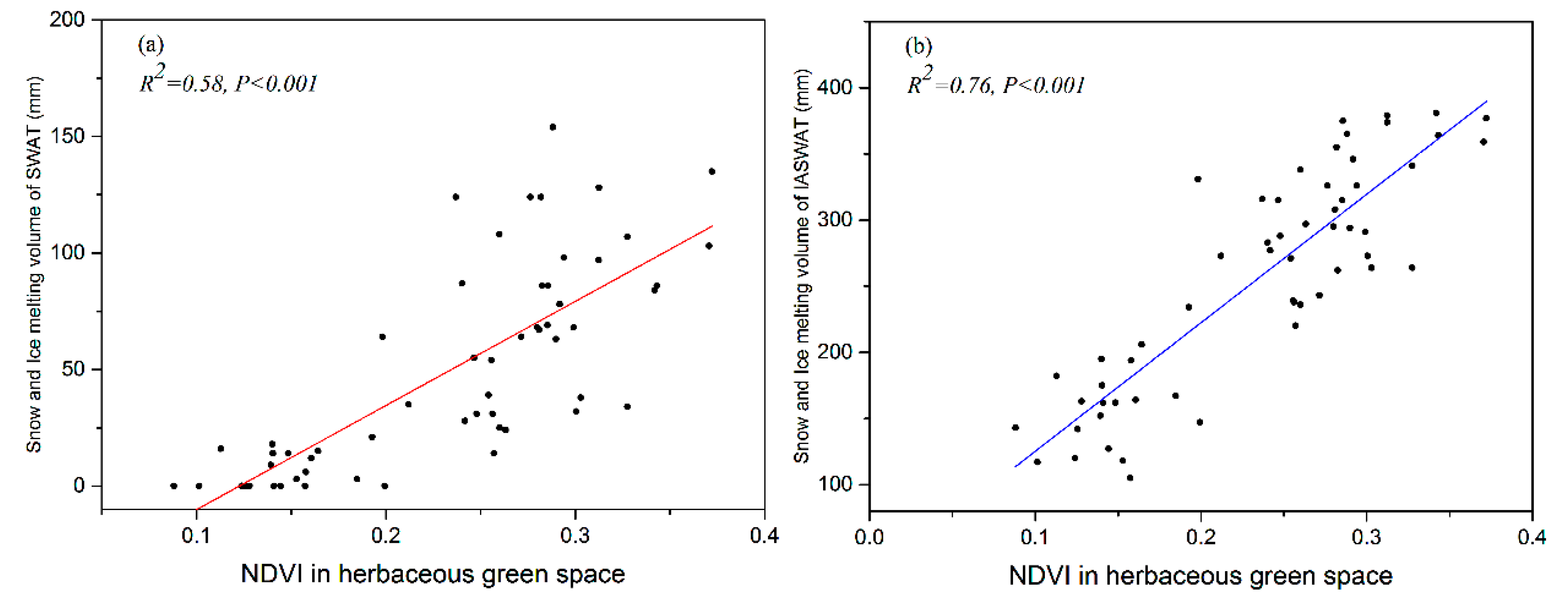
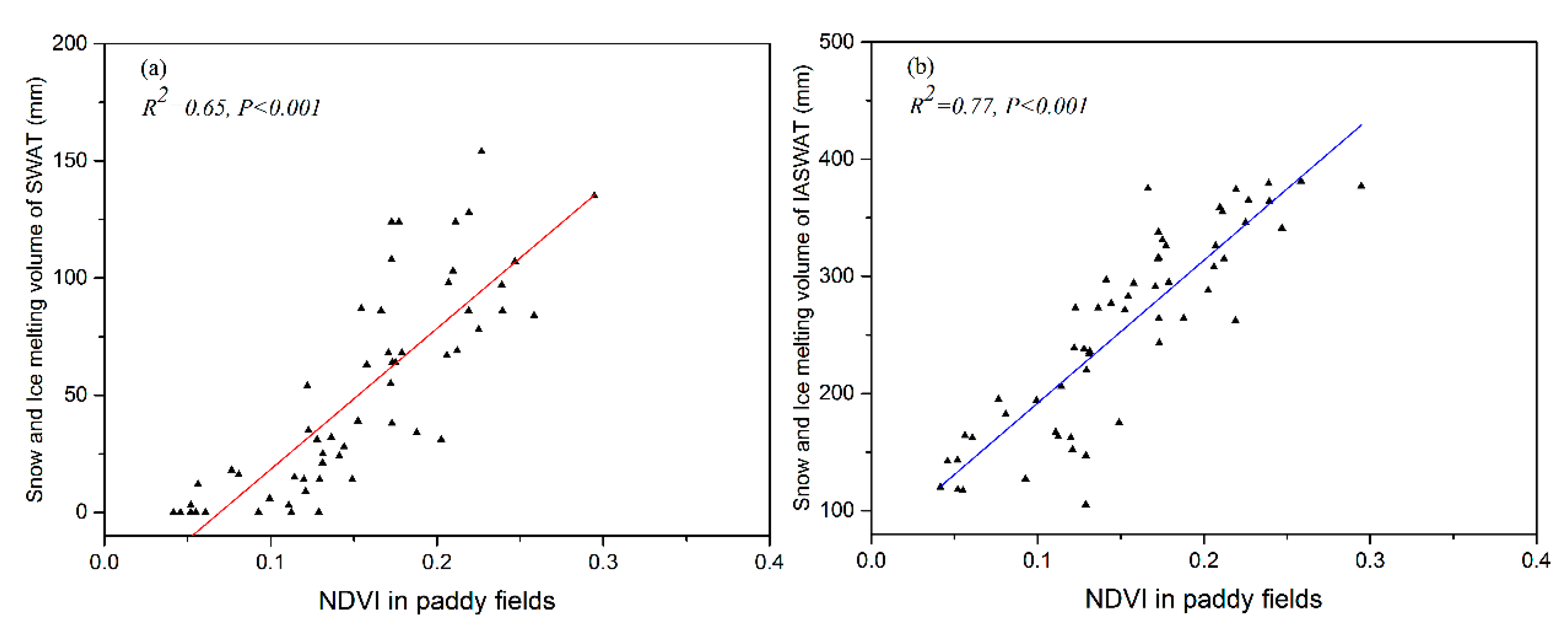
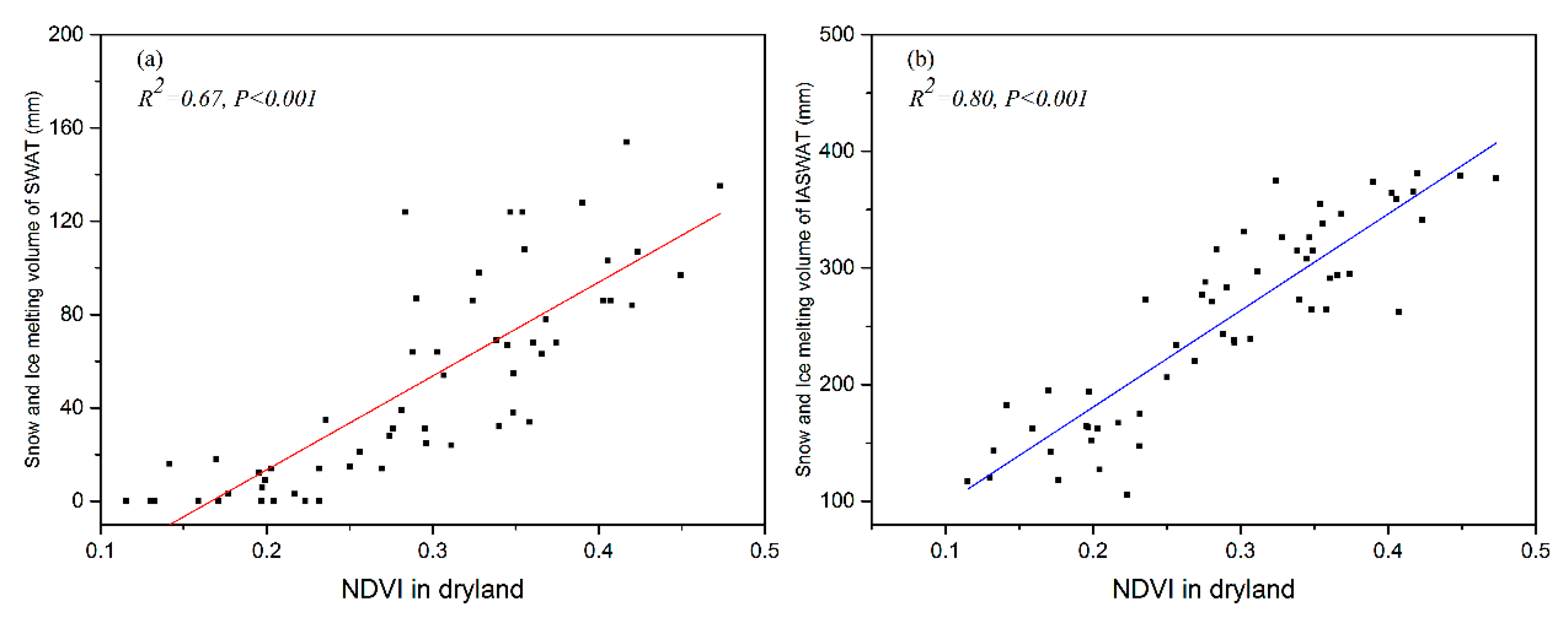
3.4. Relationship between NDVI and Model Modification
4. Discussion
4.1. Model Modification
4.2. Model Performance Comparison
4.3. Analysis of Parameter Sensitivity and Uncertainty
4.4. Relationship Between NDVI and Snow and Ice Melt in Spring
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Campbell, J.L.; Driscoll, C.T.; Pourmokhtarian, A.; Hayhoe, K. Streamflow responses to past and projected future changes in climate at the hubbard brook experimental forest, new hampshire, United States. Water Resour. Res. 2011, 47, 15. [Google Scholar] [CrossRef]
- Fischer, A. Glaciers and climate change: Interpretation of 50 years of direct mass balance of hintereisferner. Glob. Planet. Chang. 2010, 71, 13–26. [Google Scholar] [CrossRef]
- Gaudard, L.; Romerio, F.; Dalla Valle, F.; Gorret, R.; Maran, S.; Ravazzani, G.; Stoffel, M.; Volonterio, M. Climate change impacts on hydropower in the Swiss and Italian alps. Sci. Total Environ. 2014, 493, 1211–1221. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Arnold, J.; Liu, S.Y.; Wang, X.Y.; Chen, X. Inclusion of glacier processes for distributed hydrological modeling at basin scale with application to a watershed in Tianshan mountains, northwest China. J. Hydrol. 2013, 477, 72–85. [Google Scholar] [CrossRef]
- Singh, P.; Bengtsson, L. Impact of warmer climate on melt and evaporation for the rainfed, snowfed and glacierfed basins in the Himalayan region. J. Hydrol. 2005, 300, 140–154. [Google Scholar] [CrossRef]
- Bolch, T. Climate change and glacier retreat in northern Tienshan (Kazakhstan/Kyrgyzstan) using remote sensing data. Glob. Planet. Chang. 2007, 56, 1–12. [Google Scholar] [CrossRef]
- Li, B.L.; Zhu, A.X.; Zhang, Y.C.; Pei, T.; Qin, C.Z.; Zhou, C.H. Glacier change over the past four decades in the middle Chinese Tienshan. J. Glaciol. 2006, 52, 425–432. [Google Scholar] [CrossRef]
- Liu, S.Y.; Ding, Y.J.; Shangguan, D.H.; Zhang, Y.; Li, J.; Han, H.D.; Wang, J.; Xie, C.W. Glacier retreat as a result of climate warming and increased precipitation in the Tarim River basin, northwest China. Ann. Glaciol. 2006, 43, 91–96. [Google Scholar] [CrossRef]
- Liu, Z.F.; Xu, Z.X.; Huang, J.X.; Charles, S.P.; Fu, G.B. Impacts of climate change on hydrological processes in the headwater catchment of the Tarim River basin, China. Hydrol. Process. 2010, 24, 196–208. [Google Scholar] [CrossRef]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M. Precipitation, melt and runoff in the northern Tienshan. J. Hydrol 1996, 186, 229–251. [Google Scholar] [CrossRef]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M.; Dozier, J. Climatic and hydrologic changes in the Tienshan, central Asia. J. Clim. 1997, 10, 1393–1404. [Google Scholar] [CrossRef]
- Aizen, V.B.; Kuzmichenok, V.A.; Surazakov, A.B.; Aizen, E.M. Glacier changes in the Tienshan as determined from topographic and remotely sensed data. Glob. Planet. Chang. 2007, 56, 328–340. [Google Scholar] [CrossRef]
- Xiao, C.D.; Qin, D.H.; Yao, T.D.; Ding, Y.J.; Liu, S.Y.; Zhao, L.; Liu, Y.J. Progress on observation of cryospheric components and climate-related studies in China. Adv. Atmos. Sci. 2008, 25, 164–180. [Google Scholar] [CrossRef]
- Khromova, T.E.; Osipova, G.B.; Tsvetkov, D.G.; Dyurgerov, M.B.; Barry, R.G. Changes in glacier extent in the eastern pamir, central Asia, determined from historical data and aster imagery. Remote Sens. Environ. 2006, 102, 24–32. [Google Scholar] [CrossRef]
- Li, L.; Engelhardt, M.; Xu, C.Y.; Jain, S.K.; Singh, V.P. Comparison of satellite-based and re-analysed precipitation as input to glacio-hydrological modelling for Beas River basin, northern India. In Cold and Mountain Region Hydrological Systems under Climate Change: Towards Improved Projections; International Association of Hydrological Sciences: Wallingford, UK, 2013; Volume 360, pp. 45–52. [Google Scholar]
- Li, Z.Q.; Wang, W.B.; Zhang, M.J.; Wang, F.T.; Li, H.L. Observed changes in streamflow at the headwaters of the Urumqi River, eastern Tianshan, central Asia. Hydrol. Process. 2010, 24, 217–224. [Google Scholar] [CrossRef]
- Liu, L.; Luo, Y.; He, C.S.; Lai, J.B.; Li, X.B. Roles of the combined irrigation, drainage, and storage of the canal network in improving water reuse in the irrigation districts along the lower Yellow River, China. J. Hydrol. 2010, 391, 159–176. [Google Scholar] [CrossRef]
- Narama, C.; Kaab, A.; Duishonakunov, M.; Abdrakhmatov, K. Spatial variability of recent glacier area changes in the Tienshan mountains, central Asia, using corona (similar to 1970), landsat (similar to 2000), and alos (similar to 2007) satellite data. Glob. Planet. Chang. 2010, 71, 42–54. [Google Scholar] [CrossRef]
- Kriegel, D.; Mayer, C.; Hagg, W.; Vorogushyn, S.; Duethmann, D.; Gafurov, A.; Farinotti, D. Changes in glacierisation, climate and runoff in the second half of the 20th century in the Naryn basin, central Asia. Glob. Planet. Chang. 2013, 110, 51–61. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Merz, B.; Vorogushyn, S.; Hartmann, H.; Duethmann, D.; Wortmann, M.; Huang, S.; Su, B.; Jiang, T.; Krysanova, V. Analysis of changes in climate and river discharge with focus on seasonal runoff predictability in the Aksu River basin. Environ. Earth Sci. 2015, 73, 501–516. [Google Scholar] [CrossRef]
- Fontaine, T.A.; Cruickshank, T.S.; Arnold, J.G.; Hotchkiss, R.H. Development of a snowfall-snowmelt routine for mountainous terrain for the soil water assessment tool (swat). J. Hydrol. 2002, 262, 209–223. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.D.; Shea, J.M.; Hutchinson, D.; Cannon, A.J. Coupled modelling of glacier and streamflow response to future climate scenarios. Water Resour. Res. 2008, 44, 13. [Google Scholar] [CrossRef]
- Andreassen, L.M.; Elvehoy, H.; Kjollmoen, B.; Engeset, R.V.; Haakensen, N. Glacier mass-balance and length variation in Norway. Ann. Glaciol. 2005, 42, 317–325. [Google Scholar] [CrossRef]
- Andreassen, L.M.; Oerlemans, J. Modelling long-term summer and winter balances and the climate sensitivity of Storbreen, Norway. Geogr. Ann. Ser. Phys. Geogr. 2009, 91, 233–251. [Google Scholar] [CrossRef]
- Andreassen, L.M.; Van den Broeke, M.R.; Giesen, R.H.; Oerlemans, J. A 5 year record of surface energy and mass balance from the ablation zone of Storbreen, Norway. J. Glaciol. 2008, 54, 245–258. [Google Scholar] [CrossRef]
- Kutuzov, S.; Shahgedanova, M. Glacier retreat and climatic variability in the eastern Terskey-Alatoo, inner Tienshan between the middle of the 19th century and beginning of the 21st century. Glob. Planet. Chang. 2009, 69, 59–70. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Rossow, W.B.; Lacis, A.A.; Oinas, V.; Mishchenko, M.I. Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets: Refinements of the radiative transfer model and the input data. J. Geophys. Res. Atmos. 2004, 109, 27. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Stewart, I.T.; Maurer, E.P. Effects of projected climate change on the hydrology in the mono lake basin, California. Clim. Chang. 2013, 116, 111–131. [Google Scholar] [CrossRef]
- Finger, D.; Heinrich, G.; Gobiet, A.; Bauder, A. Projections of future water resources and their uncertainty in a glacierized catchment in the Swiss alps and the subsequent effects on hydropower production during the 21st century. Water Resour. Res. 2012, 48, 20. [Google Scholar] [CrossRef]
- Gan, R.; Luo, Y. Using the nonlinear aquifer storage-discharge relationship to simulate the base flow of glacier- and snowmelt-dominated basins in northwest China. Hydrol. Earth Syst. Sci. 2013, 17, 3577–3586. [Google Scholar] [CrossRef]
- Hagg, W.; Hoelzle, M.; Wagner, S.; Mayr, E.; Klose, Z. Glacier and runoff changes in the Rukhk catchment, upper Amu-Darya basin until 2050. Glob. Planet. Chang. 2013, 110, 62–73. [Google Scholar] [CrossRef]
- Spruill, C.A.; Workman, S.R.; Taraba, J.L. Simulation of daily and monthly stream discharge from small watersheds using the swat model. Trans. ASAE 2000, 43, 1431–1439. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. Swat: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. Swat2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Zhang, X.S.; Srinivasan, R.; Debele, B.; Hao, F.H. Runoff simulation of the headwaters of the Yellow River using the swat model with three snowmelt algorithms. J. Am. Water Resour. Assoc. 2008, 44, 48–61. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B. Using discrete wavelet transforms to analyze trends in streamflow and precipitation in Quebec and Ontario (1954–2008). J. Hydrol. 2012, 475, 204–228. [Google Scholar] [CrossRef]
- Osmonov, A.; Bolch, T.; Xi, C.; Kurban, A.; Guo, W.Q. Glacier characteristics and changes in the sary-jaz river basin (central Tienshan, Kyrgyzstan)-1990–2010. Remote Sens. Lett. 2013, 4, 725–734. [Google Scholar] [CrossRef]
- Pandey, P.; Venkataraman, G. Changes in the glaciers of Chandrabhaga basin, Himachal Himalaya, India, between 1980 and 2010 measured using remote sensing. Int. J. Remote Sens. 2013, 34, 5584–5597. [Google Scholar] [CrossRef]
- Wang, H.J.; Chen, Y.N.; Li, W.H.; Deng, H.J. Runoff responses to climate change in arid region of northwestern china during 1960-2010. Chin. Geogr. Sci. 2013, 23, 286–300. [Google Scholar] [CrossRef]
- Xu, X.K.; Pan, B.L.; Hu, E.; Li, Y.J.; Liang, Y.H. Responses of two branches of glacier no. 1 to climate change from 1993 to 2005, Tian Shan, China. Quat. Int. 2011, 236, 143–150. [Google Scholar] [CrossRef]
- Engelhardt, M.; Schuler, T.V.; Andreassen, L.M. Glacier mass balance of Norway 1961-2010 calculated by a temperature-index model. Ann. Glaciol. 2013, 54, 32–40. [Google Scholar] [CrossRef]
- Hirabayashi, Y.; Doll, P.; Kanae, S. Global-scale modeling of glacier mass balances for water resources assessments: Glacier mass changes between 1948 and 2006. J. Hydrol. 2010, 390, 245–256. [Google Scholar] [CrossRef]
- Shang, X.; Wang, X.; Zhang, D.; Chen, W.; Chen, X.; Kong, H. An improved swat-based computational framework for identifying critical source areas for agricultural pollution at the lake basin scale. Ecol. Model. 2012, 226, 1–10. [Google Scholar] [CrossRef]
- Strauch, M.; Volk, M. Swat plant growth modification for improved modeling of perennial vegetation in the tropics. Ecol. Model. 2013, 269, 98–112. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, J.; Shao, Q.; Zhai, X. Water quantity and quality simulation by improved swat in highly regulated Huai River basin of China. Stoch. Environ. Res. Risk Assess. 2013, 27, 11–27. [Google Scholar] [CrossRef]
- Wang, X.L.; Luo, Y.; Sun, L.; Zhang, Y.Q. Assessing the effects of precipitation and temperature changes on hydrological processes in a glacier-dominated catchment. Hydrol. Process. 2015, 29, 4830–4845. [Google Scholar] [CrossRef]
- Gan, R.; Luo, Y.; Zuo, Q.; Sun, L. Effects of projected climate change on the glacier and runoff generation in the Naryn River basin, central Asia. J. Hydrol. 2015, 523, 240–251. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, T.; Meng, F.; Luo, M.; Frankl, A.; De Maeyer, P.; Bao, A.; Kurban, A.; Feng, X. Inclusion of modified snow melting and flood processes in the swat model. Water 2018, 10, 1715. [Google Scholar] [CrossRef]
- Vigiak, O.; Malagó, A.; Bouraoui, F.; Vanmaercke, M.; Obreja, F.; Poesen, J.; Habersack, H.; Fehér,, J.; Grošelj, S. Modelling sediment fluxes in the Danube River Basin with SWAT. Sci. Total Environ. 2017, 599, 992–1012. [Google Scholar]
- Vilaysane, B.; Takara, K.; Luo, P.; Akkharath, I.; Duan, W. Hydrological stream flow modelling for calibration and uncertainty analysis using swat model in the Xedone River basin, Lao PDR. Procedia Environ. Sci. 2015, 28, 380–390. [Google Scholar] [CrossRef]
- Khalid, K.; Ali, M.F.; Rahman, N.F.A.; Mispan, M.R.; Haron, S.H.; Othman, Z.; Bachok, M.F. Sensitivity analysis in watershed model using sufi-2 algorithm. Procedia Eng. 2016, 162, 441–447. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, J.; Yang, M.; Lei, X.; Guo, B.; Yang, L.; Zeng, Z.; Qu, J. Application of swat model with CMADS data to estimate hydrological elements and parameter uncertainty based on sufi-2 algorithm in the Lijiang River basin, China. Water 2018, 10, 742. [Google Scholar] [CrossRef]
- Wu, H.; Chen, B. Evaluating uncertainty estimates in distributed hydrological modeling for the Wenjing River watershed in China by glue, sufi-2, and parasol methods. Ecol. Eng. 2015, 76, 110–121. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a swat application to the Chaohe basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Setegn, S.G.; Srinivasan, R.; Melesse, A.M.; Dargahi, B. Swat model application and prediction uncertainty analysis in the lake Tana basin, Ethiopia. Hydrol. Process. Int. J. 2010, 24, 357–367. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Tsanis, I.K.; Koutroulis, A.G. Application of the HBV hydrological model in a flash flood case in Slovenia. Nat. Hazards Earth Syst. Sci. 2010, 10, 2713–2725. [Google Scholar] [CrossRef]
- Sicart, J.E.; Hock, R.; Six, D. Glacier melt, air temperature, and energy balance in different climates: The Bolivian tropics, the French alps, and northern Sweden. J. Geophys. Res. Atmos. 2008, 113, 11. [Google Scholar] [CrossRef]
- Ohmura, A. Physical basis for the temperature-based melt-index method. J. Appl. Meteorol. 2001, 40, 753–761. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Ye, B.S.; Liu, S.Y.; Zhang, X.W.; Hagemann, S. A modified monthly degree-day model for evaluating glacier runoff changes in China. Part i: Model development. Hydrol. Process. 2012, 26, 1686–1696. [Google Scholar] [CrossRef]
- Zhao, Q.D.; Ye, B.S.; Ding, Y.J.; Zhang, S.Q.; Yi, S.H.; Wang, J.; Shangguan, D.H.; Zhao, C.C.; Han, H.D. Coupling a glacier melt model to the variable infiltration capacity (Vic) model for hydrological modeling in north-western China. Environ. Earth Sci. 2013, 68, 87–101. [Google Scholar] [CrossRef]
- Duan, Y.; Meng, F.; Liu, T.; Huang, Y.; Luo, M.; Xing, W.; De Maeyer, P. Sub-daily simulation of mountain flood processes based on the modified soil water assessment tool (swat) model. Int. J. Environ. Res. Public Health 2019, 16, 3118. [Google Scholar] [CrossRef] [PubMed]
- Fujita, K.; Ageta, Y. Effect of summer accumulation on glacier mass balance on the Tibetan plateau revealed by mass-balance model. J. Glaciol. 2000, 46, 244–252. [Google Scholar] [CrossRef]
- Khadka, D.; Babel, M.S.; Shrestha, S.; Tripathi, N.K. Climate change impact on glacier and snow melt and runoff in Tamakoshi basin in the Hindu Kush Himalayan (HKH) region. J. Hydrol. 2014, 511, 49–60. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, S.K.; Srivastava, P.K.; Narsimlu, B. Environment. Swat model calibration and uncertainty analysis for streamflow prediction of the tons river basin, India, using sequential uncertainty fitting (sufi-2) algorithm. Model. Earth Syst. Environ. 2017, 3, 30. [Google Scholar] [CrossRef]
- Zheng, Z.; Wenxi, L.U.; Chu, H.B.; Cheng, W.G.; Ying, Z. Uncertainty analysis of hydrological model parameters based on the bootstrap method: A case study of the swat model applied to the Dongliao River watershed, Jilin province, northeastern China. Sci. China Technol. Sci. 2014, 57, 219–229. [Google Scholar] [CrossRef]
- Houser, J.B.; Hauck, L.M.; Saleh, A. Modifying and validating the SWAT model to determine landuse effects on watershed water quality: using a dual level of model performance based on subbasin size. Int. J. Environ. Res. 2015, 9, 885–896. [Google Scholar]
- Strauch, M.; Bernhofer, C.; Koide, S.; Volk, M.; Lorz, C.; Makeschin, F. Using precipitation data ensemble for uncertainty analysis in swat streamflow simulation. J. Hydrol. 2012, 414, 413–424. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C. Calibration and uncertainty issues of a hydrological model (swat) applied to west Africa. Adv. Geosci. 2006, 9, 137–143. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Shao, Q.; Yang, J. Parameter estimation and uncertainty analysis of swat model in upper reaches of the Heihe River basin. Hydrol. Process. Int. J. 2009, 23, 2744–2753. [Google Scholar] [CrossRef]
- Talebizadeh, M.; Morid, S.; Ayyoubzadeh, S.A.; Ghasemzadeh, M. Uncertainty analysis in sediment load modeling using Ann and swat model. Water Resour. Manag. 2010, 24, 1747–1761. [Google Scholar] [CrossRef]
- Mu, Z.-X.; Jiang, H.-F.; Liu, F. Spatial and temporal variations of snow cover area and Ndvi in the west of Tianshan mountains. J. Glaciol. Geocryol. 2010, 32, 875–882. [Google Scholar]
- Gamon, J.A.; Huemmrich, K.F.; Stone, R.S.; Tweedie, C.E. Spatial and temporal variation in primary productivity (NDVI) of coastal Alaskan tundra: Decreased vegetation growth following earlier snowmelt. Remote Sens. Environ. 2013, 129, 144–153. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, L.; Qiu, Y.; Ji, L.; Tian, F.; Wang, C.; Wang, Z. Snow effects on alpine vegetation in the Qinghai-Tibetan plateau. Int. J. Digit. Earth 2015, 8, 58–75. [Google Scholar] [CrossRef]
- Buma, B. Evaluating the utility and seasonality of ndvi values for assessing post-disturbance recovery in a subalpine forest. Environ. Monit. Assess. 2012, 184, 3849–3860. [Google Scholar] [CrossRef]
- Delbart, N.; Kergoat, L.; Le Toan, T.; Lhermitte, J.; Picard, G. Determination of phenological dates in boreal regions using normalized difference water index. Remote Sens. Environ. 2005, 97, 26–38. [Google Scholar] [CrossRef]
- Duan, H.; Yan, C.; Tsunekawa, A.; Song, X.; Li, S.; Xie, J. Assessing vegetation dynamics in the three-north shelter forest region of China using AVHRR NDVI data. Environ. Earth Sci. 2011, 64, 1011–1020. [Google Scholar] [CrossRef]
- Ward, D.H.; Helmericks, J.; Hupp, J.W.; McManus, L.; Budde, M.; Douglas, D.C.; Tape, K.D. Multi-decadal trends in spring arrival of avian migrants to the central arctic coast of Alaska: Effects of environmental and ecological factors. J. Avian Biol. 2016, 47, 197–207. [Google Scholar] [CrossRef]
- Zhao, X.Y. Evaluation of agricultural landform types in Yecheng County, Xinjiang. Arid Land Geogr. 1994, 3, 59–65. [Google Scholar]
- Balati, M. Present situation analysis and Prospect of facility agriculture in yecheng County, Xinjiang. Agric. Sci. 2015, 6, 123–124. [Google Scholar]


| LUCC | Area (km2) | Percentage (%) |
|---|---|---|
| Glacier and snowfield | 469.96 | 8.35 |
| Bare soil | 815.54 | 14.49 |
| Bare rock | 324.38 | 5.77 |
| Meadow | 1249.17 | 22.20 |
| Sparse grass | 1324.22 | 23.54 |
| River | 69.67 | 1.24 |
| Marsh | 5.65 | 0.10 |
| Evergreen coniferous shrub | 3.98 | 0.07 |
| Grassland | 1202.74 | 21.38 |
| Broadleaved deciduous forest | 3.49 | 0.06 |
| Evergreen needleleaved forest | 138.68 | 2.46 |
| Dryland | 17.42 | 0.31 |
| Settlement place | 1.51 | 0.03 |
| Period | R2 | NSE | PBIAS (%) | |||
|---|---|---|---|---|---|---|
| SWAT | SWATAI | SWAT | SWATAI | SWAT | SWATAI | |
| Calibration (2013) | 0.80 | 0.87 | 0.73 | 0.77 | 5.42 | 4.55 |
| Validation (2014) | 0.78 | 0.84 | 0.71 | 0.75 | −6.89 | 4.85 |
| Overall (2013–2014) | 0.77 | 0.82 | 0.69 | 0.74 | 8.65 | 5.42 |
| Date | Deviation of Flood Peak Value (m3·s−1) | Deviation of Timing (h) | ||
|---|---|---|---|---|
| SWAT | SWATAI | SWAT | SWATAI | |
| 2013.5 | 14.52 | 3.88 | 7 | 0 |
| 2013.6 | 63.13 | 8.83 | 8 | −1 |
| 2013.7 | 14.33 | 11.59 | 3 | −1 |
| 2013.8 | 57.05 | 9.7 | −1 | 0 |
| 2013.9 | −2.88 | −2.16 | 2 | 1 |
| 2014.5 | 52.7 | 5.04 | −8 | 2 |
| 2014.6 | 11.23 | 4.37 | −6 | 0 |
| 2014.7 | 26.25 | −2.29 | 0 | 0 |
| 2014.8 | 96.05 | 26.94 | −2 | 1 |
| 2014.9 | −10.15 | −3.03 | 4 | −1 |
| File Extension | Parameter | Description | Range of Values | Daily Simulation Calibrated Value | Sub-daily Simulation calibrated Value |
|---|---|---|---|---|---|
| .bsn(New) | ETSI | Elevation threshold between snow and ice | 2000–6000 | 3500 | 3500 |
| .bsn(New) | IMTP | Ice-melt base temperature | −40 | 5.39 | 5.87 |
| .bsn(New) | IMTP_A | Ice-melt base accumulated temperature | 0–40 | 24.68 | 26.77 |
| .bsn(New) | IMFMX | Maximum melt rate for ice during the year | 0–20 | 12.35 | 13.04 |
| .bsn(New) | IMFMN | Minimum melt rate for ice during the year | 0–20 | 15.87 | 16.55 |
| .bsn(New) | ITIMP | Ice temperature lag factor | 0–1 | 0.61 | 0.65 |
| .bsn(New) | SFTMP_A | Snowfall accumulated temperature | 0–40 | 28 | 29 |
| .bsn | SFTMP | Snowfall temperature | −20 to 20 | 3.27 | 3.46 |
| .bsn | SMTMP | Snow-melt base temperature | −20 to 20 | 3.06 | 2.85 |
| .bsn | SMFMX | Maximum melt rate for snow during the year | 0–20 | 7.62 | 7.57 |
| .bsn | SMFMN | Minimum melt rate for snow during the year | 0–20 | 9.4 | 8.19 |
| .bsn | TIMP | Snowpack temperature lag factor | 0–1 | 0.55 | 0.54 |
| .bsn | SNOCOVMX | Minimum snow water content corresponding to 100% snow cover | 0–500 | 38.33 | 37.84 |
| .bsn | SFTMP | Snowfall temperature | −40 | 3.36 | 3.47 |
| .bsn | SURLAG | Surface runoff lag time | 0.05–24 | 11.78 | 11.43 |
| .gw | ALPHA_BF | Base flow alpha factor (days) | 0–1 | 0.15 | 0.18 |
| .gw | GW_DELAY | Groundwater delay (days) | 0–500 | 222.68 | 224.12 |
| .gw | GWQMN | Threshold water depth in the shallow aquifer required for return flow to occur (mm) | 0–5000 | 1175.84 | 1205.64 |
| .gw | SHALLST | Initial water depth in the shallow aquifer (mm) | 0–50,000 | 4903.68 | 4958.74 |
| .gw | GW_REVAP | Groundwater “revamp” coefficient | 0.02–0.2 | 0.06 | 0.05 |
| .mgt | CN2 | SCS runoff curve number | 35–98 | 70.79 | 72.35 |
| .ohru | OV_N | Manning’s “n” value for overland flow | 0.01–30 | 10.77 | 11.12 |
| .ohru | ESCO | Soil evaporation compensation factor | 0–1 | 0.37 | 0.35 |
| .ohru | EPCO | Plant uptake compensation factor | 0–1 | 0.39 | 0.32 |
| .rte | CH_N2 | Manning’s “n” value for the main channel | −0.01 to 0.3 | 0.01 | 0.01 |
| .rte | CH_K2 | Effective hydraulic conductivity in main channel alluvium | −0.01 to 500 | 47.38 | 48.12 |
| .sol | SOL_K | Saturated hydraulic conductivity | 0–2000 | 861.31 | 874.58 |
| .sol | SOL_AWC | Available water capacity of the soil layer | 0–1 | 0.32 | 0.36 |
| .sub | PLAPS | Precipitation lapse rate | −20 to 20 | −5.5 | −5.36 |
| .sub | TLAPS | Temperature lapse rate | −10 to 10 | −7.59 | −7.64 |
| .sub | CH_N1 | Manning’s “n” value for the tributary channels | 0.01–30 | 5.42 | 5.13 |
| .sub | CH_K1 | Effective hydraulic conductivity in tributary channel alluvium | 0–300 | 295.67 | 271.36 |
| .sub | SNO_SUB | Initial snow water content | 0–150 | 95.39 | 97.33 |
| Parameter | T-states | p-Value |
|---|---|---|
| CH_K2 | 21.67 | 0 |
| PLAPS | 18.53 | 0 |
| IMTP_A | 12.06 | 0 |
| SMTMP | 10.98 | 0.01 |
| TLAPS | 9.76 | 0.01 |
| IMTP | 9.05 | 0.01 |
| ETSI | 8.25 | 0.01 |
| LAT_TTIME | 6.89 | 0.02 |
| SMFMX | 6.05 | 0.02 |
| SOL_K | 5.36 | 0.03 |
| IMFMX | 5.09 | 0.03 |
| SOL_AWC | 4.68 | 0.05 |
| IMFMN | 4.47 | 0.05 |
| SURLAG | 3.28 | 0.06 |
| TIMP | 2.64 | 0.17 |
| ITIMP | 2.36 | 0.18 |
| GWQMN | 1.49 | 0.26 |
| SNO_SUB | 1.05 | 0.34 |
| REVAPMN | 1.01 | 0.57 |
| EPCO | 0.72 | 0.64 |
| SMFMN | 0.43 | 0.79 |
| CH_N2 | 0.38 | 0.82 |
| RCHRG_DP(Deep aquifer percolation fraction) | 0.21 | 0.89 |
| OV_N | −0.02 | 0.91 |
| CH_N1 | −0.57 | 0.71 |
| SNOCOVMX | −1.05 | 0.53 |
| SHALLST | −1.24 | 0.51 |
| ALPHA_BF | −2.49 | 0.43 |
| CN2 | −3.07 | 0.39 |
| CH_K1 | −3.14 | 0.34 |
| SFTMP | −3.88 | 0.26 |
| GW_DELAY | −4.01 | 0.14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Y.; Liu, T.; Meng, F.; Yuan, Y.; Luo, M.; Huang, Y.; Xing, W.; Nzabarinda, V.; De Maeyer, P. Accurate Simulation of Ice and Snow Runoff for the Mountainous Terrain of the Kunlun Mountains, China. Remote Sens. 2020, 12, 179. https://doi.org/10.3390/rs12010179
Duan Y, Liu T, Meng F, Yuan Y, Luo M, Huang Y, Xing W, Nzabarinda V, De Maeyer P. Accurate Simulation of Ice and Snow Runoff for the Mountainous Terrain of the Kunlun Mountains, China. Remote Sensing. 2020; 12(1):179. https://doi.org/10.3390/rs12010179
Chicago/Turabian StyleDuan, Yongchao, Tie Liu, Fanhao Meng, Ye Yuan, Min Luo, Yue Huang, Wei Xing, Vincent Nzabarinda, and Philippe De Maeyer. 2020. "Accurate Simulation of Ice and Snow Runoff for the Mountainous Terrain of the Kunlun Mountains, China" Remote Sensing 12, no. 1: 179. https://doi.org/10.3390/rs12010179
APA StyleDuan, Y., Liu, T., Meng, F., Yuan, Y., Luo, M., Huang, Y., Xing, W., Nzabarinda, V., & De Maeyer, P. (2020). Accurate Simulation of Ice and Snow Runoff for the Mountainous Terrain of the Kunlun Mountains, China. Remote Sensing, 12(1), 179. https://doi.org/10.3390/rs12010179








