Semi-Supervised Hyperspectral Image Classification via Spatial-Regulated Self-Training
Abstract
1. Introduction
- We have introduced a novel semi-supervised classification algorithm for HSIc based on the cooperation between deep learning models and clustering.
- Adjacent pixels in a hyperspectral image may belong to the same class. We introduce a spatial constraint in the above algorithm to give a smoothness hypothesis to improve HSIc accuracy.
- Compared with previous methods, our proposed approach has achieved competitive performance on HSIc while leveraging tiny labeled data.
2. Related Work
2.1. Hyperspectral Image Classification
2.2. Semi-Supervised Learning
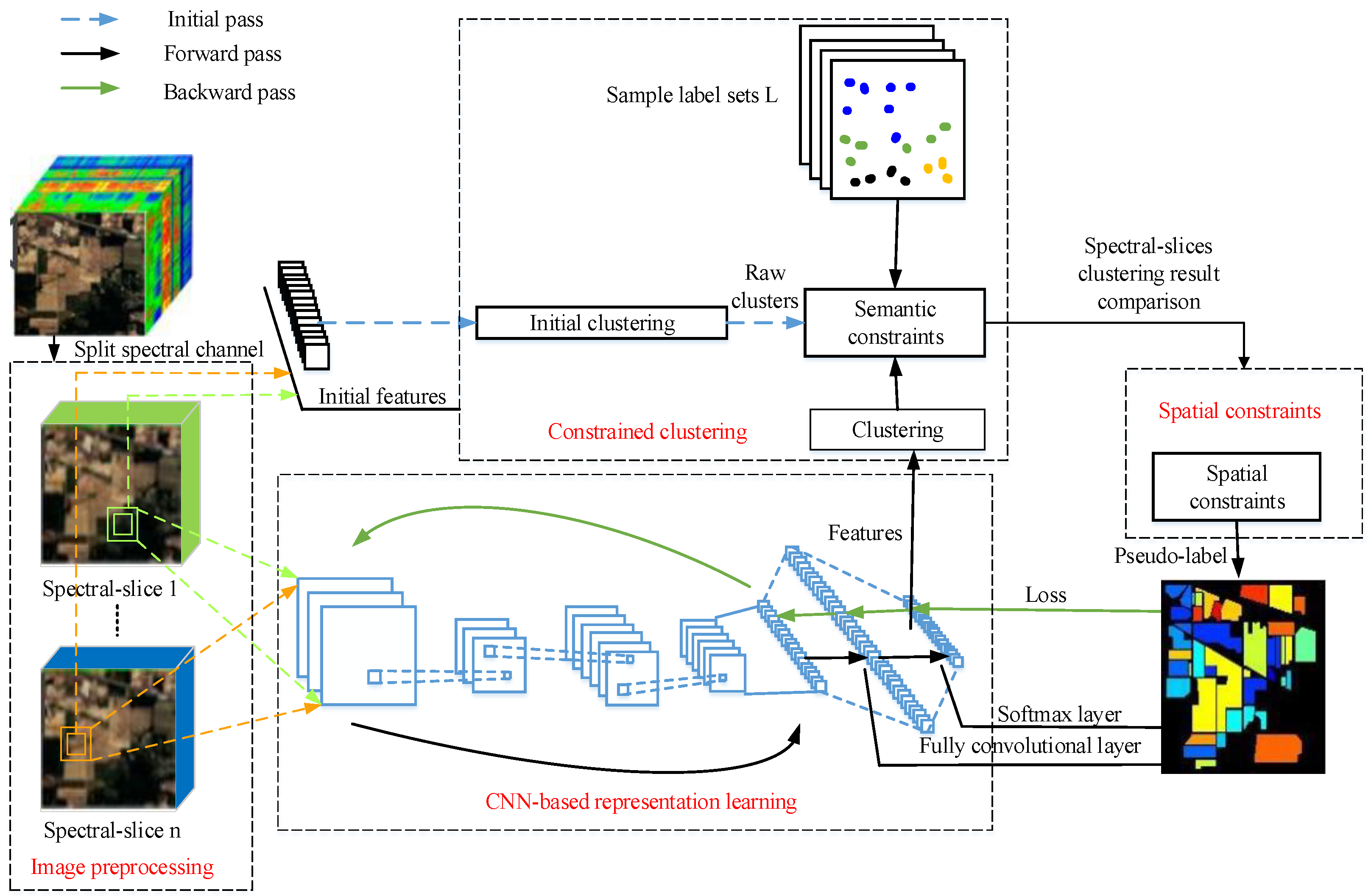
3. Proposed Method
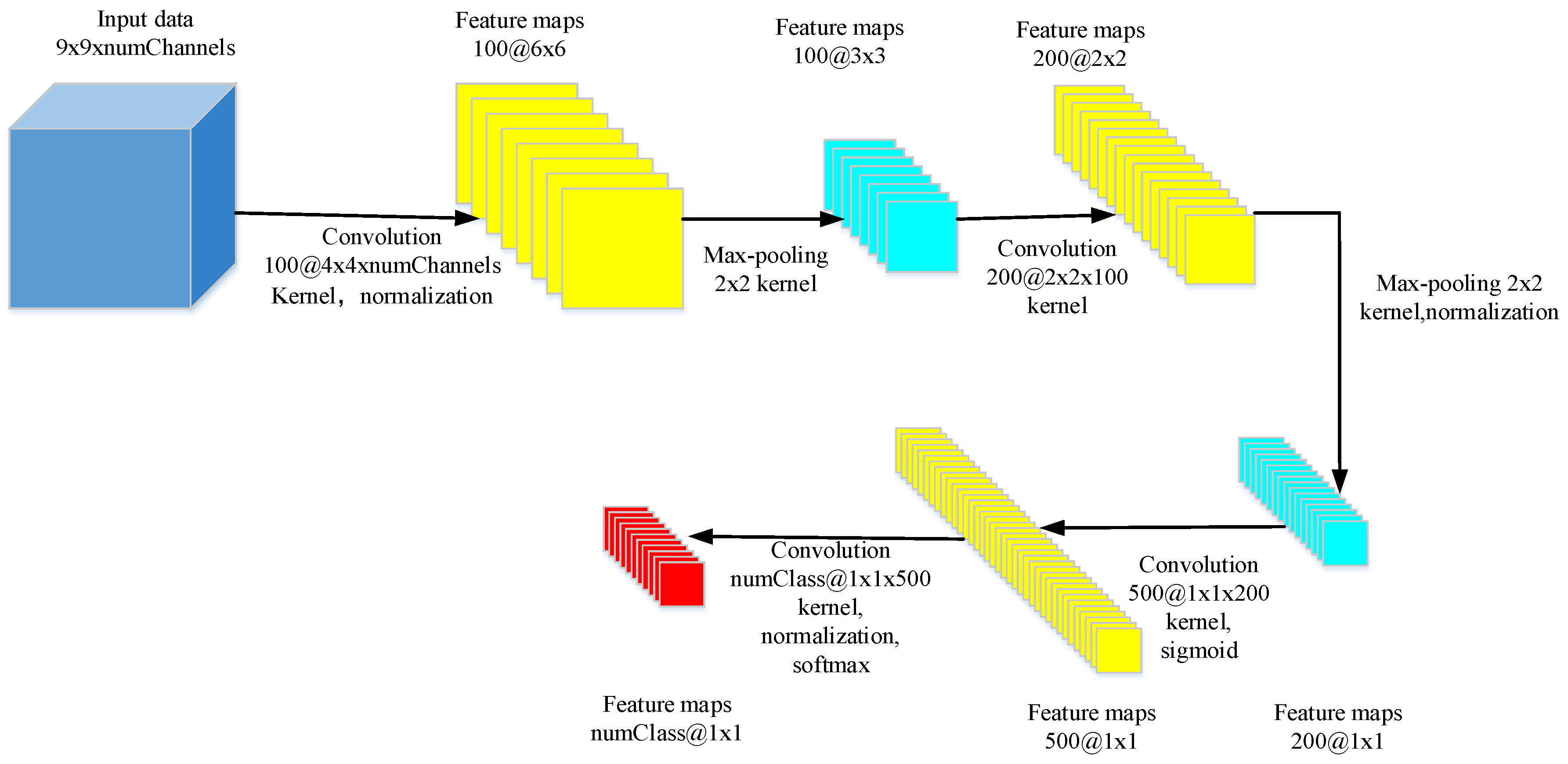
3.1. Feature Extraction Based on CNN Representation Learning
Network Structure
3.2. Classification Processing
3.2.1. Constraints Based on Semantic Information
3.2.2. Sample Confidence Calculation
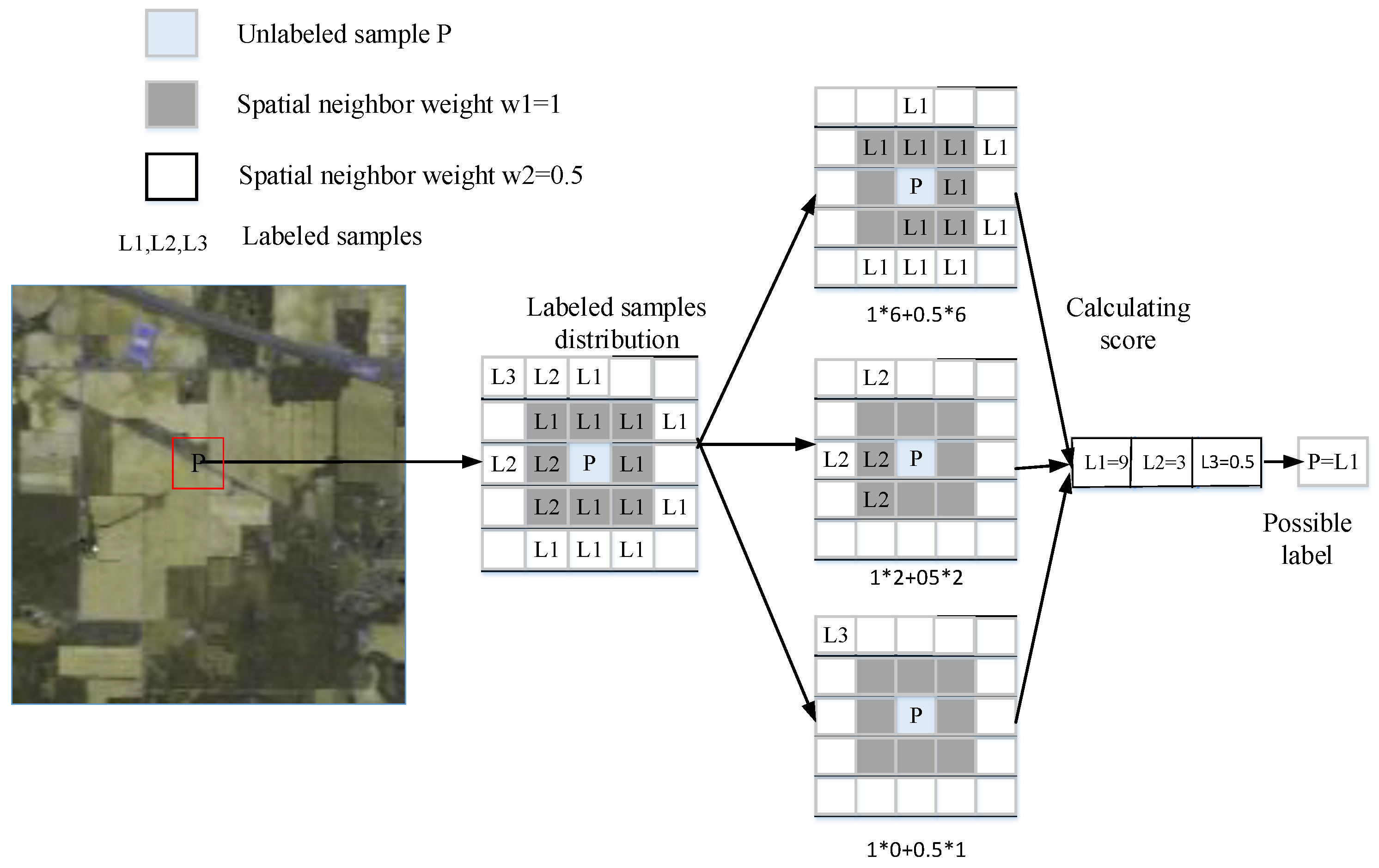
3.2.3. Constraints Based on Neighborhood Spatial Information
3.2.4. Iteration Process Based on Self-Training
| Algorithm 1 HSIc algorithm based on self-training |
|
4. Experimental Results
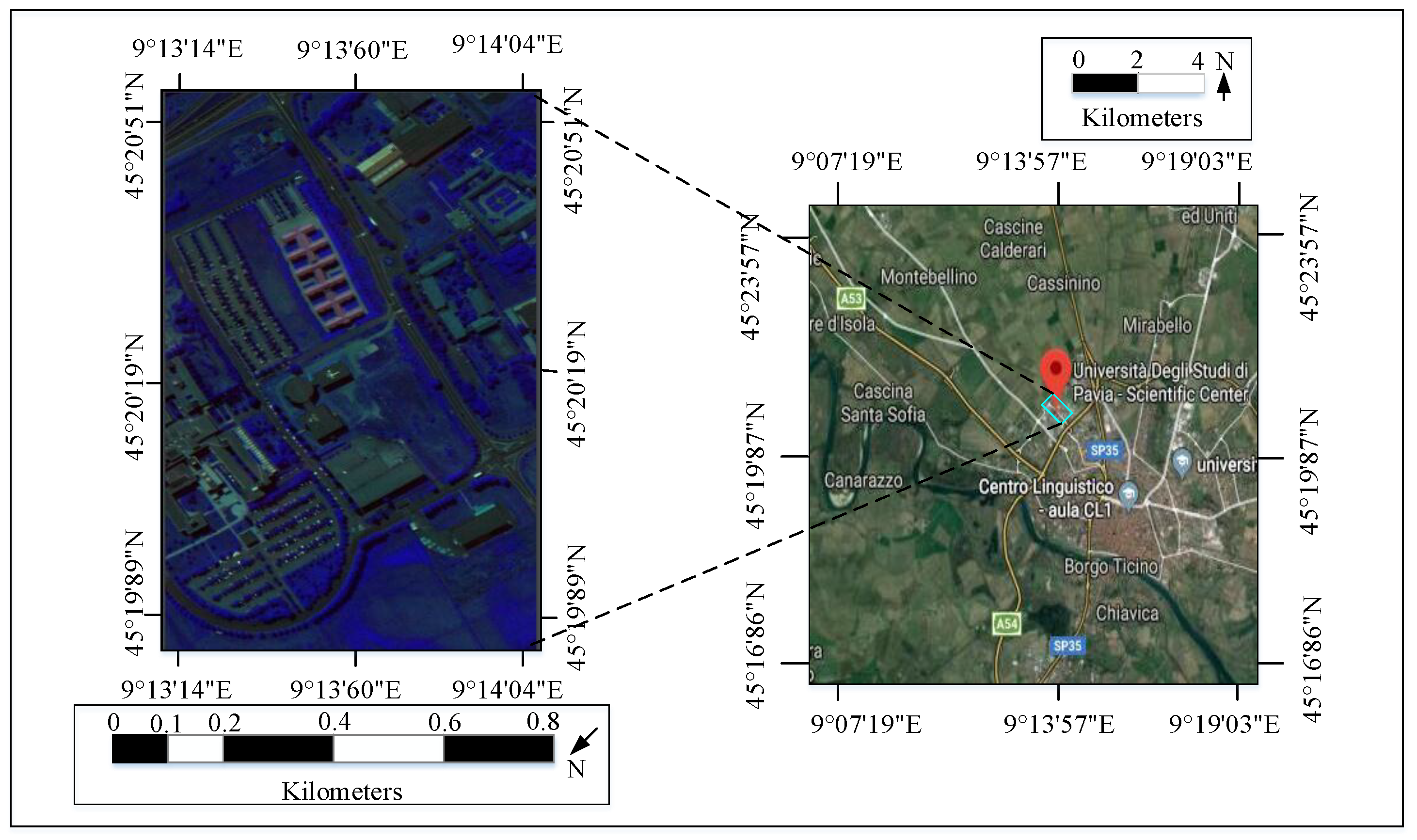
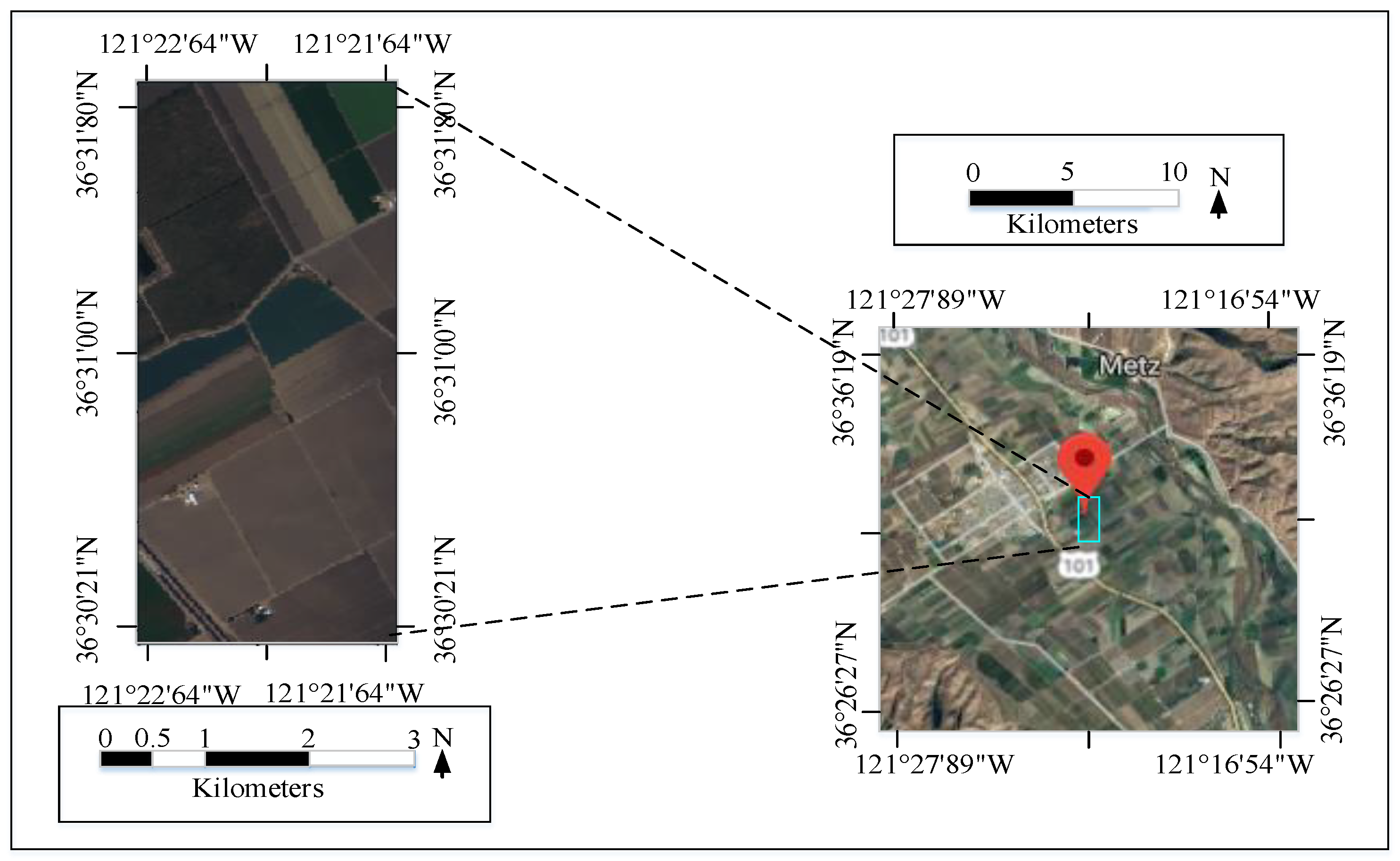
4.1. Data Sets
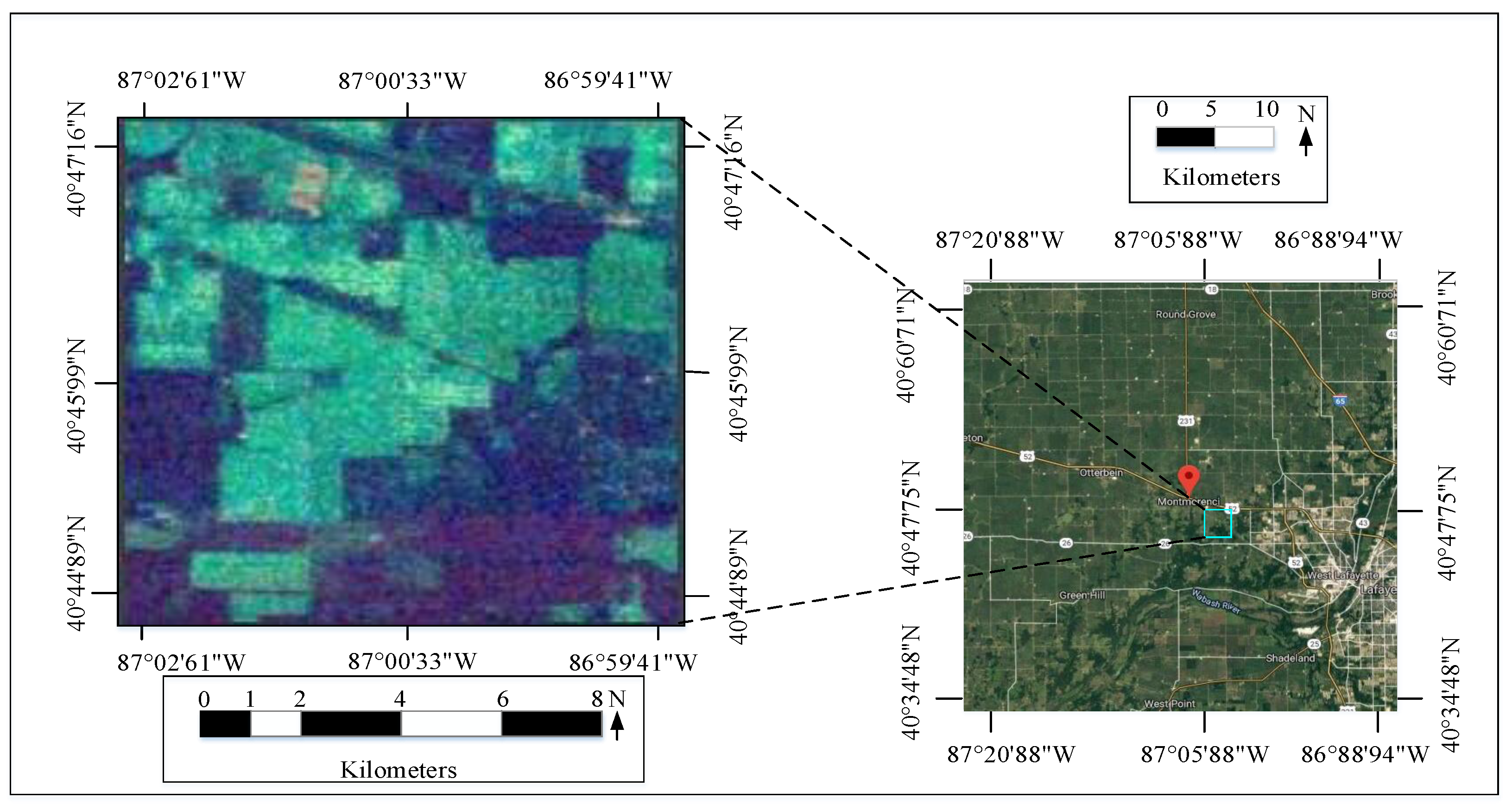
4.1.1. Indian Pines Data Set
4.1.2. Pavia University Data Set
4.1.3. Salinas Scene Data Set
4.2. Experimental Design
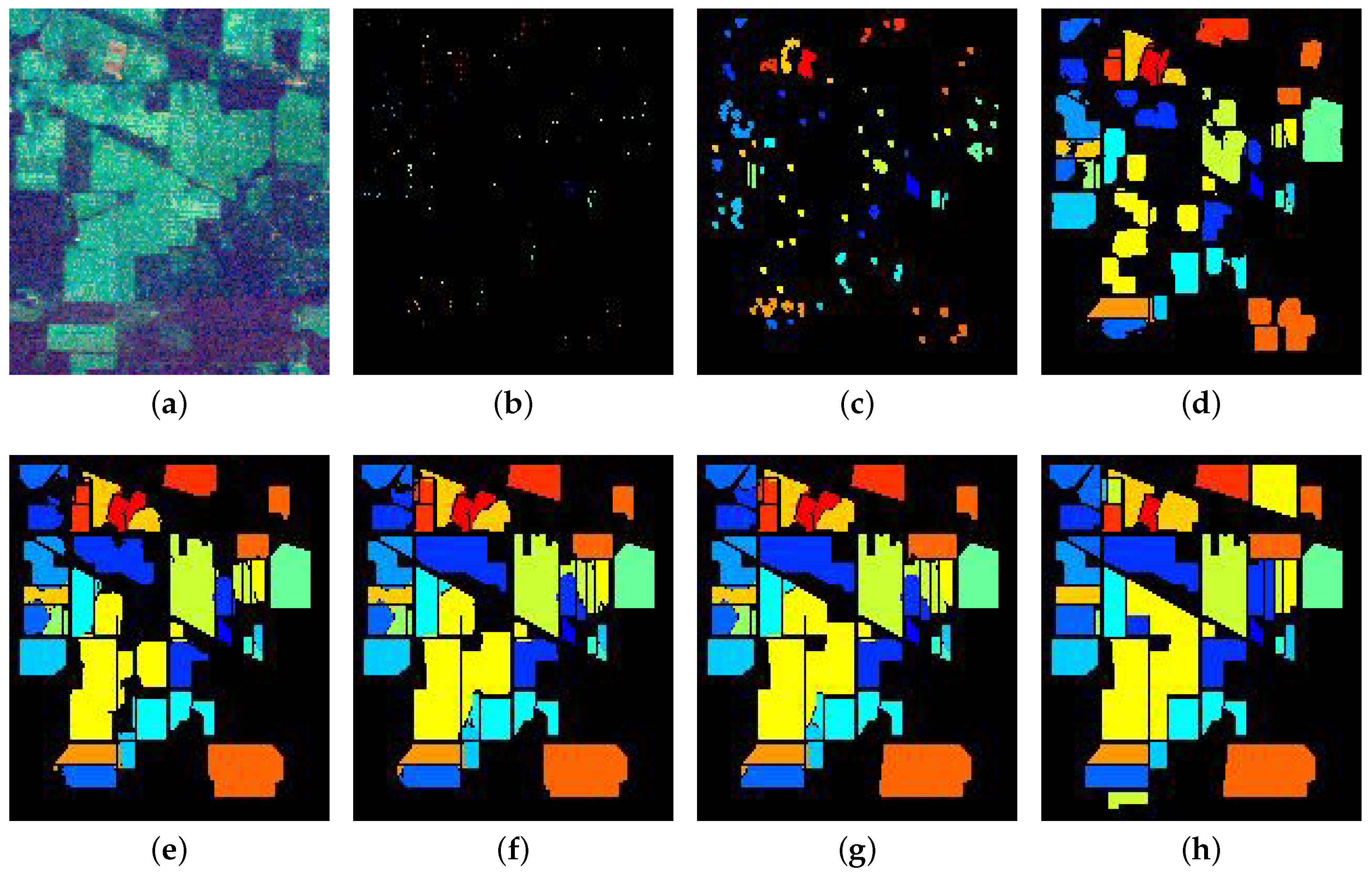
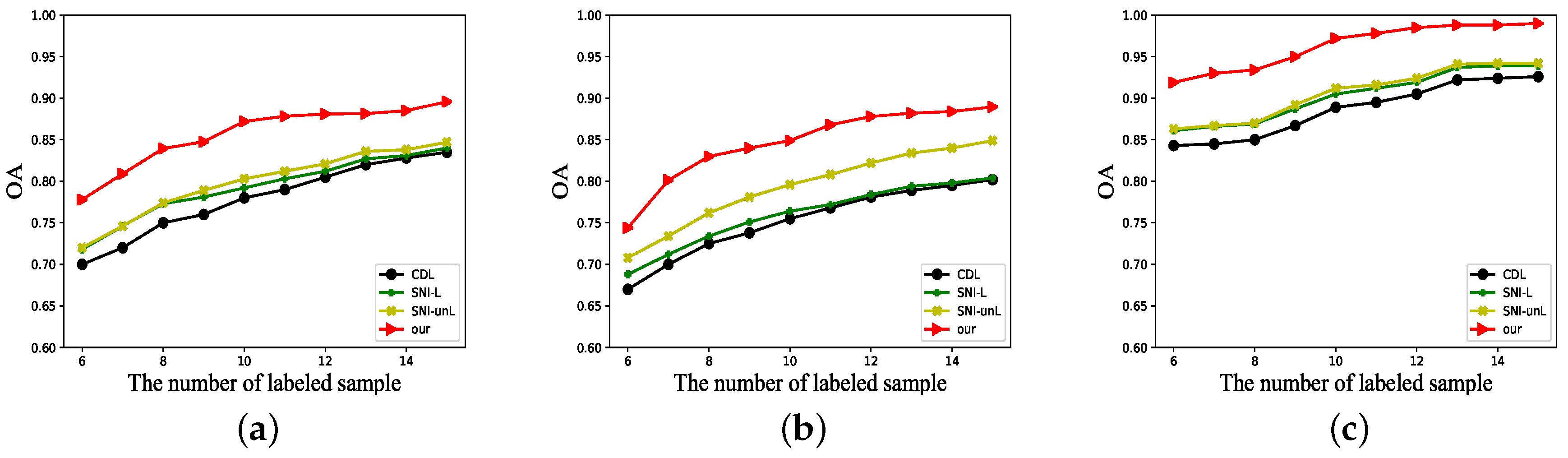
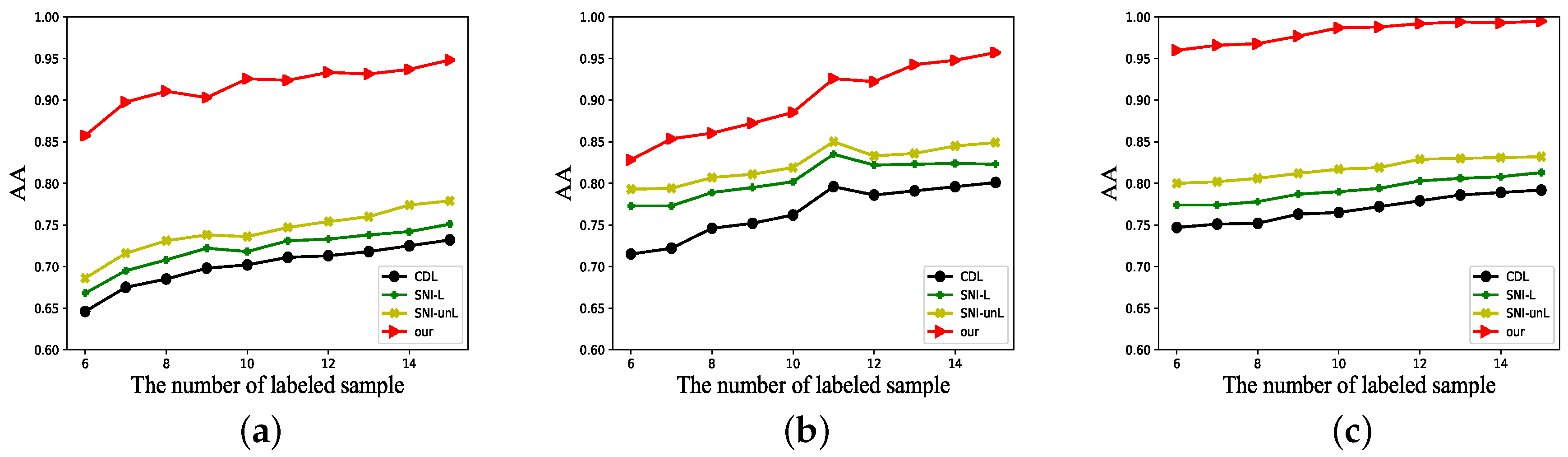
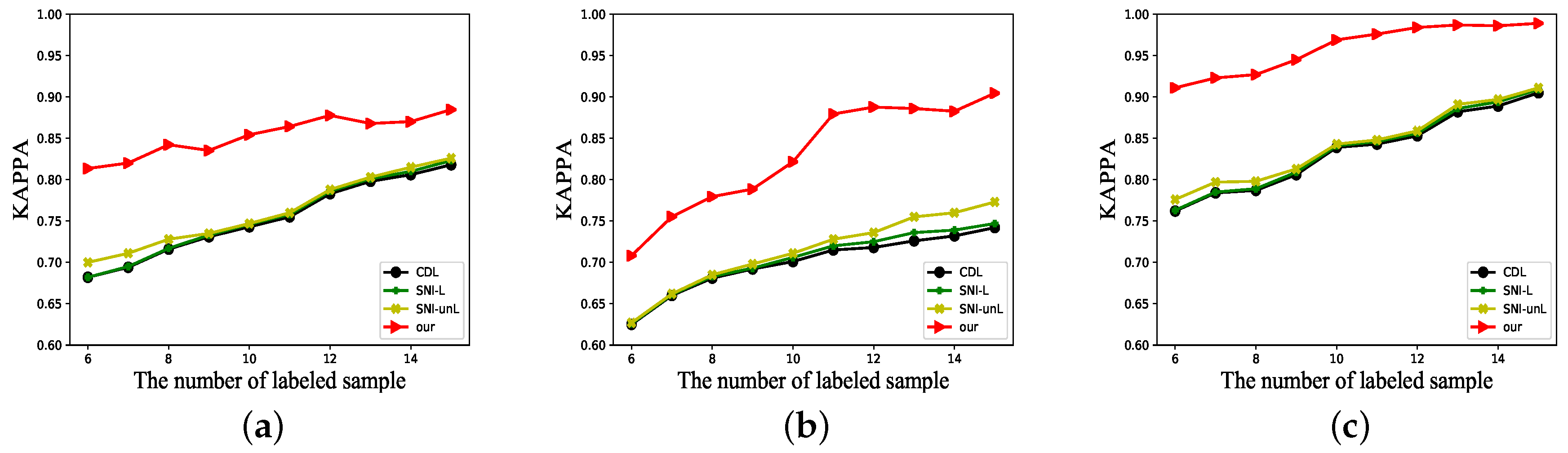
4.3. Experimental Result
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiang, J.; Chen, C.; Yu, Y.; Jiang, X.; Ma, J. Spatial-aware Collaborative Representation for Hyperspectral Remote Sensing Image Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 404–408. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Wang, Z.; Chen, C.; Liu, X. Hyperspectral Image Classification in the Presence of Noisy Labels. IEEE Trans. Geosci. Remote Sens. 2018, 57, 851–865. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Zhang, J.; An, J.; Li, C.; Gao, L. Hyperspectral Image Classification Based on Long Short Term Memory Network. In Proceedings of the Fifth International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Xi’an, China, 18–20 June 2018; pp. 1–5. [Google Scholar]
- Matsuki, T.; Yokoya, N.; Iwasaki, A. Hyperspectral Tree Species Classification of Japanese Complex Mixed Forest With the Aid of LiDAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2177–2187. [Google Scholar] [CrossRef]
- Shafri, H.Z.; Taherzadeh, E.; Mansor, S.; Ashurov, R. Hyperspectral Remote Sensing of Urban Areas: An Overview of Techniques and Applications. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 1557–1565. [Google Scholar]
- Wu, Y.; Ma, W.; Gong, M.; Su, L.; Jiao, L. A Novel Point-Matching Algorithm Based on Fast Sample Consensus for Image Registration. IEEE Geosci. Remote. Sens. Lett. 2014, 12, 43–47. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, W.; Gong, M.; Li, H.; Jiao, L. Novel Fuzzy Active Contour Model with Kernel Metric for Image Segmentation. Appl. Soft Comput. 2015, 34, 301–311. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, W.; Miao, Q.; Wang, S. Multimodal Continuous ant Colony Optimization for Multisensor Remote Sensing Image Registration with Local Search. Swarm Evol. Comput. 2017, 47, 89–95. [Google Scholar] [CrossRef]
- An, J.; Lei, J.; Song, Y.; Zhang, X.; Guo, J. Tensor Based Multiscale Low Rank Decomposition for Hyperspectral Images Dimensionality Reduction. Remote Sens. 2019, 11, 1485. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Y.; Huyan, N.; Li, C.; Feng, J.; Gao, L.; Ma, X. Spatial-Spectral Graph-Based Nonlinear Embedding Dimensionality Reduction for Hyperspectral Image Classificaiton. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 8472–8475. [Google Scholar]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-based Edge-preserving Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A Superpixelwise PCA Approach for Unsupervised Feature Extraction of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1–13. [Google Scholar] [CrossRef]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral Image Classification With Independent Component Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Zhou, P.; Han, J.; Cheng, G.; Zhang, B. Learning Compact and Discriminative Stacked Autoencoder for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4823–4833. [Google Scholar] [CrossRef]
- Abdel-Zaher, A.M.; Eldeib, A.M. Breast Cancer Classification using Deep Belief Networks. Expert Syst. Appl. 2016, 46, 139–144. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Zhang, X.; Li, X.; An, J.; Gao, L.; Hou, B.; Li, C. Natural Language Description of Remote Sensing Images Based on Deep Learning. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4798–4801. [Google Scholar]
- Pleva, M.; Liao, Y.F.; Hsu, W.; Hladek, D.; Stas, J.; Viszlay, P.; Lojka, M.; Juhar, J. Towards Slovak-English-Mandarin Speech Recognition Using Deep Learning. In Proceedings of the International Symposium ELMAR, Zadar, Croatia, 16–19 September 2018; pp. 151–154. [Google Scholar]
- Ma, X.; Wang, H.; Wang, J. Semisupervised Classification for Hyperspectral Image Based on Multi-Decision Labeling and Deep Feature Learning. J. Photogram. Remote Sens. 2016, 120, 99–107. [Google Scholar] [CrossRef]
- Duan, P.; Kang, X.; Li, S.; Benediktsson, J.A. Multi-Scale Structure Extraction for Hyperspectral Image Classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 5724–5727. [Google Scholar]
- Senthilnath, J.; Kulkarni, S.; Benediktsson, J.A.; Yang, X.S. A Novel Approach for Multispectral Satellite Image Classification Based on the Bat Algorithm. IEEE Geosci. Remote Sens. Lett. 2016, 13, 599–603. [Google Scholar] [CrossRef]
- Essa, A.; Sidike, P.; Asari, V. Volumetric Directional Pattern for Spatial Feature Extraction in Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1056–1060. [Google Scholar] [CrossRef]
- Sidike, P.; Chen, C.; Asari, V.; Xu, Y.; Li, W. Classification of hyperspectral image using multiscale spatial texture features. In Proceedings of the Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–4. [Google Scholar]
- Lee, H.; Kwon, H. Going Deeper with Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-Spatial Classification of Hyperspectral Imagery Using a Dual-Channel Convolutional Neural Network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Ma, W.; Yang, Q.; Wu, Y.; Zhao, W.; Zhang, X. Double-Branch Multi-Attention Mechanism Network for Hyperspectral Image Classification. Remote Sens. 2019, 11, 1307. [Google Scholar] [CrossRef]
- Cao, J.; Chen, Z.; Wang, B. Deep Convolutional Networks with Superpixel Segmentation for Hyperspectral Image Classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3310–3313. [Google Scholar]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Learning and Transferring Deep Joint Spectral–Spatial Features for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Meer, F.D.V.D.; Werff, H.M.A.V.D.; Ruitenbeek, F.J.A.V.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; Meijde, M.V.D.; Carranza, E.J.M.; Smeth, J.B.D.; Woldai, T. Multi- and Hyperspectral Geologic Remote Sensing: A Review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; An, Z.; Jiang, Z.; Ma, Y. A Novel Spectral-Unmixing-Based Green Algae Area Estimation Method for GOCI Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 437–449. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of Hyperspectral Remote Sensing Images with Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM-and MRF-based Method for Accurate Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in Hyperspectral Image Classification: Earth Monitoring with Statistical Learning Methods. IEEE Signal Process. Mag. 2013, 31, 45–54. [Google Scholar] [CrossRef]
- Acquarelli, J.; Marchiori, E.; Buydens, L.M.; Tran, T.; van Laarhoven, T. Convolutional Neural Networks and Data Augmentation for Spectral-Spatial Classification of Hyperspectral Images. Networks 2017, 16, 21. [Google Scholar]
- Chen, C.; Ma, Y.; Ren, G. A Convolutional Neural Network with Fletcher–Reeves Algorithm for Hyperspectral Image Classification. Remote Sens. 2019, 11, 1325. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep Supervised Learning for Hyperspectral Data Classification through Convolutional Neural Networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Wang, Z.; Du, B.; Zhang, L.; Zhang, L.; Jia, X. A Novel Semisupervised Active-Learning Algorithm for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3071–3083. [Google Scholar] [CrossRef]
- Tran, T.N.; Wehrens, R.; Hoekman, D.H.; Buydens, L.M. Initialization of Markov Random Field Clustering of Large Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1912–1919. [Google Scholar] [CrossRef]
- Cao, X.; Xu, Z.; Meng, D. Spectral-Spatial Hyperspectral Image Classification via Robust Low-Rank Feature Extraction and Markov Random Field. Remote Sens. 2019, 11, 1565. [Google Scholar] [CrossRef]
- Lu, T.; Li, S.; Fang, L.; Jia, X.; Benediktsson, J.A. From Subpixel to Superpixel: A NovelFfusion Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4398–4411. [Google Scholar] [CrossRef]
- Ma, X.; Geng, J.; Wang, H. Hyperspectral Image Classification via Contextual Deep Learning. EURASIP J. Image Video Process. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Dópido, I.; Li, J.; Marpu, P.R.; Plaza, A.; Dias, J.M.B.; Benediktsson, J.A. Semisupervised Self-Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4032–4044. [Google Scholar] [CrossRef]
- Tan, K.; Hu, J.; Li, J.; Du, P. A Novel Semi-supervised Hyperspectral Image Classification Approach Based on Spatial Neighborhood Information and Classifier Combination. ISPRS J. Photogramm. Remote Sens. 2015, 105, 19–29. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. 1977, 39, 1–38. [Google Scholar]
- Bruzzone, L.; Chi, M.; Marconcini, M. Transductive SVMs for Semisupervised Classification of Hyperspectral Data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, Korea, 29 July 2005; Volume 1, pp. 164–167. [Google Scholar]
- Camps-Valls, G.; Marsheva, T.V.B.; Zhou, D. Semi-Supervised Graph-Based Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3044–3054. [Google Scholar] [CrossRef]
- Li, F.; Clausi, D.A.; Xu, L.; Wong, A. ST-IRGS: A Region-based Self-training Algorithm Applied to Hyperspectral Image Classification and Segmentation. IEEE Trans. Geosci. Remote Sens. 2017, 56, 3–16. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Qin, C.; Gong, M.; Wu, Y.; Tian, D.; Zhang, P. Efficient Scene Labeling via Sparse Annotations. In Proceedings of the Workshops at the Thirty-Second AAAI Conference on Artificial Intelligenc, Hilton New Orleans Riverside, New Orleans, LA, USA, 2–3 February 2018; pp. 194–201. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-propagating Errors. Cogn. Model. 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Viera, A.J.; Garrett, J.M. Understanding Interobserver Agreement: The Kappa Statistic. Family Med. 2005, 37, 360–363. [Google Scholar]


| Serial Number | Colour | Class | Sample Number | Serial Number | Colour | Class | Sample Number |
|---|---|---|---|---|---|---|---|
| 1 |  | Alfalfa | 54 | 9 |  | Oats | 20 |
| 2 |  | Corn-notill | 1434 | 10 |  | Soybean-notill | 968 |
| 3 |  | Corn-mintill | 834 | 11 |  | Soybean-mintill | 2468 |
| 4 |  | Corn | 234 | 12 |  | Soybean-clean | 614 |
| 5 |  | Grass/pasture | 497 | 13 |  | Wheat | 212 |
| 6 |  | Grass/tree | 747 | 14 |  | Woods | 1294 |
| 7 |  | Grass/pasture/mowed | 26 | 15 |  | Buildings/grass/trees/drives | 95 |
| 8 |  | Hay/windrowed | 489 | 16 |  | Stone/steel/towers | 380 |
| Serial Number | Colour | Class | Sample Number | Serial Number | Colour | Class | Sample Number |
|---|---|---|---|---|---|---|---|
| 1 |  | Asphalt | 6548 | 6 |  | Bare soil | 5029 |
| 2 |  | Meadows | 18652 | 7 |  | Bitumen | 1330 |
| 3 |  | Gravel | 2099 | 8 |  | Self-blocking bricks | 3682 |
| 4 |  | Trees | 3064 | 9 |  | Shadows | 947 |
| 5 |  | Painted metal sheets | 1365 |
| Serial Number | Colour | Class | Sample Number | Serial Number | Colour | Class | Sample Number |
|---|---|---|---|---|---|---|---|
| 1 |  | Brocoli_green_weeds_1 | 2009 | 9 |  | Soil_vinyard_develop | 6203 |
| 2 |  | Brocoli_green_weeds_2 | 3726 | 10 |  | Corn_senesced_green_weeds | 3278 |
| 3 |  | Fallow | 1976 | 11 |  | Lettuce_romaine_4wk | 1068 |
| 4 |  | Fallow_rough_plow | 1394 | 12 |  | Lettuce_romaine_5wk | 1927 |
| 5 |  | Fallow_smooth | 2678 | 13 |  | Lettuce_romaine_6wk | 916 |
| 6 |  | Stubble | 3959 | 14 |  | Lettuce_romaine_7wk | 1070 |
| 7 |  | Celery | 3579 | 15 |  | Vinyard_untrained | 7268 |
| 8 |  | Grapes_untrained | 11271 | 16 |  | Vinyard_vertical_trellis | 1807 |
| Data | First | Third | Fifth | Seventh | Ninth | Variance |
|---|---|---|---|---|---|---|
| Indian Pines | 23.25% | 72.73% | 81.57% | 85.45% | 86.42% | 0.03% |
| Pavia University | 12.30% | 55.23% | 70.36% | 78.88% | 81.69% | 0.17% |
| Salinas Scene | 39.91% | 82.81% | 89.04% | 92.66% | 93.97% | 0.005% |
| Data | Measurement | CDL | SNI-L | SNI-unL | Our Method |
|---|---|---|---|---|---|
| Indian Pines | OA | 0.7751 ± 0.0270 | 0.7881 ± 0.0220 | 0.8062 ± 0.0270 | 0.8755 ± 0.0126 |
| AA | 0.7751 ± 0.0270 | 0.7757 ± 0.0223 | 0.7753 ± 0.0350 | 0.9237 ± 0.0057 | |
| Kappa | 0.7496 ± 0.0300 | 0.7818 ± 0.0200 | 0.7818 ± 0.0300 | 0.8608 ± 0.0138 | |
| Pavia University | OA | 0.7508 ± 0.0304 | 0.7556 ± 0.0471 | 0.7872 ± 0.0425 | 0.8178 ± 0.0372 |
| AA | 0.7508 ± 0.0304 | 0.7841 ± 0.0258 | 0.8031 ± 0.0302 | 0.8835 ± 0.0283 | |
| Kappa | 0.6910 ± 0.0300 | 0.6981 ± 0.0500 | 0.7341 | 0.7759 ± 0.0429 | |
| Salinas Scene | OA | 0.8890 ± 0.0230 | 0.9050 ± 0.0210 | 0.9120 ± 0.0240 | 0.9733 ± 0.0061 |
| AA | 0.7650 ± 0.0130 | 0.7900 ± 0.0121 | 0.8170 ± 0.0170 | 0.9878 ± 0.0023 | |
| Kappa | 0.8390 ± 0.0110 | 0.8410 ± 0.0100 | 0.8430 ± 0.0170 | 0.9704 ± 0.0067 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Mu, G.; Qin, C.; Miao, Q.; Ma, W.; Zhang, X. Semi-Supervised Hyperspectral Image Classification via Spatial-Regulated Self-Training. Remote Sens. 2020, 12, 159. https://doi.org/10.3390/rs12010159
Wu Y, Mu G, Qin C, Miao Q, Ma W, Zhang X. Semi-Supervised Hyperspectral Image Classification via Spatial-Regulated Self-Training. Remote Sensing. 2020; 12(1):159. https://doi.org/10.3390/rs12010159
Chicago/Turabian StyleWu, Yue, Guifeng Mu, Can Qin, Qiguang Miao, Wenping Ma, and Xiangrong Zhang. 2020. "Semi-Supervised Hyperspectral Image Classification via Spatial-Regulated Self-Training" Remote Sensing 12, no. 1: 159. https://doi.org/10.3390/rs12010159
APA StyleWu, Y., Mu, G., Qin, C., Miao, Q., Ma, W., & Zhang, X. (2020). Semi-Supervised Hyperspectral Image Classification via Spatial-Regulated Self-Training. Remote Sensing, 12(1), 159. https://doi.org/10.3390/rs12010159








