1. Introduction
Hyperspectral Imaging (HSI) is a technological tool which takes into account a wide spectrum of light instead of just primary colors such as red, green, and blue to characterize a pixel [
1,
2]. The light striking a pixel, indeed, is divided into many different spectral bands to provide more information on what is imaged. HSI has been adopted in a wide range of real-world applications including biomedical imaging, geosciences, and surveillance to mention a few [
3]. One of the main challenges in the HSI domain is the management of the data, which typically yields hundreds of contiguous and narrow spectral bands with very high spatial resolution throughout the electromagnetic spectrum [
2,
4]. Therefore, HSI classification is complex and can be dominated by a multitude of urban classes and nested regions, than the traditional monochrome or RGB images [
5].
Supervised classification methods are widely adopted in the analysis of HSI datasets. These methods include, for example, multinomial logistic regression [
6], random forests [
7], ensemble learning [
8], deep learning [
9], support vector machine (SVM) [
10], and k-nearest neighbors (KNN) [
11]. However, supervised classifiers often under-perform due to the Hughes phenomenon [
12], also known as the issue of dimensionality, which occurs whenever the number of available labeled training samples is considerably lower than the number of spectral bands required by the classifier [
11].
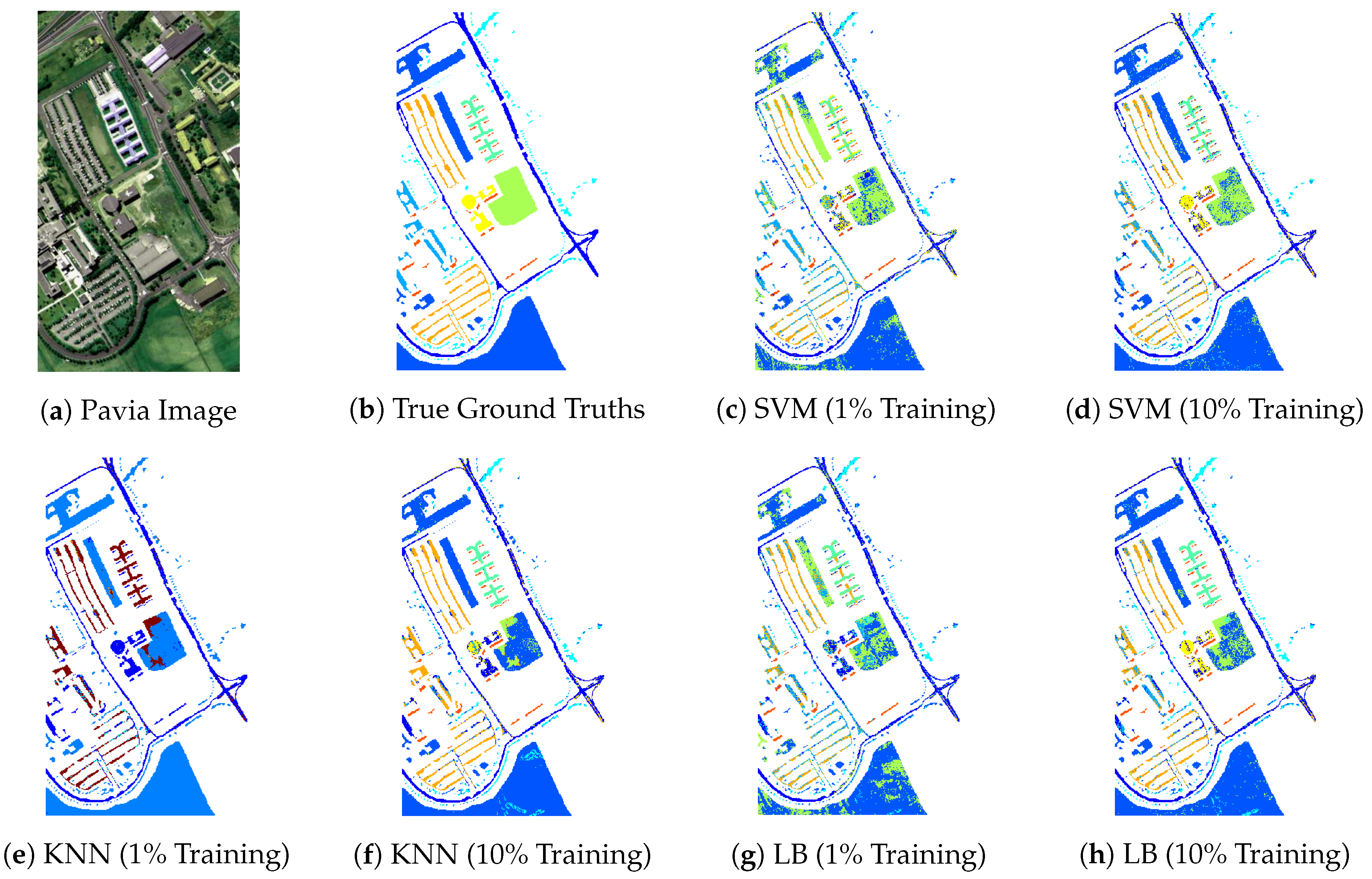
Figure 1 (Loss of accuracy in terms of ground maps) and
Table 1 (Loss of accuracy in terms of overall and kappa (
) for different number of labeled training samples i.e., 1% and 10% respectively) illustrates the loss in predictive performance of such classification methods for a particular ground image (Pavia University) when using two different sample size.
The limited availability of labelled training data in the HSI-domain is one of the motivations for the utilization of semi-supervised learning [
13]. Examples of such methods include kernel techniques [
14] such as SVM, Tri-training [
15] algorithms which generates three classifiers from the original labeled samples, then these classifiers are refined using unlabeled samples in the tri-training process, and Graph-based learning [
16,
17]. A major limitation of such approaches, however, is the low predictive performance when utilizing a small number of training samples within high dimensionality, as commonly observed in HSI classification [
18,
19] as shown in
Figure 1 and
Table 1.
Active learning (AL) is a class of semi-supervised learning method which tackles the limitations as mentioned earlier [
20,
21]. The main component of an AL method is the iterative utilization of the training model to acquire new training samples to be entered to the training set for the next iteration [
22]. AL methods can be pool-based or stream-based depending on how they enter new data to the training set, and employ measures like uncertainty, representativeness, inconsistency, variance, and error to rank and select new samples [
23]. Despite the gained success, there are still particular characteristics which can cause AL to present inflated false discovery rate and low statistical power [
11]. These characteristics include: (i) sample selection bias; (ii) high correlation among the bands; and (iii) non-stationary behavior of unlabeled samples.
This study introduces a customized AL pipeline for HSI to reduce sample selection bias whilst maintaining the data stability in the spatial domain. The presented pipeline distinguishes from standard AL methods in three relevant aspects. First, instead of simply using the uncertainty of samples to select new samples, it utilizes the fuzziness measure associated with the confidence of the training model in classifying those samples correctly. Second, it couples samples’ fuzziness with their diversity to select new training samples which simultaneously minimize the error among the training samples while maximizing the spectral angle between the selected sample and the existing training samples. In our current work, instead of measuring angle-based distances among all new samples and all existing training samples, a reference sample is selected from within the training set against which the diversity of the new samples is measured. This achieves the same goal while reducing the computational overhead as the size of training set is always much smaller than the validation set which is the source of new samples. Thirdly, the proposed Fuzziness and Spectral Angle Mapper (FSAM) method keeps the pool of new samples balanced, giving equal representation to all classes, which is achieved via softening the thresholds at run time. Experimental results on five benchmark datasets demonstrate that the customized spatial AL pipeline leads to an increased predictive power regarding kappa () coefficient and overall accuracy, precision, recall, and F1-Score.
The remainder of the paper is structured as follows.
Section 2 reviews related work on learning methods applied to HSI.
Section 3 presents the theoretical aspects of the proposed FSAM-AL pipeline followed by a theoretical explanation of the implemented objective function.
Section 4 discusses the experimental dataset and experimental settings.
Section 5 presents the experimental results and intensive discussion on obtained results.
Section 6 compare the experimental results with the state of the art sample selection methods used in AL frameworks in the recent most years. Finally,
Section 7 summarizes the contributions and future research directions.
2. Related Work
The HSI technology has been employed in several real-world applications including object detection and recognition, change detection (The process of identifying the changes occurred over the time on the earth surface), human-made material identification, semantic annotation, unmixing, and classification [
2,
16]. However, some challenges can arise from typical characteristics of HSI data, notably the limited availability of labeled data which can lead to inflated false discovery rate and low statistical power [
22]. This aspect results in a relatively poor predictive performance of supervised [
24] and semi-supervised [
25] learning methods when addressing HSI classification, as shown in
Figure 1.
AL poses as an alternative for coping with the limited amount of labeled data by iteratively selecting informative samples for the training set [
11]. Alternatives of sample selection method utilized in AL and corresponding references to the literature are shown in
Table 2.
Table 2 classifies the references in the literature according to the information utilized by the sample selection methods, being either spectral (consider only the wavelength of the pixel) or spectral–spatial (pixel location in addition to the wavelength). The latter class is particularly relevant in the HSI-domain as the acquisition of training samples depends on a large degree on the spatial distribution of the queried samples. However, only a few studies have integrated spatial constraints into AL methods [
26,
27]. In the
Table 2 we have provided a unified summary of existing sample selection methods and the information they use along with references to their respective papers.
Tuia et al. [
28] presented a detailed survey on AL methods addressing HSI analysis and contrasted non-probabilistic methods, which assume that all query classes are known before to the initialization, to probabilistic approaches that allow the discovery of new classes. The latter class was also pointed as more suitable for cases when the prior assumption is no longer fulfilled [
44]. In addition to probabilistic and non-probabilistic AL methods, large margin heuristics have been utilized as the base learner to combine the benefits of HSI analysis and AL [
28,
45]. A particular approach for selecting samples that have achieved remarkable results for several applications is query by committee (QBC) [
46]. Contrarily from previous methods, QBC selects samples based on the maximum disagreement of an ensemble of classifiers. Overall, these sampling methods suffer from high computational complexity due to the iterative training of the classifier for each sample [
28].
Pool-based AL, also known as batch-mode AL, addresses the high computational complexity observed in the aforementioned methods by concomitantly considering the uncertainty (spectral information) and diversity (spatial information) of the selected samples [
36]. A seminal work was presented by Munoz-Mari et al. [
47], which highlighted the benefits of integrating spatio-contextual information to AL even when the distribution of queried samples in the spatial space is ignored. This method was later expanded to include the position of selected samples in the feature space [
32]. One of the outcomes from such a transformation is the point-wise dispersed distribution in the spatial domain, which incurs the risk of revisiting the same geographical location several times, especially in the HSI-domain [
32].
A considerable amount of research has been conducted on AL in the recent years, often analyzing only spectral properties, whilst ignoring spatial information that plays a vital role in HSI classification as shown in [
32,
48]. Spatial and spectral HSI classification can achieve higher performance than its pixel-wise counterpart as it utilizes not only information of spectral signature but also from spatial domain [
48]. Thus, the combination of spatial and spectral information for AL represents a novel and promising contribution yet to be explored in the HSI-domain. This study proposes a customized pool-based AL pipeline which exploits both spatial and spectral information in the context of HSI classification.
3. Methodology
We address the small sample problem when classifying high dimensional HSI data by defining an AL scheme selecting a pool of diverse samples by taking into account two main criteria. The first is the fuzziness of samples, which is associated with the confidence of the trained model in properly classifying the unseen samples. The second is the diversity of the samples, thus reducing the redundancy among the selected samples. The combination of two criteria results in the selection of a pool of potentially most informative and diverse samples in each iteration.
Although there have been lots of different sampling methods (few mentioned in
Table 2), uncertainty remains one of the most popular method that can be used to select the informative samples [
11,
49]. Usually, the most uncertain samples have similar posterior probabilities for two most possible classes [
49]. Thus, probabilistic model could be directly used to evaluate the uncertainty of unlabeled sample [
49].
However, assessing the uncertainty of a sample is not as straight-forward when one is using non-probabilistic (NP) classifiers because their output does not exist in the form of posteriori probabilities [
23,
49]. The output of such classifiers can be manipulated to obtain an approximation of posteriori probability functions for the classes being trained [
23].
Suppose is an HSI cube which is composed of L spectral bands and samples per band belonging to C classes where is the sample in the cube. Let us assume , where is the class label of the sample. Let us further assume that n finite (limited) number of labeled training samples are selected from X to create the training set . The rest of the samples form the validation set . Please note that , and .
An NP classifier trained on
when tested on
would produce an output matrix
of
dimensions containing NP outputs of the classifier. Let
be the
output (membership for the
class) for
sample. There are several methods proposed in the literature to transform such NP outputs into the posteriori probabilities [
23,
49]. Such methods are computationally complex in two folds. First these methods need to compute the Bayesian decision for each samples
choosing the category
having the largest discriminant function
. Secondly, these methods assume that the training outputs are restricted as
. However, these methods also consider to manipulate each Bayes rule using Jacobin’s derivation over the limit theorem on infinite number samples to approximate the posterior probabilities in a least squares sense, i.e.,
[
49].
In order to overcome the above mentioned difficulties, in this work, we used marginal probability distribution [
32] which is obtained form the
information in the HSI data, serves as an engine in which our AL pipeline can exploit both the spatial and spectral information in the data. The posteriori class probabilities are modeled with the discriminative random field [
32,
50] in which the association potential is linked with discriminative, generative, ensemble and signal hidden layer feed forward neural network based classifiers. Thus, the posteriori probabilities are computed as similar to the work [
32]. From these posteriori probabilities we obtained the membership matrix which should satisfy the following properties [
11]:
In Equation (
1),
and
is a function that represents the membership of
sample
to the
class [
11]. For the true class, the posteriori probability would be approximated as close to 1, whereas, if the output is small (wrong class), the probability would be approximated as close to 0. However, AL methods do not require accurate probabilities, but only need a ranking of the samples according to their posteriori probabilities which would help to estimate the fuzziness [
49] and the output of the sample.
The fuzziness
upon
samples for
C classes from the membership matrix
can then be defined as expressed in Equation (
2) which must satisfy the properties defined in [
51,
52].
Then, we first associate , predicted class labels, and actual class labels with and then sort the in descending order based on the fuzziness values. We then heuristically select the number of misclassified samples which have higher fuzziness, where . The proposed strategy keeps the pool of new samples balanced, giving equal representation to all classes, which is achieved via softening the thresholds at run time.
Next, the spectral angular mapper (SAM) (More information about spectral angle mapper (SAM) function can be found in the following papers [
53,
54,
55]) function is used to discriminate the samples within the same class to minimize the redundancy among the pool of
selected samples. SAM is an automated method for directly comparing sample spectra to a known spectra. It treats both spectra as vectors and calculates the spectral angle between them. It is insensitive to illumination since it uses only the vector direction and not the vector length [
56]. The output of SAM is an image showing the best match of each pixel at each spatial location [
57]. This approach is typically used as a first cut for determining the mineralogy and works well in area of homogeneous regions.
In this work, SAM takes the arc-cosine-based dot product between the test spectrum which have higher fuzziness
to a reference (training samples) spectrum
, where
and
where
L is the total number of bands in HSI dataset, with the following objective functions:
Equation (
3) aims to compute the spectral difference among all the training samples for
C classes, respectively. We then select one reference spectrum from each class which minimizes the angular distance among others within same class, i.e., the sample which is more similar to others in the given class. This process will return the number of reference spectrum’s up to the number of classes in HSI. We then pick one reference spectrum from
to compare with all the selected test spectrum for the same class and account the angular distance among them in
as shown in Equation (
4).
where
denotes the induces of samples which have higher fuzziness,
represents the index of samples of
that are not contained in
,
provides the trade-off between diversity, and
denotes the index of the unlabeled sample that will be included in the pool. Please note that here we used a soft threshing scheme to balance the number of classes in both training and selected samples. The proposed pipeline systematically select the (
) higher fuzziness samples from
for each class, if one or more classes missed in the pool of selected samples. This process is repeated until the cardinality of
is equal to
h, i.e.,
, where
h is the size of pool. This technique guarantees that the selected samples in
are diverse regarding to their angles to all the others in (
). Since the initial size of
is zero, thus, the first sample included in
is always the higher fuzziness sample from
.
There are several advantages of using fuzziness information carried out through SAM as query function: (i) easy to implement; (ii) robust in mapping the spectral similarity for reference to higher fuzziness test spectrum only; (iii) powerful because it represents the influence of shading effects to accentuate the selected test reflectance characteristics [
55]. On the other hand, the main drawback of SAM is spectral mixture problems, i.e., SAM assumes that the reference spectrum chosen to classify the HSI represents the pure spectrum which is not the case in our problem. Such problems occur when the HSI is in low or medium spatial resolution. Furthermore, as we know, the surface of the earth is heterogeneous and complex in many ways, thus, containing many mixed samples. The spectral confusion in samples can lead to overestimation or underestimation errors for a spectral signatures. This is not the case of the proposed solution, since we iteratively select the reference spectrum from each class using Equation (
3) as a pure spectrum and comparing this with selected test spectrum respectively using Equation (
4) with the help of whiting parameter to minimize the redundancy among the selected samples. The complete work-flow of our proposed pipeline is described in Algorithm 1 and
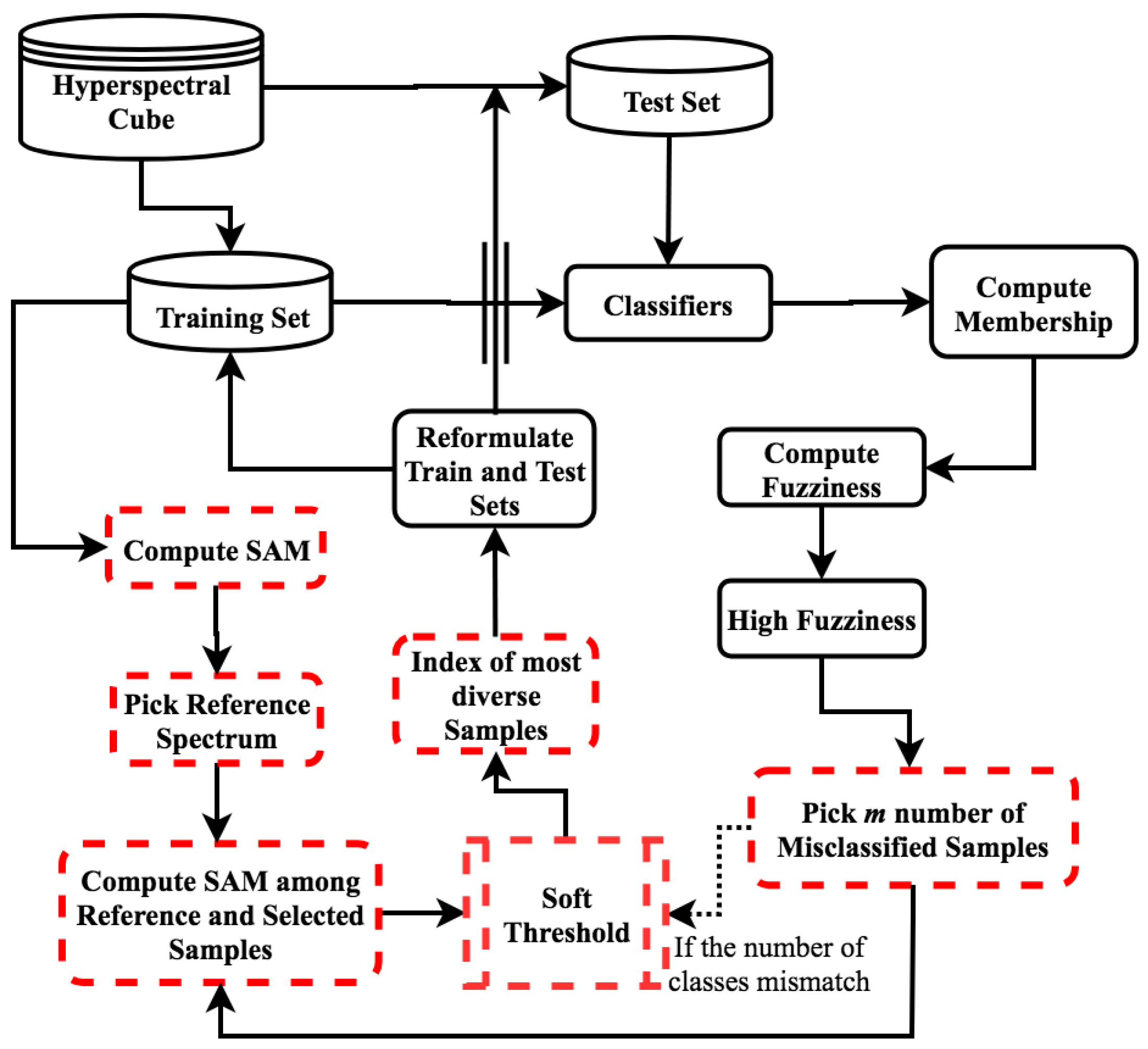
Figure 2.
| Algorithm 1: Pseudo-code of our Proposed FSAM Algorithm. |
![Remotesensing 11 01136 i001]() |
4. Experimental Datasets and Settings
The performance of our proposed FSAM-AL pipeline is validated on five benchmark HSI datasets acquired by two different sensors, e.g., Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) and Reflective Optics System Imaging Spectrometer (ROSIS). These datasets include, Salinas-A, Salinas full scene, Kennedy Space Center (KSC), Pavia University (PU), and Pavia Center (PC) (Further information about these datasets can be found in [
58]).
We evaluated the FSAM pipeline against four different classifiers: extreme learning machine (ELM) [
59], support vector machine (SVM), k-nearest neighbor (kNN), and ensemble learning (EL). These classifiers are chosen because they have been extensively studied in the literature for HSI classification and rigorously utilized for comparison purposes. Furthermore, our goal is to show that the proposed method can work well with a diverse set of classifiers. The performance of aforementioned classifiers is measured using two well know metrics: overall accuracy and kappa (
) coefficient [
11]. Furthermore, F1-score, precision, and recall rates are also compared. To further validate the real time applicability of FSAM, we compared it against four benchmark sample selection methods, namely: random sampling (RS), mutual information (MI), breaking ties (BT), and modified breaking ties (MBT).
Random Sampling (RS) [
11,
28] method relies on the random selection of the samples without considering any specific conditions.
Mutual Information (MI) [
32] of two samples is a measure of the mutual dependence between the two samples.
Breaking Ties (BT) [
33] relies on the smallest difference of the posterior probabilities for each sample. In a multiclass settings, BT can be applied by calculating the difference between two highest probabilities. As a result, BT finds the samples minimizing the distance between the first two most probable classes. The BT method generally focuses on the boundaries comprising many samples, possibly disregarding boundaries with fewer samples.
Modified Breaking Ties (MBT) [
34,
35] includes more diversity in the sampling process as compared to BT. The samples are selected by maximizing the probability of the largest class for each individual class. MBT takes into account all the class boundaries by conducting the sampling in cyclic fashion, making sure that the MBT does not get trapped in any class whereas BT could be trapped in a single boundary.
In all experiments, the initial training size is set as 100 samples from an entire HSI data. In each iteration the size of training set increases with actively selected samples by FSAM pipeline. The best part of FSAM is that there is no hyper-parameters need to be tuned except classification methods. In ELM, the hidden neurons are systematically selected from the range of . Similarly, in kNN, the nearest neighbors are set to , SVM is tested with polynomial kernel function, and ensemble learning classifiers are trained using tree-based model with number of trees. All such parameters are carefully tuned and optimized during the experimental setup. All these experiments are carried out using MATLAB (2014b) on an Intel Core i5 3.20 GHz CPU with 12 GB of RAM.
5. Experimental Results
In this section, we performed a set of experiments to evaluate our proposed FSAM pipeline using both ROSIS and AVIRIS sensors datasets. Evaluating ROSIS sensor datasets is more challenging classification problem dominated by complex urban classes and nested regions then AVIRIS. Here we evaluate the influence of the number labeled samples on the classification performance achieved by several classifiers.
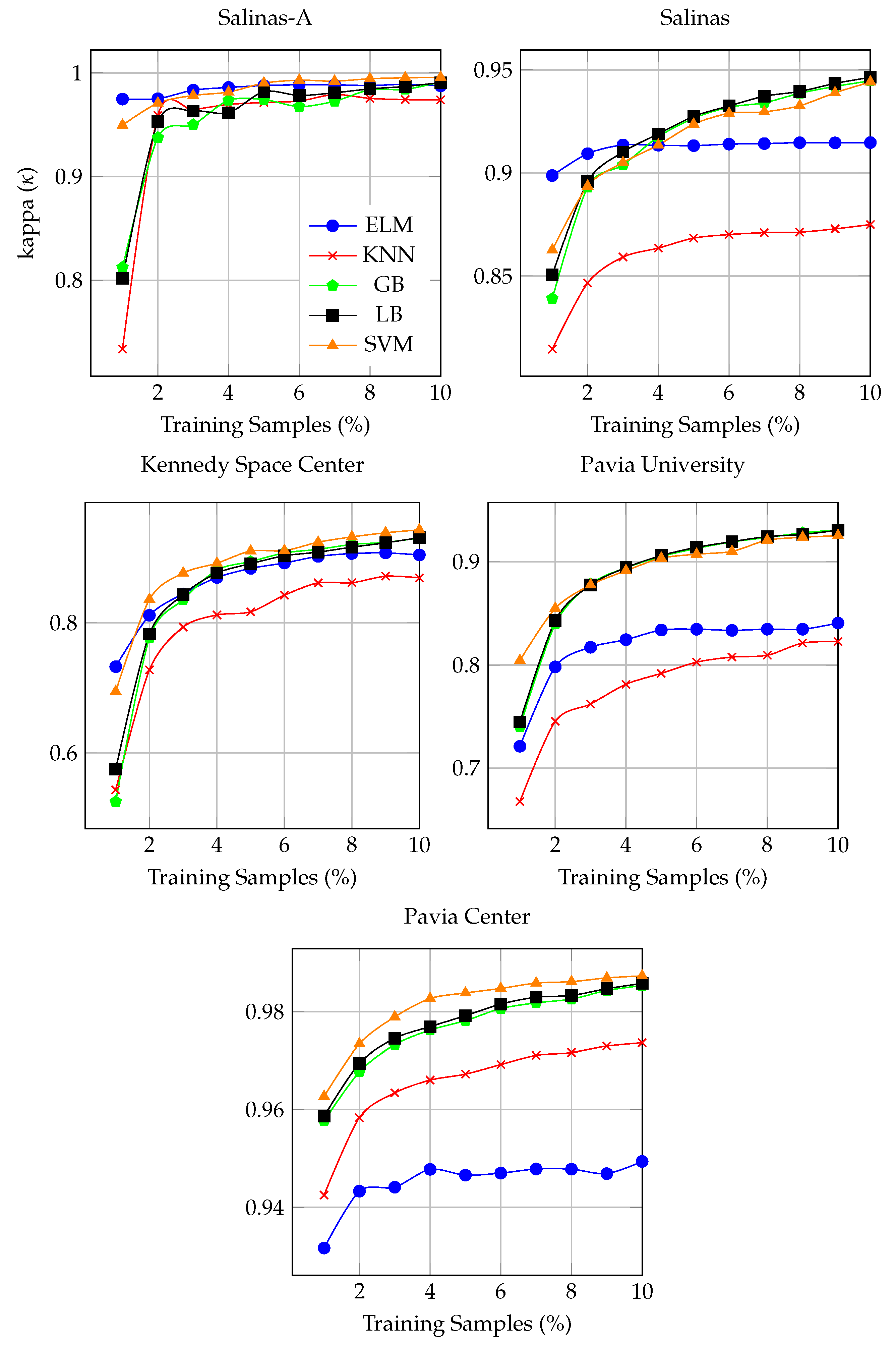
Figure 3 and
Figure 4 shows the overall and kappa
accuracy as a function of the number of labeled samples obtained by FSAM, i.e., fuzziness and SAM diversity-based active selection of most informative and diverse samples in each iteration. These labeled samples were selected by machine–machine interaction which significantly reduces the cost in terms of labeled collection through human supervisor which is the key aspects of automatic AL methods. The plots are shown in
Figure 3 and
Figure 4 and generated based on only selected samples in contrast to the entire population which reveals clear advantages of using fewer labeled samples for FSAM pipeline.
From
Figure 3 and
Figure 4, it can be observed that FSAM greatly improved the accuracy. The results also reveal that SVM and LB outperformed other classifiers in most cases, whereas, as expected, KNN provides lower classification accuracy than SVM and LB, since the candidates are more relevant when the samples are acquired from the class boundaries. Furthermore, it can also be observed that SVM always performed better than KNN, ELM, and ensemble learning classifiers. ELM could perform better with more number of hidden neurons on more powerful machines. For instance, when the 2% of labeled samples were used, the performance has been significantly increased in contrast to the 1% of actively selected samples. These observations confirm that FSAM can greatly improve the results obtained by different classifiers based on a small portion from the entire population, i.e., the classifiers trained using a limited number of selected labeled samples can produce better generalization performance rather than selecting the bulk amount of label training samples.
It is perceived form
Figure 3 and
Figure 4 that by including the samples back to the training set, the classification results are significantly improved for all the classifiers. Moreover, it can be seen that SVM and ELM classifiers are more robust then ensemble and KNN classifiers. For examples, with 1% actively selected samples in ELM classifier case, only 2% difference in classification with different number of samples can be observed, however, for the KNN and SVM classifiers, the difference is quite high. Similar observations can be made for ensemble models.
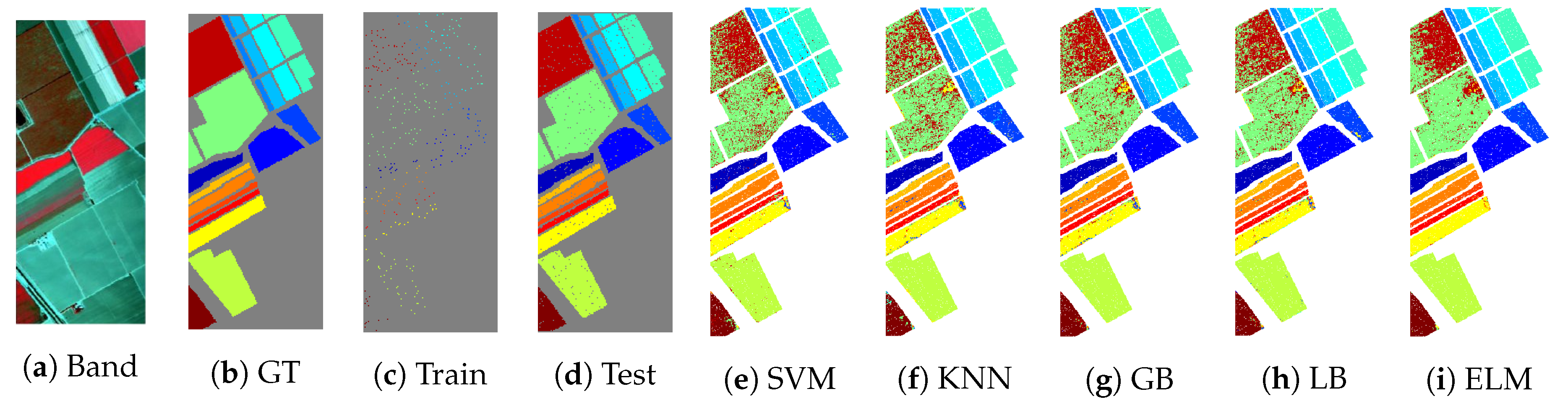
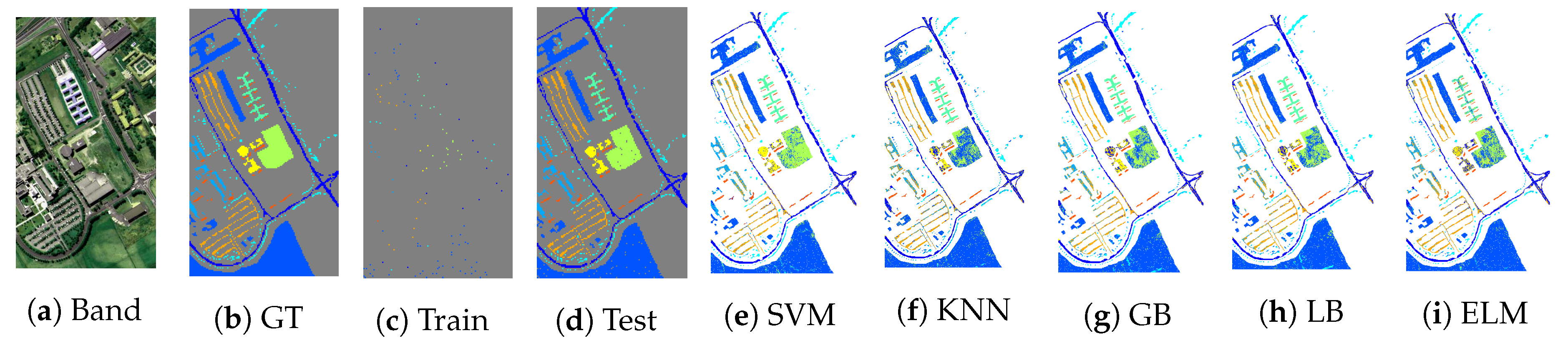
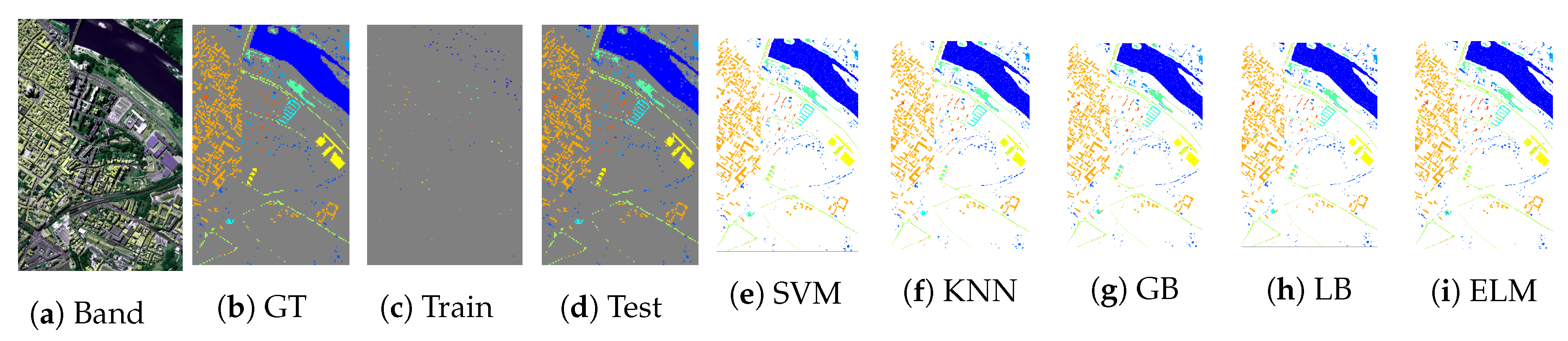
In order to present the classification results in geographical fashioned for both ROSIS and AVIRIS sensors datasets,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9 shows ground truths segmentation of all experimental datasets used in this work. These ground truths are generated using
of actively selected samples by FSAM pipeline. In all the experiments, we provide the quantity of labeled training samples and the test samples which provide an indication of the number of true versus estimated labels used in the experiments. It can be observed from listed results, that our proposed fuzziness and diversity-based active labeled sample selection pipeline is quite robust as it achieved higher classification results which are way better or at least comparable with several state-of-the-art AL methods.
To better analyze the performance of FSAM on ROSIS and AVIRIS datasets,
Table 3 shows the statistical significance in terms of recall, precision, and F1-score tests. The experiments shown in
Table 3 are performed with 2% of actively selected labeled samples from each class for all experimental datasets.
Table 3 is produced to support the results shown in
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9 for both AVIRIS and ROSIS sensor datasets. The global recall, precision, and F1-score for each classifier of these results are obtained using 5 Monte Carlo runs. Furthermore, these Tables shows the statistical significance of FSAM in terms of recall, precision, and F1-score with the 99% confidence interval. The obtained values indicate the ability of FSAM to correctly identify the unseen samples in which each classifier was trained on a very small amount of labeled training samples. For any good model, precision, recall, and F1-score values should be greater than 80% in average, and in our case, these values are almost above 80% for all experimental datasets and for all classifiers, demonstrating that the proposed FSAM-AL pipeline is not classifier sensitive.
6. Comparison and Discussion
The most advanced developments in AL are single pass context and hybrid AL. These techniques combine the concepts of incremental and adaptive learning from the field of online and traditional machine learning. These advancements have resulted in a substantial number of AL methods. The most classical and well studied AL methods include, for example, the works [
60,
61] focused on online learning. These works specifically designed for on-line single-pass setting in which the data stream samples arrive continuously, thus, does not allow classifier re-training. Furthermore, these works focused on close concepts of conflict and ignorance. Conflict models how close a query point is to the actual class boundary and ignorance represents the distance between already seen training samples and a new sample.
Similar works proposed in [
62,
63] focused only on early AL strategies such as early-stage experimental design problems. The TED method was proposed to select the samples using robust AL method incorporated with structured sparsity-inducing norms to relax the NP-hard objective of the convex formulation. Thus, these works only focused on selecting an optimal set of initial samples to kick-start the AL. However, the superiority of our proposed FSAM pipeline is that it shows state-of-the-art performance independent of how the initial labeled training samples are selected. Such methods can easily be integrated into the works which utilize the decision boundary based sample selection methods.
A novel tri-training semi-supervised hyperspectral image classification method based on regularized local discriminant embedding feature extraction (RLDE) was proposed in [
64]. In this work, the RLDE process is used for optimal number of feature extraction to overcome the limitation of singular values and over-fitting of local Fisher discriminant analysis and local discriminant embedding. At a later stage, active learning method is used to select the informative samples from the candidate set. This work solves the singularity issues of LDA, however, this may include the redundant samples back to the training set which do not provide any new information to the classifier.
Spatial–spectral multiview 3D Gabor inspired active learning for hyperspectral image classification method was proposed in [
65]. Trivial multiview active learning methods can make a comprehensive analysis of both sample selection and object characterization in active learning by using several features of multiple views. However, multiview cannot effectively exploit spatial–spectral information by respecting the 3D nature of hyperspectral imaging, therefore, the sample selection method in multiview is only based on the disagreement of multiple views. To overcome such problems, J. Hu, et al. [
65] proposed a two-step 3D Gabor inspired multiview method for hyperspectral image classification. The first step consists of the view generation step, in which a 3D Gabor filter was used to generate multiple cubes with limited bands and utilize the features assessment strategies to select cubes for constructing views. On a second stage, an active learning method was presented which used both external and internal uncertainty estimation of views. More specifically, posterior probability distribution was used to learn the internal uncertainty of each individual independent view and external uncertainty was computed using inconsistency between the views.
Of course, the frameworks proposed in the above papers can be easily integrated with our proposed FSAM sample selection method instead of selecting the samples based on uncertainty or tri-training methods. We initialize our active learning method from 100 number of randomly selected labeled training samples and we experimentally demonstrate that randomly increasing the size of the training set slightly increases the accuracy nevertheless the classifiers become computationally complex. Therefore, at the first step, we decided to separate the set of misclassified samples which have higher fuzziness values (samples fuzziness magnitude between 0.7–1.0). We then select a specific percentage of misclassified samples which have higher fuzziness to compute the spectral angle among the reference training samples. We then fused a specific percentage of selected samples with the original training set to retrain the classifier from scratch for better generalization and classification performance on those samples which were initially misclassified by the same classifier.
More specifically, the proposed solution has been rigorously investigated through comparison against some significant works recently published in the HSI classification area, adopting different sample selection methods such as random sampling (RS), mutual information (MI), breaking ties (BT), modified breaking ties (MBT), uncertainty, and fuzziness as introduced in
Section 4. This comparison is based on the Botswana hyperspectral dataset acquired by the NASA EO-1 Satellite Hyperion sensor [
58,
66]. The experiments are based on five Monte Carlo runs with 100 initial training samples selected from this dataset. In each iteration, the training set size has been increased of 50 samples selected by a specific method among the ones to be compared. The results thus obtained are presented in the
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8. Based on such results, we can argue that the FSAM pipeline outperforms the other solutions taken into account in these experiments. This is due to the dual soft thresholding method for selection of the most informative as well as spatially heterogeneous labeled training samples. Furthermore, another benefit of the proposed FSAM solution is that it systematically selects the most informative but least redundant labeled training samples by machine–machine interaction without involving any supervisor, automatically, while the other AL frameworks need that a supervisor selects the samples at each iteration, manually.
By the Botswana dataset we experimentally demonstrated that FSAM outperforms all other sample selection methods, i.e., random selection, mutual information, breaking ties, modified breaking ties, and fuzziness in terms of accuracy, starting from the same classifiers and the same number of labeled training samples as shown in
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8. Furthermore, all these sample selection methods are more often subjective and tends to bring redundancy into the classifiers. reducing the generalization performance of the classifiers. More specifically, the number of samples required to learn a model in FSAM can be much lower than the number of selected samples. In such scenarios, there is a risk, however, that the learning model may get overwhelmed because of the uninformative or spatially miscellaneous samples selected by query function.
7. Conclusions
The classification of multiclass spatial–spectral HSI with a small labeled training sample size is a challenging task. To overcome this problem, this paper introduces a customized AL pipeline for HSI to reduce the sample selection bias while maintaining the data stability in the spatial domain.
The proposed FSAM pipeline differs from traditional AL methods in three relevant aspects. First, instead of simply using the uncertainty of samples to select new samples, it utilizes the fuzziness measure associated with the confidence of the training model in classifying those samples correctly. Second, it couples the samples’ fuzziness with their diversity to select new training samples which simultaneously minimize the error among the training samples while maximizing the spectral angle between the selected sample and the existing training samples. In our work, instead of measuring angle-based distances among all new samples and all existing training samples, a reference sample is selected from within the training set against which the diversity of the new samples is measured. This achieves the same goal while reducing the computational overhead as the size of training set is always much smaller than the validation set which is the source of new samples. Thirdly, the FSAM keeps the pool of new samples balanced, giving equal representation to all classes, which is achieved via softening the thresholds at run time.
Experimental results on five benchmark datasets demonstrate that the proposed FSAM leads to an increased predictive power regarding kappa and overall accuracy, precision, recall, and F1-Score parameters. A comparison of FSAM with state-of-the-art sample selection method is performed, confirming that the FSAM is effective in terms of overall accuracy and , also with few training samples.
However, the main drawback of SAM is spectral mixture problems, i.e., SAM assumes that the reference spectra chosen to classify the HSI represents the pure spectra. Such problem occurs when the HSI is in low or medium spatial resolution. Furthermore, as we know, the surface of the earth is widely heterogeneous and complex, thus containing many mixed samples. The spectral confusion in samples can lead to overestimation or underestimation errors for a spectral signatures. Our future research direction aims to address such limitations to classify low or mid spatial resolution hyperspectral images in a computationally efficient way. Further work will be directed toward testing the FSAM pipeline in different analysis scenarios dominated by the limited availability of training samples a priori.