Field Intercomparison of Radiometers Used for Satellite Validation in the 400–900 nm Range
Abstract
1. Introduction
2. Material and Methods
2.1. Participants of the LCE-2
2.2. Venue and Measurement Setup
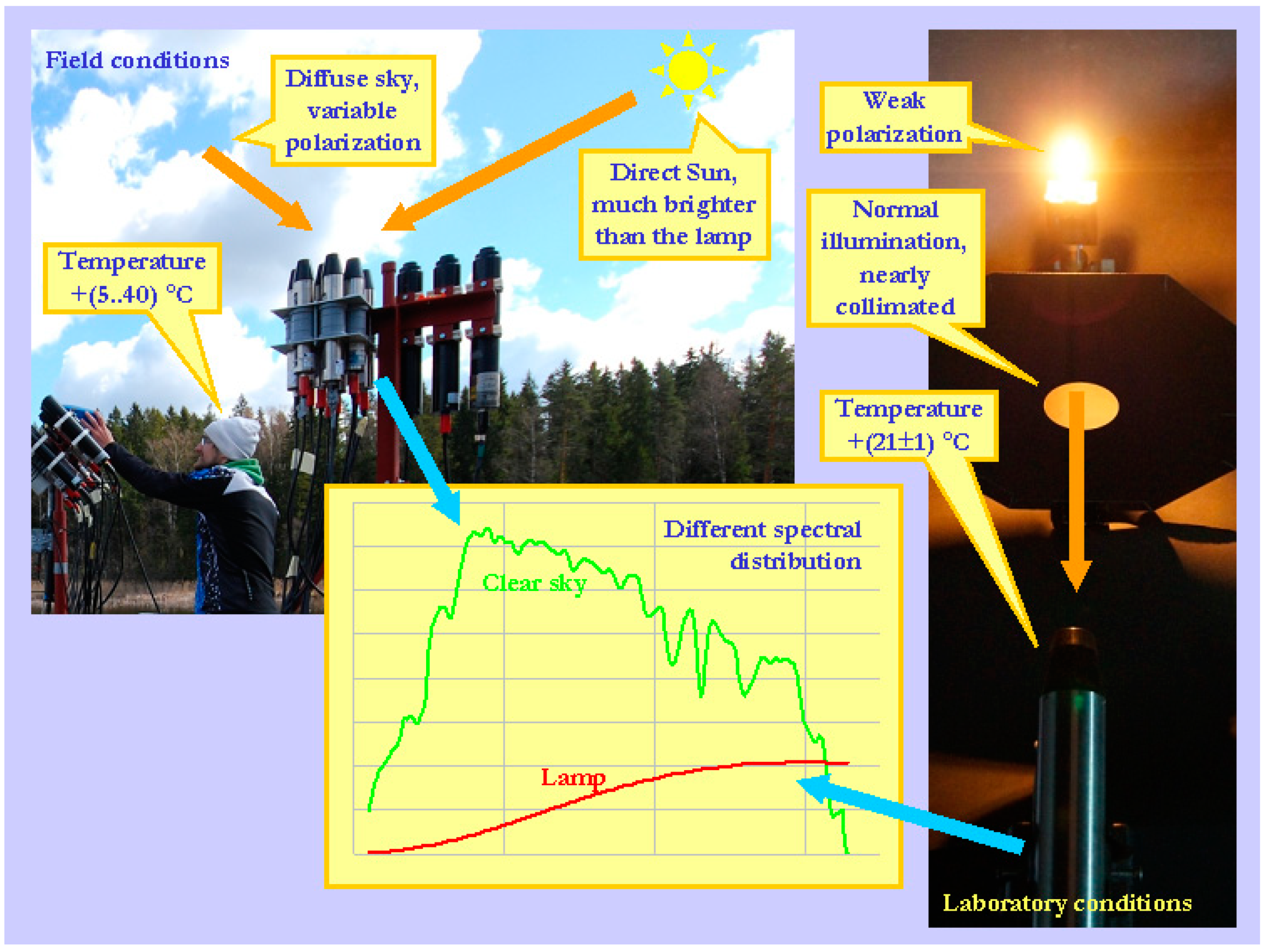
2.3. Environmental Conditions and Selection of Casts
2.4. Outdoor Experiment of the LCE-2
2.5. Data Processing
- Separation of the raw data files, based on the casts’ start and stop timestamps;
- Subtraction of the dark signal;
- Division by radiometric responsivity;
- Interpolation/convolution of spectra into the OLCI bands.
2.6. Consensus Value Used for the Analysis
2.7. Accuracy of Sensor Adjustment
3. Results
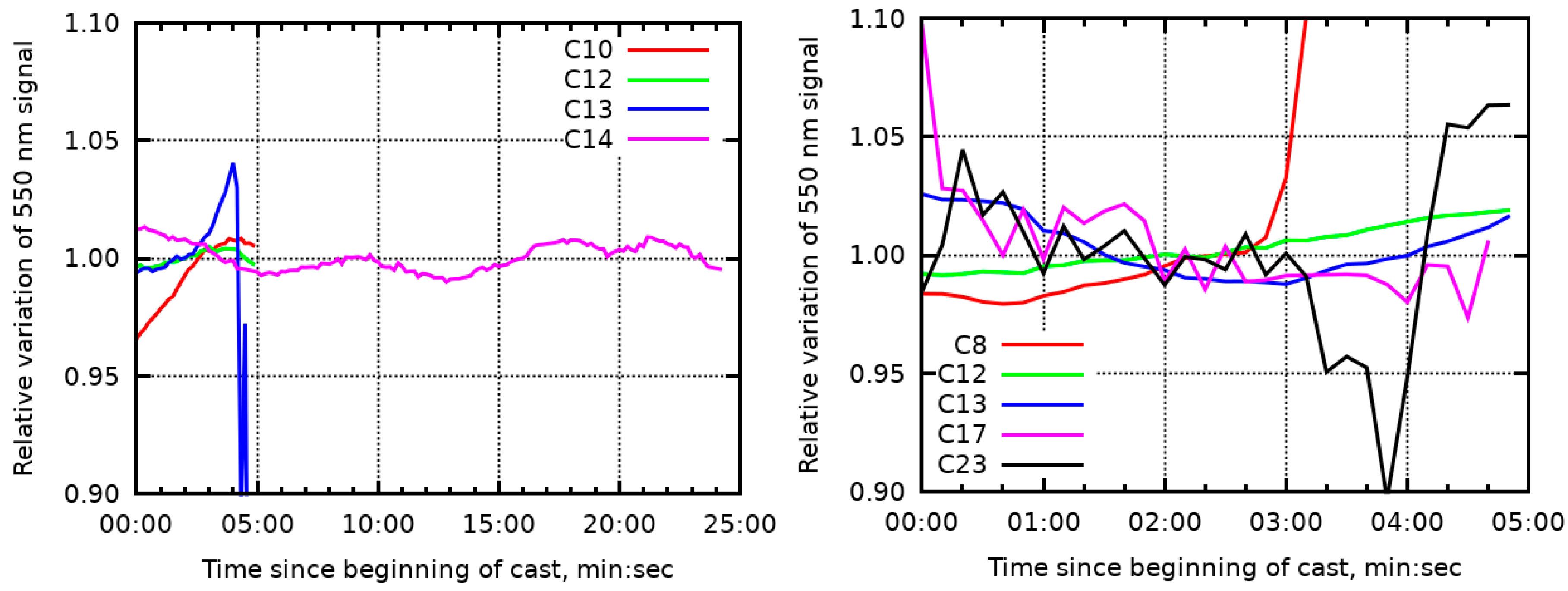
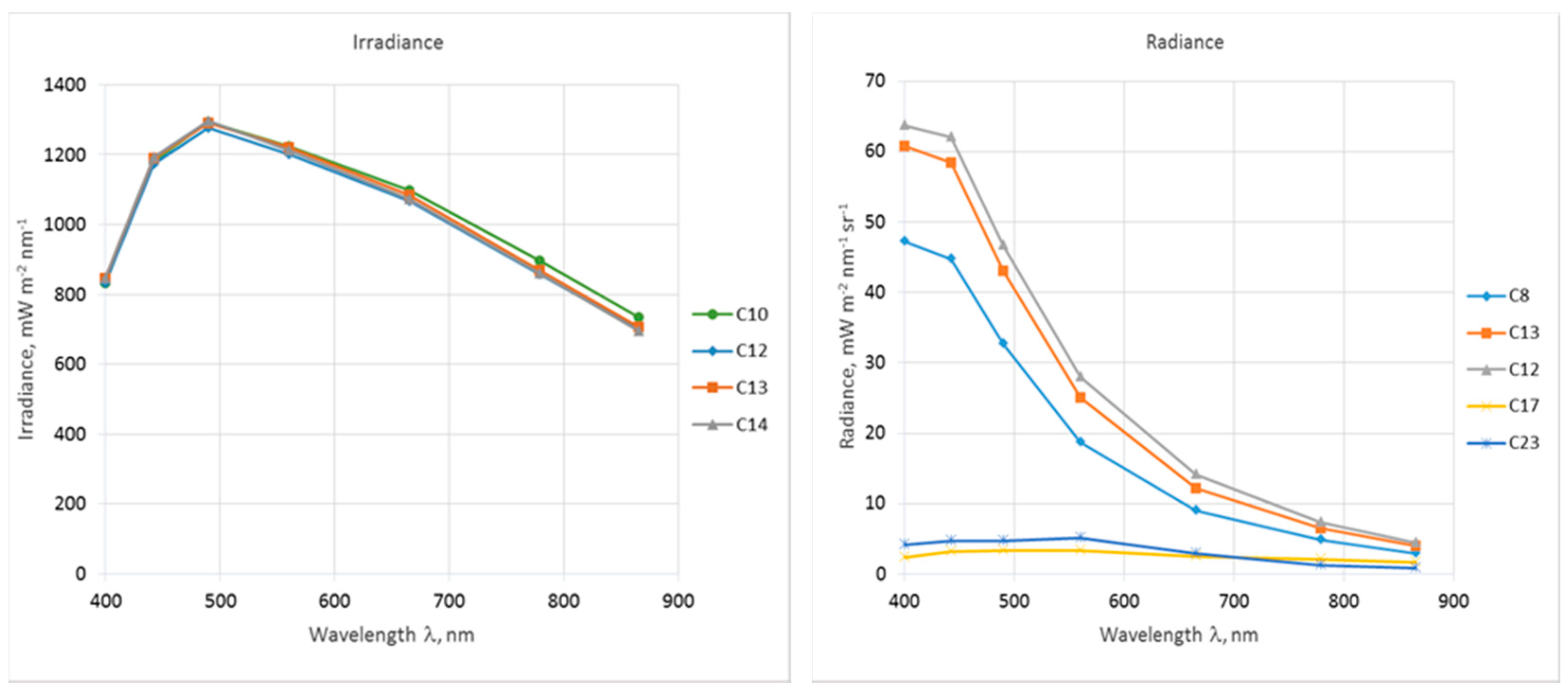
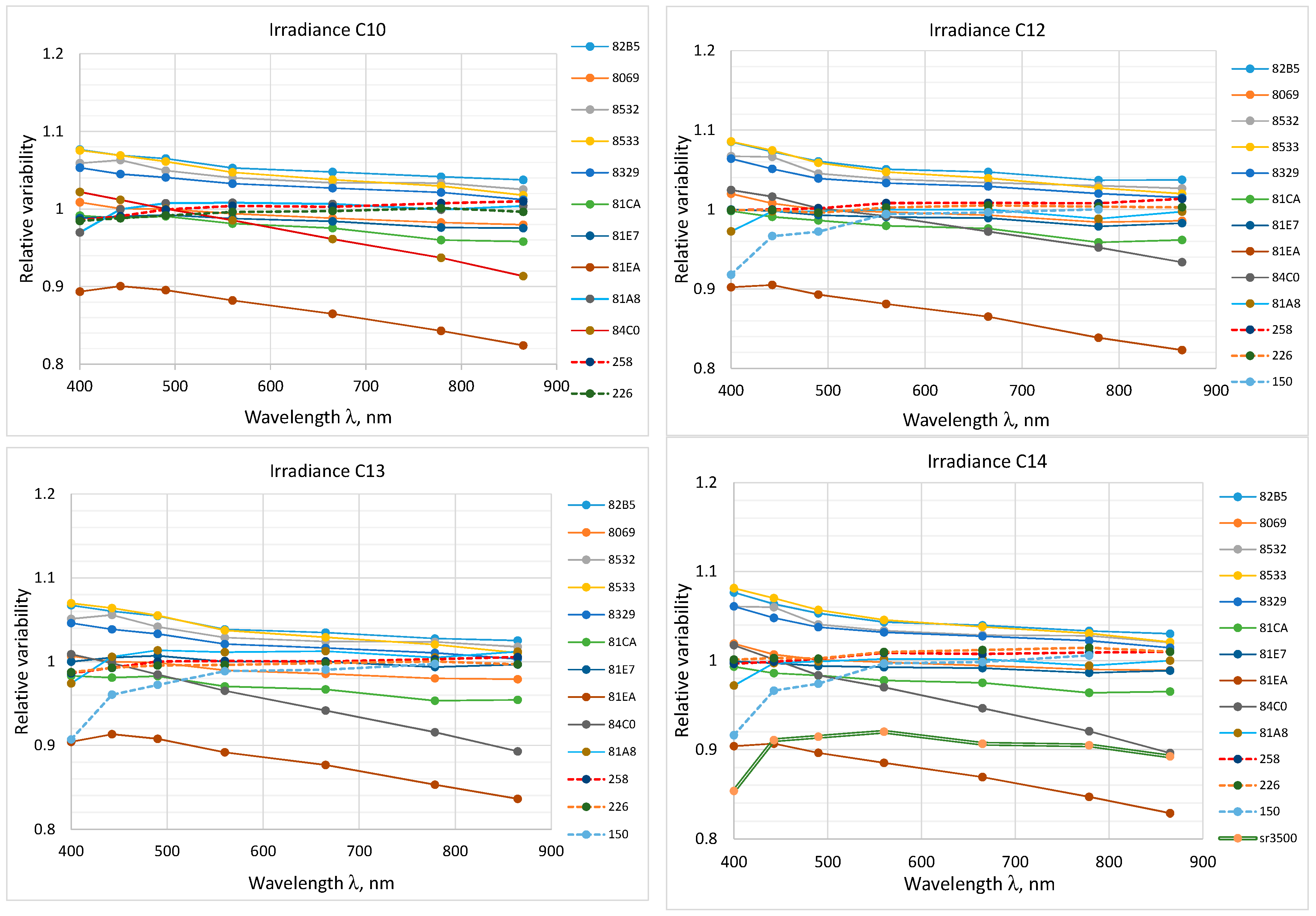
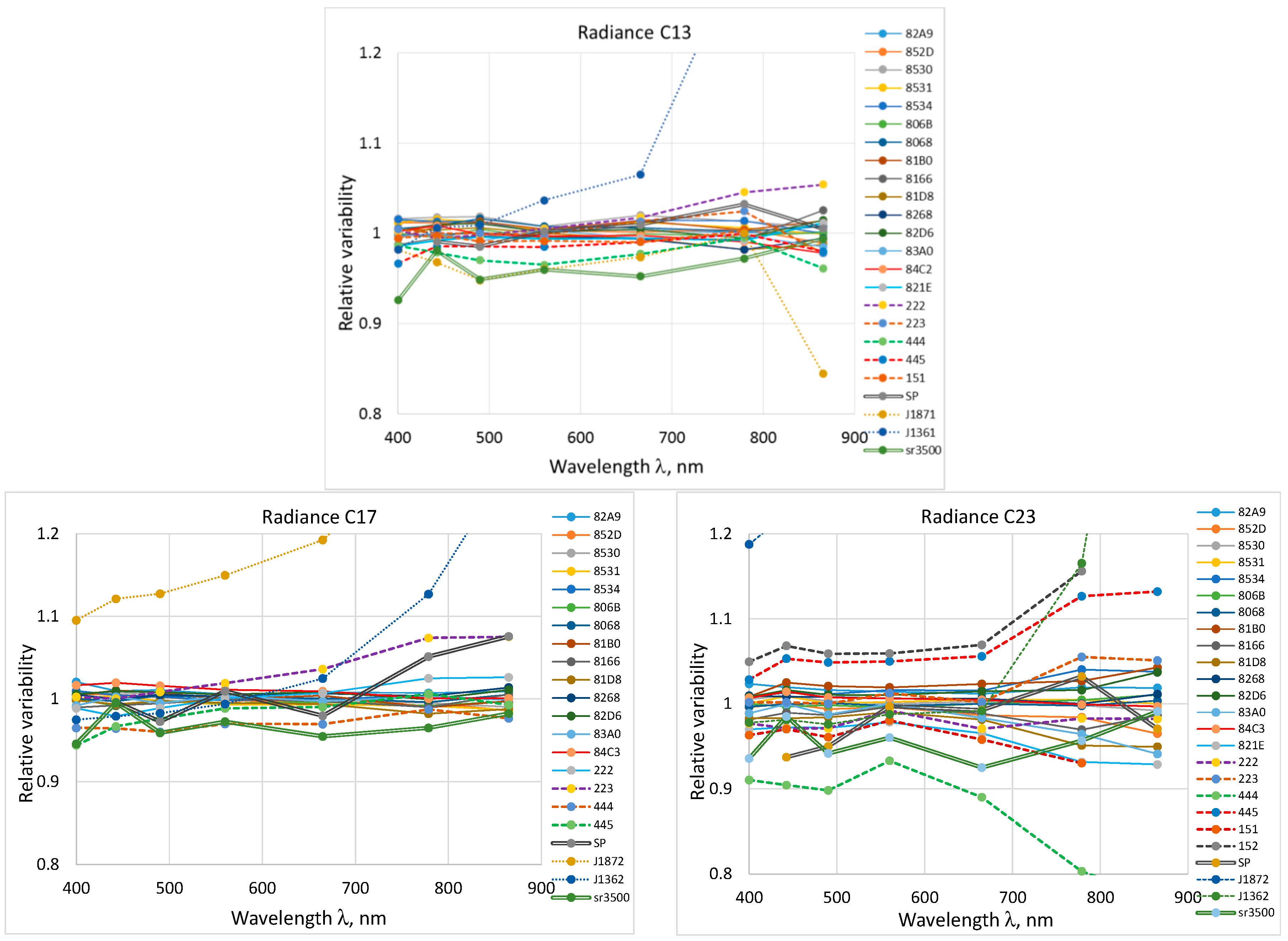
3.1. Results of Outdoor Comparison
3.2. Measurements after the End of LCE-2 Comparison
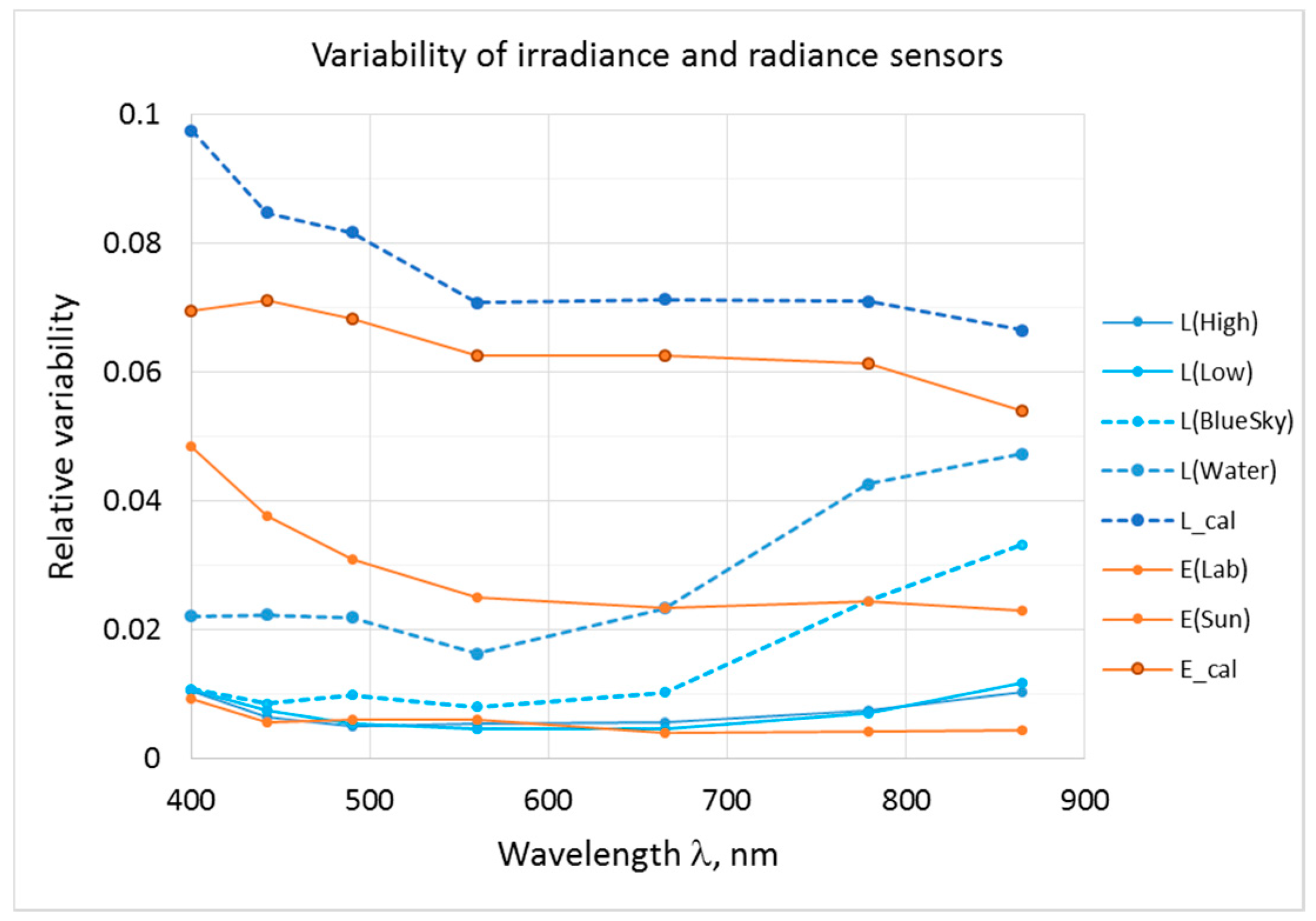
4. Uncertainty Budgets of Outdoor Comparisons
4.1. Calibration Certificate
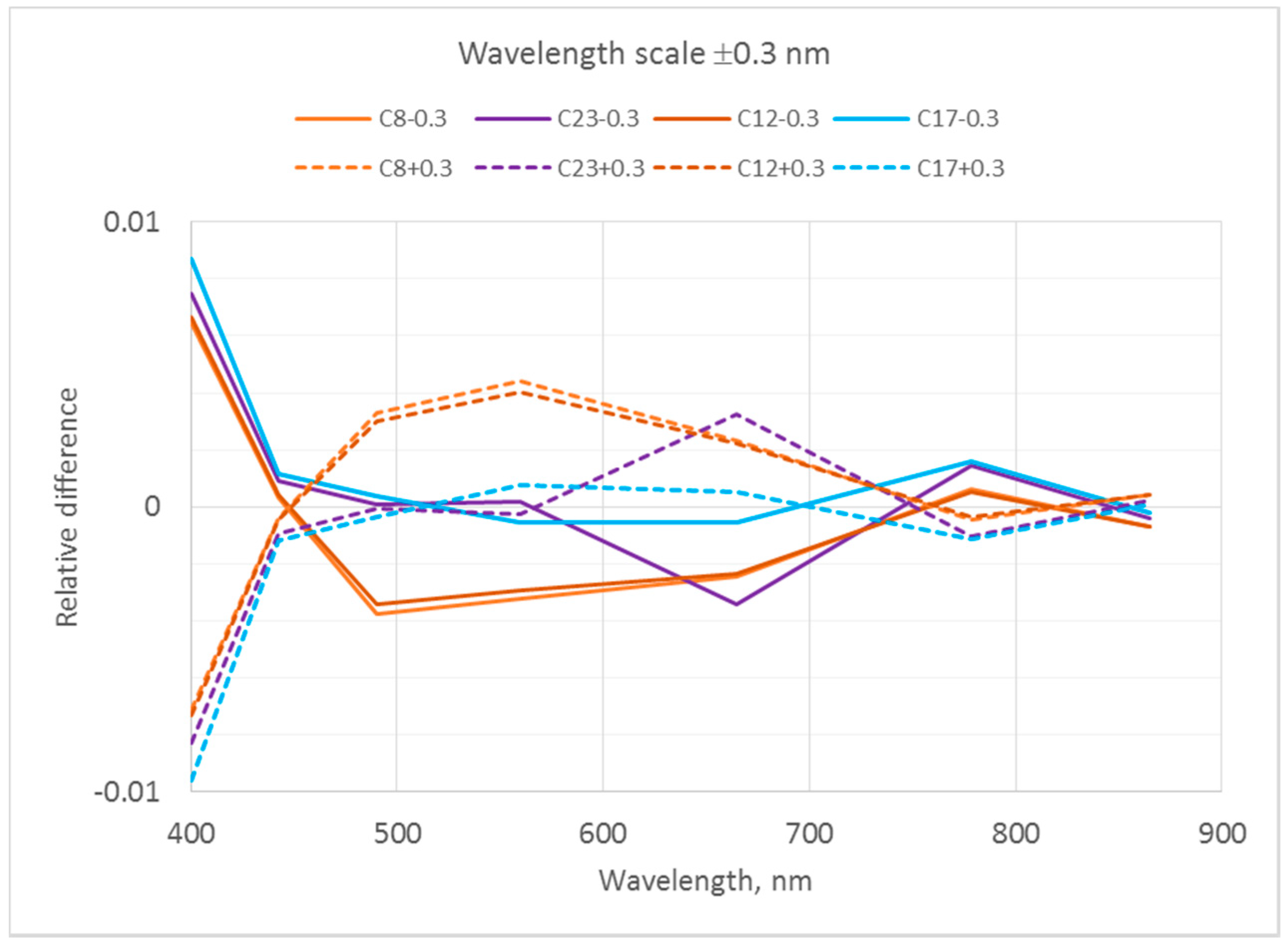
4.2. Interpolation
4.3. Temporal Instability of Sensor
4.4. Polarization
4.5. Nonlinearity
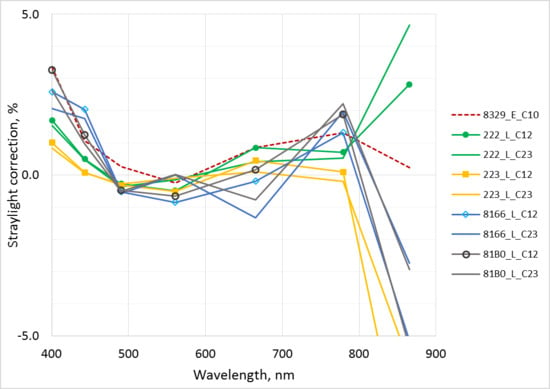
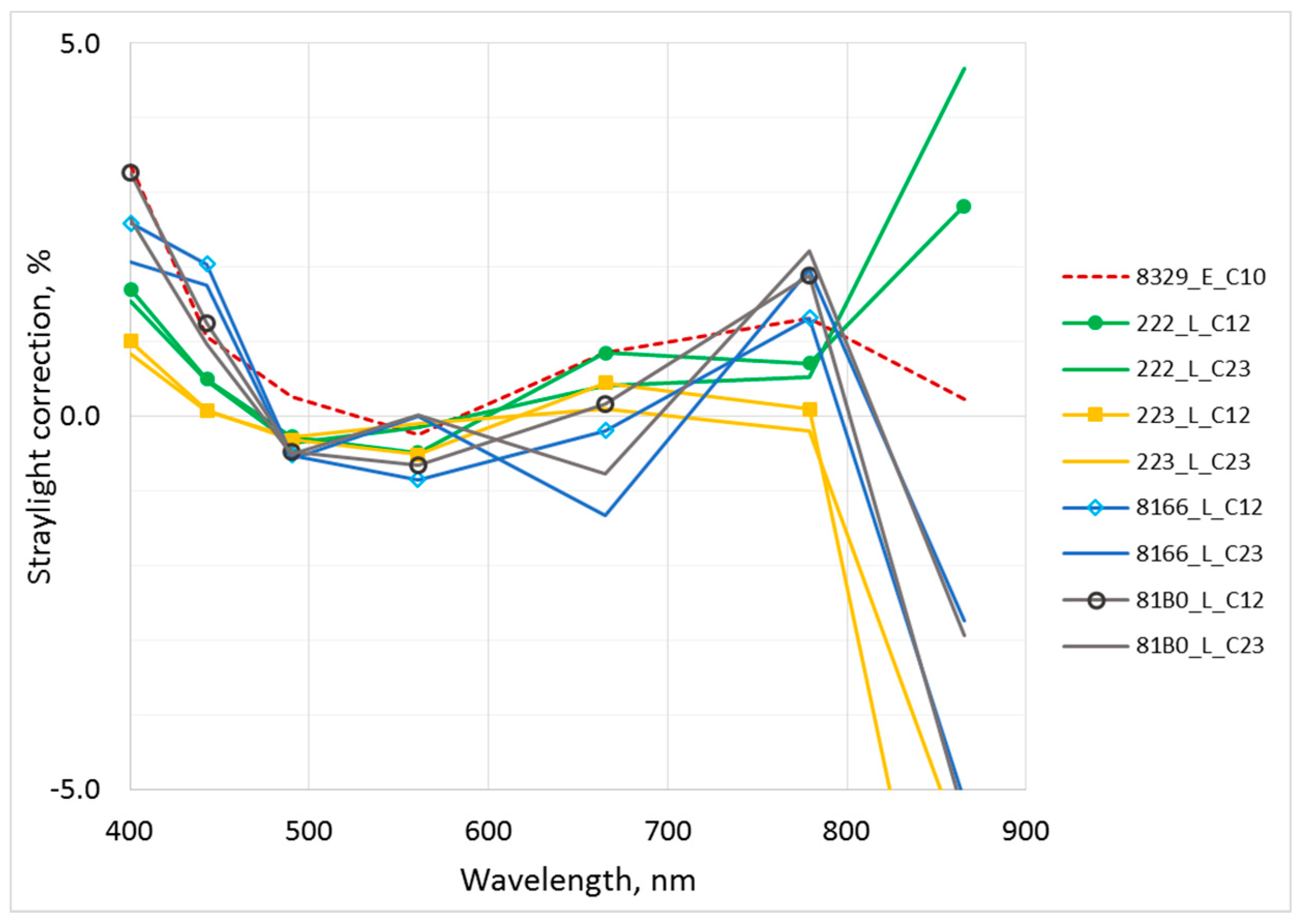
4.6. Spectral Stray Light
4.7. Temperature
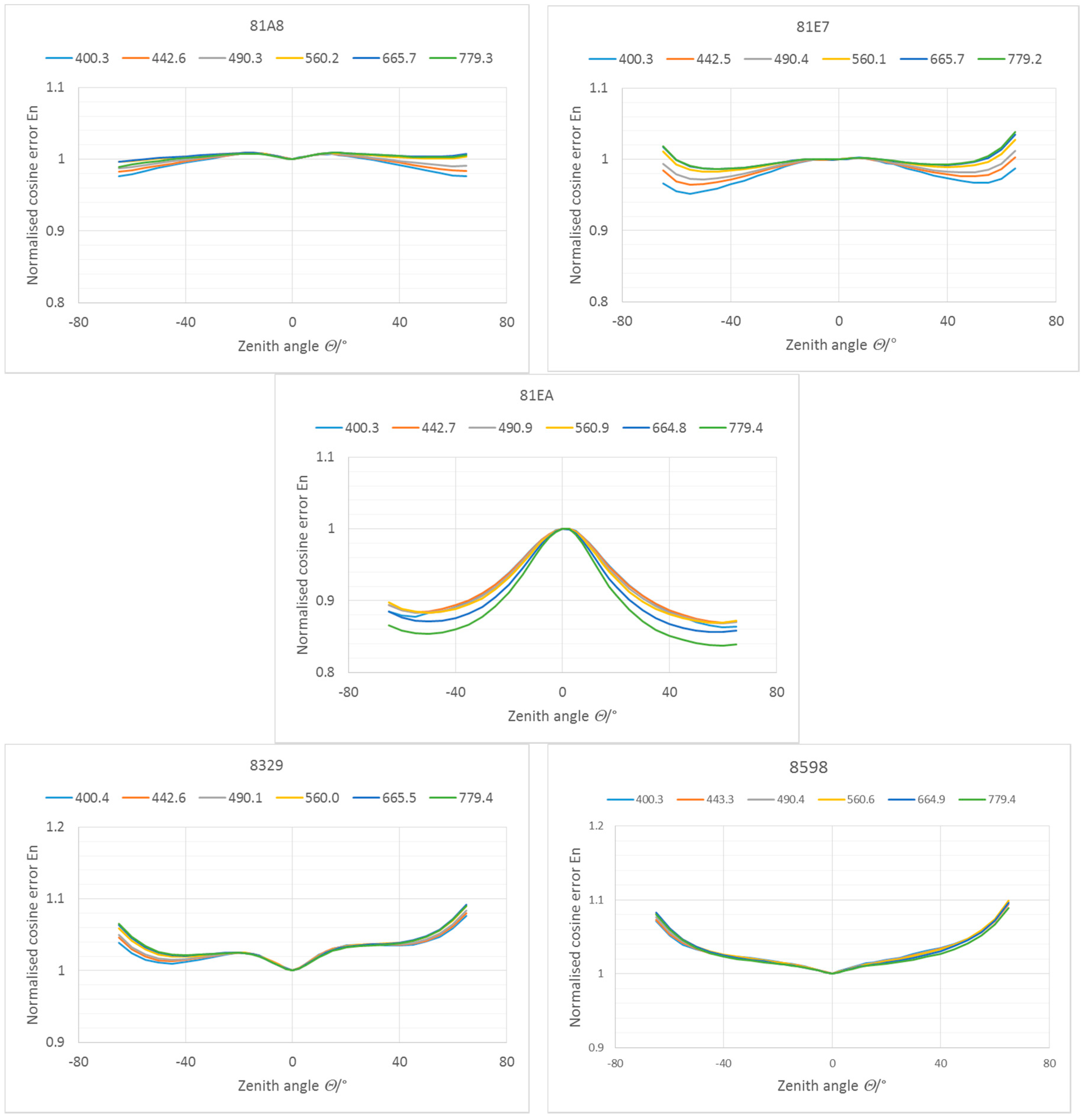
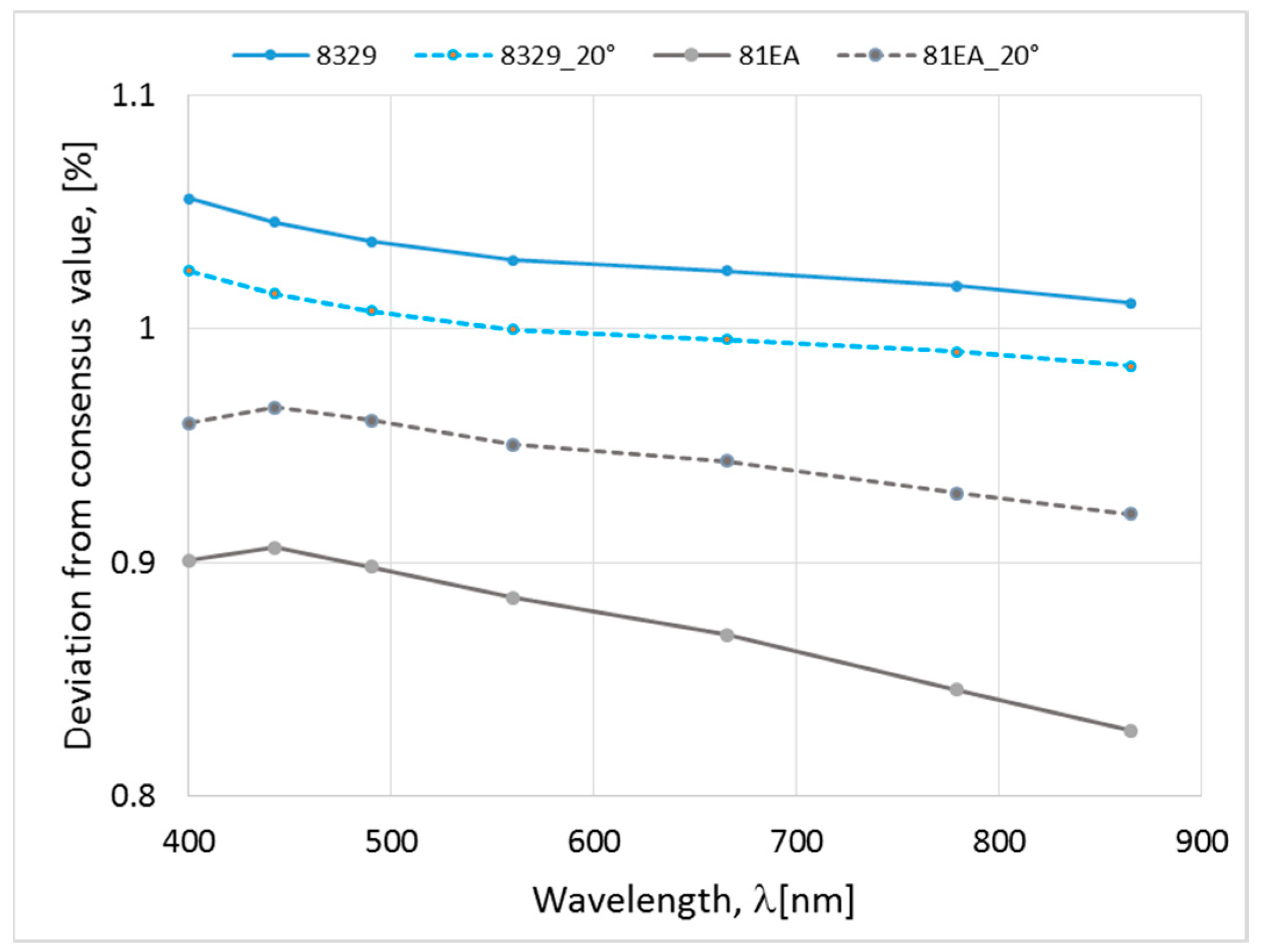
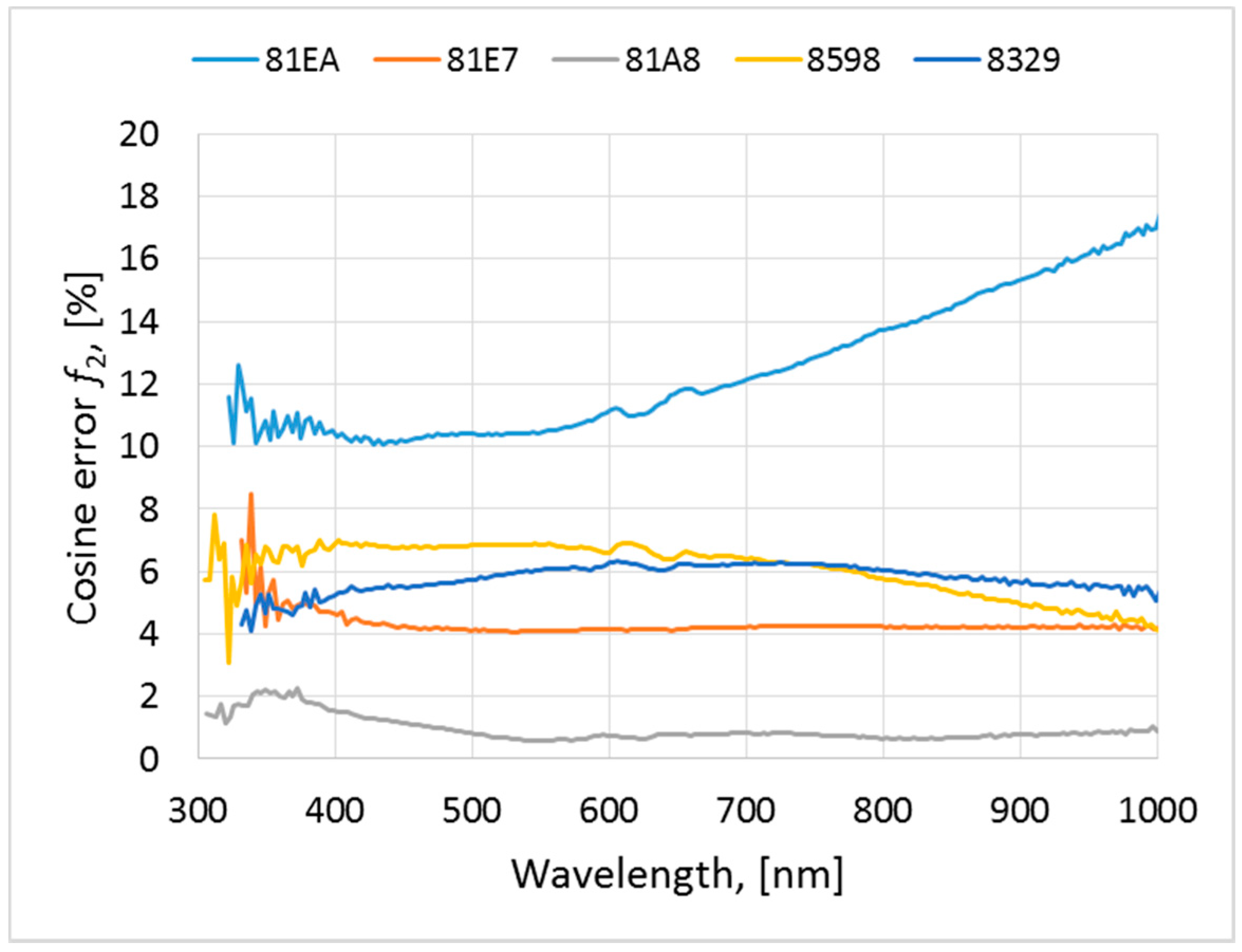
4.8. Cosine Error
4.9. Type A Uncertainty of Repeated Measurements
4.10. Alignment and Field-of-View
5. Discussion and Conclusions
Lessons Learned for the Design of Future Intercomparisons
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vabson, V.; Kuusk, J.; Ansko, I.; Vendt, R.; Alikas, K.; Ruddick, K.; Ansper, A.; Bresciani, M.; Burmester, H.; Costa, M.; D’Alimonte, D.; et al. Laboratory intercomparison of radiometers used for satellite validation in the 400–900 nm range. Remote Sens. 2019, 11, 1101. [Google Scholar] [CrossRef]
- Zibordi, G.; Ruddick, K.; Ansko, I.; Moore, G.; Kratzer, S.; Icely, J.; Reinart, A. In situ determination of the remote sensing reflectance: An inter-comparison. Ocean Sci. 2012, 8, 567–586. [Google Scholar] [CrossRef]
- Antoine, D.; Schroeder, T.; Slivkoff, M.; Klonowski, W.; Doblin, M.; Lovell, J.; Boadle, D.; Baker, B.; Botha, E.; Robinson, C.; et al. IMOS Radiometry Task Team. Final Report. 2017. Available online: http://imos.org.au/fileadmin/user_upload/shared/IMOS%20General/documents/Task_Teams/IMOS-RTT-final-report-submission-30June2017.pdf (accessed on 7 May 2019).
- Aerosol Robotic Network (AERONET) Homepage. Available online: https://aeronet.gsfc.nasa.gov/ (accessed on 9 August 2018).
- Kuusk, J.; Ansko, I.; Vabson, V.; Ligi, M.; Vendt, R. Protocols and Procedures to Verify the Performance of Fiducial Reference Measurement (FRM) Field Ocean Colour Radiometers (OCR) used for Satellite Validation; Technical Report TR-5; Tartu Observatory: Tõravere, Estonia, 2017. [Google Scholar]
- Ruddick, K.G.; de Cauwer, V.; Park, Y.-J.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef]
- Zibordi, G.; Talone, M.; Jankowski, L. Response to Temperature of a Class of In Situ Hyperspectral Radiometers. J. Atmos. Ocean. Technol. 2017, 34, 1795–1805. [Google Scholar] [CrossRef]
- Mekaoui, S.; Zibordi, G. Cosine error for a class of hyperspectral irradiance sensors. Metrologia 2013, 50, 187–199. [Google Scholar] [CrossRef]
- Sea-Bird Scientific, “Specifications for HyperOCR Radiometer”. Available online: https://www.seabird.com/hyperspectral-radiometers/hyperocr-radiometer/family?productCategoryId=54627869935 (accessed on 31 January 2019).
- TriOS, “RAMSES Technische Spezifikationen”, TriOS Mess- und Datentechnik. Available online: https://www.trios.de/ramses.html (accessed on 31 January 2019).
- Mueller, J.L.; Fargion, G.S.; McClain, C.R. (Eds.) Ocean Optics Protocols for Satellite Ocean Color Sensor Validation: Instrument Specifications, Characterization, and Calibration; NASA/TM-2003-21621/Rev-Vol II; NASA: Washington, DC, USA, 2003.
- Pulli, T.; Kärhä, P.; Ikonen, E. A method for optimizing the cosine response of solar UV diffusers. J. Geophys. Res. Atmos. 2013, 118, 7897–7904. [Google Scholar] [CrossRef]
- JCGM. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement (GUM), 1st ed.; JCGM 100, GUM 1995 with Minor Corrections; JCGM: Sèvres, France, September 2008; Available online: http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 31 January 2019).
- EUMETSAT. Requirements for Copernicus Ocean Colour Vicarious Calibration Infrastructure; Annex: Example of Quantified Uncertainty Budget; EUMETSAT: Darmstadt, Germany, 2017. [Google Scholar]
- Zibordi, G.; Voss, K.J. Chapter 3.1—In situ Optical Radiometry in the Visible and Near Infrared. In Optical Radiometry for Ocean Climate Measurements; GZibordi, I., Donlon, C., Parr, A., Eds.; Academic Press: Cambridge, MA, USA, 2014; Volume 47, pp. 247–304. [Google Scholar]
- Gergely, M.; Zibordi, G. Assessment of AERONET-OC LWN uncertainties. Metrologia 2014, 51, 40. [Google Scholar] [CrossRef]
- Talone, M.; Zibordi, G. Polarimetric characteristics of a class of hyperspectral radiometers. Appl. Opt. 2016, 55, 10092–10104. [Google Scholar] [CrossRef] [PubMed]
- IOCCG. International Network for Sensor Inter-Comparison and Uncertainty Assessment for Ocean Color Radiometry (INSITU-OCR) White Paper. 2012. Available online: http://www.ioccg.org/groups/INSITU-OCR_White-Paper.pdf (accessed on 7 February 2017).
- Alikas, K.; Ansko, I.; Vabson, V.; Ansper, A. Validation of Sentinel-3A/OLCI data over Estonian inland waters. In Proceedings of the AMT4 Sentinel FRM Workshop, Plymouth, UK, 20–21 June 2017. [Google Scholar]
- Ruddick, K. A Review of Commonly Used Fiducial Reference Measurement (FRM) Ocean Colour Radiometers (OCR) Used for Satellite OCR Validation. Technical Report TR-2. 2018. Available online: https://frm4soc.org/wp-content/uploads/filebase/FRM4SOC-TR2_TO_signedESA.pdf (accessed on 7 May 2019).
- Talone, M.; Zibordi, G.; Ansko, I.; Banks, A.C.; Kuusk, J. Stray light effects in above-water remote-sensing reflectance from hyperspectral radiometers. Appl. Opt. 2016, 55, 3966–3977. [Google Scholar] [CrossRef] [PubMed]
- Vabson, V.; Ansko, I.; Alikas, K.; Kuusk, J.; Vendt, R.; Reinat, A. Improving comparability of radiometric in situ measurements with Sentinel-3A/OLCI data. In Proceedings of the S3VT Sentinel-3 Validation Team meeting, Eumetsat, Darmstadt, Germany, 13–15 March 2018. [Google Scholar]
- Santer, B.D.; Wigley, T.M.; Boyle, J.S.; Gaffen, D.J.; Hnilo, J.J.; Nychka, D.; Parker, D.E.; Taylor, K.E. Statistical significance of trends and trend differences in layer-average atmospheric temperature time series. J. Geophys. Res. Atmos. 2000, 105, 7337–7356. [Google Scholar] [CrossRef]

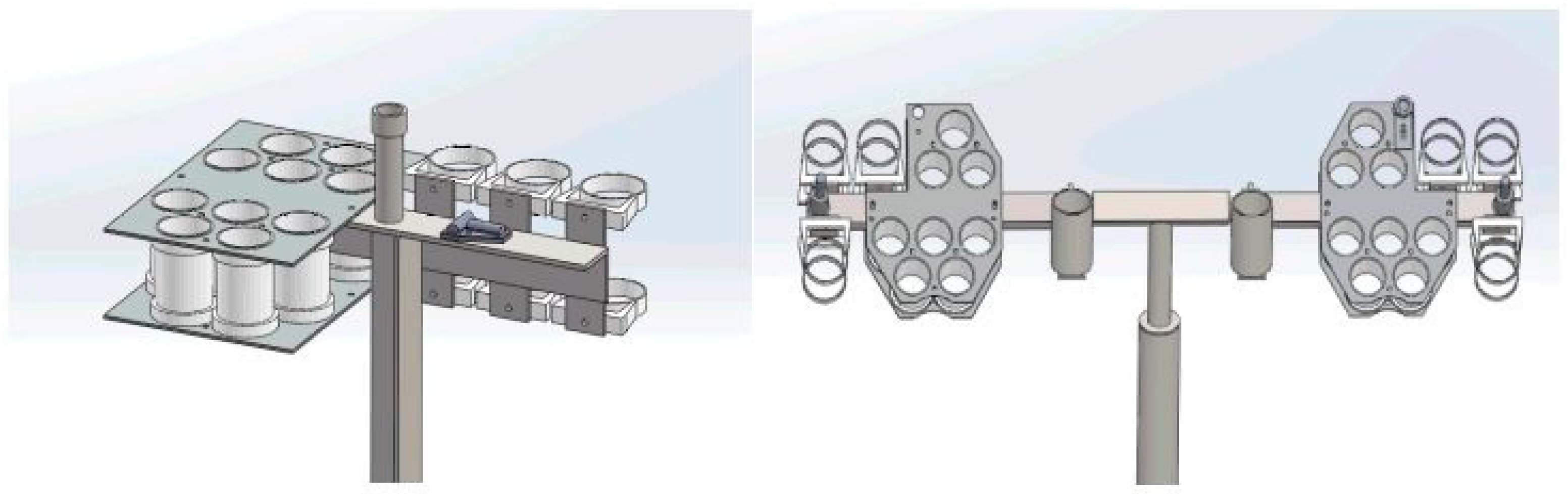




| Participant | Country | L-Radiance; E-Irradiance Sensor |
|---|---|---|
| Tartu Observatory (pilot) | Estonia | RAMSES (2 L, 1 E) WISP-3 (2 L, 1 E) |
| Alfred Wegener Institute | Germany | RAMSES (2 L, 2 E) |
| Royal Belgian Institute of Natural Sciences | Belgium | RAMSES (7 L, 4 E) |
| National Research Council of Italy | Italy | SR-3500 (1 L, 1 E) WISP-3 (2 L, 1 E) |
| University of Algarve | Portugal | RAMSES (2 L, 1 E) |
| University of Victoria | Canada | OCR-3000 (OCR-3000 is the predecessor of HyperOCR) (2 L, 1 E) |
| Satlantic; Sea Bird Scientific | Canada | HyperOCR (2 L, 1 E) |
| Plymouth Marine Laboratory | UK | HyperOCR (2 L, 1 E) |
| Helmholtz-Zentrum Geesthacht | Germany | RAMSES (2 L, 1 E) |
| University of Tartu | Estonia | RAMSES (1 L, 1 E) |
| Cimel Electronique S.A.S | France | SeaPRISM (1 L) |
| Parameter | RAMSES | HyperOCR | WISP-3 | SR-3500 | SeaPRISM |
|---|---|---|---|---|---|
| Field of View (L/E) | 7°/cos | 6°(According to the manufacturer, the HyperOCR radiance sensors 444 and 445 have 6° FOV) or 23°/cos | 3°/cos | 5°/cos | 1.2°/NA |
| Manual integration time | yes | yes | no | yes | no |
| Adaptive integration time | yes | yes | yes | yes | yes |
| Min. integration time, ms | 4 | 4 | 0.1 | 7.5 | NA |
| Max. integration time, ms | 4096 | 4096 | NA | 1000 | NA |
| Min. sampling interval, s | 5 | 5 | 10 | 2 | NA |
| Internal shutter | no | yes | no | yes | yes |
| Number of channels | 256 | 256 | 2048 | 1024 | 12 |
| Wavelength range, nm | 320…1050 | 320…1050 | 200…880 | 350…2500 | 400…1020 |
| Wavelength step, nm | 3.3 | 3.3 | 0.4 | 1.2/3.8/2.4 | NA |
| Spectral resolution, nm | 10 | 10 | 3 | 3/8/6 | 10 |
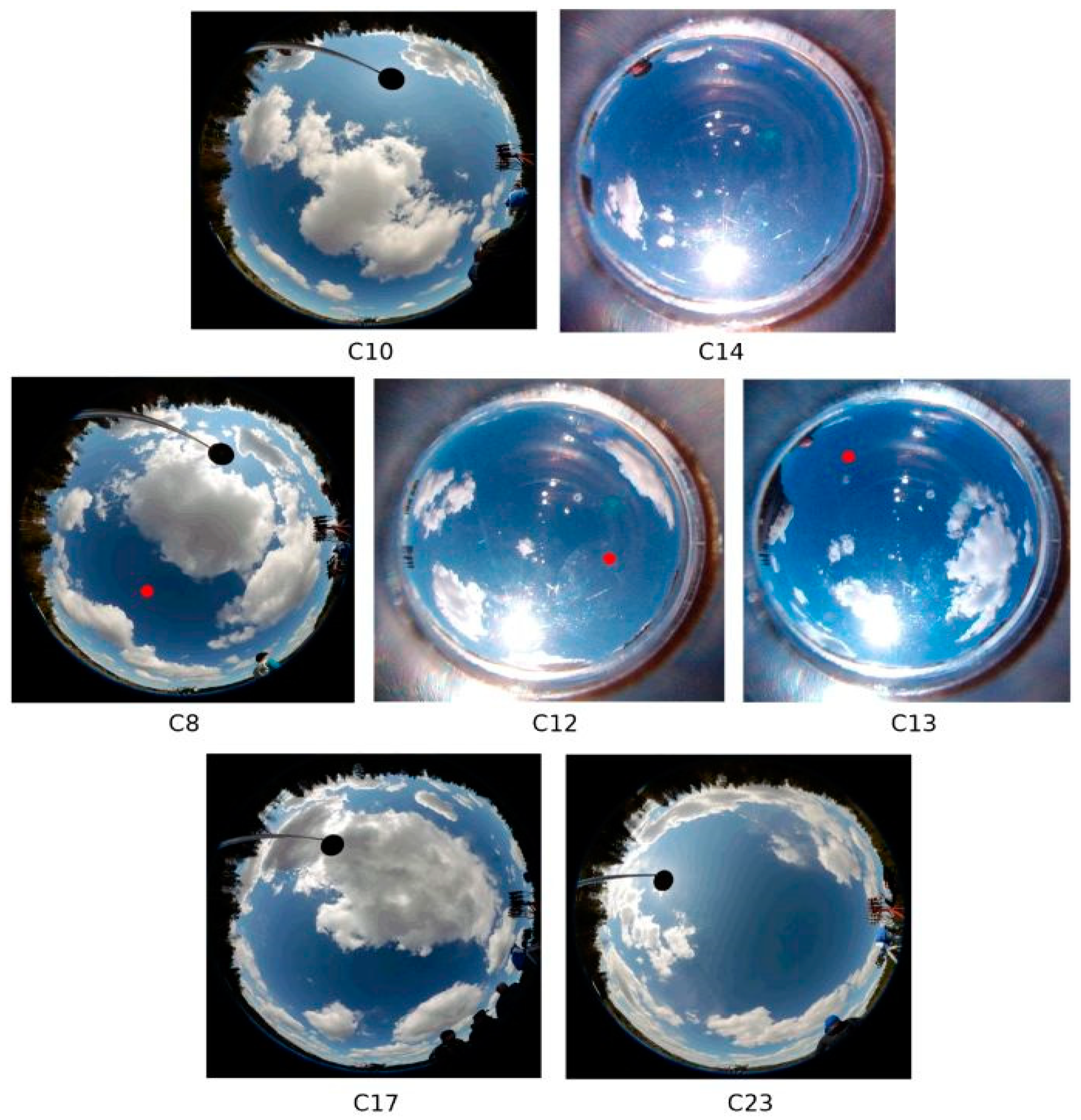
| Cast | Target | Time (UTC) | SZA | SAA | Relative VAA from Sun | VZA | Wind speed |
|---|---|---|---|---|---|---|---|
| C8 | Ld (blue sky) | 07:46:00–07:49:25 | 48° | 131° | 162° | 43° | NA |
| C10 | Ed | 08:07:00–08:12:00 | 46° | 137° | NA | NA | NA |
| C12 | Ed, Ld (blue sky) | 08:50:00–08:55:00 | 43° | 151° | 90° | 43° | NA |
| C13 | Ed, Ld (blue sky) | 09:00:00–09:03:05 | 42° | 154° | 134° | 58° | NA |
| C14 | Ed | 09:22:30–09:47:30 | 41° | 162° | NA | NA | NA |
| C17 | Lu (shadow) | 10:30:00–10:35:00 | 40° | 187° | 107° | 139° | 2 m s−1 |
| C23 | Lu (sunlit) | 11:56:00–12:01:00 | 44° | 217° | 143° | 130° | 1 m s−1 |
| 400 nm | 442.5 nm | 490 nm | 560 nm | 665 nm | 778.8 nm | 865 nm | |
|---|---|---|---|---|---|---|---|
| Certificate | 0.88 | 0.68 | 0.65 | 0.62 | 0.59 | 0.62 | 0.56 |
| Interpolation | 0.5 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Instability (sensor) | 0.05 | 0.03 | 0.04 | 0.03 | 0.04 | 0.03 | 0.02 |
| Polarization | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 |
| Nonlinearity | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.2 |
| Stray light | 0.9 | 0.7 | 0.3 | 0.3 | 0.7 | 0.9 | 1.0 |
| Temperature | 0.4 | 0.2 | 0.2 | 0.2 | 0.2 | 0.4 | 0.8 |
| Cosine error | 4.8 | 3.7 | 3 | 2.4 | 2.2 | 2.2 | 2 |
| Signal, type A | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 |
| Combined (k = 1) | 4.9 | 3.8 | 3.1 | 2.5 | 2.3 | 2.4 | 2.3 |
| Expanded (k = 2) | 9.8 | 7.6 | 6.2 | 5 | 4.6 | 4.8 | 4.6 |
| Variability (k = 2) | 9.7 | 7.6 | 6.2 | 5 | 4.7 | 4.9 | 4.6 |
| 400 nm | 442.5 nm | 490 nm | 560 nm | 665 nm | 778.8 nm | 865 nm | |
|---|---|---|---|---|---|---|---|
| Certificate | 1.2 | 0.78 | 0.76 | 0.73 | 0.71 | 0.73 | 1.35 |
| Interpolation | 0.5 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Instability (sensor) | 0.04 | 0.03 | 0.02 | 0.01 | 0.01 | 0.02 | 0.01 |
| Polarization | 0.1 | 0.1 | 0.2 | 0.2 | 0.4 | 0.4 | 0.4 |
| Nonlinearity | 0.4 | 0.4 | 0.5 | 0.5 | 0.5 | 0.6 | 0.6 |
| Stray light | 0.8 | 0.6 | 0.2 | 0.2 | 0.5 | 0.9 | 1 |
| Temperature | 0.4 | 0.2 | 0.2 | 0.2 | 0.2 | 0.4 | 0.8 |
| Alignment, FOV | 0.3 | 0.4 | 0.6 | 0.6 | 0.5 | 2 | 2.9 |
| Signal, type A | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.11 | 0.2 |
| Combined (k = 1) | 1.1 | 0.9 | 0.9 | 0.9 | 1 | 2.4 | 3.3 |
| Expanded (k = 2) | 2.2 | 1.8 | 1.8 | 1.8 | 2 | 4.8 | 6.6 |
| Variability (k = 2) | 2.2 | 1.8 | 2 | 1.6 | 2 | 4.8 | 6.6 |
| 400 nm | 442.5 nm | 490 nm | 560 nm | 665 nm | 778.8 nm | 865 nm | |
|---|---|---|---|---|---|---|---|
| Certificate | 1.2 | 0.78 | 0.76 | 0.73 | 0.71 | 0.73 | 1.35 |
| Interpolation | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Instability (sensor) | 0.04 | 0.03 | 0.02 | 0.01 | 0.01 | 0.02 | 0.01 |
| Polarization | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Nonlinearity | 0.7 | 0.8 | 0.9 | 1 | 1.1 | 1.2 | 1.3 |
| Stray light | 0.9 | 0.7 | 0.3 | 0.3 | 0.7 | 0.9 | 1 |
| Temperature | 0.4 | 0.2 | 0.2 | 0.2 | 0.2 | 0.4 | 0.8 |
| Alignment, FOV | 1.7 | 1.8 | 1.8 | 1.6 | 1.8 | 4 | 4.3 |
| Signal, type A | 0.04 | 0.07 | 0.11 | 0.11 | 0.21 | 0.55 | 0.72 |
| Combined (k = 1) | 2.2 | 2.1 | 2.1 | 1.9 | 2.3 | 4.2 | 4.6 |
| Expanded (k = 2) | 4.4 | 4.2 | 4.2 | 3.8 | 4.6 | 8.4 | 9.2 |
| Variability (k = 2) | 4.4 | 4.4 | 4.4 | 3.2 | 4.6 | 8.6 | 9.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vabson, V.; Kuusk, J.; Ansko, I.; Vendt, R.; Alikas, K.; Ruddick, K.; Ansper, A.; Bresciani, M.; Burmester, H.; Costa, M.; et al. Field Intercomparison of Radiometers Used for Satellite Validation in the 400–900 nm Range. Remote Sens. 2019, 11, 1129. https://doi.org/10.3390/rs11091129
Vabson V, Kuusk J, Ansko I, Vendt R, Alikas K, Ruddick K, Ansper A, Bresciani M, Burmester H, Costa M, et al. Field Intercomparison of Radiometers Used for Satellite Validation in the 400–900 nm Range. Remote Sensing. 2019; 11(9):1129. https://doi.org/10.3390/rs11091129
Chicago/Turabian StyleVabson, Viktor, Joel Kuusk, Ilmar Ansko, Riho Vendt, Krista Alikas, Kevin Ruddick, Ave Ansper, Mariano Bresciani, Henning Burmester, Maycira Costa, and et al. 2019. "Field Intercomparison of Radiometers Used for Satellite Validation in the 400–900 nm Range" Remote Sensing 11, no. 9: 1129. https://doi.org/10.3390/rs11091129
APA StyleVabson, V., Kuusk, J., Ansko, I., Vendt, R., Alikas, K., Ruddick, K., Ansper, A., Bresciani, M., Burmester, H., Costa, M., D’Alimonte, D., Dall’Olmo, G., Damiri, B., Dinter, T., Giardino, C., Kangro, K., Ligi, M., Paavel, B., Tilstone, G., ... Casal, T. (2019). Field Intercomparison of Radiometers Used for Satellite Validation in the 400–900 nm Range. Remote Sensing, 11(9), 1129. https://doi.org/10.3390/rs11091129