Surfaces of Revolution (SORs) Reconstruction Using a Self-Adaptive Generatrix Line Extraction Method from Point Clouds
Abstract
:1. Introduction
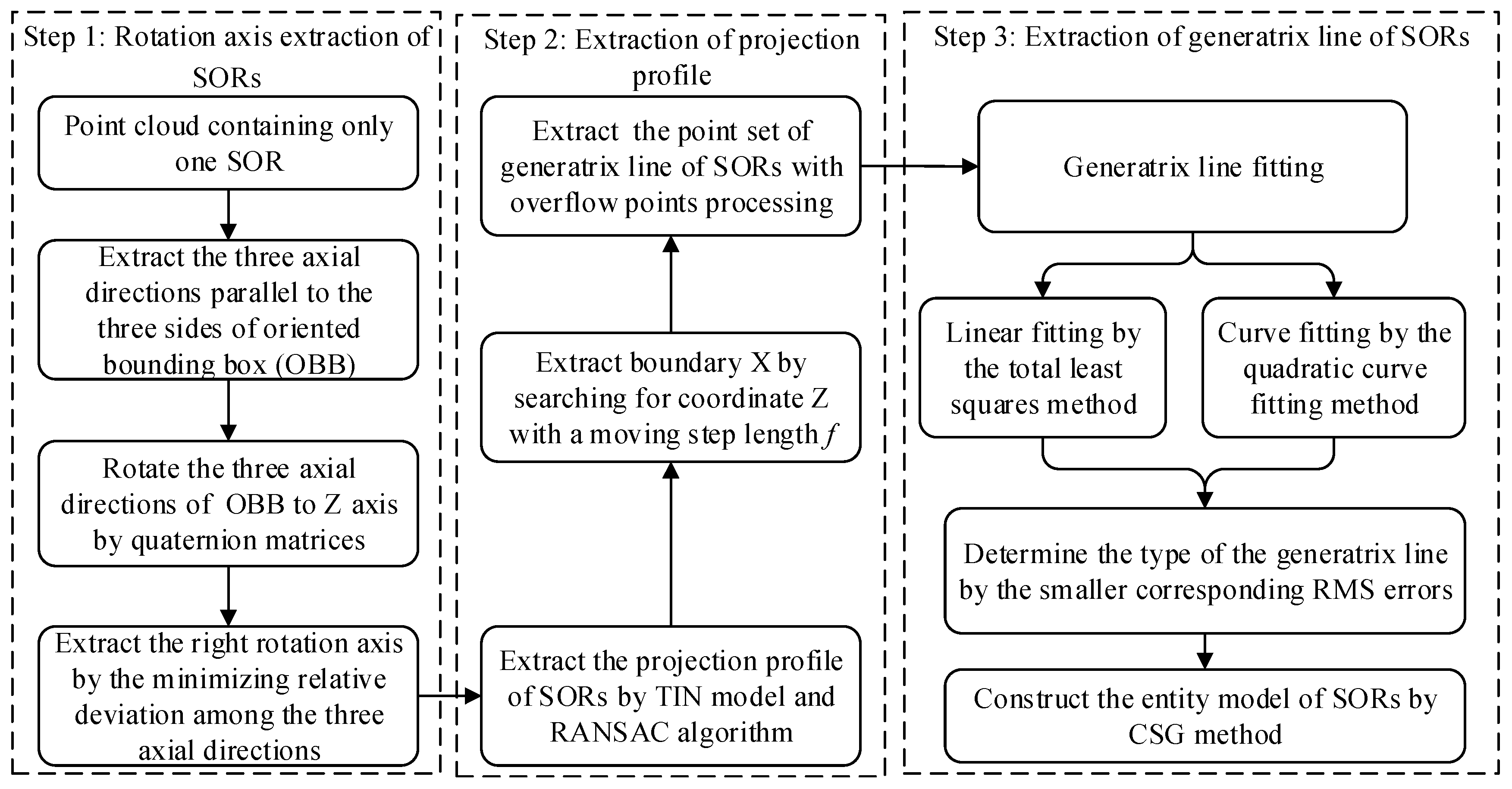
2. Methods
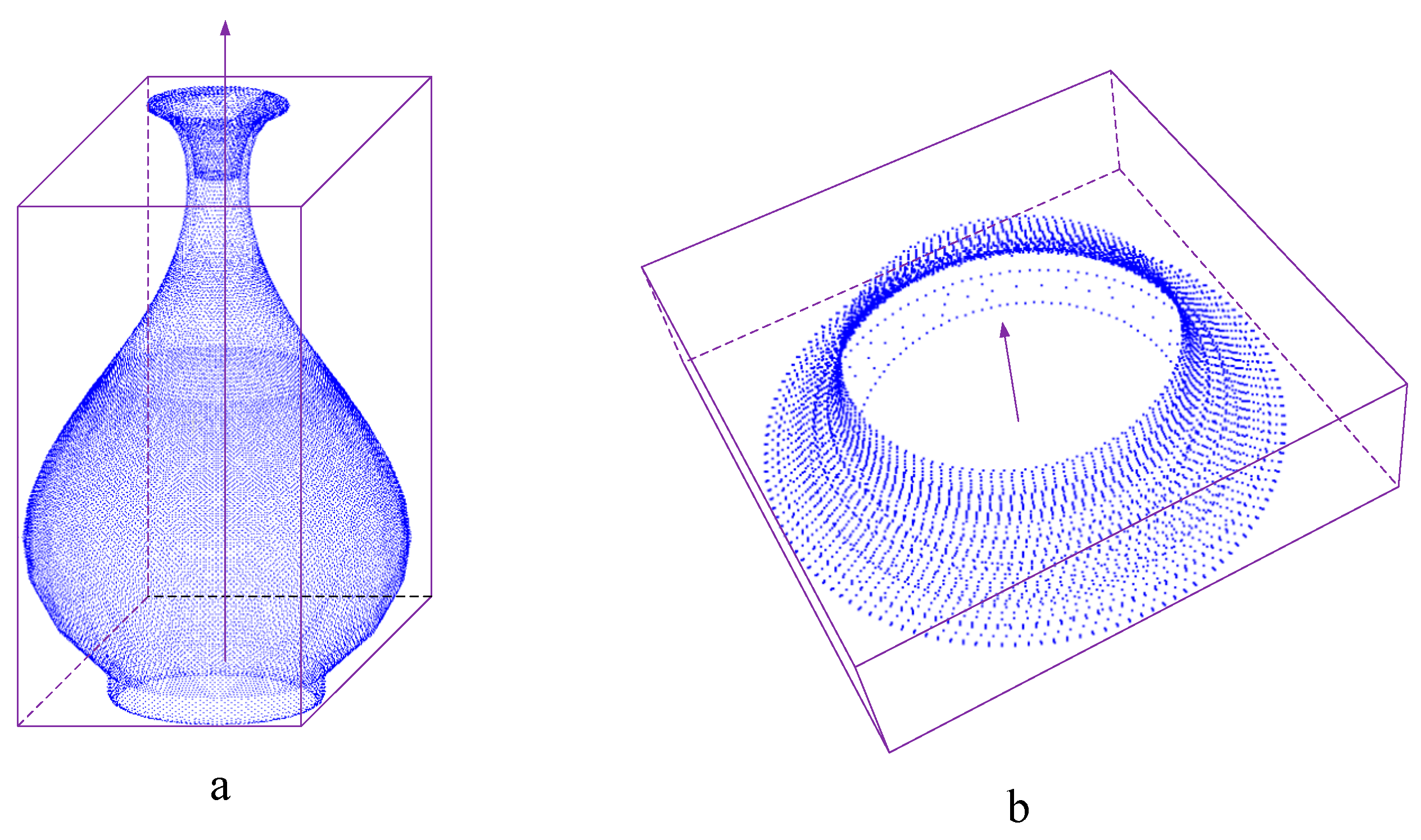
2.1. Rotation Axis Extraction of SORs
2.1.1. Quaternion Rotation
2.1.2. Extraction of Rotation Axis
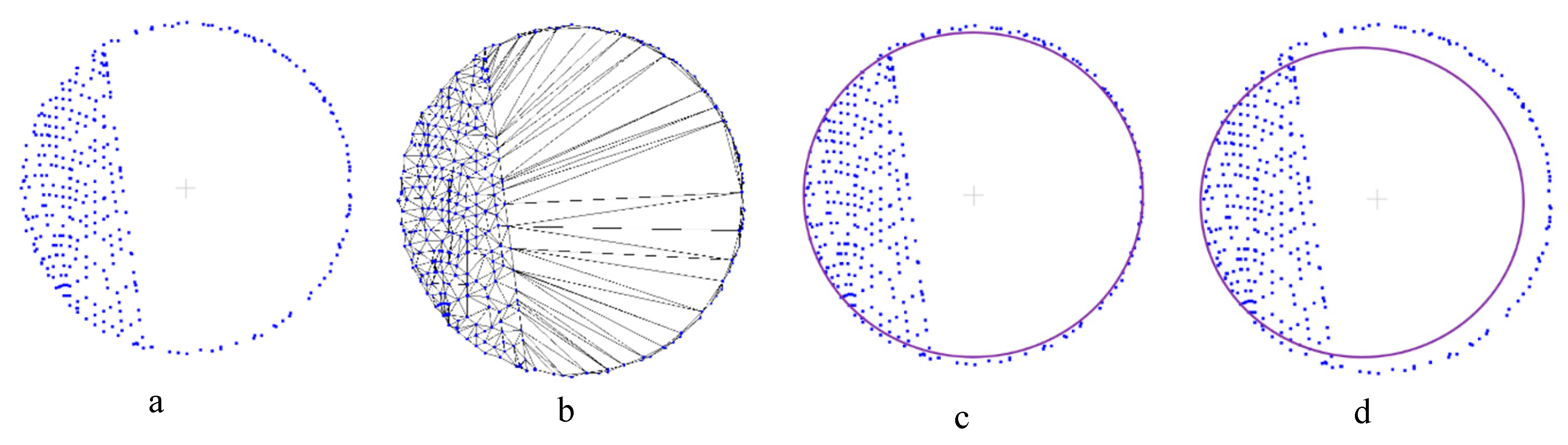
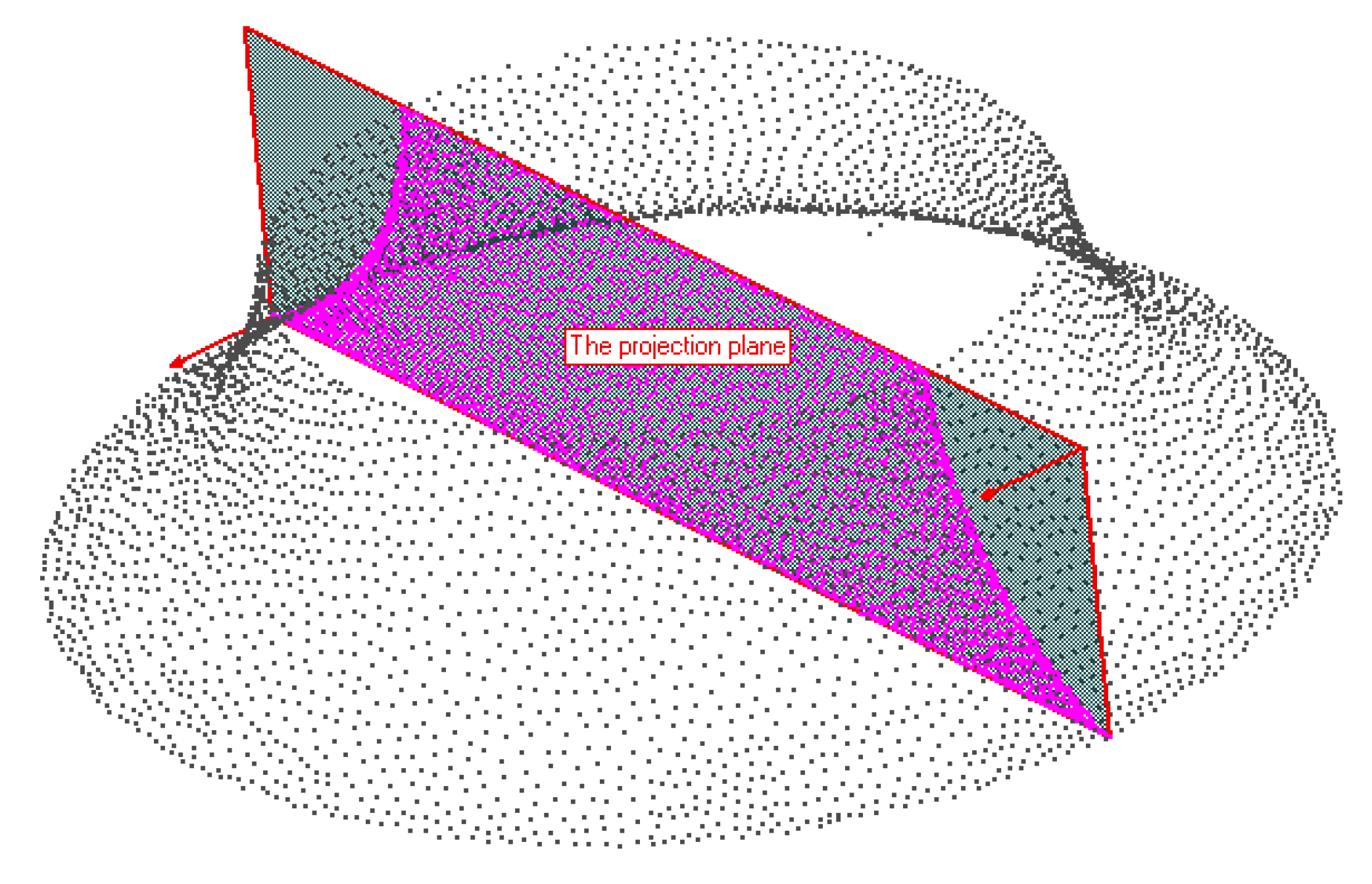
2.2. Extraction of Projection Profile
2.3. Extraction of the Generatrix Line of SORs
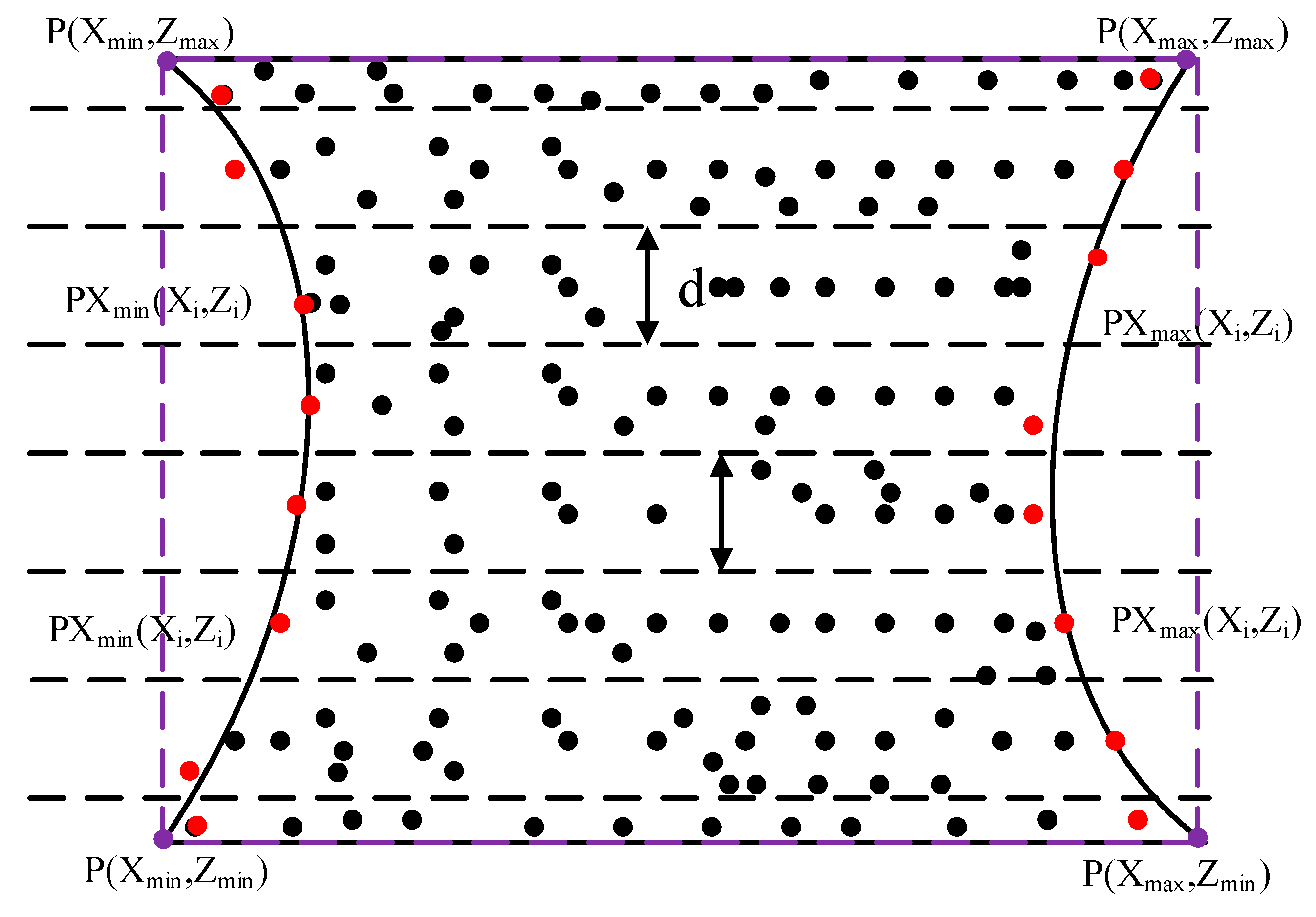
2.3.1. Extraction of the Point Set of Boundary X
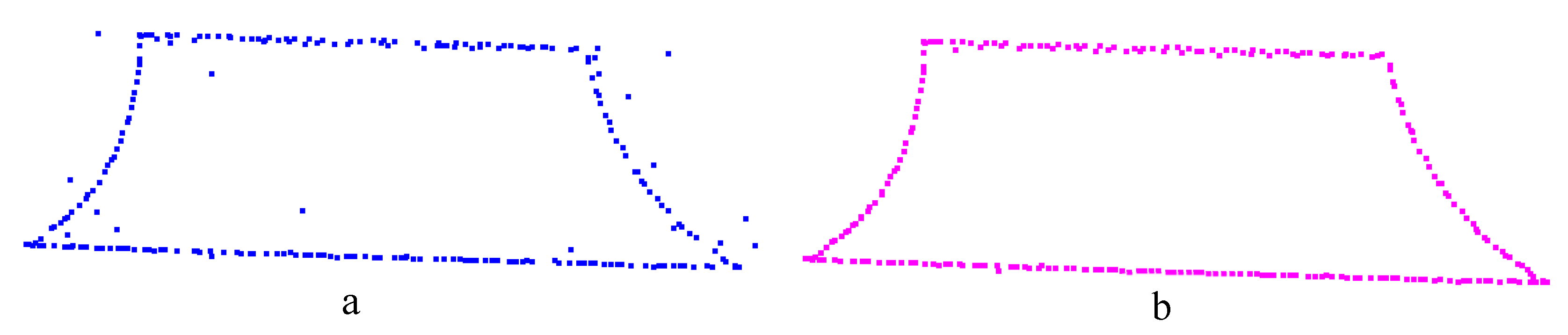
2.3.2. Extraction of the Point Set of the Generatrix Line of SORs
2.3.3. Generatrix Line Fitting
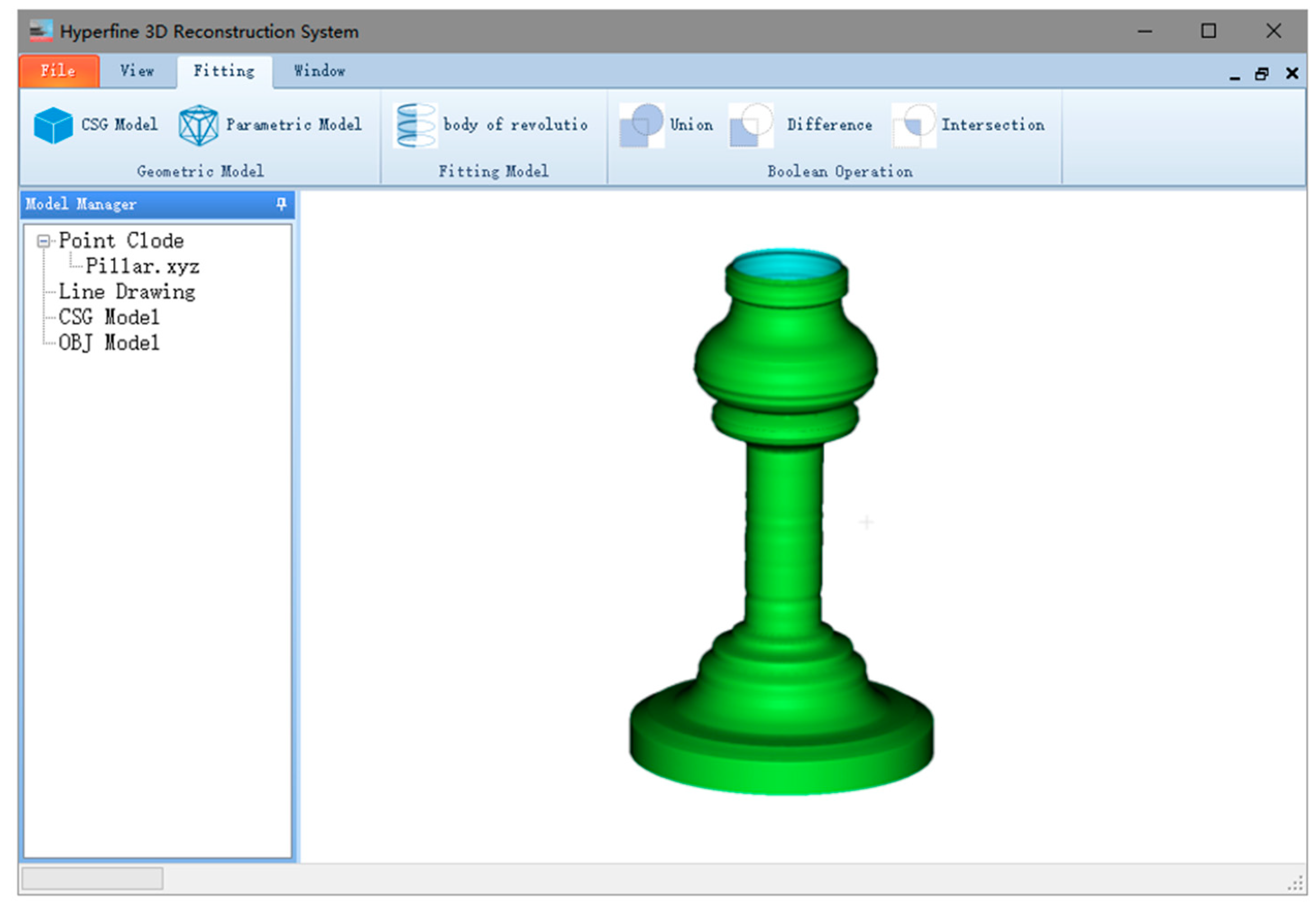
3. Experiments and Analysis
3.1. Comparison with the Curvature Computation Method
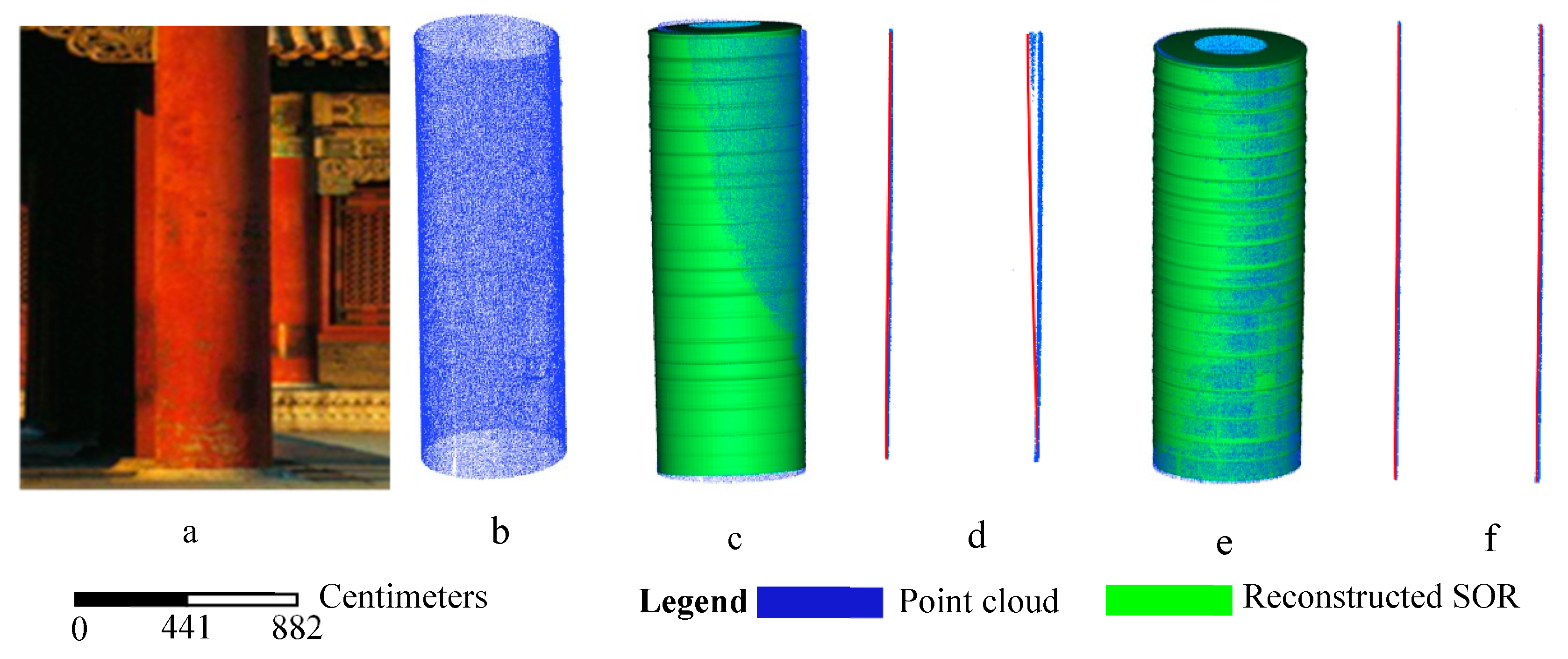
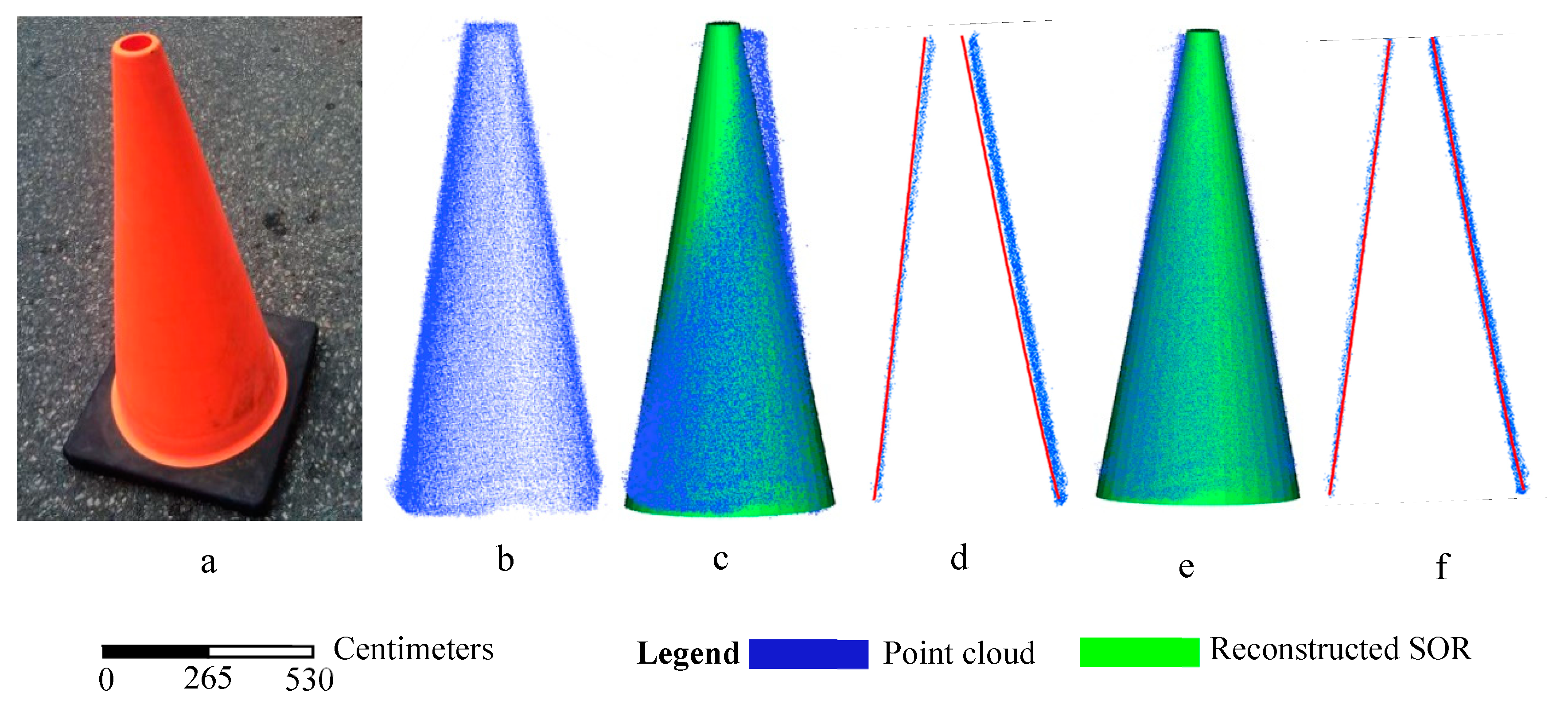
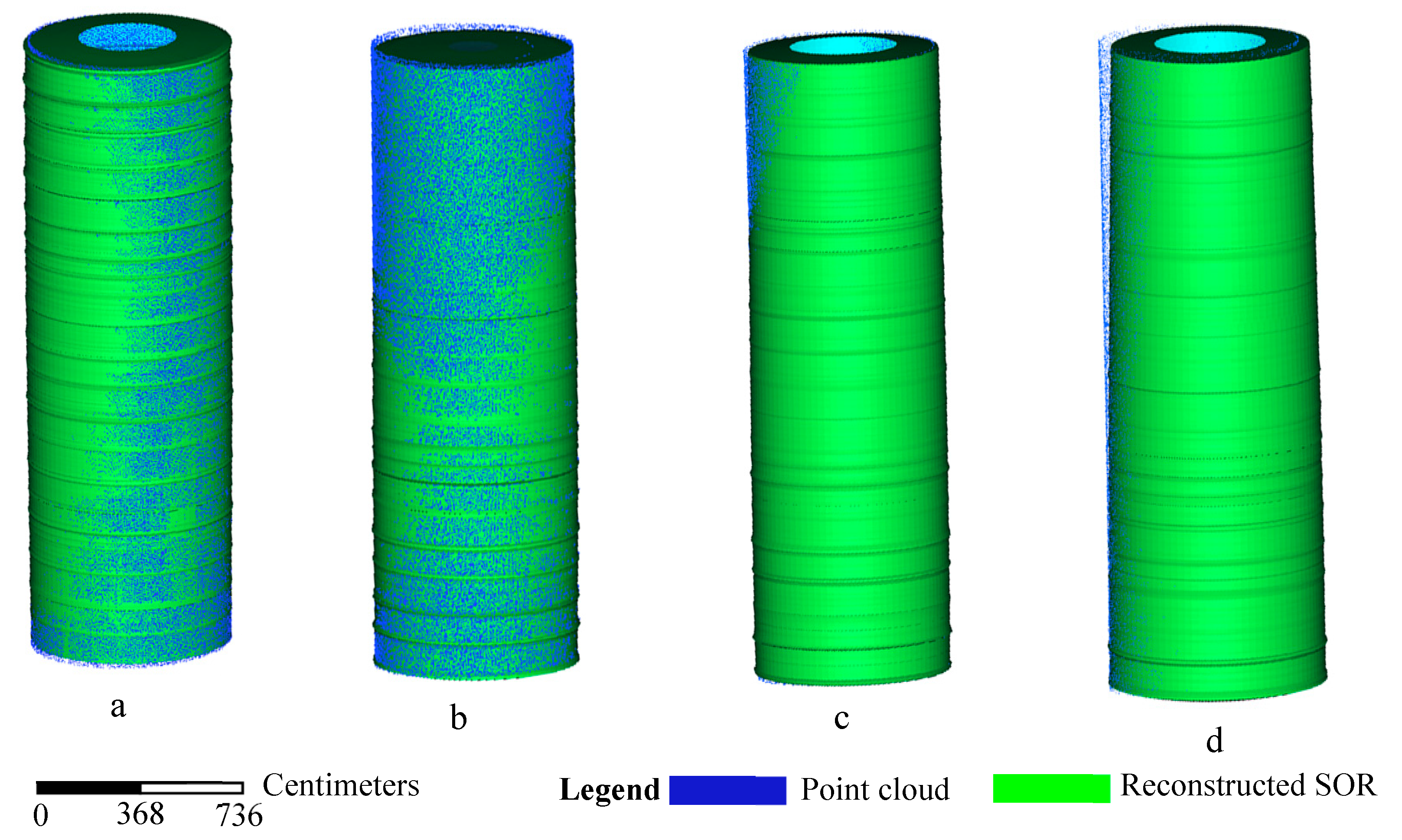
3.1.1. Simple SORs
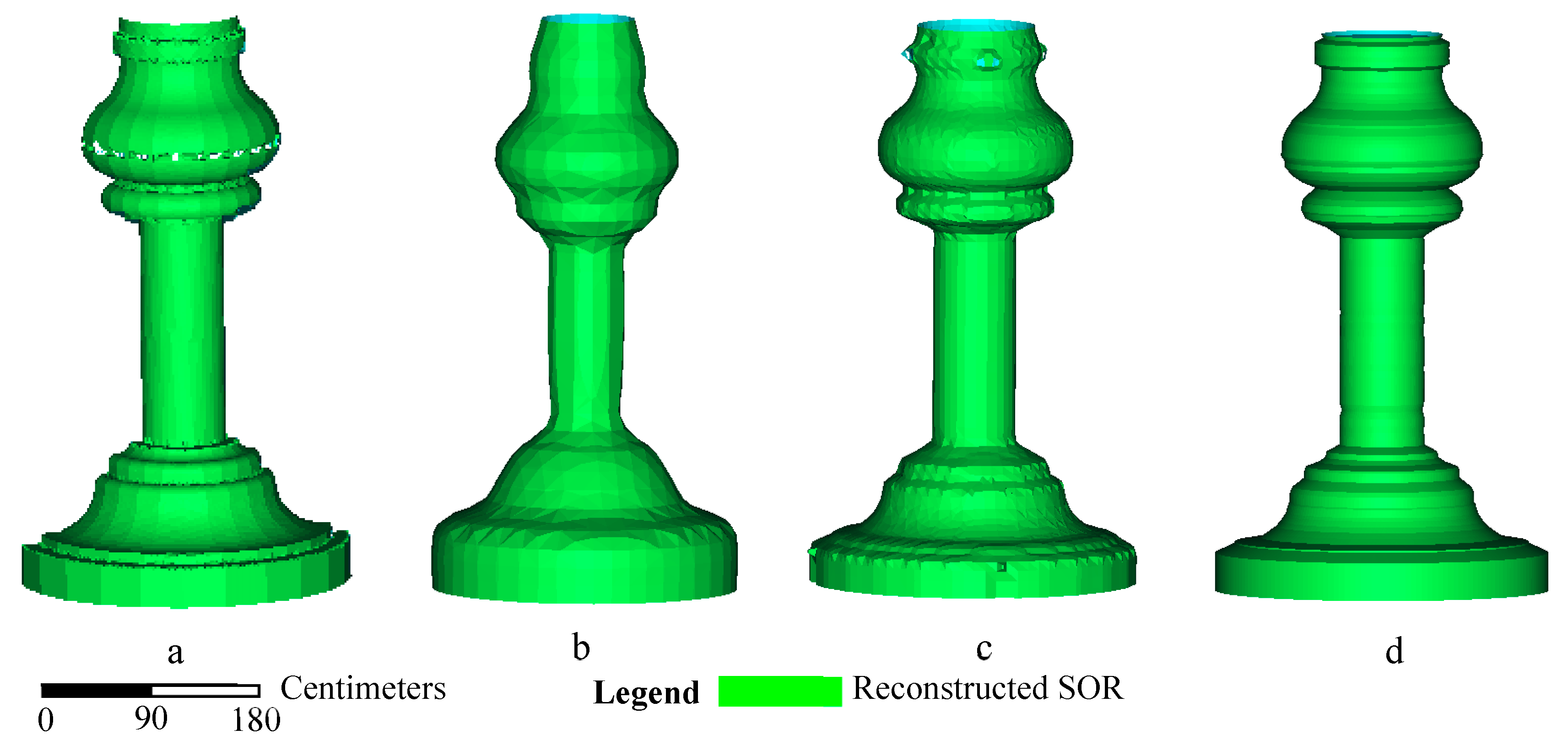
3.1.2. Tall-Thin SORs
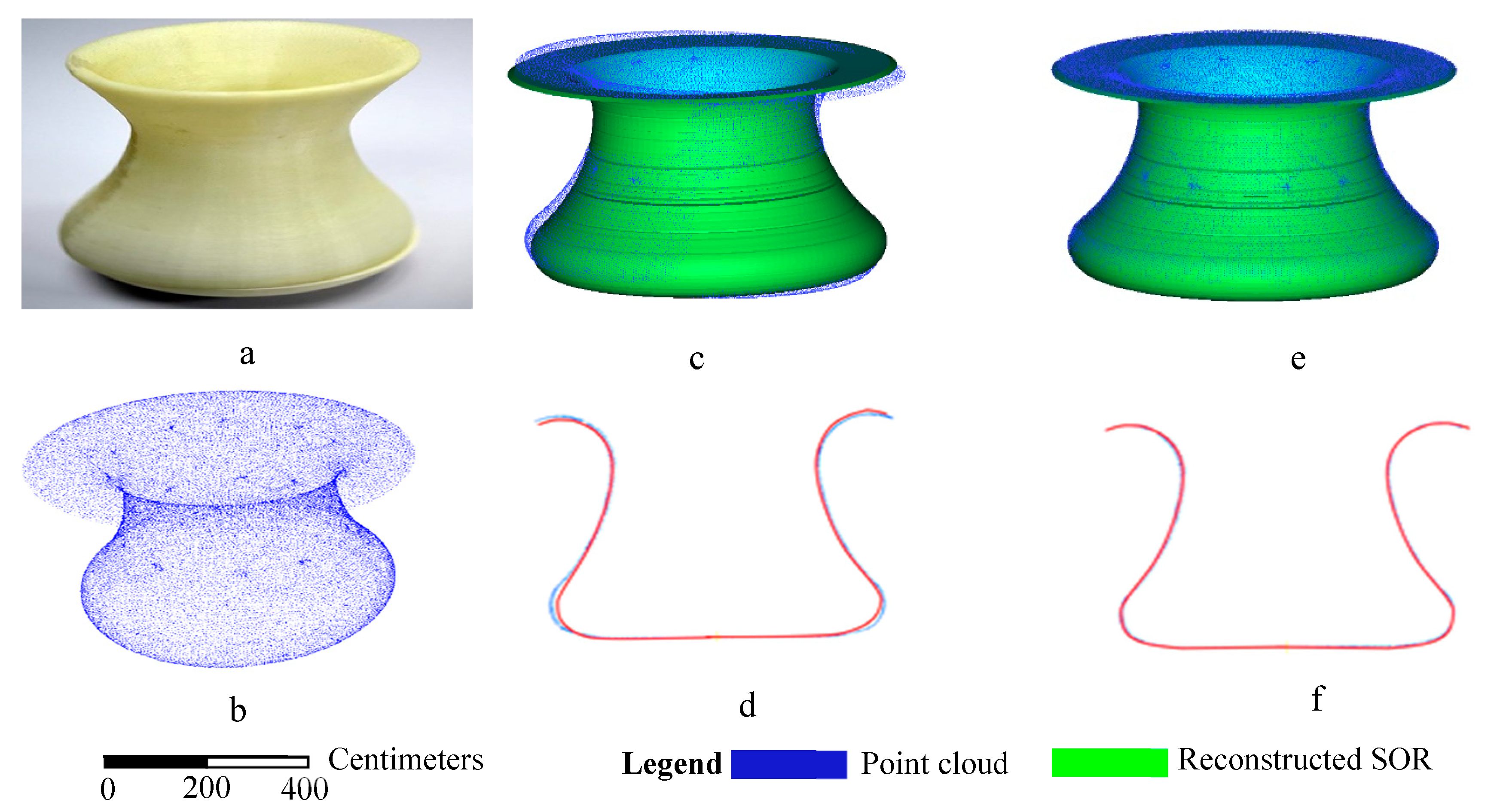
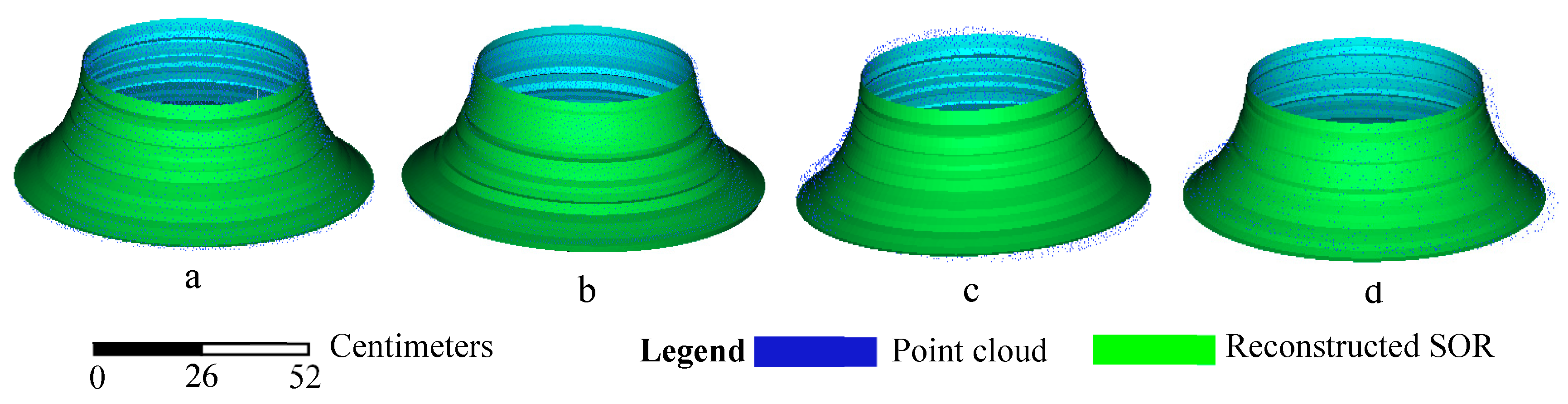
3.1.3. Short-Wide SORs
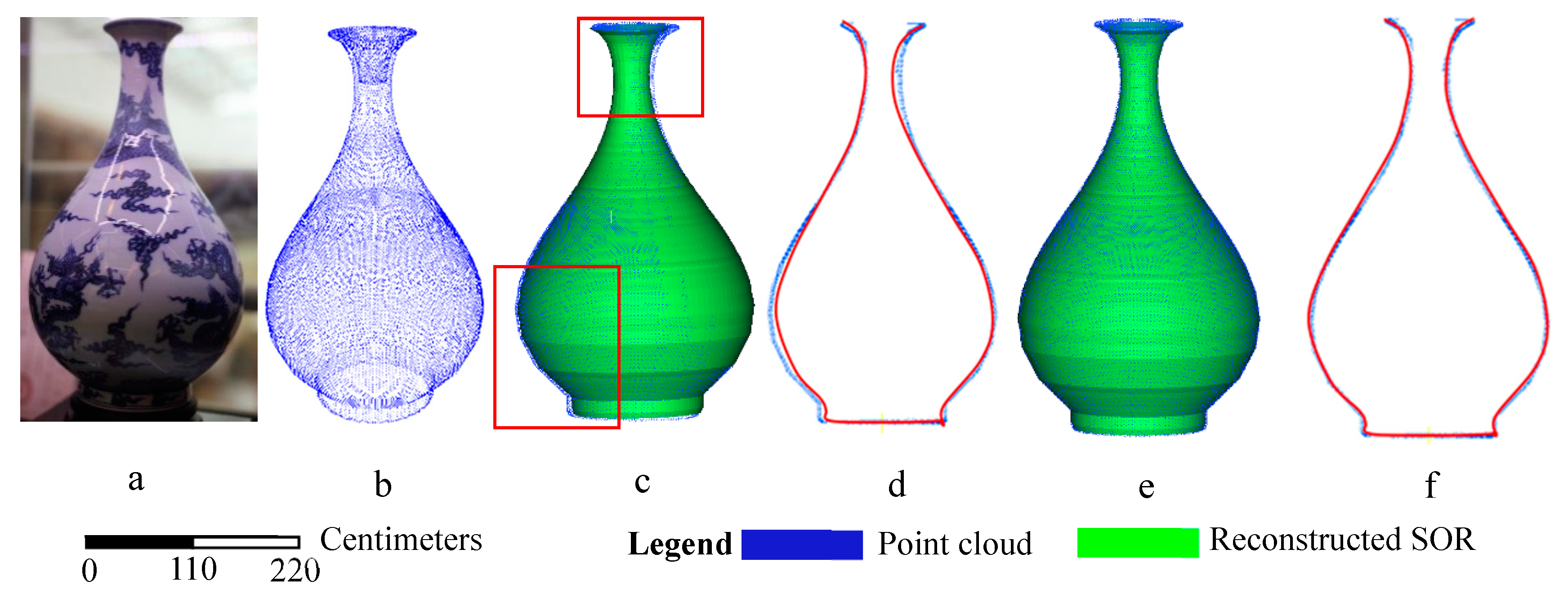
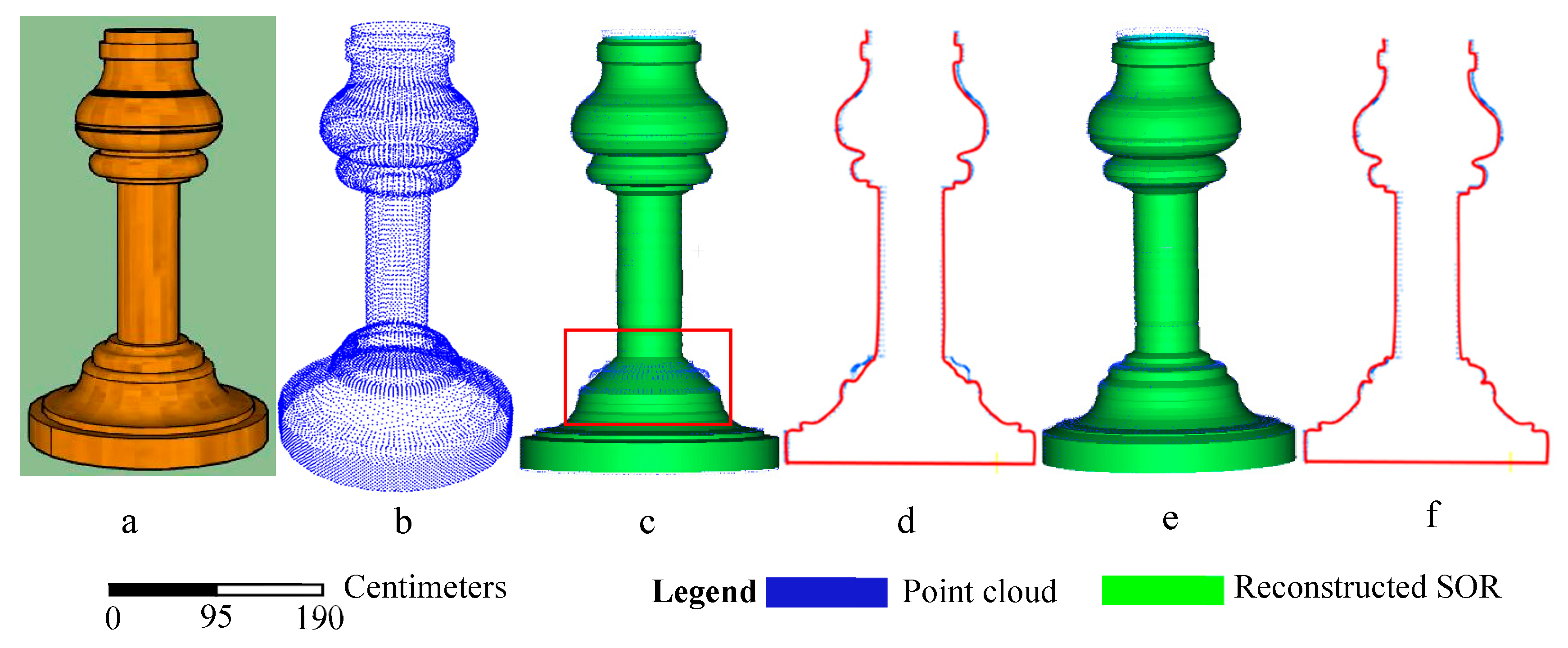
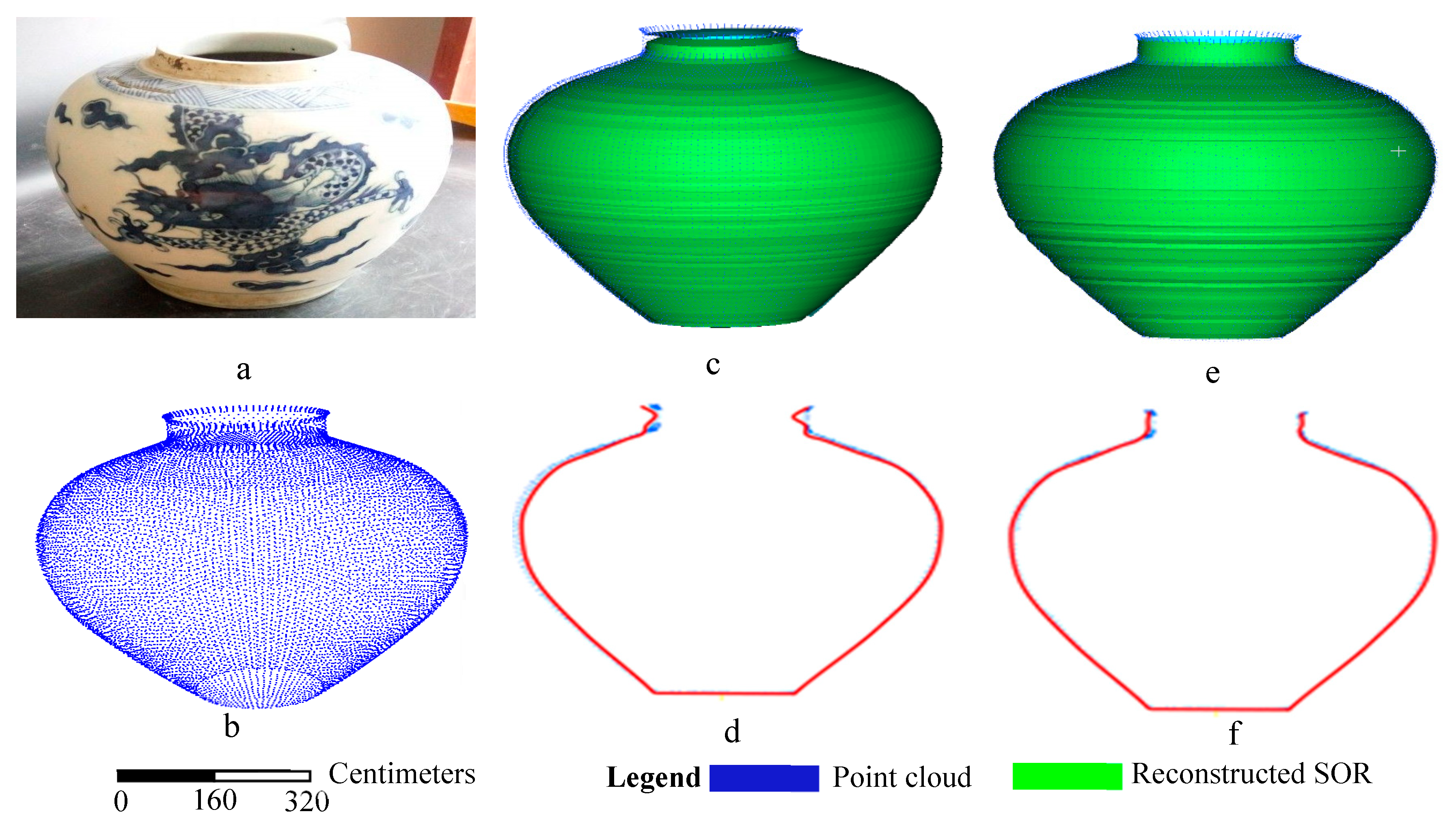
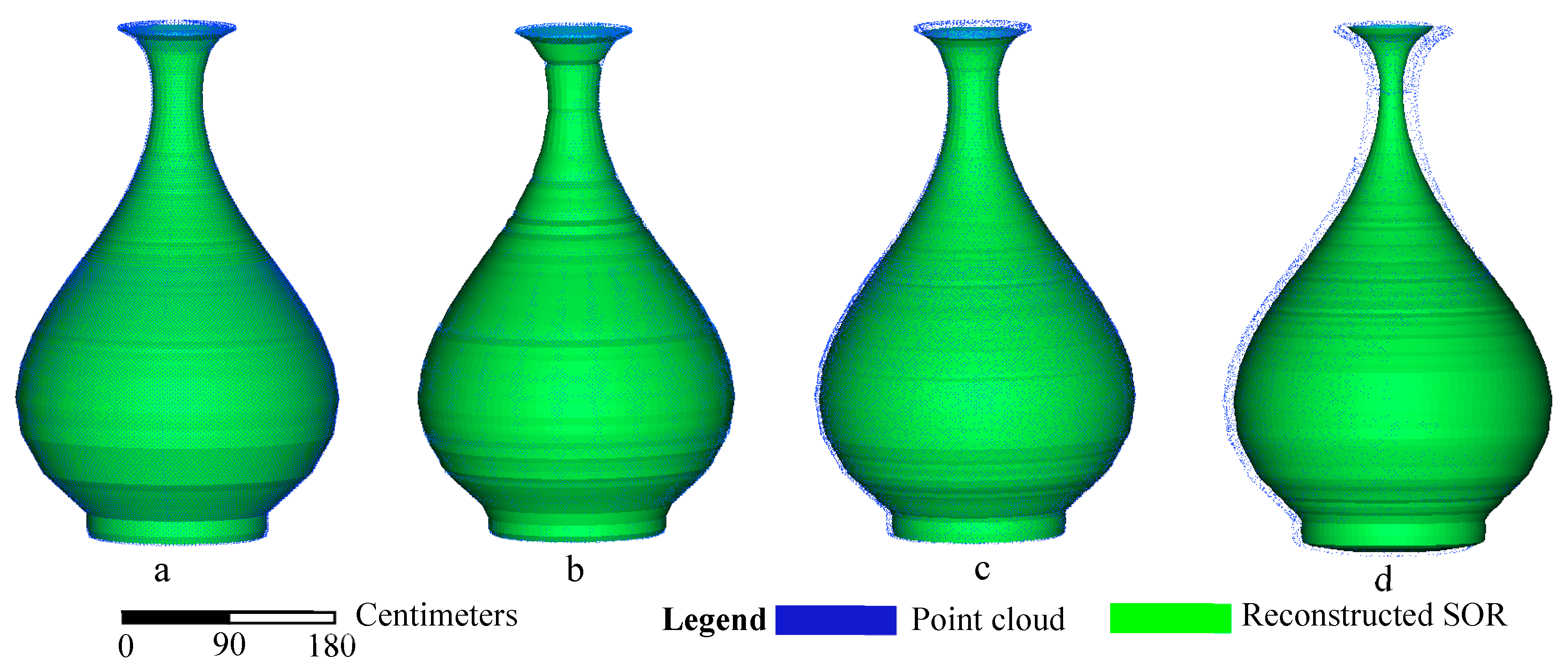
3.2. Comparison with Surface Reconstruction Methods
3.3. Accuracy Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hoover, A.; Jean-Baptiste, G.; Jiang, X.; Flynn, P.; Bunke, H.; Goldgof, D.; Bowyer, K.; Eggert, D.; FitzGibbon, A.; Fisher, R. An experimental comparison of range image segmentation algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 673–689. [Google Scholar] [CrossRef]
- Qian, X.; Huang, X. Reconstruction of surfaces of revolution with partial sampling. J. Comput. Appl. Math. 2004, 163, 211–217. [Google Scholar] [CrossRef]
- Colombo, C.; Del Bimbo, A.; Pernici, F. Metric 3D reconstruction and texture acquisition of surfaces of revolution from a single uncalibrated view. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 99–114. [Google Scholar] [CrossRef]
- Alcázar, J.G.; Goldman, R. Finding the axis of revolution of an algebraic surface of revolution. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2082–2093. [Google Scholar] [CrossRef]
- Weisstein, E.W. Surface of Revolution. From MathWorld--A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/SurfaceofRevolution.html (accessed on 1 April 2019).
- Kang, Z.; Zhang, L.; Wang, B.; Li, Z.; Jia, F. An Optimized BaySAC Algorithm for Efficient Fitting of Primitives in Point Clouds. IEEE Geosci. Sens. Lett. 2014, 11, 1096–1100. [Google Scholar] [CrossRef]
- Alcazar, J.G.; Goldman, R. Detecting When an Implicit Equation or a Rational Parametrization Defines a Conical or Cylindrical Surface, or a Surface of Revolution. IEEE Trans. Vis. Comput. Graph. 2017, 23, 2550–2559. [Google Scholar] [CrossRef] [PubMed]
- Willis, A.R.; Cooper, D.B. Computational reconstruction of ancient artifacts. IEEE Signal Proc. Mag. 2008, 25, 65–83. [Google Scholar] [CrossRef]
- Shi, X.; Goldman, R. Implicitizing rational surfaces of revolution using u-bases. Comput. Aided Geom. Des. 2012, 29, 348–362. [Google Scholar] [CrossRef]
- Vršek, J.; Lávička, M. Determining surfaces of revolution from their implicit equations. J. Comput. Appl. Math. 2015, 290, 125–135. [Google Scholar] [CrossRef]
- Lee, I.-K. Curve reconstruction from unorganized points. Comput. Aided Geom. Des. 2000, 17, 161–177. [Google Scholar] [CrossRef]
- Peternell, M.; Pottmann, H. Approximation in the space of planes: applications to geometric modeling and reverse engineering. Rev. Real Acad. Cienc. Ser. A Math 2002, 96, 243–256. [Google Scholar]
- Xu, Y.; Tuttas, S.; Hoegner, L.; Stilla, U. Geometric primitive extraction from point clouds of construction sites using vgs. IEEE Geosci. Sens. Lett. 2017, 14, 424–428. [Google Scholar] [CrossRef]
- Barazzetti, L. Parametric as-built model generation of complex shapes from point clouds. Adv. Eng. Inform. 2016, 30, 298–311. [Google Scholar] [CrossRef]
- Benkő, P.; Martin, R.R.; Várady, T. Algorithms for reverse engineering boundary representation models. Comput. Des. 2001, 33, 839–851. [Google Scholar] [CrossRef]
- Zhang, X. A system of generalized Sylvester quaternion matrix equations and its applications. Appl. Math. Comput. 2016, 273, 74–81. [Google Scholar] [CrossRef]
- Tran, T.-T.; Cao, V.-T.; Laurendeau, D. Extraction of cylinders and estimation of their parameters from point clouds. Comput. Graph. 2015, 46, 345–357. [Google Scholar] [CrossRef]
- Yang, L.; Uchiyama, H.; Normand, J.M.; Moreau, G.; Nagahara, H.; Taniguchi, R.I. Real-time surface of revolution reconstruction on dense SLAM. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 28–36. [Google Scholar]
- Pottmann, H.; Peternell, M.; Ravani, B. An introduction to line geometry with applications. Comput. Des. 1999, 31, 3–16. [Google Scholar] [CrossRef]
- Lou, C.; Zhu, L.; Ding, H. Identification and reconstruction of surfaces based on distance function. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 981–994. [Google Scholar] [CrossRef]
- Han, D.; Cooper, D.B.; Hahn, H.-s. Fast axis estimation from a segment of rotationally symmetric object. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, Rhode Island, 16–21 June 2012; pp. 1154–1161. [Google Scholar] [CrossRef]
- Pavlakos, G.; Daniilidis, K. Reconstruction of 3D pose for surfaces of revolution from range data. In Proceedings of the 2015 International Conference on 3D Vision (3DV), Lyon, France, 19–22 October 2015; pp. 648–656. [Google Scholar]
- Andrews, J.; Séquin, C.H. Generalized, basis-independent kinematic surface fitting. Comput. Des. 2013, 45, 615–620. [Google Scholar] [CrossRef]
- Son, H.; Kim, C.; Kim, C. Fully automated as-built 3D pipeline extraction method from laser-scanned data based on curvature computation. J. Comput. Civ. Eng. 2014, 29, 1943–5487. [Google Scholar] [CrossRef]
- Hoppe, H.; Derose, T.; Duchamp, T.; McDonald, J.; Stuetzle, W. Surface reconstruction from unorganized points. ACM SIGGRAPH Comput. Graph. 1992, 26, 71–78. [Google Scholar] [CrossRef]
- Li, Z.; Li, L.; Zou, F.; Yang, Y. 3D foot and shoe matching based on OBB and AABB. Int. J. Cloth. Sci. Technol. 2013, 25, 389–399. [Google Scholar] [CrossRef]
- Dasgupta, K.; Soman, S.A. Line parameter estimation using phasor measurements by the total least squares approach. In Proceedings of the IEEE Power & Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Ouyang, D.; Feng, H.-Y. Reconstruction of 2D polygonal curves and 3D triangular surfaces via clustering of Delaunay circles/spheres. Comput. Des. 2011, 43, 839–847. [Google Scholar] [CrossRef]
- Shakarji, C.M.; Srinivasan, V. Theory and Algorithms for Weighted Total Least-Squares Fitting of Lines, Planes, and Parallel Planes to Support Tolerancing Standards. J. Comput. Inf. Sci. Eng. 2013, 13, 031008. [Google Scholar] [CrossRef]
- Zhang, J.; Duan, M.; Yan, Q.; Lin, X. Automatic Vehicle Extraction from Airborne LiDAR Data Using an Object-Based Point Cloud Analysis Method. Remote Sens. 2014, 6, 8405–8423. [Google Scholar] [CrossRef]
- Cazals, F.; Giesen, J. Delaunay Triangulation Based Surface Reconstruction. Eff. Comput. Geom. Curves Surf. 2006, 231–276. [Google Scholar]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 29. [Google Scholar] [CrossRef]
- Filin, S.; Pfeifer, N. Segmentation of airborne laser scanning data using a slope adaptive neighborhood. ISPRS J. Photogramm. Sens. 2006, 60, 71–80. [Google Scholar] [CrossRef]
- Manson, J.; Petrova, G.; Schaefer, S. Streaming Surface Reconstruction Using Wavelets. Comput. Graph. Forum 2008, 27, 1411–1420. [Google Scholar] [CrossRef]
- Chiang, P.; Zheng, J.; Mak, K.H.; Thalmann, N.M.; Cai, Y. Progressive surface reconstruction for heart mapping procedure. Comput. Des. 2012, 44, 289–299. [Google Scholar] [CrossRef]
- Cuomo, S.; Galletti, A.; Giunta, G.; Starace, A. Surface reconstruction from scattered point via RBF interpolation on GPU. In Proceedings of the 2013 Federated Conference on Computer Science and Information Systems (FedCSIS), Krakow, Poland, 8–11 September 2013; pp. 433–440. [Google Scholar]
- Vosselman, G.; Dijkman, S. 3D building model reconstruction from point clouds and ground plans. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2001, 34, 37–44. [Google Scholar]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Wang, W.; Sakurada, K.; Kawaguchi, N. Incremental and Enhanced Scanline-Based Segmentation Method for Surface Reconstruction of Sparse LiDAR Data. Remote Sens. 2016, 8, 967. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, J. Segmentation-Based Filtering of Airborne LiDAR Point Clouds by Progressive Densification of Terrain Segments. Remote Sens. 2014, 6, 1294–1326. [Google Scholar] [CrossRef]
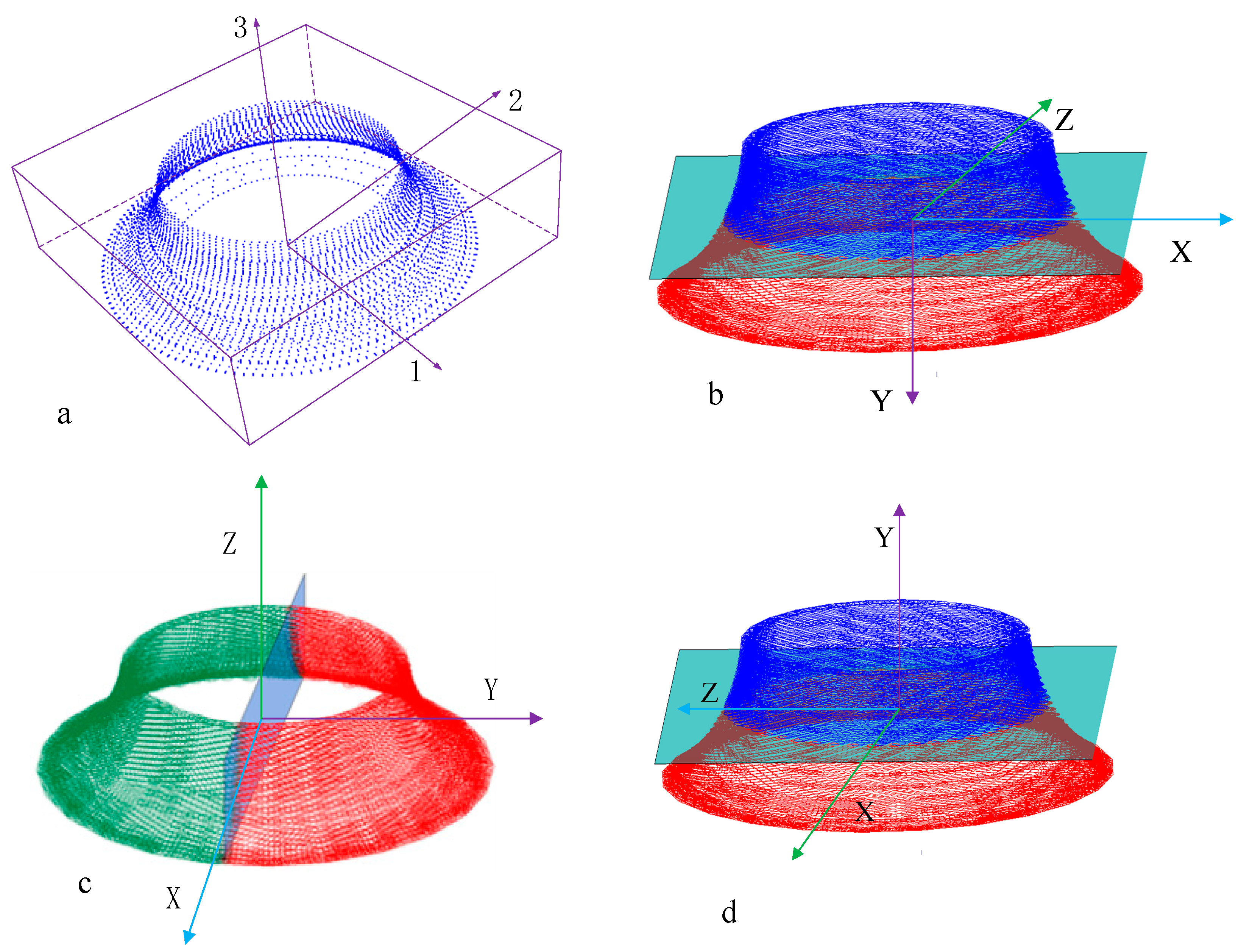
| Axial Direction | Number of Points M | Number of Points N | Number of Points M-N | Relative Deviation |
|---|---|---|---|---|
| 1 | 21,668 | 15,620 | 6048 | 0.613 |
| 2 | 21,668 | 10,966 | 10,702 | 0.02 |
| 3 | 21,668 | 6043 | 15,625 | 1.586 |
| Objects | Parameters | Curvature Computation Method | Proposed Method | Percentage Improvement |
|---|---|---|---|---|
| Cylinder | RMS (mm) | 0.42 | 0.29 | 30.1% |
| Time (ms) | 2151 | 1039 | 51.7% | |
| Frustum of a cone | RMS (mm) | 0.56 | 0.29 | 41.1% |
| Time (ms) | 1928 | 1001 | 48.1% |
| Objects | Parameters | Curvature Computation Method | Proposed Method | Percentage Improvement |
|---|---|---|---|---|
| Vase | RMS (mm) | 0.35 | 0.24 | 31.4% |
| Time (ms) | 2450 | 1835 | 25.1% | |
| Pillar | RMS (mm) | 0.43 | 0.30 | 30.2% |
| Time (ms) | 1836 | 1349 | 26.5% |
| Objects | Parameters | Curvature Computation Method | Proposed Method | Percentage Improvement |
|---|---|---|---|---|
| Pot | RMS (mm) | 0.51 | 0.21 | 58.8% |
| Time (ms) | 4020 | 3012 | 25.1% | |
| Ceramic | RMS (mm) | 0.33 | 0.23 | 30.3% |
| Time (ms) | 1548 | 1113 | 28.1% |
| Parameters | Delaunay | Poisson | RBF | Proposed Method |
|---|---|---|---|---|
| RMS (mm) | 0.06 | 0.58 | 0.45 | 0.30 |
| Time (ms) | 1936 | 1489 | 1523 | 1349 |
| Sampling Rate | 100% | 75% | 50% | 25% | |
|---|---|---|---|---|---|
| Simple SOR | Number of points | 148,400 | 111,300 | 74,200 | 37,100 |
| RMS (mm) | 0.28 | 0.88 | 3.9 | 4.5 | |
| Tall-thin SOR | Number of points | 36,114 | 27,085 | 18,057 | 9028 |
| RMS (mm) | 0.32 | 0.85 | 3.77 | 4.81 | |
| Short-wide SOR | Number of points | 10,131 | 7598 | 5065 | 2532 |
| RMS (mm) | 0.26 | 0.81 | 4.47 | 5.54 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Huang, M.; Li, S.; Ma, C. Surfaces of Revolution (SORs) Reconstruction Using a Self-Adaptive Generatrix Line Extraction Method from Point Clouds. Remote Sens. 2019, 11, 1125. https://doi.org/10.3390/rs11091125
Liu X, Huang M, Li S, Ma C. Surfaces of Revolution (SORs) Reconstruction Using a Self-Adaptive Generatrix Line Extraction Method from Point Clouds. Remote Sensing. 2019; 11(9):1125. https://doi.org/10.3390/rs11091125
Chicago/Turabian StyleLiu, Xianglei, Ming Huang, Shanlei Li, and Chaoshuai Ma. 2019. "Surfaces of Revolution (SORs) Reconstruction Using a Self-Adaptive Generatrix Line Extraction Method from Point Clouds" Remote Sensing 11, no. 9: 1125. https://doi.org/10.3390/rs11091125
APA StyleLiu, X., Huang, M., Li, S., & Ma, C. (2019). Surfaces of Revolution (SORs) Reconstruction Using a Self-Adaptive Generatrix Line Extraction Method from Point Clouds. Remote Sensing, 11(9), 1125. https://doi.org/10.3390/rs11091125





