Improving Jujube Fruit Tree Yield Estimation at the Field Scale by Assimilating a Single Landsat Remotely-Sensed LAI into the WOFOST Model
Abstract
:1. Introduction
2. Materials and Methods
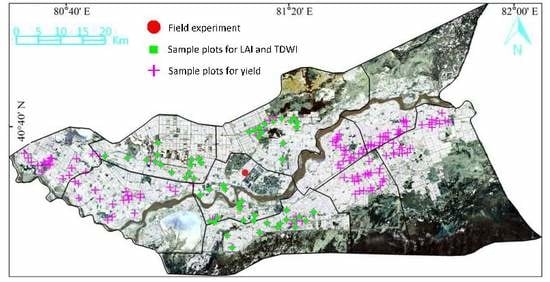
2.1. Study Region
2.2. Research Framework
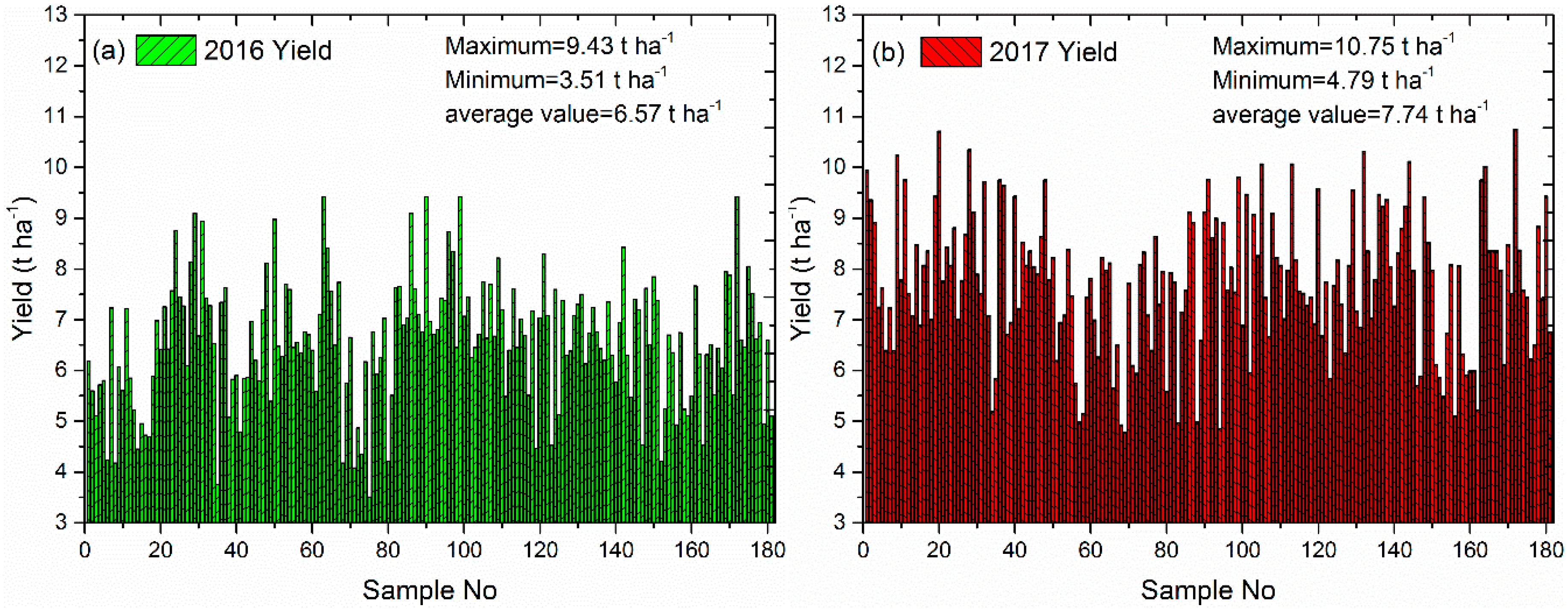
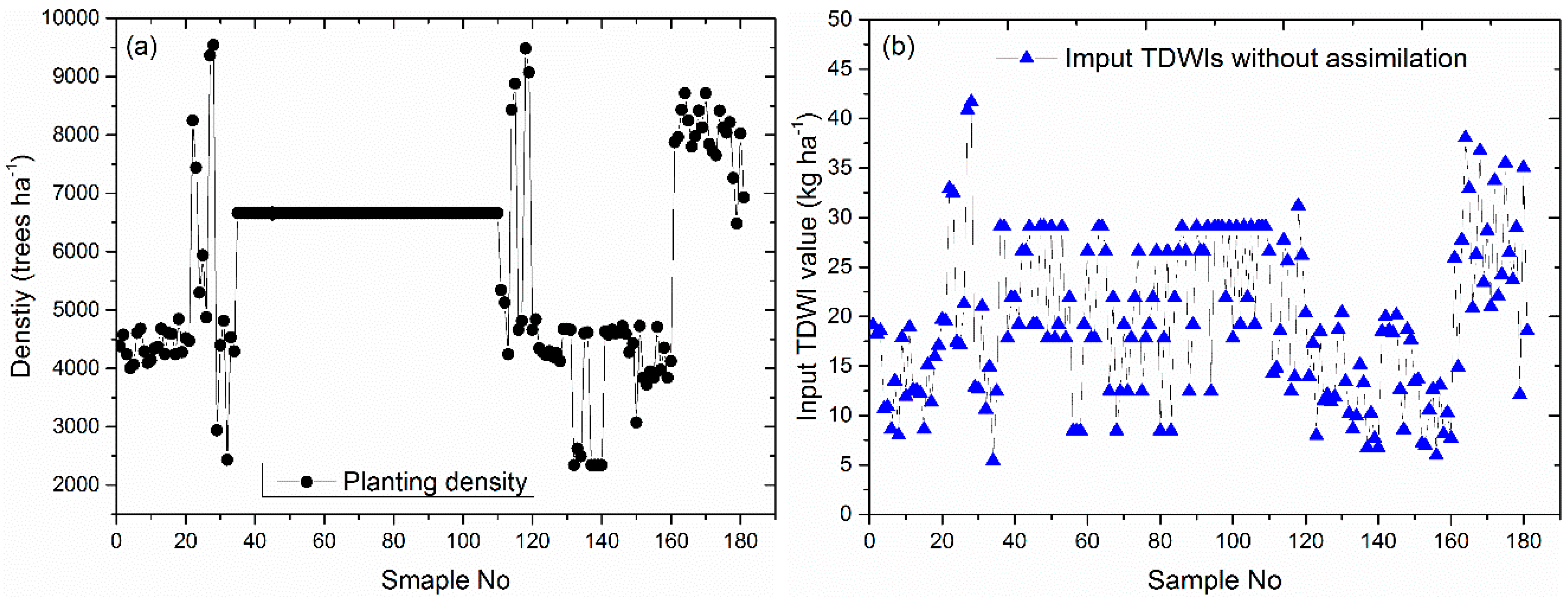
- Model calibration and yield prediction without forcing LAI: The WOFOST model parameters were calibrated and validated using field experimental data (jujube, soil, and weather data). Default values calculated using the planting density of each orchard multiplied by the average TDWI per tree were input into the calibrated model to predict yields of 181 orchard samples.
- Yield prediction using remotely-sensed vegetation indices (VIs): The correlations between the vegetation index obtained from Landsat data during the main growing period and yield data were analyzed to determine the best modeling time. A single or composite vegetation index with highest correlation was chosen to establish the yield prediction model for 181 sample spots. The prediction accuracy was cross-validated using two years of yield data.
- Yield estimation after forcing LAI: A statistical regression model between LAI and the remotely-sensed vegetation index was firstly established for LAI estimation of 181 samples. Then, a single LAI (near to maximum LAI stages) derived from Landsat data was forced into the calibrated WOFOST model to re-calculate TDWIs, thereby re-driving the model for yield prediction. The yield of 181 samples was re-estimated.
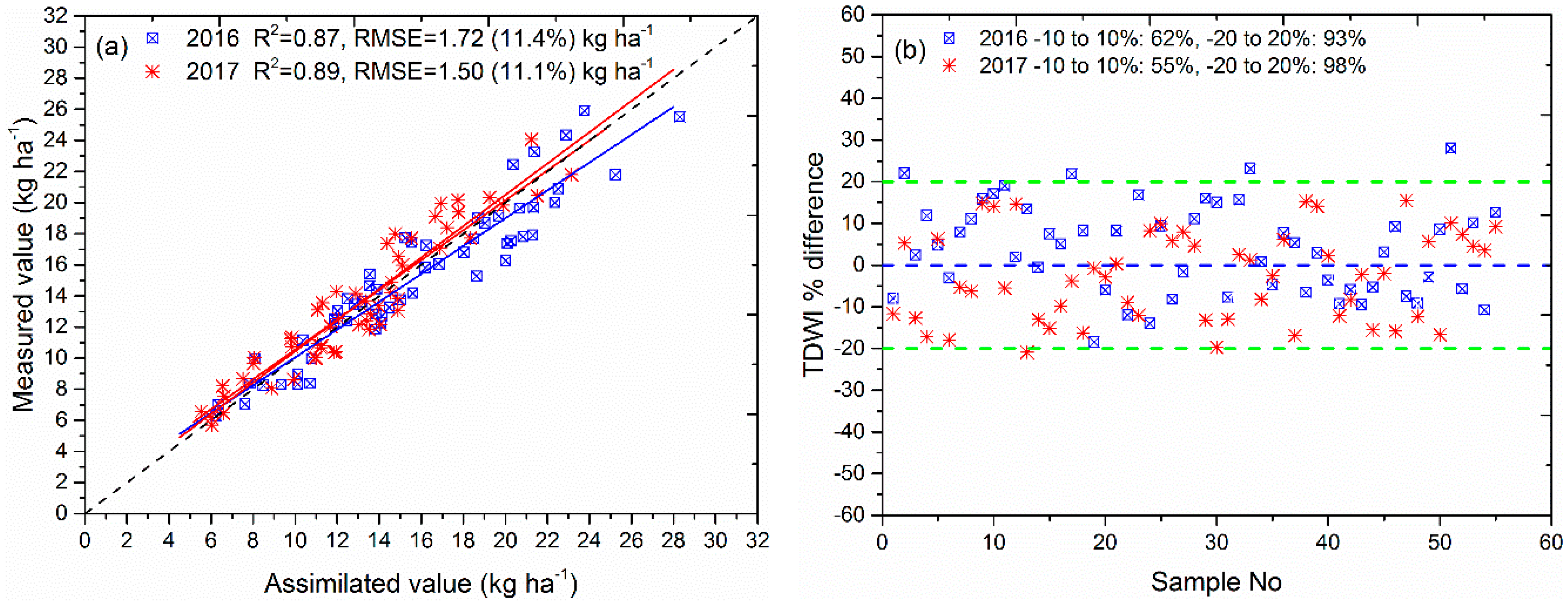
- Accuracy evaluation: In addition to comparing the yield prediction accuracy of the above three methods, the TDWI values of 55 sampled orchards obtained from the assimilation method were also verified and evaluated.
2.3. Description of the WOFOST Model
- Ia: Amount absorbed of specified radiation flux (J m−2 s−1).
- Ia,L: Amount absorbed of total radiation flux at relative depth L (J m−2 s−1).
- I0: Photosynthetically active radiation flux at top of the canopy (J m−2 s−1).
- k: The extinction coefficient for the PAR flux.
- ρ: Reflection coefficient of the canopy.
- AL: Gross assimilation rate at relative depth L (per unit leaf area) (kg ha−1 h−1).
- Am: Gross assimilation rate at light saturation (kg ha−1 h−1).
- ε: Initial light use efficiency (kg ha−1 h−1)/(J m−1 s−1).
- AC: Total gross assimilation rate for the whole canopy (kg ha−1 h−1).
- AC,t: Total gross canopy assimilation rate per unit leaf area (kg ha−1 h−1).
- AT,L,P: Total instantaneous gross assimilation rate at relative depth L (kg ha−1 h−1).
- LAI: Total leaf area of the crop (ha ha−1).
2.4. Study Data
2.4.1. Field Experimental Data for WOFOST Calibration and Validation
2.4.2. Field-Scale Observation Data for Different Orchards
2.5. Calibration of WOFOST Model
2.6. Input TDWIs for WOFOST Model without Forcing LAI and Yield Estimation
2.7. Yield Estimation Using Remotely-Sensed Vegetation Index Regression Method
2.8. Forcing Remotely Sensed LAI and Yield Estimation
2.9. Accuracy Evaluation
3. Results
3.1. Yield Estimation Using the Remote Sensing Regression Method
3.2. Calibration of the WOFOST Model
3.3. Remotely-Sensed LAI
3.4. Forcing Remotely-Sensed LAI and Yield Estimation
3.4.1. Re-Calibrated TDWI Evaluation after Forcing LAI
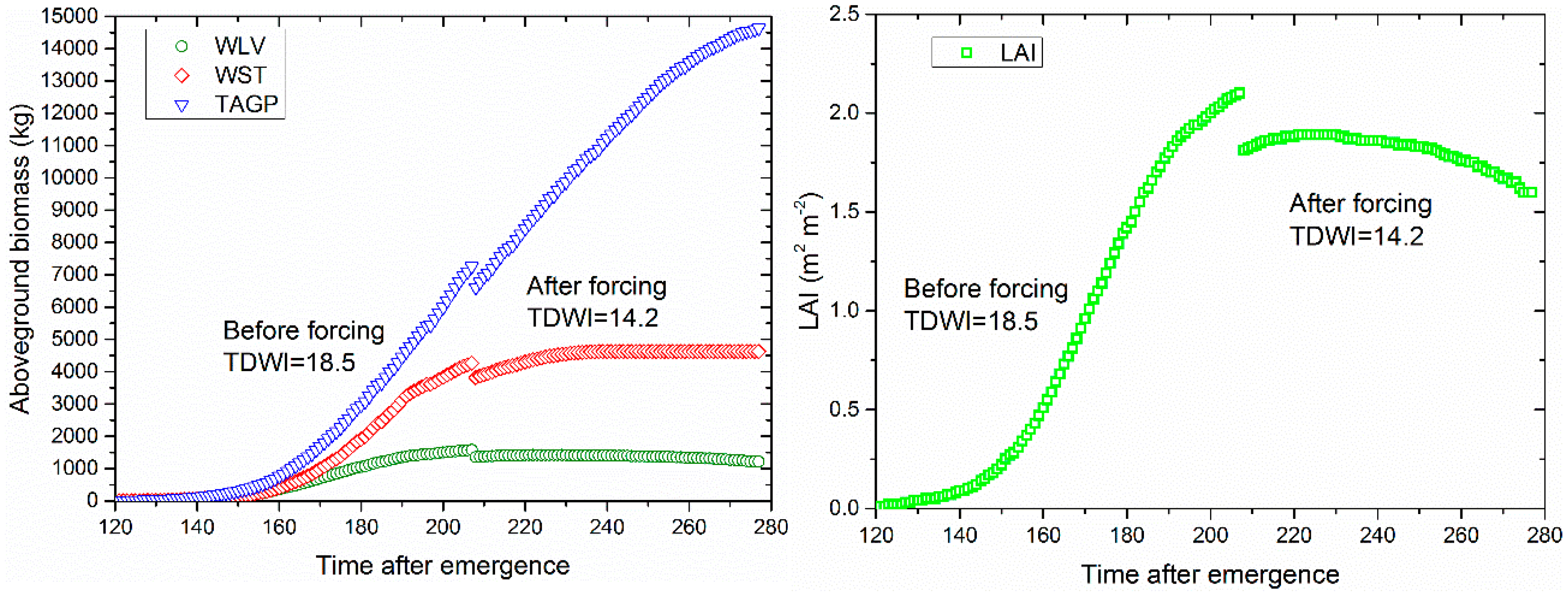
3.4.2. Aboveground Biomass Simulation after Forcing LAI
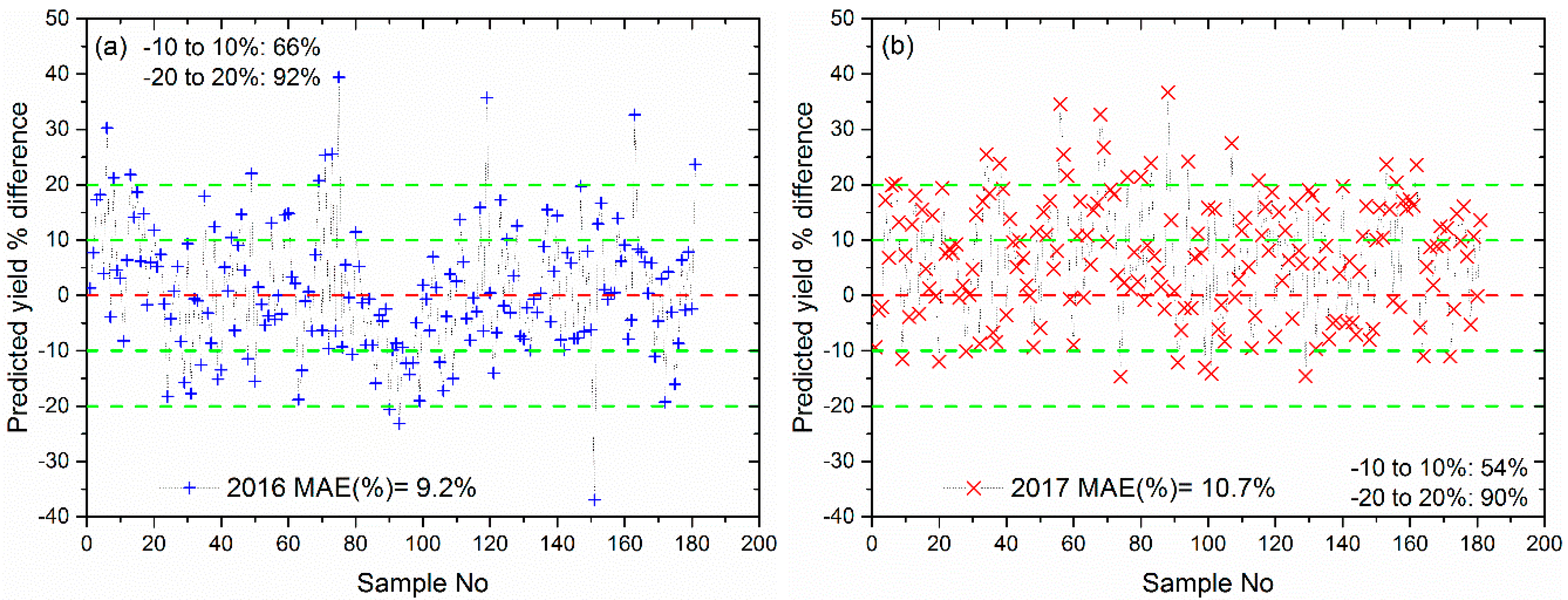
3.4.3. Yield Estimation after Forcing LAI
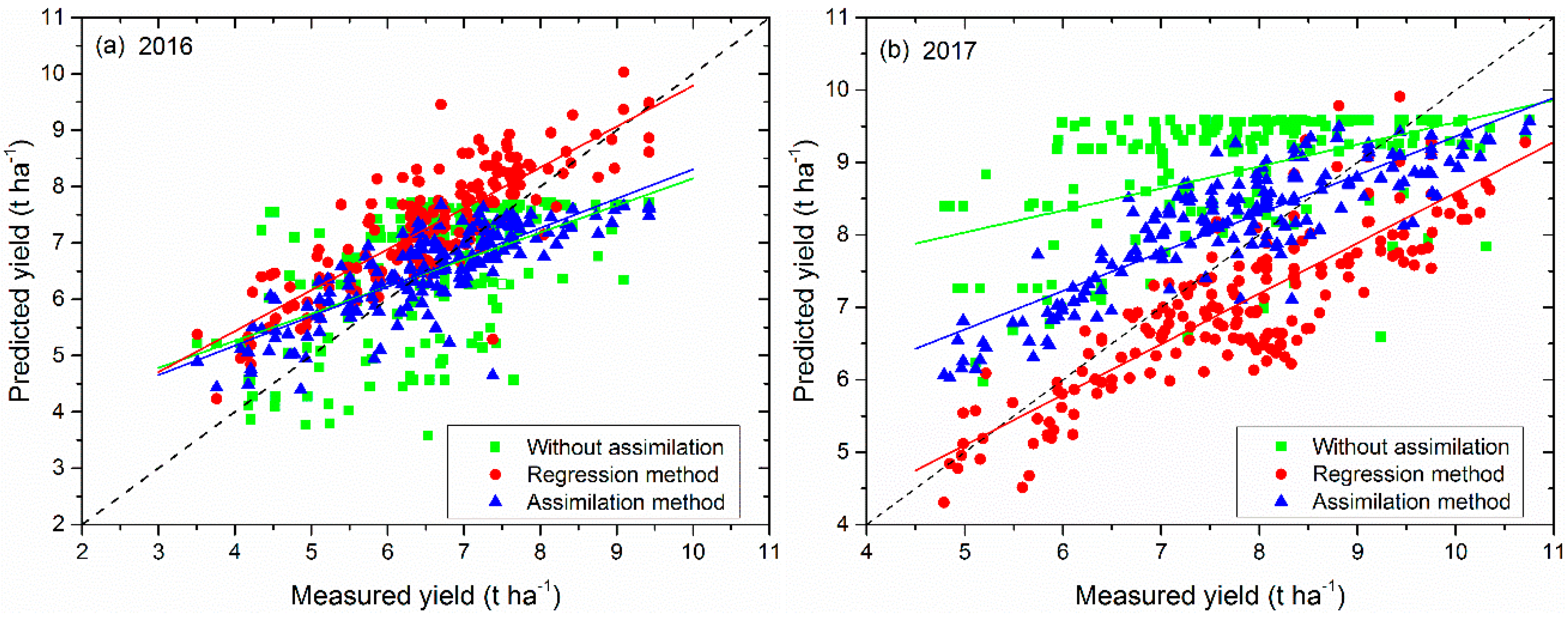
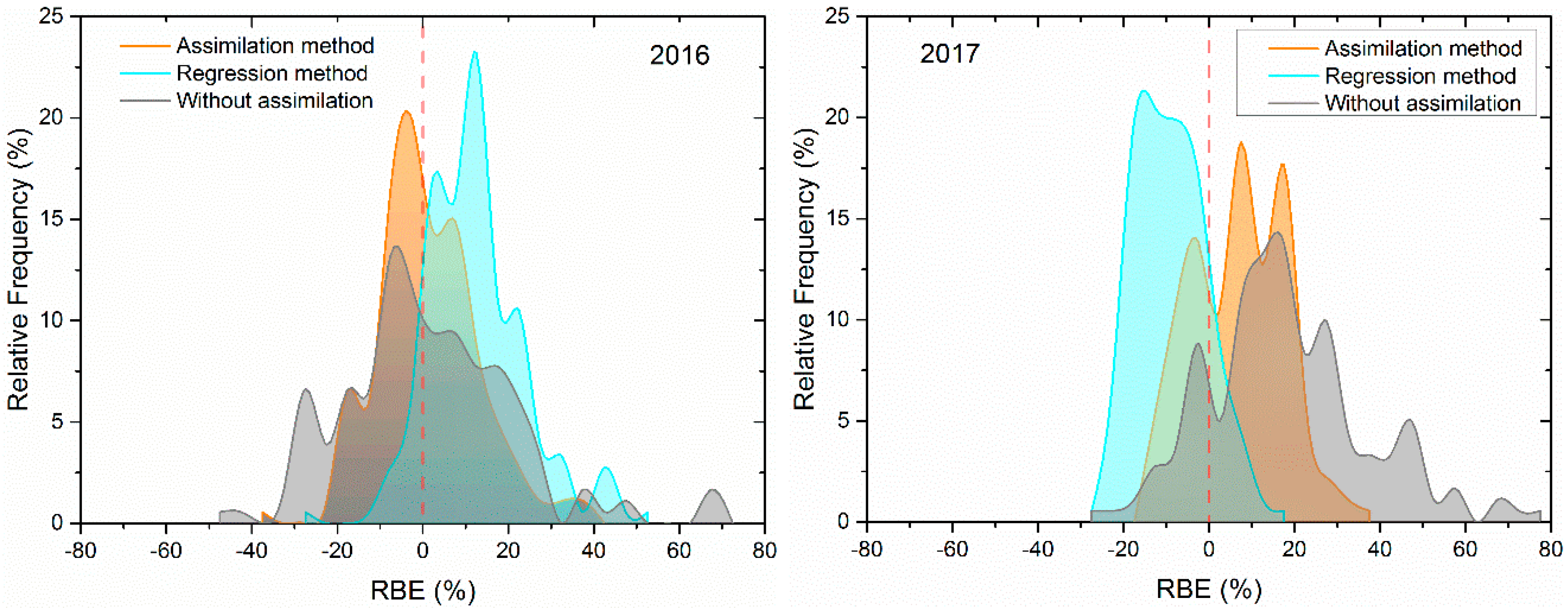
3.5. Comparison of Three Prediction Methods
4. Discussion
5. Conclusions
- Remotely-sensed state variable SM can be recommended to be assimilated into the WOFOST model in response to the effects of irrigation and rainfall on the simulation results.
- The influence of tree age and shapes on CO2 assimilation parameters and the use of remote sensing data to optimize these parameters are also worth exploring in order to improve simulation accuracy in high-yield and low-yield jujube gardens.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ouédraogo, S.J.; Bayala, J.; Dembélé, C.; Kaboré, A.; Kaya, B.; Niang, A.; Somé, A.N. Establishing jujube trees in sub-Saharan Africa: Response of introduced and local cultivars to rock phosphate and water supply in Burkina Faso, West Africa. Agrofor. Syst. 2006, 68, 69–80. [Google Scholar] [CrossRef]
- Lam, C.T.W.; Chan, P.H.; Lee, P.S.C.; Lau, K.M.; Kong, A.Y.Y.; Gong, A.G.W.; Xu, M.L.; Lam, K.Y.C.; Dong, T.T.X.; Lin, H.; et al. Chemical and biological assessment of Jujube (Ziziphus jujuba)-containing herbal decoctions: Induction of erythropoietin expression in cultures. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 2015, 1026, 254–262. [Google Scholar] [CrossRef]
- de Wit, A.; Boogaard, H.; Fumagalli, D.; Janssen, S.; Knapen, R.; van Kraalingen, D.; Supit, I.; van der Wijngaart, R.; van Diepen, K. 25 years of the WOFOST cropping systems model. Agric. Syst. 2019, 168, 154–167. [Google Scholar] [CrossRef]
- van Diepen, C.A.; Wolf, J.; van Keulen, H.; Rappoldt, C. WOFOST: A simulation model of crop production. Soil Use Manag. 1989, 5, 16–24. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Wang, X.; Williams, J.R.; Gassman, P.W.; Baffaut, C.; Izaurralde, R.C.; Jeong, J.; Kiniry, J.R. EPIC and APEX: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1447–1462. [Google Scholar] [CrossRef]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An overview of the crop model STICS. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Holzworth, D.P.; Huth, N.I.; deVoil, P.G.; Zurcher, E.J.; Herrmann, N.I.; McLean, G.; Chenu, K.; van Oosterom, E.J.; Snow, V.; Murphy, C.; et al. APSIM—Evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 2014, 62, 327–350. [Google Scholar] [CrossRef]
- Van Dam, J.C.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; Van Walsum, P.E.V.; Van Diepen, C.A. Theory of SWAP version 2.0. Softw. Man. 1997, 153. Available online: https://library.wur.nl/WebQuery/wurpubs/fulltext/222782 (accessed on 1April 2019).
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. Aquacrop-The FAO crop model to simulate yield response to water: II. main algorithms and software description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef]
- Stöckle, C.O.; Donatelli, M.; Nelson, R. CropSyst, a cropping systems simulation model. Eur. J. Agron. 2003, 18, 289–307. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- De Wit, A.; Duveiller, G.; Defourny, P. Estimating regional winter wheat yield with WOFOST through the assimilation of green area index retrieved from MODIS observations. Agric. For. Meteorol. 2012, 164, 39–52. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Hoogenboom, G.; Teasdale, J.; Cavigelli, M. Corn-yield estimation through assimilation of remotely sensed data into the CSM-CERES-Maize model. Int. J. Remote Sens. 2008, 29, 3011–3032. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, Z.; Chen, J.; Liu, J.; Ren, J.; Li, Z.; Sun, L.; Li, H. Application of Crop Model Data Assimilation With a Particle Filter for Estimating Regional Winter Wheat Yields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4422–4431. [Google Scholar] [CrossRef]
- Nearing, G.S.; Crow, W.T.; Thorp, K.R.; Moran, M.S.; Reichle, R.H.; Gupta, H. Assimilating remote sensing observations of leaf area index and soil moisture for wheat yield estimates: An observing system simulation experiment. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Yao, F.; Tang, Y.; Wang, P.; Zhang, J. Estimation of maize yield by using a process-based model and remote sensing data in the Northeast China Plain. Phys. Chem. Earth 2015, 87–88, 142–152. [Google Scholar] [CrossRef]
- Jin, X.; Yang, G.; Xu, X.; Yang, H.; Feng, H.; Li, Z.; Shen, J.; Lan, Y.; Zhao, C. Combined multi-temporal optical and radar parameters for estimating LAI and biomass in winter wheat using HJ and RADARSAR-2 data. Remote Sens. 2015, 7, 13251–13272. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, Y.; Li, W.; Cao, W.; Tian, Y. Assimilating Remotely Sensed Information with the WheatGrow Model Based on the Ensemble Square Root Filter for Improving Regional Wheat Yield Forecasts. Plant Prod. Sci. 2013, 16, 352–364. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Ali, S. A new crop yield forecasting model based on satellite measurements applied across the Indus Basin, Pakistan. Agric. Ecosyst. Environ. 2003, 94, 321–340. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Su, W.; Zhang, X.; Huang, Y.; Fan, J. Jointly Assimilating MODIS LAI and ET Products Into the SWAP Model for Winter Wheat Yield Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4060–4071. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-Wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Bongiovanni, T.; Judge, J.; Zotarelli, L.; Bayer, C. Assimilation of SMOS soil moisture for quantifying drought impacts on crop yield in agricultural regions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3867–3879. [Google Scholar] [CrossRef]
- Sakamoto, T.; Yokozawa, M.; Toritani, H.; Shibayama, M.; Ishitsuka, N.; Ohno, H. A crop phenology detection method using time-series MODIS data. Remote Sens. Environ. 2005, 96, 366–374. [Google Scholar] [CrossRef]
- Delécolle, R.; Maas, S.J.; Guérif, M.; Baret, F. Remote sensing and crop production models: Present trends. ISPRS J. Photogramm. Remote Sens. 1992, 47, 145–161. [Google Scholar] [CrossRef]
- Singh, R.; de Wit, A.J.W.; Zurita-Milla, R.; Brazile, J.; Schaepman, M.E.; Dorigo, W.A. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2006, 9, 165–193. [Google Scholar]
- Argent, R. Land Surface Observation, Modeling and Data Assimilation. Environ. Model. Softw. 2014, 57, 248–249. [Google Scholar] [CrossRef]
- Moulin, S.; Bondeau, A.; Delécolle, R. Combining agricultural crop models and satellite observations: From field to regional scales. Int. J. Remote Sens. 1998, 19, 1021–1036. [Google Scholar] [CrossRef]
- Curnel, Y.; de Wit, A.J.W.; Duveiller, G.; Defourny, P. Potential performances of remotely sensed LAI assimilation in WOFOST model based on an OSS Experiment. Agric. For. Meteorol. 2011, 151, 1843–1855. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F. Improving regional winter wheat yield estimation through assimilation of phenology and leaf area index from remote sensing data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Sedano, F.; Lewis, P.; Liang, S.; Wu, Q.; Su, W.; Zhang, X.; Zhu, D. Evaluation of regional estimates of winter wheat yield by assimilating three remotely sensed reflectance datasets into the coupled WOFOST–PROSAIL model. Eur. J. Agron. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.; Liu, G.; Jiang, Z.; Huang, C. Improving winter wheat yield estimation from the CERES-Wheat model to assimilate leaf area index with different assimilation methods and spatio-temporal scales. Remote Sens. 2017, 9, 190. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, L.; Zhou, X.; Zhu, Y.; Cao, W.; Qiu, X.; Cheng, T.; Tian, Y. Integrating remote sensing information with crop model to monitor wheat growth and yield based on simulation zone partitioning. Precis. Agric. 2017, 19, 55–78. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, P.; Bai, X.; Khan, J.; Zhang, S.; Li, L.; Wang, L. Assimilation of the leaf area index and vegetation temperature condition index for winter wheat yield estimation using Landsat imagery and the CERES-Wheat model. Agric. For. Meteorol. 2017, 246, 194–206. [Google Scholar] [CrossRef]
- Gilardelli, C.; Stella, T.; Confalonieri, R.; Ranghetti, L.; Campos-Taberner, M.; García-Haro, F.J.; Boschetti, M. Downscaling rice yield simulation at sub-field scale using remotely sensed LAI data. Eur. J. Agron. 2019, 103, 108–116. [Google Scholar] [CrossRef]
- Donohue, R.J.; Lawes, R.A.; Mata, G.; Gobbett, D.; Ouzman, J. Towards a national, remote-sensing-based model for predicting field-scale crop yield. F. Crop. Res. 2018, 227, 79–90. [Google Scholar] [CrossRef]
- Silvestro, P.C.; Pignatti, S.; Pascucci, S.; Yang, H.; Li, Z.; Yang, G.; Huang, W.; Casa, R. Estimating wheat yield in China at the field and district scale from the assimilation of satellite data into the Aquacrop and simple algorithm for yield (SAFY) models. Remote Sens. 2017, 9, 509. [Google Scholar] [CrossRef]
- Cheng, Z.; Meng, J.; Wang, Y. Improving spring maize yield estimation at field scale by assimilating time-series HJ-1 CCD data into the WOFOST model using a new method with fast algorithms. Remote Sens. 2016, 8, 303. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Xu, X.; Yang, G.; Wang, J.; Kumar, L. Estimation of winter wheat biomass and yield by combining the aquacrop model and field hyperspectral data. Remote Sens. 2016, 8, 972. [Google Scholar] [CrossRef]
- Ma, G.; Huang, J.; Wu, W.; Fan, J.; Zou, J.; Wu, S. Assimilation of MODIS-LAI into the WOFOST model for forecasting regional winter wheat yield. Math. Comput. Model. 2013, 58, 634–643. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, S.; Shen, S. Assimilating remote sensing information with crop model using Ensemble Kalman Filter for improving LAI monitoring and yield estimation. Ecol. Modell. 2013, 270, 30–42. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Hoogenboom, G. Integration of MODIS LAI and vegetation index products with the CSM-CERES-Maize model for corn yield estimation. Int. J. Remote Sens. 2011, 32, 1039–1065. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Y.; Li, W.; Cao, W.; Tian, Y. Integrating remotely sensed leaf area index and leaf nitrogen accumulation with RiceGrow model based on particle swarm optimization algorithm for rice grain yield assessment. J. Appl. Remote Sens. 2014, 8. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, L.; Zhao, C.; Wang, J.; Feng, H.; Yang, G. Integrating a very fast simulated annealing optimization algorithm for crop leaf area index variational assimilation. Math. Comput. Model. 2012, 58, 877–885. [Google Scholar] [CrossRef]
- Ding, C.; Jiang, J.; Wu, L.; Zhao, L.; Liu, X.; Liu, F. The Dynamic Assessment Model for Monitoring Cadmium Stress Levels in Rice Based on the Assimilation of Remote Sensing and the WOFOST Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1330–1338. [Google Scholar]
- Hadria, R.; Duchemin, B.; Lahrouni, A.; Khabba, S.; Er-Raki, S.; Dedieu, G.; Chehbouni, A.G.; Olioso, A. Monitoring of irrigated wheat in a semi-arid climate using crop modelling and remote sensing data: Impact of satellite revisit time frequency. Int. J. Remote Sens. 2006, 27, 1093–1117. [Google Scholar] [CrossRef]
- Schneider, K. Assimilating remote sensing data into a land-surface process model. Int. J. Remote Sens. 2003, 24, 2959–2980. [Google Scholar] [CrossRef]
- Thorp, K.R.; Hunsaker, D.J.; French, A.N. Assimilating Leaf Area Index Estimates from Remote Sensing into the Simulations of a Cropping Systems Model. Trans. ASABE. 2013, 53, 251–262. [Google Scholar] [CrossRef]
- Panigrahy, S.; Mukherjee, J.; Chaudhari, K.N.; Parihar, J.S.; Ray, S.S.; Patel, N.K.; Tripathy, R. Forecasting wheat yield in Punjab state of India by combining crop simulation model WOFOST and remotely sensed inputs. Remote Sens. Lett. 2012, 4, 19–28. [Google Scholar]
- Jongschaap, R.E.E.; Schouten, L.S.M. Predicting wheat production at regional scale by integration of remote sensing data with a simulation model. Agron. Sustain. Dev. 2005, 25, 481–489. [Google Scholar] [CrossRef]
- Aubert, D.; Loumagne, C.; Oudin, L. Sequential assimilation of soil moisture and streamflow data in a conceptual rainfall-Runoff model. J. Hydrol. 2003, 280, 145–161. [Google Scholar] [CrossRef]
- Pellenq, J.; Boulet, G. A methodology to test the pertinence of remote-sensing data assimilation into vegetation models for water and energy exchange at the land surface. Agronomie. 2004, 24, 197–204. [Google Scholar] [CrossRef]
- Crow, W.T.; Wood, E.F. The assimilation of remotely sensed soil brightness temperature imagery into a land surface model using Ensemble Kalman filtering: A case study based on ESTAR measurements during SGP97. Adv. Water Resour. 2003, 26, 137–149. [Google Scholar] [CrossRef]
- Lorenc, A.C.; Ballard, S.P.; Bell, R.S.; Ingleby, N.B.; Andrews, P.L.F.; Barker, D.M.; Bray, J.R.; Clayton, A.M.; Dalby, T.; Li, D.; et al. The Met. Office global three-dimensional variational data assimilation scheme. Q. J. R. Meteorol. Soc. 2000, 126, 2991–3012. [Google Scholar] [CrossRef]
- Trémolet, Y. Model-error estimation in 4D-Var. Q. J. R. Meteorol. Soc. 2007, 133, 1267–1280. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41, 1–17. [Google Scholar] [CrossRef]
- Sahu, S.K.; Yip, S.; Holland, D.M. Improved space-time forecasting of next day ozone concentrations in the eastern US. Atmospheric Environ. 2009, 43, 494–501. [Google Scholar] [CrossRef]
- Plant, N.G.; Holland, K.T. Prediction and assimilation of surf-zone processes using a Bayesian network. Coast. Eng. 2010, 58, 119–130. [Google Scholar] [CrossRef]
- de Wit, A.J.W.; van Diepen, C.A. Crop model data assimilation with the Ensemble Kalman filter for improving regional crop yield forecasts. Agric. For. Meteorol. 2007, 146, 38–56. [Google Scholar] [CrossRef]
- Bolten, J.D.; Reynolds, C.A.; Crow, W.T.; Zhan, X.; Jackson, T.J. Evaluating the Utility of Remotely Sensed Soil Moisture Retrievals for Operational Agricultural Drought Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 57–66. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Q.; Zhou, J.; Zhang, G.; Chen, C.; Wang, J. Assimilating remote sensing information into a coupled hydrology-crop growth model to estimate regional maize yield in arid regions. Ecol. Model. 2014, 291, 15–27. [Google Scholar] [CrossRef]
- Bai, T.; Zhang, N.; Chen, Y.; Mercatoris, B. Assessing the Performance of the WOFOST Model in Simulating Jujube Fruit Tree Growth under Different Irrigation Regimes. Sustainability 2019, 11, 1466. [Google Scholar] [CrossRef]
- Principles of WOFOST (Temporal and Spatial Scale). Available online: https://www.wur.nl/en/Research-Results/Research-Institutes/Environmental-Research/Facilities-Products/Software-and-models/WOFOST/Principles-of-WOFOST.htm (accessed on 1 April 2019).
- Ye, Z.P.; Yu, Q. Comparison of a New Model of Light Response of Photosynthesis with Traditional Models. J. Shenyang Agric. Univ. 2007, 38, 771–775. (In Chinese) [Google Scholar]
- RSI. ENVI User’s Guide. September 2001 Edition. 2001. Available online: http://www.harrisgeospatial.com/portals/0/pdfs/envi/ENVI_User_Guide.pdf (accessed on 6 May 2018).
- Pettorelli, N. The Normalized Difference Vegetation Index. 2013. Available online: https://books.google.be/books?hl=zh-CN&lr=&id=FXywAAAAQBAJ&oi=fnd&pg=PP1&dq=Pettorelli,+N.+The+Normalized+Difference+Vegetation+Index&ots=q1av97XPIL&sig=qsBfWEGJ1SbUqJTaFjGP2qVauww&redir_esc=y#v=onepage&q=Pettorelli%2C%20N.%20The%20Normalized%20Difference%20Vegetation%20Index&f=false (accessed on 15 March 2018).
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Sun, L.; Gao, F.; Anderson, M.C.; Kustas, W.P.; Alsina, M.M.; Sanchez, L.; Sams, B.; McKee, L.; Dulaney, W.; White, W.A.; et al. Daily mapping of 30 m LAI and NDVI for grape yield prediction in California vineyards. Remote Sens. 2017, 9, 317. [Google Scholar] [CrossRef]
- Rahman, M.M.; Robson, A.; Bristow, M. Exploring the potential of high resolution worldview-3 Imagery for estimating yield of mango. Remote Sens. 2018, 10, 1866. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Yang, W.; Gao, J.; Xu, C.; Wu, C.; Jin, Q. The Correlation Analysis of Leaf Area Index and Yield of Red Jujube. Xinjiang Agric. Sci. 2012, 49, 1397–1400. (In Chinese) [Google Scholar]

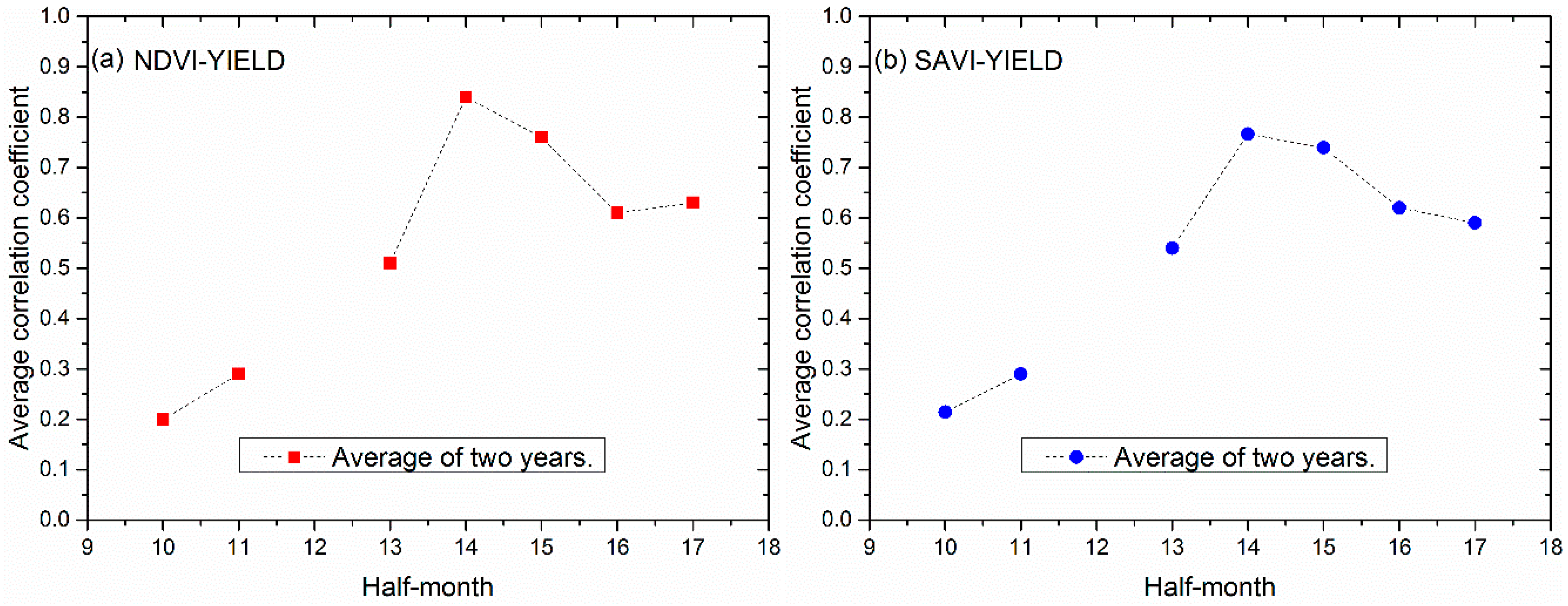
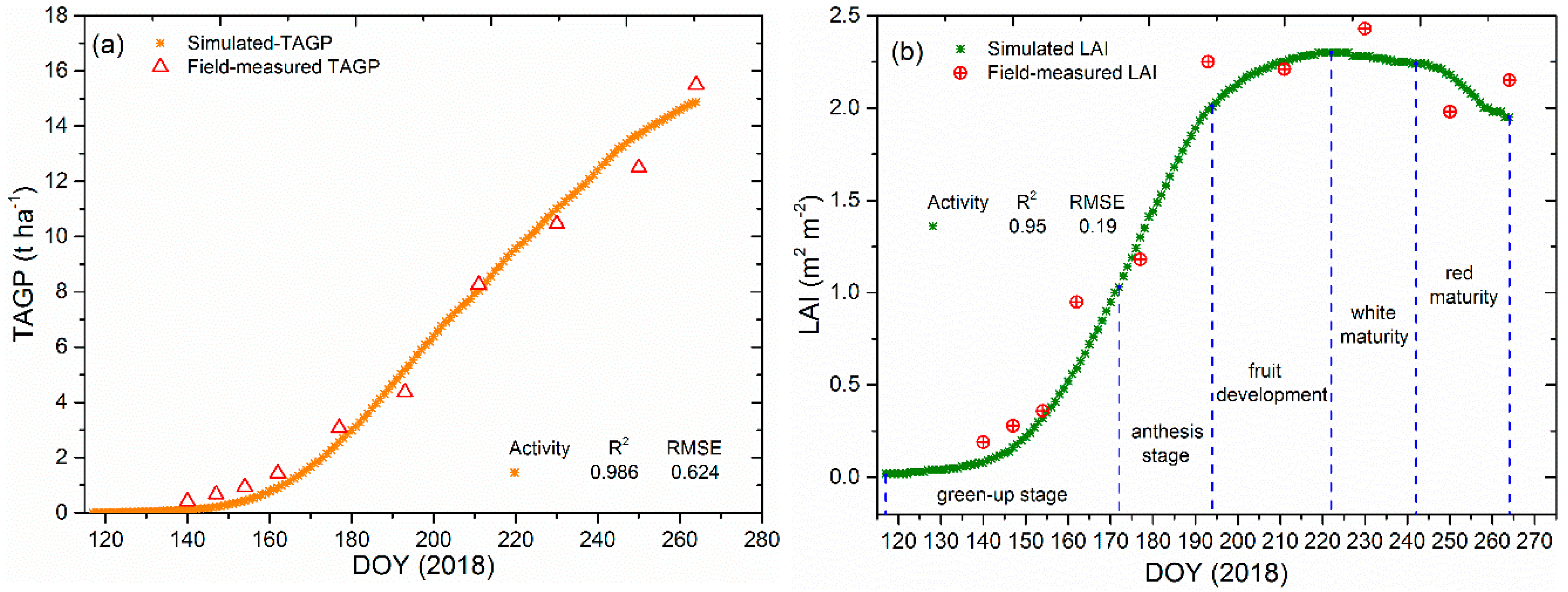
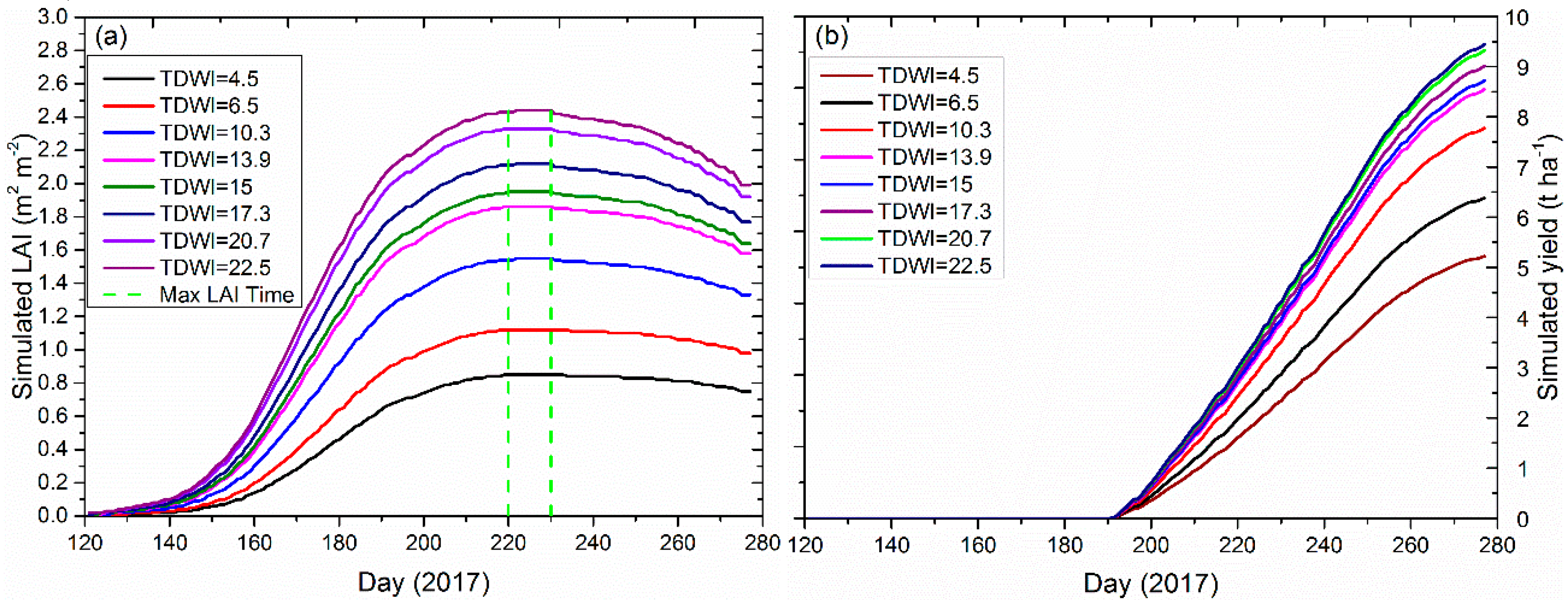
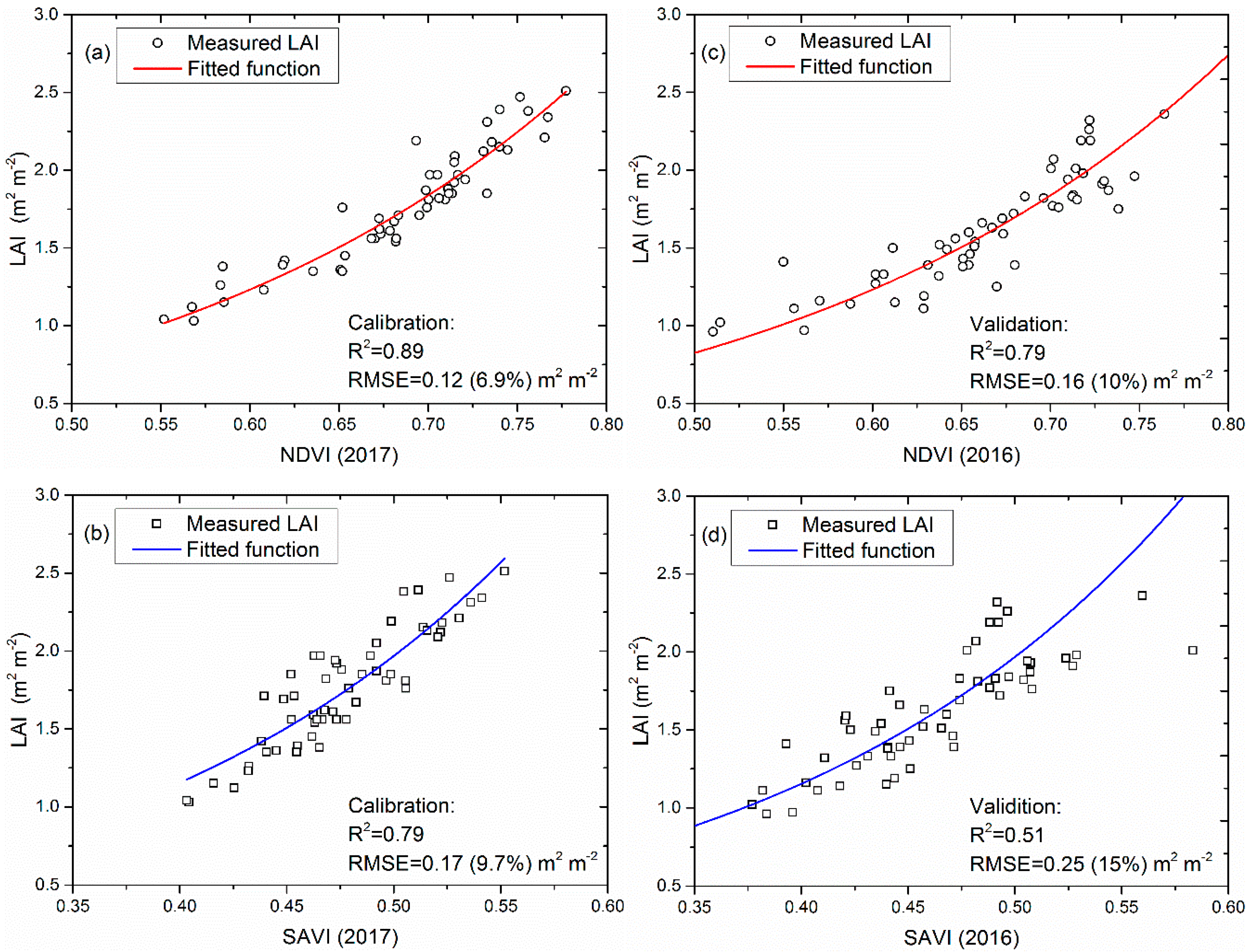
| Index Based on NDVI | Year | Cross-validation (2016 versus 2017) | |
|---|---|---|---|
| R2 | NRMSE (%) | ||
| 14th half-month | 2016 | 0.25 | 16 |
| 2017 | 0.33 | 14.3 | |
| Max | 2016 | 0.1 | 17.5 |
| 2017 | 0.24 | 15.3 | |
| Average for 7th and 8th month | 2016 | / | 21.3 |
| 2017 | / | 18.2 | |
| Average for 14th and 15th half-month | 2016 | 0.35 | 14.8 |
| 2017 | 0.43 | 13.3 | |
| Parameter | Description | Value | Units | Source |
|---|---|---|---|---|
| *Emergence | ||||
| TBASEM | Lower threshold temperature emergence | 10 | °C | e |
| TEFFMX | Max effective temperature emergence | 30 | °C | e |
| TSUMEM | Temperature sum from sowing to emergence | 230 | °C | m-c |
| *Phenology | ||||
| TSUM1 | Temperature sum from emergence to anthesis | 967 | °C d−1 | m-c |
| TSUM2 | Temperature sum from anthesis to maturity | 960 | °C d−1 | m-c |
| DTSMTB0 | Daily increase in temperature sum as function of at average = 0 °C | 0.00 | °C d−1 | e |
| DTSMTB100 | Daily increase in temperature sum as function of at average = 10 °C | 0.00 | °C d−1 | e |
| DTSMTB355 | Daily increase in temperature sum as function of at average = 35.5 °C | 25.5 | °C d−1 | e |
| DTSMTB400 | Daily increase in temperature sum as function of at average = 40 °C | 25.5 | °C d−1 | e |
| *Initial parameters | ||||
| TDWI | Redefine initial total emergence dry weight | / | kg ha−1 | m |
| LAIEM | Leaf area index at emergence | 0.0007 | ha ha−1 | d |
| RGRLAI | Maximum relative increase in LAI | 0.05 | ha ha−1 d−1 | d |
| *Green area | ||||
| SLATB000 | Specific leaf area while DVS = 0 | 0.00165 | ha kg−1 | m-c |
| SLATB55 | Specific leaf area while DVS = 0.55 | 0.0013 | ha kg−1 | m-c |
| SLATB100 | Specific leaf area while DVS = 1 | 0.0013 | ha kg−1 | m-c |
| SLATB200 | Specific leaf area while DVS = 2 | 0.0014 | ha kg−1 | m-c |
| SPAN | Life span of leaves growing at 35 °C | 60 | [d] | e |
| TBASE | Lower threshold temp. for ageing of leaves | 10 | °C | e |
| *CO2 assimilation | ||||
| KDIFTB00 | Extinction coefficient for diffuse visible light at DVS = 0 | 0.8 | \ | m-c |
| KDIFTB200 | Extinction coefficient for diffuse visible light at DVS = 2 | 0.8 | \ | m-c |
| EFFTB19.5 | Light-use efficiency single leaf at average temp. = Celsius | 0.495 | kg ha−1 hr−1J−1 m2 s | m-c |
| EFFTB355 | Light-use efficiency single leaf at average temp. = Celsius | 0.495 | kg ha−1 hr−1J−1 m2 s | m-c |
| AMAXTB00 | Maximum leaf CO2 assimilation. Rate at DVS = 0 | 39.0 | kg ha−1 hr−1 | m-c |
| AMAXTB170 | Maximum leaf CO2 assimilation. Rate at DVS = 1.7 | 39.0 | kg ha−1 hr−1 | m-c |
| AMAXTB200 | Maximum leaf CO2 assimilation. Rate at DVS = 2 | 20.0 | kg ha−1 hr−1 | m-c |
| TMPFTB10 | Reduction factor of AMAX of at 10 ℃ | 0 | \ | d |
| TMPFTB195 | Reduction factor of AMAX of at 19.5 ℃ | 1 | \ | d |
| TMPFTB355 | Reduction factor of AMAX of at 35.5 ℃ | 1 | \ | d |
| *Conversion of assimilates into biomass | ||||
| CVL | Efficiency of conversion into leaves | 0.732 | kg kg−1 | m-c |
| CVO | Efficiency of conversion into storage organs | 0.780 | kg kg−1 | m-c |
| CVR | Efficiency of conversion into roots | 0.690 | kg kg−1 | m-c |
| CVS | Efficiency of conversion into stems | 0.751 | kg kg−1 | m-c |
| *maintenance respiration | ||||
| Q10 | Relative increase in respiration rate per 10 °C temperature increase | 2 | kg CH2O kg−1 d−1 | d |
| RML | Relative maintenance respiration rate of leaves | 0.03 | kg CH2O kg−1 d−1 | d |
| RMO | Relative maintenance respiration rate of storage organs | 0.01 | kg CH2O kg−1 d−1 | d-c |
| RMR | Relative maintenance respiration rate of roots | 0.01 | kg CH2O kg−1 d−1 | d |
| RMS | Relative maintenance respiration rate of stems | 0.015 | kg CH2O kg−1 d−1 | d-c |
| *Partitioning parameters | ||||
| FRTB00 | Fraction of above-ground dry matter to roots at DVS = 0 | 0.3 | kg kg−1 | m-c |
| FRTB154 | Fraction of above-ground dry matter to roots at DVS = 1.54 | 0.0 | kg kg−1 | m-c |
| FLTB00 | Fraction of above-ground dry matter to leaves at DVS = 0 | 0.67 | kg kg−1 | m-c |
| FLTB012 | Fraction of above-ground dry matter to leaves at DVS = 0.12 | 0.31 | kg kg−1 | m-c |
| FLTB022 | Fraction of above-ground dry matter to leaves at DVS = 0.22 | 0.41 | kg kg−1 | m-c |
| FLTB032 | Fraction of above-ground dry matter to leaves at DVS = 0.32 | 0.55 | kg kg−1 | m-c |
| FLTB051 | Fraction of above-ground dry matter to leaves at DVS = 0.51 | 0.4 | kg kg−1 | m-c |
| FLTB097 | Fraction of above-ground dry matter to leaves at DVS = 0.97 | 0.15 | kg kg−1 | m-c |
| FLTB100 | Fraction of above-ground dry matter to leaves at DVS = 1.00 | 0.1 | kg kg−1 | m-c |
| FSTB00 | Fraction of above-ground dry matter to stems at DVS = 0 | 0.33 | kg kg−1 | m-c |
| FSTB012 | Fraction of above-ground dry matter to stems at DVS = 0.12 | 0.69 | kg kg−1 | m-c |
| FSTB022 | Fraction of above-ground dry matter to stems at DVS = 0.22 | 0.59 | kg kg−1 | m-c |
| FSTB032 | Fraction of above-ground dry matter to stems at DVS = 0.32 | 0.45 | kg kg−1 | m-c |
| FSTB051 | Fraction of above-ground dry matter to stems at DVS = 0.51 | 0.6 | kg kg−1 | m-c |
| FSTB097 | Fraction of above-ground dry matter to stems at DVS = 0.97 | 0.85 | kg kg−1 | m-c |
| FSTB100 | Fraction of above-ground dry matter to stems at DVS = 1.00 | 0.43 | kg kg−1 | m-c |
| FSTB145 | Fraction of above-ground dry matter to stems at DVS = 1.45 | 0.2 | kg kg−1 | m-c |
| FOTB100 | Fraction of above-ground dry matter to storage organs at DVS = 1.00 | 0.47 | kg kg−1 | m-c |
| FOTB145 | Fraction of above-ground dry matter to storage organs at DVS = 1.45 | 0.8 | kg kg−1 | m-c |
| FOTB164 | Fraction of above-ground dry matter to storage organs at DVS = 1.64 | 1.0 | kg kg−1 | m-c |
| FOTB200 | Fraction of above-ground dry matter to storage organs at DVS = 2.00 | 1 | kg kg−1 | m-c |
| *Death rates | ||||
| RDRSTB00 | Relative death rate of stems at DVS = 0 | 0 | \ | e |
| RDRSTB200 | Relative death rate of stems at DVS = 2.0 | 0 | \ | e |
| Prediction Method | Year | R2 | RMSE (%) t ha−1 | MAE (%) |
|---|---|---|---|---|
| Without assimilation | 2016 | 0.09 | 1.16 (17.6) | 14.9 |
| 2017 | 0.13 | 1.67 (21.5) | 20.3 | |
| Remotely sensed average NDVI prediction (cross-validation) | 2016 | 0.35 | 0.98 (14.8) | 13.3 |
| 2017 | 0.43 | 1.02 (13.3) | 14.9 | |
| Forcing LAI (assimilation) | 2016 | 0.62 | 0.74 (10.9) | 9.2 |
| 2017 | 0.59 | 0.87 (11.1) | 10.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, T.; Zhang, N.; Mercatoris, B.; Chen, Y. Improving Jujube Fruit Tree Yield Estimation at the Field Scale by Assimilating a Single Landsat Remotely-Sensed LAI into the WOFOST Model. Remote Sens. 2019, 11, 1119. https://doi.org/10.3390/rs11091119
Bai T, Zhang N, Mercatoris B, Chen Y. Improving Jujube Fruit Tree Yield Estimation at the Field Scale by Assimilating a Single Landsat Remotely-Sensed LAI into the WOFOST Model. Remote Sensing. 2019; 11(9):1119. https://doi.org/10.3390/rs11091119
Chicago/Turabian StyleBai, Tiecheng, Nannan Zhang, Benoit Mercatoris, and Youqi Chen. 2019. "Improving Jujube Fruit Tree Yield Estimation at the Field Scale by Assimilating a Single Landsat Remotely-Sensed LAI into the WOFOST Model" Remote Sensing 11, no. 9: 1119. https://doi.org/10.3390/rs11091119
APA StyleBai, T., Zhang, N., Mercatoris, B., & Chen, Y. (2019). Improving Jujube Fruit Tree Yield Estimation at the Field Scale by Assimilating a Single Landsat Remotely-Sensed LAI into the WOFOST Model. Remote Sensing, 11(9), 1119. https://doi.org/10.3390/rs11091119