Label Noise Cleansing with Sparse Graph for Hyperspectral Image Classification
Abstract
1. Introduction
- (1)
- We carefully analyzed and examined the core issue and the influence of label noise for HSI classification, which is an useful guideline to present a label noise-polluted classification work.
- (2)
- A novel label noise cleansing method, namely, SALP algorithm, is proposed to deal with random label noise and boundary label noise.
- (3)
- Experimental results on two publicly practical datasets show that the proposed SALP over four major classifiers can obviously reduce the impact of noisy labels, and its performance can surpass the baselines in terms of overall accuracy (OA), average accuracy (AA), Kappa coefficient, and visual classification map.
2. Problem Statement
3. Proposed Method
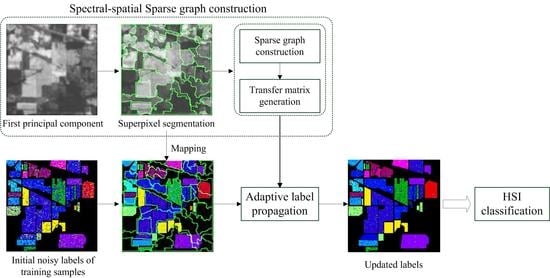
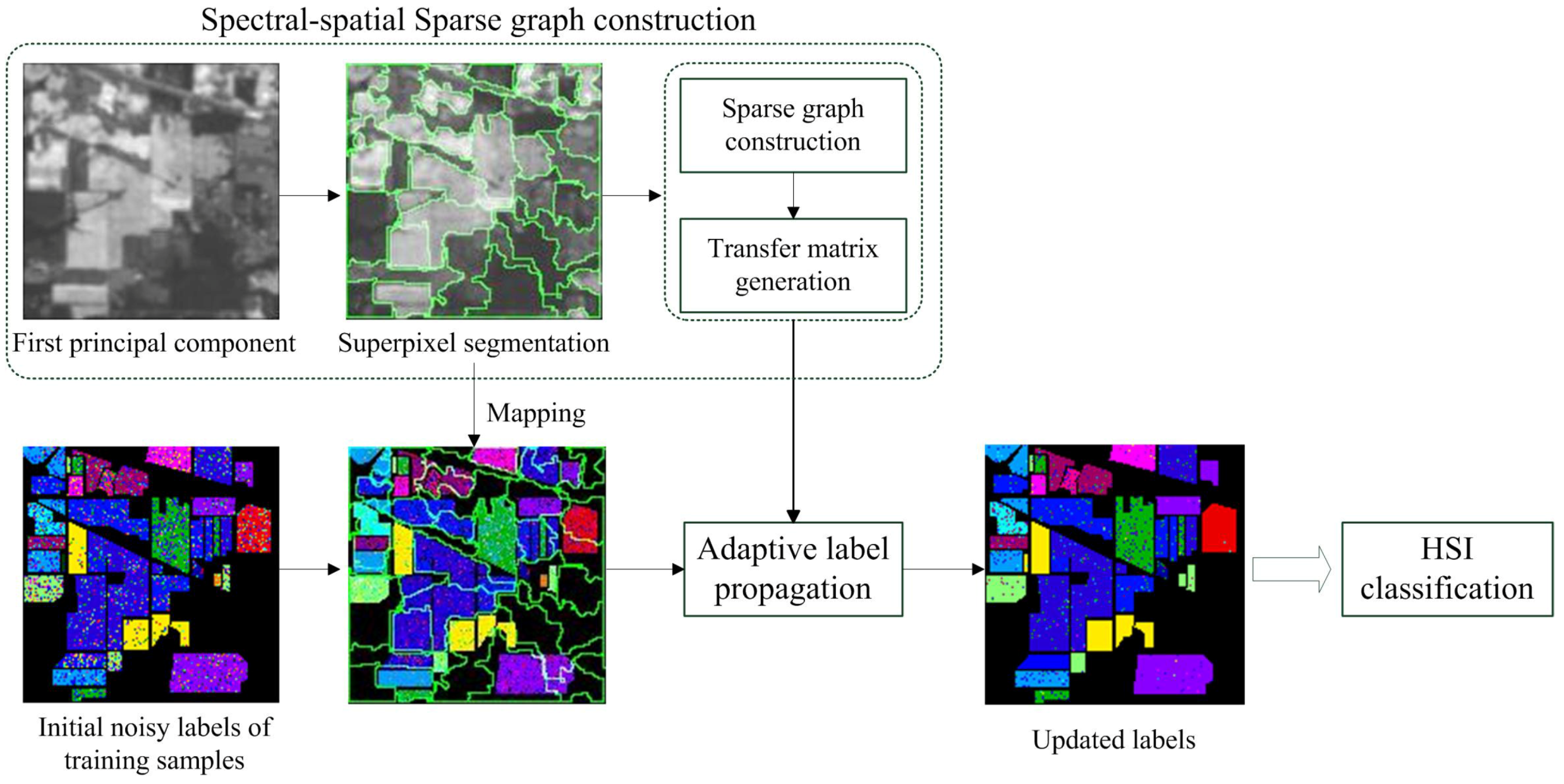
3.1. Overview of the Proposed Method
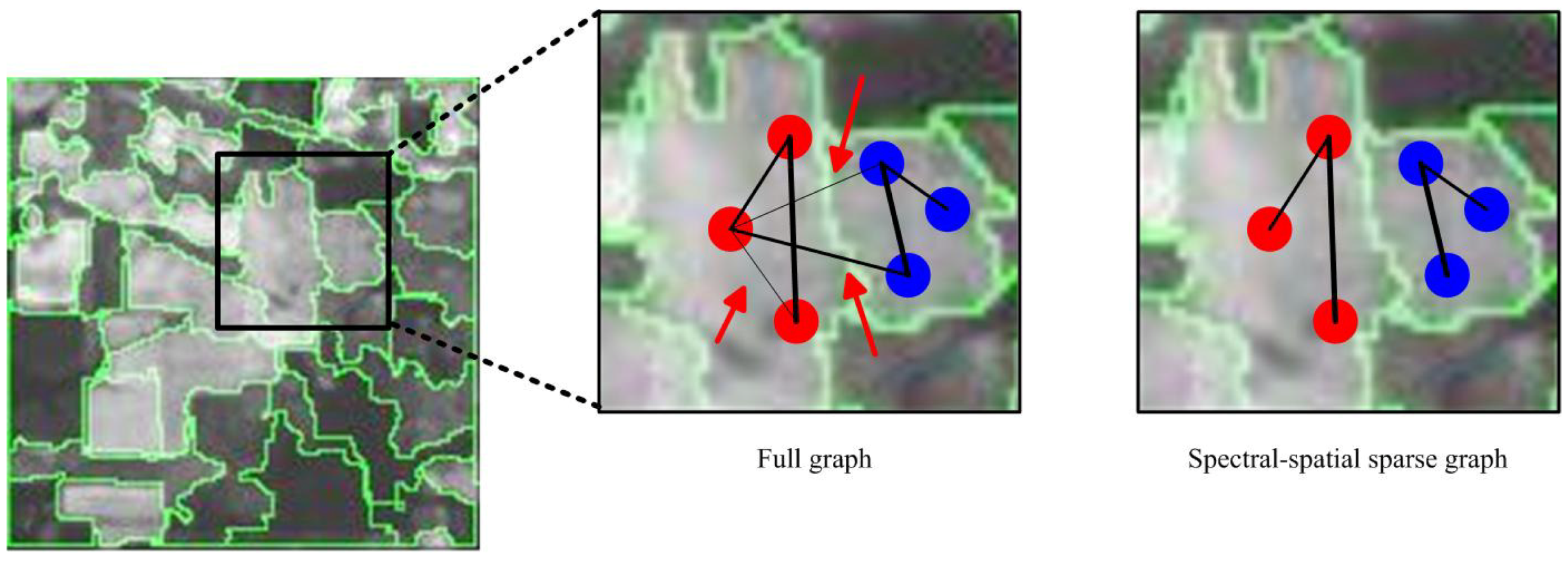
3.2. Spectral-Spatial Sparse Graph Construction
3.3. Adaptive Label Propagation
| Algorithm 1 The proposed SALP algorithm. |
Input: A hyperspectral image ; The training pixels with their labels ; Parameters and . Output: The cleaned label .
|
4. Results and Discussions
4.1. Datasets
4.2. Experimental Setup
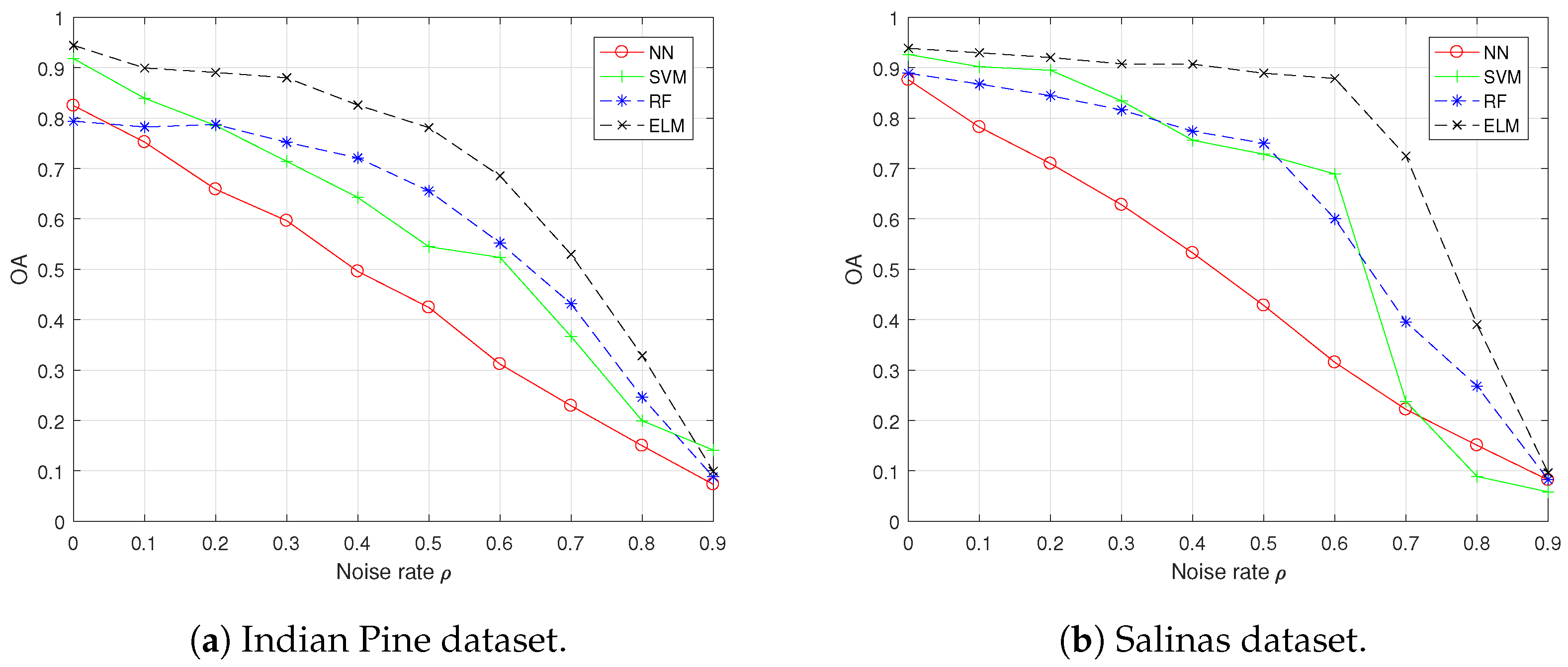
4.3. Results Comparison and Analysis with the “Random” Setting
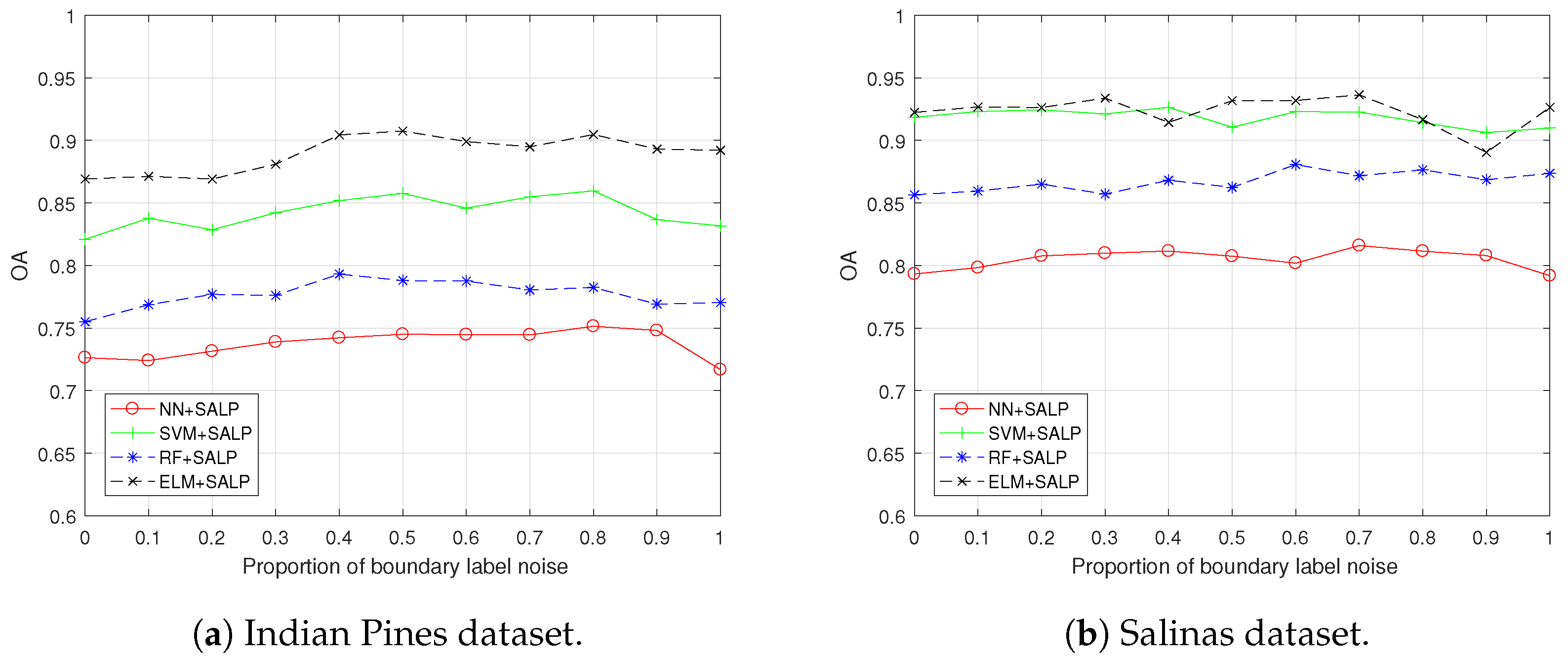
4.4. Results, Comparison and Analysis with the “both” Settings
4.5. Further Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SALP | Spectral–spatial sparse graph based adaptive label propagation |
| HSI | Hyperspectral image |
| SVM | Support vector machines |
| ELM | Extreme learning machine |
| RLPA | Random label propagation algorithm |
| ESR | Entropy rate superpixel segmentation |
| MVA | Majority vote algorithm |
| OA | Overall accuracy |
| NLA | Noisy label based algorithm |
| NN | Neighbor nearest |
| RF | Random forest |
| KNN | k-nearest neighbors |
| iForest | isolation Forest |
References
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in hyperspectral image classification: Earth monitoring with statistical learning methods. IEEE Signal Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef]
- Tuia, D.; Persello, C.; Bruzzone, L. Domain adaptation for the classification of remote sensing data: An overview of recent advances. IEEE Geosci. Remote Sens. Mag. 2016, 4, 41–57. [Google Scholar] [CrossRef]
- Schneider, S.; Murphy, R.J.; Melkumyan, A. Evaluating the performance of a new classifier—The GP-OAD: A comparison with existing methods for classifying rock type and mineralogy from hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2014, 98, 145–156. [Google Scholar] [CrossRef]
- Tiwari, K.; Arora, M.; Singh, D. An assessment of independent component analysis for detection of military targets from hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 730–740. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent advances on spectral–spatial hyperspectral image classification: An overview and new guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced spectral classifiers for hyperspectral images: A review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef]
- Landgrebe, D.A. Signal Theory Methods in Multispectral Remote Sensing; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 29. [Google Scholar]
- Ratle, F.; Camps-Valls, G.; Weston, J. Semisupervised neural networks for efficient hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2271–2282. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, C.; Yu, Y.; Jiang, X.; Ma, J. newblock Spatial-aware collaborative representation for hyperspectral remote sensing image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 404–408. [Google Scholar] [CrossRef]
- Jiang, X.; Song, X.; Zhang, Y.; Jiang, J.; Gao, J.; Cai, Z. Laplacian regularized spatial-aware collaborative graph for discriminant analysis of hyperspectral imagery. Remote Sens. 2019, 11, 29. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local binary patterns and extreme learning machine for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Samat, A.; Du, P.; Liu, S.; Li, J.; Cheng, L. Ensemble Extreme Learning Machines for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1060–1069. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative adversarial networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Liang, P.; Li, C.; Jiang, J. FusionGAN: A generative adversarial network for infrared and visible image fusion. Inf. Fusion 2019, 48, 11–26. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Marais Sicre, C.; Dedieu, G. Effect of training class label noise on classification performances for land cover mapping with satellite image time series. Remote Sens. 2017, 9, 173. [Google Scholar] [CrossRef]
- Angluin, D.; Laird, P. Learning from noisy examples. Mach. Learn. 1988, 2, 343–370. [Google Scholar] [CrossRef]
- Lawrence, N.D.; Schölkopf, B. Estimating a kernel Fisher discriminant in the presence of label noise. In Proceedings of the Eighteenth International Conference on Machine Learning, ICML ’01, Williamstown, MA, USA, 28 June–1 July 2001; Volume 1, pp. 306–313. [Google Scholar]
- Natarajan, N.; Dhillon, I.S.; Ravikumar, P.K.; Tewari, A. Learning with noisy labels. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 1196–1204. [Google Scholar]
- Liu, T.; Tao, D. Classification with noisy labels by importance reweighting. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 447–461. [Google Scholar] [CrossRef]
- Tu, B.; Zhang, X.; Kang, X.; Zhang, G.; Li, S. Density Peak-Based Noisy Label Detection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1573–1584. [Google Scholar] [CrossRef]
- Kang, X.; Duan, P.; Xiang, X.; Li, S.; Benediktsson, J.A. Detection and correction of mislabeled training samples for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5673–5686. [Google Scholar] [CrossRef]
- Gao, Y.; Ma, J.; Yuille, A.L. Semi-supervised sparse representation based classification for face recognition with insufficient labeled samples. IEEE Trans. Image Process. 2017, 26, 2545–2560. [Google Scholar] [CrossRef] [PubMed]
- Frénay, B.; Verleysen, M. Classification in the presence of label noise: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 845–869. [Google Scholar] [CrossRef]
- You, Y.L.; Kaveh, M. Fourth-order partial differential equations for noise removal. IEEE Trans. Image Process. 2000, 9, 1723–1730. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; You, X.; Chen, C.P.; Tao, D.; Ou, W.; Jiang, X.; Zou, J. An adaptive hybrid pattern for noise-robust texture analysis. Pattern Recognit. 2015, 48, 2592–2608. [Google Scholar] [CrossRef]
- Condessa, F.; Bioucas-Dias, J.; Kovačević, J. Supervised hyperspectral image classification with rejection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2321–2332. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Wang, Z.; Chen, C.; Liu, X. Hyperspectral image classification in the presence of noisy labels. IEEE Trans. Geosci. Remote Sens. 2019, 57, 851–865. [Google Scholar] [CrossRef]
- Ji, R.; Gao, Y.; Hong, R.; Liu, Q.; Tao, D.; Li, X. Spectral–spatial constraint hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1811–1824. [Google Scholar]
- Pu, H.; Chen, Z.; Wang, B.; Jiang, G.M. A novel spatial–spectral similarity measure for dimensionality reduction and classification of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7008–7022. [Google Scholar]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral–spatial hyperspectral image classification with edge-preserving filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Zheng, X.; Yuan, Y.; Lu, X. Dimensionality reduction by spatial–spectral preservation in selected bands. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5185–5197. [Google Scholar] [CrossRef]
- Bin, C.; Jianchao, Y.; Shuicheng, Y.; Yun, F.; Huang, T. Learning with l1-graph for image analysis. IEEE Trans. Image Process. 2010, 19, 858–866. [Google Scholar]
- Gu, Y.; Feng, K. L1-graph semisupervised learning for hyperspectral image classification. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1401–1404. [Google Scholar]
- Wang, X.; Zhang, X.; Zeng, Z.; Wu, Q.; Zhang, J. Unsupervised spectral feature selection with l1-norm graph. Neurocomputing 2016, 200, 47–54. [Google Scholar] [CrossRef]
- Liu, L.; Chen, L.; Chen, C.P.; Tang, Y.Y. Weighted joint sparse representation for removing mixed noise in image. IEEE Trans. Cybern. 2017, 47, 600–611. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Chen, C.P.; You, X.; Tang, Y.Y.; Zhang, Y.; Li, S. Mixed noise removal via robust constrained sparse representation. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2177–2189. [Google Scholar] [CrossRef]
- Fan, F.; Ma, Y.; Li, C.; Mei, X.; Huang, J.; Ma, J. Hyperspectral image denoising with superpixel segmentation and low-rank representation. Inf. Sci. 2017, 397, 48–68. [Google Scholar] [CrossRef]
- Liu, M.Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2097–2104. [Google Scholar]
- Freund, Y. Boosting a weak learning algorithm by majority. Inf. Comput. 1995, 121, 256–285. [Google Scholar] [CrossRef]
- Kalai, A.T.; Servedio, R.A. Boosting in the presence of noise. J. Comput. Syst. Sci. 2005, 71, 266–290. [Google Scholar] [CrossRef]
- Chen, C.; Li, W.; Su, H.; Liu, K. Spectral–spatial classification of hyperspectral image based on kernel extreme learning machine. Remote Sens. 2014, 6, 5795–5814. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Zhu, L.; Liu, Y. Centroid and Covariance Alignment-Based Domain Adaptation for Unsupervised Classification of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2305–2323. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A superpixelwise PCA approach for unsupervised feature extraction of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, X.; Li, Q. Spectral–Spatial Hyperspectral Image Classification Using ℓ1/2 Regularized Low-Rank Representation and Sparse Representation-Based Graph Cuts. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2473–2484. [Google Scholar] [CrossRef]
- Ma, D.; Yuan, Y.; Wang, Q. Hyperspectral anomaly detection via discriminative feature learning with multiple-dictionary sparse representation. Remote Sens. 2018, 10, 745. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Jiang, J.; Zhou, H.; Guo, X. Locality preserving matching. Int. J. Comput. Vis. 2019, 127, 512–531. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Fu, W.; Fang, L. Multiscale superpixel-based sparse representation for hyperspectral image classification. Remote Sens. 2017, 9, 139. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L. Efficient superpixel-level multitask joint sparse representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5338–5351. [Google Scholar]
- Xue, Z.; Du, P.; Li, J.; Su, H. Simultaneous sparse graph embedding for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6114–6133. [Google Scholar] [CrossRef]
- Chen, M.; Wang, Q.; Li, X. Discriminant analysis with graph learning for hyperspectral image classification. Remote Sens. 2018, 10, 836. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Donoho, D.L. For most large underdetermined systems of linear equations the minimal ℓ1-norm solution is also the sparsest solution. Commun. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Kothari, R.; Jain, V. Learning from labeled and unlabeled data. In Proceedings of the 2002 International Joint Conference on Neural Networks, IJCNN’02 (Cat. No. 02CH37290), Honolulu, HI, USA, 12–17 May 2002; Volume 3, pp. 2803–2808. [Google Scholar]
- Zhu, X.; Ghahramani, Z. Learning from Labeled and Unlabeled Data with Label Propagation; Technical Report CMU-CALD-02-107; Carnegie Mellon University: Pittsburgh, PA, USA, 2002. [Google Scholar]
- Cheng, G.; Li, Z.; Han, J.; Yao, X.; Guo, L. Exploring hierarchical convolutional features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6712–6722. [Google Scholar] [CrossRef]
- Qin, Y.; Bruzzone, L.; Li, B.; Ye, Y. Cross-Domain Collaborative Learning via Cluster Canonical Correlation Analysis and Random Walker for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 3. [Google Scholar] [CrossRef]


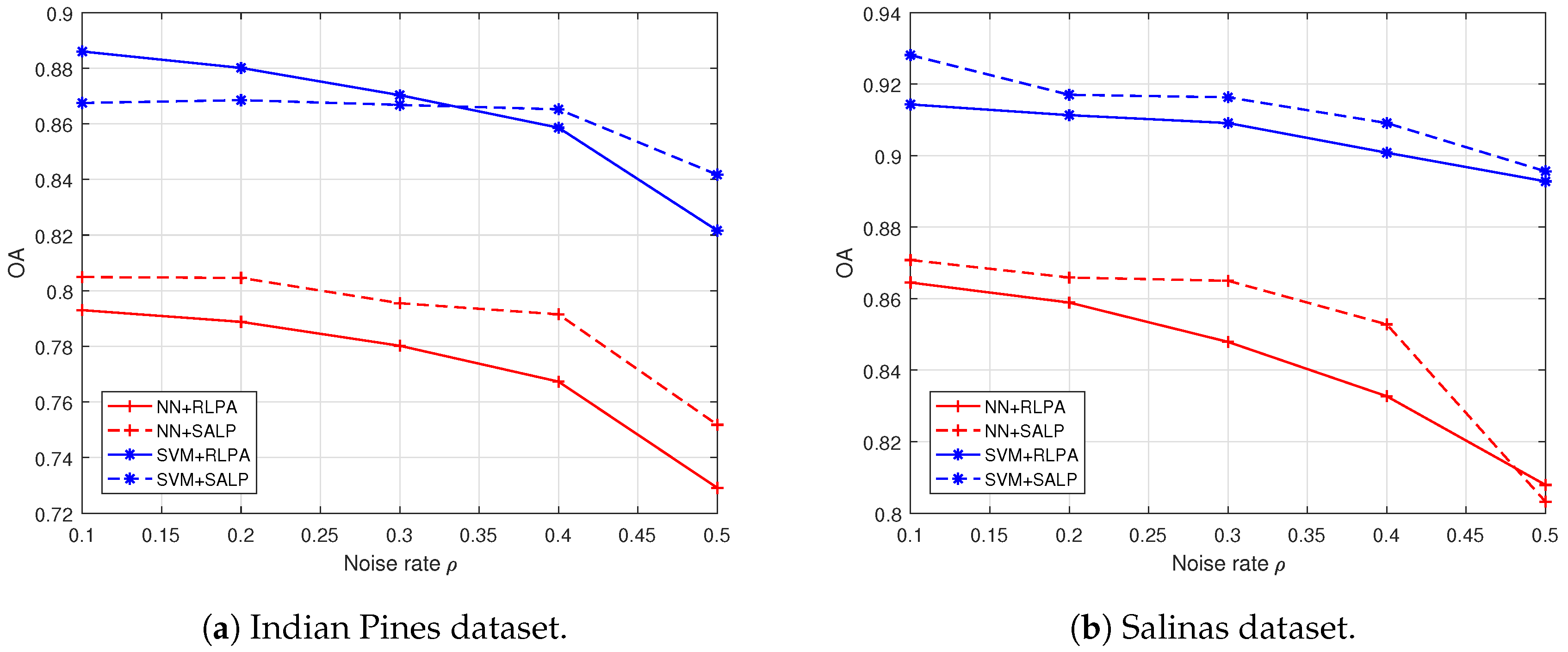
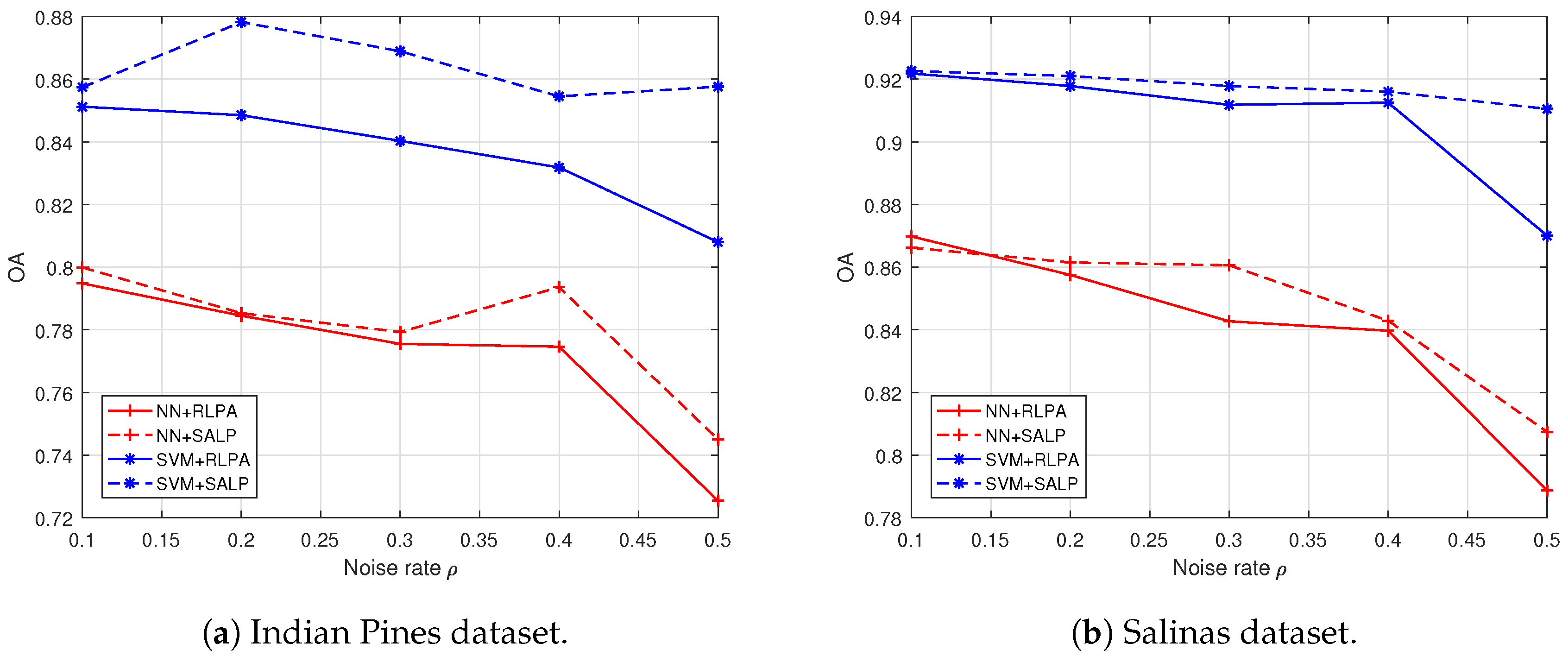
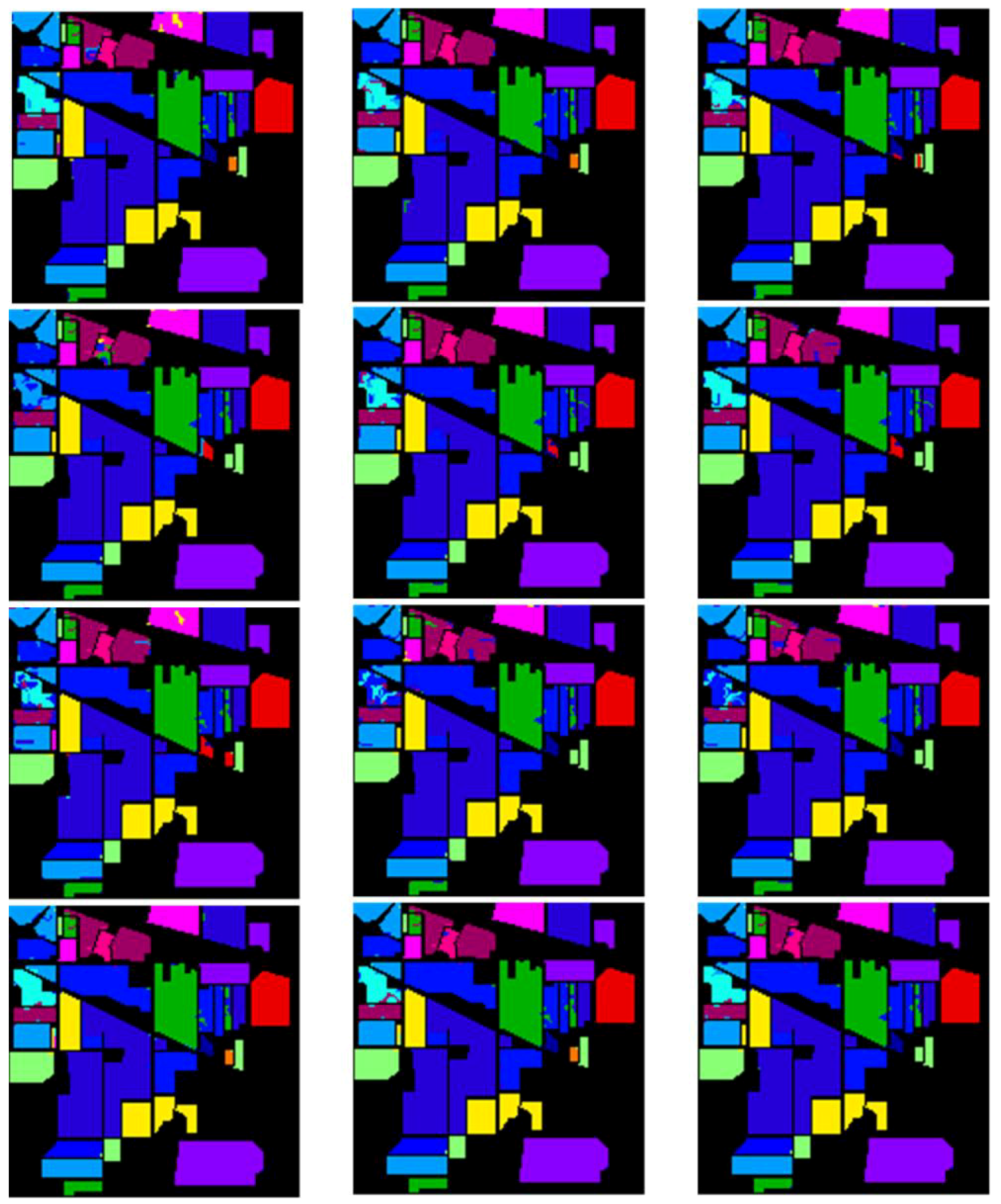
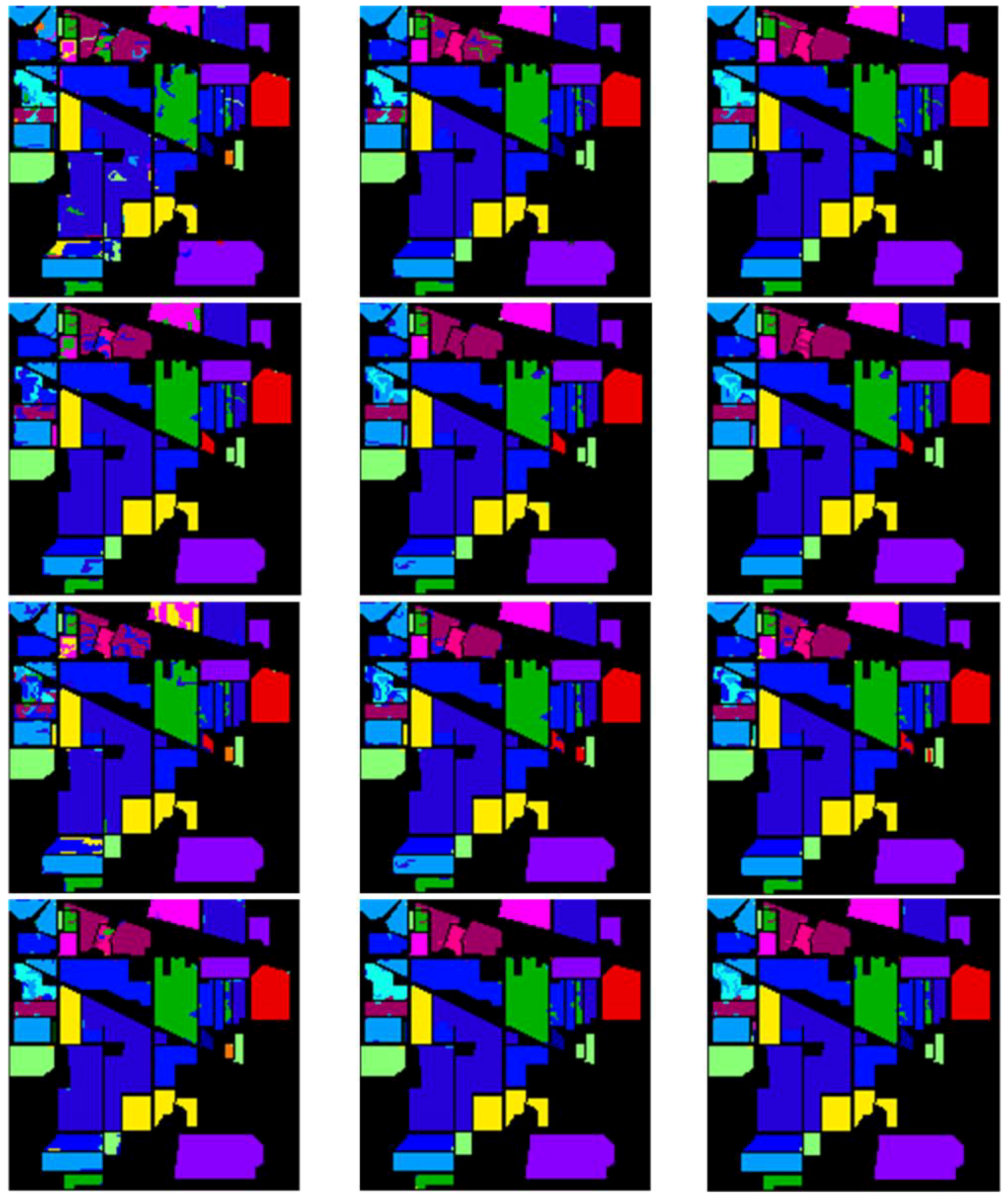

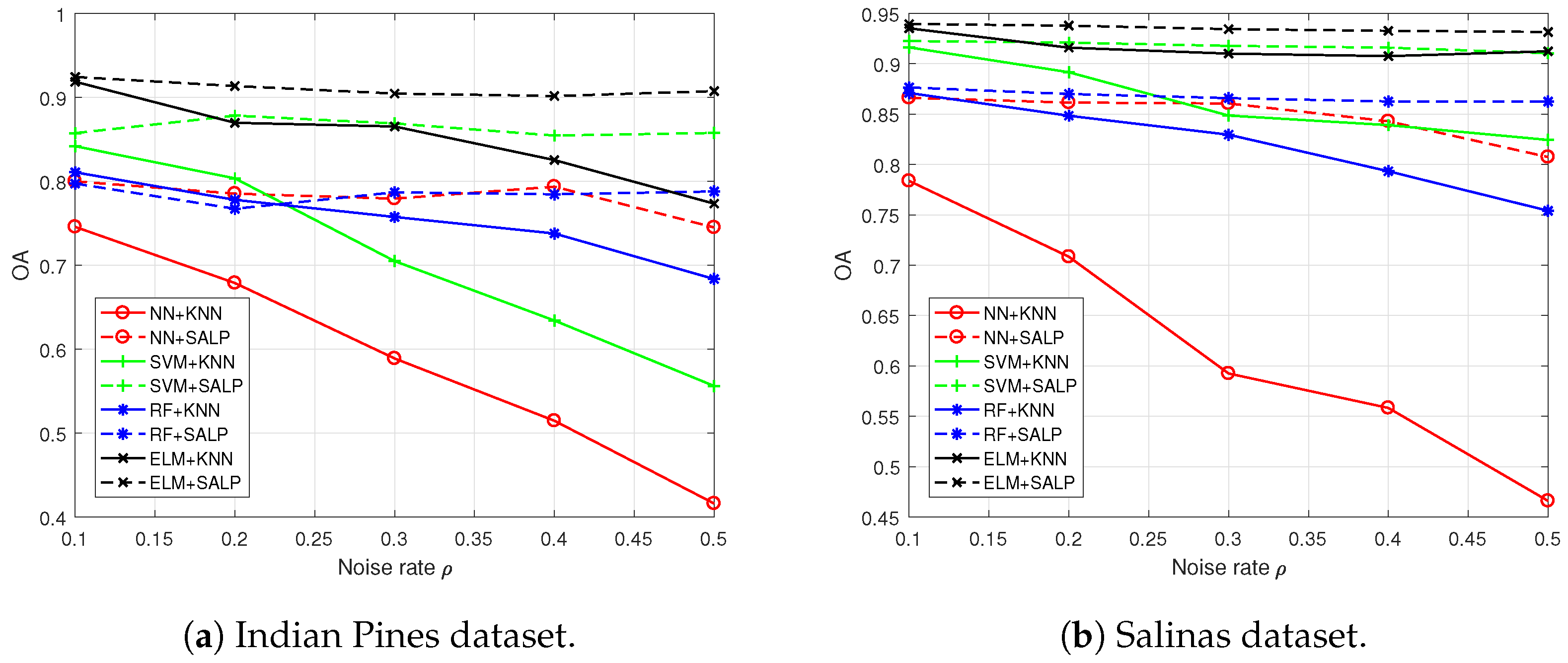
| Classifier | OA [%] | AA [%] | Kappa Coefficient | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NLA | iForest | RLPA | SALP | NLA | iForest | RLPA | SALP | NLA | iForest | RLPA | SALP | ||
| 0.1 | NN | 73.24 | 74.34 | 79.30 | 69.55 | 69.50 | 72.63 | 0.6966 | 0.7085 | 0.7635 | |||
| SVM | 84.21 | 83.73 | 86.75 | 61.37 | 64.28 | 74.56 | 0.8176 | 0.8122 | 0.8480 | ||||
| RF | 79.11 | 79.72 | 78.69 | 66.68 | 66.26 | 65.85 | 0.7597 | 0.7665 | 0.7538 | ||||
| ELM | 90.11 | 91.66 | 90.07 | 82.53 | 83.31 | 81.88 | 0.9012 | 0.8869 | 0.8844 | ||||
| 0.2 | NN | 65.24 | 73.08 | 78.88 | 62.73 | 66.14 | 72.32 | 0.6086 | 0.6925 | 0.7587 | |||
| SVM | 77.16 | 77.96 | 86.85 | 54.93 | 62.78 | 74.67 | 0.7340 | 0.7444 | 0.8491 | ||||
| RF | 78.41 | 74.03 | 78.96 | 61.26 | 66.12 | 66.64 | 0.7518 | 0.7006 | 0.7571 | ||||
| ELM | 88.65 | 83.30 | 90.03 | 82.26 | 73.44 | 82.50 | 0.8704 | 0.8082 | 0.8860 | ||||
| 0.3 | NN | 57.46 | 70.95 | 78.02 | 54.28 | 61.75 | 70.31 | 0.5247 | 0.6688 | 0.7491 | |||
| SVM | 71.10 | 76.82 | 86.68 | 46.58 | 58.29 | 71.18 | 0.6603 | 0.7315 | 0.8514 | ||||
| RF | 75.95 | 72.54 | 79.13 | 64.40 | 58.52 | 65.55 | 0.7243 | 0.6837 | 0.7598 | ||||
| ELM | 86.41 | 81.51 | 89.70 | 77.28 | 68.72 | 80.94 | 0.8447 | 0.7878 | 0.8822 | ||||
| 0.4 | NN | 49.76 | 68.71 | 76.73 | 47.82 | 60.12 | 69.66 | 0.4421 | 0.6426 | 0.7348 | |||
| SVM | 65.04 | 73.01 | 85.86 | 39.00 | 57.25 | 71.21 | 0.5851 | 0.6867 | 0.8381 | ||||
| RF | 72.43 | 69.59 | 78.64 | 61.06 | 56.91 | 65.61 | 0.6844 | 0.6494 | 0.7538 | ||||
| ELM | 82.93 | 76.91 | 89.62 | 72.53 | 64.61 | 80.63 | 0.8050 | 0.7345 | 0.8815 | ||||
| 0.5 | NN | 40.56 | 64.64 | 72.91 | 40.06 | 55.39 | 65.31 | 0.3458 | 0.5967 | 0.6923 | |||
| SVM | 61.91 | 68.90 | 82.16 | 35.80 | 53.36 | 64.02 | 0.5469 | 0.6388 | 0.7952 | ||||
| RF | 66.68 | 66.08 | 76.39 | 57.04 | 53.39 | 63.47 | 0.6212 | 0.6096 | 0.7329 | ||||
| ELM | 76.94 | 72.43 | 87.07 | 67.74 | 58.94 | 76.69 | 0.7373 | 0.6826 | 0.8522 | ||||
| Classifier | OA [%] | AA [%] | Kappa Coefficient | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NLA | iForest | RLPA | SALP | NLA | iForest | RLPA | SALP | NLA | iForest | RLPA | SALP | ||
| 0.1 | NN | 78.07 | 85.10 | 86.45 | 83.95 | 91.72 | 93.01 | 0.7579 | 0.8350 | 0.8497 | |||
| SVM | 84.44 | 88.22 | 91.43 | 91.74 | 93.14 | 95.45 | 0.8272 | 0.8694 | 0.9047 | ||||
| RF | 86.97 | 86.71 | 88.09 | 92.18 | 92.33 | 93.27 | 0.8553 | 0.8526 | 0.8677 | ||||
| ELM | 92.69 | 90.54 | 92.96 | 96.31 | 95.20 | 96.58 | 0.9186 | 0.8949 | 0.9216 | ||||
| 0.2 | NN | 70.22 | 84.93 | 85.89 | 75.12 | 91.33 | 92.76 | 0.6721 | 0.8331 | 0.8436 | |||
| SVM | 85.87 | 88.24 | 91.13 | 91.30 | 93.16 | 95.20 | 0.8415 | 0.8694 | 0.9013 | ||||
| RF | 85.54 | 85.98 | 87.82 | 90.54 | 91.66 | 93.12 | 0.8395 | 0.8445 | 0.8648 | ||||
| ELM | 92.27 | 89.63 | 92.82 | 95.92 | 94.59 | 96.49 | 0.9139 | 0.8848 | 0.9201 | ||||
| 0.3 | NN | 60.85 | 84.08 | 84.79 | 65.44 | 90.26 | 92.14 | 0.5710 | 0.8237 | 0.8318 | |||
| SVM | 76.62 | 85.99 | 90.91 | 89.47 | 91.48 | 95.12 | 0.7437 | 0.8445 | 0.8989 | ||||
| RF | 82.59 | 84.69 | 87.12 | 87.52 | 90.34 | 92.78 | 0.8070 | 0.8301 | 0.8571 | ||||
| ELM | 91.34 | 88.22 | 92.56 | 95.07 | 93.52 | 96.31 | 0.9036 | 0.8692 | 0.9172 | ||||
| 0.4 | NN | 53.99 | 83.72 | 83.27 | 57.83 | 89.91 | 91.28 | 0.4958 | 0.8197 | 0.8150 | |||
| SVM | 77.52 | 84.79 | 90.08 | 85.98 | 90.52 | 94.37 | 0.7525 | 0.8313 | 0.8897 | ||||
| RF | 79.03 | 84.27 | 86.47 | 83.62 | 90.01 | 92.54 | 0.7675 | 0.8256 | 0.8500 | ||||
| ELM | 90.44 | 86.89 | 92.03 | 94.17 | 92.69 | 96.10 | 0.8936 | 0.8545 | 0.9114 | ||||
| 0.5 | NN | 44.86 | 82.89 | 80.32 | 47.17 | 88.53 | 89.22 | 0.3978 | 0.7879 | 0.783 | |||
| SVM | 75.03 | 84.52 | 89.28 | 75.97 | 89.54 | 93.85 | 0.7206 | 0.8281 | 0.8808 | ||||
| RF | 73.19 | 83.25 | 85.10 | 77.06 | 88.62 | 91.50 | 0.7034 | 0.8143 | 0.8352 | ||||
| ELM | 89.39 | 86.39 | 91.55 | 93.26 | 91.70 | 95.43 | 0.8819 | 0.8490 | 0.9061 | ||||
| Classifier | OA [%] | AA [%] | Kappa Coefficient | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NLA | RLPA | SALP | NLA | RLPA | SALP | NLA | RLPA | SALP | ||
| 0.1 | NN | 75.23 | 79.48 | 67.80 | 72.14 | 0.7071 | 0.7513 | |||
| SVM | 83.93 | 85.12 | 62.57 | 76.38 | 0.8150 | 0.8362 | ||||
| RF | 78.24 | 78.90 | 62.71 | 66.06 | 0.7498 | 0.7568 | ||||
| ELM | 89.94 | 92.02 | 81.42 | 82.63 | 0.8850 | 0.9089 | ||||
| 0.2 | NN | 65.86 | 78.45 | 63.31 | 71.81 | 0.6169 | 0.7566 | |||
| SVM | 78.51 | 84.85 | 55.69 | 73.41 | 0.7539 | 0.8481 | ||||
| RF | 77.65 | 76.73 | 62.06 | 64.70 | 0.7422 | 0.7314 | ||||
| ELM | 89.06 | 91.35 | 80.48 | 81.22 | 0.8752 | 0.9009 | ||||
| 0.3 | NN | 59.63 | 77.55 | 56.04 | 71.27 | 0.5368 | 0.7446 | |||
| SVM | 71.41 | 84.03 | 45.48 | 72.47 | 0.6693 | 0.8395 | ||||
| RF | 75.20 | 77.98 | 63.96 | 64.15 | 0.7149 | 0.7475 | ||||
| ELM | 87.99 | 90.45 | 79.40 | 82.13 | 0.8625 | 0.8909 | ||||
| 0.4 | NN | 49.58 | 77.46 | 44.97 | 71.97 | 0.4417 | 0.7439 | |||
| SVM | 64.24 | 83.18 | 36.40 | 64.37 | 0.5783 | 0.8129 | ||||
| RF | 72.11 | 78.62 | 58.67 | 64.98 | 0.6823 | 0.7524 | ||||
| ELM | 82.57 | 90.16 | 69.94 | 81.73 | 0.8010 | 0.8875 | ||||
| 0.5 | NN | 42.42 | 72.54 | 42.18 | 66.20 | 0.3665 | 0.6892 | |||
| SVM | 54.47 | 80.80 | 28.55 | 61.92 | 0.4615 | 0.7898 | ||||
| RF | 65.53 | 78.05 | 53.61 | 62.89 | 0.6061 | 0.7468 | ||||
| ELM | 78.10 | 89.98 | 67.51 | 81.26 | 0.7505 | 0.8856 | ||||
| Classifier | OA [%] | AA [%] | Kappa Coefficient | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NLA | RLPA | SALP | NLA | RLPA | SALP | NLA | RLPA | SALP | ||
| 0.1 | NN | 78.20 | 86.62 | 84.43 | 93.52 | 0.7602 | 0.8528 | |||
| SVM | 90.19 | 92.18 | 94.09 | 95.85 | 0.8906 | 0.9082 | ||||
| RF | 86.75 | 87.65 | 92.23 | 93.25 | 0.8640 | 0.8632 | ||||
| ELM | 92.96 | 93.86 | 96.68 | 96.97 | 0.9281 | 0.9309 | ||||
| 0.2 | NN | 70.96 | 85.75 | 76.77 | 93.01 | 0.6803 | 0.8368 | |||
| SVM | 89.49 | 91.78 | 91.79 | 95.78 | 0.8831 | 0.9014 | ||||
| RF | 84.44 | 86.48 | 90.37 | 92.86 | 0.8272 | 0.8503 | ||||
| ELM | 92.02 | 93.79 | 95.67 | 96.12 | 0.9113 | 0.9191 | ||||
| 0.3 | NN | 62.78 | 84.27 | 66.43 | 92.16 | 0.5911 | 0.8287 | |||
| SVM | 83.4 | 91.18 | 88.29 | 94.98 | 0.8136 | 0.9021 | ||||
| RF | 81.60 | 86.11 | 88.21 | 92.29 | 0.7967 | 0.8544 | ||||
| ELM | 90.76 | 93.44 | 93.96 | 96.10 | 0.8970 | 0.9116 | ||||
| 0.4 | NN | 53.23 | 83.97 | 58.89 | 91.21 | 0.4891 | 0.8080 | |||
| SVM | 75.60 | 91.25 | 83.71 | 94.31 | 0.7301 | 0.9004 | ||||
| RF | 77.40 | 85.99 | 82.90 | 91.95 | 0.7501 | 0.8450 | ||||
| ELM | 90.70 | 93.27 | 93.47 | 96.08 | 0.8989 | 0.9144 | ||||
| 0.5 | NN | 42.82 | 78.87 | 46.64 | 87.47 | 0.3788 | 0.7521 | |||
| SVM | 72.84 | 87.00 | 79.77 | 92.66 | 0.6986 | 0.8563 | ||||
| RF | 75.00 | 86.24 | 77.21 | 91.05 | 0.7222 | 0.8313 | ||||
| ELM | 88.90 | 93.16 | 93.16 | 95.51 | 0.8767 | 0.9073 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, Q.; Yang, H.; Jiang, J. Label Noise Cleansing with Sparse Graph for Hyperspectral Image Classification. Remote Sens. 2019, 11, 1116. https://doi.org/10.3390/rs11091116
Leng Q, Yang H, Jiang J. Label Noise Cleansing with Sparse Graph for Hyperspectral Image Classification. Remote Sensing. 2019; 11(9):1116. https://doi.org/10.3390/rs11091116
Chicago/Turabian StyleLeng, Qingming, Haiou Yang, and Junjun Jiang. 2019. "Label Noise Cleansing with Sparse Graph for Hyperspectral Image Classification" Remote Sensing 11, no. 9: 1116. https://doi.org/10.3390/rs11091116
APA StyleLeng, Q., Yang, H., & Jiang, J. (2019). Label Noise Cleansing with Sparse Graph for Hyperspectral Image Classification. Remote Sensing, 11(9), 1116. https://doi.org/10.3390/rs11091116