Hyperspectral Unmixing with Gaussian Mixture Model and Low-Rank Representation
Abstract
:1. Introduction
2. Related Models
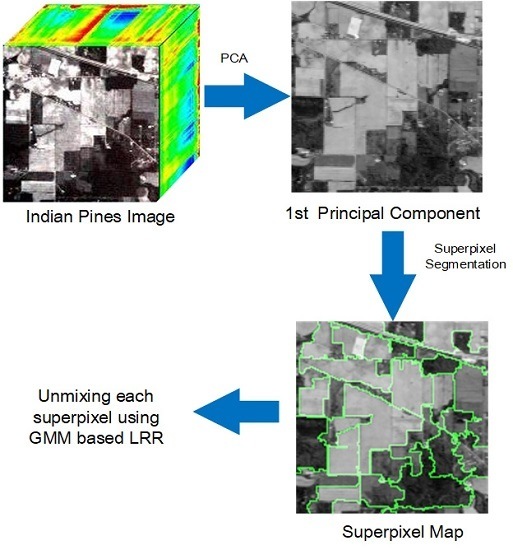
3. GMM Unmixing with Superpixel Segmentation and Low-Rank Representation
3.1. Formulation of the Proposed GMM-SS-LRR
3.2. Optimization of the Proposed GMM-SS-LRR
| Algorithm 1 Solving Equation (15) with EM. |
| Input: Collect mixed pixel matrix , endmember , the parameter of smoothness and sparse constraint , and the parameter of low-rank property ; Output: The estimated abundance matrix ; 1: Implement PCA and set as initialization; 2: Using the KL divergence to get the number of components ; 3: Using CVIC to correct for the bias; 4: while not converged do 5: E step: 6: M step: 7: Update and A; 8: end while 9: Return . |
| Algorithm 2 Proposed GMM-SS-LRR. |
| Input: Collect mixed pixel matrix , endmember , the parameter of smoothness and sparse constraint , and the parameter of low-rank property and the number of the superpixels S; Output: The estimated abundance matrix ; 1: Implement PCA on and obtain the first principal component; 2: Segment into homogeneous regions based on its first principal component by using entropy rate [42]; 3: for each homogeneous region do 4: |Recover with Algorithm 1; 5: end for 6: Obtain from each homogeneous region; 7: Return . |
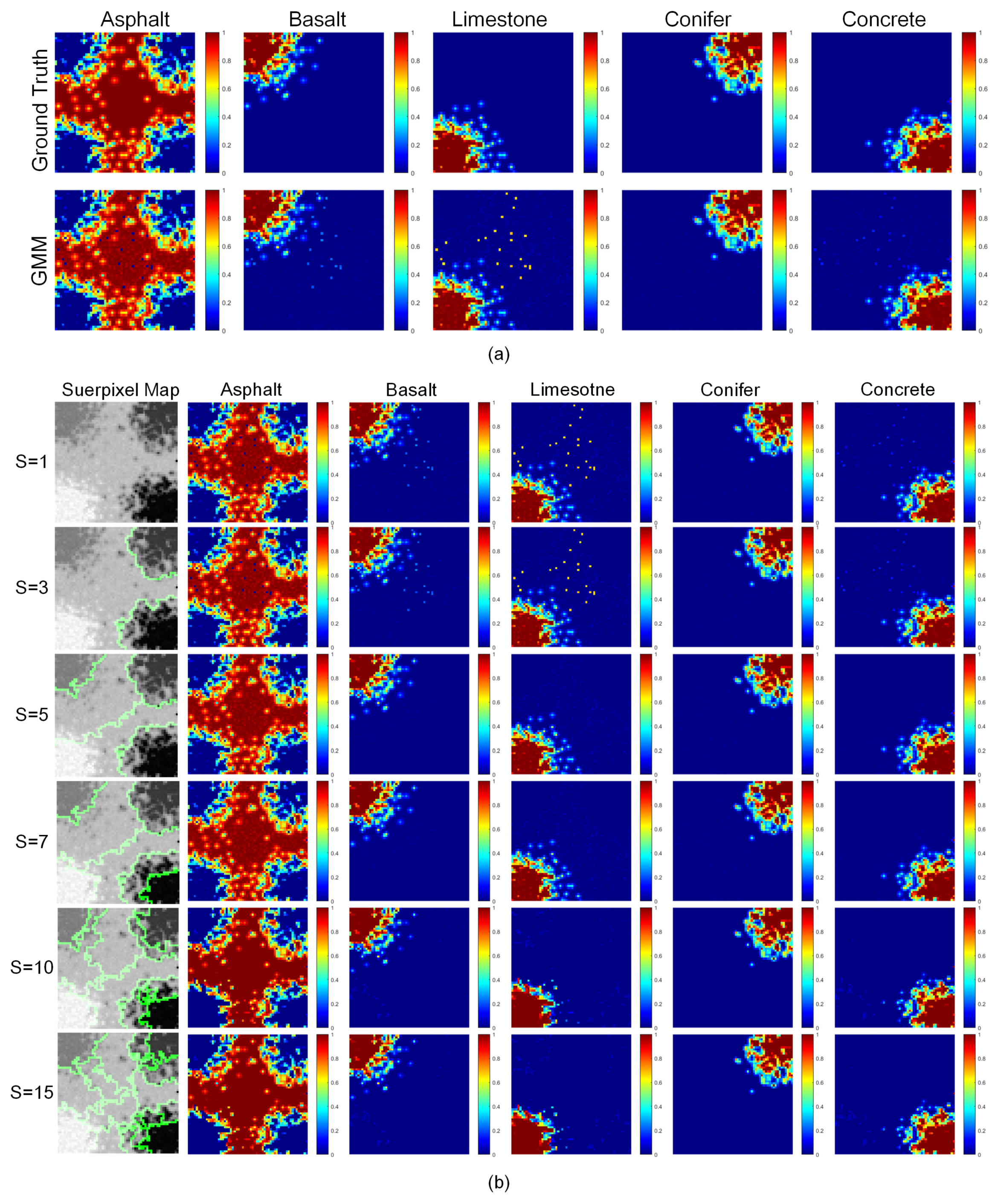
4. Experimental Result
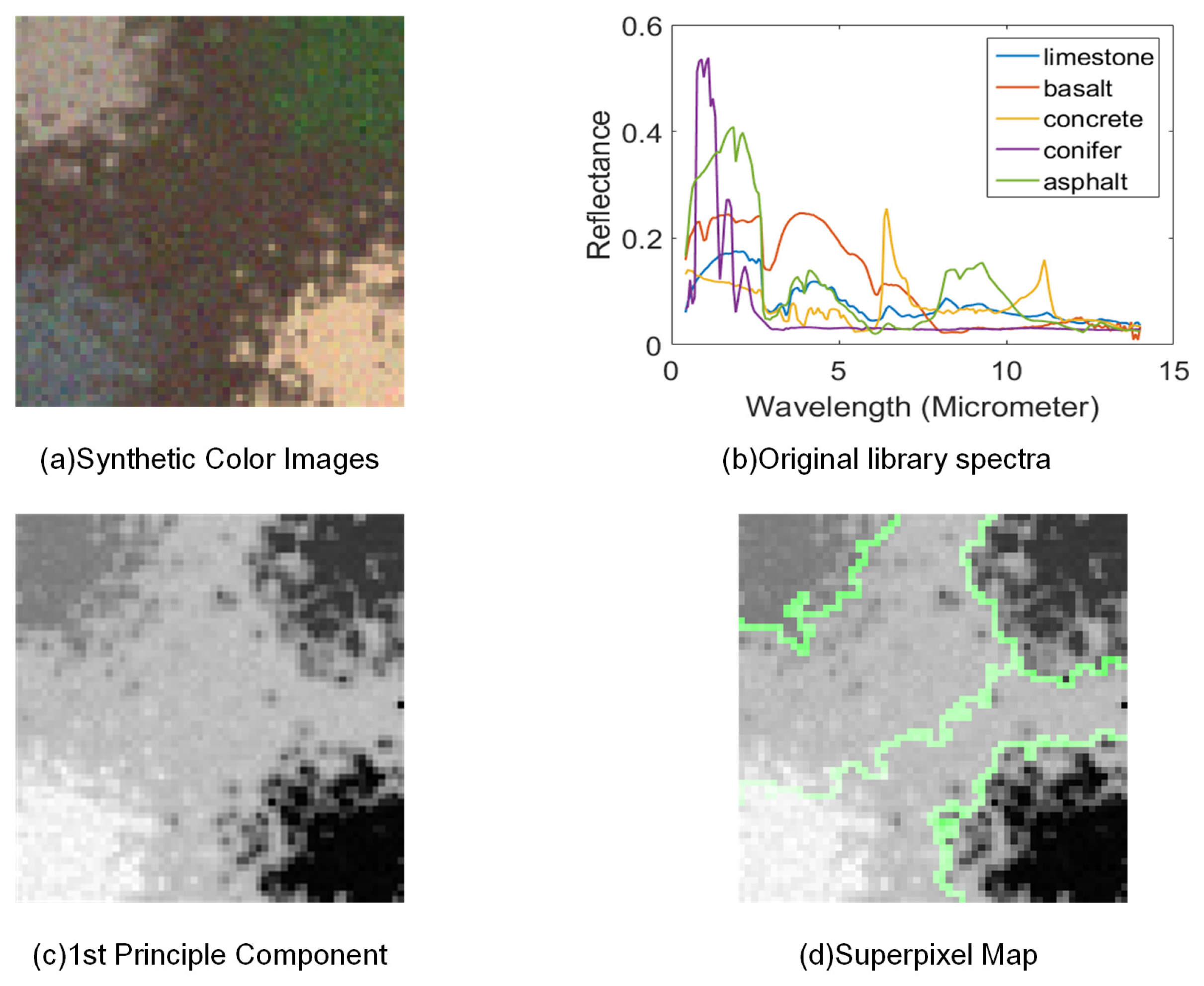
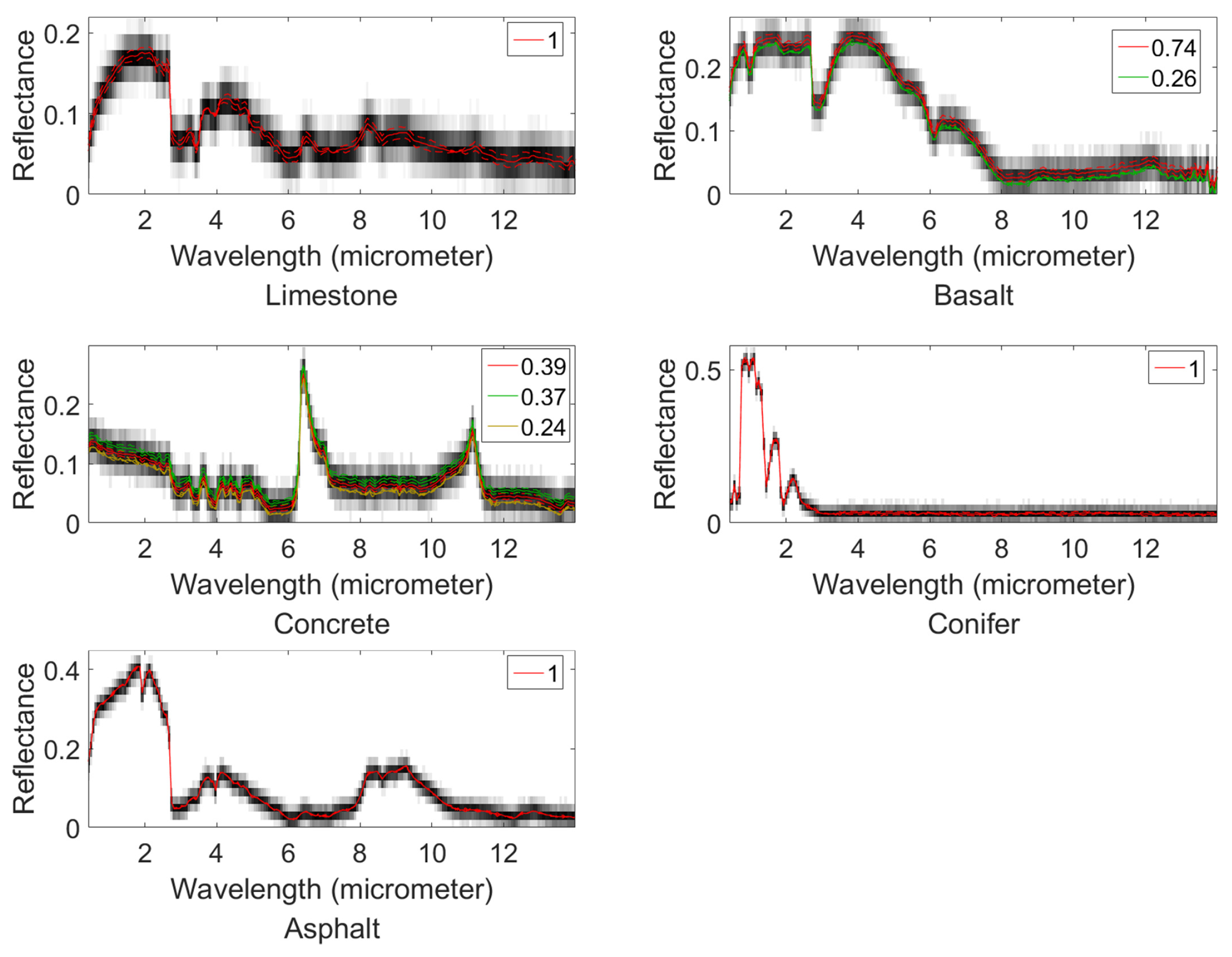
4.1. Synthetic Datasets
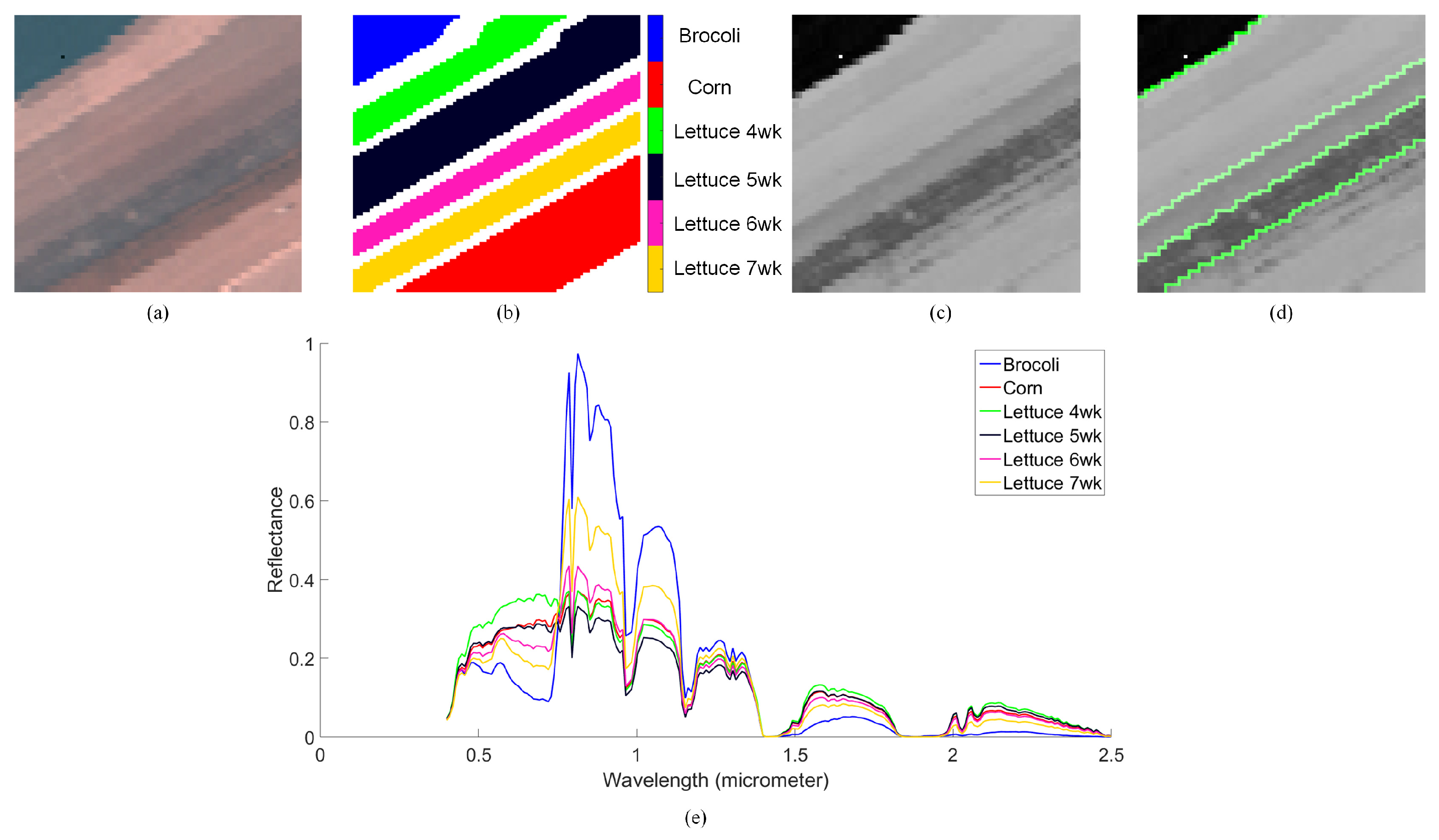
4.2. Mississippi Gulfport Datasets
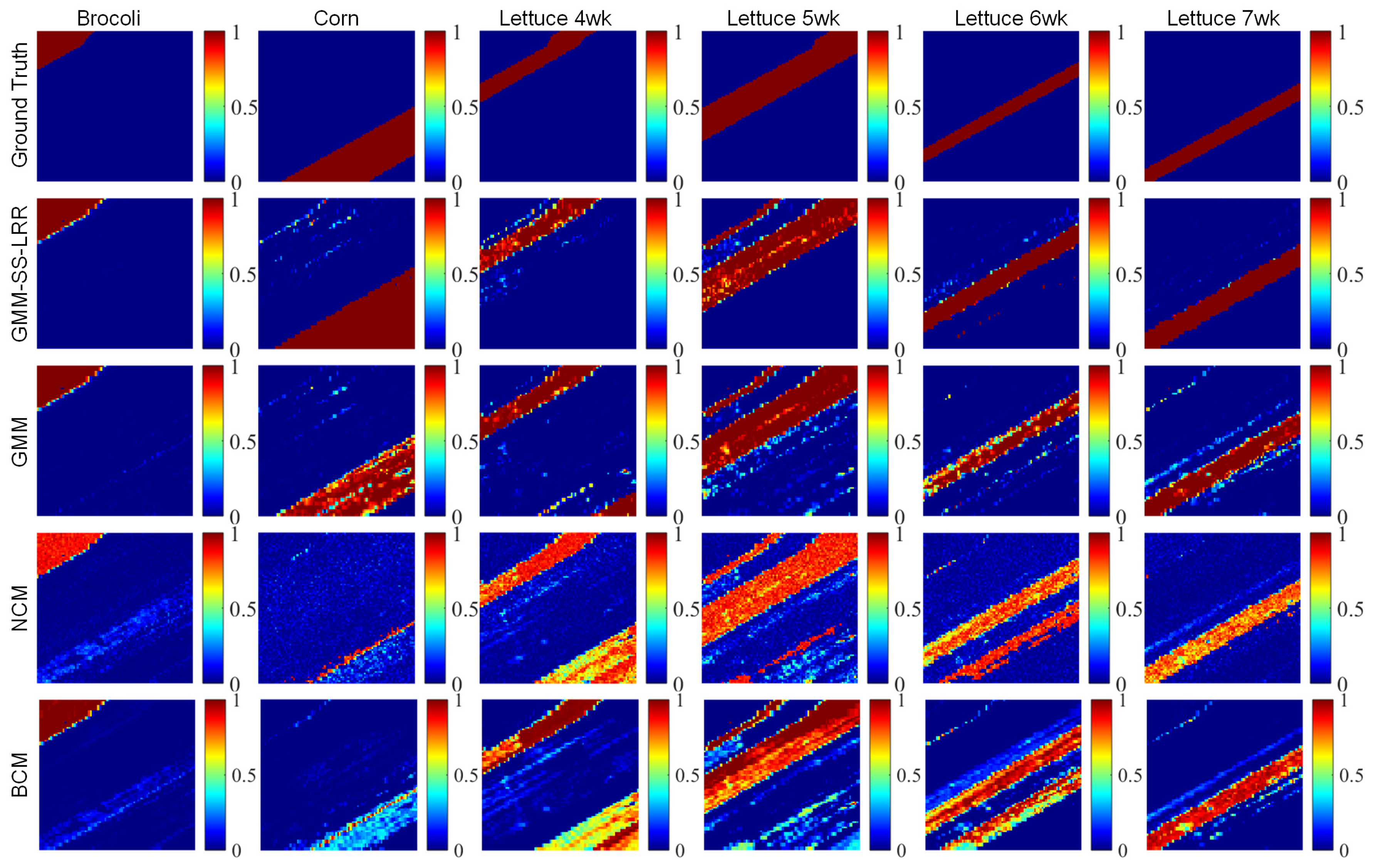
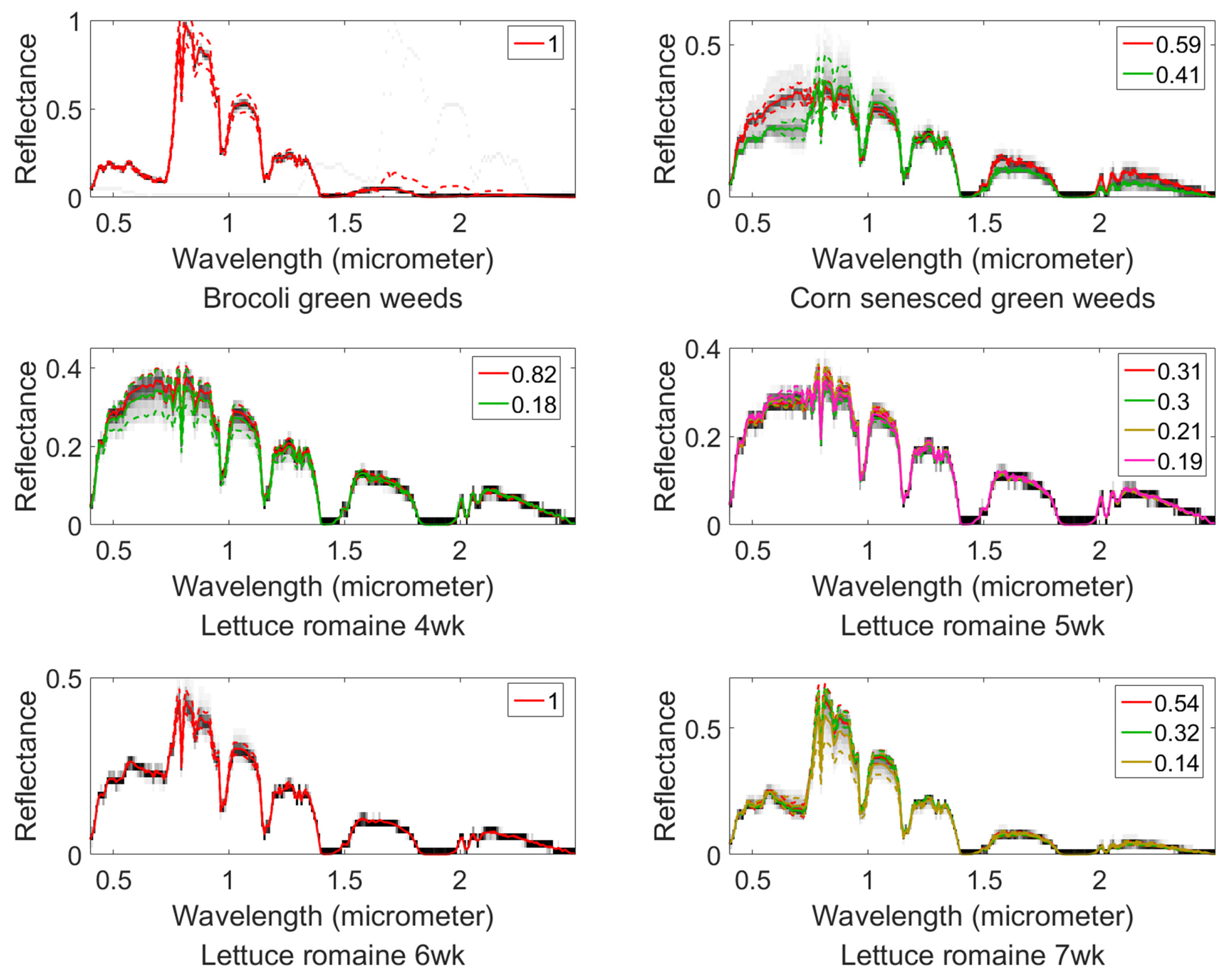
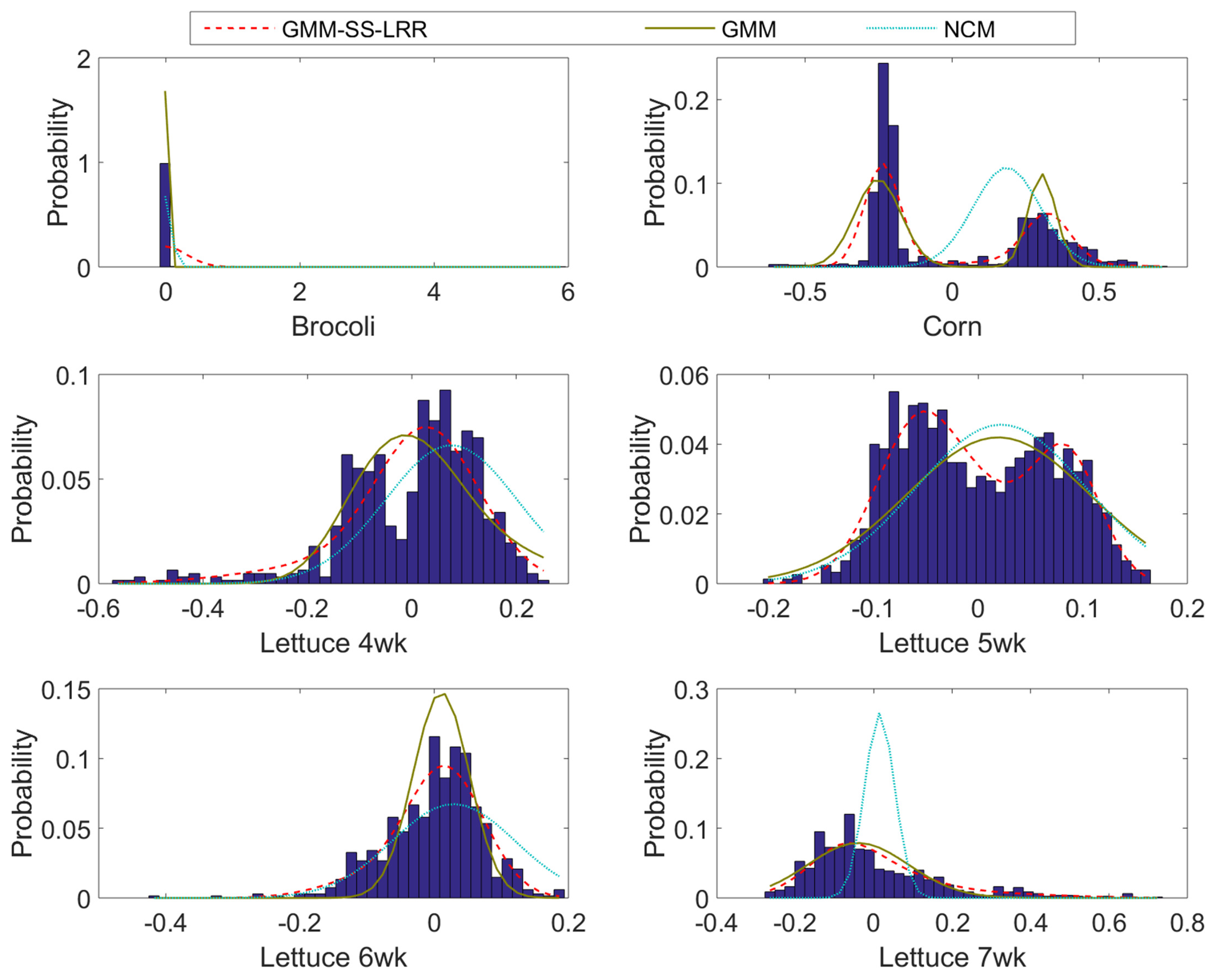
4.3. Salinas-A Datasets
4.4. Effects of the Size of the Superpixels
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Mei, X.; Ma, Y.; Li, C.; Fan, F.; Huang, J.; Ma, J. Robust GBM hyperspectral image unmixing with superpixel segmentation based low rank and sparse representation. Neurocomputing 2018, 275, 2783–2797. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Wang, Z.; Chen, C.; Liu, X. Hyperspectral Image Classification in the Presence of Noisy Labels. IEEE Trans. Geosci. Remote Sens. 2019, 57, 851–865. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, H.; Zhao, J.; Gao, Y.; Jiang, J.; Tian, J. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Manolakis, D.; Siracusa, C.; Shaw, G. Hyperspectral subpixel target detection using the linear mixing model. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1392–1409. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Zhu, L.; Liu, Y. Centroid and Covariance Alignment-Based Domain Adaptation for Unsupervised Classification of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2305–2323. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A Superpixelwise PCA Approach for Unsupervised Feature Extraction of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Jiang, J.; Zhou, H.; Guo, X. Locality preserving matching. Int. J. Comput. Vis. 2019, 127, 512–531. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Boardman, J.W.; Kruse, F.A.; Green, R.O. Mapping Target Signatures via Partial Unmixing of AVIRIS Data. 1995. Available online: http://hdl.handle.net/2014/33635 (accessed on 14 April 2019).
- Ren, H.; Chang, C.I. Automatic spectral target recognition in hyperspectral imagery. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1232–1249. [Google Scholar]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Chan, T.H.; Ma, W.K.; Ambikapathi, A.; Chi, C.Y. A simplex volume maximization framework for hyperspectral endmember extraction. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4177–4193. [Google Scholar] [CrossRef]
- Berman, M.; Kiiveri, H.; Lagerstrom, R.; Ernst, A.; Dunne, R.; Huntington, J.F. ICE: A statistical approach to identifying endmembers in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2085–2095. [Google Scholar] [CrossRef]
- Halimi, A.; Altmann, Y.; Dobigeon, N.; Tourneret, J.Y. Nonlinear unmixing of hyperspectral images using a generalized bilinear model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4153–4162. [Google Scholar] [CrossRef]
- Altmann, Y.; Halimi, A.; Dobigeon, N.; Tourneret, J.Y. Supervised nonlinear spectral unmixing using a postnonlinear mixing model for hyperspectral imagery. IEEE Trans. Image Process. 2012, 21, 3017–3025. [Google Scholar] [CrossRef]
- Broadwater, J.; Chellappa, R.; Banerjee, A.; Burlina, P. Kernel fully constrained least squares abundance estimates. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 4041–4044. [Google Scholar]
- Broadwater, J.; Banerjee, A. A generalized kernel for areal and intimate mixtures. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Zare, A.; Ho, K. Endmember variability in hyperspectral analysis: Addressing spectral variability during spectral unmixing. IEEE Signal Process. Mag. 2014, 31, 95–104. [Google Scholar] [CrossRef]
- Roberts, D.A.; Gardner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, R. Mapping chaparral in the Santa Monica Mountains using multiple endmember spectral mixture models. Remote Sens. Environ. 1998, 65, 267–279. [Google Scholar] [CrossRef]
- Combe, J.P.; Le Mouélic, S.; Sotin, C.; Gendrin, A.; Mustard, J.; Le Deit, L.; Launeau, P.; Bibring, J.P.; Gondet, B.; Langevin, Y.; et al. Analysis of OMEGA/Mars express data hyperspectral data using a multiple-endmember linear spectral unmixing model (MELSUM): Methodology and first results. Planet. Space Sci. 2008, 56, 951–975. [Google Scholar] [CrossRef]
- Asner, G.P.; Lobell, D.B. A biogeophysical approach for automated SWIR unmixing of soils and vegetation. Remote Sens. Environ. 2000, 74, 99–112. [Google Scholar] [CrossRef]
- Asner, G.P.; Heidebrecht, K.B. Spectral unmixing of vegetation, soil and dry carbon cover in arid regions: Comparing multispectral and hyperspectral observations. Int. J. Remote Sens. 2002, 23, 3939–3958. [Google Scholar] [CrossRef]
- Dennison, P.E.; Roberts, D.A. Endmember selection for multiple endmember spectral mixture analysis using endmember average RMSE. Remote Sens. Environ. 2003, 87, 123–135. [Google Scholar] [CrossRef]
- Bateson, C.A.; Asner, G.P.; Wessman, C.A. Endmember bundles: A new approach to incorporating endmember variability into spectral mixture analysis. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1083–1094. [Google Scholar] [CrossRef]
- Somers, B.; Asner, G.P.; Tits, L.; Coppin, P. Endmember variability in spectral mixture analysis: A review. Remote Sens. Environ. 2011, 115, 1603–1616. [Google Scholar]
- Jin, J.; Wang, B.; Zhang, L. A novel approach based on fisher discriminant null space for decomposition of mixed pixels in hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2010, 7, 699–703. [Google Scholar] [CrossRef]
- Eches, O.; Dobigeon, N.; Mailhes, C.; Tourneret, J.Y. Bayesian estimation of linear mixtures using the normal compositional model. Application to hyperspectral imagery. IEEE Trans. Image Process. 2010, 19, 1403–1413. [Google Scholar] [CrossRef]
- Stein, D. Application of the normal compositional model to the analysis of hyperspectral imagery. In Proceedings of the 2003 IEEE Workshop on Advances in Techniques for Analysis of Remotely Sensed Data, Greenbelt, MD, USA, 27–28 October 2003; pp. 44–51. [Google Scholar]
- Halimi, A.; Dobigeon, N.; Tourneret, J.Y. Unsupervised unmixing of hyperspectral images accounting for endmember variability. IEEE Trans. Image Process. 2015, 24, 4904–4917. [Google Scholar] [CrossRef]
- Zhang, B.; Zhuang, L.; Gao, L.; Luo, W.; Ran, Q.; Du, Q. PSO-EM: A hyperspectral unmixing algorithm based on normal compositional model. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7782–7792. [Google Scholar] [CrossRef]
- Du, X.; Zare, A.; Gader, P.; Dranishnikov, D. Spatial and spectral unmixing using the beta compositional model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1994–2003. [Google Scholar]
- Zhou, Y.; Rangarajan, A.; Gader, P.D. A Gaussian mixture model representation of endmember variability in hyperspectral unmixing. IEEE Trans. Image Process. 2018, 27, 2242–2256. [Google Scholar] [CrossRef]
- Eches, O.; Dobigeon, N.; Tourneret, J.Y. Enhancing hyperspectral image unmixing with spatial correlations. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4239. [Google Scholar] [CrossRef]
- Giampouras, P.V.; Themelis, K.E.; Rontogiannis, A.A.; Koutroumbas, K.D. Simultaneously sparse and low-rank abundance matrix estimation for hyperspectral image unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4775–4789. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.Y.; Chang, C.I. Semi-supervised linear spectral unmixing using a hierarchical Bayesian model for hyperspectral imagery. IEEE Trans. Signal Process. 2008, 56, 2684–2695. [Google Scholar] [CrossRef]
- Dobigeon, N.; Moussaoui, S.; Coulon, M.; Tourneret, J.Y.; Hero, A.O. Joint Bayesian endmember extraction and linear unmixing for hyperspectral imagery. IEEE Trans. Signal Process. 2009, 57, 4355–4368. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Qu, Q.; Nasrabadi, N.M.; Tran, T.D. Abundance estimation for bilinear mixture models via joint sparse and low-rank representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4404–4423. [Google Scholar]
- Meng, X.L.; Rubin, D.B. Maximum likelihood estimation via the ECM algorithm: A general framework. Biometrika 1993, 80, 267–278. [Google Scholar] [CrossRef]
- Liu, M.Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 2097–2104. [Google Scholar]
- Fang, L.; Li, S.; Duan, W.; Ren, J.; Benediktsson, J.A. Classification of hyperspectral images by exploiting spectral–spatial information of superpixel via multiple kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef]
- Horn, R.A.; Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef]
- Vlassis, N.; Likas, A. A greedy EM algorithm for Gaussian mixture learning. Neural Process. Lett. 2002, 15, 77–87. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, J.; Liu, C.; Li, Y. Feature guided Gaussian mixture model with semi-supervised EM and local geometric constraint for retinal image registration. Inf. Sci. 2017, 417, 128–142. [Google Scholar] [CrossRef]
- Achlioptas, D.; McSherry, F. On spectral learning of mixtures of distributions. In Proceedings of the International Conference on Computational Learning Theory, Bertinoro, Italy, 27–30 June 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 458–469. [Google Scholar]
- Lange, K. The MM algorithm. In Optimization; Springer: New York, NY, USA, 2013; pp. 185–219. [Google Scholar]
- McLachlan, G.J.; Rathnayake, S. On the number of components in a Gaussian mixture model. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 341–355. [Google Scholar] [CrossRef]
- Smyth, P. Model selection for probabilistic clustering using cross-validated likelihood. Stat. Comput. 2000, 10, 63–72. [Google Scholar] [CrossRef]
- Zhou, Y.; Rangarajan, A.; Gader, P.D. A spatial compositional model for linear unmixing and endmember uncertainty estimation. IEEE Trans. Image Process. 2016, 25, 5987–6002. [Google Scholar] [CrossRef]

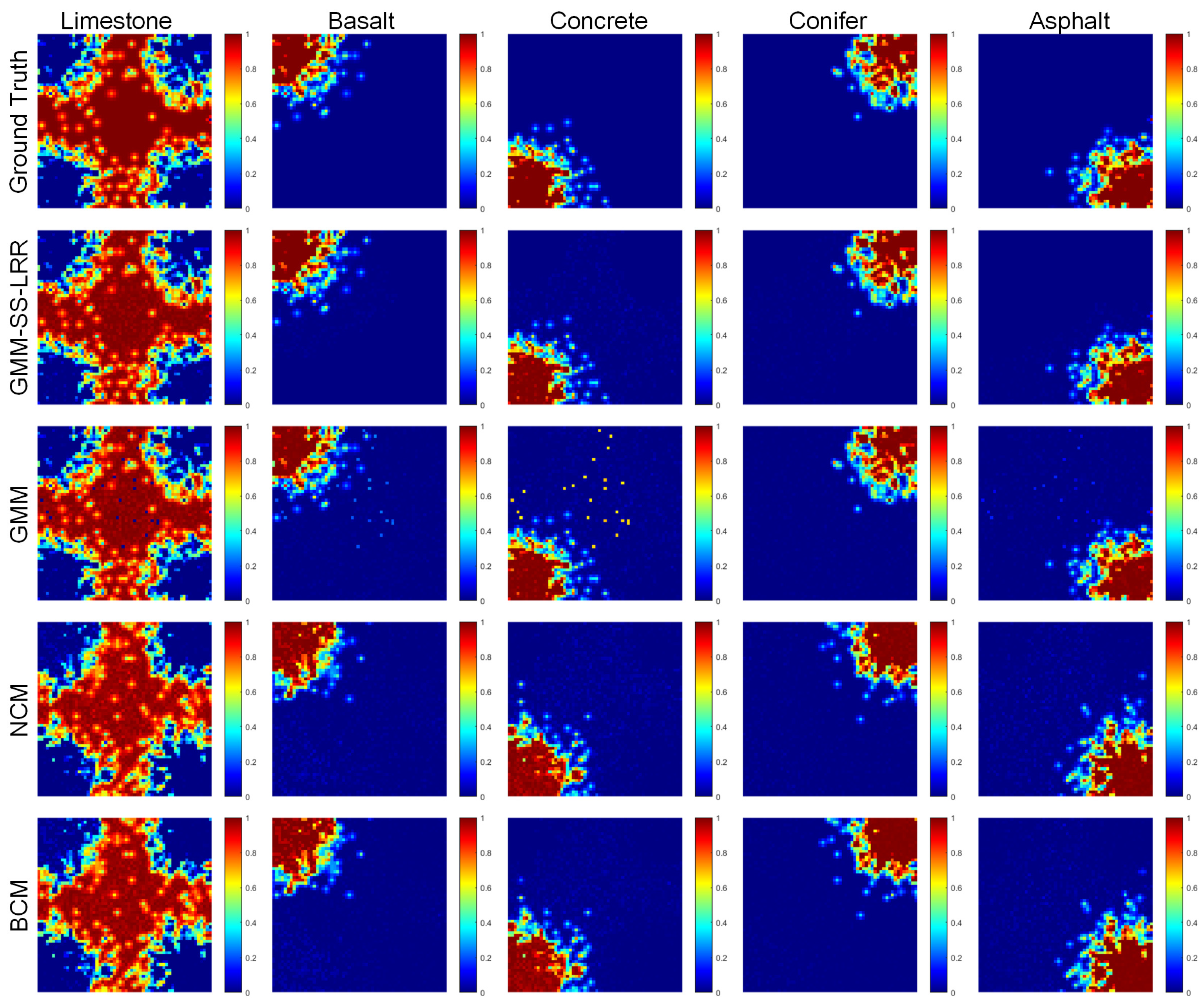
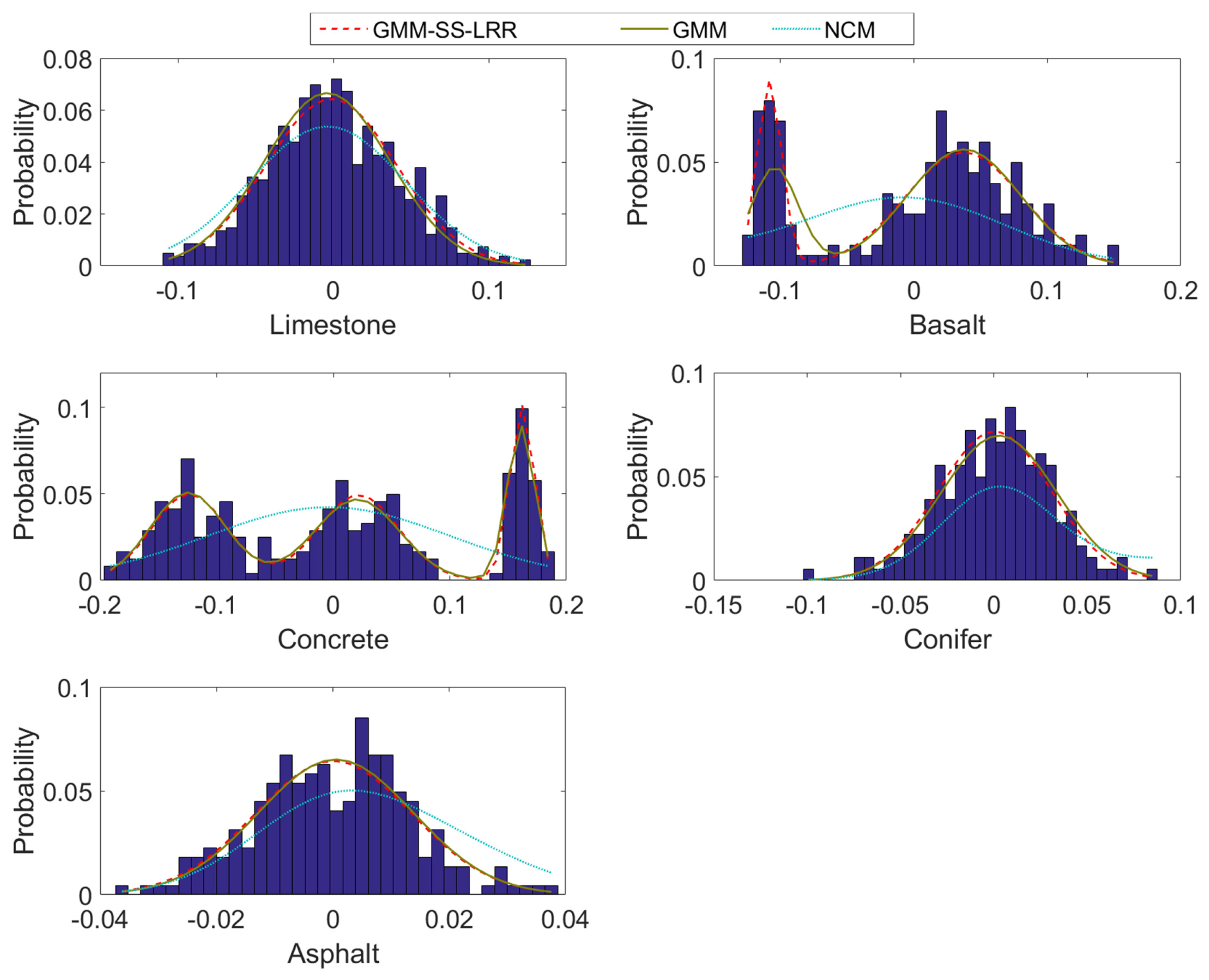
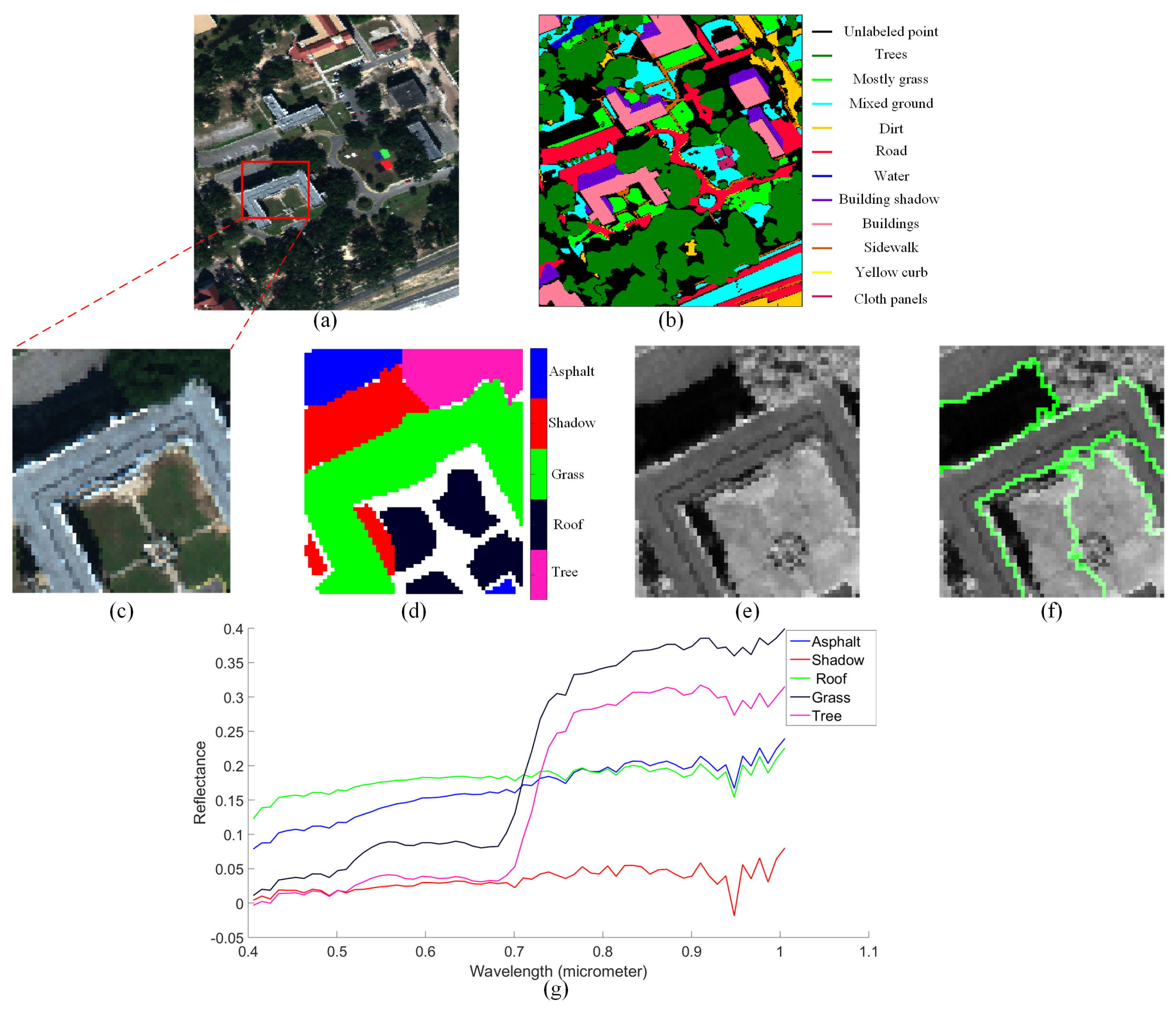

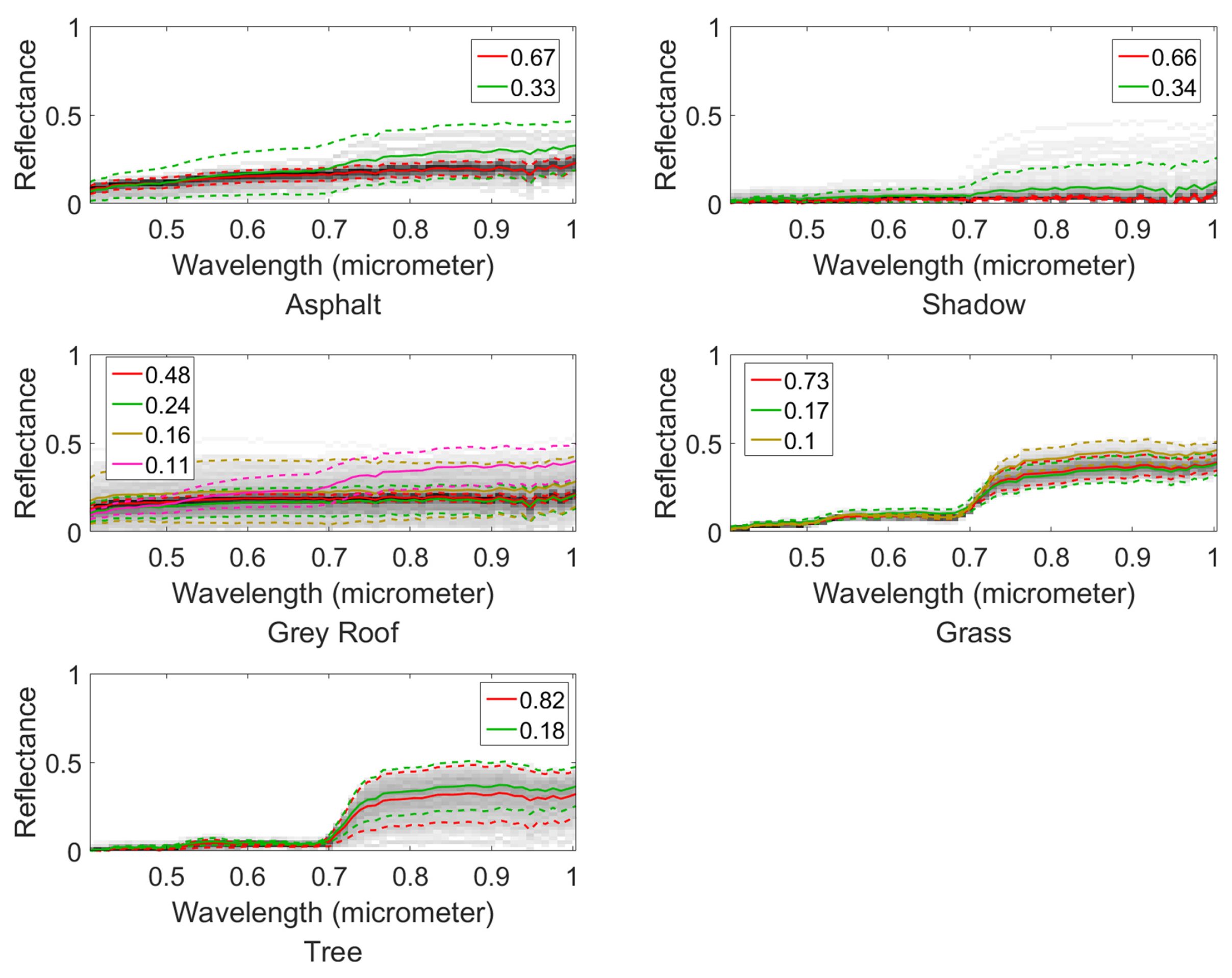
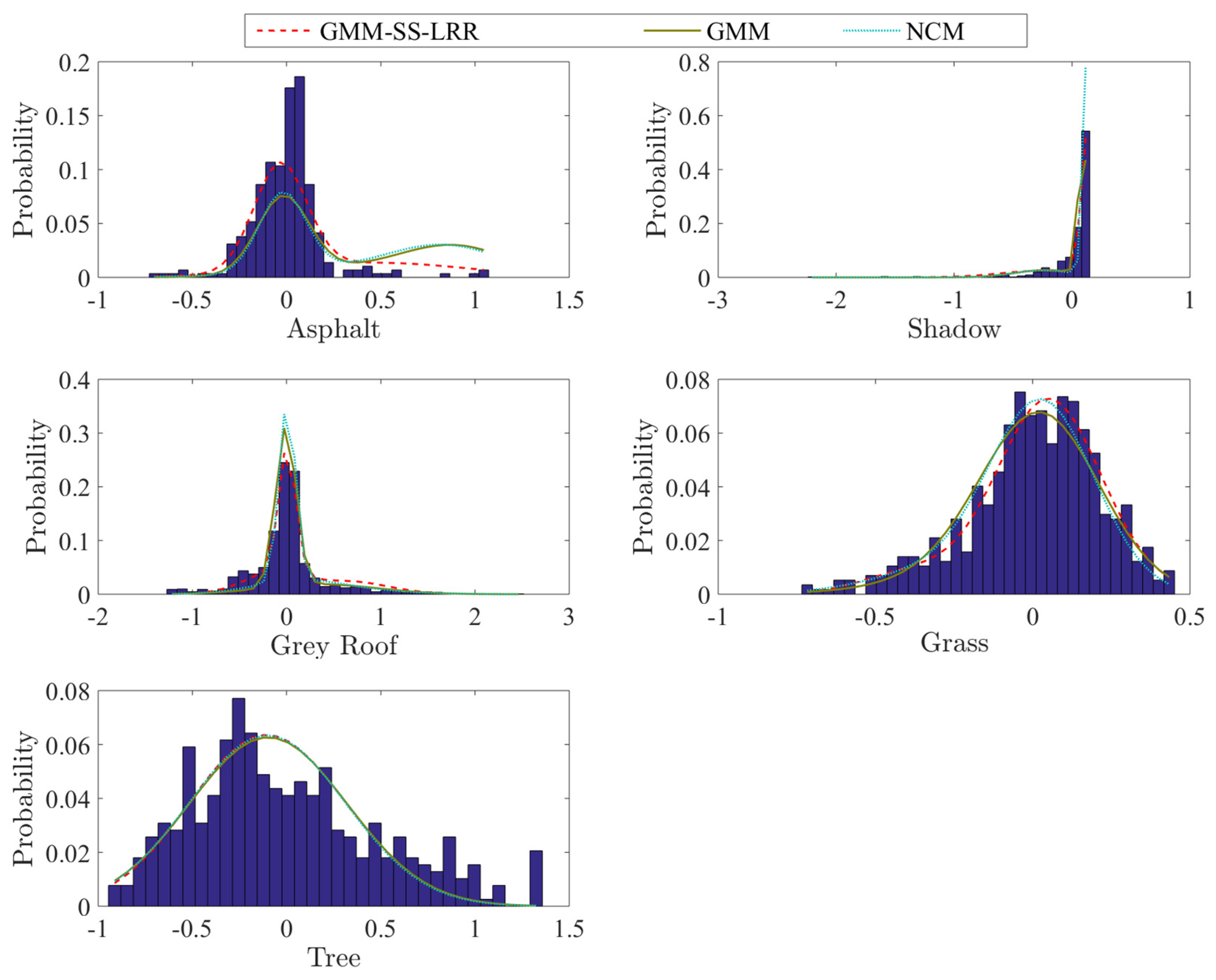
| GMM-SS-LRR | GMM | NCM | BCM | |
|---|---|---|---|---|
| Limestone | 142 | 816 | 566 | 743 |
| Basalt | 59 | 182 | 278 | 311 |
| Concrete | 94 | 539 | 460 | 586 |
| Conifer | 50 | 50 | 248 | 273 |
| Asphalt | 45 | 123 | 262 | 277 |
| Whole map | 78 | 342 | 363 | 438 |
| GMM-SS-LRR | GMM | NCM | |
|---|---|---|---|
| Limestone | 60 | 62 | 81 |
| Basalt | 89 | 134 | 248 |
| Concrete | 90 | 93 | 259 |
| Conifer | 72 | 72 | 160 |
| Asphalt | 94 | 94 | 140 |
| GMM-SS-LRR | GMM | NCM | BCM | |
|---|---|---|---|---|
| Asphalt | 161 | 202 | 383 | 865 |
| Shadow | 136 | 149 | 151 | 888 |
| Roof | 216 | 338 | 627 | 536 |
| Grass | 10 | 21 | 166 | 341 |
| Tree | 197 | 183 | 647 | 761 |
| Whole map | 99 | 140 | 278 | 328 |
| GMM-SS-LRR | GMM | NCM | |
|---|---|---|---|
| Asphalt | 229 | 322 | 332 |
| Shadow | 137 | 273 | 473 |
| Roof | 91 | 163 | 186 |
| Grass | 81 | 88 | 70 |
| Tree | 110 | 110 | 111 |
| GMM-SS-LRR | GMM | NCM | BCM | |
|---|---|---|---|---|
| Brocoli | 506 | 715 | 1421 | 511 |
| Corn | 386 | 2087 | 8790 | 8021 |
| Lettuce 4wk | 2090 | 2096 | 2732 | 2396 |
| Lettuce 5wk | 710 | 520 | 1858 | 1536 |
| Lettuce 6wk | 551 | 1975 | 2529 | 1597 |
| Lettuce 7wk | 1061 | 1046 | 3053 | 2423 |
| Whole map | 498 | 802 | 2268 | 2006 |
| GMM-SS-LRR | GMM | NCM | |
|---|---|---|---|
| Brocoli | 1303 | 1196 | 552 |
| Corn | 264 | 342 | 607 |
| Lettuce 4wk | 140 | 159 | 164 |
| Lettuce 5wk | 51 | 112 | 120 |
| Lettuce 6wk | 122 | 187 | 138 |
| Lettuce 7wk | 110 | 133 | 599 |
| GMM-SS-LRR | S = 1 | S = 3 | S = 5 | S = 7 | S = 10 | S = 15 |
|---|---|---|---|---|---|---|
| Limestone | 816 | 813 | 142 | 142 | 628 | 645 |
| Basalt | 182 | 180 | 59 | 58 | 168 | 170 |
| Concrete | 539 | 537 | 93 | 93 | 491 | 508 |
| Conifer | 50 | 47 | 50 | 48 | 96 | 96 |
| Asphalt | 123 | 120 | 45 | 46 | 182 | 186 |
| Whole map | 342 | 339 | 78 | 77 | 313 | 321 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Jin, Q.; Mei, X.; Dai, X.; Fan, F.; Li, H.; Huang, J. Hyperspectral Unmixing with Gaussian Mixture Model and Low-Rank Representation. Remote Sens. 2019, 11, 911. https://doi.org/10.3390/rs11080911
Ma Y, Jin Q, Mei X, Dai X, Fan F, Li H, Huang J. Hyperspectral Unmixing with Gaussian Mixture Model and Low-Rank Representation. Remote Sensing. 2019; 11(8):911. https://doi.org/10.3390/rs11080911
Chicago/Turabian StyleMa, Yong, Qiwen Jin, Xiaoguang Mei, Xiaobing Dai, Fan Fan, Hao Li, and Jun Huang. 2019. "Hyperspectral Unmixing with Gaussian Mixture Model and Low-Rank Representation" Remote Sensing 11, no. 8: 911. https://doi.org/10.3390/rs11080911
APA StyleMa, Y., Jin, Q., Mei, X., Dai, X., Fan, F., Li, H., & Huang, J. (2019). Hyperspectral Unmixing with Gaussian Mixture Model and Low-Rank Representation. Remote Sensing, 11(8), 911. https://doi.org/10.3390/rs11080911