Use of WorldView-2 Along-Track Stereo Imagery to Probe a Baltic Sea Algal Spiral
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Selection of Wavelength Bands to Analyze
2.3. Treatment of Noise Stripes
2.4. Method for Calculating Currents
3. Results
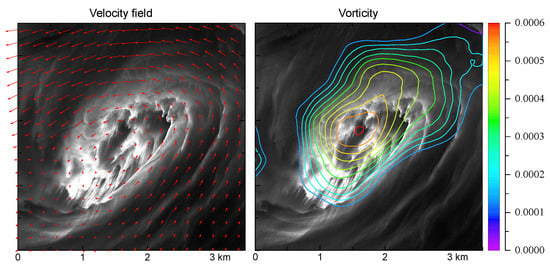
3.1. Spiral Pattern (Band 3 Data)
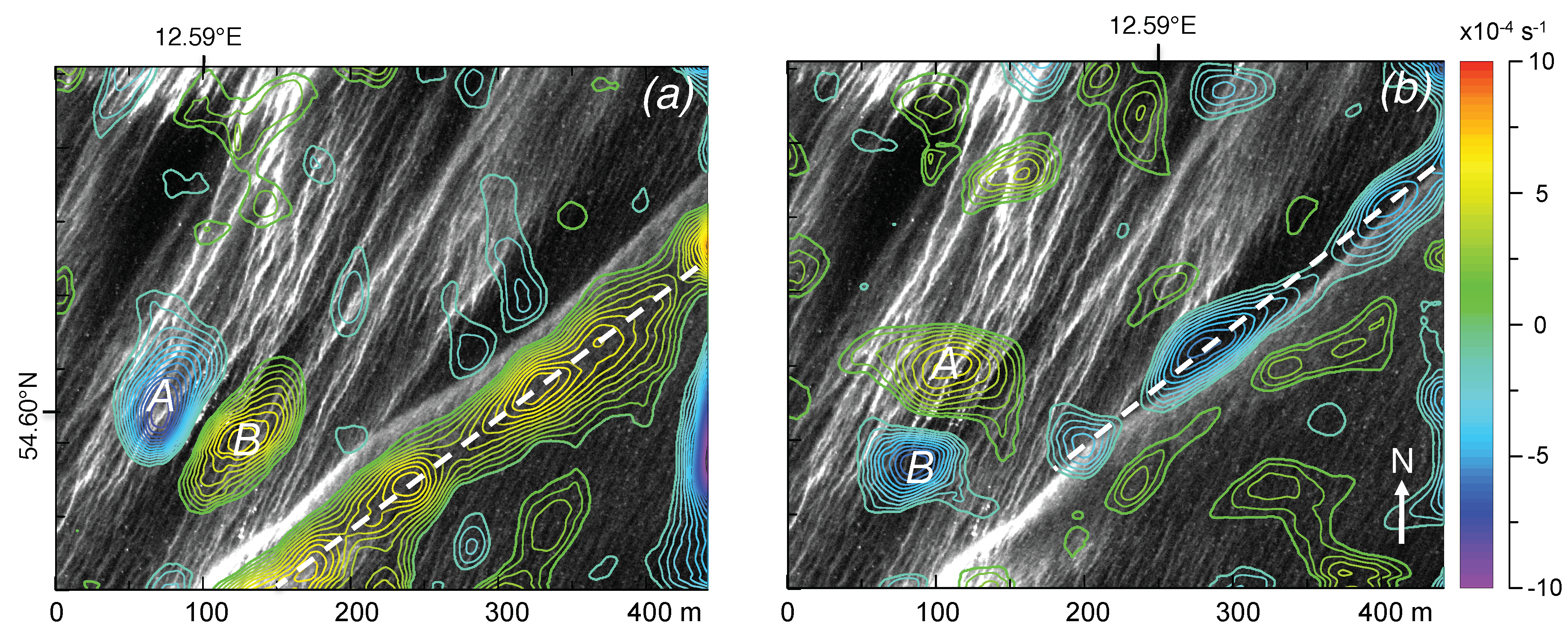
3.2. Algal Aggregations (Panchromatic Data)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kääb, A.; Leprince, S. Motion detection using near-simultaneous satellite acquisitions. Rem. Sens. Environ. 2014, 154, 164–179. [Google Scholar] [CrossRef]
- Qazi, W.A.; Emery, W.J.; Fox-Kemper, B. Computing ocean surface currents over the coastal California current system using 30-min-lag sequential SAR images. IEEE Trans. Geosci. Rem. Sens. 2014, 52, 7559–7580. [Google Scholar] [CrossRef]
- Matthews, J.P.; Yoshikawa, Y. Synergistic surface current mapping by spaceborne stereo imaging and coastal HF radar. Geophys. Res. Letts. 2012, 39. [Google Scholar] [CrossRef]
- Gade, M.; Seppke, B.; Dreschler-Fischer, L. Mesoscale surface current fields in the Baltic Sea derived from multi-sensor satellite data. Int. J. Remote Sens. 2012, 33, 3122–3146. [Google Scholar] [CrossRef]
- Chen, W. A global optimal solution with higher order continuity for the estimation of surface velocity from infrared images. IEEE TGRS 2010, 48, 1931–1939. [Google Scholar]
- Chen, W. Nonlinear inverse model for velocity estimation from an image sequence. J. Geophys. Res. 2011, 116, C06015. [Google Scholar] [CrossRef]
- Chen, W.; Mied, R.P. River velocities from sequential multispectral remote sensing images. Water Resour. Res. 2013, 49, 3093–3103. [Google Scholar] [CrossRef]
- Delandmeter, P.; Lambrechts, J.; Marmorino, G.O.; Legat, V.; Wolanski, E.; Remacle, J.F.; Chen, W.; Deleersnijder, E. Submesoscale tidal eddies in the wake of coral islands and reefs: Satellite data and numerical modelling. Ocean Dyn. 2017, 67, 897–913. [Google Scholar] [CrossRef]
- Marmorino, G.; Chen, W.; Mied, R.P. Submesoscale Tidal-Inlet Dipoles Resolved Using Stereo WorldView Imagery. IEEE Geosci. Rem. Sens. Lett. 2017, 14, 1705–1709. [Google Scholar] [CrossRef]
- D’Asaro, E.A.; Shcherbina, A.Y.; Klymak, J.M.; Molemaker, J.; Novelli, G.; Guigand, C.M.; Haza, A.C.; Haus, B.K.; Ryan, E.H.; Jacobs, G.A.; et al. Ocean convergence and the dispersion of flotsam. Proc. Natl. Acad. Sci. USA 2018, 115, 1162–1167. [Google Scholar] [CrossRef]
- Taylor, J.R. Accumulation and subduction of buoyant material at submesoscale fronts. J. Phys. Oceanogr. 2018, 48, 1233–1241. [Google Scholar] [CrossRef]
- Huisman, J.; Codd, G.A.; Paerl, H.W.; Ibelings, B.W.; Verspagen, J.M.; Visser, P.M. Cyanobacterial blooms. Nature Rev. Microbiol. 2018, 16, 471. [Google Scholar] [CrossRef]
- Kahru, M. Using satellites to monitor large-scale environmental change: A case study of cyanobacteria blooms in the Baltic Sea. In Monitoring Algal Blooms: New Techniques for Detecting Large-Scale Environmental Change; Springer: Berlin, Germany, 1997; pp. 43–61. [Google Scholar]
- Flohr, P.; Vassilicos, J.C. Accelerated scalar dissipation in a vortex. J. Fluid Mech. 1997, 348, 295–317. [Google Scholar] [CrossRef]
- Updike, T.; Comp, C. Radiometric Use of WorldView-2 Imagery; Tech. Note; DigitalGlobe Inc.: Longmont, CO, USA, 2010. [Google Scholar]
- Corsini, G.; Diani, M.; Walzel, T. Striping removal in MOS-B data. IEEE Trans. Geosci. Rem. Sens. 2000, 38, 1439–1446. [Google Scholar] [CrossRef]
- Lyon, P.E. An automated de-striping algorithm for Ocean Colour Monitor imagery. Int. J. Rem. Sens. 2009, 30, 1493–1502. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671. [Google Scholar] [CrossRef]
- Karimova, S.; Gade, M. Improved statistics of sub-mesoscale eddies in the Baltic Sea retrieved from SAR imagery. Int. J. Rem. Sens. 2016, 37, 2394–2414. [Google Scholar] [CrossRef]
- Karimova, S. Spiral eddies in the Baltic, Black and Caspian seas as seen by satellite radar data. Adv. Space Res. 2012, 50, 1107–1124. [Google Scholar] [CrossRef]
- Eldevik, T.; Dysthe, K.B. Spiral eddies. J. Phys. Oceanogr. 2002, 32, 851–869. [Google Scholar] [CrossRef]
- Fennel, W.; Seifert, T.; Kayser, B. Rossby radii and phase speeds in the Baltic Sea. Cont. Shelf Res. 1991, 11, 23–36. [Google Scholar] [CrossRef]
- Marmorino, G.; Smith, G.; North, R.; Baschek, B. Application of airborne infrared remote sensing to the study of ocean submesoscale eddies. Front. Mech. Eng. 2018, 4. [Google Scholar] [CrossRef]
- Thorpe, S.A. Langmuir circulation. Annu. Rev. Fluid Mech. 2004, 36, 55–79. [Google Scholar] [CrossRef]
- Szekielda, K.H.; Marmorino, G.O.; Maness, S.J.; Donato, T.F.; Bowles, J.H.; Miller, W.D.; Rhea, W.J. Airborne hyperspectral imaging of cyanobacteria accumulations in the Potomac River. J. Appl. Rem. Sens. 2007, 1, 013544. [Google Scholar]
- McKinna, L.I. Three decades of ocean-color remote-sensing Trichodesmium spp. in the World’s oceans: A review. Progr. Oceanogr. 2015, 131, 177–199. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marmorino, G.; Chen, W. Use of WorldView-2 Along-Track Stereo Imagery to Probe a Baltic Sea Algal Spiral. Remote Sens. 2019, 11, 865. https://doi.org/10.3390/rs11070865
Marmorino G, Chen W. Use of WorldView-2 Along-Track Stereo Imagery to Probe a Baltic Sea Algal Spiral. Remote Sensing. 2019; 11(7):865. https://doi.org/10.3390/rs11070865
Chicago/Turabian StyleMarmorino, George, and Wei Chen. 2019. "Use of WorldView-2 Along-Track Stereo Imagery to Probe a Baltic Sea Algal Spiral" Remote Sensing 11, no. 7: 865. https://doi.org/10.3390/rs11070865
APA StyleMarmorino, G., & Chen, W. (2019). Use of WorldView-2 Along-Track Stereo Imagery to Probe a Baltic Sea Algal Spiral. Remote Sensing, 11(7), 865. https://doi.org/10.3390/rs11070865