1. Introduction
Data acquired using a hyperspectral camera contains a plethora of information related to the chemical and physical properties of the in situ materials. Each pixel of a hyperspectral image has many dimensions pertaining to the absorption characteristics of a material at specific wavelengths in the visible, near infrared, and short-wave infrared (SWIR). As such, the data have been used for a variety of remote-sensing tasks, such as mapping/classification of surface materials [
1,
2,
3], target detection [
4,
5] and change detection [
6]. Because of the information content of each pixel in a hyperspectral image, the advantage of using hyperspectral imagery over conventional RGB and multispectral cameras is that many of the aforementioned tasks can be done at the pixel level.
The high dimensionality of hyperspectral data can also be problematic. With more dimensions, exponentially more data points are required to accurately represent the distribution of the data (i.e., the curse of dimensionality [
7,
8,
9]). A low ratio between the number of data points and the number of dimensions may limit many algorithms from working well where the data have many dimensions. Most of the mass of a high dimensional multivariate Gaussian distribution is near its edges. Thus, many algorithms designed around an intuitive idea of ‘distance’ in two- or three-dimensional space, cease to work at higher dimensions, where those intuitions no longer hold. This problem is compounded by variability present in a hyperspectral image due to intrinsic factors such as keystone, smile, and noise and extrinsic factors such as the incident illumination. The incident illumination is dependent on the position of the sun, surface geometry and prevailing atmospheric conditions [
10]. This variability demands more data points to adequately represent the distribution of the data.
It is often the case that key information necessary for a high-level task such as classification resides either in only a subset of the dimensions or in a lower-dimensional subspace within the high dimensional space. For example, proximal wavelengths in hyperspectral data are usually highly correlated, resulting in many redundant dimensions [
11]. Features that are either selected or extracted (via some transformation) from the data in the spectral domain leverage this to represent the key information in the data with fewer dimensions. In many cases, a good feature space will actually enhance the important information, simplifying the task for higher-level algorithms using the data. For example, a good feature space for a classification task will separate distributions of points belonging to different classes (increasing inter-class variation), while making the distribution for each given class more compact in the space (decreasing intra-variation) [
12]. In the case of hyperspectral data, the feature space should ideally have greater representation power than the raw intensity or reflectance space.
One approach for obtaining features from hyperspectral data is to manually hand-craft them. In [
13], layers of clay on a mine face are mapped using the width and depth of a spectral absorption feature at 2200 nm. The Normalized Difference Vegetation Index (NDVI), which is a simple function of the reflectance at two wavelengths, is typically used for mapping vegetation [
14]. While these features usually work very well for the application they were designed for, they are often difficult to design, require sufficient expertise and at times do not generalize well to new scenarios.
An alternative approach to obtaining features is to learn them directly from the data. This can be done using either supervised methods (e.g., Linear Discriminant Analysis (LDA) [
15], kernel methods [
16], autoencoder with logistic regression layer [
17]) or unsupervised methods (e.g., Principal Component Analysis (PCA) [
18,
19], Independent Component Analysis (ICA) [
20], basis functions [
21]). Supervised feature-learning methods require labelled data. In many applications labelled hyperspectral data is limited due to the challenges associated with annotation [
22]. This motivates a need for unsupervised feature-learning methods which extract important information from the data without the need for any labelling. Unsupervised learning methods are particularly good as a feature extractor for higher-level unsupervised tasks such as clustering. Clustering, as opposed to classification, can be used to map a scene without the need for any labelled data [
23,
24]. Thus, an entire pipeline, from the feature-learning to the mapping, can be unsupervised.
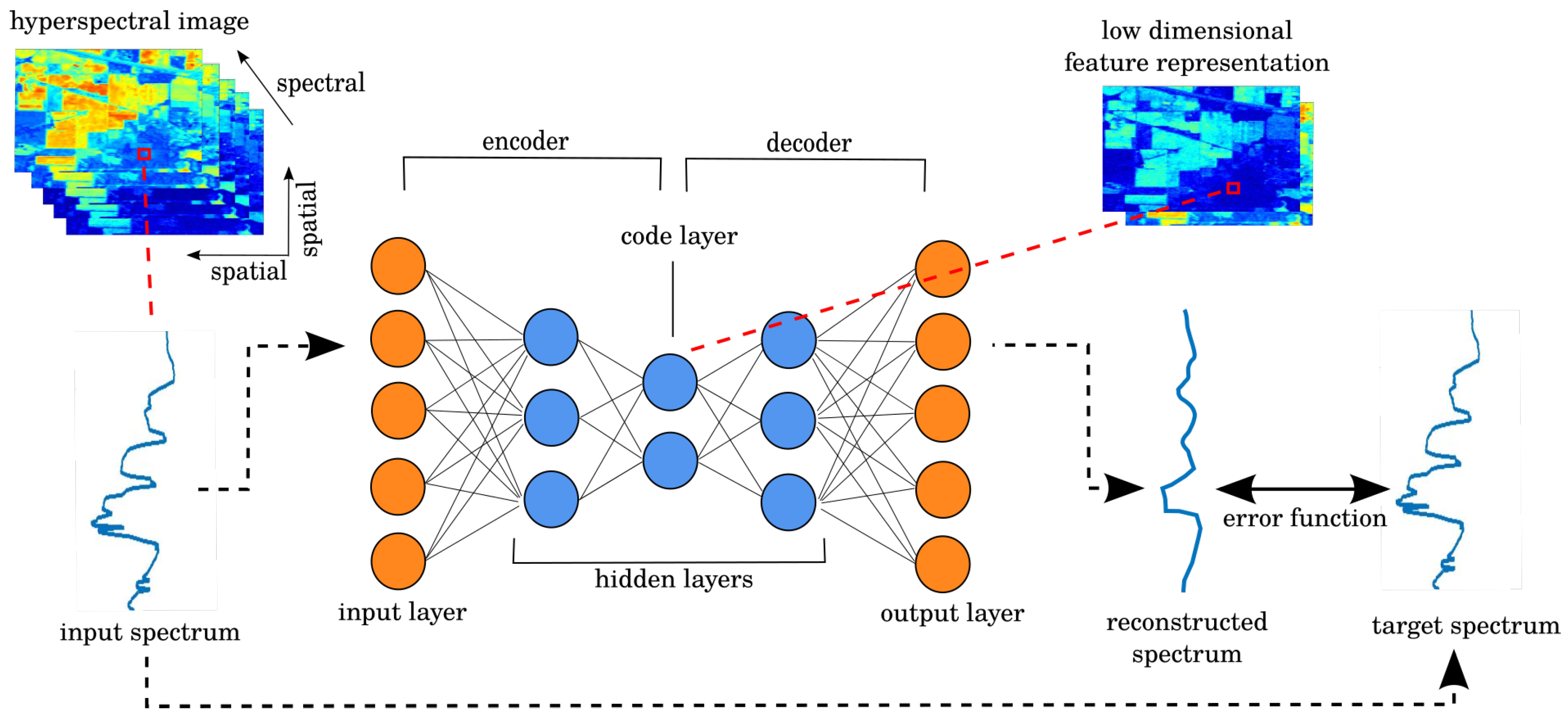
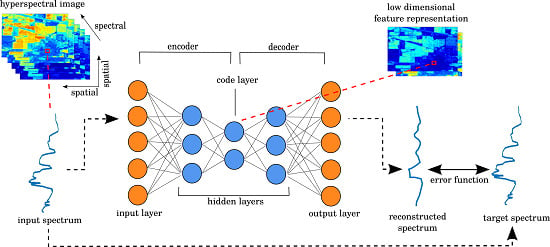
Autoencoders [
25,
26,
27] are a useful tool for unsupervised feature-learning that have been used to obtain features from hyperspectral data [
11,
28,
29,
30,
31]. An autoencoder is a neural network trained to reconstruct its input in the output. Through constraints imposed by the architecture, the network is forced to learn a condensed representation of the input that possess enough information to be able to reconstruct (i.e., decode) it again. This condensed layer can be used as a feature representation. With multiple layers of non-linear functions in the encoder and decoder, the network can learn a non-linear feature mapping.
When designing an autoencoder for hyperspectral data, a common approach, and the one used in [
11,
28,
29,
30,
31], is to train the network to minimize a reconstruction objective based on a squared-error function. A squared-error function works generically well in most domains—not just hyperspectral. However, in the remote-sensing literature, there are alternative error measures more suited to spectral data. Unlike the squared-error measure, these measures are predominantly dependent on the shape of the spectra rather than their magnitude. Previous work [
32] has incorporated a spectral measure, the cosine of the spectral angle, into the reconstruction objective of an autoencoder. The work presented in this paper further explores this space with novel autoencoders proposed which have spectral measures from the remote-sensing literature, the Spectral Information Divergence (SID) [
33] and the spectral angle [
34,
35], incorporated into the reconstruction objective.
The contributions of this work are:
Two novel autoencoders that use remote-sensing measures, the SID, and spectral angle, for unsupervised feature-learning from hyperspectral data in the spectral domain.
An experimental comparison of these techniques with other unsupervised feature-learning techniques on a range of datasets.
Further experimental evaluation of the autoencoder based on the cosine of the spectral angle proposed in previous work [
32].
The outline of this paper is as follows:
Section 2 provides a background on applying autoencoders to hyperspectral data,
Section 3 describes the proposed autoencoders,
Section 4 provides the experimental method and results which are discussed in
Section 5 before conclusions are drawn in
Section 6.
4. Experimental Results
The performance of the features learnt with the proposed hyperspectral autoencoders were evaluated experimentally with several datasets to demonstrate the algorithm’s ability to work with different scenes, illumination conditions and sensors used to capture the images. The evaluation involved an analysis of the separability of the feature spaces as well as the performance of the feature spaces for clustering and classification tasks.
4.1. Datasets
The datasets used to evaluate the proposed feature learners were captured from different distances to the scene and hence have different spatial resolutions. They were also captured from both airborne and field-based sensor platforms. The scenes covered simple, structured and complex, unstructured geometries, and exemplified a variety of illumination conditions.
Table 1 summarizes the datasets used, and
Figure 2 visualizes them as color composites. For these datasets, each multi-channel pixel of a hyperspectral image corresponds to a data point (i.e., a single spectrum).
Mineral spectra from the USGS spectral library [
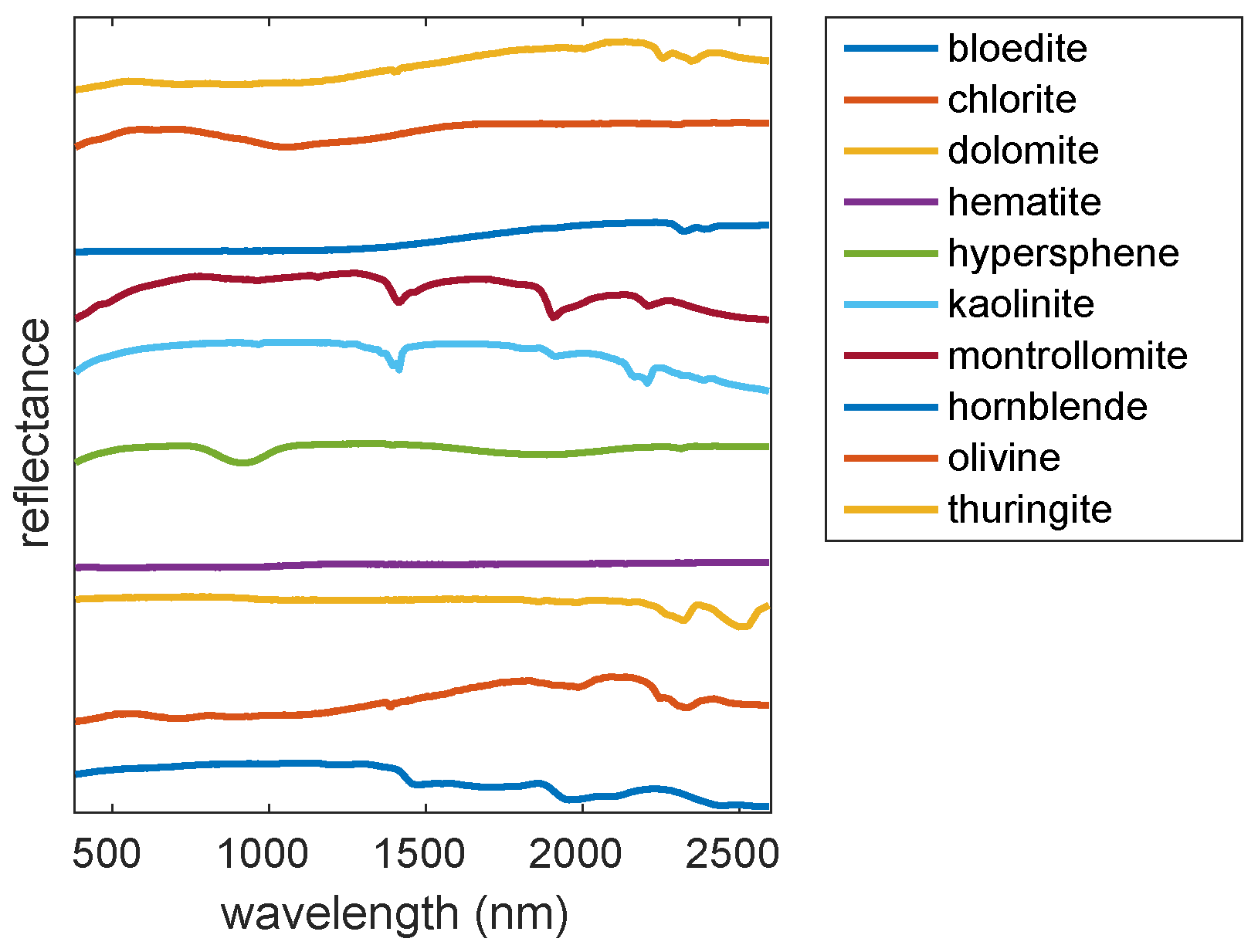
39] were used to simulate a dataset. Ten minerals were selected to generate spectral samples (
Figure 3). The data was simulated using the principle that the radiance at the sensor
is the product of the material reflectance
and the terrestrial sunlight
with some additive noise:
where
is a scaling factor controlling the brightness. The terrestrial sunlight was generated using an atmospheric modeler [
40]. Spectra from a calibration panel were also simulated. These data are used to normalize the simulated radiance data to reflectance. Each dataset consisted of 10,000 spectral samples (1000 samples for each of the ten classes in
Figure 3).
The X-rite ColorChecker is an array of 24 different colored squares. They reflect light in the visible spectrum in the same way as many naturally colored objects. A Visible and Near Infrared (VNIR) image of an X-rite colorChecker was captured indoors with a Specim sensor under a 3500 K temperature light source [
37]. The geometry is very uniform and there is little cause for variation in the illumination. The image was normalized to reflectance using the white square on the colorChecker.
A VNIR scan of The University of Sydney’s Great Hall was captured with a field-based Specim AISA Eagle sensor [
38]. The outdoor scene consists predominantly of a structured urban environment, with different material classes including roof, sandstone building, grass, path, tree, and sky. The roof and path classes are very similar spectrally; however, the other classes are quite discriminable, including the tree and grass. Data were collected under clear-sky conditions, with shadows being evenly distributed across the structure. A calibration panel of known reflectance is attached to a tripod and placed in the scene so that the incident illumination can be measured. The apparent reflectance across the image was calculated using flat-field correction.
An aerial VNIR image is acquired over Pavia University using the ROSIS-3 sensor. The spectra in the image have been normalized to reflectance. The scene consists of nine classes, encompassing both urban and natural vegetation classes. Some of the classes are spectrally similar. The Pavia University dataset has been provided by Professor Paolo Gamba, Pavia University.
The Kennedy Space Centre (KSC) image was acquired by the AVIRIS VNIR/SWIR sensor. The water absorption bands have been removed from this image. The 13 classes are a mix of urban and natural and the data are normalized to reflectance.
4.2. Evaluation Metrics
Three metrics were used to evaluate the performance of the features extracted from the above datasets. These were the Fisher’s discriminant ratio, Adjusted Rand Index (ARI) and F1 score.
Fisher’s discriminant ratio is a measure of how separable classes are in a feature space. Fisher’s discriminant ratio [
41] is used in feature selection algorithms as a class separability criterion [
42,
43]. The measure is calculated for a pair of classes and takes the ratio of the between-class scatter and the within-class scatter. A pair of classes has a high score if their means are far apart and points within each class are close to other points in the same class, indicating good separability. For
p dimensional data points from class
A and class
B, with respective means of
and
over all points in each class, the Fisher’s discriminant ratio is calculated as:
where
J is the ratio,
is the
norm, and
is the within-class scatter of class
i, given by:
where
is a point in class
i, which has
points in total.
An important property of this measure is that it is invariant to the scale of the data points. This allows feature spaces found using different approaches to be compared consistently. It is also important that the measure is invariant to the number of dimensions p so that the data with the original dimensionality can be compared to data with reduced dimensionality in the new feature space. For multi-class problems, the mean of the Fisher’s discriminant ratio for all possible pairs of classes can be found.
The ARI is an evaluation metric for clustering [
44,
45]. It measures the similarity of two data clusterings. If one of those data clustering is the actual class labels, then the ARI can be considered the accuracy of the clustering solution. This measure is useful as an indirect measure of how separable classes are in a feature space [
46]. If the classes are well separated, then they should be easy to cluster, and the ARI should be high.
If
and
are the number of points in class
and cluster
respectively and
is the number of points that are in both class
and cluster
, then the ARI is calculated as:
This adjustment of the rand index makes it more likely that random label assignments will get a value close to zero. The best clustering score has an ARI of 1, and the worst clustering score (equivalent to randomly allocating cluster association) has an adjusted rand index of 0.
The F1 score (also known as the F-score) is a commonly use evaluation metric for classification accuracy [
47]. It is calculated as the harmonic mean of precision and recall:
where the precision and recall are defined as:
where
,
, and
are the number of true positives, false positives, and false negatives respectively. The F1 score ranges from 0 to 1, with 1 indicating perfect classification performance. The F1 score is calculated separately for each class.
4.3. Implementation
The network architecture and tunable parameters of the autoencoder were found in preliminary experiments using a coarse grid search, minimizing the reconstruction error. A common architecture was chosen for the experiments that performed well across all the datasets. For the Great Hall VNIR, KSC, Pavia Uni, Simulated and X-rite datasets, unless otherwise stated, an encoder architecture of K-100-50-10 was used with symmetric decoders (six layers in total), where the input size K is the original dimensionality of the data (i.e., number of bands). Because the code layer has 10 neurons, the dimensionality of the data in the new feature space is 10.
For all datasets, the regularization parameter was set to
, the activation function used was a sigmoid and 1000 epochs of L-BFGS [
48] was used to optimize the networks. As this method is unsupervised, the method is trained on the same image it is evaluated on (similar to the evaluation of a dimensionality-reduction approach). Hence, for each experiment, the number of data points used to train the autoencoders was the number of pixels in the image.
As is the case with standard SAEs, training a network with many layers using backpropagation often results in poor solutions [
25]. Hence, an initial solution is found using a greedy pre-training step [
49] whereby layers are trained in turn while keeping other layers frozen. The network parameters learnt in the layerwise pre-training are then used to initialize the full network for end-to-end fine-tuning with the same data, whereby all layers are trained at the same time. In [
50], it was showed that it is possible to also pre-train networks on different hyperspectral datasets.
A property of the spectral angle reconstruction cost is that it is undefined for . Hence, an activation function f must be chosen that does not include zero in its range. This removes the chance of having an undefined reconstruction cost. A sigmoid function is chosen as the activation function because it is bound by a horizontal asymptote at zero such that its range is . It is, therefore, impossible for to equal zero, which is not the case if functions such as ReLU and the hyperbolic tangent are used.
All experiments were carried out in MATLAB.
4.4. Results
The proposed autoencoders, the SID-SAE and SA-SAE, were compared with other unsupervised feature-extraction/dimensionality-reduction methods based on their ability to discriminate spectra of different classes and similarly represent spectra of the same class with a reduced number of dimensions. These included PCA, Factor Analysis (FA), an equivalent autoencoder (referred to as SSE-SAE) that used the squared error for its reconstruction cost function (similar to [
11,
28,
29,
30,
31]), an autoencoder using the cosine of the spectral angle as in [
32] (referred to as CSA-SAE) and the raw data without any dimensionality reduction. The degree of variability in the scene differed between datasets, and the algorithms were evaluated on how robust they were to this variability. All the chosen datasets were used in normalized reflectance form, and the simulated and Great Hall VNIR datasets were also evaluated in Digital Number (DN) form.
The first set of results compared each methods ability to represent different classes with fewer dimensions. It is desirable that in the new feature space, spectra from different classes are separated and spectra from the same class are closer together. This was measured with the Fisher’s discriminant ratio. If classes are well represented in the low-dimensional space, then it is expected that the data will cluster into semantically meaningful groups (rather than groups that have a similar incident illumination). Hence, as an additional method of evaluation, the low-dimensional data was clustered using
k-means [
51], where the number of clusters was set to the number of classes in the dataset. The clustering performance was measured using the ARI. Furthermore, the classification accuracy when using the unsupervised features with several common supervised classifiers was used to evaluate the proposed methods. The classifiers used were Support Vector Machines (SVM),
k-Nearest Neighbors (KNN) and Decision Trees (DT). To train the classifier, the training sets comprised 1000, 500, and 50 data points, the validation sets comprised 100, 50, and 5 and the test sets comprised the remainder of the points for the Great Hall, Pavia Uni and KSC datasets respectively (these values were chosen based on the class with the fewest number of labelled points for each dataset). The classification accuracy was measured using the F1 score.
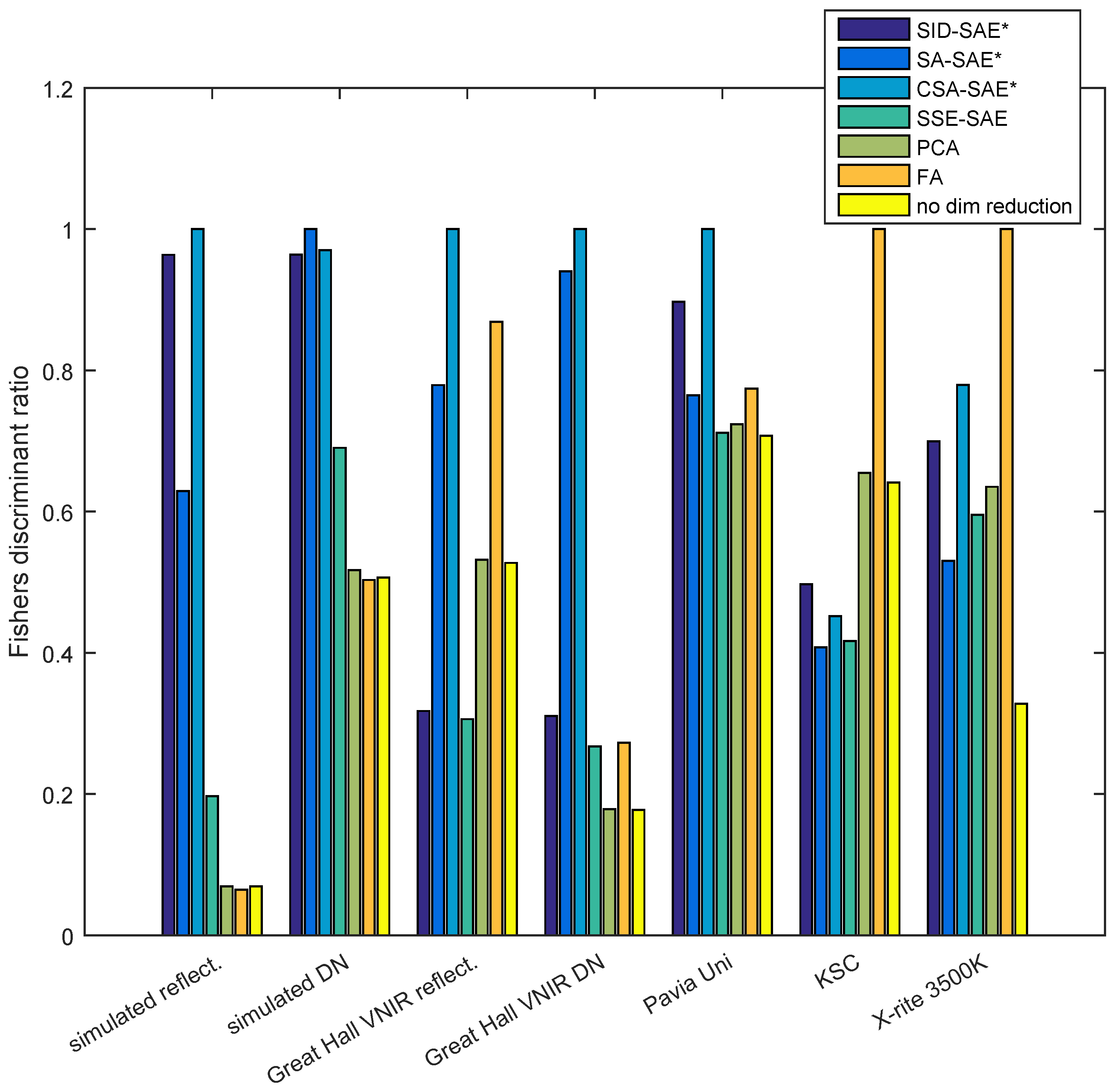
The Fisher’s ratio results showed that for most datasets, the hyperspectral autoencoders that utilized remote-sensing measures (SID-SAE, SA-SAE and CSA-SAE) represented the different classes with fewer dimensions with more between-class discriminability and within-class uniformity than the other approaches (
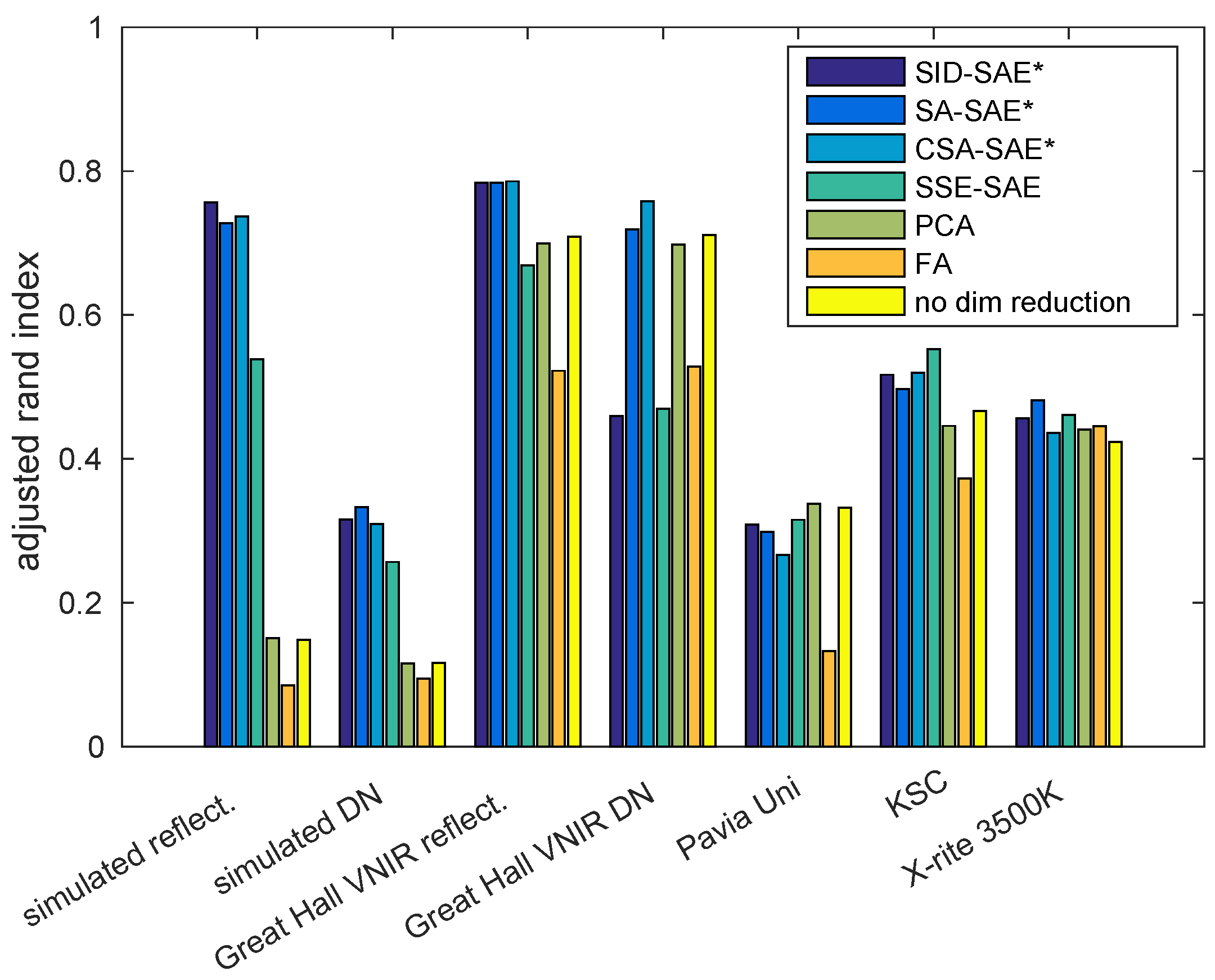
Figure 4). Clustering performance was also higher when using these autoencoders to represent the data (
Figure 5). The hyperspectral autoencoder based on the cosine of the spectral angle (CSA-SAE) had the best overall performance. The results of
Figure 4 indicated that this method performed well in comparison to the other methods on the simulated reflectance, simulated DN, Great Hall VNIR reflectance, Great Hall VNIR DN, and Pavia Uni datasets. The clustering results of
Figure 5 supported the Fisher’s ratio results in terms of relative performance, especially in comparison to the no-dimensionality reduction, PCA and FA results. The CSA-SAE had ARI scores of above 0.7 for the simulated reflectance dataset, Great Hall VNIR reflectance and Great Hall VNIR DN datasets. In terms of Fisher’s score, the SID-SAE approach performed well on the simulated reflectance, simulated DN and Pavia Uni datasets, but only performed marginally better than the standard autoencoder, the SSE-SAE, on the other datasets. All methods had similar class separation on the Pavia Uni and simulated DN datasets, and the clustering performance of all methods for these datasets was low (ARI below 0.4). FA had the best separation for the KSC and X-rite 3500K datasets. There appeared to be no real advantage to using the raw spectral angle (SA-SAE) over the cosine of the spectral angle (CSA-SAE).
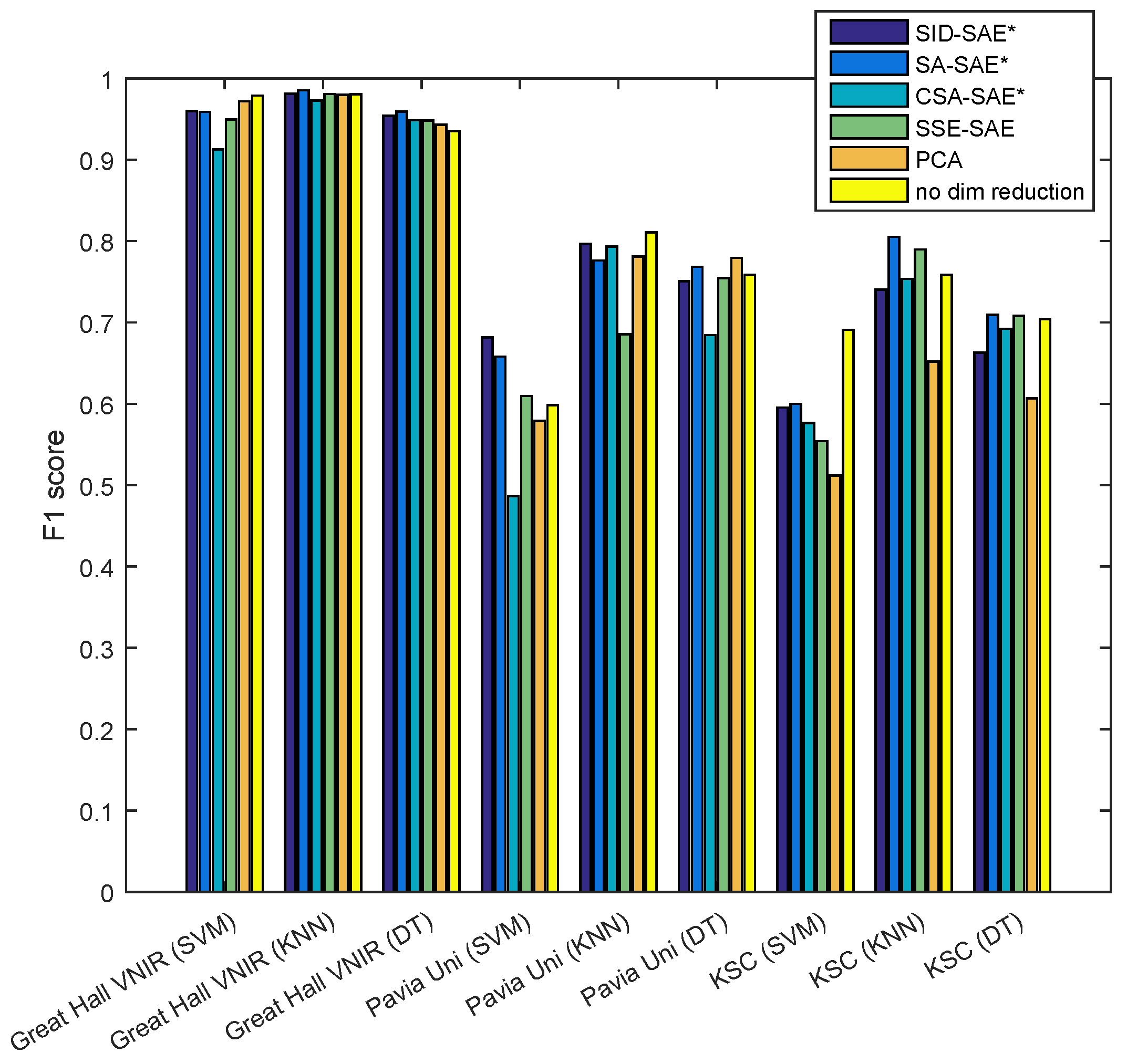
For the classification results (
Figure 6), for any given classifier there were no clear trends across the datasets as to which feature method produced the best result. Observations can be made, such as for DTs, the SA-SAE performs comparatively well across all three datasets. However, in the Pavia Uni dataset it is outperformed by PCA, and in the KSC dataset, it performs similarly to SSE-SAE and the original reflectance features (raw spectra). In other cases, such as applying the SVM to the KSC dataset, the original reflectance features performed well (in this case it outperformed all other methods by a large margin). For the Great Hall dataset, all methods performed similarly well except for the CSA-SAE, which produced results that were slightly worse than the other methods.
Figure 7 visualizes how invariant the low-dimensional feature representations were to changes in brightness. Using the data that was simulated with different brightness, dimensionality-reduction mappings were learnt by training on data illuminated by a source with a given intensity (scaling factor equal to 1), and then applied to two different datasets: the said dataset as well as the same dataset illuminated by a source with a different intensity (scaling factor equal to 0.3).
Figure 7 compares the low-dimensional representation of four different material spectra under the two different illumination intensities, for each of the autoencoder approaches. Bright refers to the dataset with scaling factor equal to 1, and dark has a scaling factor equal to 0.3. If a feature is invariant, a material illuminated with different intensities should appear similar in the feature representation. In a real-world outdoor dataset, differences in brightness can arise due to the variations in geometry with respect to the sun, and also changes in the brightness of the sun (for example, in a dataset of the same scene captured at different times).
Table 2 compares the performance of the learnt features using the two proposed hyperspectral autoencoder methods with different numbers of neurons in the code layer. Experiments were conducted on the Pavia University dataset, and code layer neurons varied from 6 to 14 with increments of 2 (the rest of the architecture remained the same). The results show that for a given method, there is not much variance when the number of nodes is varied. For the SID-SAE, the best score is achieved with 6 nodes, and for the SA-SAE, the best score is achieved with 14 nodes.
5. Discussion
The autoencoder approaches were expected to have better overall performance than PCA as they were able to learn non-linear mappings to the low-dimensional spaces. This property allowed for more complex transformations to occur. The results (
Figure 4 and
Figure 5) supported this for some of the datasets. The hyperspectral autoencoders that used remote-sensing measures had a better overall performance than the SSE-SAE, and further, the autoencoders based on the spectral angle performed better than the SID-SAE. By using the spectral angle as the reconstruction cost function, the autoencoders learnt complex mappings that captured features describing the shape of the spectra. This was in comparison to the autoencoder that used the squared-error measurement of reconstruction error. These autoencoders learnt features which described the intensity of the spectra. The intensity is highly dependent on the illumination conditions and hence was not the best characteristic on which features should be based on. The autoencoder using the SID performed slightly better than the SSE-SAE approach because the distance function could account for small variations in the probability distribution of each spectra and was also unaffected by wavelength-constant multiplications. Hence, the learnt mapping was invariant to intensity changes. FA performed best on the X-rite 3500K dataset. However, this was likely to be because the X-rite 3500K dataset was the only dataset that had almost no intraclass variability. Thus, features were learnt which maximized the variability between classes and there was very small separation created within each class.
In some cases, the hyperspectral autoencoders using remote-sensing methods did not outperform the other approaches. There was almost no performance improvement in
Figure 4 from using the angle-based methods for the KSC and X-rite 3500 K datasets. However, the clustering results (
Figure 5) were relatively low for these datasets for all methods, suggesting that they were particularly difficult to represent with unsupervised approaches. Clustering results were also low for the simulated DN and Pavia Uni datasets. The KSC, Pavia Uni and X-rite 3500 K datasets contain many classes (greater than eight), many of which are very similar. For example, the KSC dataset contains several different ’marsh’ classes. With that said, the hyperspectral autoencoders still outperformed the PCA, FA and no-dimensionality reduction approaches for the KSC dataset. Thus, the limitations of the proposed hyperspectral autoencoder are similar to those of any unsupervised method. In certain cases, such as when there are many similar classes as in the KSC dataset, a supervised method is more suitable. However, in situations where unsupervised learning techniques have utility, it is beneficial to use the proposed hyperspectral autoencoders.
Regarding the simulated DN dataset, the spectral angle methods were expected to achieve similar results on both the reflectance and DN datasets, because the shape of the spectra is unique for different classes regardless of normalization. For the Fisher’s score results (
Figure 4) this was true, but for the clustering results, this was only the case for the Great Hall datasets and not the simulated datasets. The clustering results show that all methods performed badly on the simulated DN dataset, suggesting that if not normalized, the differences in the spectra can become very small, making it difficult for any unsupervised methods to separate the classes.
From the results of
Figure 6, there was no obvious feature and classifier combination that performed definitively better than other combinations across all datasets. Thus, it is difficult to draw conclusions about the benefit of using the proposed unsupervised feature methods with supervised classifiers. The added complexity of the classifier makes it hard to determine whether a combination worked well or poorly with a particular dataset due to the features or the classifier. From the results, in general the proposed features can be used with a classifier for adequate performance, but in many cases the raw spectra were equally as or more effective than using the features. It is possible that in some cases the hyperspectral features suppress information that is valuable for classification. For example, differences in the magnitude of the spectra could be due to brightness variations, promoting undesirable intraclass variation, but they could also indicate a different semantic class, such as the roof and path classes of the Great Hall dataset. These two classes have spectra with a similar shape, but with different magnitudes. Because the hyperspectral autoencoders emphasize spectral shape, they could be less effective at distinguishing these classes, where shape is not a valuable cue. This could explain the slightly worse performance of the CSA-SAE on the Great Hall dataset when using the SVM. The raw spectra perform well because it captures the differences in magnitude needed to distinguish the classes, but not at the cost of performance due to brightness variability because there are enough labelled training examples of each class under varying illumination for the supervised classifier to learn to generalize. Thus, it is recommended that if sufficient labelled data is available, it is best to use either the raw spectra or a supervised feature learner such as a neural network optimized with a classification loss function [
22], rather than the unsupervised remote-sensing specific reconstruction loss functions proposed in this paper.
For the autoencoders using remote-sensing measures, the encodings of spectra with different brightnesses appeared similar in the learnt feature space (
Figure 7), indicating a degree of invariance to brightness. Mappings learnt on simulated data, illuminated with a specific brightness, were able to generalize to simulated data illuminated with a brightness that the mappings were not trained on. This was expected from the proposed hyperspectral autoencoders because their reconstruction cost functions are robust to brightness variations. Interestingly, the SSE-SAE also exhibited some brightness invariance despite the reconstruction cost function being dependent on the intensity of the spectra. It was expected that this occurred because there was no brightness variability within the training set. As a result, the SSE-SAE learnt to ignore brightness variability because it did not require reconstruction. If, however, there was variability in the brightness of the training data then it is likely that the SSE-SAE would capture the very basic intensity multiplication in the training dataset with its non-linear function approximators and encode these variations in several features/dimensions. If the trained encoder was then applied to new data with a different intensity of the source brightness, then some of the features in the encoding would vary depending on the brightness.
The results of
Table 2 indicate that there is flexibility in the choice of the number of nodes in the code layer, which is good for unsupervised tasks. This is because cues for the design of the code layer, such as the intrinsic dimensionality of the data or the number of classes, are often unknown. The results show a slight trend for both methods: that for the Pavia University dataset, the optimal number of neurons in the code layer is fewer for the SID-SAE than the SA-SAE. This could suggest that for this particular dataset, the SID-SAE is more efficient at representing the data. However, the performance margin (across neuron numbers) is too small to be able to conclude this decisively from the results.