Monitoring Cliff Erosion with LiDAR Surveys and Bayesian Network-based Data Analysis
Abstract
1. Introduction
2. Materials and Methods
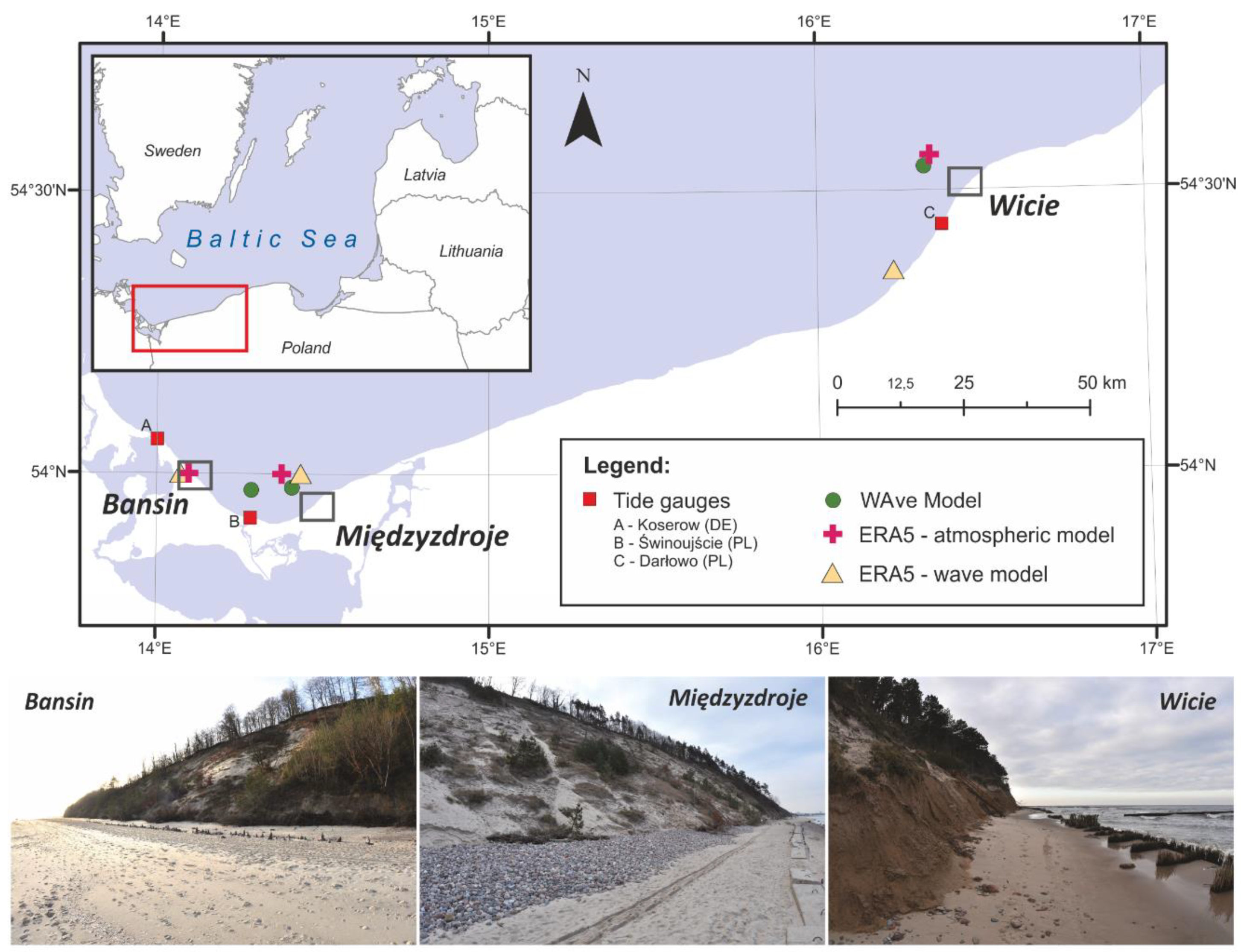
2.1. Study Sites
2.2. Data
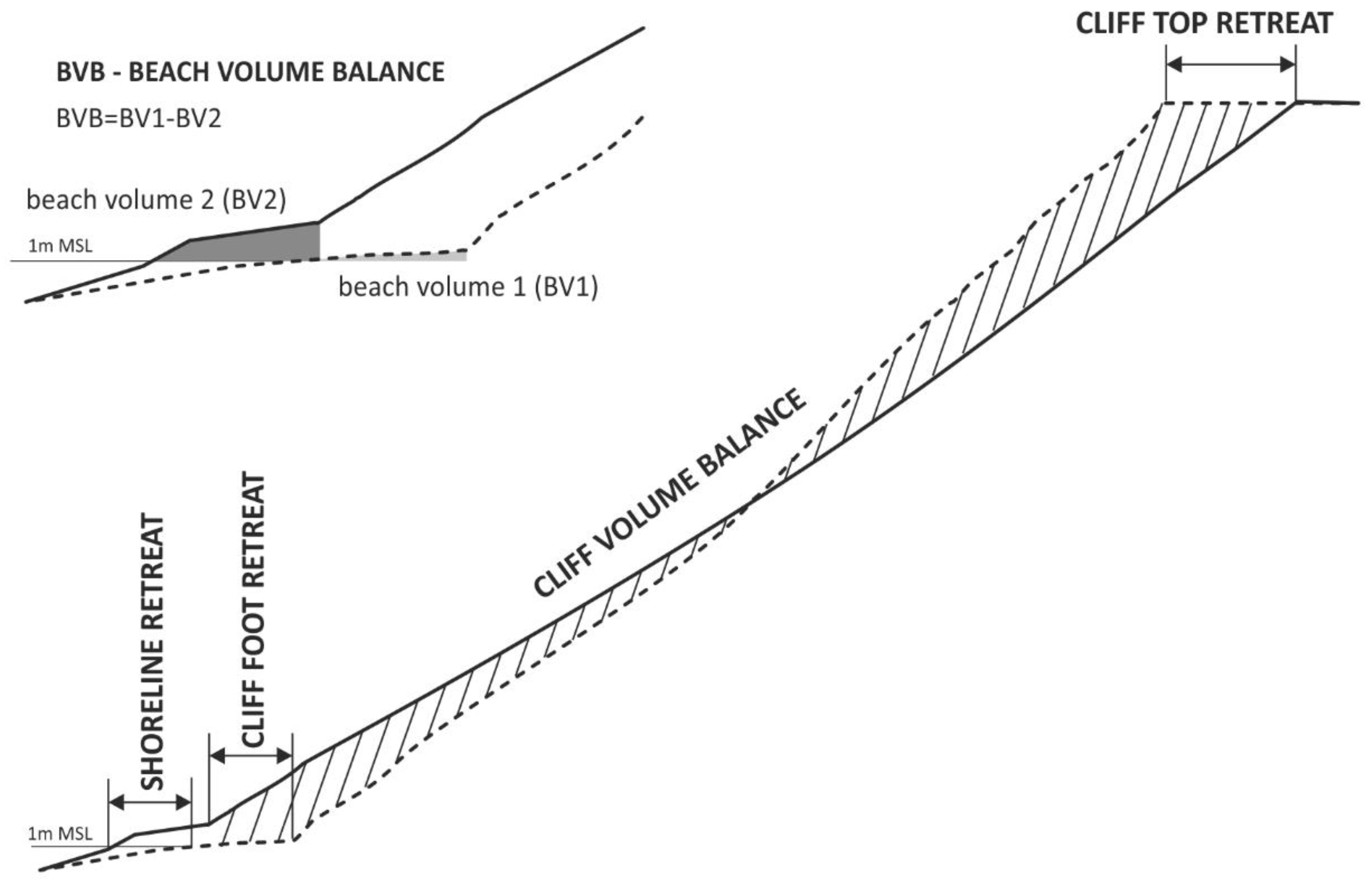
2.3. Geomorphological Indicators
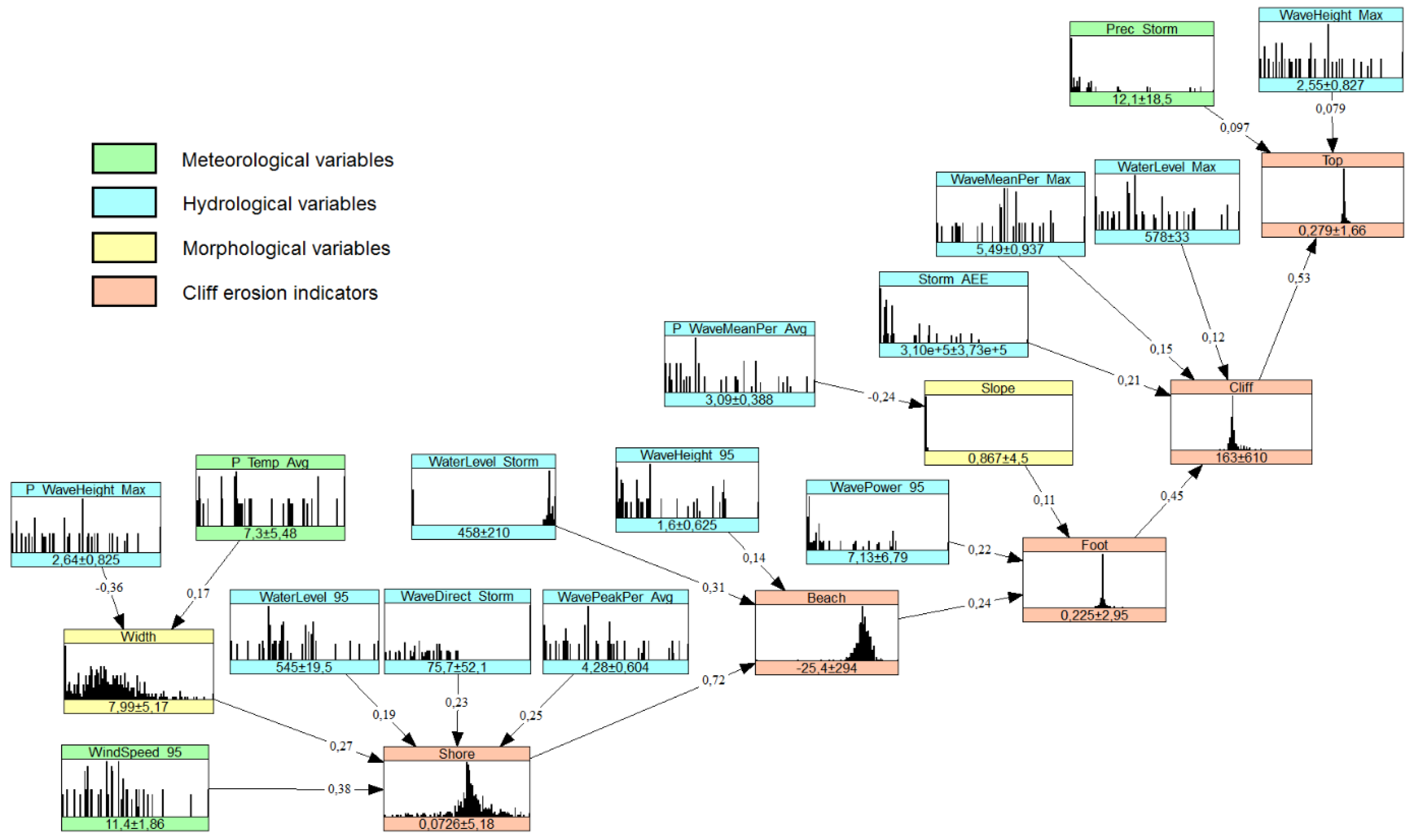
2.4. Bayesian Networks
- Cliff erosion indicators were connected with each other, starting from the shoreline retreat indicator and moving toward the cliff top.
- In every case, the cliff erosion indicator was used as the first parent node when other parent nodes were added.
- Meteorological, hydrological, and morphological variables were added starting from the shoreline retreat (Shore) node and moving toward the cliff top.
- Each variable was connected only to one node containing a cliff erosion indicator.
- Meteorological and hydrological variables were not given any parent nodes and were not connected with each other.
- The first meteorological or hydrological variable to be connected with a cliff erosion indictor was the variable with the highest unconditional correlation within the model. The unconditional correlation matrix is shown in Supplementary Information 2.
- Further meteorological or hydrological variables were selected based on the conditional correlation with cliff erosion indicators.
- Only parent nodes with (conditional) correlations higher than 0.1 were included in the model, except for the parents of cliff top retreat (Top), where only the correlation with the cliff volume balance (Cliff) exceeded this threshold.
3. Results
3.1. Hydrological Conditions during the Period of Study
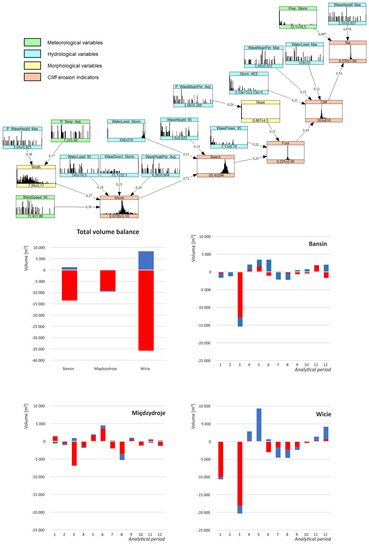
3.2. Descriptive Analysis of Cliff Erosion
3.3. Statistical Analysis of Cliff Erosion
4. Discussion
5. Conclusions
- Our study demonstrates the advantages of using Bayesian network for analysis of surface morphological changes on cliff coasts even on relatively short analyzed shore segments. Despite the site-specific geomorphological settings for different test areas, the implementation of the proposed Bayesian network model enabled the determination of relationships between the erosion rates and selected factors. The proposed model explained the general behavior of the cliff coast with respect to different hydrometeorological conditions, indicating variables most relevant at each segment along the profile. Validation of the model showed good performance along the beach and cliff foot, but weaker in predicting cliff mass balance or cliff top recession.
- Our study proves that high temporal resolution in TLS surveys enables the analysis of correlations between the influence of several factors (wave height, length and period, water level, storm energy, precipitation, etc.) and the geomorphological response of coast during isolated storm events, as well as with cumulative effects for season-long analysis. In general, a presentation of short and mid-term analyses expands possibilities in coastal morphological studies. Although we have seen a rapid increase of TLS usage in recent years, most of these have focused on a small quantity of realized surveys or long-term analysis.
- The automatic extraction of all geomorphological indicators from DEMs enabled reproducible and comparable cliff recession analysis. However, caution should be taken when interpreting the beach recovery, because some erosion and deposition processes may be masked by an automatic delineation of the cliff base line.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Terefenko, P.; Giza, A.; Paprotny, D.; Kubicki, A.; Winowski, M. Cliff retreat induced by series of storms at Międzyzdroje (Poland). J. Coastal Res. 2018, 85, 181–185. [Google Scholar] [CrossRef]
- Furmańczyk, K.; Andrzejewski, P.; Benedyczak, R.; Bugajny, N.; Cieszyński, Ł.; Dudzińska-Nowak, J.; Giza, A.; Paprotny, D.; Terefenko, P.; Zawiślak, T. Recording of selected effects and hazards caused by current and expected storm events in the Baltic Sea coastal zone. J. Coastal Res. 2014, 70, 338–342. [Google Scholar] [CrossRef]
- Paprotny, D.; Andrzejewski, P.; Terefenko, P.; Furmańczyk, K. Application of Empirical Wave Run-Up Formulas to the Polish Baltic Sea Coast. PLoS ONE 2014, 9, e105437. [Google Scholar] [CrossRef] [PubMed]
- Bugajny, N.; Furmańczyk, K. Comparison of Short-Term Changes Caused by Storms along Natural and Protected Sections of the Dziwnow Spit, Southern Baltic Coast. J. Coastal Res. 2017, 33, 775–785. [Google Scholar] [CrossRef]
- Deng, J.; Harff, J.; Zhang, W.; Schneider, R.; Dudzińska-Nowak, J.; Giza, A.; Terefenko, P.; Furmańczyk, K. The Dynamic Equilibrium Shore Model for the Reconstruction and Future Projection of Coastal Morphodynamics. In Coastline Changes of the Baltic Sea from South to East; Harff, J., Furmańczyk, K., VonStorch, H., Eds.; Springer: Cham, Switzerland, 2017; pp. 87–106. [Google Scholar]
- Uścinowicz, G.; Szarafin, T. Short-term prognosis of development of barrier-type coasts (Southern Baltic Sea). Ocean Coast. Manag. 2018, 165, 258–267. [Google Scholar] [CrossRef]
- Prémaillon, M.; Regard, V.; Dewez, T.J.B.; Auda, Y. GlobR2C2 (Global Recession Rates of Coastal Cliffs): A global relational database to investigate coastal rocky cliff erosion rate variations. Earth Surf. Dyn. 2018, 6, 651–668. [Google Scholar] [CrossRef]
- Hall, J.W.; Meadowcroft, I.C.; Lee, E.M.; van Gelder, P.H.A.J.M. Stochastic simulation of episodic soft coastal cliff recession. Coast. Eng. 2002, 46, 159–174. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Garcin, M.; Yates, M.; Idier, D.; Meyssignac, B. Approaches to evaluate the recent impacts of sea-level rise on shoreline changes. Earth-Sci. Rev. 2014, 138, 47–60. [Google Scholar] [CrossRef]
- Beuzen, T.; Splinter, K.D.; Marshall, L.A.; Turner, I.L.; Harley, M.D.; Palmsten, M.L. Bayesian Networks in coastal engineering: 5 Distinguishing descriptive and predictive applications. Coast. Eng. 2018, 135, 16–30. [Google Scholar] [CrossRef]
- Hapke, C.; Plant, N. Predicting coastal cliff erosion using a Bayesian probabilistic model. Mar. Geol. 2010, 278, 140–149. [Google Scholar] [CrossRef]
- Gutierrez, B.T.; Plant, N.G.; Thieler, E.R. A Bayesian network to predict coastal vulnerability to sea level rise. J. Geophys. Res. 2011, 116, F02009. [Google Scholar] [CrossRef]
- Yates, M.L.; Le Cozannet, G. Brief communication “Evaluating European Coastal Evolution using Bayesian Networks”. Nat. Hazards Earth Syst. Sci. 2012, 12, 1173–1177. [Google Scholar] [CrossRef]
- Jäger, W.S.; Christie, E.K.; Hanea, A.M.; den Heijer, C.; Spencer, T. A Bayesian network approach for coastal risk analysis and decision making. Coast. Eng. 2018, 134, 48–61. [Google Scholar] [CrossRef]
- Le Mauff, B.; Juigner, M.; Ba, A.; Robin, M.; Launeau, P.; Fattal, P. Coastal monitoring solutions of the geomorphological response of beach-dune systems using multi-temporal LiDAR datasets (Vendee coast, France). Geomorphology 2018, 304, 121–140. [Google Scholar] [CrossRef]
- Kolander, R.; Morche, D.; Bimböse, M. Quantification of moraine cliff erosion on Wolin Island (Baltic Sea, northwest Poland. Baltica 2016, 26, 37–44. [Google Scholar] [CrossRef]
- Nunes, M.; Ferreira, O.; Loureiro, C.; Baily, B. Beach and cliff retreat induced by storm groups at Forte Novo, Algarve (Portugal). J. Coastal Res. 2011, 64, 795–799. [Google Scholar]
- Warrick, J.A.; Ritchie, A.C.; Adelman, G.; Adelman, K.; Limber, P.W. New techniques to measure cliff change form historical oblique aerial photographs and structure-for-motion photogrammetry. J. Coastal Res. 2017, 33, 39–55. [Google Scholar] [CrossRef]
- Palaseanu-Lovejoy, M.; Danielson, J.; Thatcher, C.; Foxgrover, A.; Barnard, P.; Brock, J.; Young, A. Automatic Delineation of Seacliff Limits using Lidar-derived High-resolution DEMs in Southern California. J. Coastal Res. 2016, 76, 162–173. [Google Scholar] [CrossRef]
- Rokiciński, K. Geograficzna i hydrometeorologiczna charakterystyka Morza Bałtyckiego jako obszaru prowadzenia działań asymetrycznych. Zeszyty Naukowe Akad. Marynarki Wojennej 2007, 48, 65–82. [Google Scholar]
- Wolski, T.; Wiśniewski, B.; Giza, A.; Kowalewska-Kalkowska, H.; Boman, H.; Grabbi-Kaiv, S.; Hammarklint, T.; Holfort, J.; Lydeikaitė, Ž. Extreme sea levels at selected stations on the Baltic Sea coast. Oceanologia 2014, 56, 259–290. [Google Scholar] [CrossRef]
- Paprotny, D.; Terefenko, P. New estimates of potential impacts of sea level rise and coastal floods in Poland. Nat. Hazards 2017, 85, 1249–1277. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Annunziato, A.; Giardino, A.; Feyen, L. Projections of extreme storm surge levels along Europe. Clim. Dyn. 2016, 47, 3171–3190. [Google Scholar] [CrossRef]
- Kostrzewski, A.; Zwoliński, Z.; Winowski, M.; Tylkowski, J.; Samołyk, M. Cliff top recession rate and cliff hazards for the sea coast of Wolin Island (Southern Baltic). Baltica 2015, 28, 109–120. [Google Scholar] [CrossRef]
- Schumacher, W. Coastal dynamics and coastal protection of the Island of Usedom. Greifswalder Geogr. Arbeiten 2002, 27, 131–134. [Google Scholar]
- Schwarzer, K.; Diesing, M.; Larson, M.; Niedermeyer, R.O.; Schumacher, W.; Furmanczyk, K. Coastline evolution at different time scales: Examples from the Pomeranian Bight, southern Baltic Sea. Mar. Geol. 2003, 194, 79–101. [Google Scholar] [CrossRef]
- Andrews, B.P.; Gares, P.A.; Colby, J.B. Techniques for GIS modeling of coastal dunes. Geomorphology 2002, 48, 289–308. [Google Scholar] [CrossRef]
- Vousdoukas, M.; Kirupakaramoorthy, T.; Oumeraci, H.; de la Torre, M.; Wübbold, F.; Wagner, B.; Schimmels, S. The role of combined laser scanning and video techniques in monitoring wave-by-wave swash zone processes. Coast. Eng. 2014, 83, 150–165. [Google Scholar] [CrossRef]
- Almeida, L.P.; Masselink, G.; Russell, P.E.; Davidson, M.A. Observations of gravel beach dynamics during high energy wave conditions using a laser scanner. Geomorphology 2015, 228, 15–27. [Google Scholar] [CrossRef]
- Terefenko, P.; Zelaya Wziątek, D.; Dalyot, S.; Boski, T.; Pinheiro Lima-Filho, F. A High-Precision LiDAR-Based Method for Surveying and Classifying Coastal Notches. ISPRS Int. J. Geo-Inf. 2018, 7, 295. [Google Scholar] [CrossRef]
- Cieślikiewicz, W.; Paplińska-Swerpel, B. A 44-year hindcast of wind wave fields over the Baltic Sea. J. Coastal Eng. 2008, 55, 894–905. [Google Scholar] [CrossRef]
- Hersbach, H.; Dee, D. ERA5 Reanalysis Is in Production. 2016. Available online: https://www.ecmwf.int/en/newsletter/147/news/era5-reanalysis-production (accessed on 23 November 2018).
- Rosser, N.J.; Brain, M.J.; Petley, D.N.; Lim, M.; Norman, E.C. Coastline retreat via progressive failure of rocky coastal cliffs. Geology 2013, 41, 939–942. [Google Scholar] [CrossRef]
- Johnstone, E.; Raymond, J.; Olsen, J.M.; Driscoll, N. Morphological Expressions of Coastal Cliff Erosion Processes in San Diego County. J. Coastal Res. 2016, 76, 174–184. [Google Scholar] [CrossRef]
- Hapke, C.J.; Reid, D. National Assessment of Shoreline Change, Part 4: Historical Coastal Cliff Retreat along the California Coast; USGS Open-File Report 2007-1133; U.S. Department of the Interior, U.S. Geological Survey: Santa Cruz, USA, 2007; 51p.
- Kurowicka, D.; Cooke, R. Uncertainty Analysis with High Dimensional Dependence Modelling; John Wiley & Sons Ltd.: Chichester, UK, 2006. [Google Scholar]
- Hanea, A.M.; Kurowicka, D.; Cooke, R.M. Hybrid Method for Quantifying and Analyzing Bayesian Belief Nets. Qual. Reliab. Eng. Int. 2006, 22, 709–729. [Google Scholar] [CrossRef]
- Hanea, A.; Morales Nápoles, O.; Dan Ababei, D. Non-parametric Bayesian networks: Improving theory and reviewing applications. Reliab. Eng. Sys. Saf. 2015, 144, 265–284. [Google Scholar] [CrossRef]
- Joe, H. Dependence Modeling with Copulas; Chapman & Hall/CRC: London, UK, 2014. [Google Scholar]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Furmańczyk, K.K.; Dudzińska-Nowak, J.; Furmańczyk, K.A.; Paplińska-Swerpel, B.; Brzezowska, N. Critical storm thresholds for the generation of significant dune erosion at Dziwnow Spit, Poland. Geomorphology 2012, 143, 62–68. [Google Scholar] [CrossRef]
- Hackney, C.; Darby, S.E.; Leyland, J. Modelling the response of soft cliffs to climate change: A statistical, process-response model using accumulated excess energy. Geomorphology 2013, 187, 108–121. [Google Scholar] [CrossRef]
- Earlie, C.; Masselink, G.; Russell, P. The role of beach morphology on coastal cliff erosion under extreme waves. Earth Surf. Process. Landf. 2018, 43, 1213–1228. [Google Scholar] [CrossRef]
- Wiśniewski, B.; Wolski, T. Katalogi Wezbrań i Obniżeń Sztormowych Poziomów Morza oraz Ekstremalne Poziomy wód na Polskim Wybrzeżu; Maritime University of Szczecin: Szczecin, Poland, 2009. [Google Scholar]
- Young, A.P. Recent deep-seated coastal landsliding at San Onofre State Beach, California. Geomorphology 2015, 228, 200–212. [Google Scholar] [CrossRef]
- Marques, F.; Matildes, R.; Redweik, P. Statistically based sea cliff instability hazard assessment of Burgau—Lagos coastal section (Algarve, Portugal). J. Coastal Res. 2011, 64, 927–993. [Google Scholar]
- Varnes, D.J. Slope Movement Types and Processes. In Special Report 176: Landslides: Analysis and Control; Schuster, R.L., Krizek, R.J., Eds.; Transportation and Road Research Board; National Academy of Science: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Bray, M.J.; Hooke, J.M. Prediction of soft-cliff retreat with accelerating sea-level rise. J. Coastal Res. 1997, 13, 453–467. [Google Scholar]
- Paprotny, D.; Morales-Nápoles, O. Estimating extreme river discharges in Europe through a Bayesian network. Hydrol. Earth Syst. Sci. 2017, 21, 2615–2636. [Google Scholar] [CrossRef]
- Morales Nápoles, O.; Hanea, A.M.; Worm, D.T.H. Experimental results about the assessments of conditional rank correlations by experts: Example with air pollution estimates. In Safety, Reliability and Risk Analysis: Beyond the Horizon; CRC Press/Balkema: Leiden, Holland, 2013; pp. 1359–1366. [Google Scholar]


| Variable | Source | Provider | Resolution |
|---|---|---|---|
| Wave parameters | WAM wave model hindcast | Interdisciplinary Centre for Mathematical and Computational Modelling of Warsaw University (ICM) | hourly, 1/12° |
| Wave parameters | ERA5 wave reanalysis | European Center for Medium-Range Weather Forecasts (ECMWF) | hourly, 0.36° |
| Sea level | Observations at Koserow, Świnoujście and Darłowo | German Federal Institute of Hydrology (BfG), Institute of Meteorology and Water Management (IMGW) | hourly, at tide gauges |
| Temperature, precipitation | ERA5 atmosphere reanalysis | European Center for Medium-Range Weather Forecasts (ECMWF) | hourly, 0.28° |
| Study Area | Source of Data | Variable | ||||||
|---|---|---|---|---|---|---|---|---|
| Shore | Beach | Foot | Cliff | Top | Width | Slope | ||
| All | All | 0.50 | 0.60 | 0.36 | 0.31 | 0.19 | 0.40 | 0.24 |
| All (split-sample) | 0.48 | 0.59 | 0.35 | 0.30 | 0.18 | 0.37 | 0.24 | |
| Bansin | 0.50 | 0.59 | 0.34 | 0.30 | 0.17 | 0.33 | 0.23 | |
| Międzyzdroje | 0.49 | 0.62 | 0.34 | 0.25 | 0.18 | 0.36 | −0.11 | |
| Wicie | 0.47 | 0.59 | 0.34 | 0.31 | 0.17 | 0.37 | 0.13 | |
| Bansin | All | 0.60 | 0.74 | 0.32 | 0.25 | 0.01 | 0.26 | 0.19 |
| Międzyzdroje + Wicie | 0.59 | 0.71 | 0.32 | 0.19 | 0.01 | 0.20 | 0.19 | |
| Międzyzdroje | All | 0.41 | 0.29 | 0.46 | 0.10 | −0.16 | 0.42 | −0.02 |
| Bansin + Wicie | 0.41 | 0.28 | 0.46 | 0.07 | −0.16 | 0.40 | −0.02 | |
| Wicie | All | 0.50 | 0.72 | 0.22 | 0.50 | 0.45 | 0.15 | 0.01 |
| Bansin + Międzyzdroje | 0.47 | 0.70 | 0.26 | 0.47 | 0.31 | 0.12 | 0.02 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terefenko, P.; Paprotny, D.; Giza, A.; Morales-Nápoles, O.; Kubicki, A.; Walczakiewicz, S. Monitoring Cliff Erosion with LiDAR Surveys and Bayesian Network-based Data Analysis. Remote Sens. 2019, 11, 843. https://doi.org/10.3390/rs11070843
Terefenko P, Paprotny D, Giza A, Morales-Nápoles O, Kubicki A, Walczakiewicz S. Monitoring Cliff Erosion with LiDAR Surveys and Bayesian Network-based Data Analysis. Remote Sensing. 2019; 11(7):843. https://doi.org/10.3390/rs11070843
Chicago/Turabian StyleTerefenko, Paweł, Dominik Paprotny, Andrzej Giza, Oswaldo Morales-Nápoles, Adam Kubicki, and Szymon Walczakiewicz. 2019. "Monitoring Cliff Erosion with LiDAR Surveys and Bayesian Network-based Data Analysis" Remote Sensing 11, no. 7: 843. https://doi.org/10.3390/rs11070843
APA StyleTerefenko, P., Paprotny, D., Giza, A., Morales-Nápoles, O., Kubicki, A., & Walczakiewicz, S. (2019). Monitoring Cliff Erosion with LiDAR Surveys and Bayesian Network-based Data Analysis. Remote Sensing, 11(7), 843. https://doi.org/10.3390/rs11070843