An Efficient Framework for Mobile Lidar Trajectory Reconstruction and Mo-norvana Segmentation
Abstract
1. Introduction
2. Related Work
2.1. Use of Mobile Lidar Trajectory Information
2.2. Segmentation for Mobile Lidar Data
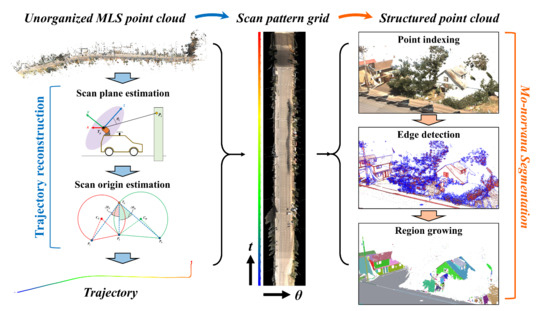
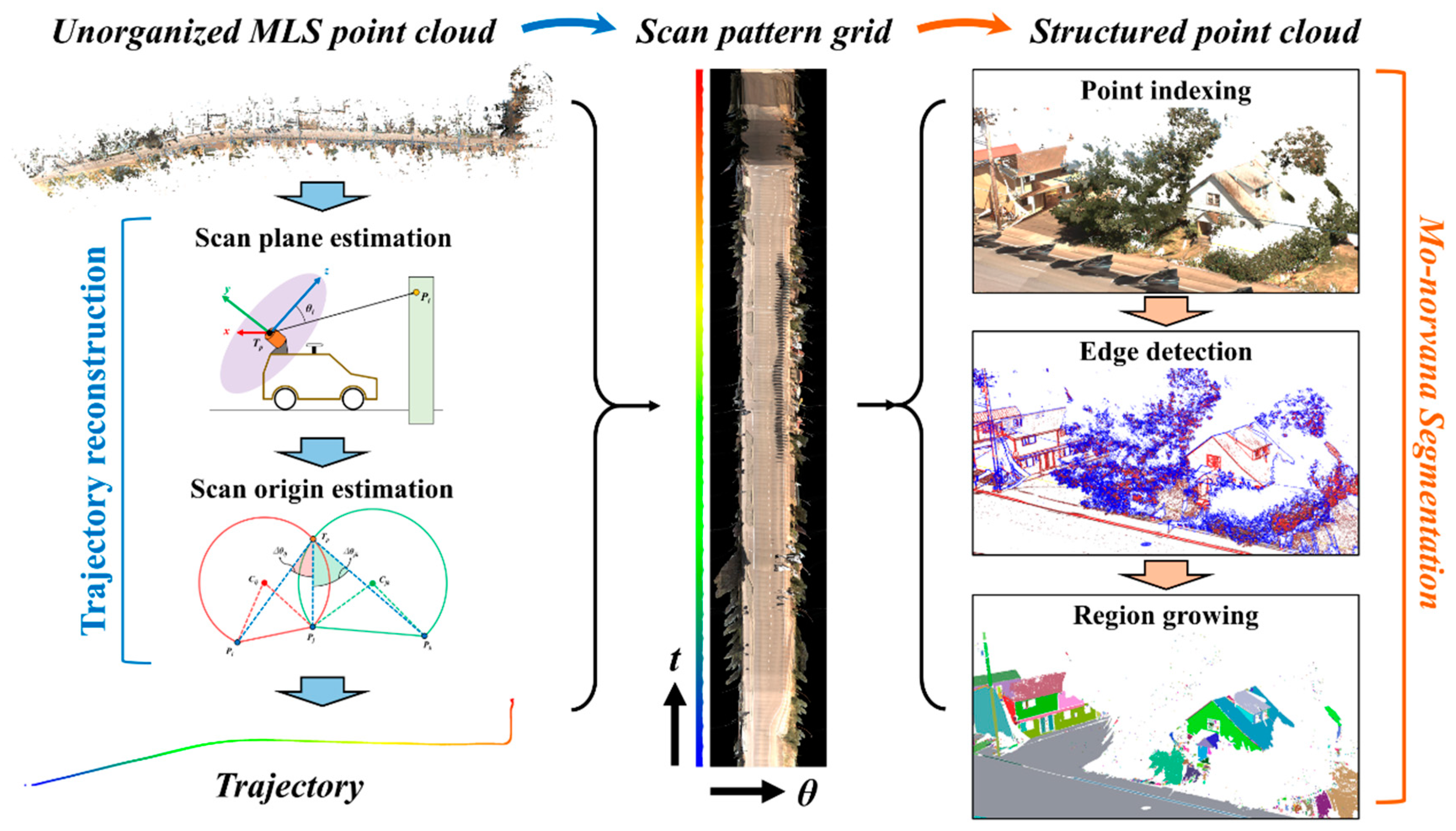
3. Methodology
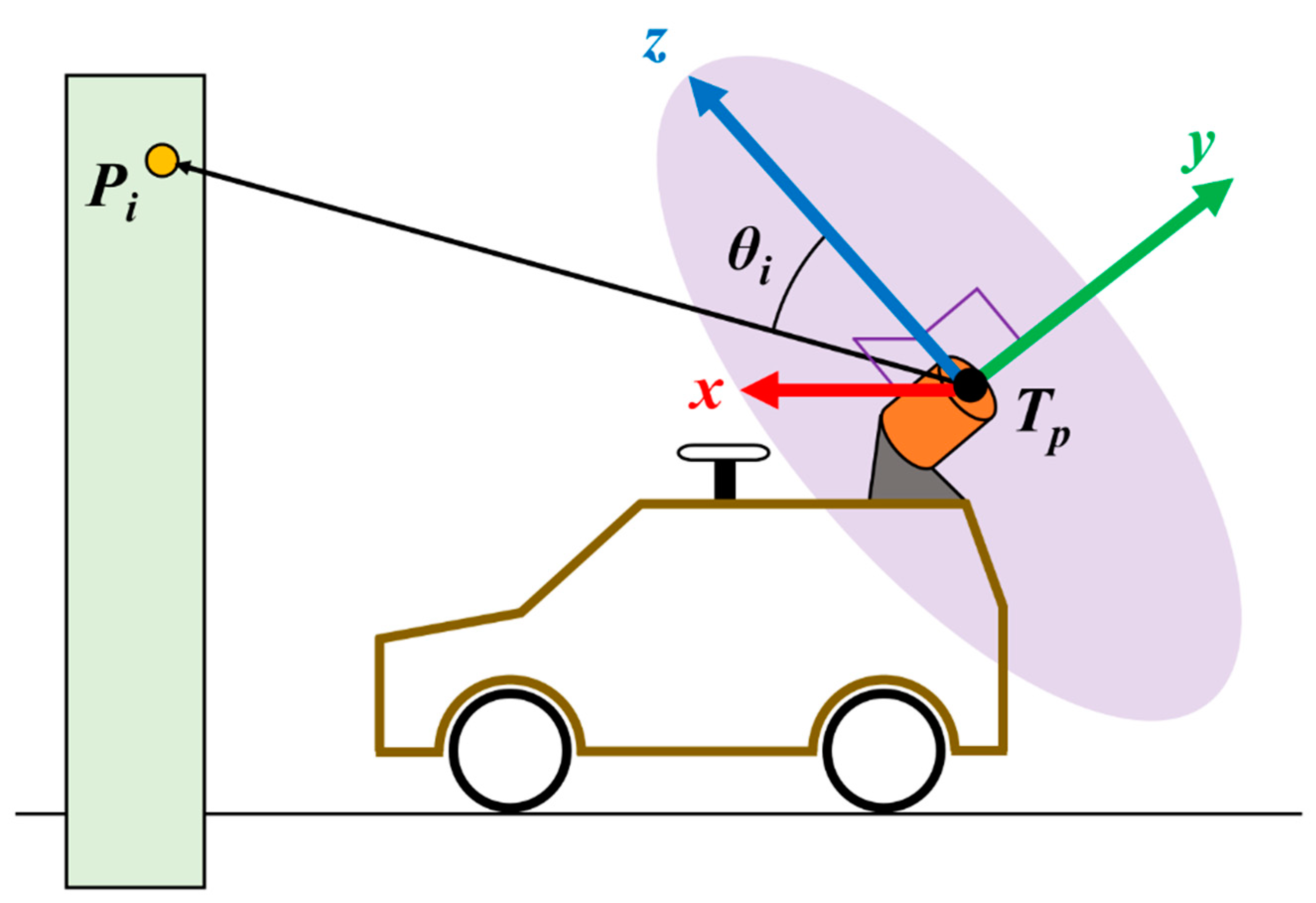
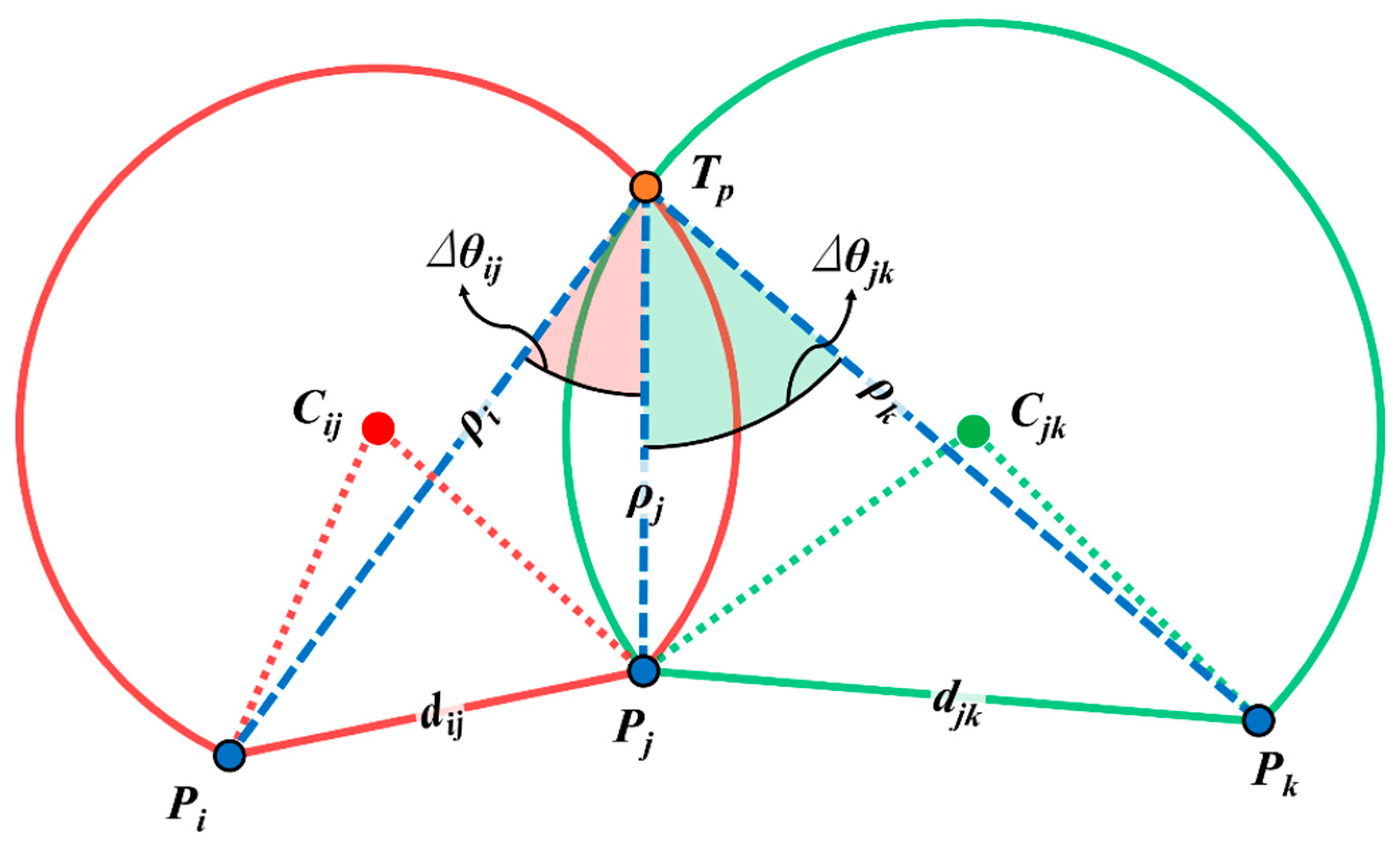
3.1. Trajectory Reconstruction
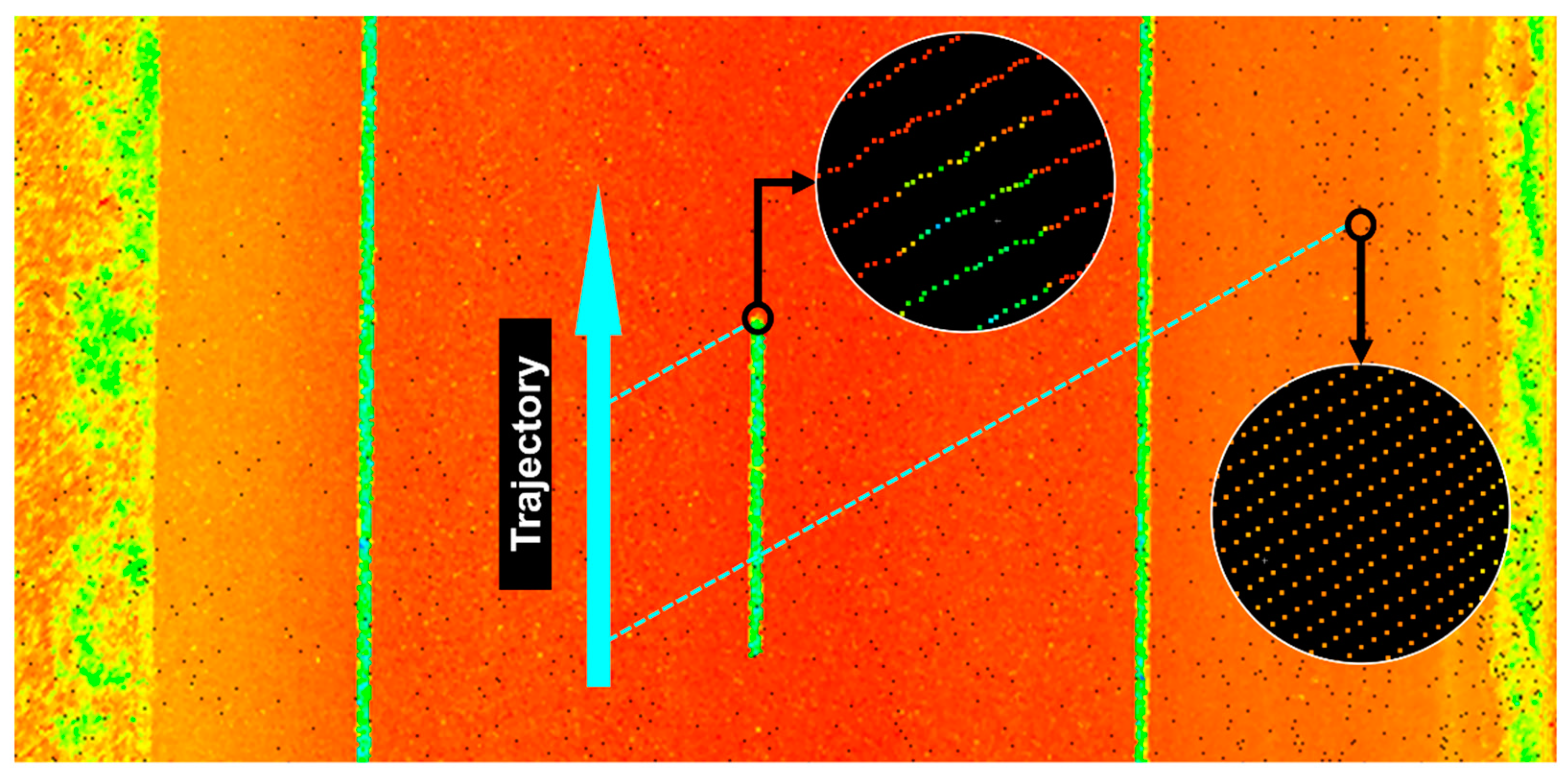
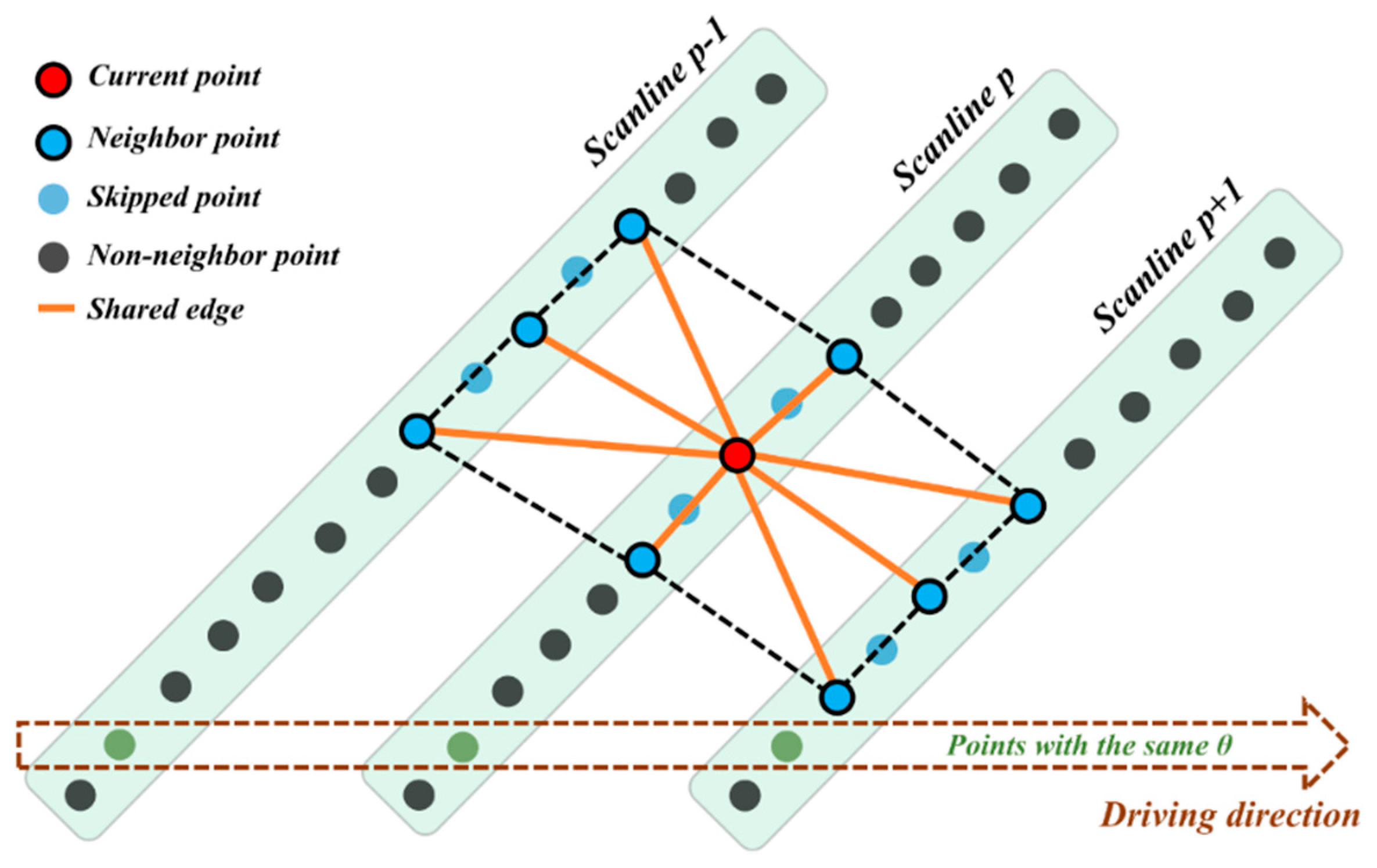
3.2. Scan Pattern Grid
3.3. Mo-norvana Segmentation
4. Experiment
4.1. Test Datasets
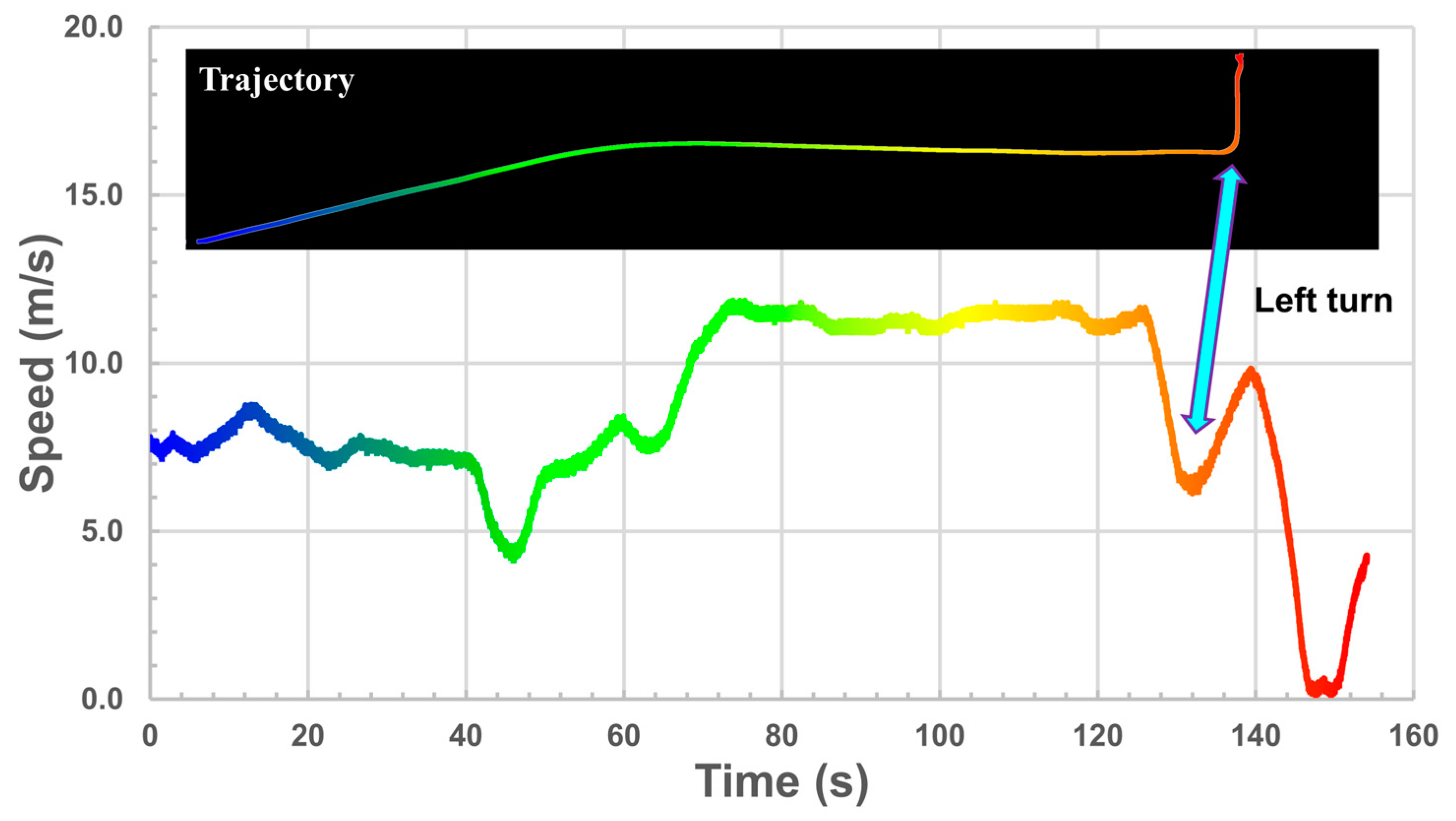
4.2. Trajectory Reconstruction
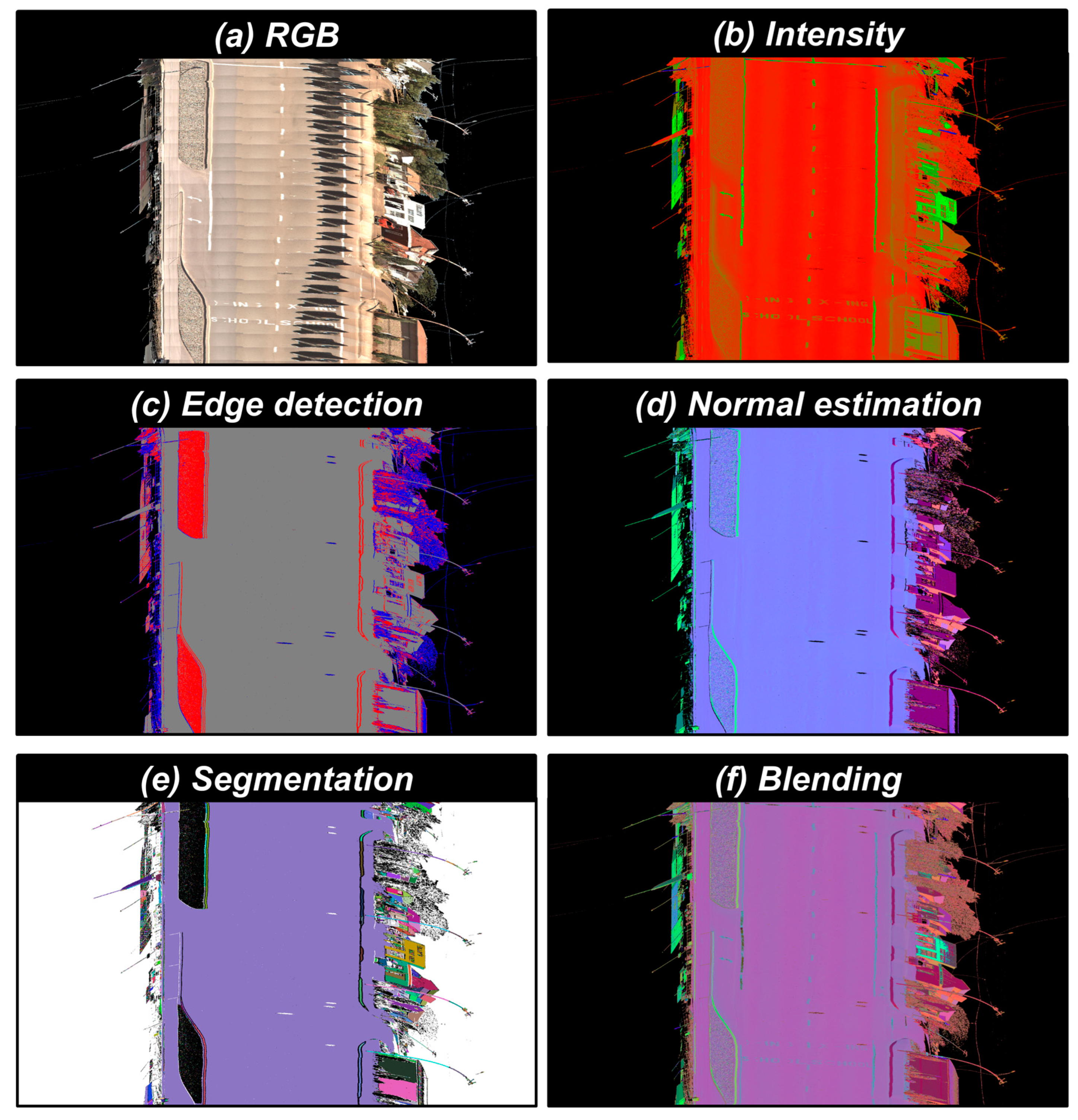
4.3. Visualization Based on Scan Pattern Grid
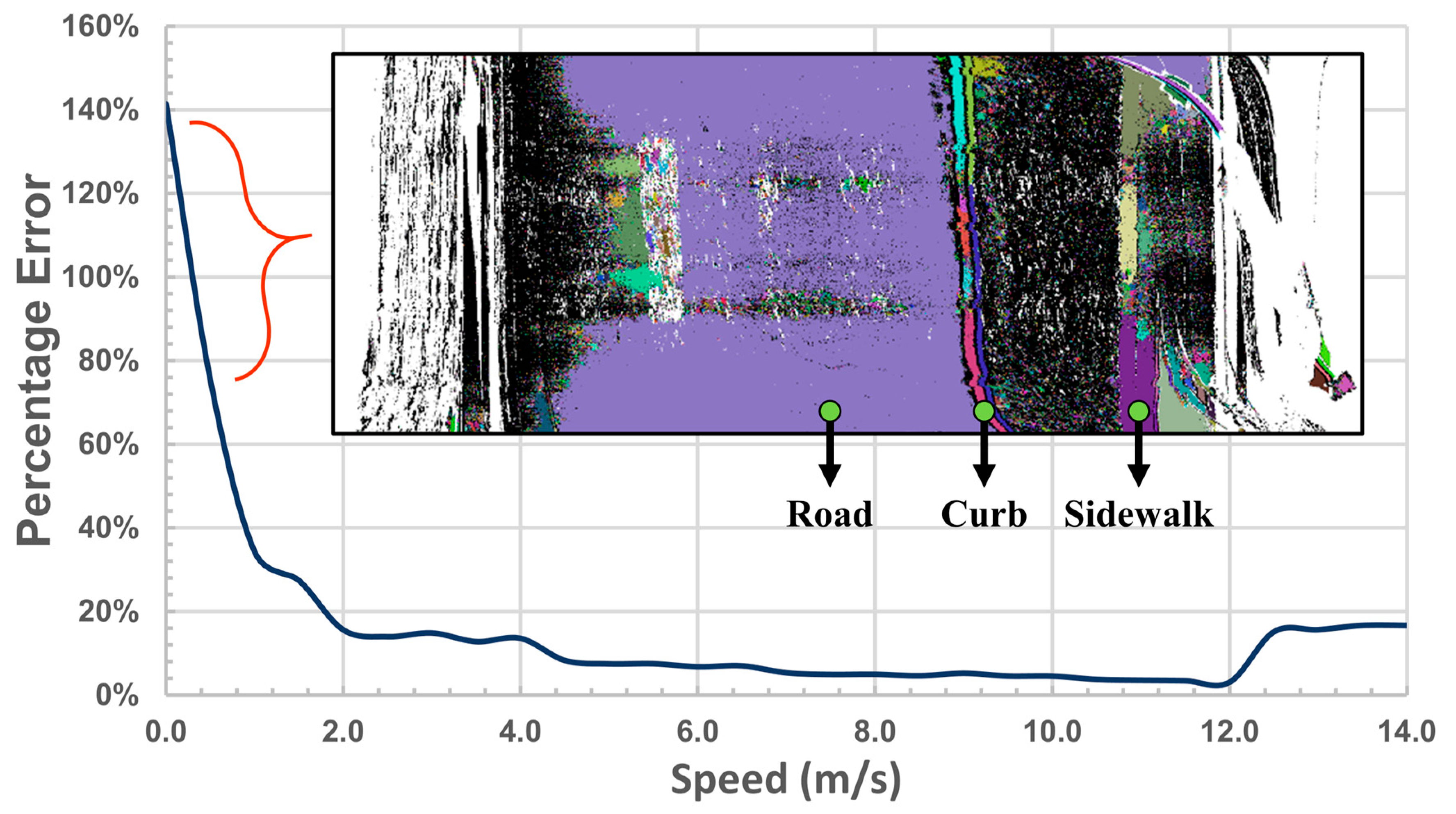
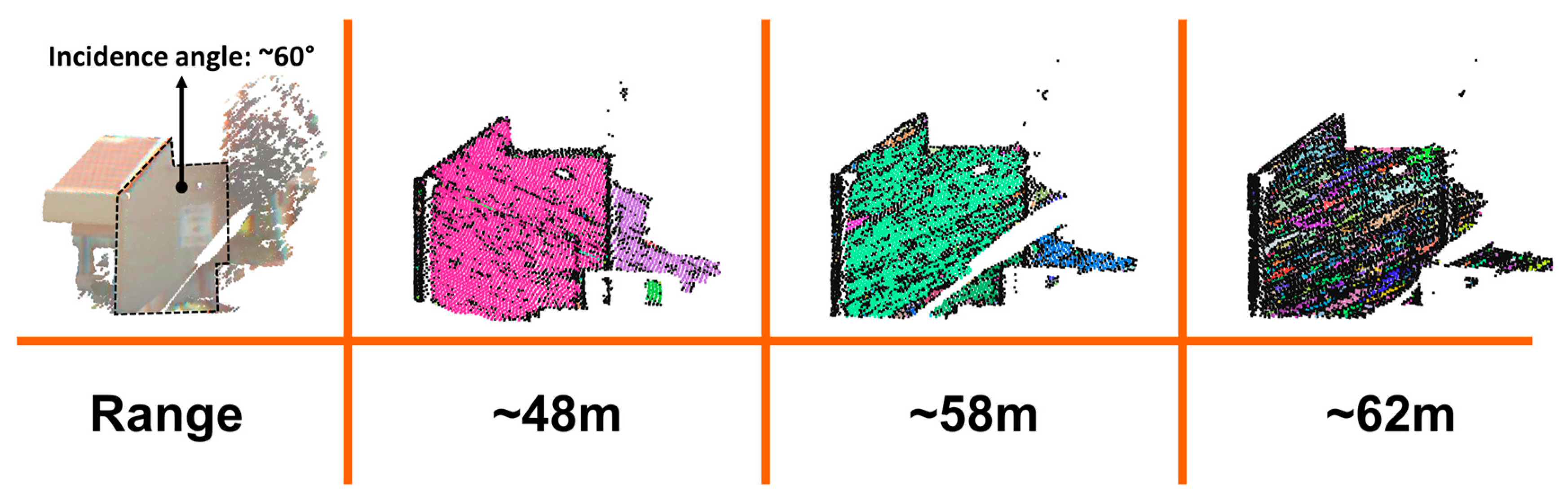
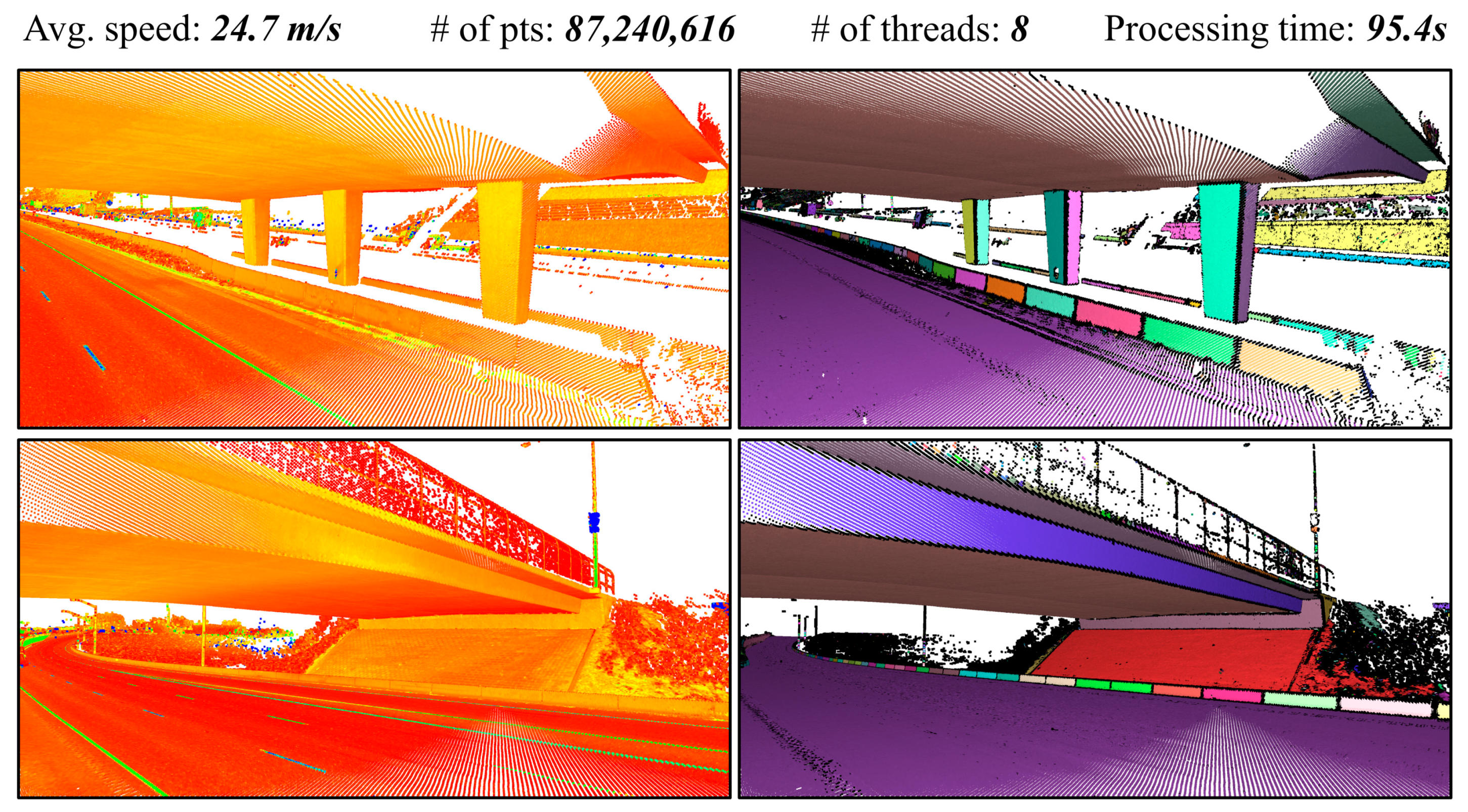
4.4. Mo-norvana Segmentation
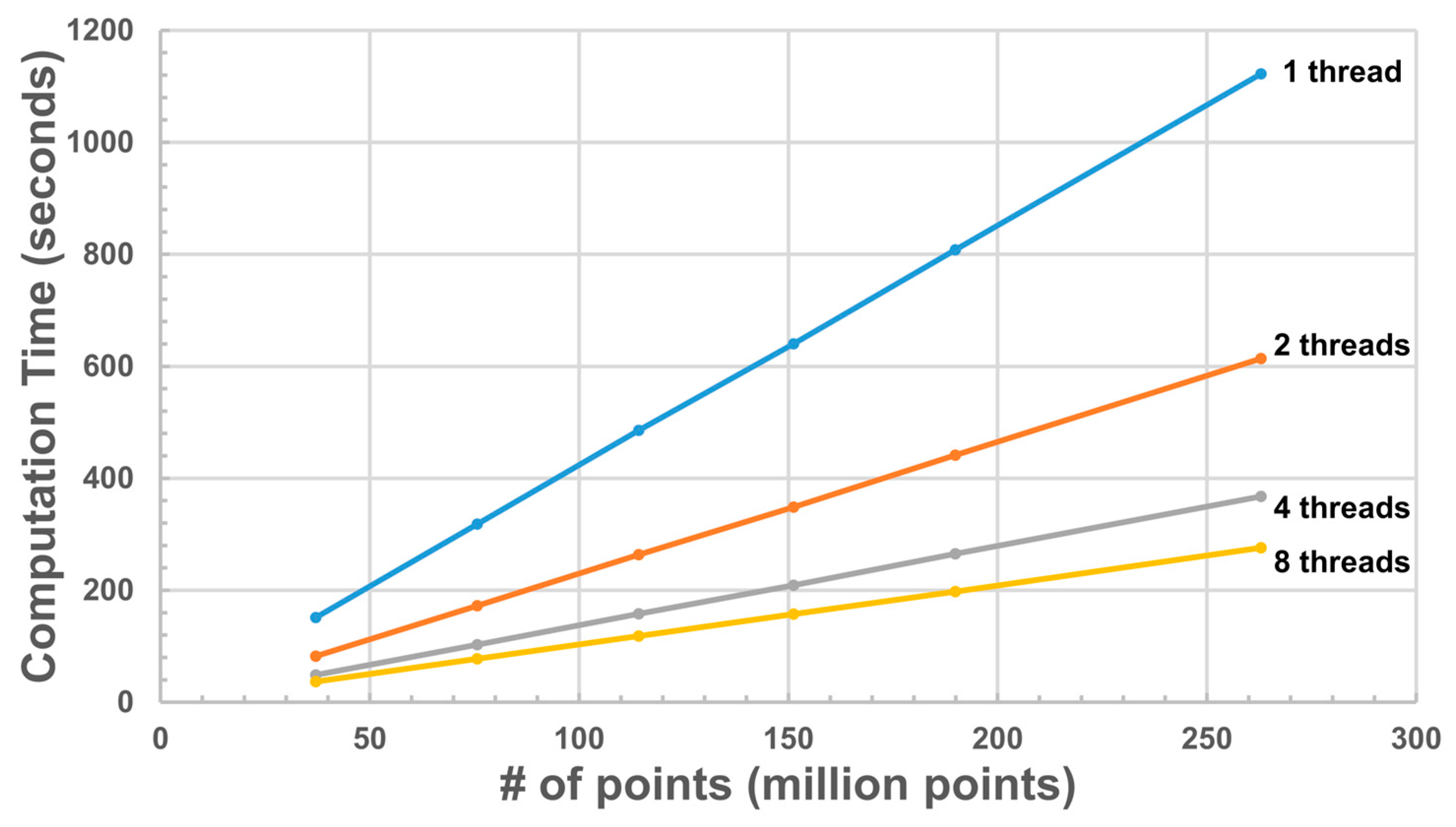
4.5. Computational Efficiency
4.6. Versatility
5. Conclusions
- (1)
- A novel approach to accurately reconstructing the scanner trajectory (both position and state) is proposed only with angular resolution as input.
- (2)
- By using the reconstructed trajectory, the unorganized mobile lidar point cloud can be structured into a scan pattern grid, which can support efficient data indexing and visualization.
- (3)
- Exploiting the scan pattern grid, we extend the concept of our previous work only applicable to structured TLS data (Norvana segmentation) to be able to process mobile lidar data.
- (4)
- The proposed framework is efficient because the process is conducted exploiting the scan pattern grid, and further improved by taking advantage of parallel programming.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Olsen, M.J.; Roe, G.V.; Glennie, C.; Persi, F.; Reedy, M.; Hurwitz, D.; Williams, K.; Tuss, H.; Squellati, A.; Knodler, M. Guidelines for the Use of Mobile LIDAR in Transportation Applications; TRB NCHRP Final Report; Transportation Research Board: Washington, DC, USA, 2013. [Google Scholar]
- Balsa-Barreiro, J.; Fritsch, D. Generation of visually aesthetic and detailed 3D models of historical cities by using laser scanning and digital photogrammetry. Digit. Appl. Archaeol. Cult. Herit. 2018, 8, 57–64. [Google Scholar] [CrossRef]
- Che, E.; Jung, J.; Olsen, M.J. Object Recognition, Segmentation, and Classification of Mobile Laser Scanning Point Clouds: A State of the Art Review. Sensors 2019, 19, 810. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Cuenca, B.; García-Cortés, S.; Ordóñez, C.; Alonso, M.C. Automatic detection and classification of pole-like objects in urban point cloud data using an anomaly detection algorithm. Remote Sens. 2015, 7, 12680–12703. [Google Scholar] [CrossRef]
- Puente, I.; Akinci, B.; González-Jorge, H.; Díaz-Vilariño, L.; Arias, P. A semi-automated method for extracting vertical clearance and cross sections in tunnels using mobile LiDAR data. Tunn. Undergr. Space Technol. 2016, 59, 48–54. [Google Scholar] [CrossRef]
- Chen, X.; Kohlmeyer, B.; Stroila, M.; Alwar, N.; Wang, R.; Bach, J. Next generation map making: Geo-referenced ground-level LIDAR point clouds for automatic retro-reflective road feature extraction. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; pp. 488–491. [Google Scholar]
- Wang, H.; Cai, Z.; Luo, H.; Wang, C.; Li, P.; Yang, W.; Ren, S.; Li, J. Automatic road extraction from mobile laser scanning data. In Proceedings of the 2012 International Conference on Computer Vision in Remote Sensing (CVRS), Xiamen, China, 16–18 December 2012; pp. 136–139. [Google Scholar]
- Holgado-Barco, A.; Gonzalez-Aguilera, D.; Arias-Sanchez, P.; Martinez-Sanchez, J. An automated approach to vertical road characterisation using mobile LiDAR systems: Longitudinal profiles and cross-sections. ISPRS J. Photogramm. Remote Sens. 2014, 96, 28–37. [Google Scholar] [CrossRef]
- Wang, H.; Luo, H.; Wen, C.; Cheng, J.; Li, P.; Chen, Y.; Wang, C.; Li, J. Road Boundaries Detection Based on Local Normal Saliency From Mobile Laser Scanning Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2085–2089. [Google Scholar]
- Wu, B.; Yu, B.; Huang, C.; Wu, Q.; Wu, J. Automated extraction of ground surface along urban roads from mobile laser scanning point clouds. Remote Sens. Lett. 2016, 7, 170–179. [Google Scholar] [CrossRef]
- Zai, D.; Li, J.; Guo, Y.; Cheng, M.; Lin, Y.; Luo, H.; Wang, C. 3-D road boundary extraction from mobile laser scanning data via supervoxels and graph cuts. IEEE Trans. Intell. Transp. Syst. 2018, 19, 802–813. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Yu, Y.; Wang, C.; Chapman, M.; Yang, B. Using mobile laser scanning data for automated extraction of road markings. ISPRS J. Photogramm. Remote Sens. 2014, 87, 93–107. [Google Scholar] [CrossRef]
- Kumar, P.; McElhinney, C.P.; Lewis, P.; McCarthy, T. Automated road markings extraction from mobile laser scanning data. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 125–137. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Jia, F.; Wang, C. Learning hierarchical features for automated extraction of road markings from 3-D mobile LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 709–726. [Google Scholar] [CrossRef]
- Yan, L.; Liu, H.; Tan, J.; Li, Z.; Xie, H.; Chen, C. Scan line based road marking extraction from mobile LiDAR point clouds. Sensors 2016, 16, 903. [Google Scholar] [CrossRef] [PubMed]
- Soilán, M.; Riveiro, B.; Martínez-Sánchez, J.; Arias, P. Segmentation and classification of road markings using MLS data. ISPRS J. Photogramm. Remote Sens. 2017, 123, 94–103. [Google Scholar] [CrossRef]
- Jung, J.; Che, E.; Olsen, M.J.; Parrish, C. Efficient and robust lane marking extraction from mobile lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2019, 147, 1–18. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Wang, C.; Yu, J. Semiautomated extraction of street light poles from mobile LiDAR point-clouds. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1374–1386. [Google Scholar] [CrossRef]
- Teo, T.-A.; Chiu, C.-M. Pole-like road object detection from mobile lidar system using a coarse-to-fine approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4805–4818. [Google Scholar] [CrossRef]
- Wang, J.; Lindenbergh, R.; Menenti, M. SigVox–A 3D feature matching algorithm for automatic street object recognition in mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 128, 111–129. [Google Scholar] [CrossRef]
- Teo, T.-A.; Yu, H.-L. Empirical radiometric normalization of road points from terrestrial mobile LiDAR system. Remote Sens. 2015, 7, 6336–6357. [Google Scholar] [CrossRef]
- Ai, C.; Tsai, Y.J. An automated sign retroreflectivity condition evaluation methodology using mobile LIDAR and computer vision. Transp. Res. Part C Emerg. Technol. 2016, 63, 96–113. [Google Scholar] [CrossRef]
- Pu, S.; Rutzinger, M.; Vosselman, G.; Elberink, S.O. Recognizing basic structures from mobile laser scanning data for road inventory studies. ISPRS J. Photogramm. Remote Sens. 2011, 66, S28–S39. [Google Scholar] [CrossRef]
- González-Jorge, H.; Puente, I.; Riveiro, B.; Martínez-Sánchez, J.; Arias, P. Automatic segmentation of road overpasses and detection of mortar efflorescence using mobile LiDAR data. Opt. Laser Technol. 2013, 54, 353–361. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Li, D.; Yang, F.; Liu, Y. A density-based clustering method for urban scene mobile laser scanning data segmentation. Remote Sens. 2017, 9, 331. [Google Scholar] [CrossRef]
- Varela-González, M.; González-Jorge, H.; Riveiro, B.; Arias, P. Automatic filtering of vehicles from mobile LiDAR datasets. Measurement 2014, 53, 215–223. [Google Scholar] [CrossRef]
- Ibrahim, S.; Lichti, D. Curb-based street floor extraction from mobile terrestrial LiDAR point cloud. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, B5. [Google Scholar] [CrossRef]
- Kashani, A.G.; Olsen, M.J.; Parrish, C.E.; Wilson, N. A review of LiDAR radiometric processing: From ad hoc intensity correction to rigorous radiometric calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef]
- Williams, K.; Olsen, M.J.; Roe, G.V.; Glennie, C. Synthesis of transportation applications of mobile LiDAR. Remote Sens. 2013, 5, 4652–4692. [Google Scholar] [CrossRef]
- Ma, L.; Li, Y.; Li, J.; Wang, C.; Wang, R.; Chapman, M. Mobile laser scanned point-clouds for road object detection and extraction: A review. Remote Sens. 2018, 10, 1531. [Google Scholar] [CrossRef]
- Vo, A.-V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Demantke, J.; Mallet, C.; David, N.; Vallet, B. Dimensionality based scale selection in 3D lidar point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, W12. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Fast Semantic Segmentation of 3D Point Clouds with Strongly Varying Density. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 177–184. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z. A shape-based segmentation method for mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 81, 19–30. [Google Scholar] [CrossRef]
- Serna, A.; Marcotegui, B. Detection, segmentation and classification of 3D urban objects using mathematical morphology and supervised learning. ISPRS J. Photogramm. Remote Sens. 2014, 93, 243–255. [Google Scholar] [CrossRef]
- Xu, S.; Wang, R.; Zheng, H. An optimal hierarchical clustering approach to segmentation of mobile LiDAR point clouds. arXiv Preprint, 2017; arXiv:1703.02150. [Google Scholar]
- Samberg, A. An implementation of the ASPRS LAS standard. In Proceedings of the ISPRS Workshop on Laser Scanning and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; pp. 363–372. [Google Scholar]
- Che, E.; Olsen, M.J. Multi-scan segmentation of terrestrial laser scanning data based on normal variation analysis. ISPRS J. Photogramm. Remote Sens. 2018, 143, 233–248. [Google Scholar] [CrossRef]
- Che, E.; Olsen, M.J. Fast ground filtering for TLS data via Scanline Density Analysis. ISPRS J. Photogramm. Remote Sens. 2017, 129, 226–240. [Google Scholar] [CrossRef]
- Mahmoudabadi, H.; Olsen, M.J.; Todorovic, S. Efficient terrestrial laser scan segmentation exploiting data structure. ISPRS J. Photogramm. Remote Sens. 2016, 119, 135–150. [Google Scholar] [CrossRef]
- Guinard, S.; Vallet, B. Sensor-topology based simplicial complex reconstruction. arXiv Preprint, 2018; arXiv:1802.07487. [Google Scholar]
- Barnea, S.; Filin, S. Segmentation of terrestrial laser scanning data using geometry and image information. ISPRS J. Photogramm. Remote Sens. 2013, 76, 33–48. [Google Scholar] [CrossRef]
- Olsen, M.J.; Ponto, K.; Kimball, J.; Seracini, M.; Kuester, F. 2D open-source editing techniques for 3D laser scans. In Proceedings of the Computer Applications and Quantitative Methods in Archaeology, CAA 2010, Granada, Spain, 6–9 April 2010; pp. 47–50. [Google Scholar]


| Applications | Use of Trajectory Data | References | ||
|---|---|---|---|---|
| Data Partitioning | Road Extraction | Radiometric Calibration | ||
| Road surface extraction | ✓ | ✓ | Chen, et al. [6] | |
| ✓ | Wang, et al. [7] | |||
| ✓ | ✓ | Holgado-Barco, et al. [8] | ||
| ✓ | Wang, et al. [9] | |||
| ✓ | Wu, et al. [10] | |||
| ✓ | ✓ | Zai, et al. [11] | ||
| Road marking extraction | ✓ | ✓ | Guan, et al. [12] | |
| ✓ | Kumar, et al. [13] | |||
| ✓ | Yu, et al. [14] | |||
| ✓ | ✓ | Yan, et al. [15] | ||
| ✓ | ✓ | ✓ | Soilán, et al. [16] | |
| ✓ | ✓ | Jung, et al. [17] | ||
| Pole-like object extraction | ✓ | Yu, et al. [18] | ||
| ✓ | ✓ | Teo and Chiu [19] | ||
| ✓ | Wang, et al. [20] | |||
| Asset condition assessment | ✓ | Teo and Yu [21] | ||
| ✓ | Ai and Tsai [22] | |||
| General segmentation and classification | ✓ | Pu, et al. [23] | ||
| ✓ | González-Jorge, et al. [24] | |||
| ✓ | Li, et al. [25] | |||
| Duration (s) | Length (m) | Speed (m/s) | ||||
|---|---|---|---|---|---|---|
| Max. | Min. | Median | Avg. | Std. | ||
| 154 | 1319 | 14.17 | 0.15 | 8.15 | 8.62 | 2.76 |
| Vert. Offset (m) | Horz. Offset (m) | 3-D Offset (m) | |
|---|---|---|---|
| Max. | 0.494 | 0.630 | 0.672 |
| Min. | 0.228 | 0.356 | 0.574 |
| Median | 0.352 | 0.483 | 0.599 |
| Avg. | 0.352 | 0.485 | 0.599 |
| Std. | 0.018 | 0.020 | 0.008 |
| Lever arm (Calibration) | 0.358 | 0.491 | 0.608 |
| Vert. Error (m) | Horz. Error (m) | 3-D Error (m) | |
|---|---|---|---|
| Max. | 0.086 | 0.142 | 0.200 |
| Min. | -0.140 | 0.000 | 0.000 |
| Median | 0.000 | 0.002 | 0.002 |
| Avg. | 0.000 | 0.004 | 0.004 |
| RMSE | 0.004 | 0.008 | 0.009 |
| Method | CPU | # of pts | Time(s) | pts/sec. |
|---|---|---|---|---|
| Mo-norvana | Intel Core E5620 @ 2.40 GHz (4 cores, 8 threads) | 37 M | 37 | 1.003 M |
| 76 M | 78 | 0.974 M | ||
| 114 M | 118 | 0.964 M | ||
| 151 M | 157 | 0.961 M | ||
| 190 M | 198 | 0.959 M | ||
| 263 M | 276 | 0.953 M | ||
| Vo, et al. [31] | Intel Core i7-3770 @ 3.40 GHz | 6 M | 38 | 0.158 M |
| Xu, et al. [37] | Intel Core i7-4790 @ 3.60 GHz | 13 M | 14,400 | 0.001 M |
| Yang and Dong [35] | Intel Core i3-540 @ 3.07 GHz | 105 M | 3241 | 0.032 M |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, E.; Olsen, M.J. An Efficient Framework for Mobile Lidar Trajectory Reconstruction and Mo-norvana Segmentation. Remote Sens. 2019, 11, 836. https://doi.org/10.3390/rs11070836
Che E, Olsen MJ. An Efficient Framework for Mobile Lidar Trajectory Reconstruction and Mo-norvana Segmentation. Remote Sensing. 2019; 11(7):836. https://doi.org/10.3390/rs11070836
Chicago/Turabian StyleChe, Erzhuo, and Michael J. Olsen. 2019. "An Efficient Framework for Mobile Lidar Trajectory Reconstruction and Mo-norvana Segmentation" Remote Sensing 11, no. 7: 836. https://doi.org/10.3390/rs11070836
APA StyleChe, E., & Olsen, M. J. (2019). An Efficient Framework for Mobile Lidar Trajectory Reconstruction and Mo-norvana Segmentation. Remote Sensing, 11(7), 836. https://doi.org/10.3390/rs11070836