Next Article in Journal
Spatiotemporal Image Fusion in Remote Sensing
Next Article in Special Issue
Evaluation of Sentinel-1 and 2 Time Series for Land Cover Classification of Forest–Agriculture Mosaics in Temperate and Tropical Landscapes
Previous Article in Journal
Alternative Vegetation States in Tropical Forests and Savannas: The Search for Consistent Signals in Diverse Remote Sensing Data
Previous Article in Special Issue
Effective Band Ratio of Landsat 8 Images Based on VNIR-SWIR Reflectance Spectra of Topsoils for Soil Moisture Mapping in a Tropical Region
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 11
Issue 7
10.3390/rs11070817
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Quantifying Canopy Tree Loss and Gap Recovery in Tropical Forests under Low-Intensity Logging Using VHR Satellite Imagery and Airborne LiDAR

by
Ricardo Dalagnol
1,2,*,
Oliver L. Phillips
2,
Emanuel Gloor
2,
Lênio S. Galvão
1,
Fabien H. Wagner
1,
Charton J. Locks
3 and
Luiz E. O. C. Aragão
1,4
1
Remote Sensing Division, National Institute for Space Research—INPE, São José dos Campos SP 12227-010, Brazil
2
School of Geography, University of Leeds, Leeds LS2 9JT, UK
3
Brazilian Forest Service, Brasília DF 70818-900, Brazil
4
Geography, College of Life and Environmental Sciences, University of Exeter, Exeter EX4 4RJ, UK
*
Author to whom correspondence should be addressed.
Remote Sens. 2019, 11(7), 817; https://doi.org/10.3390/rs11070817
Submission received: 13 February 2019 / Revised: 26 March 2019 / Accepted: 3 April 2019 / Published: 4 April 2019
(This article belongs to the Special Issue Remote Sensing of Tropical Environmental Change)
Browse Figures
Versions Notes

Abstract

:
Logging, including selective and illegal activities, is widespread, affecting the carbon cycle and the biodiversity of tropical forests. However, automated approaches using very high resolution (VHR) satellite data (≤1 m spatial resolution) to accurately track these small-scale human disturbances over large and remote areas are not readily available. The main constraint for performing this type of analysis is the lack of spatially accurate tree-scale validation data. In this study, we assessed the potential of VHR satellite imagery to detect canopy tree loss related to selective logging in closed-canopy tropical forests. To do this, we compared the tree loss detection capability of WorldView-2 and GeoEye-1 satellites with airborne LiDAR, which acquired pre- and post-logging data at the Jamari National Forest in the Brazilian Amazon. We found that logging drove changes in canopy height ranging from −5.6 to −42.2 m, with a mean reduction of −23.5 m. A simple LiDAR height difference threshold of −10 m was enough to map 97% of the logged trees. Compared to LiDAR, tree losses can be detected using VHR satellite imagery and a random forest (RF) model with an average precision of 64%, while mapping 60% of the total tree loss. Tree losses associated with large gap openings or tall trees were more successfully detected. In general, the most important remote sensing metrics for the RF model were standard deviation statistics, especially those extracted from the reflectance of the visible bands (R, G, B), and the shadow fraction. While most small canopy gaps closed within ~2 years, larger gaps could still be observed over a longer time. Nevertheless, the use of annual imagery is advised to reach acceptable detectability. Our study shows that VHR satellite imagery has the potential for monitoring the logging in tropical forests and detecting hotspots of natural disturbance with a low cost at the regional scale.

Graphical Abstract

1. Introduction

Logging, including illegal and selective activities, causes mostly small-scale but spatially widespread disturbances in tropical forests. Illegal logging accounts for ~40% of all logging in tropical forests and up to 72% of all logging in the Brazilian Amazon [1,2]. Despite the large uncertainties, it has been estimated to affect ~12,000 km2 year−1 of forests in the Brazilian Amazon and is responsible for gross carbon losses of ~0.08 Pg C year−1 or ~33% of the Amazon’s annual carbon budget between 1999 and 2002 [3,4]. Besides the direct implications on the carbon cycle, logging also causes ecological impacts, such as the increased mortality of remaining trees, increased fire risk, and losses of floral and faunal biodiversity [3,5,6]. Furthermore, the long-term effects of logging on forest dynamics and turnover remain poorly understood, but likely persist for decades [7].
Given the impacts of logging on a forest’s carbon stocks and biodiversity, there is a growing interest in tracking these direct human-induced forest disturbances [8]. This is critical for better understanding the contribution of logging to the carbon budget and ultimately supporting actions for climate change mitigation [4]. However, unlike forest clear-cutting, logging is not easily detected by remote sensing. Compared to clear-cutting, logging causes comparably subtler changes to the canopy, such as opening gaps over logging decks and roads, but most of the canopy damage is due to the direct impacts of tree-falls [3]. Furthermore, the detection challenge increases for low-impact logging (i.e., selective or reduced impact logging), since these activities are carefully planned to minimize environmental impacts, by only extracting targeted individual trees of non-endangered species with high market value.
Satellite imagery from the Landsat series (30 m resolution) has been successfully used to map logging disturbances in Amazon forests using mono-temporal, e.g., [3,9], or multi-temporal, e.g., [10], approaches. However, although Landsat satellites provide the longest historical time series (1984-today), the spatial resolution of their instruments is limited with respect to capturing all the small-scale disturbances associated with logging and especially low-impact logging. Alternatively, studies have shown that VHR satellite imagery (≤1 m spatial resolution) is a promising way to map small-scale disturbances from natural mortality and logging by the visual inspection of multi-date imagery [11,12,13]. More recently, Kellner and Hubbell [14] applied an automated method to detect the mortality of canopy tree species Handroanthus guayacan in tropical forests based on synchronous flowering. However, their method only works for tree species with synchronous annual flowering. At this time, we still lack information about the effects of tree size, tree-fall gap opening, and time after the event on the sensitivity of the disturbance detection from the VHR satellite data.
Automated disturbance detection using VHR satellite imagery still poses technical challenges, as differences in view-illumination geometries between the pairs of images may cause a mismatch of tree crown geo-location, e.g., [15,16]. Thus, the appearance of artifacts due to canopy shadowing can induce misclassification of disturbance [15], and the high local canopy spectral variability hampers the success of pixel-based change detection approaches [16]. To solve these problems, some studies suggest the application of object-based analyses [15,16] focusing on physically meaningful features rather than pixels. This is often done by the segmentation of images into individual tree crown (ITC) polygon objects, which minimizes the high local spectral variability in the canopy, and reduces the problems of tree crown geo-misallocation.
Airborne LiDAR data have also been used to investigate the impacts of selective logging [17,18,19] and natural tree mortality [20] in the Amazon. These studies pointed out that the height difference between a pair of LiDAR data, acquired pre- and post-logging, was strongly related to the aboveground biomass (AGB) change. These approaches enabled the estimation of AGB loss due to logging with fairly low (2–18%) uncertainty, and with precise observation of canopy gaps. Although they achieved a high precision for estimating small-scale disturbance impacts, airborne LiDAR data are not ideal for operational monitoring over large and remote areas because of the high costs associated with data acquisition. Nevertheless, studies suggest that the combination of airborne LiDAR and VHR satellite data could prove useful to quantitatively assess and validate how VHR satellite data can observe individual canopy tree loss, e.g., [11].
In this study, we explore the potential of VHR satellite imagery as a means to detect canopy tree loss associated with low-intensity logging in closed-canopy tropical forests. Specifically, we address the following questions: (1) How does logging drive changes in forest canopy height? (2) Can low-intensity logging events be detected by VHR satellite data? (3) Which remote sensing metrics are the most important for tree loss detection? (4) For how long after a disturbance can VHR satellite data still detect it? (5) Is the satellite-based tree loss map consistent across disturbed and undisturbed forests?
To answer these questions, we acquired a complete dataset of multi-date (pre- and post-logging) airborne LiDAR and VHR satellite data from WorldView-2 and GeoEye-1 satellites, and a comprehensive field dataset of tree-by-tree georeferenced logged trees at Jamari National Forest in the Brazilian Amazon. This enabled us to evaluate the potential of optical remote sensing to detect tree-by-tree disturbances against a carefully collected airborne LiDAR and ground record of logging.

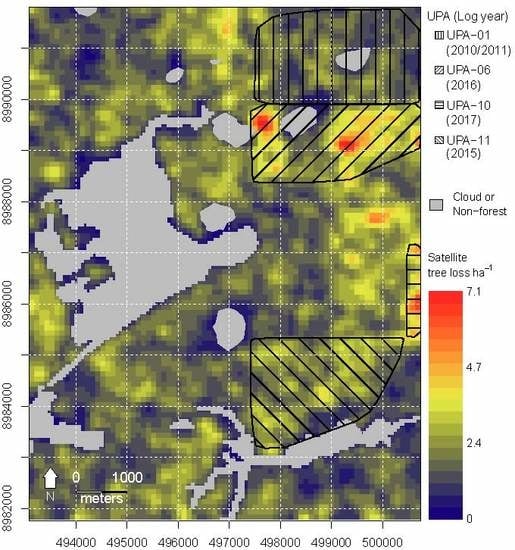
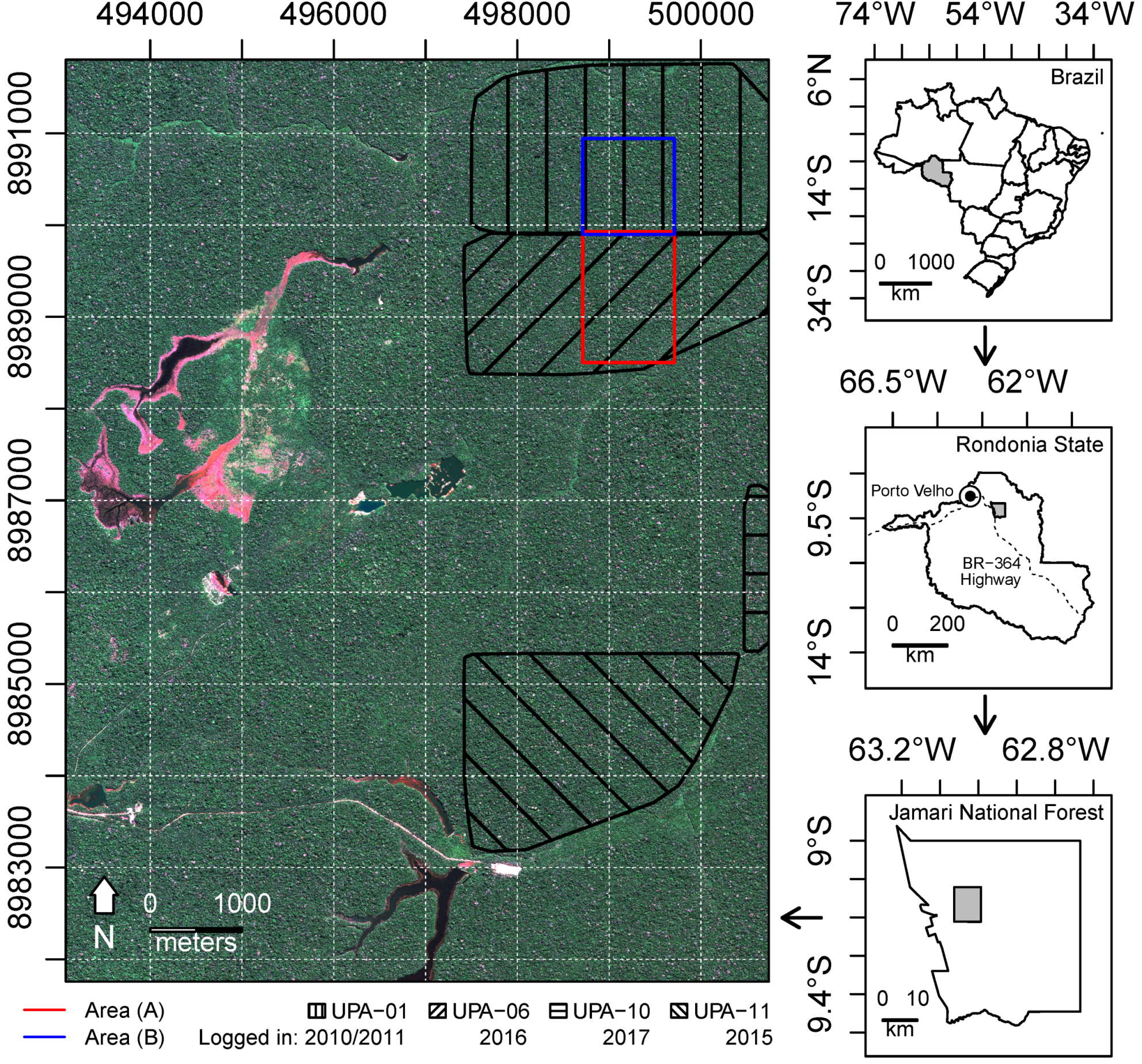
2. Study Area

The study area is located in the Jamari National Forest (09°10′S, 63°01′W), next to the BR-364 highway, 90 km from Porto Velho city, capital of the Rondônia state, Brazil (Figure 1). The Jamari Forest covers 2200 km2 of terra firme lowland ombrophilous open forests [21], with tree species of high commercial value. From the total area, 960 km2 (44%) has been allocated for private selective logging concessions since 2008. The forest concessions are administered and managed by the Brazilian Institute of Environment and Renewable Mineral Resources (IBAMA) and the Brazilian Forest Service, respectively. Wood extraction is limited to (i) non-endangered species allowed by IBAMA; (ii) trees with a diameter at breast height (DBH) greater than 50 cm; and (iii) an extraction density of up to 25.8 m3 ha−1. The managed areas are left to recover naturally for 25 years after extraction.
This study focuses on an area of 76.6 km2 inside the total managed area, with the availability of images from a pair of VHR satellites (WorldView-2 and GeoEye-1). The area covers four annual production units (UPA): UPA-01 (logged in 2010/2011), UPA-06 (logged in 2016), part of UPA-10 (logged in 2017), and UPA-11 (logged in 2015). Two smaller sections of the study area were analyzed using LiDAR datasets (Figure 1): (A) 1.4 km2 over UPA-06 observed pre- and post-logging by the satellite and LiDAR instruments (analyses of Section 3.1 and Section 3.2), and (B) 1.04 km2 over UPA-01 evaluated by a time series of LiDAR data from 2011 to 2017 (analysis of Section 3.3). The imagery also covers an active legal mining site of Cassiterite ore, located in the western part of the study area. The forests outside of UPAs and away from the mining site are nominally undisturbed.
Based on a forest inventory of the UPA-06 conducted by the concessionaire in 2015 (prior to logging), the logged trees include at least 18 different species, with DBH ranging from 50 to 185 cm (mean = 92 cm) and height ranging from 11 to 28 m (mean = 20 m). The region has two well-defined seasons: a wet season from December to May, and a dry season from June to November, with annual precipitation of 2000 mm, varying from 14 mm in the driest month (July) to 318 mm in the wettest (January), as indicated by Tropical Rainfall Measuring Mission (TRMM) data (product TRMM 3B43 v7 at 0.25 deg). Monthly mean temperature ranges from 24 °C in June/July to 27 °C in October, according to the Climatic Research Unit (product v4.01) [22]. The terrain is hilly, with heights ranging from 90 to 158 m above the sea level as measured by the Shuttle Radar Topography Mission v2.1 [23].

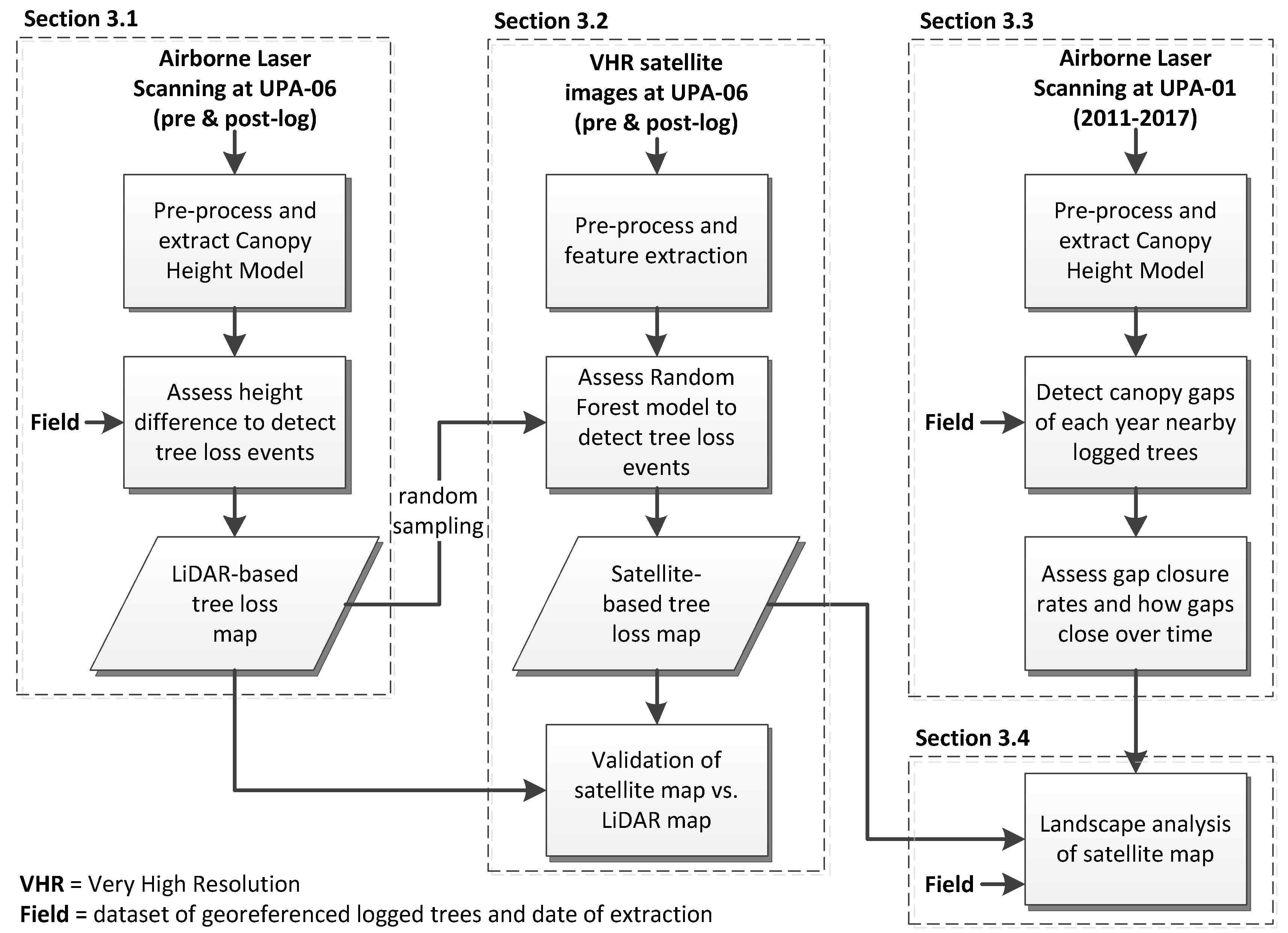
3. Material and Methods

The overview of this study is shown in Figure 2. In the first section, we used airborne LiDAR data and logged trees’ geolocation to assess height differences related to logging and create a LiDAR-based tree loss map. In the second section, using the LiDAR map as a reference for tree loss samples, we trained an RF model with VHR satellite metrics to create a satellite-based tree loss map. The satellite map was validated using the whole LiDAR map. Then, we conducted a sensitivity analysis to explore the variability of results regarding the forest structure and changes. In the third section, we analyzed a time series of airborne LiDAR data to detect tree-fall gaps and track vegetation recovery and gap closure over time. Finally, in the fourth and last section, we analyzed the whole satellite map over previously known selectively logged areas and undisturbed forests to detect hotspots of disturbances and discuss the detection capabilities using VHR satellite data.

3.1. Tree Loss Detection Using LiDAR Data

We used airborne LiDAR data and field logged tree coordinates to characterize canopy height changes associated with tree loss events derived from logging. Using this information, we created a tree loss map. We acquired airborne LiDAR data over 1.4 km2 of forests at the UPA-06 during 2015 (pre-logging) and 2017 (post-logging) (Table 1 and area A in Figure 1). The LiDAR point cloud (x, y, z coordinates) was processed into a canopy height model (CHM) following four steps of pre-processing: point classification, generation of a Digital Terrain Model (DTM), height normalization, and extraction of CHM. First, we classified the points into ground or vegetation classes using the lasground, lasheight, and lasclassify functions from LAStools 3.1.1 [24]. Second, to ensure that potential acquisition effects between the two datasets did not interfere with the analysis, we merged their points classified as ground and created a combined DTM with a 1 × 1 m pixel using the TINSurfaceCreate function from FUSION/LDV 3.6 [25]. Third, we normalized the point’s height to height above ground by subtracting the combined DTM height from their values. Finally, we extracted the CHMs considering the highest height of vegetation on each 1 × 1 m pixel using the CanopyModel function from FUSION/LDV. No adjustment for horizontal displacement between the datasets was necessary because tree crowns’ positioning agreed nearly perfectly. Both LiDAR collections had very high point densities (≥12 points m−2), which vary across studies, depending on the platform used for data collection.
As already mentioned, we adopted an object-based approach instead of a pixel-based analysis for both LiDAR and VHR analysis. To delineate the ITCs using the LiDAR data, we applied the voronoi-based method (FindTreesCHM and ForestCAS functions) from the rLiDAR R-package [26]. More details on ITC delineation are described in the Supplementary Material S1. The pre-logging LiDAR CHM was used as the input because the tree crowns from logged trees were still intact.
To characterize canopy height changes associated with tree loss events and to define a threshold to detect canopy tree loss from logging, we assessed the LiDAR CHM height difference between the acquisitions (ΔCHM = CHMdate2 – CHMdate1) considering 172 ground-mapped logged trees. Tree geolocation was acquired by the forest concessionaire in 2015, prior to the logging activities that occurred in August 2016, using a Garmin 64S handheld global positioning system (GPS) (~10 m precision). We assessed the distribution of most negative height differences in a 30 m radius around logged trees (n = 172) and around non-logged trees areas (n = 146). This radius was chosen to account for (1) tree coordinate displacement due to GPS location error and differences of geo-location between tree trunks and crowns, and (2) displacement between tree coordinates and the areas actually impacted by the tree losses. To ensure that the non-logged tree areas did not overlap with each other nor with areas included within logged trees’ radii, we randomly distributed points across the area at least 60 m away from the logged tree coordinates and from each other. We defined the ΔCHM threshold that maximally separated the distributions of height difference from logged and non-logged areas by fitting a logistic regression model and inspecting the results.
Using the ΔCHM threshold, we detected tree losses associated with logging and generated the LiDAR-based tree loss map. To assess how far the detected tree loss events occurred from logged trees, we analyzed the nearest neighbor distances between the two datasets. We also calculated the rate of tree loss occurrence per area and the percentage of canopy change between 2015 and 2017.

3.2. Tree Loss Detection Using VHR Satellite Data and RF Model

3.2.1. Satellite Data Acquisition and Preprocessing

We acquired VHR satellite data of the study area during 2014 (WorldView-2) and 2017 (GeoEye-1) (Table 1). The intersection of the two images covered an area of 76.6 km2, of which 1.4 km2 overlapped with the LiDAR data of UPA-06 forests (Figure 2). In order to convert the VHR data into surface reflectance, we applied the 6S radiative transfer model [27]. This was conducted using the OpticalCalibration function implemented in the Orfeo Toolbox (OTB) 6.4 [28]. After the correction, we selected only the blue, green, red, and near infrared (NIR) bands, because these bands were available for both GeoEye-1 and WorldView-2 satellites. To resample the pixel size of the multispectral data at the resolution of the panchromatic imagery (0.5 m), we applied the Bayes data fusion method [29] implemented in OTB 6.4. This fusion method is a probabilistic approach that combines the higher spatial resolution from the panchromatic band with the spectral bands. It is considered one of the best methods for preserving the spectral information from VHR satellite images when compared to other traditional fusion methods [29].
In order to match the tree crowns between LiDAR and satellite datasets, we co-registered (i.e., aligned) the VHR satellite data with the LiDAR CHM. Only a translation of a few pixels was necessary to match the datasets. As the pair of images was acquired under different sun-sensor geometry angles and by different sensors (Table 1), to ensure that the signals of VHR satellite images were comparable, we normalized the post-logging image based on the pre-logging image. The normalization was done using the histogram matching method by the histMatch function from the RStoolbox R-package [30]. This method extracts the cumulative distribution functions from both images, adjusting the target histogram as a function of the source histogram.

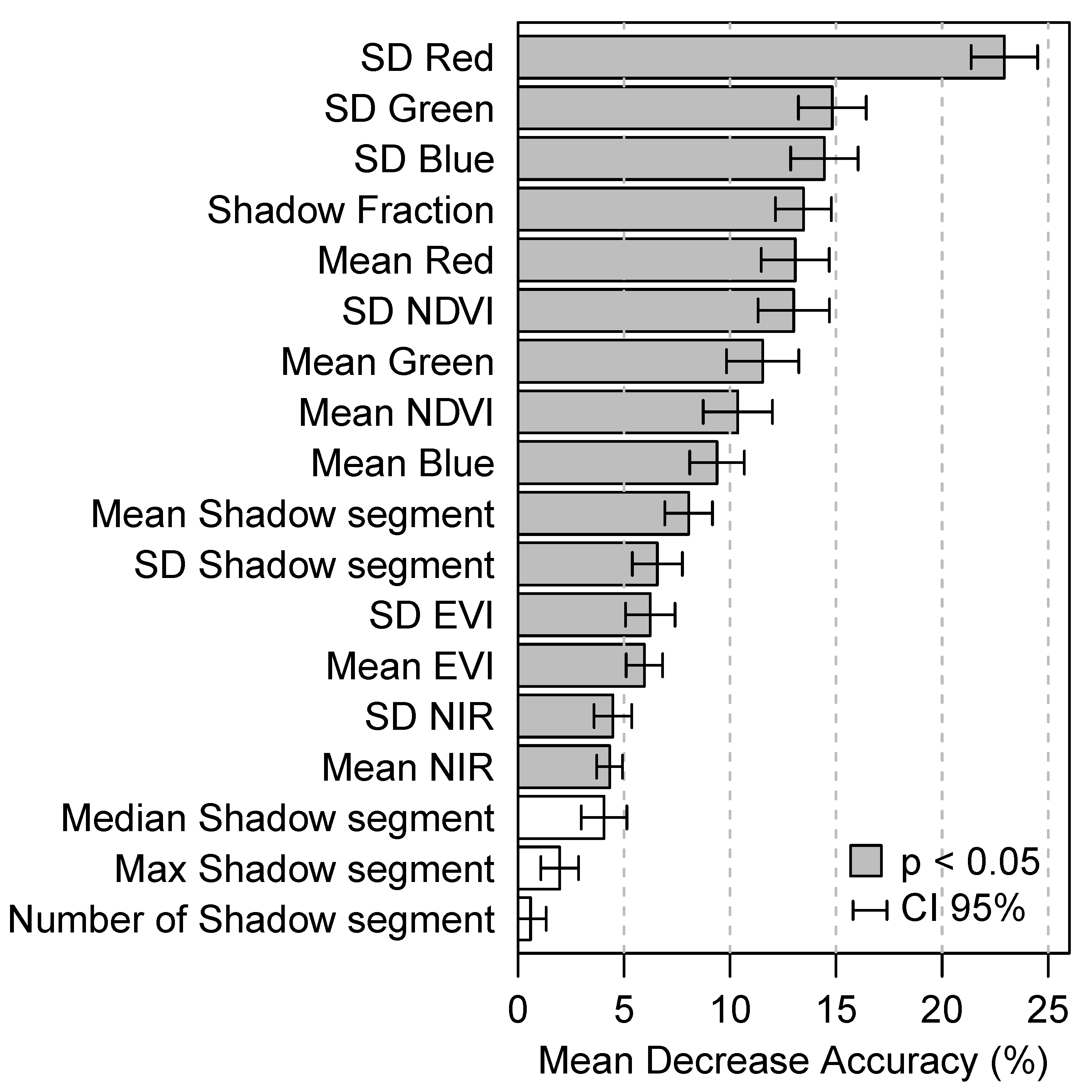
3.2.2. Selection and Extraction of VHR Satellite Metrics

In addition to the reflectance of the spectral bands, we calculated two widely used vegetation indices to explore forest structural changes: the normalized difference vegetation index (NDVI) [31] and the enhanced vegetation index (EVI) [32]. Since shade is known to be associated with tree mortality, e.g., [33], we also calculated a set of shadow metrics to be used in the modeling. To detect the shadow, we employed a simple thresholding method using the NIR band of the post-logging VHR image. We manually sampled shaded (n = 100) and non-shaded (n = 100) pixels to define a threshold separating the two classes. The threshold was determined considering the first percentile of NIR reflectance (NIR = 0.21) that covered the non-shaded pixels. Hence, all pixels with values below this threshold were classified as shadow. This shadow map was later used to calculate shadow metrics for RF modeling after performing the ITC delineation.
Using the NIR band from the pre-logging VHR data, we delineated ITCs with the marker-controlled watershed segmentation (MCWS) method. The vwf and mcws functions from the ForestTools R-package were used [34] (more details in Supplementary Material 1).
Based on the LiDAR-based tree loss map, we selected ITC samples representing tree loss and non-tree loss events (n = 200 each) to train the RF model. The tree loss samples were collected randomly from the LiDAR tree loss map. To collect non-tree loss samples, we selected samples at least 5 m away from the LiDAR tree loss detections to minimize potential mismatches of tree crown locations between LiDAR and VHR data. Then, we extracted the VHR satellite data (reflectance of the red, green, blue, and NIR bands; NDVI and EVI; and shadow) from date1 and date2 for each sample.
Using the extracted data, we created a total of 18 metrics for RF modeling. Since each ITC contains hundreds of pixels, we first summarized the values inside the ITCs of each of the four reflectance bands and two vegetation indices by calculating the mean and standard deviation (SD); then, we calculated the mean and SD differences (date2 – date1) metrics for each attribute. For the shadow attribute, considering only the values from date2, we calculated six metrics to describe the distribution of shadows inside the tree crowns. The first metric was the shadow fraction, which consisted of the ratio between the area occupied by shadow pixels and the total ITC area. The shadow pixels inside ITC were segmented and the segments were analyzed to create the remaining five metrics: number of segments and maximum, mean, median, and SD of segments’ size. To remove noise, we filtered out segments consisting of only one pixel.

3.2.3. RF Model

RF is a machine-learning algorithm, which consists of an ensemble of decision trees [35]. RF reduces the prediction variance by using a large number of decision trees. We trained RF models using 18 VHR satellite metrics as predictors to classify 400 samples as tree loss or non-tree loss events. This was performed using the randomForest R-package v4.6-12 [36]. Thus, to create the model, we generated 1000 decision trees; each tree was created using a random subset consisting of 2/3 of the samples; and for each node of a tree, only three from the 18 predictors were randomly chosen for that node classification.
Since each decision tree has a classification response for a given sample, the ensemble of responses corresponds to a pseudo-probability for classifying that sample as tree loss or non-tree loss. In general, the majority of votes is chosen as the response. However, since our classification problem was binary (presence or absence of tree loss) and our interest was to optimize the precision (inverse of commission error) of the tree loss occurrence class, we used a weighted voting approach towards this class, minimizing commission errors, but increasing omission errors. Finally, we applied the model to predict the class of every ITC and create a satellite-based tree loss map.

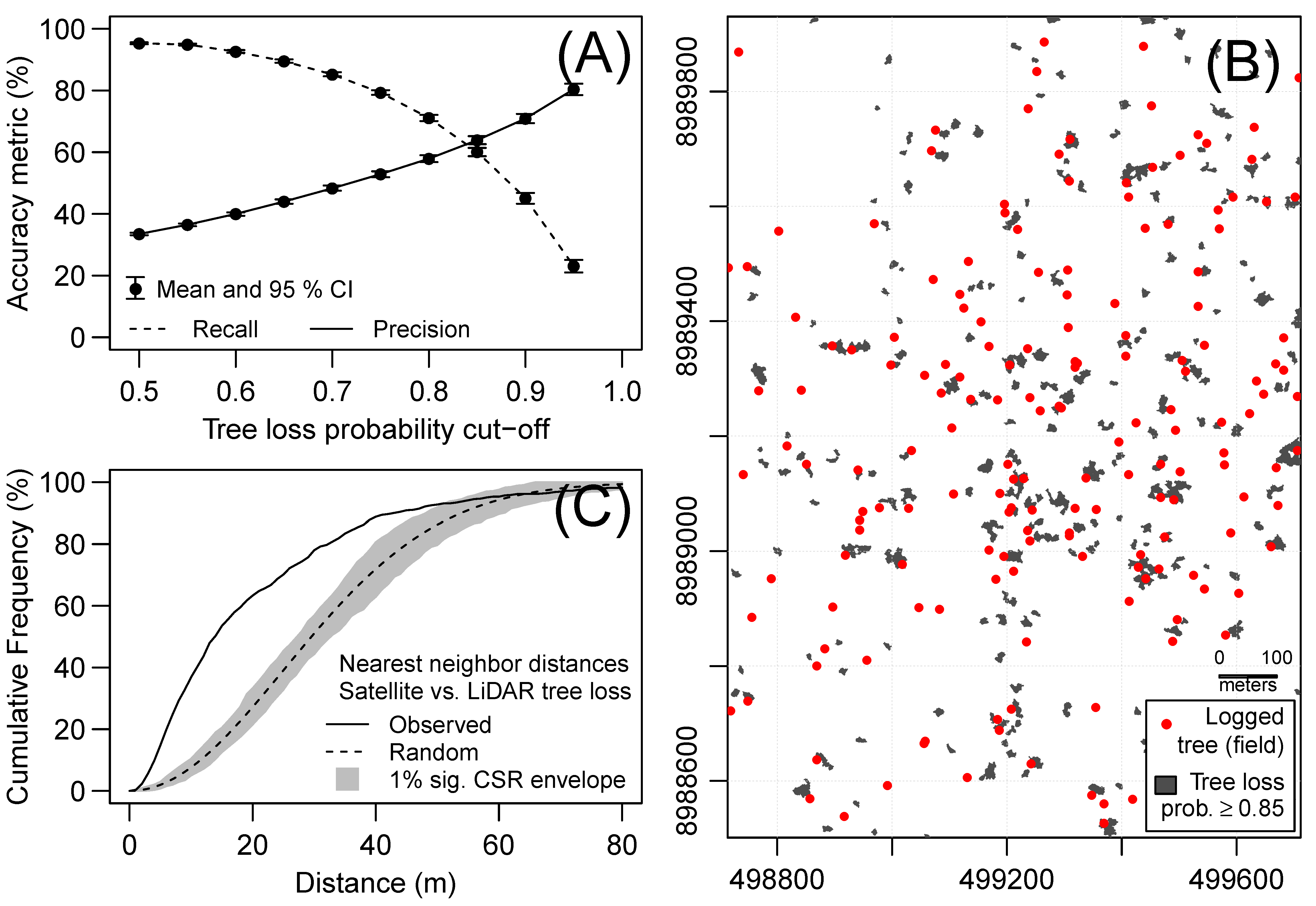
3.2.4. Validation of the Satellite-Based Tree Loss Map

To validate the satellite map, we used the LiDAR map as a reference. We intersected both maps and obtained the number of true positives (TP), false positives (FP), and false negatives (FN). TP is defined as the number of ITCs correctly identified by the satellite map, judged by whether they intersected with the ITCs of the LiDAR map; FN is the number of ITCs not identified by the satellite map, but identified by the LiDAR map; and FP is the number of ITCs incorrectly identified by the satellite map, i.e., ITCs which do not occur in the LiDAR map. For the intersections, we used a small buffer of one meter around the tree loss detections to minimize effects of artificial tree crown displacement between satellite and LiDAR datasets. To evaluate the accuracy of the model, we used TP, FP, and FN to calculate two accuracy metrics: precision (P) and recall (R) (Equations (1) and (2)). Precision is the inverse of the commission error and measures how much of the satellite detections coincided with the LiDAR detections. The recall is the inverse of omission error and measures how many ITCs of the LiDAR map were detected by the satellite map.
P = TP/(TP + FP)
R = TP/(TP + FN)
We performed additional analyses to explore the model sensitivity to random sampling and tree loss probability cutoff, the spatial dependence of detections between satellite and LiDAR maps, variable importance for modeling, and sensitivity of detections to vertical structure change and tree height. To explore the model sensitivity to sampling, we trained 30 RF models using different random sampling runs. The accuracy metrics (P and R) from the models were aggregated into mean and 95% confidence intervals. To explore the tree loss probability cutoff sensitivity and select a threshold to generate a map, while ensuring that the model predictions had a high precision, we assessed the model performance as a function of the RF tree loss probability ranging from 0.5 to 0.95.
As an independent measure of detection capability, we tested if there was significant spatial dependence between tree losses detected by VHR satellite imagery and LiDAR data. For this purpose, we extracted the nearest neighbor distances between the tree loss detections of the two maps, and compared the cumulative distribution of nearest neighbor distances with a completely random (Poisson) point process. We simulated 199 realizations of the random point process using a Monte Carlo approach and created an envelope of complete spatial randomness (CSR) with a 1% significance level. This was done using the envelope and Gcross functions from the spatstat R-package v1.47 [37]. If the observed distribution was located inside the CSR envelope, that would mean that VHR satellite detections occurred independently in space from the LiDAR detections and vice versa.
The sensitivity of detection success to vertical structure change and tree height was assessed by exploring the LiDAR CHM pre- and post-logging heights, and ΔCHM over correct VHR satellite detections.
Finally, to explore the importance of the different VHR satellite variables for the modeling, we ranked the variables according to the mean decrease accuracy (MDA) metric [35]. Once each node had been determined in a decision tree, this metric was computed by removing a single variable from the pool of variables and assessing the decrease in the model accuracy. The mean and 95% confidence interval of MDA for each variable were computed for the 30 models. The variables with the largest MDA were ranked highest in importance. To further test whether a variable was significantly important in the voting process of the RF, we compared the observed MDA versus a null distribution of MDA. We created this null distribution by running the model 30 times while shuffling the sample responses randomly. This was performed using the rfPermute v2.1.6 R-package [38]. We reported which variables showed MDAs significantly different from the null distribution considering a 5% significance level.

3.3. Assessment of Tree-Fall Gaps Recovery Using LiDAR Data

Following the assumption that the VHR detection of tree loss events depends on the observation of forest canopy gaps created by the tree-falls, and given that gaps recover over time through new recruitment and recovery of existing trees, we expect a time dependence between the tree loss detection and the time since disturbance. Therefore, we investigated the rate and mechanisms of gap closure over time using a time series of airborne LiDAR observations of a 1.04 km2 forest section collected in 2011, 2013, 2014, 2015, and 2017 over UPA-01 (Table 2 and area B in Figure 1), which was logged during 2010 and 2011. We processed the data to obtain the LiDAR CHM for each date following the same procedures described in Section 3.1.
We defined canopy gaps as holes in the forest canopy extending up to 10 m in height above the ground and with at least 5 m2 of contiguous area. Although this height threshold is higher than the classic Brokaw’s gap definition of 2 m height above ground [39], previous studies of gap dynamics with airborne LiDAR in tropical forests showed that gaps extending up to different heights above ground (e.g., 10 to 11 m) were consistent with gaps observed in the field, e.g., [40,41]. Following previous studies, e.g., [42], the minimum gap area was chosen as a small value (5 m2) in order to assess the gap filling variability from smaller to bigger gap sizes. Moreover, the optimal choice of height and minimum area varies across forest types. Hence, the gaps were delineated as follows: (1) all CHM pixels with a height below 10 m were classified as gaps; (2) the pixels defined as gaps were segmented into polygons; (3) polygons were filtered for a minimum area of 5 m2. Since the logging activities in 2010 and 2011 occurred earlier than the first LiDAR acquisition in 2011, we were unable to exactly extract the areas affected exclusively by the selective logging. Thus, to prioritize the observation of logging disturbance rather than gaps caused by natural mortality, we only selected gaps occurring within a 30 m distance from the logged tree’s locations in UPA-01 (n = 215).
To estimate the rate of gap closure over time, we calculated each gap’s relative size with respect to its initial size in 2011. We extracted the average gap size change considering all gaps, but also by size classes of up to 25, 25–50, 50–100, 100–500, and larger than 500 m2. We defined gap closure as decreases of gap size over time. This means that the vegetation inside the gap is reaching an average height of 10 m. In addition, we estimated the gap fraction (percentage of area occupied by gaps) for each year and the percentage of gaps that have fully closed.
To improve our understanding of the mechanisms of gap filling, we also assessed the percentage of height gains and losses inside gaps and whether the gaps closed by horizontal and/or vertical vegetation regrowth. To separate vertical from horizontal growth, we followed the procedures described in Hunter et al. [40]. First, we estimated a maximum possible tree height growth rate per year, which we defined as the mean plus three standard deviations of the mean height change inside gaps. Then, we applied this threshold to classify pixels inside gaps as horizontal (height change above maximum growth) or vertical growth (height change below maximum growth). Horizontal growth means the ingrowth of trees to the sides instead of actual growth in height. For those pixels classified as vertical growth, we estimated an average growth rate. To estimate the maximum tree height growth and obtain a stable estimate, we only extracted the values from pixels near to the center of the gaps, that is, at least 5 m from the edges. Therefore, the smaller gaps were not included in this estimate.

3.4. Landscape Analysis of Satellite-Based Tree Loss Map

We applied the VHR satellite data and RF model to detect tree loss events for the whole study area. This area is much larger (area = 76.6 km2) than that analyzed in Section 3.2 (1.4 km2). Thus, in order to be able to visualize the spatial distribution of tree loss events, we created a map using the isotropic kernel-smooth density estimator for aggregating the events into cells of 100 × 100 m [43]. We identified areas of greater tree loss occurrence (hotspots) according to the Z-score statistic, the absolute difference between each pixel’s tree loss value, and tree loss mean normalized by the standard deviation and a 5% significance level. To compare our results with an independent source of disturbance mapping, we acquired the global forest cover loss 2000–2017 dataset (available at https://earthenginepartners.appspot.com/science-2013-global-forest). This product, created by Hansen et al. [44] using Landsat data (30 m spatial resolution), has been widely used for forest disturbance monitoring around the world.
We assessed and compared the number of tree loss events inside each UPA and the undisturbed forest areas. The undisturbed forests were those outside of UPAs, excluding water bodies and deforestation up to 2017, according to the INPE-PRODES deforestation product [45]. We also excluded areas of cloud cover of the pre-logging image by manually delineating the clouds using a true-color composite. We estimated the canopy turnover time simply as the ratio of the average number of ITCs (canopy tree crowns) to the annualized number of tree losses per unit of area.
To explore how much of the variability of satellite tree loss detections is explained by the logged trees recorded in the field dataset, we used the same kernel approach to estimate the density of logged trees inside the managed areas (UPA-01, UPA-06, UPA-10, and UPA-11). We then overlaid the two maps and extracted the pixel-by-pixel density of tree loss events from satellite and field estimates. The relationship between the two variables using linear regression models was then assessed.

4. Results

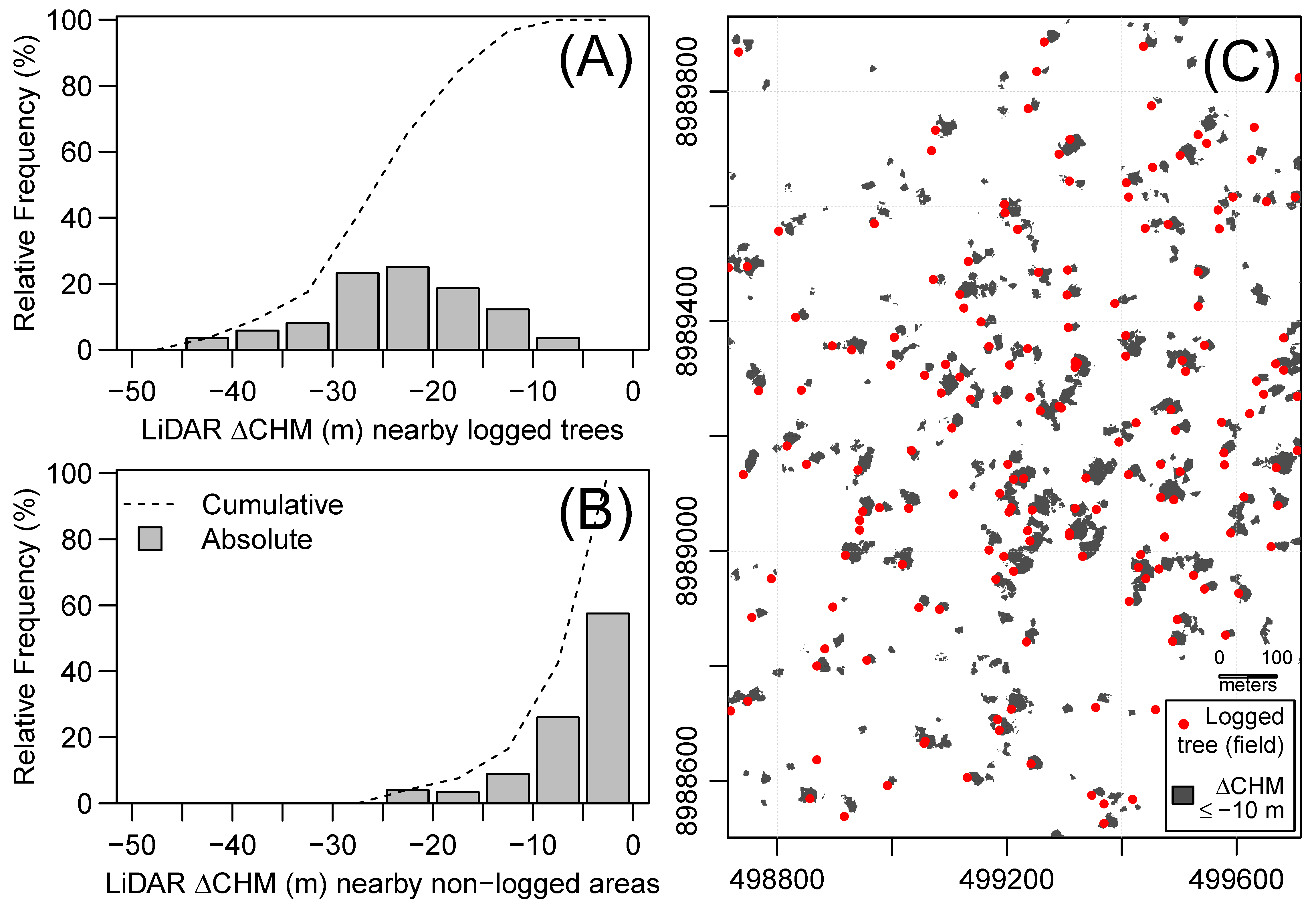
4.1. Detecting Tree Loss Events Using LiDAR Data

We observed LiDAR ΔCHM ranging from −5.6 to −42.2 m, with a mean of −23.5 m, for the ITCs nearby (within 30 m of distance) the 172 logged trees in Jamari National Forest (Figure 3A). For the non-logged areas (n = 146), we noted a distribution of ΔCHM values ranging from −0.3 to −22 m, with a mean of −5.9 m (Figure 3B). This means that, between 2015 and 2017, the largest canopy changes occurred nearby logged trees’ locations. The distributions in Figure 3A,B did not show positive values because we only assessed the most negative height difference in the area’s neighborhood.
We obtained a ΔCHM threshold of −10 m, where 96.5% of the logged trees (n = 166/172) were detected and only 16.4% of the non-logged random areas were misattributed (n = 24/146). Using this threshold, 888 tree loss events (634 trees km−2) were detected between 2015 and 2017 (Figure 3C). This corresponded to a canopy change of 6.15% in terms of area. While this detection rate was larger than the number of logged trees of 172 trees (122 trees km−2), it also included trees that were eventually killed during the logging activities and tree losses from natural mortality that occurred during the studied period. This rate was likely also influenced by the average overestimate of the number of trees of about 30% (Supplementary Material 1). Nevertheless, the detected tree loss events occurred predominantly nearby logged trees’ location, with an average nearest neighbor distance of 25.86 m, while only 10% of the tree loss events were located farther than 50 m from the logged trees (see also Figure 3C).

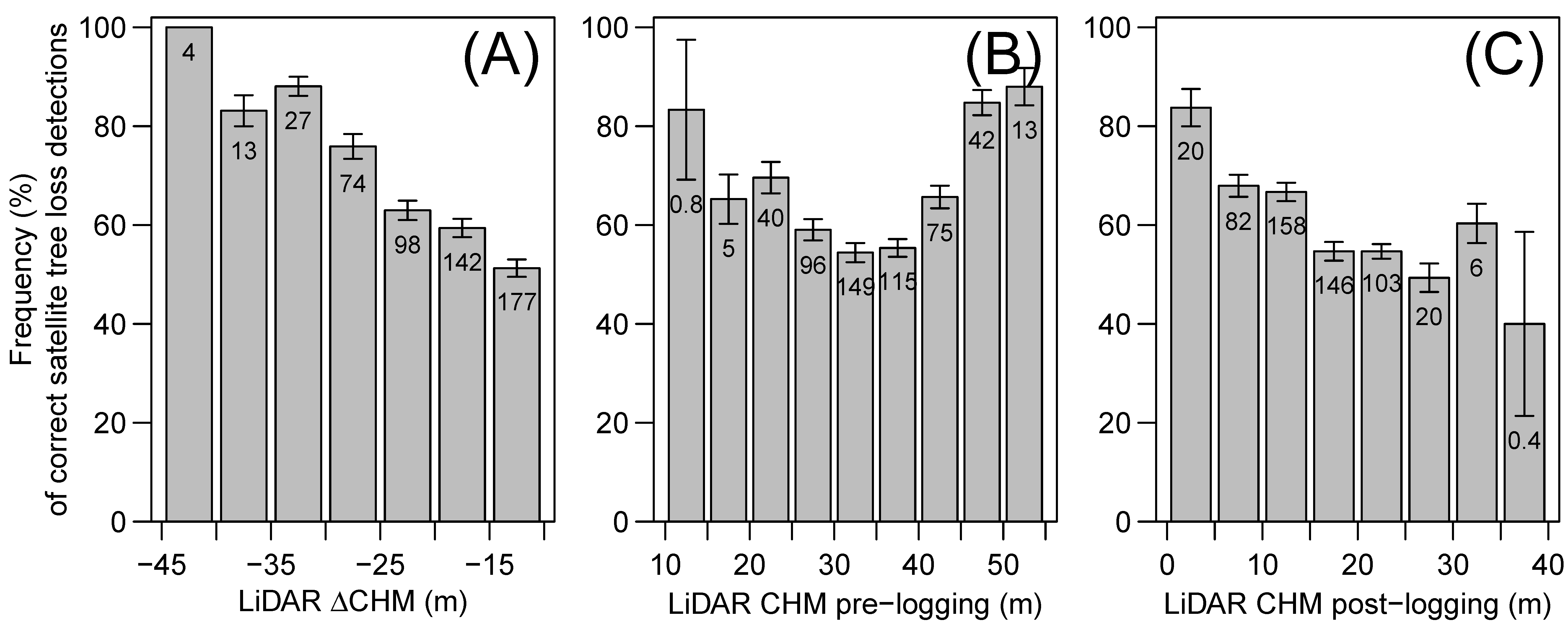
4.2. Detecting Tree Loss Events Using VHR Satellite Data and RF Model

We trained RF models using VHR satellite data to detect tree loss or non-tree loss areas (Figure 4). Overall, we observed that an increase in the cut-off of tree loss occurrence probability (0.5 to 0.95) was associated with an increase in precision (33 to 80%) and a decrease in recall (95 to 23%) (Figure 4A). Given that a useful model requires high precision, we chose a tree loss probability cut-off of 0.85, which resulted in a moderate-to-high precision of 63.9% (95% CI: 62.6%, 65.2%), and a moderate recall of 60.1% (95% CI: 58.7%, 61.4%). Thus, taking the LiDAR map as a reference, on average, 64% of the satellite detections were correct, and more than half (60%) of the total tree losses were detected.
We generated a map using the average of the 30 RF models and a tree loss probability cut-off of 0.85 (Figure 4B). This map detected 357 tree loss events (255 trees km−2), of which 74.5% intersected the tree losses detected in the LiDAR map, and 25.5% did not intersect it (commission errors). Part of these errors should represent actual tree losses captured by the VHR satellite data due to its extended observation period in comparison to LiDAR data (Table 1). We detected 50.8% of the tree loss events from the LiDAR map (omission error of 49.2%). The detections corresponded to 2.55% of canopy area change between 2014 and 2017. Even though, in this map, we only detected 51% of the total tree loss events, the satellite detections were predominantly located nearby LiDAR detections, with a mean nearest neighbor distance of 21.2 m (95% CI: 19.8 m, 22.7 m) (Figure 4C). Moreover, the observed distribution of nearest neighbor distances between the two maps (solid line in Figure 4C) lied beyond the upper-part of the 1% significance CSR envelope (p < 0.01), which meant that the satellite detections were not simply randomly distributed, but were clustered with the LiDAR detections (Figure 4C).
The accuracy of satellite tree loss detections was sensitive to the magnitude of changes in the vertical structure of the canopy and size (height) of the trees (Figure 5). Tree losses with higher ΔCHMs (−45 to −25 m) were more easily detected (>75% frequency) compared with tree losses with lower ΔCHMs (−25 to −10 m) (45 to 60%) (Figure 5A). Tree losses from the tallest trees (≥45 m) were more successfully detected (>80%) than for other height classes (Figure 5B). However, the high accuracy for the shortest trees (10–15 m) was probably associated with the low average number of samples (n = 1) and does not truly mean a higher accuracy for this height class. Finally, tree losses that created deep gap openings (0 to 5 m height above ground) were the most successfully detected (>80%) (Figure 5C).
Variables used in the RF modeling were ranked for importance according to their MDA (Figure 6). The SD of the red band was ranked highest (23% MDA) among all the variables. In general, the SD metrics were ranked higher than the mean metrics, and the most important variables were the SD of the three visible spectrum bands (Red, Green, Blue), followed by the shadow fraction, mean of visible bands, and SD and mean NDVI. Meanwhile, the NIR band and EVI were the least important of the significant variables (p < 0.05). Only the median, max, and number of shadow segments variables did not significantly contribute to the model (p > 0.05).

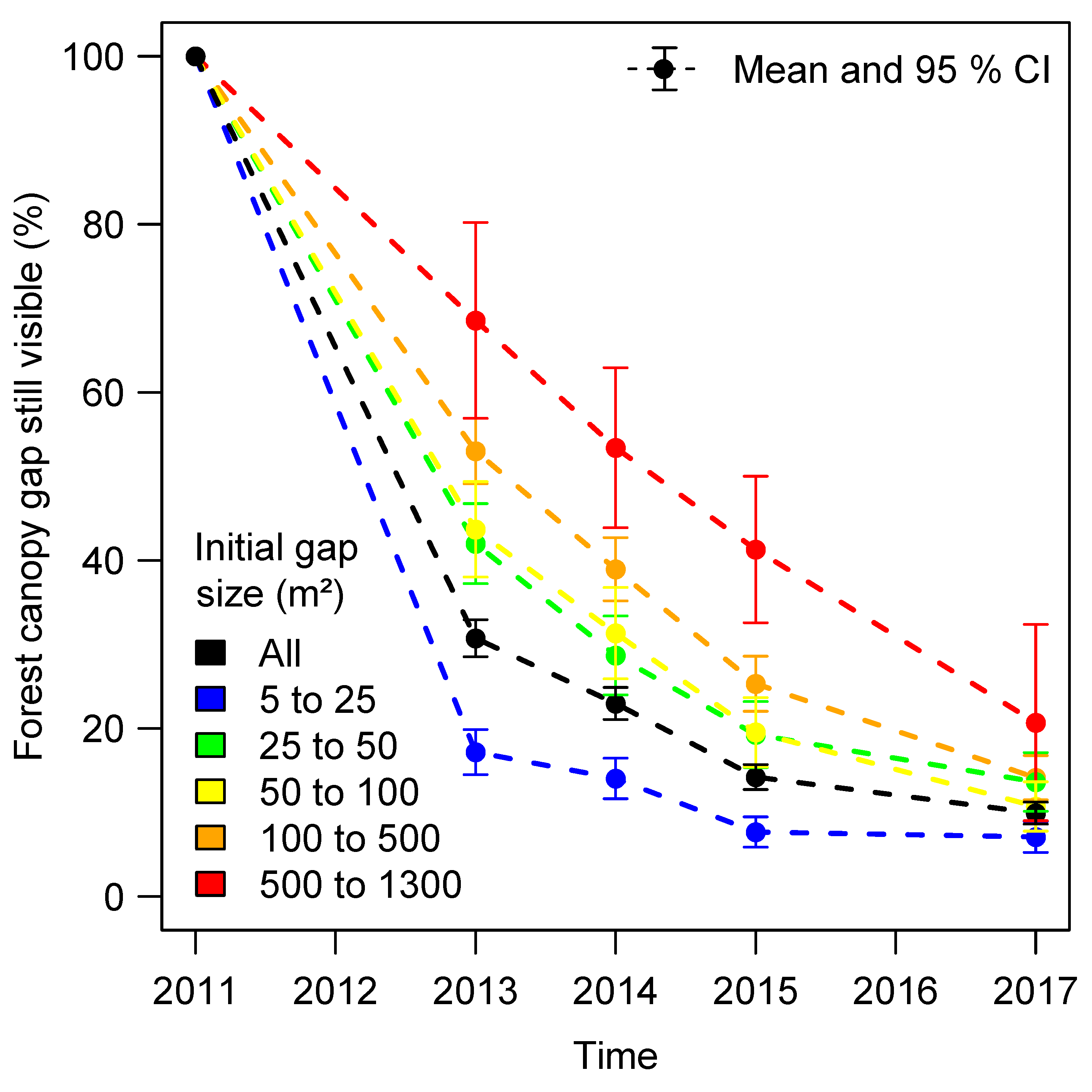
4.3. Tree-Fall Gap Recovery Assessment Using LiDAR Data

We delineated 724 canopy gaps in the 1.04 km2 of forests inside UPA-01 in Jamari National Forest using the LiDAR data of 2011. The detected gaps were predominantly small: 55.3% from 5 to 25 m2, 16.4% from 25 to 50 m2, 8.8% from 50 to 100 m2, 18.5% from 100 to 500 m2, and 1% from 500 to 1300 m2. From 2011 to 2017, the total gap fraction decreased from 4.61 to 1.96%, whereas 63% of the initial gaps completely closed (Figure 7). The average rate of gap filling was 35.4% yr−1 considering all gap sizes and 30% yr−1 when excluding smaller gaps (area < 25 m2). After 1.8 years (2011–2013) and 5.4 years (2011–2017) of recovery, the average gap size consisted of 47% and 13% of their original size, respectively, excluding smaller gaps (area < 25 m2). Therefore, larger gaps were still visible after ~2 years of recovery, but were almost completely closed and invisible after ~5 years.
We found that 23.3% of pixels inside gap areas experienced further height loss over time. These were probably caused by delayed mortality of remaining vegetation, natural disturbances, or the decomposition of trees that were killed during logging activities. The majority of pixels (76.7%), however, showed height gain. We estimated a maximum vertical growth rate of 3.9 m yr−1 from 2011 to 2013 considering only the gap centers. Using this threshold to separate horizontal from vertical tree growth inside gaps, we estimated that horizontal ingrowth (height change >3.9 m) corresponded on average to 21.2% of the height gains. The remaining 78.8% of height gains were due to vertical tree growth, with an average growth rate of 1.65 m yr−1 (SD = 0.6).

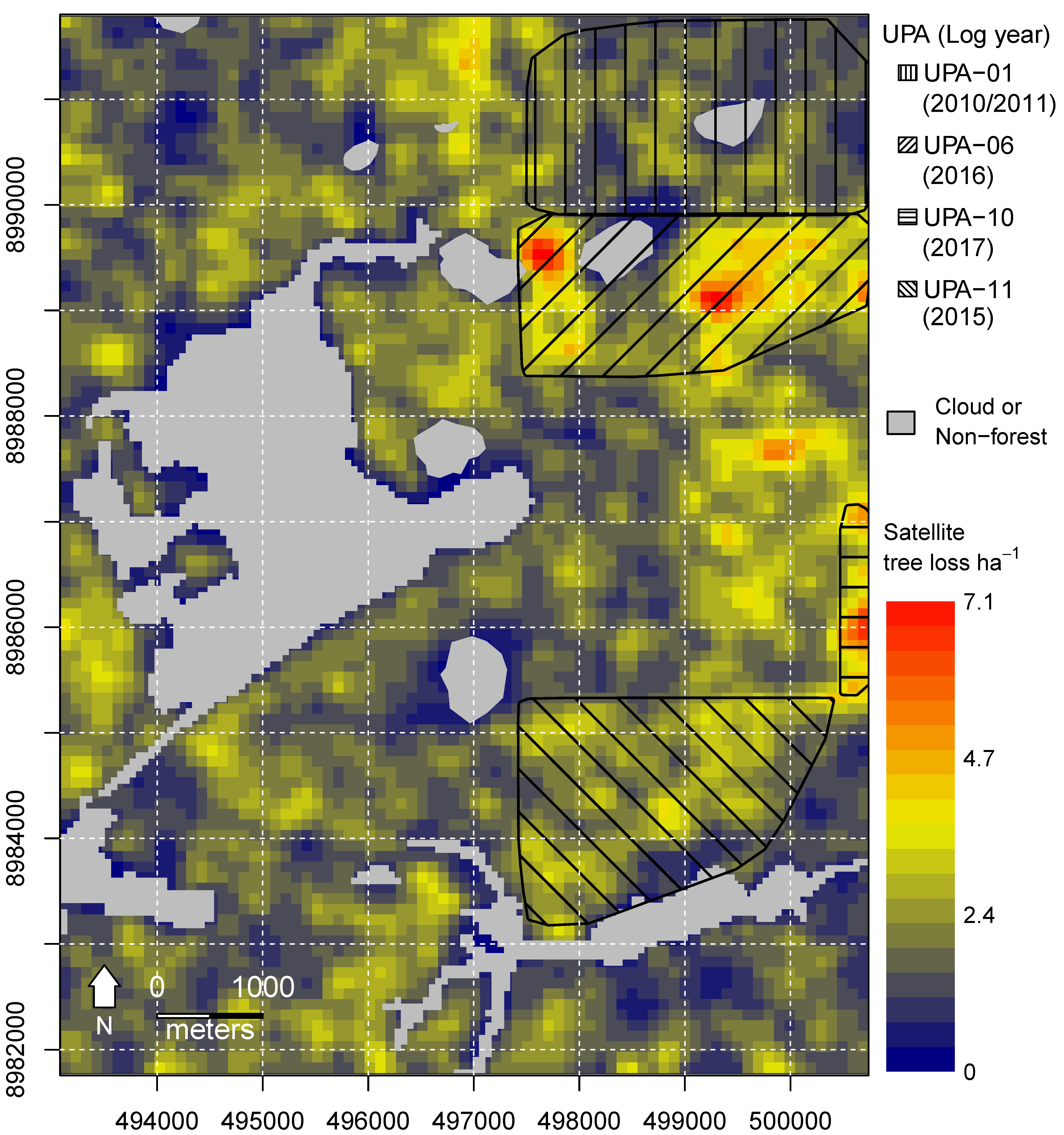
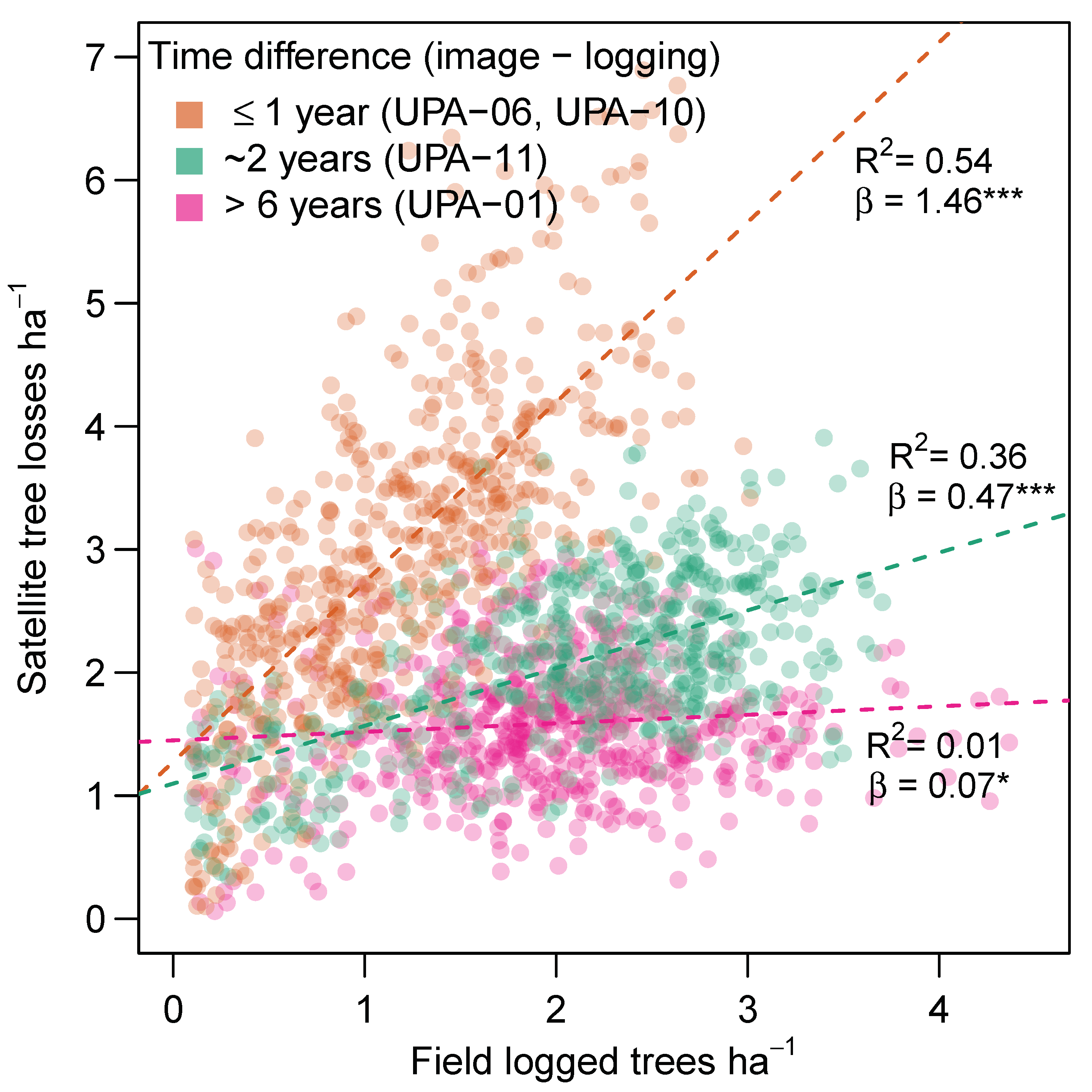
4.4. Landscape Analysis of Satellite-Based Tree Loss Map

Using the VHR satellite data and the RF model, we mapped tree losses over a larger area (76.6 km2) of the Jamari National Forest than covered by LiDAR (Figure 8). We found that tree losses were widespread and only a few areas exhibited hotspots of losses up to 7.1 trees ha−1 (red in Figure 8): two at UPA-06 and one at UPA-10. Another area outside of the UPAs, located at undisturbed forests near UPA-06 and UPA-10, showed an unexpected higher frequency of tree loss (5.15 trees ha−1).
We observed a greater frequency of tree loss events (1.63 to 4.39 trees ha−1) inside UPAs compared to the frequency of field logged trees (1.28 to 2.21 logged trees ha−1) (Table 3). In addition, tree loss events occurred more frequently (3.08 to 4.39 trees ha−1) in the recently logged areas (UPA-06 and UPA-10) compared to the other UPAs, even though they had the lowest frequency of logged trees in the field (1.28 to 1.38 logged trees ha−1). This was clearly seen in Figure 8, where these two UPAs were the only ones with hotspots. Furthermore, the undisturbed forests exhibited a similar but slightly greater frequency of tree loss (1.8 trees ha−1) as UPA-01 (1.63 trees ha−1), but less than the rest of the UPAs. The most likely explanations for the lower frequency of detections in UPA-01 were that the forest in this area had a long time to recover since logging occurred in 2010/2011, and that the logging process removed the tallest trees at the canopy level. Meanwhile, these trees are those that open the largest gaps when they fall. Based on the tree losses over undisturbed forests during the interval between VHR images (2.72 years), and the average number of ITCs (85 trees ha−1), we inferred a canopy turnover time of 129 years. The global forest cover loss product from Landsat data (30 m resolution) did not show any forest loss over the study area.
When we overlaid the kernel density estimates of satellite tree losses and field logged trees of the UPAs, we found that the field logged trees explained part of the satellite tree loss variability for areas that were logged less than one year (R2 = 0.54) and two years (R2 = 0.36) before image acquisition. The same was not verified for areas logged six years before image acquisition (Figure 9). The areas that had been logged up to two years before image acquisition also showed very significant regression slopes (p < 0.001).

5. Discussion

Using a unique dataset of multi-date airborne LiDAR and VHR satellite data (pre- and post-logging), and a tree-by-tree field dataset of georeferenced logged trees, we showed that it is possible to use VHR satellite data to detect canopy tree loss associated with logging. Nonetheless, we advise caution regarding the image acquisition frequency, because it can severely affect how well tree loss can be detected, and thus the suitability to use these data for disturbance monitoring. We discuss each of the scientific questions in the paragraphs below.
Besides these general insights, our findings showed that logging drove pervasive changes in the canopy vertical structure. The estimated height difference threshold (−10 m) that we used to define tree loss using LiDAR data should represent a general approximation of the minimal logging impacts to the forest structure and could be used in other studies for rough estimates of canopy tree loss. However, we recommend additional tests in other study sites for more precise detection. In a study of forest dynamics in Tapajós National Forest, located in central-east of the Brazilian Amazon, Leitold et al. [20] found a mean height difference of −11.7 m corresponding to natural tree-fall events from single or multiple trees. While this value is similar to our height difference threshold, it is only half of the mean height difference that we found. This could indicate that even though logging conducted at Jamari Forest is considered “low-impact”, these human-disturbances cause more drastic changes to the forest structure than small-scale natural disturbances.
Our results show that tree losses associated with logging and other disturbances, most probably natural, can be automatically mapped using VHR satellite imagery and the RF model with an average precision of 64%, while capturing 60% of the events detected by the LiDAR dataset. Even though the accuracy is not optimal, the detected tree losses show a strong spatial correlation with LiDAR detections and logged trees coordinates. Since the model accuracy varied with the model probability cutoff, this parameter must be chosen carefully. It is important to note, however, that our imagery had distinct sun-sensor geometry properties, with a big difference in sun elevation angles between images (~20 degrees), which affected the accuracy. The effects of such differences include the obfuscation of smaller trees by taller trees and potential attribution as a tree loss event. In a scenario where both images have a similar acquisition geometry, we expect an improved detection accuracy. Nevertheless, this result, based on an automatic detection algorithm, advances the visual analysis and manual delineation of tree mortality of Read et al. [11] and Clark et al. [12,13], and opens up new venues for monitoring small-scale disturbances.
The sensitivity of our VHR satellite tree loss detection methodology increased with the presence of more pervasive changes to the canopy, such as bigger gap openings and loss of the tallest trees. Because large trees store most of the aboveground biomass in tropical forests [46], these disturbances are likely the most impactful to carbon loss. The accurate detection of these bigger events enables the identification of disturbance hotspots, where multiple small-scale events may be occurring locally and simultaneously. Furthermore, our results confirmed the possibility of detecting some of the tree-falls that do not create gaps following Brokaw’s definition of ≤2 m height above ground [39].
Seasonality effects on plant phenology can reduce our ability to extract biophysical information from remote sensing observations in the Amazon, e.g., [47]. Without tree-by-tree phenology field data to support a proper analysis, we are unable to determine the exact impact of seasonality on our detection, but we expect that it may have a minor to moderate impact. Trees that are leafless in one of the two images, or have completely different colors, due to flowering, could indeed be erroneously attributed as a tree loss event. However, if these effects occur roughly at random across the forest, because of the high tree species diversity in tropical forests, they would not prevent the detection of hotspots associated with disturbance. This is because these occur more clustered in space and time. A way to reduce seasonal effects on detection is to fix the multi-year imagery analysis within a fixed period (e.g., dry season).
The most important VHR satellite metrics for tree loss detection were the SD of the reflectance of the visible bands and the shadow fraction and amongst those, especially the red band. The fact that these SD metrics were more important than the mean metrics suggests that there were marked increases in spectral variability in tree loss areas due to logging. This variability is associated with shadows cast by nearby trees, and the signal mixture from non-photosynthetically active responses of leaves, branches, and trunks, and possibly exposed soil. For the same reason, the shadow fraction turned out to be one of the most important variables. Other studies have also shown that shadow was related to tree mortality, e.g., [33]. However, although shadow metrics were important in our study, their performance can vary in other study areas and across sensors, depending on the view-illumination geometry during image acquisition.
Findings of this study also showed that tree loss detection depends on the time difference between disturbance occurrence and image acquisition, ideally of less than two years. This is explained by the slower in-filling and longer persistence of bigger gaps in the forest, up to five years or more, in comparison to smaller gaps (<25 m2), which close up very rapidly. In either case, the lateral ingrowth was an important process for gap filling, especially for the smaller gaps. These results are corroborated by the findings of Hunter et al. [40], which also show a strong influence of gap size on closure rates; as well as similar, or slightly higher, gap persistence estimates in two Amazonian forests sites: Ducke (8.1 years) and Tapajós (9.1 years). Our estimates of annual tree height gains inside gaps (mean = 1.65 m yr−1, max. = 3.9 m yr−1) were slightly higher than field observations of pioneer species commonly found in tropical forest gaps (e.g., Cecropia spp., mean = 1.2–1.5 m yr−1, max 2–3 m yr−1) [48]. Nevertheless, hotspots were evident in our map in areas with time differences, between disturbance and image acquisition, up to one year. The implication of these findings for small-scale disturbances’ monitoring is that disturbances associated with small gaps will most probably be underestimated unless annual imagery is being used.
Our satellite-based map of tree loss disturbances was spatially coherent. It showed a greater density of events in selective logging disturbed forests than in undisturbed forests. However, the rate of tree losses was up to three times greater than the on-the-ground determined logging rate and depended on the time between disturbance and image acquisition. This is probably related to additional damage caused by logging onto the adjacent trees and natural mortality events. In addition, potential explanations for the observed hotspot of tree loss estimates outside the UPAs include: (i) the presence of a road that crosses that exact location—visible in the pre-logging image—which was likely used for timber transportation; (ii) preparation activities (e.g., opening of trails) for exploration of this area in the near future; and (iii) enhanced and/or delayed natural mortality associated with human-disturbances during the opening of the roads. Our estimate of canopy turnover time (129 years) was lower than the estimate of Hunter et al. [40] for canopy trees at two Central-East Amazon sites (300–370 years). This was probably because of our relatively high rate of omission errors (~40%). Nevertheless, we expect that the presented mapping approach using VHR satellite data can also be useful for the detection of hotspots of natural disturbance.
As a comparison exercise, we acquired and visualized the global forest cover loss product from Hansen et al. [44] obtained from Landsat data (30 m resolution), and it did not show any forest loss over the study area, even over the managed forests. We believe that this indicates the potential advantages of using VHR imagery for small-scale disturbance detection and monitoring.
A caveat regarding the current mapping approach is the requirement of LiDAR data to calibrate the model before extending the VHR satellite estimates into larger areas. However, as shown in this study, LiDAR data acquisition in small areas can be used for this purpose. For example, in our experiment, the LiDAR calibration area covered 1.4 km2 (1 by 1.4 km), while the VHR satellite imagery covered 76.6 km2 of forests. Hence, the satellite imagery area was 55 times bigger than the LiDAR area, and has the potential to cover much larger areas, such as >5000 km2, with a single-pass of either WorldView-2 or GeoEye-1 satellites. In addition, further studies can take advantage of the recent technological advances associated with unmanned aerial vehicles to cover larger areas at reduced costs, with caution to current constraints, e.g., space for taking off, landing, and piloting in dense forest environments. On the other hand, the current mapping approach using an RF model was primarily used as a benchmark to test the VHR imagery potential; other machine learning or statistical approaches, or, perhaps, simpler methods that bypass the calibration step (e.g., thresholding), are possible and should be tested for a more general application over different areas. In the absence of LiDAR data to be used as a reference for model training, other sources of publicly available training data should be considered. For instance, tree loss data at an individual level from forest inventories obtained by the Brazilian Forest Service and/or forest management concessionaires can be useful.
Although the study used WorldView-2 and GeoEye-1 satellite imagery for the experiment, the current method is not, by any means, restricted to these spectral data. The mapping approach could be applied with other available VHR satellite data, e.g., Ikonos, QuickBird, WorldView-3, WorldView-4, and Planet satellites, or, indeed, from future satellites to be launched. Moreover, the combined use of multi-sensors should be required to adapt the current method for detecting canopy tree loss and recovery at broader scales. In this context, the advent of the nanosatellite constellations is an alternative to obtain low-cost data at a very high spatial and temporal resolution. Band positioning and bandwidth should be considered in instrument selection for analysis.

6. Conclusions

Logging activities disturb large areas in Amazon forests every year, affecting flora and fauna diversity, impacting forest structure and carbon balance, and enhancing fire probability. To address the remote sensing challenges of detecting canopy tree loss associated with logging, we explored the use of multi-date VHR satellite imagery (≤1 m resolution) and airborne LiDAR to detect these events. Logging caused pervasive changes in the canopy vertical structure, with a mean of −23.5 m, but applying a simple LiDAR height difference threshold of −10 m was sufficient to map almost all the logged trees. We show that canopy tree losses associated with logging can be detected using VHR satellite imagery and an automated machine-learning method with an average precision of 64%. Events associated with large gap openings or tall trees were most successfully detected. The standard deviation metrics were the most important for the mapping, because they indicate change in spectral variability with the tree losses. The detection was also dependent on the time difference between the disturbance occurrence and the image acquisition, thus annual imagery acquisition is highly recommended. Our study showed the potential of VHR satellite imagery for monitoring the logging in tropical forests and detecting hotspots of natural forest disturbance with a low cost at the regional scale. Future research can build upon our work and improve the accuracy of detection using pairs of images with similar sun-sensor geometry properties, and testing additional satellite-based metrics (e.g., texture) and alternative modeling approaches.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/11/7/817/s1: Supplementary Material 1: Individual tree crown (ITC) delineation; Table S1: ITC delineation assessment per plot for VHR satellite data; Table S2: ITC delineation assessment per plot for airborne LiDAR data.

Author Contributions

All authors contributed to the research conceptualization; C.J.L. provided resources (LiDAR and field data) for the experiment; R.D., O.L.P, E.G., and F.H.W. conducted the formal analysis; R.D. wrote the first draft of the manuscript; All authors reviewed and edited the manuscript and provided critical feedback on the paper’s discussion and improvement; L.E.O.C.A. and O.L.P. supervised the research.

Funding

Ricardo Dalagnol was supported by the São Paulo Research Foundation—FAPESP, Brazil, grants 2015/22987-7 and 2017/15257-8. Oliver Phillips and Emanuel Gloor were supported by the Natural Environment Research Council—NERC, UK, BIO-RED grant NE/N012542/1 and ARBOLES grant NE/S011811/1. Lênio S. Galvão was supported by the Brazilian National Council for Scientific and Technological Development—CNPq, grant 301486/2017-4. Fabien H. Wagner was supported by the FAPESP, grants 2015/50484-0 and 2016/17652-9. Luiz Aragão was supported by the CNPq, grant 305054/2016-3.

Acknowledgments

We thank Devon I. Libby and Digital Globe Foundation for providing the very high resolution satellite imagery which made this study possible. We thank the Brazilian Forest Service, and the Sustainable Landscapes Brazil project supported by the Brazilian Agricultural Research Corporation (EMBRAPA), the US Forest Service, USAID, and the US Department of State, for providing the airborne LiDAR data. Finally, we thank four anonymous referees whose helpful comments and suggestions helped improve and clarify this manuscript.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Contreras-Hermosilla, A.; Doornbosch, R.; Lodge, M. The Economics of Illegal Logging and Associated Trade. Round Table Sustain. Dev. 2007, 33, 8–9. [Google Scholar]
  2. Lawson, S.; Macfaul, L. Illegal Logging and Related Trade: Indicators of the Global Response; Chatham House Rep. 132 + xix; Chatham House: London, UK, 2010. [Google Scholar]
  3. Asner, G.P.; Knapp, D.E.; Broadbent, E.N.; Oliveira, P.J.C.; Keller, M.; Silva, J.N. Selective Logging in the Brazilian Amazon. Science 2005, 310, 480–482. [Google Scholar] [CrossRef] [PubMed]
  4. Aragão, L.E.O.C.; Poulter, B.; Barlow, J.B.; Anderson, L.O.; Malhi, Y.; Saatchi, S.; Phillips, O.L.; Gloor, E. Environmental change and the carbon balance of Amazonian forests. Biol. Rev. 2014, 89, 913–931. [Google Scholar] [CrossRef] [PubMed]
  5. Cochrane, M.A. Fire science for rainforests. Nature 2003, 421, 913–919. [Google Scholar] [CrossRef]
  6. LaManna, J.A.; Martin, T.E. Logging impacts on avian species richness and composition differ across latitudes and foraging and breeding habitat preferences. Biol. Rev. 2017, 92, 1657–1674. [Google Scholar] [CrossRef] [PubMed]
  7. Osazuwa-Peters, O.L.; Jiménez, I.; Oberle, B.; Chapman, C.A.; Zanne, A.E. Selective logging: Do rates of forest turnover in stems, species composition and functional traits decrease with time since disturbance? A 45 year perspective. For. Ecol. Manag. 2015, 357, 10–21. [Google Scholar] [CrossRef]
  8. Buchanan, G.M.; Beresford, A.E.; Hebblewhite, M.; Escobedo, F.J.; De Klerk, H.M.; Donald, P.F.; Escribano, P.; Koh, L.; Martínez-López, J.; Pettorelli, N.; et al. Free satellite data key to conservation. Science 2018, 361, 139–140. [Google Scholar]
  9. Stone, T.A.; Lefebvre, P. Using multi-temporal satellite data to evaluate selective logging in Pará, Brazil. Int. J. Remote Sens. 1998, 19, 2517–2526. [Google Scholar] [CrossRef]
  10. Wang, Y.; Ziv, G.; Adami, M.; Mitchard, E.; Batterman, S.A.; Buermann, W.; Schwantes, B.; Hur, B.; Junior, M.; Matias, S.; et al. Mapping tropical disturbed forests using multi-decadal 30 m optical satellite imagery. Remote Sens. Environ. 2019, 221, 474–488. [Google Scholar] [CrossRef]
  11. Read, J.M.; Clark, D.B.; Venticinque, E.M.; Moreira, M.P. Application of merged 1-m and 4-m resolution satellite data to research and management in tropical forests. J. Appl. Ecol. 2003, 40, 592–600. [Google Scholar] [CrossRef]
  12. Clark, D.B.; Castro, C.S.; Alvarado, L.D.A.; Read, J.M. Quantifying mortality of tropical rain forest trees using high-spatial-resolution satellite data. Ecol. Lett. 2004, 7, 52–59. [Google Scholar] [CrossRef]
  13. Clark, D.B.; Read, J.M.; Clark, M.L.; Cruz, A.M.; Dotti, M.F.; Clark, D.A. Application of 1-m and 4-m resolution satellite data to ecological studies of tropical rain forests. Ecol. Appl. 2004, 14, 61–74. [Google Scholar] [CrossRef]
  14. Kellner, J.R.; Hubbell, S.P. Adult mortality in a low-density tree population using high-resolution remote sensing. Ecology 2017, 98, 1700–1709. [Google Scholar] [CrossRef] [PubMed]
  15. Wulder, M.A.; White, J.C.; Coops, N.C.; Butson, C.R. Multi-temporal analysis of high spatial resolution imagery for disturbance monitoring. Remote Sens. Environ. 2008, 112, 2729–2740. [Google Scholar] [CrossRef]
  16. Guo, Q.; Kelly, M.; Gong, P.; Liu, D. An Object-Based Classification Approach in Mapping Tree Mortality Using High Spatial Resolution Imagery. GISci. Remote Sens. 2007, 44, 24–47. [Google Scholar] [CrossRef]
  17. Asner, G.P.; Powell, G.V.N.; Mascaro, J.; Knapp, D.E.; Clark, J.K.; Jacobson, J.; Kennedy-Bowdoin, T.; Balaji, A.; Paez-Acosta, G.; Victoria, E.; et al. High-resolution forest carbon stocks and emissions in the Amazon. Proc. Natl. Acad. Sci. USA 2010, 107, 16738–16742. [Google Scholar] [CrossRef] [PubMed]
  18. d’Oliveira, M.V.N.; Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.E. Estimating forest biomass and identifying low-intensity logging areas using airborne scanning lidar in Antimary State Forest, Acre State, Western Brazilian Amazon. Remote Sens. Environ. 2012, 124, 479–491. [Google Scholar] [CrossRef]
  19. Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J.; d’Oliveira, M.V.N.; Keller, M. Monitoring selective logging in western amazonia with repeat lidar flights. Remote Sens. Environ. 2014, 151, 157–165. [Google Scholar] [CrossRef]
  20. Leitold, V.; Morton, D.C.; Longo, M.; dos-Santos, M.N.; Keller, M.; Scaranello, M. El Niño drought increased canopy turnover in Amazon forests. New Phytol. 2018, 219, 959–971. [Google Scholar] [CrossRef]
  21. IBGE. Mapa Temático-Mapa de Vegetação do Brasil; Brazilian Institute of Geography and Statistics: Rio de Janeiro, Brazil, 2006. [Google Scholar]
  22. Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
  23. USGS Shuttle Radar Topography Mission, 1 Arc Second, v.2.1; United States Geological Survey: Pasadena, LA, USA, 2006.
  24. Isenburg, M. LAStools—Efficient Tools for LiDAR Processing v.3.1.1; Rapidlasso: Gilching, Germany, 2018. [Google Scholar]
  25. McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization v. 3.6; United States Department of Agriculture: Seattle, WA, USA, 2016.
  26. Silva, C.A.; Crookston, N.L.; Hudak, A.T.; Vierling, L.A.; Klauberg, C.; Cardil, A. rLiDAR: LiDAR Data Processing and Visualization v.0.1.1; NASA Goddard Space Flight Center: Greenbelt, ML, USA, 2017.
  27. Vermote, E.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcrette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum (6S). 6S User Guide Version 2. Appendix III: Description of the subroutines. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
  28. Grizonnet, M.; Michel, J.; Poughon, V.; Inglada, J.; Savinaud, M.; Cresson, R. Orfeo ToolBox: Open source processing of remote sensing images. Open Geospat. Data Softw. Stand. 2017, 2, 15. [Google Scholar] [CrossRef]
  29. Fasbender, D.; Radoux, J.; Bogaert, P. Bayesian data fusion for adaptable image pansharpening. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1847–1857. [Google Scholar] [CrossRef]
  30. Leutner, B.; Horning, N.; Schwalb-Willmann, J. RStoolbox: Tools for Remote Sensing Data Analysis v0.2.1; University of Würzburg: Würzburg, Germany, 2018. [Google Scholar]
  31. Rouse, J.W.; Hass, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. Third Earth Resour. Technol. Satell. Symp. 1974, 1, 301–317. [Google Scholar]
  32. Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
  33. Anderson, L.O.; Malhi, Y.; Aragão, L.E.O.C.; Ladle, R.; Arai, E.; Barbier, N.; Phillips, O. Remote sensing detection of droughts in Amazonian forest canopies. New Phytol. 2010, 187, 733–750. [Google Scholar] [CrossRef]
  34. Plowright, A. ForestTools: Analyzing Remotely Sensed Forest Data v.0.2; University of British Columbia: Vancouver, BC, Canada, 2018. [Google Scholar]
  35. Breiman, L.E.O. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  36. Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
  37. Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Patterns: Methodology and Applications with R, 1st ed.; Chapman and Hall/CRC Press: London, UK, 2015; ISBN 9781482210200. [Google Scholar]
  38. Archer, E. rfPermute: Estimate Permutation p-Values for Random Forest Importance Metrics v.2.1.6; National Oceanic and Atmospheric Administration: Maryland, ML, USA, 2018.
  39. Brokaw, N.V.L. The Definition of Treefall Gap and Its Effect on Measures of Forest Dynamics. Biotropica 1982, 14, 158. [Google Scholar] [CrossRef]
  40. Hunter, M.O.; Keller, M.; Morton, D.; Cook, B.; Lefsky, M.; Ducey, M.; Saleska, S.; De Oliveira, R.C.; Schietti, J.; Zang, R. Structural dynamics of tropical moist forest gaps. PLoS ONE 2015, 10, 1–19. [Google Scholar] [CrossRef]
  41. Goulamoussène, Y.; Bedeau, C.; Descroix, L.; Linguet, L.; Hérault, B. Environmental control of natural gap size distribution in tropical forests. Biogeosciences 2017, 14, 353–364. [Google Scholar] [CrossRef]
  42. Lobo, E.; Dalling, J.W. Spatial scale and sampling resolution affect measures of gap disturbance in a lowland tropical forest: Implications for understanding forest regeneration and carbon storage. Proc. Biol. Sci. 2014, 281, 20133218. [Google Scholar] [CrossRef]
  43. Diggle, P. A Kernel Method for Smoothing Point Process Data. Appl. Stat. 1985, 34, 138. [Google Scholar] [CrossRef]
  44. Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
  45. INPE PRODES: Deforestation Monitoring Program; National Institute for Space Research: São José dos Campos, Brazil, 2018.
  46. Bastin, J.F.; Rutishauser, E.; Kellner, J.R.; Saatchi, S.; Pélissier, R.; Hérault, B.; Slik, F.; Bogaert, J.; De Cannière, C.; Marshall, A.R.; et al. Pan-tropical prediction of forest structure from the largest trees. Glob. Ecol. Biogeogr. 2018, 27, 1366–1383. [Google Scholar] [CrossRef]
  47. de Moura, Y.M.; Galvão, L.S.; Hilker, T.; Wu, J.; Saleska, S.; do Amaral, C.H.; Nelson, B.W.; Lopes, A.P.; Wiedeman, K.K.; Prohaska, N.; et al. Spectral analysis of amazon canopy phenology during the dry season using a tower hyperspectral camera and MODIS observations. ISPRS J. Photogramm. Remote Sens. 2017, 131, 52–64. [Google Scholar] [CrossRef]
  48. Clark, D.A.; Clark, D.B. Getting to the canopy: Tree height growth in a neotropical rain forest. Ecology 2001, 82, 1460–1472. [Google Scholar] [CrossRef]
Remotesensing 11 00817 g001 550
Figure 1. Study area at the Jamari National Forest, Rondônia state, Brazil. The background of the left image is a true color composite from the GeoEye-1 satellite acquired on 02 July 2017 (UTM, datum WGS-84). The red and blue rectangles represent the areas A and B covered by the LiDAR datasets, which were analyzed in Section 3.1 and Section 3.3, respectively. The black lines represent the boundaries of the UPAs. The satellite image is courtesy of the DigitalGlobe Foundation.
Figure 1. Study area at the Jamari National Forest, Rondônia state, Brazil. The background of the left image is a true color composite from the GeoEye-1 satellite acquired on 02 July 2017 (UTM, datum WGS-84). The red and blue rectangles represent the areas A and B covered by the LiDAR datasets, which were analyzed in Section 3.1 and Section 3.3, respectively. The black lines represent the boundaries of the UPAs. The satellite image is courtesy of the DigitalGlobe Foundation.
Remotesensing 11 00817 g001
Remotesensing 11 00817 g002 550
Figure 2. Main steps of the data processing and analyses.
Figure 2. Main steps of the data processing and analyses.
Remotesensing 11 00817 g002
Remotesensing 11 00817 g003 550
Figure 3. Tree loss detection using LiDAR ΔCHM in the Jamari National Forest over the UPA-06. Relative frequency of the most negative ΔCHM within a 30 m radius of (A) logged trees and (B) non-logged areas. (C) LiDAR-based tree loss map considering ΔCHM ≤ −10 m (UTM, datum WGS-84).
Figure 3. Tree loss detection using LiDAR ΔCHM in the Jamari National Forest over the UPA-06. Relative frequency of the most negative ΔCHM within a 30 m radius of (A) logged trees and (B) non-logged areas. (C) LiDAR-based tree loss map considering ΔCHM ≤ −10 m (UTM, datum WGS-84).
Remotesensing 11 00817 g003
Remotesensing 11 00817 g004 550
Figure 4. Tree loss detection using VHR satellite data and RF model in the Jamari National Forest over the UPA-06. (A) Detection accuracy as a function of the tree loss probability cut-off. (B) Satellite-based tree loss map considering a tree loss probability ≥0.85 (UTM, datum WGS-84). (C) Nearest neighbor distances between satellite and LiDAR tree loss detections, as a function of distance (m). The gray area represents a CSR envelope with a 1% significance level (n = 199).
Figure 4. Tree loss detection using VHR satellite data and RF model in the Jamari National Forest over the UPA-06. (A) Detection accuracy as a function of the tree loss probability cut-off. (B) Satellite-based tree loss map considering a tree loss probability ≥0.85 (UTM, datum WGS-84). (C) Nearest neighbor distances between satellite and LiDAR tree loss detections, as a function of distance (m). The gray area represents a CSR envelope with a 1% significance level (n = 199).
Remotesensing 11 00817 g004
Remotesensing 11 00817 g005 550
Figure 5. Relative frequency of correct satellite tree loss detections for intervals of (A) LiDAR CHM height differences (ΔCHM), (B) LiDAR CHM pre-logging, and (C) LiDAR CHM post-logging. Mean and error bars (95% confidence interval) were calculated considering the 30 model runs. Numbers inside bars represent the average number of ITCs within that class among the 30 model runs.
Figure 5. Relative frequency of correct satellite tree loss detections for intervals of (A) LiDAR CHM height differences (ΔCHM), (B) LiDAR CHM pre-logging, and (C) LiDAR CHM post-logging. Mean and error bars (95% confidence interval) were calculated considering the 30 model runs. Numbers inside bars represent the average number of ITCs within that class among the 30 model runs.
Remotesensing 11 00817 g005
Remotesensing 11 00817 g006 550
Figure 6. Variables’ importance derived from the RF model using VHR satellite data to map tree loss events in Jamari National Forest ranked by their MDA. SD corresponds to the standard deviation.
Figure 6. Variables’ importance derived from the RF model using VHR satellite data to map tree loss events in Jamari National Forest ranked by their MDA. SD corresponds to the standard deviation.
Remotesensing 11 00817 g006
Remotesensing 11 00817 g007 550
Figure 7. Filing of forest canopy gaps over time (2011 to 2017) in Jamari National Forest (UPA-01), as a function of the initial gap size class (m2).
Figure 7. Filing of forest canopy gaps over time (2011 to 2017) in Jamari National Forest (UPA-01), as a function of the initial gap size class (m2).
Remotesensing 11 00817 g007
Remotesensing 11 00817 g008 550
Figure 8. Satellite-based tree loss map during 2014–2017 for a section of 76.6 km2 inside the Jamari National Forest (UTM, datum WGS-84). The background corresponds to the isotropic kernel-smooth density of satellite-based tree losses per hectare. Black lines are the boundaries of the UPAs.
Figure 8. Satellite-based tree loss map during 2014–2017 for a section of 76.6 km2 inside the Jamari National Forest (UTM, datum WGS-84). The background corresponds to the isotropic kernel-smooth density of satellite-based tree losses per hectare. Black lines are the boundaries of the UPAs.
Remotesensing 11 00817 g008
Remotesensing 11 00817 g009 550
Figure 9. Relationship between satellite-based tree loss and field logged trees per hectare in the UPAs labeled by the time difference (years) between the logging and last image acquisition (2017). Each point represents a pixel of 100 × 100 m (1 ha) from which the estimates are extracted. Lines represent linear regression models between the two variables. Significance levels for regression slopes (β) are represented by asterisks: * ≤ 0.05, ** ≤ 0.01, and *** ≤ 0.001.
Figure 9. Relationship between satellite-based tree loss and field logged trees per hectare in the UPAs labeled by the time difference (years) between the logging and last image acquisition (2017). Each point represents a pixel of 100 × 100 m (1 ha) from which the estimates are extracted. Lines represent linear regression models between the two variables. Significance levels for regression slopes (β) are represented by asterisks: * ≤ 0.05, ** ≤ 0.01, and *** ≤ 0.001.
Remotesensing 11 00817 g009
Table
Table 1. Acquisition details of Airborne LiDAR and VHR satellite data used for tree loss analyses.
Table 1. Acquisition details of Airborne LiDAR and VHR satellite data used for tree loss analyses.
InformationLiDAR Date 1LiDAR Date 2Satellite Date 1Satellite Date 2
SensorLaser scan Optech 3100Laser scan Optech ALTM GeminiWorldView-2 satelliteGeoEye-1 satellite
Acquisition date21 Sep 201520 Apr 201710 Oct 201402 Jul 2017
Acquisition altitude750 m700 m770 km770 km
Scan frequency100 kHz100 kHz--
Off-nadir angle15°15°26°20°
View elevation--60°68°
View azimuth--74°64°
Sun elevation--69°49°
Sun azimuth--85°38°
Data type, bands, and spatial resolutionPoint cloud (x,y,z) with 33.6 points m−2Point cloud (x,y,z) with 12 points m−2PAN - 0.5 m;
Spectral - 2.4 m: coastal, B, G, Y, R, Red edge, NIR-1, NIR-2		PAN - 0.5 m;
Spectral - 1.8 m: B, G, R, NIR
PAN = Panchromatic; B = blue; G = green; Y = yellow; R = red; NIR = Near infrared.
Table
Table 2. Acquisition details of Airborne LiDAR data used for gap recovery analysis.
Table 2. Acquisition details of Airborne LiDAR data used for gap recovery analysis.
Information20112013201420152017
Laser Scan SensorOptech 3100Optech, OrionTrimble, Harrier 68iOptech 3100Optech ALTM Gemini
Acquisition Date17 Nov 201120 Sep 201309 Oct 201421 Sep 201520 Apr 2017
Acquisition Altitude (m)850853500750700
Scan Frequency59.8 kHz67.5 kHz400 kHz100 kHz100 kHz
Off-Nadir Angle11.1°11.1°15°15°15°
Point Cloud Density m−215.4315.4830.3933.6312
Table
Table 3. Frequency of satellite-based tree loss events and field logged trees per hectare for the UPAs and undisturbed forests.
Table 3. Frequency of satellite-based tree loss events and field logged trees per hectare for the UPAs and undisturbed forests.
RegionArea
(ha)		Satellite – 2017
(Tree Losses ha−1)		Field – Multiple Years
(Logged Trees ha−1)
UPA-01—Logged in 2010/20115541.632.08
UPA-11—Logged in 20154952.152.21
UPA-06—Logged in 20164263.081.28
UPA-10—Logged in 2017474.391.38
Undisturbed Forest50521.80-

Share and Cite

MDPI and ACS Style

Dalagnol, R.; Phillips, O.L.; Gloor, E.; Galvão, L.S.; Wagner, F.H.; Locks, C.J.; Aragão, L.E.O.C. Quantifying Canopy Tree Loss and Gap Recovery in Tropical Forests under Low-Intensity Logging Using VHR Satellite Imagery and Airborne LiDAR. Remote Sens. 2019, 11, 817. https://doi.org/10.3390/rs11070817

AMA Style

Dalagnol R, Phillips OL, Gloor E, Galvão LS, Wagner FH, Locks CJ, Aragão LEOC. Quantifying Canopy Tree Loss and Gap Recovery in Tropical Forests under Low-Intensity Logging Using VHR Satellite Imagery and Airborne LiDAR. Remote Sensing. 2019; 11(7):817. https://doi.org/10.3390/rs11070817

Chicago/Turabian Style

Dalagnol, Ricardo, Oliver L. Phillips, Emanuel Gloor, Lênio S. Galvão, Fabien H. Wagner, Charton J. Locks, and Luiz E. O. C. Aragão. 2019. "Quantifying Canopy Tree Loss and Gap Recovery in Tropical Forests under Low-Intensity Logging Using VHR Satellite Imagery and Airborne LiDAR" Remote Sensing 11, no. 7: 817. https://doi.org/10.3390/rs11070817

APA Style

Dalagnol, R., Phillips, O. L., Gloor, E., Galvão, L. S., Wagner, F. H., Locks, C. J., & Aragão, L. E. O. C. (2019). Quantifying Canopy Tree Loss and Gap Recovery in Tropical Forests under Low-Intensity Logging Using VHR Satellite Imagery and Airborne LiDAR. Remote Sensing, 11(7), 817. https://doi.org/10.3390/rs11070817

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop