Spatial and Temporal Monitoring of Pasture Ecological Quality: Sentinel-2-Based Estimation of Crude Protein and Neutral Detergent Fiber Contents
Abstract
1. Introduction
2. Materials and Methods
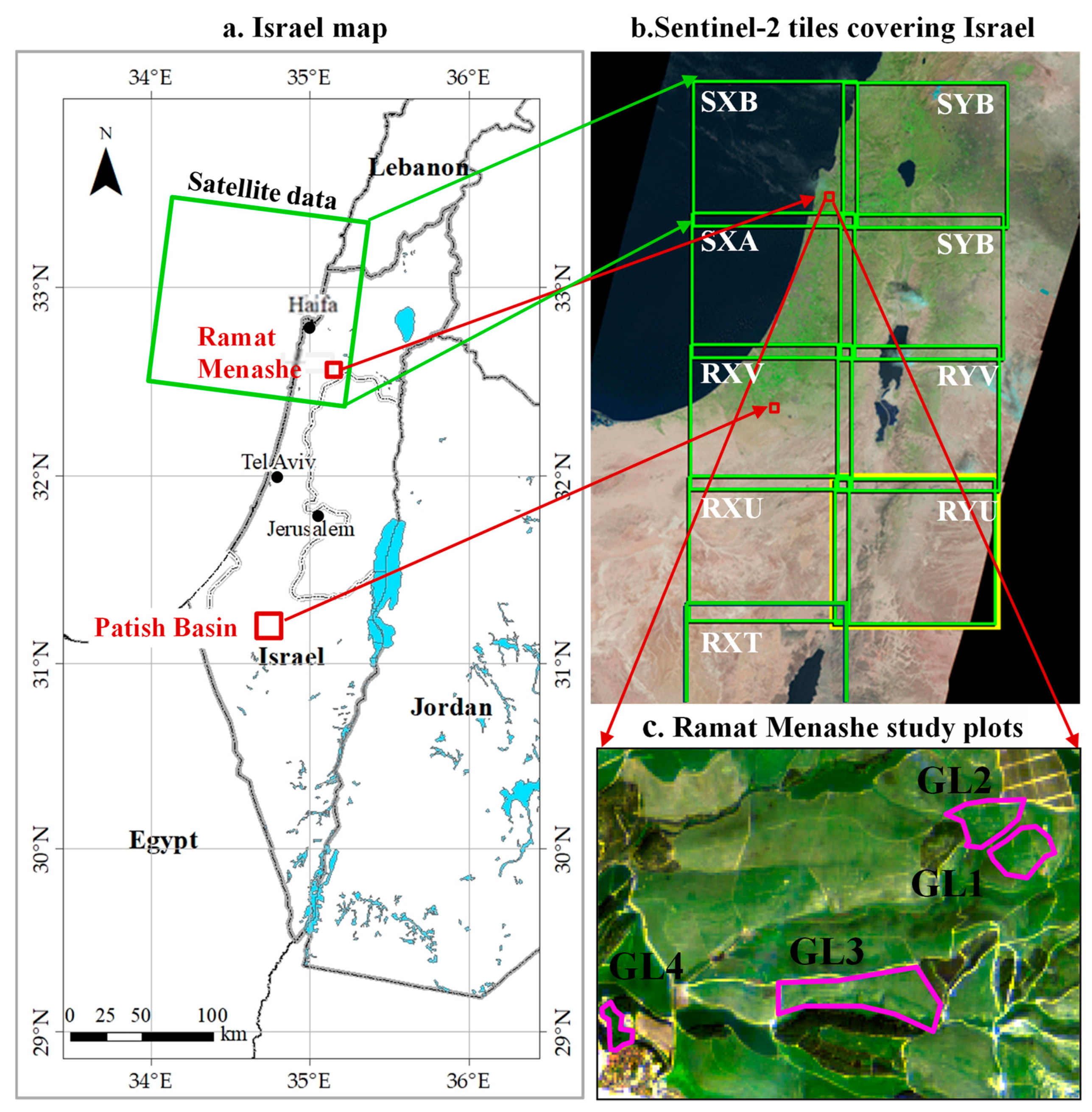
2.1. Study Areas
2.2. Sample Site Identification: Ecological Approach
2.3. Chemical Analyses: Reference Measurements
2.4. Field Measurements
2.4.1. Sample Collection
2.4.2. Spectral Measurements
2.4.3. Data Pre-Processing
2.5. Imagery Data: Sentinel-2
2.5.1. Data Collection
2.5.2. Sentinel-2 Image Pre-Processing
2.6. Meteorological Data
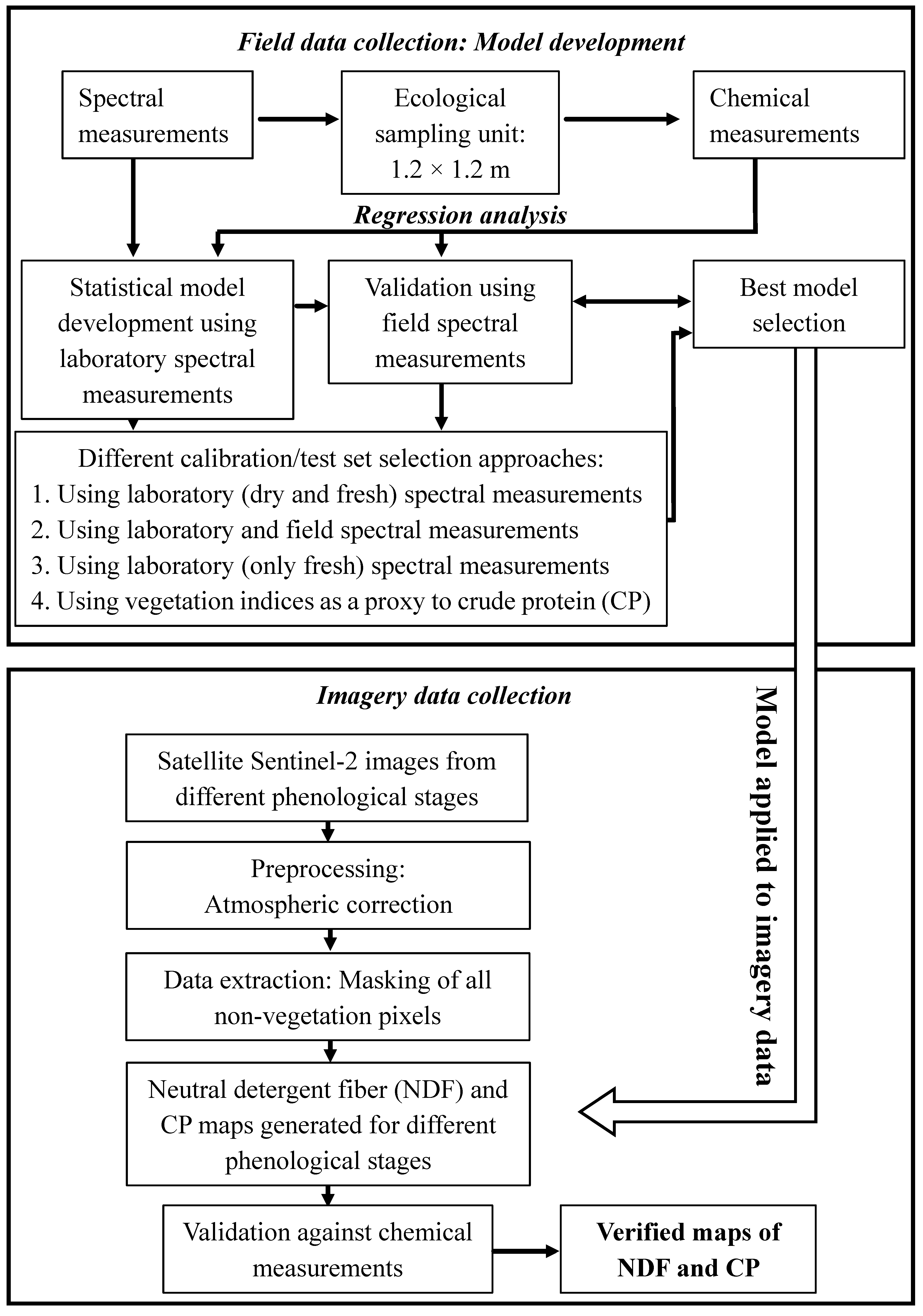
2.7. Statistical Analysis: Regression Models
2.8. Model Development: Selection of Calibration/Test Sample Sets
2.9. Model Validation
3. Results
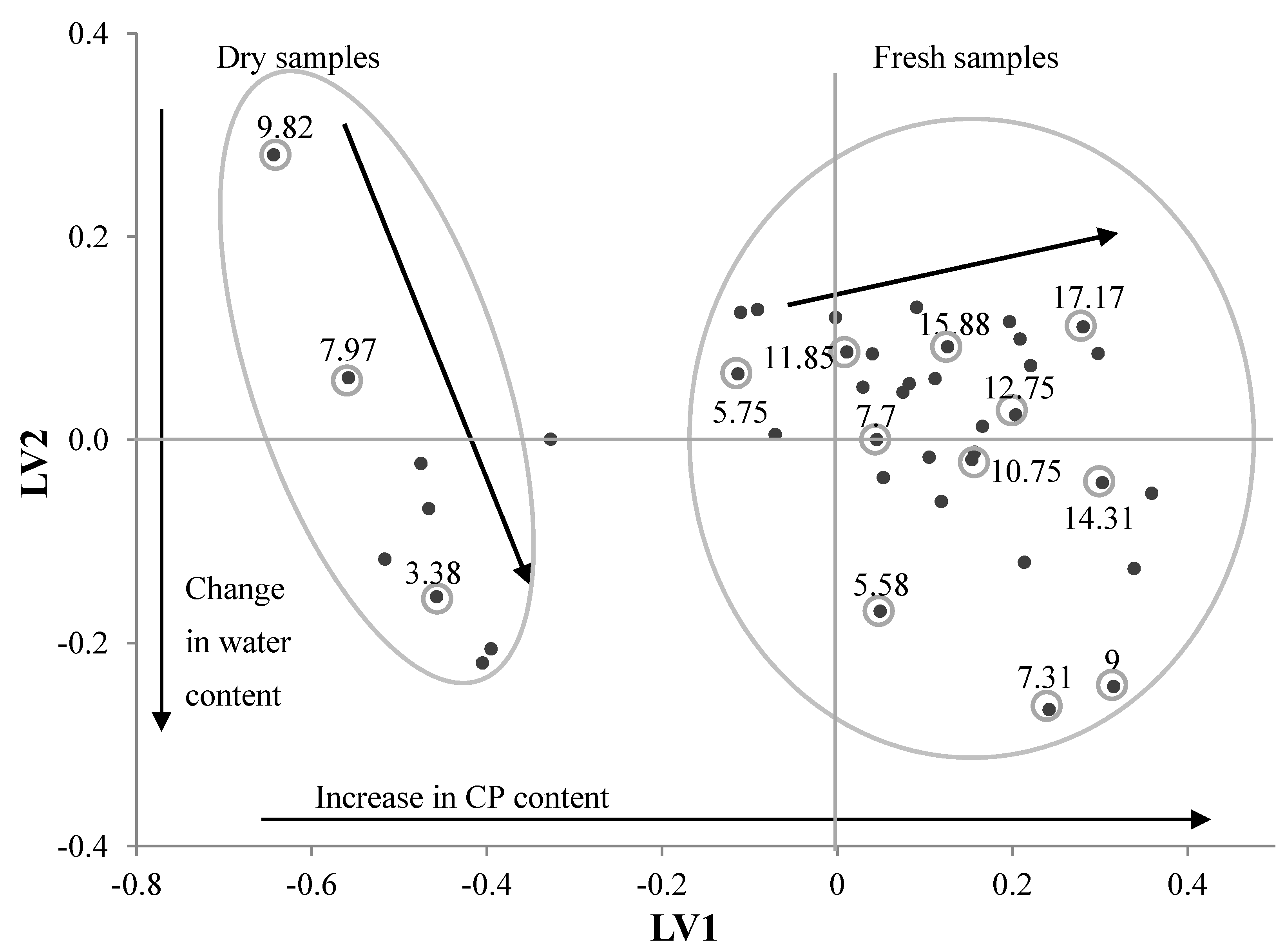
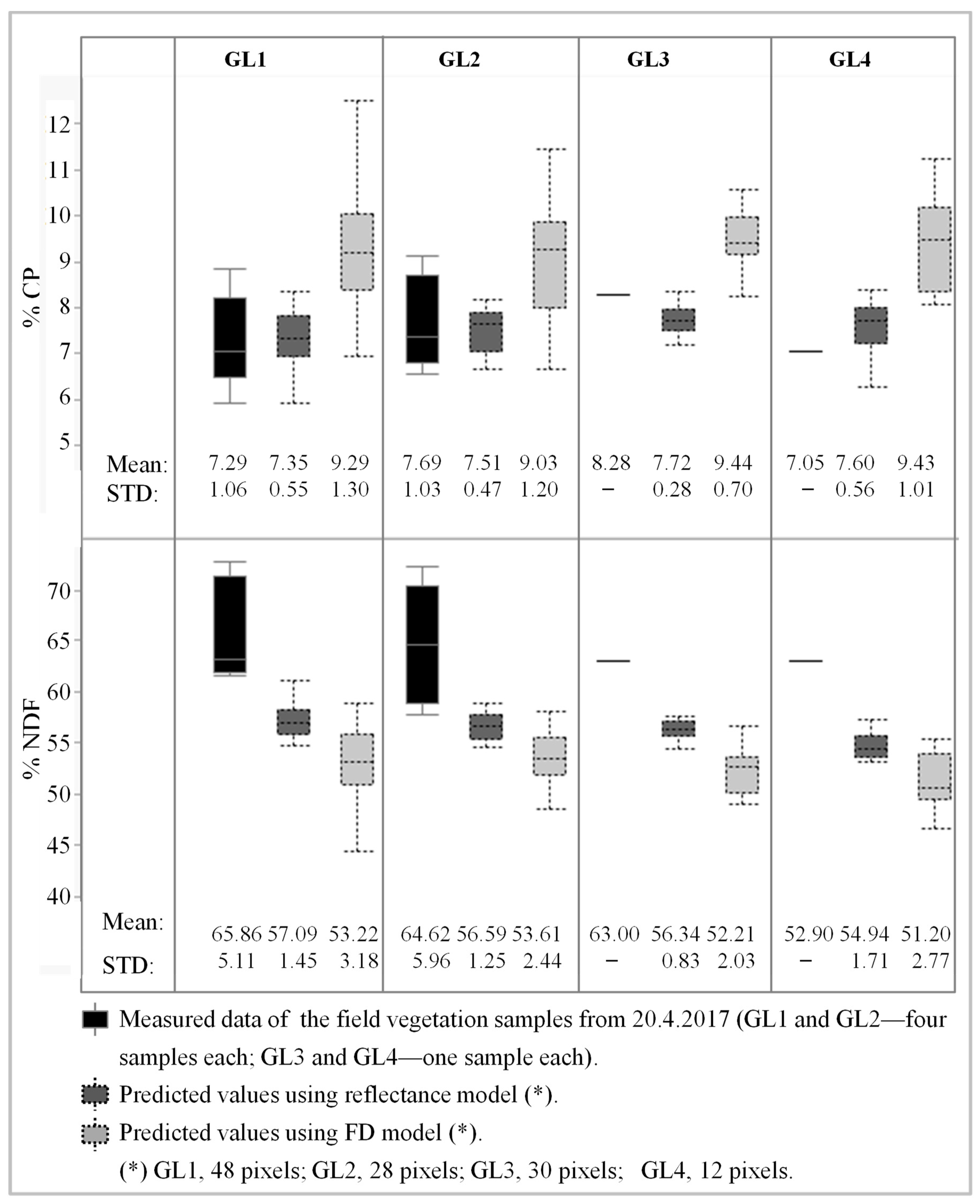
3.1. Chemical References: CP and NDF
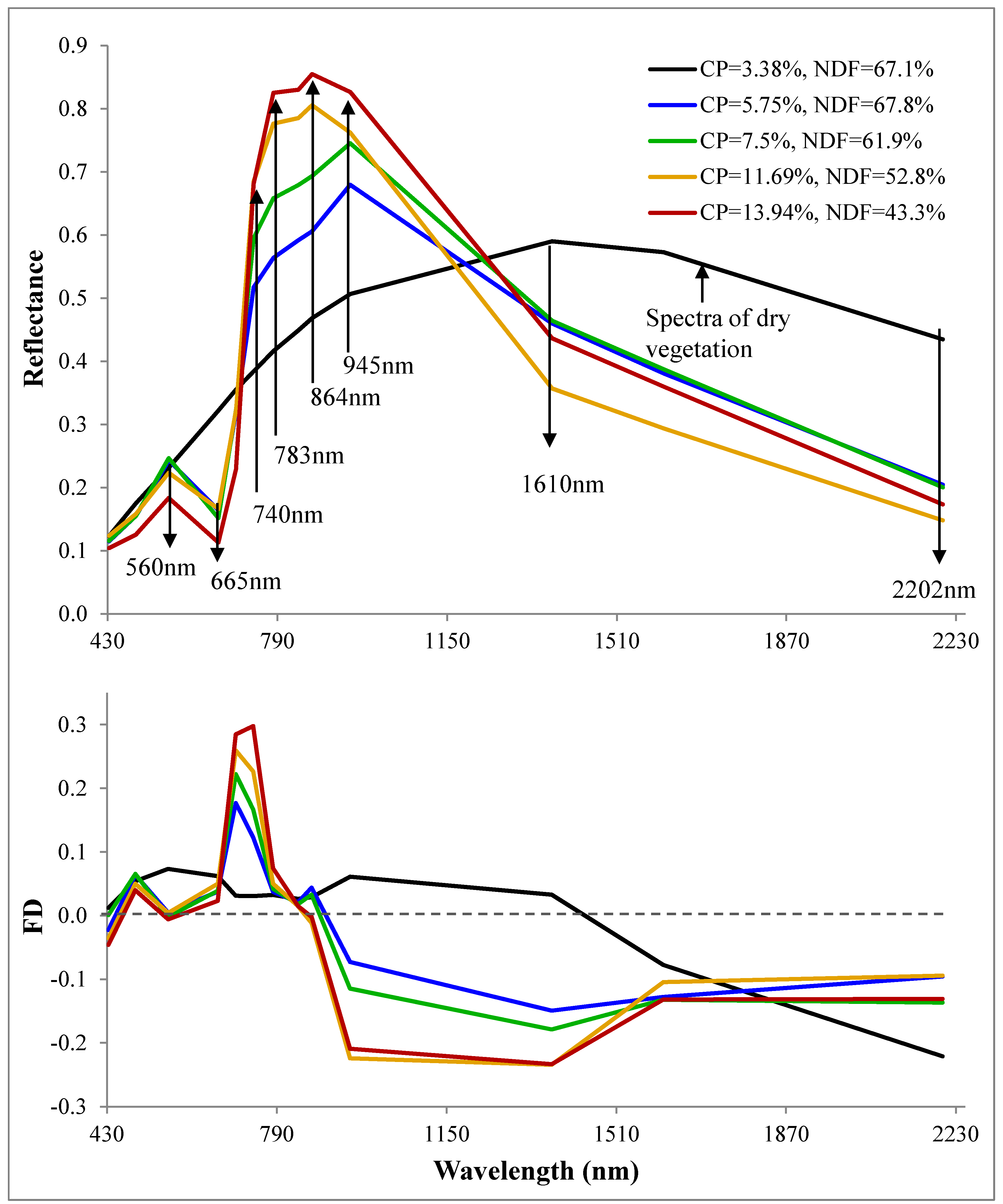
3.2. Spectral Analysis
3.3. PLS Analysis of Different Selection Models
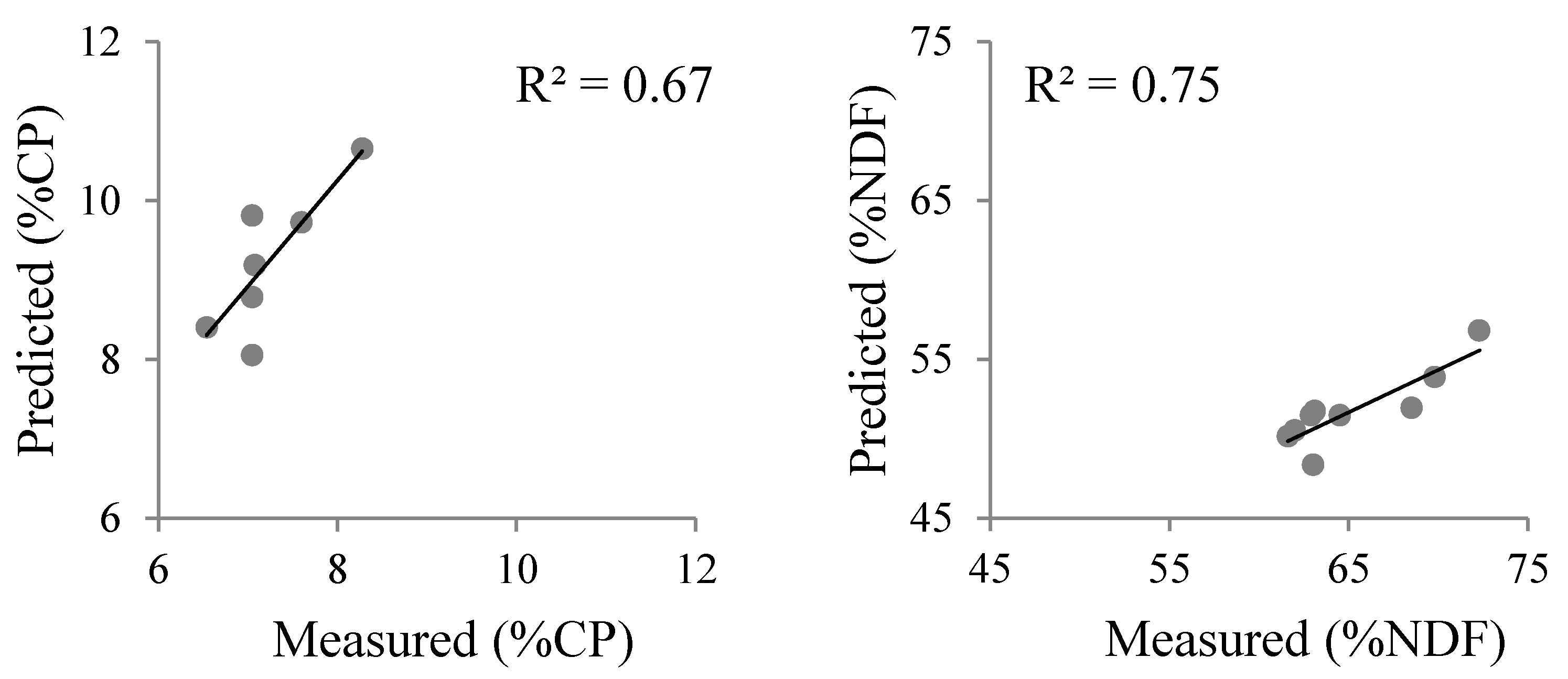
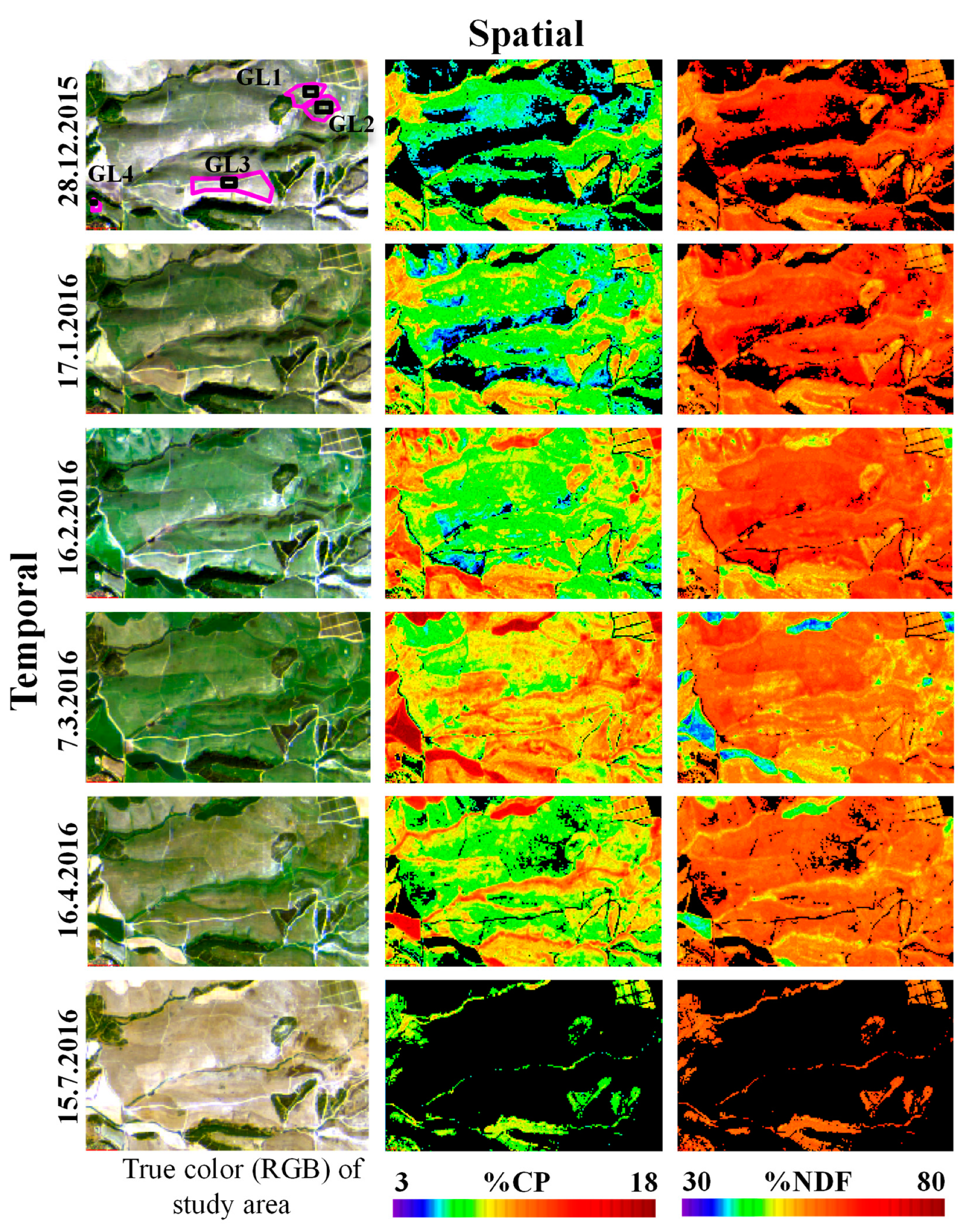
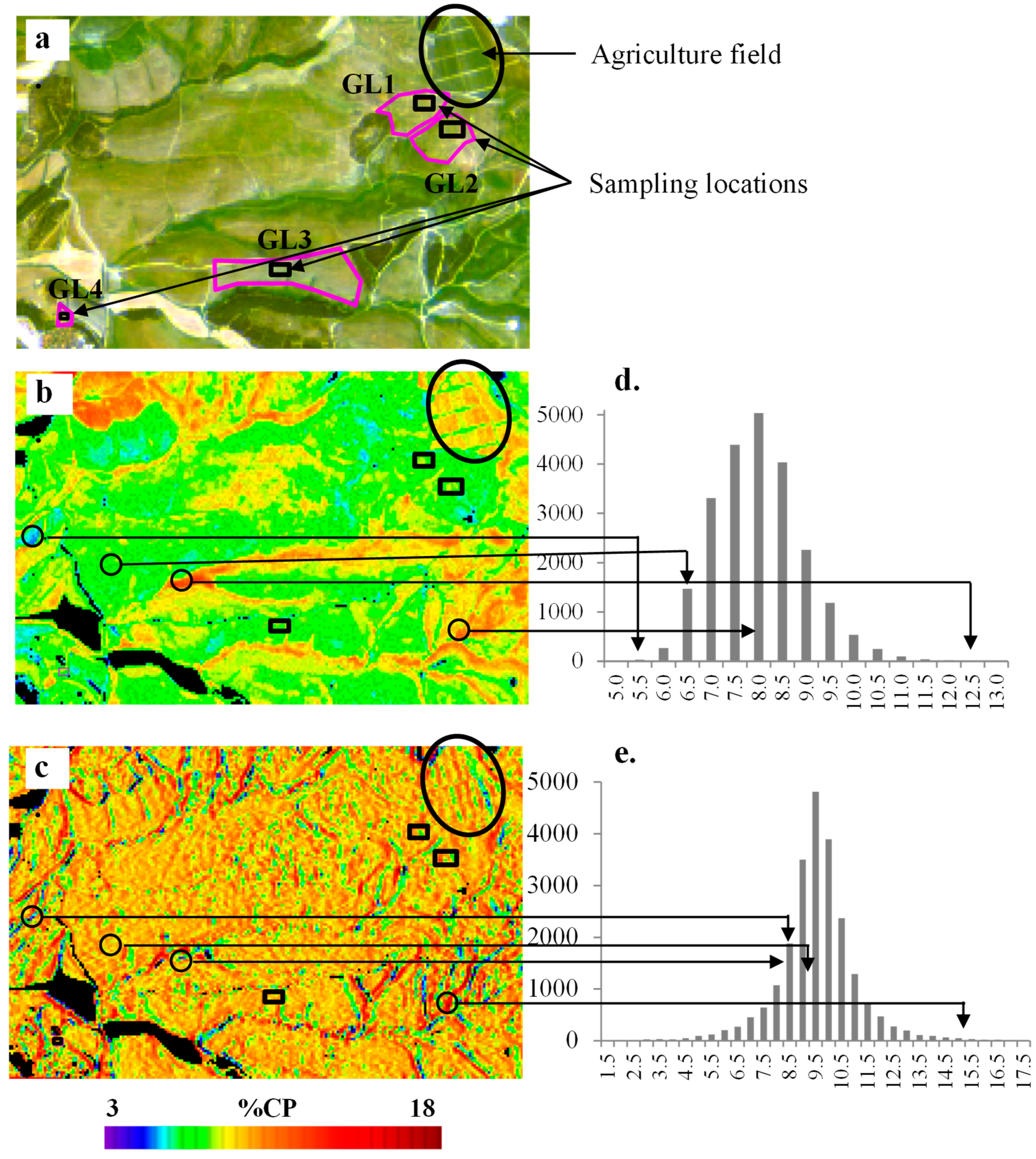
3.4. Mapping CP and NDF Contents using Sentinel-2 Images
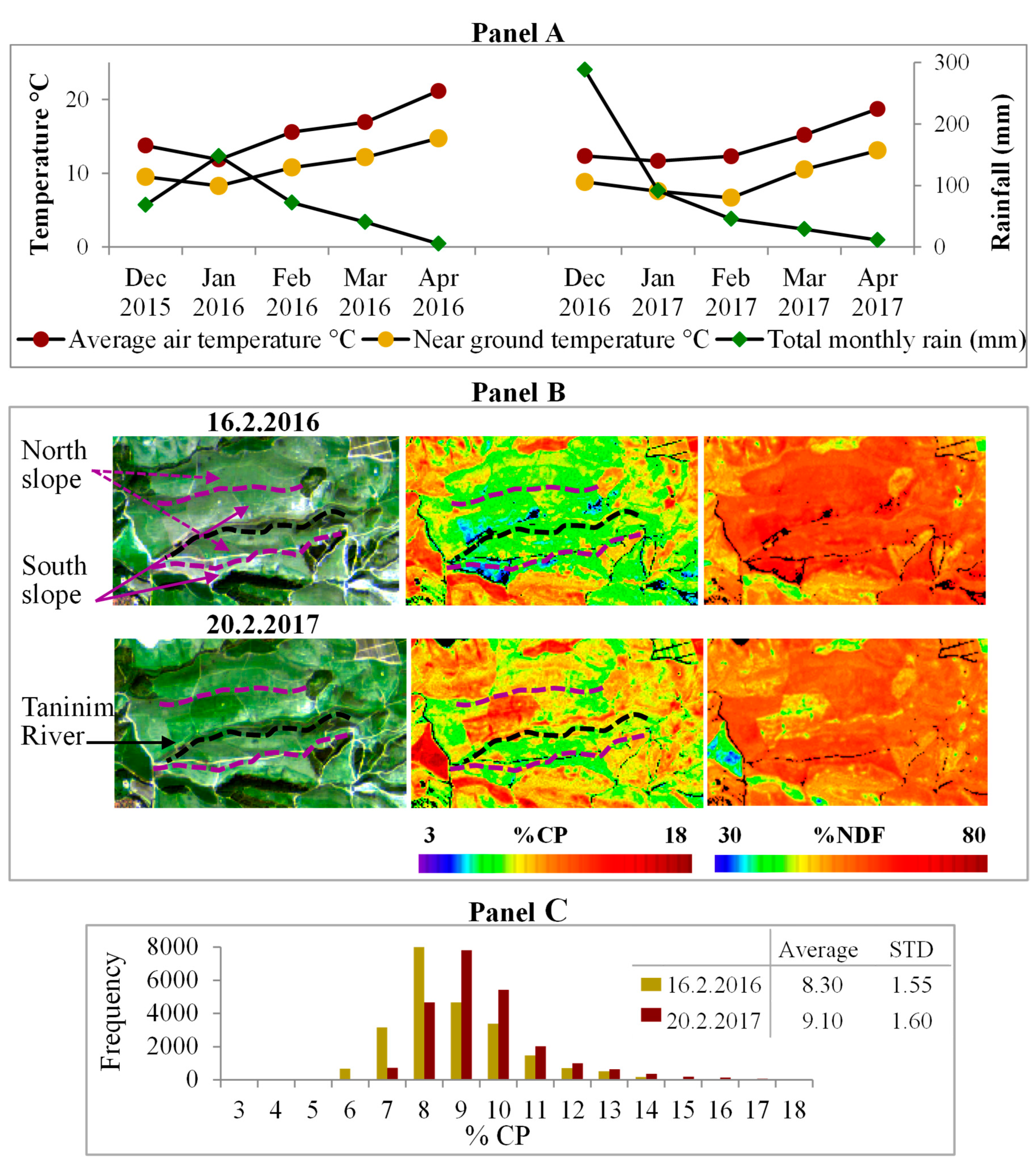
3.5. The Influence of the Meteorological Conditions on the Patterns of CP and NDF
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- IPCC. Climate Change 2014: Synthesis Report; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Balvanera, P.; Daily, G.C.; Ehrlich, P.R.; Ricketts, T.H.; Bailey, S.-A.; Kark, S.; Kremen, C.; Pereira, H. Conserving Biodiversity and Ecosystem Services. Science 2001, 291, 2047. [Google Scholar] [CrossRef] [PubMed]
- DeFries, R.; Hansen, A.; Turner, B.L.; Reid, R.; Liu, J. Land Use Change Around Protected Areas: Management to Balance Human Needs and Ecological Function. Ecol. Appl. 2007, 17, 1031–1038. [Google Scholar] [CrossRef]
- MA, M.E.A. Ecosystems and Human Well-Being: Desertification Synthesis; World Resources Institute: Washington, DC, USA, 2005. [Google Scholar]
- Ali, I.; Cawkwell, F.; Dwyer, N.; Barrett, B.; Green, S. Satellite remote sensing of grasslands: From observation to management—A review. J. Plant Ecol. 2016, 9, 649–671. [Google Scholar] [CrossRef]
- Lugassi, R.; Chudnovsky, A.; Zaady, E.; Dvash, L.; Goldshleger, N. Estimating Pasture Quality of Fresh Vegetation Based on Spectral Slope of Mixed Data of Dry and Fresh Vegetation—Method Development. Remote Sens. 2015, 7, 8045–8066. [Google Scholar] [CrossRef]
- Lugassi, R.; Chudnovsky, A.; Zaady, E.; Dvash, L.; Goldshleger, N. Spectral Slope as an Indicator of Pasture Quality. Remote Sens. 2015, 7, 256–274. [Google Scholar] [CrossRef]
- Foley, W.; Mcilwee, A.; Lawler, I.; Aragones, L.; Woolnough, A.; Berding, N. Ecological applications of near infrared reflectance spectroscopy—A tool for rapid, cost-effective prediction of the composition of plant and animal tissues and aspects of animal performance. Oecologia 1998, 116, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P. Biophysical and Biochemical Sources of Variability in Canopy Reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Asner, G.P.; Townsend, A.; Bustamante, M.M. Spectrometry of Pasture Condition and Biogeochemistry in the Central Amazon. Geophys. Res. Lett. 1999, 26, 2769–2772. [Google Scholar] [CrossRef]
- Garcia, J.; Cozzolino, D. Use of Near Infrared Reflectance (NIR) Spectroscopy to Predict Chemical Composition of Forages in Broad-Based Calibration Models. Agric. Técnica 2006, 66, 41–47. [Google Scholar] [CrossRef]
- Landau, S.; Friedman, S.; Brenner, S.; Bruckental, I.; Weinberg, Z.G.; Ashbell, G.; Hen, Y.; Dvash, L.; Leshem, Y. The value of safflower (Carthamus tinctorius) hay and silage grown under Mediterranean conditions as forage for dairy cattle. Livest. Prod. Sci. 2004, 88, 263–271. [Google Scholar] [CrossRef]
- Landuar, S.; Nitzan, R.; Barkai, D.; Dvash, L. Excretal Near Infrared Reflectance Spectrometry to monitor the nutrient content of diets of grazing young ostriches (Struthio camelus). S. Afr. J. Anim. Sci. 2006, 36, 248–256. [Google Scholar]
- Landau, S.; Glasser, T.; Dvash, L. Monitoring nutrition in small ruminants with the aid of near infrared reflectance spectroscopy (NIRS) technology: A review. Small Rumin. Res. 2006, 61, 1–11. [Google Scholar] [CrossRef]
- Landau, S.; Giger-Reverdin, S.; Rapetti, L.; Dvash, L.; Dorléans, M.; Ungar, E.D. Data mining old digestibility trials for nutritional monitoring in confined goats with aids of fecal near infra-red spectrometry. Small Rumin. Res. 2008, 77, 146–158. [Google Scholar] [CrossRef]
- Norris, H.K.; Barnes, F.R.; Moore, E.J.; Shenk, S.J. Predicting forage quality by infrared reflectance spectroscopy. Anim. Sci. 1976, 43, 889–897. [Google Scholar] [CrossRef]
- Siesler, H.W. Introduction. In Near-Infrared Spectroscopy: Principles, Instruments, Applications; Siesler, H.W., Ozaki, Y., Kawata, S., Heise, H.M., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2002; pp. 1–12. ISBN 978-3-527-61266-6. [Google Scholar]
- Kokaly, R.F.; Clark, R.N. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sens. Environ. 1999, 67, 21. [Google Scholar] [CrossRef]
- Marten, G.C.; Shenk, J.S.; Barton, F.E. Near-Infrared Reflectance Spectroscopy (NIRS): Analysis of Forage Quality; Handbook 643; United States Department of Agriculture (USDA): Washington, DC, USA, 1985; p. 110.
- Chudnovsky, A.; Golberg, A.; Linzon, Y. Monitoring complex monosaccharide mixtures derived from macroalgae biomass by combined optical and microelectromechanical techniques. Process. Biochem. 2018, 68, 136–145. [Google Scholar] [CrossRef]
- Peleg, Y.; Shefer, S.; Anavy, L.; Chudnovsky, A.; Israel, A.; Golberg, A.; Yakhini, Z. Sparse NIR optimization method (SNIRO) to quantify analyte composition with visible (VIS)/near infrared (NIR) spectroscopy (350 nm–2500 nm). Anal. Chim. Acta 2019, 1051, 32–40. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.; Prins, H.H. Predicting in situ pasture quality in the Kruger National Park, South Africa, using continuum-removed absorption features. Remote Sens. Environ. 2004, 89, 393–408. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.; Kumar, L.; Ferwerda, J. Estimating tropical pasture quality at canopy level using band depth analysis with continuum removal in the visible domain. Int. J. Remote Sens. 2005, 26, 1093–1108. [Google Scholar] [CrossRef]
- Friedl, M.; Henebry, G.; Reed, B.; Huete, A.; White, M.; Morisette, J.; Nemani, R.; Zhang, X.; Myneni, R. Land Surface Phenology. Available online: ftp://zeus.geog.umd.edu/Land_ESDR/Phenology_Friedl_whitepaper.pdf (accessed on 14 February 2018).
- Starks, P.J.; Zhao, D.; Phillips, W.A.; Brown, M.A.; Coleman, S.W. Productivity and Forage Quality of Warm Season Grass Pastures in Relation to Canopy Reflectance in Aster Wavebands. In Proceedings of the American Society for Photogrammetry and Remote Sensing, Weslaco, TX, USA; 2006; pp. 135–141. [Google Scholar]
- Starks, P.J.; Zhao, D.; Phillips, W.A.; Coleman, S.W. Development of Canopy Reflectance Algorithms for Real-Time Prediction of Bermudagrass Pasture Biomass and Nutritive Values. Crop Sci. 2006, 46, 927–934. [Google Scholar] [CrossRef]
- Adjorlolo, C.; Mutanga, O.; Cho, M.A. Estimation of Canopy Nitrogen Concentration Across C3 and C4 Grasslands Using WorldView-2 Multispectral Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 4385–4392. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Observ. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Pullanagari, R.; Yule, I.; Hedley, M.; Tuohy, M.; Dynes, R.; King, W. Multi-spectral radiometry to estimate pasture quality components. Precis. Agric. 2012, 13, 442–456. [Google Scholar] [CrossRef]
- Mobasheri, M.; Rahimzadegan, M. Introduction to Protein Absorption Lines Index for Relative Assessment of Green Leaves Protein Content Using EO-1 Hyperion Datasets. J. Agric. Sci. Technol. 2012, 14, 135–147. [Google Scholar]
- Skidmore, A.K.; Ferwerda, J.G.; Mutanga, O.; Van Wieren, S.E.; Peel, M.; Grant, R.C.; Prins, H.H.T.; Balcik, F.B.; Venus, V. Forage quality of savannas—Simultaneously mapping foliar protein and polyphenols for trees and grass using hyperspectral imagery. Remote Sens. Environ. 2010, 114, 64–72. [Google Scholar] [CrossRef]
- Segl, K.; Guanter, L.; Gascon, F.; Kuester, T.; Rogass, C.; Mielke, C. S2eteS: An End-to-End Modeling Tool for the Simulation of Sentinel-2 Image Products. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5560–5571. [Google Scholar] [CrossRef]
- MSI Instrument—Sentinel-2 MSI Technical Guide—Sentinel Online. Available online: https://earth.esa.int/web/sentinel/technical-guides/sentinel-2-msi/msi-instrument (accessed on 8 April 2018).
- Haas, J.; Ban, Y. Mapping and Monitoring Urban Ecosystem Services Using Multitemporal High-Resolution Satellite Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 669–680. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Lugassi, R.; Goldshleger, N.; Chudnovsky, A. Studying Vegetation Salinity: From the Field View to a Satellite-Based Perspective. Remote Sens. 2017, 9, 122. [Google Scholar] [CrossRef]
- Beamish, A.; Coops, N.; Chabrillat, S.; Heim, B. A Phenological Approach to Spectral Differentiation of Low-Arctic Tundra Vegetation Communities, North Slope, Alaska. Remote Sens. 2017, 9, 1200. [Google Scholar] [CrossRef]
- Hill, M.J. Vegetation index suites as indicators of vegetation state in grassland and savanna: An analysis with simulated SENTINEL 2 data for a North American transect. Remote Sens. Environ. 2013, 137, 94–111. [Google Scholar] [CrossRef]
- Frampton, W.; Dash, J.; Watmough, G.; James Milton, E. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Mark, H. Quantitative Spectroscopic Calibration. In Encyclopedia of Analytical Chemistry: Applications, Theory and Instrumentation; John Wiley & Sons, Ltd.: Chichester, UK, 2000; ISBN 978-0-470-02731-8. [Google Scholar]
- Shoshany, M.; Svoray, T. Multidate adaptive unmixing and its application to analysis of ecosystem transitions along a climatic gradient. Remote Sens. Environ. 2002, 82, 5–20. [Google Scholar] [CrossRef]
- IMS—Israel Meteorological Service. Available online: http://www.ims.gov.il/IMSEng/All_tahazit (accessed on 19 February 2018).
- Seligamn, N.; Ron, N. Fertilization of Natural and Rainfed Range in Ramat Menashe’e Research; Ministry of Agriculture, Department of Soil Conservation: Bet-Dagan, Israel, 1976.
- Zaady, E.; Yonatan, R.; Shachak, M.; Perevolotsky, A. The Effects of Grazing on Abiotic and Biotic Parameters in a Semiarid Ecosystem: A Case Study from the Northern Negev Desert, Israel. Arid Land Res. Manag. 2001, 15, 245–261. [Google Scholar] [CrossRef]
- Dan, J.; Yaalon, D.; Kundzimzinsky, H.; Raz, Z. The Soil of Israel; Agriculture Research Organization; Soil and Water Conservation; Ministry of Agriculture Publication: Bet-Dagan, Israel, 1977; p. 37.
- Feinbrun-Dothan, N.; Danin, A. Analytical Flora of Eretz-Israel; Cana Publishers: Jerusalem, Israel, 1991. [Google Scholar]
- Perry, N.J.; Liebhold, A.; Rosenberg, M.; Dungan, J.L.; Miriti, M.; Jakomulska, A.; Citron-Pousty, S. Illustrations and Guidelines for Selecting Statistical Methods for Quantifying Spatial Pattern in Ecological Data. Ecography 2002, 25, 578–600. [Google Scholar] [CrossRef]
- Smith, P.G. Quantitative Plant. Ecology; University of California Press: Berkeley, CA, USA, 1983; ISBN 978-0-520-05080-8. [Google Scholar]
- Williams, W.T.; Lambert, J.M. Multivariate Methods in Plant Ecology: I. Association-Analysis in Plant Communities. J. Ecol. 1959, 47, 81–101. [Google Scholar] [CrossRef]
- Goering, H.K.; Van Soest, P. Forage Fiber Analyses (Apparatus, Reagents, Procedures, and Some Applications); U.S. Agricultural Research Service: Washington, DC, USA, 1970.
- Tilley, J.M.A.; Terry, R.A. A Two-Stage Technique for the in Vitro Digestion of Forage Crops. Grass Forage Sci. 1963, 18, 104–111. [Google Scholar] [CrossRef]
- Van Soest, P.J.; Robertson, J.B.; Lewis, B.A. Methods for Dietary Fiber, Neutral Detergent Fiber, and Nonstarch Polysaccharides in Relation to Animal Nutrition. J. Dairy Sci. 1991, 74, 3583–3597. [Google Scholar] [CrossRef]
- Spectroscopy Solutions|Spectroscopy Applications & Instruments|ASD Inc. Available online: https://www.asdi.com/ (accessed on 12 February 2018).
- Labsphere—Labsphere|Internationally Recognized Photonics Company. Available online: http://labsphere.com/ (accessed on 12 February 2018).
- Kokaly, R.F. Investigating a Physical Basis for Spectroscopic Estimates of Leaf Nitrogen Concentration. Remote Sens. Environ. 2001, 75, 153–161. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Sellitto, V.M.; Fernandes, R.B.A.; Barrón, V.; Colombo, C. Comparing two different spectroscopic techniques for the characterization of soil iron oxides: Diffuse versus bi-directional reflectance. Geoderma 2009, 149, 2–9. [Google Scholar] [CrossRef]
- Curcio, D.; Ciraolo, G.; D’Asaro, F.; Minacapilli, M. Prediction of Soil Texture Distributions Using VNIR-SWIR Reflectance Spectroscopy. Procedia Environ. Sci. 2013, 19, 494–503. [Google Scholar] [CrossRef]
- Noomen, M.F.; Skidmore, A.K.; van der Meer, F.D.; Prins, H.H.T. Continuum removed band depth analysis for detecting the effects of natural gas, methane and ethane on maize reflectance. Remote Sens. Environ. 2006, 105, 262–270. [Google Scholar] [CrossRef]
- User Guides—Sentinel-2 MSI—Resolutions—Sentinel Online. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi/resolutions (accessed on 8 April 2018).
- EarthExplorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 5 February 2018).
- Products and Algorithms—Sentinel-2 MSI Technical Guide—Sentinel Online. Available online: https://earth.esa.int/web/sentinel/technical-guides/sentinel-2-msi/products-algorithms (accessed on 8 April 2018).
- Sen2Cor|STEP Science Toolbox Exploration Platform. Available online: http://step.esa.int/main/third-party-plugins-2/sen2cor/ (accessed on 5 February 2018).
- ESA Sentinel-2 MSI—Level-2A Prototype Processor Installation and User Manual. Available online: https://step.esa.int/thirdparties/sen2cor/2.2.1/S2PAD-VEGA-SUM-0001-2.2.pdf (accessed on 8 April 2018).
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS; NASA: Washington, DC, USA, 1974; pp. 309–317.
- Esbensen, K.H.; Guyot, D.; Westad, F.; Houmoller, L.P. Multivariate Data Analysis: In Practice: An Introduction to Multivariate Data Analysis and Experimental Design; CAMO: Woodbridge, NJ, USA, 2002; ISBN 978-82-993330-3-0. [Google Scholar]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Evaluation of Model Performance in Physical Geography. In Spatial Statistics and Models; Gaile, G.L., Willmott, C.J., Eds.; Theory and Decision Library; Springer: Dordrecht, The Netherlands, 1984; pp. 443–460. ISBN 978-94-017-3048-8. [Google Scholar]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant. Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Prabhakara, K.; Hively, W.D.; McCarty, G.W. Evaluating the relationship between biomass, percent groundcover and remote sensing indices across six winter cover crop fields in Maryland, United States. Int. J. Appl. Earth Observ. Geoinf. 2015, 39, 88–102. [Google Scholar] [CrossRef]
- Jin, Y.; Yang, X.; Qiu, J.; Li, J.; Gao, T.; Wu, Q.; Zhao, F.; Ma, H.; Yu, H.; Xu, B. Remote Sensing-Based Biomass Estimation and Its Spatio-Temporal Variations in Temperate Grassland, Northern China. Remote Sens. 2014, 6, 1496–1513. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Analytical Flora|Online Flora of Israel Online. Available online: http://flora.org.il/en/plants/ (accessed on 18 February 2018).
- Albayrak, S. Use of Reflectance Measurements for the Detection of N, P, K, ADF and NDF Contents in Sainfoin Pasture. Sensors 2008, 8, 7275–7286. [Google Scholar] [CrossRef]
- Guo, X.; Wilmshurst, J.; Li, Z. Comparison of Laboratory and Field Remote Sensing Methods to Measure Forage Quality. Int. J. Environ. Res. Public Health 2010, 7, 3513–3530. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.G.; Hare, J.D.; Compton, S.J. Measuring plant protein with the Bradford assay. J. Chem. Ecol. 1989, 15, 979–992. [Google Scholar] [CrossRef]
- Kawamura, K.; Watanabe, N.; Sakanoue, S.; Inoue, Y. Estimating forage biomass and quality in a mixed sown pasture based on PLS regression with waveband selection. Grassland Sci. 2008, 54, 131–145. [Google Scholar] [CrossRef]
- Ollinger, S.V.; Richardson, A.; Martin, M.E.; Hollinger, D.Y.; Frolking, S.E.; Reich, P.B.; Plourde, L.C.; Katul, G.G.; Munger, J.W.; Oren, R.; et al. Canopy nitrogen, carbon assimilation, and albedo in temperate and boreal forests: Functional relations and potential climate feedbacks. Proc. Natl. Acad. Sci. USA 2008, 105, 19336–19341. [Google Scholar] [CrossRef] [PubMed]
- Ramoelo, A.; Cho, M.A.; Mathieu, R.; Madonsela, S.; van de Kerchove, R.; Kaszta, Z.; Wolff, E. Monitoring grass nutrients and biomass as indicators of rangeland quality and quantity using random forest modelling and WorldView-2 data. Int. J. Appl. Earth Observ. Geoinf. 2015, 43, 43–54. [Google Scholar] [CrossRef]
- Wang, Z.J.; Wang, J.H.; Liu, L.Y.; Huang, W.J.; Zhao, C.J.; Wang, C.Z. Prediction of grain protein content in winter wheat (Triticum aestivum L.) using plant pigment ratio (PPR). Field Crops Res. 2004, 90, 311–321. [Google Scholar] [CrossRef]
- Clifton, K.; Bradbury, J.W.; Vehrencamp, S.L. The fine-scale mapping of grassland protein densities. Grass Forage Sci. 1994, 49, 1–8. [Google Scholar] [CrossRef]
- Wright, L.D.; Rasmussen, V.; Ramsey, R.; Baker, D.J.; Ellsworth, J.W. Canopy Reflectance Estimation of Wheat Nitrogen Content for Grain Protein Management. Gisci. Remote Sens. 2004, 41, 287–300. [Google Scholar] [CrossRef]
- Scheromm, S.; MARTINMartin, G.; Bergoin, A.; Autran, C. Influence of Nitrogen Fertilization on the Potential Bread-Baking Quality of Two Wheat Cultivars Differing in Their Responses to Increasing Nitrogen Supplies. Cereal Chem. 1992, 69, 664–670. [Google Scholar]
- Shi, S.-M.; Chen, K.; Gao, Y.; Liu, B.; Yang, X.-H.; Huang, X.-Z.; Liu, G.-X.; Zhu, L.-Q.; He, X.-H. Arbuscular Mycorrhizal Fungus Species Dependency Governs Better Plant Physiological Characteristics and Leaf Quality of Mulberry (Morus alba L.) Seedlings. Front. Microbiol. 2016, 7, 1030. [Google Scholar] [CrossRef]
- Woodard, H.J.; Bly, A. Relationship of nitrogen management to winter wheat yield and grain protein in South Dakota. J. Plant Nutr. 1998, 21, 217–233. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mõttus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Carmona, P.L.; Kaufmann, R.K.; Lewis, P.; et al. Hyperspectral remote sensing of foliar nitrogen content. Proc. Natl. Acad. Sci. USA 2013, 110, E185–E192. [Google Scholar] [CrossRef]
- Cunniff, P. Official Methods of Analysis of AOAC International, 16th ed.; AOAC International: Arlington, VA, USA, 1995; Volume 1. [Google Scholar]
- Martin, M.E.; Plourde, L.C.; Ollinger, S.V.; Smith, M.-L.; McNeil, B.E. A generalizable method for remote sensing of canopy nitrogen across a wide range of forest ecosystems. Remote Sens. Environ. 2008, 112, 3511–3519. [Google Scholar] [CrossRef]
- Menesatti, P.; Antonucci, F.; Pallottino, F.; Roccuzzo, G.; Allegra, M.; Stagno, F.; Intrigliolo, F. Estimation of plant nutritional status by Vis—NIR spectrophotometric analysis on orange leaves [Citrus sinensis (L) Osbeck cv Tarocco]. Biosyst. Eng. 2010, 105, 448–454. [Google Scholar] [CrossRef]
- Schleicher, T.D.; Bausch, W.C.; Delgado, J.A.; Ayers, P.D. Evaluation and Refinement of the Nitrogen Reflectance Index (NRI) for Site-Specific Fertilizer Management; Paper No. 011151; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2001. [Google Scholar]
- Orman, A.B.; Schumann, A.R. Comparison of near-infrared spectroscopy calibration methods for the prediction of protein, oil, and starch in maize grain. J. Agric. Food Chem. 1991, 39, 883–886. [Google Scholar] [CrossRef]
- Rushing, B.J.; Saha, U.; Lemus, R.; Sonon, L.; Baldwin, B.S. Analysis of Some Important Forage Quality Attributes is Southeastern Wildrye (Elymus glabriflrous) using Near-Infrared Spectroscopy. Am. J. Anal. Chem. 2016, 7, 642–662. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, R.; Xu, R.; Zhang, W.; Shen, Y.; Zhang, Y. Evaluation of Leymus chinensis quality using near-infrared reflectance spectroscopy with three different statistical analyses. PeerJ 2015, 3, e1416. [Google Scholar] [CrossRef]
- Cozzolino, D. Use of Infrared Spectroscopy for In-Field Measurement and Phenotyping of Plant Properties: Instrumentation, Data Analysis, and Examples. Appl. Spectrosc. Rev. 2014, 49, 564–584. [Google Scholar] [CrossRef]
- Givens, I.; Boever, J.; Deaville, E.R. The principles, practices and some future applications of near infrared spectroscopy for predicting the nutritive value of foods for animals and humans. Nutr. Res. Rev. 1997, 10, 83–114. [Google Scholar] [CrossRef] [PubMed]
- Petisco, C.; Garcia-Criado, B.; Garcia-Criado, L.; Vazquez de Aldana, B.; Ciudad, A. Quantitative Analysis of Chlorophyll and Protein in Alfalfa Leaves Using Fiber-Optic Near-Infrared Spectroscopy. Commun. Soil Sci. Plant Anal. 2009, 40, 2474–2484. [Google Scholar] [CrossRef]
- Yang, Z.; Nie, G.; Pan, L.; Zhang, Y.; Huang, L.; Ma, X.; Zhang, X. Development and validation of near-infrared spectroscopy for the prediction of forage quality parameters in Lolium multiflorum. PeerJ 2017, 5, e3867. [Google Scholar] [CrossRef]
- Tkachuk, R. Oil and protein analysis of whole rapeseed kernels by near infrared reflectance spectroscopy. J. Am. Oil Chem Soc. 1981, 58, 819–822. [Google Scholar] [CrossRef]
- Card, D.H.; Peterson, D.L.; Matson, P.A.; Aber, J.D. Prediction of leaf chemistry by the use of visible and near infrared reflectance spectroscopy. Remote Sens. Environ. 1988, 26, 123–147. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Murray, I.; Williams, P.C. Chemical principles of near infrared technology. In Near Infrared Technology in Agriculture and Food Industries; American Association of Cereal Chemistry Inc: St. Paul, MN, USA, 1987; pp. 17–31. [Google Scholar]
- Schwanninger, M.; Rodrigues, J.; Fackler, K. A review of band assignments in near infrared spectra of wood and wood components. J. Near Infrared Spectrosc. 2011, 19, 287–308. [Google Scholar] [CrossRef]
- Workman, J.J.; Weyer, I. Practical Guide to Interpretive Near Infrared Spectroscopy; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2008. [Google Scholar]
- Arzani, H.; Zohdi, M.; Fish, E.; Zahedi Amiri, G.H.; Nikkhah, A.; Wester, D. Phenological Effects on Forage Quality of Five Grass Species. Rangel. Ecol. Manag. 2004, 57, 624–629. [Google Scholar] [CrossRef]
- Henkin, Z.; Ungar, E.D.; Dvash, L.; Perevolotsky, A.; Yehuda, Y.; Sternberg, M.; Voet, H.; Serge Yan, L. Effects of cattle grazing on herbage quality in a herbaceous Mediterranean rangeland. Grass Forage Sci. 2011, 66, 516–525. [Google Scholar] [CrossRef]
- Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Sicre, C.; Le Dantec, V.; Demarez, V. Estimating maize biomass and yield over large areas using high spatial and temporal resolution Sentinel-2 like remote sensing data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
- Dong, J.; Kaufmann, R.K.; Myneni, R.B.; Tucker, C.J.; Kauppi, P.E.; Liski, J.; Buermann, W.; Alexeyev, V.; Hughes, M.K. Remote sensing estimates of boreal and temperate forest woody biomass: Carbon pools, sources, and sinks. Remote Sens. Environ. 2003, 84, 393–410. [Google Scholar] [CrossRef]
- Filella, I.; Peñuelas, J.; Llorens, L.; Estiarte, M. Reflectance assessment of seasonal and annual changes in biomass and CO2 uptake of a Mediterranean shrubland submitted to experimental warming and drought. Remote Sens. Environ. 2004, 90, 308–318. [Google Scholar] [CrossRef]
- le Maire, G.; Marsden, C.; Nouvellon, Y.; Grinand, C.; Hakamada, R.; Stape, J.-L.; Laclau, J.-P. MODIS NDVI time-series allow the monitoring of Eucalyptus plantation biomass. Remote Sens. Environ. 2011, 115, 2613–2625. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Tucker, C.J.; Newcomb, W.W.; Los, S.O.; Prince, S.D. Mean and inter-year variation of growing-season normalized difference vegetation index for the Sahel 1981–1989. Int. J. Remote Sens. 1991, 12, 1133–1135. [Google Scholar] [CrossRef]
- Wessels, K.J.; Prince, S.D.; Zambatis, N.; MacFadyen, S.; Frost, P.E.; Zyl, D.V. Relationship between herbaceous biomass and 1-km2 Advanced Very High Resolution Radiometer (AVHRR) NDVI in Kruger National Park, South Africa. Int. J. Remote Sens. 2006, 27, 951–973. [Google Scholar] [CrossRef]
- Svoray, T.; Shafran-Nathan, R.; Henkin, Z.; Perevolotsky, A. Spatially and temporally explicit modeling of conditions for primary production of annuals in dry environments. Ecol. Model. 2008, 218, 339–353. [Google Scholar] [CrossRef]
- Jin, M.S.; Mullens, T. A Study of the Relations between Soil Moisture, Soil Temperatures and Surface Temperatures Using ARM Observations and Offline CLM4 Simulations. Climate 2014, 2, 279–295. [Google Scholar] [CrossRef]
- Zweifel-Schielly, B.; Leuenberger, Y.; Kreuzer, M.; Suter, W. A herbivore’s food landscape: Seasonal dynamics and nutritional implications of diet selection by a red deer population in contrasting Alpine habitats. J. Zool. 2012, 286, 68–80. [Google Scholar] [CrossRef]
- Kirkby, M.J.; Atkinson, K.; Lockwood, J. Aspect, vegetation cover and erosion on semi-arid hillslopes. In Vegetation and Erosion. Processes and Environments; Wiley: New York, NY, USA, 1990; pp. 25–39. [Google Scholar]
- Nevo, E. Evolution in Action across Phylogeny Caused by Microclimatic Stresses at “Evolution Canyon”. Theor. Popul. Biol. 1997, 52, 231–234. [Google Scholar] [CrossRef]
- Sternberg, M.; Shoshany, M. Influence of slope aspect on Mediterranean woody formations: Comparison of a semiarid and an arid site in Israel. Ecol. Res. 2001, 16, 335–345. [Google Scholar] [CrossRef]
- Bar (Kutiel), P.; Lavee, H. Effect of slope aspect on soil and vegetation properties along an aridity transect. Israel J. Plant. Sci. 1999, 47, 169–178. [Google Scholar]
- Nevo, E. Asian, African and European biota meet at ‘Evolution Canyon’ Israel: Local tests of global biodiversity and genetic diversity patterns. R. Soc. 1995, 262, 149–155. [Google Scholar]
- Herrmann, I.; Pimstein, A.; Karnieli, A.; Cohen, Y.; Alchanatis, V.; Bonfil, D.J. LAI assessment of wheat and potato crops by VENμS and Sentinel-2 bands. Remote Sens. Environ. 2011, 115, 2141–2151. [Google Scholar] [CrossRef]
- Cohen, Y.; Alchanatis, V.; Zusman, Y.; Dar, Z.; Bonfil, D.J.; Karnieli, A.; Zilberman, A.; Moulin, A.; Ostrovsky, V.; Levi, A.; et al. Leaf nitrogen estimation in potato based on spectral data and on simulated bands of the VENμS satellite. Precis. Agric. 2010, 11, 520–537. [Google Scholar] [CrossRef]


| Method | Selected Bands\Slopes | Number of Samples | R2 | RMSE | p Value of Model | p Value | Index of Agreement | |
|---|---|---|---|---|---|---|---|---|
| First Derivative | CP | 703 nm | 44 | 0.764 | 2.022 | <0.0001 | <0.0001 | 0.72 |
| 740 nm | <0.0001 | |||||||
| 865 nm | 0.0103 | |||||||
| 945 nm | 0.0009 | |||||||
| 2202 nm | 0.0126 | |||||||
| NDF | 703nm | 43 | 0.740 | 6.274 | <0.0001 | <0.0001 | 0.73 | |
| 740 nm | 0.0039 | |||||||
| 865 nm | 0.1992 | |||||||
| 945 nm | <0.0001 | |||||||
| 2202 nm | 0.4370 | |||||||
| Reflectance | CP | 560 nm | 43 | 0.711 | 2.102 | <0.0001 | 0.0002 | 0.71 |
| 665 nm | 0.0013 | |||||||
| 865 nm | <0.0001 | |||||||
| 2202 nm | <0.0001 | |||||||
| NDF | 560 nm | 43 | 0.775 | 5.525 | <0.0001 | <0.0001 | 0.73 | |
| 665 nm | <0.0001 | |||||||
| 865 nm | <0.0001 | |||||||
| 2202 nm | <0.0001 | |||||||
| Slope | CP * | Slope (443–865 nm) | 40 | 0.739 | 1.251 | <0.0001 | 0.0307 | 0.78 |
| Slope (665–865 nm) | 0.0572 | |||||||
| Slope (496–865 nm) | 0.0056 | |||||||
| Slope (783–1610 nm) | 0.0660 | |||||||
| NDF | Slope (443–865 nm) | 43 | 0.778 | 5.581 | <0.0001 | <0.0001 | 0.78 | |
| Slope (665–865 nm) | <0.0001 | |||||||
| Slope (496–865 nm) | <0.0001 | |||||||
| Slope (783–1610 nm) | 0.0054 | |||||||
| Kubelka Munk | CP | 496 nm | 44 | 0.721 | 2.230 | <0.0001 | 0.0169 | 0.71 |
| 665 nm | 0.1119 | |||||||
| 740 nm | 0.0043 | |||||||
| 835 nm | 0.0388 | |||||||
| 865 nm | 0.0808 | |||||||
| 2202 nm | 0.0018 | |||||||
| NDF | 433 nm | 43 | 0.748 | 6.052 | <0.0001 | <0.0001 | 0.74 | |
| 703 nm | 0.0150 | |||||||
| 865 nm | 0.2555 | |||||||
| 2202 nm | <0.0001 | |||||||
| Reflectance (fresh vegetation samples only) | CP | 560 nm | 36 | 0.592 | 2.150 | <0.0001 | 0.0003 | 0.64 |
| 665 nm | 0.0012 | |||||||
| 865 nm | <0.0001 | |||||||
| 2202 nm | 0.0039 | |||||||
| NDF | 560 nm | 36 | 0.698 | 6.868 | <0.0001 | 0.0001 | 0.72 | |
| 665 nm | <0.0001 | |||||||
| 865 nm | 0.0003 | |||||||
| 2202 nm | <0.0001 | |||||||
| Model Name | Value Predicted | Model Description |
|---|---|---|
| S2_CP_RI * | CP | 7.63 − 54.39 × b1 + 31.37 × b2 + 21.23 × b3 − 25.33 × b4 |
| S2_NDF_RI ** | NDF | 54.49 + 207.53 × b1 − 193.99 × b2 − 54.19 × b3 + 111.15 × b4 |
| Where b1, b2, b3 and b4 are the reflectances at the 560 nm, 665 nm, 865 nm, and 2202 nm bands, respectively. | ||
| Randomly Selected Samples | Partial Least-Squares (PLS) Calibration of 33 Samples | Validation of 10 Samples (Test) | Prediction of Seven Samples (External Test) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSEC (%) | R2 | p Value | Index of Agreement | RMSEP (%) | R2 | p Value | Slope | R2 | |
| Data1 | 2.136 | 0.70 | 0.0001 | 0.70 | 2.219 | 0.72 | 0.0018 | 0.660 | 0.66 |
| Data2 | 2.159 | 0.71 | 0.0001 | 0.71 | 2.082 | 0.71 | 0.0022 | 0.683 | 0.68 |
| Data3 | 2.172 | 0.71 | 0.0001 | 0.70 | 1.854 | 0.77 | 0.0002 | 0.663 | 0.66 |
| Data4 | 2.142 | 0.72 | 0.0001 | 0.71 | 1.549 | 0.82 | 0.0039 | 0.673 | 0.67 |
| Data5 | 1.951 | 0.74 | 0.0001 | 0.74 | 2.858 | 0.59 | 0.097 | 0.643 | 0.64 |
| Randomly Selected Samples | PLS Calibration (39 Samples) | Validation (10 Samples) | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSEC (%) | R2 | Index of Agreement | p Value | RMSEP (%) | R2 | p Value | ||
| CP | Data1 | 2.02 | 0.69 | 0.71 | 0.0001 | 2.17 | 0.73 | 0.0015 |
| Data2 | 2.15 | 0.69 | 0.69 | 0.0001 | 1.53 | 0.78 | 0.0006 | |
| Data3 | 2.01 | 0.72 | 0.71 | 0.0001 | 1.76 | 0.71 | 0.0023 | |
| Data4 | 2.04 | 0.69 | 0.70 | 0.0001 | 1.79 | 0.82 | 0.0003 | |
| Data5 | 2.12 | 0.70 | 0.72 | 0.0001 | 1.56 | 0.81 | 0.0004 | |
| NDF | Data1 | 7.12 | 0.69 | 0.74 | 0.0001 | 7.31 | 0.60 | 0.0086 |
| Data2 | 7.21 | 0.66 | 0.72 | 0.0001 | 6.41 | 0.78 | 0.0006 | |
| Data3 | 6.67 | 0.71 | 0.72 | 0.0001 | 8.79 | 0.61 | 0.0074 | |
| Data4 | 7.47 | 0.63 | 0.69 | 0.0001 | 5.30 | 0.86 | 0.0001 | |
| Data5 | 7.57 | 0.64 | 0.70 | 0.0001 | 4.63 | 0.86 | 0.0001 | |
| Model (N = 43) | Estimated Parameter | RMSE | R2 | p-Value of Model |
|---|---|---|---|---|
| Reflectance | CP | 2.102 | 0.71 | <0.0001 |
| NDF | 5.525 | 0.78 | <0.0001 | |
| NDVI [66] | CP | 3.006 | 0.36 | <0.0001 |
| NDF | 11.719 | 0.06 | 0.1283 | |
| SAVI [73] | CP | 2.987 | 0.37 | <0.0001 |
| NDF | 11.713 | 0.06 | 0.1247 | |
| WDRVI [70] | CP | 3.028 | 0.35 | <0.0001 |
| NDF | 11.823 | 0.04 | 0.2060 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lugassi, R.; Zaady, E.; Goldshleger, N.; Shoshany, M.; Chudnovsky, A. Spatial and Temporal Monitoring of Pasture Ecological Quality: Sentinel-2-Based Estimation of Crude Protein and Neutral Detergent Fiber Contents. Remote Sens. 2019, 11, 799. https://doi.org/10.3390/rs11070799
Lugassi R, Zaady E, Goldshleger N, Shoshany M, Chudnovsky A. Spatial and Temporal Monitoring of Pasture Ecological Quality: Sentinel-2-Based Estimation of Crude Protein and Neutral Detergent Fiber Contents. Remote Sensing. 2019; 11(7):799. https://doi.org/10.3390/rs11070799
Chicago/Turabian StyleLugassi, Rachel, Eli Zaady, Naftaly Goldshleger, Maxim Shoshany, and Alexandra Chudnovsky. 2019. "Spatial and Temporal Monitoring of Pasture Ecological Quality: Sentinel-2-Based Estimation of Crude Protein and Neutral Detergent Fiber Contents" Remote Sensing 11, no. 7: 799. https://doi.org/10.3390/rs11070799
APA StyleLugassi, R., Zaady, E., Goldshleger, N., Shoshany, M., & Chudnovsky, A. (2019). Spatial and Temporal Monitoring of Pasture Ecological Quality: Sentinel-2-Based Estimation of Crude Protein and Neutral Detergent Fiber Contents. Remote Sensing, 11(7), 799. https://doi.org/10.3390/rs11070799







