Abstract
Digital aerial photogrammetric (DAP) techniques applied to unmanned aerial system (UAS) acquired imagery have the potential to offer timely and affordable data for monitoring and updating forest inventories. Development of methods for individual tree crown detection (ITCD) and delineation enables the development of individual tree-based, rather than stand based inventories, which are important for harvesting operations, biomass and carbon stock estimations, forest damage assessment, and forest monitoring in mixed species stands. To achieve these inventory goals, consistent and robust DAP estimates are required over time. Currently, the influence of seasonal changes in deciduous tree structure on the consistency of DAP point clouds, from which tree-based inventories can be derived, is unknown. In this study, we investigate the influence of the timing of DAP acquisition on ITCD accuracies and estimation of tree attributes for a deciduous-dominated forest stand in New Brunswick, Canada. UAS imagery was acquired five times between June and September 2017 over the same stand and consistently processed into DAP point clouds. Airborne laser scanning (ALS) data, acquired the same year, was used to reconstruct a digital terrain model (DTM) and served as a reference for UAS-DAP-based ITCD. Marker-controlled watershed segmentation (MCWS) was used to delineate individual tree crowns. Accuracy index percentages between 55% (July 25) and 77.1% (September 22) were achieved. Omission errors were found to be relatively high for the first three DAP acquisitions (June 7, July 5, and July 25) and decreased gradually thereafter. The commission error was relatively high on July 25. Point cloud metrics were found to be predominantly consistent over the 4-month period, however, estimated tree heights gradually decreased over time, suggesting a trade-off between ITCD accuracies and measured tree heights. Our findings provide insight into the potential influence of seasonality on DAP-ITCD approaches to derive individual tree inventories.
1. Introduction
Forest inventories are a critical component of sustainable forest management and offer key information on a range of spatial and temporal scales [1]. Conventionally, forest inventories have employed a combination of field plots, aerial photographic interpretation, and remote sensing techniques that facilitate forest management decision making such as operational planning, wood supply, and regeneration strategies [2]. Maintaining and updating forest inventories is costly however for both field plot establishment and the measurement and interpretation of the aerial imagery, which is often undertaken manually [3,4]. Research advancements in remote sensing have demonstrated accurate derivation of key forest attributes, and offer detailed tree-level information when compared to more common stand inventory approaches [5]. This offers the potential for the accurate estimation of parameters such as tree height, canopy cover, age class, tree density, and tree spatial patterns [6], which in turn inform harvesting operations, carbon stock and biomass estimations, forest monitoring, and forest damage assessment [7,8].
Tree-level inventory information derived from remote sensing data can be extracted from individual tree crown detection (ITCD) methods which refer to the detection of trees, delineation of crowns, and derivation of tree attributes [9]. Past research on ITCD was focused on passive aerial and satellite imagery, however, more recently this has shifted to airborne laser scanning (ALS) [9], which is often considered a best available technology for digital terrain model (DTM) generation [10] and forest inventory modeling [11,12].
Koch et al. [13] grouped ITCD approaches into four categories: raster-based; point cloud-based; raster, point, and a priori data combined; and tree shape reconstruction methods. Most ITCD research follows a raster-based approach using a canopy height model (CHM) [14,15,16,17,18] incorporating local maxima (LM) filtering and watershed segmentation algorithms [19]. Watershed segmentation incorporates edge-detection and region-growing methods [20]. Marker-controlled watershed segmentation (MCWS) was first proposed by Meyer and Beucher [21] and is performed using user-specified markers rather than LM, to avoid over-segmentation. Several papers have successfully applied LM filtering with a variable window using a marker function for detecting tree apexes [22,23,24].
ITCD studies using ALS data have predominantly focused on coniferous forest stands with few focusing on deciduous species [7,22,23,25,26,27]. Generally, results of ITCD methods using ALS have found that tree detection and individual tree height estimation were impacted by forest structure, particularly tree stocking density and spatial clustering of the tree boles [26], across a range of forest types including boreal, deciduous, broadleaf, and tropical pulpwood stands. ITCD studies in deciduous forests have generally indicated lower accuracies due to the more complex structure, crown shape, and a relatively flat canopy surface [23,28]. The LM filter that is often used for detecting trees is known to be more successful for conifer trees due to their cone shape and well-defined apex [27]. The mentioned studies also applied the ITCD approaches in perceived optimum conditions of either leaf-on or leaf-off conditions rather than during the transition periods of spring and fall. As a result, the consistency of these ITCD based approaches using imagery acquired within a single year is seldom addressed. Nevalainen et al. [16] noted that most studies have focused on a single plot at a single time and suggested that more extensive studies over time and across a wider range of forest types are needed. In this paper, consistency covers the seasonal influences on ITCD accuracy and corresponding metrics.
Unmanned aerial systems (UAS) offer the capacity to obtain high spatial resolution imagery and allow for more timely and cost-efficient data acquisitions compared to ALS [29,30]. They are of great interest to the forestry inventory community as dense 3D point clouds can be produced by digital aerial photogrammetric (DAP) processing techniques which can, in turn, be used to derive inventory-related information [17]. As a result, the research focus for ITCD based algorithms is shifting towards the application of datasets derived from these platforms. UAS have seen significant growth and adaptation in commercial markets [29]. Currently, UAS have the potential to aid in near real-time operational forest inventory updates [31]. UAS allow rapid and quick data acquisition, give flexible control over temporal and spatial resolution, have low operational costs, and are user-friendly [29,32]. Recent advancements have focused on maximizing flight times, improving payload capacity, automating navigation, and reducing weight and size [33]. Responsive data acquisition and analysis can provide information about disturbance such as windthrow [34], fire [35], and harvest [4] as well as long term assessments of regeneration and growth [36], which can help to inform operational forest management initiatives.
DAP data generated from UAS imagery are capable of producing high-density digital surface models (DSMs) that characterize the outer envelope of the dominant forest canopy and provide multi-spectral information in a 3D environment [37]. Unlike ALS, DAP cannot reliably penetrate canopies to characterize internal canopy structure and terrain [38]. DAP has however proven effective and accurate for the creation of DTMs under open stand conditions [31], estimating inventory attributes for trees in the dominant canopy [39], and following canopy phenological dynamics and morphological changes [40].
Research on ITCD derived from high spatial resolution UAS-DAP has been limited but is an active area of research [14,15,16,17,18]. To date, the main findings suggest that UAS-DAP can generate spatially and temporally accurate forest inventory attributes for dominant stems, such as tree height, crown diameter, and species, even under poor and variable illumination conditions [16]. Challenges for UAS-DAP ITCD concerning the consistency of results are likely due to a combination of factors including varying image acquisition conditions as well as changing forest parameters [17]. Early studies on building tree-level inventories from airborne data highlight some of the environmental factors influencing the extraction of tree-level information, such as illumination, bidirectional reflectance distribution, canopy geometry, viewing angle, wind speed, and fog [41,42]. A small number of studies have examined the application of ITCD to derive tree-growth from UAS derived CHMs [36]. Additionally, [43] demonstrates the capability of UAS for measuring within-season individual tree growth, using a novel approach incorporating derived CHMs. Notably, UAS-DAP ITCD research addressing seasonal changes, such as seasonal leaf green up and senescence has been limited. It is likely that deciduous crowns, in particular, will appear different on consecutive multi-season acquired DAP point clouds and these variations in characterization should be investigated to determine their influence on ITCD results and the extraction of tree-level inventory attributes.
In this study, we undertake a multi-temporal UAS-based analysis to assess both the multi-seasonal accuracy and consistency of ITCD attribute extraction using DAP. Five DAP acquisitions were examined over a 4-month time period and compared to a reference ALS acquisition. Tree apex detection and crown delineation were performed based on the CHMs of all data acquisitions. Statistics were calculated for segmented trees including tree height, crown size, crown shape complexity indices, and measures of the vertical distribution of points. DAP’s ITCD errors and accuracies were assessed using the segmented ALS reference. Trees were matched across all data acquisitions to investigate metric consistency through time. It is anticipated that results will help to improve understanding of ITCD accuracy and consistency in deciduous stands, furthering knowledge on the influence of seasonal and phenological variation for characterizing the crown size, shape, and density. Insight into acquisition planning and data parameterization will help guide planning and decision making for UAS acquisitions.
2. Materials and Methods
2.1. Study Area
The study area is located in the central uplands of New Brunswick, approximately 300 m above sea level (47°27′08″N, 68°06′32″W; Figure 1). The 0.9 ha site has a slightly sloping terrain towards the south. The site has a continental climate, receiving an average of 475–525 mm of rain from May to September [44]. The site had a total stem density of approximately 447 stems ha−1 with 118 stems ha−1 typical of trees in the dominant canopy. The region has a varied history of forest management including research-based plots, as well as public and private forest management activities [44]. The stands are dominated by deciduous hardwood trees, comprised of sugar maple (Acer saccharum), yellow birch (Betula alleghaniensis), red maple (Acer rubrum), and beech (Fagus). A number of smaller conifer softwood stands exists, comprised primarily of balsam-fir (Abies balsamea).
Figure 1.
Study area near Edmundston; an orthophoto of 25 July 2017 is displayed in a false color composite of red, green, and near-infrared. Both maps are projected in WGS 84/UTM zone 19N.
2.2. Field Measurements
Height, diameter at breast height (DBH), crown size, and species were recorded for each stem within the field site [45]. The stem density within the dominant canopy was approximately 118 stems ha−1 with an average crown size of 12.4 m and a DBH of 36 cm. More details on forest layout can be found in Table 1.

Table 1.
Forest layout based on field measurements.
2.3. ALS Data
ALS data with a mean point density of 25.6 points m−2 was acquired between June 12 and June 13 2017 as part of a province-wide ALS acquisition campaign by the Government of New Brunswick. Pulses had a maximum of 5 returns. The ALS point cloud was used for DTM extraction and served as a reference for UAS-DAP ITCD.
2.4. UAS-DAP Data
Five UAS flights were undertaken in 2017 over a 4-month period (June 7, July 5 and 25, August 29, and September 22). Aerial images were acquired using a Sequoia multi-spectral camera which consists of a true-colour composite camera, a sunlight sensor to capture the sun angle and irradiance, and four individual monochrome sensors measuring in green (530–570 nm), red (640–680 nm), red-edge (730–740 nm), and near-infrared (770–810 nm) [46]. The sensor was mounted to a senseFly eBee UAS, which is capable of semi-autonomous mapping. The mean flying altitude varied between approximately 73 and 89 m and the mean ground sample distance between 6.6 and 8.2 cm (Table 2). The imagery had a forward and lateral overlap of approximately 85% and 80%, respectively. Details of the multi-spectral camera are shown in Table 3. In total, 106 trees were individually located and matched with overstorey tree crown locations from acquired ortho-imagery.

Table 2.
Imagery acquisition dates and corresponding season, mean above ground flight altitude, mean ground sample distance (GSD), mean sun angle, and mean point cloud point density.

Table 3.
Sensor characteristics including platform type, spectral sensitivity, and spatial resolution. Source: Pix4D (2018) [46].
Photogrammetric processing followed Agisoft Photoscan’s workflow including conjugate tie-point pixels matching in three or more overlapping images, image alignment using tie-points and measurements of GPS and inertial measurement unit, and radiometric calibration using pre-flight target images [47]. Following image alignment, an orthomosaic was built and dense DAP point clouds were generated at the original image scale with mean point densities between 35.5–46 points m−2. DAP point clouds were co-registered and aligned with the ALS point cloud using the iterative closest point (ICP) algorithm due to lack of available ground control data [48].
2.5. Processing and Analysis
The processing approach developed in this study comprised four steps: point cloud processing, ITCD, tree matching, and time-series analysis. First, the UAS derived data was pre-processed which included: normalization of the DAP point cloud against the ALS-derived DTM, and CHM modeling. Second, an ITCD routine was applied to locate individual trees in both the DAP and the ALS 3D data. Third, individual tree metrics were derived and tracked across the multi-temporal DAP data acquisitions using the segmented tree locations that were matched across all acquisitions. Finally, a time series analysis of the extracted attributes and an accuracy comparison was undertaken. Figure 2 presents a conceptual workflow of the followed methodology.
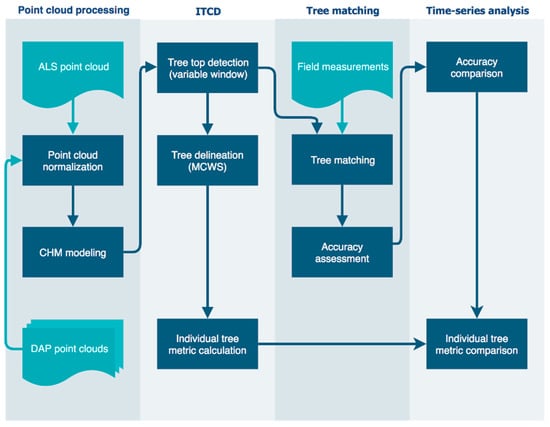
Figure 2.
Conceptual workflow detailing the methodological process used for point cloud processing, individual tree crown detection and delineation (ITCD), tree matching (accuracy assessment), and time-series analysis.
2.5.1. Point Cloud Processing
The DAP point clouds were normalized using reference ALS ground returns. To do so a triangulated irregular network (TIN) was developed from the ALS ground returns. Separate CHMs were constructed from either the ALS first returns or from the normalized DAP acquisitions. A pit-free algorithm developed by Khosravipour et al. [49] was used for CHM creation in all cases. Dominant vegetation cover was determined for each date by calculating the proportion of points > 15 m based on the assumption that points > 15 m represented the dominant deciduous canopy [31]. The threshold used was conservative to account for the fact that DAP only characterizes the outer canopy layer [50]. CHM height change was calculated cell-by-cell for each subsequent DAP acquisition resulting in four height change maps. An average CHM height change was determined for five sample areas of each 50 m2.
2.5.2. ITCD
Dominant tree apexes were detected on each DAP CHM using a variable window filter algorithm. A circular search window was used due to the generally circular shape of tree crowns. The moving window marks a single LM within the window as a tree apex. The CHM cell value in each window’s center is used to define the radius of the search window. The radius is dependent on a marker function describing the relationship between tree height and crown size. In this work, a variable window filter algorithm and marker function developed for deciduous forest stands by Popescu and Wynne [22] was adopted.
The marker-controlled watershed segmentation (MCWS) algorithm was used to segment the continuous CHM into crown segments. The watershed transformation computed the reversed catchment basins at starting locations identified by the previous defined LM. Neighboring pixels around each LM were given priority based on the gradient magnitude of the pixel. The pixel with the lowest priority (lowest gradient magnitude) was extracted and labeled the same as the neighboring marker. Non-labeled neighbor pixels, including new ones, were again evaluated based on their gradient magnitude. Neighboring pixels with the lowest priority rank were added to the marked area until all neighboring pixels were marked [21].
For each segmented crown, the individual tree point clouds were extracted in order to compute a number of vertical structural variability, geometric, and landscape metrics (Table 4). Landscape metrics relate to the normalized perimeter-area ratio. Shape index values reach from 1 (square shape) to infinity (complex shape). Fractal dimension index values lie between 0–3, representing point (0), line (1), plane (2), and cube (3) shapes.

Table 4.
List and description of airborne laser scanning (ALS) and digital aerial photogrammetric (DAP) derived forest variables.
Lastly, a non-parametric Kruskal–Wallis with Dunn’s posthoc test was applied to all computed metrics to determine whether population medians for data acquisitions were significantly different (p < 0.01). Dunn’s post hoc test is a common method for multiple pairwise comparisons with non-parametric data [51]. The non-parametric tests are required because they do not assume normality nor homoscedasticity [52,53].
2.5.3. Tree Matching
Segmented tree crowns from the DAP acquisitions were matched to their corresponding ALS-derived LM to assess the DAP ITCD accuracies. A tree segment was considered a correct match if it contained a reference ALS LM. If a segment contained multiple reference LM then it was matched with the reference LM closest to the LM of the segment. Trees crossing the plot boundary and thus only partially segmented were removed. Note that the boundary of the plot slightly changed for each DAP acquisition due to edge effect correction. Only references of ALS LM within the plot boundary were used for accuracy assessment. To evaluate the accuracy, recall (r), precision (p), omission (OM) and commission (COM) error percentage, and accuracy index (AI) were calculated as [56,57]:
where TP, FP, and FN are the true positives, false positives and false negatives respectively produced by the segmentation algorithm and where REF is the number of used reference trees in the study area. Omission and commission error percentages are inversely related to recall and precision respectively [57]. The accuracy index (AI) quantifies the trade-off between omission (false positives) and commission (false negatives) errors [56].
r = TP/(TP + FN)
p = TP/(TP + FP)
OM = 100 (1 − r)
COM = 100 (1 − p)
AI = 100 (1 − (FP + FN)/REF),
For point cloud processing LASTools software was used including the tools: lastile, lasnoise, lasmerge, and lasheight. LidR’s R package function grid_tincanopy was used for CHM creation. ForestTools R package was used for the implementation of the variable search window and MCWS using the functions: vwf and mcws. Vertical structural variability metrics were produced with LidR’s lasclassify and tree_metrics functions. SDMTools’ R package function PatchStat produced the geometric and landscape metrics. PMCMR’s R package function posthoc.kruskal.dunn.test was used for the time series analysis.
3. Results
3.1. ITCD
On average, 84 trees were mapped based on the DAP acquisitions from June 7 to Sept 22 showing detection rates from 80.2%–89.3% (Table 5). In total, 65 tree crowns were matched between the DAP acquisitions and thus consistently mapped over time. Of these 65 crowns, 61 could also be delineated in the ALS dataset and matched with the DAP acquisitions. A total of 58 tree crowns were matched through all datasets including the field measurements. Table A1 (Appendix A) shows the ITCD accuracies using multiple matching operations.

Table 5.
A temporal trajectory by date of segmentation results, vegetation cover, and an average cell-by-cell canopy height model (CHM) height change for each following DAP acquisition using five 50 m2 sample areas. Recall, precision, errors, detection rate, and accuracy index are presented using ALS local maxima as a reference for accuracy assessment.
Figure 3 shows the errors and accuracies of ITCD for the DAP acquisitions over time compared to ALS-based LM. The DAP acquisitions show accuracies between 55.0–77.1% with an average of 66.0%. The DAP acquisition on July 25 showed the lowest accuracy with an omission error of 19.8% and commission error of 24.3%. The last DAP acquisition on September 22 had the highest accuracy with an omission error of 12.4% and a commission error of 10.7%. Both errors for this DAP acquisition were distinctly lower than for other times of the year. The mean omission and commission errors were 17.3% and 16.4%, respectively. The omission error had a variance of 8.4 while the commission error had a variance of 19.3. The omission error indicated a downward trend for the last two DAP acquisitions. The commission showed a notable outlier for July 25. Table 5 reports the accuracies and errors over time in more detail.
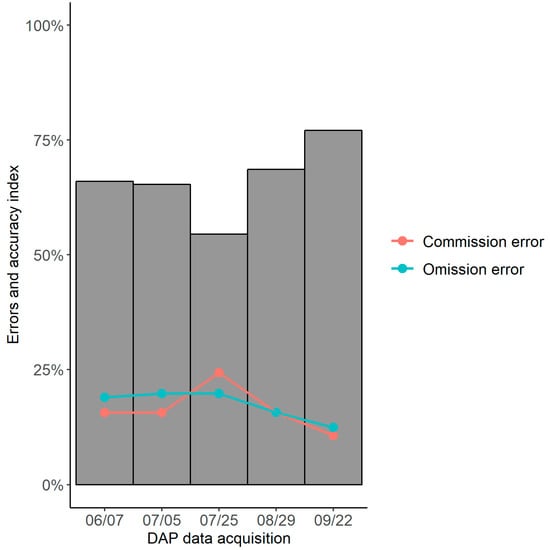
Figure 3.
Bar and line chart presenting a temporal trajectory by date of ITCD accuracies (accuracy index) and commission and omission errors for segmented DAP point clouds, using ALS local maxima (LM) as a reference for accuracy assessment.
When ITCD results were compared with field measurements, ALS showed an overall accuracy of 79.2%. DAP acquisitions showed accuracies from 59–72% with an average of 67%. The variance of commission error was smaller than for the ALS-based results, namely 12.7 compared to 19.3. This led to smaller differences between the accuracy percentages. The DAP acquisitions of July 5 (59%) and July 25 (61%) had the lowest accuracies of the five acquisitions. Table A2 (Appendix A) provides further detail on accuracies and errors over time, using the field measurements as a reference.
3.2. Time Series Analysis
Figure 4 shows the differences in tree crown-based point heights across DAP- and ALS-based point clouds by height percentile. Up to the 50th percentile and above the 80th percentile DAP acquisitions were not significantly different, determined with Dunn’s posthoc test (p < 0.01). Between the 60th and 80th height percentiles, the acquisition on June 7 in spring was significantly different from the DAP acquisition on September 22 in fall.
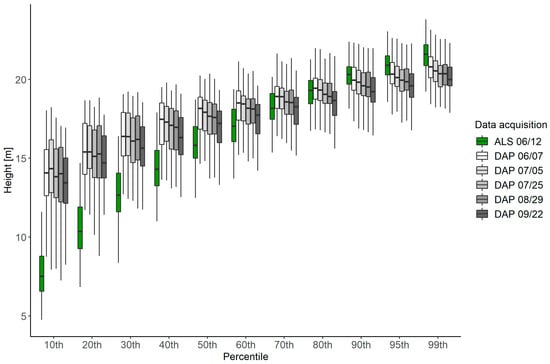
Figure 4.
Boxplots presenting a temporal trajectory by date of tree crown-based point heights of ALS and DAP point clouds by height percentile.
For the 50th and 60th percentiles, only the DAP acquisition on September 22 in fall was not significantly different from ALS. For 70th and 80th height percentile, the DAP acquisitions matched ALS. For the 90th height percentile, ALS was not significantly different from the four DAP acquisitions in spring and summer. For 95th height percentile, ALS was not significantly different from the two DAP acquisitions on June 7 in spring and July 5 in early summer. Finally, for the 99th height percentile, ALS was not significantly different from the DAP acquisition in spring.
Other than kurtosis, all metrics concerning the vertical structural variability of points were not significantly different over time, as shown in Figure 5. For mean height and standard deviation, ALS was significantly different compared to the DAP segmentations. DAP characterizes only the outer canopy and shows smaller variation across point heights compared to ALS. For both ALS and DAP acquisitions there was no significant difference in the negative skewness across all data acquisitions. For kurtosis, the ALS was significantly different to the DAP acquisitions on June 7 and August 29. This means the distribution of the point heights of those two DAP acquisitions was slightly more heavy-tailed relative to the other acquisitions.
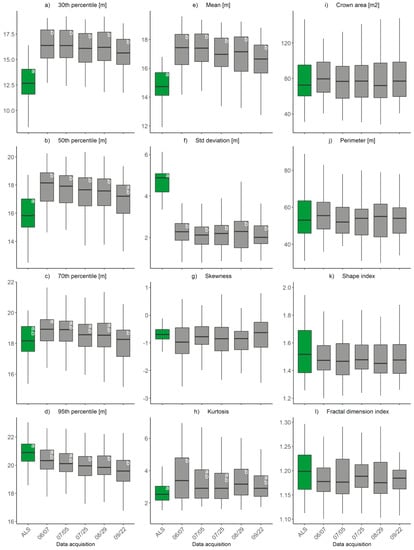
Figure 5.
Boxplots presenting a temporal trajectory of eight vertical structural variabilities (a–h), and two geometric (i,j) and two landscape (k,l) metrics of the segmented trees, by date. Groups that share the same letter (or no letter) are not significantly different (p < 0.01), determined with Kruskal–Wallis and Dunn’s posthoc test.
All landscape and geometric metrics were not significantly different across DAP acquisitions and ALS, as shown in Figure 5, confirming the crown areas and shapes were not significantly different over time. Although, ALS seemed to show slightly more shape complexity compared to the DAP, as shown in Figure 5.
Table 5 shows the temporal trajectory of vegetation cover by date and an average cell-by-cell CHM height change for each following DAP acquisition using five 50 m2 sample areas. Highest canopy cover occurred on June 7 in spring and July 5 in early-summer with 81.1% and 81.8% respectively. The canopy cover gradually decreased to 78.8% on July 25 and 78.5% on August 29. Into fall, there was a drop in canopy cover to 75.8% on September 22 which was the lowest canopy cover of all DAP acquisitions. June 7 and September 22 were more than one standard deviation (2.83) from mean canopy cover (79.2%). Mean CHM height change was from –0.02–0.48 m, with the change between July 5 and July 25 being the greatest (0.48 m), and change variation between other CHMs lower (0–0.14 m).
4. Discussion
Three-dimensional tree level information derived using UAS acquired imagery and DAP data could fundamentally alter approaches for developing fine scale operational forest inventories. This is especially relevant in operational forest environments where acquisition timing is important. The purpose of this work is to examine the complexity associated with mapping crowns consistently over time and the potential influence of seasonality on estimated forest inventory attributes. Previous research has not focused on the influence of seasonal transition periods on ITCD accuracy, rather focusing on either open canopy conditions or non-changing conifer trees. Although tree segmentation in deciduous dominated stands is challenging, both height and shape related tree metrics were found to be relatively consistent through time.
4.1. ITCD
The accuracies of the UAS-DAP ITCD through time were similar to those of ALS-based research using comparable methodologies and deciduous forest stands. Popescu and Wynne [22] found an omission and commission error of 27.07% and 27.61%, respectively, compared to 17.34% (12.4%–19.8%) and 16.38% (10.7–24.3%) respectively in this research. It is known that the quality of photogrammetrically-derived information describing conditions below the dominant canopy surface is highly dependent on the density of the forest [58]. As mentioned previously, deciduous forest stands have a relatively flat outer canopy envelope and generally have more complex crown structures. Coniferous trees are more conical and maintain a stronger relationship between tree height and crown size. Single deciduous trees can contain several local maxima and can have inter-growth amongst individuals [56]. Several local maxima could lead to high commission errors, where inter-growth could cause omission errors. The two highest ITCD accuracies in our study occurred on August 29 in late-summer and on September 22 in early-fall when canopy-cover was decreasing, due to relatively low omission and commission errors. This potentially indicates that having larger canopy openings allows for better detection of individual deciduous trees. The omission error is constantly higher for the first three acquisitions on June 7, July 5, and July 25 and decreased thereafter. Omission error showed a gradual downward trend over the season. The accuracies of the remaining DAP acquisitions during spring and summer varied due to a single high outlier of commission error on July 25 in summer. Variations in commission error could be related to challenges related to detecting trees in complex, closed-canopy, and highly dense deciduous forest stands [56]. This suggests an influence of multiple local maxima on the ITCD results from leaf-on conditions. Particularly from spring to mid-summer, DAP point clouds presented ITCD challenges. Results suggest that leaf-off conditions are more conducive for ITCD, but other environmental and point cloud accuracy-related influences should also be acknowledged.
Note that the variation in the mean CHM height over the time-series varied by a maximum of almost 0.5 m between July 25 and the preceding data acquisition (Table 5). This indicates possible errors related to imagery orientation and alignment on that date, and as a result, may explain some of the tree matching errors. In addition, the small variations in CHM height for the other data acquisitions indicated a reduced influence of these registration errors. Alternatively, a high commission error could also be caused by using too small of an LM search window [27]. Adjustment of the marker function could further improve ITCD results.
This research focused on examining the seasonal influences related to ITCD. The influence of shadows within and between crowns was not specifically addressed; shadow is related to canopy density and foliar crown health [41]. In addition, ITCD algorithms can have problems with segmenting crowns over bright backgrounds caused by, for example, exposed soil and understory vegetation [12]. Acquisition parameters were consistent over time except for a lower sun angle on July 25. It is acknowledged that DAP generation errors can propagate from many sources such as shadowing, solar angle/illumination, occlusion from neighboring tree canopies, bidirectional reflectance distribution, canopy geometry, and tree swaying caused by wind [38,59].
4.2. Forest Inventory Attributes
Some vertical structural variability metrics such as the 90th, 95th, and 99th height percentiles have shown correlation with tree attributes such as mean tree height and maximum tree height in previous research [25]. There appeared to be no consistent pattern between the timing of acquisition between spring and early-fall and changes for these three percentiles. Nevertheless, a slight downward trend of estimated tree heights over the season was shown, in Figure 4. An indicator of the impact of canopy cover is apparent on the 60th–80th percentile height where the estimated heights of the first acquisition in spring and last acquisition in fall are significantly different. The downward trend was likely related to seasonality and change of canopy cover, however differences in measured tree heights could also be due to damaged trees. To quantify decreasing heights in relation to such natural occurrences, field measurements and validation would be needed [15]. It is likely that the influence of artifacts in the CHMs, such as errors related to orientation and alignment and irregularities in canopy surface elevation, are limited because the CHM is pit-free, and because mean CHM heights were stable or increasing (Table 5).
Geometric, landscape, and other vertical distribution of points metrics were not significantly different between both DAP and ALS acquisitions and therefore not likely to be influenced by seasonality. Note that all derived individual tree height metrics could have been influenced by segment characteristics such as area, perimeter, and location. However, the area and perimeter of the segments were not significantly different for the acquisitions. Furthermore, when crown locations slightly differ because of minor misalignments between point clouds, the ITCD approach accounts for misalignment effects because it adjusts crown locations and plot extent accordingly.
Another indicator of seasonal influence can be found in the comparison between ALS and DAP-based tree heights. DAP acquisitions on August 29 in late-summer and September 22 in fall were significantly different compared to ALS above the 80th height percentile. Also below the 70th height percentile significant height differences between ALS and DAP were found, however this is likely due to technical characteristics of both methods [58,60]. This work suggests that leaf-on conditions may have a positive influence on measured tree heights, and it is plausible that heights will be underestimated in leaf-off conditions. This suggests updating ALS-based forest inventory height attributes is preferably done with DAP acquired in leaf-on conditions. These findings agree with the earlier research [39], who found more similarity for height metrics between ALS and DAP when canopy cover increased using an area-based approach.
This research shows consistency between DAP-based individual tree heights, but also shows a pattern of slightly decreasing tree heights for acquisitions with a lower canopy cover while ITCD accuracies increase. This indicates a trade-off related to canopy cover, between ITCD accuracy, and measured tree heights. Future research should take into account a larger time-span to investigate if ITCD accuracies could improve in situations with leave-off conditions and if estimated tree heights further decrease. When tree heights of relevant height percentiles start to be significantly different over a larger period, only then could such a trade-off be confirmed.
4.3. Future Outlook
Operational forest management decisions are likely to rely on detailed tree-level inventories increasingly. This research indicates that DAP-ITCD based approaches should anticipate lower extracted tree heights in fall and lower detection rates in spring and early-summer. When these seasonal influences are taken into account, managers could have a more detailed understanding of forest characteristics such as tree density and forest damage based on ITCD results compared to stand wise-inventories. A foreseen UAS-as-a-service data collection market together with automated ITCD could allow tree-level inventories to become an integral part of operational forest management.
A shift towards point cloud-based ITCD methods is becoming more prominent in the literature [3,9,27,57,61]. Point cloud-based algorithms could increase ITCD accuracies and detection of understory trees in conifer stands using ALS data, however, may not be as successful in deciduous stands with larger and more complex crowns or using DAP point cloud data with less penetration of the outer canopy [57]. In addition, spectral data can be used to classify forests by stand type which can, in turn, be used to apply appropriate ITCD methods [22]. Future research could focus on determining how to take into account spectral information in combination with seasonality in areas with various forest stand types.
5. Conclusions
Using five multi-temporal UAS-based DAP datasets, ITCD accuracies were found to vary. The highest ITCD accuracy was observed on September 22 in fall (77.1%) when canopy cover is relatively low (Table 5). The capability of tree detection algorithms is lowest in deciduous forest stands with complex crown structures. Multiple local maxima and inter-growth amongst individual trees are likely the cause of relatively high commission and omission errors respectively in leaf-on situations. In addition, it is acknowledged that the high ITCD errors and low accuracy (54.5%) on July 25 are likely influenced by point cloud orientation and alignment errors. Estimated tree heights, as well as other measures related to crown shape, are consistent over the period with only the 60th–80th percentile heights being significantly different between spring and fall. Estimated tree heights gradually decreased over time, suggesting a trade-off between ITCD accuracies and measured tree heights. Future research should incorporate a larger time-span to confirm this trade-off.
Author Contributions
Conceptualization, R.J.G.N., N.C.C., and T.R.H.G.; pre-processing, T.R.H.G.; formal analysis, R.J.G.N.; investigation, R.J.G.N.; methodology, R.J.G.N.; resources, G.P.; supervision, N.C.C. and T.R.H.G.; visualization, R.J.G.N.; writing—original draft, R.J.G.N.; writing—review and editing, R.J.G.N., N.C.C., T.R.H.G., and G.P.
Funding
This research was funded by AWARE (Assessment of Wood Attributes from Remote Sensing NSERC; grantee Prof Nicholas Coops, UBC). The project was realized with direct funding from the NHRI (Northern Hardwoods Research Institute) for UAV flight missions, surveying, and plot establishment. The ALS point cloud data was provided by the government of New Brunswick.
Acknowledgments
We thank Pamela Hurley Poitras for her dedication to UAS imagery acquisition. This research was funded by the AWARE (Assessment of Wood Attributes using Remote Sensing) Natural Sciences and Engineering Research Council of Canada Collaborative Research and Development grant to a team led by Nicholas Coops with support from NHRI. We thank all anonymous reviewers and journal editorial staff for their efforts in improving the quality of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Accuracy index values for all segmented data acquisitions using field measurements, ALS-based, and DAP-based detected LM as a reference.
Table A1.
Accuracy index values for all segmented data acquisitions using field measurements, ALS-based, and DAP-based detected LM as a reference.
| Segmented Data Acquisitions | ||||||
|---|---|---|---|---|---|---|
| Reference Data | ALS | June 7 | July 5 | July 25 | August 29 | September 22 |
| Field data | 79.2 | 72 | 59.2 | 61 | 71.8 | 72.3 |
| ALS | x | 66 | 65.3 | 54.5 | 68.6 | 77.1 |
| DAP June 7 | 63.2 | x | 77.1 | 71 | 68 | 75.5 |
| DAP July 5 | 50 | 71.6 | x | 69.7 | 59.8 | 71.7 |
| DAP July 25 | 54.4 | 76 | 70.1 | x | 78.4 | 68.2 |
| DAP August 29 | 69.2 | 60.6 | 58.3 | 58.3 | x | 63.7 |
| DAP September 22 | 71.4 | 68 | 71.4 | 72.1 | 68.7 | x |

Table A2.
Segmentation results for the five DAP acquisitions; ITCD accuracies and errors using ALS local maxima as a reference. Recall, precision, errors, detection rate, and accuracy index are presented.
Table A2.
Segmentation results for the five DAP acquisitions; ITCD accuracies and errors using ALS local maxima as a reference. Recall, precision, errors, detection rate, and accuracy index are presented.
| DAP Acquisitions | ||||||
|---|---|---|---|---|---|---|
| ALS | June 7 | July 5 | July 25 | August 29 | September 22 | |
| True positives | 95 | 84 | 77 | 84 | 88 | 88 |
| False positives | 11 | 12 | 19 | 23 | 14 | 15 |
| False negatives | 11 | 16 | 21 | 16 | 15 | 13 |
| Recall | 0.897 | 0.840 | 0.786 | 0.840 | 0.854 | 0.871 |
| Precision | 0.896 | 0.875 | 0.802 | 0.785 | 0.863 | 0.854 |
| Omission error (%) | 10.3 | 16 | 21.4 | 16 | 14.6 | 12.9 |
| Commission error (%) | 10.4 | 12.5 | 19.8 | 21.5 | 13.7 | 14.6 |
| Detection rate (%) | 89.6 | 84 | 78.6 | 84 | 85.4 | 87.1 |
| Accuracy index (%) | 79.2 | 72 | 59.2 | 61 | 71.8 | 72.3 |
References
- Bechtold, W.A.; Patterson, P.L. The Enhanced Forest Inventory and Analysis Program—National Sampling Design and Estimation Procedures; US Department of Agriculture Forest Service, Southern Research Station: Asheville, NC, USA, 2005; Volume SRS-80.
- Prandi, F.; Magliocchetti, D.; Poveda, A.; De Amicis, R.; Andreolli, M.; Devigili, F. New approach for forest inventory estimation and timber harvesting planning in mountain areas: The SLOPE project. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B3, 775–782. [Google Scholar] [CrossRef]
- Lee, H.; Slatton, K.C.; Roth, B.E.; Cropper, W.P., Jr. Adaptive clustering of airborne LiDAR data to segment individual tree crowns in managed pine forests. Int. J. Remote Sens. 2010, 31, 117–139. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Tompalski, P.; Crawford, P.; Day, K.J. Updating residual stem volume estimates using ALS- and UAV-acquired stereo-photogrammetric point clouds. Int. J. Remote Sens. 2016, 38, 2938–2953. [Google Scholar] [CrossRef]
- Tompalski, P.; Wężyk, P.; Weidenbach, M.; De Kok, R.; Hawryło, P. A comparison of LiDAR and image-derived canopy height models for individual tree crown segmentation with object based image analysis. South-Eastern Eur. J. Earth Obs. Geomat. 2014, 3, 21–24. [Google Scholar]
- Brosofske, K.D.; Froese, R.E.; Falkowski, M.J.; Banskota, A. A review of methods for mapping and prediction of inventory attributes for operational forest management. For. Sci. 2014, 60, 733–756. [Google Scholar] [CrossRef]
- Ene, L.; Næsset, E.; Gobakken, T. Single tree detection in heterogeneous boreal forests using airborne laser scanning and area-based stem number estimates. Int. J. Remote Sens. 2012, 33, 5171–5193. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in automatic individual tree crown detection and delineation-evolution of LiDAR data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; White, J.C.; Wulder, M.A.; Yuill, A. Characterizing streams and riparian areas with airborne laser scanning data. Remote Sens. Environ. 2017, 192, 73–86. [Google Scholar] [CrossRef]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ. 2010, 114, 911–924. [Google Scholar] [CrossRef]
- Coops, N.C.; Wulder, M.A.; Culvenor, D.S.; St-Onge, B.A. Comparison of forest attributes extracted from fine spatial resolution multispectral and lidar data. Can. J. Remote Sens. 2004, 30, 855–866. [Google Scholar] [CrossRef]
- Koch, B.; Kattenborn, T.; Straub, C.; Jari, V. Forestry applications of airborne laser scanning: Concepts and case studies. In Managing Forest Ecosystems; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 27, pp. 89–112. ISBN 9789401786621. [Google Scholar]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M.; et al. Using UAV-based photogrammetry and hyperspectral imaging for mapping bark beetle damage at tree-level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Marshall, P.L.; Tompalski, P.; Crawford, P. Unmanned aerial systems for precision forest inventory purposes: A review and case study. For. Chron. 2017, 93, 71–81. [Google Scholar] [CrossRef]
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.; et al. Individual tree detection and classification with UAV-based photogrammetric point clouds and hyperspectral imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef]
- Mohan, M.; Silva, C.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.; Dia, M. Individual tree detection from unmanned aerial vehicle (UAV) derived canopy height model in an open canopy mixed conifer forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining tree height and crown diameter from high-resolution UAV imagery. Int. J. Remote Sens. 2017, 38, 2392–2410. [Google Scholar] [CrossRef]
- Pirotti, F.; Kobal, M.; Roussel, J.R. A comparison of tree segmentation methods using very high density airborne laser scanner data. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W7, 285–290. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis: Principles and Applications, 2nd ed.; Springer: Berlin, Germany, 2003; ISBN 3662050889. [Google Scholar]
- Meyer, F.; Beucher, S. Morphological segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint LiDAR data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Impact of tree-oriented growth order in marker-controlled region growing for individual tree crown delineation using airborne laser scanner (ALS) data. Remote Sens. 2013, 6, 555–579. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkanen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2012, 85, 27–40. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. A robust approach for tree segmentation in deciduous forests using small-footprint airborne LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 532–541. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of individual tree crowns in airborne LiDAR data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Lim, Y.S.; La, P.H.; Park, J.S.; Lee, M.H.; Pyeon, M.W.; Kim, J.-I. Calculation of Tree Height and Canopy Crown from Drone Images Using Segmentation. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2016, 33, 605–614. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Hermosilla, T.; Tompalski, P.; Pelletier, G. Vegetation Phenology Driving Error Variation in Digital Aerial Photogrammetrically Derived Terrain Models. Remote Sens. 2018, 10, 1554. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, J.; Lian, J.; Fan, Z.; Ouyang, X.; Ye, W. Seeing the forest from drones: Testing the potential of lightweight drones as a tool for long-term forest monitoring. Biol. Conserv. 2016, 198, 60–69. [Google Scholar] [CrossRef]
- Peasgood, S.; Valentin, M. Drones: A Rising Market; Sophic Capital: Toronto, ON, Canada, 2015; Available online: http://sophiccapital.com/wp-content/uploads/2015/09/Download-Sophic-Capitals-Aerial-Drone-Report-Here.pdf (accessed on 10 December 2018).
- Mokroš, M.; Výbošťok, J.; Merganič, J.; Hollaus, M.; Barton, I.; Koreň, M.; Tomaštík, J.; Čerňava, J. Early stage forest windthrow estimation based on unmanned aircraft system imagery. Forests 2017, 8, 306. [Google Scholar] [CrossRef]
- McKenna, P.; Erskine, P.D.; Lechner, A.M.; Phinn, S. Measuring fire severity using UAV imagery in semi-arid central Queensland, Australia. Int. J. Remote Sens. 2017, 38, 4244–4264. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; González-Ferreiro, E.; Monleón, V.; Faias, S.; Tomé, M.; Díaz-Varela, R. Use of multi-temporal UAV-derived imagery for estimating individual tree growth in Pinus pinea stands. Forests 2017, 8, 300. [Google Scholar] [CrossRef]
- Vastaranta, M.; Wulder, M.A.; White, J.C.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Kankare, V.; Holopainen, M.; Hyyppä, H. Airborne laser scanning and digital stereo imagery measures of forest structure: Comparative results and implications to forest mapping and inventory update. Can. J. Remote Sens. 2013, 39, 382–395. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; White, J.C. Digital Aerial Photogrammetry for Updating Area-Based Forest Inventories: A Review of Opportunities, Issues, and Future Directions. Curr. For. Rep. 2019, 1–22. [Google Scholar]
- White, J.C.; Stepper, C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparing ALS and image-based point cloud metrics and modelled forest inventory attributes in a complex coastal forest environment. Forests 2015, 6, 3704–3732. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Goodwin, N.; Coops, N.C.; Stone, C. Assessing plantation canopy condition from airborne imagery using spectral mixture analysis and fractional abundances. Int. J. Appl. Earth Obs. Geoinf. 2005, 7, 11–28. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Dempewolf, J.; Nagol, J.; Hein, S.; Thiel, C. Measurement of Within-Season Tree Height Growth in a Mixed Forest Stand Using UAV Imagery. Forests 2017, 8, 231. [Google Scholar] [CrossRef]
- Zelazny, V.F. Our Landscape Heritage: The Story of Ecological Land Classification in New Brunswick; Government of New Brunswick: Fredericton, NB, Canada, 2007; ISBN 978-1-55396-203-8.
- Soucy, M. Protocole d’Installation, Marteloscope 2014 McCoy; Université de Moncton: Edmundston, NB, Canada, 2013; Available online: https://www.researchgate.net/publication/311742145_Protocole_d’installation_des_marteloscopes_Horseback (accessed on 10 December 2018).
- Pix4D. Parrot Sequoia+ Multispectral Camera. Available online: https://www.pix4d.com/product/sequoia/faq (accessed on 23 November 2018).
- Agisoft LLC. Agisoft PhotoScan Professional Edition 2018; Agisoft LLC: St. Petersburg, Russia, 2018; Available online: https://www.agisoft.com/pdf/photoscan-pro_1_4_en.pdf (accessed on 10 December 2018).
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Sensor Fusion IV: Control Paradigms and Data Structures; SPIE: Bellingham, WA, USA, 1992; Volume 1611, pp. 586–606. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/1611/1/Method-for-registration-of-3-D-shapes/10.1117/12.57955.full?SSO=1 (accessed on 10 December 2018).
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating pit-free canopy height models from airborne LiDAR. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A Best Practices Guide for Generating Forest Inventory Attributes from Airborne Laser Scanning Data Using an Area-Based Approach; Natural Resources Canada: Victoria, BC, Canada, 2013.
- Ruxton, G.D.; Beauchamp, G. Time for some a priori thinking about post hoc testing. Behav. Ecol. 2008, 19, 690–693. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple Comparisons Using Rank Sums. Technometrics 1964, 6, 241–252. [Google Scholar] [CrossRef]
- Patton, D.R. A diversity index for quantifying habitat “edge”. Wildl. Soc. Bull. 1975, 3, 171–173. [Google Scholar]
- Mandelbrot, B.B. The Fractal and the Geometry of Nature; W. H. Freeman and Co.: New York, NY, USA, 1982; ISBN 978-0716711865. [Google Scholar]
- Pouliot, D.A.; King, D.J.; Bell, F.W.; Pitt, D.G. Automated tree crown detection and delineation in high-resolution digital camera imagery of coniferous forest regeneration. Remote Sens. Environ. 2002, 82, 322–334. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the LiDAR point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Tomaštík, J.; Mokroš, M.; Saloň, Š.; Chudý, F.; Tunák, D. Accuracy of photogrammetric UAV-based point clouds under conditions of partially-open forest canopy. Forests 2017, 8, 151. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A. Geometric-Optical Modeling of a Conifer Forest Canopy. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 705–721. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Karjalainen, M.; Karila, K.; Kaasalainen, S.; Honkavaara, E.; Hyyppä, J. Forest inventory attribute estimation using airborne laser scanning, aerial stereo imagery, radargrammetry and interferometry—Finnish experiences of the 3D techniques. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W4, 63–69. [Google Scholar] [CrossRef]
- Wang, Y.; Weinacker, H.; Koch, B. A Lidar point cloud based procedure for vertical canopy structure analysis and 3D single tree modelling in forest. Sensors 2008, 8, 3938–3951. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).