3D Forest Mapping Using A Low-Cost UAV Laser Scanning System: Investigation and Comparison

1. Introduction

Forests, one of the main terrestrial ecosystems on Earth, play a vital role in climate change, conservation of biological diversity, and terrestrial ecosystems itself. 3D forest mapping at individual tree level is becoming essential for forest management and ecosystem sustainability [1]. Traditionally, the detailed information of the individual tree is acquired through a statistical field inventory, which is labor-intensive, time-consuming, and accessibility-constrained [2,3]. Therefore, accurate, efficient, and cost-effective methods for accessing the individual tree structure are of great importance [4,5].

With the development of laser scanning in the last twenty years, most researches on forest structure metrics have focused on laser scanning point clouds from different platforms. More specifically, applications of terrestrial laser scanning (TLS) using the single-scan and multi-scan approach for forest inventory have been thoroughly investigated [2]. To further improve the efficiency of data collection using TLS, mobile laser scanning (MLS) is used in forestry surveys because of its ability to measure complex forest areas [6,7]. However, MLS is restricted by the global navigation satellite system (GNSS) shadows in forests. Complementing TLS and MLS in different observational perspectives, airborne laser scanning (ALS) has a high potential in forest applications, providing a good solution for accessing various forest characteristics, such as tree height [8], crown diameter [9], wood volume [10], and biomass [11]. Nevertheless, the spatial and temporal resolutions of the ALS system is limited because of the inflexibility and the high costs.

In recent years, improvements in the convenience and minimization of unmanned aerial vehicles (UAVs) have made it a powerful tool for 3D forest mapping, providing a distinctive combination of high spatial and temporal resolution. Jaakkola et al. [12] provided the first investigation of forest mapping using the unmanned aerial vehicle laser scanning (ULS) and demonstrated that data collected by the ULS system was feasible for automatic measurements of forest. Liu et al. [13] estimated the forest structure attributes using ULS in Ginkgo plantations, in which the effectiveness of plot-level metrics and individual-tree-summarized metrics derived from ULS point clouds were assessed. Furthermore, Jaakkola et al. [14] presented a new concept, “ULS based automatic tree field reference collection”, and demonstrated the feasibility of this concept, even though the whole topic needs further research. In most reported studies of ULS based forest mapping [12,13,15,16], the standard ULS systems were equipped with high-end positioning and orientation system (POS), which has high survey costs and limits the widespread use of the ULS in forest applications. The drawback of such platforms is that the size and budget are significantly larger than what could be considered useful as an operational tool in forest management [17]. Thus, 3D forest mapping using a low-cost ULS system equipped with only low-cost sensors has a high practical meaning. However, studies focusing on 3D forest mapping using low-cost ULS, including data quality evaluation, and individual tree characteristics estimation, are still lacking and attract the attention of the academic community [17,18].

As far as the low-cost ULS system is concerned, system integration is limited by the cost, payload, and the rapid consumption of battery power. A tradeoff must often be made among the accuracy, weight, and cost of sensors [17]. It is difficult to obtain accurate point clouds using the direct georeferencing data estimated by the GNSS and a low-cost inertial measurement unit (IMU) because of insufficient quality control [19]. Therefore, 3D forest mapping with the low-cost ULS system is a great challenge. To optimize the trajectory estimated by the low-cost sensors, Wallace et al. [17] utilized a structure from motion (SfM) algorithm first, then coupled the results of SfM with GNSS/IMU using sigma point Kalman Filter. They handled the SfM algorithm and GNSS/IMU information separately and achieved good accuracy of the trajectory. However, independent SfM processing may suffer from drift, which could be effectively controlled by GNSS/IMU aided bundle adjustment [20]. Furthermore, the performance of the 3D forest mapping (i.e., automatic individual tree segmentation, tree characteristics estimation) using the low-cost ULS system is not yet thoroughly investigated or compared with the commercial ULS system in the previous studies.

The main objectives of this paper are to (1) reconstruct point clouds accurately in mapping frame using the low-cost sensors, and (2) investigate the performance of the low-cost ULS system in 3D forest mapping by comparing it with a high-end commercial ULS system. The low-cost ULS system, named Kylin Cloud, equipped with multiple low-cost sensors (i.e., GNSS, IMU, camera, and laser scanner) is used in the experiments. To overcome the poor performance of the low-cost sensors, an automatic multisensory integration method is proposed. It reconstructs point clouds accurately in a mapping frame by integrating the GNSS data, IMU data, and image sequence utilizing GNSS and IMU aided bundle adjustment. Then individual tree segmentation and tree characteristics (i.e., tree height and crown diameter) estimation are performed using the reconstructed point clouds.

This paper is structured as follow: Section 2 illustrates the study area and the collected data. Section 3 elaborates the proposed method, which integrates the multisensory data and investigates the potential of the low-cost ULS system for 3D forest mapping. Section 4 reports the results of the experiments. Section 5 discusses the results of the experiments. Conclusions and future work are drawn at the end of this paper.

2. Study Area and Material

To investigate the feasibility of the low-cost ULS system in 3D forest mapping, two sets of data were collected by different systems (the low-cost ULS system and a commercial ULS system). In addition, both approaches, including a direct comparison of the point clouds reconstructed by two systems, and comparison of individual tree characteristics (i.e., tree height and crown diameters), were applied to validate the performance of the low-cost system. In this section, detailed information about the study area, the two ULS systems, and the collected data are provided.

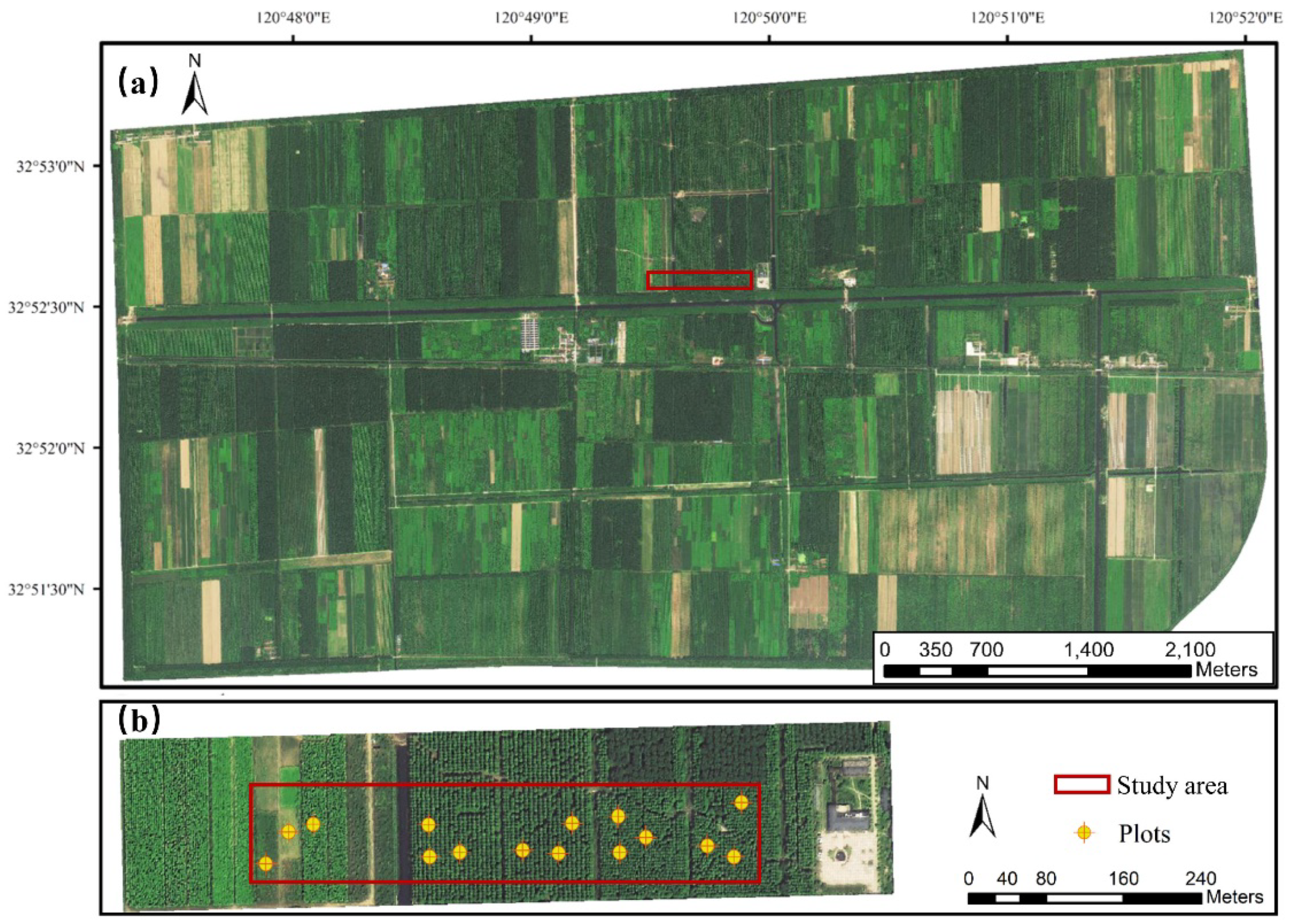
2.1. Study Area

The study area, located in the Dongtai forest farm (32°52′N, 120°50′E), Yancheng City, Jiangsu Province, China. An 800 m * 100 m of nursery land was selected for data collection as shown in Figure 1a. Fifteen sample plots were randomly selected from the study area as shown in Figure 1b. Each sample plot is a circular area with a radius of 15 m. The main planted tree species include Dawn redwood (Metasequoia glyptostroboides) and Poplar (Populus deltoids). The seedlings, including Maple (Acer L.), Weeping willow (Salix babylonica Linn.) and Ligustrum lucidum (Ligustrum lucidum Ait.), are planted in the nursery land.

2.2. The Low-Cost ULS System and the Collected Data

The low-cost ULS system, named Kylin Cloud, is illustrated in Figure 2. Kylin Cloud consists of a low-cost IMU (Xsens Mti-300), a double-frequency GNSS receiver (KQ GEO), a GNSS antenna, a global shutter camera (Pointcrey Flea3), and a laser scanner (Velodyne Puck VLP-16). Kylin Cloud is mounted on a DJI M600Pro UAV with a maximum payload of 6 kg and 25 min flying time. The synchronization between the laser scanner, the camera, the GNSS receiver, and the IMU is fulfilled electronically. The raw data of the sensors is recorded by an onboard control unit based on advanced RISC machine (ARM) cortex A9, which has low power and is sufficient for the data log.

Table 1. Sensor specifications of the Kylin Cloud.

Sensor	Manufacturer	Description	Approximate Price
GNSS receiver (Base)	M8 made by KQ GEO Technologies *	Double frequency, supporting BDS/GPS/GLONASS	1500 USD
GNSS receiver (Rover)	P8 made by KQ GEO Technologies *	Double frequency, supporting BDS/GPS/GLONASS	1500 USD
IMU	Xsens MTI-300	Gyroscope in-run bias stability is 12°/h; accelerometer in-run bias stability is 0.015 mg	2500 USD
Global shutter camera	Pointgrey Flea3	1280 × 1024 pixels, color, with a pixel size of 5.3 µm	1000 USD
Laser scanner	Velodyne VLP16	16 channels; 300,000 points per second; 905 nm wavelength; 100 m measurement range	6000 USD
Lens	Kowa wide-angle lens	3.5 mm/F1.4	200 USD

* KQ GEO Technologies is a Chinese company (http://www.kanq.com.cn/).

lists the specifications of the sensors. The Xsens Mti-300 is a low-cost and light IMU, which provides 200 Hz raw inertial measurements. Its gyroscope bias stability and accelerometer bias stability are 12°/h and 0.015 mg, respectively. The intrinsic parameters of the IMU were provided by the manufacturer. The Pointgrey Flea3 is a global shutter color camera with 1280 × 1024 pixels. It captures image data at 5 Hz and is not affected by rolling-shutter distortion. The initial intrinsic parameters of the camera were pre-calibrated using a camera calibration toolbox in MATLAB [21] with an industrial checkerboard (1.5 m * 1.2 m), and then they were optimized in the proposed GNSS and IMU aided bundle adjustment. The Velodyne Puck VLP16 is a light-weight and low-cost laser scanner, which operates at a wavelength of 905 nm. It has 16 channels and supports 300,000 points per second. The measurement range of Velodyne Puck VLP16 is 100 m. The range error of the Velodyne Puck VLP16 laser scanner is about 0.03 m (1 $\sigma$), and it could be improved by 10 to 20% after interior calibration [22]. The range error of the Velodyne Puck VLP16 laser scanner is about 0.03 m (1 $\sigma$), and it could be improved by 10% to 20% after interior calibration. As reported by Jaakkola et al. [14], using the VLP-16 laser scanner with a range error of 3 cm is sufficient for the forest applications, so the manufacture values were used without calibration in this paper.

Data of Kylin Cloud were collected in December 2018. To ensure data quality and flight safety, the Kylin Cloud was programmed to automatically follow the pre-designed flight lines using DJI GS PRO. The flight height was set to 70 m above the ground, and the flying speed was nearly 3 m/s. It took 15 min to collect the raw data of the study area. There were 3760 images and approximately 2 GB raw laser scanning data (7,993,351 points) collected in this study area. The forward overlap of the images is over 90%, and the side overlap of the images is 70%. The density of the resulted laser point clouds (with double-echo) is 11.85 points per m².

2.3. The High-End Commercial ULS System and the Collected Point Clouds

The commercial ULS was integrated by Green Valley International. The hardware system is composed of 6 units, including a Hexa-rotor UAV, a high-end POS (Novatel IMU-IGM-S1), a GNSS antenna, a high-end laser scanner (Riegl VUX-1), a micro-computer, a long-range Wi-Fi, as shown in Figure 3. The survey grade laser scanner, Riegl VUX-1, has high accuracy (0.01 m) and long measurement range (300 m). Its scan speed and measurement rate are up to 200 scans per second and 550 kHz, respectively. To obtain the georeferenced point clouds according to trajectory, the Novatel IMU-IGM-S1 is mounted. The raw IMU and GNSS data are post-processed using a loosely coupled Kalman Filtering via Novatel Inertial Explorer software to generate accurate trajectory. A micro-computer is integrated to log raw data. In addition, the raw data is transmitted to the ground station through the long-range Wi-Fi system. The total price of this system is over 120,000 USD, which is much higher than the low-cost system.

The laser scanning data for the study area was collected in August 2018. The UAV system was programmed to automatically follow the pre-designed flight lines using an autopilot system of the Hexa-rotor UAV. The flying height was 140 m, the flying speed was nearly 4 m/s, and it took 8.7 min to collect the raw data of the study area. The average point density of the reconstructed point clouds is 224.33 points per m².

3. Methodology

The proposed method is to integrate multisensory data collected by the low-cost ULS system and investigate its feasibility for 3D forest mapping. Workflow of the proposed method is shown in Figure 4. Due to the poor performance of the low-cost sensors, direct georeferencing data estimated by low-cost IMU and GNSS leads to inaccurate point clouds. Thus, a novel data integration strategy using GNSS and IMU aided SfM is proposed. It estimates accurate trajectory and reconstructs the point clouds accurately in a mapping frame as shown in Figure 4b. To investigate the feasibility of the low-cost UAV system for 3D forest mapping, individual trees are extracted for tree characteristics (e.g., tree height and crown diameter) estimation as shown in Figure 4c. Details of the proposed method are described below.

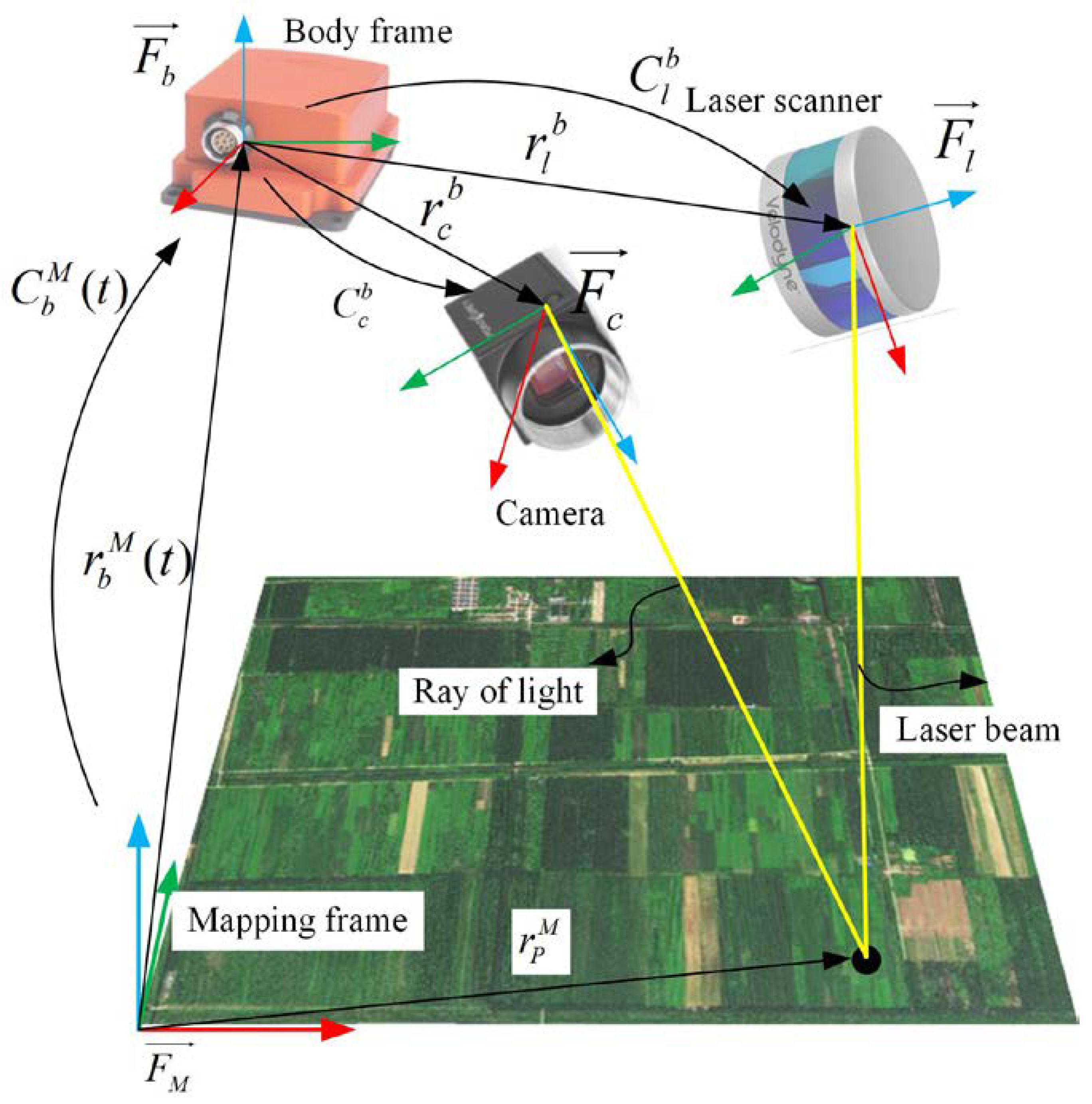
3.1. Coordinate Definitions

To integrate multisensory data collected by the low-cost ULS system, coordinate definitions involved in the proposed method are introduced first. Following the notation of coordinate and transformation used in [23], $\stackrel{\rightharpoonup }{{\mathit{F}}_A}$ denotes a reference frame $A$, and a point $\mathit{P}$ in frame $\stackrel{\rightharpoonup }{{\mathit{F}}_A}$ is written as a vector ${\mathit{r}}_P^A$. The rotation matrix between $\stackrel{\rightharpoonup }{{\mathit{F}}_A}$ and $\stackrel{\rightharpoonup }{{\mathit{F}}_B}$ is represented by ${\mathit{C}}_B^A$. The corresponding quaternion is represented by ${\mathit{q}}_B^A$.

As illustrated in Figure 5, four coordinate systems are involved in the proposed integration (i.e., mapping frame $\stackrel{\rightharpoonup }{{\mathit{F}}_M}$, body frame $\stackrel{\rightharpoonup }{{\mathit{F}}_b}$, camera frame $\stackrel{\rightharpoonup }{{\mathit{F}}_c}$, and laser scanner frame $\stackrel{\rightharpoonup }{{\mathit{F}}_l}$). We let the system states to be estimated at time $t$ be $x_s\left(t\right)$, which can be written as:

$${\mathit{x}}_{\mathit{s}}\left(t\right)={\left[{\mathit{r}}_b^M{\left(t\right)}^{\mathrm{T}},{\mathit{v}}_b^M{\left(t\right)}^{\mathrm{T}},{\mathit{q}}_b^M{\left(t\right)}^{\mathrm{T}},{\mathit{b}}_a{\left(t\right)}^{\mathrm{T}},{\mathit{b}}_g{\left(t\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}$$

(1)

where ${\mathit{r}}_b^M\left(t\right)$ is the position of body frame in the mapping frame; ${\mathit{q}}_b^M\left(t\right)$ is the quaternion that rotates a vector from the mapping frame to the body frame; ${\mathit{v}}_b^M\left(t\right)$ is the velocity in the mapping frame; and ${\mathit{b}}_a^k\left(t\right)$ and ${\mathit{b}}_g^k\left(t\right)$ are the biases of the accelerometer and gyroscope, respectively. The trajectory used for reconstructing the laser point clouds in the mapping frame is composed of ${\mathit{r}}_b^M\left(t\right)$ and ${\mathit{q}}_b^M\left(t\right)$. If a point ${\mathit{r}}_P^M$ in the world frame $\stackrel{\rightharpoonup }{{\mathit{F}}_M}$ is observed by the camera and the laser scanner simultaneously, the corresponding points in the camera and laser scanner coordinate system are ${\mathit{r}}_P^c$ and ${\mathit{r}}_P^l$. Then the ${\mathit{r}}_P^M$ can be reconstructed in the mapping frame using the following equations:

$$\{\begin{array}{c}{\mathit{r}}_P^M={\mathit{C}}_b^M\left(t_1\right){\mathit{C}}_c^b{\mathit{r}}_P^c+{\mathit{C}}_b^M\left(t_1\right){\mathit{r}}_c^b+{\mathit{r}}_b^M\left(t_1\right)\\ {\mathit{r}}_P^c=\lambda {\left(x,y,-c\right)}^{\mathrm{T}}\end{array}$$

(2)

$${\mathit{r}}_P^M={\mathit{C}}_b^M\left(t_2\right){\mathit{C}}_l^b{\mathit{r}}_P^l+{\mathit{C}}_b^M\left(t_2\right){\mathit{r}}_l^b+{\mathit{r}}_b^M\left(t_2\right)$$

(3)

where $x$, $y$, and $-c$ are the coordinates of the point ${\mathit{r}}_P^c$ in the camera frame with scale factor $\lambda$; $t_1$ and $t_2$ are the observing times from camera and laser scanner, respectively. ${\mathit{r}}_c^b$ and ${\mathit{r}}_l^b$ are the level-arm parameters of the camera/IMU and the laser/IMU, respectively; and ${\mathit{C}}_c^b$ and ${\mathit{C}}_l^b$ are the boresight matrix of the camera/IMU and the laser/IMU, respectively. The values of these boresight and level-arm parameters are calibrated before data collection.

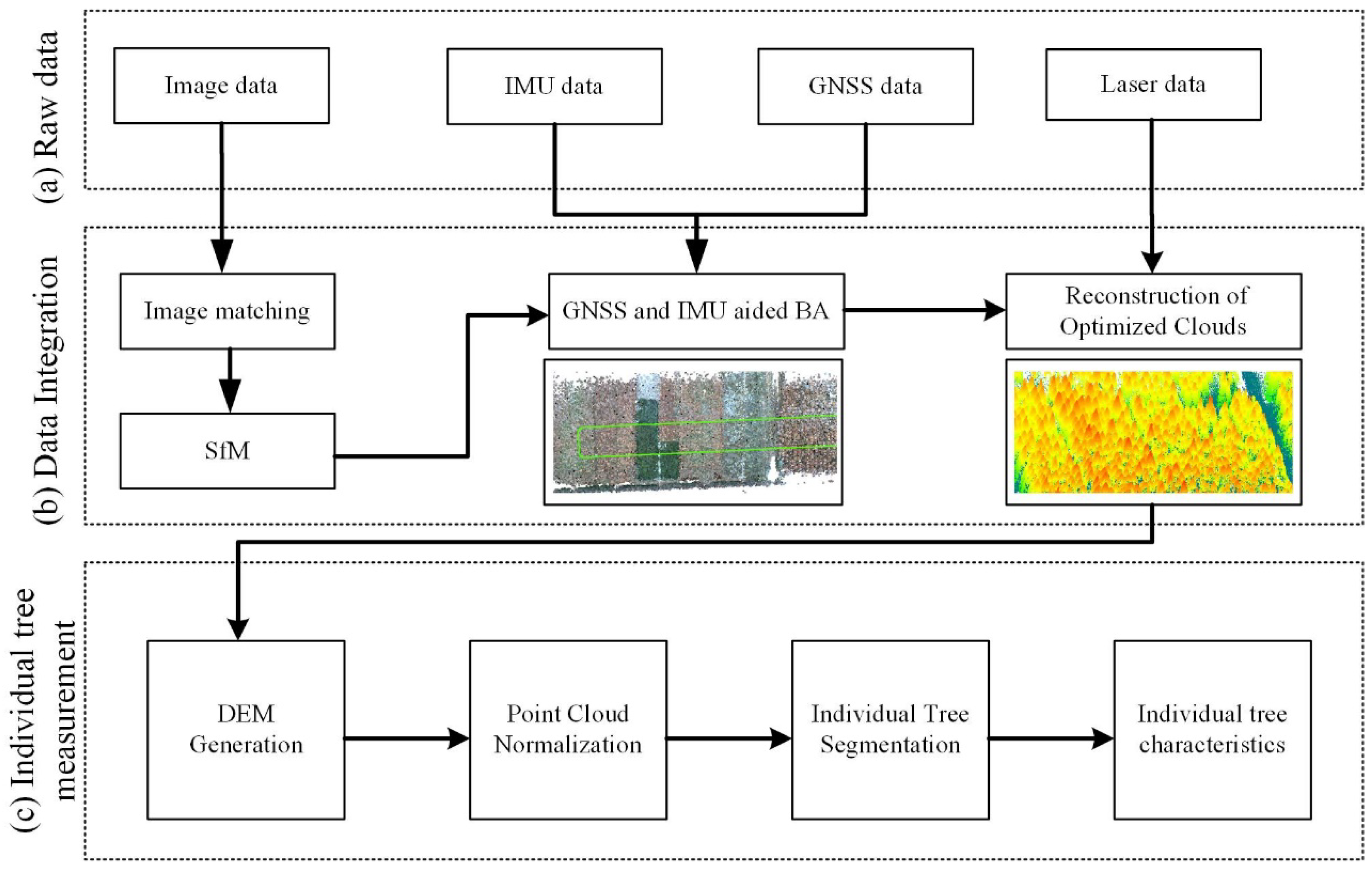
3.2. Data Integration

As the inaccurate direct georeferencing data resulted from the poor performance of the low-cost IMU, a modified SfM algorithm with the aid of GNSS and IMU is adopted to estimate the trajectory for accurate point clouds. First, the low-cost IMU measurements are integrated using the pre-integration technique. Second, sequent images matching is performed, and a scale-free graph is built using incremental SfM. Finally, the trajectory is estimated using a carefully designed GNSS and IMU aided bundle adjustment.

3.2.1. IMU Integration

The low-cost IMU kinematics model proposed by Shin and El-Sheimy [24] is used in the proposed registration model. In addition, an IMU pre-integration technique [25,26] is adopted to overcome the re-propagation of the IMU measurements when states change in optimization steps. If we assume that two images are captured at times $t_i$ and $t_{i+1}$, then the update equations of the position ${\mathit{r}}_b^M\left(t\right)$, velocity ${\mathit{v}}_b^M\left(t\right)$, and orientation ${\mathit{q}}_b^M\left(t\right)$ are derived as follows:

$${\mathit{r}}_b^M\left(t_{i+1}\right)={\mathit{r}}_b^M\left(t_i\right)+{\mathit{v}}_b^M\left(t_i\right)\Delta t+0.5{\mathit{g}}^M\Delta t^2+{\mathit{C}}_b^M\left(t_i\right)\Delta {\mathit{p}}_{i+1}^i$$

(4)

$${\mathit{v}}_b^M\left(t_{i+1}\right)={\mathit{v}}_b^M\left(t_i\right)+{\mathit{g}}^M\Delta t+{\mathit{C}}_b^M\left(t_i\right)\Delta {\mathit{v}}_{i+1}^i$$

(5)

$${\mathit{q}}_b^M\left(t_{i+1}\right)={\mathit{q}}_b^M\left(t_i\right)\otimes \Delta {\mathit{q}}_{i+1}^i$$

(6)

where ${\mathit{g}}^M$ is the gravity vector in the mapping frame. $\otimes$ is the multiplier for quaternion [23]. $\Delta {\mathit{p}}_{i+1}^i$, $\Delta {\mathit{v}}_{i+1}^i$, and $\Delta {\mathit{q}}_{i+1}^i$ are the pre-integration components of the time duration $\left[t_i,t_{i+1}\right]$. The covariance matrix ${\mathit{P}}_{IMU}^{i,i+1}$ for the pre-integration parts can be propagated according to [25,26].

3.2.2. Image Sequence Matching and SfM

To integrate the image information for accurate trajectory estimation, a SfM algorithm is utilized to build a scale-free graph of the image sequence, which determines relative orientations of the images captured at certain times. First, features are extracted from all the images for the matching. In this research, the scale-invariant feature transform (SIFT) [27] feature detector is used. The feature matching operations between the two feature point sets are achieved by searching nearest Euclidian distance among a 128-dimensional descriptor space. To speed up feature extraction and matching options, a GPU-based SIFT implementation [28] is applied. Second, image matching and the key-frames selection are performed simultaneously as follow: the first image was selected as the key-frame, then the following images are matched with the last key-frame sequentially. If a current frame had less than ${\mathrm{N}}_{corres}$ correspondences (e.g., 800) with the last key-frame, it is selected as a new key-frame. Then the key-frames are matched with each other. Using this strategy, we can avoid matching all the images with each other and reduce the computation cost. Then all the key frames are matched with each other according to their GNSS positions. Third, the scale free graph of image sequence is initialized and reconstructed using an incremental SfM strategy proposed in [29]. This graph contains information of relative orientations of images, correspondences of tie points, and projection relationships between 2D tie points and 3D triangulated points, which are used for following GNSS and IMU aided bundle adjustment.

3.2.3. GNSS and IMU Aided Bundle Adjustment

The GNSS and IMU aided bundle adjustment is performed to reduce the drift of SfM and estimate all the states involved in trajectory estimation [30]. The cost function $\mathrm{J}{\left({\mathit{x}}_{\mathit{s}}\right)}_{BA}$ for bundle adjustment consists of three parts: the re-projection error term ${\mathit{e}}_r^{j,i}$, the inertial error term ${\mathit{e}}_{IMU}^{i,i+1}$, and the GNSS error term ${\mathit{e}}_g^i$, as follows:

$$\mathrm{J}{\left(x_s\right)}_{BA}≔\underset{inertial}{\underbrace{{\displaystyle \sum }_{i=1}^{N-1}{\mathit{e}}_{IMU}^{i,i+1}{}^{\mathrm{T}}{\mathit{P}}_{IMU}^{i,i+1}{}^{-1}{\mathit{e}}_{IMU}^{i,i+1}}}+\underset{re\text{-}projection}{\underbrace{{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j\in \mathcal{J}\left(i\right)}{e}_r^{j,i}{}^{\mathrm{T}}{\mathit{P}}_r^{j,i}{}^{-1}{\mathit{e}}_r^{j,i}}}+\underset{GNSS}{\underbrace{{\displaystyle \sum }_{i=1}^N{\mathit{e}}_g^i{}^{\mathrm{T}}{\mathit{P}}_g^i{}^{-1}{\mathit{e}}_g^i}}$$

(7)

If the ith image is captured at time $t_i$, and the jth feature point is observed in this image, j belongs to set $\mathcal{J}\left(i\right)$. $\mathcal{J}\left(i\right)$ represents a set of all the feature points observed in the image. ${\mathit{P}}_r^{j,i}$, ${\mathit{P}}_{IMU}^{i,i+1}$, and ${\mathit{P}}_g^i$ are covariance matrices of the re-projection error term, the inertial error term, and the GNSS error term, respectively. The covariance matrix ${\mathit{P}}_g^i$ for GNSS part is obtained by the software Inertial Explorer after applying carrier-phase differential post-processing. The covariance matrix ${\mathit{P}}_r^{j,i}$ for re-projection error is set to an identity matrix, for the accuracy of SIFT feature points is within one pixel. The general framework for graph optimization (g2o) [31] is used to optimize above cost function.

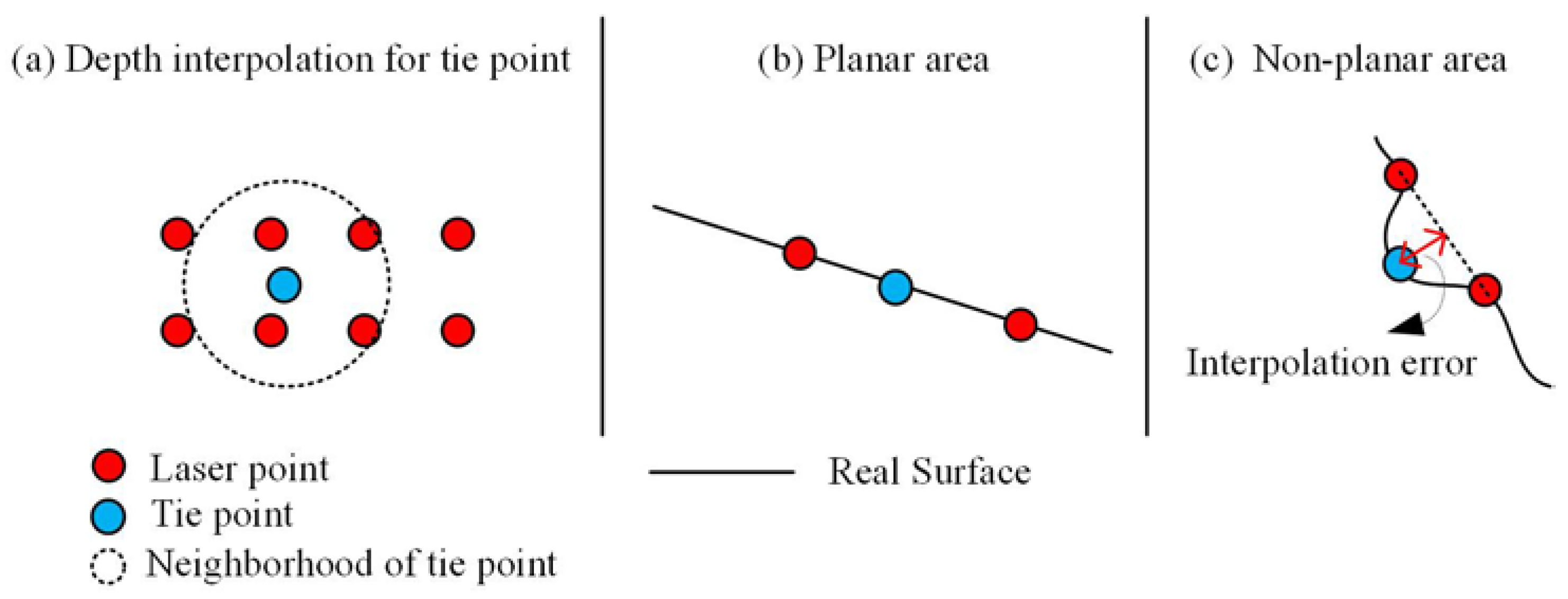
3.2.4. Reconstruction of the Point Clouds

After the optimization using the proposed GNSS and IMU aided bundle adjustment, accurate trajectory composed of ${\mathit{r}}_b^M\left(t\right)$ and ${\mathit{q}}_b^M\left(t\right)$ is obtained. As time synchronization of all the sensors are fulfilled electronically, the point clouds are reconstructed using the estimated trajectory by projecting laser scanning measurement from laser scanner coordinate system $\stackrel{\rightharpoonup }{{\mathit{F}}_l}$ to mapping coordinate system $\stackrel{\rightharpoonup }{{\mathit{F}}_M}$ via Equation (3). The point clouds are used as input for the following forest applications.

3.3. Individual Tree Segmentation and Evaluation

3.3.1. Non-Ground Points Classification and Point Clouds Normalization

The reconstructed point clouds are classified into ground points and non-ground points using multi-scale morphological filtering [32] with default parameter setting. We recommend readers to see [32] for more details of the classification. Digital elevation model (DEM) is generated by interpolated the ground points using Kriging interpolation. By subtracting the corresponding value in the generated DEM, the non-ground points are normalized [33]. The z value of a point in normalized points indicates the relative height from ground to this point. If a point is located on the top of a tree, its height represents the height of the tree.

3.3.2. Hierarchical Segmentation of the Normalized Point Clouds

In most conditions, there is horizontal spacing between individual trees and the spacing of the tree top is larger than the spacing of the tree bottom. According to this assumption, the individual trees in the normalized point clouds are segmented hierarchically from top to bottom using a growing strategy proposed in [34]. After the individual tree is segmented, the individual tree height is obtained by finding the highest point of one point segment. The crown diameter is estimated by fitting the individual tree segment on the horizontal plane using a circular region.

4. Results

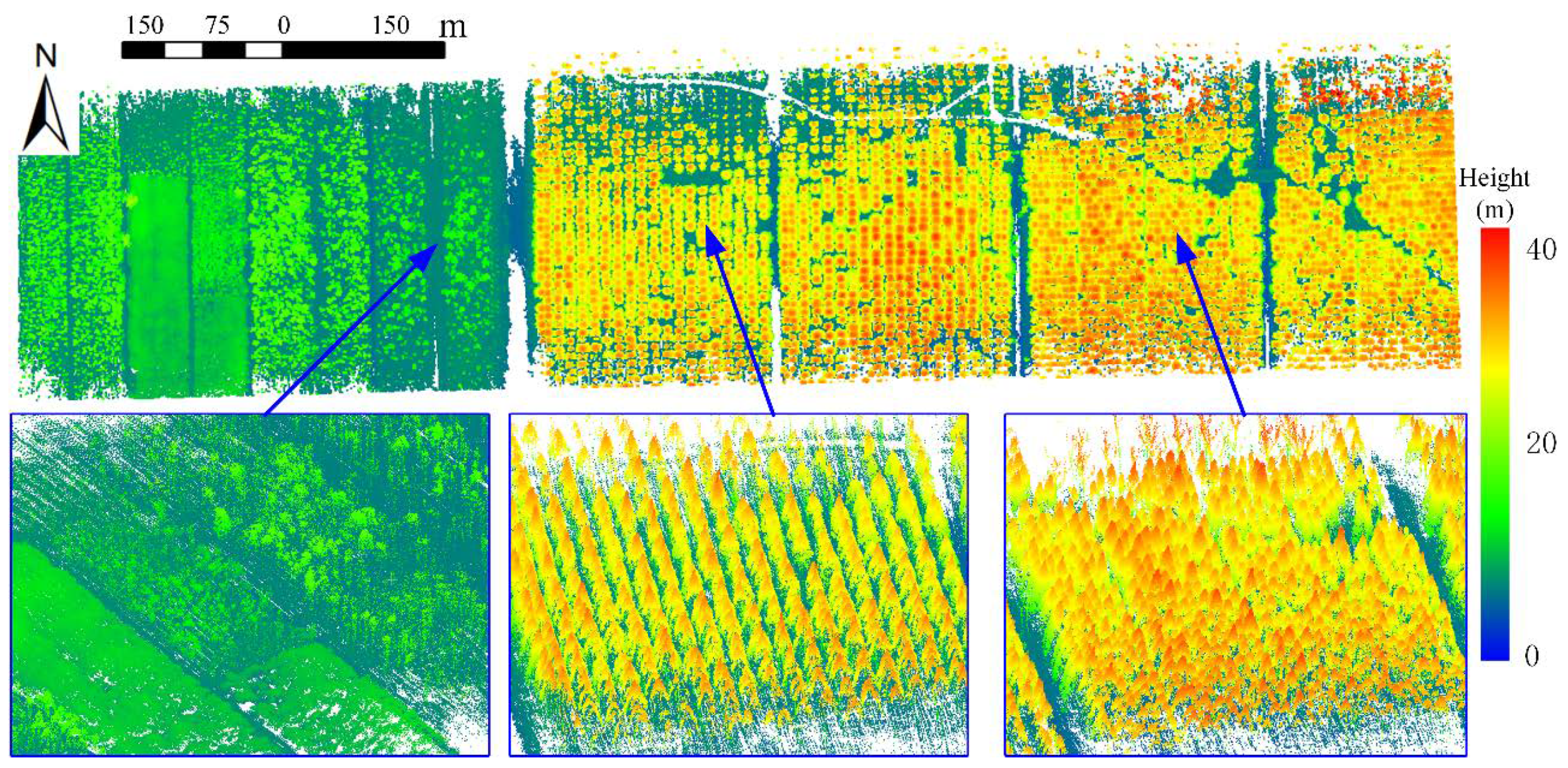
4.1. Reconstruction of the Point Clouds in Mapping Frame

The trajectory was estimated by integrating image sequence, IMU and GNSS data. As shown in Figure 6a, the green line was the estimated trajectory, and colorful points were triangulated 3D tie points. There were 909,442 triangulated tie points evenly distributed in the study area. We only used tie points observed in three or more images in the proposed bundle adjustment. To detect the outliers of tie points observed in three or more images, “three-ray points” error was used. The coordinates of 3D tie points observed in more than three images were adjusted according to redundancy, resulting in a more reliable solution [35]. Figure 6b showed the observability of all remained 3D tie points. As images were captured at 5 Hz and had a wide field of view, more than 80% tie points could be observed in more than 10 images, resulting in reliable adjustment results. However, check-points in the forest can hardly be observed by the UAV images due to the occlusion of tall and dense vegetation, especially for the plantation. Thus, the accuracy of the GNSS and IMU aided bundle adjustment in the study area was not directly evaluated with check-points. However, in the proposed method, reconstructing good point cloud is relying on an accurate result of GNSS and IMU aided bundle adjustment. Therefore, the accuracy of the bundle adjustment could be validated indirectly by evaluating the accuracy of the reconstructed point cloud.

Using the estimated trajectory, the low-cost point clouds were reconstructed accurately by projecting the laser measurements from laser scanner frame to the mapping frame as shown in Figure 7. The point density of reconstructed point clouds was 11.85 points per m². A visual inspection indicated that the point clouds were of good quality, with fairly low noise. We also reconstructed the point clouds using the trajectory merely relying on GNSS and IMU data via a loosely coupled Kalman filter. The comparison of these two point clouds was shown in Figure 8. Due to the poor performance of low-cost IMU, point clouds reconstructed using trajectory estimated by loosely coupled filtering of GNSS and IMU measurements were with high noise, and suffered from significant distortion as shown in Figure 8b. With the aid of the image information, distortion was removed using the proposed method, demonstrating the improvement of data quality and the effectiveness of the proposed data integration.

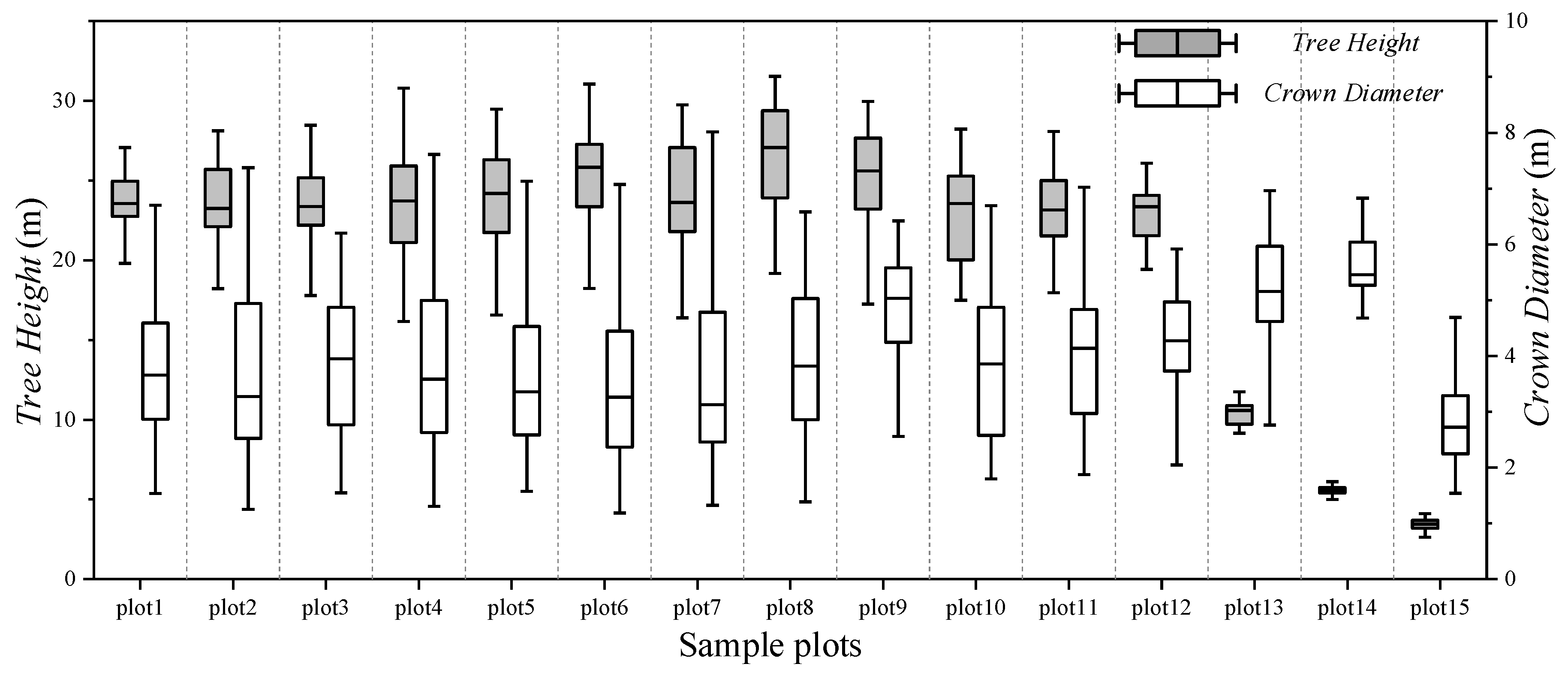
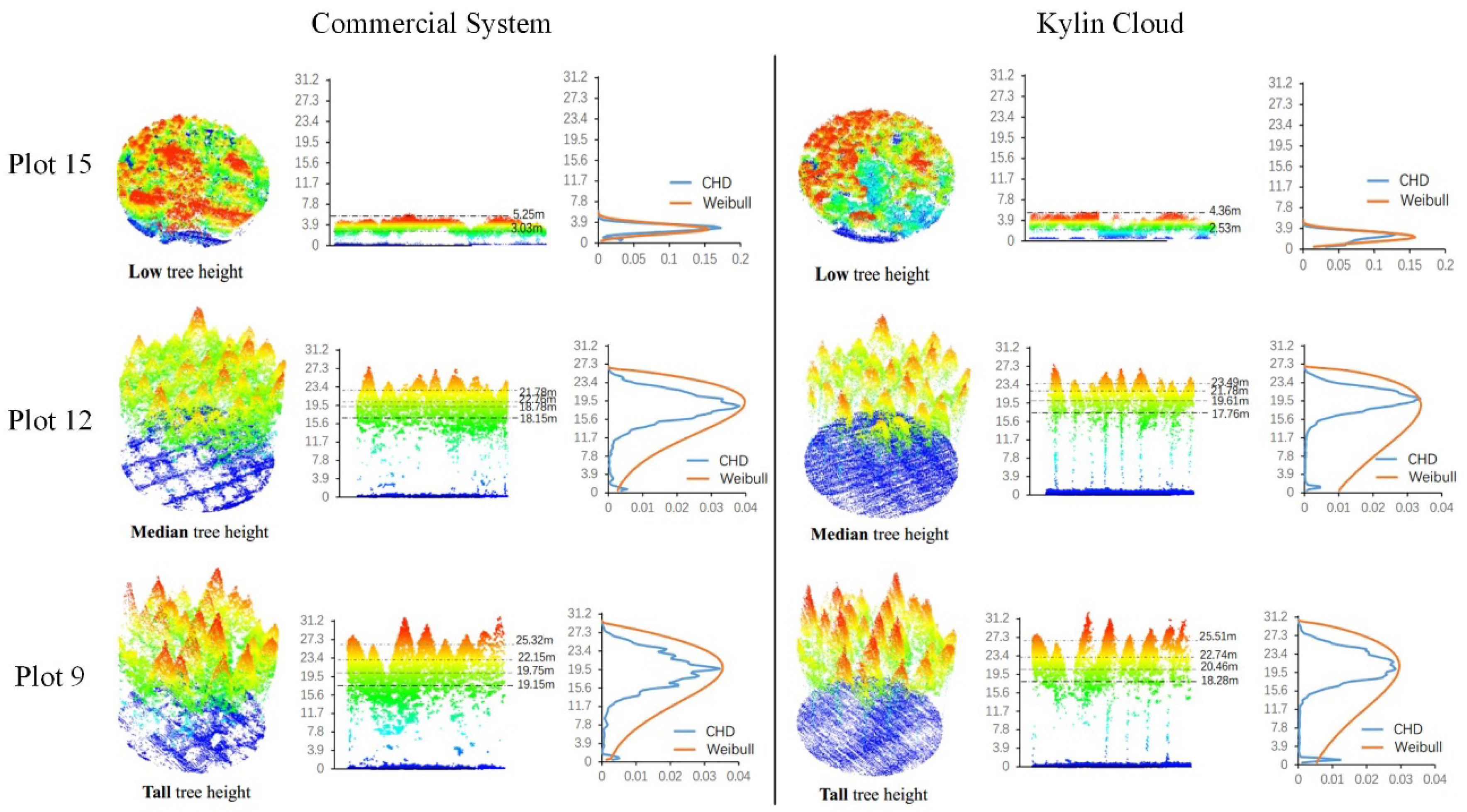
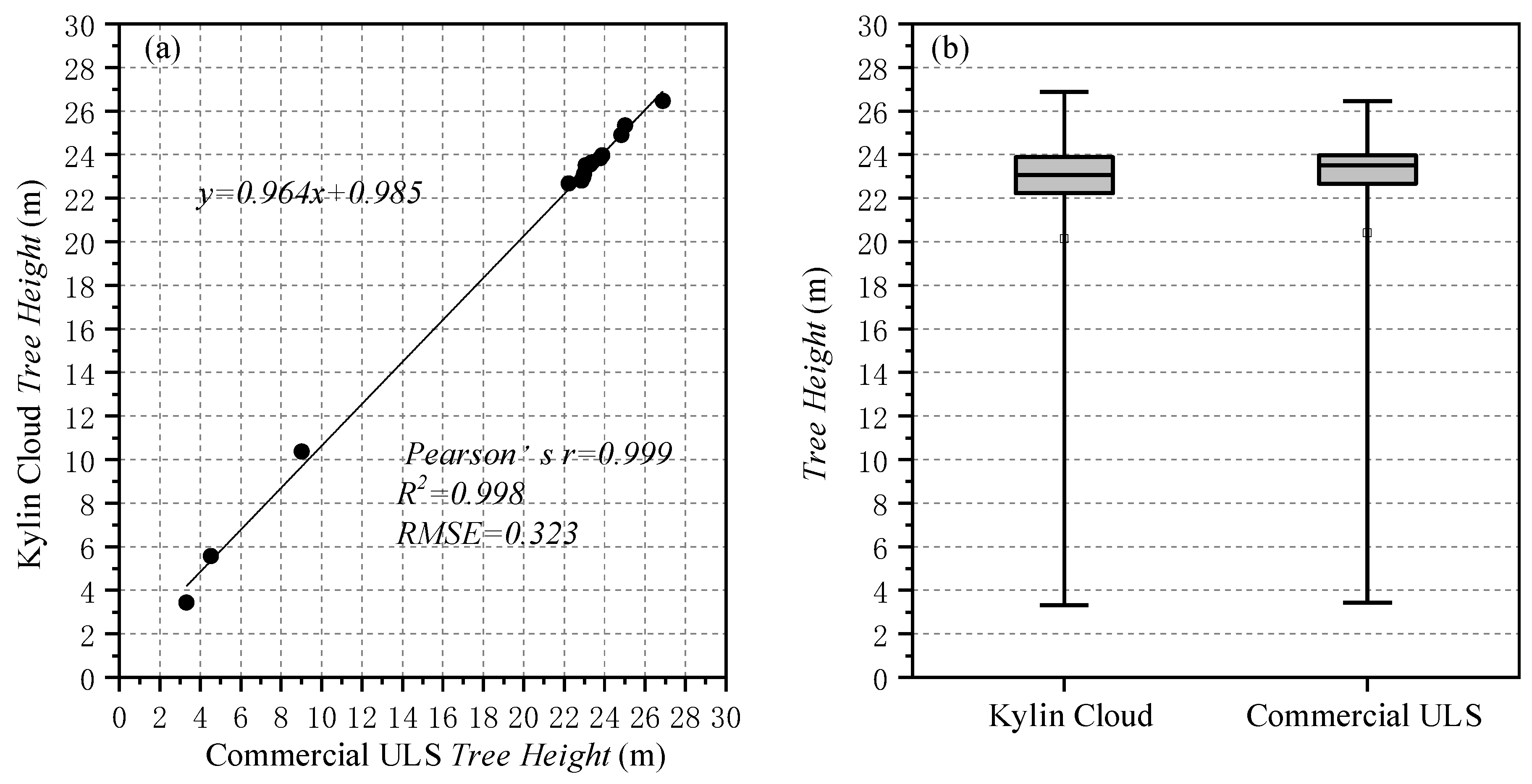
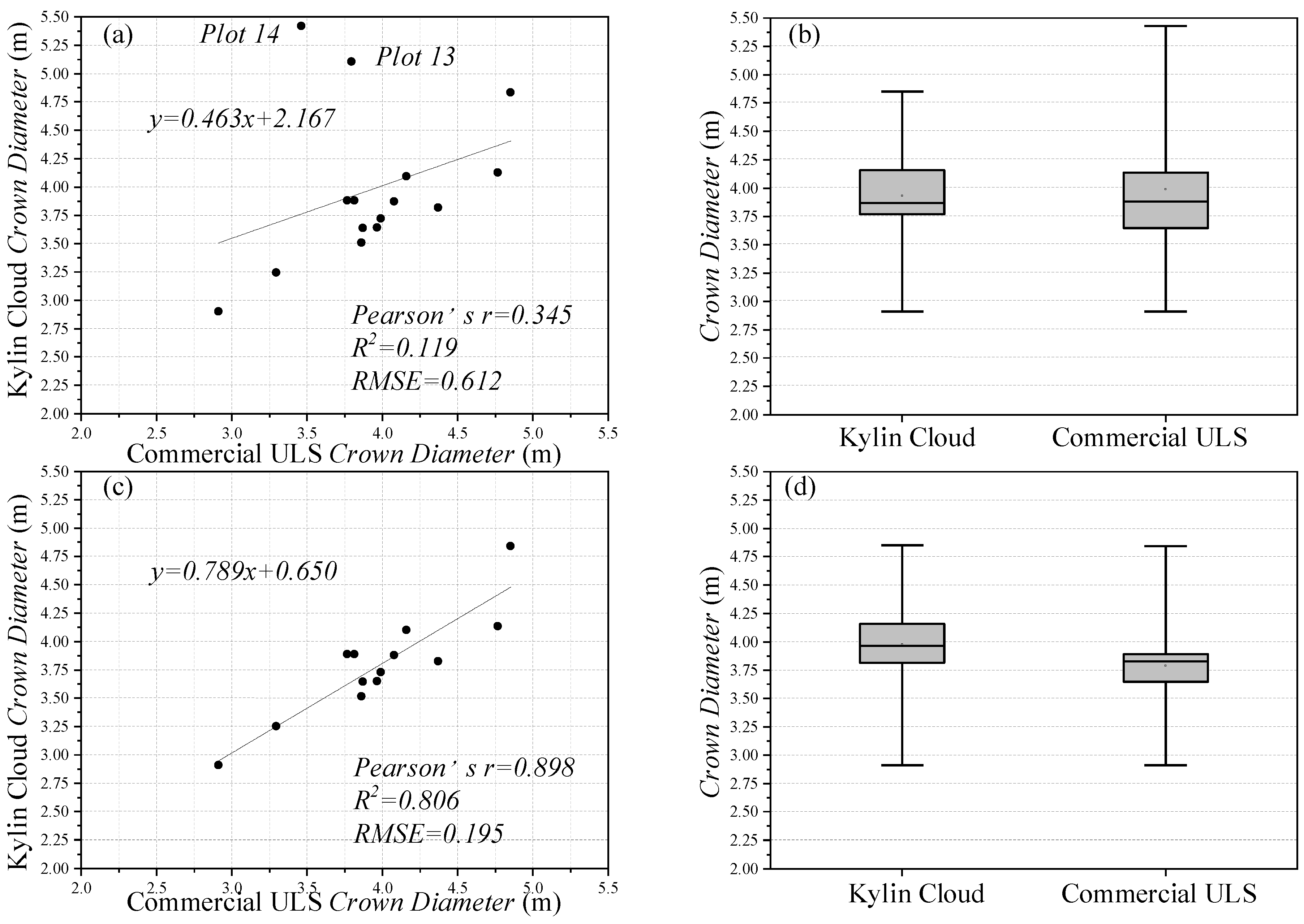
4.2. Individual Tree Measurement

Individual trees were segmented using the point clouds collected by the low-cost ULS. The individual tree segmentation results of these 15 sample plots are illustrated in Figure 9. The green triangles indicate detected trees. The circles with black line indicate the tree crowns. Starting from the top of a tree, a target tree can be segmented by including nearby points and exclude points of other trees according to their relative spacing. Using this segmentation strategy, points with a spacing larger than a specified threshold are excluded from the target tree; points with spacing smaller than the threshold are classified based on a minimum spacing rule. The threshold should be approximately equal to the crown radius (e.g., 2 m used in the experiments). According to the individual tree segments, tree height and crown diameter were estimated and plotted using boxplot as shown in Figure 10.

5. Discussion

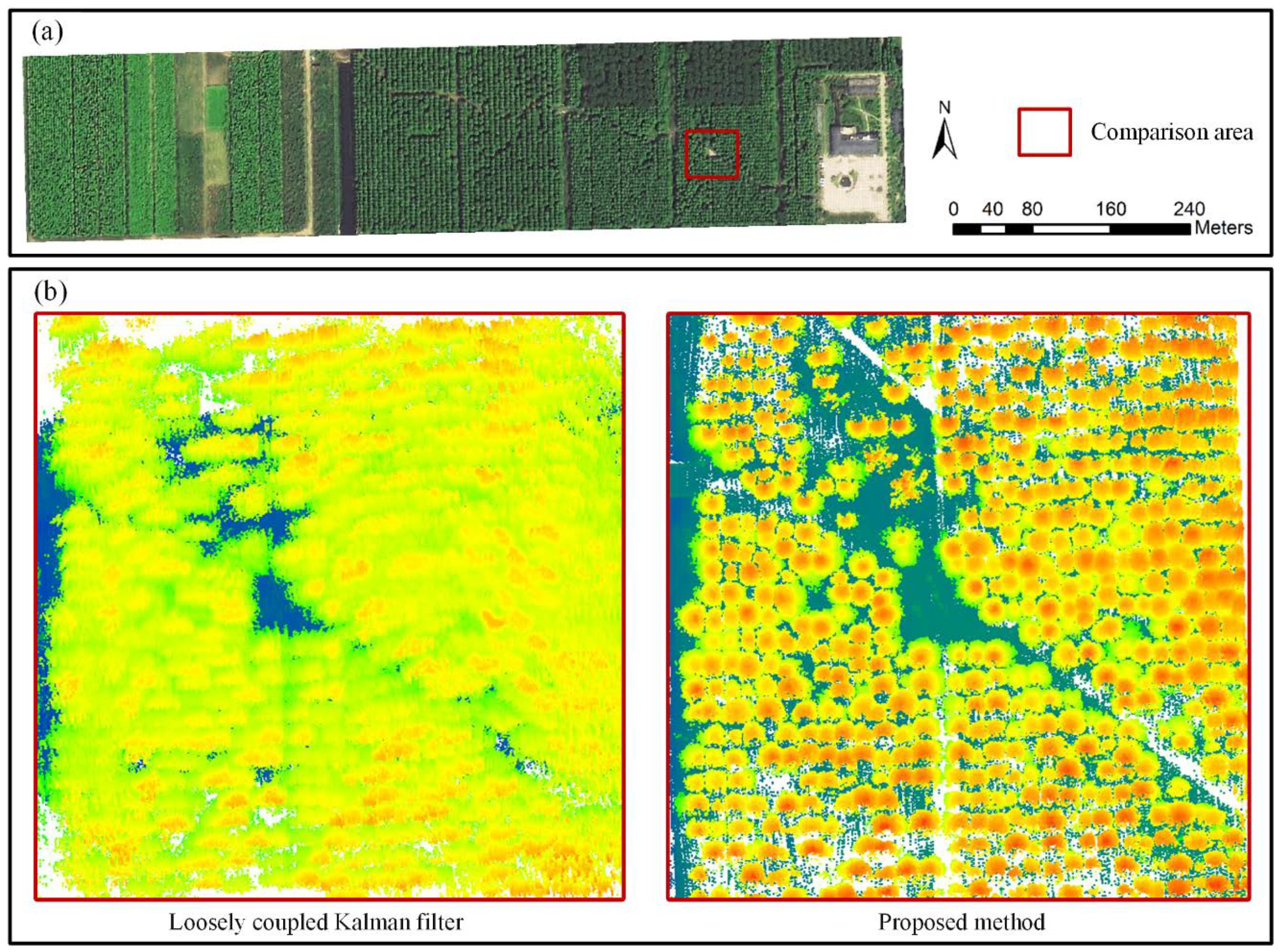
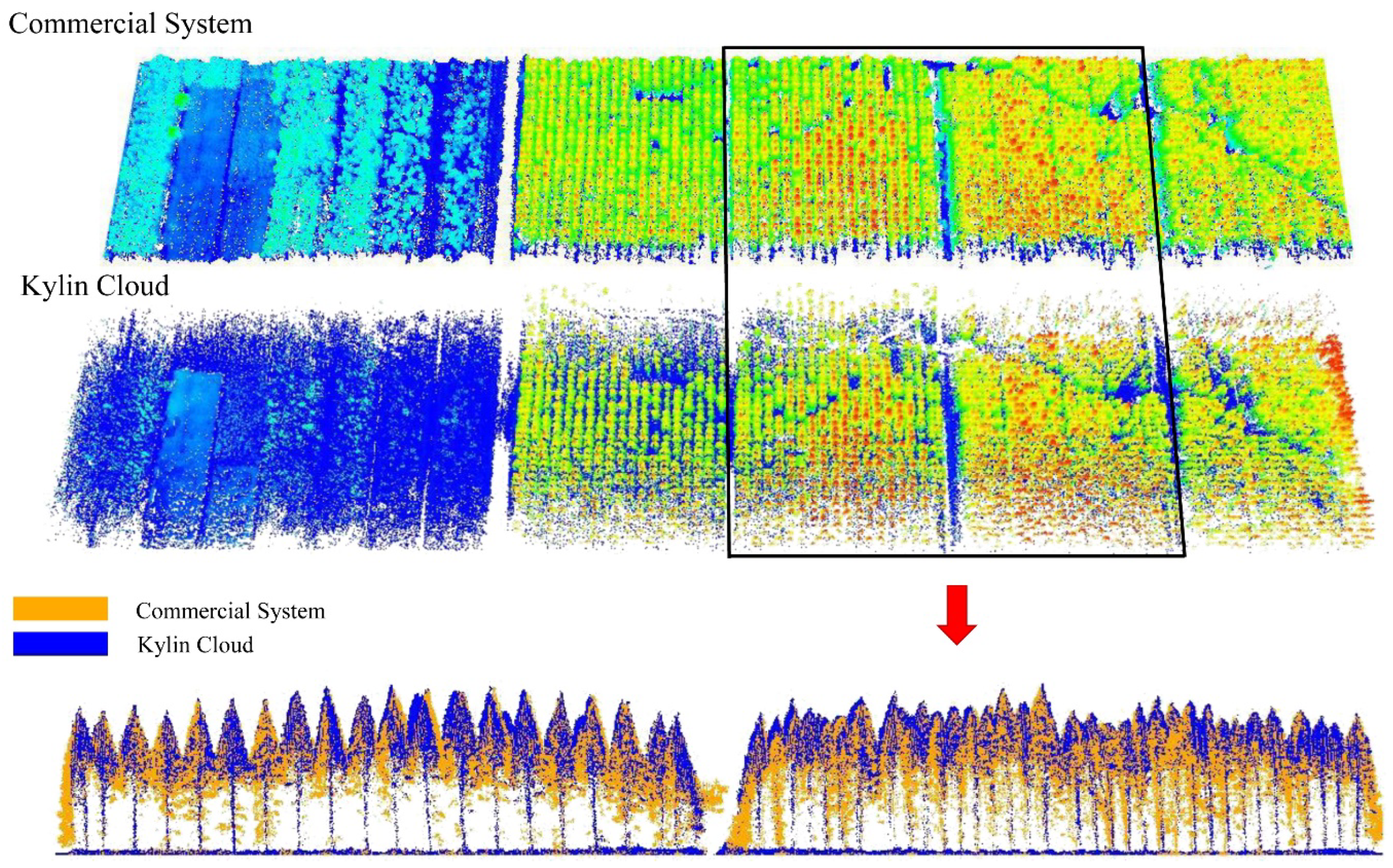
5.1. Comparison of the Point Clouds Quality from Different Platforms

To validate the feasibility of the low-cost ULS system for forest applications, we compared the low-cost point clouds with ground truth data collected by the commercial system. We first visually compared the two point clouds by overlaying the low-cost point clouds and the ground truth data. Part of the overlapping results is shown in Figure 11. Visually, the two data overlapped well, showing a comparable data quality of the low-cost system with the commercial system. For further comparison, the 15 sample plots were selected to further evaluate the feasibility of the low-cost point clouds. Plots from different point clouds were compared by calculating the canopy height distribution (CHD) and fitting Weibull distribution curves. Comparison of three typical plots with different height levels (low, median, high) is shown in Figure 12. Due to the fact that the low-cost data were collected in winter and the ground truth data were collected in summer, the leaf points of the low-cost point clouds were relatively sparse, and the ground points of the low-cost point clouds were relative dense, resulting in the difference between the Weibull distribution curves. Visual inspection indicates that the low-cost point clouds provided a reliable CHD, which can be further used to calculate the individual tree characteristics.

5.2. Comparison of the Individual Tree Segmentation from Different Platforms

Individual trees of the selected 15 plots were segmented using the low-cost point clouds and compared with the ground truth data derived from the commercial system. To evaluate the accuracy of segmentation results, three indices (“recall”, “precision”, and “F-measure”) were adopted in this study. “recall” ($r$), “precision” ($P$) and “F-measure” (F) are defined as follow:

$$r=\frac{TP}{TP+FN}$$

(8)

$$P=\frac{TP}{TP+FP}$$

(9)

$$F=\frac{2\ast r\ast P}{r+P}$$

(10)

where $TP$ (True Positive) was the number of individual trees that were detected correctly, $FN$ (False Negative) was the number of trees were not detected, and $FP$ (False Positive) represented the number of point cluster was detected as a tree that did not exist. The segmentation results derived from the low-cost system were overlapped with the ground truth first as shown in Figure 13. Then the results were validated manually according to the following rules:

(1)

If a detected tree center is located in a crown area of ground truth, it is treated as TP.

(2)

If more than one detected tree centers (over-segmentation) are located in one crown of ground truth, only one detected tree is treated as TP, and the other ones are treated as FP.

(3)

If a detected tree center (under-segmentation) is located in more than one crown area of ground truth, it belongs to the closer crown of ground truth.

(4)

If a detected tree center is not located in any crown area of ground truth, it is treated as FP.

(5)

If no detected tree center is located in a crown area of ground truth, it is treated as FN.

Table 2. Results of Individual Trees Segmentation in 15 Sample Plots.

Plot ID	Reference Trees	Detected Trees	TP1	FN2	FP3	recall	Precision	F-Measure
1	50	46	43	7	3	0.86	0.93	0.89
2	53	50	46	7	4	0.87	0.92	0.89
3	51	46	44	7	2	0.86	0.96	0.91
4	37	44	34	3	10	0.92	0.77	0.84
5	50	53	48	2	5	0.96	0.91	0.93
6	48	52	46	2	6	0.96	0.88	0.92
7	40	50	38	2	12	0.95	0.76	0.84
8	40	46	36	4	10	0.90	0.78	0.84
9	27	29	26	1	3	0.96	0.90	0.93
10	26	35	24	2	11	0.92	0.69	0.79
11	34	40	33	1	7	0.97	0.83	0.89
12	34	35	33	1	2	0.97	0.94	0.95
13	52	26	25	27	1	0.48	0.96	0.64
14	53	26	25	28	1	0.47	0.96	0.63
15	78	75	65	13	10	0.83	0.87	0.85
Overall	673	653	566	107	87	0.84	0.87	0.85

¹ TP: True Positive; ² FN: False Negative; ³ FP: False Positive.

indicated that out of 673 reference trees, 566 trees were successfully detected using the low-cost point clouds. However, the recall of Plot 13, and 14 (0.48 and 0.47) was significantly lower than the average value (0.84). The trees in Plot 13 and 14 were mainly Maple and Weeping willow, which were relatively low and had more deciduous leaves in winter. The laser scanner (VLP-16) produced a 9 to 15 cm footprint (from 30 to 50 m distance), which was approximately ten times bigger than the typical ALS laser scanner. Thus, individual tree segmentation may fail (low recall) due to less laser reflection on the vegetation in these two plots because of the limitation of the low-cost laser scanner and the sparse leaves. Overall, the average detection precision and recall were 0.87 and 0.84, respectively, showing the feasibility of the low-cost ULS system in individual tree detection and segmentation.

5.3. Comparison of the Individual Tree Characteristics Estimation Using Different Platforms

To evaluate the accuracy of the individual tree height estimation results using the low-cost ULS system, we compared the results with the ground truth data derived from the commercial system. Figure 14 shows the scatterplot for the validation of the low-cost system and different distributions presented by a boxplot. Tree height estimated by different platforms showed a strong linear relationship (Pearson’s correlation (Pearson’s r) = 0.999). The coefficient of determination (R²) and root-mean-square error (RMSE) of low-cost system for tree height estimation were 0.998 and 0.323 m, respectively, illustrating that tree height estimation using the low-cost system worked well compared with the commercial system. It satisfied the accuracy level of the tree height measurement [36].

To evaluate the accuracy of the tree crown diameter estimation using the low-cost ULS system, we compared the results with the ground truth data derived from the commercial system. Figure 15a,b shows the scatterplot and crown diameter distributions for the validation of the low-cost system. Crown diameter estimated by different platforms showed a low linear relationship (Pearson’s r = 0.345). The R² and RMSE of low-cost system for crown diameter estimation were 0.119 and 0.612 m, respectively. In the scatter plots, there were obviously two outliers, namely, Plot 13 and Plot 14, respectively. As discussed before, trees in Plot 13 and 14 were mainly Maple and Weeping willow, which were relatively low and have more deciduous leaves in winter. Thus, there were relatively fewer points collected from the trees because of the limitation of the low-cost laser scanner and the sparse leaves. This may result in failures of individual tree segmentation and inaccurate crown diameter calculation. Figure 15c,d showed the scatterplot and crown diameter distributions of the plots except Plot 13 and Plot 14. By eliminating the two outliers, crown diameter estimated by different platforms showed a high linear relationship (Pearson’s r = 0.898). The R² and RMSE for crown diameter estimation were 0.806 and 0.195 m, respectively, which indicated that tree diameter estimation of the low-cost system worked well for the most plots, showing the high potential of the low-cost system for 3D forest mapping.

5.4. Deficiencies and Future Work

In this paper, a GNSS and IMU aided SfM was performed to obtain the accurate trajectory. Then the laser scanning points were reconstructed in mapping frame according to the estimated trajectory. However, laser scanning data was not used in the trajectory estimation step. As reported by some works of simultaneous localization and mapping (SLAM), with the depth information from the laser scanner, visual-laser SLAM could achieve better trajectory accuracy [37,38]. Establishing correspondences of the image tie points and laser scanning points, and adding them in the adjustment may achieve better results. As reported by [39], they use laser control information for camera calibration. But only the laser scanning points distributed on the planar area were selected as the “good points”. Thus, the main difficulty lies in the correspondence establishment and selection. If we attach an image tie point with a laser depth, the raw laser depths should be interpolated as shown in Figure 16. The interpolated depth is reliable in the planar area (e.g., roof, ground). However, it is not reliable in the non-planar area (e.g., tree). Hence, using correspondences of image tie points and laser points may result in unreliable optimization in a forest environment. Therefore, how to combine the image tie points and laser points for trajectory estimation in forest environment is worth being explored.

Individual tree segmentation is performed merely based on the reconstructed laser scanning points in this paper. Image sequences collected by the low-cost ULS is not used for the forest application. As reported by [40], individual tree segmentation will benefit from the spectral information. Thus, individual tree segmentation by fusing images and point clouds will also be explored in the future.

6. Conclusions

The low-cost ULS system is a newly developed tool for collecting 3D information in a cost-effective way. However, 3D forest mapping with the low-cost ULS is still a great challenge because of the poor performance of the low-cost sensors. In this paper, we investigated the feasibility of the low-cost ULS for 3D forest mapping and compared the low-cost ULS system with a high-end commercial system. First, to overcome the poor performance of low-cost sensors, we proposed a multisensory integration manner for reconstructing point clouds accurately. Second, individual trees were segmented using the point clouds reconstructed by the proposed multisensory integration. Then the individual tree characteristics (e.g., tree height and crown diameter) were estimated according to the segmented trees. Results indicated that the low-cost ULS system achieved comparable accuracy of tree height and crown diameter with that of the high-end commercial system. However, for the mapping results of low and complex trees, there was still a gap between the data quality of low-cost UAV system and high-end commercial system because of insufficient point density. In general, the low-cost ULS system has shown a high potential for 3D forest mapping, even though 3D forest mapping using low-cost ULS system requires further research.

Some issues are still worthy of attention. With the development of laser technology, many low-cost laser scanners with longer measurement range (e.g., 200 m) and smaller footprint have been produced. They promote the performance of low-cost ULS systems and are more efficient for mapping in forest. What is more, the proposed trajectory estimation and individual tree segmentation have not taken advantage of the multisensory data. Thus, (1) trajectory estimation combining laser and image information; (2) individual tree segmentation by fusing images and point clouds will be explored in the future.