Estimation of Cargo Handling Capacity of Coastal Ports in China Based on Panel Model and DMSP-OLS Nighttime Light Data
Abstract
1. Introduction
2. Materials and Methods
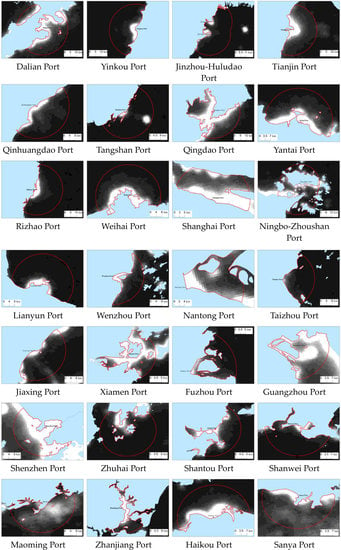
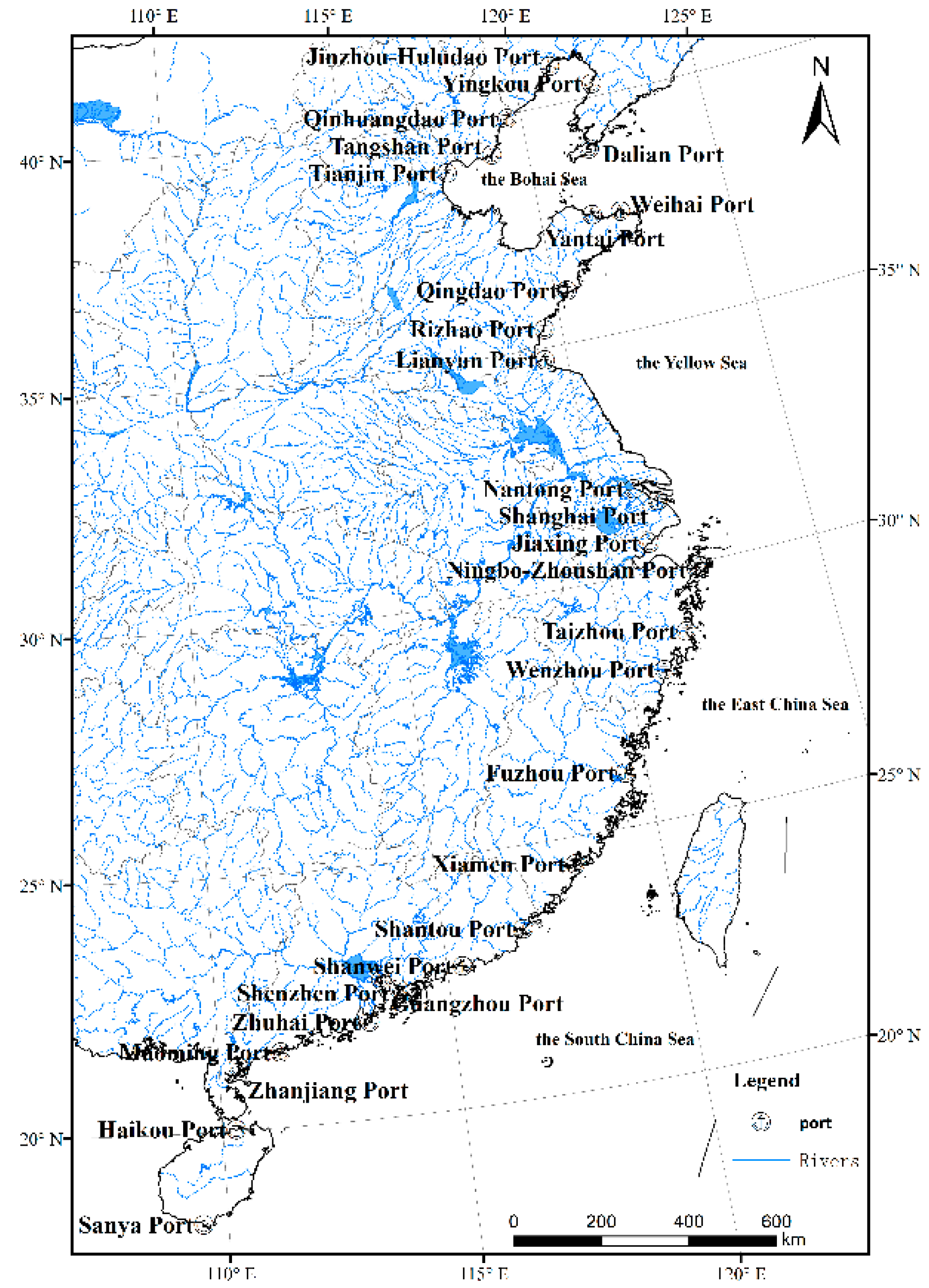
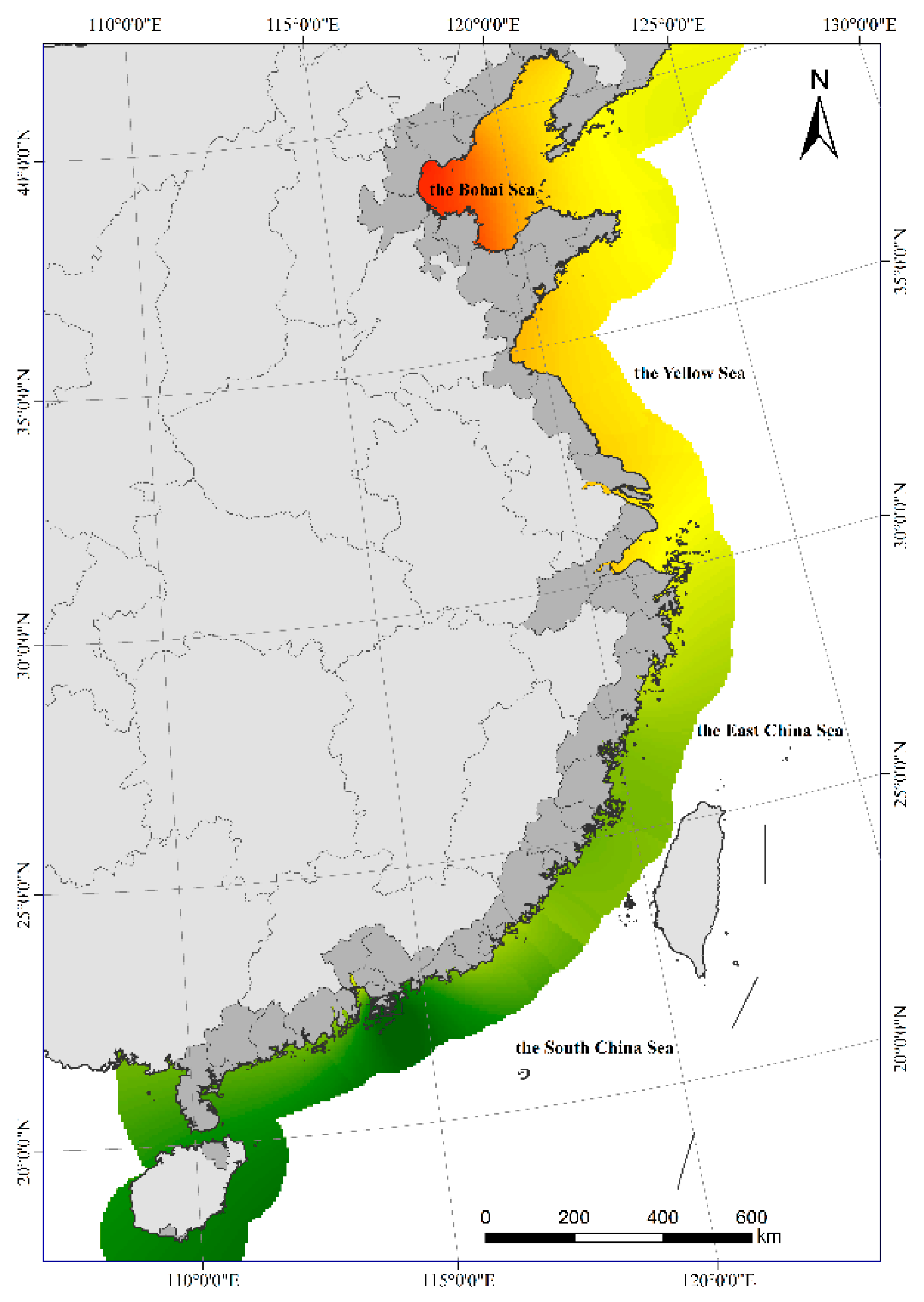
2.1. Study Area
2.2. Data Source
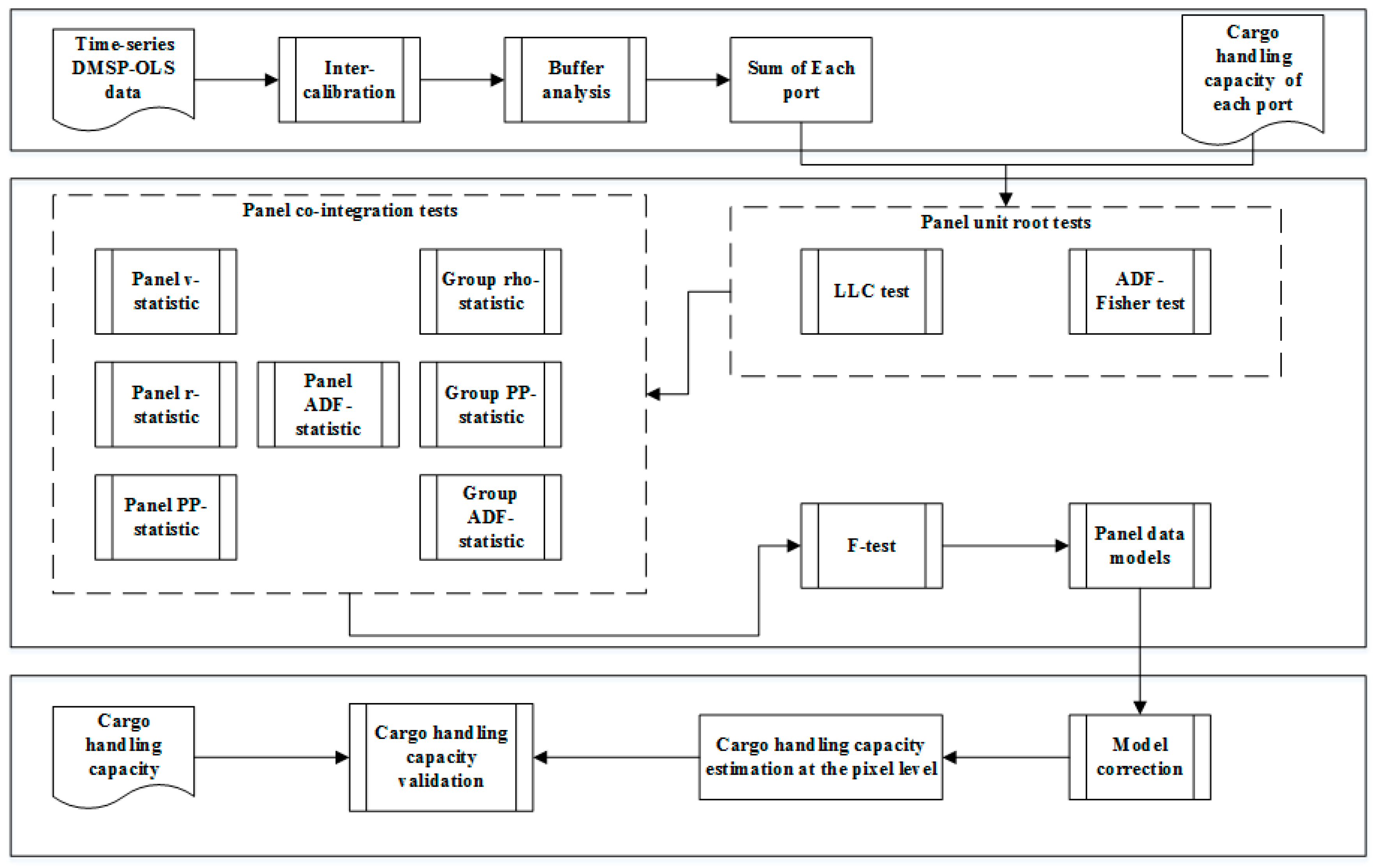
2.3. Data Pre-Processing
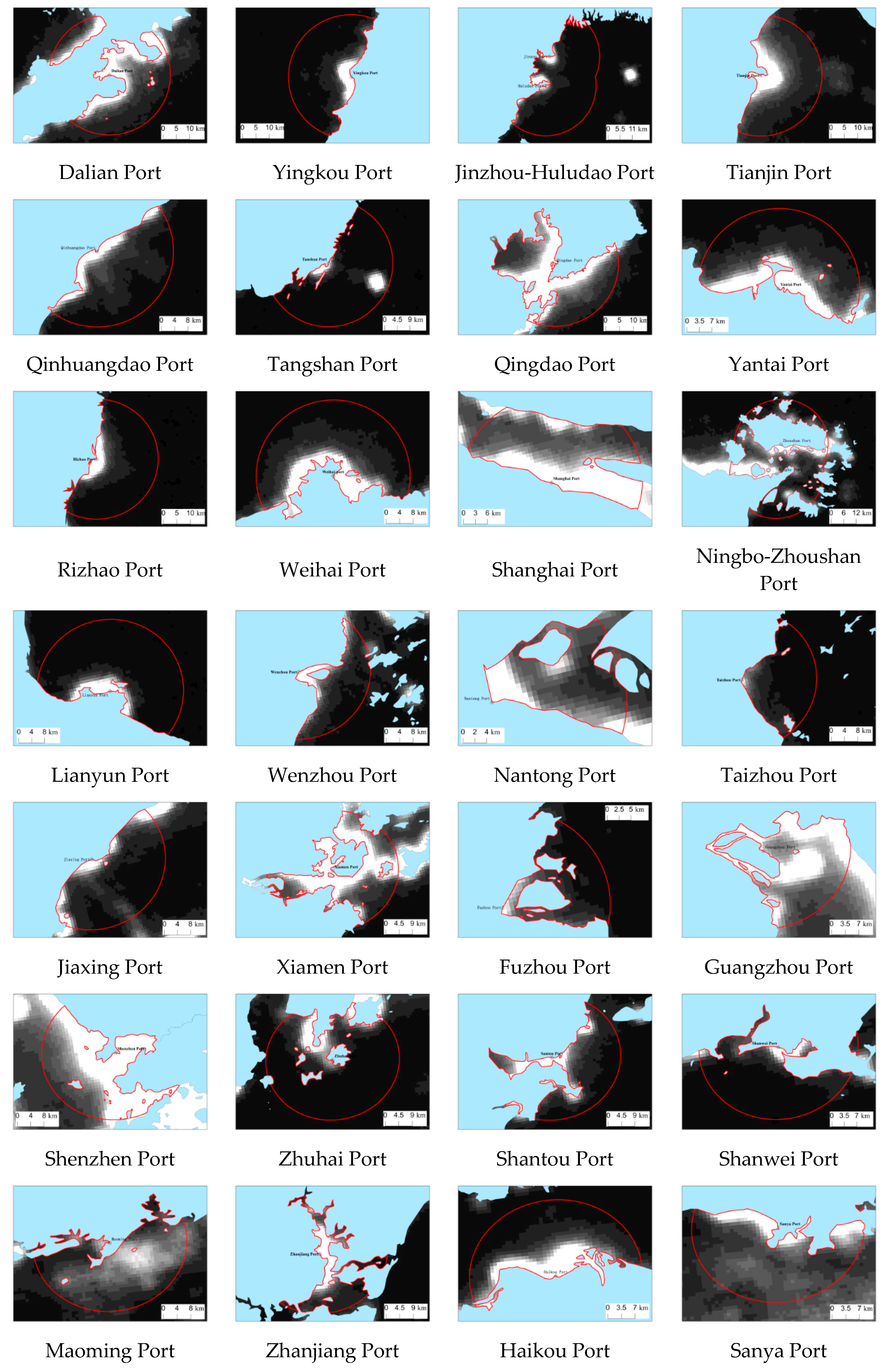
2.4. Generation of the Port Buffer Zone and Statistics of Light Values
2.5. Establishment of Panel Model
2.5.1. Unit Root Test of Panel Data
2.5.2. Co-Integration Test of Panel Data
2.5.3. Panel Model Estimation
- Case 1:
- (constant coefficient model);
- Case 2:
- (variable intercept model);
- Case 3:
- (variable parameter model).
3. Results
3.1. Results of Unit Root Test of Panel Data
3.2. Results of the Co-Integration Test of Panel Data
3.3. Parameter Estimation of the Panel Model
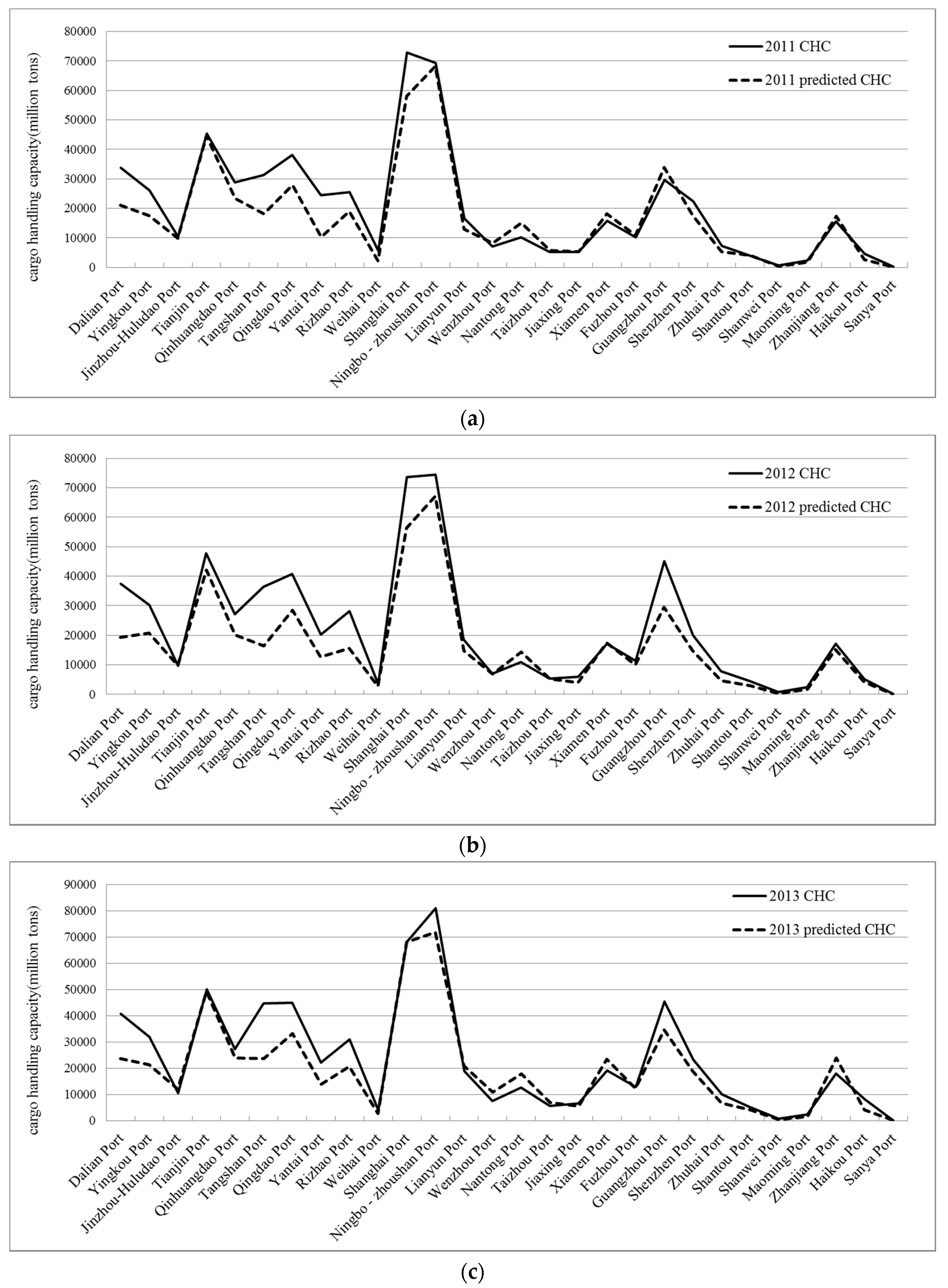
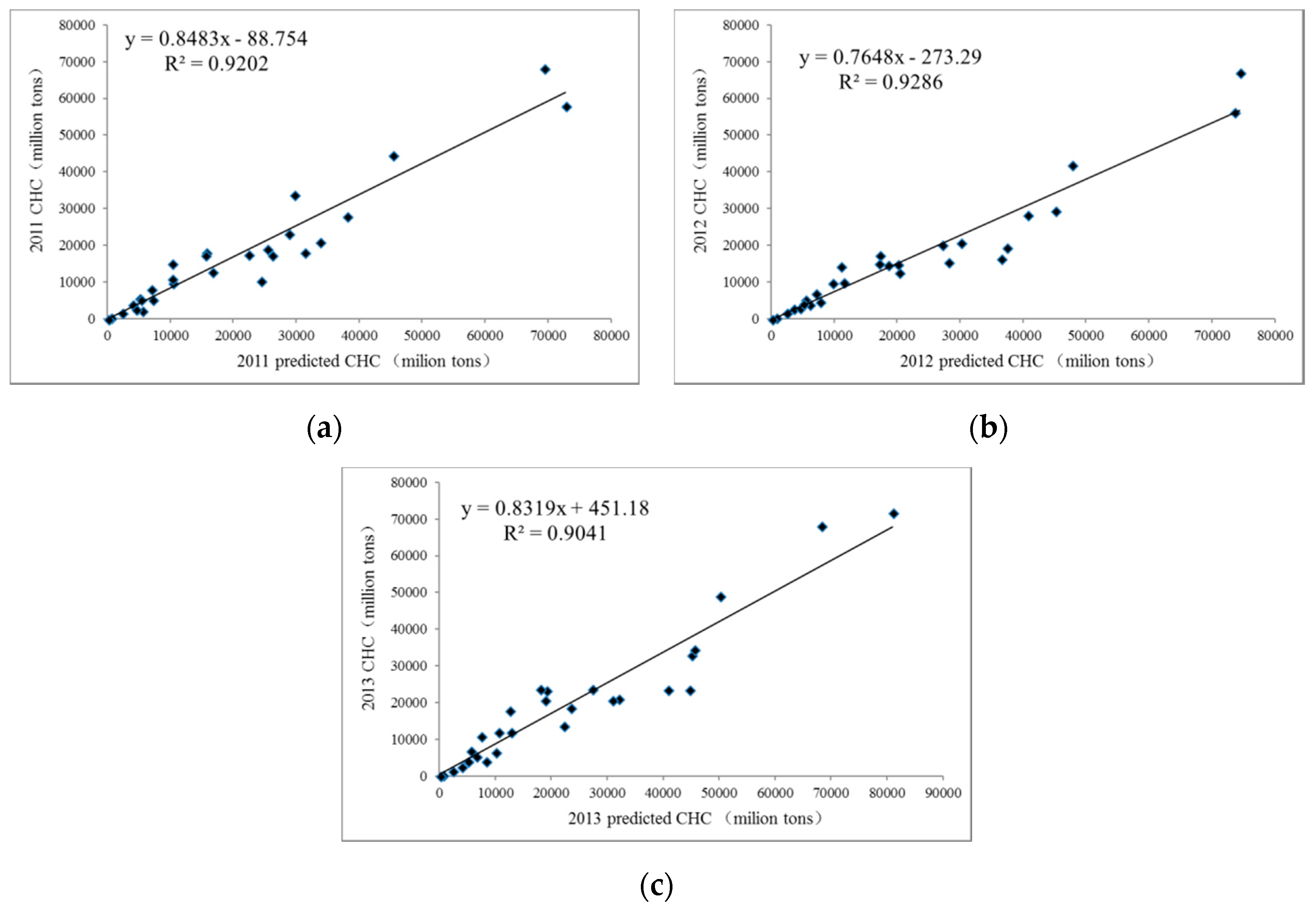
3.4. Verification of the Panel Model
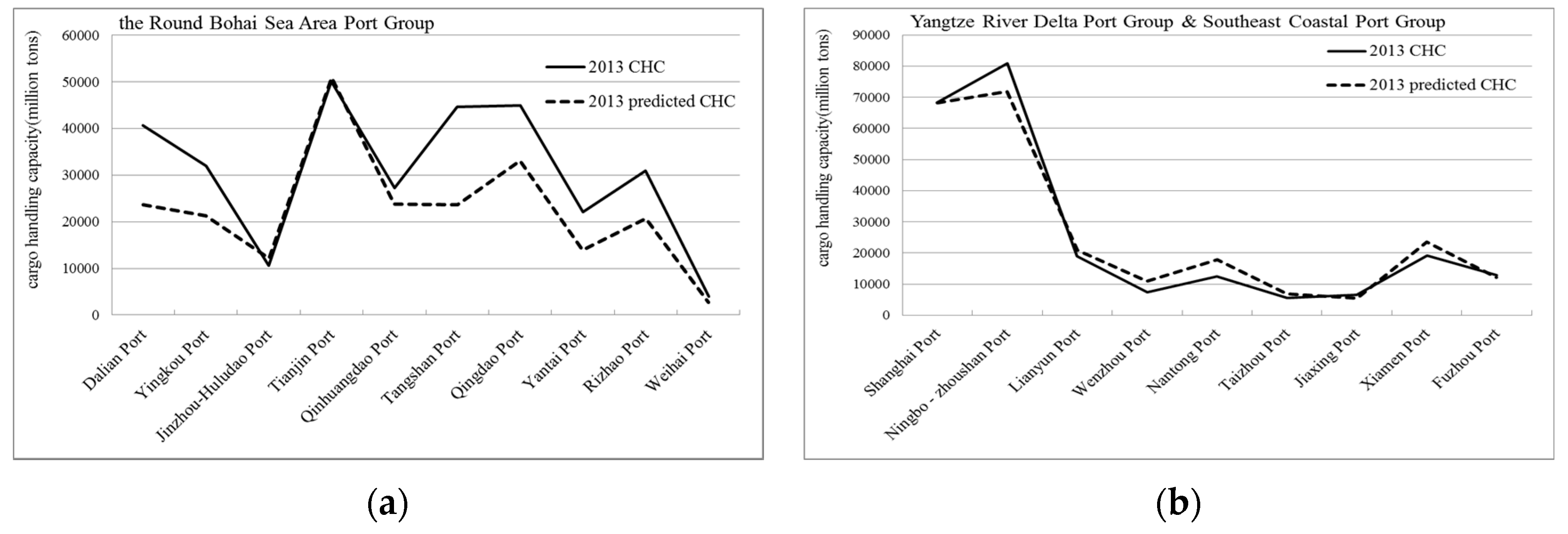
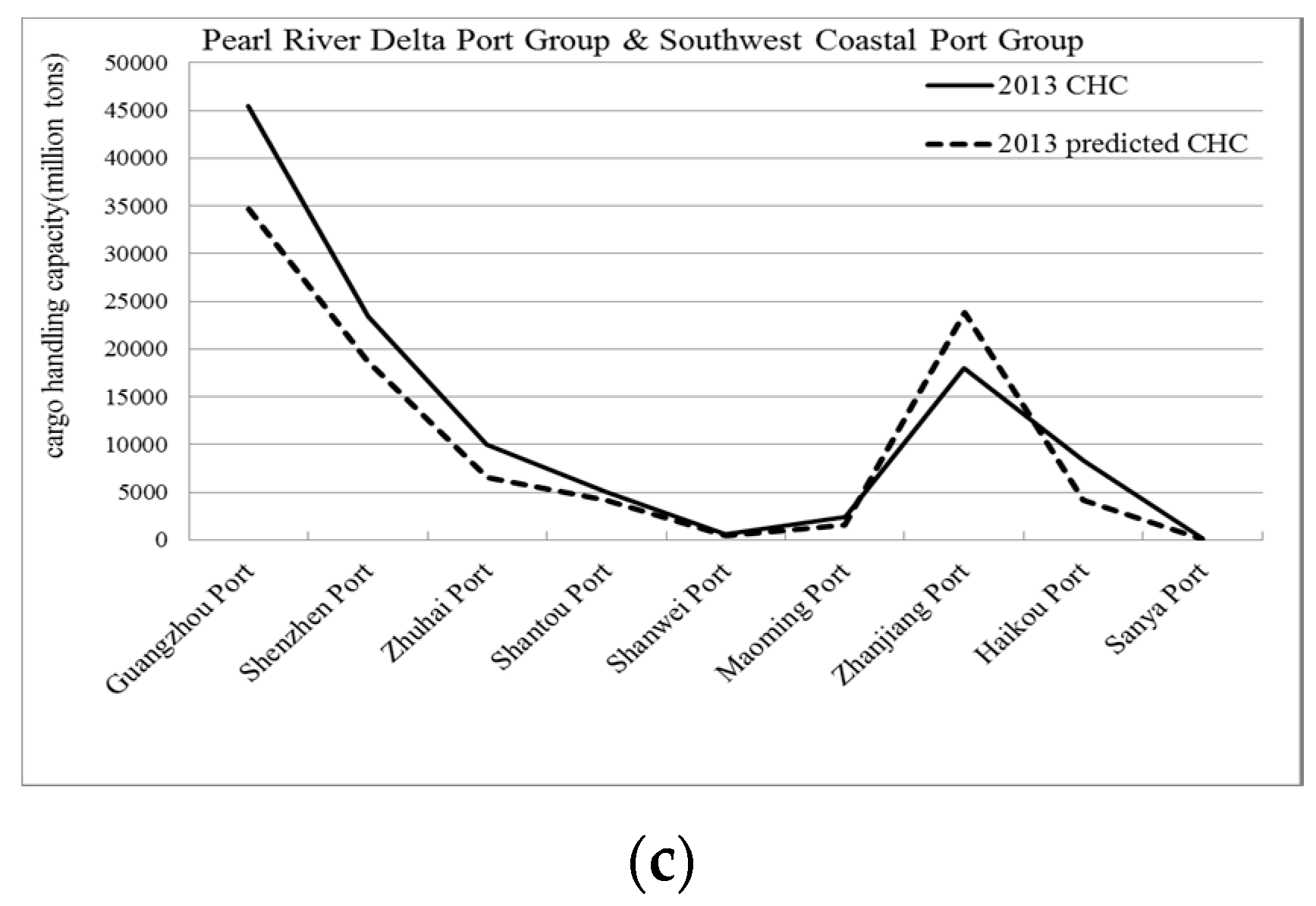
3.4.1. Accuracy Test for All Ports
3.4.2. Accuracy Test for Three Port Groups
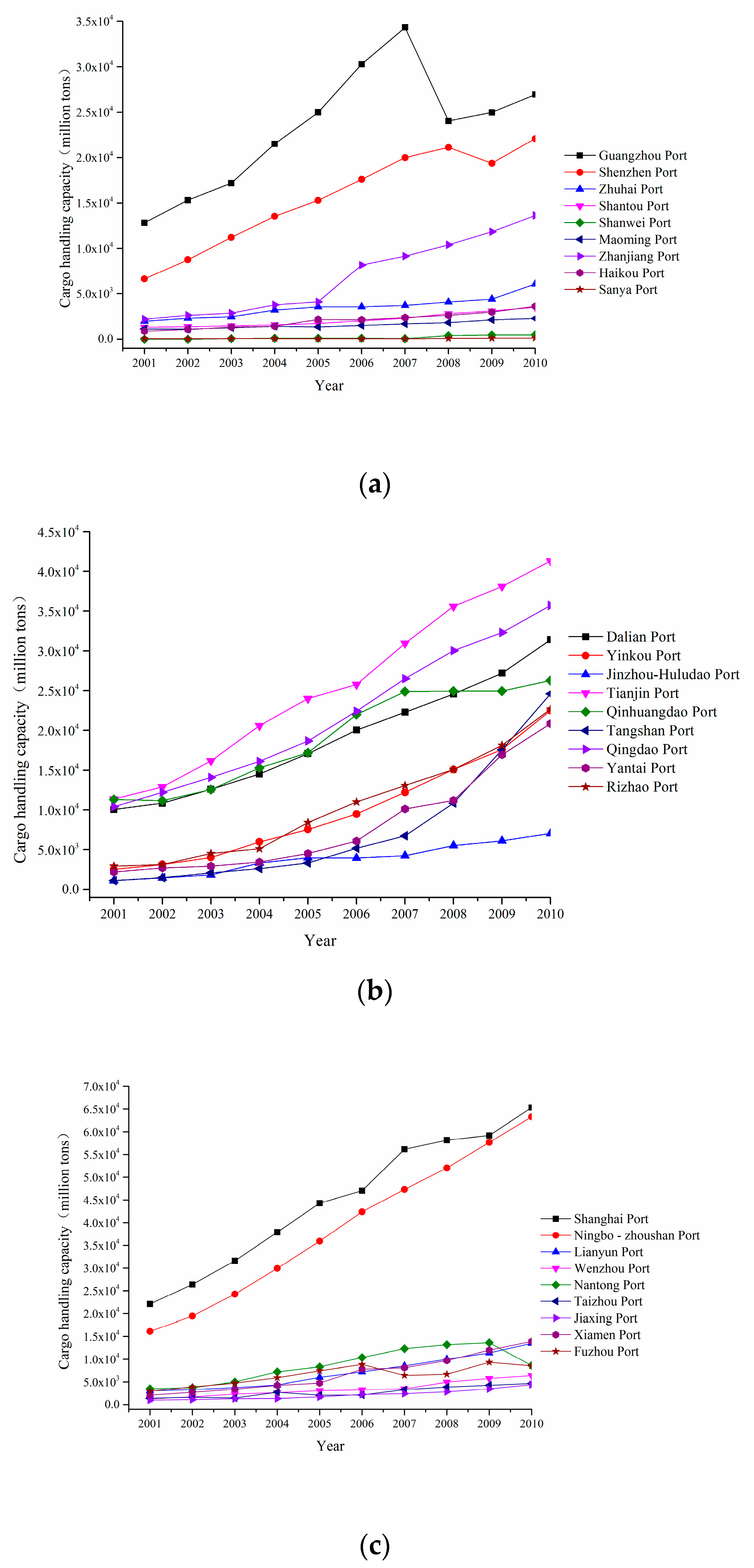
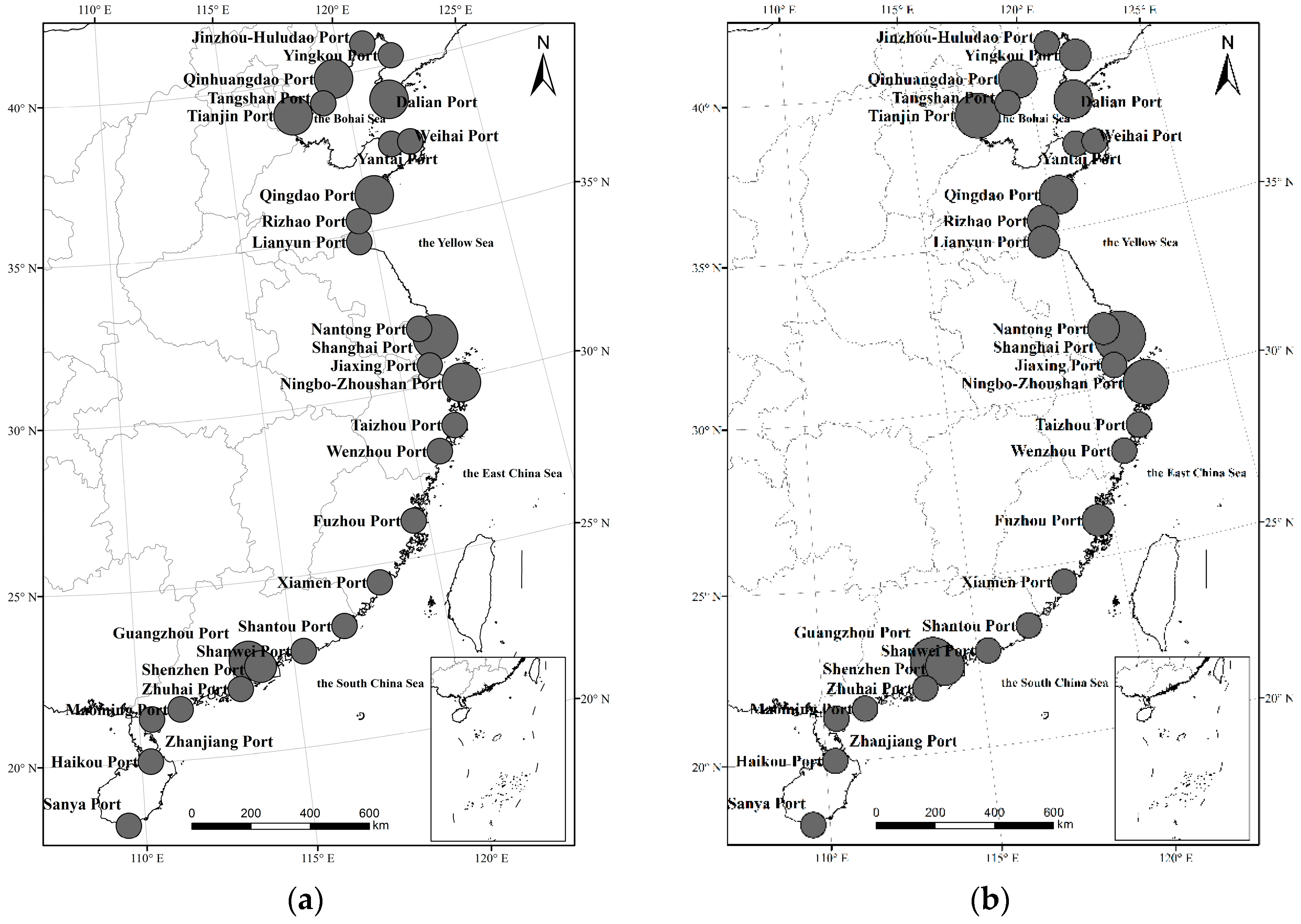
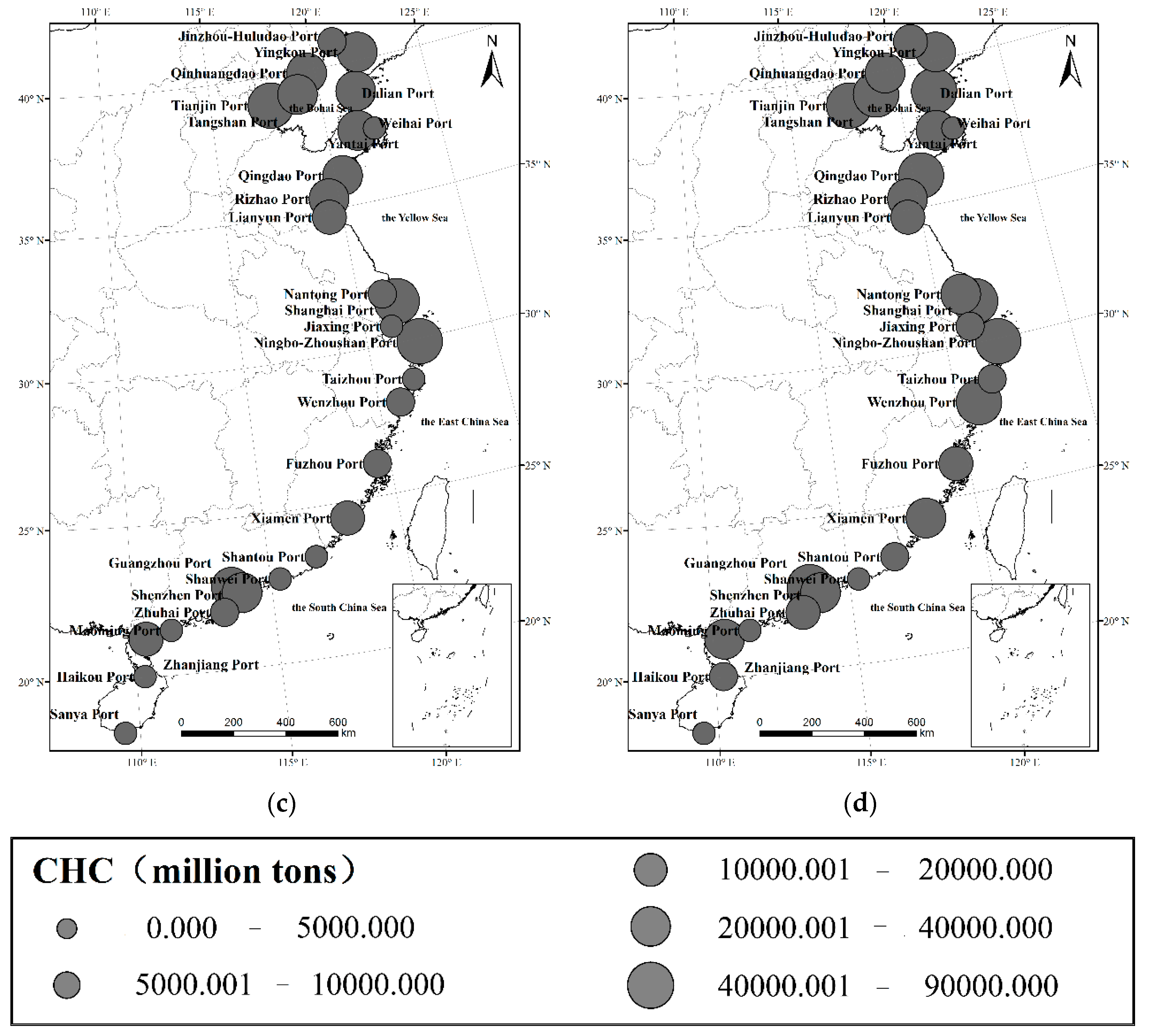
3.5. Spatial Pattern and Evolution of CHC for Coastal Ports in China from 2001 to 2015
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chang, S. Production function and capacity utilization of the port of Mobile. Marit. Policy Manag. 1978, 5, 297–305. [Google Scholar] [CrossRef]
- Kim, M.; Sachish, A. The structure of production, technical change and productivity in a port. Int. J. Ind. Econ. 1986, 35, 209–223. [Google Scholar] [CrossRef]
- Tongzon, J.L. The Port of Melbourne Authority’s pricing policy: Its efficiency and distribution implications. Marit. Policy Manag. 1993, 20, 197–203. [Google Scholar] [CrossRef]
- Sun, L.; Tan, D. Research on probability distribution of port cargo throughput. J. Mar. Sci. Appl. 2008, 7, 65–68. [Google Scholar] [CrossRef]
- Eddie, C.H.; Man, H.N.; Jane, J.X.; Tsz, L.Y. The cargo throughput response to factor cost differentials-an analysis for the port of Hong Kong. Transportmetrica 2010, 6, 235–248. [Google Scholar] [CrossRef]
- Chang, B.K. Impact of Exchange Rate Movements, Global Economic Activity, and the BDI Volatility on Loaded Port Cargo Throughput in South Korea. Asian J. Shipp. Logist. 2016, 32, 243–248. [Google Scholar] [CrossRef]
- Elvidge, C.D. Mapping City Lights with Nighttime Data from the DMSP Operational Linescan System. Photogramm. Eng. Remote Sens. 1997, 63, 727–734. [Google Scholar]
- Elvidge, C.D.; Baugh, K.E.; Dietz, J.B.; Bland, T.; Sutton, P.C.; Herbert, W.K. Radiance Calibration of DMSP-OLS Low-Light Imaging Data of Human Settlements. Remote Sens. Environ. 1999, 68, 77–88. [Google Scholar] [CrossRef]
- Witmer, F.W.; Loughlin, J. Detecting the Effects of Wars in the Caucasus Regions of Russia and Georgia Using Radiometrically Normalized DMSP-OLS Nighttime Lights Imagery. Mapp. Sci. Remote Sens. 2011, 48, 478–500. [Google Scholar] [CrossRef]
- Propasti, P.; Kappas, M. Assessing Satellite-Observed Nighttime Lights for Monitoring Socioeconomic Parameters in the Republic of Kazakhstan. Mapp. Sci. Remote Sens. 2012, 49, 538–557. [Google Scholar] [CrossRef]
- Butt, M.J. Estimation of Light Pollution Using Satellite Remote Sensing and Geographic Information System Techniques. Mapp. Sci. Remote Sens. 2012, 49, 609–621. [Google Scholar] [CrossRef]
- He, C.; Ma, Q.; Li, T.; Yang, Y.; Liu, Z. Spatiotemporal dynamics of electric power consumption in Chinese Mainland from 1995 to 2008 modeled using DMSP-OLS stable nighttime lights data. J. Geogr. Sci. 2012, 22, 125–136. [Google Scholar] [CrossRef]
- He, C.; Ma, Q.; Li, T.; Yang, Y.; Liu, Z.; Zhang, Q. Modeling the spatiotemporal dynamics of electric power consumption in Mainland China using saturation-corrected DMSP-OLS nighttime stable light data. Int. J. Digit. Earth 2014, 7, 993–1014. [Google Scholar] [CrossRef]
- Tian, J.; Zhao, N.; Samson, E.L.; Wang, S. Brightness of Nighttime Lights as a Proxy for Freight Traffic: A Case Study of China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 206–212. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, W.; Zhou, C.; Li, M.C.; Huang, K.; Wang, N. Assessing Spatiotemporal Characteristics of Urbanization Dynamics in Southeast Asia Using Time Series of DMSP-OLS Nighttime Light Data. Remote Sens. 2018, 10, 47. [Google Scholar] [CrossRef]
- Addison, D.M.; Stewart, B.P. Nighttime Lights Revisited: The Use of Nighttime Lights Data as a Proxy for Economic Variables. Soc. Sci. Electron. Publ. 2015, 53, 86–87. [Google Scholar] [CrossRef]
- Yücer, E.; Erener, A. Examining Urbanization Dynamics in Turkey Using DMSP–OLS and Socio-Economic Data. J. Indian Soc. Remote Sens. 2018, 46, 1159–1169. [Google Scholar] [CrossRef]
- Doll, C.N.H. The DMSP-OLS sensor and its data products. In CIESIN Thematic Guide to Night-Time Light Remote Sensing and Its Applications, 1st ed.; Doll, C.N.H., Ed.; Columbia University: New York, NY, USA, 2008; Volume 3, pp. 6–11. [Google Scholar]
- Ma, T.; Xu, T.; Huang, L.; Zhou, A. A Human Settlement Composite Index (HSCI) Derived from Nighttime Luminosity Associated with Imperviousness and Vegetation Indexes. Remote Sens. 2018, 10, 455. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, Z.; Liu, F. Monitoring Population Evolution in China Using Time-Series DMSP-OLS Nightlight Imagery. Remote Sens. 2018, 10, 194. [Google Scholar] [CrossRef]
- Stathakis, D.; Baltas, P. Seasonal population estimates based on night-time lights. Comput. Environ. Urban Syst. 2018, 68, 133–141. [Google Scholar] [CrossRef]
- Croft, T.A. Nighttime Images of the Earth from Space. Sci. Am. 1978, 239, 86–98. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Lawrence, W.T.; Stutzer, D.C.; Elvidge, C.D. A technique for using composite DMSP-OLS ‘City Lights’ satellite data to map urban area. Remote Sens. Environ. 1997, 61, 361–370. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Imhoff, M.L.; Baugh, K.E.; Hobson, V.R.; Nelson, I.; Satran, J.; Dietz, J.B.; Tuttle, B.T. Night-time lights of the world: 1994–1995. ISPRS J. Photogramm. Remote Sens. 2001, 56, 81–99. [Google Scholar] [CrossRef]
- Shi, K.F.; Yu, B.L.; Huang, Y.X.; Wu, J.P. Evaluating the Ability of NPP-VIIRS Nighttime Light Data to Estimate the Gross Domestic Product and the Electric Power Consumption of China at Multiple Scales&58; A Comparison with DMSP-OLS Data. Remote Sens. 2014, 6, 1705–1724. [Google Scholar] [CrossRef]
- Kim, S.W.; Cho, K.D.; Kim, Y.S.; Choi, Y.S.; Ahn, Y.H.; Kim, Y.S. Distribution of Fishing Boats at Night in the East Sea Derived from DMSP-OLS Imagery. Korean J. Fish. Aquat. Sci. 2005, 38, 323–330. [Google Scholar] [CrossRef]
- Nagatani, I. A methodology to create DMSP-OLS night-time mosaic image for monitoring fishing boats. Proc. Asia-Pac. Adv. Netw. 2010, 30, 229. [Google Scholar] [CrossRef]
- Shi, K.F.; Yu, B.L.; Hu, Y.J.; Huang, C.; Chen, Y.; Huang, Y.X.; Chen, Z.Q.; Wu, J. Modeling and mapping total freight traffic in China using NPP-VIIRS nighttime light composite data. Mapp. Sci. Remote Sens. 2015, 52, 274–289. [Google Scholar] [CrossRef]
- Li, C.; Chen, G.; Luo, J.; Li, S.; Ye, H. Port economics comprehensive scores for major cities in the Yangtze Valley, China using the DMSP-OLS night-time light imagery. Int. J. Remote Sens. 2017, 38, 1–23. [Google Scholar] [CrossRef]
- Chu, Z.F. Logistics and economic growth: A panel data approach. Ann. Reg. Sci. 2012, 49, 87–102. [Google Scholar] [CrossRef]
- Lakew, P.A. Essays on Air Cargo Cost Structures, Airport Traffic, and Airport Delays: Panel Data Analysis of the U.S. Airline Industry. Ph.D. Dissertation, University of California, Irvine, CA, USA, 2014. Available online: https://escholarship.org/uc/item/9vp9621m (accessed on 21 January 2019).
- Guo, X.; Ren, D.; Shi, J. Carbon emissions, logistics volume and GDP in China: Empirical analysis based on panel data model. Environ. Sci. Pollut. Res. 2016, 23, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Baltagi, B.H. Econometric analysis of panel data. Econom. Theory 2001, 5, 747–754. [Google Scholar]
- Seto, K.C.; Kaufmann, R.K. Modeling the Drivers of Urban Land Use Change in the Pearl River Delta, China. Land Econ. 2003, 79, 106–121. [Google Scholar] [CrossRef]
- Hsiao, C. Analysis of Panel Data; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Shi, K.; Chen, Y.; Yu, B.; Xu, T.; Chen, Z.; Liu, R.; Li, L.; Wu, J. Modeling spatiotemporal CO2 (carbon dioxide) emission dynamics in China from DMSP-OLS nighttime stable light data using panel data analysis. Appl. Energy 2016, 168, 523–533. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, H.; Song, W.; Yu, B.; Xiu, C. Normalization of time series DMSP-OLS nighttime light images for urban growth analysis with Pseudo Invariant Features. Landsc. Urban Plan. 2014, 128, 1–13. [Google Scholar] [CrossRef]
- Elvidge, C.; Ziskin, D.; Baugh, K.; Tuttle, B.; Ghosh, T.; Pack, D.; Erwin, E.; Zhizhin, M. A Fifteen Year Record of Global Natural Gas Flaring Derived from Satellite Data. Energies 2009, 2, 595–622. [Google Scholar] [CrossRef]
- Adhikari, R. A neural network based linear ensemble framework for time series forecasting. Neurocomputing 2015, 157, 231–242. [Google Scholar] [CrossRef]
- Chang, Y.T.; Park, H.; Lee, S.; Kim, E. Have Emission Control Areas (ECAs) harmed port efficiency in Europe? Transp. Res. Part D Transp. Environ. 2018, 58, 39–53. [Google Scholar] [CrossRef]
- Rassam, M.; Hadi, R.F.; Hadi, G. Estimation of perishable cargo transportation demand by a panel data model. Urban Manag. 2015, 13, 93–102. [Google Scholar]
- Wang, S.S.; Zhou, D.Q.; Zhou, P.; Wang, Q.W. CO2 emissions, energy consumption and economic growth in China: A panel data analysis. Energy Policy 2011, 39, 4870–4875. [Google Scholar] [CrossRef]
- Levin, A.; Lin, C.; James, C. Unit root tests in panel data: Asymptotic and finite-sample properties. Economet 2002, 108, 1–24. [Google Scholar] [CrossRef]
- Fleissig, A.R.; Strauss, J. Unit root tests on real wage panel data for the G7. Econ. Lett. 1997, 56, 149–155. [Google Scholar] [CrossRef]
- Rault, C.; Drine, I. Does the Balassa-Samuelson Hypothesis Hold for Asian Countries? In An Empirical Analysis Using Panel Data Cointegration Tests; William Davidson Institute Working Papers; William Davidson Institute: Ann Arbor, MI, USA, 2002; p. 4. [Google Scholar] [CrossRef]
- Pedroni, P. Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxf. Bull. Econ. Stat. 1999, 61, 653–670. [Google Scholar] [CrossRef]
- Örsal, D.D.K. Comparison of panel cointegration tests. Econ. Bull. 2007, 3, 1–20. [Google Scholar]
- Kim, C.J.; Nelson, C.R. Estimation of a forward-looking monetary policy rule: A time-varying parameter model using ex post data. J. Monet. Econ. 2006, 53, 1949–1966. [Google Scholar] [CrossRef]
- Yang, J.; Guan, Y.Y.; Xia, J.H.; Jin, C.; Li, X.M. Spatiotemporal variation characteridtics of green space ecosystem service value at urban fringes: A case study on Ganjingzi District in Dalian, China. Sci. Total Environ. 2018, 639, 1453–1461. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, J.; Wang, S.H.; Wang, J.F.; Deng, G.P. Analysis and simulation of the spatiotemporal evolution pattern of tourism lands at the Natural World Heritage Site Jiuzhaigou, China. Habitat Int. 2018, 79, 74–88. [Google Scholar] [CrossRef]
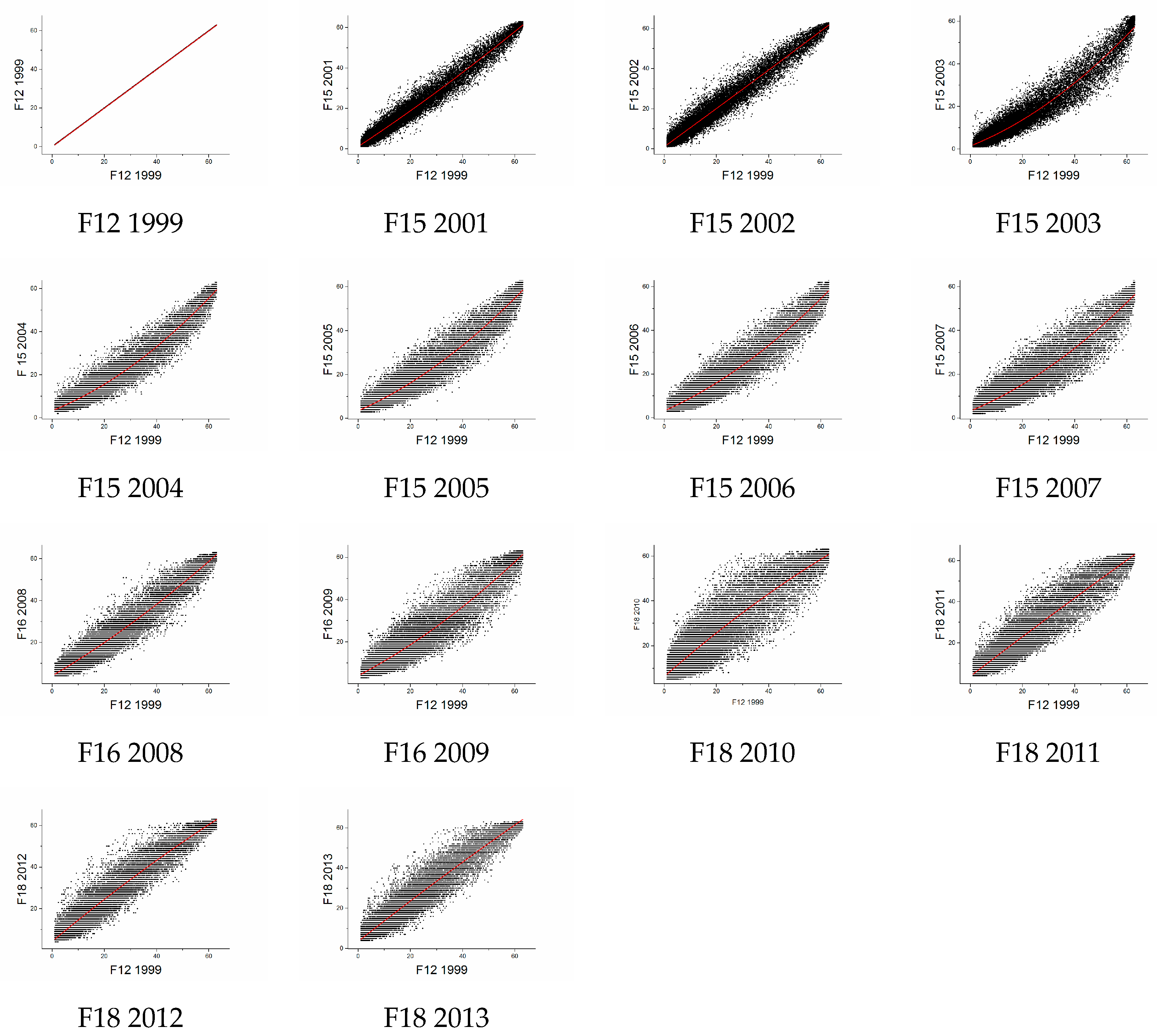
| Port Group | Variable | ADF | ADF | LLC | LLC |
|---|---|---|---|---|---|
| Level | First Difference | Level | First Difference | ||
| RBAPG | CHC | 11.8788 | 42.5880 *** | 1.11674 | −8.35618 *** |
| NAL | 34.9262 ** | 71.2847 *** | −11.8514 *** | −12.2575 *** | |
| YRDPG & SECPG | CHC | 9.33534 | 24.1933 | −1.64247 ** | −4.75277 *** |
| NAL | 17.3270 * | 23.2828 *** | −4.28212 *** | −6.69991 *** | |
| PRDPG & SWCPG | CHC | 3.61232 | 33.1364 *** | 4.31733 | −4.81040 *** |
| NAL | 23.6416 | 40.1869 *** | −3.13365 *** | −7.74467 *** |
| Port Group | Panel v-Statistic | Panel rho-Statistic | Panel PP-Statistic | Panel ADF-Statistic | Group rho-Statistic | Group PP-Statistic | Group ADF-Statistic |
|---|---|---|---|---|---|---|---|
| RBAPG | −0.902304 | 0.705141 | −5.877560 *** | −2.594381 *** | 2.137482 | −9.447249 *** | −3.073088 *** |
| YRDPG & SECPG | 3.448060 *** | −2.467861 *** | −4.330827 *** | 0.403685 | 0.809806 | −0.960831 | 0.814878 |
| PRDPG & SWCPG | 3.966106 *** | 0.335334 | −8.996168 *** | −3.608918 *** | 1.950330 | −7.409503 *** | −3.075394 *** |
| Port Group | R-Squared | Adjusted R-Squared | F-Statistic | Prob (F-Statistic) |
|---|---|---|---|---|
| RBAPG | 0.873629 | 0.843616 | 29.10834 | 0.000000 |
| YRDPG & SECPG | 0.978657 | 0.973618 | 794.2081 | 0.000000 |
| PRDPG & SWCPG | 0.927828 | 0.910787 | 54.44777 | 0.000000 |
| Port Group | Port | βi | αi |
|---|---|---|---|
| RBAPG | Dalian Port | 2.97316480967 | −29,800.8460021 |
| Yingkou Port | 1.51259165806 | 10,139.6909277 | |
| Jinzhou Port | 1.08230668582 | 9611.7506492 | |
| Tianjin Port | 2.28021081738 | 8339.30420347 | |
| Qinhuangdao Port | 2.93348582808 | 14,313.2481409 | |
| Tangshan Port | 4.35352549308 | 5723.6833558 | |
| Qingdao Port | 2.69021227798 | −34,697.1797607 | |
| Yantai Port | 1.44303547357 | 1888.39510679 | |
| Rizhao Port | 3.54326127447 | 5922.03727201 | |
| Weihai Port | 0.365999992386 | 8559.91610698 | |
| YRDPG & SECPG | Shanghai Port | 5.30720435849 | −38,838.5697443 |
| Ningbo-Zhoushan Port | 2.34490630312 | 10,038.0934431 | |
| Lianyun Port | 3.49366796774 | 6480.15261962 | |
| Wenzhou Port | 2.40333674731 | 7381.84050485 | |
| Nantong Port | 1.66437462899 | 12,547.3393606 | |
| Taizhou Port | 1.90768606351 | 11,490.8742163 | |
| Jiaxing Port | 0.668939673475 | 9850.14836242 | |
| Xiamen Port | 2.37719613324 | −31,316.9531034 | |
| Fuzhou Port | 5.46452736258 | 12,367.0743408 | |
| PRDPG & SWCPG | Guangzhou Port | 1.43838402662 | 12,127.2906713 |
| Shenzhen Port | 2.57695331345 | −45,905.6297616 | |
| Zhuhai Port | 0.538321113604 | 9563.65544466 | |
| Shantou Port | 0.699682060439 | 7324.55617453 | |
| Shanwei Port | 0.23474882113 | 8506.50287551 | |
| Maoming Port | −0.130224114145 | 10,683.1372926 | |
| Zhanjiang Port | 7.1384914425 | −15,059.5314971 | |
| Haikou Port | 0.888932009617 | 4145.79490213 | |
| Sanya Port | 0.0291353214443 | 8614.22389788 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, A.; Wei, Y.; Yu, B.; Song, W. Estimation of Cargo Handling Capacity of Coastal Ports in China Based on Panel Model and DMSP-OLS Nighttime Light Data. Remote Sens. 2019, 11, 582. https://doi.org/10.3390/rs11050582
Liu A, Wei Y, Yu B, Song W. Estimation of Cargo Handling Capacity of Coastal Ports in China Based on Panel Model and DMSP-OLS Nighttime Light Data. Remote Sensing. 2019; 11(5):582. https://doi.org/10.3390/rs11050582
Chicago/Turabian StyleLiu, Aoshuang, Ye Wei, Bailang Yu, and Wei Song. 2019. "Estimation of Cargo Handling Capacity of Coastal Ports in China Based on Panel Model and DMSP-OLS Nighttime Light Data" Remote Sensing 11, no. 5: 582. https://doi.org/10.3390/rs11050582
APA StyleLiu, A., Wei, Y., Yu, B., & Song, W. (2019). Estimation of Cargo Handling Capacity of Coastal Ports in China Based on Panel Model and DMSP-OLS Nighttime Light Data. Remote Sensing, 11(5), 582. https://doi.org/10.3390/rs11050582