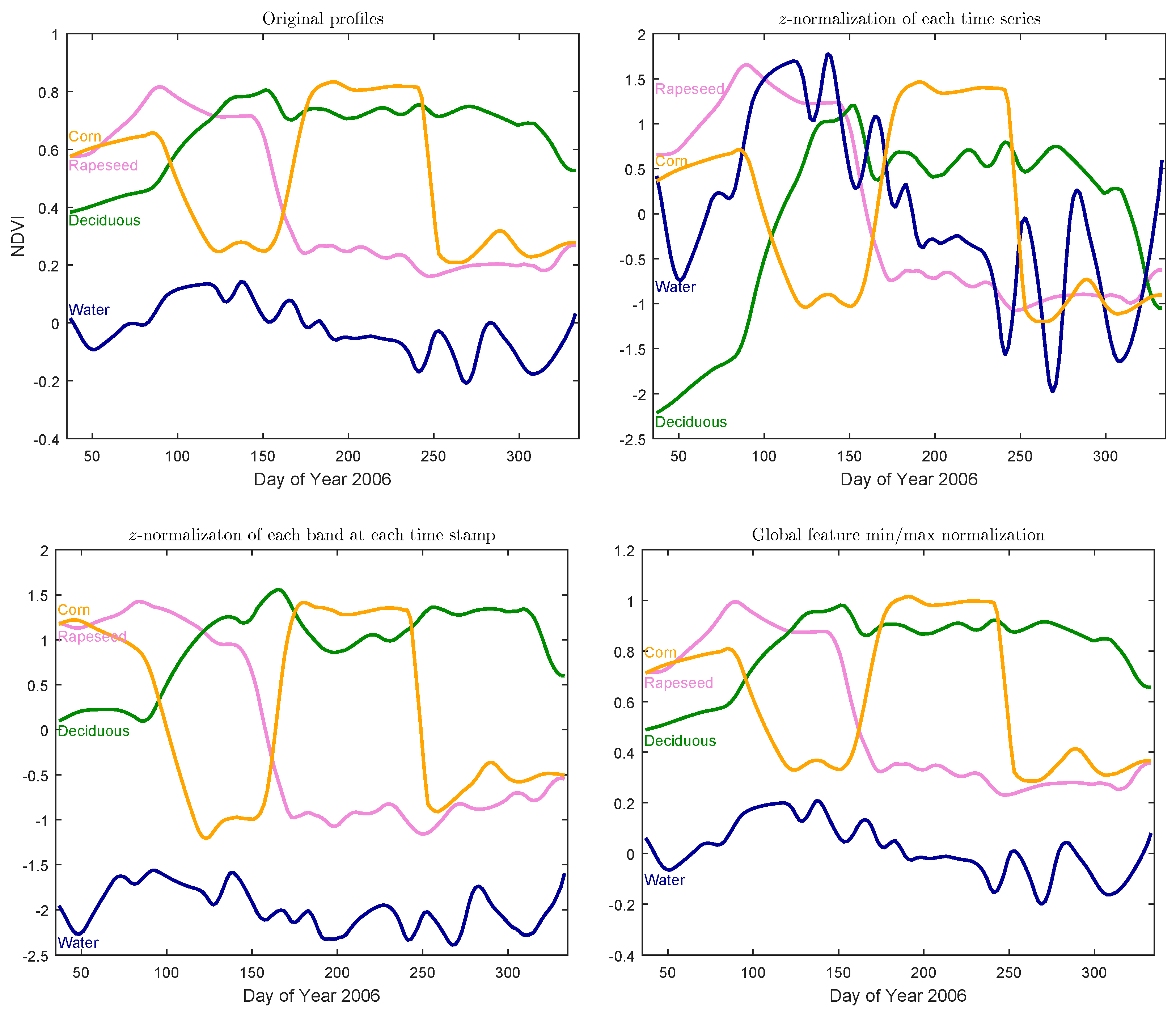
A last section is dedicated to the visual analysis of the produced land cover maps.
4.1. Benefiting from Both Spectral and Temporal Dimensions
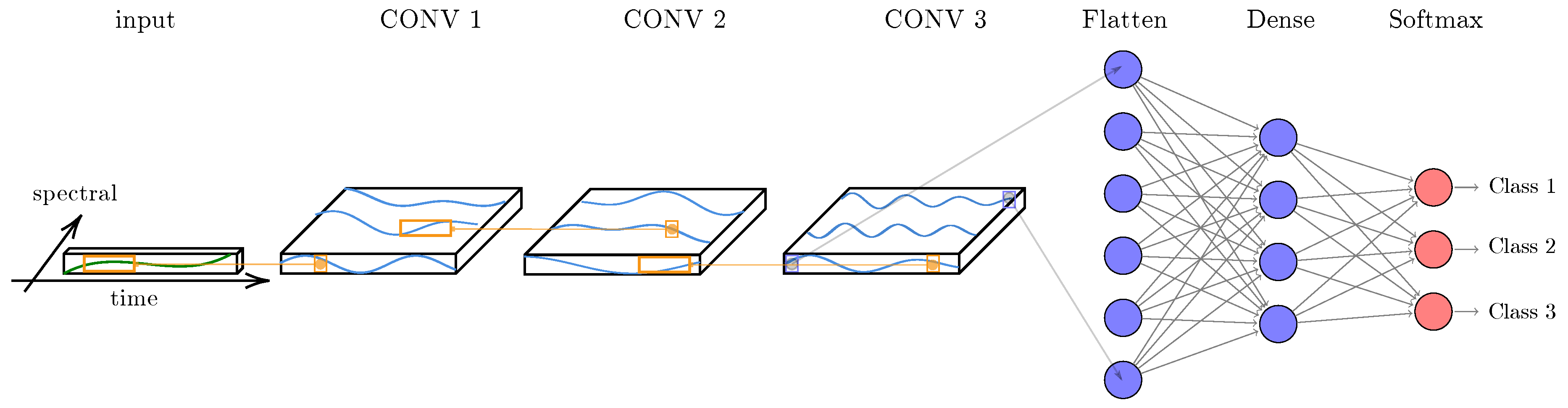
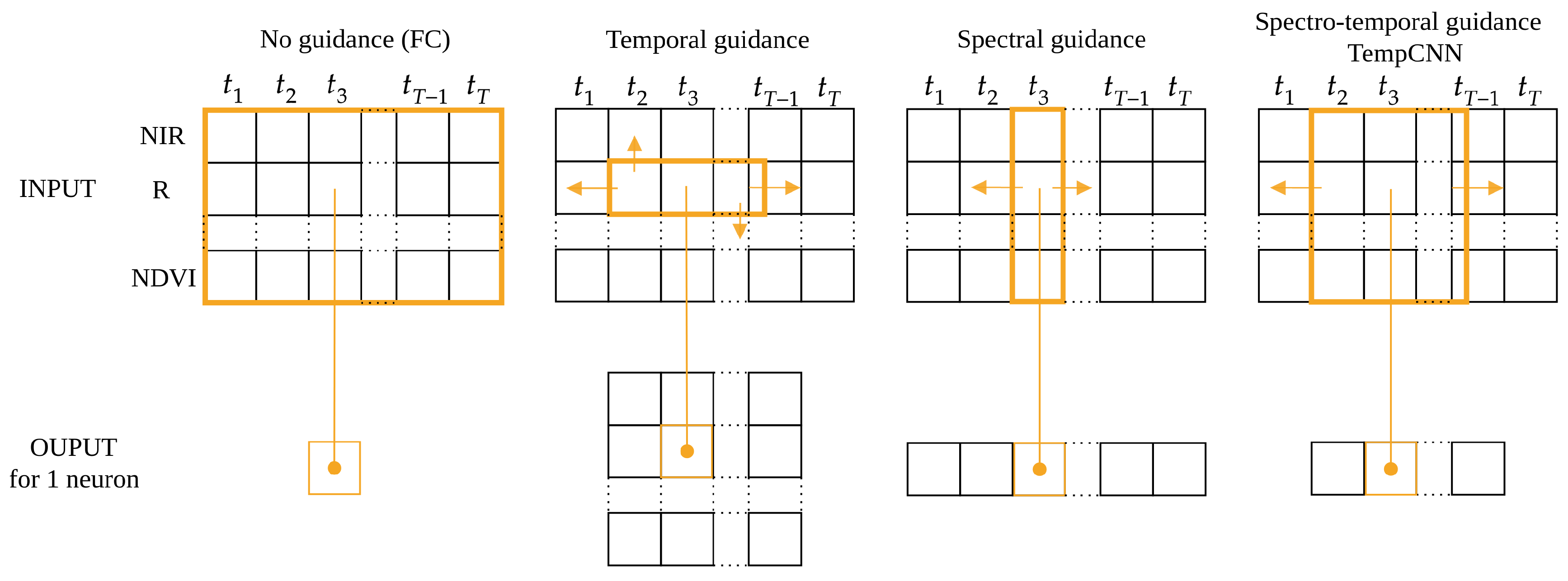
In this experiment, we compare four configurations: (1) no guidance, (2) only temporal guidance, (3) only spectral guidance, and (4) both temporal and spectral guidance (TempCNNs). Before presenting the obtained results, we first describe the trained models for these fourth types of guidance, which are illustrated in
Figure 8.
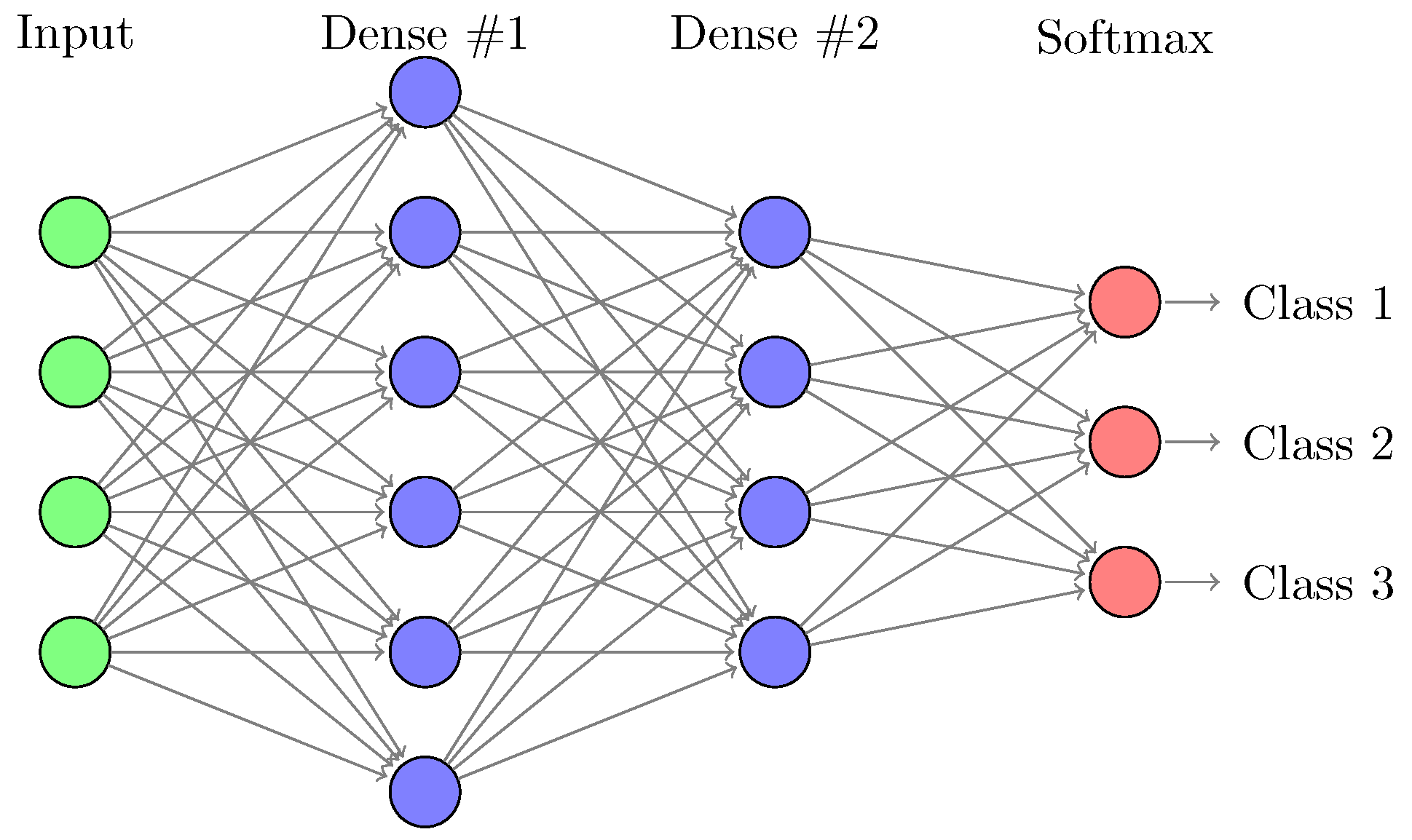
No guidance: Similar to a traditional classifier, such as the RF algorithm, the first considered type of model ignores the spectral and temporal structures of the data, i.e., the expected model is the same regardless of the order in which the features (spectral and temporal) are given. For this configuration, we decided to train two types of algorithms: (1) the RF classifier selected as the competitor [
3], and (2) a deep learning model composed of three dense layers of 1024 units—this specific architecture is named FC in the following. Both models are trained the whole dataset with
features, with
T the length of the times series and
D the number of spectral features (see
Table 2). As both RF and FC models do not require regular temporal sampling, the use of 2-day sampling is not necessary and can even lead to under-performance. The use of high dimensional space composed of redundant and sometimes noisy features may indeed decrease accuracy. Hence, the results of both models are displayed for the original temporal sampling, i.e.,
.
Temporal guidance: The second type of model provides guidance only along the temporal dimension. We train an architecture with convolution filters of size
. In other words, the same convolution filters are applied across the temporal dimension, identically for all the spectral dimensions (second column in
Figure 8).
Spectral guidance: The third type of model includes guidance only on the spectral dimension (third column in
Figure 8). For this purpose, a convolution of size
is first applied without padding, reducing the spectral dimension to one for the next convolution layers of size
.
Spectro-temporal guidance: The last type of model corresponds to the one presented in
Section 2.3 (TempCNNs), where the first convolutions have size
(last column in
Figure 8). The choice of this architecture is explained in the following sections. We also compare this architecture to RNNs, which also provide a spectro-temporal guidance (
Section 3.4).
It is interesting to note that studying temporal and spectral guidance separately is not standard; we only include it here as a means to disentangle the contribution of the different components of our TempCNN model. As illustrated by
Figure 8, all the applied convolutions are 1D-convolutions as they slide over one dimension only: over time for both TempCNN and the temporal guidance, and the spectral dimension for the spectral guidance.
Table 3 displays the Overall Accuracy (OA) and one standard deviation for the four levels of guidance. As the use of engineering features may help the different models, we train all the models for the three types of features presented in
Section 3.3: NDVI alone, spectral bands (SB), and spectral bands with three spectral indices (SB-SF). For both models using temporal guidance, the filter size
f is set to five. All the models are learned as specified in
Section 2.3, including dropout and batch normalization layers, weight decay and the use of a validation set.
Table 3 shows that the OA increases for CNN models when adding more guidance, regardless of the type of used features. Note that the case of only using the spectral guidance with NDVI feature is a particular “degenerate” case: the spectral dimension is composed of only one feature (NDVI). The trained model applies convolutions of size (1,1), leading to a model that does not provide any guidance.
When using at least the spectral bands in the feature vector (SB and SB-SF columns), our TempCNN model outperforms all other algorithms with variations in OA between 1 and 3%. We have also performed a paired t-test to compare the mean accuracy obtained over the different folds of TempCNNs against the three other competitors. The p-values are lower than for TempCNN vs both FC and RF, and for TempCNN vs RNN; TempCNN thus significantly outperforms the three models at the traditional 5% significance threshold.
Interestingly, models based on only spectral convolutions with spectral features (fifth row, second column) slightly outperform models that used only temporal guidance (fourth row, second column). This result confirms the importance of the spectral domain for land cover mapping application. In addition, the use of convolutions in both temporal and spectral domains leads to slightly better OA compared to the other three levels of guidance. Finally,
Table 3 shows that the use of spectral indices in addition of the available spectral bands does not help to improve the accuracy of traditional and deep learning algorithms.
To explore this result further,
Table 4 gives the producer’s accuracy (PA), the user’s accuracy (UA) and the F-Score per class for the three main classification algorithms: RFs, RNNs and TempCNNs.
Table 4 shows that TempCNNs outperform other algorithms with the highest F-Scores for all but two classes, while obtaining very close results for the two remaining classes. TempCNNs obtain very good results on the most frequent classes (wheat, sunflower, and grassland), but also on the rarer ones (peas, sorghum, and conifer).
4.2. Influence of the Filter Size
For CNN models using a temporal guidance, it is also interesting to study the filter size. Considering the 2-day regular temporal sampling, a filter size of f (with f an odd number) will abstract the temporal information over days, before and after each point of the series. Given this natural expression in number of days, we name the reach of the convolution: it corresponds to half of the width of the temporal neighborhood used for the temporal convolutions.
Table 5 displays the OA values as a function of reach for TempCNN. We study five size of filters
corresponding to a reach of 2, 4, 8, 16, and 32 days, respectively.
Table 5 shows that the maximum OA is obtained for a reach of 8 days, with a similar OA for 4 days. The F-Score values per class corroborate this results where maxima are often achieved for a reach of 4 or 8 days. Although the OA values are close for the different reach values, there are some observable differences per class: conifer, sorgo, and pea have F-Score differences that range from 2.8 to 8.9%. This result shows the importance of the high temporal resolution SITS, such as the one provided at five days by both Sentinel-2 satellites. The frequency of acquisition indeed allows CNNs to abstract enough temporal information from the temporal convolutions. In general, the reach of the convolutions will mainly depend on the patterns that need to be abstracted at a given temporal resolution. For example, even though the F-scores are very similar w.r.t. reach, the conifer class seems to require the lowest reach and the deciduous to require the highest reach.
4.3. Are Local and Global Temporal Pooling Layers Important?
In this Section, we explore the use of pooling layers for different reach values. Pooling layers are generally used in image classification task to both speed-up the computations and make the learnt features more robust to noise [
74]. They can be seen as a de-zooming operation, which naturally induces a multi-scale analysis when interleaved between successive convolutional layers. For a time series, these pooling layers simply reduce the length, and thus the resolution, of the time series that are output by the neurons—and this by a factor
k.
Two types of pooling have received most of the attention in the literature in computer vision: 1) the local max-pooling [
75], and 2) the global average pooling [
76]. For time series, global average pooling seems to have been more successful [
9,
37]. We want to see here if these previous results can be generalized for time series classification.
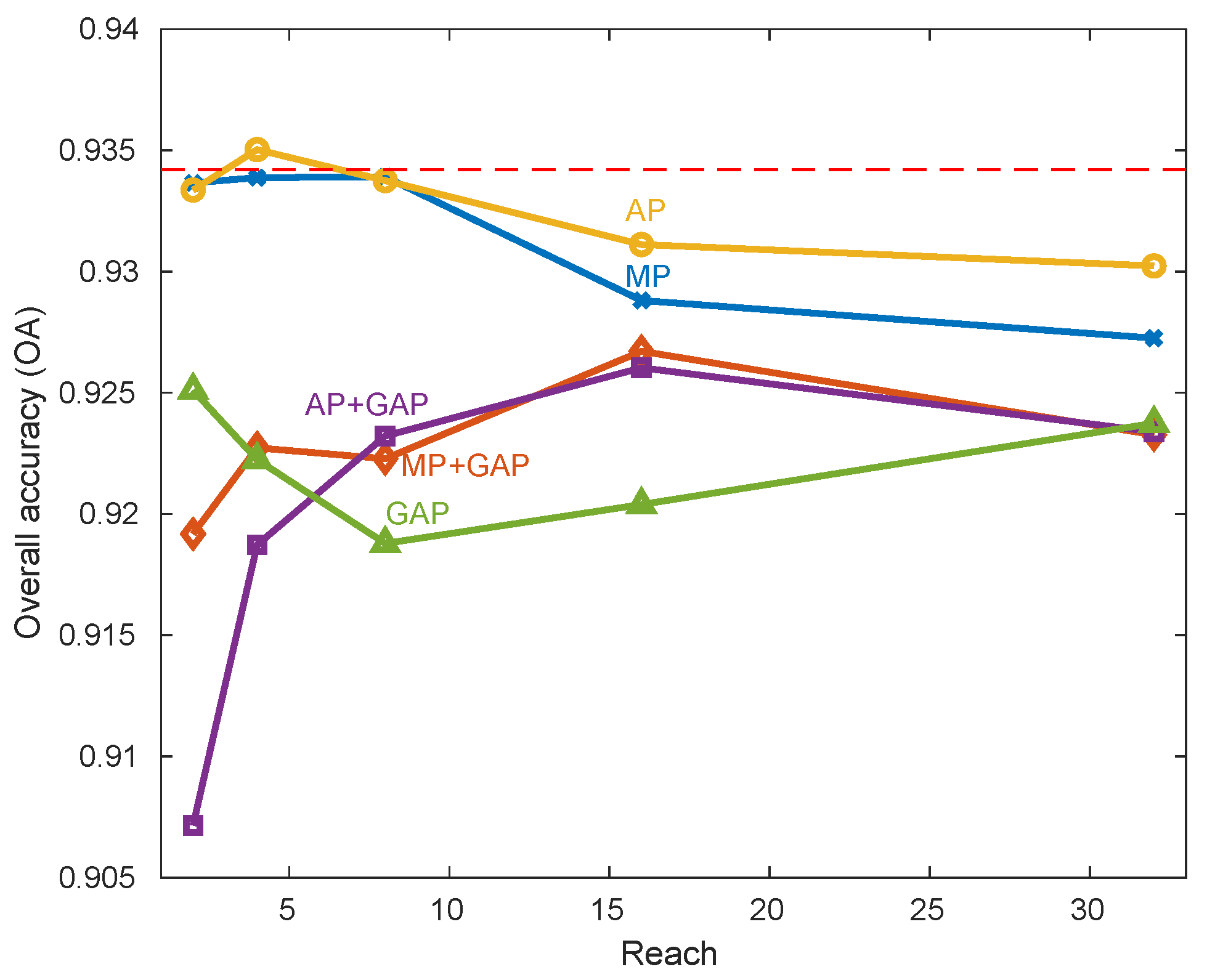
For this purpose, we train models with a global average pooling layer added after the third convolution layers for the following reach: 2, 4, 8, 16, and 32 days. We also train models with local pooling layers interleaved between each convolution layer with a window size k of 2. As local pooling layers virtually increase the reach of the following convolutional layers for this experiment, we kept the reach constant—2, 4, 8, 16, and 32 days—by reducing the convolution filter size f after each convolution. For example, a constant reach of 8 is obtained by applying successively three convolutions with filter sizes of 9, 5, and 3, with a local pooling layer after each convolutional one.
Figure 9 displays the OA values as a function of reach. Each curve represents a different configuration: local max-pooling (MP) in blue, local max-pooling and global average pooling (MP + GAP) in orange, local average pooling (AP) in yellow, local and global average pooling (AP + GAP) in purple, and global average pooling (GAP) in green. The horizontal red dashed line corresponds to the OA values obtained without pooling layers in the previous experiment.
Figure 9 shows that the use of pooling layers performs poorly: the OA results are almost always below the one obtained without pooling layers (red dashed line). Let us describe in more details the different findings for both global and local pooling layers.
The use of a global average pooling layer leads to the biggest decrease in accuracy. This layer is generally used to drastically reduce the number of trainable parameters by reducing the size of the last convolution layer to its depth. It thus performs an extreme dimensionality reduction, that decreases here the accuracy performance.
Regarding the use of only local pooling layers,
Figure 9 shows similar results for both max and average pooling layers. The OA values tend to decrease when the reach increases. The results are similar to those obtained by the model without pooling layers (horizontal red dashed line) for reach values lower than nine days, with even a slight improvement when using a local average pooling layer with a constant reach of four days.
This last result contrasts with results obtained in computer vision tasks for which: (1) max-pooling tends to give better results than average pooling, and (2) the use of local pooling layers helps to improve the classification performance. The main reason for this difference is probably task-related. In image classification, local pooling layers are known to extract features that are invariant to the scale and small transformations leading to models that can detect objects in an image no matter their locations or their sizes. However, the location of the temporal features, and their amplitude, are critical for SITS classification. For example, winter and summer crops, that we want to distinguish, may have similar profiles with only a shift in time. Removing the temporal location of the peak of greenness might prevent their discrimination.
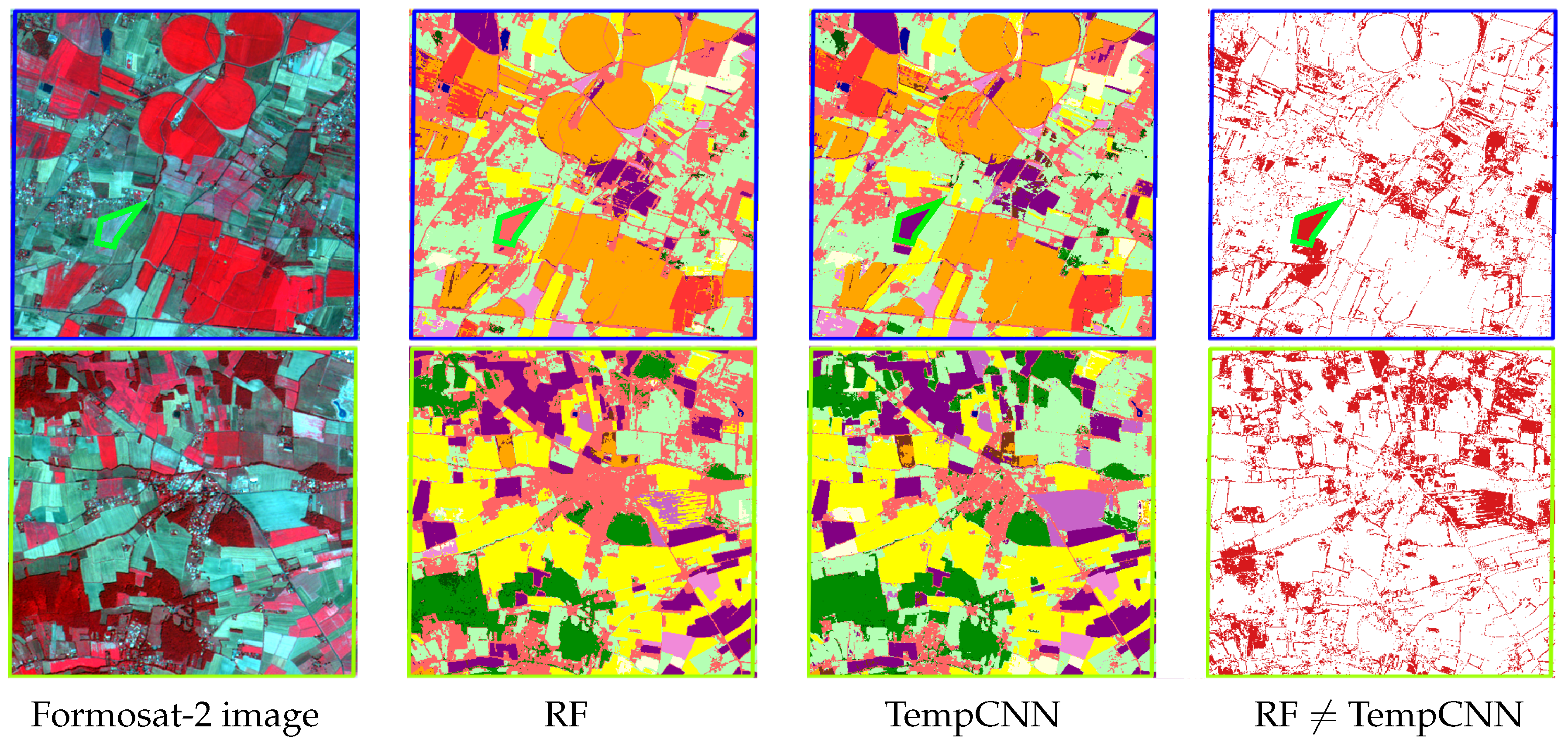
4.7. Visual Analysis
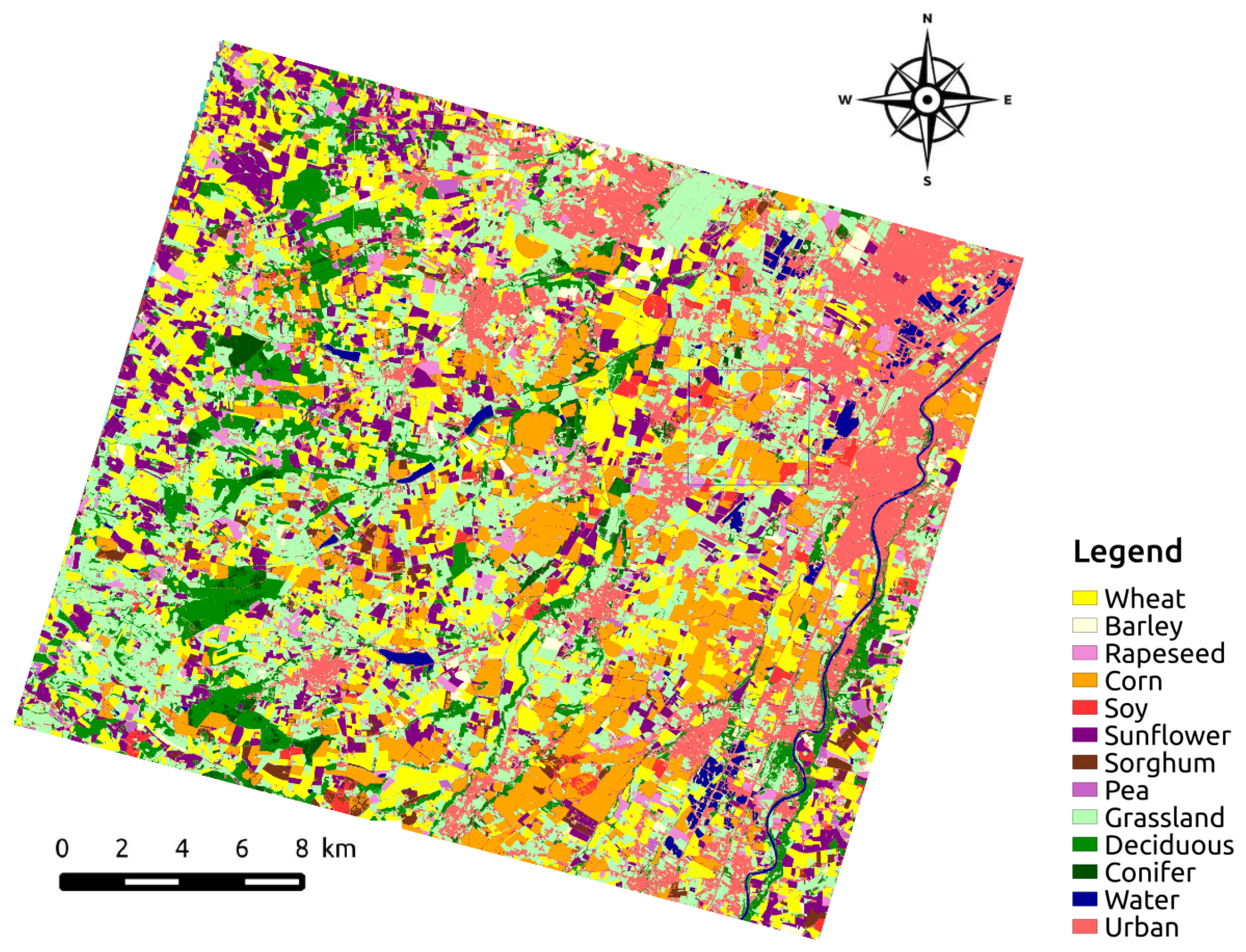
This experimental section ends with a visual analysis of the results for both blue and green areas of size 3.7 km × 3.6 km (465 pixels × 450 pixels) displayed in
Figure 5. The analysis is performed for RF and TempCNN. The original temporal sampling is used for RF, whereas the regular temporal sampling at two days is used to train TempCNN. Both models are trained on the datasets with three spectral bands. The full maps are available in our online repository at
https://github.com/charlotte-pel/temporalCNN.
Figure 11 displays the produced land cover maps. The first row displays the results for the blue area, whereas the second row displays the one for the green area. The first column displays the Formosat-2 image in false color for 14 July 2006 (zoom of
Figure 6). The second and third columns give the results for the RF and the TempCNN algorithms, respectively. Images in the last column display the disagreements between both classifiers in red. Legend of land cover maps can be found in
Table 1.
Although the results look visually similar, the disagreement images between both classifiers highlight some strong differences on the delineations between several land cover, but also at the object-level (e.g., crop, urban areas, forest). Regarding the delineation disagreements, we found that RF spreads out the majority class, i.e., urban areas, leading to an over-detection of this class, especially for mixing pixels. Regarding object disagreements, one can observe that RF mistakenly classifies an area as ‘urban’ (light pink) while it is a sunflower crop (purple). That crop, which was part of the test set, is highlighted with a green outline in the top-row results. Finally, this visual analysis shows that both classification algorithms exhibit some salt and pepper noise, that could be potentially removed by a post-processing procedure or by incorporating some spatial information into the classification framework.